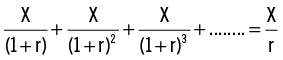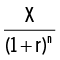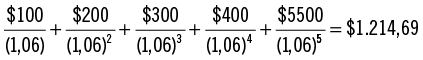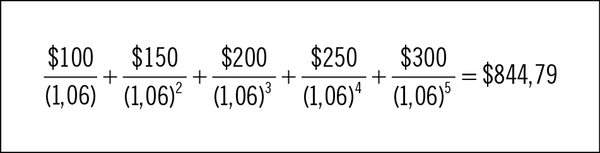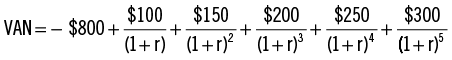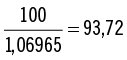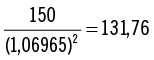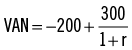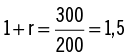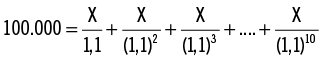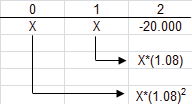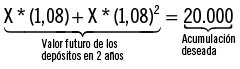Capítulo 2El valor del dinero en el tiempo
1.Concepto General
Este capítulo trata el aspecto más básico en finanzas: valor futuro, valor presente, valor actual neto y tasa interna de retorno. Estos conceptos le dirán cuánto crecerá su dinero si lo deposita en un banco (valor futuro); cuál es el valor hoy de promesas de pago futuras (valor actual); cuál es el valor de una inversión (valor actual neto); y qué tasa de retorno obtiene de su inversión (tasa interna de retorno).
Los activos financieros y la planificación financiera siempre tienen una dimensión temporal. Presentamos ahora algunos ejemplos.
 Deposita $100 en el banco hoy en una caja de ahorros, ¿cuánto dinero tendrá en tres años?
Deposita $100 en el banco hoy en una caja de ahorros, ¿cuánto dinero tendrá en tres años?
 Deposita $100 en el banco hoy en una caja de ahorros y planea agregar $100 cada año por los próximos 10 años, ¿cuánto dinero tendrá en su cuenta dentro de 20 años?
Deposita $100 en el banco hoy en una caja de ahorros y planea agregar $100 cada año por los próximos 10 años, ¿cuánto dinero tendrá en su cuenta dentro de 20 años?
 La empresa XYZ vendió recientemente un bono a su madre por $860. El bono le pagará a ella $20 anuales durante los próximos 5 años. En 6 años obtendrá un pago de $1020. ¿Ha pagado ella un precio justo por el bono?
La empresa XYZ vendió recientemente un bono a su madre por $860. El bono le pagará a ella $20 anuales durante los próximos 5 años. En 6 años obtendrá un pago de $1020. ¿Ha pagado ella un precio justo por el bono?
 Vuestra tía Sara está analizando si realizar una inversión, la cual tiene un costo de $1.000 y pagará $50 mensuales cada uno de los próximos 36 meses. ¿Debería hacerla o dejar su dinero en el banco, donde gana el 5 %?
Vuestra tía Sara está analizando si realizar una inversión, la cual tiene un costo de $1.000 y pagará $50 mensuales cada uno de los próximos 36 meses. ¿Debería hacerla o dejar su dinero en el banco, donde gana el 5 %?
Conceptos de finanzas tratados
 Valor Futuro.
Valor Futuro.
 Valor Presente.
Valor Presente.
 Valor Actual Neto.
Valor Actual Neto.
 Tasa Interna de Retorno.
Tasa Interna de Retorno.
 Fondos de Pensión y ahorro y otros problemas de acumulación.
Fondos de Pensión y ahorro y otros problemas de acumulación.
Funciones de excel utilizadas
 Funciones de Excel: VF, VA, VNA, TIR, PAGO, NPER.
Funciones de Excel: VF, VA, VNA, TIR, PAGO, NPER.
 Buscar Objetivo.
Buscar Objetivo.
2.Valor futuro
El valor futuro es el valor en alguna fecha futura de un pago (o pagos) hechos con anterioridad a dicha fecha. El valor futuro incluye el interés ganado sobre los pagos.
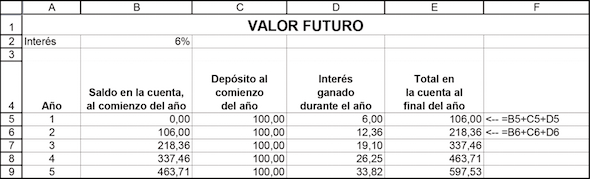
El valor futuro (VF) es un concepto que relaciona el valor en el futuro de una suma depositada en una cuenta bancaria hoy y a través del tiempo y dejada en la cuenta para generar intereses. Suponga, por ejemplo, que deposita $100 en la cuenta bancaria hoy y el banco le paga 6 % de interés al final de cada año. Si usted deja el dinero en el banco, tendrá $106 después de 1 año; $100 del depósito original + $6 de interés. Los $106 son el valor futuro después de 1 año del depósito inicial de $100 al 6 % anual de interés.
Ahora, suponga que deja el dinero en la cuenta por un segundo año: al final de dicho año, usted tendrá lo siguiente:
|
$106
|
Saldo final de la cuenta bancaria al final del primer año
|
|
+
|
|
|
6 %* $106 = 6,36
|
Interés de dicho importe por el segundo año
|
|
= $112,36
|
Total en la cuenta al final de 2 años
|
Los $112,36 son el valor futuro tras 2 años del depósito inicial de $100 al 6 % anual de interés. Otra manera de expresarlo es $112,36 = $100 * (1 + 6%)2:
Observe que el valor futuro utiliza el concepto de interés compuesto: el interés ganado en el primer año ($6) también gana interés el segundo año. Resumiendo:
El valor futuro de X $ depositado hoy en una cuenta que paga r % de interés anual y dejado en la misma por n años es: VF = X * (1 + r)n.
Notación
En este libro utilizaremos nuestra notación matemática más que la empleada por Excel. Dado que en Excel la multiplicación se indica mediante el asterisco, “*”, algunas veces escribiremos 6 % * $106 = $106,36, aunque no sea necesario. Del mismo modo, algunas veces escribiremos (1,10)3 como 1,10^3.
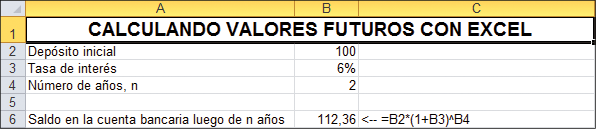
Los cálculos de valor futuro son fácilmente realizados en Excel.
Observe que el uso del carácter ^ es para indicar el exponente: en Excel (1 + 6%)2 se escribe como (1 + B3) ^ B4, donde la celda B3 contiene la tasa de interés y la celda B4 el número de años.
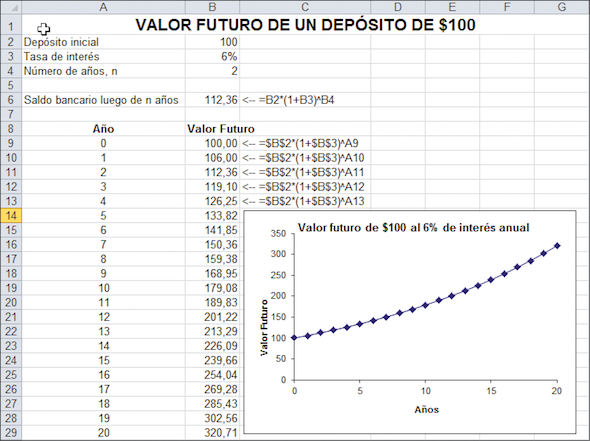
Podemos utilizar Excel para construir una tabla de cómo los valores futuros crecen con los años y luego utilizar las funciones gráficas de Excel para plasmar en una gráfica dicho crecimiento.
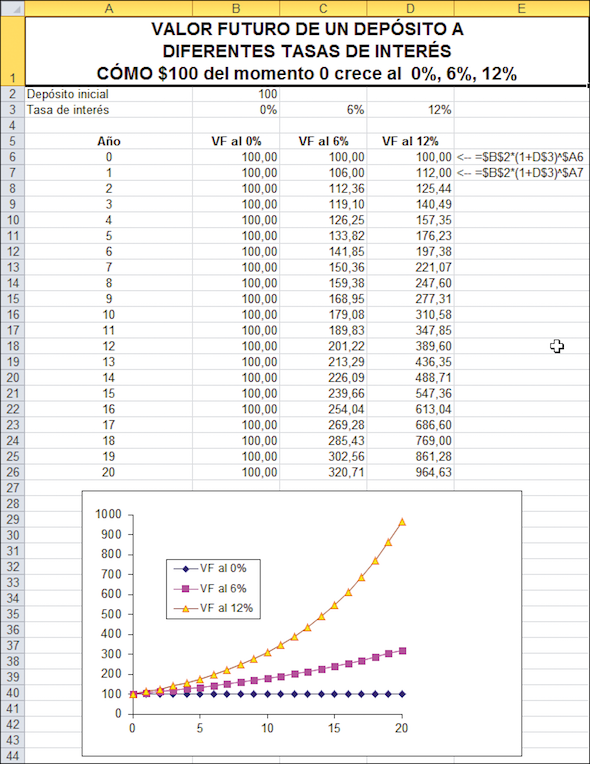
En la hoja de cálculo de abajo presentamos un cuadro y gráfico que muestra el valor futuro de $100 para las tres diferentes tasas de interés: 0,6 y 12 %. Como muestran las hojas, el valor futuro es muy sensible a la tasa de interés. Observe que cuando la tasa de interés es 0 %, el valor futuro no crece.
Nota sobre Excel
Observe que la fórmula en las celdas B9:B29 en la tabla tiene signo $ en las referencias, por ejemplo, =$B$2*(1+$B$3)^A9. Este uso de referencia absoluta en Excel se explica en el capítulo 17.
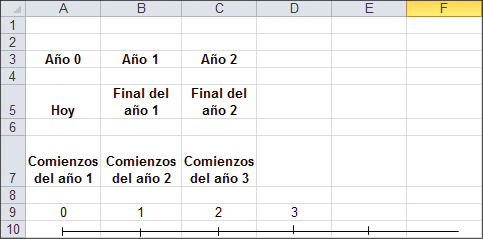
Terminología: ¿Qué es un año? ¿Cuándo comienza?
A pesar de que esta cuestión pueda parecer obvia, no lo es. Hay mucha confusión semántica sobre esta materia en los cursos y textos de finanzas.
A lo largo de este libro utilizaremos los siguientes sinónimos:
Para reiterar, los términos “año 0”, “hoy” y “comienzo del año 1” son sinónimos. Por ejemplo, $100 “a comienzos del año 2” es lo mismo que “$100 al final del año 1”. Si a usted le cuesta entender lo que alguien quiere decir, pida un gráfico, o mejor aún, una hoja de Excel.
Acumulación – Planes de ahorro y valor futuro
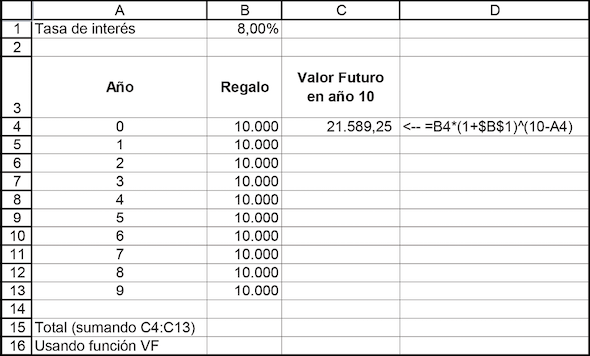
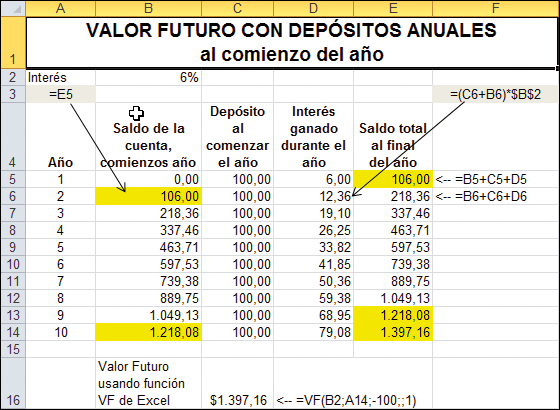
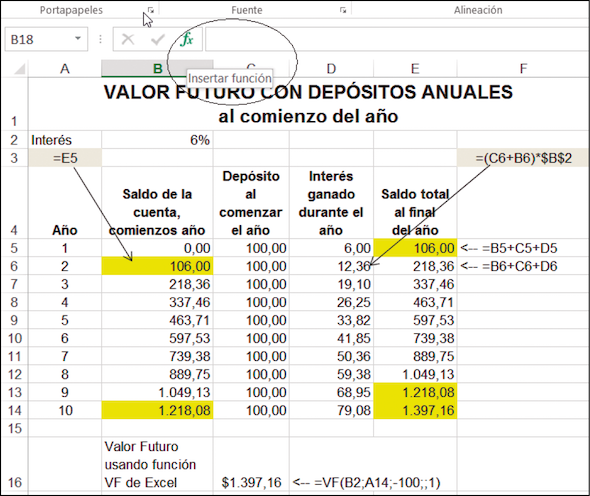
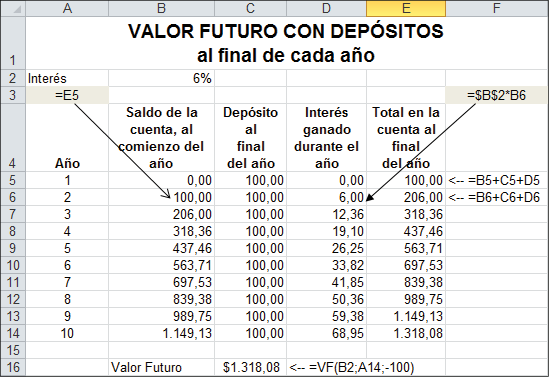
En el ejemplo anterior usted depositó $100 y lo dejó en el banco. Suponga que intenta realizar 10 depósitos anuales de $100 cada uno, con el primer depósito en el año 0 (hoy) y cada uno de los depósitos sucesivos al final de los años 1, 2,…, 9. El valor futuro de todos esos depósitos al final del año 10 le dice cuanto tendrá acumulado en su cuenta. Si usted está ahorrando para el futuro (sea para comprar un coche al finalizar la universidad o para financiar una pensión al finalizar su vida laboral), este es un cálculo importante e interesante.
Entonces, ¿cuánto tendrá acumulado al final del año 10? Hay una función de Excel para calcular esta respuesta que trataremos después. Por el momento plantearemos dicho problema en Excel y realizaremos los cálculos detalladamente, mostrando cuánto tendremos al final de cada año.
Para clarificar, analicemos un año en particular. Al final del año 1 (celda E5) usted tiene $106 en la cuenta. Esta es también la cantidad que habrá en la cuenta al comenzar el año 2 (celda B6). Si entonces deposita otros $100 y deja el total del dinero, $206, para generar intereses durante el año, ganará $12,36 de interés. Usted tendrá $218,36 = (106 + 100) * 1,06 al final del año 2.
Finalmente, vemos las columnas 13 y 14: al final del año 9 (celda E13) usted tiene $1.218,08 en la cuenta; esta es también la suma en la cuenta el comienzo del año 10 (celda B14). Entonces deposita $100 y los $1.318,08 resultantes generan $79,08 de intereses durante el año, acumulando $1.397,16 al final del año 10.
La función VF de Excel
La hoja de la sección anterior ilustra paso a paso la manera en la que el dinero se acumula en un plan típico. Para simplificar esta serie de cálculos, Excel tiene la función VF que computa el valor futuro de cualquier serie de pagos constantes. Esta función es ilustrada en la celda C16.
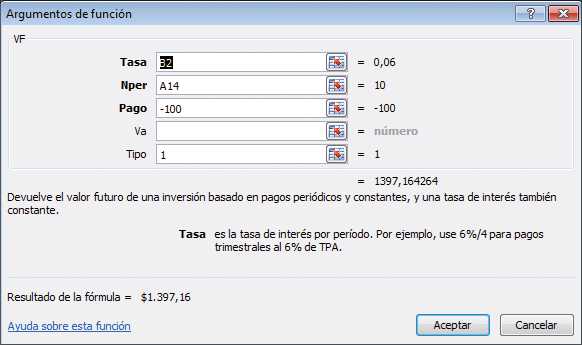
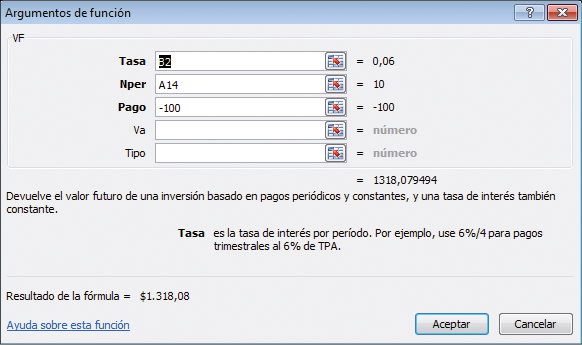
La función VF y los datos necesarios pueden computarse utilizando un cuadro de diálogo —una importante característica que viene con cada función de Excel—. La nota de Excel que sigue ilustra cómo generar el cuadro de diálogo para el cómputo de la celda C16. Si usted ya conoce cómo utilizar un cuadro de diálogo, aquí la indicamos para este ejemplo.
La función VF requiere ingresar la Tasa de interés, el Número de períodos, Nper, y el Pago anual. También puede indicar el Tipo, que le dice a Excel si el pago es realizado al comienzo del período (Tipo 1 como en nuestro ejemplo) o al final del período (Tipo 0).
Nota sobre Excel
Funciones y cuadros de diálogo
La celda C16 del ejemplo previo contiene la función VF (B2, A14,-100,,1). En esta nota ilustramos el uso del cuadro de diálogo para la función VF para generar dicha función. La última parte de esta nota de Excel trata por qué el pago de $100 se ingresa en esta función como un número negativo. Esta es una particularidad de la función VF de Excel compartida por otras tantas funciones financieras de Excel.
Avanzando por el asistente de la Función
Suponga que se encuentra en la celda C16 y desea ingresar la función para valor futuro en la misma celda. Con el cursor en C16, mueva el ratón hacia el siguiente icono en la barra de herramientas.
Haciendo clic en el mismo icono se despliega el cuadro de diálogo que mostramos abajo. Elegimos la categoría funciones Financieras y nos desplazamos hacia abajo en la siguiente sección para posicionar el cursor en la función VF.
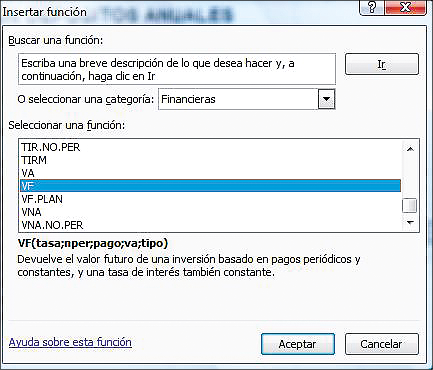
Haciendo clic en Aceptar se despliega el cuadro de diálogo de la función VF, que puede ser completado como se ilustra abajo.
Los cuadros de diálogo en Excel dan lugar a dos tipos de variables.
 Las indicadas en Negrita deben completarse obligatoriamente - en la función VF son la Tasa de interés, el número de períodos, Nper, y el Pago. (siga leyendo para ver por qué hemos escrito el pago en negativo).
Las indicadas en Negrita deben completarse obligatoriamente - en la función VF son la Tasa de interés, el número de períodos, Nper, y el Pago. (siga leyendo para ver por qué hemos escrito el pago en negativo).
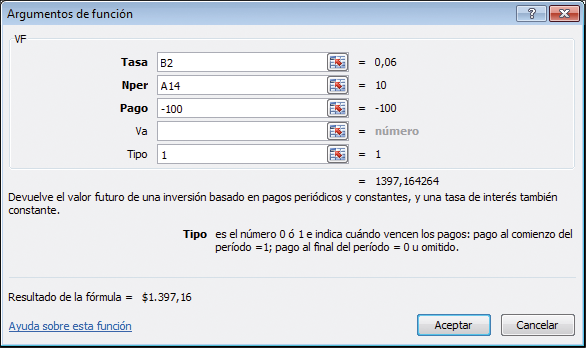
 Las no indicadas en negrita son optativas. Por ejemplo, Tipo se refiere a cuando se realiza el pago y, por lo tanto, tiene solo dos opciones: -1 cuando el pago se efectúa al comienzo del período y 0 cuando se realiza al final del mismo. En el ejemplo de arriba hemos indicado un 1 para Tipo; lo que indica (como se explica en el cuadro de diálogo mismo) que el valor futuro se calcula para pagos efectuados al comienzo del período. Si hemos omitido dicha variable o puesto 0, Excel calcularía el valor futuro para una serie de pagos realizados al final del período; vea la subsección de la sección 2.1 titulada “Comienzos versus final del período” para una ilustración.
Las no indicadas en negrita son optativas. Por ejemplo, Tipo se refiere a cuando se realiza el pago y, por lo tanto, tiene solo dos opciones: -1 cuando el pago se efectúa al comienzo del período y 0 cuando se realiza al final del mismo. En el ejemplo de arriba hemos indicado un 1 para Tipo; lo que indica (como se explica en el cuadro de diálogo mismo) que el valor futuro se calcula para pagos efectuados al comienzo del período. Si hemos omitido dicha variable o puesto 0, Excel calcularía el valor futuro para una serie de pagos realizados al final del período; vea la subsección de la sección 2.1 titulada “Comienzos versus final del período” para una ilustración.
Observe que el cuadro de diálogo ya nos dice (aún antes de hacer clic en ACEPTAR) que el valor futuro de $100 anuales por 10 años capitalizados al 6 % es $1.397,16.
Una manera abreviada de desplegar el cuadro de diálogo
Si usted conoce el nombre de la función que quiere utilizar, puede directamente escribirla en la celda y luego hacer clic en el siguiente icono en la barra de herramientas:
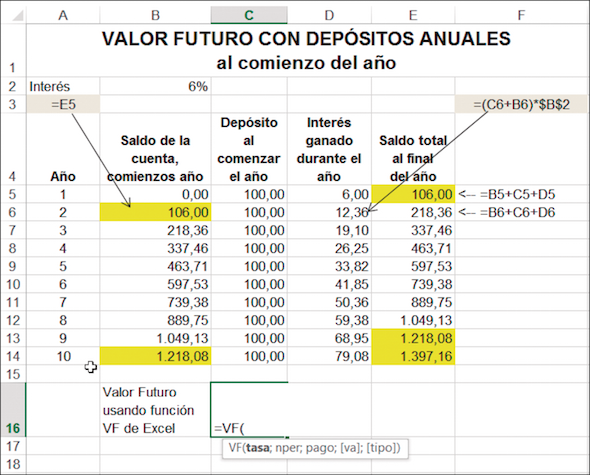
Como se ilustra abajo, usted debe escribir: = VF (
Y luego hacer clic en el mismo icono anterior - Observe que hemos escrito un signo igual, el nombre de la función y luego hemos abierto paréntesis.
Aquí veremos cómo se ve la hoja de cálculo:
Observe en el texto que despliega Excel debajo de la celda C16: como se ilustra aquí, algunas versiones de Excel muestran el formato de la función cuando la escribe en la celda.
Otra alternativa
¡Usted no está obligado a utilizar un cuadro de diálogo! Si conoce el formato de la función, entonces directamente escriba los datos de sus variables y listo. En el ejemplo de la sección 2.1 podría haber escrito = VF (B2, A14, -100,, 1) en la celda. Presionando [Enter] daría la respuesta.
¿Por qué la variable pago es un número negativo?
En el cuadro de diálogo de la función VF hemos ingresado en el parámetro Pago, un número negativo, -100. La función VF tiene la particularidad (compartida por otras funciones financieras de Excel) de que un depósito positivo genera una respuesta negativa. No entraremos en la (¿extraña?) lógica que produce tal razonamiento: cuando nos encontramos con ella, directamente ingresamos un valor negativo.
Comienzos versus final del período
En el ejemplo anterior usted realizó depósitos de $100 a comienzos de cada año. En términos temporales, usted realizó los depósitos en los momentos 0, 1, 2, 3… 9. Aquí presentamos una manera esquemática de verlo, mirando el valor futuro de cada depósito al final del año 10.
Suponga que usted realizó 10 depósitos de $100 al final de cada año. ¿Cómo afectaría ello a la acumulación en la cuenta al final de los 10 años? El diagrama esquemático de abajo ilustra la temporalidad y acumulación de los pagos.
La acumulación en la cuenta es menor cuando se deposita al final de cada año que en el caso previo, en que se depositaba al comienzo de cada año. Cuando usted deposita al final de cada año, cada depósito permanece en la cuenta 1 año menos y, en consecuencia, gana 1 año menos de interés. En una hoja, se ve como sigue.
La celda C16 ilustra el uso de la fórmula de Excel VF para resolver el problema. Aquí presentamos el cuadro de diálogo de la función VF de la celda C16.
Cuadro de diálogo para VF con depósitos al final del período
En el ejemplo hemos omitido toda entrada en el campo Tipo. También podríamos haber puesto un 0 en el campo Tipo y obtenido el mismo resultado.
Algo de jerga financiera y la función VF de Excel
Una anualidad es una serie de pagos periódicos iguales realizados por un período de tiempo específico. Ejemplos de anualidades hay por todos lados:
 El dinero que los padres les dan al hijo para que estudie ($1.000 mensuales durante los próximos 4 años de universidad) es una anualidad con 48 pagos.
El dinero que los padres les dan al hijo para que estudie ($1.000 mensuales durante los próximos 4 años de universidad) es una anualidad con 48 pagos.
 Los fondos de pensión a menudo conceden al beneficiario que se jubila un pago fijo durante el período en el que permanezca con vida. Esto es un poco más complicado porque el número de pagos es incierto.
Los fondos de pensión a menudo conceden al beneficiario que se jubila un pago fijo durante el período en el que permanezca con vida. Esto es un poco más complicado porque el número de pagos es incierto.
 Ciertos tipo de créditos son pagados en cuotas fijas, periódicas (generalmente mensuales, algunas veces anuales). Las hipotecas y créditos para estudiantes son dos ejemplos.
Ciertos tipo de créditos son pagados en cuotas fijas, periódicas (generalmente mensuales, algunas veces anuales). Las hipotecas y créditos para estudiantes son dos ejemplos.
Una anualidad con pagos al final de cada período generalmente es denominado “anualidad regular”. Como usted podrá haber observado en esta sección, el valor de una anualidad regular se calcula con = VF (B2, A14, -100). Una anualidad con pagos al comienzo de cada año generalmente se denomina “anualidad adelantada” y su valor es calculado con la función de Excel = VF (B2, A14, -100,,1).
3.Valor actual
El valor actual es el valor hoy de un pago (o pagos) que serán realizados en el futuro.
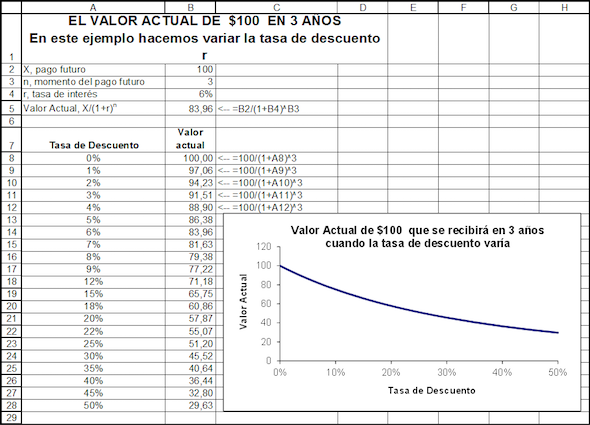
Presentamos aquí un ejemplo: suponga que usted prevé recibir de su tío Miguel, cuyo compromiso es tan válido como el de un banco, $100 en tres años. Suponga que el banco paga el 6 % de interés por los depósitos de ahorros. ¿Cuál es el valor actual de los pagos futuros previstos? La respuesta es:
Si usted pone $83,96 en el banco hoy al 6 % anual de interés, entonces en 3 años tendría $100 (vea la “prueba” en las filas 8 y 9). El valor de $83,96 es también llamado el valor presente o valor actual de $100 en 3 años al 6 % de interés.
Para sintetizar,
El valor actual de X $ que se recibirán en n años cuando la tasa apropiada de interés es r % es:
La tasa de interés r es también conocida como “tasa de descuento”. Podemos utilizar Excel para crear una tabla que muestra cómo el valor actual decrece con la tasa de descuento. Como podrá ver, mayores tasas de descuento generan menores valores presentes.
3.1.¿Por qué el valor actual disminuye cuando la tasa de interés crece?
La tabla de Excel de arriba muestra que $100 que el tío Miguel le prometió a usted en 3 años valen hoy $83,96 si la tasa de descuento es 6 %, pero valen solo $40,64 si la tasa de interés es 35 %. La razón mecánica para ello es que calcular el valor actual de $100 significa dividir por un denominador menor que calcular el valor actual al 35 %:
La razón económica se relaciona al valor futuro: si el banco le paga el 6 % de interés por sus ahorros, usted tendría que depositar $83,96 hoy para ahorrar $100 en 3 años. Si el banco paga el 35 % de interés, entonces $40,64 de hoy crecerían a $100 en 3 años porque $40,64 * (1,35)3 = $100.
Lo que este breve análisis muestra es que el valor actual es inverso al valor futuro.
3.2.Valor actual de una anualidad
Recordemos que una anualidad es una serie de pagos periódicos iguales. El valor actual de una anualidad le dice el valor hoy de todos los pagos futuros de la anualidad.
El valor actual de una anualidad de $ X al ser recibida al final de los años 1, 2, 3,… N cuando la tasa apropiada de descuento es r % es:
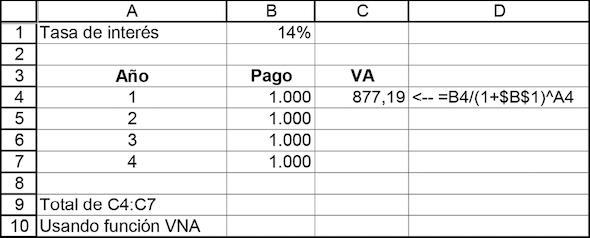
Ahora un ejemplo: suponga que le prometen $100 al final de cada uno de los próximos 5 años. Asumiendo que puede obtener un 6 % del banco, la promesa tiene un valor de $421,64 hoy.
El ejemplo anterior muestra tres maneras de obtener el valor actual de $421,24:
 Puede sumar los valores actuales individuales. Eso se hizo en la celda C13.
Puede sumar los valores actuales individuales. Eso se hizo en la celda C13.
 Puede utilizar la función VA de Excel, la cual calcula el valor actual de una anualidad (celda C14).
Puede utilizar la función VA de Excel, la cual calcula el valor actual de una anualidad (celda C14).
 Puede utilizar la función VNA de Excel (celda C15). Esta función calcula el valor actual de cualquier serie de pagos periódicos (ya se trate de pagos fijos, como en una anualidad, o de variables).
Puede utilizar la función VNA de Excel (celda C15). Esta función calcula el valor actual de cualquier serie de pagos periódicos (ya se trate de pagos fijos, como en una anualidad, o de variables).
 Le dedicamos subsecciones separadas para las funciones VA y VNA.
Le dedicamos subsecciones separadas para las funciones VA y VNA.
3.3.Valor actual de una perpetuidad
Una perpetuidad es una anualidad que continúa para siempre. En el apéndice 2.1 al final de este capítulo mostramos que:
El valor actual de una perpetuidad de X $ a ser recibidos al final de los años 1, 2, 3… cuando la tasa apropiada de descuento es r % es:
Suponga, por ejemplo, que a usted le ofrecen un pago de $100 anuales al final de cada año 1, 2, 3… Suponga que la tasa apropiada de interés es r = 5 %. Como la siguiente hoja muestra, el valor actual de esta perpetuidad es $2.000.
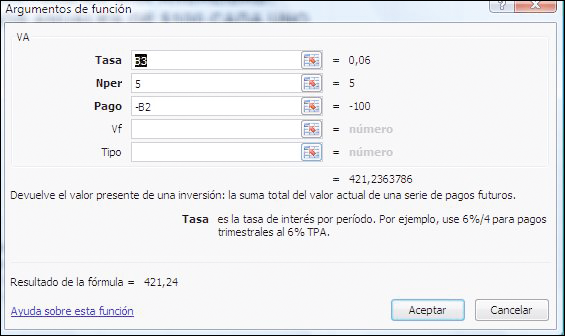
3.4.La función VA de Excel
La función VA calcula el valor presente de una anualidad (una serie de pagos iguales). Se ve muy parecida a la función VF antes tratada y como VF, también tiene la particularidad de que los pagos positivos dan resultados negativos (y ese es el motivo por el que se ingresa -100 en el Pago). Como en el caso de la función VF, Tipo denota si el pago es realizado al comienzo o al final del año. Dado que al final del año se toma por defecto, puede ingresarse 0 o deja Tipo en blanco (si el pago es al comienzo del período debe ingresarse 1 en el cuadro Tipo).
Cuadro de diálogo para la función VA
El cuadro “Resultado de la fórmula” en el cuadro de diálogo muestra que el resultado es $421,24.
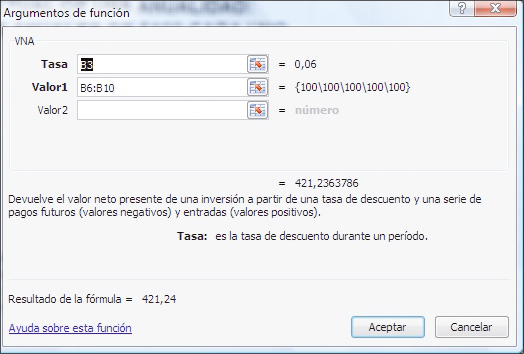
3.5.La función VNA de Excel
La función VNA de Excel computa el valor presente de una serie de pagos. Los pagos no necesariamente deben ser iguales, a pasar de que en el actual ejemplo lo son. La habilidad de la función VNA para tratar con pagos no constantes la hace una de las funciones más útiles de las funciones financieras de Excel.
Cuadro de diálogo para la función VNA
La función VNA de Excel computa el valor presente de una serie de pagos. Puede ingresar los pagos separadamente (como Valor 1, Valor 2...) o —como se ilustra arriba—puede ingresarse un rango de pagos en el cuadro Valor 1.
Nota importante sobre terminología
Los profesionales de finanzas utilizan “VNA” (o “VAN” en español) para indicar “valor actual neto”, un concepto que explicaremos en la sección siguiente. La función VNA de Excel calcula el valor presente de una serie de pagos. Casi todos los profesionales y textos de finanzas llamarían al número calculado por la función VNA de Excel como VA. Es decir, el uso que hace Excel de VNA difiere del estándar utilizado en finanzas, el cual es explicado en la sección 2.3.
Haremos un uso extensivo de esta función a lo largo del libro. En el ejemplo actual, dado que los pagos son iguales, el resultado es el mismo ($421,24) si usamos la función VA que si utilizamos la función VNA.
3.6.Eligiendo una tasa de descuento
Hemos definido el valor actual de $ X a ser recibidos en n años como:
La tasa de interés r en el denominador de esta expresión es también conocida como “tasa de descuento”. ¿Por qué es 6 % una tasa de descuento apropiada para el dinero que le ha prometido el tío Miguel? El principio básico es elegir una tasa de descuento que sea apropiada al riesgo y durabilidad de los flujos de fondos que serán descontados. La promesa de $100 anuales del tío Miguel por los próximos 5 años se asume tan buena como un banco local, que paga 6 % por los depósitos de ahorros. Por lo tanto, 6 % es una tasa de descuento adecuada.
3.7.El valor actual de una “no anualidad” de flujos de fondos (o sea, no constantes)
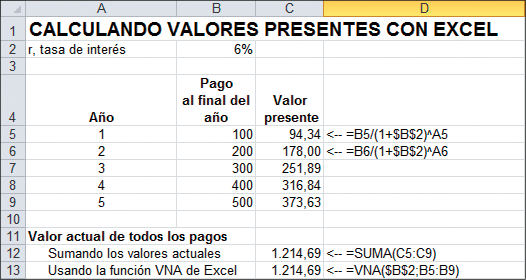
El concepto de valor actual también puede aplicarse a una corriente no constante de flujos de fondos, significando flujos de fondos que no son iguales en cada período. Suponga que, por ejemplo, su tío Juan le ha prometido pagarle $100 al final del año 1; $200 al final del año 2; $300 al final del año 3; $400 al final del año 4; y $500 al final del año 5. Eso no constituye una anualidad y, por lo tanto, no puede ser solucionada con la función VA. Pero podemos hallar el valor presente de dicha promesa futura mediante la función VNA.
El ejemplo muestra que el valor actual de la promesa de pago del tío Juan durante los próximos 5 años es $1.214,69:
Nota de Excel
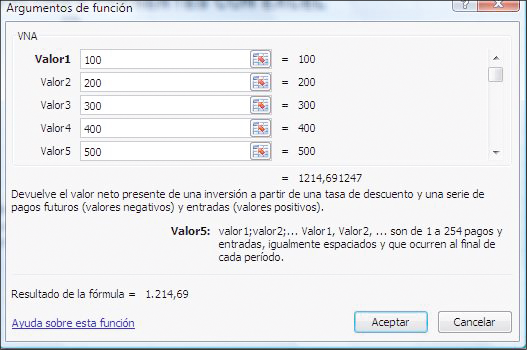
La función VNA le permite ingresar hasta 29 pagos directamente en el cuadro de diálogo de la función. Ahora, se incluye una ilustración para el ejemplo anterior.
4.Valor actual neto
El valor actual neto (VAN) de una corriente de pagos futuros es el valor actual menos la inversión inicial requerida para obtener los flujos de fondos futuros. El VAN = VA de los flujos de fondos futuros - inversión inicial. El VAN de una inversión representa el incremento en riqueza que se obtiene si realiza la inversión.
Presentamos un ejemplo basado en la hoja de cálculo de página anterior. ¿Pagaría usted $1.500 hoy para obtener una serie de pagos futuros como los de la serie B5: B9? Ciertamente, no —solo valen $1.214,69—, entonces ¿por qué pagar $1.500? Si le piden pagar $1.500, el VAN de su inversión sería:
Si usted paga $1.500 por esa inversión, estaría pagando $285,31 de más por la inversión y se empobrecerá en dicha suma. ¡Es un mal negocio!
Por otro lado, si a usted le ofrecen el mismo flujo de fondos futuros a $1.000, usted aprovecharía la propuesta porque estaría pagando $214,69 menos por la inversión que su valor:
En este caso, la inversión le haría $214,69 más rico. Como dijimos antes, el VAN de una inversión representa el incremento en su riqueza si realiza la inversión.
En síntesis:
 El valor actual neto (VAN) de una serie de flujos de fondos se utiliza para tomar decisiones de inversión. Una inversión con VAN positivo es una buena inversión y una con VAN negativo es mala inversión. Una inversión con VAN igual a cero es un “juego justo” —el valor futuro de los flujos de fondos compensa exactamente el costo inicial de la inversión—.
El valor actual neto (VAN) de una serie de flujos de fondos se utiliza para tomar decisiones de inversión. Una inversión con VAN positivo es una buena inversión y una con VAN negativo es mala inversión. Una inversión con VAN igual a cero es un “juego justo” —el valor futuro de los flujos de fondos compensa exactamente el costo inicial de la inversión—.
 El valor actual neto es una herramienta básica de análisis financiero. Es utilizada para determinar si una inversión en particular debe ser emprendida; en los casos en que podamos llevar adelante solo una de entre varias alternativas, es la herramienta de decisión para elegir cuál emprender.
El valor actual neto es una herramienta básica de análisis financiero. Es utilizada para determinar si una inversión en particular debe ser emprendida; en los casos en que podamos llevar adelante solo una de entre varias alternativas, es la herramienta de decisión para elegir cuál emprender.
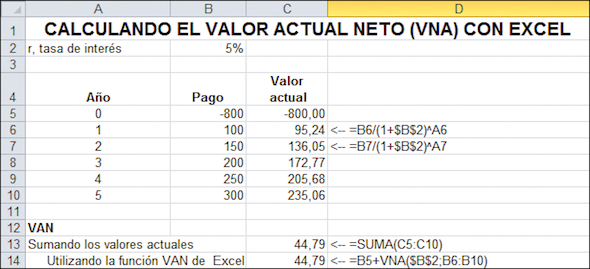
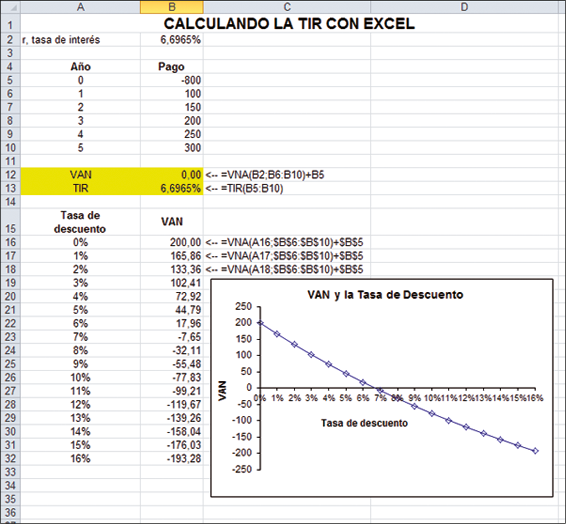
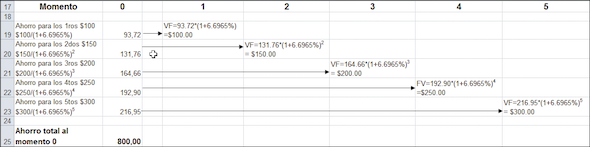
A continuación, otro ejemplo de VAN: usted encontró una inversión interesante —si paga $800 hoy a una caja de créditos local, dicha empresa le promete pagarle $100 al final del año 1; $150 al final del año 2; $200 al final el año 3; $250 al final del año 4; y $300 al final del año 5. Usted considera que dicha caja de crédito es tan digna de su confianza como un banco, que actualmente paga 5 % de interés. La hoja siguiente muestra el VAN de dicha inversión de $800.
La plantilla muestra que el valor de la inversión —el VAN de los pagos, incluyendo el pago inicial de - $800— es $44,79:
A una tasa de descuento del 5 %, usted debería llevar a cabo la inversión, dado que su VAN es $44,79; que es positivo.
Nota de Excel
Como se mencionó antes, el nombre de la función VNA de Excel no se corresponde con el uso estándar de término valor actual neto en finanzas4. En finanzas, el valor presente generalmente se refiere al valor actual de una corriente futura de flujos de fondos, en el ejemplo anterior, el valor actual es:
Los profesionales de finanzas utilizan VAN para representar el valor actual de la corriente de pagos futuros menos el costo de la inversión inicial, en el ejemplo anterior esto es $844,79 - $800 = $44,79. En este libro utilizaremos el término VAN para expresar su verdadero significado en finanzas. La función de Excel VNA aparecerá siempre en negrita. Esperamos que no origine confusión.
4.1.VAN depende de la tasa de descuento
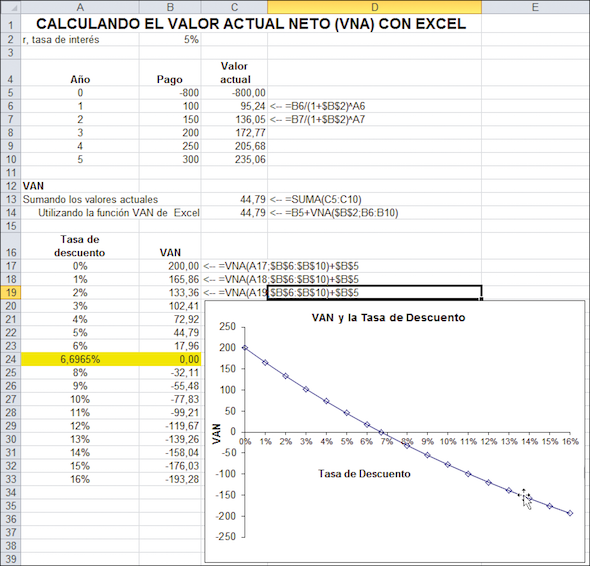
Veamos el ejemplo de la caja de crédito de la página anterior y usemos Excel para crear una tabla que muestre la relación entre tasa de descuento y VAN. Como muestra el gráfico, a mayor tasa de descuento, menor es el VAN de la inversión.
Observe que hemos resaltado una tasa de descuento en especial: cuando la tasa de descuento es 6,6965 %, el valor actual neto de la inversión es cero. La tasa de 6,6965 % se refiere a la tasa interna de retorno (TIR). Para tasas de descuento menores que la TIR, el VAN es positivo y para tasas de descuento mayores que la TIR, el VAN es negativo. Trataremos la TIR con mayor detalle en la sección 2.5.
4.2.Utilizando VAN para seleccionar entre inversiones
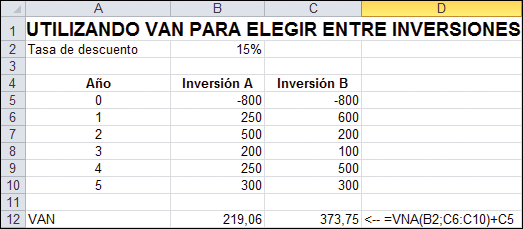
En los ejemplos analizados hasta el momento hemos utilizado VAN solo para decidir si llevar a cabo una inversión en particular, pero VAN también puede usarse para seleccionar entre inversiones mutuamente excluyentes. Observe la hoja de cálculo siguiente: usted dispone de $800 para invertir y le han ofrecido elegir entre las alternativas A y B. La hoja muestra que, a una tasa del 15 %, la inversión A tiene un VAN de $219,06 y la B tiene un VAN de $373,75. Si las inversiones no son mutuamente excluyentes, usted querría invertir en ambas porque cada una de ellas tiene un VAN positivo. Pero si se ve forzado a elegir solo una inversión, debería elegir la alternativa B porque tiene un mayor VAN. La alternativa A incrementará su riqueza en $219,06, mientras que la alternativa B incrementará su riqueza en $373,75.
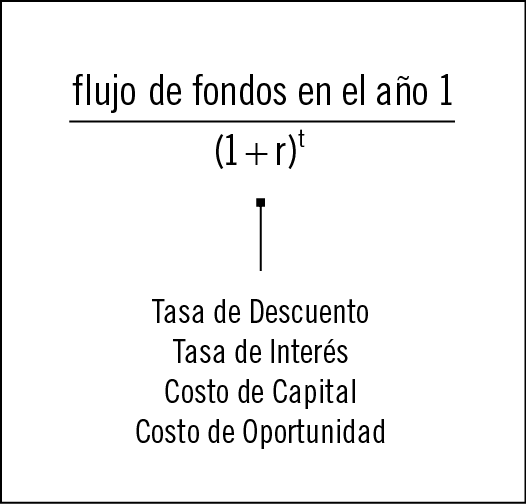
Terminología - ¿es una tasa de descuento o una tasa de interés?
En algunos de los ejemplos precedentes hemos utilizado tasa de descuento en lugar de tasa de interés para describir la tasa usada en el cálculo de VAN. Como verá en los capítulos siguientes de este libro, la tasa que se usa en el cálculo de VAN tiene mucho sinónimos: tasa de descuento, tasa de interés, costo de capital, costo de oportunidad; esos son solo unos cuantos de los nombres para la tasa que aparece en el denominador del VAN:
En síntesis,
Al utilizar VAN para seleccionar entre dos inversiones mutuamente excluyentes con VAN positivo, elegimos la inversión con mayor VAN.
5.Tasa Interna de Retorno (TIR)
La tasa interna de retorno (TIR) de una serie de flujos de fondos es la tasa de descuento que hace el valor actual neto de los flujos de fondos igual a cero.
Antes de explicar en profundidad (en la sección siguiente) la TIR, explicamos cómo calcularla. Volvamos al ejemplo anterior: si usted paga $800 hoy a una caja de crédito local, el dueño le ofrece pagarle $100 al final del año 1; $150 al final del año 2; $200 al final del año 3; $250 al final del año 4 y $300 al final del año 5. Descontando esos flujos de fondos a la tasa r, el VAN puede escribirse como:
En las celdas B16: B32 de la hoja de cálculo de abajo calculamos el VAN para varias tasas de descuento. Como ve, en algún lugar entre r = 6 % y r = 7 %, el VAN se torna negativo.
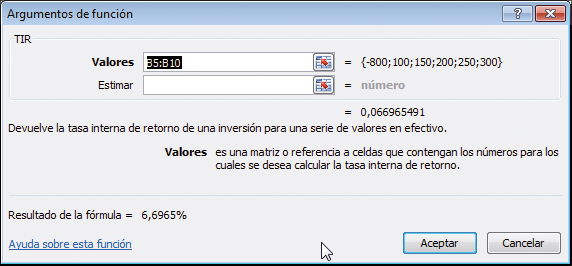
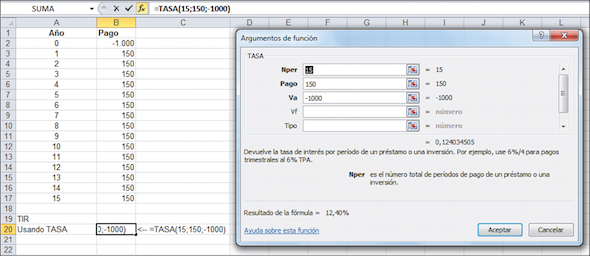
En la celda B13 usamos la función de Excel TIR para calcular la tasa de descuento exacta a la cual el VAN se torna igual a cero. La respuesta es 6,6965 %; a esa tasa de descuento, el VAN de los flujos de fondos es igual a cero (observe la celda B12). Podemos utilizar el cuadro de diálogo para la función TIR de Excel.
Cuadro de diálogo para la funcion tir de excel
Observe que no hemos utilizado la segunda opción (Estimar) para calcular nuestra TIR. Trataremos esta opción en el capítulo 5.
5.1.¿Cuál es el significado de la TIR?
Suponga que puede obtener 6,6965 % de interés en el banco y suponga que quiere ahorrar hoy para obtener para usted mismo el flujo futuro de fondos del ejemplo anterior:
 Para obtener $100 al final del año 1, debería poner su valor presente en el banco hoy:
Para obtener $100 al final del año 1, debería poner su valor presente en el banco hoy:
 Para obtener $150 al final del año 2, debería poner su valor presente en el banco hoy.
Para obtener $150 al final del año 2, debería poner su valor presente en el banco hoy.
 Y así sucesivamente (vea el cuadro siguiente).
Y así sucesivamente (vea el cuadro siguiente).
La cantidad total que debería ahorrar es $800, exactamente el costo de esta oportunidad de inversión. Eso es lo que significa cuando decimos que:
La TIR es la tasa de interés compuesta que usted gana en una inversión.
5.2.Utilizando TIR para tomar decisiones de inversión
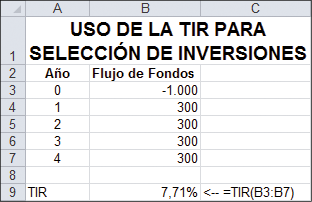
La TIR se utiliza generalmente para toma de decisiones de inversión. Suponga que a su tía Carmen le ha ofrecido su bróker la siguiente inversión: por un pago de $1.000, una compañía financiera de buena reputación le pagará a ella $300 al final de cada uno de los próximos 4 años. La tía Carmen actualmente obtiene un 5% en su depósito de ahorros bancario. ¿Debería ella retirar su dinero del banco para llevar a cabo la inversión? Para responder esa pregunta, calculamos la TIR de la inversión y la comparamos con la tasa de interés del banco:
La TIR de la inversión, 7,71 %, es mayor que el 5 % que Carmen puede obtener en su inversión alternativa (la cuenta bancaria). Por lo tanto, debería llevar a cabo la inversión.
En síntesis,
Al utilizar TIR para toma de decisiones de inversión, una inversión con TIR mayor que la tasa de interés alternativa es una buena inversión y si la tasa de interés es menor que la tasa de interés alternativa, entonces es una mala inversión.
5.3.Utilizando TIR para elegir entre dos inversiones
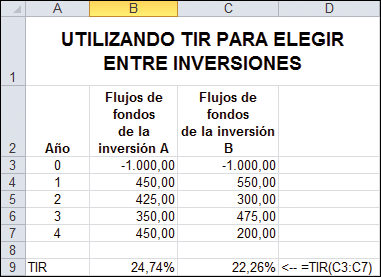
Podemos también utilizar la tasa interna de retorno para seleccionar entre dos inversiones. Suponga que a usted le han ofrecido dos inversiones. Ambas alternativas A y B con un costo de $1.000, pero con diferentes flujos de fondos. Si usted está utilizando la TIR para toma de decisiones de inversión, entonces elegirá la inversión con mayor TIR. Se presenta un ejemplo a continuación.
Deberíamos elegir la inversión A, ya que es la de mayor TIR.
En síntesis,
Al utilizar TIR para seleccionar entre dos inversiones comparables, se debe elegir la inversión que tenga la mayor TIR. Ello asume que: (1) ambas inversiones tienen una TIR mayor que la tasa alternativa y (2) las inversiones son de riesgo comparable.
Usando van y tir para toma de decisiones de inversión
En este capítulo hemos desarrollado dos herramientas, VAN y TIR, para toma de decisiones de inversión. También hemos tratado dos tipos de decisiones. Ahora presentamos un ejemplo:
|
|
“Sí” o “No”: decidir cuándo aceptar una inversión
|
“Ranking de inversiones”: comparar dos inversiones mutuamente excluyentes
|
|
Criterio de VAN
|
La inversión debería ser aceptada si VAN > 0
|
La inversión A es preferible a la inversión B si VAN (A) > VAN(B)
|
|
Criterio de TIR
|
La inversión debería ser aceptada si TIR > r, donde r es la tasa apropiada de descuento.
|
La inversión A es preferible a la inversión B si TIR (A) > TIR(B)
|
En el capítulo 4 trataremos en forma adicional la implementación de estas dos reglas junto a dos problemáticas de decisión.
6.¿Qué significa la TIR? Tablas de créditos y amortización de inversiones
En la sección anterior dimos un ejemplo simple de lo que pretendemos expresar cuando decimos que la TIR es la tasa de interés compuesta que usted gana de un activo. En esta corta oración subyace un montón de aplicaciones financieras: cuando los profesionales de finanzas discuten sobre la “tasa de retorno” de una inversión o la “tasa de interés efectiva” de un crédito, casi siempre se están refiriendo a la TIR. En esta sección exploraremos algunas significaciones de la TIR. Prácticamente, el capítulo 3 al completo se dedica a este asunto.
6.1.Un ejemplo simple
Suponga que adquiere un activo por $200 hoy y suponga que dicho activo le pagará a usted $300 en 1 año. Entonces la TIR del activo es 50 %. Para verlo, recuerde que la TIR es la tasa de interés que hace el VAN cero. Dado que:
ello implica que el VAN será cero cuando:
Resolviendo esta ecuación obtenemos que r = 50 %.
Presentamos ahora otra manera de pensar sobre esta inversión y su TIR de 50 %:
 En el momento 0 usted paga $200 por la inversión.
En el momento 0 usted paga $200 por la inversión.
 En el momento 1, los $300 que paga la inversión cancelan los $200. Los restantes $100 representan el 50 % de retorno sobre los $200 de inversión inicial. Esta es la TIR.
En el momento 1, los $300 que paga la inversión cancelan los $200. Los restantes $100 representan el 50 % de retorno sobre los $200 de inversión inicial. Esta es la TIR.
La TIR es la tasa de retorno de una inversión; es la tasa que paga, a lo largo de la vida del activo, la inversión inicial en el mismo. Y paga intereses sobre los saldos pendientes de la inversión.
6.2.Un ejemplo más complejo
Exponemos ahora un ejemplo más complicado, el cual ilustra el mismo punto. Esta vez se compra un activo cuyo costo es $200 y su flujo de fondos es $130,91 al final del año 1 y $130,91 al final del año 2. A continuación, nuestro análisis de la TIR sobre esta inversión.
 La TIR de la inversión es 20 %. Observe cómo la hemos calculado —simplemente hemos introducido en la celda B2 la fórmula = TIR ({-200; 130, 91; 130, 91}) (si usted utiliza este método para calcular la TIR en Excel, debe poner los flujos de fondos entre paréntesis).
La TIR de la inversión es 20 %. Observe cómo la hemos calculado —simplemente hemos introducido en la celda B2 la fórmula = TIR ({-200; 130, 91; 130, 91}) (si usted utiliza este método para calcular la TIR en Excel, debe poner los flujos de fondos entre paréntesis).
 Utilizando la TIR del 20 %, $40 (= 20 % * $200) del pago del primer año es interés y los $90,91 restantes son el repago de la inversión. Otro modo de pensar en los $40 es considerar que para adquirir el activo, usted entrega al vendedor el costo de $200. Cuando él le paga $130,91 al final del año 1; $40 (20 % * $200) son de interés —o sea, su beneficio por haber entregado a alguien para que use su dinero—. Los $90,91 restantes son una devolución parcial del dinero entregado.
Utilizando la TIR del 20 %, $40 (= 20 % * $200) del pago del primer año es interés y los $90,91 restantes son el repago de la inversión. Otro modo de pensar en los $40 es considerar que para adquirir el activo, usted entrega al vendedor el costo de $200. Cuando él le paga $130,91 al final del año 1; $40 (20 % * $200) son de interés —o sea, su beneficio por haber entregado a alguien para que use su dinero—. Los $90,91 restantes son una devolución parcial del dinero entregado.
 Ello deja como saldo pendiente al comienzo del segundo año $109.09. De los $130.91 que paga la inversión al final del segundo año, $21,82 (= 20 % * 109.09) es interés y el resto, (exactamente $109,09) es repago del principal.
Ello deja como saldo pendiente al comienzo del segundo año $109.09. De los $130.91 que paga la inversión al final del segundo año, $21,82 (= 20 % * 109.09) es interés y el resto, (exactamente $109,09) es repago del principal.
 El saldo de la inversión al comienzo del año 3 (año siguiente al que la inversión termina de ser pagada) es cero.
El saldo de la inversión al comienzo del año 3 (año siguiente al que la inversión termina de ser pagada) es cero.
Como en el primer ejemplo de esta sección, la TIR es la tasa de retorno sobre la inversión, definida como la tasa que repaga sobre la vida del activo la inversión inicial en el mismo y los intereses sobre los saldos pendientes de la inversión inicial.
Utilizando valor futuro, valor actual neto y tasa interna de retorno del resto del capítulo
En las restantes secciones aplicaremos los conceptos aprendidos en el capítulo para resolver varios problemas habituales:
 Secciones 2.7 – 2.9. Ahorrando para el futuro
Secciones 2.7 – 2.9. Ahorrando para el futuro
 Sección 2.10. Pagando un crédito de cuotas constantes de capital e interés
Sección 2.10. Pagando un crédito de cuotas constantes de capital e interés
 Sección 2.12. ¿Cuánto tiempo lleva cancelar un crédito?
Sección 2.12. ¿Cuánto tiempo lleva cancelar un crédito?
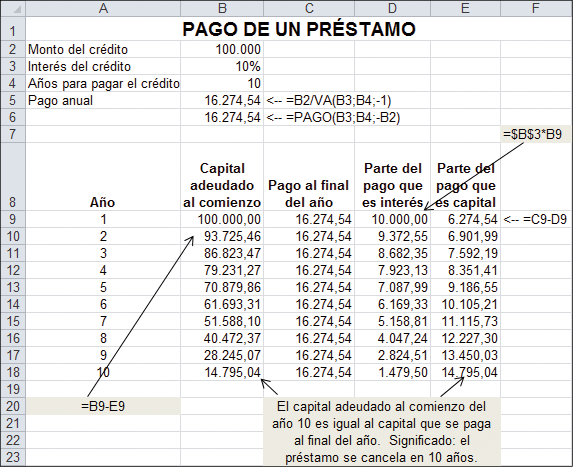
7.Cálculo del pago “fijo” anual de un préstamo – función PAGO de Excel
Usted acaba de graduarse y tiene que pagar en 10 años un préstamo de $100.000 que pidió para sus estudios. El préstamo tiene una tasa de interés anual de 10 % y su pago es constante, en el sentido de que paga la misma cantidad cada año. ¿Cuánto tiempo le llevará cancelar su préstamo?
Suponga que llamamos X al monto que paga anualmente. Entonces, el X correcto se caracterizará porque el valor actual de todos los pagos será igual al monto del préstamo:
Reescribiendo el lado derecho, puede ver que:
A continuación, todo esto en una hoja de Excel.
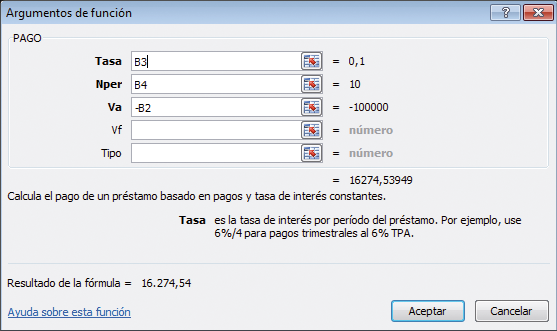
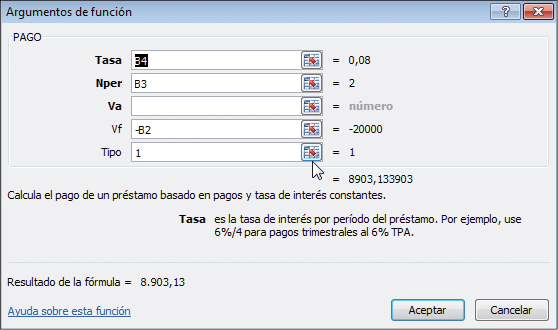
En la celda B6 utilizamos la función PAGO de Excel, que efectúa el cálculo del pago del préstamo directamente (vea el cuadro de diálogo de abajo).
7.1.Tablas de amortización de préstamos
“Amortizar” significa pagar algo a través del tiempo. Una tabla de amortización de préstamo muestra cómo el pago de un préstamo se subdivide entre interés y repago del capital inicial. A continuación, presentamos el ejemplo anterior, con la tabla de amortización adjunta (filas 9-18).
Cuando ponemos todos los pagos en una tabla de préstamos (filas 9-18 de la siguiente hoja de cálculo) se puede ver la subdivisión de cada pago de fin de año entre interés sobre el saldo remanente del capital al comienzo del año y repago del capital. Si usted debe efectuar pagos de impuestos, la columna D es deducible a efectos impositivos; mientras que la columna del repago del capital no lo es (columna E).
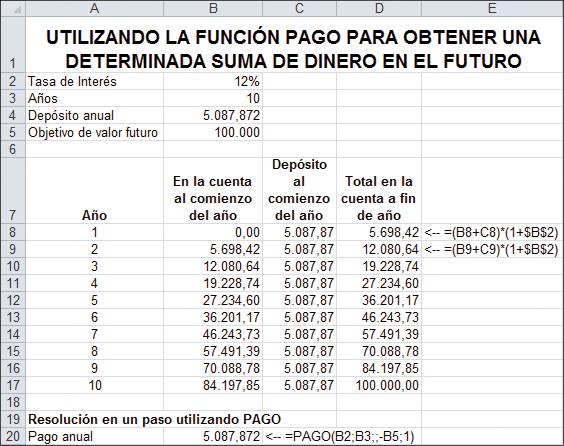
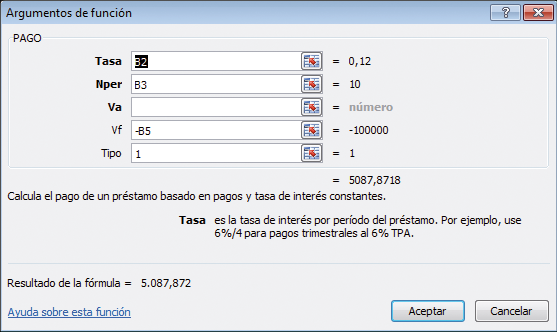
8.La función PAGO puede resolver problemas de valor futuro
La función PAGO puede también ser utilizada para calcular el pago anual requerido para obtener una determinada suma de dinero en el futuro. Tal como demuestra la siguiente hoja, si usted deposita $5.087,87 anualmente al comenzar cada año durante 10 años, acumulará $100.000 al 12 % de interés.
En la celda B20 realizamos este cálculo en un solo paso, mediante la función PAGO de Excel.
El cuadro de diálogo para la celda B20 se muestra abajo.
9.Ahorrando para el futuro – compramos un coche para Mario
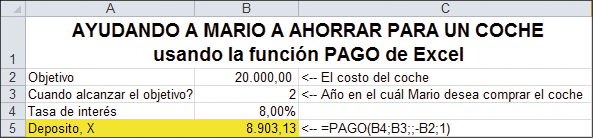
Mario tiene el ojo puesto en un coche que cuesta $20.000. Desea adquirirlo en 2 años. Planea abrir una cuenta bancaria y depositar X $ hoy y X $ en 1 año. Los saldos en la cuenta ganarán un 8 %. ¿Cuánto necesita Mario depositar para alcanzar $20.000$ en 2 años? En esta sección se lo mostraremos.
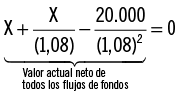
Para financiar un consumo futuro con un plan de ahorro, el valor actual neto de todos los flujos de fondos debe ser cero. En la jerga financiera, el consumo futuro planeado es totalmente financiado si el valor actual neto de los flujos de fondos es cero.
Para verlo, comencemos con una representación gráfica de lo que ocurre.
En el año 2 Mario tendrá acumulado X * (1,08)2. Esto debe financiar los $20.000 del coche, por lo que:
Ahora, reste los $20.000 de ambos lados de la ecuación y divida por (1,08)2:
Si usted deseara resolver esta ecuación, encontraría que X = $8.903,13. Para financiar completamente la adquisición futura del coche, Mario debe depositar $8.903,13 hoy y otros $8.903,13 en 1 año a partir de ahora. Si él deposita eso, el VAN de sus pagos es cero:
Solución con Excel
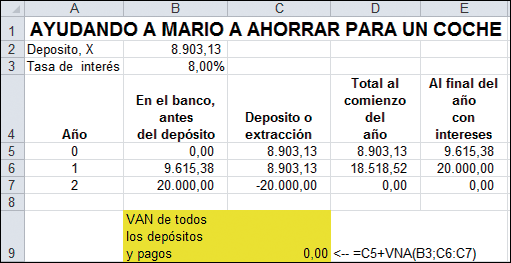
Por supuesto, esta solución es fácilmente alcanzada utilizando Excel:
Si Mario deposita $8.903,13 en los años 0 y 1, entonces la acumulación en la cuenta al comienzo del año 2 será exactamente $20.000 (celda B7). El VAN de todos los pagos (celda B9) es cero.
En la siguiente sección trataremos tres métodos para resolver el problema de ahorro de Mario.
10.Resolver los problemas de ahorro de Mario – tres soluciones
Podemos resolver el problema de Mario mediante cualquiera de los 3 métodos: prueba y error, usando Buscar Objetivo de Excel o la función PAGO de Excel. Cada uno de estos tres métodos se ilustra en esta sección.
10.1.Método 1: prueba y error
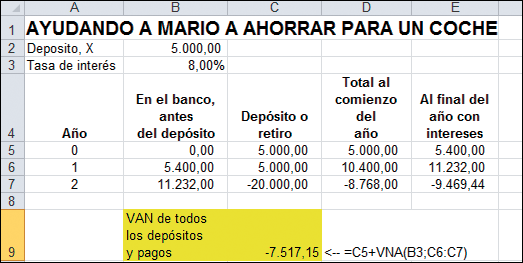
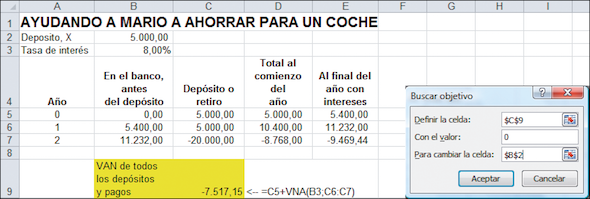
Usted puede “jugar” con la hoja de cálculo, ajustando la celda B2 hasta que la celda C9 sea igual a cero. Por ejemplo, si pone $5.000 en la celda B2 observará que el VAN en la celda C9 es negativo, indicando que Mario está ahorrando demasiado poco.
Si pone 10.000$ en la celda B2, la celda C9 será positiva: ello indica que la respuesta está en algún lugar entre 5.000 y 10.000. Mediante prueba y error usted puede llegar a la respuesta correcta.
10.2.Método 2: usar la función Buscar Objetivo de Excel
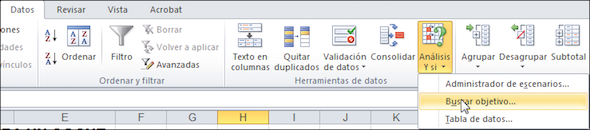
Buscar objetivo es una función de Excel que busca un número específico en una celda ajustando el valor de otra celda (para una revisión sobre el uso de Buscar Objetivo, vea el capítulo 21). Para resolver el problema de Mario, podemos usar Buscar Objetivo para hacer que la celda C9 sea igual a 0. En el menú de Excel 2007 se selecciona Datos l Herramientas de Datos l Análisis Y Si l Buscar Objetivo.
Habiendo elegido Buscar Objetivo veremos el cuadro de diálogo que aparece a continuación:
Y al hacer clic en Aceptar, Buscar Objetivo encontrará la solución de $8.903,13.
10.3.Método 3: usar la función PAGO de Excel
La función PAGO de Excel puede resolver directamente el problema de Mario, como se ilustra en la siguiente hoja:
El cuadro de diálogo para esta función se presenta a continuación:
11.Ahorrar para el futuro – problemas más complejos
En esta sección presentamos 2 versiones más complicadas que el problema de Mario de la sección 2.8.
Comenzamos intentando determinar si los padres de una niña pequeña están ahorrando suficiente dinero para su educación universitaria. A continuación el problema:
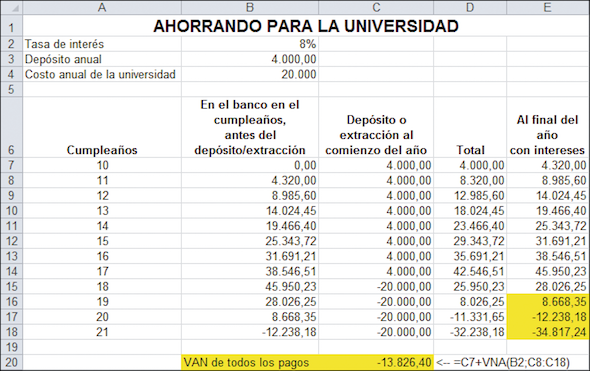
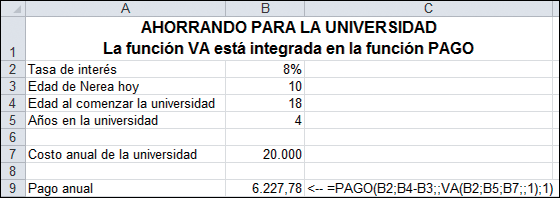
 El día en que Nerea García cumplió 10 años sus padres decidieron depositar $4.000 en una cuenta bancaria para su hija. Ellos pretenden depositar $4.000 adicionales en la cuenta cada año el día de su cumpleaños de 11, 12… hasta el de 17.
El día en que Nerea García cumplió 10 años sus padres decidieron depositar $4.000 en una cuenta bancaria para su hija. Ellos pretenden depositar $4.000 adicionales en la cuenta cada año el día de su cumpleaños de 11, 12… hasta el de 17.
 Todos los saldos bancarios generan un 8 % de interés.
Todos los saldos bancarios generan un 8 % de interés.
 El día del cumpleaños de 18, 19, 20 y 21, sus padres sacarán $20.000 para pagar la universidad.
El día del cumpleaños de 18, 19, 20 y 21, sus padres sacarán $20.000 para pagar la universidad.
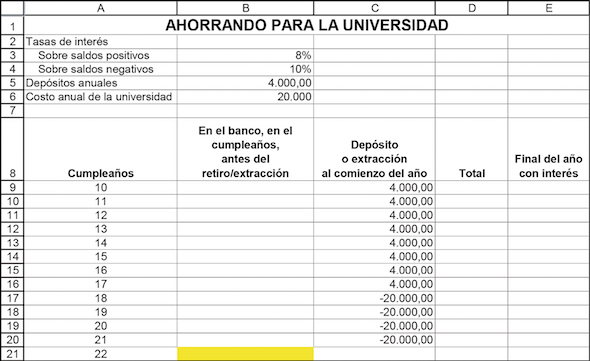
¿Son los $4.000 anuales suficientes para cubrir los aranceles universitarios previstos? Podemos resolver fácilmente este problema en una hoja.
Observando la columna de saldo al final del año en la columna E, los $4.000 no son suficientes —Nerea y sus padres se quedarán sin dinero en algún momento entre el cumpleaños 19 y 20—. Al final de su carrera universitaria habrá $34.817 “en descubierto” (celda E18). Otra forma de verlo es observar el cálculo de VAN en la celda C20: como vimos en la sección anterior, un plan que combina depósitos / extracciones está completamente financiado cuando el VAN de todos los pagos / extracciones es cero. En la celda C20 se comprueba que el VAN es negativo – El plan de Nerea es subfinanciado.
¿Cuánto deberán ahorrar los padres de Nerea cada año? Hay muchas maneras de responder a esta pregunta, en las cuales se profundizará más adelante. Estos métodos son básicamente iguales que los tratados para resolver el problema de Mario presentado en la sección anterior, pero para que quede completo vamos a presentarlos nuevamente.
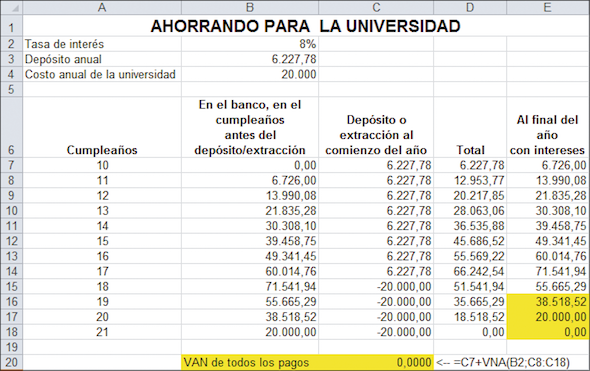
11.1.Método 1: prueba y error
Asumiendo que usted ha puesto las fórmulas correctas en la hoja, puede “jugar” con la celda B3 hasta que la celda E18 o la celda C20 sean igual a cero. Haciéndolo podemos ver que los padres de Nerea deberían haber planeado depositar $6.227,78 anualmente.
Note que el VAN de todos los pagos (celda C20) es cero cuando la solución es alcanzada. Los pagos futuros son totalmente financiados cuando el VAN de todos los flujos de fondos es cero.
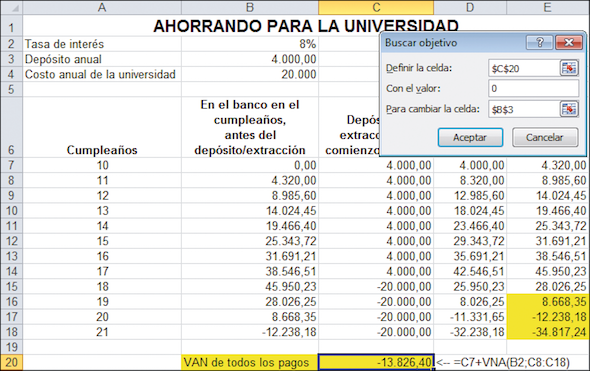
11.2.Método 2: usar Buscar Objetivo de Excel
Podemos usar Buscar Objetivo para hacer que la celda E18 sea cero. Tras pulsar en Datos l Herramientas de Datos l Análisis Y Si l Buscar Objetivo, se completa el cuadro de diálogo.
Cuando se hace clic en Aceptar, Buscar Objetivo busca la solución. El resultado es el mismo que antes: $6.227,78.
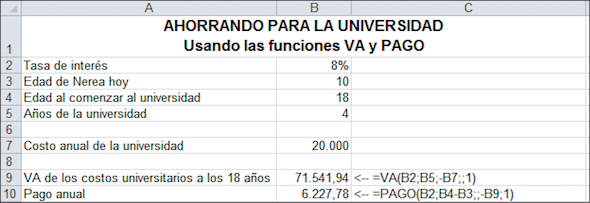
11.3.Método 3: usar las funciones VA y PAGO de Excel
Podemos usar VA de Excel y la función PAGO para resolver este problema directamente, como se ilustra en la siguiente hoja.
Explicación: la celda B9 es el valor actual de los aranceles universitarios al comenzar los 18 años de edad. La función PAGO computa el pago anual requerido tal que el valor futuro de los pagos (capitalizados al 8 % durante 8 años) sea igual a $71.541,94.
Podemos, por supuesto, integrar la función VA en la función PAGO, de modo que la solución sea aún más simple.
11.4.Planes de pensiones
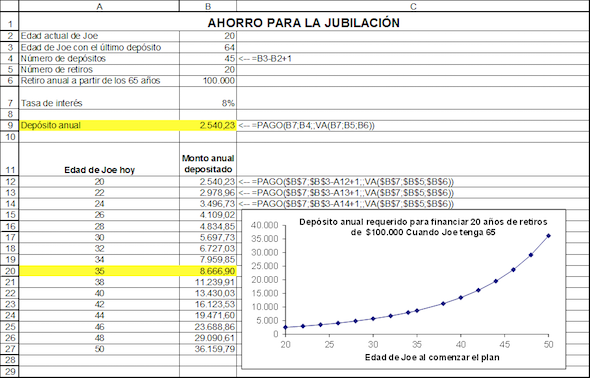
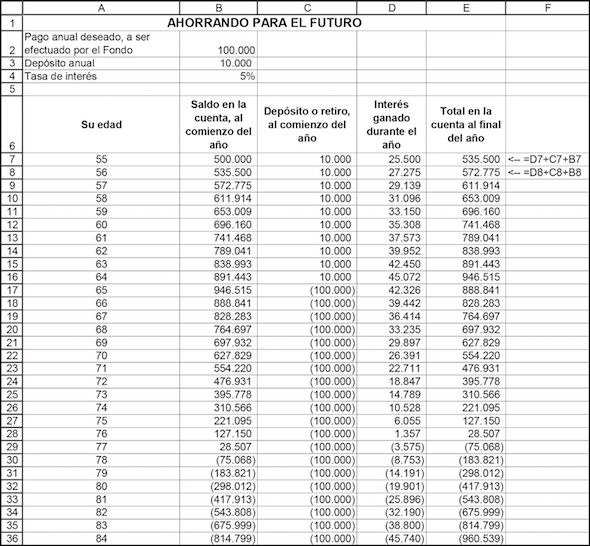
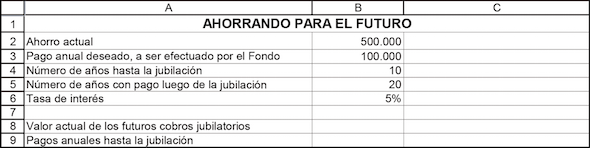
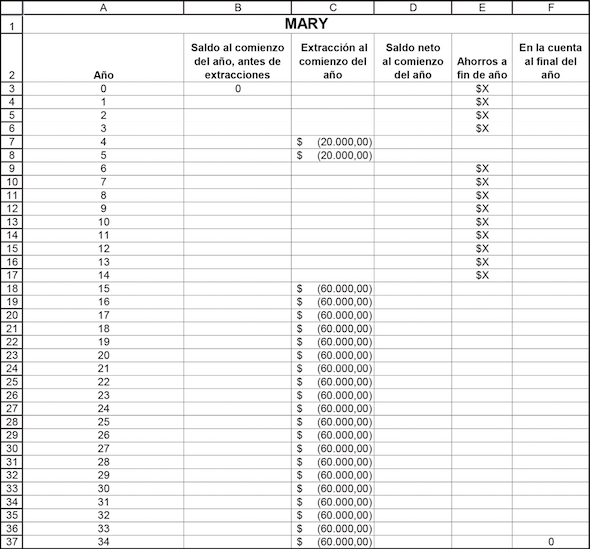
El problema de ahorro de los padres de Nerea es exactamente el mismo que el que enfrenta un individuo que pretende ahorrar para su retiro. Suponga que Joe tiene 20 años hoy y desea comenzar a ahorrar de modo que cuando tenga 65 pueda disponer durante 20 años de $100.000 para retirar anualmente. Adaptando la hoja previa, obtenemos lo siguiente.
En la tabla, en las filas 12-27 usted ve el poder del interés compuesto: si Joe comienza a ahorrar a la edad de 20 años para su retiro, un depósito de $2.540,23 crecerá para proveerle de sus $100.000 necesarios de jubilación durante 20 años a partir de la edad de 65 años. Por otro lado, si comienza a ahorrar a la edad de 35 años, necesitará $8.666,90 anuales.
12.¿Cuánto tiempo lleva pagar un préstamo?
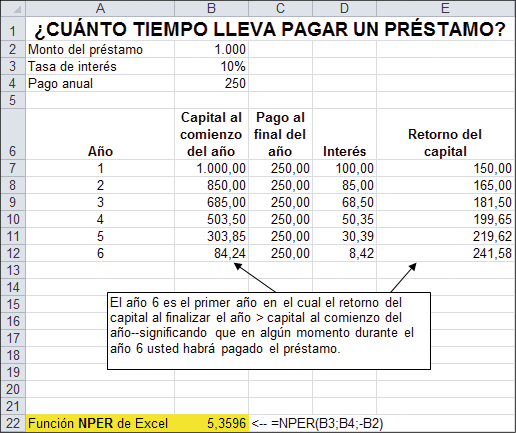
Usted está interesado en pedir un préstamo de un banco al 10 % de interés. El monto máximo que usted puede pagar es $250 por año. ¿Cuánto tiempo le llevará pagar el préstamo? Hay una función de Excel que responde a esta pregunta, la cual le mostraremos enseguida. Primero, vamos a desarrollarlo en forma analítica de modo que podamos entender la pregunta. En la hoja de abajo vemos la tabla del préstamo como la vista en la sección 2.5.
Como puede observar de la fila 12, el año 6 es el primer año en el cual el retorno del capital al final del año es mayor que el capital al comienzo del año. Por lo tanto, en algún momento entre los años 5 y 6 usted habrá cancelado el préstamo.
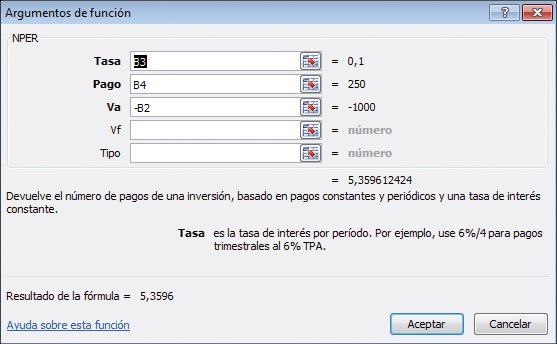
La función NPER de Excel, como se ilustra en la celda B22, provee una respuesta exacta a la pregunta.
Cuadro de diálogo para la función NPER
Al igual que la funciones PAGO, VA y VF tratadas en algún lugar de este capítulo, la función NPER requiere que el monto se ingrese en negativo para obtener una respuesta positiva.
13.Resumen
En este capítulo se han tratado los conceptos básicos del valor del dinero en el tiempo:
 Valor Futuro (VF): el monto que usted acumula en alguna fecha futura por los depósitos realizados en el presente.
Valor Futuro (VF): el monto que usted acumula en alguna fecha futura por los depósitos realizados en el presente.
 Valor Actual (VA): el valor hoy de flujos de fondos anticipados en el futuro.
Valor Actual (VA): el valor hoy de flujos de fondos anticipados en el futuro.
 Valor Actual Neto (VAN): el valor hoy de una serie de pagos futuros, incluyendo el costo de adquirir dichos flujos de fondos.
Valor Actual Neto (VAN): el valor hoy de una serie de pagos futuros, incluyendo el costo de adquirir dichos flujos de fondos.
 Hemos hecho grandes esfuerzos para destacar la diferencia entre el concepto financiero de VAN y la función de Excel VNA. La función de Excel VNA calcula el valor presente de los flujos de fondos futuros, mientras que el concepto en finanzas de VAN computa el valor presente de los flujos de fondos menos el flujo de fondos inicial.
Hemos hecho grandes esfuerzos para destacar la diferencia entre el concepto financiero de VAN y la función de Excel VNA. La función de Excel VNA calcula el valor presente de los flujos de fondos futuros, mientras que el concepto en finanzas de VAN computa el valor presente de los flujos de fondos menos el flujo de fondos inicial.
 Tasa Interna de Retorno (TIR): la tasa de interés compuesta que paga una serie de flujos de fondos, incluyendo el costo de su adquisición.
Tasa Interna de Retorno (TIR): la tasa de interés compuesta que paga una serie de flujos de fondos, incluyendo el costo de su adquisición.
 NPER: el número de períodos para pagar una inversión.
NPER: el número de períodos para pagar una inversión.
También se han mostrado las funciones de Excel (VF, VA, VNA, TIR, y NPER) que realizan estos cálculos y analizado algunas de sus particularidades. Finalmente, le hemos indicado cómo realizar estos cálculos mediante fórmulas.
Ejercicios de repaso y autoevaluación
1.Usted ha depositado $600 en al banco y prevé dejarlos por 10 años. Si el banco le paga un 15 % de interés por año, ¿cuánto dinero tendrá usted al final de los 10 años?
2.Su generosa abuela ha anunciado que ha abierto una cuenta bancaria para usted con un depósito de $10.000. Más aún, ella prevé efectuar nueve regalos similares más, al final de este año, el año próximo, etc. Si la cuenta bancaria paga un 8 % de interés, ¿cuánto dinero tendrá usted acumulado al final de 10 años (1 año después del último regalo)?
Sugerencia: resuelva este problema de dos maneras, como se muestra abajo: a) tome cada importe y calcule su valor futuro en el año 10 (como se ilustra en las celdas C4:C13) y luego súmelos; b) use la función VF de Excel. Tenga en cuenta que en este caso los importes se realizan al comienzo del año (usted deberá ingresar “1” en el campo Tipo como se describe en la sección 2.1).
3.Su tío ha anunciado que le dará $10.000 anualmente a usted, al final de cada uno de los próximos 4 años (él es menos generoso que su abuela...). Si la tasa de interés correspondiente es del 7 %, ¿cuál es el valor actual de dicha promesa? (Si usted va a utilizar VA para resolver este problema, tenga presente que la opción Tipo es 0 u omitida).
4.¿Cuál es el valor actual de una serie de cuatro pagos, cada uno de $1.000, al ser efectuados al final de los años 1, 2, 3 y 4? Asuma que la tasa de interés es 14 %.
Sugerencia: resuelva este problema de dos maneras, como se indica en las filas 9 y 10 de abajo.
5.Belleza y Salud Corporación (BYS) ha anunciado un título revolucionario: si usted le paga a BYS $1.000 ahora, obtendrá $150 al final de cada uno de los próximos 15 años. ¿Cuál es la TIR de dicha inversión?
Sugerencia: resuelva este problema de dos maneras: una, utilizando la función TIR de Excel y la otra, usando la función TASA (como se ilustra abajo).
6.Tecno Comunicación (TC) tiene un título especial para vender: usted le paga $1.000 a TC y la empresa le devolverá $100 al final del primer año, $200 al final del año 2,... $1.000 al final del año 10.
a.Calcule la TIR de esa inversión.
b.Diseñe una tabla de amortización para la inversión.
7.Usted está pensando en comprar un bono con un valor nominal de $1.000 emitido por las autoridades de Desarrollo Ibérico. El bono pagará $120 de interés al final de cada uno de los próximos 5 años. Al final del año 6, pagará $1.120 (esto es, $1.000 de su valor nominal más el interés). Si la tasa de interés correspondiente es 7 %, ¿cuál es el valor actual de los pagos futuros del bono?
8.Luisa Flores cumplió 55. Luisa planea jubilarse en 10 años y posee actualmente $500.000 en su fondo de pensión. Basándose en el patrón de longevidad de su familia, ella asume que vivirá durante 20 años más pasada la edad de retiro y durante cada uno de esos años ella quiere retirar $100.000 del fondo de pensión. Si la tasa de interés es
5 % anual, ¿cuándo dinero tendrá que ahorrar anualmente Luisa durante los próximos 10 años? Asuma que el primer depósito al fondo de pensión será hoy, seguido de nueve depósitos adicionales anuales; y el retiro a partir de la edad de 65 será al comienzo de cada año.
Utilice la hoja siguiente (los números no son correctos) y Buscar Objetivo para encontrar la respuesta.
9.Resuelva el problema anterior utilizando las funciones VA y PAGO y la plantilla siguiente:
10.Si usted deposita $10.000 hoy, Union Bank le ofrece pagarle $50.000 al cabo de 10 años. ¿Cuál es la tasa de interés?
11.Asuma que la tasa de interés es del 5 %, ¿cuál de los siguientes tiene mayor valor?
a.$5.000 hoy.
b.$10.000 al final de 10 años.
c.$9.000 al final de 4 años.
d.$300 por año a perpetuidad (lo que significa para siempre), con el primer pago al final de este año.
12.Usted recibe un bono de $15.000 por parte de su nuevo empleador y decide invertirlo durante 2 años. Su banco le ofrece dos alternativas, ambas requieren un compromiso durante los dos años. La primera de ellas le genera intereses por 8 % anual por año, durante ambos años. La segunda alternativa genera el 6 % para el primer año y 10 % para el segundo. El interés se capitaliza en forma anual. ¿Cuál debería usted elegir?
13.Su sueldo anual es de $100.000. Le ofrecen dos opciones como indemnización: la primera alternativa es un pago de 6 meses de sueldo ahora. La opción 2 consiste en un pago anual de $6.000 para usted o sus herederos a perpetuidad (el primer pago al final de este año). Si la tasa de retorno requerida es 11 %, ¿qué opción debería elegir usted?
14.Hoy es su cumpleaños número 40. Usted espera retirarse a la edad de 65 y las tablas actuariales sugieren que usted vivirá hasta los 100 años. Usted planea mudarse a Canarias cuando se jubile, estima que le costará $200.000 efectuar tal traslado (al cumplir los 65) y que sus gastos anuales serán $25.000 por año a partir de entonces. Usted espera obtener una tasa del 7 % sobre sus ahorros.
a.¿Cuánto dinero necesitará haber ahorrado en el momento de su jubilación?
b.Usted ya cuenta con $50.000 ahorrados. ¿Cuánto necesitará ahorrar al final de cada año, durante los próximos 25 años, para estar en condiciones de afrontar el plan de jubilación previsto?
c.Si usted no cuenta con ningún ahorro en el momento y no está en condiciones de comenzar a ahorrar durante los próximos 5 años (es decir, su primer ahorro lo efectuará al cumplir 45 años), ¿cuánto deberá ahorrar por año a partir de entonces para estar en condiciones de afrontar el plan jubilatorio?
15.Usted ha invertido $10.000 en un nuevo fondo de inversiones que le reportan $1.500 al final de los próximos 10 años. ¿Cuál es la tasa de interés compuesta ofrecida por el fondo? (Sugerencia: resuelva este problema de dos maneras: usando la función TIR de Excel y usando la función TASA).
16.John cumple 13 años hoy. Su decisión en el día del cumpleaños es comenzar a ahorrar para comprar un coche cuando tenga 18 años. El coche cuesta $15.000 hoy y espera que el precio crezca al 2 % por año.
John ha escuchado que un banco local ofrece una cuenta de ahorro que paga un interés del 5 % anual. Él planea realizar 6 depósitos de $1.000 c/u en la cuenta (el primer depósito será efectuado hoy); y utilizará los fondos de la cuenta el día de su cumpleaños de 18 como anticipo para la compra del automóvil, financiando el resto con la agencia.
Él espera que la agencia le ofrezca las siguientes condiciones de financiamiento: siete pagos iguales anuales (siendo el primero de ellos un año después de tomar posesión del coche) y una tasa de interés anual de 7 %.
a.¿Cuánto deberá financiar John con la agencia de coches?
b.¿Cuál será el valor de la cuota que deberá pagar anualmente a la agencia?
17.Mary ha completado recientemente sus estudios universitarios en la Universidad Europea de Madrid y está planeando cursar un programa MBA dentro de 4 años. El coste del curso será de $20.000 por año durante los 2 años de duración, que deben pagarse al comienzo de cada año. Además, Mary desea jubilarse dentro de 15 años a partir de ahora y recibir una pensión de $60.000 anuales durante 20 años; siendo el primer pago dentro de 15 años a partir de ahora. Mary puede prestar y tomar prestado todo lo que quiera a la tasa del 7 %, compuesta anual. Para financiar sus gastos, Mary ahorrará dinero al final de los años 0-3 y al final de los años 6-14.
Calcule la cantidad constante de pesos que Mary debe tener al final de cada uno de esos años para cubrir todos sus gastos (cuota del MBA y jubilación). (Ayuda: puede ser útil utilizar Buscar Objetivo).
Nota: Solo para eliminar dudas, aquí le mostramos los flujos de fondos:
18.Usted es el gerente financiero de Termination Inc. Su empresa tiene 40 empleados y cada uno gana $40.000 por año. Los salarios crecen a una tasa del 4 % anual. Comenzando a partir del año próximo y cada dos años desde entonces, 8 empleados se retiran y no se contrata ninguno nuevo. La empresa tiene vigente un programa de jubilaciones, bajo el cual los empleados que se jubilan perciben una suma anual igual a su salario anual en el momento de la jubilación. La expectativa de vida es de 20 años tras la jubilación y la pensión anual se paga a fin de año. La tasa de rendimiento sobre las inversiones es del 10 %. ¿Cuál es el valor total de su deuda por jubilaciones?
19.Usted tiene 30 años de edad y está considerando cursar un MBA. Acaba de cobrar su sueldo anual de $50.000 y espera que este crezca al 3 % anual. Los graduados de MBA generalmente ganan $60.000 tras su graduación, con salarios creciendo a la tasa del 4 % anual.
El programa MBA que usted está considerando es de jornada completa, de 2 años de duración y cuesta $20.000 anuales, los cuales se pagan al final de cada año lectivo. Usted quiere jubilarse a los 65 años de edad. La tasa de interés aplicable es 8 %. ¿Es conveniente para usted dejar su trabajo y cursar el MBA (ignore impuesto a las ganancias)? ¿Cuál es la tasa interna de retorno del BMA?
20.Usted tiene 55 años de edad y quiere comenzar a ahorrar para su jubilación. Estos son los parámetros:
 Usted pretende realizar un depósito hoy y al comienzo de cada mes, durante los próximos 19 años (es decir, en su cumpleaños de 55, 56... 64).
Usted pretende realizar un depósito hoy y al comienzo de cada mes, durante los próximos 19 años (es decir, en su cumpleaños de 55, 56... 64).
 A partir de los 65 y hasta los 84, usted quiere retirar $50.000 al año (no tiene planes a partir de entonces).
A partir de los 65 y hasta los 84, usted quiere retirar $50.000 al año (no tiene planes a partir de entonces).
 La tasa de interés es 12 %.
La tasa de interés es 12 %.
a.¿Cuánto dinero debería depositar usted en cada uno de los años iniciales para financiar por completo las extracciones?
b.Si usted comienza a ahorrar a la edad de 45, ¿cuál es su respuesta?
c.(Más difícil). Configure una fórmula para el monto de los depósitos de modo que pueda resolverlo para varias edades de comienzo. Realice un análisis de sensibilidad que muestre la cantidad de dinero que usted precisa ahorrar, como función de la edad a la que comienza a ahorrar.
21.Los padres de Nerea deciden comenzar a ahorrar para sus estudios universitarios, al cumplir ella 10 años. Depositarán $4.000 ese mismo día y así hasta su cumpleaños de 17 años.
A usted se le pide que programe la siguiente hoja: asuma que el banco le paga a los padres de Nerea el 8 % sobre los saldos positivos en la cuenta, pero le cobra un 10 % sobre saldos negativos. Si los padres de Nerea necesitan retirar $20.000 al año desde su cumpleaños de 18 hasta el de 21, ¿cuánto dinero adeudarán al banco al comenzar el año 22? (el año posterior a que Nerea termine la universidad).
Nota de Excel: para configurar esta hoja necesitará utilizar la función SI de Excel (si no está familiarizado con esta función, vea el capítulo correspondiente).
22.Una inversión de $10.000 está previsto que pague $250 al final de cada año a perpetuidad. ¿Cuál es la TIR de la inversión? (No hay ninguna función de Excel que responda esta pregunta – ¡use la lógica!).
23.En la hoja de abajo calculamos el VF de 5 depósitos de $100, siendo el primero de ellos efectuado en el momento 0. Como se indica en la primera sección de este capítulo, este cálculo también puede llevarse a cabo utilizando la función = VF (Tasa, períodos, -pago, 1).
a.Demuestre que también puede calcularlo haciendo = VF (Tasa, períodos, -pago) * (1 + interés)
b.¿Puede explicar por qué = VF (r, 5, -100, 1) = VF (r, 5, -100) * (1 + r)?
24.Abner y Maude tienen más de 80 años. Están pensando en vender sus casas por $500.000 y mudarse a un complejo de apartamentos para la tercera edad. El apartamento les costará $50.000 al año y se pagan por adelantado.
a.Si pueden ganar el 6 % anual por el dinero producido de la venta de su casa y viven durante 10 años más, ¿cuánto dinero podrán dejarle a sus nietos como herencia?
b.¿Cuánto es lo máximo que pueden vivir con el dinero producido de la venta de su casa antes de quedarse sin dinero?
25.¿Cuál sería su respuesta a la pregunta anterior si la tasa de interés es 7 % y 5 %?
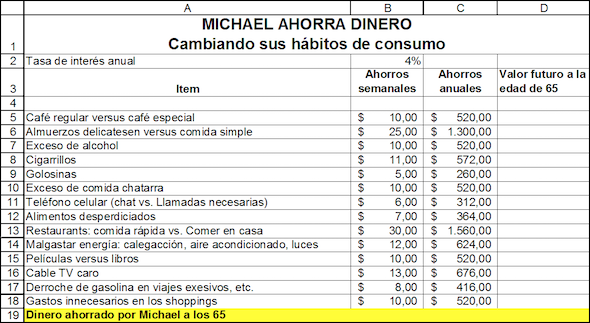
26.Michael está reconsiderando sus hábitos de consumo, tratando de ver la manera de ahorrar dinero. Se da cuenta de que puede ahorrar $2 al día consumiendo café normal en lugar de uno especial en el bar. Dado que adquiere una taza de café cada día laborable, ello representa $10 a la semana, y $520 al año.
a.Si Michael tiene 25 años de edad ahora y prevé jubilarse a los 65, ¿cuánto dinero habrá acumulado por el ahorro en el café? Asuma que la tasa de interés anual es 4 % y que el ahorro de $520 ocurre al final de cada año.
b.Michael se ha asombrado por la respuesta a la parte (a) de este ejercicio. Se ha dado cuenta de que tiene hábitos impropios y ha elaborado una lista de posibles ahorros para ver cuánto más rico podría ser a la edad de 65. ¿Cuáles son las recompensas a la austeridad de Michael?
 Deposita $100 en el banco hoy en una caja de ahorros, ¿cuánto dinero tendrá en tres años?
Deposita $100 en el banco hoy en una caja de ahorros, ¿cuánto dinero tendrá en tres años? Deposita $100 en el banco hoy en una caja de ahorros y planea agregar $100 cada año por los próximos 10 años, ¿cuánto dinero tendrá en su cuenta dentro de 20 años?
Deposita $100 en el banco hoy en una caja de ahorros y planea agregar $100 cada año por los próximos 10 años, ¿cuánto dinero tendrá en su cuenta dentro de 20 años? La empresa XYZ vendió recientemente un bono a su madre por $860. El bono le pagará a ella $20 anuales durante los próximos 5 años. En 6 años obtendrá un pago de $1020. ¿Ha pagado ella un precio justo por el bono?
La empresa XYZ vendió recientemente un bono a su madre por $860. El bono le pagará a ella $20 anuales durante los próximos 5 años. En 6 años obtendrá un pago de $1020. ¿Ha pagado ella un precio justo por el bono? Vuestra tía Sara está analizando si realizar una inversión, la cual tiene un costo de $1.000 y pagará $50 mensuales cada uno de los próximos 36 meses. ¿Debería hacerla o dejar su dinero en el banco, donde gana el 5 %?
Vuestra tía Sara está analizando si realizar una inversión, la cual tiene un costo de $1.000 y pagará $50 mensuales cada uno de los próximos 36 meses. ¿Debería hacerla o dejar su dinero en el banco, donde gana el 5 %? Valor Futuro.
Valor Futuro. Valor Presente.
Valor Presente. Valor Actual Neto.
Valor Actual Neto. Tasa Interna de Retorno.
Tasa Interna de Retorno. Fondos de Pensión y ahorro y otros problemas de acumulación.
Fondos de Pensión y ahorro y otros problemas de acumulación. Funciones de Excel: VF, VA, VNA, TIR, PAGO, NPER.
Funciones de Excel: VF, VA, VNA, TIR, PAGO, NPER. Buscar Objetivo.
Buscar Objetivo.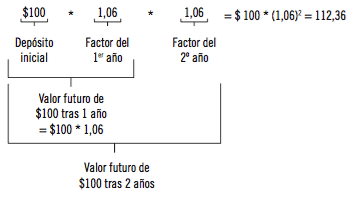





 Las indicadas en Negrita deben completarse obligatoriamente - en la función VF son la Tasa de interés, el número de períodos, Nper, y el Pago. (siga leyendo para ver por qué hemos escrito el pago en negativo).
Las indicadas en Negrita deben completarse obligatoriamente - en la función VF son la Tasa de interés, el número de períodos, Nper, y el Pago. (siga leyendo para ver por qué hemos escrito el pago en negativo). Las no indicadas en negrita son optativas. Por ejemplo, Tipo se refiere a cuando se realiza el pago y, por lo tanto, tiene solo dos opciones: -1 cuando el pago se efectúa al comienzo del período y 0 cuando se realiza al final del mismo. En el ejemplo de arriba hemos indicado un 1 para Tipo; lo que indica (como se explica en el cuadro de diálogo mismo) que el valor futuro se calcula para pagos efectuados al comienzo del período. Si hemos omitido dicha variable o puesto 0, Excel calcularía el valor futuro para una serie de pagos realizados al final del período; vea la subsección de la sección 2.1 titulada “Comienzos versus final del período” para una ilustración.
Las no indicadas en negrita son optativas. Por ejemplo, Tipo se refiere a cuando se realiza el pago y, por lo tanto, tiene solo dos opciones: -1 cuando el pago se efectúa al comienzo del período y 0 cuando se realiza al final del mismo. En el ejemplo de arriba hemos indicado un 1 para Tipo; lo que indica (como se explica en el cuadro de diálogo mismo) que el valor futuro se calcula para pagos efectuados al comienzo del período. Si hemos omitido dicha variable o puesto 0, Excel calcularía el valor futuro para una serie de pagos realizados al final del período; vea la subsección de la sección 2.1 titulada “Comienzos versus final del período” para una ilustración.


 El dinero que los padres les dan al hijo para que estudie ($1.000 mensuales durante los próximos 4 años de universidad) es una anualidad con 48 pagos.
El dinero que los padres les dan al hijo para que estudie ($1.000 mensuales durante los próximos 4 años de universidad) es una anualidad con 48 pagos. Los fondos de pensión a menudo conceden al beneficiario que se jubila un pago fijo durante el período en el que permanezca con vida. Esto es un poco más complicado porque el número de pagos es incierto.
Los fondos de pensión a menudo conceden al beneficiario que se jubila un pago fijo durante el período en el que permanezca con vida. Esto es un poco más complicado porque el número de pagos es incierto. Ciertos tipo de créditos son pagados en cuotas fijas, periódicas (generalmente mensuales, algunas veces anuales). Las hipotecas y créditos para estudiantes son dos ejemplos.
Ciertos tipo de créditos son pagados en cuotas fijas, periódicas (generalmente mensuales, algunas veces anuales). Las hipotecas y créditos para estudiantes son dos ejemplos.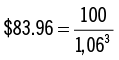

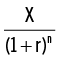
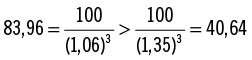
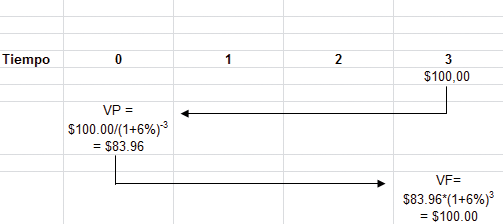
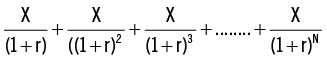
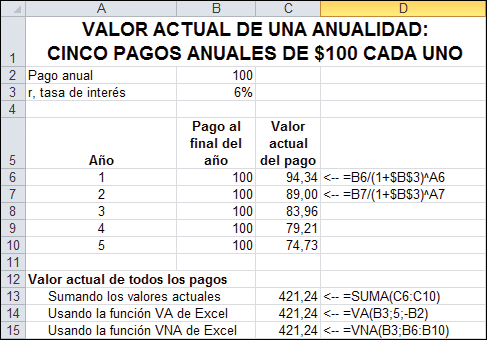
 Puede sumar los valores actuales individuales. Eso se hizo en la celda C13.
Puede sumar los valores actuales individuales. Eso se hizo en la celda C13. Puede utilizar la función VA de Excel, la cual calcula el valor actual de una anualidad (celda C14).
Puede utilizar la función VA de Excel, la cual calcula el valor actual de una anualidad (celda C14). Puede utilizar la función VNA de Excel (celda C15). Esta función calcula el valor actual de cualquier serie de pagos periódicos (ya se trate de pagos fijos, como en una anualidad, o de variables).
Puede utilizar la función VNA de Excel (celda C15). Esta función calcula el valor actual de cualquier serie de pagos periódicos (ya se trate de pagos fijos, como en una anualidad, o de variables). Le dedicamos subsecciones separadas para las funciones VA y VNA.
Le dedicamos subsecciones separadas para las funciones VA y VNA.