LO QUE NOS CUENTA LA HISTORIA

Comenzaremos este capítulo con un breve repaso histórico a lo que puede llamarse como «criptografía clásica» o de los clásicos, de modo que mostraremos los primeros métodos utilizados para cifrar información. Así, repasaremos los principales sistemasempleados por griegos y romanos, para seguir con algunos otros utilizados en la Edad Media y en el Renacimiento.

El lector interesado podrá consultar las referencias que se incluyen tanto en este como en los siguientes capítulos, dado que hay una amplia colección de obras que tratan el tema de la historia de la criptografía. En este volumen nos limitaremos a dar algunas pinceladas de los aspectos que consideramos más relevantes de esta historia.

En particular, si el lector desea ampliar la información que se presenta en este capítulo, le recomendamos el excelente libro de Kahn (1968), en el que se ofrece una visión de los inicios de la criptografía, lo que abarca un lapso de 3 000 años.¹

CRIPTOGRAFÍA CLÁSICA: GRIEGOS, ROMANOS Y MÁS

Esparta o Lacedemonia era una ciudad-estado de la antigua Grecia situada en la península del Peloponeso. Los espartanos utilizaron el primer sistema de criptografía militar que se conoce: la escítala. El historiador romano Plutarco (ca. 46-ca. 120) la describe minuciosamente, pero una forma más abreviada puede servirnos: se trata de una vara o cilindro de madera en la que un pergamino se enrollaba en espiral y a lo largo de la misma. El texto a ocultar se escribía de arriba a abajo de la vara y luego se desenrollaba el pergamino, de modo que las letras del texto original aparecían a lo largo del mismo, pero desordenadas.

A modo de ejemplo, en la figura escítala se muestra una escítala con el pergamino enrollado y una parte del texto a ocultar: «LO QUE NO SABEMOS DE LA CRIPTOLOGÍA». Una vez retirado el pergamino de la escítala, el texto pasaría a ser el siguiente: loociossroqadigubepieeltanmao, en el que se han eliminado los espacios y los signos de puntuación. Para leer el texto oculto, bastaría con volver a enrollar el pergamino en una vara con un diámetro idéntico.

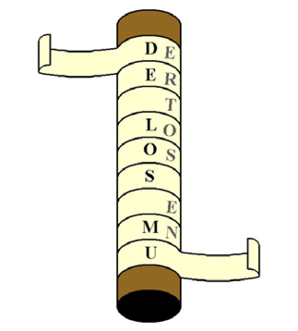
Figura 2. Recreación de una escítala lacedemonia.

Otro de los métodos clásicos para el cifrado de mensajes se debe a Julio César (100 a. C.-44 a. C.). Suetonio (ca. 70-ca. 126) fue un historiador romano que en el siglo II d. C. escribió unas biografías cortas de los primeros emperadores romanos; en la parte de Julio César dice lo siguiente:

Para los negocios secretos utilizaba una manera de cifrar que hacía el sentido ininteligible, estando ordenadas las letras de manera que no podía formarse ninguna palabra; para descifrarlas tiene que cambiarse el orden de las letras, tomando la cuarta por la primera, esto es «d» por «a», y así las demás.

Esto es, César cifraba sus mensajes sustituyendo cada letra por la tercera letra siguiente en el alfabeto, de modo que su famosa frase «VENI VIDI VINCI» pasaría a cifrarse como yhql ylgl ylfl. Para descifrarla, bastaría con sustituir cada letra por la tercera anterior. Es fácil deducir que el cifrado de César se puede modificar de modo que en lugar de usar la tercera letra que sigue a una dada, se emplee la que ocupe cualquier otra posición de las que forman el alfabeto utilizado.

Otro historiador griego fue Polibio (200 a. C.-118 a. C.) que narró los acontecimientos que se sucedieron en los países mediterráneos, especialmente en Roma, entre los años 250 a. C. y 146 a.C. Polibio se cita en los libros de criptografía como inventor de un método para escribir las letras como pares de números, utilizando una tabla. A modo de ejemplo, en la tabla Polibio que se muestra a continuación, cada una de las veinticinco letras se representa por dos números, que indican la fila y la columna correspondiente, de modo que «POLIBIO» se escribiría como 35 34 31 24 12 24 34 (nótese que la «i» y la «j» se consideran como la misma letra).

	1	2	3	4	5
1	A	B	C	D	E
2	F	G	H	I/J	K
3	L	M	N	O	P
4	Q	R	S	T	U
5	V	W	X	Y	Z

Tabla 3. Tabla de Polibio con veinticinco celdas.

Polibio no concibió la tabla como una forma de escritura secreta sino como un medio de comunicarse a distancia por medio de antorchas, a modo de telégrafo primitivo. Sin embargo, al igual que con el cifrado de César, también es sencillo generalizar la tabla de Polibio dotándola, además, de una clave. Basta con considerar una palabra sin letras repetidas o sin tenerlas en cuenta, y colocar sus letras en las primeras celdas de la tabla, completando luego el resto de las celdas con las letras no utilizadas. Así, si se usa la palabra «CLAVE» como clave, la nueva tabla de Polibio se muestra en la Tabla Polibio1, de modo que «POLIBIO» pasará a cifrarse ahora como 41 35 12 31 21 31 35.

	1	2	3	4	5
1	C	L	A	V	E
2	B	D	F	G	H
3	I/J	K	M	N	O
4	P	Q	R	S	T
5	U	W	X	Y	Z

Tabla 4. Tabla de Polibio con la clave «CLAVE».

Hay dos propiedades a destacar de este método: la primera reduce el número de caracteres de veinticinco a solo cinco, por lo que la transmisión de un mensaje es muy sencilla, y la segunda transforma los caracteres alfabéticos en duplas de números, por lo que es posible llevar a cabo operaciones aritméticas con tales parejas, dificultado el proceso de descifrado.

A lo largo de los años se han propuesto diferentes métodos de cifrado, mucho más modernos que el de Polibio, pero basados en el mismo, que ilustran cómo determinados sistemas de cifrado pueden complicarse con solo el añadido de algunas modificaciones. Aquí vamos a presentar dos de ellos. El primero se conoce como «cifrado de los nihilistas». Los nihilistas fueron revolucionarios rusos que, durante la segunda mitad del siglo XIX lucharon contra el régimen zarista. El cifrado nihilista consiste en la codificación del mensaje mediante una tabla de Polibio con una clave, luego se considera una segunda clave que se codifica también con la misma tabla. A continuación se suman las parejas de números obtenidos para el mensaje y la clave, repitiendo la codificación de la clave tantas veces como sea preciso. A modo de ejemplo, si se quiere cifrar el mensaje «NO A LA RUSIA ZARISTA» mediante la tabla de Polibio con la clave «CLAVE» que mostramos en la Tabla Polibio1 y como segunda clave la palabra «LIBERTAD», se obtienen que las siguientes codificaciones del mensaje y de la segunda clave:

N	O		A		L	A		R	U	S	I	A		Z	A	R	I	S	T	A
34	35		13		12	13		43	51	44	31	13		55	13	43	31	44	45	13

L	I	B	E	R	T	A	D
13	31	21	15	43	45	13	22

Sumando ahora las parejas de números se tiene el mensaje cifrado:

34	35	13	12	13	43	51	44	31	13	55	13	43	31	44	45	13
13	31	21	15	43	45	13	22	13	31	21	15	43	45	13	22	13
47	66	34	27	56	88	64	66	44	44	76	28	86	76	57	67	26

Para descifrar el mensaje, el receptor resta al texto cifrado los números que corresponden a la segunda clave según la tabla de Polibio acordada, y luego recupera el mensaje original transformando los números resultantes mediante la misma tabla de Polibio.

El segundo de los métodos de cifrado basado en la tabla de Polibio lo debemos al francés Félix-Marie Delastelle (1840-1902). En este cifrado se transforma cada par de letras del mensaje original en duplas de números de acuerdo con la tabla de Polibio con la clave que se haya elegido (seguiremos usando, a modo de ejemplo, la Tabla Polibio1) y se escriben las dos cifras en vertical, debajo de la letra correspondiente. Después, se leen las duplas de iniciales que constituyen el texto cifrado. Así, para cifrar, por ejemplo, el mensaje «BÍFIDO» (nombre con el que se conoce a este cifrado por combinar el cifrado de una tabla de Polibio con una trasposición sobre parejas de letras), se elaboraría la Tabla Bífido y se obtiene como texto cifrado el dado por «fc fj fh». Para descifrar se hacen las mismas operaciones que para cifrar.

B	I		F	I		D	O
2	3	f	2	3	f	2	3	f
1	1	c	3	1	j	2	5	h

Tabla 5. Sistema de cifrado bífido o de Delastelle.

Otro método de cifrado, que recuerda al de Polibio, aunque muy diferente, es el conocido como cifrado de Playfair. Lord Lyon Playfair (1818-1898) popularizó este sistema, de ahí que lleve su nombre, a pesar de haber sido inventado por su amigo Sir Charles Wheatstone (1802-1875). En este caso, las letras se distribuyen también en un cuadrado de 5×5 celdas y se selecciona una palabra como clave, de modo que las letras repetidas tampoco se consideran. La primera modificación con respecto al cifrado de Polibio es que emisor y receptor, además de la clave, acuerdan en qué posición de la tabla comienza dicha clave. Si la clave fuera precisamente «Wheatstone», esta se convertiría realmente en «WHEATSON» y si el lugar de inicio fuera el centro de la tabla, se tendría la Tabla 6:

I/J	K	L	M	P
Q	R	U	V	X
Y	Z	W	H	E
A	T	S	O	N
B	C	D	F	G

Tabla 6. Tabla de Playfair con la clave «WHEATSTONE».

Una vez establecida la tabla, el mensaje a cifrar se divide en grupos de dos letras, de modo que, si alguna pareja estuviera formada por dos letras iguales, la norma establece que se debe insertar entre ambas una letra ficticia (o nula). También, al igual que en el caso del cifrado de Delastelle, si el número de letras fuera impar, se añade una nula. El proceso para cifrar cada pareja de letras es el siguiente: se buscan las dos letras en cuestión en la tabla Playfair y se observa si las mismas están en la misma fila, en la misma columna o no. En cualquiera de los dos primeros casos, cada letra del par considerado se cambia por la letra que le sigue (de arriba abajo si están en la misma columna o de izquierda a derecha si están en la misma fila). Si las letras están en diferentes filas y columnas, se dibuja mentalmente el rectángulo que ambas determinan si fueran dos de los vértices del mismo, y se sustituyen por las letras que están en los vértices opuestos de dicho rectángulo, y se elige como primera letra para el cifrado la que está en la misma fila que la letra original.

A modo de ejemplo, si el mensaje fuera «El cifrado de Playfair», su separación en pares de letras daría lugar a «EL CI FR AD OD EP LA YF AI RX», de modo que el texto cifrado sería wp bk cv bs sf nx js bh bq uq. Está claro que el proceso de descifrado sigue los pasos inversos al de cifrado.

Hasta aquí hemos mostrado algunos métodos, más o menos ingeniosos, que ocultaban la información a transmitir modificando el mensaje original, llevando a cabo determinadas acciones con números y tablas y, en ocasiones, utilizando claves.

Sin embargo, con la excusa de la tabla de Polibio, nos hemos adelantado al curso de la historia y hemos presentado métodos más imaginativos de los que realmente aparecieron a lo largo de la historia, sobre todo hasta la Edad Moderna.

De hecho, los métodos de «sustitución simple», esto es, los que consisten en sustituir cada letra por un símbolo, más o menos extraño, o por otras letras o números, con la finalidad de que el mensaje no se revele a no ser que se conozca el diccionario de sustitución empleado, han sido una de las formas más extendidas de cifrado a lo largo de la historia. Estos métodos también se conocen como «monoalfabéticos», dado que solo se emplea un alfabeto para sustituir el alfabeto original, esto es, cada letra siempre se sustituye por el mismo símbolo durante el proceso de cifrado. A lo largo de este libro vamos a presentar algunos de los métodos más llamativos o curiosos, en particular cuando mencionemos ciertos personajes históricos de los que se sabe que emplearon dichos métodos y los describiremos con algo más de detalle.

Ahora solo mencionaremos uno de ellos, que nos permitirá presentar una forma muy sencilla de generalizar el método de cifrado de Julio César. Se trata de extender este tipo de cifrado con claves diferentes haciendo uso de un modelo mecánico, esto es, utilizar cualquier otra letra como base que no sea la tercera letra siguiente del alfabeto a la que se desea cifrar, y de realizarlo de modo efectivo. El sencillo artilugio se conoce como «regleta de SaintCyr», debido a que se empleó durante el siglo XIX en la escuela de oficiales del mismo nombre del ejército de tierra francés.

Esta regleta se puede elaborar de forma sencilla escribiendo en una regla o tablilla base el conjunto de los caracteres del alfabeto que se va a emplear y se realizan dos ranuras verticales debajo y a izquierda y derecha de los extremos del alfabeto. Además, se deben escribir en una tira de papel los mismos caracteres, pero dos veces, una a continuación de la otra. La tira de papel se introduce en la tablilla a través de las dos ranuras, haciendo coincidir los caracteres de la tablilla con los de la tira de papel, según el número de posiciones que se desee (véase la figura 3). Así, si el cifrado fuera el de César, coincidirían la «A» de la tablilla con la «D» de la tira, procediendo a cifrar o descifrar con la sustitución mostrada. Para cifrar con una clave diferente, bastará con alinear la letra «A» de la tablilla con la letra de la tira de papel que se desee.

…

Figura 3. Ejemplo sencillo de regleta de SaintCyr.

Por otra parte, es fácil generalizar el uso de esta regleta de modo que, por ejemplo, la tira tenga el alfabeto duplicado, pero en un orden diferente del habitual. Ello daría lugar a un cifrado con una sustitución diferente. También se podría usar con una clave de modo que, una vez elegida una palabra como clave, bastaría con ir cifrando cada letra del texto claro con la letra que le corresponda en la tira. Así, para cifrar cada letra se mueve la tira haciendo coincidir la letra «A» de la tablilla con cada una de las letras de la clave. Las sustituciones monoalfabéticas presentan una debilidad que puede que el lector haya notado con antelación cuando hemos presentado algunos de estos métodos, como el cifrado de César, el empleado por Poe en su novela o la regleta de SaintCyr. Al cifrarse cada letra con el mismo símbolo o letra, parece factible hacer uso de la frecuencia con la que las letras aparecen en un idioma para obtener información del texto cifrado que lleve a determinar el texto claro. Así pues, en los siguientes párrafos vamos a desempeñar el papel de criptoanalista y no el de criptógrafo.

No se conoce quién o cuándo alguien se dio cuenta de esta característica de los cifrados monoalfabéticos. Sí se sabe que el primero en publicar esta técnica de descifrado en el siglo IX fue Al-Kindi. Este personaje polifacético escribió la obra Tratado sobre el descifrado de mensajes criptográficos, donde explica de forma clara cómo proceder. De forma resumida, Al-Kindi (801-873) señala que, conociendo el idioma en el que está escrito un mensaje, para descifrar el texto cifrado correspondiente se puede analizar la frecuencia con la que aparece de forma habitual cada una de las letras de ese idioma en un texto claro cualquiera, siempre que sea lo suficientemente largo. Una vez conocemos estas frecuencias, la letra o símbolo que aparece más veces en el texto cifrado se sustituye por la letra más frecuente en el idioma considerado, la segunda del texto cifrado por la segunda del idioma y así sucesivamente, hasta completar todas las letras o símbolos del texto cifrado.

En la actualidad, hay numerosas tablas publicadas donde se listan las frecuencias de las letras en diferentes idiomas, lo que simplifica el análisis de frecuencias propuesto por Al-Kindi. Sin embargo, a pesar de que no todas las tablas para un mismo idioma presentan los mismos valores, dado que estos dependen de los textos que se hayan utilizado para hacer el recuento, los resultados suelen ser muy parecidos. A modo de ejemplo, una de tales distribuciones porcentuales de frecuencias podría ser la que se muestra en la Tabla Frecuencias (Fúster et al. 2004).

A	B	C	D	E	F	G	H	I	J	K
12,69	1,41	3,93	5,58	13,15	0,46	1,12	1,24	6,25	0,56	0,00

L	M	N	Ñ	O	P	Q	R	S	T	U
5,94	2,65	6,63	3,20	9,49	2,43	1,16	6,25	7,60	3,91	4,63

V	W	X	Y	Z	Vocales
1,07	0,00	0,13	1,06	0,35	46,21

Tabla 7. Distribución de frecuencias de las letras en español.

Estas distribuciones de frecuencias de letras en español (al igual que las de otros idiomas) tienen las mismas características, a saber, las letras más frecuentes son las vocales «a» y «e», con frecuencias muy parecidas y que acaparan más del 25% del total, la mitad de las consonantes con menor frecuencia no llegan al 12% del total, y finalmente las vocales, que componen el 18,5% del total de las letras, representan más del 46% de la frecuencia. En definitiva, esta distribución de frecuencias sigue el típico diagrama de Pareto, esto es, muy pocas letras acumulan una alta frecuencia mientras que un elevado número de ellas apenas aparecen.

Una sencilla prueba práctica pone de manifiesto que no se debe seguir al pie de la letra el método de Al-Kindi para criptoanalizar un texto cifrado. En efecto, si el texto a analizar es pequeño, es muy probable que la distribución de las frecuencias de las letras que lo componen se distancie de la mostrada en la Tabla Frecuencias, mientras que cuanto más largo sea, más se parecerá a la misma. Incluso en este último caso, no siempre la letra más repetida en el texto cifrado corresponderá a la letra más repetida en el idioma del mensaje.

Como anécdota, si bien extrema, de que en ocasiones no siempre el método de Al-Kindi será aplicable, podemos citar el libro de doscientas páginas de Georges Perec (1936-1982), titulado El secuestro en el que el autor no usó ninguna palabra con la letra «e». Reproducimos un breve fragmento,traducido al español, donde no se emplea la letra «a»: a continuación:

Siempre he tenido en secreto el oscuro embrollo de tu origen. Si pudiese, te hubiese dicho hoy el Tormento que pende sobre nosotros. Pero mi Ley prohíbe referirlo. Ningún individuo puede en ningún momento vender el inconsistente porqué, el desconocido mínimo, el completo veto que, desde el origen, oscurece nuestros discursos, desluce nuestros deseos y pudre nuestros movimientos.

De hecho, es muy recomendable considerar las frecuencias de dígrafos y trígrafos del idioma que se considere, lo que afecta considerablemente a la distribución de frecuencias. Así, basta con tener en cuenta que, por ejemplo, en español, la «a» precede a la «b» con una frecuencia de más del 50%; mientras que en muy pocas ocasiones está precedida por la «e». Los dígrafos, ordenados por su mayor frecuencia en español, son: de, el, la, as, en, es, os, ra, an, al, er, ue, ad, do, re, on, ab, nt, ar, ia, ta, se, co, qu y ba. Por su parte, los trígrafos más frecuentes, ordenados de la misma forma, son: que, del, aba, ela, sde, ent, nte, los, ode, era, ade, las, ado, con y des. En estos casos se puede observar que, como ya hemos dicho, las letras «a» y «e» aparecen con una frecuencia muy parecida, pero cada una se presenta acompañada de letras diferentes. Por ejemplo, la «e» suele ir precedida por la «d», mientras que la «b» precede y sigue frecuentemente a la letra «a» pero no a la «e», etcétera.

Para verificar en un caso concreto y divertido los aspectos que acabamos de señalar, recomendamos al lector una lectura detallada de El escarabajo de oro de Poe, donde debe tenerse en cuenta que se trata de una traducción por lo que el autor aplica el análisis de frecuencia de las letras, dígrafos y trígrafos del idioma inglés.

Por lo dicho hasta aquí, se puede deducir que los métodos de cifrado por sustitución simple no son muy seguros y, en definitiva, con algo de trabajo se pueden descifrar. Los criptógrafos eran conscientes de este problema y, a medida que pasaron los años, propusieron nuevos métodos para intentar paliar el problema que suponía utilizar las frecuencias de las letras como método de descifrado. Una de las primeras soluciones propuestas fue la del uso de «nulos», es decir, símbolos, valores o letras que no tenían significado criptográfico, pero que permitían alterar la frecuencia real de las letras. Otra solución fue utilizar, además de las sustituciones de letras por símbolos, nomenclátores, esto es, colecciones de nombres de personas, cargos o lugares que se sustituían por un único símbolo como si se tratara de una única letra o sílaba. A modo de ejemplo, la Figura 4 reproduce un documento, datado entre 1619 y 1620 y conservado en los archivos de Estrasburgo, que muestra una sustitución simple (columna de la izquierda), una colección de nulos (parte superior), un nomenclátor (a la derecha de la columna y debajo de los nulos) y un ejemplo de su utilización.

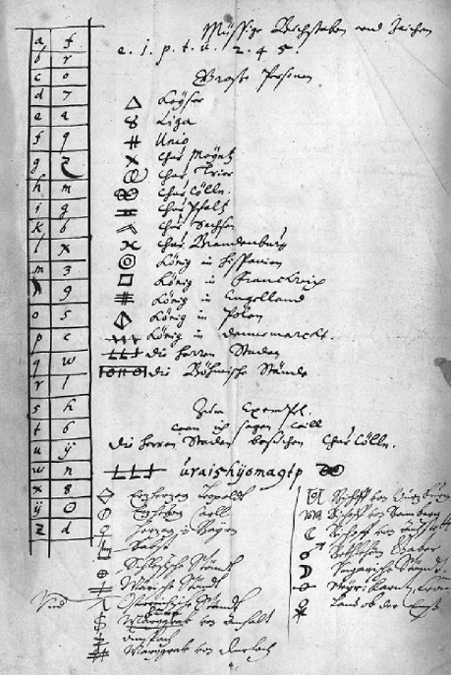
Figura 4. Ejemplo de nomenclátor (Hervé Lehning).

Leon Battista Alberti (1404-1472), en su tratado De cifris (Alberti 1997), propuso el uso de un artilugio queadmite el cifrado de César y que permite emplear un cifrado en el que se use más de un alfabeto, es decir, que permite utilizar varios alfabetos diferentes en el mismo proceso de cifrado, lo que supone que una misma letra puede cifrarse con letras diferentes a lo largo de todo el proceso. Estos métodos se conocen como cifrados por «sustitución polialfabética». Nos vamos a detener en detallar el artilugio de Alberti porque es el primer método polialfabético que se propuso en la historia.

El artilugio, denominado «discos de Alberti» o «cifrador por rotación», consta de dos discos concéntricos que pueden girar sobre su eje común (véase la Figura 5). El disco exterior contiene veinte letras del alfabeto y los números del 1 al 4. El disco interior tiene un alfabeto de veinticuatro letras (veintitrés letras y el signo &). Si se gira un disco sobre el otro y no se lleva a cabo ninguna otra acción, lo que se tiene es una sustitución monoalfabética, como la del cifrado de César. Ahora bien, si rotamos el disco interior tras un determinado período durante un proceso de cifrado (según un patrón o regla acordada de antemano), lo que se obtiene es una sustitución polialfabética, dado que se cambia de alfabeto de cifrado (de hecho, se pueden obtener hasta 24 alfabetos diferentes).

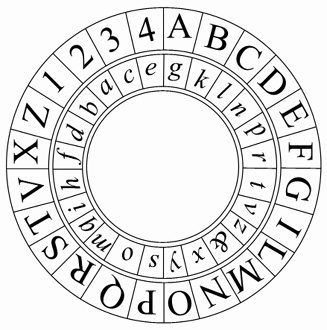
Figura 5. Cifrador de rotación (discos) de Alberti (ASC).

A modo de ejemplo, para cifrar el texto «DISCOS DE ALBERTI» se puede proceder como sigue. En primer lugar, se ha de convenir con el destinatario cuándo debe girar el disco interior y cuál será la nueva posición relativa de los mismos, acordando, por ejemplo, el número de giros a derecha a realizar. Este número de giros puede ser siempre el mismo, o variar en cada ocasión. En nuestro caso, el número 2 señalará que el primer giro será de trece posiciones, mientras que el segundo serán siete. Además, el destinatario debería conocer la posición inicial de los discos, lo que puede hacerse comenzando el texto cifrado con la letra que correspondería a la letra «A», en este caso, será la letra «g».

Así pues, el mensaje que se va a cifrar pasará a ser «-DISCOS2DEAL2BERTI» con las acciones acordadas ya mencionadas. Este acuerdo con el receptor supone que el primer alfabeto de cifrado será el indicado en la figura Alberti, mientras que el segundo y el tercero pasarán a ser «ysomqihfdbacegklnprtvz&x» y «prtvz&xysomqihfdbacegkln», respectivamente. En definitiva, el texto cifrado, que escribimos debajo del texto claro, será la segunda fila de la Tabla 8:

Tabla 8. Ejemplo de cifrado de Alberti.

Es importante destacar algunas características de este cifrado. En primer lugar, se puede ver cómo la misma letra se cifra de forma diferente a lo largo del proceso según la posición que ocupe en el texto claro. Así, la «I» pasa a ser una «v» o una «y», y la «E» se convierte en una «q» o una «z»; o que la misma letra del texto cifrado corresponda a diferentes letras en el texto claro, como la «y», que puede corresponder tanto a una «O» como a la «A» o a la «I». Por otra parte, también se pueden detectar algunas posibles debilidades, como que una letra repetida se cifre de la misma manera si no ha habido un giro en los discos, como le sucede a la «S». Finalmente, cabe señalar que el proceso de descifrado se lleva a cabo invirtiendo las operaciones realizadas en el de cifrado, teniendo en cuenta el giro que se debe realizar con los discos cuando se encuentre que el valor descifrado es un 2. En todo caso, insistimos en que este método requiere de un acuerdo previo entre las dos partes que se intercambian los mensajes.

Hay que aclarar además que, con los discos de Alberti, un mismo mensaje se puede cifrar de diferentes maneras, según la posición inicial de los discos o la regla establecida para el cambio de alfabeto.

Finalmente, es importante comentar que la inclusión de los números 1 al 4 en el disco exterior de Alberti no es caprichosa. Se trata de una especie de codificación añadida que permite asignar a cada colección de dos, tres o cuatro números un mensaje concreto acordado por emisor y receptor de antemano. Por ejemplo, ٢٤ podría significar «visita inminente» y ٣٢١ «cita suspendida». Es interesante señalar que el número de estos posibles mensajes acordados es elevado. Basta tener en cuenta que el número de grupos que se pueden formar con dos, tres y cuatro números con los cuatro disponibles es, respectivamente, 4², 4³ y 4⁴, por lo que el total es de 336.

Los discos de Alberti requieren de una preparación previa y de un acuerdo entre ambas partes, amén de una labor algo tediosa si el mensaje a transmitir es largo. Por ello, no es de extrañar que sea mucho más sencillo emplear discos cifradores que solo contengan los dos alfabetos y solo haga falta conocer la posición relativa inicial de los dos discos. Estos discos simplificados fueron utilizados por los sudistas durante la guerra de Secesión americana (véase la Figura 6).

Figura 6. Réplica de la NSA (National Security Agency) del disco empleado en la guerra de Secesión americana por los sudistas (CCN).

Otro de los padres de los sistemas de cifrado polialfabéticos fue Johannes Trithemius o Tritemio (1462-1516). A Tritemio se le deben, principalmente, dos sistemas. El primero de ellos, descrito en Polygraphiae libri sex (1518), consiste en sustituir cada una de las letras del texto claro por otra en el texto cifrado de modo que la primera letra del texto claro se mantiene tal cual en el texto cifrado, la segunda letra del texto claro se cambia por la letra que le sigue en el alfabeto, la tercera por la segunda que le sigue y así sucesivamente. De este modo es como si se tuvieran veinticinco alfabetos de cifrado diferentes compuestos por veintiséis letras cada uno: el primero empezaría con la letra «B», el segundo con la «C», etcétera. A modo de ejemplo, «TRITHEMIUS» se cifraría como tskuljspdc.

El segundo método ideado por Tritemio consistía en sustituir cada letra del alfabeto por una palabra o frase en latín, a modo de letanía o rezo litúrgico. En la tabla Tritemio se muestran solo algunos ejemplos que permiten cifrar la palabra «CEBADA» con la siguiente expresión en latín creator universorum qui gloriosus in caelis benefactor pater. Al margen de que haría falta saber latín para conocer si tal expresión tiene sentido o no, aún más en la época de Tritemio, otro inconveniente del método es la enorme diferencia entre la longitud del texto claro y la del texto cifrado.

A	Pater	Noster qui	Es in	Caelis
B	Dominus	Nostrum qui	Gloriosus in	Celo
C	Creator	Omnium qui	Graditur in	Altis
D	Benefactor	Cunctorum qui	Extas in	Alto
E	Sanator	Universorum qui	Existis in	Exelsi

Tabla 9. Sustitución de letras por palabras o frases de Tritemio.

Giovanni Battista della Porta (1535-1615) escribió el libro De furtivis literarum notis-vulgo de ziferis (Porta 1563), por el que se le considera como otro de los padres de la criptografía. Entre otras aportaciones, Battista della Porta es el autor del método de sustitución poligráfico más antiguo que se conoce. Se trata de una sustitución digráfica, esto es, cada dos letras se cambian por un símbolo siguiendo la figura Porta. Es decir, el par formado por la letra que encabeza una columna seguida por una letra final de una fila, se sustituye por uno de los cuatrocientos símbolos extraños, en particular, por el que está en la celda en la que se cruzan la columna y la fila de ambas letras.

Figura 7. Sustitución digráfica propuesta por Battista della Porta.

Posiblemente, de todos los primeros padres de la criptología, el más famoso sea Blaise de Vigenère (1523-1596), cuya fama se debe, en gran medida, a la claridad de su obra Traicte des chiffres (1585) y cuyo método, al parecer irresoluble en su época, recibió el apodo de «código indescifrable» (chiffre indéchiffrable). Vigenère estudió los métodos propuestos por Alberti, Tritemio y della Porta y presentó su sistema de cifrado que utilizaba veintiséis alfabetos diferentes. En cierto modo similar al utilizado por Tritemio, aunque empleado de modo diferente, porque además añadía la opción de usar una clave. En este caso, los veintiséis alfabetos son los mismos que los de Tritemio, es decir, a excepción del primero que funciona como alfabeto original, los restantes se forman comenzando cada uno de ellos por la segunda, tercera, cuarta letra y así sucesivamente, hasta la última. Una versión reducida del cuadro de Vigenère se muestra en la Tabla 10.

…

Tabla 10. Cuadro de Vigenère con los veinticinco alfabetos cifrantes.

Una vez construido el cuadro, una versión del método consiste en cifrar cada una de las letras de la primera fila usando el alfabeto que se define mediante la letra de la clave que le corresponde y que está en la primera columna, de modo que la letra cifrante la encontramos en la celda en la que la fila y la columna se cruzan. Así, la letra «M» se cifra mediante el alfabeto «C» como la letra «o», mientras que la misma letra se cifra con el alfabeto «Y» como la «k».

A modo de ejemplo, si se desea cifrar el mensaje «LA CIFRA INDESCIFRABLE» mediante la clave «BLAISE», bastará con escribir el texto claro y debajo la clave, repetida tantas veces como sea preciso, de modo que la primera fila contiene las letras a cifrar y la segunda los alfabetos cifrantes. Realizado el proceso de cifra de cada letra, se obtiene el texto cifrado. En la Tabla 11 puede verse el resultado de este ejemplo.

Texto claro

Clave

Texto cifrado

Tabla 11. Proceso de cifrado de Vigenère con la clave «BLAISE».

El método de Vigenère es invulnerable al método de las frecuencias de Al-Kindi, así como a las restantes sustituciones polialfabéticas ya comentadas, pero, además, este incluye la opción de utilizar una clave, lo que lo hace mucho más seguro, dado que se puede modificar la clave cuando se desee, siempre que se comparta entre emisor y receptor.

No obstante, existe otra forma de atacar y descifrar el «cifrado indescifrable» de Vigenère. Aquí solo daremos unas pinceladas de cómo llevar a cabo este ataque.

El ataque al método de Vigenère se conoce como método de Kasiski por Friedrich Wilhelm Kasiski (1805-1881), quien lo publicara en su libro Die Geheimschriften und die Dechiffrierkunst, (La escritura secreta y el arte del descifrado) en 1860, aunque todo apunta a que fue Charles Babbage (1791-1871) el primero en desarrollarlo, si bien nunca lo publicó.

De forma muy resumida, el método de Kasiski consiste en determinar, en primer lugar, la longitud de la clave para luego calcularla, reduciendo el cifrado polialfabético a varios cifrados monoalfabéticos. Para obtener la longitud de la clave, se buscan palabras repetidas en el texto cifrado (dígrafos o trígrafos, principalmente) que, presumiblemente, corresponderán a palabras repetidas en el texto claro que se cifran con la misma clave. Este hecho permite deducir que las diferentes distancias a las que aparecen estas palabras repetidas pueden ser un múltiplo de la longitud de la clave empleada. A partir de las distancias obtenidas y las longitudes de las palabras repetidas se puede hacer una suposición de la longitud de la clave. Entonces se divide el texto en bloques cuyo tamaño sea el mismo que el de la clave y se aplica un ataque a un cifrado monoalfabético (de tipo César) para obtener la clave.

Al margen de los posibles métodos para atacar un sistema de cifrado, que antes o después acaban apareciendo, es muy importante que tal sistema se utilice siguiendo las pautas con las que se diseñó o, al menos, teniendo en cuenta sus recomendaciones, dado que su autor es quien más lo ha estudiado y conoce sus propiedades. En este sentido, es de destacar que la sustitución polialfabética de Vigenère se empleara a lo largo de la historia en múltiples ocasiones, aunque ya se conocieran formas de atacarlo, y no siempre como se debía.

Así, por ejemplo, en la guerra de Secesión americana (1861-1865), los soldados del sur emplearon esta sustitución, pero redujeron su complejidad al usar solo tres claves diferentes: Manchester Bluff, Complete Victory y Come Retribution, lo cual facilitaba enormemente el trabajo de descifrado de sus enemigos.

También durante la Segunda Guerra Mundial (1939-1945) varias redes alemanas de espionaje emplearon este método. La complejidad añadida en este caso era la forma de elegir la clave de cifrado a emplear. Dicha clave era una palabra, frase o párrafo de un libro compartido por emisor y receptor, de modo que el emisor seleccionaba una clave al azar contenida en el libro y hacía llegar al receptor la página y la posición en la misma de la palabra, frase o párrafo elegido.

Otro ejemplo de mal uso del método de Vigenère lo encontramos en la guerra de Indochina (1946-1954) entre Francia y el Viet Minh de Ho Chi Minh. En este caso, el Viet Minh utilizaba claves de longitud constante igual a cinco que, además, siempre iban escritas al inicio del mensaje. Hasta aquí un breve repaso de lo que podemos considerar el nacimiento de la criptología, con mención expresa de los principales personajes que aportaron su saber, ciencia e ingenio para ello. En la siguiente sección comentaremos otros personajes históricos que son más conocidos por otras razones más que por su aportación a la criptografía, pero que la utilizaron para sus fines particulares.

ALGUNOS PERSONAJES DE LA HISTORIA

A lo largo de la historia, han sido numerosos los personajes que han utilizado diferentes métodos para enviar cartas o mensajes con la intención de que su contenido no fuera accesible por sus adversarios y solo lo conociera el destinatario de los mismos. Sería interminable detallar aquí todos los sistemas concretos que emplearon tales personajes, por lo que solo mencionaremos aquellos que puedan ser de especial interés para el lector (exceptuando a los españoles que los trataremos en el capítulo 3), bien sea por la relevancia del personaje, bien por la originalidad del sistema específico empleado.

Debe tenerse en cuenta que tales sistemas se engloban en los métodos criptográficos que se han mencionado en la sección anterior. Además, se da la circunstancia de que algunos de los personajes que mencionaremos más adelante no utilizaron los métodos más novedosos, que ya existían en su época, que evitaban el criptoanálisis y, por tanto, obtener los textos claros a partir de los cifrados, aún sin conocer la clave. Este retraso en la aplicación de tales métodos más seguros supuso, en algunos casos, graves consecuencias.

El primer personaje que mencionaremos es el emperador Carlomagno (742-814), quien utilizó la criptografía en sus misivas usando una sustitución simple. En el libro de Vigenère Traicté des chiffres, ou secrètes manières d’écrire se reproducen cuatro de los diferentes sistemas de sustitución que usó el emperador y que se muestran en la figura Carlomagno.

Figura 8. Sustituciones simples de Carlomagno.

Como se puede ver, cada una de las letras del alfabeto se sustituía por un símbolo, más o menos extraño, con el fin de ocultar el contenido del mensaje.

La característica principal de la francmasonería era el secretismo, pues utilizaban un sistema para intercambiar información. Este sistema asocia a cada letra una figura, relacionada con símbolos arquitectónicos y de la construcción que recuerdan su profesión. La forma más sencilla de recordar esta sustitución es hacer uso de la distribución de las letras como se muestra en la figura francmasonería.

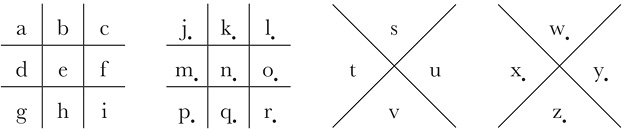
Figura 9. Disposición de las letras según los francmasones.

Así, la letra «b» se sustituye el símbolo , la «e» por ,la «f» por , la «n» por , la «s» por ν, la «v» por ʌ, etcétera.

Una sustitución simple, similar a la anterior, era la utilizada por los caballeros templarios, al parecer de antes del siglo XIII. Los símbolos empleados para cada una de las letras recuerdan, vagamente, a la cruz de la orden. En la Figura 10 se puede ver esta forma de sustitución y la cruz de la orden.

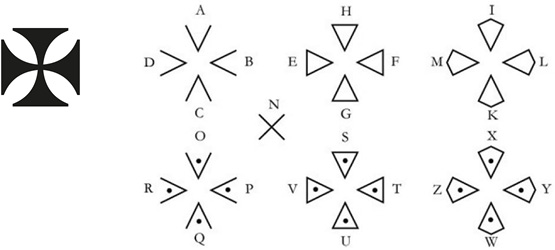
Figura 10. Sustitución simple usada por los templarios (LEHNING 2021).

Algunos personajes históricos deben agradecer a grandes criptoanalistas sus éxitos en diferentes batallas, como el rey Enrique II de Francia (1519-1559), que utilizó la habilidad de Antoine de Rossignol (1600-1682) y a quien el Cardenal Richelieu (1585-1642) tomó a su cargo. Más adelante volveremos a mencionar la capacidad de Rossignol como criptólogo.

Un conocido caso de uso incorrecto de la criptografía, con fatales consecuencias, es el de María Estuardo (1542-1587), reina de Escocia. No entraremos en los detalles de la historia, pero es sabido que a María se la acusó, y posteriormente condenó a muerte, por conspirar para asesinar a la reina Isabel I de Inglaterra y hacerse con la corona inglesa. Mientras María estuvo en prisión mantuvo correspondencia cifrada con sus partidarios. En el juicio contra ella se pudo probar, gracias a la labor de los criptoanalistas de la reina Isabel, que estaba al tanto de la conspiración, por lo que se la condenó a muerte. El nomenclátor utilizado (véase la Figura 11), esto es, la colección de símbolos empleados para el cifrado, en lo que se llamó la «conspiración Babington», lo formaban veintitrés símbolos para las letras del alfabeto (a excepción de la «j», la «v» y la «w»), cuatro nulos (símbolos sin significado) y treinta y cinco símbolos para abreviar palabras o frases de uso común.

https://upload.wikimedia.org/wikipedia/commons/b/bd/Mary-cipher-code.jpg

Figura 11. Nomenclátor empleado por María Estuardo (THE UK NATIONAL ARCHIVES).

Probablemente, uno de los ejemplos más destacables de modificación del cifrado monoalfabético es la conocida como la Gran Cifra (Grande Chiffre) empleada por Luis XIV (1638-1715), el Rey Sol. Uno de los nomenclátores de la Gran Cifra se muestra en la figura Luis XIV. Su importancia se debe a que fueron necesarios doscientos años para poder descifrarla. Los artífices de este sistema de cifrado fueron Antoine Rossignol y su hijo Bonaventure, que la emplearon para cifrar los mensajes más secretos del rey. También Antoine Rossignol fue el fundador del Gabinete negro (Cabinet noir), el servicio de descifrado de los reyes de Francia. Con el paso del tiempo este tipo de gabinetes se instauraron en otros países, destacando el austriaco y el americano.

Figura 12. Uno de los nomenclátores de la Gran Cifra de Luis XIV (THE UK NATIONAL ARCHIVES).

El gran criptógrafo francés Étienne Bazeries (1846-1931) fue el responsable del descifrado de la Gran Cifra. Su análisis para desentrañar los textos cifrados con este método es digno de mención y, por ello, lo comentaremos brevemente. Bazeries observó que los documentos cifrados contenían miles de números, pero sólo había quinientos ochenta y siete grupos de números diferentes. La primera hipótesis que estableció en su análisis es que como una sustitución simple solo necesita veintiséis números diferentes, el resto podrían ser homófonos, es decir, grupos de números que tenían el mismo significado y que pretendían enmascarar la frecuencia de su repetición. Sin embargo, tuvo que descartar esta hipótesis porque no le llevó a ninguna conclusión.

La segunda hipótesis que planteó es que cada grupo de números podría representar un dígrafo, debido a que el número de dígrafos con veintiséis letras es seiscientos setenta y seis (= 26²), lo que se aproxima mucho a los quinientos ochenta y siete existentes. Este planteamiento le llevó a tratar de emparejar los dígrafos más empleados en francés con los grupos de números más repetidos, pero tampoco obtuvo buenos resultados. Finalmente, optó por asociar a cada número una sílaba, de modo que repitió la idea de emparejar los grupos de números más frecuentes con las sílabas de uso más corriente. Esta hipótesis le llevó a suponer que el grupo de números 124-22-125-46-345, que aparecía varias veces en cada página, podía significar «les-en-ne-mi-s» o «les enemis» (los enemigos). A partir de este sencillo dato y con un enorme esfuerzo, Bazeries logró descifrar el método ideado por los Rossignol.

Otro personaje ilustre fue María Antonieta de Austria (1755-1793), quien utilizaba la criptografía para cifrar la correspondencia que mantenía con sus amantes. El método de cifrado era una sustitución polialfabética para cada uno de los destinatarios de sus cartas, con cada uno de los cuales empleaba una clave diferente. Una de tales sustituciones puede verse en la figura Antonieta, donde se aprecia que solo se emplean veintidós letras dado que para las parejas (I, J), (U, V), (C, K) y (V, W), solo se emplea una de las letras.

Figura 13. Cuadro de sustitución empleado por María Antonieta (HERVÉ LEHNING).

El proceso de cifrado no es muy cómodo y puede llevar a errores. La sustitución es como sigue: una vez elegida la palabra clave, se cifra cada una de las letras del texto claro haciendo uso de cada una de las letras de la clave de modo iterativo. Así, la primera letra a cifrar se sustituye por la que está en la misma celda (encima o debajo) donde se encuentra la letra a cifrar y que está en la fila determinada por la primera letra de la clave. La segunda letra y las siguientes se cifran de la misma manera, usando cada una de las letras de la clave. A modo de ejemplo, si se usa el cuadro de sustitución de la figura Antonieta y se desea cifrar el texto claro «ANTONIETA» con la clave «MAR», para cifrar la primera letra, la «A», se busca qué letra la acompaña en la fila correspondiente a la «M», que es la «S»; a continuación se localiza la letra que está en la misma celda que la «N» en la fila correspondiente a la letra «A», que es la «M» y así sucesivamente, de modo que el texto cifrado es smmhmryfv.

Si el lector ha seguido el ejemplo anterior, puede imaginar la complicación que resulta si se intenta cifrar una carta larga, de ahí que María Antonieta empleara un proceso más sencillo, probablemente sugerido por algún criptógrafo conocido (y podríamos decir que amateur). Este consistió en cifrar solo una de cada dos letras, por ejemplo, las que ocupaban las posiciones pares, pero esta estrategia, aunque simplifica el proceso de cifrado y de descifrado, hace que sea más inseguro.

Otro ilustre personaje fue Napoleón Bonaparte (1769-1821), pero todo apunta a que no era un gran entusiasta en el uso de la criptografía, si bien se tiene noticia de que empleó dos tipos de cifrado: la grand chiffre y varias petit chiffre. La primera tenía mil doscientos grupos y se utilizaba para las comunicaciones con el estado mayor; mientras que las segundas solo tenían ciento cincuenta grupos.

Al margen de estos personajes históricos, fundamentalmente relacionados con la política, queremos incluir aquí a otros personajes ilustres, sobre todo escritores, que usaron la criptología en algunas de sus obras y la ayudaron a su divulgación. Nos referimos, por orden de nacimiento, a Honoré de Balzac (1799-1850), Edgar Allan Poe, Julio Verne (1828-1905) y Arthur Conan Doyle (1859-1930).

Balzac, en el capítulo dedicado a las Religiones y confesiones, consideradas en sus relaciones con el matrimonio de su Fisiología del matrimonio, uno de sus trabajos dentro de la Comedia Humana, escribe lo siguiente:

Ha dicho La Bruyere muy espiritualmente: Es demasiado para un marido requerir tanto devoción como galantería; una esposa debiera elegir.

El autor piensa que La Bruyere se ha equivocado. En efecto…

A continuación, siguen cuatro páginas ilegibles formadas por letras escritas al revés, de costado, etcétera, sin un sentido aparente y diferentes según la edición del libro de que se trate (véase la Figura 14).

Figura 14. Reproducción de una página de Fisiología del matrimonio de Honoré de Balzac (ASC).

En la fe de erratas del libro en la que se advierte de «los errores que puede haber cometido el lector al leer esta obra», Balzac menciona estas cuatro páginas y a propósito de ellas señala:

Para comprender realmente el sentido de estas páginas, un lector honesto consigo mismo debe releer sus pasajes principales varias veces; porque el autor ha puesto todo su pensamiento allí.

El criptólogo Bazeries, a quien ya hemos mencionado anteriormente, trató de descifrar estas páginas y, al no poder con la tarea, concluyó que se debía tratar de una broma del autor. Más tarde, André Lange observó que el aparente texto cifrado era distinto en diferentes ediciones de la obra y, analizando una de tales ediciones (la de Furne de 1846), descifró el mensaje al comprobar que se trataba de un sistema de trasposición.

5	3	‡	†	3	0	5	)	)	6	*	4	8	2	6	)	4	‡	.	)	‡	)	;	8	0	6
*	;	4	8	‡	8	¶	6	0	)	)	8	5	;	1	‡	(	;	:	‡	*	8	†	8	3	(
8	8	)	5	*	†	;	4	6	(	;	8	8	*	9	6	*	?	;	8	)	‡	(	;	4	8
5	)	;	5	*	†	2	:	*	‡	(	;	4	9	5	6	*	2	(	5	*	–	4	)	8	¶
8	*	;	4	0	6	9	2	8	5	)	;	)	6	†	8	)	4	‡	‡	;	1	(	‡	9	4
8	0	1	;	8	:	8	‡	1	;	4	8	†	8	5	;	4	)	4	8	5	†	5	2	8	8
0	6	*	8	1	(	‡	9	;	4	8	;	(	8	8	;	4	(	‡	?	3	4	;	4	8	)
4	‡	;	1	6	1	;	:	1	8	8	;	‡	?	;

Tabla 12. Mensaje, en inglés, objeto de criptoanálisis en El escarabajo de oro de Edgar Allan Poe.

Si el lector aún no ha leído con detalle, como recomendamos unas páginas antes, esta excelente novela, daremos unas pinceladas de cómo el protagonista de la obra aborda la tarea de intentar descifrar el mensaje secreto. En el caso de que el lector desee disfrutar de la obra de Poe en todo su esplendor, le recomendamos que se salte el siguiente párrafo, para evitar que le destripemos la trama.

Como se puede apreciar, el texto cifrado contiene veinte símbolos diferentes por lo que Legrand supone que se trata de un cifrado por sustitución simple. De modo que procede a asignar las letras y símbolos según la frecuencia de los mismos en el idioma inglés. Después de este proceso, observa que no ha obtenido un texto legible al completo por lo que sigue determinadas estrategias alternativas, como hacer uso de los dígrafos y trígrafos más empleados en inglés y asignarles los grupos de dos y tres símbolos, en especial del trígrafo «THE». Hecho esto, repite el proceso de sustitución y aplica nuevas estrategias hasta lograr su propósito.

Julio Verne, por su parte, escribió varias novelas en las que emplea la criptología como parte de sus tramas, que comentaremos brevemente.

En Viaje al centro de la Tierra, Verne presenta un pergamino con caracteres rúnicos que oculta un mensaje, como vemos en la figura centro.

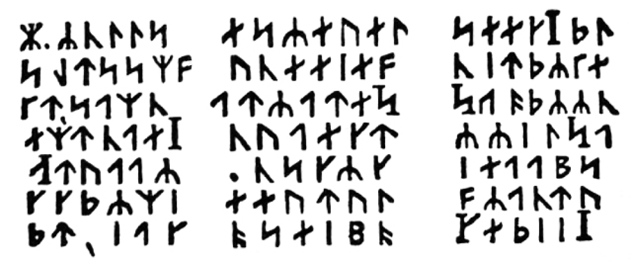
Figura 15. Reproducción del criptograma de Viaje al centro de la Tierra de Julio Verne (ASC).

El primer paso de los protagonistas de la conocida historia consiste en deshacer la sustitución inicial para escribir las runas como caracteres latinos, de modo que obtienen el mensaje que aparece en la tabla centro1. El siguiente paso es descifrar el texto cifrado mediante una trasposición, que permite conocer el camino para llegar al centro de la Tierra (eso sí, de nuevo, conviene saber algo de latín).

mm.rnlls	esreuel	seecJede
sgtssmf	unteief	niedrke
kt,samn	atrateS	Saodrrn
emtnael	nuaect	rrilSa
Atvaar	nscrc	ieaabs
ccdrmi	eeutul	frantu
dt,iac	oseibo	KediiY

Tabla 13. Caracteres latinos de las runas de Viaje al centro de la Tierra de Julio Verne.

Julio Verne vuelve a hacer uso de la criptología en la trama de la novela La Jangada: 800 leguas por el Amazonas. El personaje de esta obra, Juan Garral, ha heredado una hacienda y por este motivo se desplaza por el Amazonas junto a su familia y criados en una jangada. Al margen de los problemas de la travesía en sí, Garral parece tener problemas con la justicia, pero podría librarse de estos si accede a un chantaje del que es objeto, dado que el chantajista posee un manuscrito cifrado que le libraría de la justicia. Juan rechaza el chantaje, por lo que los protagonistas de la novela tratarán de hacerse con el manuscrito y descifrarlo para poder salvar a Juan de la muerte. En la Tabla 14 mostramos el contenido, en francés, del citado manuscrito.

Tabla 14. Mensaje objeto de criptoanálisis en La Jangada de Julio Verne.

En este caso, el texto claro se ha cifrado usando el método de Vigenère y una de las suposiciones de los que intentan descifrarlo, después de varias pistas, es que lo ha firmado su autor, un tal Ortega, por lo que las últimas seis letras del texto cifrado deberían corresponder al apellido. Un primer paso en el proceso de descifrado sería la siguiente asignación de letras: «s» con «O», «u» con «R», «v» con «T», «j» con «E», «h» con «G», y «d» con «A». Esta asignación correspondería a la serie con desplazamiento 432513. El lector podría intentar descifrar el manuscrito con esta pista o utilizar el método de Kasiski. Si no pudiera con ello o la tarea le parece demasiado complicada, siempre puede leer el libro y seguir los pasos que Julio Verne señaló en su novela.

Como es bien conocido, en Los hijos del capitán Grant, lord Edward Glenarvan descubre, durante un viaje de recreo por barco, dentro de una botella tres trozos de papel, parcialmente destruidos por el agua, que han sido escritos por el capitán Grant. Los hijos del capitán le piden llevar a cabo una expedición de rescate. El problema es que necesitan descifrar los tres mensajes, que parecen ser el mismo, pero escritos en tres idiomas diferentes: francés, inglés y alemán. En la tabla Grant se muestran los tres mensajes parciales en los tres idiomas. En este caso, no daremos ninguna pista acerca del contenido del mensaje original ni sobre las interpretaciones que se hacen del mismo a lo largo de la novela. Sugerimos al lector que disfrute de la lectura de esta novela.

Inglés
62	Bri	gow
sink	tra
aland
skripp	Gr
that	monit	of	long
and	ssistance	lost

Alemán
7	juni	Glas
swei	atrosen
graus
bring	ihnen

Francés
troj	ats	tannia
gonie	austrel	gonie
abor
contin	pr	cruel	indi
jete	ongit
et	37°11	lat

Tabla 15. Los tres mensajes encontrados en Los hijos del capitán Grant de Julio Verne.

Finalmente, el uso de la criptología en la novela Matías Sandorf (Verne 1987) nos parece más interesante por cuanto nos permite hablar de un célebre matemático, Girolamo Cardano (1501-1576) y del coronel austriaco Edouard Fleissner von Wostrowitz (1825-1888). En este caso no se trata de un mensaje que se haya cifrado mediante el método de Vigenère, sino de una sustitución monoalfabética a la que le faltan palabras que hay que suponer y en las que se dispone como pista el hecho de que se ha escrito en diferentes idiomas, como si el lector tuviera que emprender una aventura como la de Champollion ante la piedra Rosetta (salvando las distancias, claro está).

Antes de presentar el método empleado por Julio Verne en su novela, comentaremos la idea original en la que se basa el método de von Wostrowitz y que se debe a Cardano. Cardano es especialmente conocido por publicar las fórmulas que permiten resolver una ecuación cúbica o de tercer grado, mediante operaciones algebraicas. No obstante, lo incluimos aquí por haber diseñado la rejilla que lleva su nombre. Se trata de una especie de tarjeta perforada que, situada sobre un texto, permite leer ciertas partes del mismo, de modo que el mensaje cifrado se diluye dentro del resto del mensaje.

Esta	carta	que	me	escribiste
ayer	por	la	noche,	no
puedo	admitirla	y,	en	vano,
para	verte,	debo	matar	veinte
siglos	esperando	horas	y	horas

Tabla 16. Mensaje aparentemente inocente.

Tabla 17. Rejilla de Cardano.

Esta	carta	que	me	escribiste
ayer	por	la	noche,	no
puedo	admitirla	y,	en	vano,
para	verte,	debo	matar	veinte
siglos	esperando	horas	y	horas

Tabla 18. Lectura de un mensaje secreto con la rejilla de Cardano.

Como hemos dicho, basándose en la rejilla de Cardano, von Wostrowitz ideó un método de trasposición, conocido como rejilla giratoria. En este caso, se trata de una rejilla cuadrada de 6×6 celdas, de modo que se perforan nueve celdas y que permite tanto cifrar mensajes de treinta y seis letras como descifrarlos. Para que el método funcione correctamente, las posiciones de las celdas perforadas deben ser tales que cuando se gire la rejilla noventa grados tres veces en el mismo sentido (en general en el de las agujas del reloj), nunca deberán coincidir en la misma posición dos celdas perforadas.

Para cifrar las treinta y seis letras del texto claro (si la longitud es menor, se puede hacer uso de nulos y si es mayor, bastará con repetir el proceso las veces que sea preciso) se colocará la rejilla en su posición inicial (que deberá señalarse de alguna manera, por ejemplo, con una marca en la parte superior izquierda) y se escribirán las nueve primeras letras, ordenadas, en las nueve casillas perforadas. A continuación, se gira la rejilla noventa grados y se vuelven a escribir las siguientes nueve letras. El proceso se repite hasta completar el cifrado del mensaje. Para descifrar el mensaje, bastará con proceder de forma inversa.

Hemos comentado que las posiciones de las celdas perforadas de la rejilla no pueden ser cualesquiera, dado que han de distribuirse a lo largo de las filas y columnas de modo que las posiciones que ocupan no coincidan con las de otras celdas perforadas cuando la rejilla se gira noventa, ciento ochenta y doscientos setenta grados. Este diseño no es fácil, pero tampoco es demasiado complicado. En particular, podrían diseñarse rejillas de 4×4 (con cuatro celdas perforadas), 8×8 (dieciséis celdas perforadas), etcétera, pero no de tamaño 5×5 o 7×7, puesto que, en estos últimos casos, al haber un número impar de celdas, habría una celda central que, si se perfora, lo estaría en todos los giros y si no se perfora, nunca podría usarse para cifrar o descifrar letras.

A modo de ejemplo, la Tabla 19 muestra una rejilla de 6×6 celdas que verifica esta propiedad, análoga a la empleada por Julio Verne en la novela Matías Sandord.

Tabla 19. Ejemplo de rejilla de tamaño 6×6.

En el caso de que el mensaje a cifrar con esta rejilla fuera «JULIO VERNE FUE EL AUTOR DE MATÍAS SANDORF», como tiene treinta y cinco letras, añadiríamos al final una más, por ejemplo, una «X», y procederíamos como se ha indicado. Así, las primeras nueve letras que escribiríamos serían las que se muestran en la tabla 17.

J				U
A	L		I
O					V
		E
R			N

Tabla 20. Cifrado de las primeras nueve letras del texto claro.

Repitiendo el proceso como se ha indicado, el texto cifrado, fruto de la trasposición con esta rejilla, sería el que mostramos en la Tabla 21.

j	e	s	f	u	u
s	l	o	i	e	r
o	a	e	d	n	v
e	l	e	d	a	m
r	o	a	n	i	u
r	i	f	t	x	a

Tabla 21. Texto cifrado con la rejilla diseñada anteriormente.

Conviene señalar que tanto el emisor del mensaje como su receptor deberán tener la misma rejilla y compartirla en secreto. Finalmente, recomendamos al lector que lleve a cabo este proceso con el mensaje de la novela de Julio Verne para practicar con este método.

Un último ejemplo de presencia de la criptografía en una novela es la aventura de Sherlock Holmes, de Arthur Conan Doyle, titulada El misterio de los bailarines (Doyle 2013), en ocasiones publicada como Los hombres danzantes. En esta aventura, el señor Cubitt pide ayuda a Holmes porque su esposa está muy asustada desde que recibió unos papeles en los que se muestran unos muñecos que bailan o danzan, como los que se muestran en la Figura 16.

Figura 16. Hombres danzando de El misterio de los bailarines de Doyle (ASC).

En su investigación, Holmes se plantea la hipótesis de que se trate de un cifrado monoalfabético de modo que los muñecos se corresponden con letras que ocultan un mensaje. En el proceso deductivo que lleva a cabo, observa que hay bailarines idénticos, pero, en ocasiones, uno de ellos porta una bandera, por lo que una de sus primeras conclusiones es que tal hecho significa que dicho bailarín marca el final de una palabra o frase. Dejamos al lector que disfrute de la novela y no le destripamos más aspectos de los procesos deductivos del detective.

LAS GUERRAS MODERNAS

Qué duda cabe de que las situaciones bélicas son las que más han repercutido en el desarrollo de los métodos criptológicos, pues en ellas no se trata de ocultar información entre amantes o en aventuras, sino que el descifrado de un código puede acarrear consecuencias catastróficas, como es la pérdida de vidas humanas. Dado que son innumerables los casos que se pueden mencionar, comentaremos solo algunos de ellos, en especial los más importantes acaecidos durante el siglo XX. El lector interesado puede consultar alguno de los libros que citamos en las referencias para ampliar este tipo de información.

Las guerras del siglo XX se caracterizaron, entre otras cosas, por el progreso espectacular del armamento bélico y por el desarrollo de nuevos métodos de cifrado. En particular, en la segunda mitad del siglo, con el uso de máquinas cifradoras mecánicas y electromecánicas, hasta la aparición del ordenador. En el capítulo 4 trataremos este tipo de máquinas de cifrado, por lo que aquí nos vamos a limitar a comentar algunos hechos y situaciones que consideramos dignos de destacar.

Probablemente, uno de los episodios más llamativos y que pone de manifiesto la gran importancia que tiene no sólo descifrar la información del enemigo, sino también el cómo y con quién se gestiona dicho conocimiento, es el caso del telegrama Zimmermann. De modo resumido, la historia de este telegrama es la siguiente.

El llamado «telegrama Zimmermann» fue una comunicación secreta enviada en enero de 1917 por el Ministerio de Asuntos Exteriores alemán (el Secretario de Relaciones Exteriores alemán era Arthur Zimmermann, de ahí el nombre con el que ha pasado a la historia el telegrama) al embajador alemán en Washington D. C., en el que se ofertaba una alianza militar entre Alemania y México. El telegrama lo envió un diplomático alemán desde la embajada americana en Berlín, vía Copenhague y luego, por cable submarino, a la embajada alemana en Estados Unidos, pasando por Gran Bretaña, donde se interceptó.

La conocida como «Room 40», a la sazón una unidad de la Inteligencia Naval Británica, lo descifró parcialmente. El sistema de cifrado empleado por los alemanes, descifrado por los ingleses, se conocía como 0075, de modo que los ingleses pudieron hacerse una idea de su contenido. El mensaje, que debía enviarse desde Washington a Ciudad de México, proponía al gobierno mexicano una alianza con la causa alemana para lanzar un ataque militar contra los Estados Unidos, en caso de que estos entraran en la Primera Guerra Mundial, a cambio de ayuda financiera y militar para que México recuperara Texas, Arizona y Nuevo México.

El gobierno británico deseaba dar a conocer al gobierno estadounidense el contenido del telegrama y aprovechar esta situación para que los Estados Unidos se unieran a la guerra e inclinaran la balanza hacia el lado aliado. Sin embargo, se enfrentaba a un grave dilema. Por un lado, si daba a conocer el contenido del telegrama, pondría de manifiesto que los ingleses también espiaban las comunicaciones diplomáticas estadounidenses, además cabía la posibilidad de que el espionaje alemán acabara conociendo que su sistema de cifrado ya no era seguro, por lo que sería sustituido de inmediato, provocando un claro perjuicio a los británicos. Por el contrario, si no se lo daban a conocer, perderían la oportunidad de que los Estados Unidos se unieran al bando aliado.

Los británicos contaban con que la embajada alemana en Washington D. C. enviaría el mensaje contenido en el telegrama a su embajada en Ciudad de México, posiblemente mediante el sistema telegráfico estándar, de hecho, se envió por medio de la Western Union, para evitar las posibles sospechas americanas, dado que ambos países no estaban enfrentados. Los agentes británicos consiguieron una copia del telegrama en la oficina de telégrafos de Ciudad de México y la suerte los acompañó pues este estaba cifrado con un sistema viejo que los ingleses podían descifrar completamente (véase Figura 17).

Figura 17. Telegrama Zimmermann enviado desde Washington D. C. a Ciudad de México (NATIONAL ARCHIVES AND RECORDS ADMINISTRATION).

De este modo, los ingleses obtuvieron dos ventajas adicionales a la hora de revelar el telegrama Zimmermann a los estadounidenses: podían alegar que lo habían obtenido mediante sus agentes en México (sin usar las líneas telegráficas americanas) y no les importaba compartir con estos que habían descifrado un antiguo sistema de cifrado alemán y, a la vez, mantener en secreto que podían descifrar parcialmente el sistema 0075, mucho más nuevo y seguro. El caso del telegrama Zimmermann pone de manifiesto la gran importancia del trabajo de los criptoanalistas.

Otra situación dramática, también durante la Primera Guerra Mundial, fue no haber preparado o no disponer de equipos de criptógrafos lo suficientemente preparados como para poner en marcha un sistema de cifrado eficiente y seguro. La invasión de Prusia oriental por parte de los rusos contra el ejército alemán es un claro ejemplo de esto. El ejército ruso, en su rápido avance, no tuvo tiempo de entregar a sus tropas de vanguardia los libros de códigos imprescindibles para cifrar los mensajes, por lo que las transmisiones se hacían en claro a través de la radio, que, claro está, también escuchaban los alemanes, por lo que eran conocedores de los movimientos de tropas y planes de batalla del ejército ruso. La consecuencia de esto fue la derrota rusa en la batalla de Tannenberg (1914), por lo que de forma inmediata los rusos comenzaron a cifrar sus mensajes. No obstante, dicha solución no fue suficiente dado que el ejército alemán, con una estructura criptológica mucho mejor preparada, fue capaz de descifrar los mensajes rusos hasta el final de la guerra.

Esta falta de preparación rusa no terminó con la Gran Guerra. En efecto, en 1920, la ya Unión Soviética se lanzó a la conquista de Polonia, con la convicción de que su ejército era mucho más potente y que la guerra terminaría pronto. Sin embargo, Polonia tenía un excelente servicio de criptoanálisis en su Oficina de Cifrado. Destacamos este hecho porque allí trabajaban Waclaw Sierpinski (1882-1969) y su alumno Stefan Mazurkiewicz (1888-1945), ambos excelentes y reputados matemáticos. El primero de ellos es conocido, sobre todo, por las curvas fractales que llevan su nombre y el segundo por el Teorema de Hahn-Mazurkiewicz acerca de curvas que rellenan el espacio. Hoy en día, se considera que la intervención de ambos en el descifrado de los mensajes rusos influyó decisivamente para que los polacos vencieran en la batalla de Varsovia (también conocida como el «Milagro del Vístula»).

Por otra parte, uno de los sistemas de cifrado más conocidos de todos los empleados en la Primera Guerra Mundial se conoció entre los aliados como ADFGX y posteriormente modificado como ADFGVX. Su fama no se debe a su especial diseño sino al proceso de criptoanálisis logrado por los franceses.

Al margen de los avatares de la guerra (en los que no entraremos en detalle), el ejército alemán, justo antes de la gran ofensiva de 1918, tenía claro que sus sistemas de cifrado no eran demasiado secretos para los enemigos, por lo que decidieron emplear un nuevo método que les reportara ventajas. El método lo diseñó el coronel Fritz Nebel (1891-1977) y consistía en una sustitución seguida de una trasposición, denominado originalmente como «Cifrado de los radiotelegrafistas 18» (Geheimschrift der Funker 18).

El método consistía en una cuadrícula de 5×5, como la que se muestra en la tabla de Polibio, pero con dos diferencias: la primera es que las veinticinco letras se distribuían al azar, o acordadas entre emisor y receptor mediante una clave compartida, y en lugar de emplear números en la parte externa de la tabla, se escribían las letras ADFGX, como se muestra en la tabla ADFGX. En este caso, vamos a seguir la notación contraria a la que es habitual cuando se presenta este método, dado que hemos acordado que, a lo largo de este libro, los textos claros los escribiremos con letras mayúsculas y los cifrados con letras minúsculas y en cursiva. De ahí que las letras exteriores las escribamos en minúsculas y en cursiva. La razón de que Nebel eligiera las letras ADFGX se debe a que son muy diferentes en su codificación con el alfabeto Morse, lo que evitaba, en gran medida, los errores a la hora de transmitir los mensajes por telégrafo.

	a	d	f	g	x
a	O	L	D	R	G
d	Z	E	A	C	S
f	F	M	X	Q	P
g	V	B	U	H	K
x	Y	N	I/J	T	W

Tabla 22. Ejemplo de tabla de sustitución para el cifrado ADFGX.

Una vez elaborada la cuadrícula, el mensaje se cifraba como en el caso de Polibio, pero ahora cada letra del texto claro se convertía en dos letras del texto cifrado. Así, si el mensaje es: «EL ATAQUE SERÁ A LAS CUATRO HORAS», el cifrado mediante esta sustitución daría lugar, letra por letra, a: «dd ad df xg df fg gf dd dx dd ag df df ad df dx dg gf df xg ag aa gg aa ag df dx». Después de la sustitución, Nebel propuso hacer una trasposición regida por una clave, acordada por las dos partes. En el caso de que esta fuera, por ejemplo, «FRITZNEBL», la trasposición se llevaba a cabo escribiendo esta clave como primera fila de una nueva cuadrícula y debajo, en las filas siguientes, se escriben todas las letras del primer cifrado, de modo que se tendría la distribución mostrada en la Tabla 23. Si el número de letras no completa la cuadrícula, las celdas vacías se completan con letras al azar.

F	R	I	T	Z	N	E	B	L
d	d	a	d	d	f	x	g	d
f	f	g	g	f	d	d	d	x
d	d	a	g	d	f	d	f	a
d	d	f	d	x	d	g	g	f
d	f	x	g	a	g	a	a	g
g	a	a	a	g	d	f	d	x

Tabla 23. Distribución del primer cifrado ADFGX por sustitución.

Finalmente, el texto cifrado definitivo se obtenía al recolocar las columnas según el orden alfabético de la clave elegida, esto es, EFKNRU, y volver a escribir las letras de la sustitución como corresponda según esta nueva ordenación (véase la Tabla 24), separándolas en grupos del tamaño que convenga.

B	E	F	I	L	N	R	T	Z
g	x	d	a	d	f	d	d	d
d	d	f	g	x	d	f	g	f
f	d	d	a	a	f	d	g	d
g	g	d	f	f	d	d	d	x
a	a	d	x	g	g	f	g	a
d	f	g	a	x	d	a	a	g

Tabla 24. Distribución del segundo cifrado ADFGX por trasposición.

Este proceso proporciona, usando el ejemplo anterior, el siguiente texto cifrado: gxdad fdddd dfgxd fgffd daafd gdggd ffddd xaadx ggfga dfgax daag.

Esta forma de cifrado resultó, inicialmente, imposible de descifrar para el ejército francés, hasta que entró en escena Georges Jean Painvin (1886-1980), profesor de Paleontología, quien logró descifrarlo. Debe tenerse en cuenta que, para mayor complicación, los alemanes habían aprendido la lección de errores pasados y cambiaban la clave todos los días.

Como ya mencionamos anteriormente, nos parece más interesante destacar el proceso seguido por Painvin para romper el cifrado ADFGX que el de su diseño, que, al fin y a la postre, era una sustitución seguida de una trasposición. Parece que su perseverancia por intentar romper este cifrado le llevó a perder, en el proceso, quince kilos. Veamos el método que siguió Painvin para descifrar este sistema de cifrado que parecía indescifrable.

En primer lugar, el hecho de que todos los mensajes estuvieran formados por solo cinco letras daba pie a pensar que se trataba de un cifrado de tipo Polibio, es decir, de una sustitución. Pero tenía que haber algo más porque el ataque por los métodos conocidos contra las sustituciones no daba resultado. Así pues, lo lógico era pensar que después de la sustitución hubiera una trasposición. Al margen del trabajo continuo y perseverante de Painvin, también la suerte acompaña a veces a las mentes preparadas, y en este caso, sucedió que el mismo día, el criptoanalista francés recibió dos mensajes con muchas similitudes. Parece lógico pensar que la similitud entre dos mensajes no podía deberse al azar sino más bien a que ambos mensajes eran muy parecidos. Con esta idea en mente, Painvin estudió la posición de las coincidencias y dedujo cuál sería el número de columnas en la trasposición, esto es, la longitud de la segunda clave. A continuación escribió los mensajes en columnas, lo que le permitió aplicar el análisis de frecuencias de las parejas de letras, dado que se trataba de una sustitución monoalfabética, y obtener el texto claro. A partir de entonces, y conocedores del método de cifrado, los franceses pudieron descifrar un gran número de los mensajes secretos alemanes.

Sin embargo, más adelante, las cosas se volvieron a complicar porque los alemanes cambiaron de nuevo el sistema de cifrado y pasaron del ADFGX al ADFGVX, es decir, añadieron una letra y, por tanto, pasaron a una cuadrícula de 6×6 celdas, lo que les permitía utilizar treinta y seis símbolos. Painvin notó, evidentemente, el cambio y supuso que el sistema seguiría siendo el mismo con la diferencia de que el paso de veinticinco a treinta y seis celdas solo consistiría en añadir una letra del alfabeto y los diez dígitos.

Esta aparente complicación resultó en perjuicio de los alemanes porque a partir del cambio de método, sus mensajes comenzaban por la dirección del remitente, escrito con todas las letras, por lo que tales encabezamientos eran solo ligeramente diferentes de unos mensajes a otros (la que puede haber entre la 1ª división de infantería y la 5ª división de infantería se reduce a una palabra), y en muchas ocasiones, además, el contenido del mensaje era el mismo. Todo ello se traducía en que muchos mensajes solo diferían en unas pocas letras, por lo que la permutación utilizada en la trasposición era fácilmente recuperable y con ello el texto cifrado.

Como ya hemos visto, uno de los problemas más serios a la hora de llevar a cabo el proceso de cifrado, cualquiera que sea este, es el de elegir una clave adecuada, de modo que no sea fácilmente deducible por el adversario. Este problema nos va a permitir tratar uno de los temas más importantes en la criptografía: el del uso de claves aleatorias. Parece que el primer criptólogo que se lo planteó fue el comandante Joseph Oswald Mauborgne (1881-1971), jefe de la investigación criptográfica del ejército de Estados Unidos. De hecho, Mauborgne introdujo el concepto de la clave aleatoria, esto es, una clave que estaría formada por una colección de letras o palabras irreconocibles, mezcladas al azar y propuso su uso como parte del cifrado de Vigenère, para dotarlo de un nivel de seguridad mucho mayor. De forma más precisa, su propuesta consistía en elaborar dos cuadernos iguales, uno para el emisor y otro para el receptor, cada uno de ellos con muchas páginas que contenían una extensa colección de letras escritas al azar. Una vez elaborados los cuadernos, se cifraría un mensaje con el método de Vigenère utilizando como clave todas las letras de una de las páginas. El receptor, con el mismo cuaderno, podría descifrar, sin problema, el texto cifrado recibido, de modo que, una vez finalizado el proceso, la página utilizada se destruiría, esto es, la clave solo se usaría una vez. Este método se denomina «cuaderno de uso único» (en inglés se conoce como one time pad). Claramente este método de cifrado es resistente a todos los ataques que hemos mencionado hasta ahora, incluso al ataque que consistiera en probar todas las posibles claves, esto es, al ataque por fuerza bruta. Si este ataque fuera factible, los mensajes sin sentido se podrían eliminar porque corresponderían a claves incorrectas, pero además de recuperar el mensaje original, el atacante también recuperaría otros muchos textos que tendrían sentido y no podría saber cuál de ellos sería el correcto.

La cuestión es, entonces, por qué no se emplea este método. Lo cierto es que casi nunca se ha usado porque aun siendo teóricamente perfecto, tiene sus fallos. Por ejemplo, en la práctica es casi imposible crear tales cantidades de claves aleatorias y un ejército puede generar en un solo día cientos de mensajes, largos o cortos, en cuyo caso, los expertos en cifra deberían disponer de ingentes cantidades de cuadernos de un solo uso, dado que deberían compartir uno diferente con cada uno de los posibles destinatarios, lo que conlleva un problema de distribución.

Así pues, el cuaderno de uso único es solo factible en aquellos entornos en los que la comunicación entre las dos partes debe ser extremadamente segura y, además, que pueden soportar su creación y mantenimiento, como fue el caso de los presidentes John Fitzgerald Kennedy (1917-1963) de Estados Unidos y Nikita Serguéyevich Jrushchov Khrushchev (1894-1971) de la Unión Soviética. En realidad, el llamado «teléfono rojo» era una línea directa de fax entre ambos dignatarios cuyo sistema de cifrado se basaba en el cuaderno de uso único con mensajes escritos en código binario, esto es, empleando solo ceros y unos. Para establecer la clave de uso único, cada país generaba su propia clave de modo que la clave compartida que se empleaba luego era la suma, bit a bit, de ambas. Las claves de cada país se transportaban por valija diplomática y se destruían después de cada uso.

Volviendo a la parte teórica del cuaderno de uso único, conviene destacar a dos expertos en la Teoría de la Información: Gilbert Sandorf Vernam (1890-1960) y Claude Elwood Shannon (1916-2001). Al primero se le debe el conocido como «cifrado de Vernam»: es un sistema de cifrado que requiere de una clave aleatoria tan larga como el propio mensaje y de un solo uso. De forma más precisa, el mensaje a cifrar se codifica en base binaria, es decir, como una colección de ceros y unos. Por otra parte, se genera una clave, también en binario, que sea completamente aleatoria y que se comparte con el receptor del mensaje. A continuación, se suman los bits del texto claro con los de la clave, bit a bit, y se destruye la clave. A modo de ejemplo, en la primera fila de la tabla Vernam se muestra el texto claro, «Unico», en la segunda su codificación en binario, en la tercera la clave aleatoria y en la última el correspondiente texto cifrado.

U								n								i								c								o
0	1	0	1	0	1	0	1	0	1	1	0	1	1	1	0	0	1	1	0	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	0	1	1	1	1
1	1	0	0	1	0	1	0	1	1	0	0	0	1	1	0	0	0	1	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	1	1	0	0	1	0
1	0	0	1	1	1	1	1	1	0	1	0	1	0	0	0	0	1	0	1	1	0	1	1	1	0	1	0	0	1	0	1	1	0	0	1	1	1	0	1

Tabla 25. Ejemplo de cifrado de Vernam de la palabra «Unico».

Shannon, al desarrollar la Teoría de la Información, demostró que este cifrado es matemáticamente seguro, es decir, que, si se utiliza tal y como se ha definido, resulta indescifrable. Tal afirmación se puede comprender fácilmente, dado que, si el texto claro se cifra con una clave realmente aleatoria, el texto cifrado también se convierte en aleatorio. Ahora bien, es fundamental que la clave sea de uso único, aleatoria y tan larga como el mensaje. El hecho de que la prueba de la indescifrabilidad del cifrado de Vernam sea un teorema matemático con unas hipótesis muy restrictivas supone que, si las mismas no se cumplen, entonces el teorema ya no es aplicable. Esta es la diferencia entre la teoría y la práctica, ya que, aunque en teoría, ambas son iguales, en la práctica no sucede así. De hecho, el método es apenas aplicable en la práctica porque no hay forma de que las hipótesis del teorema se cumplan para un cifrado de Vernam que se emplee de forma asidua.

En esta línea, un caso curioso fue el de la cifra empleada por Ernesto «Che» Guevara (1928-1967), el revolucionario cubano. Una vez terminada la revolución en Cuba, el «Che» intentó repetirla en Bolivia, donde lo capturaron y ejecutaron. Entre sus pertenencias se encontró la descripción del sistema de cifrado que empleaba para comunicarse con Fidel Alejandro Castro Ruiz (1926- 2016). El método comenzaba con una sustitución simple de letras por números de una o dos cifras, tal y como ya hemos visto en varias ocasiones. Esta sustitución, en concreto, se muestra en la Tabla 26. Además, había dos indicadores: el símbolo «/» (73) señalaba que se procedía al cambio de letras a números; mientras que el símbolo «\» (77) indicaba el cambio contrario, es decir, de números a letras.

	8	2	0	6	4	9	1	3	7	5
	e	s	t	a	d	o	y
3	b	c	f	g	h	i	j	.	;	,
7	k	l	m	n	ñ	p	q	/	\
5	r	u	v	w	x	z

Tabla 26. Sustitución simple empleada por el Che en sus comunicaciones con Fidel Castro.

Después de hacer esta sustitución, las cifras se agrupaban de cinco en cinco y a cada una de ellas se le sumaba una serie de números aleatorios, que pueden verse en la Figura 18. Dado que los mensajes eran fundamentalmente tácticos, eran muy cortos, por lo que la longitud de la clave era la misma que la del mensaje, pero no era de uso único, incumpliendo así una de las hipótesis necesarias para que el teorema de Shannon se verificara.

Figura 18. Tabla de números aleatorios usada por el Che para comunicarse con Fidel Castro (CASLab).

En algunas ocasiones se ha dicho que la Primera Guerra Mundial fue la guerra de los químicos, porque, por primera vez, se utilizaron el gas mostaza y el cloro como armas contra el enemigo. De la Segunda Guerra Mundial se ha dicho que fue la guerra de los físicos, porque se lanzó la bomba atómica. En esta ocasión, nos apuntamos a los que han afirmado que también fue la guerra de los matemáticos y de las máquinas de cifrado porque los primeros han sido, en gran parte, los responsables del gran desarrollo de los sistemas de cifrado que se utilizaron para proteger, sobre todo, la información militar; mientras que el desarrollo y expansión de las máquinas de cifrado, dio lugar a máquinas como la Enigma alemana o la Purple (Púrpura) japonesa.

También hemos comentado anteriormente que la robustez de un sistema de cifrado no depende solo de la complejidad de su diseño para evitar ser vulnerado, sino también y, en gran medida, de cómo usan dicho sistema los especialistas de cifra o personal encargado del cifrado y descifrado. Una adecuada preparación y formación de los mismos es indispensable para que las cosas funcionen como es debido. Un ejemplo de esta importancia lo muestra el conocido como código JN-25B empleado para las comunicaciones de mando y control principal utilizado por la Armada Imperial Japonesa durante la guerra del Pacífico, en la Segunda Guerra Mundial.

El nombre de JN-25B se lo asignaron los americanos por la expresión Japanese Navy (Armada Japonesa). El JN-25B no utilizaba una máquina de cifrado, como la que se emplearía luego para el código Purple, sino que era un método manual en uso durante la Primera Guerra Mundial. Este sistema, como todos los sistemas japoneses de cifrado que se conocen, estaba compuesto por tres documentos: un libro de códigos, que contenía alrededor de cuarenta y cinco mil palabras o expresiones, que tenían asignados números de cinco cifras (véase Figura 19), y dos libros, cada uno de los cuales constaba de unos cincuenta mil números, también de cinco cifras, que se empleaban para llevar a cabo un supercifrado. Cada uno de ellos se usaba como una tabla sumatoria formada por números colocados en filas y columnas y también identificados con números. Para incrementar la seguridad del sistema, esas tablas se reemplazaban cada seis meses. Si en alguna ocasión hacía falta utilizar una palabra que no estuviera contenida en el libro de códigos, por ejemplo, el nombre de un militar o de un lugar, se escribía en kana (silabario japonés), usando de nuevo un número de cinco dígitos.

Figura 19. Extracto del libro de códigos del JN-25B (HERVÉ LEHNING).

Para cifrar un mensaje con este método, el emisor codificaba el texto claro haciendo uso del libro de códigos (o del silabario kana), de modo que cada palabra se sustituía por la colección correspondiente de números de cinco cifras. A continuación, elegía al azar uno de los dos libros de tablas sumatorias y tantos números de cinco cifras consecutivos como grupos de números hubiera dado lugar el texto claro. Luego se sumaban los grupos de números, dos a dos, pero sin acarreo, esto es, sin considerar las «llevadas» que pudieran producirse en cada una de las sumas parciales, lo que permite sumar tanto de derecha a izquierda como de izquierda a derecha. La colección de grupos de cinco números obtenida con tales sumas constituía el texto cifrado. A la hora de transmitir el texto cifrado, se incluían las referencias al libro de supercifrado empleado y la posición del primer grupo de números elegido del mismo.

A modo de ejemplo mostramos este proceso en la Tabla 27, de modo que la codificación del mensaje corresponde a la primera fila, la colección de grupos a sumar a la segunda y el texto cifrado a la tercera.

Texto codificado	76153	98450	12643	21472
Grupos a sumar	55842	65214	21145	89745
Texto cifrado	21995	53664	33788	00117

Texto codificado	38455	99578	66524	62587
Grupos a sumar	52457	25458	55633	33654
Texto cifrado	80802	14926	11157	95131

Tabla 27. Ejemplo de proceso de cifrado con el código JN-25B.

Una vez conocidas las referencias adecuadas y el texto cifrado, el descifrado se llevaba a cabo siguiendo el proceso inverso al del cifrado, esto es, restando de cada grupo de cinco números del mensaje cifrado los correspondientes grupos del libro de supercifrado, también sin considerar el acarreo necesario para proceder a la resta, como se muestra en la Tabla 25, y de la misma forma se puede realizar la resta tanto de derecha a izquierda como de izquierda a derecha.

Texto cifrado	21995	53664	33788	00117
Grupos a restar	55842	65214	21145	89745
Texto decodificado	76153	98450	12643	21472

Texto cifrado	80802	14926	11157	95131
Grupos a restar	52457	25458	55633	33654
Texto decodificado	38455	99578	66524	62587

Tabla 28. Ejemplo de proceso de descifrado con el código JN-25B.

Cuando antes nos referíamos a una adecuada formación de los especialistas en cifra lo hacíamos porque si bien este sistema de cifrado podría haber sido indescifrable, los operadores cometieron el error (humano) de empezar siempre con el mismo número de supercifrado, lo que supone que transformaban el cifrado anterior en un clásico libro de códigos.

Que el ejército americano fuera capaz de descifrar el código JN-25B resultó trascendental para el desarrollo de la Guerra del Pacífico pues influyó decisivamente tanto en la batalla del mar del Coral como en la de Midway. Otro hecho, también determinante en el desarrollo de esta guerra, fue que los criptoanalistas estadounidenses lograron descifrar un mensaje en el que se indicaba el itinerario que seguiría el almirante Isoruku Yamamoto (1884-1943), a la sazón comandante en jefe de la flota japonesa, en una visita a las islas Salomón. El almirante norteamericano Chester William Nimitz (1885-1966) decidió enviar varios aviones de caza para interceptar y derribar el avión donde viajaría Yamamoto, cosa que logró, en parte por la obsesiva puntualidad del japonés.

Una de las ideas que se ha utilizado a lo largo de la historia en varias ocasiones, y sobre todo en las grandes guerras del siglo pasado, con diferente resultado, es la de transmitir información utilizando un idioma poco extendido. Probablemente el método más conocido es el de los indios navajos en la Segunda Guerra Mundial. De hecho, hay un día nacional en EE. UU. dedicado a los mensajeros de código navajo, el 14 de agosto, e incluso se hizo una película titulada Windtalkers, dirigida por John Woo y protagonizada por Nicolas Cage y Christian Slater (en la Figura 20 se puede ver el monumento dedicado a los indios navajos que participaron en la Segunda Guerra Mundial).

Figura 20. Monumento a los indios navajos, en Ocala, Florida (MLPEARC).

Ya en la antigüedad, Julio César utilizó el griego para algunas de sus comunicaciones secretas; los ingleses emplearon el latín en la guerra de los Bóers (1880-1881) y el ejército francés usó a los bretones durante la guerra de Indochina. En la guerra de los Bóers esta estrategia tuvo nefastas consecuencias porque no solo había muy pocos oficiales británicos que supieran latín, sino porque sus enemigos tenían personal que sí que lo conocía. También los norteamericanos utilizaron como operadores de radio en el norte de Francia, durante la Primera Guerra Mundial, a los indios nativos choctaw, originarios de los estados de Oklahoma y Alabama. Estas comunicaciones jamás fueron descifradas por el ejército alemán; sin embargo, el principal inconveniente del idioma de los choctaw, llamado muskogi, es que no tenía palabras que pudieran representar al armamento y otros términos utilizados en la guerra.

La idea de utilizar el idioma de los navajos parece que surgió con motivo de una visita de representantes de este pueblo indio al presidente Theodore Roosevelt (1858-1919). Durante la misma, cuando los navajos hablaban entre sí, el presidente no entendía absolutamente nada y pensó que podría utilizarse como método para las comunicaciones; bastaba con tener a un navajo en cada uno de los extremos de la misma. El sistema, llamado «código navajo», se puso en práctica en la Guerra del Pacífico y los japoneses nunca pudieron descifrarlo.

A la hora de ponerlo en marcha, los indios navajos tenían que seguir un proceso de aprendizaje para memorizar el código que permitía relacionar palabras de su idioma con términos usados en la guerra y en entornos militares, de ese modo se evitaba tenerlas escritas y que pudieran caer en las manos del enemigo. Así, a modo de ejemplo, un tanque era una «tortuga», un torpedo era un «marisco», un avión de caza era un «colibrí» o un avión bombardero era un «halcón comepollos». El código lo formaban doscientas setenta y cuatro palabras, pero como este número no era suficiente para codificar todos los posibles términos, se elaboró otro código que asignaba a cada letra del alfabeto una palabra en inglés y esta se correspondía con otra palabra en navajo, obteniendo así una especie de nomenclátor. Esto permitía transmitir nombres de personas, ciudades o ríos, por ejemplo. Así, el emperador de Japón, «HIROHITO» (1901-1989) se cifró en navajo como: Lin Tkin Gah Ne-ash-jsh Lin Tkin Tfian-zie Ne-ash-jsh, siguiendo la equivalencia mostrada a continuación:

Letra	Palabra	Traducción	Navajo
H	Horse	Caballo	Lin
I	Ice	Hielo	Tkin
R	Rabitt	Conejo	Gah
O	Owl	Búho	Ne-ash-jsh
H	Horse	Caballo	Lin
I	Ice	Hielo	Tkin
T	Turkey	Pavo	Tfian-zie
O	Owl	Búho	Ne-ash-jsh

Tabla 29. Algunos términos navajos de su nomenclátor.

¹ Otros libros de interés donde se incluyen aspectos históricos de la criptología se encuentran citados en la bibliografía: Bauer 2007; Hernández 2016; Lehning 2021; Sgarro 1990; Singh 2000.

34	35	13	12	13	43	51	44	31	13	55	13	43	31	44	45	13
13	31	21	15	43	45	13	22	13	31	21	15	43	45	13	22	13
47	66	34	27	56	88	64	66	44	44	76	28	86	76	57	67	26

5	3	‡	†	3	0	5	)	)	6	*	4	8	2	6	)	4	‡	.	)	‡	)	;	8	0	6
*	;	4	8	‡	8	¶	6	0	)	)	8	5	;	1	‡	(	;	:	‡	*	8	†	8	3	(
8	8	)	5	*	†	;	4	6	(	;	8	8	*	9	6	*	?	;	8	)	‡	(	;	4	8
5	)	;	5	*	†	2	:	*	‡	(	;	4	9	5	6	*	2	(	5	*	–	4	)	8	¶
8	*	;	4	0	6	9	2	8	5	)	;	)	6	†	8	)	4	‡	‡	;	1	(	‡	9	4
8	0	1	;	8	:	8	‡	1	;	4	8	†	8	5	;	4	)	4	8	5	†	5	2	8	8
0	6	*	8	1	(	‡	9	;	4	8	;	(	8	8	;	4	(	‡	?	3	4	;	4	8	)
4	‡	;	1	6	1	;	:	1	8	8	;	‡	?	;

F	R	I	T	Z	N	E	B	L
d	d	a	d	d	f	x	g	d
f	f	g	g	f	d	d	d	x
d	d	a	g	d	f	d	f	a
d	d	f	d	x	d	g	g	f
d	f	x	g	a	g	a	a	g
g	a	a	a	g	d	f	d	x

B	E	F	I	L	N	R	T	Z
g	x	d	a	d	f	d	d	d
d	d	f	g	x	d	f	g	f
f	d	d	a	a	f	d	g	d
g	g	d	f	f	d	d	d	x
a	a	d	x	g	g	f	g	a
d	f	g	a	x	d	a	a	g

U								n								i								c								o
0	1	0	1	0	1	0	1	0	1	1	0	1	1	1	0	0	1	1	0	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	0	1	1	1	1
1	1	0	0	1	0	1	0	1	1	0	0	0	1	1	0	0	0	1	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	1	1	0	0	1	0
1	0	0	1	1	1	1	1	1	0	1	0	1	0	0	0	0	1	0	1	1	0	1	1	1	0	1	0	0	1	0	1	1	0	0	1	1	1	0	1

34	35	13	12	13	43	51	44	31	13	55	13	43	31	44	45	13
13	31	21	15	43	45	13	22	13	31	21	15	43	45	13	22	13
47	66	34	27	56	88	64	66	44	44	76	28	86	76	57	67	26

5	3	‡	†	3	0	5	)	)	6	*	4	8	2	6	)	4	‡	.	)	‡	)	;	8	0	6
*	;	4	8	‡	8	¶	6	0	)	)	8	5	;	1	‡	(	;	:	‡	*	8	†	8	3	(
8	8	)	5	*	†	;	4	6	(	;	8	8	*	9	6	*	?	;	8	)	‡	(	;	4	8
5	)	;	5	*	†	2	:	*	‡	(	;	4	9	5	6	*	2	(	5	*	–	4	)	8	¶
8	*	;	4	0	6	9	2	8	5	)	;	)	6	†	8	)	4	‡	‡	;	1	(	‡	9	4
8	0	1	;	8	:	8	‡	1	;	4	8	†	8	5	;	4	)	4	8	5	†	5	2	8	8
0	6	*	8	1	(	‡	9	;	4	8	;	(	8	8	;	4	(	‡	?	3	4	;	4	8	)
4	‡	;	1	6	1	;	:	1	8	8	;	‡	?	;

F	R	I	T	Z	N	E	B	L
d	d	a	d	d	f	x	g	d
f	f	g	g	f	d	d	d	x
d	d	a	g	d	f	d	f	a
d	d	f	d	x	d	g	g	f
d	f	x	g	a	g	a	a	g
g	a	a	a	g	d	f	d	x

B	E	F	I	L	N	R	T	Z
g	x	d	a	d	f	d	d	d
d	d	f	g	x	d	f	g	f
f	d	d	a	a	f	d	g	d
g	g	d	f	f	d	d	d	x
a	a	d	x	g	g	f	g	a
d	f	g	a	x	d	a	a	g

U								n								i								c								o
0	1	0	1	0	1	0	1	0	1	1	0	1	1	1	0	0	1	1	0	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	0	1	1	1	1
1	1	0	0	1	0	1	0	1	1	0	0	0	1	1	0	0	0	1	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	1	1	0	0	1	0
1	0	0	1	1	1	1	1	1	0	1	0	1	0	0	0	0	1	0	1	1	0	1	1	1	0	1	0	0	1	0	1	1	0	0	1	1	1	0	1

34	35	13	12	13	43	51	44	31	13	55	13	43	31	44	45	13
13	31	21	15	43	45	13	22	13	31	21	15	43	45	13	22	13
47	66	34	27	56	88	64	66	44	44	76	28	86	76	57	67	26

5	3	‡	†	3	0	5	)	)	6	*	4	8	2	6	)	4	‡	.	)	‡	)	;	8	0	6
*	;	4	8	‡	8	¶	6	0	)	)	8	5	;	1	‡	(	;	:	‡	*	8	†	8	3	(
8	8	)	5	*	†	;	4	6	(	;	8	8	*	9	6	*	?	;	8	)	‡	(	;	4	8
5	)	;	5	*	†	2	:	*	‡	(	;	4	9	5	6	*	2	(	5	*	–	4	)	8	¶
8	*	;	4	0	6	9	2	8	5	)	;	)	6	†	8	)	4	‡	‡	;	1	(	‡	9	4
8	0	1	;	8	:	8	‡	1	;	4	8	†	8	5	;	4	)	4	8	5	†	5	2	8	8
0	6	*	8	1	(	‡	9	;	4	8	;	(	8	8	;	4	(	‡	?	3	4	;	4	8	)
4	‡	;	1	6	1	;	:	1	8	8	;	‡	?	;

F	R	I	T	Z	N	E	B	L
d	d	a	d	d	f	x	g	d
f	f	g	g	f	d	d	d	x
d	d	a	g	d	f	d	f	a
d	d	f	d	x	d	g	g	f
d	f	x	g	a	g	a	a	g
g	a	a	a	g	d	f	d	x

B	E	F	I	L	N	R	T	Z
g	x	d	a	d	f	d	d	d
d	d	f	g	x	d	f	g	f
f	d	d	a	a	f	d	g	d
g	g	d	f	f	d	d	d	x
a	a	d	x	g	g	f	g	a
d	f	g	a	x	d	a	a	g

U								n								i								c								o
0	1	0	1	0	1	0	1	0	1	1	0	1	1	1	0	0	1	1	0	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	0	1	1	1	1
1	1	0	0	1	0	1	0	1	1	0	0	0	1	1	0	0	0	1	1	0	0	1	0	1	1	0	0	0	1	1	0	1	1	1	1	0	0	1	0
1	0	0	1	1	1	1	1	1	0	1	0	1	0	0	0	0	1	0	1	1	0	1	1	1	0	1	0	0	1	0	1	1	0	0	1	1	1	0	1