Capítulo 2.
Las redes que nos acercan
Cuando llegué a Galicia allá por el año 1999, era común que, al pasear por el campo con los perros, alguien amigablemente me preguntara: e logo, ¿ti de quen vés sendo?25. Mi interlocutor en realidad quería saber a qué «grupo social primario» pertenecía. Un grupo social es un conjunto de individuos que desarrollan roles e interacciones sociales de un tipo determinado en una sociedad. En particular, nuestro grupo social primario está constituido por nuestro círculo más íntimo, tal como la familia, con el que tenemos mayor interacción y cooperación. Aunque mi interlocutor estaba interesado en saber a qué familia pertenecía, por lo general de la pregunta, cualquiera podría responder a la misma mencionando: la peña deportiva a la que «pertenece», o el nombre del partido político al que está afiliado o con quien simpatiza, o que es miembro del grupo de graduados de cierta carrera, o mencionar el nombre de la tribu urbana con cuyo estilo se identifica, o que forma parte de los que toman café todos los días en el bar de la esquina, etc. En definitiva, podría enumerar todos los subconjuntos a los que «pertenece», que tengan una forma y estructura fácilmente identificables y que sean relativamente duraderos. Dentro de cada uno de estos grupos sociales, las personas actúan de acuerdo con las normas, valores y objetivos que sean necesarios para el buen funcionamiento del grupo social, así como para lograr sus fines. Por eso es importante a veces saber de quen vés sendo.
Por tanto, podemos considerar que un grupo social está formado por un conjunto de individuos dentro de la sociedad que tienen un tipo de interacción entre ellos que los diferencian del resto de individuos, con quienes pueden tener otros tipos de interacciones. Por ejemplo, en la Figura 12 se ilustra un conjunto de individuos dibujados en negro quienes tienen un tipo de relación marcada con conexiones grises más gruesas. Aunque forman parte de la sociedad en general, este grupo se diferencia del resto de individuos, representados en gris, por la existencia de la relación antes mencionada. Notemos que los miembros del grupo pueden tener otros tipos de relaciones con el resto de los individuos, pero, o este tipo de relación es diferente, o no es tan fuerte como la que define al grupo. Por tanto, si obviamos todas aquellas interacciones que no definen al grupo como unidad social tendremos una red formada por un conjunto de individuos y sus relaciones de un tipo determinado. A esta red la llamaremos una red social.
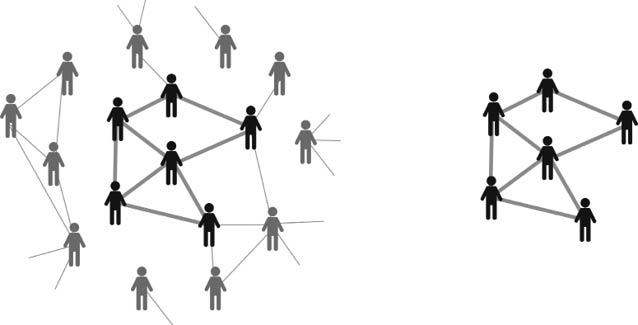
Figura 12. Esquema de lo que sería una red social de amistad/familia imbuida en la red de la sociedad como un todo (izquierda), así como la abstracción de dicha red (derecha) de su entorno.
Las redes sociales pueden ser de diferentes tipos. En general, podríamos centrarnos en aquellas en las que los nodos representan a individuos, aunque también lo podríamos extender a grupos de diversos tipos y tamaños. Si nos ceñimos a las redes entre individuos, entonces la característica diferenciante de las mismas será el tipo de relación que se establezca entre estos. Lo más sencillo es comenzar con una red en la que los nodos son individuos, y las aristas representan sus relaciones de amistad. Un ejemplo de este tipo de redes sociales es la formada por 31 médicos que participaron en un famoso estudio, conocido como el Estudio de Medicamentos de la Universidad de Columbia [23], donde se investigó la difusión de la prescripción de un nuevo medicamento (el antibiótico tetraciclina) entre los médicos. A los médicos, quienes debían prescribir el nuevo medicamento, se les pidió que nombraran a tres médicos que consideraran amigos personales. Por tanto, los médicos conforman los nodos, y sus relaciones de amistad, las aristas de esta red social. A esta red la denominaremos «Galesburgo-amistad», debido al hecho de que los médicos vivían en la ciudad de Galesburgo, en el condado de Knox, en el estado estadounidense de Illinois.
A los mismos 31 médicos se les pidió que nombraran a tres médicos con los que elegirían discutir asuntos de trabajo. Esta información permite establecer una nueva red social, en la que los nodos son los mismos que en la anterior, pero las aristas no representan relaciones de amistad sino de asesoramiento técnico. A esta red la llamaremos «Galesburgo-asesoramiento».
Otro tipo de relación social es la que se establece, por ejemplo, entre los adolescentes, entre los cuales es bastante común estar junto con los «colegas», aunque estos no sean a quienes ellos llaman propiamente sus «amigos». Por tanto, hay veces que es más conveniente preguntar, por ejemplo: «¿Hay chicos en este curso que anden juntos muy frecuentemente?». Esta fue justamente la pregunta que Killeya-Jones y colaboradores [24] hicieron a los chicos del séptimo curso de varias escuelas del centro-norte de Carolina del Norte en los EE. UU. Los chicos «nominaban» a los que consideraban que andaban frecuentemente juntos, de modo que los autores del estudio establecieron una red de 156 miembros de entre 12 y 15 años, de los cuales el 51% eran chicas. Como resultado, esta red social está constituida por 156 adolescentes y sus relaciones sociales. A esta red la denominaremos simplemente «Adolescentes».
Otro tipo de red social es la que se crea cuando los individuos que conforman los nodos de la red «pertenecen» a una organización dada. Un ejemplo es la formada por los directores de las 625 mayores empresas de los EE. UU., seleccionadas de la lista Fortune 1000 en 1999 y que informaron de la composición de sus consejos de administración. Esta red que denominaremos «Corporación» fue estudiada por Gerald F. Davis, de la Universidad de Michigan en el año 2003 [25], y en ella los nodos representan a los directivos de dichas empresas, mientras que las aristas representan el hecho de que dos directivos estén en el comité de dirección de la misma empresa.
Un ejemplo bien diferente de red social de «pertenencia» a una organización es la que forman los miembros de una red criminal, tal como una banda. Giles Oatley y Tom Crick de la Universidad de Cardiff en el Reino Unido estudiaron las redes formadas por los miembros de cuatro bandas criminales en el área de Mánchester, Reino Unido, y que denominaremos «Bandas» [26]. La información sobre la pertenencia a dichas bandas fue propiciada sobre la base del trabajo de campo, así como de inteligencia de la policía local. Los nodos representan a los miembros de las bandas y las aristas representan algún tipo de relación relacionada con el crimen, de tipo familiar, de amistad o de otro tipo entre los miembros de las bandas.
Finalmente, me referiré a las redes de colaboración científica. En estas redes los nodos representan a científicos que han publicado algún trabajo en conjunto. Por tanto, las aristas de la red representarán el hecho de que dos científicos hayan colaborado en la consecución de un resultado que haya sido publicado en la literatura científica. A estas redes sociales las denominaremos «Colaboración» [27] [28].
Cuando una persona está buscando patrones comunes entre objetos, ya sean datos numéricos, objetos cotidianos o personas, está haciendo, de forma intuitiva y quizás subconsciente, matemáticas. El objetivo de las matemáticas es siempre encontrar patrones de regularidad entre los objetos de su estudio. Así pues, si queremos estudiar las redes sociales desde un punto de vista matemático, lo primero que deberíamos hacer es definir algunos patrones que se puedan encontrar con gran frecuencia en las redes sociales de diferentes tipos. Pero ¿qué buscar? Pensemos en cómo se podrían haber formado estas redes, ya que de estos mecanismos de formación se podrían desprender algunas características de las redes.
Pensemos por un momento en nuestra red de amistades y conocidos: aquellas redes que hemos creado, por ejemplo, en la escuela donde estudiamos, o en el centro de trabajo donde desempeñamos nuestras labores, o en cualquier otra institución donde nos relacionamos y socializamos con otros. Lo primero que veremos es que, si en esta red hay, por ejemplo, 50 individuos (contándonos a nosotros mismos), cada uno de nosotros no tendremos relaciones de amistad con todos los otros 49 miembros de ésta. Lo mismo, obviamente, les sucederá a los otros miembros de la red. O sea, que en la red no estarán presentes todas las conexiones posibles entre todos los pares de individuos26. Dicho en términos de la red, nuestra red social no será una red completa. La determinación del número total de aristas en esta red completa surge de combinar el número de sus miembros en pares. La rama de las matemáticas que estudia dichas combinaciones se denomina «Combinatoria»27. El término procede de la obra Ars Combinatoria escrita por Ramón Llull, filósofo, poeta, místico, teólogo y misionero nacido en Mallorca en 1235 [29], y que influyó grandemente en el pensamiento matemático posterior a su época.
Una segunda característica que seguramente podemos observar en nuestra red social es que no todos sus miembros tenemos el mismo número de conexiones. Habrá un pequeño número de miembros con muy pocas relaciones, que son aquellos más tímidos e introvertidos, mientras que siempre habrá alguien más popular con un mayor número de relaciones. Sin embargo, la mayoría tendremos más o menos el mismo número de relaciones en la red.
¿Cómo es posible que nuestra red se haya formado para tener estas características? Para responder a esta pregunta tendríamos que interiorizar en los detalles de cómo se formaron cada una de nuestras redes sociales, lo cual quizás ni nosotros mismos seamos capaces de recordar. Por tanto, haremos uso de lo que denominamos un modelo. Un modelo no es más que una abstracción de la realidad que usamos para reproducir algunos aspectos de la misma de forma que podamos controlar su funcionamiento para poderlo entender. Para hacerlo lo menos aburrido posible, el primero de nuestros modelos consistirá: ¡en una fiesta!
Supón que has recibido una invitación para una fiesta. En la invitación se indica el lugar y la hora exacta a la que deberías llegar. El organizador de la fiesta ha cursado dicha invitación a un número dado de personas, a sabiendas de que todas ellas son mutuamente desconocidas entre sí. O sea, vas a asistir a una fiesta en la que todas las otras personas son desconocidas para ti, y lo mismo le pasará al resto. Así que a la hora exacta de la reunión estarán todos los participantes sin ninguna conexión entre sí. Aunque no lo parezca, esto es también una red. Se conoce como red trivial porque no contiene ninguna arista entre sus nodos. En la fiesta habrá música, bebidas y canapés. Lo más normal es que dentro de unos instantes te acerques a alguien y te presentes. En este mismo instante se habrá formado una primera conexión en la red.
Este proceso, mediante el cual unos individuos se van presentando a otros y estableciendo conversaciones entre ellos, avanzará a medida que avanza la fiesta. Por tanto, al cabo de un tiempo podemos observar que el número de conexiones entre participantes ha aumentado. En una red como la formada a partir de las conexiones de los individuos asistentes a una fiesta como la que estamos considerando aquí, las aristas se forman al azar. Para un observador ajeno a la fiesta, en un instante dado de tiempo se ha establecido una nueva arista entre dos nodos de forma completamente aleatoria. Por consiguiente, si quisiéramos «simular» el proceso que está ocurriendo en la fiesta usando lápiz y papel, podríamos proceder del siguiente modo.
Dibujamos en un papel un nodo por cada uno de los participantes en la fiesta. Para crear las aristas, procedemos de la siguiente manera. Primero, todos sabemos que hay fiestas en las que el ambiente no es muy propicio para entablar nuevas relaciones, mientras que hay otras que sí propician la búsqueda de dichos nuevos contactos. Por tanto, fijaremos un valor de «factibilidad» del ambiente de la fiesta para establecer relaciones sociales entre los individuos28, que tomará valores entre cero y uno, donde «cero» indica un ambiente no propiciador de nuevas relaciones y «uno» el mejor ambiente posible para entablar nuevas relaciones.
Ahora seleccionamos dos nodos de manera completamente al azar. Para saber si conectamos o no este par de nodos con una arista, generamos un número entre cero y uno de manera aleatoria. Por ejemplo, podemos lanzar una moneda al aire un número de veces, y contamos el número de veces que ha salido cara. La razón del número de veces que ha salido cara al número total de tiradas es un número aleatorio entre cero y uno. Este nuevo número nos indica la probabilidad de que las dos personas seleccionadas al azar se atrevan a «romper el hielo» y entablar una nueva relación29. Si esta probabilidad es menor o igual que la factibilidad de la fiesta, conectaremos a los dos individuos con una arista en la red.
Nótese que, si el ambiente de la fiesta es muy factible para establecer relaciones (factibilidad igual a uno), entonces la barrera que habría que vencer por parte de cualquier par de individuos sería siempre menor o igual a este valor, por lo que todos los participantes terminarían por formar un grupo en el que todos serían amigos de todos. Si por el contrario el ambiente fuera muy poco factible para establecer relaciones (factibilidad igual a cero), entonces, por muy baja que fuera la barrera para establecer una relación entre dos personas, no se entablarían nuevas relaciones, por lo que la fiesta terminaría como empezó; sin ninguna nueva relación.
Este modelo fue desarrollado, sin apelar a la idea de la fiesta, naturalmente, por los matemáticos húngaros Paul Erdős30 y Alfred Rényi, y se conoce como el modelo de Erdős-Rényi [30]. La imagen que tenemos de un matemático es la de un tipo solitario, casi ermitaño, que suele estar abstraído de la realidad e inmerso en su mundo de teoremas y fórmulas. Erdős cumplía muy bien con la segunda parte del estereotipo, pero para nada con la primera. Era un matemático muy sociable, matemáticamente hablando. Quiero decir que Erdős era capaz de colaborar con muchos, con muchísimos otros matemáticos. Tantos, que existe una red con todos aquellos matemáticos, más de 500, que publicaron un artículo con Erdős. Estos son los matemáticos que tienen un número de Erdős igual a uno. Aquellos que colaboraron con los coautores de Erdős tienen un número de Erdős igual a dos, y así sucesivamente31 [31]. Erdős nació en Budapest, Hungría, el 26 de marzo de 1913 y murió a los 83 años en Varsovia, Polonia, un 20 de septiembre. Fue uno de los matemáticos más prolíficos del siglo XX, llegó a publicar 1.525 artículos matemáticos, la mayoría de ellos con alguno de sus 511 colaboradores. Era bastante excéntrico, todas sus posesiones cabían en su maleta, llevaba una vida itinerante, viajando entre conferencias científicas, universidades y casas de colegas de todo el mundo para resolver o proponer problemas matemáticos. Los premios y otros ingresos que obtenía los donaba, generalmente a personas necesitadas, y a diversas causas benéficas, así como para pagar «premios» que daba a quien resolviera algunos de los problemas matemáticos que proponía (véase [32]). Hizo contribuciones de gran alcance en las áreas de la teoría de números y la teoría de grafos, siempre desde un enfoque de las matemáticas puras. El desarrollo de la teoría de Ramsey, el método probabilístico y la combinatoria extrema le deben su desarrollo actual a Erdős. Fue él quien descubrió la primera demostración elemental del teorema de los números primos, junto con Atle Selberg. Sin embargo, los desacuerdos acerca del papel de cada uno en la demostración llevaron a una amarga disputa entre ambos.
Según decía Alfred Rényi: «Un matemático es una máquina que bebe café y produce teoremas»32. Esta máxima era también cumplida por Erdős, quien dormía muy poco y, para mantenerse despierto, bebía ingentes cantidades de café. Rényi también nació en Budapest, el 20 de marzo de 1921, y falleció el 1 de febrero de 1970. Hizo importantes contribuciones en estadísticas, particularmente en la teoría de la probabilidad, aunque también contribuyó de forma significativa en combinatoria, teoría de grafos y teoría de números.
Volvamos al modelo de Erdős-Rényi. En la Figura 13 se ilustran tres ejemplos de redes de este tipo para diferentes valores de factibilidad, p. La primera red está muy fragmentada en pequeños grupos, de hecho, 25 nodos están completamente desconectados (aislados). En términos de la fiesta, esto significa que la mitad de los participantes se mantienen aislados y que no se ha formado ningún grupo significativo entre los asistentes. En el caso de la segunda red se observa la «semilla» de lo que puede constituir un grupo. En efecto, existe un componente conexo33 que agrupa a 13 de los 50 participantes en la fiesta. En este caso el número de asistentes que permanecen aislados es bastante menos de la mitad. En el último caso la red forma un único componente conexo. Aquí, a pesar de que la densidad34 de aristas de la red es relativamente baja, existen menos del 10% de las aristas que pueden existir; la red es conexa35.
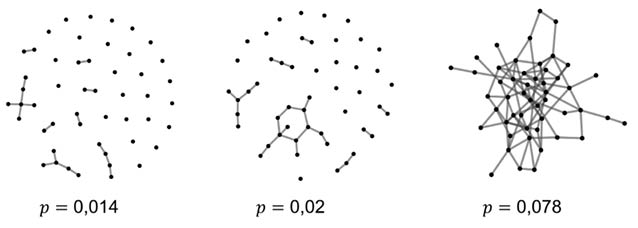
Figura 13. Ejemplo de tres instancias de la evolución de una red del tipo Erdős-Rényi con 50 nodos para diferentes «factibilidades».
Estas características de conectividad de las redes del tipo Erdős-Rényi fueron demostradas matemáticamente por los propios Erdős y Rényi en 1960 [30], quienes encontraron las condiciones para que la red sea conexa y que todos los participantes en la fiesta creen un grupo único y no varias facciones.
Por razones obvias, la mayoría de las redes sociales en el mundo real son conexas. Esto es particularmente así cuando nos referimos a un grupo en concreto. Lo que consideramos como nuestro grupo de relaciones es obviamente conexo, ya que, si alguien no está unido al grupo, no es miembro de nuestro círculo de relaciones. Pero, nuestra red social (como hemos visto al principio del Capítulo) no es una red completa y no todos sus miembros tienen el mismo grado, tal y como se puede reproducir a través del modelo de Erdős-Rényi. En el caso de las redes reales, se observan las mismas características. Por ejemplo, en el caso de las bandas criminales del área de Mánchester que analizaron Oatley y Crick, si no estás conectado a los miembros de la banda, no eres miembro de ésta y ya está. Sin embargo, en otros casos, las redes pueden contener varios componentes conexos, e incluso nodos aislados. Este es el caso, por ejemplo, de la red Adolescentes en la que existían 17 chicos aislados en el curso de otoño y 24 en el de primavera. Esto no es raro, ya que la red se creó preguntando a los chicos a quiénes veían juntos más frecuentemente. Por tanto, es posible que hayan reportado que veían a algunos chicos siempre solos. En el caso de la red Corporación también existe un componente gigante formado por 4.538 directivos de las empresas de un total de 5.311. En las redes de colaboración científica tampoco es raro encontrar varios componentes conexos. Lo que es realmente sorprendente es que los componentes gigantes de dichas redes incluyan a la mayoría de los científicos en un área dada. Por ejemplo, según los resultados de Mark Newman de la Universidad de Michigan, de los 1.520.251 autores de artículos en la base de datos Medline36, 1.407.752 forman un componente conexo de colaboración entre autores [28]. Esto es un 92.6% de todos los autores en las áreas de publicación relacionados con las ciencias médicas. Este porcentaje es también elevado para autores en otras áreas. Por ejemplo, en matemáticas37 es del 82% y en físicas38 del 85%.
Una característica común a todas estas redes sociales del mundo real es su baja densidad. Con la excepción de las redes Galesburgo-amistad y Galesburgo-asesoramiento, ambas con solo 31 nodos, que tienen densidades de 0,13 y 0,14, respectivamente, el resto tiene densidades por debajo del 10%. Por ejemplo: la red Adolescentes tiene una densidad de 6,6% en otoño y 5,7% en primavera; la de Corporación tiene una densidad (en su componente gigante) de solo 0.3%; mientras que las cuatro bandas criminales tienen densidades de 3,9%, 5,5%, 6,5% y 5,3%, respectivamente39. Las densidades de las redes de colaboración científica son incluso menores del 0.02%. O sea, que en general, las redes sociales son muy poco densas en términos de aristas. Es como si nos costara establecer muchas relaciones, o no las necesitásemos, ¿verdad?
Es que: «El mundo es un pañuelo»
Las dos características simples de las redes sociales que hemos visto antes pueden ser muy reveladoras. Primero, el hecho de que exista un componente gigante que agrupa a la mayoría de los nodos, nos indica que se puede pasar información paso-a-paso a través de la red entre prácticamente todos sus integrantes. La segunda, el hecho de que las densidades de aristas sean bajas, nos podría estar indicando que dicha comunicación quizás no requiera que todos estemos conectados con todos. Quizás exista una característica que nos facilite la comunicación entre los miembros de una red. Analicemos si este es el caso.
Pensemos, por ejemplo, que uno de los participantes en la fiesta, David, quiere darle una noticia a otro de los asistentes a la misma, Laura (véase la Figura 14). Pero David no tiene el número de Wasap de Laura. Obviamente, David solo posee el número de Wasap de aquellos con los que estableció amistad, pero no del resto. Una estrategia sería preguntar a sus contactos si estos tienen el Wasap de Laura, y si éstos no lo tienen, que les preguntasen a sus contactos y así sucesivamente. ¿Cuántos pasos de Wasap le llevaría a David contactar a Laura entre todos los asistentes? En una red conexa siempre existe un camino de longitud mínima entre cualquier par de nodos. Esta longitud, o distancia topológica40, corresponde al número de reenvíos que habría que hacer para mandar el recado de uno de estos nodos al otro41. Usemos un ejemplo más reducido que la red de la fiesta para ilustrar la situación. Para ello, consideraré la red de seis miembros que se muestra en la Figura 14.
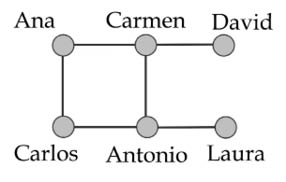
Figura 14. Ejemplo de una pequeña red social con seis personas y diferentes conexiones de amistad entre ellas.
Es obvio que David puede enviar un Wasap a Carmen directamente, pero para comunicarse con Ana, tendría que hacerlo en dos pasos: primero escribirle a Carmen y que Carmen le escriba a Ana. Si David quisiera comunicarse con Carlos, tendría que hacerlo en tres pasos: enviar un Wasap a Carmen, que Carmen le envíe otro a Ana y/o a Antonio y finalmente que Ana o/y Antonio le escriban a Carlos. Por tanto, decimos que la distancia entre David y Carmen es de uno (un solo Wasap basta para comunicarse), la de David y Ana es de dos, y la de David y Carlos es de tres (nótese que la distancia entre A y B es la misma que entre B y A). Las distancias entre todos los pares de personas en esta red se pueden representar a través de una tabla (la matriz de distancias topológicas):
|
David |
Carmen |
Ana |
Carlos |
Toni |
Laura |
|
|
David |
0 |
1 |
2 |
3 |
2 |
3 |
|
Carmen |
1 |
0 |
1 |
2 |
1 |
2 |
|
Ana |
2 |
1 |
0 |
1 |
2 |
3 |
|
Carlos |
3 |
2 |
1 |
0 |
1 |
2 |
|
Toni |
2 |
1 |
2 |
1 |
0 |
1 |
|
Laura |
3 |
2 |
3 |
2 |
1 |
0 |
Esta tabla se conoce como «matriz de distancia» de la red. Si promediamos las entradas de esta matriz, obtendremos un estimado de cuantos reenvíos harían falta en la misma para que un nodo cualquiera envíe una información a otro nodo de la red. En el caso que nos ocupa, este promedio es de 1,8 reenvíos. O sea, como promedio, a una persona de esta red le llevaría dos reenvíos de Wasap para comunicarse con otra persona. A esta medida, el promedio de las distancias entre todos los pares de nodos de una red se le conoce como «longitud media de caminos simples»42 de la red y la designamos por 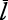 .
.
Pues bien, he aquí un descubrimiento de gran relevancia para nuestra vida. En una red del tipo Erdős-Rényi, la longitud media de caminos simples es del orden del logaritmo43 del número de nodos de la red. ¿Qué nos indica este resultado? Pues, que en la red de 50 nodos que se generó en la fiesta, el número de reenvíos de Wasap que una persona necesita como promedio para comunicarse con cualquier otra en la red es de aproximadamente 3,9. Si la red tuviese cinco mil nodos, la distancia promedio entre pares de nodos sería de solo 8,5 pasos. Incluso en una red con cinco millones de nodos esta distancia media sería de solo 15,4 reenvíos de Wasap. Si la población total de España formara una red de Wasap del tipo Erdős-Rényi nos llevaría solo aproximadamente 17,6 (menos de 18) reenvíos de Wasap para comunicarnos con cualquier ciudadano de este país. Y ya puestos, se necesitarían menos de 23 reenvíos para comunicarnos con cualquier ciudadano del mundo si todos los habitantes del planeta formáramos una red con la estructura de las redes de Erdős-Rényi. No cabe duda, ¡este mundo es un pañuelo!
El fenómeno antes descrito se conoce en la literatura científica como el efecto del «mundo pequeño» (small-world en inglés). No está de más advertir que estos números se refieren a los valores promedios y al supuesto de que las redes mencionadas tengan una estructura como las de Erdős-Rényi. Cabría aquí citar a Bernard Shaw e indicar que, si yo he comido un pollo y usted no ha comido ninguno, el promedio nos indica que «ambos hemos comido medio pollo». Por tanto, es obvio que habrá pares de nodos en una red Erdős-Rényi que para comunicarse necesitarán más reenvíos44 de Wasap que lo que 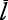 nos sugiere, al igual que habrá pares de nodos que necesitarán menos.
nos sugiere, al igual que habrá pares de nodos que necesitarán menos.
Esta característica de las redes Erdős-Rényi se observa claramente en las redes sociales del mundo real. Las redes de amistad y de asesoramiento entre los médicos de Galesburgo tienen longitud media de caminos simples (distancia media) de 2,80 y 2,26, respectivamente. Notemos que el logaritmo del número de nodos en esta red es 3,43. La red de adolescentes tiene distancia media de 3,6 (5,05), donde en paréntesis hemos escrito el logaritmo del número de nodos en la red. Para pasar información entre dos directivos de las empresas en la red Corporación, como media harían falta 4,33 (8,42) pasos. Las cuatro bandas criminales de Mánchester tienen distancias medias entre sus miembros de 3,37-4,11 (6,07-6,76). La red de colaboración científica en ciencias biomédicas tiene una distancia media entre científicos de solo 4,6 (14,15). Para transmitir una información desde un autor en físicas a otros nos llevaría 5,9 (10,71) pasos como promedio. Los matemáticos están un poco más distantes entre sí, y para pasar información de un matemático a otro nos llevaría como media 7,73 (12,24) pasos.
Así que, sin lugar a duda, las redes sociales son pequeños mundos, incluso podríamos decir que son mundos muy pequeños, dado sus tamaños. Como se puede observar, los valores de las distancias topológicas medias de las redes reales coinciden en el orden de magnitud con los de las redes de Erdős-Rényi del mismo tamaño y densidad de aristas. Por esta razón, el modelo de Erdős-Rényi es apropiado para reproducir esta propiedad del mundo real.
Para muchos, el concepto de la amistad es algo recíproco. Más que decir que «soy amigo de Tere» o que «Tere es mi amiga», decimos que «Tere y yo somos amigos». Esto implica una doble direccionalidad en la relación y por lo tanto también en las aristas de la red que representa estas relaciones. Esta doble direccionalidad no existe en todo tipo de redes. Está claro que en una ciudad hay calles con una sola dirección. En una comunicación a través del correo electrónico, puedo haber enviado un correo a Tere, pero no haber recibido ninguno de ella, por lo que habrá una dirección en la arista que nos conecta. Cuando la red incluye este tipo de direccionalidad, se dice que es una «red dirigida».
Mi sorpresa fue mayúscula cuando, al analizar algunas redes sociales de amistad por primera vez, vi que éstas eran dirigidas. ¿Cómo era posible? Recuerdo una red de amistad entre adolescentes en que el hecho de que A fuera amigo de B no implicaba que B lo fuera de A. La relación de amistad no parecía recíproca. Esto puede ocurrir por la forma en que se extraen los datos para crear dichas redes. Supongamos que preguntemos: ¿cuáles son tus tres mejores amigos? Es posible que, si nombro a Marta, Carlos y José, luego alguno de ellos no me tenga entre sus tres mejores amigos, lo que no indica que no tengamos una amistad recíproca. Esto es, por ejemplo, lo que ha sucedido en la red de amistad entre los médicos de Galesburgo, la cual fue creada justamente con una pregunta de este tipo. Las redes de amistad que considero aquí serán siempre bidireccionales, o como se dice en el argot de la teoría de redes, «no dirigidas».
En 1967, el psicólogo experimental Stanley Milgram condujo un experimento que cambió notablemente nuestra concepción del universo social [33]. Milgram es considerado como uno de los más influyentes psicólogos experimentales del siglo XX. Su experimento de psicología social publicado en 196345 con el título Estudio comportamental de la obediencia y resumido en su libro de 1974 Obediencia a la autoridad. Una perspectiva experimental46, le lanzaron a la fama tanto para bien como para mal. Pero el experimento de 1967 al que hago referencia aquí tenía como objetivo falsificar la hipótesis del mundo pequeño en la sociedad que hemos avanzado antes. O sea, ver si el hecho de que dos individuos seleccionados al azar en «el mundo» están relativamente cerca el uno del otro, socialmente hablando.
El experimento diseñado por Milgram fue muy ingenioso e innovador. Dicho experimento consistió en seleccionar aleatoriamente a individuos de dos ciudades de los EE. UU. A cada uno de los individuos se les daba un paquete con información acerca del propósito del experimento e instrucciones de a quién y cómo deberían enviar dicho paquete. El objetivo final del paquete era que llagara a una de las dos personas seleccionadas por Milgram como destinatarios finales. Ambos destinatarios finales residían en Boston, Massachusetts, a 2.100 km del origen del experimento (ver Figura 15). Entre los datos que se daban a los participantes estaban: el nombre de la persona destinataria, su dirección aproximada, su profesión, y demografía. Cada uno de los receptores del paquete, ya fueren los iniciales o cualquier eslabón de la cadena, debía registrar su nombre y enviar una tarjeta a Milgram. El paquete podía ser entregado únicamente a alguien a quien el participante conociera en una relación personal de tú a tú.
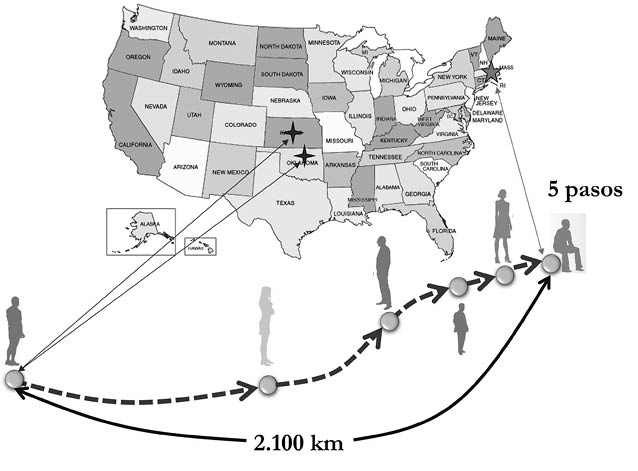
Figura 15. Resumen esquemático del experimento de Milgram del año 1967. El mapa ubica las ciudades donde se eligieron los participantes en el experimento, así como el destino final de las cartas y la separación en kilómetros entre ellas.
Podríamos ponernos en la piel de un participante fácilmente. Si conocemos al destinatario final, el trabajo será fácil: le enviamos el paquete y ya está. Si no lo conociéramos, entonces deberíamos pensar un poco. Podríamos pensar «geográficamente» y enviar el paquete a algún conocido nuestro que resida en la misma zona donde vive el destinatario final. También podríamos pensar acerca de la profesión de este. Si el destinatario fuera «médico» o «artista» o «maestro» podríamos enviar el paquete a alguien que conociéramos en dicha profesión, ya que quizás se conozcan de algún evento en que hayan participado o incluso haber estudiado juntos. Finalmente, podríamos pensar en los datos demográficos que nos han dado. Si el destinatario pertenece a una etnia o a alguna minoría, podríamos enviar el paquete a algún conocido de la misma etnia o minoría.
Como Milgram iba recibiendo los datos de cada eslabón de la cadena podía fácilmente contabilizar la longitud de éstas. Los resultados de Milgram fueron muy interesantes. Según los mismos, la longitud promedio de la cadena de conexiones fluctuaba entre las 5,5 y las 6 personas (véase el panel izquierdo de la Figura 16). O sea, solo 6 pasos eran necesarios para conectar a dos personas elegidas al azar entre los doscientos millones de habitantes que vivían en los EE. UU. en 1967. ¡Esto sí que es un pequeño mundo! Había nacido el mito de los «seis grados de separación».
Figura 16. Reproducción de los resultados del experimento de Milgram. A la izquierda el histograma y a la derecha una indicación de la transitividad de las relaciones indicada por el propio Milgram en su artículo de 1967 [33].
¿Significa este resultado que la distancia topológica promedio en la población de los EE. UU. es de seis? Esta identificación entre el resultado de Milgram y el concepto de la teoría de redes que hemos analizado aquí con anterioridad se puede leer en algunos textos sobre redes. Sin embargo, la misma es totalmente errónea. Vayamos por partes. Lo primero que debemos tener en cuenta es que, de las 296 personas seleccionadas para el estudio, el histograma solo reporta los resultados de 44 cadenas. O sea, que los resultados de la media de seis grados de separación se basan en el 15% de las posibles cadenas incluidas en el estudio. ¿Qué pasó con los otros paquetes? Pues que muchos de los participantes abandonaron el experimento. Es probable que una gran parte de los que abandonaron el experimento se encontraran entre los individuos socialmente más alejados del destinatario final, por lo que el completamiento de sus cadenas hubiera alargado considerablemente la media de Milgram. El propio Milgram analiza una posible causa de este abandono; lo llama la «endogamia» de las relaciones y se ilustra en el panel derecho de la Figura 16. O sea, pasaba muchas veces que John enviaba el paquete a Mary, Mary se lo enviaba a Tom, pero como Tom conocía también a John, se lo enviaba a este. Así que después de varios círculos en los que John recibía de vuelta el paquete, este se aburría del experimento y lo abandonaba. Por otra parte, es imposible identificar esta media obtenida por Milgram con la distancia topológica entre los individuos, porque los participantes no tenían un mapa de la red social de los EE. UU. Por tanto, en muchas ocasiones no estarían enviando el paquete a través del camino más corto, algo que ellos desconocían, sino incluso a través de un camino mucho más largo que el que los separaba del destinatario.
Aun así, el experimento de Milgram nos aporta la intrigante cuestión de que la distancia social entre dos individuos en el mundo no sea muy grande. Además, el tema «descubierto» por Milgram acerca de la endogamia de las relaciones sociales es en extremo atractivo e importante, como veremos a continuación.
El amigo de mi amigo es mi amigo
¿Qué significa el hallazgo de Milgram en relación con la «endogamia social»? Es mejor llamar a este fenómeno transitividad social. La transitividad la podemos entender desde el punto de vista de las relaciones entre tres personas. Si Ana y Carmen son amigas y Carmen es también amiga de Toni, existen muchas posibilidades de que Ana y Toni terminen siendo amigos. Podemos pensar, por ejemplo, que Carmen sale frecuentemente con Ana y que también lo hace con Toni. Por ello, existen muchas posibilidades de que coincidan los tres y que por tanto Carmen termine presentando a Ana y a Toni. Por otra parte, Carmen es amiga de Ana y de Toni porque comparte con estos varios gustos, valores, jobis, etc. Es de esperar entonces que dichos valores, gustos y hobbies sean también comunes a Ana y Toni, lo que los acercaría a establecer una amistad.
Si Carmen, Ana y Toni tienen una relación transitiva, esto se evidenciará en la red por la formación de un triángulo entre ellos. Podríamos pensar entonces que contando el número de triángulos en los que una persona participa en la red nos daría una idea de su nivel de transitividad. Pero comparemos los dos casos siguientes (Figura 17):
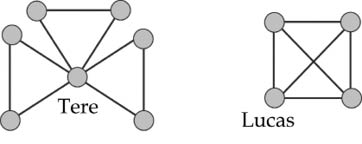
Figura 17. Ilustración de las diferencias en el grado de transitividad de las relaciones para dos individuos en sus respectivas redes. Aunque Tere (izquierda) y Lucas (derecha) tienen el mismo número de relaciones, las de Lucas están más interconectadas entre sí, indicando una mayor transitividad para estas relaciones con respecto a las de Tere.
Tanto Tere como Lucas participan en tres triángulos en sus respectivas redes. Sin embargo, mientras que todos los amigos de Lucas son amigos entre sí, los amigos de Tere en dos triángulos diferentes no tienen relación entre ellos. Por tanto, la transitividad se debe cuantificar contando el número de triángulos que se podrían formar a partir de todas las triadas en que un nodo participa. Lucas participa en tres triadas y todas ellas han dado lugar a triángulos, por lo que su transitividad es la máxima posible. Por otro lado, Tere participa en 15 triadas, de las cuales solo tres han dado lugar a triángulos, por lo que su transitividad es muy baja.
Esta idea de cuantificar el grado de transitividad de un nodo i en una red no es muy antigua, sino que vio la luz a finales del siglo XX. En 1998, Duncan Watts y Steven Strogatz publicaron un artículo seminal [34] (véase la próxima sección) en el que propusieron cuantificar el grado de transitividad de un nodo en la red como el índice Ci que divide el número de triángulos en los que participa el nodo i entre el número total de triadas en las que i es su centro47.
Este índice de transitividad de un nodo se puede calcular para todos los nodos de la red y luego calcular su promedio 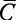 ,48 como una medida de cuán transitiva es la red como un todo. El índice de transitividad de un nodo toma valores entre cero y uno, como se puede observar en el siguiente ejemplo (Figura 18):
,48 como una medida de cuán transitiva es la red como un todo. El índice de transitividad de un nodo toma valores entre cero y uno, como se puede observar en el siguiente ejemplo (Figura 18):
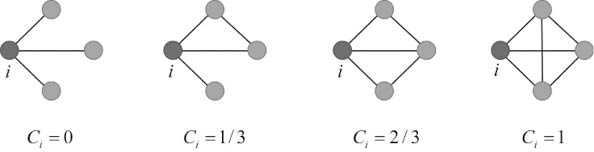
Figura 18. Valores del índice de transitividad de Watts-Strogatz para el nodo marcado.
Pensemos en la transitividad de un nodo de la siguiente manera. Si el nodo i es muy egoísta, entonces no presentará a sus amigos entre sí, quizás por el temor a que la amistad entre ellos se haga más fuerte que la que mantiene con los mismos. Este es el caso donde la transitividad es cero. En la medida en que el nodo es menos egoísta y confía más en sí mismo, presentará más a sus amigos entre sí, dando lugar a valores más altos de la transitividad, la cual será máxima cuando el nodo sea lo menos egoísta posible y presente a todos sus amigos entre sí.
Por otra parte, la transitividad promedio de cada red se ilustra en la Figura 19:
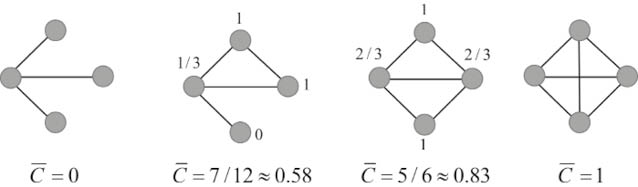
Figura 19. Valores de la transitividad media de Watts-Strogatz para las redes de cuatro nodos y diferentes patrones de conectividad.
Las redes del tipo Erdős-Rényi tienen transitividad promedio iguales a su densidad. O sea, para que una red Erdős-Rényi tenga una transitividad promedio relativamente alta debería tener una alta densidad de conexiones. Sin embargo, como hemos visto anteriormente, las redes sociales del mundo real tienen densidades muy bajas, por lo que si éstas hubiesen sido generadas por procesos del tipo Erdős-Rényi, deberían tener transitividades muy, muy bajas.
No obstante, si preguntase ahora a qué debería parecerse más la transitividad de una red social que se haya formado bajo los principios de que «el amigo de mi amigo es también mi amigo», creo que no habría dudas en responder que a aquellas más a la derecha de la Figura 19, o sea, a redes con altas transitividades promedio.
De hecho, las redes sociales del mundo real tienen transitividades relativamente altas. Las redes de amistad y de asesoramiento entre los médicos de Galesburgo tienen transitividades de 0,279 y 0,352, respectivamente. Estos valores contrastan con las transitividades de las redes del mismo tamaño y densidad generadas por el modelo de Erdős-Rényi, que son 0,136 y 0,144, respectivamente. En el caso de las redes de adolescentes, la transitividad es de entre 0,16 y 0,18 (otoño y primavera, respectivamente), en contraste con sus análogos de Erdős-Rényi, que tienen transitividades de 0,07 y 0,06, respectivamente. Mucha mayor diferencia se observa en la red que forman los directivos de las mayores corporaciones de los EE. UU., que tienen transitividad media de 0,87, versus 0,003 de la red aleatoria. Las cuatro bandas criminales tienen transitividades entre 0,12 y 0,19, mientras que sus homólogas del tipo Erdős-Rényi tienen transitividades casi 30 veces inferiores, de entre 0,004 y 0,0065. Finalmente, la red de colaboración en el área de biomedicina tiene una transitividad de 0,066, que, aunque baja, es mil veces superior a lo esperado para una red análoga creada con el modelo de Erdős-Rényi. En el caso de la red de colaboración en física, la transitividad es bastante elevada, de 0,43, que es 4.000 veces superior a la de la red de tipo Erdős-Rényi con igual número de nodos y aristas. La red de colaboración entre matemáticos muestra una transitividad de 0,15, que supera en más de diez mil veces a la esperada para una red de su tipo creada por el modelo de Erdős-Rényi.
Los datos aportados en el párrafo anterior nos ilustran una realidad obvia. Las redes sociales del mundo real no parecen, al menos en términos de sus transitividades, que se hallan formado por un mecanismo semejante al de la fiesta aleatoria que hemos descrito en este capítulo. En otras palabras, el modelo de Erdős-Rényi no es capaz por sí solo de reproducir todas las características que se presentan en las redes sociales del mundo real. Para comenzar a solucionarlo, ¡vayamos a otra fiesta!
Esta vez, la invitación a la fiesta indica que ocuparás un lugar determinado en un círculo, junto a los otros invitados. La invitación también indica que podrás establecer relaciones con un número dado de participantes que sean tus vecinos más cercanos en el círculo. La mitad a cada lado de tu asiento49.
Imaginemos que hemos llegado a la fiesta y formado parte del círculo. Siguiendo las indicaciones que especificaban de que podíamos entablar relaciones con 4 vecinos, hemos entablado conversación con las dos personas inmediatamente a nuestra derecha y con igual número a la izquierda. Como todos hemos recibido las mismas invitaciones, habremos creado una red como la que se muestra en la Figura 20.
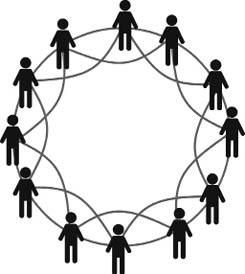
Figura 20. Ilustración de una red «circulante» formada por un grupo de individuos sentados alrededor de una mesa y que se pueden relacionar solo con sus primeros y segundos vecinos más cercanos.
Este tipo de redes se conoce como «circulantes» y tiene algunas características singulares. Por ejemplo, la transitividad media en estas redes es relativamente alta, de aproximadamente un 75% de la máxima posible. Esta característica concuerda con la que hemos encontrado antes en las redes sociales del mundo real. Sin embargo, en las redes «circulantes» la distancia promedio entre los individuos no es tan pequeña como en las redes del mundo real. O sea, no son «mundos pequeños», sino más bien mundos relativamente grandes. Esto es evidente, porque las personas que están sentadas en las antípodas una respecto a la otra están separadas por un número bastante grande de aristas.
Desde el punto de vista de la fiesta, también podemos considerar que estas redes son muy aburridas. Supongamos que a mi lado me ha tocado el típico «tostón» que solo habla de un tema tan alejado de mis intereses como el participante que está sentado frente a mí en la mesa. Así que, si revisamos la invitación, leeremos con alegría que podemos romper alguna de las relaciones con nuestros vecinos más cercanos y establecer alguna otra con otro participante de la fiesta. Esta «reconexión» de una de nuestras relaciones consistente en relocalizar una de nuestras aristas para conectarnos a un nodo seleccionado al azar. Es mostrada en la Figura 21.
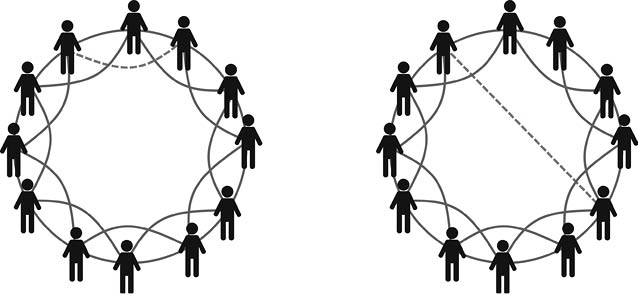
Figura 21. Evolución de la estructura de una red circulante al redireccionar una arista (marcada en línea discontinua) aleatoriamente entre dos nodos.
Como es de esperar, esta situación no solo nos ocurrirá a nosotros, sino que posiblemente también otros participantes reconecten algunas de sus conexiones originales. Así que, al cabo de un tiempo, podríamos tener una red diferente a la que encontramos al inicio de la fiesta.
Esta original idea fue propuesta en 1998 en un trabajo seminal publicado en la revista Nature por el matemático Steven Strogatz de la Universidad de Cornell en Nueva York, EE. UU., y su estudiante de doctorado Duncan Watts [34]. Watts y Strogatz se dieron cuenta de algo realmente sorprendente: si un pequeño porcentaje de los participantes reconecta alguna de sus relaciones originales en la red circulante, la transitividad de la red se mantiene prácticamente invariable. Pero, sorprendentemente, la distancia promedio entre los individuos cae abruptamente a valores parecidos a los que existen en una red del mundo real.
Para estudiar este efecto de manera sistemática, Watts y Strogatz propusieron crear una probabilidad de reconexión en la red. En términos de la fiesta, esta probabilidad indica que la media de los participantes haya caído entre «tostones» cuando se sentaron originalmente a la mesa. Por ejemplo, si la misma es cero, nadie se siente incómodo con los vecinos que le han tocado y no se establecerá ninguna reconexión en la red. Si, por el contrario, dicha probabilidad es uno, todo el mundo estará incómodo con sus vecinos, por lo que se realizará el 100% de las reconexiones posibles, tal y como se ilustra en la Figura 22.
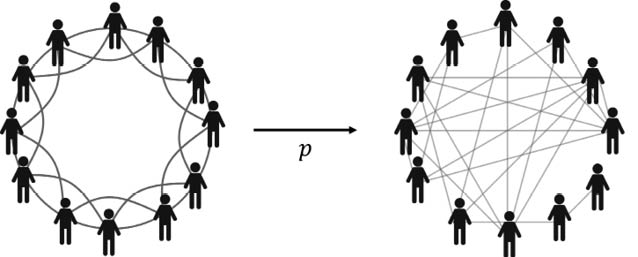
Figura 22. Punto de partida (izquierda) y de llegada (derecha) en la evolución de una red circulante por el redireccionamiento de sus aristas cuya selección se realiza de acuerdo con la probabilidad .
Está claro que, cuando todas las aristas se reconectan, obtenemos una red que es idéntica a la que se crearía si todas las conexiones se hubieran establecido completamente al azar. O sea, que en este caso estamos en presencia, una vez más, del modelo de Erdős-Rényi. Así que Watts y Strogatz graficaron los valores de la transitividad media 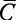 de los nodos y de las distancias medias entre todos los pares de nodos para diferentes valores de la probabilidad de reconexión. En la Figura 23 se ilustran los resultados de Watts y Strogatz, donde se han normalizado los valores de la transitividad media y de las distancias topológicas medias
de los nodos y de las distancias medias entre todos los pares de nodos para diferentes valores de la probabilidad de reconexión. En la Figura 23 se ilustran los resultados de Watts y Strogatz, donde se han normalizado los valores de la transitividad media y de las distancias topológicas medias 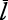 por los valores de estas medidas en las redes circulantes, y los he denotado como
por los valores de estas medidas en las redes circulantes, y los he denotado como 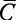 o y
o y 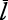 o, respectivamente.
o, respectivamente.
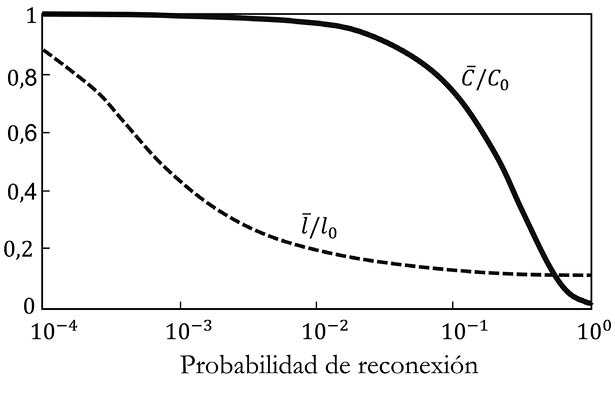
Figura 23. Reproducción de los resultados del modelo de Watts y Strogatz. En el eje horizontal se da la probabilidad de redireccionamiento de las aristas. En el eje vertical están los valores normalizados de la distancia topológica media 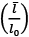 y del grado medio de transitividad
y del grado medio de transitividad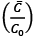 .
.
Como se puede observar en la Figura 23 existe una región relativamente amplia del gráfico en la que las redes tienen valores relativamente altos de la transitividad media y valores relativamente pequeños de la distancia topológica media. Las redes en esta región se conocen como redes de mundo pequeño, y en general se asemejan bastante a las redes del mundo real.
Veamos cuán bien o mal el modelo de Watts-Strogatz es capaz de reproducir las transitividades y distancias topológicas medias de las redes sociales del mundo real. Para ello, solo tenemos que construir el modelo de Watts-Strogatz con el mismo número de nodos y aristas que el de las redes reales. Los resultados revelan que las redes sociales del mundo real son semejantes a las redes de Watts-Strogatz para valores de la probabilidad entre cero y uno, casi siempre más cercanos a cero que a uno. Las redes circulantes (probabilidad de reconexión igual a cero), son redes «ordenadas» en las que no existe una heterogeneidad en el número de conexiones que tiene cada nodo: son redes en las que cada individuo interactúa con exactamente el mismo número que otros individuos. Por otra parte, las redes Erdős-Rényi, (probabilidad de reconexión igual a uno), son redes completamente aleatorias en las que no queda casi ningún vestigio del orden establecido en la red circulante. Las redes sociales del mundo real se encuentran a medio camino entre este orden «absoluto» impuesto por la red circulante y la aleatoriedad total de las redes Erdős-Rényi. Ellas, las redes del mundo real, parecen tener cierto orden, cierta estructura, que se manifiesta en su transitividad media, sin llegar al orden absoluto. También parecen tener cierta aleatoriedad que se refleja en su distancia topológica media, sin llegar a la aleatoriedad total de las redes Erdős-Rényi. Esta característica refleja la complejidad del mundo real.
Una de las características que hemos destacado antes de nuestra red social es la de que no todos tenemos el mismo número de relaciones. Un pequeño número de participantes tienen muy pocos o muchos amigos en la red, mientras que la mayoría tendrá un número medio de relaciones. Para ver cómo el modelo de Erdős-Rényi describe estos números de amistades de los miembros de la red, hagamos lo siguiente.
A la salida de la fiesta, preguntemos a cada participante con cuántos otros establecieron relaciones, o sea, el grado de cada individuo. Ahora registremos el grado de cada individuo y luego contemos el número total de aristas que se crearon en la fiesta. Debido al «Lema del apretón de mano» este número es la suma de los grados de todos los participantes. Con estos números podemos hallar la probabilidad de encontrar a un individuo que terminó la fiesta con un número dado de contactos50. Si graficamos los valores de estas probabilidades versus los grados de los individuos, obtenemos el «histograma», que es el nombre técnico que recibe esta gráfica de la Figura 24.
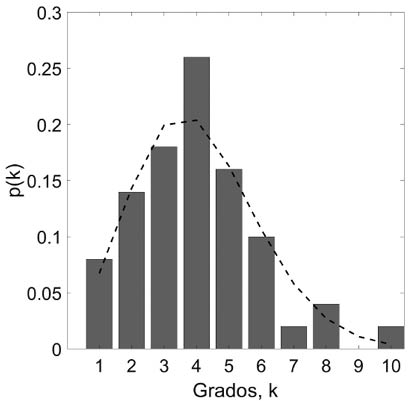
Figura 24. Histograma de la distribución de los grados de los nodos en una red. En el eje horizontal se dan los valores de los grados y en el vertical la probabilidad de encontrar un nodo con dicho grado. La línea de puntos representa el ajuste a la distribución de Poisson.
Aprendamos a leer la información de este histograma. La primera barra nos indica la probabilidad de hallar un participante en la fiesta que terminó con un solo contacto. La segunda nos da dicha probabilidad para los que hicieron dos amigos, y así sucesivamente. El histograma nos indica que menos del 10% de participantes estableció solo una relación. Tampoco es muy probable que los participantes (en un grupo de 50 individuos) hayan establecido más de 7 relaciones. Lo que vemos en el histograma es que la mayoría de los asistentes estableció como media cuatro nuevas relaciones. Estos resultados concuerdan con cierta «normalidad» de las relaciones, según lo que deberíamos esperar en una fiesta de estas características51.
La «normalidad» del histograma quizás sea una consecuencia de que, en una población, dada el grado de extroversión y sociabilidad de los individuos, se distribuya de forma que no haya muchos extremadamente asociales ni muchos extremadamente sociales. Así, la mayoría de los asistentes tendrá un grado medio de extroversión y sociabilidad. Lo anterior es justamente lo que nos dicen las matemáticas para una fiesta que se haya desarrollado según los principios establecidos aquí. Según los resultados de Erdős y Rényi, los valores de la probabilidad de encontrar nodos con un cierto grado deberán obedecer una distribución denominada binomial (la línea de puntos en la figura), que como puede verse se aproxima muy bien a las barras del histograma.
Esto es justo lo que hemos visto cualitativamente en nuestra red social personal. Pero ¿qué pasaría si obtuviéramos estas distribuciones en redes sociales del mundo real? Pues que veríamos una gran disparidad de una red a la otra. Mientras que en las redes de Galesburgo observamos unas distribuciones bastante «normales» (ver Figura 25), aunque no sean ciertamente distribuciones binomiales, en otras observamos un fenómeno no descrito por el modelo de Erdős y Rényi, ni por el de Watts-Strogatz.
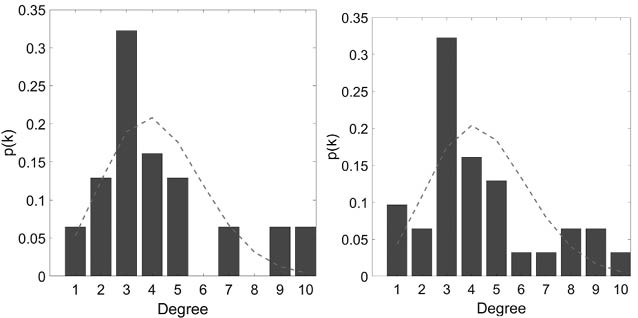
Figura 25. Distribuciones de los grados de los nodos en las redes sociales de los médicos de Galesburgo. En la izquierda está la distribución de los grados en la red social de amistad y en derecha los de la red de asesoramiento.
Para entender por qué surgen estas distribuciones «anómalas», que veremos más adelante en detalle, pensemos en la red de colaboración entre matemáticos que he mencionado antes. La media de colaboraciones entre matemáticos según esta red es de cuatro. Una gran mayoría de matemáticos se acerca bastante al estereotipo de trabajador aislado y solitario, por lo que en su gran mayoría publicará trabajos con muy pocos colaboradores durante su vida activa en las matemáticas. Por ejemplo (ver [35]), el medallista Fields52 Atle Selberg, a quien le gustaba «trabajar por su cuenta, penetrando los problemas por su cuenta y a su propio ritmo», reveló lo siguiente en una entrevista: «Debo decir que nunca pensé en colaborar con nadie. Tengo un trabajo conjunto, y este fue con Chowla53, pero debo decir que fue Chowla quien vino a mí con una pregunta». Sin embargo, hemos visto el caso de Paul Erdős, quién publicó trabajos con 511 matemáticos, o sea, que mientras que la mayoría de los matemáticos tiene solo colaboraciones con otros 4, Erdős tuvo con 511. Está claro que no hay muchos «Erdős» en este mundo, por lo que tenemos una distribución muy poco «normal», con muchos nodos que tienen un grado muy pequeño (los «Selberg» de la red) y muy pocos nodos que tienen un grado excepcional (los pocos «Erdős» de la red).
Mark Newman, de la Universidad de Michigan, ya había observado que las redes de colaboración entre científicos no seguían la distribución de Poisson, sino otras distribuciones más asimétricas [28]. Esto no es exclusivo de las redes de colaboración científica. Por ejemplo, Oatley y Crick [26] hallaron que las redes del crimen organizado en Mánchester tampoco tienen distribuciones de grados simétricas. La misma característica se observa en la red que agrupa a los directivos de las más importantes corporaciones de los EE. UU. (Corporación).
Para tener una idea de qué estamos hablando echémosle una ojeada a la Figura 26. En el panel de la izquierda vemos una distribución del tipo «binomial» o simétrica. En la misma observamos una distribución «democrática» de las conexiones. La mayoría de los nodos tiene el mismo número de conexiones y muy pocos nodos tienen números de conexiones extremos: ni muy pocas ni muchísimas. En la distribución de la derecha vemos el típico cuadro de distribución «no equitativa», en la que la mayoría de los nodos tienen un pequeño número de conexiones mientras que unos pocos, muy pocos, acaparan un gran número de uniones. El lector seguramente dirá: «sí, como la riqueza, que la mayoría tenemos muy poca y una minoría tiene un gran acaparamiento de ésta». ¡Pues, tiene toda la razón! ¿Cómo puede surgir esta gran desigualdad en el número de conexiones entre individuos en una red social?
Figura 26. Comparación esquemática de una distribución «normal» o equitativa (a veces llamada democrática) (izquierda) y otra distribución más egoísta donde unos pocos nodos acaparan la mayor concentración de conexiones.
Para entender cómo puede generarse una distribución tan asimétrica del número de conexiones en una red social, retornemos a nuestra fiesta original. Ahora, en lugar de que todos los asistentes arriben a la hora establecida al local de la fiesta, pensemos que algunos pueden llegar un poco más tarde. Supongamos que a la hora prefijada para el comienzo de la fiesta, un pequeño grupo de individuos llega al local. Llamemos a estos individuos los «tempraneros». Estos tempraneros, como hemos visto en el caso del modelo de Erdős-Rényi, comenzarán a establecer relaciones de forma aleatoria, de tal modo que al cabo de cierto tiempo habrá un número de conexiones entre ellos. La mayoría de los tempraneros habrá establecido un número medio de conexiones. Sin embargo, debido a la distribución binomial que dicta el modelo de Erdős-Rényi, habrá una pequeña minoría con muy pocos contactos y otra pequeña minoría con más contactos que la media. Digamos que esa última minoría está formada por aquellos individuos más extrovertidos o populares entre los tempraneros.
Supongamos que, pasado un tiempo desde la hora preestablecida para el comienzo de la fiesta, llega al local uno de los invitados y se encuentra con el grupo de los tempraneros. Este nuevo asistente puede entonces seguir una estrategia racional a la hora de establecer sus contactos. De seguro, pensará este, que establecer relaciones con aquellos individuos que son más populares en la fiesta merecerá más la pena que establecer dichas relaciones con alguien que está aislado o poco conectado al resto. Así que el nuevo asistente se presentará «preferencialmente» a aquellos individuos más conectados (populares) de la red. Esto tiene una consecuencia inmediata: que aquellos individuos que ya eran populares en la red se hacen más populares porque han ganado una nueva conexión. Si los próximos individuos que llegan a la fiesta siguen la misma estrategia de conectarse «preferencialmente» a los individuos más conectados, estaremos siguiendo un mecanismo en el que «el rico se hace cada vez más rico» en conexiones.
Este mecanismo de «unión preferencial» fue propuesto en un artículo de extraordinario impacto publicado por Albert-Lazslo Barabási y su estudiante de doctorado Reka Albert en la revista Science en 1999 [36]. Las características más sobresalientes de este modelo son las siguientes. La primera y más importante es que genera redes en las que la distribución de los grados es muy asimétrica. La misma sigue la llamada «ley de potencias»54 en la que la probabilidad de encontrar un nodo con un cierto grado decae como una potencia de dicho grado. La segunda característica es que las redes generadas por el modelo de Barabási-Albert tienen características de muy pequeños mundos, o sea, que las distancias topológicas medias entre los pares de nodos en las redes de este tipo son más pequeñas que en el caso de las redes del tipo Erdős-Rényi.
En el modelo de Barabási-Albert primero se genera una red pequeña siguiendo el esquema de Erdős-Rényi como se ilustra en la Figura 27 (panel izquierdo). Para cada nodo se calcula el grado y se divide por la suma de los grados de todos los nodos (recuerde el Lema del apretón de manos). Esto se ilustra en la Figura 27 (izquierda), donde se ve que los dos nodos señalados con flechas tienen los valores más alto de esta razón. Por tanto, el proceso continúa añadiendo nodos que se van enlazando preferencialmente a aquellos que tienen la mayor razón del grado entre la suma de los grados, como se ilustra en la parte derecha de la Figura 27.
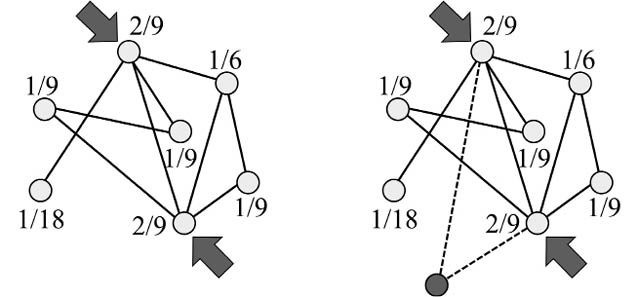
Figura 27. Ilustración del proceso de evolución de una red de acuerdo con el mecanismo de unión preferencial.
Hoy en día hay suficiente evidencia para afirmar que la mayoría de las redes en el mundo real no siguen exactamente una distribución de grados del tipo «ley de potencia». En su lugar, hay un «zoológico» de distribuciones, muchas de las cuales son bastante asimétricas [37]. Pero la lección que nos enseña este modelo es tremendamente importante. Por ejemplo, pensemos en una red con una distribución de los grados como en la red del tipo de Barabási-Albert. En este caso, la mayoría de los nodos tienen un pequeño grado. Así pues, si seleccionamos varios nodos al azar y los «borramos» de la red (junto con todas las conexiones que estos nodos tenían), estaremos borrando algunos de los muchos nodos cuya «importancia» no es tan relevante en mantener la conectividad de la red. Sin embargo, si «borramos intencionalmente» algunos de los nodos de mayor grado de ésta, entonces estaremos eliminando a aquellos que «pegan» a gran cantidad de otros nodos entre sí y estaremos destruyendo la conectividad de la red. Esto nos enseña que las redes con una distribución asimétrica de los grados son muy robustas a la eliminación aleatoria de nodos. Por ejemplo, nuestra red de amigos no se destruye si algunos de sus miembros dejan de pertenecer a la misma. Pero, si esos amigos que tienen la mayor conectividad de la red dejan de ser miembros de nuestro círculo de amigos, nuestra red se desvanece.
Desde el punto de vista de una red de amistad, de asesoramiento o de colaboración, el hecho de que los principales conectores de la red se desconecten de la misma es una mala noticia, ya que estaremos desarticulando redes que nos sirven en nuestra vida cotidiana. Pero ¿qué pasaría si la policía estuviera intentando desarticular una banda criminal? Imaginemos que este es el caso de la banda presentada en la Figura 28. Capturar a algunos miembros de la banda al azar no significaría mucho desde el punto de vista de su desarticulación, como se aprecia en la parte superior de la figura. La banda aún tiene estructura para comunicarse entre los miembros que permanecen activos: la red que queda al apresar a cuatro de los miembros es aún una red conexa. Sin embargo, la captura de los dos principales cabecillas, en términos de sus conexiones, descabezaría la organización, como se observa en la parte baja de la figura. Ahora no existe una banda; hay cuatro trozos de la banda desperdigados y sin enlaces entre ellos. La banda como tal ha desaparecido.
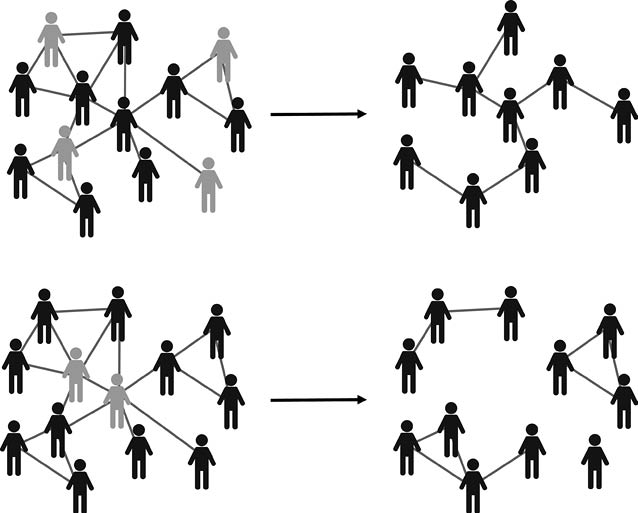
Figura 28. Efectos sobre una red de la «eliminación» aleatoria de nodos (panel superior) como por ejemplo el apresamiento aleatorio de miembros de una banda. En el panel inferior se da un ejemplo de la «eliminación» selectiva de los nodos más conectados, como podría ser el apresamiento de los cabecillas de una banda.
Como hemos visto, los nodos de mayor grado en una red sirven como conectores de otros nodos, por lo que desempeñan un importante papel estructural en la red. Por otra parte, podemos pensar que estos nodos tienen también un papel primordial en las dinámicas de transmisión de información en las redes sociales. Un nodo muy conectado tiene la capacidad de transmitir un mensaje de Wasap a muchos miembros de la red con un solo clic. De igual forma, estos nodos podrían transmitir una infección a muchos más nodos que la media (comportase como superpropagadores), o tener mayor probabilidad de ser contagiados por otros individuos de la red (véase el Capítulo 3). En resumen, el grado de un nodo es una buena medida de la «importancia» que este juega en la red, tanto desde el punto de vista estructural como desde el punto de vista funcional. Cualquier medida cuantitativa de los nodos de la red que esté diseñada para aportar información acerca de la importancia estructural del nodo y/o de su papel funcional en la red se denomina una medida de centralidad del nodo.
Supongamos que la red que se ha generado en una de las fiestas (modelos) que hemos analizado antes es la que se ilustra en la Figura 29. Pensemos en un agente ajeno a la red que quiere distribuir una información entre todos los miembros de ésta de la forma más efectiva posible, por ejemplo, usando el menor número posible de clics de Wasap.
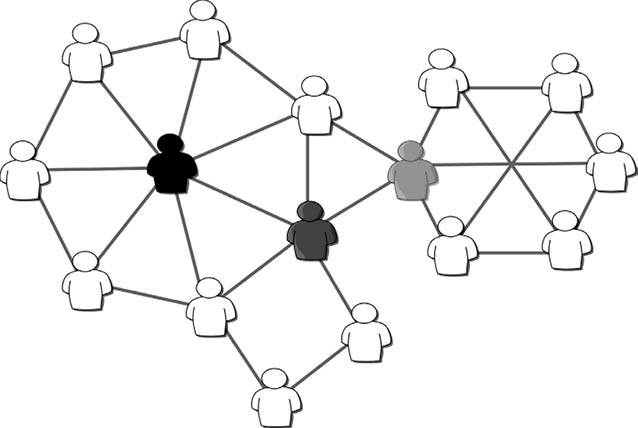
Figura 29. Ejemplo de tres nodos, marcados en tres tonos de grises, que son detectados como los más «importantes» de la red de acuerdo con tres medidas diferentes de centralidad de la red.
El nodo más «central», de acuerdo con el número de conexiones (grado), es el nodo marcado en negro, el cual tiene siete conexiones. Si el agente le da la información a este nodo lo cierto es que este la podrá distribuir a siete otros individuos con un solo clic. Pero ahí no termina la historia: cada uno de estos individuos deberá pasar la información a sus contactos y éstos a los suyos, y así sucesivamente. Si el nodo negro es el comienzo de la cadena, habrá dos nodos que recibirán la información solo después de cuatro clics. El número medio de clics que habrá que efectuar para distribuir la información a todos los miembros de la red, partiendo del nodo negro, será de 1,87.
Sin embargo, si el agente le da la información originalmente al nodo gris oscuro este distribuirá la misma en no más de tres clics a todos los miembros de la red. Como promedio se necesitarán solo 1,69 clics en toda la red para alcanzar a todos los miembros partiendo del nodo gris oscuro. Por tanto, desde el punto de vista de la «cercanía» al resto de los nodos de la red, el nodo gris oscuro es más «central» que el nodo negro. Pero ¿Cómo podemos saber si el nodo gris oscuro es el más «central» de todos los nodos en términos de cercanía en la red? Para ello definimos una nueva medida de centralidad en la red: la «centralidad de cercanía»55.
Para calcular la centralidad de cercanía de un nodo procedemos de la siguiente forma. Primero, identificamos todos los caminos más cortos que unen este nodo al resto de nodos en la red (asumimos siempre que la red es conexa). En una red pequeña esto lo podemos hacer a mano, pero para redes más grandes usamos algoritmos computacionales como el de Dijkstra56 para calcular todos los caminos más cortos entre todos los pares de nodos. Una vez que tengamos este dato, procedemos a calcular la distancia topológica desde este nodo al resto de nodos, es decir, el número de aristas en sus caminos más cortos. La suma de estos números nos dará la «lejanía» de este nodo al resto de nodos en la red. La centralidad de cercanía se define como el recíproco de la lejanía. Haciendo este cálculo podemos ver que el nodo marcado en gris oscuro es el más central, de acuerdo con su cercanía a los otros nodos de la red.
Si observamos detenidamente la red podemos ver que existen dos partes fácilmente identificables en la misma. En la parte derecha hay un grupo formado por seis individuos y sus interacciones, mientras que a la izquierda existe un grupo de diez personas. Ambos grupos están conectados a través del nodo marcado en gris claro. O sea, toda la información que fluye desde el grupo de la izquierda al de la derecha y viceversa, tiene necesariamente que pasar por el nodo gris claro. Digamos entonces que este nodo tiene una gran «centralidad de intermediación» entre otros pares de nodos en la red57. Nótese que, si el nodo gris claro desaparece, los dos grupos quedarían desconectados entre sí, indicando la importancia estructural de este nodo. Para cuantificar la centralidad de intermediación de un nododebemos contar todos los caminos más cortos entre cualquier par de nodos de la red que atraviesan al nodo en cuestión. Este número es entonces dividido por el número total de caminos más cortos entre cualquier par de nodos, atraviesen o no el nodo que analizamos. Haciendo este cálculo podemos saber que el nodo gris claro es el de mayor centralidad de intermediación de todos los nodos de la red.
En este ejemplo sencillo hemos aprendido una lección. La centralidad o «importancia» de un individuo en una red social es relativa. No por ser el más «popular» en términos del número de amigos que tengas serás el más importante para pasar una información en el menor tiempo posible al resto de miembros de la red, o para mantener comunicados a dos (o más) grupos en la red. Esta situación fue ya identificada por los estudiosos de las redes sociales desde la mitad del siglo XX.
El concepto de centralidad en redes data de los estudios que los científicos sociales comenzaron a realizar ya desde finales de los años 1940 y principios de los 50. Como señaló Linton C. Freeman en un artículo [38], los estudios de centralidad se pueden trazar hacia finales de la década de 1940 cuando Alex Bavelas58 y sus estudiantes -en particular Harold Leavitt59- realizaron una serie de experimentos sobre el impacto de la forma organizativa en la productividad y la moral, donde manipularon la centralidad de cada sujeto experimental en el patrón de comunicación que los unía. Durante la década de 1950 se desarrollaron trabajos sobre centralidad basados en el álgebra matricial por Leo Katz60 (1953) quien introdujo un índice de «estatus» basado en las potencias sucesivas de una matriz de adyacencia. Luego Charles Hubbell amplió en 1965 el índice de estatus de Katz, y en dos trabajos publicados en 1972 y 1987, respectivamente, Phil Bonacich61 caracterizó tanto el índice de Katz como el de Hubbell como medidas de centralidad. Un par de trabajos muy importantes fueron publicados por Linton Freeman en 1977 y 1979, donde formalizó las medidas de grado, cercanía e intermediación como centralidades de los nodos en redes sociales.
Existen varias circunstancias en las que la centralidad de un nodo en una red depende no solo de su posición en la red, sino también de la posición de sus vecinos. Es decir, la centralidad de un nodo depende no solo de cuántos vecinos este tiene, sino también de cuán centrales son estos vecinos. De este modo dos nodos que tienen el mismo grado pueden tener diferentes centralidades si uno de los nodos está conectado a vecinos de mayor centralidad, digamos de mayor grado, que el otro. Lo interesante es que esta clasificación no la logran ni el grado, ni la centralidad de cercanía, ni la centralidad de intermediación. Dos ejemplos de este tipo de centralidad son la centralidad de vector propio62 propuesta por Phillip Bonacich de la Universidad de California en los Ángeles (UCLA) [39] y la centralidad de subgrafos63 [40] propuesta por mí cuando trabajaba en la Universidad de Santiago de Compostela junto con Juan Alberto Rodríguez Velázquez de la Universidad Rovira i Virgili, ambas en España. Un ejemplo de las diferencias en la clasificación de nodos en una red entre estas centralidades y el grado es ilustrado en la Figura 30.
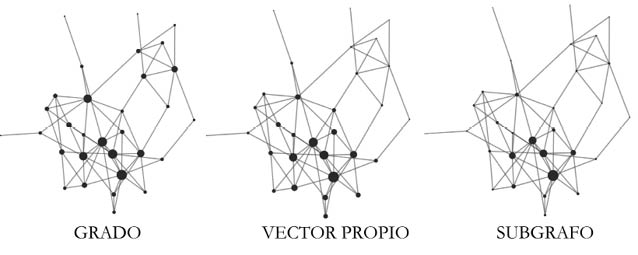
Figura 30. Clasificación de los nodos de la red de asesoramiento entre los médicos de Galesburgo de acuerdo con tres tipos de centralidad (grado, vector propio y subgrafo). Los nodos son dibujados como círculos con radios proporcionales a dichas centralidades.
Como se puede ver en la Figura 30 que representa las relaciones de asesoramiento entre los médicos de Galesburgo, el grado identifica como centrales a varios nodos que son periféricos en el sentido de que sus vecinos no tienen una alta centralidad. Este efecto se elimina con las otras dos centralidades que identifican como más «relevantes» a aquellos médicos que tienen muchas conexiones fundamentalmente con otros médicos «relevantes» en la red.
Las medidas de centralidad son de gran relevancia para entender el papel de los diferentes individuos en una red social real. Por ejemplo, según los resultados del estudio de Killeya-Jones y colaboradores [24], la centralidad de vector propio y la de intermediación son fundamentales para entender la posición de los diferentes adolescentes en sus redes sociales. Estos autores estudiaron el consumo de alcohol y cigarrillos entre los adolescentes de una muestra étnicamente diversa de 156 adolescentes masculinos y femeninos muestreados en dos momentos del séptimo grado (primavera y otoño) como se ilustra en la Figura 31.
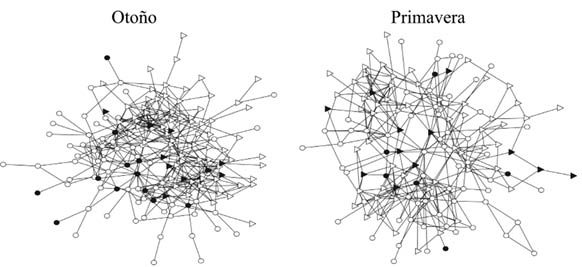
Figura 31. Redes de amistad entre adolescentes estudiadas por Killeya-Jones. Los triángulos representan a las chicas y los círculos a los chicos. En negro se representan los que consumen alcohol y/o cigarrillos y en blanco los que no.
En el curso de otoño, las variables que más impacto tuvieron en el consumo de cigarrillos y alcohol entre los adolescentes fueron «el impacto social» y la «popularidad», seguidas de la centralidad de vector propio y la centralidad de intermediación. El índice de impacto social mide el grado de visibilidad de los individuos en su entorno social y es evaluado a través de la percepción subjetiva de unos individuos respecto a otros. También la popularidad es en este caso un criterio subjetivo que mide el grado en que los adolescentes son identificados explícitamente como miembros de la red, lo que refleja tanto la reputación como el impacto en el entorno social. Las medidas de centralidad no dependen, sin embargo, de ninguna evaluación subjetiva de los miembros de la red, sino únicamente de la estructura social creada por los adolescentes a través de sus interacciones sociales. En el curso de primavera, esta relación entre consumo y centralidad desaparece, lo que indica que las posiciones relativas de los adolescentes en la red social (centralidades) son importantes solo a comienzos del curso escolar. Según estos resultados, es importante identificar qué adolescentes tienen poder para influir en sus compañeros con miras a establecer políticas para la prevención del consumo de sustancias en este grupo de edad temprana, especialmente al comienzo del año escolar.
Otro resultado interesante es el que aporta el trabajo de Oatley y Crick [26] sobre las bandas criminales en Mánchester. Los autores encontraron que los líderes de las bandas no son identificables por el grado de sus nodos en la red. O sea, que los nodos más conectados no corresponden a los jefes de las organizaciones. Esto ocurre posiblemente porque, como ha demostrado la información de inteligencia suministrada por la policía, existe una jerarquía en las bandas, por lo que los jefes posiblemente se conectan solo a sus lugartenientes y no al resto de miembros. Adicionalmente, los resultados del análisis de Oatley y Crick concluyen que los delincuentes que cometen asesinatos tampoco son necesariamente los individuos de mayor grado en la red. De hecho, los asesinatos se cometen por individuos periféricos, lo cual podría ser una consecuencia del hecho que la red tiene una distribución de nodos asimétrica y, por tanto, hay muchos más nodos de poco grado que nodos con un grado significativo.
Los resultados anteriores no son muy alentadores desde el punto de vista policial, ya que hace más difícil la tarea de detección de líderes y asesinos desde un punto de vista del análisis de la red. Sin embargo, el análisis de la red sí que ha revelado una información importante. Ésta es que hay un número importante de conexiones comunes entre bandas rivales. Estos nodos que conectan diferentes bandas entre sí son caracterizados por su significativa centralidad de intermediación. Por consiguiente, la identificación policial de estos individuos de mayor intermediación en las redes hace posible el trabajo de vigilancia de las interacciones entre las bandas rivales, facilitando su desarticulación.
Oatley y Crick concluyeron que el uso de redes, tanto como herramienta de visualización de la información, como de su análisis, es operacionalmente ventajoso desde el punto de vista del intercambio de información, entrenamiento, así como para la identificación de los principales infractores en el crimen organizado. Todo esto en la vida real, no en la serie «CSI».
Cuantas veces habremos oído a alguno de nuestros amigos decir: «mis amigos tienen más amigos que yo» o «mis colaboradores tienen más colaboradores que yo» o cualquiera de las posibles variantes que puedan surgir de nuestras redes sociales. No se trata de que nuestros amigos tengan baja su autoestima y piensen que los demás son más «populares» que ellos. Se trata de un efecto real y cuantificable que ocurre en las redes y que se explica únicamente a través de las características de estas. Con «real y cuantificable» me refiero a que podemos verlo ahora mismo en cualquier red social. Por ejemplo, consideremos la red social hipotética mostrada en la Figura 32. Es fácil obtener el número de amigos que cada uno tiene en la red, o sea, su grado.
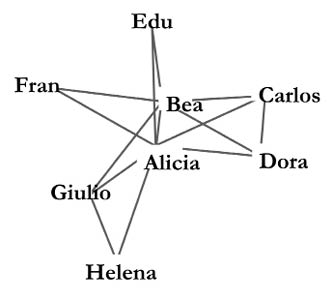
Figura 32. Ejemplo de una red social hipotética.
Ahora contemos el número de amigos que tienen los amigos de cada individuo. Por ejemplo, si preguntamos a Alicia, nos dirá que sus amigos tienen amigos (esto corresponde al grado de los amigos de Alicia). Por tanto, los amigos de Alicia tienen como media 3 amigos. Los amigos de Bea tienen amigos lo que da una media de 3,33. Los de Carlos tienen , que da una media de 5,33 amigos, y así sucesivamente. En la Figura 33 ilustro el número de amigos que cada persona tiene en la red (gráfico de la izquierda) y el promedio de amigos que cada amigo tiene (gráfico de la derecha).
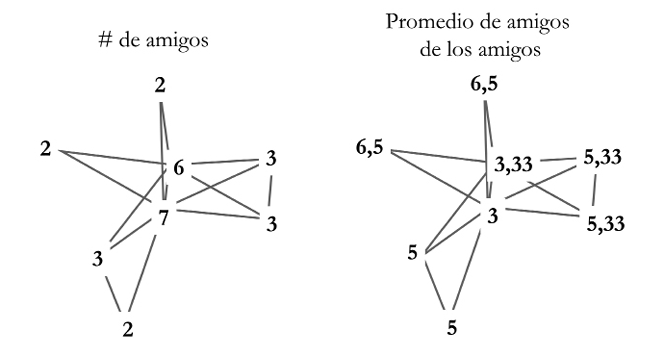
Figura 33. Ilustración del número de amigos que cada miembro de una hipotética red tiene (izquierda) así como del número medio de amigos que tienen los amigos de cada individuo (derecha).
Si comparamos los valores de los nodos en los gráficos de la derecha y de la izquierda nos damos cuenta de que, excepto para Alicia y Bea, el resto de las personas tiene menos amigos que sus amigos (véase la Figura 34). De hecho, la probabilidad de que encontremos a una persona en esta red para quien sus amigos tienen más amigos que ella, es del 75% de los miembros de la red. He aquí la «paradoja de la amistad»: como promedio en una red, nuestros amigos siempre tienen más amigos que nosotros.
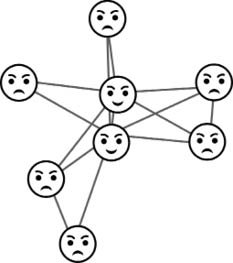
Figura 34. Ilustración de los miembros de una hipotética red mostrando sus «estados» como contentos o tristes en dependencia de si sus amigos tienen menos o más amigos que ellos, respectivamente.
Esta aparente paradoja fue estudiada por primera vez en el año 1991 [41] por Scott L. Feld de la Universidad del Estado de Nueva York, en Stony Brooks, EE. UU. No hay ningún misterio en esta paradoja que las matemáticas no puedan resolver. En realidad, esta no es más que la consecuencia de una conocida desigualdad matemática [42] que se evidencia en las redes de cualquier tipo. O sea, que podemos observar que los vecinos de los nodos de cualquier red tienen como promedio mayor grado que los nodos por sí mismos, independientemente de que la red sea una red social o represente las interacciones entre proteínas en una célula. ¡Un ejemplo más de que estamos a merced de las redes!
El consenso es un acuerdo o conformidad en algo de todas las personas que pertenecen a una colectividad. Por tanto, si nuestro grupo es de más de dos individuos tenemos que llegar a acuerdos entre todos los pares de individuos conectados que conforman nuestra red. Para lograr el consenso tiene que haber una predisposición de todos los miembros del grupo de llegar a dicho acuerdo. Este consenso puede ser acerca de cualquier aspecto de nuestra vida social, desde qué hacer el «finde», hasta ajustar nuestras velocidades al caminar para que nadie en el grupo se quede detrás.
Para explicar en qué consiste el proceso de consenso en una red voy a usar el ejemplo de tres caminantes que forman una pequeña red como se ilustra en la Figura 35. Al salir a caminar, Clara lleva una velocidad de 5 km/h, va seguida por Puri, que lleva una velocidad de 3 km/h y luego por Marta, que va más lento; a 2 km/h. Si las caminantes continúan con estas velocidades el grupo se dispersará, pero si logran ajustar sus velocidades a un nivel de consenso llegarán juntas al destino. Para Clara, ir a solo 2 km/h resulta tedioso, mientras que, para Marta, ir a 5 km/h resulta muy agotador. Hay que llegar a un punto medio de las velocidades para que todas disfruten de la caminata.

Figura 35. Ilustración de las velocidades medias de tres caminantes al principio de una excursión (izquierda) y después de cierto tiempo en que han sincronizado sus pasos (derecha).
Debido a las conexiones existentes en la red, Clara tiene que ajustar su velocidad solo con la de Puri, al igual que Marta, pero Puri debe ajustar su velocidad con las de ambas caminantes. Las velocidades se pueden ajustar a mayor o menor prisa. Llamémosle ε>0 a dicha rapidez de ajuste. Por tanto, al cabo de un tiempo, Clara calculará la diferencia de velocidades con Puri, que es de 5-3=2km/h. Entonces actualizará su velocidad restándole la diferencia anterior multiplicada por . De este modo, su nueva velocidad será: 2εkm/h, lo que indica que deberá disminuir su velocidad en 2εkm/h.
Al mismo tiempo, Puri obtendrá la diferencia de velocidades con Clara: 3-5=2km/h (el signo negativo indica que va más lenta que Clara) y con Marta: 3-2=1km/h. Ahora sumará ambas diferencias: -2+1=-1km/h y actualizará su velocidad actual restándole la diferencia anterior multiplicada por ε: 3-1 ε =3+ ε km/h. Esto indica que Puri tendrá que darse un poco de prisa sumando ε a su velocidad actual. Por último, Marta encontrará la diferencia entre su velocidad actual y la de Puri, 2-3=-1km/h y actualizará su velocidad actual restándole la diferencia anterior multiplicada por ε: 2-1 ε =2+ ε km/h.
Si tomamos, por ejemplo, que ε=0.5, las velocidades iniciales se actualizarán como sigue:
•Clara: de 5 km/h a 5-2 ε =4km/h (disminución),
•Puri: de 3 km/h a 3+ ε =3,5km/h (aumento),
•Marta: de 2 km/h a 2+ ε =2,5km/h (aumento).
La segunda vez que cada caminante actualice su velocidad partirá del hecho de que ahora van a velocidades de 4, 3,5 y 2,5 km/h, respectivamente. El proceso es idéntico al anterior, calculando las diferencias entre las velocidades y luego restándole dichas diferencias multiplicadas ε por a las nuevas velocidades. Así se sigue hasta que se haya alcanzado el consenso, o sea, que todas las velocidades sean la misma.
El proceso se puede observar mucho mejor si lo graficamos. En el eje de las x vamos a considerar la iteración, denominada h en el gráfico, que representa las veces que las caminantes actualizan sus velocidades. En el eje de las graficamos la velocidad de cada una de las caminantes en la iteración correspondiente. Esto se muestra en la Figura 36. Como se puede observar en la figura, pasadas unas 15 actualizaciones, las velocidades de las tres caminantes son idénticas. Han llegado a un consenso que resulta ser el promedio de las velocidades iniciales64.
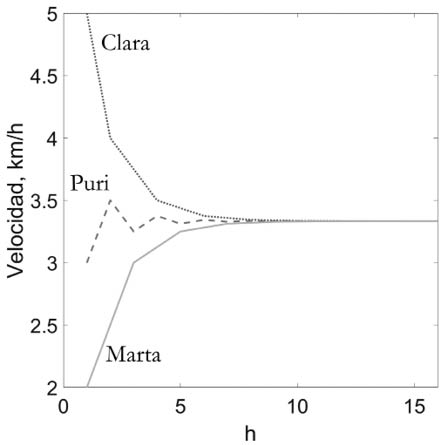
Figura 36. Diagrama de la dinámica de consenso de las velocidades de tres caminantes. En el eje horizontal se representa el tiempo transcurrido (en horas) desde que comenzaron a caminar. El eje vertical representa las velocidades de cada caminante a un tiempo dado.
El lector pensará que cuando camina no hace ningún cálculo mental para ajustar su velocidad a la del resto de caminantes, y tiene razón. Lo hacemos a base de prueba y error, si vamos muy rápido disminuimos la velocidad, pero quizás la disminuyamos demasiado y tengamos que darnos prisa a continuación, etc. Nótese que algo parecido le sucede a Puri, quien tiene que coordinarse con Clara y con Marta, y que primero aumenta su velocidad para luego reducirla y a continuación volverla a aumentar, y así sucesivamente hasta llegar al consenso. Si en lugar de tres chicas fuesen tres robots los que tienen que llegar al consenso en sus velocidades, programarlos a base de prueba y error sería muy ineficiente. Por eso se hace usando el «protocolo de consenso» que he descrito antes.
Si en lugar de una variable física, como la velocidad, estuviéramos interesados en el consenso respecto a una variable sociológica, tal como el grado de preferencia a un tema determinado o el grado de aceptación de algún cambio propuesto, usaríamos el mismo esquema anterior, siempre y cuando exista una predisposición de los miembros de la red a lograr el consenso. Incluso, si existiera más de una variable, por ejemplo, velocidad y posición, o las opiniones respecto a dos o más temas, el modelo anterior sería aún válido (si el lector está interesado en profundizar sobre los aspectos matemáticos del consenso ver por ejemplo [43]).
¿Cómo afecta al consenso la estructura de la red?
Comenzaré por aclarar que el tipo de consenso que considero aquí se logra solo si hay voluntad por las partes para lograrlo. Como escriben Michael Hechter y Christine Horne [8] «para que el orden social emerja y se mantenga, se deben vencer dos problemas separados. Los individuos deben ser capaces de coordinar sus acciones y deben cooperar para lograr los objetivos comunes». En una red sin direcciones, como las redes sociales que estamos considerando en este Capítulo, se obtiene un estado de consenso si, y solo si, la red es conexa. Si la red no es conexa entonces se alcanzan estados de consenso entre los individuos que forman cada componente de conexión de la red como se observa en la Figura 37. Debido al hecho de que los diferentes componentes conexos de una red no pueden intercambiar información entre ellos no se puede lograr el consenso global en la red si esta no es conexa.
Figura 37. Ilustración de una red no conexa (izquierda) y de la evolución de la dinámica de consenso en la misma (derecha) indicando la existencia de dos equilibrios separados por grupo de nodos en los componentes conexos de la red.
Cuando una red es conexa, existen caminos que conectan a cualquier par de nodos de la red. Por tanto, la información se puede intercambiar entre todos los individuos de la red, lo que permite lograr el consenso. Pero no todas las redes tienen la misma facilidad de conectar a sus nodos entre sí. Dicho en otras palabras, no todas las redes tienen la misma conectividad. Existen dos tipos de conectividad en una red: la conectividad de nodos y la conectividad de aristas. La conectividad de nodos es el mínimo número de nodos que deberíamos eliminar para que la red se desconecte. Por su parte, la conectividad de aristas es el mínimo número de aristas que al borrarse se desconecta la red. Si estos números son pequeños, digamos uno, entonces la red correspondiente tiene una baja conectividad. Estas medidas no son muy útiles para nuestro propósito: conocer la influencia de la estructura de la red en la dinámica del consenso. Para darnos cuenta, tomemos las dos redes que se muestran en la Figura 38. Ambas tienen conectividades de nodos y aristas iguales a uno. O sea, si eliminamos solo un nodo o solo una arista en ambas redes, las desconectamos. Pero el resultado que se obtiene de dichas desconexiones es bien distinto. Tomemos como ejemplo la eliminación de una arista. En la red de la izquierda, la eliminación de la arista marcada en línea discontinua nos deja un componente conexo que contiene más del 80% de todos los nodos de la red original. Sin embargo, la eliminación de la arista marcada en línea discontinua en la red de la derecha nos divide la red en dos componentes que tienen el 50% de los nodos de la red original. En términos del consenso, esto nos indica que en la red de la izquierda hay un nodo que no está bien «comunicado» con el resto de la red. Mientras que en la red de la derecha nos dice que hay dos bloques idénticos que no están bien comunicados entre sí. Las consecuencias son evidentes: en la red de la izquierda el consenso se alcanza en menos de 400 iteraciones, ya que al grupo solo le cuesta «convencer» al nodo aislado; mientras que en la de la derecha se necesitan 800 iteraciones para lograrlo, debido al hecho de que hay dos facciones difícilmente convencibles mutuamente.
Figura 38. Ilustración de la influencia de la conectividad de las redes en el proceso de consenso.
Muchas veces los avances más importantes en un área de investigación provienen del matrimonio de esta con otra área diferente. En el caso de la teoría de redes, en particular de su área matemática denominada teoría de grafos, se debe a su matrimonio con el álgebra lineal. De ahí ha surgido la teoría algebraica de grafos que ha dado lugar no solo a muchos resultados elegantes, sino también importantes para entender la estructura y dinámica de redes. Uno de ellos es el siguiente. En el año 1973, el matemático checoslovaco65 Miroslav Fiedler publicó una de las joyas de este campo [44]. El trabajo fue publicado en la revista checoslovaca de matemáticas y ha recibido el mayor número de citas de todos los artículos publicados en dicha revista hasta la fecha (más de 4.700 citas). Fiedler publicó más de 200 artículos matemáticos y seis libros en sus áreas de investigación, que abarcaban la geometría, la teoría de grafos y el algebra lineal. Cuando conocí a Fiedler en 2008, ya tenía 82 años, pero estaba lleno de vitalidad y de brillantes ideas matemáticas. Falleció en 2015 a sus 89 años.
El trabajo de Fiedler de 1973 lleva por título Algebraic connectivity of graph (Conectividad algebraica de grafos). Aquí, su autor define un término algebraico que caracteriza cuán bien conectada está una red. Este término se denomina la «conectividad algebraica» de la red66. En las redes de la Figura 38 la conectividad algebraica es 0,72 para la red de la izquierda y 0,43 para la de la derecha, indicando que la red de la izquierda está mejor conectada que la de la derecha. Pero lo más importante de todo es que exactamente este término, la conectividad algebraica de la red, es el que determina la velocidad de convergencia de un proceso de consenso en una red. Por tanto, ahora podemos entender que la velocidad de convergencia de un proceso de consenso en una red social depende de la estructura de dicha red, en particular de cuán bien conectados estén sus nodos entre sí. Está claro que el consenso en una red donde sus miembros quieran llegar a tal estado queda a merced de la estructura de las redes que forman dichos individuos.
En el estudio sobre la adopción de un nuevo antibiótico entre los médicos de Galesburgo, el objetivo de los promotores de la investigación era lograr el consenso entre los médicos sobre la adopción de este medicamento. Obviamente, mientras más rápido se lograse este consenso, mejor. El consenso se puede lograr a través de las interacciones de amistad entre los médicos o a través de su red de asesoramientos. El dilema es cuál de las dos redes es la mejor vía de difusión para lograr el consenso cuanto antes. Si analizamos las dos redes, nos damos cuenta de que ambas son distintas. O sea, dos médicos intercambian información en una red, pero no necesariamente en la otra. Por ello, es posible que una de ellas sea una mejor vía de difusión que la otra. Para realizar nuestro análisis, calculamos la conectividad algebraica de ambas redes, para lo cual solo necesitamos saber quién se conecta a quién en la red. Los valores son los siguientes: para la red de amistad, 0,3351; y para la red de asesoramiento, 0,4392. Los números por sí mismos no deben preocupar al lector, solo el hecho de que la red de asesoramiento entre los médicos está mejor conectada que la red de amistad (tiene mayor conectividad algebraica). Por tanto, hemos de esperar que el consenso se logre más rápido si difundimos la información y promovemos el debate a través de la red de asesoramiento que si lo hacemos usando la red de amistad. Obviamente podemos hacer la simulación y observar qué sucede. Al hacer la simulación, podemos calcular el «desacuerdo medio» entre los médicos como una función del tiempo, partiendo del punto en que todos los médicos tienen un «valor» diferente de su grado de aceptación del nuevo medicamento. En una escala arbitraria, este desacuerdo medio (el promedio de las diferencias entre las opiniones de todos los médicos) es de 10 puntos. Nuestro objetivo es que este desacuerdo medio caiga a cero, y en dicho punto habremos llegado a un consenso. Como vemos en la Figura 39, ambas redes se encaminan hacia el consenso con velocidades diferentes. La red de asesoramiento logra reducciones del desacuerdo más grandes que la red de amistad para los mismos intervalos de tiempo, y logra el consenso global (cero desacuerdos) antes que usando la red de amistad.
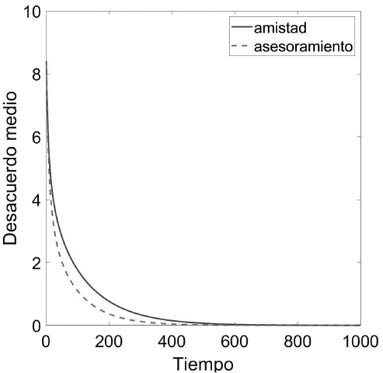
Figura 39. Evolución de la dinámica de consenso entre los médicos de las redes de Galesburgo. En el eje horizontal se da el tiempo en unidades genéricas y en el vertical el estado de desacuerdo medio entre los médicos.
El análisis original de estas redes sociales entre los médicos de Galesburgo fue hecho por James Coleman, de la Universidad de Chicago, y colaboradores en 1957 [23]. Los resultados, después de 18 meses de estudio de dichas redes, fueron que solo 17 médicos adoptaron la tetraciclina como prescripción en sus consultas. No podemos saber qué pasaría si el estudio se hubiera extendido a más tiempo, quizás los 14 médicos restantes estuvieran «rezagados» en la adopción de la innovación (ver próxima sección) y necesitaran más tiempo. Otra posibilidad es que estos médicos partieran de una base de no adopción de dicha innovación por razones diferentes. Este tipo de «cabezonería» es totalmente ajena a la estructura y dinámica de la red y no es necesariamente predecible a partir de estas. Recordemos que en el modelo de consenso que analizamos aquí los individuos de la red tienen predisposición a llegar al consenso. Las situaciones donde existen miembros de la red que se oponen al consenso, conocidos como «testarudos» en el argot de las redes (ver [45]), son diferentes y no se tratarán en este libro.
Una innovación no es más que una idea o tecnología que es percibida como nueva y que se difunde entre los individuos de una sociedad a un ritmo dado. La misma se puede referir a un nuevo atuendo de moda, a los teléfonos móviles, a las redes sociales en línea, o al uso de una nueva técnica por parte de profesionales de un sector dado.
Una cuestión evidente es que no todos los individuos de una red adoptan una innovación al mismo tiempo. Everett Rogers, quien en 1962 era profesor de sociología rural en la Universidad de Estado de Ohio en los EE. UU., publicó ese año el libro titulado Difusión de las innovaciones [46], en el que estudió cómo una innovación se propaga a lo largo del tiempo entre los participantes de un sistema social siguiendo una curva característica (como la que se ilustra en la Figura 40).
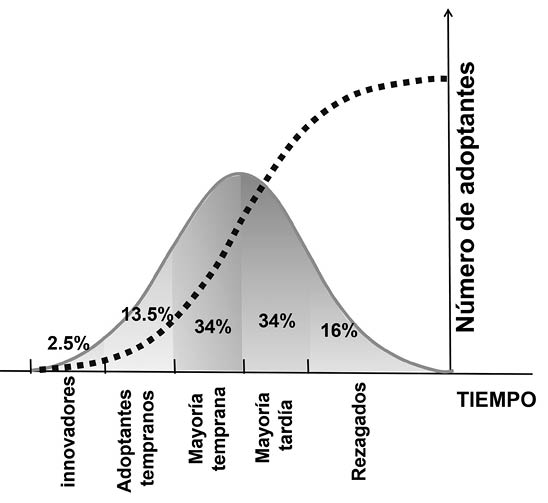
Figura 40. Diagrama de Rogers sobre la evolución temporal de la adopción de innovaciones por parte de un grupo social.
O sea, al principio solo unos pocos de los potenciales usuarios de una nueva innovación, alrededor del 2,5%, la adoptan. Estos suelen ser los más atrevidos, los que están dispuestos (y pueden) asumir los riesgos. Luego llegan los adoptantes tempranos que representan un 13,5% del total y suelen tener un alto grado de liderazgo. Las dos mayorías (temprana y tardía) están caracterizadas por los individuos más conservadores y los más escépticos, respectivamente. Al final, solo quedan los rezagados, aquellos que por diversas razones se apegan más a la tradición y les cuesta cambiar a una nueva innovación.
Para ilustrar cómo el modelo de consenso se puede aplicar al estudio de la difusión de innovaciones me referiré a dos estudios. El primero consiste en la difusión de un moderno método matemático entre los sistemas escolares que combinan programas de primaria y secundaria en el condado de Allegheny (Pensilvania, EE. UU.) a finales de los años cincuenta [47]. La red consiste en las relaciones (fundamentalmente de amistad) entre los superintendentes escolares que llevaban al menos dos años en el cargo. A estos se les preguntó por sus vínculos de amistad con otros superintendentes del condado mediante la pregunta: «entre los principales administradores escolares del condado de Allegheny, ¿quiénes son sus tres mejores amigos?». Este estudio fue impulsado por matemáticos de alto nivel y patrocinado por la Fundación Nacional de la Ciencia y el Departamento de Educación de Estados Unidos. De este modo, tenemos una red de 30 superintendentes y sus relaciones de amistad durante un periodo de 5 años.
En el segundo ejemplo se analizan tres redes generadas mediante un estudio longitudinal sobre la forma en que los agricultores brasileños adoptaron las semillas híbridas de maíz [48]. En este caso, las redes sociales corresponden a las relaciones de amistad entre los campesinos en diferentes comunidades. En este estudio se reporta el número acumulado de adoptantes de la nueva variedad de maíz a lo largo de 20 años entre los individuos del componente conexo gigante para tres comunidades diferentes del estudio, identificadas como comunidades 23, 70 y 71.
Primero analizaré la difusión del método matemático entre los institutos. En la Figura 41 muestro en forma de estrellas el número de adoptantes del método matemático en cada año del estudio. Como se ve, en el segundo año hubo cuatro escuelas que adoptaron la innovación. Luego, en el tercer año la adoptaron otras 10 escuelas, lo que da un total de 14 escuelas aplicando el nuevo método en el tercer año. La curva continua ilustrada representa el mejor ajuste de estos datos a la curva «sigmoidal»67 o tipo-S que corresponde con la teoría de Rogers. Notemos que en este caso el porcentaje de «innovadores» fue del 13%, más característico del porcentaje de «adoptantes tempranos». Posiblemente, algunos adoptaron el método en el primer año, pero esto no fue reportado en el estudio. Ahora vamos a intentar reproducir los resultados del experimento, o sea, los datos que hemos mostrado antes, con el uso únicamente de la información que aporta la red. Para ello, tenemos que buscar una forma de identificar que un individuo en la red haya adoptado la innovación. Lo primero que tenemos que hacer es encontrar una equivalencia entre el número de iteraciones en la simulación y el tiempo real del experimento. Comenzamos encontrando el tiempo de consenso para toda la red. Por ejemplo, diremos que el consenso se ha logrado si la diferencia de opiniones entre dos individuos no es mayor que 0,04 (este número es arbitrario, representa menos de un 4% de discrepancia). Entonces dividimos este tiempo por el número de años que duró el estudio; en este caso, 5 años. De este modo encontramos que, para este caso, 24 iteraciones del modelo representan un año de la vida real. A continuación, contamos el número de nodos que han adoptado la innovación como la diferencia entre el valor del estado de un nodo y el consenso medio. Cuando el valor absoluto de esta diferencia es menor o igual al 4%, consideramos que el nodo está en el régimen de consenso y que ha adoptado la innovación. Los resultados se ilustran en la Figura 41, usando círculos para los valores estimados del número de adoptantes cada año y su ajuste sigmoidal se da en forma de línea discontinua.
Como se puede observar en la Figura 41, el modelo basado en la red de amistad entre los superintendentes reproduce bastante bien los resultados del experimento. En particular, el modelo predice un mayor número de adopciones a principios de la difusión. Sin embargo, el modelo concuerda muy bien con el experimento en encontrar que la mitad de las escuelas adoptarían el nuevo método matemático a los 3 años de haber comenzado el estudio. Este ejemplo nos ilustra cómo la difusión de una innovación a través de una red puede ser claramente dependiente de la conectividad de los individuos que forman la misma.
Figura 41. Evolución temporal de la adopción de un nuevo método matemático entre los institutos del condado de Allegheny. Las estrellas y la línea que las unen representan los datos reales del experimento. Los círculos y la línea de puntos que los conectan representan los resultados del modelo matemático.
Pasamos ahora a estudiar las redes de amistad entre los campesinos en tres comunidades brasileñas y su influencia en la adopción de las semillas híbridas de maíz. La red de los superintendentes de las escuelas que acabamos de estudiar tiene una densidad de aristas del 14% respecto a la red completa del mismo tamaño. Las redes de amistad entre los campesinos son menos densas: la comunidad 23 tiene una densidad de 7,4%, la comunidad 70 de 5,7% y la comunidad 71 de 5,9%. Lo más importante es, sin embargo, el hecho de que estas tres redes tienen una conectividad algebraica muy baja: 0,0407 para la comunidad 23; 0,0422 para la comunidad 70; y 0,0624 para la comunidad 71 (véase la Figura 42). Si los comparamos con la conectividad algebraica de la red de los superintendentes (que es de 0,4469), podemos entender por qué la adopción de las semillas híbridas de maíz por parte de los campesinos brasileños llevó 20 años, mientras que el nuevo método matemático se adoptó en solo 5. Este análisis nos demuestra una vez más lo importante que es la estructura de las redes de interconexión social en la difusión de una innovación. La conectividad algebraica nos revela algo que intuimos fácilmente: los campesinos crean redes sociales de amistad con muy poca conectividad, posiblemente por la separación geográfica de sus viviendas o la propia naturaleza de sus labores, mientras que los superintendentes de las escuelas, quienes laboran en la ciudad, crean redes mucho más conexas. Sigamos adelante entonces.
Figura 42. Ilustración de las redes de amistad entre los campesinos de tres comunidades en Brasil.
En la Figura 43 ilustro los resultados de las evoluciones de la adopción de las semillas híbridas de maíz por parte de los campesinos brasileños en las tres comunidades estudiadas. En forma de estrellas represento las adopciones acumuladas reales en cada comunidad y con círculos las estimadas por el modelo de difusión de innovaciones. Como se puede observar en la figura, los resultados del modelo para las comunidades 23 y 71 son bastante parecidos a los observados en la realidad, particularmente para los primeros 10 años del estudio. Sin embargo, en el caso de la comunidad 70, los resultados de la simulación no siguen el mismo patrón que la evolución real de la dinámica. Está claro que existe alguna razón en la estructura de la red de la comunidad 70 que hace que la adopción de la innovación vaya más rápido de lo esperado según el modelo. Veamos algunas posibles causas.
Figura 43. Ilustración del curso de las dinámicas de adopción de innovaciones (consenso) para tres comunidades de campesinos brasileños. Las curvas con estrellas corresponden a los totales acumulados de adopciones en la comunidad, y los círculos a las simulaciones del modelo.
Liderazgo para lograr el consenso
Una posibilidad que pudiera existir en la comunidad 70, donde el modelo y los resultados de la dinámica real no coinciden, podría ser la existencia de líderes que guiaran a sus seguidores hacia la adopción de la innovación. El termino «líder» proviene del inglés «leader», y significa según la RAE: «persona que dirige o conduce un partido político, un grupo social u otra colectividad». Por tanto, en el contexto de un grupo social que quiere llegar a un consenso, un líder es una persona de la red que conduce al resto del grupo hacia dicho estado. Sabemos que matemáticamente la única condición que existe para que haya consenso en una red no dirigida es que esta sea conexa. Así pues, cualquier nodo en la red va a conducir al resto de nodos hacia el estado de consenso. La cuestión es quiénes lo hacen en el menor tiempo posible.
Pensemos, por consiguiente, en las situaciones analizadas en la sección anterior; en la que se quería lograr el consenso entre los superintendentes o entre los campesinos de tres comunidades diferentes para que sus colectivos adoptaran ciertas innovaciones. ¿Quiénes serían los individuos en cada red que conducirían al resto hacia el consenso en menor tiempo? ¿Se podrían reducir los tiempos de 5 o 20 años necesitados en ambos experimentos, seleccionando líderes apropiados?
Para contestar a las preguntas antes formuladas debemos cambiar un tanto el modelo de consenso que hemos venido considerando. Esta transformación nos conduce a un modelo conocido como consenso con «líderes y seguidores», cuya evolución se muestra en la Figura 44. En la misma, consideramos un proceso de consenso sobre dos opiniones simultáneamente.
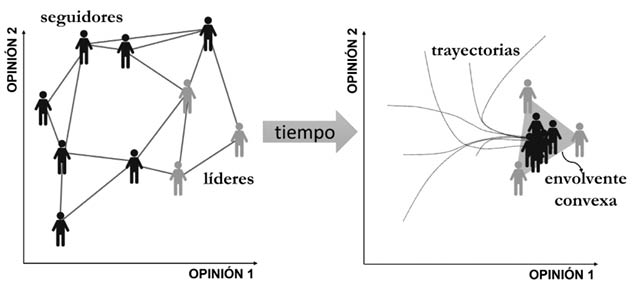
Figura 44. Representación esquemática del modelo de «líderes-seguidores». En la izquierda se representa una red social con tres líderes (gris) y siete seguidores en un espacio de dos opiniones. En la derecha, el resultado de cómo las opiniones de los seguidores han convergido al área demarcada por los líderes en el espacio de opiniones.
¿En qué consiste el modelo de consenso con líderes y seguidores? Lo primero es que hay dos grupos de nodos: los líderes (marcados en gris en la figura) y los seguidores (en negro). Esto es, dada una red cualquiera, «elegimos» un subconjunto de los nodos a los que designamos como «líderes». Ahora habrá conexiones líder-líder, líder-seguidor y seguidor-seguidor. Pues bien, la primera asunción del modelo es que los líderes no cambian su opinión en el tiempo. Está claro que esto no es una asunción realista si queremos que estos líderes sean como algunos políticos, que cambian continuamente sus opiniones según sus conveniencias. Pero si suponemos unos líderes concienciados en lograr el consenso del grupo, la asunción cumple bien su objetivo. En términos prácticos, esto quiere decir que el consenso estará determinado por las interacciones entre los seguidores y las de estos con sus líderes, pero no por las interacciones líder-líder.
Lo que ocurrirá en este proceso de consenso es que los seguidores tratarán de llegar a un consenso entre ellos, tal y como ocurre en el proceso de consenso sin líderes. Sin embargo, al mismo tiempo, los líderes estarán «tirando» de los seguidores hacia el espacio de opiniones definido por estos, la llamada «envolvente convexa» de los líderes.
Polarización, polarización, polarización
Si hubiera un solo líder, al final, el consenso se lograría cuando todos los seguidores tengan exactamente la misma opinión que el líder. Veamos ahora qué pasa si hay varios líderes. En primer lugar, supongamos que todos los nodos están conectados entre sí (una red completa). En la Figura 45 represento la red completa de seis nodos con dos líderes marcados con los nodos más grandes (aquí el tamaño no significa nada, solo se han agrandado para una mejor visualización). En este sistema, los dos líderes tiran de todos los seguidores en la misma dirección. Esto es independiente de que los líderes estén o no conectados entre sí (recordemos que en este modelo las interacciones líder-líder no nos interesan). Lo importante es que todos los líderes están conectados de igual forma a todos los seguidores. Si esto se cumple, entonces al final todos los seguidores tendrán exactamente la misma opinión y esta coincidirá con el punto medio de los líderes.

Figura 45. Ilustración de cómo la posición de los líderes en la red afecta el resultado del proceso de consenso. En este caso, un par de líderes en una red completa hacen que los seguidores converjan sus opiniones justo en el medio de las de los líderes.
Pasemos al próximo ejemplo. Ahora consideramos una cadena lineal de seis nodos, como se ilustra en la parte izquierda de la Figura 46. En este sistema, el líder que está a la izquierda se conecta con el seguidor a su izquierda, quien a su vez se conecta a otro seguidor también del lado izquierdo. El líder a la derecha se conecta a un seguidor a su derecha, que a su vez se conecta con otro seguidor en la parte derecha. De este modo, el líder a la izquierda no puede «tirar» de los seguidores a su derecha, porque así se lo impide el líder que está a su derecha (recordemos que la posición de los líderes es inamovible). Lo mismo le sucederá al líder de la derecha con los seguidores a su izquierda. El resultado se muestra en la figura, donde se ve que los dos nodos a la izquierda terminan con exactamente la misma posición que el líder a la izquierda, y los dos a la derecha terminan en consenso con el líder a la derecha (en la figura, el aparente auto-lazo es solo la conexión entre los nodos a la izquierda o derecha de cada líder). Por tanto, todos los seguidores no terminan con la misma opinión, sino que ha «emergido» una polarización en las opiniones como consecuencia de la estructura de la red. Obviamente, si hay más líderes y estos no están muy cohesionados en sus opiniones, habrá polarización en término de las diferentes posiciones de estos líderes.

Figura 46. Ilustración de cómo la posición de los líderes en la red afecta el resultado del proceso de consenso. En este caso, los líderes situados en el centro de una red simétrica tiran cada uno de los seguidores más próximos a ellos. Como consecuencia, se crea una polarización del estado de consenso, en la que los seguidores de un líder terminan con sus opiniones coincidentes con la de este y los otros con opiniones idénticas a las del otro líder.
El tema de la polarización de la sociedad está ahora en boca de todos. El periódico El País del 6 de febrero de 2022 tituló uno de sus artículos como «La polarización se dispara y embarra la política», mientras que La Vanguardia del 21 de octubre de 2022 publicó el artículo «Una España cada vez más extrema: la polarización de la sociedad se dispara un 5.000% en 10 años». La mayoría de las tertulias dedican tiempo a este tema en la radio y la televisión. ¿De qué polarización se está hablando? Está claro que, en parte, se habla de polarización política, pero también de polarización de opiniones respecto a diferentes temas de actualidad. Aclaremos el asunto.
El lector estará de acuerdo conmigo en que podemos hablar de una alta polarización dentro de un grupo si este se divide en dos partes extremas que mantienen opiniones opuestas. En este caso, la polarización será mayor, mientras mayor sea la separación de estos dos grupos en el espacio de opiniones. Un ejemplo concreto sería una mayor polarización a los extremos de las opiniones entre la izquierda y la derecha políticas. Pero ¿qué diríamos si el grupo se divide no en dos, sino en tres facciones de opiniones en las que se «atrincheran» sus miembros? ¿Está este grupo más polarizado que el anterior?
El modelo de líderes y seguidores nos ofrece algunas respuestas a ambos tipos de polarización. En el primer caso, supongamos que tenemos un número de líderes en un grupo, región o país. Las opiniones de los seguidores convergerán a la envolvente convexa de los líderes (ver Figura 47). La envolvente convexa de los líderes será mayor o menor en dependencia de si estos tienen opiniones más o menos cohesionadas. Por tanto, como los seguidores tienen diferentes conectividades con los líderes, se producirá una mayor o menor polarización de sus opiniones en dependencia de la cohesión de la opinión de sus líderes. A mayor cohesión de los líderes, menor polarización. Es posible que, en términos de los grupos políticos más representativos, lo que estamos viendo en la actualidad es una menor cohesión de opiniones entre los líderes que hace que sus bancadas terminen cada vez más polarizadas.
Figura 47. Ejemplo del estado final de consenso de varios seguidores (en negro) cuando los líderes del grupo (en gris) están más (izquierda) o menos (derecha) cohesionados. La envolvente convexa es el área sombreada entre los líderes.
Por otra parte, el modelo de líderes y seguidores nos permite también ver claramente los efectos del aumento de líderes en el grupo (ver Figura 48). En este caso, si hay pocos líderes, las opiniones de los seguidores se repartirán entre estos creando un polígono de polarización pequeño, por ejemplo, un triángulo. Sin embargo, si hay muchos líderes, las opiniones de los seguidores se repartirán entre todos, creando polígonos de polarización de muchos vértices. En una sociedad real, estos líderes y sus seguidores no lo son sobre un único tema, sino sobre muchos. Habrá un par de líderes de opinión sobre «cambio climático», otro par sobre «vacunación», otro par sobre «aborto», otros sobre «feminismo», etc. Esto ocasionará que la sociedad como un todo esté polarizada en muchos grupos de opinión diferentes. Es obvio que esta situación se puede haber visto agravada más recientemente por la inundación de información en las redes sociales, donde no solo las personas, sino también los bots de información, difunden sus opiniones como líderes y seguidores (ver capítulo sobre redes sociales en línea).
Figura 48. Ejemplo del estado final de consenso de varios seguidores (en negro) cuando hay pocos (izquierda) o muchos (derecha) líderes (en gris) en el grupo. La envolvente convexa es el área sombreada entre los líderes.
Pero siempre habrá líderes que guíen mejor a sus seguidores que otros, por lo que cabe preguntarse acerca de quiénes son los mejores líderes en una red.
La respuesta a esta pregunta depende obviamente de lo que creamos que significa «mejor». Así que de forma general tendrá tantas respuestas como personas hayan sido interrogadas con esta pregunta. Por ello, aquí nos centramos en una definición muy concreta de lo que entendemos por «mejor». En nuestro caso, el «mejor» líder es aquel que logra el consenso de los seguidores en el menor tiempo en relación con otros posibles líderes. Es decir, supongamos que en un grupo dado seleccionamos a tres líderes para lograr el consenso. Calculamos el tiempo que se demora en lograr el consenso global del grupo. Ahora, seleccionamos otros tres líderes y volvemos a calcular el tiempo que demora llegar al consenso. Los líderes que hayan logrado el consenso en un menor tiempo son «mejores» que los que lo han logrado en un mayor tiempo.
Para analizar quiénes son los potenciales mejores líderes usaré la siguiente estrategia. Primero, selecciono tres líderes completamente al azar. Estos serán nuestros primeros candidatos a «mejores» líderes. Luego, selecciono los tres individuos que tengan el mayor número de conexiones en la red, o sea, el mayor grado. Finalmente, selecciono a los tres individuos con la mayor centralidad de intermediación.
Veamos los resultados para la red de los médicos de Galesburgo, para la cual tenemos las conexiones de amistad y las de asesoramiento técnico. En la red de amistad vemos claramente que la elección aleatoria de los líderes no es una buena estrategia (véase la Figura 49), ya que el tiempo para lograr el consenso es muy grande (superior a las 800 iteraciones del modelo). Dicho de otra manera, cualquiera en la red no es un buen líder para lograr el consenso de sus seguidores. Los médicos más conectados en la red logran el consenso en un tiempo mucho más rápido (menos de 400 iteraciones). Esto es de esperar, ya que los mismos pueden «convencer» a un gran número de seguidores quienes están conectados directamente a ellos, lo que les llevaría menos tiempo que el hecho de convencer a seguidores más alejados socialmente. Sin embargo, los médicos que tienen la mayor centralidad de intermediación son los más efectivos en lograr el consenso en toda la red de amistad (menos de 200 iteraciones). La diferencia es que, mientras que los médicos de mayor grado (estrellas en la figura) están conectados entre sí y apiñados en la misma región de la red, los de mayor intermediación (círculos en la figura) están desperdigados por diferentes partes de la red. Por el contrario, la selección aleatoria de los nodos no produce buen resultado, porque la probabilidad de elegir líderes con poca centralidad es muy alta, aunque estos estén dispersos en toda la red. En resumen, si usted representara a la autoridad o compañía que quiere propagar el uso de la tetraciclina entre los médicos del condado y conociera los resultados descritos en el párrafo anterior, solo tendría que visitar a los tres médicos marcados con círculos e intentar convencerlos de la importancia del uso de este nuevo antibiótico. Ellos se encargarían de hacer el resto en la red.
Figura 49. Ilustración de cómo diferentes líderes pueden lograr diferentes niveles de consenso en un mismo grupo. En este caso, se ilustra para la red de amistad entre los médicos de Galesburgo. Se seleccionan líderes de acuerdo con sus grados, intermediación o de forma aleatoria. Los nodos más centrales son indicados en la figura de la derecha: círculos para la intermediación y estrellas para el grado. Las dinámicas se muestran en la figura de la izquierda.
Ahora consideremos la red de asesoramiento entre los mismos médicos. En la Figura 50 (panel izquierdo) se muestra el progreso del proceso de consenso en dicha red.
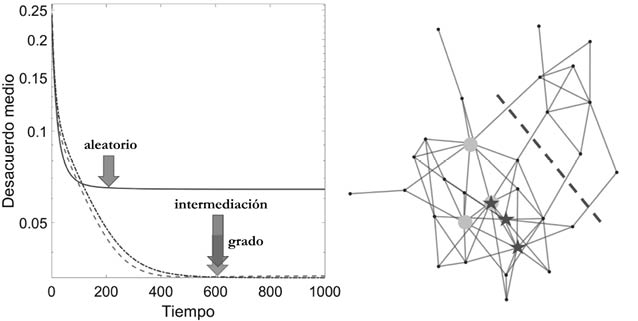
Figura 50. Ilustración de cómo diferentes líderes pueden lograr diferentes niveles de consenso en un mismo grupo. En este caso, se ilustra para la red de asesoramiento entre los médicos de Galesburgo. Se seleccionan líderes de acuerdo con sus grados, intermediación o de forma aleatoria. Los nodos más centrales son indicados en la figura de la derecha: círculos para la intermediación y estrellas para el grado. Las dinámicas se muestran en la figura de la izquierda.
A diferencia del caso anterior, aquí los resultados son un tanto «alocados». Resulta que los líderes seleccionados completamente al azar llevan a los seguidores al consenso más rápidamente que los médicos más conectados o con mayor intermediación en la red. ¿Qué pasa aquí? Para entenderlo, tenemos que visualizar la red, la que se muestra en el panel de la derecha de la figura. He dibujado una línea discontinua que separa dos partes de la red. Como se puede observar, estas dos partes están conectadas entre sí solo por cuatro aristas: es como si una ciudad tuviera dos partes divididas por un río, al cual cruzan cuatro puentes. Cada una de estas regiones se conoce en el argot de la teoría de redes como una «comunidad». Una comunidad, topológicamente hablando, se define como un conjunto de nodos cuya densidad de conexiones es mayor que la densidad de conexiones entre estos nodos y el resto de los nodos de la red (ver Figura 51). Existen diferentes metodologías y algoritmos para hallar comunidades en una red (véase por ejemplo [49]).
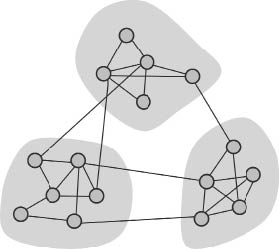
Figura 51. Ejemplo de comunidades en una red. Cada comunidad se caracteriza por tener mayor densidad de conexiones entre los nodos que pertenecen a ella que con los nodos que no pertenecen a la misma.
La nueva cuestión que surge en esta red es que los líderes seleccionados de acuerdo con el grado (estrellas en la figura) o a la intermediación (círculos en la figura) están todos en la misma comunidad (la de la izquierda en la Figura 50). Por tanto, estos líderes llevarán a «su comunidad» al consenso de manera muy rápida y eficiente, pero no a los médicos que están en la otra comunidad. Cuando existen comunidades tan bien demarcadas como en este caso (pensemos en las bancadas de izquierda y derecha en un parlamento, algo que veremos más adelante), se logran consensos en cada bancada relativamente rápido, pero el consenso global es mucho más lento. ¿Qué pasa al elegir líderes al azar? Cuando elegimos líderes al azar tenemos la posibilidad de que los elegidos sean de diferentes comunidades. En este caso, cada líder «local» llevará a su propia comunidad al consenso de forma efectiva y luego se logrará el consenso global. Por tanto, en este simple experimento se ha puesto de manifiesto que, cuando en las redes existen comunidades o bandos bien definidos, los líderes locales son más eficientes que los líderes globales para lograr el consenso. Obviamente, podemos elegir ahora los nodos más centrales en cada comunidad y lograr un consenso más efectivo que eligiendo los líderes globalmente.
Los resultados anteriores surgieron del análisis del modelo de líderes-seguidores durante la tesis de mi estudiante de doctorado Eusebio Vargas Estrada en la Universidad de Strathclyde en Glasgow, quien es ahora profesor en el Instituto Tecnológico de Monterrey en México. Los resultados de este trabajo fueron publicados en 2013 [50]. Algo que también aprendimos con este trabajo es que muchas veces los «mejores» líderes para lograr el consenso en el menor tiempo posible no eran los «mejores» en lograr la menor «polarización» de los seguidores. Por ejemplo: en la red de amistad entre los médicos, el mayor desacuerdo medio entre los seguidores y sus líderes es el que se obtiene con los líderes de mayor intermediación, mientras que el menor desacuerdo se logra con los líderes seleccionados al azar. Por el contrario, en la red de asesoramiento, el menor desacuerdo es el que se logra por los líderes de mayor centralidad. El desacuerdo entre los individuos es mayor debido a que, como pasaba en el caso de la cadena lineal analizada en la sección anterior, unos seguidores «siguen» más a un líder, mientras que otros seguidores «siguen» más a otro. O sea, se genera una polarización en el estado de consenso. La razón para esta «polarización» es que los líderes tienen diferentes grupos de seguidores, que no necesariamente están bien conectados entre sí. En otras palabras, los líderes no tienen un liderazgo cohesivo. En términos de la red podemos decir que el área que abarca la envolvente convexa de los líderes es muy grande. Esto provoca que todas las opiniones de los seguidores no converjan en el centro mismo de la envolvente, sino en diferentes regiones de esta, creando polarización. Para lograr una menor polarización de los seguidores, los líderes deberán tener una alta cohesión, como se demostró en el trabajo antes mencionado con Vargas Estrada. Desafortunadamente, en el mundo real cada día se ve menos cohesión de los líderes, no solo en política, sino en temas vitales como el cambio climático, la economía, vacunación, etc. Es posible que esta sea una de las causas por las que cada vez observamos mayor polarización de opiniones y menos consenso global.
Retornemos a la comunidad 70 de los campesinos brasileños. Como se puede observar en la Figura 52 (panel izquierdo), esta comunidad de campesinos está dividida en dos módulos, cuyos nodos se ilustran entre líneas discontinuas. Solo existe una conexión entre los campesinos de un módulo con los campesinos del otro.
Figura 52. Ilustración de los dos módulos existentes en la comunidad 70 de campesinos brasileños (izquierda). Los nodos en cada módulo se demarcan con línea discontinua. Los módulos fueron hallados en el método de Girvan y Newman [51]. Dinámica de la difusión de innovaciones en la comunidad 70 de campesinos brasileños (panel derecho) con la elección de dos líderes locales (señalados con flechas en el panel izquierdo). La curva con estrellas corresponde a los totales acumulados de adopciones en la comunidad, y los círculos a las simulaciones del modelo.
En este caso, como hemos visto antes, la existencia de líderes locales (al menos uno en cada módulo), es muy efectivo para lograr el consenso, el cual se lograría en cada módulo por separado y luego en la red como un todo. En el panel derecho muestro la dinámica de la difusión de innovaciones en esta comunidad de campesinos seleccionando dos líderes locales (aquellos con mayor grado en sus respectivas comunidades). Como podemos comprobar, los resultados de las simulaciones coinciden mucho mejor ahora con los datos reales, lo que indica la posible existencia de líderes locales en el proceso de consenso que tuvo lugar en esta comunidad de campesinos.
Pero aún puede haber otro efecto, más sutil que los anteriores, que puede influir en la dinámica del consenso: la presión social indirecta.
Hasta ahora hemos considerado solo la «presión» que ejercen sobre un individuo aquellos que están directamente conectados a este en la red. En alguna de las fiestas ficticias que hemos mostrado antes, alguno de los participantes seguramente recibió la presión de sus amistades para que bebiera, fumara o bailara. Un simple «vamos, por favor» (o «venga, mujer, una copita nada más» o «no pasa nada, un día es un día», etc.), por parte de sus amistades ejercería dicha presión. Esta presión social (o de grupo) es la influencia directa de los compañeros con intereses, experiencias o estatus sociales similares. Debido al hecho antes considerado de que las conexiones entre personas en una red social revelan intereses comunes entre las partes, es más probable que los miembros de un grupo de iguales influyan en las creencias, los valores y el comportamiento de una persona. De esta forma, un individuo puede verse animado y querer seguir a sus compañeros cambiando sus actitudes, valores o comportamientos para ajustarse a los de los compañeros que ejercen la influencia. Obviamente, esta presión no solo puede tener connotaciones negativas, haciendo que un individuo adopte hábitos no saludables, sino que también puede ser la fuerza motriz de la adopción de innovaciones como las que hemos considerado antes.
La cuestión es que, en la fiesta (y en la sociedad en general), estamos expuestos no solo a las actitudes y presiones directas de nuestras amistades, sino a las influencias indirectas del grupo (o sociedad) como un todo. Es probable que un adolescente no sienta la presión de sus amistades para que adopte cierto hábito como fumar o beber alcohol. Sin embargo, este es capaz de observar que otros adolescentes como él tienen normalizados dichos hábitos y estos se perciben como una atracción a ser «normal» respecto a sus pares. La misma presión indirecta la podrían experimentar los superintendentes de las escuelas en Allegheny si «perciben» que otras escuelas están adoptando el nuevo método matemático, aunque no sean aquellas cuyos superintendentes son sus amigos. Esto los dejaría un tanto fuera de la norma social y los «presionaría» indirectamente a aceptar la innovación.
Para analizar la presión de grupo indirecta debemos tener en cuenta lo siguiente. En el caso de la presión directa, el efecto se transmite solo entre los nodos conectados entre sí en la red. No obstante, la presión indirecta se transmite entre pares de nodos que no están conectados en la red. La intuición nos dicta que dos personas que están separadas solo por un intermediario en la red social tienen más características (gustos, valores, intereses, etc.) en común que otras dos que estén separadas entre sí por una cadena de diez aristas. Existe la posibilidad de que en algún momento las personas separadas entre sí por solo dos pasos en la red se conviertan en amigos debido a la transitividad característica de la amistad. Las dos personas que están a una distancia de diez pasos en la red difícilmente se convertirán en amigos, al menos sobre la base de la transitividad social. Nótese que esta separación no es geográfica, sino social. Dos personas geográficamente distantes pueden tener una distancia social muy pequeña si pertenecen al mismo grupo social. Al mismo tiempo, dos personas que viven en el mismo barrio pueden estar muy distantes socialmente entre sí. Por tanto, es de esperar que las primeras dos personas tengan una influencia indirecta la una sobre la otra mucho mayor que las segundas que están separadas a una distancia de diez pasos.
En el año 2012, mientras trabajaba en la Universidad de Strathclyde en Glasgow, Reino Unido, definí una forma matemática de capturar esta influencia indirecta de los nodos en una red [52]. Para entenderla mejor, usemos el ejemplo de la red social mostrada en la Figura 53.
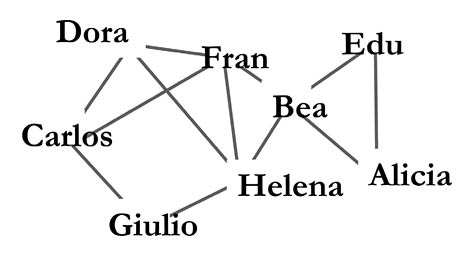
Figura 53. Ilustración de una red social hipotética.
Ahora represento las ego-redes de influencia directa e indirecta para cada uno de los miembros de este pequeño grupo social. Una ego-red es una red donde se muestran solo las interacciones de una persona. En este caso mostraremos no solo las interacciones, sino las influencias indirectas a dicha persona. Veamos un ejemplo: Alicia está influenciada directamente por Bea y por Edu, que son sus amistades en la red. Sin embargo, Alicia puede estar influenciada indirectamente por Helena y Fran, quienes se encuentran a solo dos pasos de ella en la red. De este modo, Alicia está más débilmente influenciada por Carlos, Dora y Giulio, quienes están a tres pasos de ella. En el panel de la ego-red de Alicia (primer panel de la Figura 54) represento las influencias directas por líneas más gruesas. Las influencias de las personas a distancia dos las represento por líneas algo menos gruesas y las influencias más débiles por líneas mucho más delgadas. En la figura represento a cada persona por la primera letra de su nombre. De este modo, podemos crear las ego-redes de cada individuo en la red como se ilustra en la Figura 54. El grosor de la línea, que representa la fortaleza de la interacción entre un par de individuos, es fácilmente representable a través de una función matemática que dependa de la separación entre los pares de personas en la red.
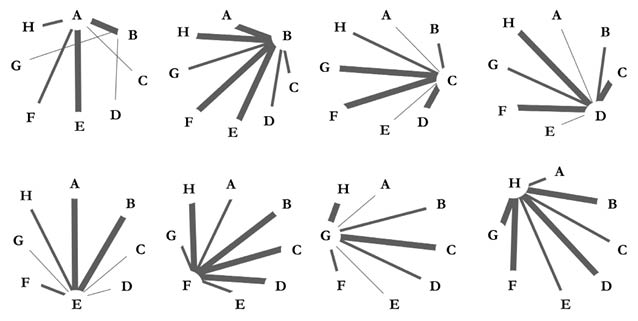
Figura 54. Representación de los diferentes tipos de interacciones entre un grupo de 8 individuos cuando interacciones sociales indirectas. Cada letra representa la inicial de un nombre en la red de la Figura 46. El grosor de las aristas indica la fortaleza de las interacciones, las cuales decaen con la separación de los nodos en términos de distancias de caminos más cortos.
La superposición de las 8 ego-redes correspondientes a cada individuo en la red creará una representación de las presiones de grupo directas e indirectas entre todos los pares de individuos en la red. Si tomamos que la presión directa recibe un valor de uno para cada par de individuos directamente conectados en la red, entonces la presión indirecta es un número entre 0 y 1, que decae con la distancia de camino más corto en la red entre los individuos. Por ejemplo, podemos asumir que esta dependencia con la distancia topológica es del tipo de ley de potencias dij-s, donde s es un número positivo y dij es la distancia del camino más corto entre los individuos i y j. Pongamos que s=3, entonces los pares de nodos unidos entre sí tendrán una influencia mutua del 100%; los que estén separados por dos pasos en la red tendrán una influencia mutua del 12,5% y los que lo estén a tres se influirán con una potencia de solo el 3,7% de la potencia que tendría dicha influencia si los nodos estuvieran conectados. Si dos nodos están separados a una distancia de cinco pasos en la red, su influencia mutua sería de menos de un uno por ciento respecto al hecho de si estuvieran unidos directamente. Si queremos que estas influencias decaigan menos con la separación entre los individuos, debemos aumentar el valor del exponente s.
Este modelo, que incluye la presión de grupo directa e indirecta, fue aplicado al estudio del consenso en redes reales en la tesis de Eusebio Vargas Estrada que mencionamos antes y publicado en 2013 [50]. Para mostrar un ejemplo de la influencia que tiene la presión social indirecta en la adopción de una innovación, tomemos la red de la comunidad 71 de los campesinos brasileños que he mostrado antes. Como sabemos, en esta comunidad la adopción de las semillas híbridas de maíz por parte de toda la comunidad llevó 20 años. Esto es justamente lo que se muestra en el panel izquierdo de la Figura 55, donde he calibrado el tiempo de simulación al tiempo real en que sabemos se adoptó el consenso, o sea, a 20 años. Si ahora tomamos exactamente la misma red, con exactamente el mismo estado inicial de cada nodo (su opinión en valor numérico entre cero y uno), pero añadimos cierta presión indirecta de grupo definida por la ley de potencias dij-3 (que, como hemos visto antes, es relativamente pequeña), observamos el gráfico de la derecha en la figura. En otras palabras, el tiempo que ahora se necesita para lograr exactamente el mismo nivel de consenso es de solo 5 años, un 20% del tiempo necesario si no hubiera ninguna influencia indirecta entre los campesinos.
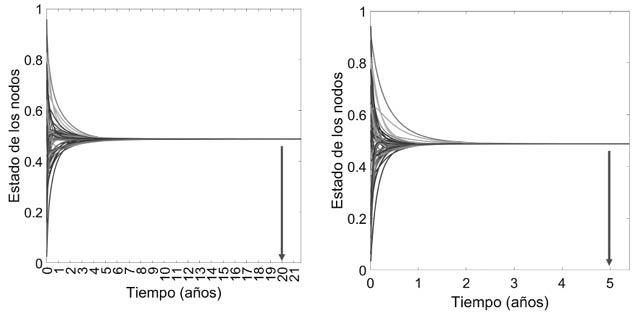
Figura 55. Ilustración del efecto de la presión social indirecta para la adopción de innovaciones en la comunidad 71 de campesinos en Brasil sin (izquierda) y con (derecha) presión social indirecta. La flecha indica el tiempo en que se logró la adopción de la innovación en cada caso.
Debo aclarar algunos puntos antes de continuar. En los resultados de la adopción de las semillas híbridas de maíz, no sabemos a ciencia cierta si hubo presión indirecta de grupo o no. Estamos asumiendo que el tiempo de 20 años que duró la adopción de la innovación fue sin dicha presión indirecta. Si la hubiera habido, entonces los resultados obtenidos al usar dij-3 equivaldrían a considerar que se aumente la presión social indirecta con respecto a la que había cuando se desarrolló el estudio original. Este estudio se desarrolló en los años 60 del pasado siglo, por lo que podemos garantizar que los participantes no usaban redes sociales en línea. ¿Por qué es importante mencionar esto aquí? Resulta que una forma de aumentar la presión indirecta de un grupo es a través de dichas redes (que veremos en la próxima sección). Pensemos en lo que sucede, por ejemplo, en Twitter. Un usuario de esta red social puede leer no solo lo que han publicado aquellos a quienes sigue, sino también lo que escribieron otros a quienes sus contactos en la red puedan seguir y retuiteen sus tuits. Por tanto, un usuario puede estar recibiendo una avalancha de influencias indirectas de otros usuarios no directamente conectados a este y de ese modo influir en la adopción de una innovación. Este es lógicamente el lado positivo de estas nuevas tecnologías, pero exactamente el mismo proceso ocurre si la adopción de que se trata es un mal hábito, un adoctrinamiento u otra conducta antisocial.
Para ver de forma más clara cómo los diferentes campesinos de la comunidad 71 fueron adoptando las semillas híbridas de maíz, graficamos los resultados del estudio original en la Figura 56, donde el número de adoptantes acumulado en cada año del estudio se ilustra con círculos. Al mismo tiempo, los resultados en el hipotético caso de aumentar la presión indirecta de grupo para los mismos campesinos se ilustran en forma de estrellas.
Figura 56. Ilustración del efecto de la presión social indirecta para la adopción de innovaciones en la comunidad 71 de campesinos en Brasil sin (círculos) y con (estrellas) presión social indirecta.
Obviamente, la influencia de la presión indirecta de grupo sigue dependiendo de la estructura de la red. Por tanto, habrá redes en las que, para lograr una aceleración del proceso de consenso, sus miembros tendrán que ejercer una mayor influencia indirecta que en otras redes.
¿Influyen las interacciones indirectas en la elección de los «mejores» líderes?
La cuestión que nos ataña ahora es saber si los líderes que hemos considerado como los «mejores» para lograr el consenso en un grupo siguen siendo los mismos cuando hay presión indirecta de grupo. Para entender el papel que juega la centralidad en la elección de los líderes, veamos en la Figura 57 lo que pasa en la red de amistad entre los campesinos de la comunidad 71 si elegimos dos campesinos con muy diferente conectividad en la red. Por ejemplo, si elegimos un campesino que solo tiene un amigo en la red (panel izquierdo en la Figura 57, cuando no hay influencias indirectas, al cabo de un año la información sobre las semillas híbridas de maíz ha sido compartida con su único amigo, este la compartió con su único amigo y al final del año se pueden contar con los dedos de una mano aquellos quienes se habían enterado de la innovación. Si, por el contrario, elegimos al campesino que más amigos tiene en la red (panel derecho de la Figura 57), al cabo de un año más de la mitad de la comunidad ha tenido conocimiento de la innovación. El mecanismo usado para la transmisión sin presión social indirecta es que un campesino pasa la información a sus amigos, estos a sus propios amigos y así sucesivamente.
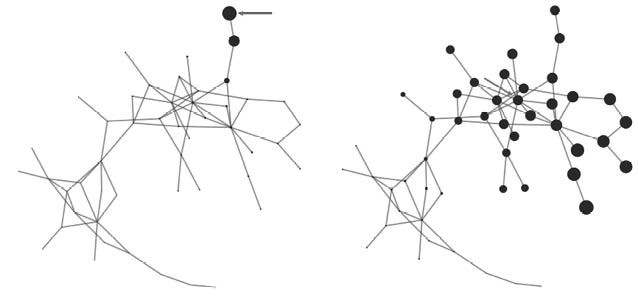
Figura 57. Dinámica de la adopción de innovaciones en la comunidad 71 de campesinos en Brasil sin presión social indirecta cuando se eligen diferentes líderes (señalados con una flecha). El tamaño de los nodos es proporcional a la probabilidad de que el nodo haya adoptado la innovación a un tiempo dado.
¿Qué pasa cuando hay presión social indirecta? Si ahora damos la información al campesino que solo tiene un amigo en la red, al cabo de un año todos los campesinos de la red estarán enterados en mayor o menor medida de la innovación como se ilustra en el panel izquierdo de la Figura 58. Lo mismo ocurre, aunque en un grado algo mayor, si le damos la información al campesino más conectado de la comunidad (véase panel derecho de la Figura 58). Es decir, en este caso la diferencia tan grande que existía entre darle la información a un campesino muy poco conectado o al más conectado de todos, se diluye casi completamente. La razón de esta diferencia es que ahora el campesino más alejado de aquel a quien le damos la información inicial es capaz de «ver» lo que está pasando en la red. Aunque reciba una influencia relativamente pequeña, estará enterado de «que algo se está cocinando» en la comunidad con respecto a unas semillas híbridas de maíz. O sea, cuando hay transmisión indirecta de información, además de la directa, parece menos importante quién es el «líder» de la comunidad. Veamos si es esto cierto o no.
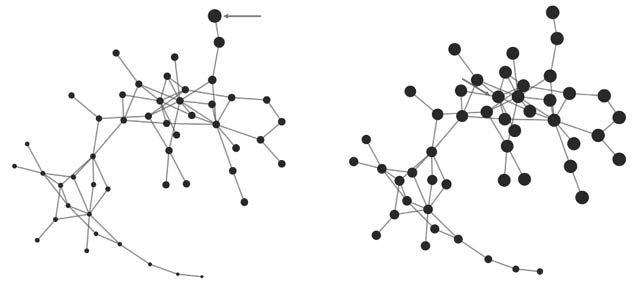
Figura 58. Dinámica de la adopción de innovaciones en la comunidad 71 de campesinos en Brasil cuando hay presión social indirecta y se eligen diferentes líderes (señalados con una flecha). El tamaño de los nodos es proporcional a la probabilidad de que el nodo haya adoptado la innovación a un tiempo dado.
Para falsificar nuestra hipótesis sobre la menor importancia de la centralidad en la elección de los líderes cuando hay presión indirecta de grupo, haré lo siguiente. En la red de amistad entre campesinos de la comunidad 71 compararé el tiempo de consenso para tres líderes elegidos al azar con el de los tres líderes más conectados o con mayor intermediación en la comunidad. Cuando no hay interacciones indirectas, el resultado es muy parecido a lo que ocurría en el caso de los médicos que vimos antes. Por decirlo de otra manera, los líderes más conectados o de mayor intermediación en la red son los que logran el consenso en menor tiempo (ver panel izquierdo de la Figura 59). Sin embargo, cuando hay presión social indirecta, esta diferencia prácticamente desaparece por completo (panel derecho de la Figura 59). Ahora los líderes emergidos al azar son casi tan «buenos» como los líderes elegidos de acuerdo con su centralidad en la red. Estos resultados no se observan únicamente en esta red, sino en una gran variedad de redes sociales del mundo real como hemos publicado Eusebio Vargas Estrada y yo en el año 2013 [50].
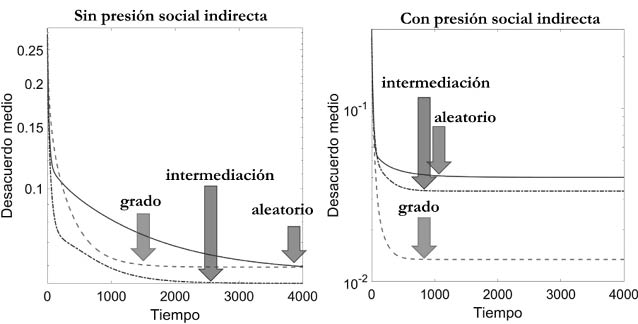
Figura 59. Comparación de las dinámicas de la adopción de innovaciones en la comunidad 71 de campesinos en Brasil sin (izquierda) y con (derecha) presión social indirecta cuando se eligen líderes de acuerdo con diferentes criterios de centralidad.
La importancia de este resultado va más allá del análisis de los líderes en pequeñas comunidades para la adopción de una innovación. Aunque no es el objetivo de este capítulo, quisiera llamar la atención del lector sobre la evolución del liderazgo en los movimientos sociales a lo largo de la historia. Tomemos por ejemplo las revoluciones sociales, las cuales son cambios fundamentales en la estructura y organización del poder establecido. Sin entrar en las complejidades técnicas del análisis de los líderes y las revoluciones que estos lideraron, cabe señalar lo siguiente. La gran mayoría de las revoluciones hasta finales del siglo XX tuvieron líderes bien reconocibles. Así, Oliver Cromwell se identifica claramente como líder de la guerra civil inglesa, mientras que Thomas Jefferson y George Washington, junto a otros, se identifican como los líderes de la revolución de los EE. UU. Lenin, Trotsky y Stalin, junto a Bukharin, fueron los líderes de la Revolución rusa, mientras que Mao Tse Tung se identifica con la Revolución china (junto con Lin Piao y Liu Chao Sh’i) y la Revolución cubana tuvo como líder principal a Fidel Castro. Por otra parte, la duración de estas revoluciones varía de una a la otra, pero en ningún caso fueron procesos instantáneos. La revolución norteamericana duró unos 9 años, mientras que Mao estuvo cerca de 20 años en la lucha por el poder. Estas revoluciones tienen por tanto mucho en común con el modelo de «líderes-seguidores» para lograr un estado de consenso, que en este caso es el apoyo de las masas. En estos movimientos hubo también influencia indirecta de los líderes a los seguidores mediante la identificación de los líderes con ciertas clases sociales. Como apunta Mehram Kanrava del Instituto de Estudios Internacionales de Los Ángeles en los EE. UU. [53], las revoluciones china y cubana ofrecen los mejores ejemplos de revoluciones en las cuales los propios revolucionarios forjaron las condiciones socioculturales o psicológicas necesarias para atraer a las masas de seguidores. Las guerrillas Fidelistas en Cuba, por ejemplo, se identificaban como los «humildes», atrayendo así el apoyo del campesinado cubano. Sin embargo, no se puede decir que esta influencia indirecta fuera muy fuerte debido a las presiones que ejercían los gobiernos para evitar la propagación de dichos mensajes, así como a la propia propaganda de descrédito hacia dichas guerrillas por parte del poder establecido.
En claro contraste con estos procesos de tipo «líder-seguidor» encontramos los que ocurrieron en el corto periodo entre el 17 de diciembre de 2010 y diciembre de 2012. En este periodo ocurrieron una serie de protestas antigubernamentales, levantamientos y rebeliones armadas en Túnez, Libia, Egipto, Yemen, Siria y Bahréin. Los ecos llegaron también a Marruecos, Irak, Argelia, Líbano, Jordania, Kuwait, Omán y Sudán donde se produjeron manifestaciones callejeras sostenidas. Los manifestantes coreaban «el pueblo quiere derribar el régimen» y esto se logró en varios de los países donde estas «revoluciones árabes» ocurrieron.
¿Quiénes fueron los líderes de estas revoluciones? Según comenta Sari Hanafi, profesor de sociología de la Universidad Americana de Beirut en el Líbano [54], «no hay líderes entre los autoproclamados líderes de las ONG, ni entre los líderes de los partidos políticos, ni entre los jeques tribales. Más bien, estamos asistiendo a revoluciones post-leninistas sin líderes». Podríamos pensar entonces que quizás hayan sido líderes anónimos, individuos no necesariamente centrales en sus redes sociales, pero con un gran uso de las interacciones sociales indirectas. Pero ¿cómo lograr tal nivel de presión social indirecta para que «cualquiera» pudiera ser un líder de estas revoluciones? Nahed Eltantawy y Julie B. Wiest de la Universidad High Point en los EE. UU. sostienen que «las redes sociales en línea jugaron un papel instrumental en el éxito de las protestas antigubernamentales que terminaron con la destitución del líder dictatorial» en Egipto [55]. Estos autores claman por la necesidad de considerar a las redes sociales en línea como una fuente importante de acción colectiva y en la organización de los movimientos sociales contemporáneos. De hecho, en su análisis anual de los derechos humanos en el mundo en el 2011, Amnistía Internacional elogió el papel de sitios web como Twitter y Facebook en el inicio de la mayor revuelta contra regímenes opresivos desde el final de la Guerra Fría. Estas revoluciones se han llamado con frecuencia las «revoluciones de Facebook» o las «revoluciones de Twitter» para destacar el papel de los medios sociales en línea en su organización. Como hemos visto más arriba, a mayor presión social indirecta, mayor dilución de la necesidad de que los líderes sean los individuos más centrales de la red. Por tanto, si esta interacción indirecta es muy grande, como ocurre con el uso de las redes sociales en línea, es posible que el liderazgo tome otra forma a la que conocíamos en el siglo XX. Alea jacta est!
El ser humano siempre ha tenido la imperiosa necesidad de comunicarse con otros seres humanos. El lenguaje apareció hace como mínimo cien mil años [56]. Este período de cultura oral o prehistoria fue seguido por el nacimiento de la «historia humana», que comenzó con la invención de la escritura hace unos 5.000 años. Con el uso de la escritura, el ser humano podía comunicarse no solo con los humanos de su tiempo, sino que podía dejar su mensaje para que lo leyéramos 5.000 años después. Los métodos de escritura, sin embargo, eran lentos y no permitían comunicar una idea a muchas personas a la vez. Una tablilla o un pergamino escritos podían estar en un solo sitio a la misma vez. Pero la invención de la escritura impresa revolucionaría esta concepción. Primero fueron los chinos quienes plasmaron sus caracteres de forma impresa. Los primeros dispositivos de tipo móvil se introdujeron en China en el siglo XI y el primer libro impreso con esta tecnología fue «Notas del Jade Hall» publicado en 1193. Esta técnica se basa en usar una gran cantidad de caracteres individuales en bloques pequeños, los que luego se unían para formar una página. Pero, teniendo cerca de veinte mil ideogramas, a los chinos les era imposible desarrollar la imprenta de forma funcional [57]. No fue hasta que Johann Gutenberg, cerca de 1440, introdujo los tipos móviles metálicos que esta revolución se materializó. Ahora se podían imprimir varias copias del mismo texto permitiendo la comunicación entre muchos humanos al mismo tiempo. Aunque quizás tenga razón el personaje del cuento Utopía de un hombre que está cansado, del gran escritor argentino Jorge Luis Borges [58], cuando dijo: «La imprenta, ahora abolida, ha sido uno de los peores males del hombre ya que tendió a multiplicar hasta el vértigo textos innecesarios».
Pero la difusión de la información a través de los libros era todavía lenta. Si se querían enviar varias copias de material impreso en Europa hacia América había que atravesar el Atlántico en una de las naves disponibles, por lo que demoraría varios días en llegar a su destino. Si no, se perdía antes de llegar.
En el siglo XIX la comunicación interpersonal pasaría a otro nivel cualitativo: la telecomunicación. Esta se refiere a la transmisión de sonidos e imágenes a través de la distancia usando señales electrónicas, ópticas o electromagnéticas. De esta forma, y con el esfuerzo de varios titanes de la ciencia y la tecnología, se lograba la comunicación interoceánica casi instantáneamente. El 25 de enero de 1915 Alexander Graham Bell habló telefónicamente desde Nueva York con Thomas Watson, quien se encontraba a casi 5.000 km de distancia en San Francisco, California. Otros inventos también tenían como objetivo principal la comunicación con muchas personas a la vez. Este es el caso del desarrollo de la radio en 1896 y de la televisión a principios del siglo XX. Ya en la segunda mitad del siglo XX, en 1973, el ingeniero Martin Cooper desarrolló el primer teléfono sin cables, cuyo posterior perfeccionamiento dio lugar a los teléfonos móviles en los años 90 del siglo XX.
Pero «ninguna de estas formas de comunicación interpersonal jugó un papel tan significativo en la vida humana como lo ha hecho la comunicación mediante el uso de ordenadores conectados a una red» [57]. Esta infraestructura se conoce como la Internet y es una red de redes a nivel global en las que los ordenadores están interconectados a través de líneas de transmisión de datos. La Internet nació oficialmente el 1 de enero de 1983. Fue en esta fecha cuando se comenzó a usar un nuevo protocolo de comunicaciones entre ordenadores en diferentes redes, llamado Protocolo de Control de Transferencia/Protocolo de Red (TCP/IP). Una de las motivaciones de crear esta red estaba en el hecho de que en los años 1960 los ordenadores que existían eran enormes y pesados, y a nadie se le ocurría viajar con uno a bordo, por lo que había que ir al sitio donde estaba el ordenador para ver la información que este contenía. Así que uno de los objetivos era que los investigadores gubernamentales compartieran información. La otra motivación era de índole militar y estratégica. En plena guerra fría, y con la amenaza de un ataque nuclear desde el bloque soviético, el Departamento de Defensa de Estados Unidos se planteó la posibilidad de crear una red que le permitiera seguir difundiendo información incluso después de un ataque nuclear. Es poco conocido que también la Unión Soviética había comenzado con la idea de desarrollar una red de redes, aunque esta tenía motivaciones diferentes y no llegó a concretarse [59].
Ya a finales del siglo XX había una infraestructura que nos permitía comunicarnos mediante los ordenadores. Fue entonces que en 1997 se lanzó la primera «red social en línea». Ese año se lanzó «SixDegrees.com», en completa alusión al fenómeno mencionado en este libro sobre los «seis grados de separación». En esta red los usuarios podían crear sus «perfiles», tener una lista de amigos y compartir información con una comunidad. El sitio atrajo a millones de usuarios, pero tuvo que cerrar en el año 2000 por problemas económicos. Sin embargo, a partir del año 2003 se produce una explosión de redes sociales en línea. Primero fue la creación de LinkedIn, MySpace, Last.FM, Delicious, Hi5, Xing y Picso en 2003 y luego de varias otras que incluyen: Facebook (solo en Harvard) en 2004, YouTube en 2005, la extensión de Facebook de forma global y la creación de Twitter ambas en 2006.
¿Cómo «es» una red social en línea?
Una red social en línea es, de acuerdo con George Pallis y colaboradores de la Universidad de Chipre [60], un sitio web que: (i) actúa como un centro para que los individuos establezcan relaciones con otras personas (amigos, colegas, etc.), cada usuario articula una lista de otros usuarios con los que se comparte una conexión; (ii) incluye una amplia gama de herramientas para que las personas construyan un sentido de comunidad de manera informal y voluntaria, los usuarios en línea interactúan entre sí, aportan información al espacio de información común, y participan en diferentes actividades interactivas (por ejemplo, subir fotos, etiquetar, etc.); (iii) contiene componentes específicos que permiten a las personas: definir un perfil en línea, hacer una lista de sus conexiones (por ejemplo, amigos, colegas), recibir notificaciones sobre las actividades de esas conexiones, participar en actividades de grupos o comunidades y controlar la configuración de permisos, preferencias y privacidad. O sea, una red para compartir información. Algunas características generales de las redes sociales en línea más conocidas son las siguientes.
Facebook (www.facebook.com): fue fundada por Mark Zuckerberg en febrero de 2004 y en 24 horas ya tenía 1.200 usuarios entre los estudiantes de la Universidad de Harvard, entre los que se había distribuido. En septiembre de 2006, la red se amplió a cualquier persona con una dirección de correo electrónico registrada. En abril de 2022 esta red tenía casi tres millardos68 de usuarios activos mensuales. Según el análisis de George Pallis y sus colaboradores en 2011 los usuarios pasaban una media de 20 minutos diarios en el sitio, aportaban cuatro millardos de informaciones, mas de ochocientos millardos de fotos y ocho millones de vídeos cada mes. En 2011, Alessandro Provetti del Departamento de Físicas de la Universidad de Mesina y sus colaboradores analizaron una porción de Facebook creando una red de mas de ocho millones de nodos [61]. Cada nodo representa un usuario de Facebook y las aristas de la red representan las conexiones entre usuarios. En total, la red contenía mas de doce millones de aristas69. Por tanto, la densidad de aristas de la red es de 3,7 ·10-7. Esto es una densidad extremadamente baja, en la que solo existe una de cada diez millones de las posibles conexiones entre usuarios en la red. Como medida de la separación media entre los usuarios Provetti y colaboradores usaron el diámetro efectivo, que es el número mínimo de aristas en los que una fracción (o cuantil q, digamos q=0,9) de todos los pares de nodos conectados pueden alcanzar a los demás. Este valor resultó ser 8,75, lo que indica que en el 90% de la red un par de usuarios están separados por menos de 9 clics. El logaritmo del número de usuarios considerados es de 15,9, por lo que la red, en este sentido, es claramente un «mundo pequeño». El índice de transitividad media de la red fue de 0,0789. Esta transitividad es cinco millones de veces más alta que la que se debería esperar si la red se hubiera creado por las conexiones aleatorias de los usuarios. Por tanto, es evidente que las conexiones siguen los patrones de transitividad de las relaciones sociales: si Joan está conectado a Marga y Marga lo está con Julia, entonces hay una alta probabilidad de que Julia y Joan estén también conectados en Facebook. El grado medio de los usuarios según el análisis de Provetti y colaboradores es de 396,8. Es decir, que como media cada usuario de Facebook tiene unos 400 contactos. Esto obviamente sobrepasa con creces el número de Dunbar, lo que significa que contactos y «amigos» son dos cosas bien distintas.
Twitter (www.twitter.com): fue fundada por Jack Dorsey, Biz Stone y Evan Williams en marzo de 2006, y lanzado públicamente en julio de 2006. En esta red se combina un servicio de redes sociales y microblogging lo que permite a los usuarios publicar sus últimas actualizaciones. Cada actualización se limita a 140 caracteres (llamados tuits) y puede publicarse a través de un formulario web, un mensaje de texto o un mensaje instantáneo. Los tuits se envían a los suscriptores del autor, a los que se les llaman «seguidores». Los seguidores pueden indicar si les gusta el tuit («like») y también pueden reenviarlo (retuitear). Twitter se ha utilizado para hacer campañas políticas, con fines educativos, relaciones públicas, etc. Según los datos publicados en septiembre de 2022, esta red social en línea tenía mas de trescientos millones de usuarios activos. Sofía Aparicio y sus colaboradores del Instituto de Tecnologías Físicas y de la Información «Leonardo Torres Quevedo», del CSIC en Madrid, España [62], han estudiado 51.217.93670 usuarios de Twitter conectados a través de los casi dos millardos de aristas. Esto indica que existen 7,5 aristas por cada diez millones de pares de usuarios. Como media, cada usuario tiene 38,33 conexiones, mientras que los más conectados tienen una media de 47,35 amigos y de 67,62 seguidores. La transitividad media de las relaciones en Twitter es de 0,096, lo cual es más de 250.000 veces mayor que la esperada para una red aleatoria de igual tamaño y densidad. Los autores estimaron una cota superior para la distancia media entre los pares de usuarios de solo 5,28 clics. O sea, la red es sin duda un «mundo pequeño». Además, Twitter mostró una distribución de grados muy similar a las redes del tipo «libre de escala» como las de Barabási-Albert que hemos visto antes.
Flickr (www.flickr.com): fue fundada por Stewart Butterfield y Caterina Fake en febrero de 2004 y adquirida por Yahoo! en marzo de 2005. Es una red social en línea dedicada a compartir fotos y vídeos, donde se suben, etiquetan y organizan millones de fotos. En 2013 se reportaban un total de casi noventa millones de usuarios, y unos tres millones y medio de imágenes eran subidas a diario. Cada usuario introduce/selecciona nuevas etiquetas para una determinada foto/vídeo y el sistema sugiere al usuario etiquetas relacionadas, basadas en las que el usuario u otras personas han utilizado en el pasado junto con (algunas de) las etiquetas ya introducidas. En un estudio conducido por Alan Mislove y colaboradores del Instituto Max Planck para Sistemas de Software se obtuvieron datos de casi dos millones71 de usuarios y cerca de veintitrés millones de enlaces mediante un rastreo realizado el 9 de enero de 2007 [63]. La densidad de la red es, por tanto, de algo más de un enlace por cada cien mil pares de usuarios en la red. Cada usuario tenía un promedio de 12,24 «amigos», mientras se reportaban 103.648 grupos de usuarios. Cada usuario pertenecía como media a 4,62 grupos. La red tenía una distribución de grados bastante asimétrica, incluso mayor que las de las redes del tipo Barabási-Albert. Como media, dos usuarios elegidos al azar están separados por 5,67 clics, y no hay dos usuarios a más de 27 clics en Flickr. La transitividad de las relaciones entre los usuarios de esta red es muy alta con un índice de transitividad de 0,313 el cual es 47.200 veces superior a si la red se hubiera creado con el modelo de Erdős-Rényi.
YouTube (www.youtube.com): fue fundada por Steve Chen, Chad Hurley y Jawed Harim en febrero de 2005. Esta red social permite a los usuarios publicar sus vídeos. En noviembre de 2006, YouTube fue comprada por Google por $1.650.000.000. En mayo de 2022, YouTube ha sido clasificado como el sitio web más visitado en Internet. En la misma fecha había cuatro millardos y medio de usuarios activos en YouTube. Todos los usuarios pueden ver vídeos abiertos, mientras que los usuarios registrados pueden subir un número ilimitado de vídeos. Mislove y colaboradores [63] obtuvieron datos de mas de un millón de usuarios y casi cinco millones de enlaces mediante un rastreo realizado el 15 de enero de 2007. Esto da una densidad de algo más de siete conexiones por cada millón de pares de usuarios. Cada usuario tenía como media 4,29 «amigos» y pertenecía a una media de 0,25 de los más de 30.000 grupos existentes. La distribución de grados es bastante parecida a la de la red Flick, o sea, del tipo «libre de escala». Aquí, cada par de usuarios está separado como media por solo 5,10 clics y ningún par de ellos está a más de 21 clics de distancia. La transitividad de las relaciones entre los usuarios muestra un índice de transitividad de 0,136 el cual es 36.900 veces superior al de una red similar obtenida con el método de Erdős-Rényi.
En resumen, podemos ver que las redes sociales en línea son bastante parecidas a las redes sociales cara-a-cara en cuanto a que: (i) tienen muy bajas densidades; (ii) son pequeños mundos; (iii) tienen distribuciones de grados asimétricas; (iv) tienen altas transitividades en relación con las redes completamente aleatorias; y (v) forman comunidades.
A pesar de estas similitudes estructurales entre ambos tipos de redes sociales, existen un número de diferencias que es bueno conocer. En nuestras relaciones sociales cara-a-cara sabemos quiénes son nuestros interlocutores, somos capaces de ver sus gesticulaciones y detectar sus estados de ánimo: si están contentos o irritados, si están siendo sarcásticos o no, etc. Pero en una red social en línea no necesariamente sabemos quién es nuestro interlocutor, ni siquiera si es real o ficticio. Esto trae una serie de problemas que se estudian en el contexto específico de las redes sociales en línea y que Umit Can de la Universidad Manzur y Bilal Alatas de la Universidad Firat, ambas en Turquía, han estudiado recientemente [64]. Me gustaría mencionar aquí algunos de estos problemas para que el lector tenga una idea clara de los riesgos reales que existen en la comunicación en línea mediate estas redes sociales72:
Preservación de la privacidad: con el desarrollo de dispositivos con capacidad de localización de nuestra ubicación se han desarrollado redes sociales móviles basadas en la proximidad. Cuando dos usuarios se envían perfiles entre sí, pueden revelar algunos datos personales e información privada que aumenta el riesgo de violación de la privacidad cuando el canal de transmisión no es seguro. Si dicha información se filtra a personas malintencionadas, estas pueden analizar la vida de los usuarios siguiendo sus hábitos en línea y recopilando otros datos sensibles. De esta forma, los usuarios pueden estar expuestos a delitos informáticos (acoso, robo de coches, secuestro, etc.).
Incapacidad de detectar «anomalías»: con «anomalías» nos referimos al comportamiento inesperado de un usuario o grupo de usuarios que resulta inusual cuando se compara con los comportamientos normales de los usuarios en la red. Es difícil para un usuario detectar por sí mismo dicha anomalía, ya que le es difícil conocer «los comportamientos normales de los usuarios en la red». Estas anomalías representan un comportamiento irregular y generalmente ilegal, e incluye a los «spammers», a los abusadores sexuales, los fraudes en tarjetas de crédito y seguros, hostilidades y violencia, etc.
Víctimas de «ciberdelincuencia»: la ciberdelincuencia se refiere a cualquier delito o daño realizados aprovechando las oportunidades creadas por las tecnologías de red. Esto incluye cualquier tipo de actividad ilegal y/o de piratería llevada a cabo mediante el uso de fuentes y herramientas de información, que interfieren con la vida privada de las personas e instituciones, y que causan daños económicos a las personas e instituciones. Ejemplos son: (i) el ciberacoso, que consiste en «enviar textos o imágenes para dañar o avergonzar a otro individuo mediante el uso de Internet, teléfonos móviles u otros dispositivos»; (ii) spam, consistente en el envío indiscriminado de texto a un gran número de personas con el propósito de realizar «phishing», propagar «malware», etc., utilizando herramientas como el correo electrónico, mensajería, blogs, grupos de noticias, redes sociales, búsquedas en la web, etc.; (iii) malware, tales como los virus, gusanos, troyanos y «bots» que pueden introducirse en nuestros dispositivos mediante el uso de las redes; (iv) fraudes, tales como el fraude con tarjetas de crédito, fraude en las telecomunicaciones, fraude en los seguros, fraude corporativo, fraude informático, fraude en la red y fraude aduanero; (v) phishing, que es un tipo de ataque informático que transmite un mensaje electrónico al usuario a través de canales de comunicación electrónica para persuadirlo de que realice determinadas acciones en beneficio del atacante; (vi) ataque de clonación de perfiles, que crea identidades falsas de ciertos usuarios aprovechando que los mismos no suelen ser precavidos a la hora de aceptar solicitudes de amistad. Los principales objetivos del malintencionado en este ataque son: obtener la información personal de los amigos de la víctima imitando el perfil del usuario real y realizar más actividades fraudulentas en el futuro ganando la confianza de los amigos comunes.
Exposición a rumores y noticias falsas: se trata en lo fundamental de la difusión de información incorrecta, es decir, la manipulación de la información.
Exposición a ironía y sarcasmo: esto quizás lo detectemos de inmediato en una conversación cara-a-cara, pero la distinción entre textos irónicos (sarcásticos) y textos no irónicos (no sarcásticos) no es trivial en la comunicación en línea. La ironía se define como una negación que no contiene ningún negador (la mayoría de los enunciados que contienen ironía son afirmativos, e irónicamente se utiliza la negación indirecta). O sea, una ironía transmite lo contrario de lo que se dice y esto puede ser malinterpretado en la red, particularmente por niños y adolescentes.
Estos son algunos de los precios a pagar por «navegar» en unas redes cuya información es a veces irrelevante, trivial o maliciosa, o como dijera el protagonista del ya mencionado cuento de Jorge Luis Borges Utopía de un hombre que está cansado [58], porque «todo esto se leía para el olvido, porque a las pocas horas lo borrarían otras trivialidades».
Ahora se dice con frecuencia que vivimos en la época de la «posverdad». El término, aunque fue acuñado en los años 1990, se hizo popular a partir de los medios anglosajones luego de la elección de Donald Trump en los EE. UU. y del Brexit en el Reino Unido. La verdad es que es un concepto dicotómico: algo es verdad o es mentira. Así que no veo por qué disfrazar a la mentira con un maquillaje de «posverdad» para que parezca otra cosa. Los eufemismos han sido usados durante años para engañar a las masas y ocultarles situaciones dramáticas, como decir que la más profunda crisis económica a la que se enfrentaba un país en su historia era un «periodo especial», por citar solo un ejemplo sufrido en carne propia. Las formas de la mentira no han cambiado en siglos, solo la forma y velocidad de transmitirlas. Seguimos inculpando a Nerón del incendio de Roma producido en la noche del 19 de julio de 64, a pesar de que el emperador, según Tácito, se encontraba a 42 kilómetros de la capital del imperio. Pero Nerón era odiado por muchos, y seguramente no les faltaron razones a Suetonio y a Dio Casio para extender la teoría de que el emperador causó el incendio para poder reconstruir la ciudad a su gusto. El objetivo de propagar esta mentira podría ser variado, pero seguramente la propagación del odio hacia el emperador era uno de ellos. Esta mentira se propagó boca a boca y mediante la escritura de textos que serían luego transcritos y así propagados en el tiempo. Alcanzaría multitudes en el espacio (todo el Imperio) y en tiempo (hasta nuestros días), pero de forma lenta.
Hoy en día la velocidad de propagación de una mentira es el tiempo que nos lleve reenviar un mensaje que «alguien» ha escrito a través de una red social en línea. Y la gran diferencia con otros tiempos es que «alguien» no es necesariamente una persona. El experto en desinformación en redes sociales en línea Filippo Menczer de la Universidad de Indiana en los EE. UU. junto con sus colaboradores [65] ha definido el término «desinformación» como todo el conjunto de noticias falsas o engañosas, bulos, teorías de la conspiración, «titulares de cebo», ciencia basura e incluso sátira que se propaga por las redes sociales en línea. Los motivos para difundir esta desinformación son variados e incluyen la motivación económica (se reciben dividendos por número de seguidores), hasta los motivos políticos. La cuestión es que, como indica Pio Baroja: «A una colectividad se le engaña siempre mejor que a un hombre». Ahora tenemos, a través de las redes sociales en línea, colectividades cada vez más grandes y accesibles que nunca, que pueden llegar a los millones, o a los miles de millones de potenciales engañados.
Cuando Menczer y sus colaboradores analizaron catorce millones de mensajes que difundían 400.000 artículos en Twitter durante diez meses, en 2016 y 2017 encontraron evidencia de que los «bots sociales» jugaban un papel desproporcionado en la difusión de artículos de fuentes de baja credibilidad. Estos bots son generadores automáticos de tuits que se usan para colmar las redes de mensajes que defienden ciertas ideas, apoyan campañas y relaciones públicas, ya sea como una cuenta falsa que reúne seguidores o como «adeptos» a una cierta cuenta de Twitter. Según encontraron Menczer y sus colaboradores, estos bots amplifican los contenidos de su conveniencia en los primeros momentos de la difusión, antes de que un artículo se vuelva viral. También se dirigen a usuarios con muchos seguidores mediante respuestas y menciones. Es evidente que los humanos somos vulnerables a esta manipulación, ya que podemos compartir el contenido publicado por los bots. Los autores encontraron que las fuentes de baja credibilidad que tienen éxito están fuertemente apoyadas por los bots sociales. Un ejemplo citado por Menczer y colaboradores fue la repercusión en Twitter de un informe de noticias fabricado, altamente viral, titulado Spirit cooking en el que se difundía la siguiente desinformación: «El presidente de la campaña de Clinton practica un extraño ritual oculto». Esto fue publicado 4 días antes de las elecciones estadounidenses de 2016 y fue compartido en más de 30.000 tuits. El análisis de este tuit permitió descubrir una amplia distribución de bots que se usaron para amplificar la noticia falsa y un número elevado de potenciales usuarios humanos que participaron consciente o inconscientemente en la difusión del bulo.
Los autores del artículo mencionado hicieron también una verificación sobre una muestra aleatoria de tuits a efectos de verificación, adoptando una definición de «información errónea» que incluye que la misma sea: contenido fabricado, contenido manipulado, contenido impostor, contexto falso, contenido engañoso, conexión falsa y sátira. Además, añadieron una categoría para las afirmaciones que no pudieron ser verificadas. Se comprobó que menos del 15% de los artículos podían ser verificados. O sea, más del 75% de la información que analizaron era falsa, dudosa o no verificable.
No crea nuestro amigo lector que está libre de caer en estas redes. Si estás expuesto a las mismas, tienes una gran probabilidad de sentir el llamado del bot algún día. Solo hace falta que leas lo que quieres leer, si es falso, a quien le importa. Está claro que frenar a los bots sociales puede ser una estrategia eficaz para mitigar la difusión de la desinformación en línea. El nuevo dueño de Twitter, el multimillonario Elon Musk, ha despedido a la mitad de su plantilla, pero nada ha dicho de frenar a los bots que difunden informaciones falsas. ¡Saque usted sus propias conclusiones!
25 La traducción literal sería: «y entonces, ¿tú de quién eres?».
26 El máximo número de aristas en una red de n nodos esta dado por 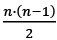 .
.
27 El número de formas posibles en que objetos se pueden combinar en grupos de k elementos se representa matemáticamente como: 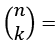
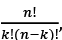 donde n! es el «factorial» de n, que se calcula como: n!=n∙(n-1)⋯1. Por ejemplo, 3!=3∙2∙1=6.
donde n! es el «factorial» de n, que se calcula como: n!=n∙(n-1)⋯1. Por ejemplo, 3!=3∙2∙1=6.
28 Matemáticamente, este término es la probabilidad de que dos nodos se conecten al azar.
29 Esta probabilidad se puede designar como .
30 Erdős se pronuncia «Erdich».
31 Como información irrelevante, diré que tengo número de Erdős igual a tres.
32 Mencionada por P. Turán, «The Work of Alfréd Rényi», Matematikai Lapok 21 (1970) 199-210. Muchas veces la frase es erróneamente atribuida a Erdős.
33 Una parte de la red en la que se puede viajar de un nodo a otro usando las aristas de dicho á.
34 La densidad de aristas es el número de aristas que tiene la red con relación al máximo número que pudiera tener. Matemáticamente, la densidad de la red es: 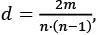 donde es el número de nodos y el de aristas.
donde es el número de nodos y el de aristas.
35 Una red en la que se puede viajar de un nodo a otro a través de sus aristas.
36 Medline es una base de datos de bibliografía médica.
37 Según los datos de Mathematical Reviews.
38 Según los datos del Physics E-print Archive.
39 Por si os interesa, las bandas se denominan: Gooch, Doddington/pepperhill, Longsight crew y Rusholme crew gangster, respectivamente.
40 Matemáticamente, una distancia debe cumplir los siguientes axiomas: (i) ser no negativa, (ii) tomar el valor de cero si y solo si el origen y el final son el mismo, (iii) la distancia entre A y B es igual a la distancia entre B y A, (iv) la desigualdad triangular, esto es que la suma de las distancias A-B y B-C sea menor o igual que la distancia A-C. La longitud del camino más corto cumple estos cuatro axiomas.
41 En una red conexa siempre existe un camino entre dos nodos de la red. Un camino es una secuencia de nodos v1,v2,⋯,vl+1 y aristas e1,e2,⋯, el tales que ei La longitud del camino es el número de aristas que este contiene. Si v1=vl+1 el camino es cerrado. Un camino simple es un camino en que no hay repeticiones de nodos ni de aristas. Si v1=vl+1 el camino simple es un ciclo.
42 También la denominaremos aquí como distancia topológica media o distancia media si no hay confusión con otras distancias.
43 El logaritmo natural de x (lnx) es la función que «deshace» la exponenciación. Así, si x=ea, entonces lnx=lnxea =a.
44 El número máximo de reenvíos necesarios en una red se conoce como su «diámetro».
45 Milgram, S. Journal of Abnormal and Social Psychology 67, 1963, 371-378.
46 Milgram, S. Obediencia a la autoridad: El experimento de Milgram. Capitán Swing, 1988.
47 Si ti es el número de triángulos que inciden en el nodo i y k es el grado del nodo i, entonces la transitividad del nodo i (llamado en inglés «clustering coefficient») es:
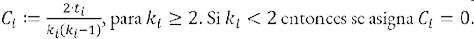
48 La transitividad media es obviamente 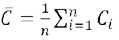 , donde n es el número de nodos.
, donde n es el número de nodos.
49 Si llamamos a este número, se establecerán relaciones con los k/2 vecinos más cercanos a la derecha y con el mismo número de los vecinos más cercanos a la izquierda.
50 Esta probabilidad es 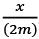 .
.
51 Una distribución de probabilidad es una función matemática que da las probabilidades de ocurrencia de los diferentes resultados posibles de un fenómeno aleatorio. Si es el grado de un nodo, entonces es la probabilidad de que un nodo elegido al azar tenga dicho grado. En el caso de una red del tipo Erdős-Rényi con nodos y probabilidad la distribución de probabilidades es: 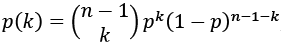 , la cual se conoce como distribución binomial. Cuando es muy grande y es constante, la distribución converge a:
, la cual se conoce como distribución binomial. Cuando es muy grande y es constante, la distribución converge a: 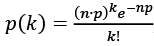 , la cual se conoce como distribución de Poisson.
, la cual se conoce como distribución de Poisson.
52 La medalla Fields es el máximo galardón que otorga la comunidad matemática internacional a un matemático de no más de 41 años. Se otorga cada cuatro años en el Congreso Internacional de Matemáticos.
53 Se refiere al matemático indio-americano Sarvadaman D. S. Chowla (22 octubre 1907-10 diciembre 1995) quien fuera especialista en teoría de números.
54 La variable sigue una ley de potencia respecto a una variable si estas se relacionan de la siguiente forma:  , donde es el exponente de la ley. Por tanto, si aplicamos logaritmos obtenemos:
, donde es el exponente de la ley. Por tanto, si aplicamos logaritmos obtenemos: 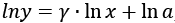 , la cual es la ecuación de una línea recta con pendiente e intercepto
, la cual es la ecuación de una línea recta con pendiente e intercepto 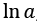 .
.
55 La centralidad de cercanía de un nodo i es: 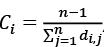 , donde n es el número de nodos y di, j es la distancia topológica entre el nodo i y cualquier otro nodo j en la red.
, donde n es el número de nodos y di, j es la distancia topológica entre el nodo i y cualquier otro nodo j en la red.
56 Edsger Wybe Dijkstra fue un científico de la computación de los Países Bajos, quien propuso un algoritmo para la determinación de los caminos más cortos desde un nodo origen, hacia el resto de los nodos en una red.
57 La intermediación de un nodo i es: 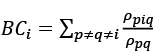 , donde
, donde 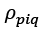 es el número de caminos más cortos entre los nodos p y q que pasan por el nodo i, y ppq es el número total más cortos entre los nodos p y q.
es el número de caminos más cortos entre los nodos p y q que pasan por el nodo i, y ppq es el número total más cortos entre los nodos p y q.
58 Psicólogo estadounidense conocido por sus contribuciones al análisis de redes sociales y por iniciar el estudio formal de la centralidad.
59 Psicólogo estadounidense.
60 Estadístico estadounidense que contribuyó en gran medida al área del análisis de redes sociales.
61 Sociólogo estadounidense amante de las matemáticas que contribuyó al desarrollo de las medidas de centralidad.
62 Técnicamente, es la entrada correspondiente al nodo en el vector propio asociado al valor propio más grande de la matriz de adyacencia del grafo.
63 Matemáticamente, la centralidad de subgrafos de un nodo se define como 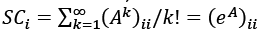 , donde A es la matriz de adjacencia del grafo eAy es la matriz exponencial de A.
, donde A es la matriz de adjacencia del grafo eAy es la matriz exponencial de A.
64 Matemáticamente, el proceso de consenso se describe por la ecuación 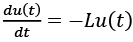 ,
, 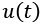 donde es un vector que contiene los estados de los nodos y L=K-Aes la matriz Laplaciana de la red, en la que es una matriz diagonal de los grados de los nodos y es la matriz de adyacencia. Se asume una condición inicial
donde es un vector que contiene los estados de los nodos y L=K-Aes la matriz Laplaciana de la red, en la que es una matriz diagonal de los grados de los nodos y es la matriz de adyacencia. Se asume una condición inicial  .
.
65 En el año 1973 las actuales República Checa y Eslovaquia formaban un estado soberano llamado República Socialista Checoslovaca. Checoslovaquia como tal existió desde 1918 hasta su disolución en 1992.
66 La conectividad algebraica es el segundo valor propio más pequeño de la matriz Laplaciana de la red, y normalmente se designa por μ2.
67 Una sigmoide es una curva en forma de «S» que se describe por la ecuación:  .
.
68 Un millardo son mil millones.
69 ¡Imagínese dibujar esta red con lápiz y papel!
70 Estos son más de cincuenta millones de usuarios. Es decir, alrededor del 20% de los usuarios totales de Twitter.
71 Estos casi dos millones de usuarios representan alrededor del 27% del número total de usuarios de Flickr.
72 El objetivo no es atemorizar sino alertar sobre estos riesgos para estar preparados.