FIGURA 2.1. Comparación entre la disposición horizontal y vertical
Una vez expuestos los conceptos relacionados con los procesos y los tipos de distribución física, estamos en condiciones de abordar un primer diseño y dimensionado muy general de una planta, sin entrar en detalles, pero incluyendo no solo las operaciones de producción, sino también los almacenes, otros departamentos, servicios anexos (administración y otros) y los sistemas de comunicación interna y con el exterior. En este aspecto se trata de un diseño integral, aunque sin profundizar.
Para conseguirlo, será preciso lograr un conjunto equilibrado en terrenos, edificios, máquinas, equipos, instalaciones y personal, que reduzca al mínimo la circulación de todo tipo (materiales, personas y elementos de producción), adecuadamente dimensionado y que se ajuste a los criterios que se consideren oportunos.
Hay que tener en cuenta que una deficiente distribución supondrá una fuente constante de pérdidas para la empresa. Por contra, una ordenada y eficiente distribución de los elementos que componen una planta de producción (equipamientos, maquinaria, materia prima y recursos humanos) incidirá positivamente en la eficacia de los procesos, en la eficiencia del sistema productivo y, por supuesto, en el resultado económico de la empresa.
En una implantación adecuada como la referida, interrelacionaremos los diversos elementos que componen los procesos productivos y todos los servicios anexos, bien sea en una superficie o en varias de ellas dispuestas en niveles. Dicha implantación puede verse afectada por diversos factores, como por ejemplo:
• Longitud de los recorridos de materiales, equipos y personas.
• Superficies necesarias para ubicar todos los elementos.
• Plantilla de personal precisa.
• Tiempos perdidos en desplazamientos y esperas dentro de la planta.
El objetivo principal del análisis de una distribución será la economía de espacio y la reducción de los recorridos de los circuitos. En este sentido, los errores que más comúnmente encontramos en muchas plantas industriales se concentran en que el espacio útil disponible no se emplea del modo más racional y en que los circuitos son, a menudo, demasiado complicados. El origen de estas deficiencias puede responder a causas tales como:
• Distribución inicialmente correcta que no ha sabido adaptarse al variar las condiciones de producción.
• Locales ya existentes que no permiten una óptima distribución.
• Complejidad del estudio que una buena distribución supone, en el que a menudo confluyen soluciones de compromiso.
Optar por mejorar la distribución de una planta ya en funcionamiento puede resultar una tarea muy costosa ya que, además de los gastos directos que acarrea, hay que considerar los derivados de la pérdida de producción. Sin embargo, de no hacerlo, incurriremos en otra serie de gastos invisibles derivados de las mejoras de producción que no obtendremos, los cuales afectan al coste de fabricación de los productos. Algunos de los factores que conciernen a la obtención de una correcta distribución en planta son:
• Movimiento de materiales, de acuerdo con las distancias que deben recorrer, la complejidad de los itinerarios y la posibilidad de ayudarse con la gravedad.
• Movimiento de personal, tanto del interno como del externo a la empresa, que deba moverse ocasionalmente por ella.
• Eliminación de los despilfarros en tiempos perdidos de personas y materiales, sea en los procesos productivos u otros.
• Aspectos de la distribución que pueden afectar a la calidad de los productos y al mantenimiento de los equipos de producción.
• Construcción e instalaciones de las plantas facilitadas por su diseño, dimensionado y distribución.
• Previsión de posibles ampliaciones futuras.
• Seguridad y condiciones de trabajo: eliminación de riesgos, ergonomía de la planta y sus puestos de trabajo, iluminación, etc.
Por lo que hace referencia a la disposición de los procesos en superficie, dos son los enfoques básicos, con relación a la superficie: la disposición horizontal y la vertical. En la figura 2.1 se muestran las ventajas de una y otra. Muchas veces estos factores afectarán de forma contradictoria a la resolución del problema, haciendo que no sea fácil encontrar la solución óptima.
Asimismo, en lo referente al proceso de análisis necesario para la implantación de cuanto abarca la distribución en planta integral, nos ocuparemos, ante todo, de los desplazamientos de los materiales a lo largo de los procesos de elaboración de los diversos productos. Dicha descripción se iniciará en el momento de la recepción de las materias primas, en su correspondiente almacén y finalizará en el lugar de destino de los productos terminados. Otros aspectos que tener en cuenta son:
• Los puestos de trabajo: producción que se espera de los mismos, espacio necesario, equipamiento, útiles, herramientas, etc.
FIGURA 2.1. Comparación entre la disposición horizontal y vertical
• Los almacenes: cantidades de materiales y productos que deben contener, así como sus características físicas, peso y volumen.
• Las vías de enlace (pasillos, transportadores, etc.): volumen de materiales y productos que desplazar por unidad de tiempo, frecuencia del transporte, características físicas de los mismos, peso y volumen.
• Tipo de disposición de los procesos: talleres, células, en cadena, flujo continuo, etc., ya expuestos anteriormente, y el tipo de operaciones y movimiento de materiales (manutención) que conlleven.
Para cada posible implantación se deberán determinar las superficies necesarias y no solo las correspondientes a la maquinaria y equipamiento de producción, sino también el espacio precisado para la alimentación y evacuación de materiales de la maquinaria, mantenimiento de la misma, circulación de personal, stocks, etc.
El dimensionado de la planta comienza, en efecto, con la determinación de la cantidad de equipos necesaria por puesto de trabajo, para abordar toda la producción programada. Para ello nos basaremos en una evaluación ajustada de las horas de trabajo por puesto en la que utilizaremos la siguiente nomenclatura:
• Horas empleadas en el puesto i para procesar una unidad del producto j: hij.
• Número total de unidades del producto j a procesar en el puesto i: Nij.
• Número total de horas en el puesto i para procesar todos los productos: Hi.
• Número total de equipos necesarios en el puesto i: Ei.
Para llevar a cabo esta evaluación, nos ayudaremos de la figura 2.2.
Para determinar el número de equipos, haremos uso de la siguiente expresión:
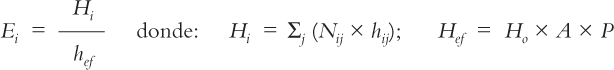
Siendo: |
Hef = Número de horas efectivas en el puesto HO = Número de horas operativas en el puesto A = Coeficiente de absentismo P = Coeficiente de productividad media en el puesto |
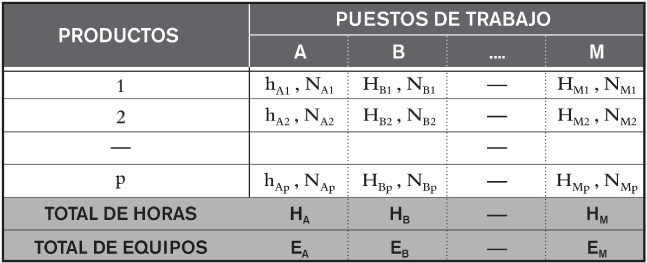
FIGURA 2.2. Evaluación de los equipos necesarios por puestos
De ser necesario, se podría incluir, además, cualquier otro coeficiente corrector conveniente.
Una vez determinada la cantidad de equipos productivos necesarios para cada puesto de trabajo, vamos a evaluar la superficie que se precisa para los mismos y la planta de producción completa. Según el método de Guerchet, la superficie total vendrá dada por la suma de tres superficies parciales (figura 2.3):
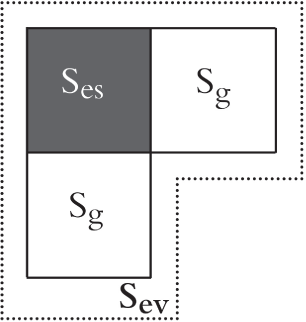
FIGURA 2.3. Superficies de Guerchet
1. Superficie estática: Ses. Esta es la superficie productiva, es decir, la que ocupa físicamente la maquinaria, el mobiliario y las demás instalaciones.
2. Superficie de gravitación: Sg. Se trata de la superficie utilizada por los operarios que están trabajando y por la materia que está procesándose en un puesto de trabajo. Esta se obtiene multiplicando la superficie estática por el número de lados (n) de esta que deban estar operativos, es decir, por los que utilizará el equipamiento productivo: Sg = Ses × n. En el caso de almacenes o de máquinas automáticas, el número de lados operativos es menor que en el caso de máquinas o equipos productivos con trabajadores operando en ellos.
3. Superficie de evolución: Sev. Contempla la superficie necesaria que reservar entre diferentes puestos de trabajo para el movimiento del personal y del material y sus medios de transporte. Se obtiene como suma de la superficie estática más la de gravitación afectada por un coeficiente k. Este variará en función de la proporción entre el volumen del material, personal y equipos de manutención que se muevan entre los puestos de trabajo y el tamaño de las máquinas y equipos e instalaciones productivas de dichos puestos, lo que se traduce en un «pasillo» de anchura relacionada con el coeficiente k alrededor del conjunto de las superficies Ses y Sg, con lo que la superficie de evolución vendrá dada por:
Sev = (Ses + Sg) × k.
A modo de ejemplo, en la figura 2.4 se dan una serie de valores del coeficiente k.
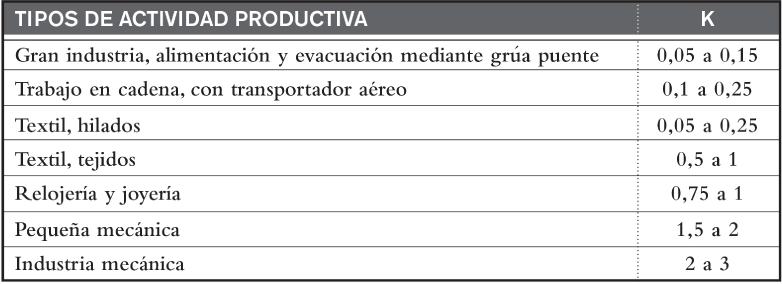
FIGURA 2.4. Coeficientes para la superficie de evolución
Un elemento muy a tener en cuenta es el material dispuesto junto a la máquina en espera de ser procesado o evacuado de la misma. Si el volumen es pequeño, como suele ocurrir en los procesos gestionados bajo los principios del lean manufacturing, ello no afectará a la superficie calculada, pero si se trata de lotes voluminosos, deberá calcularse la superficie por separado, como si de un stock se tratara, y sumarla a la superficie total.
Así pues, teniendo en cuenta los tres tipos de superficie considerados, la superficie total St que debe destinarse por puesto de trabajo vendrá dada por:
St = Ses+Sg+Sev = Ses+ (Ses × n) + [Ses+ (Ses × n)] × k = = Ses × [1+n+k+(n × k)]
Teniendo en cuenta todos los puestos de trabajo involucrados en la planta, se precisará una superficie igual a:
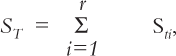donde: r es el número de puestos de trabajo de la planta.
Finalmente, para la evaluación de la superficie que ocupar no debemos olvidar añadir la correspondiente a los centros técnicos no productivos, a la superficie total ST anteriormente definida.
Más adelante, en un caso completo de diseño integral de una planta en desarrollo, se aplicará el método de Guerchet, que permitirá seguir así la aplicación del mismo a un caso concreto.
Llamaremos eslabón a la trayectoria del producto en un proceso que une entre sí dos puestos de trabajo. Con este método se pretende encontrar la distribución óptima reduciendo al mínimo el número de manutenciones. El problema se plantea cuando tenemos una planta (o varias) con diversos circuitos de materiales que dan lugar a producciones distintas.
Imaginemos un taller en el que se fabrican tres piezas (A, B, C) y en el que disponemos de 10 puestos de trabajo (numerados del 1 al 10). Los recorridos o gamas de cada una de las piezas son las de la primera tabla de la figura 2.5, por lo que los enlaces (eslabones) entre puestos de trabajo serán los de la segunda tabla de dicha figura.
Seguidamente, haremos uso de la matriz o cuadro de eslabones, la cual nos permitirá determinar la frecuencia con que aparecen los distintos eslabones. Ello se realizará anotando en la citada matriz, con el símbolo X, todos y cada uno de los eslabones existentes como fruto de recorridos reales de los productos en los procesos, sin tener en cuenta el sentido del trayecto. Así, retomando nuestro ejemplo, construiríamos el cuadro de eslabones de la figura 2.6.
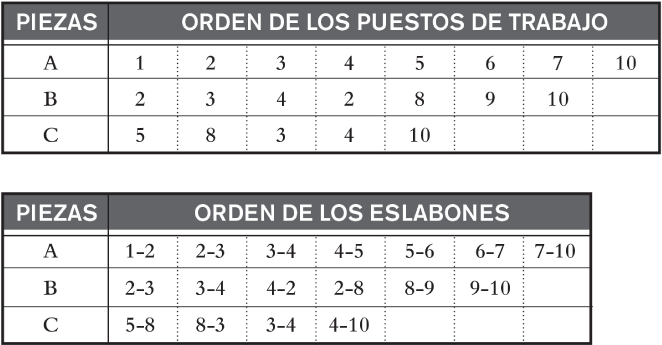
FIGURA 2.5. Gamas de piezas y enlaces entre sus puestos de trabajo
Podemos observar que en la diagonal del cuadro de eslabones hemos sumado, para cada puesto de trabajo, el número de enlaces o eslabones que realizar, es decir, hemos determinado la cantidad total de las X existentes en filas y columnas. Por ejemplo, el puesto de trabajo 2 tiene 5 eslabones: 1-2, 2-3 (2), 2-8 y 4-2 (señalados con un fondo tramado en la figura). En este recuento de enlaces por puesto no consideramos el orden de los enlaces.
Partiendo del cuadro, el siguiente paso será diseñar la disposición de los puestos para reducir al mínimo la importancia de los transportes. La distribución deberá realizarse teniendo en cuenta los valores obtenidos en dicha diagonal, situando más juntos aquellos puestos de trabajo con mayor número de enlaces entre sí. El procedimiento que seguir será el siguiente:
1. Colocar el puesto de trabajo con mayor número de enlaces en el centro de la distribución, la cual podrá estar basada en esquemas con reticulado rectangular, triangular, hexagonal, etc. En nuestro ejemplo, el puesto elegido podría ser tanto el 3 como el 4 (puestos para los que hemos introducido un fondo oscuro en su celda en la diagonal del cuadro de eslabones).
2. Alrededor de este puesto central se situarán aquellos puestos que tengan una relación más fuerte con él, es decir, un mayor número de uniones. O sea, si el puesto central es el 4, el puesto 3, con el que tiene tres uniones, deberá estar, necesariamente, lo más próximo posible.
3. A continuación, se considerará la posibilidad de situar los puestos que tengan algún enlace con el central (en nuestro caso, los puestos 2, 5 y 10) lo más próximo posible a este.
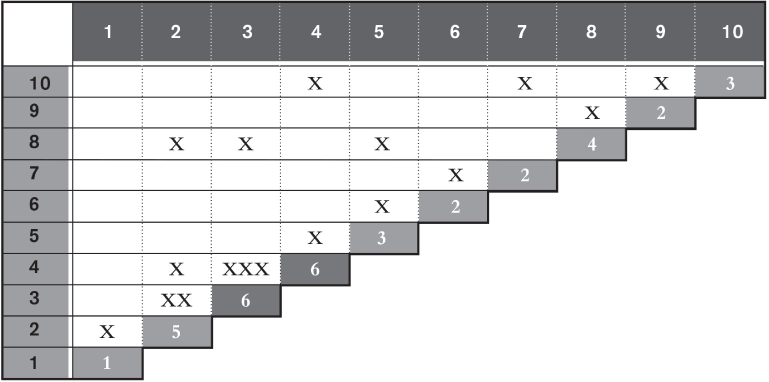
FIGURA 2.6. Cuadro de eslabones
4. Finalmente, trataremos de situar alrededor de los puestos con mayor número de enlaces con el central, aquellos que tengan el mayor número de uniones respecto a ellos. Este último paso se irá repitiendo sucesivamente hasta haber colocado todos los puestos existentes, vigilando que cada uno quede cerca de aquellos con los que la relación sea máxima, pero teniendo en cuenta que algunos de ellos pueden tener una ubicación especial predeterminada o condicionada.
Tal como podemos deducir, no existirá una solución única ya que dependerá del criterio elegido. Así, por ejemplo, la figura 2.7 muestra una posible solución sobre retícula triangular, con los enlaces de cada eslabón resaltados.
Ahora bien, hasta el momento hemos supuesto la misma complejidad en todos los eslabones, es decir, que el flujo de materiales en todos los enlaces sea el mismo. Sin embargo, este caso no será el más usual ya que pueden darse eslabones por los que circule una mayor cantidad de materiales que en otros o que sean más pesados, voluminosos o difíciles de transportar. Por tanto, será preciso ponderar de alguna manera la importancia de los eslabones al situarlos en una distribución.
En este sentido, supongamos que en nuestro ejemplo introducimos ahora los volúmenes de fabricación de las distintas piezas y su tamaño relativo. Así, podríamos establecer como criterio, a efectos de ponderación, el producto de las unidades fabricadas por su tamaño relativo, como se observa en la figura 2.8.
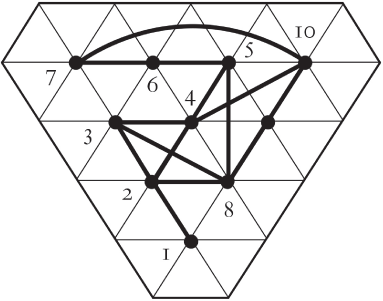
FIGURA 2.7. Implantación sobre retícula triangular
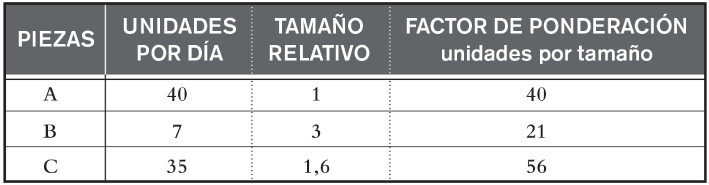
FIGURA 2.8. Factor de ponderación que integra dos aspectos
En dicha figura, hemos introducido junto a cada una de las piezas que ya componían el caso anterior, el volumen de producción diario, el tamaño relativo de cada una, y hemos obtenido un factor de ponderación de su importancia que tiene en cuenta ambos aspectos, por cuanto se obtiene por producto de los dos.
El cuadro de eslabones, ponderado de esta forma, recibe el nombre de cuadro de intensidades de tráfico (o cuadro de tránsito). La figura 2.9 muestra el cuadro de tránsito del caso que nos ocupa.
Una vez obtenido este cuadro, procederíamos del modo anteriormente descrito, a propósito del cuadro de eslabones, para proponer soluciones de disposición de los puestos de trabajo.
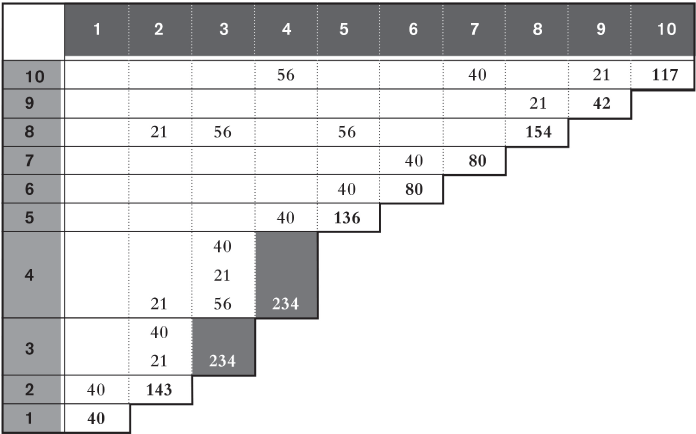
FIGURA 2.9. Cuadro de tránsito
En el nivel de abstracción más elevado, podemos reemplazar el concepto de distribución de puestos de trabajo dentro de una planta, por el de distribución de subplantas o secciones dentro de una planta. En este caso, el concepto de eslabón sigue siendo válido y aplicable, solo que ahora unirá subplantas enteras en lugar de puestos de trabajo.
A partir de las soluciones obtenidas en la implantación sobre retícula y del dimensionado de los centros contenidos en ellas, se obtienen las posibles soluciones de la distribución en planta, las cuales deberán compararse para elegir la mejor. Para mayor claridad, se muestra, a continuación cómo aplicar todo lo dicho en un caso práctico completo.
CASO EJEMPLO
Con el fin de desarrollar la metodología que permita obtener la distribución en planta integral de los procesos y servicios anexos de una planta industrial, vamos a desarrollar esta metodología sobre un caso práctico, con la aplicación de los conceptos y técnicas expuestos anteriormente. Se trata de una planta, con servicios anexos, para la fabricación y ensamblaje de aparatos reproductores de DVD, las máquinas y equipos que precisen y las operaciones correspondientes.
Dicha planta ocupará una superficie de 2.000 m2 en un polígono industrial, en una parcela de geometría concreta sobre la que se llevará a cabo la implantación. Se proyectará para una producción diaria de 600 unidades de producto. Se ha previsto, asimismo, la necesidad de contratar 32 operarios, 20 empleados de oficinas (administrativos y vendedores) y 5 directivos. La planta se compondrá de los centros de trabajo que muestra la figura 2.10, junto con los procesos y estaciones de trabajo.
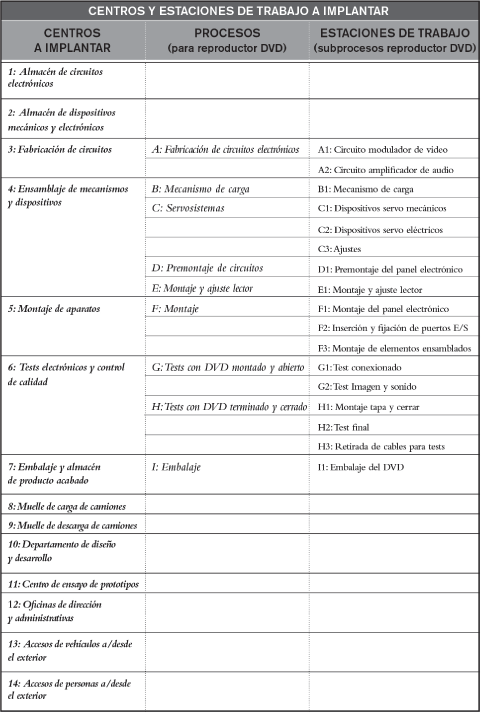
FIGURA 2.10. Centros, procesos y estaciones de trabajo de una planta de reproductores de DVD
La secuencia de producción de la planta es la que viene reflejada en el gráfico de la figura 2.11, en el denominado «diagrama de precedencias», en el que los procesos A, B, C, D y E fabrican o premontan elementos y dispositivos del aparato DVD y el proceso F lleva a cabo el ensamblaje de los aparatos, para luego ser testeados y embalados en los procesos G, H e I. Este conjunto de procesos se configurará a partir de las operaciones que se desarrollarán en departamentos o talleres muy concretos y se llevará a cabo, básicamente y para una implantación convencional (con la que comenzaremos nuestros diseños en esta obra), sobre una distribución por talleres, aunque el ensamblaje pueda hacerse en cadena. La optimización de la producción se obtendrá, como corresponde a la gestión más convencional, a base a trabajar por lotes, arbitrando el stock necesario en cada centro-taller para la implantación de este tipo de producción.
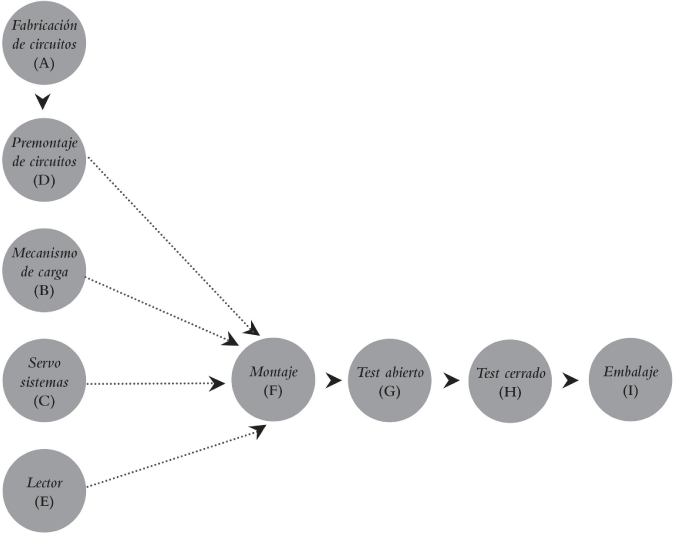
FIGURA 2.11. Diagrama de flujo del proceso de la planta
El siguiente paso consistirá en construir el cuadro de tránsito por centros. En este caso, construiremos un cuadro muy completo con los tránsitos de productos y materiales. Por un lado, el acarreo de materiales y productos por parte de unas personas y de herramientas, utillajes, equipamientos y documentación, por parte de otras, así como elementos de transporte que acarrean materiales, productos y otros elementos. Ello supondrá que cada celda del cuadro de tránsito se compondrá de seis celdillas con los seis tipos de información a los que acabamos de hacer referencia. La figura 2.12 muestra dicho cuadro.
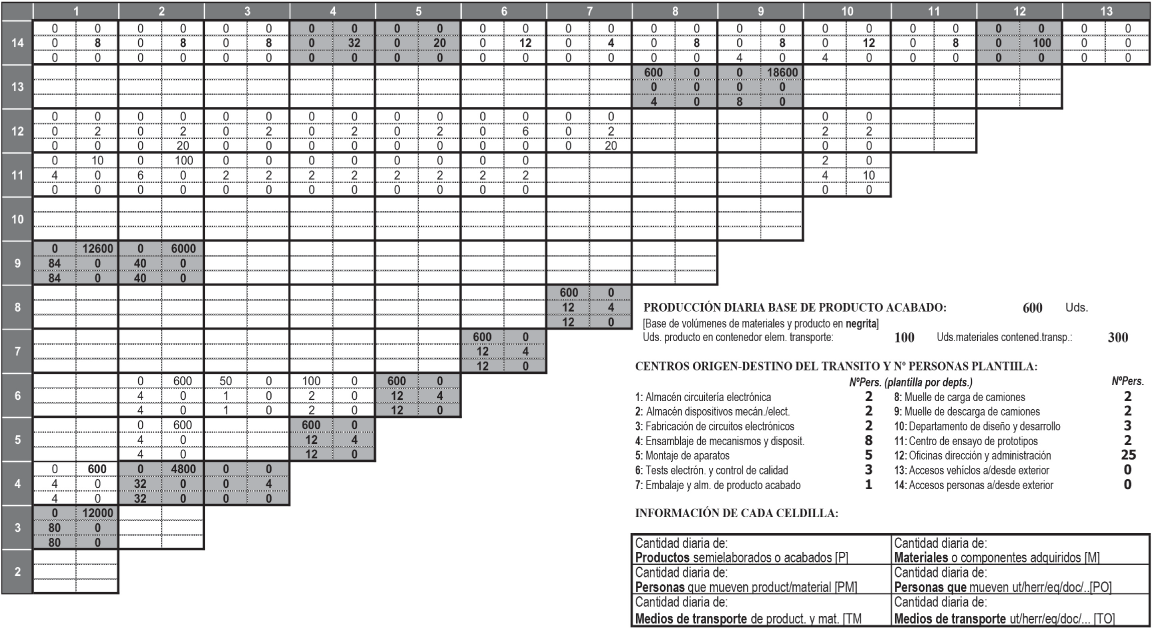
Figura 2.12. Cuadro de tránsito del caso
Las celdas de los centros cuyo tráfico mutuo es importante se han destacado con fondo gris en la figura 2.12. Los datos de los que se alimentan todas las celdas provienen de los mostrados en la parte inferior derecha de la citada figura, tanto en lo referente a los volúmenes de producción y de movimiento de materiales, como al personal de cada centro. Debajo de estos datos se halla detallada la composición de las celdillas de cada celda.
Todo ello permitirá realizar múltiples propuestas de implantaciones con la ayuda de un reticulado, disponiendo en el mismo los centros con mayor tráfico mutuo lo más cerca posible, de acuerdo con las siguientes normas:
1. Situar los accesos desde/al exterior y los muelles de carga/descarga y entradas de personal.
2. A partir de ellos, situar los centros de máxima prioridad con los mismos, de acuerdo con las reglas de priorización que siguen, cuyos objetivos son impulsar el flujo correcto del producto y eliminar despilfarros en movimientos de personal y transportes de materiales:
• Prioridad absoluta para el tránsito de personal [PM y PO].
• Prioridad segunda para el tránsito de productos y materiales [P y M].
• Prioridad tercera para medios de transporte [TM].
• Prioridad cuarta para otros tránsitos [TO].
3. Ubicar nuevos centros con relación a los anteriores, de acuerdo con las prioridades y sus reglas.
4. Continuar así, hasta agotar el total de centros que ubicar.
5. Reajustar el conjunto de los centros ubicados.
6. Evaluar la solución: para las celdillas de encuentro de dos centros en el cuadro de tránsito, que tengan valores relevantes (con fondo gris en el cuadro de tránsito efectuado), se determinará la siguiente expresión, sumando luego los valores de tales expresiones:
n × [Kp × (PM + PO) + Km × (P + M) + Kt × (TM + TO)]
donde:
n = Número de lados o segmentos de red que distan los centros cuya celdilla se evalúa
Kp = Factor de priorización del personal (valor empleado: 5)
Km = Factor de priorización de los materiales (valor empleado: 3)
Kt = Factor de priorización de otros tránsitos (valor empleado: 2)
Vamos a elaborar, pues, con estas normas, tres posibles soluciones que, a su vez, darán lugar a tres posibles distribuciones de la planta, persiguiendo en todo momento acercar al máximo los centros que soportan un mayor tráfico entre sí pero sin olvidar tener en cuenta la secuencia de fabricación del proceso productivo de dicha planta.
En las figuras 2.13a, 2.13b y 2.13c presentamos las tres posibles soluciones sobre red bidireccional.
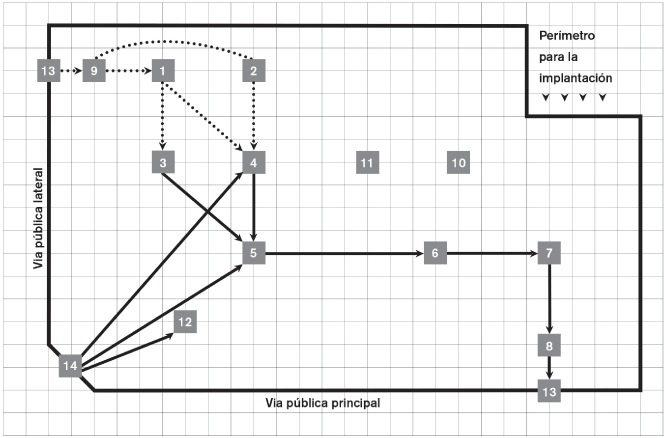
FIGURA 2.13a. Primera solución a la implantación sobre red bidireccional
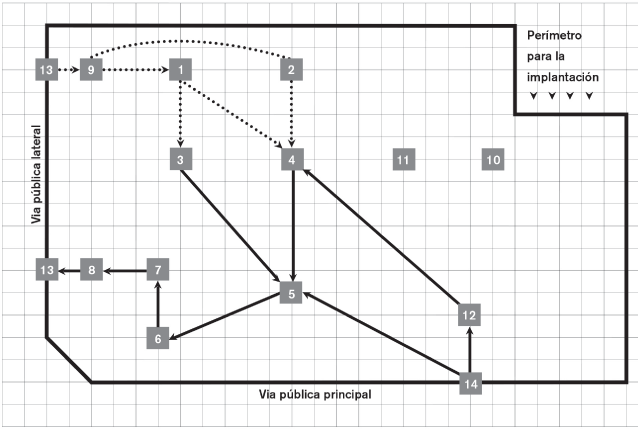
FIGURA 2.13b. Segunda solución a la implantación sobre red bidireccional
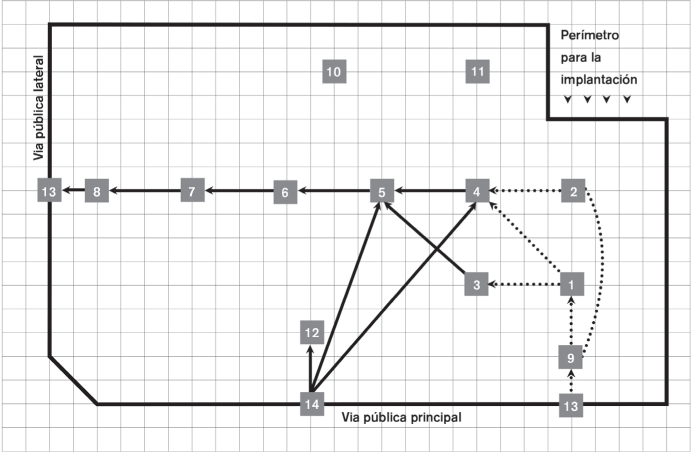
FIGURA 2.13c. Tercera solución a la implantación sobre red bidireccional
Cada una de ellas viene, como se verá, acompañada de la implantación real a escala, obtenida tras convertir los puntos de la red donde se propone cada solución, en un área o departamento con una superficie dada (a partir del cálculo de equipos, máquinas o puestos necesarios, es decir, a partir de las expresiones ya expuestas del tipo Ei=Hi /hef y de la superficie que se precisa, calculada por el método de Guerchet).
Por el momento, vamos a proceder a evaluar las soluciones planteadas, de acuerdo con la expresión ya expuesta para ello y los coeficientes que hemos acordado emplear.
La expresión que nos dará la evaluación de cada solución es, como sabemos:
n × [Kp × (PM + PO) + Km × (P + M) + Kt × (TM + TO)]
siendo así que la expresión entre corchetes depende de los datos de las seis celdillas de cada celda del cuadro de tránsito y n (el número de lados de la red bidireccional) depende de la solución adoptada. Veamos, ante todo, cuál es la expresión entre corchetes, para los pares de centros con tránsito importante, los que se hallan con fondo gris en el cuadro de tránsito de la figura 2.12. La figura 2.14 nos da los valores para dichas celdas.
La figura 2.14 muestra el cálculo del factor base (expresión entre corchetes) de la evaluación de las soluciones, a partir de las celdas con valores relevantes.
Este factor es el valor que se va a multiplicar por el valor de n de cada celda para cada una de las soluciones, a fin de determinar la evaluación completa de las mismas. La figura 2.15 muestra dicha valoración completa: la primera columna identifica las celdas que evaluar y la segunda, el factor base de cada una, de acuerdo con la figura 2.14. A partir de ahí hay un columnado para cada una de las soluciones, con una columna con el valor de n (tramos o lados sobre la red) y otra con el valor final de la expresión completa de la evaluación de cada celda (n multiplicado por el factor base).
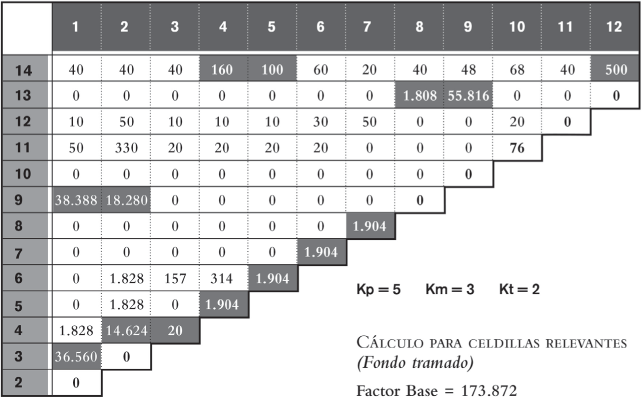
FIGURA 2.14. Determinación del factor base de la evaluación de las soluciones
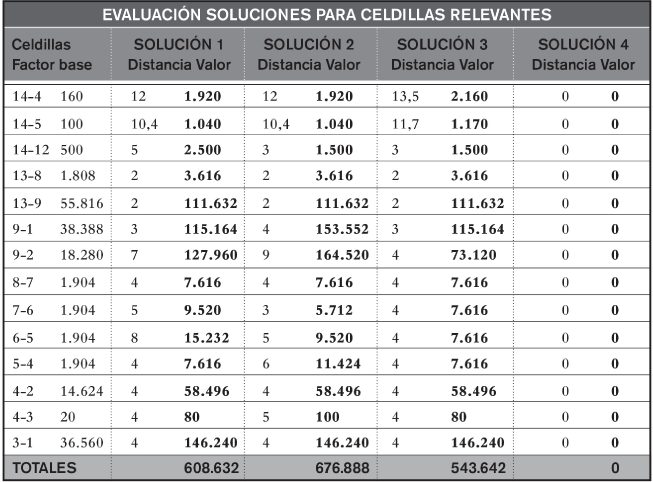
FIGURA 2.15. Evaluación final de cada una de las soluciones aportadas
Sumando el conjunto de estos valores finales, se obtiene el valor total de cada solución, siendo así que el menor es el mejor, ya que supone el menor consumo de recursos posible, entre las soluciones aportadas. Como puede observarse, la tercera solución, con un valor total de 543.642, es la mejor.
Una vez que hemos decidido la mejor solución (sobre red), en la que solo se ha determinado la posición relativa de cada centro, hemos de pasar a dimensionar tales centros, para convertir la solución en una planteamiento con los centros correctamente situados y dimensionados. A título de ejemplo, vamos a proceder a realizarlo para un centro concreto (el 4, de ensamblaje de dispositivos), aplicando cuanto se ha expuesto anteriormente sobre la determinación del número de puestos y/o equipos de producción necesarios en cada centro y su dimensionado por el método de Guerchet:
• Horas productivas anuales por puesto: 2.000.
• Coeficiente de absentismo: 85 %.
• Coeficiente de productividad laboral: 95 %.
• Coeficiente de rendimiento (sin mantenimiento - averías) de máquinas: 80 %.
• Coeficiente global de rendimiento: 0,85 × 0,95 × 0,8 = 0,646.
• Número de horas efectivas por año: 2.000 × 0,646 = 1.292.
La figura 2.16 recoge el cálculo necesario para evaluar la cantidad de puestos de trabajo por operación precisados.
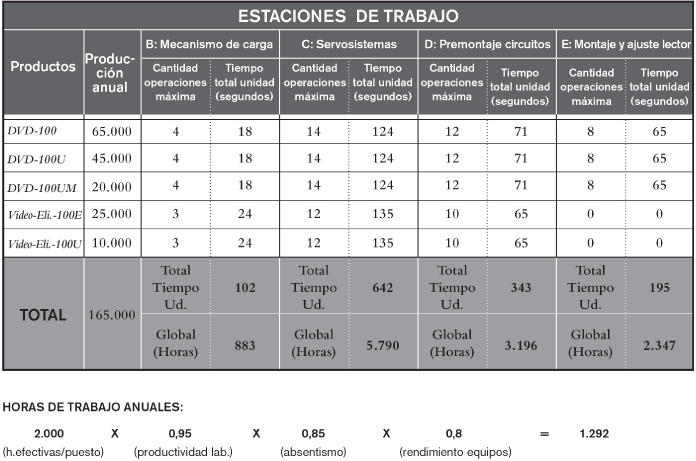
FIGURA 2.16. Determinación de los datos para evaluar los equipos necesarios
El cuadro de dicha figura permite calcular las necesidades en tiempo de los equipos que conforman el centro 4. Estas necesidades dependen de las operaciones que se deban efectuar en cada producto y de qué máquinas intervengan en ellas.
De acuerdo con el número de horas de trabajo que se precisarán de cada equipo y teniendo en cuenta la disponibilidad efectiva de horas ya calculada (1.292), podemos ya determinar, tal como hacemos en la figura 2.17, la cantidad de puestos que se precisarán de cada tipo.
Ahora evaluaremos la superficie necesaria para la ubicación de los puestos que vamos a necesitar. La figura 2.18 permite determinar las superficies precisadas para estos puestos, aunque también habrá que tener en cuenta otras superficies adicionales necesarias. Concretamente:
• Pasillo central con accesos (en el inicio y el fin) a otros talleres según el proceso (podría haberse introducido como un elemento más en el cálculo).
• Zona mínima para una posible ampliación futura que no exija invadir otros talleres (coeficiente de seguridad en el cálculo de superficies).
Cálculo del número de estaciones necesarias:
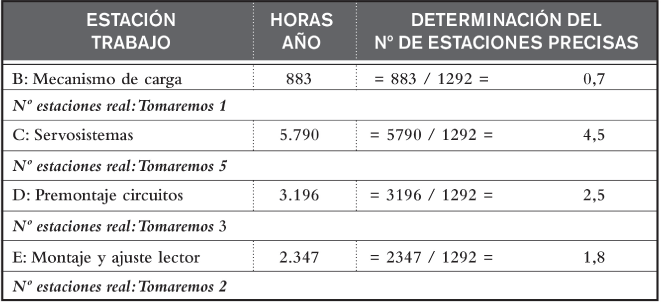
FIGURA 2.17. Determinación de la cantidad de estaciones necesarias de cada tipo
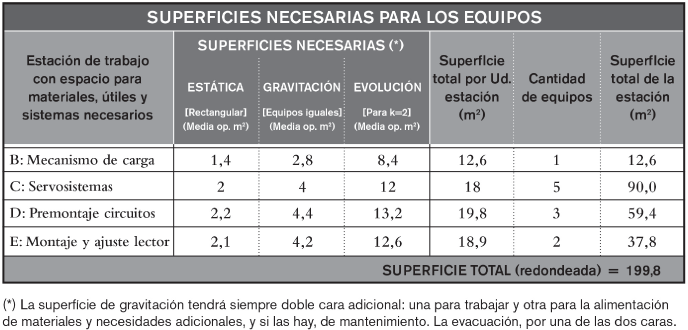
FIGURA 2.18. Determinación de la superficie total necesaria para un centro
Las figuras 2.19a y 2.19b muestran el centro de ensamblaje de dispositivos con su distribución interna, en dos variantes: flujo lineal y distribución funcional (talleres). La superficie que ocupan las máquinas y, por tanto, ampliación aparte, es:
20 × 10 = 200 m2
la que debía ser, según se había calculado en la figura 2.18, que daba un total de 199,8 m2. Además, puede observarse que se ha previsto una ampliación, con superficies de un 10 % de la calculada anteriormente para el centro.
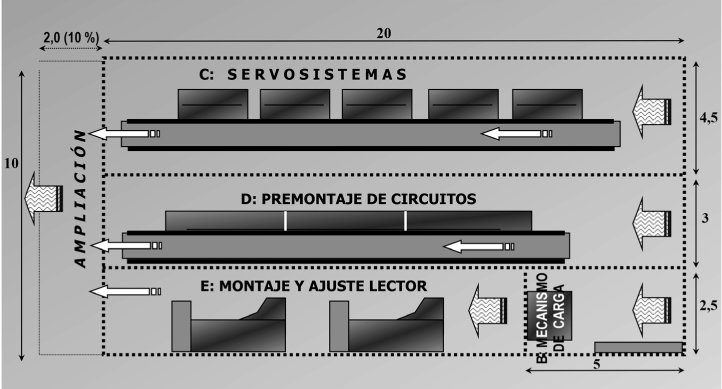
FIGURA 2.19a. Centro dimensionado para operativa en flujo
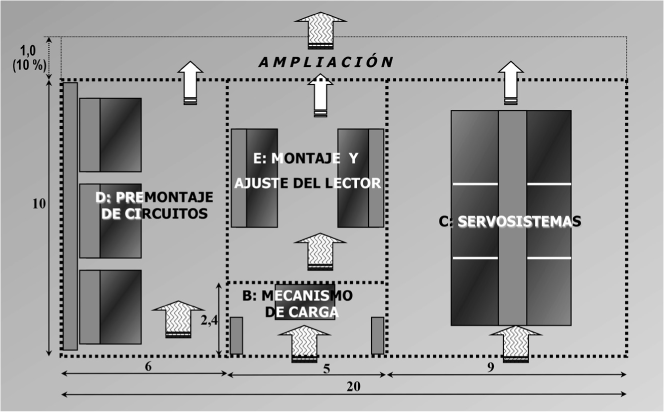
FIGURA 2.19b. Centro dimensionado para operativa funcional
Procederíamos igual con todos los demás centros de la planta, sean de producción o servicios anexos; una vez tengamos la superficie de cada uno de ellos, podremos, por fin, convertir las soluciones de la distribución en planta realizadas sobre red (con los centros indicados por puntos y por tanto sin ocupación física), en una planta real con una ocupación real.
Las figuras 2.20a, 2.20b y 2.20c, muestran las tres soluciones desarrolladas sobre la red (figuras 2.13a, 2.13b y 2.13c), convertidas en las correspondientes distribuciones en planta, con los centros ocupando la superficie que les corresponde, toda vez que ya han sido debidamente dimensionados. En algunos casos, por motivos prácticos relacionados con la propia distribución, se han asignado superficies mayores que las obtenidas, si puede ser de interés y no afecta al conjunto, pero en ningún caso podrán ser menores. Ahora podemos pasar ya a la selección de la solución óptima.
Esta es la última fase, que nos permitirá obtener la distribución en planta definitiva, lo que se llevará a cabo a partir de la serie de soluciones que hemos desarrollado, las cuales serán evaluadas según los criterios que se juzgue convenientes en cada caso. Dichos criterios deberán ser ponderados según su importancia, estableciendo un sistema que los haga compatibles.
Muchos podrían ser los criterios a partir de los cuales evaluar las soluciones. Sin embargo, en general, se consideran de gran interés por su trascendencia los siguientes:
• Racionalidad de la implantación.
• Inversiones y costes relacionados con la implantación que acarrea.
• Costes de funcionamiento del conjunto.
• Flexibilidad a cambios y ampliaciones.
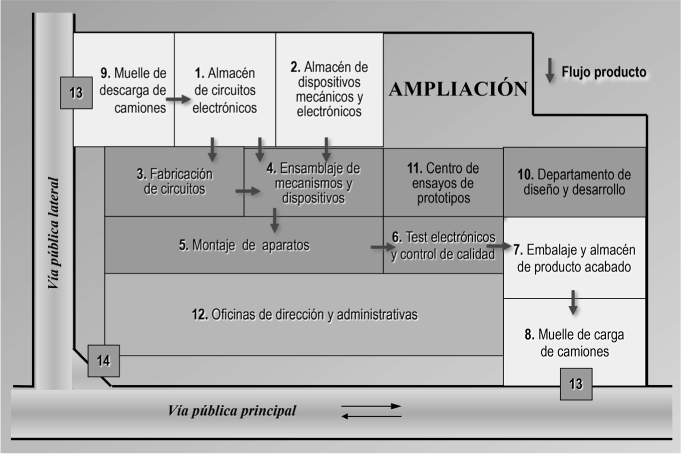
FIGURA 2.20a. Propuesta correspondiente a la primera solución
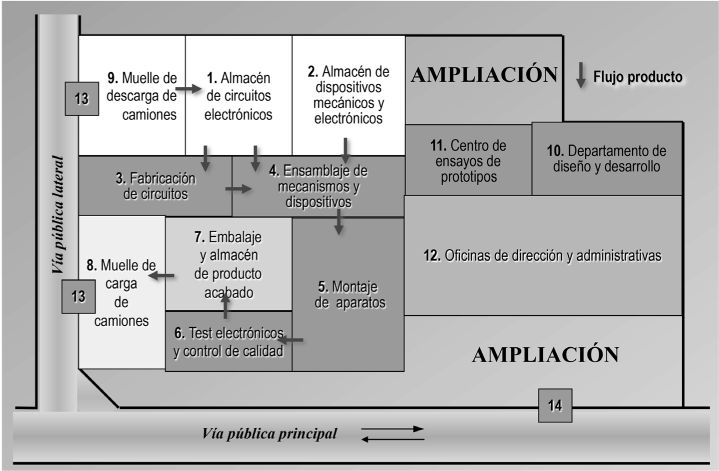
FIGURA 2.20b. Propuesta correspondiente a la segunda solución
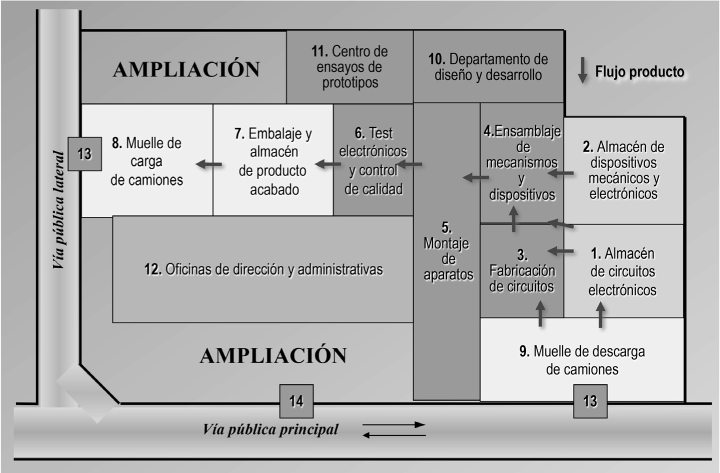
FIGURA 2.20c. Propuesta correspondiente a la tercera solución
• Superficie libre y facilidades para ampliaciones.
• Minimización y racionalización de recorridos de materiales, personas y elementos de transporte.
• Seguridad.
• Adaptación a normativas generales y locales.
• Facilidad de puesta en marcha y control de los procesos.
Así pues, el procedimiento de selección consistirá en someter todas las soluciones encontradas al juicio de un equipo integrado por todas aquellas personas que, de algún modo, interesa que emitan su valoración (incluso los futuros usuarios de la instalación), acerca de todos los aspectos susceptibles de crítica. Cada uno de estos aspectos será evaluado mediante un coeficiente de ponderación cuyo valor reflejará la importancia del mismo.
En este sentido, retomando el caso práctico de nuestra planta en el que, recordemos, habíamos obtenido tres posibles soluciones, los criterios que se han elegido para escoger la mejor de ellas, así como sus coeficientes de ponderación, son:
1. Secuencia de operaciones: debe ser lo más uniforme posible. Ponderación: 10.
2. Seguridad: referida, especialmente, a la situación alejada del almacén de seguridad. Ponderación: 9.
3. Reforma departamental: deben poder preverse reformas en los centros sin romper la secuencia, así como posibilitar subdivisiones en los mismos. Ponderación: 7.
4. Posibilidades de ampliación: sobre todo en los almacenes de materias primas y expediciones. Ponderación: 6.
5. Circulación de personal fluida. Ponderación: 5.
Una vez se han elegido los criterios que considerar, estos serán puntuados (en nuestro caso, de 1 a 5) para todas y cada una de las soluciones presentadas para, posteriormente, efectuar el producto de tales puntuaciones por sus respectivos coeficientes de ponderación (que en este caso irán de 1 a 10). Así pues, las puntuaciones totales de cada alternativa de solución se obtendrán de la suma de los productos anteriormente citados. Para el caso que hemos venido desarrollando, el cuadro con las puntuaciones ponderadas sería el de la figura 2.21.
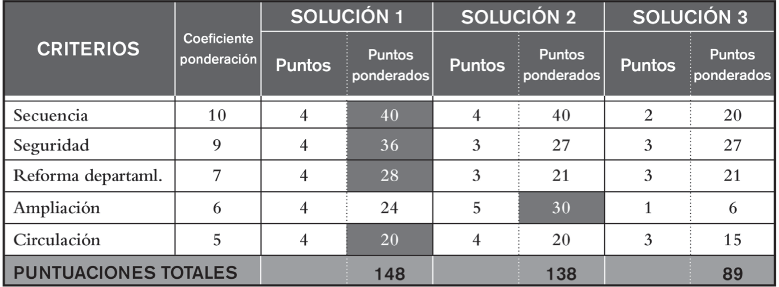
FIGURA 2.21. Cuadro de valoraciones ponderadas de las soluciones
Como puede observarse, guiándonos por el criterio de que aquella solución que haya obtenido la máxima puntuación total es la mejor, la distribución que se implementará será la que se derive de la solución 1. Ello no supone, sin más, que la solución 1 sea la mejor, sobre todo si otra tiene una puntuación similar; la optimización efectiva de la solución elegida exige mejorarla al máximo. Así, aunque en algunos aspectos la solución 1 sea óptima, tales como los que hemos resaltado con fondo gris y caracteres en negrita, no deben despreciarse aquellas soluciones de puntuación similar (solución 2), siendo necesario fijarnos en aquellos criterios concretos (destacados de la misma manera) en los que otras soluciones superen a la óptima, llegando incluso a modificarla de modo que obtengamos una solución mixta que contenga las mejores cualidades de las distintas soluciones.
Así pues, en nuestro caso y de acuerdo con los resultados de la figura 2.21, la solución 1 es la idónea, aunque en el criterio con mayor ponderación (secuencia del proceso) la solución 2 sea igual de buena, además de que en el criterio que hace referencia a las ampliaciones resulta mejor la solución 2, especialmente por lo que se refiere a situación de la zona de verificación, que puede mejorar la posibilidad de ampliar. En consecuencia, la solución definitiva podría ser la 1 con una corrección en este sentido, tal como muestra la figura 2.22, en la cual se destacan los cambios en fondo oscuro y caracteres en blanco.
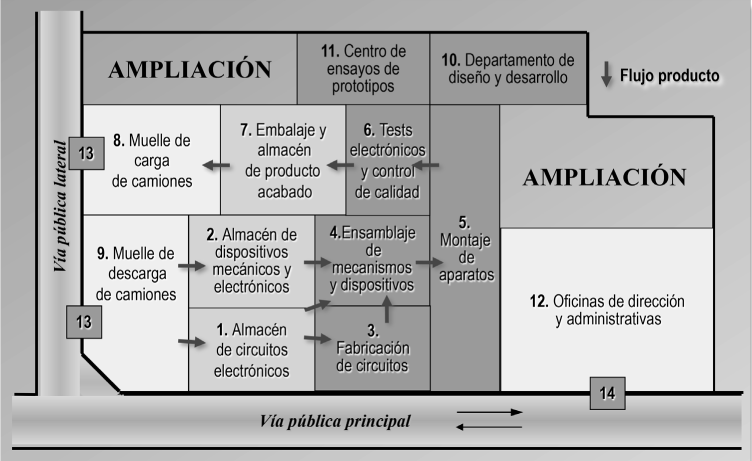
FIGURA 2.22. Distribución en planta definitiva, desarrollada sobre la solución 1 mejorada