1.7. EL TIEMPO EN LA RELATIVIDAD GENERAL DE EINSTEIN
Antes de tratar con algo más de detalle el espaciotiempo 5-dimensional de la teoría de Kaluza-Klein, será preciso que analicemos el método para describir las interacciones electromagnéticas que, en última instancia, pasó a formar parte de la teoría estándar. En particular, lo que nos interesará aquí será la manera en que se describen las interacciones electromagnéticas de las partículas cuánticas (la versión cuántica de la extensión de Lorentz a la teoría de Maxwell que, como se ha mencionado en §1.5, muestra cómo las partículas cargadas responden a un campo electromagnético), así como las generalizaciones de lo anterior a las interacciones fuerte y débil del modelo estándar. Este es el esquema que puso en marcha en 1918 el gran matemático (y físico teórico) alemán Hermann Weyl. (Weyl se convirtió en uno de los pilares del Instituto de Estudios Avanzados de Princeton durante la misma época, 1933-1955, en que Einstein estuvo allí, aunque, como en el caso de este último, sus principales contribuciones a la física las había hecho antes, en Alemania y Suiza.) La muy original idea inicial de Weyl consistió en ampliar la teoría de la relatividad general de Einstein para que el electromagnetismo de Maxwell (la gran teoría que se menciona brevemente en §§1.2 y 1.6) pudiese incorporarse de forma natural a la estructura geométrica del espaciotiempo. Para conseguirlo, introdujo el concepto de lo que ahora se denomina conexión de gauge. En última instancia, tras una serie de ligeros retoques, la idea de Weyl se convirtió en el eje de la manera en que se tratan por regla general las interacciones en el modelo estándar de la física de partículas. En términos matemáticos (en gran medida debido a la influencia de Andrzej Trautman [1970]), esta idea de una conexión de gauge se entiende ahora a través del concepto de fibrado (§A.7) que hemos visto ilustrado en la figura 1-12 (y que ya se ha insinuado en §1.3). Es importante que entendamos las diferencias y las semejanzas que la idea original de la conexión de gauge de Weyl tenía con la propuesta ligeramente posterior de Kaluza-Klein.
En §1.8 describiré con algo más de detalle cómo Weyl introdujo su extensión geométrica de la relatividad general de Einstein para incorporar la teoría de Maxwell. Veremos que la teoría de Weyl no implica ningún aumento de la dimensionalidad del espaciotiempo, pero sí introduce un debilitamiento de la noción de métrica, en la que se basa la teoría de Einstein. Así pues, como preámbulo, tendré que abordar la función física real del tensor métrico g del esquema de Einstein, que es la magnitud básica que define la estructura pseudoriemanniana del espaciotiempo. Los físicos normalmente utilizarían una notación como gab (o gij, o gmn , o algo por el estilo) para denotar el conjunto de componentes de esta magnitud tensorial g, pero no tengo la intención de entrar aquí en los detalles de estas cuestiones ni de explicar lo que el término «tensor» significa en verdad en un sentido matemático. Lo que aquí necesitamos conocer en realidad es simplemente la interpretación física directa que se le puede atribuir a g.
Supongamos que tenemos una curva C que conecta dos puntos —o eventos— P y Q, en la variedad espaciotemporal M, donde C representa la historia de una partícula con masa que se desplaza desde el evento P al evento posterior Q. (El término «evento» suele emplearse para un punto en el espaciotiempo.) Llamamos a la curva C la línea de universo de esa partícula. Entonces, lo que g hace, en la teoría de Einstein, es determinar una «longitud» para la curva C, longitud que se interpreta físicamente como el intervalo temporal (en lugar de como una medida de la distancia) entre P y Q que mediría un reloj ideal que se moviese con la partícula (véase la figura 1-14(a)).
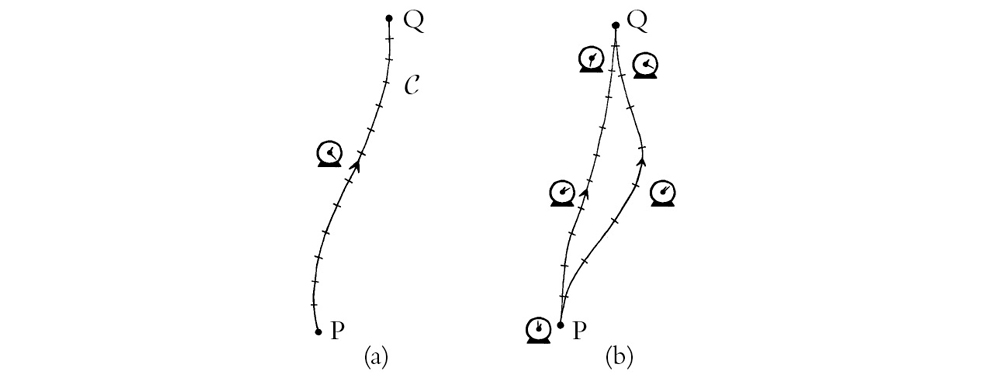
FIGURA 1-14. (a) La métrica espaciotemporal g asigna una «longitud» a cada segmento de la línea de universo C de una partícula, que se corresponde con el intervalo temporal que mediría un reloj ideal que siguiese dicha línea de universo; (b) si dos de esas líneas de universo diferentes conectan dos determinados eventos P, Q, las medidas del tiempo pueden ser distintas.
Debemos tener en cuenta que, según la relatividad de Einstein, el «paso del tiempo» no es algo absoluto que venga dado y ocurra simultáneamente a lo largo y ancho del universo, sino que debemos entenderlo en términos plenamente espaciotemporales. No existe un «troceo» dado del espaciotiempo en secciones espaciales 3-dimensionales, cada una de las cuales representaría la familia de eventos que ocurren «todos al mismo tiempo». No disponemos de un «reloj universal» absoluto que marque el tiempo, de tal modo que, para cada tictac de dicho reloj universal, hubiese todo un espacio 3-dimensional de eventos simultáneos, etc., y todos estos 3-espacios encajasen para formar el espaciotiempo (como en la figura 1-15, donde podemos imaginar que nuestro reloj universal suena todos los días al mediodía). No pasa nada por pensar provisionalmente en el espaciotiempo de esta manera, solo para poder relacionar esta representación 4-dimensional con nuestra experiencia cotidiana de un espacio 3-dimensional en el que las cosas «evolucionan en el tiempo», pero debemos adoptar el punto de vista de que no hay nada especial, o «de origen divino», en esta manera de trocear el espaciotiempo, respecto a cualquier otra forma de hacerlo. Es el espaciotiempo entero el que es absoluto, pero no debemos interpretar cualquier troceo del espaciotiempo como el preferido, de acuerdo con el cual existiría un concepto universal que podríamos llamar «el» tiempo. (Todo esto forma parte del principio de covariancia general al que se hace mención en §1.7 y que se describe de forma más específica en §A.5, lo cual nos indica que una determinada elección de coordenadas —en particular, una coordenada «temporal»— no debería tener relevancia física directa.) En cambio, la línea de universo de cada partícula distinta posee su propia noción del paso del tiempo, que viene determinada por la línea de universo concreta de la partícula y por la métrica g, como se ha descrito antes. No obstante, las discrepancias entre la noción de tiempo de una partícula y la de otra partícula son muy pequeñas (a menos que las velocidades relativas entre ambas sean significativas en relación con la velocidad de la luz, o que nos encontremos en una región donde los efectos de la gravedad sobre la curvatura del espaciotiempo sean enormes); este hecho es un requisito necesario para que no percibamos tales discrepancias en nuestra experiencia cotidiana del paso del tiempo.
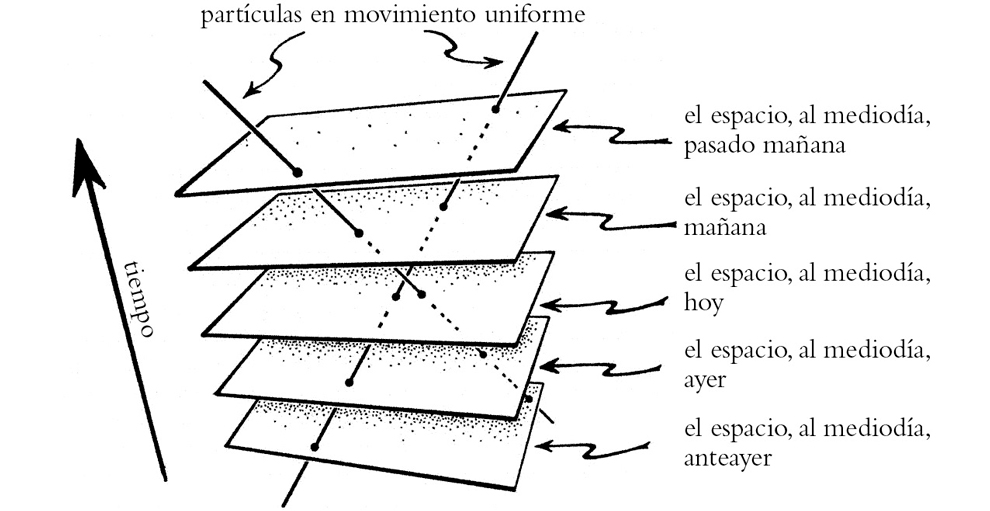
FIGURA 1-15. La visión newtoniana de un tiempo universal (en la que, aquí, podríamos imaginar que un reloj suena todos los días al mediodía). En la teoría de la relatividad se rechaza este punto de vista, pero, de momento, podemos considerar así el espaciotiempo como una excelente aproximación para objetos cuyo movimiento es mucho más lento que la velocidad de la luz.
En la relatividad de Einstein, si tenemos dos líneas de universo que conectan dos determinados eventos P y Q (figura 1-14(b)), esta «longitud» (es decir, esta medida del tiempo transcurrido) puede diferir en ambos casos (un efecto que se ha medido directamente en repetidas ocasiones, por ejemplo mediante el uso de relojes a bordo de aviones que se desplazan a gran velocidad, o que viajan a altitudes muy distintas respecto al suelo) [Will, 1993]. Este hecho tan poco intuitivo es básicamente una expresión de la conocida (supuesta) paradoja de los gemelos de la relatividad especial, según la cual un astronauta que viajase a gran velocidad desde la Tierra a una estrella remota y de vuelta a nuestro planeta experimentaría un paso del tiempo considerablemente menor que el hermano gemelo que permaneciese en la Tierra durante el viaje del astronauta. Ambos gemelos tienen líneas de universo distintas, aunque conectan los mismos dos eventos P (cuando están juntos y el astronauta está a punto de partir de la Tierra) y Q (cuando el astronauta vuelve a nuestro planeta).
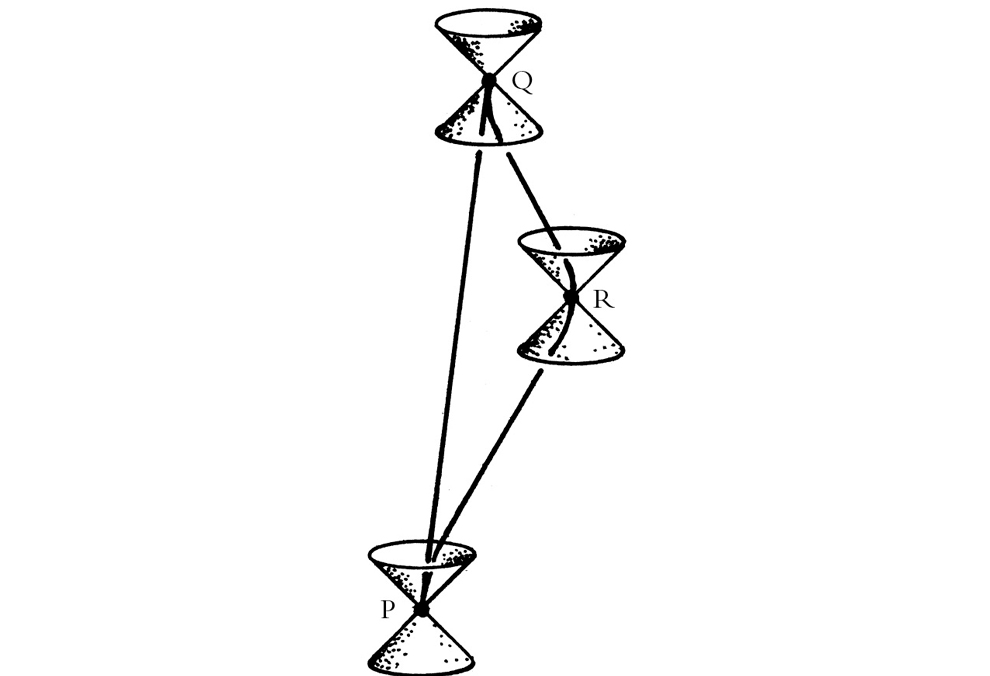
FIGURA 1-16. La llamada paradoja de los gemelos de la relatividad especial. El gemelo que permanece en la Tierra con línea de universo PQ experimenta un tiempo más largo que el que viaja al espacio, con línea de universo PQR (en una curiosa inversión de la conocida desigualdad triangular de la geometría euclídea: PR+ RQ > PQ). Los conos (dobles) se explican en la figura 1-18.
En la figura 1-16 se muestra una representación espaciotemporal de esta situación, en relatividad especial (con movimientos en gran medida uniformes), donde, además, R es el evento que marca la llegada del astronauta a la estrella remota. La figura 1-17 ilustra análogamente cómo la métrica determina el lapso experimentado, lo cual vale también para la situación más general de la relatividad general, en la que, para una partícula (masiva), la «longitud» de un segmento de la línea de universo está determinada por g, que proporciona el intervalo temporal experimentado durante ese periodo. En cada imagen, se representan los conos nulos, que son una importante manifestación física de la g de Einstein y proporcionan una descripción espaciotemporal de la velocidad de la luz en cada evento en el espaciotiempo. Vemos que, en cada evento a lo largo de la línea de universo del astronauta o de la partícula, la dirección de la línea debe estar contenida dentro del (doble) cono nulo en dicho evento, lo que pone de manifiesto la importante restricción de que la velocidad de la luz no se puede superar (localmente).
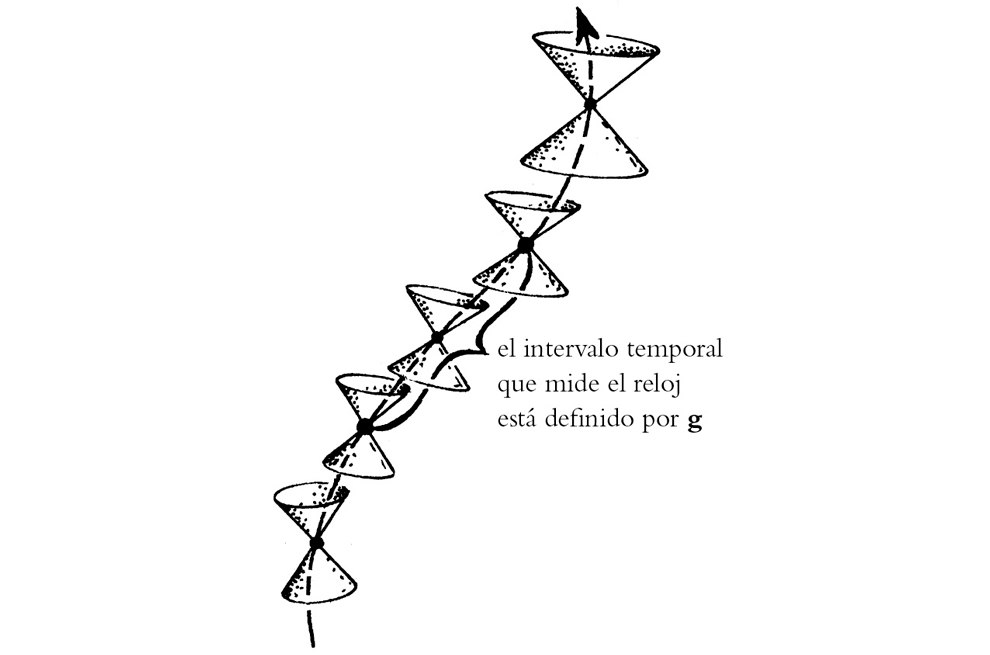
FIGURA 1-17. En el espaciotiempo curvo de la relatividad general, el tensor métrico g proporciona la medida del tiempo experimentado. Esto generaliza la imagen del espaciotiempo de la relatividad especial que muestra la figura 1-16.
La figura 1-18 representa la interpretación física de la parte futura del (doble) cono nulo, como la historia inmediata de un (hipotético) rayo de luz que parte de un evento X. La figura 1-18(a) muestra la representación plenamente 3-dimensional, mientras que en la figura 1-18(b) se puede ver la correspondiente imagen espaciotemporal, en la que se ha eliminado una dimensión espacial. El cono nulo pasado se representa asimismo mediante un rayo de luz (hipotético) que converge en X. La figura 1-18(c) nos dice que el cono nulo es en realidad una estructura infinitesimal en cada evento X, que existe solo localmente en lo que es estrictamente el espacio tangente en X (véanse §A.5 y la figura A-10).
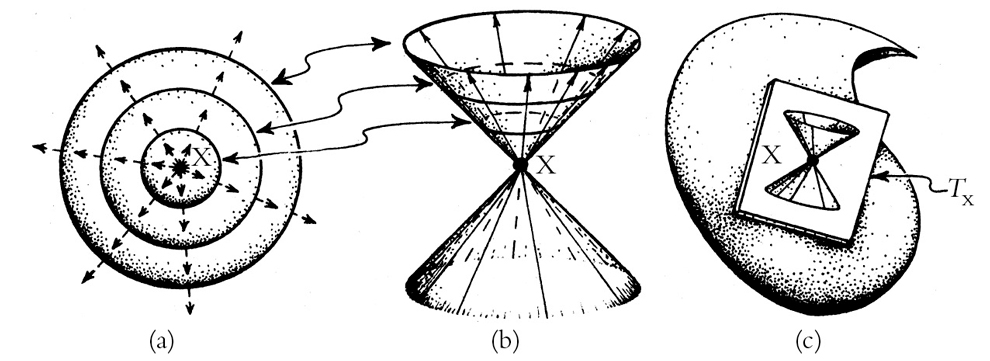
FIGURA 1-18. En cada punto X del espaciotiempo hay un (doble) cono nulo, determinado por la métrica g y compuesto de un cono nulo pasado y un cono nulo futuro, a lo largo de cuyas direcciones la medida del tiempo desaparece. El cono nulo futuro tiene una interpretación (local) como la historia de un hipotético rayo de luz emitido en X: (a) imagen espacial; (b) imagen espaciotemporal (habiendo eliminado una dimensión espacial), donde el cono nulo pasado representaría la historia de un hipotético rayo de luz que converge en X; (c) técnicamente, el cono nulo es una estructura infinitesimal en el entorno del evento X, esto es, ubicada en el espacio tangente TX.
Estos conos (dobles) representan las direcciones espaciotemporales a lo largo de las cuales la medida «temporal» desaparece. Esta característica se debe a que la geometría del espaciotiempo es, en sentido estricto, pseudoriemanniana en lugar de riemanniana (como se ha señalado en §1.1). Con frecuencia, se utiliza el término «lorentziana» para este tipo particular de geometría pseudoriemanniana, en la cual la estructura espaciotemporal posee únicamente 1 dimensión temporal y (n – 1) dimensiones espaciales, y en la que existirá un doble cono nulo en cada punto de la variedad espaciotemporal. Los conos nulos constituyen la característica más importante de la estructura del espaciotiempo, ya que nos dicen cuáles son los límites para la propagación de la información.
¿Cuál es la relación directa entre la medida temporal que proporciona g y estos conos nulos? Hasta ahora, las líneas de universo que he estado considerando son las historias de partículas ordinarias con masa, que están abocadas a desplazarse a velocidades inferiores a la de la luz, por lo que sus líneas de universo deben estar contenidas dentro de los conos nulos. Pero también debemos considerar partículas (libres) sin masa, como los fotones (las partículas de luz), las cuales viajarían a la velocidad de la luz. Según la relatividad, si un reloj se desplazase a dicha velocidad, ¡no registraría ningún paso del tiempo en absoluto! Así pues, la «longitud» de la línea de universo (medida a lo largo de la curva) de una partícula sin masa es siempre cero entre dos eventos P y Q situados sobre dicha línea (figura 1-19), por muy separados que puedan estar el uno del otro. Estas líneas de universo se denominan líneas nulas. Algunas de ellas son geodésicas (lo veremos más adelante), y a la línea de universo de un fotón libre se la considera una geodésica nula.
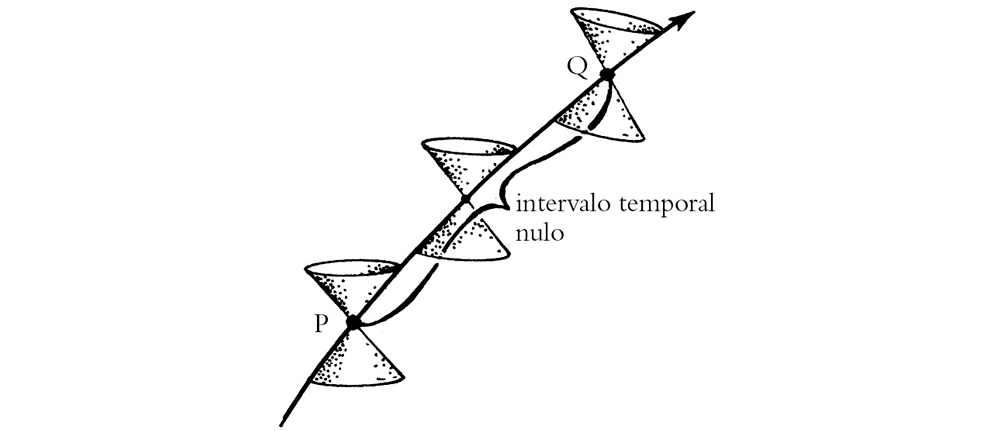
FIGURA 1-19. A lo largo de un rayo de luz (o de cualquier curva nula) la medida del tiempo transcurrido entre dos eventos P y Q es siempre cero.
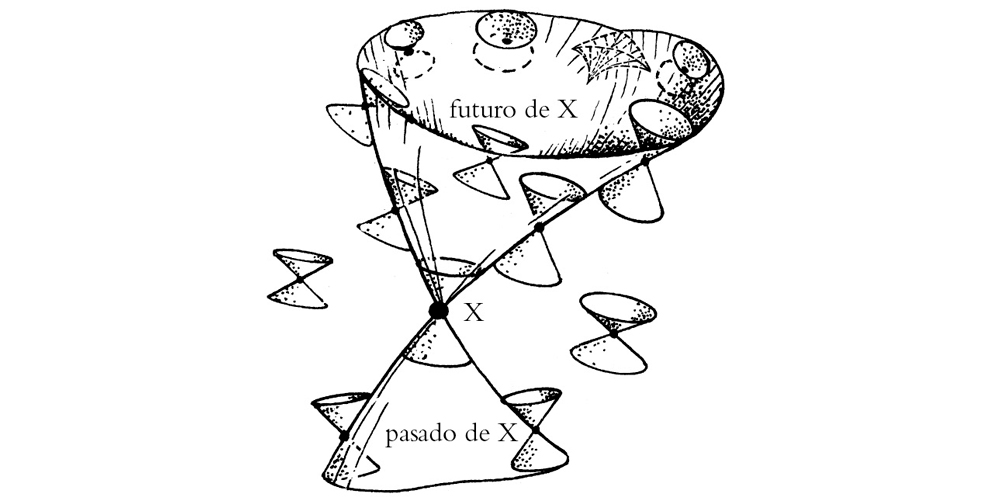
FIGURA 1-20. El cono de luz de un evento X es el lugar geométrico en el espaciotiempo que es barrido por todas las geodésicas nulas que pasan por X. La estructura tangente en su vértice X es el cono nulo en X.
La familia de todas las geodésicas nulas que pasan por un determinado punto P en el espaciotiempo barre por completo el cono de luz de P (figura 1-20), y el cono nulo en P describe únicamente la estructura infinitesimal en el vértice del cono de luz de P (véase la figura 1-18). El cono nulo nos da las direcciones espaciotemporales en P que definen la velocidad de la luz, esto es, la estructura en el espacio tangente en el punto P que da las direcciones de «longitud» nula, según la métrica g. (En la literatura, la expresión «cono de luz» suele emplearse también en el sentido que aquí estoy reservando para «cono nulo».) El cono de luz (igual que el cono nulo, como hemos visto antes) posee dos partes, una que define las direcciones nulas futuras y otra que define las direcciones nulas pasadas. El requisito impuesto por la relatividad general de que las partículas masivas no puedan superar la velocidad de la luz local se expresa explícitamente como el hecho de que las direcciones tangentes a las líneas de universo de las partículas masivas están todas ellas dentro de los conos nulos en sus respectivos eventos (figura 1-21). Las curvas suaves cuyas direcciones tangentes están todas estrictamente dentro de los conos nulos se denominan curvas de género tiempo. Por lo tanto, las líneas de universo de las partículas masivas son curvas de género tiempo.
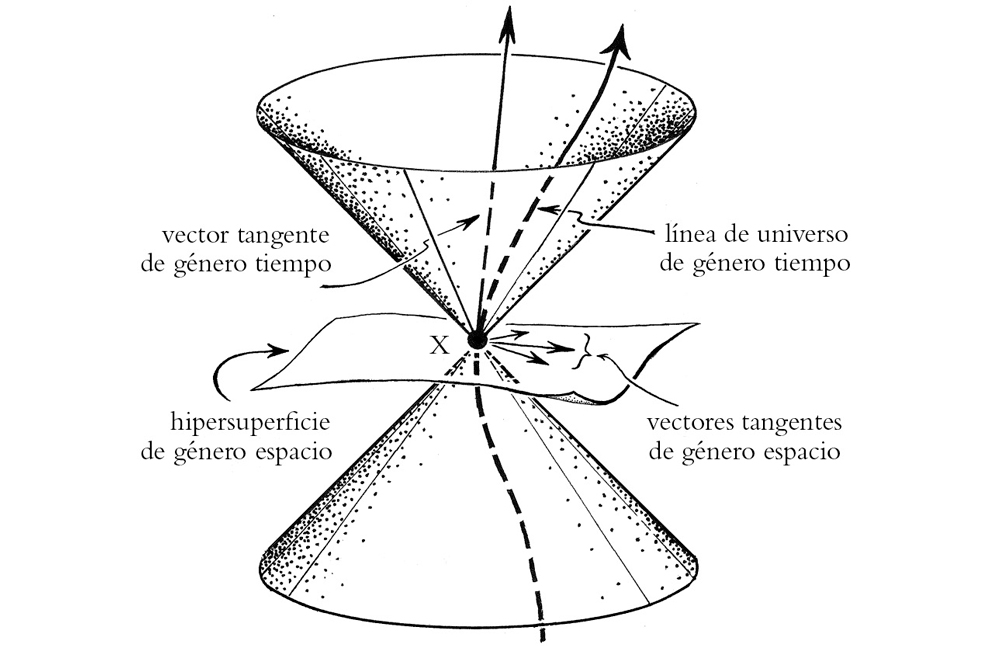
FIGURA 1-21. Los vectores tangentes nulos en X generan el cono nulo, como en la figura 1-18, pero también los hay de género tiempo que, si señalan hacia el futuro, describen vectores tangentes (4-velocidades) a las líneas de universo de las partículas masivas, y de género espacio, que señalan fuera del cono y son tangentes a las superficies de género espacio que pasan por X.
Un concepto complementario al de la curva de género tiempo es el de una 3-superficie de género espacio (o (n – 1)-superficie de género espacio, o hipersuperficie de género espacio, si pensamos en un espaciotiempo n-dimensional. Las direcciones tangentes a tal hipersuperficie son todas externas a los conos nulos pasado y futuro (figura 1-21). En relatividad general, esta es la generalización apropiada de la idea de «un instante en el tiempo» o un «t = espacio constante», donde t es una coordenada temporal adecuada. Claramente, existe una gran arbitrariedad a la hora de elegir tal hipersuperficie, pero esto es lo que se necesita si queremos referirnos a cuestiones como el determinismo en el comportamiento dinámico, donde podemos pedir que se especifiquen los «datos iniciales» sobre dicha hipersuperficie, datos destinados (localmente) a determinar la evolución del sistema hacia el pasado o hacia el futuro, según las ecuaciones adecuadas (normalmente, ecuaciones diferenciales; véase §A.11).
Como otra característica de la teoría de la relatividad, podemos destacar que si la «longitud» (en este sentido de lapso transcurrido) de una línea de universo C que conecta P con Q es mayor que la de cualquier otra línea de universo de P a Q, entonces C debe ser lo que se denomina una geodésica,[5] que es análoga, en un espaciotiempo curvo, a una «línea recta» (véase la figura 1-22). Curiosamente, esta propiedad de las «longitudes» de maximizarse en el espaciotiempo funciona de manera opuesta a lo que sucede en la geometría euclídea corriente, donde la línea recta que une dos puntos P y Q marca la longitud mínima de los caminos que unen P y Q. De acuerdo con la teoría de Einstein, la línea de universo de una partícula que se mueve libremente bajo el efecto de la gravedad es siempre una geodésica. Sin embargo, en el viaje del astronauta de la figura 1-16 hay movimiento acelerado, por lo que no es una geodésica.
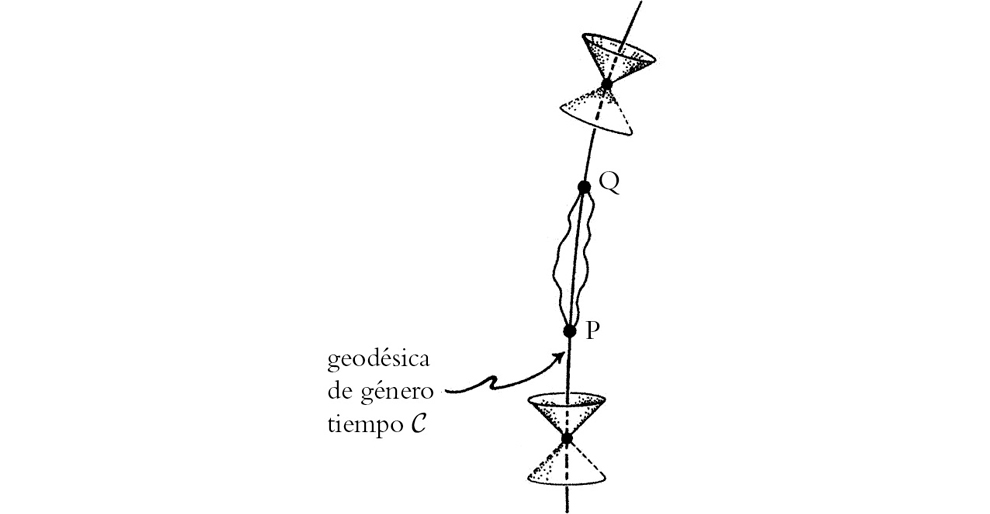
FIGURA 1-22. Una curva de género tiempo que maximiza la medida del tiempo entre dos eventos P y Q separados por un intervalo de género tiempo es necesariamente una geodésica.
El espaciotiempo plano de la relatividad especial, donde no hay campo gravitatorio, se denomina espacio de Minkowski (que por lo general representaré mediante el símbolo M) en honor del matemático germano-ruso Hermann Minkowski, quien introdujo la idea del espaciotiempo en 1907. Aquí los conos nulos están distribuidos uniformemente (figura 1-23). La relatividad general de Einstein sigue esa misma línea, pero los conos nulos ahora pueden no estar distribuidos uniformemente, debido a la presencia de un campo gravitatorio (figura 1-24). La métrica g (10 componentes por punto) define la estructura de conos nulos, pero no está del todo definida por ella. Algunos se refieren a esta estructura de conos nulos como la estructura conforme del espaciotiempo (9 componentes por punto); véase, en particular, §3.5. Además de esta estructura conforme lorentziana, g determina el escalamiento (1 componente por punto), lo cual fija el ritmo al que los relojes miden el tiempo en la teoría de Einstein (figura 1-25). Para más información sobre la manera en que se comportan los relojes en la teoría de la relatividad, véanse, por ejemplo, Rindler [2001] y Hartle [2003].
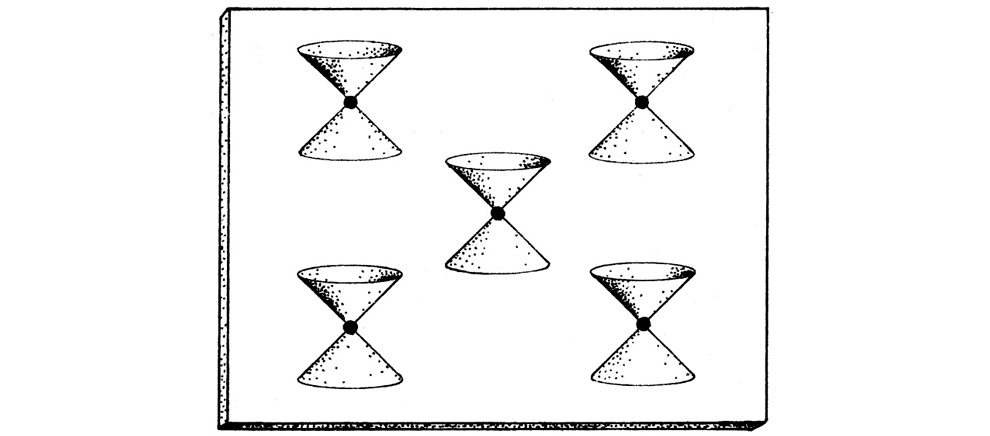
FIGURA 1-23. El espacio de Minkowski es el espaciotiempo plano de la relatividad especial. Sus conos nulos están distribuidos de manera completamente uniforme.
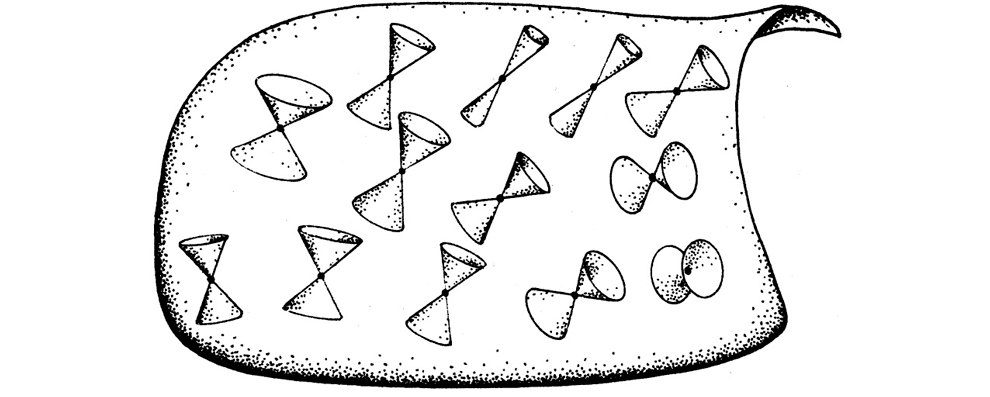
FIGURA 1-24. En relatividad general, los conos nulos no tienen por qué exhibir ninguna uniformidad particular.
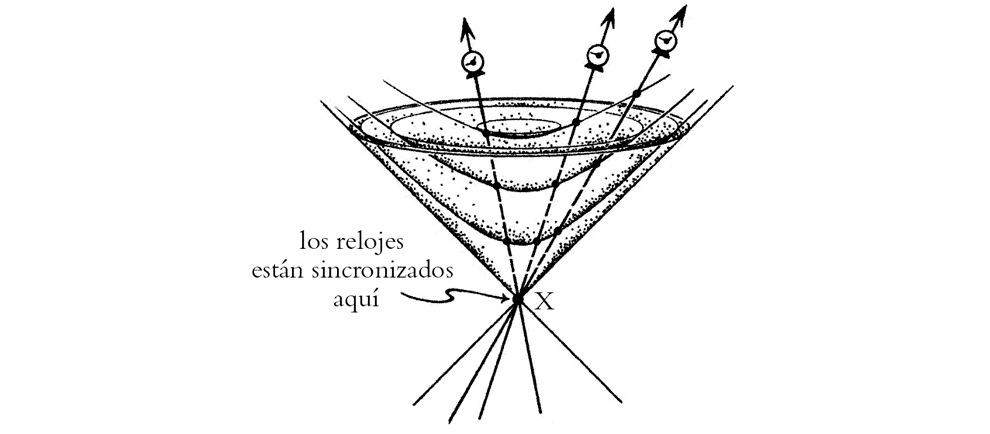
FIGURA 1-25. El escalamiento métrico en un evento X estaría determinado por los ritmos de los relojes ideales que pasan por X. Aquí, varios relojes ideales idénticos pasan por X, y cada uno de ellos determina el mismo escalamiento métrico, en el que los «tics» de los relojes estarían relacionados entre sí a través de las superficies con forma de cuenco que se muestran (denominadas 3-superficies hiperboloides).
1.8. LA TEORÍA DE GAUGE DEL ELECTROMAGNETISMO DE WEYL
La idea original de Weyl de 1918 para incorporar el electromagnetismo a la relatividad general implicaba debilitar la estructura métrica del espaciotiempo hasta dar lugar a una estructura conforme, como se ha descrito antes, de manera que ahora no existe una medida absoluta de los ritmos a los que transcurre el tiempo, aunque los conos nulos siguen estando definidos [Weyl, 1918]. Además de lo anterior, en la teoría de Weyl persiste el concepto de «reloj ideal», de manera que podemos definir una medida de la «longitud» asociada a una curva de género tiempo con respecto a cualquiera de estos relojes en concreto, aunque el ritmo al que el reloj midiese el paso del tiempo dependería de cuál se tratase. Pero en la teoría de Weyl no existe una escala temporal absoluta, porque ninguno de los relojes ideales se prefiere sobre ningún otro. Lo que es más, podríamos tener dos relojes que marcasen el tiempo exactamente al mismo ritmo cuando estuviesen en reposo uno respecto al otro en algún evento P, pero, si toman distintos caminos espaciotemporales hacia un segundo evento Q, podríamos ver que, al llegar a este segundo evento, existe una discrepancia entre los dos ritmos, esto es, ya no marcan el tiempo al mismo ritmo estando en reposo uno respecto al otro en Q; véase la figura 1-26(a). Es importante señalar que esta figura es distinta de —y más extrema que— la «paradoja de los gemelos» de la relatividad de Einstein. En aquel caso, mientras que las lecturas de los relojes podían depender de sus historias, no sucedía lo mismo con los ritmos. La geometría de Weyl, de una clase más general, conduce a un tipo curioso de «curvatura» espaciotemporal a través del concepto de los relojes ideales, curvatura que mide esta discrepancia entre los ritmos de los relojes a una escala infinitesimal (véase la figura 1-26(b)). Es análogo a la manera en que la curvatura de una superficie mide una discrepancia en los ángulos, como veremos en breve (en la figura 1-27). Weyl logró demostrar que la magnitud F que describe este tipo de curvatura satisface exactamente las mismas ecuaciones que la magnitud que describe el campo electromagnético libre en la teoría de Maxwell, motivo por el que propuso que esta F debía identificarse físicamente con el campo electromagnético de Maxwell.
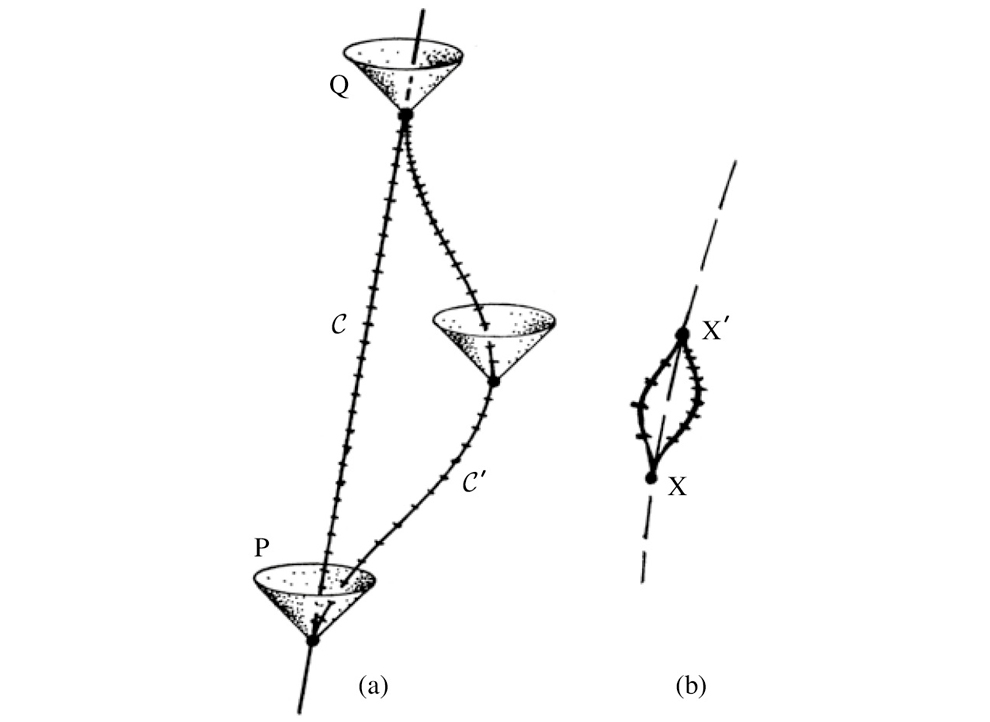
FIGURA 1-26. (a) La idea de Weyl de una conexión de gauge propone que la escala métrica no sea algo dado, sino que se pueda transferir de un punto P a otro punto Q a lo largo de una curva conectora C, de manera que se podría obtener un resultado diferente con una curva distinta C’ de P a Q. (b) La curvatura gauge de Weyl surge de la versión infinitesimal de esta discrepancia. En un principio, Weyl propuso que esta curvatura fuera el tensor del campo electromagnético de Maxwell.
Las medidas espaciales y temporales son esencialmente equivalentes entre sí en el entorno de cualquier evento P una vez que tenemos el concepto del cono nulo en P, puesto que eso fija la velocidad de la luz en P. En particular, dicho en términos corrientes, la velocidad de la luz permite la conversión entre medidas espaciales y temporales, y viceversa. Así, por ejemplo, el intervalo temporal de un año se convierte en la distancia espacial de un año luz; de un segundo se pasa a un segundo luz, etc. De hecho, en las mediciones modernas, los intervalos temporales se determinan directamente con mucha más precisión que los espaciales, por lo que el metro ahora se define como exactamente 1/299.792.458 de un segundo luz (de manera que la velocidad de la luz tiene ahora el valor entero exacto de 299.792.458 metros por segundo). De ahí que la expresión cronometría (en lugar de geometría) para la estructura del espaciotiempo, como propuso el destacado teórico relativista J. L. Synge [1921 y 1956], resulte particularmente pertinente.
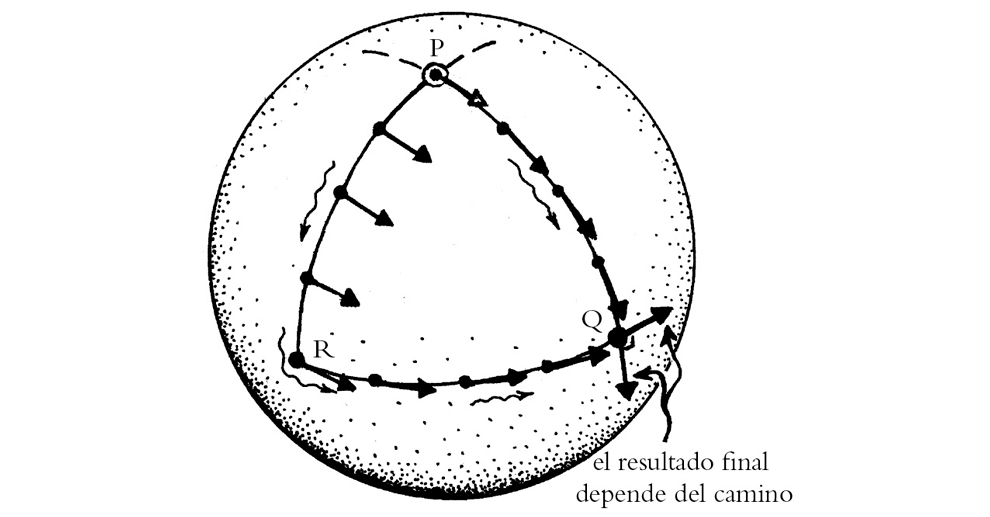
FIGURA 1-27. Una conexión afín expresa la idea del transporte paralelo de vectores tangentes a lo largo de curvas, donde la discrepancia al transportar a lo largo de distintas curvas proporciona una medida de la curvatura. Podemos verlo explícitamente en una esfera, en la que el transporte de un vector tangente a lo largo de la ruta directa de un círculo máximo desde P a Q da un resultado extremadamente diferente que el que se obtiene mediante la ruta consistente en un arco de círculo máximo de P a R seguido de otro arco similar desde R hasta Q.
He descrito la idea de Weyl en términos de medidas temporales, pero es probable que él tuviera más en mente desplazamientos espaciales, y su esquema es lo que se denomina una teoría de gauge, donde «gauge» («calibre», en inglés) hace referencia a la escala en función de la cual se miden las distancias físicas. Lo importante de la notable idea de Weyl es que un gauge no tenía por qué determinarse globalmente, a la vez para todo el espaciotiempo, pero si se especifica en un evento P, y se tiene una curva C que conecta P con otro evento Q, entonces el gauge puede ser transportado de forma unívoca a lo largo de C desde P hasta Q. Pero si se tiene también otra curva C’ que conecta P con Q, entonces transportar el gauge hasta Q a lo largo de C’ puede dar un resultado diferente. La magnitud matemática que define este procedimiento de «transporte de gauge» se denomina conexión gauge, y las discrepancias fruto de emplear distintos caminos son una medida de la curvatura gauge. Debemos señalar que es probable que la genial idea de una conexión gauge se le ocurriese a Weyl gracias a su familiaridad con otro tipo de conexión, que posee automáticamente cualquier variedad (pseudo) riemanniana —conocida como conexión afín—, que tiene que ver con el transporte paralelo de vectores tangentes a lo largo de curvas y que también depende del camino que se recorra, como queda a todas luces de manifiesto, para el caso de una esfera, en la figura 1-27.
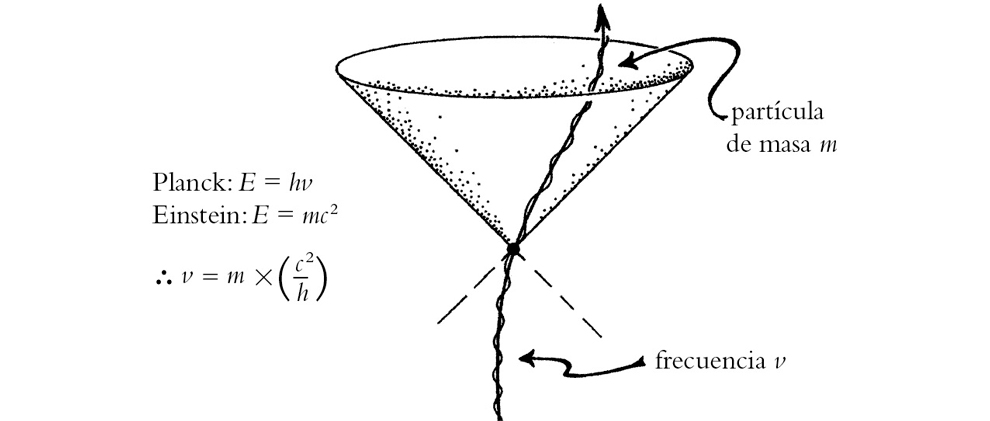
FIGURA 1-28. Cualquier partícula masiva estable de masa m es un preciso reloj mecanocuántico de frecuencia n = mc2/h.
Cuando Einstein supo de la ingeniosa idea de Weyl sintió mucha curiosidad, pero señaló que, desde un punto de vista físico, el esquema tenía un grave defecto, básicamente debido a la razón física de que la masa de la partícula proporciona una medida definida del tiempo a lo largo de su línea de universo. Esto se obtiene (figura 1-28) al combinar la relación cuántica de Max Planck
E = hn
con la del propio Einstein
E = mc2.
Aquí, E es la energía de la partícula (en su sistema de referencia en reposo), m es su masa (en reposo) y v es la frecuencia (esto es, el «ritmo del tictac») que la partícula adquiere según la mecánica cuántica básica (véase §2.2), y donde h y c son, respectivamente, la constante de Planck y la velocidad de la luz. Así, combinando lo anterior haciendo uso de que hn (= E) = mc2, vemos que siempre existe una frecuencia precisa determinada por una partícula individual, que es directamente proporcional a su masa:
n = m × ,
donde la magnitud c2 / h es una constante universal. La masa de cualquier partícula estable, por lo tanto, determina con mucha precisión un ritmo del reloj, dado por su frecuencia.
Sin embargo, en la propuesta de Weyl este ritmo del reloj no sería necesariamente una magnitud fija, sino algo que dependería de la historia de la partícula. En consecuencia, la masa de la partícula tendría que depender de su historia. En particular, en la situación de antes, si dos electrones se considerasen partículas idénticas (como de hecho exige la mecánica cuántica) en un evento P, es probable que acabasen con masas distintas en un segundo evento Q si llegaron a él siguiendo caminos diferentes, en cuyo caso no podrían ser partículas idénticas en Q. Esto es, de hecho, profundamente incompatible con los principios bien establecidos de la teoría cuántica, que exigen que las reglas que son de aplicación para partículas idénticas sean esencialmente diferentes de las que corresponden a partículas no idénticas (véase §1.14).
Así pues, parecía que la idea de Weyl no cumplía con varios principios cuánticos muy básicos. Sin embargo, en un extraordinario giro de los acontecimientos, fue la propia teoría cuántica la que acudió al rescate de la idea de Weyl una vez que fue formulada por completo, alrededor de 1930 (principalmente por Dirac [1930] y Von Neumann [1932], así como por el propio Weyl [1927]). Como veremos en el capítulo 2 (véanse §§2.5 y 2.6), la descripción cuántica de las partículas viene dada en términos de una descripción mediante números complejos (§A.9). Ya hemos visto, en §1.4, esta función esencial de los números complejos al aparecer como coeficientes (las magnitudes w y z) en el principio de superposición de la mecánica cuántica. Veremos más adelante (§2.5) que, si multiplicamos todos estos coeficientes por el mismo número complejo u de módulo unidad (esto es, |u| = = 1, de forma que u está situado sobre el círculo unidad en el plano de Wessel (véase §A.10, figura A-13)), la situación física no varía. Observemos que la fórmula de Cotes-De Moivre-Euler (véase §A.10) demuestra que dicho número complejo unimodular siempre puede escribirse como
u = eiq = cos q + i sin q,
donde q es el ángulo (medido en radianes, en sentido antihorario) que la línea que une el origen con u forma con el eje real positivo (figura A-13 en §A.10).
En el contexto de la mecánica cuántica, un multiplicador complejo unimodular se conoce habitualmente como una fase (o un ángulo de fase), y en el formalismo cuántico se considera algo que no es directamente observable (véase §2.5). La sutil variación que convierte la ingeniosa pero extraordinaria idea de Weyl en un ingrediente clave de la física moderna consiste en sustituir el factor de escala real positivo —o gauge— de Weyl por la fase compleja de la mecánica cuántica. Por estas razones históricas, el término «gauge» ha persistido, aunque quizá habría sido más apropiado referirse a la teoría de Weyl, modificada de esta manera, como una teoría de fase, y a la conexión gauge como una conexión de fase. Sin embargo, cambiar la terminología a estas alturas probablemente confundiría a más gente que a la que ayudaría.
Para ser más precisos, la fase que aparece en la teoría de Weyl no es exactamente la misma que la fase (universal) del formalismo cuántico, ya que existe entre ambas un factor multiplicador que viene dado por la carga eléctrica de la partícula en cuestión. La característica fundamental en la que se basa la teoría de Weyl es la presencia de lo que se denomina un grupo continuo de simetrías (véase el último párrafo de §A.7), que se aplica sobre cualquier evento P en el espaciotiempo. En la teoría original de Weyl, el grupo de simetrías está formado por todos los factores reales positivos mediante los que se podría aumentar o reducir el gauge. Estos posibles factores son simplemente los distintos números reales positivos, cuyo espacio los matemáticos denominan R+, por lo que el grupo de simetría de relevancia se conoce aquí como grupo multiplicativo R+. En la versión posterior, y más relevante desde un punto de vista físico, de la teoría electromagnética de Weyl, los elementos del grupo son las rotaciones en el plano de Wessel (sin reflexión), denominado SO(2) o a veces U(1), y los elementos de este grupo se representan mediante números complejos eiq de módulo unidad, que proporcionan los distintos ángulos de rotación del círculo unidad en el plano de Wessel (este círculo unidad lo denoto simplemente como S1).
Cabría señalar (véase asimismo el párrafo final de §A.7 en relación con esta notación, y también para el concepto de «grupo») que la «O» en «SO(2)» significa «ortogonal», lo que quiere decir que estamos tratando con un grupo de rotaciones (esto es, que preserva la ortogonalidad —los ángulos rectos—, que en este caso es de rotaciones en 2 dimensiones, tal y como señala el «2» en «SO(2)»). La «S» significa «especial» (special en inglés), lo cual hace referencia al hecho de que aquí se excluyen las reflexiones. En cuanto a «U(1)», la «U» viene de «unitario» (que preserva la naturaleza de norma unidad de los vectores complejos), lo que alude a una clase especial de rotación en el espacio de los números complejos que veremos en §§2.5-2.8. Con independencia de cómo las denominemos, de lo que hablamos es simplemente de las rotaciones, sin reflexión, del círculo ordinario S1.
Observamos que ahora la conexión de Weyl no es realmente un concepto que se aplique simplemente a la variedad espaciotemporal M, ya que el círculo S1 no forma en verdad parte del espaciotiempo sino que hace referencia a un espacio abstracto que tiene que ver específicamente con la mecánica cuántica. No obstante, podemos seguir pensando que S1 tiene una función geométrica, en particular como la fibra de un fibrado B cuyo espacio base es la variedad espaciotemporal M. Esta geometría se ilustra en la figura 1-29. Las fibras son los círculos S1, pero vemos en la imagen que es más conveniente entenderlos como los círculos unitarios dentro de copias del plano (de Wessel) complejo (§A.10). (Se remite al lector a la exposición en §A.7 sobre el concepto de «fibrado».) El concepto de Weyl de una conexión de gauge es en efecto geométrico, pero no proporciona estructura al espaciotiempo puro y duro, sino que dicha estructura se asigna al fibrado B, que es una 5-variedad íntimamente relacionada con la 4-variedad espaciotemporal.
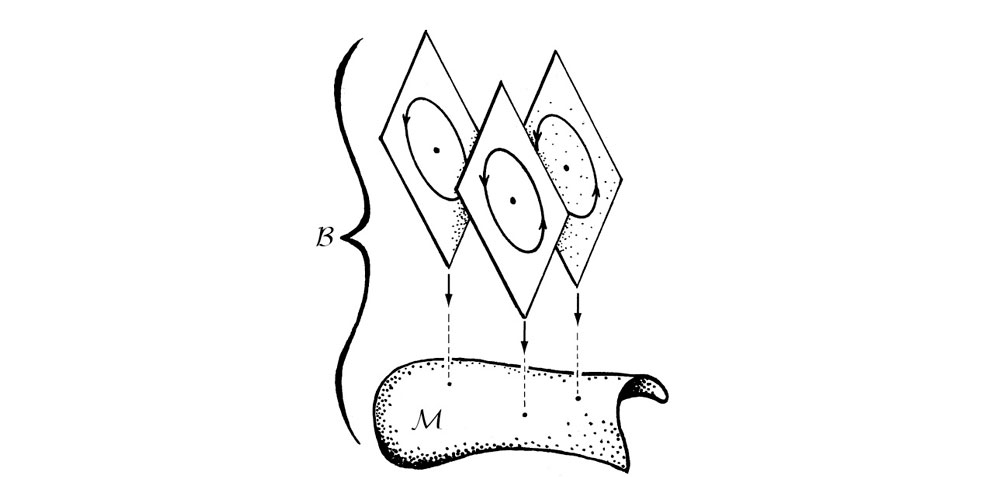
FIGURA 1-29. La geometría de Weyl expresa el electromagnetismo como una conexión en un fibrado B sobre el espaciotiempo M. Es preferible entender las fibras (circulares) S1 como círculos unitarios en copias del plano (de Wessel) complejo.
Las extensiones de las ideas de Weyl que expresan las interacciones fuerte y débil de la física de partículas también se formulan, en el modelo estándar de §1.3, en función de una conexión de gauge, y de nuevo es apropiada la descripción mediante fibrados de §A.7. En cada caso el espacio base es el espaciotiempo 4-dimensional, como antes, pero la fibra tendría que ser un espacio F de dimensionalidad superior a la del 1-dimensional S1 que, como ya se ha mencionado, puede utilizarse para expresar el electromagnetismo. Estas extensiones de la aproximación gauge a la teoría de Maxwell se conocen como teorías de Yang-Mills [Chan y Tsou, 1998]. En el caso de las interacciones fuertes, F sería un espacio con la misma simetría que el de los colores que puede tener un quark, de acuerdo con las descripciones dadas en §1.3. Aquí, el grupo de simetría es el denominado SU(3). El caso de las interacciones débiles es aparentemente similar, y ahora el grupo es el llamado SU(2) (o bien U(2)), pero hay algo que enturbia la situación en la teoría de la interacción débil al romperse la simetría, como consecuencia de un proceso de ruptura de la simetría que se entiende que tuvo lugar en los primeros momentos de la expansión del universo. De hecho, en las descripciones habituales de este procedimiento hay varias cuestiones que a mí me resultan algo preocupantes, ya que, en sentido estricto, la propia idea de una simetría gauge no funciona a menos que la simetría sea exacta [véanse §A.7, y §28.3 de ECalR]. Afortunadamente, a mi juicio, hay reformulaciones del procedimiento habitual en las que las fuerzas débiles surgen a través de un mecanismo con una interpretación física algo distinta de la estándar, en la que, en efecto, se postulan componentes de los leptones de tipo quark y con color (análogos a los quarks componentes de hadrones) en los cuales se considera que la simetría de la interacción débil es siempre exacta [’t Hooft, 1980b; Chan y Tsou, 1980].
1.9. LIBERTAD FUNCIONAL EN MODELOS DE KALUZA-KLEIN Y DE CUERDAS
Tenemos ahora dos espacios 5-dimensionales alternativos, cada uno de los cuales proporciona un procedimiento geométrico para incorporar el electromagnetismo de Maxwell a una geometría espaciotemporal curva. ¿Cuál es la relación de la 5-variedad B en la representación mediante fibrados de S1 del procedimiento de Weyl que se describe en §1.8 con la representación de Kaluza-Klein de las interacciones electromagnéticas a través de un espaciotiempo 5-dimensional que se comenta en §1.6? De hecho, ambas están íntimamente relacionadas, y no hay ningún inconveniente en pensar que son idénticas. El espaciotiempo 5-dimensional de Kaluza, modificado por Klein para que tuviese un minúsculo círculo (S1) como su dimensión «adicional», y el fibrado B, que obtenemos en el procedimiento de Weyl, son topológicamente idénticos, ya que (por regla general) ambos son simplemente el espacio producto M × S1 del espaciotiempo 4-dimensional ordinario M con el círculo S1(véanse la figura A-25 en §A.7 y la figura 1-29). Además, el espacio de Kaluza-Klein posee automáticamente una especie de estructura de fibrado de S1, en la que, para identificar las fibras S1, solo buscamos geodésicas que sean cerradas (y pertenezcan a la familia topológica correcta). Existe, no obstante, una pequeña diferencia entre los 5-espacios de Weyl y de Kaluza-Klein en el tipo de estructura que se asigna en cada caso. El procedimiento de Weyl exige que asignemos una conexión de gauge (§1.8) a B, considerado como un fibrado sobre el espaciotiempo 4-dimensional M, mientras que, en la teoría de Kaluza-Klein, se considera que la 5-variedad en su conjunto es «espaciotiempo» y, en consecuencia, se asigna una métrica g a toda la estructura. Sin embargo, resulta que la conexión de gauge de Weyl ya está implícita en la construcción de Kaluza, pues viene determinada simplemente por el concepto ordinario de conexión afín, que se analiza en §1.8 (cosa que es válida para cualquier espacio de Riemann, y por lo tanto para el 5-espacio de Kaluza), aplicada a las direcciones ortogonales a las fibras S1. Así pues, el 5-espacio de Kaluza ya contiene la conexión de gauge de Weyl, y de hecho puede identificarse con el fibrado B de Weyl.
Pero el espacio de Kaluza-Klein nos da algo más, porque posee una métrica con la propiedad de que, si satisface las correspondientes ecuaciones de campo de Einstein del vacío 5G = 0 (que afirman que el tensor energía 5T del 5-espacio se considera nulo), entonces no solo obtenemos la conexión de Weyl sino que, notablemente, también obtenemos el hecho de que el campo electromagnético de Maxwell, F, que surge de la conexión de Weyl, actúa (a través de su densidad de masa/energía) como una fuente del campo gravitatorio (las ecuaciones se emparejan debidamente de esta manera denominada ecuaciones de Einstein-Maxwell). Este hecho sorprendente no es algo que se derive de manera directa del enfoque de Weyl.
Para ser algo más preciso sobre la estructura del 5-espacio de Kaluza-Klein, debo señalar que existe una salvedad a la afirmación anterior: a saber, que la versión de la teoría de Kaluza-Klein que estoy empleando aquí es aquella que requiere que la longitud asignada a los bucles S1 sea la misma a través del 5-espacio. (Algunas versiones de la teoría permiten que esta longitud varíe, dejando así margen para un campo escalar adicional.) Yo también requiero que esta longitud constante se elija de tal manera que la constante 8πγ en las ecuaciones de Einstein (véase §1.1) aparezca correctamente, y, lo más importante, insisto en que, cuando hablo de la teoría de Kaluza-Klein, me refiero a la versión original, en la que se impone la existencia de una simetría exacta en todo el 5-espacio, para que posea simetría rotacional completa en la dirección de S1 (véase la figura 1-29, básicamente similar). Dicho de otro modo, el vector k es un vector de Killing, de manera que el 5-espacio puede deslizarse sobre sí mismo a lo largo de las líneas de las S1 sin que eso afecte a su estructura métrica.
Abordemos ahora la cuestión de la libertad funcional en la teoría de Kaluza-Klein. Si usamos la forma de la teoría que acabamos de comentar, entonces la dimensión adicional no contribuye a un exceso de libertad funcional. Debido a la simetría rotacional impuesta a lo largo de las curvas S1, la libertad es la misma que para un espaciotiempo 4-dimensional ordinario con una evolución determinista estándar a partir de los datos en un 3-espacio inicial; de hecho, la misma que para las ecuaciones de Einstein-Maxwell, a las cuales es equivalente, a saber
∞8∞3,
que es el valor que debería tener, para una teoría física clásica apropiada para nuestro universo.
Algo que quiero recalcar aquí es que una característica esencial de las teorías de gauge —esa clase de teorías que han tenido un éxito extraordinario a la hora de explicar las fuerzas básicas de la naturaleza— es que exista una simetría (de dimensiones finitas) asociada a las fibras F del fibrado sobre el que se aplica la teoría de gauge. Como se señala insistentemente en §A.7, es la posesión de una simetría (continua) en nuestra fibra F lo que hace posible que la teoría de gauge funcione. Esta simetría, en el caso de la teoría de Weyl de las interacciones electromagnéticas, es el grupo circular U(1) (o, de forma equivalente, SO(2)) que debe aplicarse, exactamente, a las fibras F. (Véase el final de §A.7 para el significado de estos símbolos.) Es también esta simetría la que en la aproximación de Weyl se extiende al conjunto de la variedad 5-dimensional B, y la que se ha especificado en el procedimiento original de Kaluza-Klein. Para preservar esta estrecha relación entre el enfoque espaciotemporal en más dimensiones, propuesto inicialmente por Kaluza, y el de la teoría de gauge de Weyl, parece esencial conservar la simetría de las fibras y no incrementar (enormemente) la libertad funcional al tratar los espacios fibras F como si fuesen en efecto partes del espaciotiempo con grados de libertad internos.
¿Y qué hay de la teoría de cuerdas? Aquí, la historia parece ser por completo distinta, ya que se exige explícitamente que la o las dimensiones espaciales adicionales participen plenamente de la libertad funcional. Dichas dimensiones espaciales adicionales están destinadas a desempeñar su función como verdaderas dimensiones espaciales. Esto forma parte de la filosofía en la que se basa la teoría de cuerdas tal y como se ha desarrollado, ya que se propone que, de alguna manera, las «oscilaciones» que estas dimensiones adicionales hacen posibles deben permitir explicar todas las complicadas fuerzas y parámetros que se necesitan, para así disponer de margen para acomodar todas las características necesarias de la física de partículas. En mi opinión, esta es una filosofía gravemente errónea, ya que permitir que las dimensiones espaciales adicionales participen con libertad en la dinámica constituye una verdadera caja de Pandora de grados de libertad no deseados, pero con escasas esperanzas de que alguna vez lleguemos a controlarlos.
Sin embargo, haciendo caso omiso de las dificultades de este estilo que surgirían de manera natural de la excesiva libertad funcional existente en las dimensiones adicionales, quienes propusieron la teoría de cuerdas escogieron esta vía, muy alejada del esquema original de Kaluza-Klein. Como parte de sus intentos de resolver las anomalías que surgieron como consecuencia de sus requisitos de invariancia parametral para su teoría cuántica de cuerdas, se vieron abocados, desde alrededor de 1970 en adelante, a tratar de adoptar (para las cuerdas bosónicas) un espaciotiempo 26-dimensional plenamente dinámico, en el que habría 25 dimensiones espaciales y 1 dimensión reservada para el tiempo. Posteriormente, en la estela del muy influyente trabajo teórico realizado en 1984 por Michael Green y John Schwarz, los teóricos de cuerdas lograron reducir esta dimensionalidad espacial a 9 (para cuerdas fermiónicas) con la ayuda de lo que se conoce como supersimetría (véase §1.14, aunque ya se ha mencionado en §1.6), pero esta reducción de la dimensionalidad espacial adicional (ya que no la reduce hasta el valor 3 que experimentamos directamente) no supone una gran diferencia para las objeciones que expondré aquí.
En mis intentos de captar los distintos avances en teoría de cuerdas, me he encontrado con otro punto de potencial confusión para mí, sobre todo al tratar de entender los problemas de libertad funcional. La cuestión es que a menudo ha habido un cambio del punto de vista acerca de cuál se entiende que es la dimensionalidad del espaciotiempo. Supongo que muchas otras personas ajenas a este campo se topan con dificultades similares en sus intentos por comprender la estructura matemática de la teoría de cuerdas. La idea de tener un espaciotiempo ambiente de una determinada dimensionalidad parece desempeñar un papel menor en la teoría de cuerdas que en la física convencional, y desde luego menor que el tipo de papel con el que yo me sentiría cómodo. Es especialmente difícil evaluar la libertad funcional que implica una teoría física, a menos que se tenga una idea clara de su dimensionalidad espaciotemporal.
Para ser más explícito sobre esta cuestión, permítanme que vuelva sobre uno de los aspectos particularmente atractivos de las primeras ideas sobre cuerdas, tal y como se ha esbozado en §1.6. Me refiero al hecho de que se pueda entender que las historias de cuerdas son superficies de Riemann, esto es, curvas complejas (véase §A.10), que son estructuras de una elegancia notable desde el punto de vista matemático. La expresión hoja de universo se usa a veces para referirse a esta historia de cuerdas (en analogía con la idea de la línea de universo de una partícula en la teoría de la relatividad convencional; véase §1.7). En los primeros tiempos de la teoría de cuerdas, el asunto se veía en ocasiones desde el punto de vista de una teoría de campo conforme 2-dimensional [Francesco et al., 1997; Kaku, 2000; Polchinski, 1994: cap. 1, y 2001: cap. 2], en la que, a grandes rasgos, el análogo del espaciotiempo sería la propia hoja de universo 2-dimensional. (Recordemos el concepto de conforme, en un contexto espaciotemporal, visto en §1.7.) Esto nos llevaría a una representación en la que la libertad funcional tendría la forma
∞a∞1
para un número positivo a. ¿Cómo conseguir que esto cuadre con la libertad funcional mucho mayor, de ∞b∞3, que exige la física ordinaria?
La respuesta parece ser que la hoja de universo, en algún sentido, «palparía» el espaciotiempo y la física a su alrededor en términos de alguna clase de expansión de serie de potencias, donde la información necesaria (los coeficientes efectivos de la serie de potencias) se obtendría en función de un número infinito de parámetros (de hecho, magnitudes holomorfas sobre la hoja de universo; véase §A.10). Tener un número infinito de tales parámetros es a grandes rasgos como poner «a = ∞» en la expresión anterior, pero no resulta muy útil (por una razón del tipo de la que se menciona hacia el final de §A.11). Lo que quiero dejar claro aquí no es desde luego que la libertad funcional pueda, en algún sentido, estar mal definida o ser irrelevante, sino que, para una teoría formulada de tal manera que depende de aspectos como los coeficientes de una serie de potencias o el análisis de modos, puede que no resulte nada fácil determinar cuál es realmente esa libertad funcional (§A.11). Por desgracia, parece que las formulaciones de este tipo suelen ser las que se emplean en varios enfoques de la teoría de cuerdas.
Al parecer, en cierta medida, entre los teóricos de cuerdas se cree que no es demasiado importante tener una visión clara de cuál es realmente la dimensionalidad del espaciotiempo. En cierto sentido, podría suponerse que esta dimensionalidad es un efecto de la energía, de forma que podría suceder que, a medida que la energía del sistema aumenta, vayan estando disponibles más dimensiones espaciales. En consecuencia, se podría adoptar el punto de vista de que existen dimensiones ocultas, un mayor número de las cuales se van revelando a medida que se eleva la energía. La falta de claridad en esta representación es algo perturbadora para mí, sobre todo en lo que respecta a la cuestión de la libertad funcional intrínseca a la teoría.
Un ejemplo de lo anterior es lo que se denomina una teoría de cuerdas heteróticas. Existen dos versiones de esta propuesta, que se conocen como teoría HO y teoría HE. La diferencia entre ambas no nos interesa ahora, pero en breve diré algo al respecto. La extraña característica de la teoría de cuerdas heteróticas es que parece que se comporta al mismo tiempo como una teoría en 26 y en 10 dimensiones espaciotemporales (en el segundo caso, acompañada de supersimetría), dependiendo de si nos fijamos en las excitaciones de la cuerda levógiras o dextrógiras. Esta diferencia (que depende de una orientación que ha de asignársele a la cuerda) también requiere una explicación, que daré en breve. Este conflicto dimensional podría causarnos problemas si intentásemos calcular la libertad funcional en cuestión (donde, para este propósito, cada esquema se trata como una teoría clásica).
El aparente dilema se aborda oficialmente tratando el espaciotiempo como si fuese 10-dimensional en ambos casos (1 dimensión temporal y 9 espaciales), pero hay 16 dimensiones espaciales adicionales que deben tratarse de manera diferente en los dos casos. Para las excitaciones levógiras se deben tomar conjuntamente las 26 dimensiones y se ha de considerar que todas ellas forman el espaciotiempo en el que la cuerda puede agitarse. Sin embargo, para las excitaciones dextrógiras, distintas direcciones dentro de las 26 dimensiones se interpretan de maneras diferentes: 10 de ellas proporcionan direcciones en las que la cuerda puede oscilar, mientras que las otras 16 se consideran direcciones de fibra, por lo que, en lo tocante a la cuerda cuando se encuentra en dichos modos de vibración hacia la derecha, la representación es la de un fibrado (véase §A.7) con un espacio base 10-dimensional y una fibra 16-dimensional.
Como sucede con los fibrados en general, debe haber un grupo de simetría asociado a la fibra, que para la teoría HO se considera que es SO(32) (el grupo de rotaciones no reflexivas de una esfera en 32 dimensiones; véase la parte final de §A.7), mientras que para la teoría heterótica HE es el grupo E8 × E8, donde E8 es un grupo de simetría de un tipo particularmente interesante, denominado grupo continuo simple excepcional. No cabe duda de que el interés matemático intrínseco particular de este grupo simple excepcional E8 es el más grande y el más fascinante de ellos (da cierto ánimo desde el punto de vista del atractivo estético; véase §1.1). Pero lo importante, por lo que concierne a la libertad funcional, es que, sea cual sea el grupo que se elija para la descripción del fibrado, esta libertad sería de la forma ∞a∞9, apropiada para los modos fermiónicos (dextrógiros) de oscilación de la cuerda, mientras que parecería ser de la forma ∞b∞25, como resultaría apropiado para los modos bosónicos (levógiros). Esta cuestión está estrechamente relacionada con otra con la que nos hemos topado antes, cuando analizamos la diferencia en cuanto a libertad funcional entre la teoría original de Kaluza-Klein (o teoría del fibrado circular de Weyl; véase §1.8), con una libertad funcional de ∞8∞3, y una teoría del espaciotiempo plenamente 5-dimensional cuya libertad funcional, muy superior, sería de la forma ∞b∞4. Debe establecerse aquí una clara distinción entre la dimensionalidad d + r del espacio total B de un fibrado (con fibra r-dimensional F ) y la del espacio base d-dimensional M. Esto se describe con más detalle en §A.7.
La cuestión anterior tiene que ver con la libertad funcional que posee el espaciotiempo en su conjunto, al margen de qué hoja de universo pudiera existir en su interior. Pero lo que nos interesa realmente aquí es la libertad que poseen las hojas de universo de la cuerda (véase §1.6) que se encuentran dentro de este espaciotiempo. ¿Cómo es posible que para ciertos tipos de modos de desplazamiento (los fermiónicos) el espaciotiempo parezca ser 10-dimensional y para otros (los bosónicos) parezca 26-dimensional? Para estos últimos, la situación es razonablemente sencilla. La cuerda puede vibrar a su antojo en el espaciotiempo ambiente, con una libertad funcional de ∞24∞1 (el «1» proviene del hecho de que, aunque la hoja de universo de la cuerda es una 2-superficie, estamos considerando tan solo el espacio 1-dimensional de las excitaciones dextrógiras). Pero, cuando pasamos a considerar los modos fermiónicos, debemos entender que la cuerda habita el «espaciotiempo» que es 10-dimensional, en lugar de encontrarse en el fibrado 26-dimensional situado sobre él. Lo que esto significa es que la propia cuerda debe transportar consigo las fibras del fibrado situadas sobre ella. Se trata de una entidad de un tipo realmente muy diferente de la de los modos bosónicos, pues ahora la propia cuerda es un subfibrado 18-dimensional del espacio total 26-dimensional del fibrado espaciotemporal que habita. (Este es un hecho que no suele señalarse. El espaciotiempo efectivo es un espacio cociente 10-dimensional —véanse la figura 1-32 en §1.10 y §A.7— del fibrado total 26-dimensional, de manera que la hoja de universo de la cuerda debe ser también un espacio cociente, en este caso de un subfibrado 18-dimensional.) La libertad funcional en estos modos sigue siendo de la forma ∞a∞1 (donde a depende del grupo del fibrado), pero la imagen geométrica es ahora completamente distinta de la de los modos bosónicos, ya que, para estos últimos, la cuerda debe verse como un tubo de universo 2-dimensional (como en la figura 1-11), mientras que para los modos fermiónicos las cuerdas deberían ser, desde el punto de vista técnico, subfibrados de dimensión total 18 ( = 2 + 16). Me cuesta mucho hacerme una imagen coherente de lo que sucede aquí, y nunca he visto que estas cuestiones geométricas se traten debidamente.
Además, debería ser más explícito aquí sobre la naturaleza geométrica de los modos dextrógiros y levógiros, dejando de lado la cuestión de cómo debe interpretarse el espacio ambiente, puesto que esto suscita otra cuestión que aún no he abordado. Ya he mencionado el hecho sugerente de que las hojas de universo de las cuerdas pueden verse como superficies de Riemann. Sin embargo, esto no es realmente así para las descripciones anteriores. He recurrido a cierto juego de manos muy habitual en las argumentaciones de la teoría cuántica (de campos) y que aquí se emplea a las claras al hacer uso de un recurso conocido como rotación de Wick, que no ha recibido una mención explícita hasta ahora.
¿Qué es una rotación de Wick? Es un procedimiento matemático, originalmente pensado para transformar diversos problemas en teoría cuántica de campos en el espaciotiempo de Minkowski M (el espaciotiempo plano de la relatividad especial; véase la parte final de §1.7) en otros normalmente más abordables en el 4-espacio euclídeo ordinario E4. La idea procede del hecho de que la métrica g del espaciotiempo lorentziano de la teoría de la relatividad se convierte en (menos) una métrica euclídea si una coordenada temporal estándar t se sustituye por it (donde i = ; véase §A.9). Este truco se conoce por regla general como euclideanización, y, una vez que se ha resuelto el problema en su forma euclideanizada, se convierte de vuelta mediante un proceso de extensión analítica (véase §A.10, y también §3.8) para obtener una solución en el espaciotiempo de Minkowski M en cuestión. Actualmente, es tan habitual utilizar el concepto de la rotación de Wick en teoría cuántica de campos que a menudo se considera casi un procedimiento automático en numerosas situaciones de distinto tipo, sin apenas hacer mención de él y sin que su validez se cuestione casi nunca. Tiene, en efecto, una amplia aplicabilidad, pero no es un procedimiento universalmente válido. Muy en particular, es harto discutible en el contexto de los espaciotiempos curvos que aparecen en relatividad general, donde, en circunstancias normales, el procedimiento ni siquiera se puede aplicar, porque no existe una coordenada temporal natural. En teoría de cuerdas, esto supone un problema tanto en el espaciotiempo 10-dimensional, en situaciones generales con espacios curvos, como también en la hoja de universo de las cuerdas.[6]
Me parece que una dificultad de este tipo suscita cuestiones que la teoría de cuerdas no ha abordado debidamente. No obstante, me permitiré ignorar aquí estas cuestiones generales para fijarme en cuál es el efecto de la euclideanización de la hoja de universo de una cuerda. Podemos visualizar la historia de una cuerda como un lazo único que se mueve de alguna manera, sin superar la velocidad de la luz local. Entonces, su hoja de universo sería una 2-superficie de género tiempo, que hereda una 2-métrica lorentziana de la 10-métrica lorentziana del espacio ambiente. Esta 2-métrica asignará un par de direcciones nulas a cada punto de la hoja de universo. Si seguimos sistemáticamente estas direcciones nulas en un sentido o en otro, obtenemos una curva nula helicoidal dextrógira o levógira sobre el cilindro de la hoja de universo. Las excitaciones que son constantes a lo largo de una u otra de estas familias de curvas nos darán los modos dextrógiro o levógiro a los que me he referido antes (véase la figura 1-30(b)). Sin embargo, dichas hojas cilíndricas nunca pueden ramificarse y dar lugar a imágenes como las que necesitaríamos para la figura 1-11, porque la estructura lorentziana se descompone en los lugares donde el tubo se ramifica. Esta topología solo puede darse para las cuerdas euclideanizadas que se muestran en la figura 1-30(a), que son superficies de Riemann, con una métrica de tipo riemanniano, sin direcciones nulas y susceptibles de ser interpretadas como curvas complejas (véase §A.10). Los modos dextrógiro y levógiro euclideanizados corresponden ahora a funciones holomorfas y antiholomorfas, respectivamente, sobre la superficie de Riemann (véase §A.10).
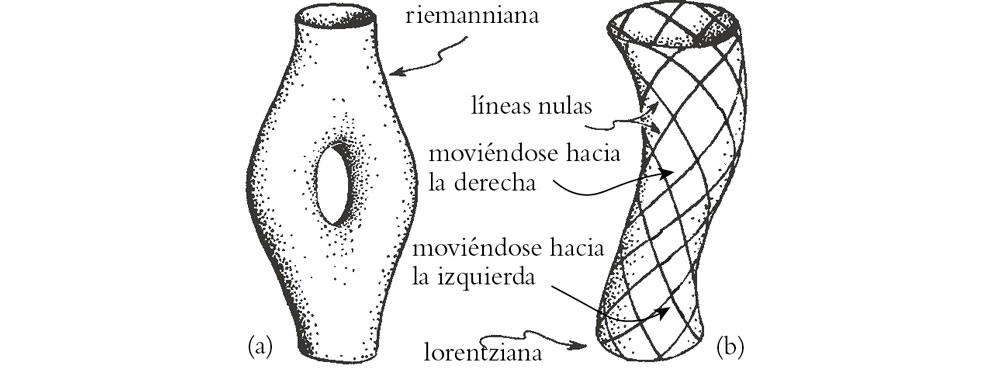
FIGURA 1-30. Esta figura compara dos puntos de vista diferentes con respecto a las hojas de universo de las cuerdas. En (a) vemos la representación de los tubos de universo como superficies de Riemann, que pueden ramificarse y volver a unirse de forma suave de diferentes maneras. En (b) tenemos la forma más directa de visualizar una historia de cuerdas (de género tiempo) como una 2-variedad lorentziana, en la que se pueden representar los modos de excitación levógiro y dextrógiro, pero donde no está permitida la ramificación. Se supone que las dos imágenes están relacionadas mediante una rotación de Wick, procedimiento muy discutible en un contexto de espaciotiempo curvo de la relatividad general.
La cuestión de la libertad funcional, que constituye mi preocupación principal en este apartado, no es la única directamente física que no se trata con suficiente profundidad en las consideraciones sobre teoría de cuerdas que he leído en la literatura estándar. De hecho, no he encontrado mucho relacionado con las consideraciones geométricas inmediatas que suscita el procedimiento aparentemente fundamental pero muy discutible de la rotación de Wick que he mencionado antes. Tengo la impresión de que muchas de las cuestiones geométricas y físicas más evidentes que surgen de la perspectiva de la teoría de cuerdas nunca se abordan como es debido.
Por ejemplo, en el caso de la teoría de cuerdas heterótica, a las cuerdas se las considera cerradas, lo que significa que no tienen agujeros. (Véase §1.6, y en particular §1.16.) Si intentamos imaginar estas cuerdas de una manera física directa —esto es, antes de que se introduzca el «truco» de la rotación de Wick—, debemos entender que la hoja de universo de una cuerda es de género tiempo, como en la figura 1-30(b). Si en dicha hoja de universo no puede haber agujeros, esta debe seguir siendo un tubo de género tiempo que se extiende indefinidamente hacia el futuro. No vale imaginar que se enrolla alrededor de las «minúsculas» dimensiones adicionales, ya que a estas dimensiones se las considera de género espacio. Solo puede continuar indefinidamente hacia el futuro, y entonces no puede considerarse cerrada. Esta es una de las muchas cuestiones que no creo que se traten debidamente en ninguna descripción de la teoría de cuerdas de las que he visto.
Me parece muy extraña esta curiosa falta de una imagen geométrica coherente de cómo la teoría de cuerdas ha de entenderse en términos físicos ordinarios, en especial para una teoría descrita con frecuencia como una teoría del todo. Es más, dicha falta de una imagen geométrica y física clara contrasta mucho con la geometría sumamente sofisticada y el análisis puramente matemático, tan minucioso, aplicados en el estudio de las 6-variedades (por regla general, espacios de Calabi-Yau; véanse §§1.13 y 1.14) que proporcionan las dimensiones adicionales del 6-espacio, enrolladas y del tamaño de la escala de Planck, que se supone que son necesarias para la coherencia de la teoría. Me resulta sumamente desconcertante que una parte muy bien informada de la comunidad física combine una sofisticación geométrica extrema y una aparente despreocupación por la coherencia geométrica general.
En la evaluación de las cuestiones relativas a la libertad funcional que ocupará los dos apartados siguientes, me expresaré como si el espaciotiempo fuese 10-dimensional, pero la validez de los argumentos no se limita a ese número concreto de dimensiones. El argumento clásico de §1.11, según el cual tales dimensiones adicionales serían catastróficamente inestables, también es válido para cualquier teoría supradimensional para la cual existan al menos 2 (minúsculas) dimensiones espaciales adicionales y que esté sujeta a las ecuaciones de Einstein 10-dimensionales (L = 0) del vacío 10G = 0 (la dimensionalidad temporal continúa siendo 1). En la literatura estándar se encuentran argumentos en el sentido de que la teoría de cuerdas bosónicas 26-dimensional original es en efecto catastróficamente inestable, pero esto no es demasiado relevante para los argumentos que expondré aquí, cuyo ámbito de aplicación es mucho más general.
El argumento expuesto en §1.10 es de un carácter completamente distinto al que figura en §1.9, que está dirigido a combatir un argumento mecanocuántico habitual según el cual las dimensiones espaciales adicionales, extraordinariamente minúsculas, serían inmunes a la excitación a cualquier escala de energía remotamente alcanzable. Aquí, de nuevo, el argumento no es específico para un determinado número de estas dimensiones espaciales adicionales, pero para concretar lo expresaré también en función de la teoría 10-dimensional, hoy en día en boga. En ninguno de los casos me preocuparé por la supersimetría, para que los conceptos geométricos puedan seguir siendo razonablemente claros. Doy por hecho que la presencia de supersimetría no afectaría de manera drástica a los argumentos, puesto que podrían referirse al «cuerpo» no supersimétrico de la geometría (véase §1.14).
En todos estos argumentos, adopto el punto de vista que la teoría de cuerdas parece exigir, según el cual las dimensiones espaciales adicionales se consideran plenamente dinámicas. Así, aunque los teóricos de cuerdas suelen destacar las semejanzas entre las dimensiones adicionales de la teoría de cuerdas y las que introducen Kaluza y Klein, debo insistir de nuevo en la diferencia enorme y esencial que existe entre el esquema original de Kaluza-Klein y el tipo de propuesta que los teóricos de cuerdas tienen en mente. En ninguna de las versiones de mayor dimensionalidad de la teoría de cuerdas que he visto, salvo quizá en relación con las 16 dimensiones de discrepancia entre los modelos heteróticos que se han descrito con anterioridad en este mismo apartado, hay un indicio de algo análogo a la simetría rotacional en las dimensiones adicionales incorporada en la teoría de Kaluza-Klein (de hecho, se niega explícitamente esa simetría [Greene, 1999]). En consecuencia, es probable que la libertad funcional en la teoría de cuerdas sea a todas luces excesiva; por ejemplo, de la forma ∞k∞9 para la teoría 10-dimensional que se considera convencional hoy en día, en lugar del valor de ∞k∞3 que esperaríamos para una teoría física realista. Lo más importante es que, mientras que en la teoría de Kaluza-Klein no existe libertad para tener variaciones arbitrarias en la estructura a lo largo de la dimensión espacial (S1) adicional (debido a la imposición de la simetría rotacional), en la teoría de cuerdas esta libertad está explícitamente permitida. Esta diferencia es la única responsable del exceso de libertad funcional que existe en la teoría de cuerdas.
Esta es una cuestión que nunca he visto que los teóricos de cuerdas profesionales traten en serio por lo que respecta a las consideraciones clásicas (esto es, no cuánticas). Por otra parte, se ha argumentado que tales consideraciones son esencialmente irrelevantes para la teoría de cuerdas, porque el problema debe abordarse desde el punto de vista de la mecánica cuántica (o la teoría cuántica de campos) en lugar de hacerlo desde la teoría clásica de campos. En efecto, cuando a los teóricos de cuerdas se les saca a colación el asunto de los excesivos grados de libertad funcional en las 6 dimensiones «pequeñas» adicionales, suelen desdeñarlo con un argumento mecanocuántico poco riguroso de naturaleza general que yo considero básicamente falaz. Evaluaré este argumento en el apartado siguiente, y a continuación (en §1.11) expondré no solo por qué creo que no es en absoluto convincente, sino que el corolario lógico de las dimensiones espaciales adicionales de los teóricos de cuerdas sería un universo por completo inestable, en el que cabría esperar que dichas dimensiones adicionales se derrumbasen dinámicamente, con consecuencias desastrosas para la geometría macroscópica del espaciotiempo tal y como la conocemos.
Estos argumentos se centran sobre todo en los grados de libertad en la propia geometría del espaciotiempo. Está también la cuestión distinta, aunque estrechamente relacionada, de la excesiva libertad funcional en otros campos definidos en variedades espaciotemporales de dimensionalidad más elevada. Analizaré con brevedad estos asuntos hacia el final de §1.10, a los que en ocasiones se ha atribuido cierta relevancia para situaciones experimentales. Comentaré de manera sucinta un problema relacionado en §2.11, y aunque los argumentos allí expuestos no resulten del todo concluyentes, sí hay cuestiones preocupantes, que no he visto tratadas en otros lugares, y que podrían ser dignas de un estudio más a fondo.
1.10. ¿OBSTÁCULOS CUÁNTICOS A LA LIBERTAD FUNCIONAL?
En este apartado (y en el siguiente) expongo un argumento que, en mi opinión, apuntala firmemente la idea de que no podemos evitar la cuestión de la excesiva libertad funcional en las teorías con dimensiones espaciales adicionales, incluso en un contexto cuántico. El argumento es, en esencia, el que presenté en el congreso organizado en Cambridge en enero de 2002 para celebrar el sexagésimo cumpleaños de Stephen Hawking [Penrose, 2003; véase también ECalR: §§31.11 y 31.12], pero aquí lo expongo de una manera más contundente. En primer lugar, para poder entender las cuestiones cuánticas relevantes tal y como suelen presentarse, necesitamos saber un poco más sobre los procedimientos de la teoría cuántica estándar.
Consideremos un sistema cuántico sencillo, como puede ser un átomo (por ejemplo, de hidrógeno) en reposo. Básicamente, lo que tenemos es que habrá una serie de niveles de energía discretos diferentes (por ejemplo, las distintas órbitas permitidas del electrón en el átomo de hidrógeno). Existirá un estado de mínima energía, denominado estado fundamental, y cabe esperar que cualquier otro estado estacionario del átomo, al tener una energía mayor, acabará cayendo hasta el estado fundamental mediante la emisión de fotones, siempre que el entorno en el que se encuentre el átomo no esté demasiado «caliente» (es decir, no sea demasiado energético). (En algunas situaciones, puede que haya reglas de selección que prohíban algunas de estas transiciones, pero esto no afecta al razonamiento general.) Por el contrario, si se suministra la suficiente energía externa (normalmente, en forma de energía electromagnética en lo que se conoce como un baño de fotones; de nuevo los fotones, en este contexto cuántico) y esta se transfiere al átomo, este puede pasar de un estado de energía baja (por ejemplo, el estado fundamental) a otro de mayor energía. En cada caso, la energía E de cada fotón estará asociada con una determinada frecuencia n, sujeta a la famosa fórmula de Planck E = hn (§§1.5, 1.8, 2.2 y 3.4).
Volvamos ahora a la cuestión de los espaciotiempos supradimensionales de la teoría de cuerdas. Cuando se les pregunta al respecto, casi todos los teóricos de cuerdas se muestran encantados con el hecho de que, de alguna manera, la (¡gigantesca!) libertad funcional que reside en las dimensiones espaciales adicionales nunca entrará en juego en circunstancias corrientes. Esto parece deberse a la opinión de que esos grados de libertad que intervienen en la deformación de la geometría de las 6 pequeñas dimensiones adicionales serían en la práctica inmunes a una posible excitación, debido a la magnitud de la energía que sería necesaria para excitarlos.
De hecho, existen ciertas deformaciones especiales de las dimensiones espaciales adicionales que se pueden excitar sin la inyección de ninguna energía. Esto es así en el caso del espaciotiempo 10-dimensional cuando se considera que las 6 dimensiones espaciales adicionales son espacios de Calabi-Yau; véanse §§1.13 y 1.14. Tales deformaciones se denominan modos nulos, y suscitan cuestiones problemáticas de las que los teóricos de cuerdas son perfectamente conscientes. Estos modos nulos no hacen uso del exceso de libertad funcional que aquí me interesa, por lo que dejaré mi análisis al respecto para §1.16. En este apartado y en el siguiente me centraré en las deformaciones que sí tienen acceso a todo ese exceso de libertad funcional, y que requieren una cantidad significativa de energía para ser excitadas.
Para estimar la escala de energía que sería necesaria, recurrimos de nuevo a la fórmula de Planck, E = hn , y no nos equivocamos mucho si tomamos para la frecuencia n un valor del orden de magnitud del inverso del tiempo que tardaría una señal en propagarse alrededor de una de estas dimensiones adicionales. Ahora bien, el «tamaño» de estas pequeñas dimensiones adicionales depende de la versión de la teoría de cuerdas que nos interese. En la teoría 26-dimensional original, podríamos estar pensando en algo del orden de 10–15 m, en cuyo caso la energía necesaria podría estar al alcance del LHC (véase §1.1). Por otra parte, la energía requerida en las teorías de cuerdas supersimétricas y 10-dimensionales sería mucho más elevada, y completamente inalcanzable para el acelerador de partículas más potente existente en la Tierra (el LHC) o para cualquier otro que pueda existir en un futuro próximo. En este tipo de teoría de cuerdas, que intenta abordar de manera concienzuda las cuestiones relativas a la gravedad cuántica, esta energía sería aproximadamente del orden de la energía de Planck, que es la energía asociada a la longitud de Planck (que se analiza brevemente en §§1.1 y 1.5,y con más detenimiento en §§3.6 y 3.10). En consecuencia, se suele argumentar que sería necesario un proceso que implicase partículas individuales aceleradas a energías al menos de una magnitud tan enorme —que sería del orden de la energía liberada en la explosión de un proyectil de artillería de buen tamaño— para excitar los grados de libertad en las dimensiones adicionales desde su estado fundamental. Al menos, para las versiones de la teoría de cuerdas con dimensiones adicionales de aproximadamente esta escala diminuta, se argumenta que estas dimensiones serían en la práctica inmunes a la excitación por cualquier medio que podamos prever actualmente.
Cabe mencionar que hay versiones de la teoría de cuerdas, por lo general consideradas alejadas de las dominantes, en las que algunas de las dimensiones adicionales pueden llegar a tener tamaños hasta del orden de un milímetro. La supuesta virtud de estos esquemas es que podrían ser sometidas a una prueba experimental [véase Arkani-Hamed et al., 1998]. Pero, desde el punto de vista de la libertad funcional, adolecen particularmente de la dificultad de que debería ser fácil excitar estas «grandes» energías de oscilación, incluso con las energías de los aceleradores actuales, y sigo sin entender por qué a quienes proponen estas ideas no les preocupa el gigantesco exceso de libertad funcional que ya debería haberse puesto de manifiesto.
Debo decir que, por las razones que expondré, no me parece nada convincente el argumento de que la libertad funcional en dimensiones espaciales adicionales incluso del tamaño de la escala de Planck debería ser inmune a las excitaciones. Por consiguiente, soy incapaz de tomarme en serio la conclusión general de que la enorme acumulación de grados de libertad en las dimensiones adicionales debería ser inmune a la excitación en las circunstancias «corrientes» de las energías disponibles en nuestro universo actual. Hay varios motivos para mi profundo escepticismo. En primer lugar, hemos de preguntarnos por qué deberíamos considerar que la energía de Planck es «grande» en este contexto. Supongo que lo que se quiere dar a entender es que la energía debe inyectarse mediante la intervención de algo como una partícula de muy alta energía, como sucedería en un acelerador de partículas (que sería análoga al fotón capaz de excitar un átomo desde su estado fundamental). Pero debemos tener en cuenta que la imagen que nos proponen los teóricos de cuerdas es una en la que el espaciotiempo —al menos cuando las dimensiones adicionales se encuentran en su estado fundamental— debería tomarse como un espacio producto M × X (véase la figura A-25 en §A.7), donde M es algo que se parece mucho a nuestra imagen clásica corriente de un espaciotiempo 4-dimensional, mientras que X es el espacio de las dimensiones «pequeñas» adicionales. En la versión 10-dimensional de la teoría de cuerdas, suele considerarse que X es un espacio de Calabi-Yau, que es un tipo particular de 6-variedad que veremos un poco más detenidamente en §§1.13 y 1.14. Si se excitasen las propias dimensiones adicionales, el «modo excitado» relevante (véase §A.11) del espaciotiempo se reflejaría en el hecho de que nuestro espaciotiempo supradimensional tendría la forma M × X´, donde X´ es el sistema de dimensiones adicionales perturbado (es decir, «excitado»). (Evidentemente, debemos entender que X´ es, en cierto sentido, un espacio «cuántico», no uno clásico, pero esto no afecta demasiado al razonamiento.) Algo que quiero dejar claro aquí es que, al perturbar M × X hasta acabar en M × X´, hemos perturbado el universo entero (todo el espacio M se ve afectado en cada punto de X ), de manera que cuando pensamos que la energía necesaria para producir este modo de perturbación es «grande» debemos entender esto en el contexto del universo en su conjunto. Me parece muy poco razonable exigir que la inyección de este cuanto de energía la efectúe necesariamente una partícula de alta energía bastante localizada.
En esa misma línea iría la consideración de cierta forma de inestabilidad presumiblemente no lineal (véanse §§A.11 y 2.4) que afecta a la dinámica del universo (supradimensional) en su conjunto. Llegados a este punto, debe quedar claro que no considero que la dinámica de los grados de libertad «internos», que rige el comportamiento de las 6 dimensiones espaciales adicionales, sea independiente de la dinámica de los grados «externos», que gobiernan el comportamiento del espaciotiempo 4-dimensional ordinario. Para que ambos puedan considerarse legítimamente componentes de un «espaciotiempo» conjunto, debería existir una dinámica que gobierne ambos conjuntos de grados de libertad en un esquema global (en lugar de que, por ejemplo, se considere que el primero es algún tipo de «fibrado» sobre el segundo; véanse §§A.7 y 1.9). De hecho, se considera que una versión de las ecuaciones de Einstein controla toda la evolución de ambos conjuntos de grados de libertad, que es, en cualquier caso, la imagen que entiendo que los teóricos de cuerdas tienen en mente, al menos a escala clásica, en que se considera que la evolución de todo el 10-espaciotiempo se aproxima adecuadamente mediante las ecuaciones de Einstein 10-dimensionales del vacío, 10G = 0 (véase, más adelante, §1.11).
Trataré la cuestión de tales inestabilidades clásicas en §1.11; la presente digresión se refiere a cuestiones cuánticas, y la conclusión a la que llegaremos será que debemos en efecto fijarnos en la imagen clásica para llegar a comprender plenamente la cuestión de la inestabilidad. En el contexto de la dinámica del universo entero, la energía de Planck no es grande en absoluto, sino extremadamente pequeña. Por ejemplo, el movimiento de la Tierra alrededor del Sol implica una energía cinética que es alrededor de un millón de millones de millones de millones (esto es, 1024) de veces más grande. No veo ningún motivo por el que una diminuta fracción de esta energía, que podría muy bien ser mucho mayor que la energía de Planck, no tuviera que invertirse en perturbar muy ligeramente el espacio X, en una región espacial M´ de la escala de la Tierra, o quizá algo más grande (y que incluya el sistema Tierra-Sol al completo). Al estar distribuida sobre una región relativamente grande, la densidad de esta energía a lo largo y ancho de M´ sería sumamente pequeña (véase la figura 1-31). En consecuencia, la geometría de estas dimensiones espaciales (X) apenas se vería alterada en M´ por una perturbación de la magnitud de la energía de Planck, y no veo ninguna razón por la que nuestra geometría espaciotemporal relativamente local M´ × X no debería experimentar una perturbación hasta dar lugar a algo como M´ × X ´, pero unido suavemente con el resto de M × X fuera de la región M´, donde la diferencia entre las geometrías X y X´ sería ridículamente minúscula y muchísimo más pequeña que la escala de Planck.
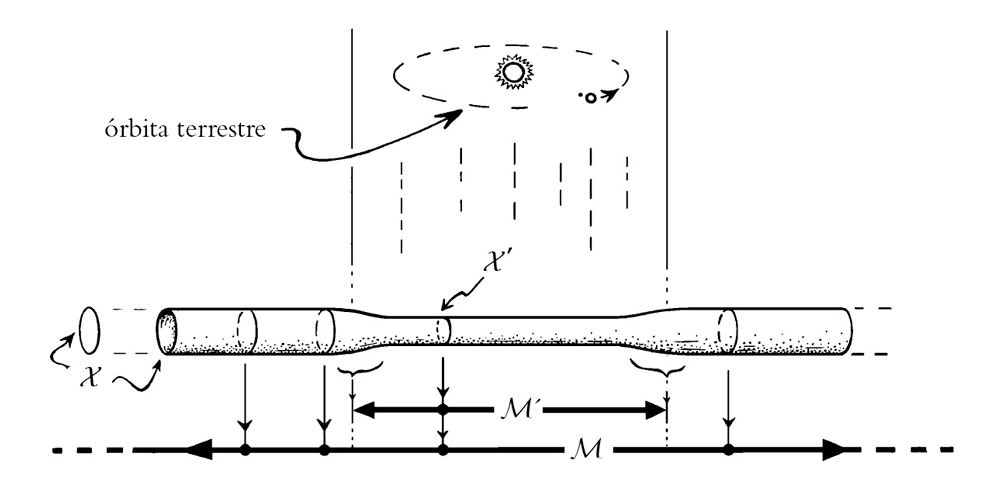
FIGURA 1-31. Se necesitaría una energía del orden de la escala de Planck para excitar el pequeño espacio compacto 6-dimensional X de dimensiones adicionales de la teoría de cuerdas, pero la energía disponible en el movimiento de la Tierra alrededor del Sol es muy superior a ese valor. Aquí M representa el 4-espaciotiempo ordinario de nuestra experiencia cotidiana y M´, una parte relativamente pequeña del mismo, que contiene el movimiento orbital de la Tierra. Una mínima proporción de la perturbación al espaciotiempo procedente de la energía del movimiento terrestre bastaría para perturbar X hasta dar un espacio X ´ muy ligeramente distinto, extendido sobre la región M´.
Las ecuaciones que gobiernan el 10-espacio entero acoplarían dinámicamente las de M con las de X, de manera que un minúsculo cambio local de la geometría de X sería una consecuencia esperada de una perturbación relativamente local (en un entorno M´) de la geometría espaciotemporal macroscópica M. Además, este acoplamiento sería mutuo. En consecuencia, el desencadenamiento de una inundación de grados de libertad supradimensionales que están en potencia ahí en virtud de la libertad existente en la geometría a la escala de Planck —que implica, dicho sea de paso, una enorme curvatura del espaciotiempo— podría perfectamente tener efectos devastadores sobre la dinámica macroscópica.
Aunque existen argumentos, basados en la supersimetría, según los cuales la geometría X del estado fundamental podría estar sumamente restringida (por ejemplo, que sea necesariamente lo que se conoce como un 6-espacio de Calabi-Yau; véanse §§1.13 y 1.14), eso no debería afectar a su potencial para alejarse de dicha geometría en situaciones dinámicas. Por ejemplo, mientras que las ecuaciones de Einstein 10G = 0, cuando se aplican a geometrías que están restringidas a ser de la forma producto M × X, pueden imponer fuertes condiciones sobre la geometría del propio X (así como sobre la de M), no cabría esperar que esta muy particular forma de producto persistiese en la situación dinámica general; y, de hecho, casi toda la libertad funcional se expresaría en soluciones que no poseen esta forma de producto (véase §A.11). En consecuencia, con independencia de los criterios que se utilicen para restringir las dimensiones adicionales de forma que tengan una estructura geométrica particular (por ejemplo, CalabiYau) cuando se encuentran en su estado fundamental, no podemos esperar que esto se mantenga en situaciones plenamente dinámicas.
En este punto es necesario hacer una aclaración en relación con la comparación que he hecho antes con las transiciones cuánticas en los átomos, ya que al principio de este apartado he pasado por alto una cuestión técnica cuando he considerado un átomo en reposo. Para que el átomo esté por completo en reposo, su estado (función de onda) debe, técnicamente, estar distribuido de manera uniforme por todo el universo (ya que, para estar en reposo, debe poseer un momento nulo, del que se deduce la uniformidad; véanse §§2.13 y 4.2), de una manera aparentemente similar a como X (o X´) están distribuidos uniformemente por el universo en el producto M × X. ¿Invalida esto en algún sentido mi razonamiento anterior? No veo por qué habría de ser así. No obstante, los procesos que implican átomos individuales deben verse como eventos localizados, en los que un cambio en el estado de un átomo sería producido por algún proceso local, como un encuentro con otra entidad razonablemente localizada, como un fotón. El hecho de que, técnicamente, se pueda entender que un estado estacionario (o una función de onda independiente del tiempo) de un átomo está distribuido por todo el universo es irrelevante para la manera en que se hacen en realidad los cálculos, ya que por regla general se entiende simplemente que todas las consideraciones espaciales se toman con respecto al centro de masas del sistema, y la dificultad antes mencionada desaparece.
Sin embargo, la situación con respecto a las perturbaciones del espacio X de la escala de Planck es por completo diferente, porque aquí el estado fundamental de X está, por su propia naturaleza, necesariamente no localizado en ningún lugar en concreto de nuestro espaciotiempo ordinario M, sino que se supone que es omnipresente, y permea la estructura del espaciotiempo por todo el universo. Se supone que el estado cuántico geométrico de X influye en los detalles de lo que sucede físicamente en la galaxia más remota tanto como aquí, en la Tierra. El argumento de los teóricos de cuerdas de que una energía del orden de la escala de Planck sería, con creces, demasiado grande para poder excitar X, en comparación con la que hay disponible, me parece un argumento inapropiado por varios motivos. No es solo que esas energías están ampliamente disponibles a través de medios no localizados (como, por ejemplo, el movimiento de la Tierra), sino que, si imaginásemos que X pasase realmente a un estado excitado X ´ a través de la transición de una partícula (gracias quizá a un avance tecnológico que hiciese posible un acelerador de partículas que operase a la energía de Planck), lo cual llevaría a M × X´ para el nuevo estado del universo, esto sería a todas luces absurdo, ya que no cabe esperar que la física en la galaxia de Andrómeda cambie instantáneamente porque se produzca un evento de este estilo aquí, en la Tierra. Deberíamos pensar más bien en términos de un evento mucho más leve en las proximidades de nuestro planeta que se propaga a la velocidad de la luz. Es mucho más admisible describir estas cosas mediante ecuaciones clásicas no lineales que a través de abruptas transiciones cuánticas.
A la vista de tales consideraciones, debería volver sobre una idea que he mencionado brevemente antes para tratar de ver de qué manera cabría esperar que un cuanto de energía de la escala de Planck, distribuido sobre una región más bien grande M´ de M, afectase a la geometría del espacio X en dicha región. Como ya se ha dicho, X se vería muy poco afectado, y, cuanto más grande fuese la región M´, menor tendría que ser el cambio de X en esa región (donde estamos suponiendo que este cambio es producido por un evento extendido cuya energía sería de la escala de Planck). En consecuencia, si examinamos las variaciones en la forma o en el tamaño de X que sean realmente significativas, y hacen que X se transforme en un espacio X * que difiere bastante de X, eso nos lleva a considerar energías muy superiores a la escala de Planck (que, evidentemente, son muy abundantes en el universo que conocemos, como, por ejemplo, en el movimiento de la Tierra alrededor del Sol). Estas energías no vienen dadas tan solo por un único cuanto «mínimo» de energía de la escala de Planck, sino por la inyección de una cantidad enorme de cuantos de variaciones de X. Propiciar una transformación de X a un X* notablemente diferente en una región grande implicaría una cantidad enorme de tales cuantos (quizá de la escala de Planck o más grandes). Se suele suponer, al considerar efectos que requieren de una cantidad de cuantos tan gigantesca, que la mejor manera de describir dichos efectos es puramente clásica (esto es, sin mecánica cuántica).
De hecho, como veremos en el capítulo 2, esta cuestión de cómo una apariencia de clasicismo puede surgir a partir de una multiplicidad de eventos cuánticos suscita toda una serie de preguntas profundas sobre la manera en que el mundo cuántico se relaciona con el clásico. De hecho, es una cuestión interesante (y polémica) la de si la apariencia de clasicismo se produce o no simplemente como consecuencia del gran número de cuantos implicados, o bien de algún otro criterio, y volveré sobre este asunto particular en §2.13. Sin embargo, para los propósitos del argumento que nos ocupa, tales sutilezas no parecen particularmente relevantes, y me limito a señalar que debería considerarse como algo razonable el uso de argumentos clásicos para abordar la cuestión de las perturbaciones del espaciotiempo M × X que alteran de manera significativa el espacio X. Esto ocasiona sus propias dificultades graves en relación con las dimensiones espaciales adicionales, como veremos en breve en el apartado siguiente.
Pero antes de llegar a esas dificultades —que tienen que ver en concreto con la forma particular de supradimensionalidad espacial que surge de la teoría de cuerdas— creo que es útil establecer una comparación con un tipo de situación experimental que a veces se considera análoga a la planteada antes. Un ejemplo de dicha situación es el denominado efecto Hall cuántico [Von Klitzing et al., 1980; Von Klitzing, 1983], que es un bien conocido fenómeno cuántico en 2 dimensiones espaciales que tiene lugar dentro de la física en 3 dimensiones espaciales. En esta situación, existe una gran barrera de energía que restringe el sistema en cuestión a una superficie 2-dimensional, y la física cuántica de este mundo de menos dimensiones puede desarrollarse al parecer ajena a la tercera dimensión espacial, porque sus contenidos no poseen suficiente energía para superar dicha barrera. Así pues, en ocasiones se argumenta que cabe considerar que un ejemplo como este nos facilita una analogía con lo que se supone que debe estar sucediendo con la supradimensionalidad de la teoría de cuerdas, en que se considera que nuestra física ordinaria en 3 dimensiones espaciales es asimismo ajena al mundo de 9 dimensiones espaciales en el que supuestamente está inmersa, debido a la existencia de una gran barrera energética.
Sin embargo, esta es una analogía completamente falsa. El ejemplo anterior es más apropiado para el punto de vista del universo de branas de §1.16, donde el espacio de menos dimensiones es un subespacio del de mayor dimensionalidad, en lugar del espacio cociente relevante para las representaciones de la teoría de cuerdas estándar que he estado evaluando (ejemplificado por la expresión M × X, de la cual M es un espacio cociente). Véanse §A.7 y la figura 1-32. La función de M como espacio cociente, en lugar de ser un subespacio, vuelve a ser pertinente para el argumento del apartado siguiente. No obstante, la representación del subespacio es relevante para la muy distinta imagen del universo de branas que se describirá con algo más de detalle en §1.16.
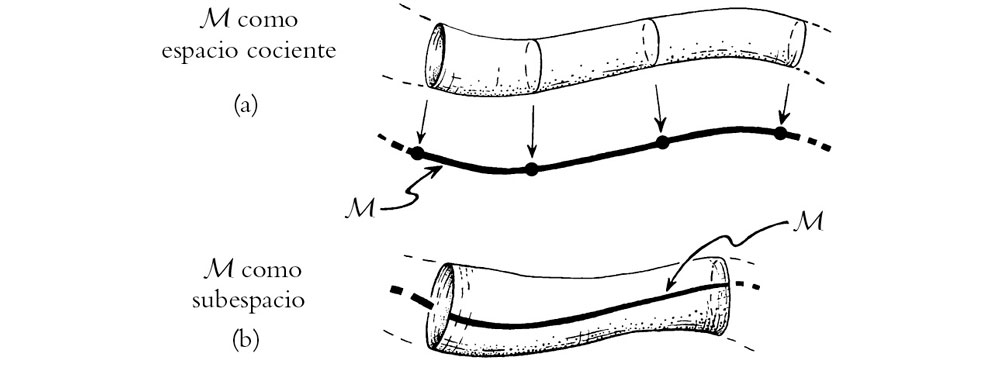
FIGURA 1-32. Comparación entre (a) una situación en la que M es un espacio cociente y (b) otra en la que M es un subespacio.
1.11. INESTABILIDAD CLÁSICA DE LA TEORÍA DE CUERDAS SUPRADIMENSIONAL
Volvamos ahora a la cuestión, que ya se ha tratado en §1.10, de la estabilidad de un espaciotiempo clásico de la forma S = M × X, donde X es un espacio compacto de tamaño minúsculo. Aunque mis argumentos no son muy específicos en cuanto a la naturaleza del espacio X, los expresaré en términos de las versiones de la teoría de cuerdas en las que X sería un tipo de espacio compacto 6-dimensional denominado variedad de Calabi-Yau, que veremos algo más detalladamente en §§1.13 y 1.14, de manera que S será un espaciotiempo 10-dimensional. Esta situación implicaría la existencia de ciertos elementos de supersimetría (§1.14), pero no desempeñarán ninguna función en el razonamiento clásico que expondré aquí (que puede considerarse de aplicación para la parte del «cuerpo» del sistema (véase §1.14), por lo que me he tomado la libertad de ignorar, de momento, la supersimetría, dejando mis reflexiones sobre ella para §1.14. De hecho, básicamente todo lo que necesitaré de X es que sea al menos 2-dimensional, que es sin duda lo que se pretende en la teoría de cuerdas actual, aunque sí necesitaré que el espaciotiempo S satisfaga unas ecuaciones de campo.
Ya he mencionado (§1.10) que, según la teoría de cuerdas, la métrica asignada a este S supradimensional debería satisfacer unas ecuaciones de campo. En una primera aproximación, podemos considerar que este conjunto de ecuaciones para S son las de Einstein del vacío 10G = 0, donde 10G es el tensor de Einstein construido a partir de la 10-métrica de S. Estas ecuaciones se imponen sobre el espacio S en el que residen las cuerdas para evitar una anomalía (que va más allá de la mencionada en §1.6, que llevó a los teóricos a incrementar la dimensionalidad espacial). De hecho, el «10G» en 10G = 0 es solo el primer término de una serie de potencias en una magnitud pequeña α´ denominada constante de cuerda, un parámetro de área sumamente minúsculo cuyo valor se suele tomar como ligeramente superior al cuadrado de la longitud de Planck (véase §1.5):
α´ ≈ 10–68 m2.
Así, tenemos unas ecuaciones de campo para S que pueden expresarse como una cierta serie de potencias (§A.10):
0 = 10G + α´H + α´2J + α´3 K + ...,
donde H, J, K, etc. serían expresiones construidas a partir de la curvatura riemanniana y sus derivadas de distintos órdenes. Sin embargo, debido al tamaño sumamente pequeño de α´, los términos de órdenes superiores se suelen ignorar en las distintas versiones particulares de la teoría de cuerdas que se proponen (aunque hay ciertas dudas acerca de hasta qué punto es válido hacerlo, pues no hay información sobre la convergencia o comportamiento final de la serie (véanse §§A.10 y A.11)). En particular, se puede considerar explícitamente que los espacios de Calabi-Yau que se han mencionado antes (véanse §§1.13 y 1.14) satisfacen la ecuación 6-espacial «6G = 0», lo que implica que la ecuación 10-espacial 10G = 0 sea válida para el espacio producto M × X, dado que también se supone que la ecuación de Einstein estándar del vacío, 4G = 0, es válida para M (lo cual sería razonable para el «estado fundamental» del vacío de los campos de materia).[7] En todo esto, estoy usando las ecuaciones de Einstein sin ningún término L (véanse §§1.1 y 3.1). La constante cosmológica sería en efecto completamente despreciable para las escalas que estamos considerando aquí.
Supongamos, de acuerdo con lo anterior, que, en efecto, las ecuaciones del vacío 10G = 0 se satisfacen para S = M × X. Nos interesa lo que sucede si se aplican pequeñas perturbaciones sobre el espacio (por ejemplo, de Calabi-Yau) X de «dimensiones adicionales». Debemos hacer aquí una precisión importante sobre la naturaleza de la perturbación que consideraré. En el seno de la comunidad de los teóricos de cuerdas hay muchos debates sobre perturbaciones que deforman un ejemplo de espacio de Calabi-Yau y dan lugar a otro ligeramente diferente al alterar los módulos que veremos en §1.16, que definen la forma específica de una variedad de Calabi-Yau dentro de una clase topológica particular. Entre las perturbaciones que alteran los valores de dichos módulos están los modos nulos que se han mencionado en §1.10. En este apartado, no me interesan especialmente las deformaciones de este tipo, que no nos sacan de la familia de los espacios de Calabi-Yau. En la teoría de cuerdas convencional, normalmente se considera que uno debe permanecer dentro de esta familia, porque se piensa que estos espacios son estables debido a criterios de supersimetría que obligan a que las 6 dimensiones espaciales adicionales constituyan una variedad. Sin embargo, estas consideraciones de «estabilidad» están dirigidas a demostrar que estos son los únicos 6-espacios que satisfacen los criterios de supersimetría exigidos. La idea normal de estabilidad consistiría en que una pequeña perturbación que provoque la salida de un espacio de Calabi-Yau lo devolviera a dicho estado; pero no se considera la posibilidad de que dicha perturbación diverja, alejándose de esta familia y conduciendo en última instancia a algo singular, donde no exista ninguna métrica suave. De hecho, esta última posibilidad de una evolución desbocada hacia tal configuración singular es la consecuencia evidente de los argumentos que siguen.
Para poder estudiar esto, lo más fácil sería que antes tratásemos explícitamente el caso básico donde M no experimenta ninguna perturbación; esto es, donde M = M, siendo M el 4-espacio plano de Minkowski de la relatividad especial (§1.7). Al ser M plano, puede reformularse como el espacio producto
M = E3 × E1
(véase §A.4, figura A-25; ello no implica básicamente más que agrupar las coordenadas x, y, z y t como (x, y, z) por una parte, y t por la otra). El 3-espacio euclídeo E3 es el espacio ordinario (coordenadas x, y y z), y el espacio euclídeo 1-dimensional E1 es el tiempo ordinario (coordenada t), que es simplemente una copia de la recta real R. Con M escrito de esta manera, el conjunto del espaciotiempo 10-dimensional (sin perturbar) S se puede expresar (al ser M y X espacios cocientes de S) como
S = M × X
= E3 × E1 × X
= E3 × Z,
con tan solo reagrupar las coordenadas, y donde Z es el espaciotiempo 7-dimensional
Z = E1 × X
(las coordenadas de Z son: en primer lugar, t, y después las de X).
Me gustaría considerar una perturbación (pequeña, pero no infinitesimalmente pequeña) del 6-espacio X (por ejemplo, de Calabi-Yau) hasta dar un nuevo espacio X*, en t = 0, donde podemos entender que esto se propaga en la dirección temporal dada por E1 (con coordenada temporal t), para darnos un espaciotiempo 7-dimensional evolucionado Z*. De momento, supongo que la perturbación afecta solo a X, mientras que el 3-espacio euclídeo externo E3 permanece inalterado. Esto es perfectamente compatible con las ecuaciones de evolución, pero, puesto que se esperará de esta perturbación que altere de alguna manera la 6-geometría de X* a medida que el tiempo avance, no esperamos que Z* conserve la forma de un producto como E1 × X*, donde la 7-geometría exacta de Z* esté gobernada por las ecuaciones de Einstein 7G = 0. Sin embargo, el espaciotiempo S entero sí que conservaría la forma de producto E3 × Z* a medida que evoluciona, porque dicha forma de producto satisfaría las ecuaciones de Einstein completas 10G = 0 si Z* satisface 7G = 0, ya que 3G = 0 ciertamente se cumple en el espacio plano E3.
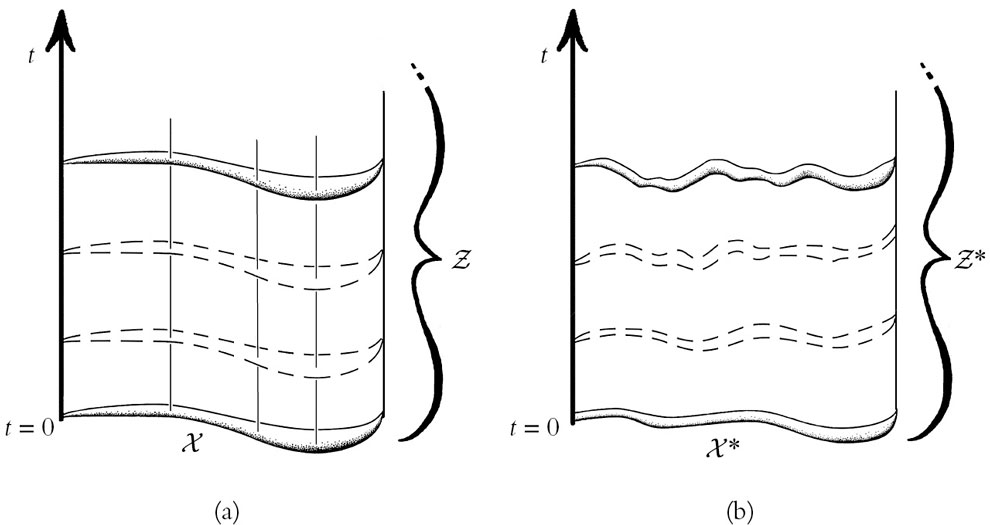
FIGURA 1-33. (a) El minúsculo espacio compacto X, cuando un espacio de Calabi-Yau continúa siéndolo con el paso del tiempo, pero (b) cuando, ligeramente perturbado hasta X*, evoluciona hacia algo diferente.
El 6-espacio X* se toma como la superficie de valor inicial t = 0 para la evolución Z* (figura 1-33). A continuación, las ecuaciones 7G = 0 propagan la perturbación en dirección temporal hacia el futuro (dada por t > 0). Hay ciertas ecuaciones de ligadura que deben cumplirse en X, y, en un sentido matemáticamente riguroso, cerciorarse de que dichas ecuaciones pueden satisfacerse en todo el espacio compacto X* puede ser un asunto algo delicado. No obstante, la libertad funcional que esperamos para tales perturbaciones iniciales de X es
∞28∞6,
donde el «28» que aparece aquí procede de poner n = 7 en la expresión n (n – 3), siendo este el número de componentes iniciales independientes por punto en una (n – 1)-superficie inicial, para un n-espacio con tensor de Einstein nulo, y el «6» es la dimensionalidad de la 6-superficie inicial X* [Wald, 1984]. Esto incluye tanto las perturbaciones intrínsecas del propio X como las extrínsecas debidas a cómo X está inmerso en Z. Esta libertad clásica es, evidentemente, mucho mayor que el valor de ∞k∞3 que esperamos para una teoría física apropiada para el tipo de actividad que experimentamos en el mundo 3-dimensional que percibimos.
Pero la situación es mucho peor, porque casi todas esas perturbaciones darán lugar a una evolución de Z que es singular (véase la figura 1-34). Lo cual significa, en efecto, que debe esperarse que las dimensiones adicionales se arruguen hasta que las curvaturas diverjan hacia el infinito y que la posterior evolución de las ecuaciones clásicas se vuelva imposible. Esta conclusión se deriva de los teoremas matemáticos de singularidad demostrados a finales de la década de 1960, y muy en particular del que Stephen Hawking y yo establecimos poco antes de 1970 [Hawking y Penrose, 1970], que demostraba, entre otras cosas, que casi cualquier espaciotiempo n-dimensional (n > 3) que contenga una (n – 1)-superficie compacta de género espacio (aquí, el 6-espacio de Calabi-Yau inicial X*), pero que no contenga bucles cerrados de género tiempo, debe evolucionar hacia una singularidad espaciotemporal si su tensor de Einstein nG satisface una condición sobre la energía (de no negatividad) denominada condición fuerte para la energía (que ciertamente se cumple aquí, ya que 7G = 0 en todo Z*). Aquí se pueden ignorar las salvedades que introducen el «casi» y la ausencia de «bucles cerrados de género tiempo», ya que estas posibles escapatorias podrían ocurrir, en todo caso, únicamente en circunstancias excepcionales de mucha menor libertad funcional que la que se daría en una perturbación genérica de Z.
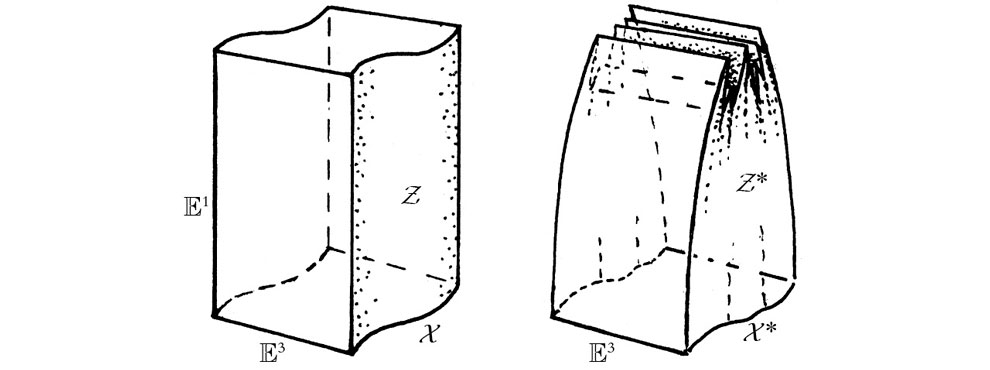
FIGURA 1-34. La inestabilidad clásica de las dimensiones adicionales de la teoría de cuerdas. La evolución Z* del 6-espacio supradimensional perturbado X* es, casi con toda certeza, singular, por un teorema de 1970 formulado por Hawking y el autor.
Debo comentar aquí un detalle técnico. Este teorema no afirma realmente que las curvaturas deban divergir hacia el infinito, sino tan solo que, en general, la evolución no se puede extender más allá de cierto punto. Aunque en principio pueden darse otras alternativas en casos excepcionales, también cabe esperar que el motivo general para la imposibilidad de que continúe la evolución es que las curvaturas, en efecto, sí que divergen [Clarke, 1993]. Otro detalle importante es que la condición fuerte para la energía que aquí se da por supuesta, aunque se satisface automáticamente para 7G = 0, no puede ciertamente garantizarse si hemos de considerar lo que sucede con los términos de orden más elevado en la serie de potencias en α´ mencionada antes. Aun así, la mayoría de las reflexiones actuales de teoría de cuerdas parecen operar al nivel en el que se ignoran estos términos de orden superior en α´, y se considera que X es un espacio de Calabi-Yau. Lo que este teorema de singularidad parece decirnos es que, siempre y cuando las perturbaciones puedan tratarse clásicamente (como parece que es razonable hacer, tal y como se deduce de nuestras consideraciones previas en §1.10), podemos esperar una violenta inestabilidad en las 6 dimensiones espaciales adicionales, en la cual estas se arruguen y se aproximen a un estado singular. Justo antes de que se llegue a este desastre, habría que tener muy en cuenta los términos de orden más alto en α´, u otras consideraciones cuánticas. Dependiendo de la escala de la perturbación, cabe prever que este «tiempo arrugado» se produciría probablemente transcurrida una minúscula fracción de segundo, donde debemos tener en mente que el tiempo de Planck (el tiempo que tarda la luz en recorrer una distancia de la longitud de Planck; véase §1.5) es del orden de 10–43 segundos. Con independencia de lo que las dimensiones adicionales puedan formar al arrugarse, es improbable que la física observada no se vea drásticamente afectada. La que nos proponen los teóricos de cuerdas no es una imagen demasiado tranquilizadora del espaciotiempo 10-dimensional del universo.
Otra cuestión que debe señalarse aquí es que las perturbaciones que hemos considerado más arriba son las que afectan únicamente a las 6 dimensiones adicionales, pero no a las dimensiones macroscópicas (aquí, el 3-espacio euclídeo E3). De hecho, habría muchísima más libertad funcional (en concreto, ∞70∞9) en perturbaciones del 9-espacio espacial E3 × X completo que en las que solo afectan a X, que poseen una libertad funcional de ∞28∞6. Parece posible modificar el argumento anterior para que el mismo teorema [Hawking y Penrose, 1970] siga siendo válido, pero de una manera más complicada, y conduzca a la misma conclusión singular, pero ahora para todo el espaciotiempo [ECalR: p. 1.247, nota 31.46]. Aparte de esto, es evidente que cualquier perturbación del 4-espacio macroscópico que sea comparable con las que estamos considerando aquí en lo referente a las 6 dimensiones adicionales sería desastrosa para la física corriente, ya que curvaturas tan minúsculas como las que se dan en X sencillamente no se experimentan en los fenómenos observados. Esto suscita una incómoda cuestión que es de hecho una dificultad aún por resolver en la teoría de cuerdas moderna: ¿cómo es posible que puedan coexistir sin afectarse de forma significativa escalas de curvatura tan extraordinariamente diferentes? Esta preocupante cuestión será planteada de nuevo en §2.11.