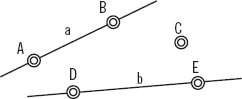
Los puntos A y B definen la recta a, D y E definen la recta b, mientras que C es un punto que no pertenece a ninguna de las rectas
Capítulo 1
Geometría aplicada al trazado de tuberías
Antes de tratar de interpretar cualquier plano de tuberías (en realidad cualquier tipo de plano) e incluso con anterioridad a conocer los tipos de representaciones de los mismos o las normas de aplicación, resulta necesario tener unas nociones básicas de dibujo.
Esto se justifica por la necesidad de establecer una disposición ordenada, coherente y económica, tanto de equipos (depósitos, calderas, hornos, bombas, etcétera) como de líneas de tuberías. Es decir, que todos los elementos de un sistema incluidos en una planta de producción industrial están dispuestos de tal forma que haga posible diseñar, montar, mantener y/o sustituir cualquiera de sus elementos sin afectar a otros componentes de la misma. No sería razonable lo contrario, por razones fundamentalmente económicas.
En la mayoría de los planos en los que se representan tuberías, se recurre al uso de elementos de dibujo, lo cuales posteriormente servirán para poder replantear y ejecutar los trabajos en taller o a pie de obra.
En este capítulo se definen dichos elementos, así como sus aplicaciones en las instalaciones de tuberías mediante ejemplos prácticos que permitan al lector desenvolverse en el trabajo diario.
Se plantean a continuación las definiciones de los elementos básicos que se presentan en los planos referidos a proyectos de tuberías.
También llamada línea recta, se entiende como tal al ente ideal, unidimensional e ilimitado que se extiende en una dirección (o su opuesta), constituido por infinidad de puntos. De lo expresado, se deduce que, para identificar una recta, bastará con determinar dos puntos no consecutivos cualesquiera que estén contenidos en la misma.

Los puntos A y B definen la recta a, D y E definen la recta b, mientras que C es un punto que no pertenece a ninguna de las rectas

Nota
Dos rectas situadas una a continuación de la otra, dan como resultado una tercera, que es el resultado de la suma de las primeras.
Se entiende como tal a la porción de plano delimitado por dos semirrectas que se cortan. Por tanto, al unir dos rectas con distinta dirección, se generarán cuatro ángulos, los cuales son complementarios entre sí. Por otra parte, para definir un ángulo, se requieren dos puntos pertenecientes a los lados formados por las semirrectas y el punto común de las mismas, denominado vértice.
Para establecer un valor a los ángulos, se consideran radianes y grados como unidades de medida.

Definición
Radián
Arco de la circunferencia cuya longitud es igual al radio.
Por otra parte, se divide el giro completo de la circunferencia en minutos.
En función de la disposición que presenten, existen dos sistemas de graduación:
En este manual y siempre que no se indique lo contrario, se considerará el sistema sexagesimal. Dicho esto, se establece la siguiente clasificación para los ángulos:


En el segundo caso, se puede establecer la siguiente subdivisión:

Se define como tal a la porción de plano delimitado por tres rectas que se cortan dos a dos. Los puntos de intersección se denominan vértices del triángulo, siendo los segmentos comunes los lados del mismo.

Nota
La suma de los ángulos de cualquier triángulo es igual a 180° sexagesimales o 200° centesimales.
Se entiende como tal a la porción de plano delimitado por cuatro segmentos que se cortan dos a dos, o dicho de otra forma, son s cerrados de cuatro lados.

Se entiende como tales a toda porción de plano delimitado por tres o más líneas rectas.
Bajo esta definición cabe incluir a los triángulos y cuadriláteros citados anteriormente, pero que se tratan de forma separada por su mayor utilización y por ser base para la construcción de elementos y/o figuras más complejas. A partir de esto, se tiende a considerar a los s cerrados a partir de los compuestos por cinco lados.

Sabía que...
Las planos de cualquier polígono de más de tres lados y cerrado pueden descomponerse en triángulos para poder medir su área.
Los s se clasifican en:

Se entiende como tales a toda porción de plano delimitado por una línea curva cerrada y plana, con inicio y fin en un mismo punto contenido en la misma.

Las rectas son el elemento básico de todo trazado, a partir del cual se elabora el resto de figuras. Al estudiar las rectas en el presente manual, se distinguen dos aspectos. El primero atiende a su clasificación, en relación a la posición que las mismas ocupan respecto de las demás. El segundo aspecto a considerar son las operaciones básicas.
La clasificación de las rectas atiende a su relación con la posición que las mismas ocupan respecto de las demás, por lo que estas serán:

Líneas paralelas. Vías de ferrocarril.

Líneas oblicuas. Columnas de la escultura de Hércules en la entrada al puerto de Ceuta.

Nota
Para dos rectas situadas en un mismo plano y que tienden a cortarse fuera de los límites del dibujo, puede determinarse el ángulo trazando paralelas a las mismas.
Por otra parte, dos rectas en el espacio tendrán una posición relativa de los puntos pertenecientes a las mismas. De acuerdo con sus posiciones relativas, estas serán:

Ejes de tubería que se cortan en el codo

Líneas de cornisa en distinto plano (no se cortan)
Aun siendo las rectas ilimitadas por definición, puede establecerse en la práctica un punto de origen, denominándose en dicho caso semirrecta, o un punto de origen y otro de final, en cuyo caso se denominará segmento.
Tanto en el primer como en el segundo caso, el valor es infinito, mientras que los segmentos son mensurables. Es decir, que estos tendrán siempre un valor finito o medible.

Nota
Para el trazado de dibujo técnico ha de tenerse en cuenta dicho valor, lo cual permite realizar divisiones, sumas de segmentos, medir tuberías o, como se verá en capítulos posteriores, acotar cualquier dibujo.
Se presentarán muchos casos en los que será necesario repartir conexiones de tuberías, a partir de otra, generalmente de mayor diámetro. Para tales casos se recurre a la técnica de división de segmentos. Para esta operación, a partir de un extremo del segmento de referencia, se traza una línea oblicua. Dicha línea se dividirá en partes iguales y consecutivas, con una medida cualquiera y en el número de veces que se necesite. A partir de la última marca obtenida, se trazará una recta hasta el extremo opuesto del segmento original. Finalmente, se trazan paralelas a esta última (tantas como divisiones de la recta auxiliar).


Importante
El método de división de segmentos se utiliza para distribuir varias tuberías de igual diámetro sobre un soporte.
Se define tangencia o enlace como la unión armónica de dos o más líneas, ya sean estas rectas o curvas, de tal manera que se vean como una sola.
En el caso realizar un enlace entre una recta y una circunferencia, se ha de trazar una línea recta desde el centro de la misma hasta cortar perpendicularmente la recta, determinando así el punto de tangencia (T). De igual forma, para el caso de dos líneas curvas, bastará con unir sus centros para determinar el punto de tangencia.
De lo dicho en el párrafo anterior, los enlaces estarán pues condicionados a las dimensiones de los elementos a unir. En el caso contrario, será necesario recurrir a elementos auxiliares para hacerlos posibles.

Es sabido que la distancia más corta entre dos puntos es la línea recta, pero en el caso de instalaciones de tuberías, rara vez es posible.

Nota
Si se observa cualquier instalación, se deduce que la disposición de equipos, pasos para personal de mantenimiento y muchas más causas condicionan la disposición de las líneas de tuberías.

Aplicación práctica
Se han de enlazar dos tuberías con ángulos distintos, mediante un tubo curvado de radio 50 cm. Las alineaciones de ambos tubos se muestran a continuación.

SOLUCIÓN
Se procederá según los siguientes pasos:


A partir de la definición efectuada en apartados anteriores, resulta conveniente conocer aspectos como su tipología y la aplicación en el contexto de las instalaciones de tuberías.

Importante
Existen distintas formas de clasificar los triángulos, lo que hace necesario un buen conocimiento de los mismos, para, una vez en el lugar de trabajo, permitir al operario desarrollar su tarea de forma fluida y casi automática.
En el caso de la geometría aplicada al diseño de tuberías, se entiende que para todo recinto cerrado se presentan unas características físicas. Por tal motivo y a partir de ahora y en lo sucesivo, se tendrán en cuenta los siguientes valores, cuyas expresiones se muestran en las tablas incluidas al final del presente manual:

Para clasificar los triángulos, se atenderá a la relación de los ángulos entre sí y/o la existente entre los lados que los componen:


Asimismo, para construir cualquier figura, es necesario conocer elementos o datos elementales, que permitan, por combinación, aplicar cualquier método existente para elaborar la figura.

Nota
El proceso de dividir superficies en triángulos se conoce como triangulación y se utiliza para el “replanteo” de los trabajos a realizar, tanto en taller como en obra.
En el caso de los triángulos, los datos elementales son:
Una vez que se pueden componer los triángulos, pueden conocerse otros puntos característicos de los mismos, que son:
Ortocentro
Punto donde se cortan las tres alturas del triángulo. Las alturas se determinan uniendo los vértices con el lado opuesto y formando ángulo recto con este o con su prolongación.
Circuncentro
Punto donde se cortan las tres mediatrices de los lados del triángulo. Se entiende como mediatriz a la línea que pasa por el punto medio de un segmento formando ángulos rectos.
Baricentro
Punto donde se cortan las tres medianas de los lados del triángulo. Se entiende como mediana a la línea que une el punto medio de cualquiera de sus lados con el vértice opuesto.
Incentro
Punto de corte de las bisectrices de los tres ángulos de cualquier triángulo.

Definición
Bisectriz
Ángulo es la línea que, pasando por el vértice, divide aquel en dos ángulos iguales.
De igual forma y a partir de todo lo anterior, pueden obtenerse otros elementos propios, entre los que se destacan los siguientes triángulos característicos:
Todos estos elementos definidos anteriormente, relacionados entre sí, dan lugar a nuevos elementos mediante técnicas de dibujo, que pueden ser aplicados a la ejecución de conjuntos de tuberías, entre otras aplicaciones.

Sabía que...
Entre todos los polígonos, el triángulo es el que menos se deforma y el más económico en su elaboración, por eso es el más utilizado en construcción.
El valor de los triángulos está en función de las dimensiones de sus lados, por lo que ya en la antigüedad clásica, Pitágoras (580-500 a.C.) formuló el siguiente teorema: “En un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.”
Se entiende por hipotenusa el lado opuesto al ángulo recto, formado por los lados restantes, que se denominan catetos.

Para todo triángulo, la suma de cualquiera de dos lados cualesquiera es mayor que el valor del tercero y menor que su diferencia. De igual forma, la suma de todos los ángulos es 180°.
Una muestra para la aplicación de este teorema en la fabricación de tuberías consiste en el replanteo de las líneas.

Ejemplo
Se precisa fabricar una línea que presenta varios tramos, unidos por codos de 30, 45, 60 y 90. Para ejecutar el replanteo, se traza un triángulo rectángulo con las medidas 30, 40 y 50 cm, correspondiendo los primeros datos a los catetos y, el tercero, a la hipotenusa.
La razón de estas medidas es por simplicidad de cálculos, ya que al aplicar el teorema de Pitágoras, se verifica:
h2 = c12 + C22
302 + 402 = 900 + 1600 = 2500
Haciendo la raíz cuadrada del resultado obtenido, se obtiene que H = 50, es decir, el valor de la hipotenusa.
Además, se obtienen ángulos de 90, 30 y 60°, con lo que bastaría trazar la bisectriz al ángulo recto para tener el que falta (véase figura).

En el caso de la geometría y continuando con el criterio expresado en el punto anterior, se definirán los valores físicos.

Por otra parte y en función a la relación entre sus lados y entre estos y los ángulos que forman, pueden clasificarse de la siguiente manera:


Sabía que...
El proyecto de edificio más grande proyectado tiene forma de pirámide con base cuadrada y 4 km de altura. Este proyecto está diseñado por los arquitectos Shimizu y Taisei para Japón.

Se define como circunferencia la curva cerrada plana caracterizada por tener un punto interior equidistante a todos y cada uno de los puntos que componen la misma. Dicho punto se denomina centro de la circunferencia.
En el caso de la geometría y continuando con el criterio expresado en el punto anterior, se definirán los valores físicos:

Asimismo, para construir cualquier circunferencia, se necesita conocer el radio (r). Todo radio tendrá un punto de aplicación, el cual se denomina centro de la circunferencia (cr).

Circunferencia realizada con tubos
Una vez se tiene la circunferencia, se deducen los siguientes elementos:

Este último elemento tiene una gran importancia en el tipo de instalaciones que se estudian en el presente manual, no solo por la forma de las tuberías, sino por el hecho de que las conducciones presentan otros elementos como codos, injertos y muchos otros elementos. Por tal motivo, es necesario conocer bien sus características.

Ejemplo
Una aplicación de este elemento es el trazado de pasos de tubería a través de techos, suelos o paredes de un recinto a otro, dentro de la misma planta o para tubuladuras en depósitos, etcétera.
Una circunferencia, como ya se ha definido con anterioridad, es una curva cerrada y, por tanto, no tiene definido ni principio ni fin. Resulta necesario, en estos casos, tener una referencia válida para situar correctamente cualquier tramo de tubería respecto de los restantes elementos que componen la instalación.
Efectivamente, ya se conoce cómo puede calcularse de forma analítica (mediante fórmulas), pero en trazado de tuberías, caso de un injerto (unión de dos tubos no alineados y/o de distinto diámetro) ha de recurrirse a métodos gráficos para ejecutarlos.
Para resolver este problema, se recurre al uso de plantillas. Para el trazado de las mismas y para que estas sean compatibles entre sí, los puntos de unión deben coincidir. Para que esto ocurra, se dividen las circunferencias en igual número de partes, haciendo coincidir dichas divisiones.

Nota
Existen numerosos procedimientos para la división de circunferencias, pero se ha preferido exponer el más sencillo y utilizado en este tipo de trabajo.
Para hacer la división de la circunferencia se procede como sigue:
A partir de aquí, puede plantearse la siguiente cuestión: ¿cuántas divisiones se deben hacer?

El número de divisiones a realizar estará en función del diámetro de los tubos y de la exactitud con la que quieran trazarse las plantillas. En la práctica, suelen dividirse en ocho partes los tubos de hasta 50 mm de diámetro, dieciséis partes para diámetros de hasta 203 mm y treintaidós partes para mayores.

Consejo
En todo caso, no se recomienda que la separación entre divisiones sea mayor de dos o tres centímetros, a riesgo de perder exactitud de la plantilla y, en consecuencia, de las piezas a unir.
Como se ha observado anteriormente, para todo polígono se obtiene el perímetro sumando los lados que lo forman. En el caso de la circunferencia, el perímetro se obtiene de la deducción de la longitud de la circunferencia.
Para determinar dicho valor, de forma analítica, se recurre a la expresión:

Cuando se recurre a métodos gráficos, estos serán siempre aproximados, idealizando la circunferencia como un polígono de infinitos lados, ya que es una curva cerrada.
No obstante, para el trazado de plantillas, se necesita conocer la distancia que se recorrería al girar sobre un plano, partiendo desde un punto cualquiera de la misma, hasta retornar al mismo punto tras rodear la figura por completo. Esto resulta necesario para trasladar las divisiones realizadas sobre la circunferencia y hacer posible la obtención de las plantillas necesarias.
Métodos para calcular la longitud de la circunferencia
Para conocer la longitud de la circunferencia, existen varios métodos, exponiéndose a continuación el más intuitivo:

Se entiende como espiral aquella curva que gira alrededor de uno o varios puntos, llamados centros, y, al tiempo, se aleja de este, tal y como se muestra en la figura.

En función del número de centros y/o de la forma base a emplear, se obtendrá una espiral u otra. Las formas básicas para los centros pueden ser: dos centros alineados, tres centros (base triangular), cuatro centros (caso en el cual se utiliza un cuadrilátero como base), de mayor número de centros (base poligonal regular, pentágono, hexágono, etcétera).

Nota
El paso de una hélice corresponde a un giro completo de la curva. Para n número de pasos, se tendrán n número de giros.
El procedimiento de la figura arriba mostrada corresponde al de dos centros alineados, situados a una distancia dada entre sí.
Para representar la espiral, se traza una recta dada donde se marcan los centros A y B. Tomando centro en A y con radio AB, se traza un arco de 180° hasta cortar la recta en el punto 1. A continuación y desde B y radio B1, se traza otro arco con el mismo sentido que el anterior, cortando el eje en el punto 2. Este proceso se repetirá sucesivas veces hasta lograr el tamaño deseado.
Cabe la posibilidad de que se mantenga fijo el radio de la curva, mientras el centro de la curva se desplaza a lo largo de un eje.

Ejemplo
Esta situación se da en los filetes de rosca de los tornillos.

Para este último caso, se procede dividiendo la base del cilindro en ocho partes. De igual forma, se divide el eje en igual número de partes. A partir de estas divisiones, se relaciona cada punto de la base, siempre siguiendo puntos consecutivos y en el mismo sentido de giro, con cada porción de paso con cada porción de giro.
Este tipo de trazado puede encontrarse en multitud de aplicaciones:
Seguidamente, se definirá de manera detallada en qué consisten estas figuras geométricas, así como la forma en que se construyen.
Se define así a toda curva cerrada plana, con centro y dos ejes perpendiculares, que son de simetría y se cortan en el centro de la figura.

Uso del óvalo como recurso ornamental e industrial
A continuación, se muestra uno de los muchos métodos existentes para la construcción de óvalos.
Cómo construir un óvalo conociendo el eje mayor
Para construir un óvalo conociendo el eje mayor, se procede como se indica:


Nota
Esta figura puede encontrarse en representación esquemática de depósitos y otros símbolos, útiles para embridar, piezas torneadas, etcétera.
Llamada también ovoide, se define por aquella curva cerrada convexa y simétrica respecto de su eje mayor y que no tiene centro.

Nota
Este tipo de trazado, además de presentarse en calderería, aparece en símbolos de representación normalizados para planos de proyecto.
El método de trazado de este tipo de figura se realizará según los datos de partida. Por ejemplo, dado el eje menor, se haría como sigue:

Ejercicio práctico
Se va a explicar el procedimiento para realizar el trazado de un soporte de una tubería colgada. Dicho soporte debe estar salvando unas tuberías que discurren paralelas, situadas entre la nueva línea y el soporte. Por tal motivo, se ha diseñado con forma ovoide en su parte inferior.
Solución
Para el trazado del soporte ovoide, se procederá según los siguientes pasos:


Basta trazar la mitad del ovoide, dejando listo para realizar el corte de la chapa, obteniendo el siguiente resultado.

La elipse es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos, denominados focos, es una cantidad constante y positiva. El valor de dicha suma es 2a (donde a es el semieje mayor). Al eje mayor también se denomina eje real, mientras que al eje menor se define como eje imaginario. La distancia entre los focos recibe el nombre de distancia focal, siendo su valor 2c. El valor de c es la distancia del eje imaginario hasta cada foco. Por otra parte, se cumple que los dos ejes de la elipse son ejes de simetría y perpendiculares entre sí. El punto de intersección de ambos ejes recibe el nombre de centro de la elipse. Finalmente, los vectores de posición se designan como r y r′.
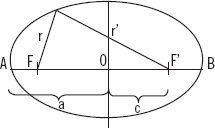
Construcción de elipse dados el eje mayor y la distancia focal

Nota
Este tipo de trazado, además de presentarse en calderería, aparece en símbolos de representación normalizados para planos de proyecto.

Ejemplo
Para realizar el trazado de una elipse en taller a partir de lo expuesto anteriormente, se procederá como sigue:
La separación entre puntos suele oscilar entre 1 y 2 cm, ya que si se realizan puntos con mucha separación, hay posibilidad de mayor de error.
Es el lugar geométrico de los puntos del plano equidistantes de un punto llamado foco y de una recta llamada directriz. Posee un solo eje de simetría, perpendicular a la directriz, el cual contiene al foco y a un solo punto de la curva, denominado vértice, siendo su tangente paralela a la directriz y, en consecuencia, perpendicular al eje.
El vértice equidista de la directriz y del foco, siendo la distancia del mismo a cada uno igual al semiparámetro (sp). Se denomina parámetro de la parábola a la longitud de cuerda que, pasando por el foco, es paralela a la directriz.

Ejercicio práctico
Se ha de trazar un hueco con forma parabólica sobre una chapa de acero para dar paso a la estructura de un equipo a montar en un compartimento de una construcción.
SOLUCIÓN
Para el trazado de dicho hueco, se procederá siguiendo los siguientes pasos:
Los puntos de la parábola se marcarán siguiendo el mismo procedimiento que se expone para el punto “1”.


Nota
Existen aplicaciones de esta figura, por ejemplo en accesorios especiales de instrumentación, moldes para conformación de chapas, estructuras de arco con perfiles de tubos (construcciones singulares), las pantallas de colectores solares (para calentar el fluido o gas que circula por las tuberías de las instalación), abrazaderas de sujeción de tubos a sus soportes, diagramas tabulados del comportamiento de fluidos, etcétera.
Se entiende como recta el ente ideal, unidimensional e ilimitado que se extiende en una dirección (o su opuesta), constituido por infinidad de puntos. Pude clasificarse según su posición relativa respecto a otra y la relación entre sus puntos.
Un ángulo es la porción de plano delimitado por dos semirrectas que se cortan en un punto, llamado vértice. El valor de cada ángulo se mide en radianes o en grados.
Se define como triángulo toda porción de plano delimitado por tres rectas que se cortan dos a dos. Sus elementos son los lados, la altura y los ángulos. Pueden clasificarse según sus lados y según sus ángulos. Se aplican como elementos auxiliares de trazado de planos y replanteos en proyectos, así como también los cuadriláteros, las circunferencias, los polígonos cerrados, las rectas y sus segmentos relacionados.
Por otra parte, el método de división de la circunferencia y el cálculo de la longitud de la misma son muy utilizados para el trazado de plantillas para trabajos con tuberías.
El trazado de espirales se aplica en fabricación de tubos, serpentines de calderas, resortes y simbología normalizada. El cálculo del valor de elipses se utiliza en aplicaciones de calderería de equipos en instalaciones de tuberías y simbología normalizada, mientras que la construcción de parábolas se emplea para diseño de accesorios de tubería y gráficas de comportamientos de fluidos.

Ejercicios de repaso y autoevaluación
1. ¿Cuál de las siguientes afirmaciones no es correcta?
2. Un triángulo se define como la porción de plano delimitada por tres rectas que se cortan dos a dos.
3. De las siguientes afirmaciones, indique cuál es la correcta.
4. Marque la solución correcta para la clasificación de los triángulos según sus lados.
5. Explique en qué consiste el teorema de Pitágoras:
6. Divida el segmento AB mostrado en cuatro partes iguales.

7. Relacione las figuras mostradas con su término.





8. Defina la elipse.
9. Los elementos de la parábola son: