1. LA MEDIDA DEL TIEMPO: UN PROBLEMA UNIVERSAL[1]

1.1. INTRODUCCIÓN

ENTRE LOS VEINTE TEXTOS ESPAÑOLES con los que la UNESCO inauguró la Biblioteca Digital Mundial se encuentra la Pragmática sobre los diez días del año, documento firmado por Felipe II ordenando la reforma del calendario gregoriano en todos sus reinos. Esta pragmática siguió a la bula Inter Gravissimas, expedida el 24 de febrero de 1582 por el papa Gregorio XIII que imponía dicha reforma sobre la cristiandad. La citada bula reformó el calendario juliano y ofreció uno nuevo llamado a partir de entonces el calendario gregoriano. La elección por parte de España de la Pragmática sobre los diez días del año[2] para una biblioteca tan emblemática como la de la UNESCO refleja, sin ninguna duda, la importancia que tuvo en su día la reforma del calendario y la que ha seguido teniendo para la historia de la humanidad, pues hasta la norma internacional para la representación de fechas y horarios, norma ISO 8601, utiliza el calendario gregoriano.

No todos nos regimos por el mismo calendario: cristianos, musulmanes, judíos, hindúes o chinos medimos el tiempo de formas distintas, de acuerdo con los acontecimiento de nuestras historias respectivas, creencias religiosas y estadio cultural (Casals, 2007). Sin embargo, el calendario gregoriano es en la actualidad el aceptado como calendario civil de la humanidad y representa un gran logro de la civilización, debido a que, a pesar de su pequeño desajuste respecto del movimiento estelar, es una medida de gran precisión (Gutiérrez, 2008).

El cometido de este trabajo radica en la publicación y estudio de los proyectos elaborados por la Universidad de Salamanca para la reforma del calendario en el siglo XVI; tema que fue de la mayor importancia científica, jurídica, política y religiosa desde que se tienen datos históricos computacionales; circunstancia que ha venido siendo destacada entre los cristianos al menos desde el concilio de Nicea (año 325).

Al acordar la cristiandad en este concilio la ligazón dogmática entre el equinoccio de primavera y la Resurrección de Jesucristo se puso de manifiesto la importancia capital que la Iglesia otorgaba a la fijación del tiempo social de los cristianos, más allá del tiempo astronómico u otros, dirigiendo su curso y asociándolo con la idea inequívoca de la luz equinoccial. Discurso que corrobora el informe salmantino de 1515, cuando dice:

...es a partir del equinoccio de primavera cuando el calor comienza a aumentar y cuando empieza a alargarse la luz del día; y es desde la luna décimocuarta hasta la luna vigésimo primera cuando la luz de este astro, tanto en plenilunio como en cuarto creciente, disipa las tinieblas de la noche [informe de 1515 (5)].

Esta premeditada y largamente buscada ligazón tripartita entre Resurrección de Jesucristo, luz y calor convertía la celebración de la principal fiesta de los cristianos en un planificado acicate de la anagogía espiritual, donde el rito de la Pascua quedaba indisolublemente trabado con el nacimiento de la primavera astronómica y con la idea de la bienaventuranza eterna: una planificación del tiempo y del dogma que me parece de una audacia magistral, a la que indiscutiblemente contribuyó el informe salmantino citado.

Para lograrlo se requería primero una conciencia clara de la necesidad nuclear del acompasamiento del paso del tiempo con el dogma, pero también se necesitaba —y aquí estuvo el problema— la invención de un procedimiento matemático que lo hiciera posible, permitiendo enlazar en un cómputo convergente el distinto ritmo del Sol y de la Luna. La búsqueda de este procedimiento consumió la energía y el ingenio de muchos matemáticos cristianos, especialmente desde el siglo XIII. El informe salmantino de 1515 lo consiguió y el de 1578 ratificó dicha consecución previa. Este hecho es de enorme importancia, no sólo por el logro, sino también porque demuestra la altura de los conocimientos matemáticos y astronómicos en la Universidad de Salamanca alrededor del año 1515.

Siempre me llamó la atención el que documentos de tanta relevancia estuvieran durmiendo el sueño de los siglos sin una puesta en valor mediante estudios sistemáticos. El que ahora presento demuestra por una parte la continuada falta de sensibilidad de los historiadores ante una documentación tan llamativa (probablemente motivada por la dificultad de interpretación de las propuestas manuscritas), y por la otra, la certeza de que el informe salmantino del año 1515 fue, si no la única, al menos sí una de las más sólidas bases de la reforma gregoriana del calendario que finalmente se ratificó en 1582. Es decir, que mediante este trabajo pretendo reivindicar para la Universidad de Salamanca la autoría, o como poco la co-autoría, de nuestro modelo actual de medir el tiempo, que hasta el día de hoy se le ha reconocido al italiano Luis Lilio.

Este trabajo se presentó originariamente como tesis doctoral en el Departamento de Filosofía, Lógica y Estética de la Universidad de Salamanca, el día 15 de junio de 2011. El tribunal que lo juzgó estuvo formado por D. Salustiano de Dios de Dios (presidente), D. Víctor Navarro Brotóns, D. ª María José Vega Ramos, D. Modesto Sierra Vázquez y D. Luis Andrés Marcos (vocales). Fueron codirectores del mismo los doctores D. Cirilo Flórez Miguel y D. Ramon Aznar i Garcia. Obtuvo la máxima calificación.

El estudio es deudor directo de D. Ambrosio Díez Escanciano y de D. Benigno Hernández Montes, que han sido coautores conmigo de la primera traducción de los textos latinos aquí presentada; sin su colaboración este trabajo hubiera sido imposible. También debo agradecer al profesor D. Raúl González Salinero su imprescindible ayuda en la Biblioteca Apostólica Vaticana; a D. ª Asunción Miralles y a D. César Ramos la colaboración prestada para la localización documental en la Real Academia de la Historia (Madrid); a D. ª María Teresa Rodríguez Blázquez su tenacidad en buscar datos sobre Juan de Ortega; a D. Jonás Castro Toledo la guía para saber quién fue el cura de Gatón (del que hablan los documentos) en el Archivo Diocesano de Valladolid; a mis hermanos Ignacio y Ángel su constante disposición a responder a mis simples preguntas sobre matemáticas; a D. Daniel Hernández Ruipérez, D. Víctor Navarro Brotóns y D. ª María José Vega sus observaciones; a los profesores D. Cirilo Flórez Miguel y D. Ramon Aznar i Garcia que me ofrecieron sabios consejos y correcciones que tanto agradezco y a D. Francisco Lorenzo Pinar su constante apoyo.

1.2. EL PROBLEMA DEL TIEMPO EN LA HISTORIA Y EN LA HISTORIOGRAFÍA

El tiempo es un elemento nuclear en las sociedades humanas y, por eso, la reflexión sobre el tiempo es uno de los hilos conductores de la historia de la filosofía. La consciencia de la temporalidad se nos encara individualmente cuando aprehendemos nuestra propia finitud y también cuando reconstruimos una memoria del pasado que nos da razón de lo que somos y del porqué de las cosas. De hecho, esta consciencia es una pre-condición de la supervivencia, pues la sociedad y el individuo no pueden sobrevivir sin afirmar y conocer parte de su relación con el pasado, pero su significado ha ido variando de acuerdo con los cambios en la cosmovisión del mundo.

¿Han intentado obviar el concepto y la palabra tiempo en su conversación y en su vida? Ello equivaldría a enmudecer, a cosernos la boca en palabras de Klein (Klein, 2005, pp. 29-39), porque es casi imposible percibir o hablar de una emoción sin expresar su trama temporal; cuando decimos que el tiempo pasa, confundimos el objeto con la función, pues es toda la realidad la que pasa, no el tiempo en sí. Esta imprecisión verbal en nuestras expresiones habituales se arrastra desde que se tiene memoria. Al principio el mundo duraba sin estar sometido al tiempo, pues el tiempo sólo entró en la escena humana al cabo de un cierto tiempo. Desde este punto de vista podemos decir que los historiadores somos los agentes del tiempo en el presente; los encargados de conservar la memoria colectiva e individualizada del grupo.

La Universidad de Salamanca presentó dos informes oficiales sobre este problema, aunque entre sus profesores, como entre los intelectuales de todos los tiempos, hubo también otros que elaboraron o propuestas de reforma del calendario o comentarios al calendario gregoriano finalmente aprobado. El primero de estos dos informes oficiales de los que hablo fue redactado por una comisión universitaria nombrada para corresponder a la doble solicitud del papa León X y Fernando el Católico, y enviado al V concilio de Letrán en Roma, en el año 1515. El segundo procede del cumplimiento de una segunda doble solicitud, en este caso del papa Gregorio XIII y de Felipe II, en el año de 1578. El estudio de estos informes representa una novedad historiográfica y puede ayudarnos a comprender tanto el peso científico de la Universidad de Salamanca en los tiempos en los que se emitieron como el planteamiento de algunas cuestiones clave de la historia social en algunas de sus muchas vertientes.

De acuerdo con la importancia que ha tenido y tiene la medida del tiempo, a lo largo de la historia cristiana encontramos gran cantidad de escritos redactados con el objetivo de acompasar el calendario eclesiástico con el astronómico, y somos hoy testigos de la compleja filigrana computacional e interpretativa a que dieron lugar los muchos y abstrusos debates sobre el tema. La historia del calendario ha convocado a su alrededor a más científicos que historiadores, a pesar de que estos últimos también se contaban ya por cientos en el siglo XX.

Haré a continuación una evaluación de la historia de la historiografía sobre el tiempo; el camino por el que hemos llegado a esta consciencia y sus múltiples facetas ha sido muy bien estudiado por la filosofía, la antropología y la historia. Un breve libro de Fernando Muñoz Box, titulado Las medidas del tiempo en la historia. Calendarios y relojes, representa una buena introducción general al tema; en el que podrá el lector encontrar información precisa, de meridiana claridad y gratificante sencillez sobre cronologías, calendarios, medidas y relojes a lo largo de la historia.

Desde el punto de vista temático, la reforma del calendario gregoriano pertenece al ámbito de la historia de la ciencia, pero la forma de abordarlo puede acercarlo a su vez a la historia de la Iglesia, la historia del derecho, la historia de las mentalidades, la historia cultural y la historia social (que en realidad lo engloba todo). Por lo que se refiere al ámbito de la historia de la ciencia, José María López Piñero expuso ya hace años el problema de la discontinuidad de la historiografía sobre la ciencia en España en sus textos «Tradición y discontinuidad en España de la historiografía de la ciencia» y «La historia de la ciencia durante los últimos 25 años» (López Piñero, 1996, pp. 13-16; López Piñero, 2001). Hizo además una evaluación global del problema en 2007, titulada «Ciencia y técnica en la sociedad española de los siglos XVI y XVII tres décadas después» (López Piñero, 2007, pp. 12-26), en la que matizaba otra previa sobre este tema, titulada «La actividad científica en la España de Felipe II» (López Piñero, 1999b, pp. 17-36), mucho después de haber dado a la imprenta su conocido libro Ciencia y técnica en la sociedad española de los siglos XVI y XVII (Barcelona: Labor, 1979). En el mismo sentido, Enrique Martínez Ruiz coordinó un espléndido libro sobre Felipe II, la ciencia y la técnica (Madrid, 1999), que representó una actualización de conocimientos y del estado de la cuestión sobre el asunto. Visión que ha sido completada últimamente por la reflexión de Navarro y Eamon sobre la revolución científica en España, en su trabajo «Spain and the Scientific Revolution: historiographical questions and conjectures» (Navarro Brotons – Eamon, 2008, pp. 27-40).

Todos estos investigadores coinciden en subrayar el cambio que se ha operado en la investigación de este tema en los últimos cincuenta años, como consecuencia de la superación de la polémica de la ciencia española y el desarrollo de una historiografía nacional sobre la temática, prácticamente inexistente hasta mediados del siglo XX. Esto ha permitido matizar los tópicos acerca del retraso científico español, superando los vacíos historiográficos y el desconocimiento de que adolecían bastantes libros, cuyos contenidos eran valiosos en lo relativo a otras cuestiones. López Piñero (especialmente, en los textos citados) y Goodman (Goodman, 1990, 1999) han abundado mucho en los tópicos sobre nuestro retraso científico, pero ninguno de ellos trata al problema de la reforma del calendario en sus obras, siendo así que este asunto fue la cuestión científica más importante de la cristiandad hasta la publicación de la reforma, en 1582, y podría ofrecerse como paradigma de los conocimientos científicos españoles a lo largo del siglo XVI. Aunque esto me parece evidente, curiosamente, ni López Piñero recuerda o analiza la historiografía sobre la reforma del calendario en los espléndidos balances historiográficos apuntados, ni Goodman lo cita siquiera en el libro Poder y penuria. Gobierno, tecnología y ciencia en la España de Felipe II (Madrid, 1990), o en su interesante artículo «Las inquietudes científicas de Felipe II», del año 1999.

A la vista de lo dicho, como era de esperar, ni estos autores, ni los profesores que forman parte del grupo del Instituto de Historia de la Medicina y de la Ciencia López Piñero, de la Universitat de València y el CSIC, ninguno de ellos recoge información específica sobre la historia del calendario en sus trabajos sobre Los impresos científicos científicos españoles de los siglos XV y XVI (López Piñero y otros, 1981-1986), ni en la Bibliografía histórica sobre la ciencia y la técnica en España, publicados entre 1968 y 1973; ni en la Bibliographia physico-mathematica hispanica (1475-1900) (Navarro Brotóns y otros, 1999), ni en estudios como «La imprenta y la difusión y comunicación científica de los saberes y las técnicas (1561-1600)» (Salabert, 1999), etc.

En realidad no ha habido historiador de la ciencia que haya hecho poco más que citar este asunto, como de puntillas. En conjunto, pues, a pesar del enorme peso científico de estos trabajos citados y otros no citados, la reforma del calendario gregoriano ha pasado inadvertida, sin pena ni gloria, para los grandes investigadores sobre la historia de la ciencia en España. Mi trabajo pretende poner el acento en este olvido y ofrecer los elementos documentales e históricos que justifiquen la importancia nuclear que yo le otorgo en la sociedad de su tiempo. Antes de centrarme en ello, sigamos haciendo una breve visita guiada global a la cuestión del tiempo en la historia y en la historiografía.

Desde el punto de vista de la historia social, es muy difícil de establecer el origen preciso de la reflexión sobre el tiempo y la duración. Todos conocemos que esta cuestión fue tratada y escrita (por eso lo sabemos) por los filósofos presocráticos y que inicialmente se mostró ligada a la idea de naturaleza, a sus constantes cambios (llamados entonces devenir) y a la vinculación de ser y tiempo. En este sentido Heráclito (535 a. C.-484 a. C.) hablaba del devenir de todas las cosas, Anaximandro (610 a. C.-546 a. C.) relacionaba la existencia del tiempo con la del cosmos y Parménides (nacido entre el 530 a. C. y el 515 a. C.) definía la eternidad del ser como la ausencia de devenir y tiempo.

Se cree que fue Platón (c. 427 a. C.-347 a. C.) el que inauguró una concepción cíclica del tiempo (en el Timeo), concibiendo una imagen móvil y circular de la eternidad. Las ideas inmutables y eternas eran para él la representación de la eternidad del tiempo; concibiendo la eternidad como un tiempo totalmente dado cuyo desarrollo permitía la apariencia sensible del transcurrir; la duración y la futilidad de las cosas sólo atañían al mundo sensible.

Aristóteles (384 a. C.-322 a. C.) interrelacionó tiempo y movimiento. En su pensamiento el movimiento adquiría las características de total, infinito y eterno, rechazando la distinción platónica entre realidad y apariencia. Recuerda las paradojas de lo uno y lo múltiple, de la identidad y la diferencia. Pero, según él, el tiempo no sólo dependía del movimiento, sino también de un alma que lo numere. El instante era al tiempo lo que el punto al movimiento.

Este tratamiento teórico del tema tiempo fue bastante menos intenso que el computacional (Neugebauer, 1957), puesto que el desfase entre los calendarios civiles y astronómicos en varias culturas aconsejaba reformas, como la que finalmente implantaría Julio César en el año 46 a. C. Hasta ese momento, el mundo romano se regía por un calendario de 304 días distribuidos en 10 meses (6 meses de 30 días y 4 de 31 días). Los reajustes con el ritmo astronómico los hacían los sacerdotes con criterios estrictamente políticos o económicos, provocando frecuentes protestas.

La necesidad de reforma del calendario entre los romanos representó un acicate de la investigación astronómica. El calendario juliano que resultó aprobado al final de estos estudios, fue elaborado por Sosígenes a petición de Julio César. Es un calendario solar, con años comunes de 365 días y uno intercalar, de 366 días, cada cuatro años; es decir, que el año trópico medía para ellos 365,25 días, mientras que la admitida hoy es de 365 días, 5 horas, 48 minutos y 45,16 segundos (o sea, 365,242189 días). Por eso, los 11 minutos de diferencia anual del año juliano, habían supuesto un retraso acumulado de 10 días en el momento que se planteó la reforma gregoriana, en 1582 (Llagostera, 2006-2007, pp. 61 ss.; Jiménez Corvo, 2002). En este año intercalar de un día más, llamado bisiesto, se añadía un día al 24 de febrero, que era el último día de ese mes en el calendario romano previo.

También la implantación de la semana de siete días en Occidente fue decisión de los romanos; concretamente del emperador Constantino I el Grande, que en año 321 d. C. la tomó del calendario lunar judío, constando de: domingo, lunes, martes, miércoles, jueves, viernes y sábado.

Pero una cosa era el calendario civil y otra el astronómico. Los continuos intentos computacionales de acompasar ambas medidas habían resultado infructuosos; entre tanto, se optó por lo más útil. Desde el punto de vista práctico, la teoría filosófica de Aristóteles, junto a los resultados de la investigación de Claudio Ptolomeo (c. 100-c. 170) en el Almagesto, servían para predecir los fenómenos, para salvar las apariencias —como decía Ptolomeo—, constituyéndose esta obra en la base del estudio y la investigación astronómica de Occidente durante siglos, siendo progresivamente completada, en cuanto a la precisión del año trópico[3], primero por las tablas Alfonsíes y después por las Pruténicas.

De forma paralela y simultánea a la investigación sobre el cómputo astronómico continuaron la reflexión y los debates teóricos sobre el tema. Aquella teoría platónica de un tiempo cíclico fue definitivamente rota por el cristianismo, que lo concibió como algo lineal e imparable. El tiempo daba sentido a la historia de los cristianos, desde la Creación hasta el Juicio Final; es decir, que —como opinaba San Agustín— el tiempo humano, presente, finito, lineal y progresivo, depende de la eternidad de Dios. Aunque al final, San Agustín subjetivizó el tiempo de la eternidad de Plotino, reduciéndolo al de la interioridad del alma[4].

Más allá de la reflexión teórica, esta temática fue haciéndose más frecuente cuando los cristianos necesitaron una precisión en la medida del tiempo para el cumplimiento del dogma. Podríamos hacer arrancar el debate sobre la reforma del calendario eclesiástico del año 314, fecha en que el concillio occidental de Arlés decició que la Pascua se celebrara el mismo día en todo el mundo, lo que promovió el interés por la fijación de esta fecha, saliendo a colación la imprecisión del calendario. Esta historia está perfectamente sintetizada en el trabajo de Pedersen «The Ecclesiastical Calendar and the Life of the Church» (Pedersen, 1983, pp. 17-74).

Tras la reunión de Arlés, la cuestión del cómputo fue amplia y largamente debatida en el concilio de Nicea (325), que fue un hito en este ámbito, por establecer que la fecha de la Pascua cristiana debía celebrarse el domingo posterior al plenilunio de primavera. Con este decreto se aseguraron los padres de la Iglesia la separación de la Pascua cristiana y la judía, que seguía los criterios bíblicos de conmemorarla el 14 del mes de Nisan, que era el primero en el calendario judío. Después abundaremos en ello.

El espíritu universalista de Nicea no fue seguido por todos y por eso, en contra de lo que se había pretendido y creído, no cesó ahí el debate sobre la medida del tiempo de los cristianos. Los alejandrinos de las iglesias del Este, por ejemplo, discreparon del criterio niceno y propusieron otras alternativas. En realidad el decreto de la fijación de la fecha de la Pascua en el concilio de Nicea sólo fue una solución provisional, pues ni los propios padres del concilio dudaban del retraso en la fecha del equinoccio vernal, el de primavera, que se produciría con los siglos cumpliendo el decreto que estaban imponiendo.

La clave del problema era la fijación de la medida del año solar o trópico, para poder después acompasarla con el ciclo de Metón y el áureo número y poder así elaborar un calendario perfecto. Recordemos que Metón fue un astrónomo ateniense que descubrió la correspondencia entre 19 años solares y 235 lunaciones; es decir, que, al cabo de esos 19 años (el llamado ciclo de Metón), las fases de la luna supuestamente se repetían en las mismas fechas. Pero fijar la medida del año trópico era un trabajo de Hércules, en palabras de Juanelo Turriano (Turriano, 1990), uno de los convocados a la reforma gregoriana como veremos; y, en esta lucha por la precisión cronológica hay que insertar a toda una serie de intelectuales que escribieron sobre la medida del tiempo, entre los que es imposible olvidar a: Eusebio (c. 275-339), Dionisio el Exiguo (c. 470-c. 544) y su verdadero divulgador: Beda el Venerable (c. 672-735; De Temporum Ratione), Alcuino (c.735-804, en su De cursu et salto lunae), Rabanus Maurus (c. 780-856, en De computo), el Magister Anianus (siglo XIII, en Computus metricus mundialis), Roberto Grosseteste (1175-1253, con su propuesta de un ciclo de 76 años), Roger Bacon (c. 1214-1294, especialmente en Opus Tertium), Johannes Campanus (1220–1296, y su De computo eclesiástico o Computus maior, escrito para Urbano VI), Johannes de Sacrobosco (1195-1256, autor del Tractatus de Sphaera, obra que era base del curriculo académico salmantino); las Tablas alfonsíes (de 1252, cuya medida del año trópico se pensó hasta hace muy poco que fue la utilizada por Lilio para establecer la reforma del calendario gregoriano). El enorme desarrollo de la ciencia astronómica entre los árabes promovió, a su vez, una importante producción científica en astronomía; pero permanecieron al margen del debate sobre la reforma del calendario que tanto preocupaba a los cristianos, por no atañerles personalmente un asunto astronómico de otra religión.

Como vemos, la cronología y el problema del tiempo adquirieron gran importancia durante la Edad Media y se han publicado excelentes trabajos contemporáneos sobre el tema[5]. El desajuste entre el año astronómico y el civil generó cierta incertidumbre y se convirtió en un lugar común de debate de matemáticos y astrónomos, algunos de ellos relacionados con las jerarquías eclesiáticas, a quienes interesaba especialmente la correcta celebración de la Pascua. Como hitos reseñables en el estudio del tema, yo destacaría la relevancia de Beda, Bacon y las tablas alfonsíes. Subrayo la obra de Beda porque, a pesar de ser este autor más conocido por su faceta de historiador, ha sido considerado como el creador de la cronología por sus obras De temporibus liber y De temporum ratione (Saint Beda, 1884). En ellas incluyó el cálculo de la edad de la Tierra, resúmenes de la historia del mundo desde la creación hasta el 725 y el 703 respectivamente, la práctica de dividir la era cristiana en antes de Cristo y después de Cristo y matices en la fecha de la celebración de la Pascua.

Puesta en valor la cronología por Beda[6], se generalizó el tratamiento libresco de cronologías y calendarios, generalmente por parte de eclesiásticos, como Roger Bacon, que se escandalizaba de la imprecisión cristiana en el cumplimiento del decreto conciliar sobre la celebración de la fecha de la Pascua. Ha pasado a la historia la opinión que le merecía esta imprecisión, a la que tachaba de intolerabilis, horribilis, et derisibilis (North, 1983, pp. 75-116), siendo el primero que propuso seriamente una reforma del calendario juliano.

El tercer hito elegido son las Tablas alfonsíes: uno de los textos medievales sobre el que la historiografía se ha volcado (Chabás-Goldstein, 2008), circunstancia que está en consonancia con la enorme importancia astronómica y computacional que tuvieron durante más de trescientos años. Obra científica y conmemorativa, que contiene las posiciones de los cuerpos celestes para Toledo el día de la coronación de Alfonso X (1221-1284), el 1 de enero de 1252. Son una revisión de las tablas toledanas de Azarquiel basadas en las observaciones llevadas a cabo en Toledo entre 1262 y 1272. Su gran repercusión se debió precisamente a que era un texto práctico para calcular las posiciones del Sol y la Luna en la época en que se fue generalizando el interés por estas medidas con vistas a la reforma del calendario y que, como dije, se basó inicialmente en ellas.

Otra de las novedades significativas de este conjunto teórico sobre la medida del tiempo fue la invención del reloj mecánico (Muñoz Box, 2003), aunque algunos teólogos lanzaron su voz contra su uso, porque usurpaba el derecho divino de medir el tiempo; pero su utilidad promovió su rápida difusión a partir del siglo XIV. Muchas iglesias y plazas públicas de florecientes ciudades medievales se engalanaron con el nuevo artilugio: Saint Andrews en Escocia, Salisbury en Inglaterra... Los escritos sobre el nuevo invento se desarrollaron y generalizaron rápidamente. Esta idea de socializar la medida del tiempo mediante la ubicación de relojes en las principales plazas se ha conservado hasta hoy, en el reloj mundial, como el que ahora luce Alexanderplatz en Berlín.

A pesar de lo anotado, la mayoría de los textos medievales sobre el tiempo tenían poco que ver con el tratamiento historiográfico del tema; eran más bien libros de cómputo eclesiástico, útiles para la fijación de fiestas religiosas y los momentos de rezo; apoyados ahora en la pauta de su uso por la mecánica de los relojes; relojes que tanto podían llamar a la oración como marcar el tiempo de los negocios o la política.

El clamor de Roger Bacon por la reforma fue asumido primero por la Iglesia en su conjunto, tratándose el tema en concilios, y en último lugar por el papa como autoridad individual, que finalmente la aprobó. La asunción eclesiástica del problema determinó su tratamiento obligado en los concilios ecuménicos. Así fue cuestión de debate primero en el concilio de Constanza (1414-1418), después en el V concilio de Letrán (1512-1517), que solicitó explícitamente informes a varias universidades (Marzi, 1896; más tarde volveremos sobre el tema, pues uno fue el de la Universidad de Salamanca) y finalmente en el concilio de Trento (1545-1563), donde, al no encontrarse tiempo para tratarlo adecuadamente, en su última sesión se decidió que fuera la autoridad del Papa (y no el concilio) la encargada de la reforma del calendario. En virtud de este decreto la firmaría Gregorio XIII. Por eso North habla de la reforma olvidada del calendario en el concilio de Trento (North, 1983, p. 100).

Estos debates y las solicitudes conciliares para la colaboración en la resolución del problema computacional promovieron un estudio inusitado de la astronomía y el cómputo en Europa. Directamente volcaron sus esfuerzos en el tema Pierre d’Ailly (c. 1350-1420) mediante solicitud que le hiciera el concilio de Constanza; Nicolás de Cusa (1401-1464, que escribió De reparatione calendarii) y colaboró en el concilio de Basilea-Ferrara-Florencia (1431-1445), y Pablo de Midleburg (1446-1534, con Paulina, de recta celebratione Pascua) en el V concilio de Letrán, para el que redactó Secundum compendium correctionis calendarii (Marzi, 1896)[7]. Nicolás Copérnico (1473-1543, Comentariolus y De revolutionibus orbium coelestium) fue también consultado por los padres del concilio de Letrán, pero su contribución al tema había sido magnificada, cuando en realidad fue bastante limitada, según demostró Proverbio (Proverbio, 1983, p. 129). De aquel período son destacables también los trabajos de John de Gmunden (1385-1442), su discípulo Georg Peurbach (1423-1461) y el discípulo de éste, Johannes Müller (Regiomontano, 1436-1476). Gran importancia tuvieron igualmente las ideas de Johannes Stöffler (1452-1531, Calendarium Romanum Magnum) y las tablas astronómicas elaboradas por el alumno de Copérnico, Erasmo Reinhold (1511-1553, Tablas pruténicas); las cuales sustituyeron a las alfonsíes en el trabajo cotidiano de los astrónomos.

Es decir, que en el tránsito de la Edad Media a la Edad Moderna la necesidad de reforma del calendario eclesiástico provocó una multiplicación de manuscritos e impresos sobre el asunto. Como esta época coincide con el período de expansión y desarrollo del Renacimiento, a los textos puramente cronológicos o técnicos solía añadírseles una parte introductoria de carácter historiográfico e incluso a veces lingüístico. Éste es el caso precisamente del informe que redactó Juan Ginés de Sepúlveda para su presentación al concilio de Trento (Sepúlveda, 1546), que no trataba tanto el fondo computacional del problema, sino sobre todo sus matices lingüísticos y que, por ello, de nada sirvió a la resolución del problema (Carabias Torres, 2003). Sepúlveda mantuvo una correspondencia científica con varios prelados de Roma y España sobre la reforma del calendario que puede ser paradigmática de la sensibilidad y el interés que había en los círculos intelectuales católicos europeos por la reforma.

De esos mismos años son los textos españoles de Jerónimo de Chaves (Cronografía o reportorio de los tiempos, el más copioso que hasta ahora ha salido a la luz, con quince ediciones en España desde 1554 a 1600, del año 1548), Bernardo Pérez de Vargas (Repertorio perpetuo, 1563), Bartolomé Antist (Almanac o pronóstico de los efectos que se esperan según las configuraciones de los planetas y estrellas que han de suceder en diversas partes del mundo y particularmente en el horizonte de Valencia, 1580), Pedro de la Hera (sus cálculos de eclipses lunares con arreglo al meridiano de Madrid), fray Juan de la Barrera (Repertorio perpetuo de los tiempos, de 1579), Jerónimo Cortés (El non plus ultra del lunario y pronóstico perpetuo general y particular para cada reino y provincia, de 1665, o el Lunario nuevo, perpetuo y general…, de 1598), fray Diego Jiménez (Kalendarium perpetuum secundum institutum patrum predicatorum, de 1563) y, sobre todo, los de Juan Salón, un franciscano valenciano que escribe De romani calendari nova emendatione, ac Paschalis solemnnitatis reductione… (Florencia, 1572), que obtuvo el aplauso papal, igual que el de Alessandro Piccolomini (1508-1579) con su De nova ecclesiastici calendarii, pro legitimo Paschalis celebrationis tempore restituendo forma…; y otros de menor difusión entre los círculos pontificios, pero de gran interés en España dado que ayudaron a popularizar el tema del calendario entre las gentes: en este grupo podemos recordar los de Juan Terréu, Agelasio Palmireno, Álvaro Piña, García de Lovas, etc.

Un ejemplo del tipo de texto que se publicaba entonces puede ser el de Johannes Stöffler citado, del que había al menos cuatro ejemplares al alcance de estudiantes y profesores en la biblioteca de Salamanca desde 1518 —lo cual sugiere que era un tratado de uso común entre los escolares—, titulado Calendarium Romanum magnum: Caesareae maiestati dicatum (...Impressum in Oppenheym: per Jacobum Ko[e]bel, 1518, véase fig. 1). Luce éste una portada con treinta escudos de armas coronados por el del emperador. A la información relacionada con el calendario añade en la hoja decimocuarta, a toda plana, la figura de un hombre anatómico con sus vasos sanguíneos numerados y la influencia del zodíaco (véase fig. 2). Contiene además un calendario con los signos del zodiaco en el margen derecho, y en el izquierdo escenas de ocupaciones del año; imágenes de eclipses solares y lunares, así como de instrumentos astronómicos. Buena prueba de que la información sobre el calendario iba unida a otra relacionada con la medicina, las ciencias naturales, la historia y la astrología.

De todos ellos, el comentario más difundido en los años setenta del siglo XVI y entre los círculos intelectuales debió ser el de Aloysius Lilio (c. 1510-1576), que precisamente es uno de los más desconocidos en la actualidad. Fue Lilio el presunto inventor de la fórmula cronológica que sirvió de base a la reforma gregoriana, en un trabajo titulado Compendium novae rationis restituendi kalendarium (Moyer, 1983, pp. 171-188), hasta el punto de que Herrera Armendía reivindicó hace poco que nuestro calendario debería llamarse liliano en lugar de gregoriano (Herrera Armendía, 2007). Por mandato papal, un compendio del trabajo de Lilio, elaborado por el antiguo profesor salmantino Pedro Chacón, fue enviado a los monarcas y a varias universidades entre 1577 y 1578 para su consulta.

De la misma forma que se había puesto de moda el tema del calendario antes de la bula Inter gravissimas, después de su publicación en 1582 abundaron los ensayos explicativos del mismo o aquellos que ofrecían propuestas alternativas a lo ordenado en ella por el papa. La reacción de los astrónomos ante la reforma está muy bien estudiada en la época contemporánea por Nobis (Nobis, 1983), Hoskin (Hoskin, 1983) y Gingerich (Gingerich, 1983). Entre los intelectuales que más duramente se enfrentaron a ella en el momento de producirse, el que quizá lo hizo con más ahínco fue Joseph Justus Scaligero (1540-1609), hasta el extremo de haber sido considerado como el promotor del auge y de la decadencia de la cronología[8], en su texto De emendatione temporum (Leyden: Officina Plantiniana, Francis Raphelengius, 1598). En esta misma línea crítica escribieron Georgius Germanus (segunda mitad del siglo XVI), Sethus Calvisius (1553-1617), Michaelem Maestlinum (1550-1630) y Franciscus Vieta (1540-1603), que deseaban simplemente restablecer la tradición del concilio de Nicea. En cambio otros, incluidos algunos protestantes —lo cual sorprende—, aceptaron y alabaron la reforma gregoriana, como Bartholomaeus Scultetus (1510-1614), Tycho Brahe (1546-1601), Johannes Kepler (1571-1630), Paulus Guldin (1577-1643), Dionysius Petavius (1583-1628) y muy especialmente Christophorus Clavius (1537-1612) (Nobis, 1983, pp. 244 ss.).

Fig. 1: STÖFFLER, Johannes. Calendarium Romanum magnum: Caesareae maiestati dicatum, D. Ioanne Stoeffler iustingensi mathematico authore...

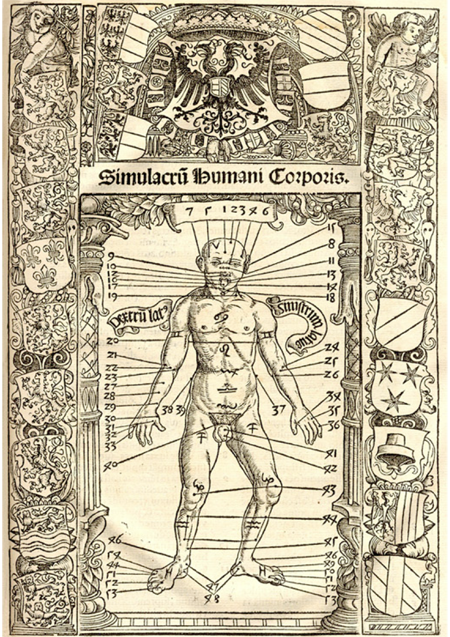
Fig. 2: STÖFFLER, Johannes. Calendarium Romanum magnum: Caesareae maiestati dicatum, D. Ioanne Stoeffler iustingensi mathematico authore... Impressum in Oppenheym: per Jacobum Ko[e]bel, 1518, die 24 Martii, p. 14.

En un momento concreto Clavio era el único de los responsables de la reforma que había sobrevivido al conjunto de los comisionados y, quizá por ello, el que escribió varios textos, tanto para su explicación y difusión, como para rebatir las teorías de quienes previamente habían escrito denostándolo. Ésta es la razón de que su nombre haya pesado tanto en la memoria de esta reforma, aunque haya sido fundamentalmente el explicador y difusor de la misma (más información en Oñate Guillén, 2000b). Explicó meticulosamente la propuesta gregoriana en tres trabajos: Computus ecclesiasticus per digitorum articulos mira facilitate traditus (Clavius, 1597), Computus ecclesiasticus per tabulas traditus, vbi omnia, quae ad Computum pertinent, vno in conspectu cernuntur (Clavius, 1597) y, especialmente, en Romani calendarii a Gregorio XIII P.M. restituti explicatio S.D.N. Clementis VIII P.M. iussu edita (Clavius, 1603), obra ésta que sería reeditada en el tomo V de su Opera mathematica (Mainz: Anton Hierat, 1611). No fue el único en hacerlo, pues la pluma de muchos intelectuales se dedicó en esos años a ese mismo cometido. Por ejemplo Ugolino Martelli (Martelli, 1583), Oñate de Escalante, en 1584 (Oñate, 1584), el catedrático de música salmantino Francisco Salinas, en 1583, (BNE. ms. 23106), el arzobispo de Toledo D. García Loaisa y Girón (BNE, ms. 13019). En España también se editó la traducción del calendario gregoriano con comentarios que hizo Tornamira (Tornamira, 1581), y otros más conocidos.

Como al mismo tiempo se habían difundido algunos textos difamatorios o descalificadores de la reforma gregoriana, Clavio también redactó varios contra-argumentos, como por ejemplo uno contra las teorías de Maestrlin, titulado Novi calendarii Romani apologia, adversus Mich. Maestlinum in Tubingensi Academiâ mathematicum (Clavio, 1588). Otro titulado Iosephi Scaligeri Elenchus, et castigatio calendarij Gregoriani (Clavio, 1595), frente al De emendatione temporum (Leyden, 1593 y 1598) de Scaligero. Giuseppe Scaligero fue quizá el mayor detractor de la reforma gregoriana del calendario (Scaliger, 1583; Secaliger, 1598). Al menos Scalígero no se limitó a descalificar sin más el resultado de la reforma, sino que hizo una crítica constructiva —lo cual le honra—, pues inventó el ciclo juliano de 7.980 años sidéreos, producto de multiplicar el ciclo lunar (19 años), el ciclo solar (28 años) y la indicción (15 años), prescindiendo del año bisiesto y de los cálculos medios, que habían sido usados en las tablas alfonsíes. Dicho ciclo comenzaba, según él, el 1 de enero del 4713 a. C. En apoyo de Clavio y de la reforma, Paul Guldin rebatió las críticas de Calvisius (1556-1615) en Refutatio elenchi calendarii gregoriani a Setho Calvisio conscripti (Moguntiae, 1616) y en ...Ad Refutationem Calvisiani elenchi calendarii gregoriani paralipomena sive Annotationes (Moguntiae, 1616). También Peter Roest entró en el debate escribiendo un texto para la disputa (Roest, 1582).

Sobrepasada la etapa inicial de recepción de la reforma, el número de textos, tanto manuscritos como impresos (cada vez más estos que aquéllos) sobre el calendario gregoriano, adquirió una mayor frecuencia relativa cuando se acercaba la celebración de su centenario; o sea, en 1682, 1782, 1882, 1982, con un interés creciente. Por ejemplo, en 1682 se editó en España la obra Nueva disposicion del Kalendario reformado, que mando obseruar la santidad de Gregorio XIII y computo eclesiástico (Fernández de Rozas, 1682). En francés, imagino que movido por un interés similar, se editó el libro titulado Histoire du calendrier romain... (Blondel, 1684), un volumen de cuatrocientas páginas con la explicación y la historia del calendario y del año litúrgico. El segundo centenario de esta reforma, el del siglo XVIII, reavivó el interés por el tema, difundiéndose explicaciones tanto manuscritas como impresas: la Ylustración de la Corrección Gregoriana (Zabaleta, 1784), el Cotejo del modo de intercalar los años bisiestos en el cómputo gregoriano (Anónimo, 1781), el Compendio individual, breve instrucción, y llave maestra, para que el inteligente computista perciba con mas claridad el contenido de los dos tratados... (Hualde, 1766), El tiempo y la cuenta acreditan la verdad (Hualde, 1782), etc.

Interesa destacar que la ciencia española estuvo al nivel de la europea en la cuestión de la reforma del calendario, pero no parece que se produjera la suficiente interrelación entre el alto nivel mostrado por varios intelectuales españoles en este conocimiento y el de otros campos del saber coetáneos. Para explicar lo que con ello deseo expresar propongo analizar el término tiempo según su definición. El primer diccionario conocido de nuestro idioma, El Tesoro de la lengua castellana o española de Sebastián de Covarrubias Orozco (Madrid, 1611), define la palabra tiempo por aproximación, con escasísima precisión según era normal en la época, como:

Tener tiempo, tener lugar. Llegar a tiempo, llegar a sazón. Andar con el tiempo, acomodarse. A un tiempo, juntamente y en una sazón. Dar tiempo al tiempo, dar lugar. En música, en el juego de la esgrima y en el de la pelota, usan deste término tiempo. Hazer buen tiempo o mal tiempo.

O sea, el tiempo como duración o como pronóstico meteorológico. Una definición ciertamente pobre si la comparamos con la precisión y la finura de los cálculos astronómicos contemporáneos a Sebastián Covarrubias. Se le achaca la culpa de esta involución al cierre ideológico practicado por Felipe II entre 1558 y 1559 por temor al contagio herético, aunque veremos después que Goodman no cree que el presunto cierre lo fuera tanto (Goodman, 1999, p. 95).

¿Esta involución terminológica y científica de los diccionarios ocurrió sólo en España? En realidad no, porque curiosamente, con el paso de los años, lo que ha ido haciéndose patente es la dificultad creciente de definir la palabra tiempo. Muchos siglos atrás Platón afirmaba que el tiempo era la imagen móvil de la eternidad que no pasa; Aristóteles dijo que era la medida del movimiento, según el antes y el después...; definiciones mucho más precisas que las de este diccionario de la lengua castellana que se publicaba veintiún siglos después. En cambio, Pascal (1623-1662) decía que era uno de esos vocablos fundamentales que sería imposible y vano definir. Etienne Klein (Klein 2005, pp. 28 y 29) ha repasado muchas de las definiciones dadas en distintas épocas y ha llegado a la conclusión de que, en realidad, son un encadenamiento de metáforas y que, más que definiciones, lo que estos intelectuales expresan son imágenes o tautologías que presuponen (no definen) la idea del tiempo[9].

Un peldaño decisivo para la matización de su definición ocurrió en el siglo XVII, en el momento en el que se consideró el tiempo como una variable. En este sentido, Klein explica en el libro citado que el descubrimiento de la ley de la caída de los cuerpos representó el verdadero arranque de la física moderna. Existía una duda sobre cuándo hizo Galileo dicho descubrimiento[10], pues no figuraba en su obra Sobre el movimiento (1590) y sí en cambio, perfectamente desarrollada, en el Diálogo sobre los dos máximos sistemas del mundo, ptolemaico y copernicano (1632), habiéndose descubierto en 2002, por parte de unos físicos del Instituto de Física Nuclear de Florencia, que las trazas de la tinta de Galileo en este texto son del año 1604. Gracias a este descubrimiento de Galileo, según Klein (Klein, 2005, pp. 15-16), la física le abrió las puertas al tiempo, y llegó a trastocar la representación que los seres humanos se hacían de él. Hasta entonces, el tiempo sólo era tenido en cuenta en relación con las cosas cotidianas; era como un medio para orientarse en el universo social y un modo de regulación de la existencia. Galileo demostraba que, tomando el tiempo como variable (en lugar de considerarlo como espacio recorrido), la velocidad era proporcional a la duración de la caída de un objeto, e independiente de la masa o de la naturaleza del sólido. Este descubrimiento destronaba la teoría de Aristóteles defensora de que cuanto mayor fuera la masa de un cuerpo, mayor sería su velocidad de caída. Ello permitió la primera formulación matemática del tiempo que desarrollaría más aún Newton, y que arrumbó el esquema filosófico dominante hasta ese momento. El tiempo se había convertido en una variable matemática, llegando después a ser considerado como una magnitud absoluta, o sea, como un escalar (porque carece de dirección) cuya medida era presuntamente idéntica para todos los observadores (tiempo absoluto). Otras revoluciones han seguido modelando durante el siglo XX esta concepción del tiempo: la relatividad restringida (Einstein), la física cuántica, la relatividad general, el descubrimiento de la interacción nuclear fuerte, de la antimateria, de la expansión del universo... Y ni aún hoy podríamos decir de qué naturaleza está hecho el tiempo y se juega a lanzar hipótesis, como las de la discontinuidad o la pluralidad del tiempo ¿Forma parte del mundo o lo contiene? De momento, el tiempo matemático de los físicos —el único verdadero según ellos— no tiene mucho que ver con la idea que acerca del mismo nos hacemos el común de los mortales.

Volviendo al tema de las definiciones tenemos que reconocer que el proceso de matización terminológica y semántica sufrió una importante e incomprensible involución en España en la Edad Moderna. A pesar de que desde la época del Renacimiento aquí se vivieron en primera persona el desarrollo de la economía mundo, los progresos de los sistemas de medición necesarios por ejemplo para fijar la raya de Tordesillas, el debate científico acerca de la propia reforma del calendario: cuestiones que exigieron y permitieron una mayor precisión —lo que debería haberse traducido en una evolución del concepto y en su definición más ajustada—; sin embargo, en el año 1737, un siglo y cuarto más tarde, el Diccionario de la lengua castellana, publicado por la Real Academia Española, lo expresaba textualmente como:

La duración sucesiva de las cosas, desde el más imperceptible instante, hasta la hora, día, mes, año y siglo; gobernada y medida por las revoluciones del primer móbil, y el movimiento de los Astros.

Obsérvese cómo esta alusión al primer móvil corrobora la continuidad de la que hablo: la persistente influencia del sistema aristotélico-ptolemaico en un sector de la intelectualidad dieciochesca dentro de nuestro territorio[11]. A pesar de que hacía ya ciento cuarenta y tres años que en Europa se conocía con precisión absoluta cómo se movían los astros (Kepler había publicado sus leyes en Mysterium Cosmographicum, en 1594) y de que hacía cincuenta años que se sabía por qué se movían (Newton expuso su teoría de la gravitación universal en Philosophiae naturalis principia matemática, editada tras mucho pensarlo, en 1687), los esclarecidos académicos de la lengua española seguían pegados al más rancio faldón de la ortodoxia tridentina, enunciando una definición de la palabra tiempo en parte completamente trasnochada: en función del primer móvil. Bien es verdad que, tras ella, los mismos académicos añadieron otras quince acepciones relativas al paso de las estaciones, la edad de las personas, la coyuntura de hacer algo, o sus significados en la música, la destreza en el uso de la espada, etc., que son ejemplo de la revolución que en este caso necesariamente tuvo que representar la generalización del valor social y objetivo de la medida del tiempo.

Fue en el tercer centenario del calendario gregoriano, en el siglo XIX, cuando comenzó el verdadero boom historiográfico sobre la historia del tiempo y de esta reforma del calendario. Ferrari publicó un discurso sobre el tema, titulado La riforma gregoriana del calendario… (Ferrari, 1883); Fritsche sacó a la luz un libro sobre cronología (Fritsche, 1886) y lo mismo hicieron Corral en España (Breve tratado del calendario ó computo eclesiástico, Corral, 1881) y Arrubia en Cuba (Arrubia, 1888). Asimismo constatamos que en aquella época también suscitaron interés otras formas de medir el tiempo y se editaron explicaciones sobre el calendario musulmán (Laredo, 1887) y el maya (Molera, 1883), de forma paralela a como lo hizo la presunta influencia del calendario en facetas de la vida alejadas de los estudios cronológicos o religiosos (Anónimo, Flora…; Anónimo, 1881; Lebeuf, 1882).

A partir de ese momento, y especialmente en torno a la celebración del tercer centenario de la publicación de la reforma gregoriana del calendario, este proceso histórico y los modelos de medir el tiempo atrajeron una buena parte de la atención de los historiadores de la ciencia y de la Iglesia, y se dieron pasos de gigante en el conocimiento del tema y en el estudio riguroso del mismo. Entre los investigadores que se dedicaron entonces a estudiar la reforma tres pueden considerarse hoy imprescindibles para su conocimiento: Ferdinand Kaltenbrunner, Joseph Schmid y Demetrio Marzi. Kaltenbrunner (1851-1902) fue catedrático de ciencias históricas en Innsbruck y realizó una ingente y fructífera labor de estudio de los documentos originales. Con estos materiales publicó tres trabajos «Die Vorgeschichte der Gregorianischen Kalenderreform» (Kaltenbrunner, 1876), «Die polemik über die Gregorianische Kalenderreform» (Kaltenbrunner, 1877) y «Beiträge zur Geschichte der Gregorianischen Kalenderreform. I Die Commission unter Gregor XIII nach Handschriften der Vaticanischen Bibliotek» (Kaltenbrunner, 1880). Estos tres artículos aportan, por primera vez, una información precisa de la historia de la reforma gregoriana, de la polémica que desencadenó y del análisis de la documentación vaticana. Sin embargo, muy poco nos dicen del informe salmantino, salvo reconocer el autor que no lo consultó en el Vaticano por encontrarse en mal estado de conservación, circunstancia que explica por qué sólo se refiere a él de pasada. Su esfuerzo fue considerable y sus resultados brillantes —aunque algunos después le criticaran varias ausencias (por ejemplo Marzi)—, ya que en pocas palabras resumió lo esencial del problema.

Inmediatamente después Schmid publicó igualmente en otras tres partes un nuevo estudio histórico de la reforma gregoriana: en «Zur Geschichte der Gregorianischen Kalenderreform» (Schmid, 1882, dos partes, y 1884, tercera parte). Este mismo investigador trabajó con posterioridad la cuestión de la Pascua en el concilio de Nicea («Die Osterfrage auf dem ersten allgemeinen Konzil von Nicäa», Schmid, 1905), tema que puede considerarse el origen del problema del calendario. Schmid citó el informe salmantino del año 1578 y realizó un resumen de uno de sus apartados, siendo el primer historiador que se hacía eco del documento; pero no dijo nada del de 1515. Tras los artículos de Kaltenbrunner y Schmid se pudo conocer con precisión el quién, el cuándo y el cómo de la reforma de 1582, que antes de estos estudios se ignoraban. Finalmente, otros esfuerzos vinieron a completar esta línea de trabajo, como el de Stiewe (Stiewe, 1880).

Para el tema de la reforma gregoriana del calendario, estas investigaciones citadas fueron muy importantes. Sin embargo, puesto que Salamanca envió uno de sus informes sobre la reforma al V concilio de Letrán, en nuestro caso son también de gran ayuda las publicaciones de Marzi sobre La questione della riforma del Calendario nel Quinto Concilio Lateranense (1512-1517) (Marzi, 1896) y el «Nuovi studii e ricerche intorno alla questione del Calendario durante i secoli XV e XVI» (Marzi, 1906). En ellas se explican los antecedentes más claros de la reforma, como lo fueron las aportaciones científicas de Regiomontano (Johan Müller), Antonio Dolciati, Giovanni Maier, Johannes Stöffler, Giovanni Tolosani, Basilio Lapi y, muy especialmente, la de Pablo de Middleburg, de quien Marzi hace un estudio pormenorizado en el apéndice documental de su libro. Esta obra recoge toda la documentación y, entre ella el compendio enviado desde el concilio de Letrán a los eclesiásticos y rectores de las más importantes universidades europeas para su evaluación y comentario (Marzi, 1896, pp. 191-195). Este texto es muy importante en nuestra investigación porque, aunque no se haya conservado rastro de él en Salamanca, es uno de los dos que recibió la Universidad salmantina en ese momento y a los que respondió con el informe de 1515 que aquí presentamos. Yo he encontrado una copia de este compendio, impresa en la época, que parece fue comprada por Hernando Colón pues tiene incluso una anotación manuscrita suya que dice: Costo vn quatrin en Roma por Julio de 1516 (fig. 23)[12]. Sin embargo, de forma que no acierto a explicar, Marzi no cita este informe salmantino entre los evaluados en este concilio.

¿Por qué Marzi no recoge el informe de Salamanca de 1515 entre los recibidos en el concilio? No cabe ninguna duda de que fue enviado a Roma, al concilio, porque así lo expresa con claridad el otro informe, el de 1578. Es posible que a Marzi le pasara lo mismo que a Kaltenbrunner, que dijo que no lo había estudiado por encontrarse en mal estado de conservación; Kaltenbrunner, pues, lo cita, aunque no lo estudie, pero Marzi ni siquiera lo nombra; simplemente no lo ha conocido.

Poco tiempo después de que Kaltenbrunner (en 1876 y 1867), Schmid (entre 1882 y 1884) y Marzi (1896), estudiaran con profundidad la documentación que habían encontrado sobre la reforma del calendario gregoriano, y de que Kaltenbrunner y Schmid citaran el informe salmantino de 1578, algunos investigadores españoles se ocuparon de esta aportación de la Universidad de Salamanca a la reforma del calendario eclesiástico. Los pioneros fueron Picatoste (1891, pp. 329-330), Fernández Vallín (1893, p. 65 ss. y 220-224) y De Bustos y Miguel (1898). Ninguno de ellos se hizo eco de las aportaciones foráneas. Picatoste, con sus Apuntes para una biblioteca científica española del siglo XVI, respondía al entusiasmo patriótico que produjo el discurso de ingreso de José Echegaray en la Academia de Ciencias, donde denostaba la tradición científica española. Su interés por desmentir tales afirmaciones le llevó a hacer una recogida de datos concienzuda sobre la ciencia y los científicos españoles de ese tiempo y este libro fue premiado por la Biblioteca Nacional de Madrid, por reunir en él los datos bio-bibliográficos de los científicos españoles del siglo XVI, recordando que hasta ese momento la hegemonía de la ciencia española fue indiscutible en geografía, cosmografía y navegación. Picatoste, en la referencia que ofrece sobre Diego de Vera, el representante de la comisión universitaria salmantina de 1578 para la reforma del calendario, proporciona un resumen bastante exacto de las propuestas concretas del informe salmantino de ese año, mientras que del de 1515 —el que es científicamente más profundo e interesante— se limita a decir que la Universidad no dio un informe completamente explícito (Picatoste, 1891, pp. 329-330), lo cual es estrictamente falso. Esto sugiere que Picatoste leyó personalmente el informe más tardío, pero no el primitivo, siempre que no tomara de alguna otra fuente desconocida para mí sus observaciones.

Este mismo entusiasmo de exaltación del nacionalismo llevó al catedrático de matemáticas de instituto en Valladolid y Madrid, Fernández Vallín, a publicar una transcripción del informe de 1578, en su obra Cultura científica de España en el siglo XVI (Fernández Vallín, 1893, pp. 220-222). Este autor resaltaba en este texto que su publicación era la primera que se realizaba de este informe (Fernández Vallín, 1893, p. 223), cosa que parece rigurosamente cierta; pero no es menos verdad que tal publicación es muy imperfecta y que su lectura resulta poco menos que ininteligible, de manera que casi habría que decir que, a efectos prácticos, dicho informe ha permanecido inédito hasta el día de hoy. Fernández Vallín era un buen conocedor del tema astronómico, como lo demostró en sus trabajos Geografía Matemática o elementos de Cosmografía; de hecho, su Cultura científica de España en el siglo XVI constituyó el contenido de su discurso de ingreso en la Academia de Ciencias Exactas, Físicas y Naturales de Madrid, de la que fue académico correspondiente el 17 de marzo de 1876 y académico numerario en diciembre de 1880; pero parece que no sabía suficiente paleografía y latín. Estas carencias le llevaron a cometer errores de transcripción que hoy producen hilaridad y que me permitan afirmar que no entendió nada del informe salmantino que publicó. Por ejemplo, donde el manuscrito 97 de la BGH dice el año de 1515, él transcribe el año de Isis (p. 222 y lo repite en p. 223); donde el documento dice ab hinc 1623, él transcribe ab hinc ibz3 (sic) (p. 221); donde el documento dice annis 134 ad mensis… él transcribe annis 139 ad mentis… (p. 222); donde se lee a nuestro (en abreviatura), él transcribe anlo; y un sinnúmero de errores de transcripción latina.

De este mismo problema adolece la obra del catedrático de física del globo de la Universidad de Salamanca don José de Bustos y Miguel (Bustos y Miguel, 1898), que trató el tema de estos informes en su discurso de apertura del curso académico 1898 a 1899 en esta Universidad y en él manifestó su intención de publicar una traducción castellana de ambos informes, tanto el de 1515 como el de 1578, pero que renunció a ello, según dice, a causa de ser muy extensos. Tanto Fernández Vallín como Bustos tenían conocimientos sobrados para haber elaborado un excelente estudio astronómico de esta documentación, pero yo opino que no entendieron los documentos, por haber fallado la transcripción y la traducción que hicieron.

Por lo que se refiere a la documentación complementaria —las cartas al papa y al rey y los datos de los libros de claustros universitarios—, la publicó en parte el P. Luis G. Alonso Getino, O.P. (Alonso Getino, 1907, pp. 281-303) a principios del presente siglo, también con no pocas deficiencias de transcripción. Parece que Alonso Getino también tropezó más de una vez en escollos de carácter paleográfico, tanto en lo que transcribió, como en lo que silenció. Así, por ejemplo, la omisión de una carta del Nuncio a la Universidad por estar en italiano antiguo y no ofrecer cosa de particular (Alonso Getino, 1907, p. 293) parece obedecer más bien a otras razones que a las aducidas.

En conclusión diré que la historiografía sobre la historia del calendario del siglo XIX, fue mayoritariamente de origen alemán e italiano y rompió con la tradición computacional como único medio de acercamiento a este asunto. Para el tema de la participación salmantina en estas reformas, en esa historiografía aparece citada la documentación pertinente, pero ni se entendió ni se analizó su contenido.

Posteriormente, durante el siglo XX, la cuestión del tiempo ha evolucionado notablemente al socaire del progreso de la ciencia histórica en su conjunto. En este sentido y según mi opinión, de forma simultánea a la revolución historiográfica del siglo XX se han desarrollado dos vías historiográficas de investigación y comentario sobre esta temática:

• La historiografía contemporánea de carácter computista, basada en cuestiones matemáticas y astronómicas.
• La historiografía contemporánea de carácter socio-político, que descubrió la importancia del tiempo histórico y lo estudió como una variable más; que en principio no se dedicó al tema de la reforma del calendario, pero que comprendió el valor político, social, económico del tiempo histórico. Esta historiografía ha sido muy fructífera en los últimos treinta años constituyendo lo que podríamos denominar la historia social del tiempo.

1.2.1. La historiografía contemporánea de carácter computista. Siglos XX y XXI

Durante la última centuria y pico, los investigadores interesados por esta temática se han dedicado por una parte a explicar y por otra a criticar la reforma del calendario gregoriano.

Los que han tratado de explicar al gran público la actual forma de medir el tiempo han continuado la trayectoria historiográfica preexistente y, por eso, una buena parte de los estudios sobre la historia del calendario realizados desde principios del siglo XX han seguido teniendo un marcado carácter matemático-divulgativo. Muchos de los autores que se han dedicado a la cronología eran teólogos y les ha interesado la forma de medir el tiempo y su historia como curiosidad o como parte de su labor educativa o pastoral. Más que historiadores eran metrólogos que, en sus trabajos de cómputo a veces han incluido un capítulo de carácter historiográfico o histórico.

Entre ellos cabe citar los trabajos de Hagen («Die Gregorianische Kalenderreform», de 1914), Obrecht (Il calendario gregoriano, de 1925), Chauve Bertrand (La Question du calendrier, de 1929; La Question de Pâques et du calendrier, de 1937; y «Vers un calendrier nouveau», de 1940), y Gazeau («La réforme du calendrier», de 1962). Dentro de los estudios de estas características publicados en España, uno de los más completos es el de Pérez Millan (El calendario: su origen, evolución y reforma, 1956), que consigue una explicación clara, concisa y sintética del hecho. De interés son asimismo los de Catalá Poch («El Calendario Gregoriano», de 1987); un breve pero no menos brillante artículo de Ojeda Nieto sobre «La reforma gregoriana del calendario: algo más que una anécdota histórica» (de 1991), que introduce además la reflexión sobre las repercusiones económicas de la reforma; el de Joaquín Lledó (1999) sobre calendarios y medidas del tiempo; varios de Fernando Muñoz Box (especialmente el editado en 2003); y el de José Casals (2007) sobre la medida del tiempo. Varios de ellos, especialmente los primeros, aparte de la explicación computacional, recogieron alguna documentación novedosa junto a la información histórica ya tratada por Kaltenbrunner. Esta línea de trabajo ha sido y sigue siendo muy fructífera. Pretende explicar el problema astronómico de la reforma del calendario y sus repercusiones; y consigue su objetivo.

A caballo entre la cronología y lo que yo denominaría la historia social del tiempo, está la magna obra de Duhem (1914-1958) sobre el sistema del mundo, especialmente interesante en nuestro caso el tomo X, sobre La cosmologie du XVe siècle; écoles et universités au XVe siècle. También pertenece a este grupo el mejor trabajo sobre la reforma gregoriana y el último de los que la tratan en su conjunto; me refiero al que publicó el propio Vaticano en conmemoración del cuarto centenario de la puesta en vigor de la reforma gregoriana, y que coordinaron Coyne, Hoskin y Pedersen, bajo el título Gregorian Reform of the Calendar (Coyne, 1983). Actualmente hay un enlace en Internet a su contenido, en el servidor de Harvard. Me parece una obra difícilmente superable, tanto por la pluralidad de temas que contempla como por la profundidad del tratamiento de los mismos. En ella los contenidos se articulan en varias partes, con distintos capítulos por cada una de ellas, sobre los antecedentes históricos, los aspectos astronómicos, los principales personajes de la reforma, el decreto de 1582, la recepción de la reforma y los proyectos posteriores encaminados a una nueva reforma que aspira a un calendario universal. A través de todos ellos puede hacerse una excelente reconstrucción del problema desde el punto de vista histórico y computista. En este libro, salvo para el caso del antiguo profesor salmantino Pedro Chacón, que fue uno de los miembros de la comisión pontificia encargada de la reforma, la intervención de Salamanca queda absolutamente desdibujada.

Esta sub-línea de investigación computista, tuvo un nuevo e inusitado desarrollo como consecuencia del cambio de milenio, momento en que el tema adquirió relevancia mediática. De estas características son los textos de Manuel Fidela Velázquez (2002) y uno breve mío (Carabias Torres, 2000b) sobre los problemas de comienzo del milenio. Abundan en Internet los de esta temática. De hecho, desde la época del cambio de milenio, la red se ha erigido en un espacio privilegiado de edición o de difusión de este tipo de estudios; hay multitud de páginas web sobre el cómputo y el calendario de profesores o de instituciones científicas de cualquier nacionalidad y crece cada día el acceso a recursos anteriores digitalizados.

Un segundo grupo de obras de cómputo han pretendido la crítica de la reforma gregoriana y el enunciado de nuevas propuestas para una posible y futura reforma del calendario. Hemos visto arriba que estas alternativas resultaron habituales desde el mismo momento en que se hizo pública la reforma (año 1582) y cómo algunas de ellas fueron rebatidas por el mismo Clavio. La historia de este proceso llega hasta el presente. Estas obras suelen comenzar por resumir brevemente la cuestión histórica antes de extenderse en sus propuestas alternativas. Estos proyectos han sido estudiados por F. Russo[13] y entre ellos están desde el calendario humanista propuesto por Compte, donde cada uno de los meses y de los días conmemoraría un personaje histórico, hasta los de carácter matemático, de Corona Martínez, García Serrano, etc.[14].

Actualmente contamos hoy con buenas recopilaciones bibliográficas de este conjunto informativo. Tenemos, por ejemplo, una «Bibliography on the Computus and the Calculation of Easter Sunday»[15], que, aparte del cálculo de la fecha de la Pascua, pone a nuestro alcance una gran cantidad de textos contemporáneos, editados tanto en papel como en formato electrónico. Ofrece la ventaja añadida de indicar, en su caso, los lugares en los que la obra citada está accesible en Internet; abundando los trabajos en Gallica (Bibliothèque Nationale de France), jstor, The sao/nasa Astrophysics Data System, o Google Libros. Dentro de este sector informativo, también son muy útiles la Bibliografía histórica sobre la ciencia y la técnica en España, de textos publicados entre 1968 y 1973 y la Bibliographia physico-mathematica hispanica (1475-1900) (Navarro Brotons y otros, 1999b).

1.2.2. La historiografía contemporánea de carácter socio-político. La valoración del tiempo histórico en el siglo XX

La reflexión historiográfica sobre la historia del tiempo es relativamente reciente y ha sido puesta en valor por Teófilo Ruiz en un trabajo sobre la cronología y la nueva historia social (Ruiz, 2001).

A mí me parece que esta preocupación del historiador por el tiempo nace con la escuela francesa de los Annales y más concretamente cuando, en su segunda generación, con Braudel, se amplió el primitivo interés desde la historia económica hacia la historia cultural. Es bien conocido que esta escuela convocó inicialmente a un grupo de historiadores (L. Febvre, y M. Bloch —franceses—, H. Pirenne —belga—), geógrafos (A. Demangeon) y socólogos (L. Lévy-Bruhl) que inspiran los Annales d’histoire économique et sociale (llamados más tarde Annales. Economies, sociétés, civilisations, y, desde 1994, Annales. Histoire, Sciences Sociales)[16]. Esta primera generación contribuyó a forjar una nueva forma de historiar, analítica, de carácter socio-económico, que se preocupaba por la masa de la sociedad, contraria a la historia política o tradicional.

La elección del propio término annal (Annales) es ya un referente temporal que seguramente no fue elegido al azar. Frente al tiempo corto del acontecimiento, habitual en la historia tradicional, Braudel incorporó la idea de un tiempo absoluto, universal e idéntico para los hombres, curiosamente cincuenta años después de que Einstein publicara lo contrario: su convencimiento de la inexistencia de un tiempo único, afirmando su relación con el espacio, la posición y la velocidad. Quizá por ello últimamente Montserrat Galcerán ha matizado las diferencias entre el tiempo de la historia, el tiempo psicológico de la experiencia vivida y el tiempo de la física.

A pesar de que se le atribuye a Braudel el mérito de esta novedad y aunque sin duda este autor fue decisivo en la afirmación del tiempo como tema histórico, quizá el primer inspirador de esa idea fuera Gianbattista Vico (1668-1744) cuando distinguía el tiempo histórico, propio de las acciones humanas, del tiempo cartesiano, relacionado con el movimiento. Detrás de él e inmediatamente antes de Braudel, Lucienn Febvre (1878-1956), con La Terre et l’évolution humaine (Paris: La Renaissance du Livre, 1922) y Gaston Bachelard (1884-1962), con la obra La dialectique de la durée (Paris: P.U.F., 1950), habían discutido el alcance del tiempo histórico y del determinismo natural. Inspiradas en esta nueva forma de historiar, vendrían después otras, no siempre necesariamente de seguidores directos de Annales, en las que el tiempo era el objeto de estudio: Histoires du temps de Atali (1982), o Les fondements de la mesure du temps de Audoin y Guinot (1998).

Braudel reivindicaba la larga duración, lo que es una ingenuidad totalizadora —en palabras de García Cárcel— (El País, 30/11/1985). Abogaba por la idea de un tiempo absoluto, universal e idéntico para los hombres; el tiempo de la historia —decía— es social y no individual; un tiempo biológico, físico; era preciso, pues, realizar mediciones concretas y variables de las distintas duraciones de los fenómenos sociales, cuya coexistencia e imbricación constituía el nuevo tiempo de la historia. Defendía que la historia económica y social podía y debía investigar ciclos, coyunturas, estructuras...; el largo plazo de los economistas, los ritmos, la pluralización de los tiempos.

Esta teoría de los diversos tiempos es una revolución en el modo de concebir y percibir el tiempo histórico. Con Braudel la naturaleza (y el tiempo como parte de ella) se convertía en un agente activo de la historia; este autor incorporaba al quehacer del historiador una nueva faceta metodológica y epistemológica, que tendría un brillante porvenir en el estudio de los interciclos de Kondratieff, o en el nacimiento más recientemente de la geohistoria[17]. Donald Woster piensa que la era ecológica nació en 1942 con el lanzamiento del proyecto Manhattan que promovió, en 1945, la explosión de la primera bomba atómica en el desierto de Nuevo México; pero Camus[18] recuerda que la acción transformadora del hombre sobre la Tierra dura desde la Antigüedad; dice que, aunque en la teología cristiana la Tierra era solamente una estación de tránsito, el estudio de la naturaleza se incentivaba al ser concebido como una forma de conocer el plan de Dios sobre el mundo. En la Edad Moderna se observan importantes acciones de dominio del hombre sobre la naturaleza, en la desecación de tierras (polders en Holanda), control del curso de los ríos, etc. Cambios, que en el siglo XIX se empiezan a ver frecuentemente como no deseados, promoviéndose el estudio de la orografía, petrografía, paleontología, etc. Pero —también según Camús— sólo a partir de la segunda mitad del siglo XX, las investigaciones respecto de las relaciones hombre-naturaleza alcanzaron una importancia más nuclear y generalizada, especialmente desde la bomba atómica. Otros opinan que el verdadero iniciador de la geohistoria fue Utterström, en su artículo sobre el clima y la población[19]. Geohistoria emparentada directamente con la historia del tiempo.

Como consecuencia de estos cambios, hoy cualquier historiador con sentido común considera el tiempo (igual que la naturaleza) como una variable más de la realidad social, una variable fundamental, distinguiendo incluso una pluralidad de tiempos: tiempo geográfico, económico, político; tiempo natural, físico, social.... Según dijera después Pierre Chaunu, todo nuestro conocimiento y nuestro pensar organiza la totalidad del ser alrededor del eje orientado del tiempo[20]. En este sentido, la labor de Braudel en la ciencia historica fue equivalente a la de Galileo en la ciencia física, pues ambos demostraron que el tiempo es una variable, en este caso tanto del conocimiento de la historia como del de la física.

Esta forma de historiar ha llegado también hasta el presente con enorme fuerza y con una renovada voluntad de utilidad, y permite un diálogo entre pasado y presente en el que insistía mucho Le Goff en su texto Pensar la historia, cuando se preguntaba:

¿Qué relaciones tiene la historia con el tiempo, con la duración, se trate del tiempo natural y cíclico del clima y las estaciones o del tiempo vivido y naturalmente registrado por los individuos y sociedades? Por una parte, para domesticar al tiempo natural, las diferentes sociedades y culturas inventaron un instrumento fundamental, que también es un dato esencial de la historia: el calendario; por otra, hoy los historiadores se interesan cada vez más por las relaciones entre historia y memoria.[21]

El calendario y la memoria. Consciente o inconscientemente, todos los hombres percibimos el tiempo, aunque haya variado la forma de hacerlo (Whitrow, 1980). Hoy en día, todos los historiadores partimos en nuestro trabajo de los presupuestos del calendario y la memoria. Herederos de estas ideas son el conocido libro Las medidas y los hombres, de Kula (1980); el titulado La medida de la realidad, de Crosby (1988) —homónimo de otro—, que a mí me parece uno de los más sugerentes; varios de los trabajos de Gordon Moyer (1982a), que ha publicado mucho y bien sobre el calendario gregoriano; la obra de Dutka (1988) sobre los calendarios juliano y gregoriano; el texto de Herbert Artur Klein (1988) sobre la ciencia de la medida; el de Duncan (1998) sobre el calendario y los diez días desaparecidos; o el de Biémon (1999) sobre los ritmos de los tiempos.

Annales ha influido en la historiografía española de la Edad Moderna, desde la lectura que en nuestro territorio se hizo de la magna obra de Braudel y desde aquellos primeros encuentros fortuitos de algunos investigadores españoles con los franceses en el Archivo General de Simancas. Bien es verdad que en los años setenta algunos pretendieron desprenderse de esta influencia, por considerarla ya innecesaria, pero lo cierto es que Annales contribuyó notablemente al progreso de nuestro modernismo y fue un lenitivo para nuestra historiografía en los años sesenta[22]. Partiendo de la revolución epistemológica de la ciencia histórica que el valimiento de Annales permitió, según pienso, se han desarrollado dos líneas de investigación derivadas de la variable tiempo que llegan hasta nuestros días: por un lado la que tiene que ver con la historia social, que fue la más temprana, y por el otro lo que yo llamaría la historia socio-política de la ciencia.

1.2.2.1. El tiempo en la historia social

El trabajo historiográfico de los últimos veinte años ha permitido matizar los extremos y las características de la historia social. Quizá sea la revista de este mismo nombre, Historia Social, la que mejor haya recogido en español la senda de este debate. En su número 60, del año 2008, Ricardo García Cárcel publicaba una reflexión titulada «Veinte años de historia social de la España moderna» (pp. 91-112) y así lo manifestaba. Antes que él, Gonzalo Pasamar e Ignacio Peiró (en 1987), Baudilio Barreiro Mallón (en 1990), Santiago Castillo (coord. en 1990), Jesús María Usunáriz (en 1999), Araceli Otero Fernández (en 1996), Carlos Barros (la última vez en 2006), María Elena Hernández Sandoica (en 2004), Judith Prat Sedeño (en 2003) y otros habían reflexionado sobre las posibilidades de esta historia social en distintos ámbitos.

Obras como Ideología y mentalidades de Vovelle (1985) o los trabajos de Ariés y su grupo (como la Historia de la vida privada, reed. 2001), se convirtieron en iconos y modelos de los modernistas españoles y de los hispanistas. Como consecuencia de ello empezaron a editarse cientos de textos sobre la actitud y mentalidad de los españoles, en los que se tenía en cuenta el factor tiempo, como el de Bennassar sobre las actitudes y mentalidades de los españoles (1976); el coordinado por César González Mínguez titulado La otra historia: sociedad, cultura y mentalidades (1999); el interesante libro dirigido por Alcalá Zamora (1995) sobre la vida cotidiana en la España de Velázquez (en el que Bouza incluye un gran trabajo sobre el tiempo y la cultura del reloj); el de la historia de las mentalidades e Inquisición, de García Cárcel (1990); el estudio de la historia cultural de Carlos Serrano Lacarra (1996); el titulado Tiempo y el cambio social, una visión sindical del tiempo editada por Jesús Vicens (2004); el interesante estudio de Peter Burke sobre Formas de historia cultural (2006); la reflexión sobre las personas de su tiempo o la historia de las mentalidades, de Darina Martykánová (2007)... El elenco de autores y obras de los últimos treinta años ocuparía muchas páginas.

Gracias a este espectacular avance del conocimiento sobre la historia y su tiempo, desde hace estos treinta años es raro encontrar un libro de carácter general sobre historia moderna que no tenga un apartado, por pequeño que sea, dedicado al tiempo, y así lo hacen Braudel en Civilización material y capitalismo (Madrid, 1984), en la p. 9; Bennassar, en su manual de Historia Moderna (Madrid, 1980) lo incluye en las pp. 7-9; Hill, en De la Reforma a la revolución industrial (Barcelona, 1980), en la página 30; Wallerstein, en El moderno Sistema Mundial (Madrid, 1984), en la p. 91; Tenenti, en La formación del mundo moderno (Barcelona, 1985), en la p. 9; Koenigsberger, en El mundo Moderno (Bardelona, 1991), en las páginas 1-3; Castellán, en «Dos modelos dialécticos: Medievalismo y Modernidad» (en Anales de Historia Antigua y Medieval, 1972), en las pp. 38-39; Berman, en Todo lo sólido se desvanece en el aire. La experiencia de la modernidad (Madrid, 1988), en las pp. 1-27…

A través de este interés por incluir la variable tiempo en los estudios históricos hemos podido saber que, a comienzos de la Edad Moderna el tiempo (igual que el espacio) era un factor sobreentendido y sobrepuesto a la vida cotidiana de los hombres. Los investigadores de la historia de las mentalidades han matizado las costumbres asociadas a cada período, espacio geográfico o festividad concreta, tanto en el ámbito público como en el privado. Es ésta la única línea historiográfica que no pretende comprender grandes procesos sino documentar hechos concretos; los historiadores que se interesan por ella se han afanado en estudiar los usos, la medida y la percepción del tiempo, las costumbres relacionadas con el trabajo (ritmos laborales, diferencias entre campo y ciudad, peculiaridades de género), el ocio (días feriados, espacios y formas de sociabilidad, diversiones en función de la edad) o las vivencias (hábitat, usos higiénicos, usos amorosos, hábitos, círculos de comunicación, costumbres). En el período que aquí estudiamos tendrá también gran importancia la modernización y la difusión del reloj y la reforma del calendario. En este sentido la historiografía nos informó de que el tiempo adquiría un significado propio en escasas ocasiones, y siempre aparecía en función del ciclo vital, la condición, el oficio o la religión de los hombres; después abundaremos en ello.

Indiscutiblemente no todos estos descubrimientos derivaron de investigaciones históricas ligadas a la Escuela de los Annales, pero esta escuela imprimió un talante y unos temas que fueron seguidos de forma fructífera por investigadores de todo el mundo, entre ellos los españoles. En los albores de esta influencia en España, José Luis Peset publicó un artículo titulado «Historia de la ciencia e historia de la cultura»[23] donde abundaba en la idea de que la historia de la ciencia ha estado en los frentes de los combates por la historia (recordando el libro homónimo de Lucienne Febvre), que asistieron al nacimiendo de la historia contemporánea de la ciencia. En él reclamaba la unión de lo que consideraba entonces divorciada pareja de las letras y las ciencias. Pues bien su deseo es hoy una realidad incuestionable en lo que se refiere a la historia del tiempo y se tratan conjuntamente antiguos temas de letras y ciencias, gracias al impulso de Annales.

¿Por qué la Escuela de los Annales cambió el sentido de la investigación historiográfica sobre el tiempo? Quizá porque Braudel escribió tras la segunda Guerra Mundial, después de una situación límite que había roto la cotidianidad y que agudizó el modo de percibir la temporalidad en Europa. Aguirre[24] opina que el período de entreguerras constituyó la época de cuestionamiento general de las formas de la conciencia y de la racionalidad modernas; una profunda revisión y crítica de la idea de progreso y, por tanto, de la moderna idea burguesa del tiempo que se encuentra vinculada a ella.

Como consecuencia de esta mutación epistemológica llevada a cabo desde Francia entre 1950 y 1970, hoy se considera que la historia es la manifestación de un proceso temporal. Ser temporal —dice Aróstegui— es la dimensión que convierte irreversible e inexcusablemente lo social en histórico[25]. La temporalidad constituye la dimensión cardinal de la historia, tanto porque el ser humano lo es en el tiempo, como porque una concreción temporal resulta exigencia inexcusable en los relatos. En el tiempo se construye la investigación y ésta refiere, ordena y jerarquiza tiempos. Pero, tanto la dirección del curso del tiempo como los límites y el ámbito cronológicos en los que se inscriben los hechos, parten o se refieren a la distribución de los hombres y de los signos de la civilización en un espacio, en el entorno geográfico y económico. De lo anterior se desprende que tiempo y espacio son las dos coordenadas elementales y básicas para la captación y comprensión de toda la estructura social.

El carácter material y objetivo tanto del espacio como del tiempo ha encontrado nuevos apoyos en la teoría de la relatividad: sucesos que observados desde un sistema determinado pueden parecer simultáneos, resultan no simultáneos si se miran desde otro. Por tanto, el espacio y el tiempo adquieren distintas dimensiones: esto es, cambian o transcurren con más o menos profundidad y con diversos grados de rapidez de acuerdo con valoraciones e interpretaciones no históricas. La velocidad del tiempo y las dimensiones del espacio dependen de los criterios que se utilicen para medir la duración de un proceso o la distancia espacial entre acontecimientos. En este sentido decía también Aróstegui que el tiempo es una realidad mensurable, pero cuya mensurabilidad, con escala múltiple, no podemos todavía aquilatar con rigor. En cuanto constitutivo de la estructura social, el tiempo es plural, encontrando:

1. El tiempo físico, considerado por Newton como un tiempo abstracto, absoluto, verdadero y matemático, que corría uniforme, sin referencia a nada externo, vacío de contenido vital; tiempo que cambió tras las aportaciones a la física de la teoría de la relatividad, para quedar corregido igualmente a cotas de relatividad y de dependencia.

2. El tiempo astronómico, casi natural, puesto que hace referencia al lugar que la Tierra ocupa respecto de su propio eje y en su vuelta alrededor del Sol, es el que regula en muchos aspectos la vida de las sociedades.

3. La presencia del reloj y el ritmo abstracto de las horas y minutos permitió captar el tiempo social.

4. El tiempo histórico, a veces interpretado como tiempo social, puesto que su curso depende de la velocidad histórica; es decir, de la densidad de eventos contenidos en el mismo tiempo natural.

Tiempos geográficos, tiempos económicos, tiempos políticos...: esta teoría de los diversos tiempos representa una revolución espiritual en el modo de concebir y percibir la realidad histórica.

La concepción del tiempo histórico se ha complicado con los avances de la física, y los más modernos métodos históricos no pueden quedar satisfechos o atendidos con una imagen puntual del mismo (el tiempo del reloj), homogeneizada y estandarizada a nivel mundial sólo hace un siglo, en la Conferencia de Washington de 1884, que se convocó para tratar de fijar un meridiano oficial, imprescindible para la fijación de la hora y la fecha. En ella se estableció Greenwich como meridiano cero internacional, lo que fue siendo aceptado por todos los países. Fue la forma más adecuada de poner orden en los complejos sistemas de transporte y comunicaciones internacionales.

El tiempo hoy, de acuerdo con la concepción de Einstein, depende básicamente del sistema en el que se opere: de forma que los intervalos del mismo deben ser medidos no de forma universal, sino conforme al sistema concreto del que se parta. Porque de la misma manera que el tiempo depende de la velocidad, la distancia temporal entre dos eventos resulta igualmente relativa si los ritmos con que pasa así lo imponen[26]. Los cambios se producen más rápidamente en unos niveles de la actividad social que en otros. Los estados sociales muestran más movilidad en algunos elementos que en otros. La solución braudeliana supone aceptar la existencia de diversos niveles del tiempo, medidos en la misma escala, la escala cronológica.

La historia es la conciencia de lo que es único y particular, y de las diferencias entre particularidades. Estas diferencias pueden situarse en el tiempo, pero también fuera del tiempo, en la conciencia que una colectividad toma de sí misma, en relación, no con otra época de su devenir, sino con la colectividad vecina, y constituye lo que Ariès llama historia particular[27], la historia de las herencias. En un mundo fundado sobre la uniformidad de las técnicas y de las funciones, la historia ha sido concebida como la ciencia de las diferencias.

Los maestros tenemos que contribuir con nuestra actividad docente e investigadora a explicar los cambios mentales que estas afirmaciones muestran. Debemos mostrar al alumno que la duración de una transformación importante en la época del Renacimiento era considerablemente mayor que la de la vida humana. El ejemplo histórico más patente es quizá el cambio operado entre los siglos XV y XVI. En este momento se produjo el paso de una serie de espacios humanos compartimentados, sin más mensajes que los propios, al esbozo del universo común: Desde el punto de vista astronómico se pasó del cosmos cerrado al Universo infinito en palabras de Koyré; desde el punto de vista económico, de una economía autárquica al nacimiento de la economía-mundo, en expresión de Wallerstein. Pero en la actualidad, la duración de un cambio es considerablemente menor que la de una vida humana y, en consecuencia, la enseñanza debería preparar a los individuos para afrontar la novedad de estas condiciones, ya que la aceleración universal de los acontecimientos provoca intranquilidad. Por eso decía yo antes que uno de los cometidos del historiador actual era el ser agente del tiempo en el presente; el encargado de conservar la memoria colectiva e individualizada del grupo, para que —como dijera León Felipe— cada cual lo vea y para que no se olvide.

En conclusión cabe subrayar que fue la historiografía francesa de entreguerras la que revalorizó la concepción temporal de la historia, dándole un nuevo sentido; y que esta revalorización se llevó a cabo primeramente en investigaciones sobre la Edad Moderna: porque el interés de esta escuela se centraba en el análisis de series de datos cuantificables (historia serial), y la documentación histórica conservada generalmente sólo permitía la formación de esas series a partir de los tiempos modernos. Los seguidores de Annales parece que lo estudiaron casi todo, menos el tema del calendario. En este campo, vuelvo a recordar el enorme hueco historiográfico que ha quedado abierto con este tema a los historiadores actuales. Un vacío que, vuelvo a repetir, ni siquiera habían detectado.

1.2.2.2. El tiempo en la historia socio-política de la ciencia

Aunque es difícil marcar los límites exactos de esta parcela historiográfica, cabe señalar la importancia que han tenido bastantes trabajos que, herederos lejanos del cómputo y hermanos de los de historia de la ciencia, conformaron lo que yo denomino una historia social de la ciencia. Entre ellos, por su relación directa con nuestro objetivo de trabajo, creo se debe recordar la colosal aportación de dos grupos de investigación españoles: el relacionado con el recientemente fallecido José María López Piñero (López Piñero 1976, 1979, 1981-1986, 1993, 1998, 1999a, 1999b, 2001, 2002, 2006), dedicado sobre todo a historia de la ciencia; entre sus colaboradores no puede olvidarse a Víctor Navarro (Navarro, 1974, 1992, 1995, 1999, 2002, 2006, 2007), E. Portela (López Piñero-Navarro-Portela, 1976), V. Salabert (Salabert, 1999, Navarro-Salabert, 1999), etc.; y el grupo de la Universidad de Valladolid, más volcado hacia la historia de la técnica, con Isabel Vicente (Vicente Maroto, 1988, 1993a, 1993b, 2006; Vicente Maroto-Esteban Piñeiro 1991), Nicolás García Tapia (con una excelente producción sobre historia de la técnica que aquí no hemos necesitado citar) o Mariano Esteban Piñeiro (Esteban Piñeiro, 1991, 1992, 1995, 2000, 2002, 2007). También han sido destacables en este campo algunos libros, como el de Alberto Elena (Elena, 1985) que en su día fue una novedad sobre el copernicanismo en España; los de José Luis y Mariano Peset como aglutinantes de otro grupo de investigadores de peso (Elena Hernández Sandoica, Amparo Felipo, Marc Baldó…), relacionados tanto con la historia de la ciencia (Peset Reig, 2002) como con la historia de las universidades (de la que enseguida hablaremos); y otros investigadores, como Pardo Tomás (1991), Muñoz Calvo (1977)... La producción científica de esta línea de investigación es quizá la que mejor se conoce, gracias precisamente a varios textos firmados por López Piñero (1996, 2001) y Navarro Brotóns (Navarro-Salabert-Roselló- Darás, 1999), que ya hemos citado.

Más cercanos aún a nuestro tema están las siguientes obras: el libro colectivo coordinado por Martínez Ruiz (1999) sobre la ciencia en la época de Felipe II, citado, el artículo de Galende Díaz (1999) sobre la reforma del calendario en la época de Felipe II, el de Ruiz Morales (1990) sobre la pragmática astronómica filipina que impuso el calendario gregoriano en España y sus territorios, y el también colectivo de María Teresa Santamaría (2008), acerca de la transmisión de la ciencia desde la Antigüedad al Renacimiento.

Gracias a todos ellos ha cambiado radicalmente el conocimiento de la actividad científica española en la época del Renacimiento. Como dijimos, se ha superado definitivamente la polémica de la ciencia española, reconociendo el apriorismo de sus planteamientos, y se han multiplicado los profesionales afanados en este tipo de investigaciones, que han logrado invalidar la negra imagen de látigo, hierro, sangre y rezos (López Piñero, 1999a, p. 17) de la España del Quinientos. Como consecuencia de esta confluencia de afanes, se han delimitado las áreas de actividad científica, cosa que no ha sido tan fácil porque previamente hubo que delimitar el contenido de lo científico en aquella época; y se ha comprobado la falta de institucionalización de esta actividad científica (salvo en el caso de la medicina, que cristalizó en una profesión).

Como la parte principal de la documentación que he utilizado para analizar la participación de Salamanca en la reforma del calendario fue realizada en esta universidad, es obligado también repasar la producción historiográfica sobre historia de las universidades. Con respecto a ella, debo recordar que en los últimos veinte años se ha producido un verdadero despertar en la investigación. Nuevos métodos, nuevos temas e investigadores que nos vamos haciendo viejos trabajándolo dimos un gran impulso a la temática y hemos forjado el nacimiento de centros específicos para su estudio. El resultado fue la creación de distintas instituciones donde se canalizó la energía de este colectivo en distintos lugares del mundo. Así contamos hoy con: el CISUI (Centro Interuniversitario per la Storia delle Università Italiane), el CIS (International Centre of the History of Universities and Science de la Universidad de Bolonia, Italia), el IISUE (Instituto de Investigaciones sobre la Universidad y la Educación, en México), el CIREMIA (Centre International de Recherche sur l’Éducation et la Culture dans le Monde Ibérique et Ibéro-Americain, de la Universidad de Tours), el HISULA (Historia de la Universidad Latinoamericana, de Colombia), o el GHUR (grupo de Investigación Historia de la Universidad del Rosario, también de Colombia).

El reflejo de esa tendencia se ha visto también materializado en España, en tres centros de gran importancia al respecto: el CESHU: Centro de Estudios sobre Historia de las Universidades de la Universidad de Valencia; el Instituto Figuerola (antiguo Antonio Nebrija en la Universidad Carlos III de Madrid y el CEHU: Centro de Historia Universitaria Alfonso IX de la Universidad de Salamanca. Recientemente el antiguo Instituto Antonio Nebrija), ha dado lugar al Programa de Historia de las Universidades de la Universidad Carlos III de Madrid, coordinado por Manuel Martínez Neira y al que pertenece mi primer director de este trabajo, el Dr. Ramon Aznar i Garcia. El segundo de mis directores, el Dr. Cirilo Flórez Miguel, pertenece al CEHU: Centro de Historia Universitaria Alfonso IX, grupo coordinado por el Dr. Luis E. Rodríguez-San Pedro Bezares. Luego, aunque no fuera más que por la vía de la dirección, el estudio que presento es netamente un estudio de historia de las universidades. A pesar de no ser un centro específico de historia de las universidades, cabe citar en este grupo también al CILUS: Centro de Investigaciones Científicas de la Universidad de Salamanca, por su labor en la investigación de manuscritos e impresos científicos de la época del Renacimiento. Entre los trabajos de este centro y en lo relativo a nuestra temática, destacan los textos de M. J. Mancho Duque (2004, 2005, 2006, 2010), sobre el léxico de la ciencia española renacentista; los de José Luis Herrero (2003), editando la Reprovación de hechicerías de Ciruelo; uno de Gregorio Hinojo (2005), sobre Nebrija y el desarrollo del léxico científico en latín y, muy especialmente, su DICTER. Diccionario de la ciencia y de la técnica del Renacimiento [M. J. Mancho Duque (dir.), <http://dicter.eusal.es>].

Partiendo de que la historia de los saberes depende de unas estructuras de poder, Mariano Peset presentó hace años una reflexión bajo el título «Historia de las universidades, historia de las ciencias»[28], que lanzaba ideas y proponía la metodología para estudios del futuro; futuro que ha llegado y se ha materializado en multitud de investigaciones e incluso de análisis historiográficos, como los de Luis E. Rodríguez-San Pedro para la Universidad de Salamanca (Rodríguez-San Pedro, 2009, pp. 329-388), Javier García Martín para las universidades italianas (Rodríguez-San Pedro, 2009, pp. 435-468), Fernando Taveira da Fonseca para las universidades portuguesas (Rodríguez-San Pedro, 2009, pp. 469-500), Águeda Rodríguez Cruz para las universidades hispánicas[29], igual que Clara Inés Ramírez y Armando Pavón (Rodríguez-San Pedro, 2009, pp. 501-533), Joaquim Prats para la Universidad de Cervera[30], Adela Mora para la universidad chilena[31], Adriana Álvarez para la Universidad de San Carlos de Guatemala[32], y Jean-Louis Guereña para la enseñanza superior en Francia[33]. Tenemos asimismo información historiográfica precisa de las universidades de Bolonia, Coimbra y Alcalá[34], de esta última también por Laura Fernando[35]; de las universidades de Santiago de Compostela, Toledo, Barcelona y Colegio de Santa Orosia de Huesca[36], de la Universidad de Valladolid, su Colegio Mayor de Santa Cruz, y de las universidades de Oñate, Oviedo y Granada[37]. En los días en que escribo, Enrique González acaba de publicar una reflexión historiográfica sobre las universidades iberoamericanas[38]…

A la vista de lo dicho, se comprenderá que exista un conocimiento preciso de la investigación realizada en historia de las universidades y que esta producción editorial es verdaderamente abundante, considerando los venticinco años de trayectoria que tiene. Ha ampliado la antigua historia institucional, de la que necesariamente es deudora (¡qué hubiéramos hecho sin los trabajos de carácter institucional de Rodríguez Cruz!), diversificando temáticas y ampliando horizontes interpretativos.

Aquí cumple recordar también el enorme empuje que ha tenido la Historia del derecho español en las últimas décadas. A día de hoy formo parte de un proyecto de investigación dirigido por el Prof. Salustiano de Dios titulado «La proyección de los Juristas de Salamanca en los ámbitos de la cultura, la política y la práctica del derecho, siglos XV-XX»; en él colaboro junto a Baltasar Cuart Moner, Eugenia Torijano Pérez, Javier Infante Miguel-Motta, Paz Alonso Romero y Pilar Arregui Zamorano. Dicho proyecto, representa la continuidad de otro anterior, asimismo dirigido por De Dios, titulado «Juristas de Salamanca, siglos XV-XX: Enseñanza, doctrina y práctica del Derecho», fruto del cual ya han visto la luz dos trabajos colectivos del grupo, titulados: Salamanca y los juristas (número monográfico de Salamanca. Revista de Estudios, n.º 47, Salamanca: 2001) y la monografía Juristas de Salamanca, siglos XV-XX (Salamanca: Ediciones Universidad de Salamanca, 2009); aparte de varios estudios particulares de los miembros del equipo.

La cronología del tema del calendario que aquí abordo fue contemporánea a hechos y procesos históricos importantísimos desde la perspectiva del derecho y de otras disciplinas, en los que también tuvieron capacidad de acción y de opinión los profesores universitarios salmantinos y los que, naturalmente, han generado la correspondiente bibliografía:

• La Conferencia de Valladolid (1527), sobre la ortodoxia de las obras de Erasmo.
• El divorcio de Enrique VIII de la princesa española Catalina (1531).
• Las juntas de Badajoz-Elvas sobre la pertenencia de las Malucas (1524), de la misma forma que también participaron universitarios salmantinos en las anteriores reuniones que concluyeron en el Tratado de Tordesilla (1494).
• Las Juntas de Valladolid (1550-1551) en las que se enfrentaron Juan Ginés de Sepúlveda y fray Bartolomé de las Casas, como enemigo y defensor respectivamente de la humanidad de los indios, saliendo de este debate el código de las Leyes Nuevas (1542), que matizaban las anteriores Leyes de Burgos (1512).
• El concilio de Trento (1543-1563).
• El nacimiento y el desarrollo de la Escuela de Salamanca que matizó las bases del derecho y la justicia (de donde proceden la Declaración Universal de los Derechos Humanos, el derecho de gentes, el desarrollo del concepto de soberanía y el concepto de guerra justa), el nacimiento de la ciencia económica y un impulso notable a la teología (acotando temas como la existencia del mal en el mundo, o la polémica De auxiliis —gracia y predestinación—).

Superada definitivamente la polémica de la ciencia española, los investigadores hemos aprovechado el empuje y la temática de esta nueva historia de la universidad y la hemos puesto en relación con la historia del poder; poder del Estado y poder de los agentes sociales. El estudio del nacimiento y formación del Estado moderno ha sido otro de los problemas históricos más debatido desde los años 50 del siglo XX, impugnándose la denominación de Estado a las sociedades de Antiguo Régimen. Para la defensa del presente estudio no es preciso entrar en ese debate, pues el poder no era sólo ostentado por el Estado. El poder, tanto civil (Maravall, 1972) como eclesiástico (Dampier, 2008, 4ª edición), se ejerce también a través de prácticas sociales, ya sea la elaboración de mapas, el ejercicio de la medicina, la implantación de nueva tecnología o mediante la elaboración de informes para la reforma del calendario, tema que a tantos humanos atañía[39]. Mi trabajo pretende ser un ejemplo de ello. Aprovecha los avances tanto de un campo como del otro: abordo la reforma del calendario como uno de los temas clave de las relaciones entre el poder y la ciencia en la época del Renacimiento.

Desde el punto de vista sociopolítico, la época del Renacimiento fue un escenario de integración científica en el que el poder y el conocimiento estuvieron muy próximos. Muchos trabajos dedicados a esta época contienen información de gran interés para explicar esta circunstancia (Maravall, 1963; G. de la Concha-Jover Zamora, 1999; García Gibert, 2010; Gil Fernández 1979, 1984; Carabias Torres 1989, 2000a). Se ha estudiado cómo la actividad científica discurrió en esta época bajo el patrocinio o control de la Iglesia y del Estado, cada vez más de éste que de aquélla. En dicho sentido, la historiografía de la ciencia en la época del Renacimiento español tiene dos vertientes; por una parte se ha investigado el procedimiento por el cual se establecieron para su transmisión los distintos saberes del momento, y por la otra las interacciones entre los aspectos políticos, socioeconómicos y culturales de la ciencia y de los científicos coetáneos.

En realidad, los factores poder y ciencia casi nunca han sido independientes. Por lo que se refiere a la variable tiempo, hubo momentos de confluencia de especial relevancia histórica. Por ejemplo, la invención del reloj mecánico descubrió otros modos de vivir el tiempo. Le Goff y Ribemont defienden que la revolución más importante en las categorías mentales del ser humano fue la relativa al concepto y a la medida del tiempo, que ocurrió a finales de la Edad Media[40]. De modo similar podemos recordar la invención del cronómetro marino por John Harrison, en 1757; instrumento imprescindible para medir la longitud, cuya determinación se había convertido en un problema de Estado desde la fijación de la raya de los Tratados de Tordesillas, dotándose en varios reinos premios apetecibles para quien lo consiguiera[41]. De este modo cabe concluir que los problemas del calendario y de la longitud fueron los más importantes de la Edad Moderna en relación con el fenómeno tiempo.

1.2.3. La historiografía sobre la ciencia en Salamanca en la época del Renacimiento

Tenemos un conocimiento exhaustivo de la historia institucional de la Universidad de Salamanca en esta época y, para el caso del siglo XVI, que aquí se aborda, están todo lo acotados que la documentación conservada permite. La conjunción de esfuerzos multidisciplinares ha configurado dos magnas obras sobre la historia de esta Universidad en los últimos años. La primera dirigida por Fernández Álvarez, Robles Carcedo y Rodríguez-San Pedro (Salamanca: Ediciones Universidad de Salamanca, 1989-1990), y la segunda coordinada por éste último profesor (Rodríguez-San Pedro, coord. 2002-2009). Precisamente en esta Historia de la Universidad de Salamanca se incluye relación de todo lo que se ha publicado durante los siglos XIX y XX relacionado con esta institución, elenco firmado por Mariano Peset y Pilar García (Peset-García, 2009) y un listado bibliográfico de todo lo editado entre 1800 y 2007, elaborado por Rodríguez-San Pedro y Polo (Rodríguez-San Pedro – Polo Rodríguez, 2009, pp. 639 ss.). Completaban ahí estos autores la información recogida previamente en otro texto (Polo – Rodríguez-San Pedro, 2008) y cabe esperar que la continuada labor del Centro de Historia Universitaria Alfonso IX, al que pertenecen, permita una actualización constante de esta información.

El grueso de la documentación que sirve de base a este trabajo fue escrito en la Universidad de Salamanca en la época del Renacimiento; concretamente en 1515 y 1578. El ambiente institucional de cada uno de esos dos momentos históricos ha sido abordado en esa misma Historia de la Universidad de Salamanca y en otros trabajos. Entre ellos cabe recordar el de Pilar Valero sobre la Universidad de Salamanca en la época de Carlos V (Valero, 1988), el de Manuel Fernández Álvarez sobre la etapa renacentista (Fernández Álvarez, 2002), el de Javier Alejo sobre esta institución en la época de Felipe II (Alejo Montes, 1988) y el de Clara Inés Ramírez sobre la corporación académica y los poderes eclesiásticos, en el siglo XVI (Ramírez, 2002). Tenemos también un estudio del profesor Alejo Montes sobre la docencia en la Universidad de Salamanca en el Siglo de Oro (Alejo, 2007).

Se han estudiado las bibliotecas, tanto la de la Universidad como las de los colegios mayores; especialmente importante en este caso es la del Colegio Mayor de San Bartolomé, que a principios del siglo XVI estaba mucho más dotada de obras astronómicas que la del propio Estudio General. Los fondos medievales de los colegios mayores fueron analizados por Beaujouand (1963) y los del siglo XVI por mí misma (1986a). Los fondos de la biblioteca de la universidad y de la ciudad en la época del Renacimiento han sido cuidadosamente estudiados por Bécares Botas (1998, 2002, 2003), Marta de la Mano (1998), Ruiz Fidalgo (1990, 1994, 2006) y parte del trabajo de Weruaga Prieto (2006).

La información bibliográfica actual sobre los conocimientos científicos en Salamanca y la forma de enseñarlos en la época del Renacimiento, es amplísima; por eso nos centraremos específicamente en la historiografía relacionada con la época y la temática de este trabajo; es decir, lo concerniente a la Facultad de Artes. La misma Historia de la Universidad de Salamanca citada al principio (Rodríguez-San Pedro coord. 2002-2009) contiene estudios que permiten la fijación de los saberes salmantinos: Cirilo Flórez presentó en ella el conocimiento en ciencias (Flórez, 2006), José Luis Fuertes los de lógica y filosofía (Fuertes, 2006), Carmen Codoñer las letras humanas en latín (Codoñer, 2006) y Vicente Bécares las letras humanas griegas (Bécares, 2006).

Por lo que se refiere a la enseñanza en la Facultad de Artes salmantina, aparte de los datos que proporcionan los trabajos citados, contamos hoy con una investigación sobre la evolución del concepto de Facultad de Artes en España (Carabias Torres, 1986), cuestión que necesitaba aclaración, y otra sobre las reformas operadas en esta facultad salmantina en el período renacentista (Carabias Torres, 1985). Asimismo se ha publicado uno sobre la enseñanza de la astronomía en Salamanca según Sánchez de las Brozas (Chaparro Gómez, 2008), y otro de Alejo Montes muy útil para conocer la docencia de las matemáticas y la astrología en Salamanca (Alejo, 1993). Muñoz Delgado (1986) investigó lo relacionado con la lógica y el nominalismo, completando el argumento de Beltrán de Heredia sobre la efímera aparición del nominalismo en Salamanca (Beltrán de Heredia, 1942). La información sobre la recepción del platonismo se la debemos a la pluma de Cirilo Flórez (Flórez, 2008).

Acerca del ambiente científico previo al informe de 1515, conviene tener presente la importancia del árabe en Salamanca en tiempos del Renacimiento, tema que trabajó hace tiempo Bataillón (1935), y la influencia de Avicena, que ha sido estudiada por Juan Bautista Riera (Riera, 2004), pensando sobre todo en las imbricaciones que tenían en aquel momento medicina y astrología. Por lo que se refiere al conocimiento y la enseñanza de la aritmética (materia importante en la cuestión del calendario) habrá que estar pendientes de los resultados que obtenga el grupo de investigación sobre esta temática, dirigido por el profesor Modesto Sierra, que actualmente trabaja sobre el análisis de las aritméticas de la Universidad de Salamanca en el siglo XVI. Excelente información ofrece asimismo el trabajo colectivo editado por María Jesús Mancho sobre la ciencia en el Renacimiento (Mancho, 2001) o el igualmente colectivo de Margarita Becedas, María Jesús Mancho y Cirilo Flórez (2005) acerca de la ciencia y la técnica en la época de Cervantes.

En los capítulos siguientes estudiaremos las personas y las obras de los comisionados por la Universidad de Salamanca para la confección de los informes sobre la reforma del calendario. Aparte de ellos, hubo varios personajes en Salamanca que investigaron la materia astronómica y cuya importancia los ha convertido en iconos científicos de obligado recuerdo. Entre ellos, por lo menos dos: Abraham Zacut y Antonio Nebrija.

1. Abraham Zacut fue una de las mayores glorias de la ciencia astronómica salmantina del tiempo, y el único astrónomo español cuyas obras se tradujeron al árabe en la época. Desde los antiguos trabajos de Cantera Burgos sobre la figura y los conocimientos y obras de Zacut (1931a, 1931b, 2008) o el de Carvalho sobre sus manuscritos inéditos (Carvalho, 1927), hasta los excelentes textos, recientes, de Carlos Carrete sobre los hebraístas judeoconversos en la Universidad de Salamanca en los siglos XV y XVI (Carrete, 1983); el de Chabás (2006) sobre la astronomía salmantina en la última parte del siglo XV; el de Chabás y Goldstein (2008) sobre Zacut y los conocimientos astronómicos en la Península Ibérica; el de Cobos Bueno sobre uno de sus manuscritos médicos (Cobos, 2000); hasta el que trata en general la ciencia hispano judía (Romano, 1992).

En este mismo rango, es importante la lectura del texto de García Avilés (1994) que relaciona la astrología con el arte; o el de Rosa María Hiniesta (2007) relativo a la bóveda astrológica de la Universidad; porque esta bóveda (véase fig. 3) que era parte del antiguo techo de la biblioteca universitaria, fue pintada por Fernando Gallego sobre un boceto supuestamente realizado por Zacut, aunque su inspiración es dudosa (García Avilés, 1994). De hecho, casi todos los textos elaborados sobre esta materia y época, citan a Zacut. En ellos se ha estudiado también la importancia de la astrología, íntimamente relacionada con la astronomía en la época del Renacimiento. En este campo, varios estudios de Martínez Frías (2006), Hiniesta Martín (2006) y Amasuno (1972), ofrecen información sobre astrología y magia en Salamanca, completando los trabajos de carácter general de otros investigadores, como Geymonat (1985), Vernet (1974), Esteban Piñeiro (1995), Pérez Jiménez (1994), etc.

Siguiendo con el valor simbólico de la iconografía universitaria de la época, es importante no olvidar el trabajo en el que Flórez Miguel habla sobre la portada del edificio universitario (2001); el de Paulette Gabaudan (2005, actualizado en 2012) sobre la misma iconografía renacentista; y la de Rodríguez de la Flor (R. de la Flor, 1996) relativo a las representaciones del saber cosmológico en el ambiente de la Contrarreforma española.

2. Los conocimientos de Nebrija sobre el cómputo y el calendario también deben ser considerados por la importancia que tuvieron en su momento y en su inmediato futuro. Vigil y Aizpiri (1944) y González Olmedo (1944) fueron algunos de los primeros en analizar la faceta científica de Nebrija; esa temática la continuó Cotarelo Valledor en otro trabajo del año 1947. Rodríguez Moñino (1949) estudió el ambiente científico que vivió Nebrija en la Casa Zúñiga; tema que también trató Segura Corvasí en dos trabajos (1949, 1950). Benítez Claros analizó su Tabla de la diversidad de los días y horas, de la que después hablaremos, en un texto que publicó en 1946. Y más recientemente Cirilo Flórez (2002), Carmen Codoñer (1994) y Katherine Elliot van Liere (2000) han abundado y matizado la influencia de Nebrija en la ciencia y en el Renacimiento salmantinos.

Fig. 3: Detalle de la bóveda de la antigua Biblioteca de la Universidad de Salamanca. Actualmente en las Escuelas Menores.

Por su relevancia para mi estudio, he dejado para el comentario final el trabajo del grupo de investigación dirigido por Cirilo Flórez Miguel y que incluye también a los profesores Pablo García Castillo y Roberto Albares, que nos permite hoy en día disfrutar de un buen conocimiento de las materias científicas relacionadas con la reforma del calendario, que como hemos dicho eran la astronomía (a veces llamada también astrología en la época) y las matemáticas. En 1989 publicaron un libro titulado La Ciencia del Cielo. Astrología y Filosofía Natural en la Universidad de Salamanca (1450-1530), que nos ayuda a conocer la situación de estas materias en el momento en que se redacta el primero de los informes salmantinos sobre la reforma del calendario; el de 1515. En 1990 sacaron una obra sobre Pedro Ciruelo que, como dicen, representó una enciclopedia humanista del saber. Ciruelo dejó escritos tratados de aritmética, geometría, matemáticas en general, la esfera, medicina, el fuego, Aristóteles, magia, astrología, súmulas, teología, Biblia, etc. (Flórez-Castillo-Albares, 1990, p. 13 ss.). De ahí que debamos tener en cuenta su pensamiento en un estudio como éste. También en 1990, el equipo dirigido por Cirilo Flórez presentó otro libro, en este caso sobre la Ciencia de la Tierra: Cosmografía y Cosmógrafos Salmantinos del Renacimiento. En él analizan la imagen del mundo en los principales científicos salmantinos del momento: Francisco Núñez de la Yerva, Antonio de Nebrija y Pedro Margallo. Después incluyen varios de sus textos, sus traducciones y comentarios. Por último, en 1998, Flórez y su equipo publicaron una obra sobre el Humanismo científico, dedicada especialmente a los conocimientos cosmográficos relacionados con el proceso del descubrimiento de América. Recordemos que en la época del Renacimiento no había una distinción clara entre las materias de la Facultad de Artes, y por eso se comprende que una obra como ésta, de cosmografía, contenga capítulos dedicados a astrología y a matemáticas (pp. 79-84).

Además de lo dicho, el profesor Flórez, en solitario, ha publicado otros dos trabajos que tienen relación directa con nuestra investigación. El primero constituye una explicación del mapa del cielo de Pedro Apiano en su Astronomicum Caesareum (Flórez, 1994), que como sabemos es un texto excepcional, aunque no sea salmantino, sobre el que yo misma hice otro comentario (Carabias Torres, 2001). El segundo, se refiere a un artículo titulado «La reforma del calendario eclesiástico» (Flórez, 1999a); conviene subrayar éste porque trata exactamente el tema que yo abordo en la presente investigación y porque sobre él se dio una situación anecdótica.

Me explico: Después de llevar yo varios años trabajando en el tema que ahora presento, y teniendo serias dificultades en la traducción de algunos pasajes latinos, en su día acudí al P. Benigno Hernández Montes solicitándole consejo y colaboración. Observando ambos que el escollo era notable, después de un tiempo decidimos en conjunto consultar al profesor Flórez, lo que hizo el P. Benigno, pero éste enseguida enfermó, muriendo poco después.

El profesor Flórez y otros, incluyéndome a mí, fuimos convocados a realizar un trabajo en homenaje al fallecido P. Benigno (1936-1996). En la visita que previamente había realizado el clérigo al Dr. Flórez para solicitarle su de colaboración, quizá por un malentendido, el profesor Flórez creyó que era sólo el P. Benigno el que pretendía realizar este trabajo sobre el calendario, de forma individual, sin saber que yo ya llevaba tiempo en el tema y que la ayuda que le pedíamos era conjunta. Ante el desafortunado desenlace y la muerte de Hernández Montes, el profesor Flórez quiso homenajearle con un comentario de los documentos sobre la reforma del calendario y, para ilustrarlo, eligió dos presuntas páginas transcritas de la mano del P. Benigno. Cuando yo vi el libro de homenaje impreso quedé sorprendida, pues aquellas dos páginas manuscritas, presuntamente escritas por el P. Benigno, tenían mi propia letra y es que habían sido en realidad transcritas por mí. Años atrás, cuando yo empecé a trabajar el tema, realicé esa transcripción semi-fotográfica del ms. 97 de la Biblioteca Universitaria de Salamanca, conservando en lo posible la grafía y disposición textual del original, ante la negativa de reproducción del mismo que me daba entonces la directora de dicha biblioteca, doña Teresa Santander Rodríguez. Aquel rigor conservador frente a ciertos investigadores que mostró doña Teresa, me llevó a mí a realizar aquella filigrana transcriptora, que el P. Benigno le entregó al Dr. Flórez y que éste interpretó como su manuscrito (véase la fig. 4). Corrijo, pues el error: dicha imagen no se corresponde con la letra del P. Benigno sino con la mía.

Fig. 4: Transcripción del f. 28v. del Ms. 97 de la Biblioteca General de Salamanca (no del ejemplar del Vaticano) atribuida a Benigno Hernández, que en realidad es de mi mano.

Anécdotas aparte, el capítulo realizado por el profesor Flórez para el citado homenaje (Flórez, 1999a, pp. 443-464) versa sobre la documentación que hoy aquí presento y son veintiuna páginas de lo poco y específico que se pueden leer en la historiografía sobre la participación de Salamanca en la reforma del calendario. Ante estas circunstancias, se comprenderá que yo solicitara al Dr. Flórez que dirigiera este trabajo, a quien tengo que agradecer que accediera gustoso.

Para terminar este estado de la cuestión en el que he tratado el redescubrimiento del tiempo como variable histórica y del conocimiento actual de la historia del calendario y de los saberes astronómicos en la Salamanca renacentista, podríamos hablar, como dijeran Rioja y Durán, de cómo la astronomía cambió el mundo (Durán, 2000, p. 110 ss.). Indudablemente la imposición de la reforma gregoriana del calendario transformó el mundo, o al menos lo recondujo. En palabras de Vidal, encaminó la narración histórica hacia un proyecto global, relacionado con el deber ser; hacia una historia humana universal, que hacia 1970 se quebró por el fin de la modernidad (Lyotard). Otra cascada bibliográfica opinaría en cambio que, aunque la modernidad se desvió de su cauce histórico y precisamente por ello, quedó expedito el camino hacia la globalización que sin ninguna duda tuvo una baza excepcionalmente útil en la imposición (o acuerdo) de hora y día para toda la humanidad[42].

Si la aplicación de la idea de progreso hasta sus últimas consecuencias conduce a su propia autodestrucción, quizá con más tiempo, la sociedad de la información, con sus recovecos e infinitos pasadizos, nos arrastre de nuevo hacia las orillas de la eternidad, como decía Castells[43], y las mismas condiciones presuntamente postmetafísicas y protohistóricas que anuncian la postmodernidad nos ofrezcan otra oportunidad para el desarrollo de un nuevo tipo de conciencia histórica[44].

1.3. LAS CIRCUNSTANCIAS HISTÓRICAS DE LOS INFORMES SALMANTINOS

1.3.1. La percepción del tiempo y su valor en la época del Renacimiento

El espacio y el tiempo fueron dos realidades estrechamente relacionadas durante los siglos XV y XVI. En la época del Renacimiento se puso de manifiesto la diferencia en la forma de percibir estas magnitudes: mientras algunos, especialmente los que se relacionaban con los negocios, se vieron abocados a vivir dentro de una nueva cultura del reloj y del calendario (Bouza, 1994, pp. 21-28), la mayoría de la gente común atendía pocas veces al reloj de hierro[45].

Desde el punto de vista histórico hoy en día encontramos interesantes matizaciones de esta evolución en la historiografía (Hale, 1983, capítulo 1; Broc, 1980; Randles, 1985, 1990; Zumthor, 1994). A través de ella sabemos que aunque hacía mucho que se realizaban largos viajes por mar y el uso del reloj era más cotidiano, a comienzos de la Edad Moderna la mayoría de la gente concebía el tiempo y el espacio en función de parámetros subjetivos y particulares: según sus conocimientos, su condición o su oficio. En general las alusiones temporales más universales seguían refiriéndose al curso de la naturaleza, y no al del reloj o el calendario y, cuando se atendía a éste último, solía ser al calendario eclesiástico el patrón de vida cotidiana de aquellos hombres. La religión y sus fiestas guiaban la conducta de los habitantes de Europa occidental: desde el bautismo hasta el entierro, todos sus actos individuales y sociales estaban marcados por el ritmo del calendario eclesiástico y por los ritos religiosos. De este modo, en el día a día, los referentes temporales habituales se relacionaban o con este calendario eclesiástico o con los actos de la vida cotidiana. Así era frecuente referirse al día de la Ascensión, la Pascua, el anochecer, alrededor del medio día… más que al día o a la hora concreta de que se tratara. Para muchos labradores o arrieros la duración de los trabajos agrícolas o lo que un hombre podía recorrer en una jornada, eran el patrón-base de estas magnitudes.

Un cambio cualitativo en esta tendencia arribó con la expansión colonial castellano-portuguesa y con la imperiosa necesidad de adecuar la fecha de la Pascua con el ritmo real de las esferas celestes. Un exacto control de la hora era absolutamente imprescindible para determinar la longitud en el mar y sólo ligeramente menos esencial para fijar la latitud; el único medio de calcular el tiempo en el mar era el reloj de arena, instrumento bien impreciso, y mucho más cuando es sometido al movimiento de un barco o al propio uso; se comprobó que el paso de la arena agrandaba el conducto, y por tanto este tipo de relojes adelantaban.

La Edad Moderna va a caracterizarse por la búsqueda de la precisión, que se puso de manifiesto en todos los ámbitos. Por lo que se refiere a los patrones universales de medida del tiempo y del espacio sabemos que el camino fue muy lento; especialmente en lo que concierne a la medida del espacio. La necesidad política de determinación de las fronteras nacionales y exploratorias reavivaron los estudios y debates conducentes a la fijación de unos patrones universales de medida, que no fueron universales hasta la Conferencia General de Pesos y Medidas de París, de 1889. Hasta ese año no se estableció un sistema de unidades de longitud de valor universal basado en el metro. En cambio, la aprobación del calendario gregoriano permitió, ya en el siglo XVI, el uso de una convención en la medida universal del tiempo, primero entre los católicos y, poco a poco, en todo la Tierra. Antes de la imposición de esta reforma (y a veces también después), la diversidad de cómputo del tiempo entre las comunidades más apartadas afectaba incluso al conteo de los días. Así, para un pechero medio de Castilla el año no comenzaba el día 1 de enero, sino más comúnmente con el deshielo de las nieves, con la explosión floral de la primavera, o con la prolongación de los días y los primeros resultados de la cosecha.

A la diversidad de las formas de cómputo, había que añadir la inexactitud de los aparatos mecánicos para la medición. De cero a veinticuatro horas contaban los días los italianos; de cero a doce horas, antes y después del mediodía los ingleses. En cualquier lugar, una milla marina representaba distinta longitud que una milla terrestre; una vara de Salamanca era distinta de una vara de León, provocando estas diferencias muchos problemas. En el caso de la vara, su largo osciló entre los 75 y 92 centímetros. Los reyes castellanos dictaron algunas normas para su unificación como medida de longitud en la Corona de Castilla: desde 1261 hasta Juan II se sucedieron las disposiciones que establecían una vara concreta (la de Toledo, la de Burgos…) como unidad de longitud universal para este reino; pero los cambios de criterio en un corto espacio de tiempo no condujeron más que a una mayor confusión. Cada ciudad y casi cada grupo humano medía de forma particular el tiempo, el espacio, el peso y la altura (Szaszdi, 1991); sin generar grandes conflictos en toda Europa, hasta que se implicaron principios políticos y económicos, como por ejemplo la delimitación de la raya del Tratado de Tordesillas, en 1494, o precisamente la reforma del calendario, que aconsejaron e impusieron la búsqueda de la precisión y de la uniformidad.

En la época del Renacimiento, solamente aquéllos que tenían que ver con documentos legales o diplomáticos sobrepasaban la pauta temporal marcada por la estación, el servicio eclesiástico o el estómago y pensaban en el comienzo del año como una fecha oficial y no relacionada con la astronomía; y aun entre estos no existía acuerdo unánime acerca del momento en que debía empezar el año, variando según los países, de ciudad en ciudad e incluso dentro de la misma ciudad en función de diferentes clases de documentos. Unos pueblos lo empezaban en el solsticio de invierno, otros en el de verano, los judíos en el equinoccio de primavera —porque así lo marca la Biblia—, los romanos anteriores a César en el solsticio de invierno, día en el que el Sol entra en Capricornio…; la mayoría de las culturas lo inauguraban en la primavera. Un ejemplo representativo de este hecho es que en Roma las bulas se fechaban de acuerdo con un año que daba comienzo el 25 de marzo y las cartas papales lo hacían en función de otro que empezaba el 25 de diciembre (Hale, 1983, capítulo 1).

El parámetro espacial más generalizado en Europa occidental era el de cristiandad, que servía como referente tanto para el tiempo desde el nacimiento del Jesucristo como para la extensión geográfica. Por eso era corriente denominar los días en función de la festividad religiosa que en ellos se celebrara, más que por las fechas del mes de que se tratara. En este sentido la cristiandad era un concepto ideológico, además de geográfico o espacial; y el calendario eclesiástico se convirtió en un elemento muy destacado, junto al cómputo natural, para la estimación y cálculo de la duración. Todo el mundo entendía que las rentas se pagaban el día de de San Miguel o el de San Martín, y no el 29 de septiembre o el 11 de noviembre (sus respectivas fechas); o que el curso académico comenzaba en Salamanca el día de San Lucas, y no el 18 de octubre; aunque celebración onomástica y fecha del calendario fueran coincidentes en esos casos.

El calendario eclesiástico, las posibilidades de movilidad física en los viajes y el estómago, marcaban la pauta del horario en el mundo rural, pero esta concepción del tiempo y el espacio no resultaba siempre satisfactoria en las ciudades comerciales, donde la hora podía ser una unidad económica y donde la diferencia de un día podía acarrear alteraciones en las tasas bancarias de cambio. Por ello en las ciudades se contó el tiempo de un modo más preciso, mediante relojes. Así pues, mientras que en el campo los habitantes acomodaban su actividad al ritmo de la luz solar, en las ciudades crecía la necesidad y el interés por la hora del reloj y por el día del calendario.

Del mismo modo que había un ritmo natural del día y otro artificial, pautado por el reloj de la ciudad, y así como había una duración oficial del año y otra que dependía de las estaciones o de los trabajos, también existía la consideración de una duración natural y otra artificial de la vida humana. Durante la Edad Media no se solían registrar los nacimientos con regularidad; esta inscripción fue impuesta por un decreto del concilio de Trento, a partir de 1563, y lo más corriente es que antes de esta fecha las personas desconocieran su propia edad. Excepción hecha del ámbito de los negocios o la política, la mayoría no sentía la necesidad de una perspectiva tan precisa. La vida, el tiempo y la distancia se medían más eficazmente por circunstancias tales como la infancia, la juventud, la madurez, la vejez, las jornadas necesarias para culminar un recorrido etc., que por años, relojes o pies romanos.

Naturalmente, era inevitable referirse a la duración de las situaciones o de las cosas al hablar o al escribir, pero la mentalidad colectiva privilegiaba más el sentido del acto que la duración del mismo, hasta que, a mediados del siglo XV, las necesidades militares y tributarias del nuevo Estado fomentaron una precisión que no existía antes. Witold Kula puso en relación esta evolución con el desarrollo del poder monárquico. Decía este autor (Kula, 1980, p. 23) que las tendencias unificadoras del poder real constituyeron el factor preponderante de la actividad organizadora general de los absolutismos renacentistas y del sojuzgamiento de las soberanías regionales. Hoy cabría cuestionar las expresiones absolutismos renacentistas y soberanías regionales, puesto que no puede hablarse de práctica política estrictamente absolutista en Europa antes del siglo XVII, y en el segundo caso sería más preciso decir derechos de entidades políticas no nacionales; pero el nuevo uso del conocimiento y de la ciencia de base matemática por parte del poder parece incuestionable (Flórez Miguel, 2001b, p. 41). La aproximación de los monarcas renacentistas a la ciencia de su tiempo fue una necesidad política; en palabras de Flórez,

…la nueva realidad del estado moderno es impensable sin el triunfo del «espíritu de cálculo» que al principio de la modernidad se extendió a todos los ámbitos de la realidad: el social, el económico y a la misma vida cotidiana en general, produciéndose un proceso de aritmetización de la realidad del que va a salir una nueva configuración del saber (Flórez Miguel, 2001b, p. 28).

La expansión colonial, la adecuación de la fecha de la Pascua con el ritmo real de las esferas celestes, y otros problemas, supusieron un gran incentivo para este intervencionismo regio y, como si de un contagio se tratara, el interés por la precisión se fue generalizando. De ahí derivan las nuevas actitudes de los monarcas del Renacimiento hacia la sanidad, la educación, la seguridad, el control de los mercados… y todas las facetas de la vida pública en general. Así se comprende fácilmente el intervencionismo real en Castilla en cuestiones que antes habían pertenecido al ámbito de los concejos, como los pesos y medidas de los mercados (institucionalización del fiel medidor en cada municipio), el ejercicio de la medicina (creación del Protomedicato en Castilla), la seguridad de los caminos (instauración de la Santa Hermandad), la proliferación de los censos o vecindarios de población (el primero es el de Alonso de Quintanilla, de 1480), la gestión de las obras públicas,… incluso las levas de soldados cuando se requerían. El aumento del control político sobre el territorio corrió paralelo al desarrollo de la burocratización, al nacimiento, en suma, del Estado Moderno, sin entrar ahora en el debate de si la expresión Estado moderno sólo identifica y califica la posterior institución política de la Edad Contemporánea (Clavero, 1981, p. 43), o si el tema, de tan manido, es ya un cadáver historiográfico (De Dios, 1988, p. 389).

Siglos atrás la Iglesia había contribuido al nacimiento y sostenimiento económico de la mayoría de las universidades europeas y fueron eclesiásticos quienes fijaron en ellas los currículos académicos. El poder monárquico había colaborado con estas iniciativas, observándose un equilibrio de poderes que permitió una gran autonomía institucional de las universidades. Pero en la época del Renacimiento se rompió este equilibrio. Los reyes intentaron asegurar la soberanía dentro de sus reinos, llegando Felipe II incluso a ordenar dejar sin valor cualquier bula ganada en Roma a favor de algún asunto que él tuviera ya dispuesto; o prohibiendo usar cualquier documento pontificio que no hubiera sido previamente aprobado por el Consejo (Carabias, 1986c, p. 105).

En el caso de la Universidad de Salamanca, el cambio de esta tendencia lo promovieron los Reyes Católicos enviando a un antiguo miembro de aquel Estudio, don Tello de Buendía († 1484), como primer visitador real. Buendía era hombre de origen humilde, de conocido talante caritativo y conciliador; había sido colegial del mayor de San Bartolomé y rector de la Universidad en 1443-1444, y era en ese momento arcediano de Toledo (Beltrán de Heredia 1970b, II, pp. 93-94). Fue recibido en el claustro el 1 de marzo de 1580 con muchos regalos, pero también con muchas reticencias. Enfrentándose a las órdenes del visitador real, la Academia, se resistió cuanto pudo frente a la injerencia en sus asuntos que esta imposición suponía (Beltrán de Heredia, 1966a, I, pp. 166 y 217). El objeto expreso de los reyes con esta inspección era solucionar un grave conflicto en el rectorado (1479-1480), aunque el visitador actuó también en la disputa en torno a una cátedra de filosofía natural a la que se presentaron el licenciado Diego de Deza, el bachiller Diego de Torres y el maestro Antón Rodríguez de Salamanca. El 2 de enero de 1480 dicha cátedra fue otorgada a Rodríguez de Salamanca, y surgió el conflicto, porque Deza, a pesar de haberse retirado de la oposición el día anterior, recurrió la colación realizada, de tal forma que Buendía tuvo que intervenir también en el caso. Por fin, el 14 de marzo, el claustro en el que participa el visitador, oye a las partes, y en la sesión celebrada el 17 del mismo mes, da definitiva posesión de la cátedra al maestro Antón, al tiempo que impone perpetuo silencio al licenciado Deza (Val Valdivieso, 1989, p. 222).

La segunda inspección real, tan conflictiva como la primera, fue ordenada por la reina Doña Juana en 1512 (Fernández Álvarez, 1984). En este caso también se envió a un buen conocedor de esta Universidad, antiguo profesor de ella, asimismo antiguo colegial del Colegio de San Bartolomé y fundador de uno de los colegios mayores de la misma: don Diego Ramírez de Villaescusa (Millán Martínez, 2009). El rechazo del claustro a su propuesta de hacer depender de los visitadores reales la designación del rector y de los diputados no catedráticos, y que las cátedras fueran temporales —lo que, aprobado, hubiera sido un golpe durísimo a la autonomía universitaria— fue sonado (Peset-García Trobat, 2004, p. 56), resultando finalmente inoperantes estos intentos de reforma. Sin embargo, tras esta inspección la figura del visitador real se generalizó y se normalizó en las universidades de todos los reinos, según puede comprobarse repasando la expedición de órdenes reales con este fin promulgadas a lo largo del siglo (Carabias, 1986c). Hablaremos después de la acción de algunos de estos visitadores en la salmantina.

Una de las consecuencias de esta domesticación de las universidades de origen medieval fue la institucionalización de la enseñanza superior —que constituyó uno de los logros del desarrollo del Estado renacentista— y el consiguiente control en la expedición de títulos (López Piñero, 1999a, p. 20).

Basándose en esta realidad, la interpretación clásica de la historiografía del siglo XX fue la del aislamiento científico de España respecto de la civilización occidental que la Inquisición provocó cuando Fernando de Valdés, asimismo antiguo colegial de San Bartolomé, incitó a Felipe II al viraje de 1558-1559 —en palabras de Joseph Pérez (2002, pp. 141 ss.) y Thomas (2001, pp. 89 ss.)—; es decir, a dictar las leyes que derivaron en el llamado cierre intelectual, entre 1558 y 1559: los autos de fe en Sevilla y Valladolid, el índice de libros prohibidos, la ley que obligaba a regresar a los estudiantes universitarios del extranjero antes de tres meses, y el proceso del arzobispo Carranza, auguraban un negro paisaje intelectual a la cultura y la ciencia nacionales. Pero, aunque indiscutiblemente el miedo a la Inquisición cundió hasta en los argumentos literarios (por ejemplo en Cervantes), un estudio más fino del tema ha llevado a Goodman (Goodman, 1999, p. 95) a afirmar que los decretos del monarca no fueron más que un gesto y que los contactos entre los científicos no se perdieron. Los debates salmantinos sobre la reforma del calendario son un ejemplo de esta realidad: los profesores que redactan los informes entendían con precisión las ideas y cálculos astronómicos que se manejaban en el resto de Europa, aparte de la ciencia clásica, que, a su vez, era el poso cultural común del conjunto de los intelectuales europeos contemporáneos. Su información era precisa: los de 1515 conocían incluso de lo que se había tratado en el concilio de Basilea sobre el calendario; ya lo veremos.

1.3.2. La tradición astronómica en la Universidad de Salamanca

En el siglo XVI la Universidad de Salamanca era un referente científico de primer orden en el mundo occidental. Hoy todos sabemos que la producción literaria salmantina del referido siglo fue importantísima en todos los órdenes y que ejerció su influencia incluso en lugares y personas lejanas, especialmente en los campos de la astronomía, la filosofía natural y la física (Beltrán de Heredia, 1970b, II, pp. 243 ss.). Podía presumir de prestigiosos especialistas en las ciencias de la tierra y del cielo; cosmógrafos y astrónomos que, desde mediados del siglo XV, habían contado con una información manuscrita e impresa de primerísimo rango en Europa; mantenido una tradición investigadora en dos núcleos institucionales adyacentes: la facultad de artes de la Universidad y el Colegio Mayor de San Bartolomé, que ya ha sido puesto de manifiesto en bastantes estudios, como por ejemplo en Florez-García-Albares, 1988, pp. 7-84 y 127-158; 1989 y 1990; Muñoz Delgado, 1986, 1976; o Beaujouand, 1962 y 1967.

¿Qué modelo de universo tenían, por cierto, los intelectuales salmantinos a comienzos del siglo XVI? ¿Qué cambios se produjeron en estas concepciones a lo largo de esa centuria? Intentaré establecer la información astronómica concreta que había en Salamanca y ver en qué medida fue aprovechada en los informes de reforma del calendario. Como suele ocurrir casi siempre, en aquellos tiempos también creyeron que las cosas eran como las veían. Dice Rubia Vila (2000), que hasta tiempos muy cercanos, casi todo el mundo ha vivido en la falsa creencia de que las cosas son como las vemos. Sin embargo, los sentidos preservan la especie y, en realidad, cada persona crea su propio modelo de realidad. De ahí que el engaño de la ciencia en todas las épocas sea esa confusión entre la realidad y nuestra creación mental: el hombre coloca los objetos de las teorías y los modelos explicativos que existen en su cerebro como si estuvieran en el exterior, donde no están. Por ejemplo, desde el punto de vista de la cosmografía, a finales del siglo XV casi nadie concebía los límites de su región; mucho menos de un estado o nación, ni tan siquiera los reyes; de ahí su preocupación constante por adquirir la mejor documentación cartográfica. La captación de los conceptos relacionados con el espacio y el tiempo corrió pareja a la de los diferentes modos de concebir el universo (Vives, 2006, pp. 27-28). Como resultado de la observación del cielo, de modo equivalente a lo que para nosotros es el modelo cosmológico del Big Bang, los griegos habían creado diferentes arquetipos cosmológicos, entre los cuales terminaron por predominar los geocéntricos y geostáticos, que seguían siendo la base teórica del aprendizaje de la astronomía en Salamanca a finales del siglo XV.

1.3.2.1. Corrientes de pensamiento

En la Europa del Renacimiento, la tradición de origen clásico continuó siendo la base general de los estudios universitarios, a la que se fueron añadiendo matices, creencias y tendencias.

Desde el punto de vista literario, una vez superados los escollos ideológico y científico (García Gibert, 2010, p. 13), penetró en España el humanismo literario en sus tres vertientes: erasmista, ciceroniana y ramista (Gil Fernández 2004, pp. 96-140). El éxito del erasmismo español fue grande, al menos hasta la muerte de Erasmo, en 1536. Decía irónicamente Juan Gil, que la historia del erasmismo español es la de un amor no correspondido, pues Erasmo sentía olímpico desprecio por un país que imaginaba orientalizado, a caballo entre la cristiandad y el islam y encima poblado de conversos judaizantes (Gil, 2000, p. 213). En aquella época también lograron hacerse notar los ciceronianos: aquellos puristas que sólo concedían la cualidad de latinistas a quienes usaban el latín con corrección, en tiempos de Cicerón o con su perfección (Núñez González, 1991, p. 239). La tercera vertiente literaria destacable fue el ramismo: la corriente intelectual anti-aristotélica de la segunda mitad del siglo XVI, formada por los seguidores de Pierre de la Ramée (1515-1572). Sus ideas sobre lógica, filosofía y las disciplinas que regulan el discurso escrito, fueron plasmadas en varias obras consideradas como temerarias y prohibidas en Francia por decreto de Francisco I (1544). Estas tendencias erasmista, ciceroniana y ramista tuvieron su reflejo en el citado humanismo literario salmantino (Asensio, 1993), aunque para nuestro estudio sólo tienen una importancia indirecta.

Desde el punto de vista científico dos corrientes de pensamiento habían dominado la cultura académica hasta mediados del siglo XV: el escolasticismo arabizado, de origen medieval y el humanismo científico, el genuinamente salmantino, (López Piñero, 1999a, p. 28 y 1999b, pp. 28-31; Flórez-García-Albares, 1998). El primero fue la consecuencia de la asimilación del saber clásico griego, helenístico e islámico por los universitarios de la Baja Edad Media europea, a partir de las traducciones desde el árabe. En contrapartida, la expresión humanismo científico se usó para designar el movimiento que también intentó recuperar el saber de la Antigüedad clásica, pero que se jactaba de hacerlo a través de ediciones filológicamente depuradas y de traducciones directas, libres de las incorrecciones de las medievales. Es el humanismo que tiene en Nebrija a su prototipo y, como imagen gráfica, la del colegio de sabios (Flórez y otros, 1988, p. 181) o colegio invisible (Chaparro, 2008, p. 20), congregado en parte alrededor del mecenas Juan de Zúñiga (1465-1504) en la villa cacereña de Gata y en parte en la Universidad de Salamanca. Esta corte cultural extremeña ha sido bien estudiada por Vigil y otros (1944), Rodríguez Moñino (1949), Cotarelo Valledor (1947), Segura Corvasí (1950), Cobos Bueno (2001), Flórez (1992), Codoñer y González Iglesias (1994) y por García de la Concha (dir., 1996). Por demanda del mecenas escribió Zacut su Tratado de las influencias del cielo.

Tanto el escolasticismo arabizado como el humanismo científico, por motivos diferentes, pesaron en el mantenimiento de la tradición científica salmantina, al tiempo que favorecieron su renovación. Esta renovación llegó a la ciudad por distintas vías y desde distintos territorios: los calculadores ingleses, el nominalismo y averroísmo parisinos, el humanismo italiano y la astronomía austriaca; geografía que se expresa en el mapa adjunto (véase la figura 5). Desde finales del siglo XIII, una parte de la filosofía escolástica intentó conciliar a Aristóteles con Averroes dando origen al llamado averroísmo. La Iglesia católica consideró el pensamiento de este científico como incompatible con la fe católica; Santo Tomás lo consideraba como una lectura incompleta del Estagirita. Aunque algunas tesis averroístas fueron condenadas por la Sorbona en 1270 y por el obispo Étienne Tempier en 1277, sobrevivió hasta el siglo XVI y sus rasgos se encuentran en los escritos de filósofos del humanismo renacentista, como Giordano Bruno, Pico della Mirandola y en algunos profesores salmantinos. Sus tesis hablan de la superioridad de los filósofos sobre la gente común y de la relación entre el intelecto y la dignidad humana.

Fig. 5: Mapa cultural del Humanismo científico en Salamanca.

El nominalismo llegó también desde París y sólo consiguió imponerse en Salamanca de forma accidentada y efímera según Beltrán de Heredia (1942, pp. 68-101). Una interpretación mucho menos pesimista de este hecho nos la ofrece Flórez (2002b, p. 431), quien atribuye su implantación en Salamanca al catedrático de Escoto, Juan de Oria, en 1509, modernizando los métodos didácticos y la investigación en filosofía natural. Su desarrollo en Salamanca se vio frenado por la acción de los dominicos que en 1507 se pronunciaron en su contra y ordenaron estudiar las Súmulas por Pedro Hispano y la Lógica Magna por Aristóteles, siguiendo las vías tomista y escotista. Aun así, Juan de Oria, Juan de Ortega, Alonso de Córdoba, Domingo de San Juan de Pie de Pueto, Juan Martínez Silíceo, Pedro Margalho, Pedro López de Espinosa y Cristóbal de Medina mantuvieron ese pulso nominalista hasta 1550.

A la urbe arribaron también las reminiscencias del grupo de calculadores de Oxford, como Bradwardine, Heytesbury o Swineshead y seguidores en París de las doctrinas de Juan Buridán (como Nicolás de Oresme) sobre el aumento y disminución de las cualidades, las teorías del continuo, de las proporciones... Por esta vía parisina vino lo que sería una nueva física que se basaba en la observación y la experimentación; corriente científica que fue continuada en esta Universidad por Pedro Margalho, Juan Martínez Silíceo y Domingo de Soto. La crítica a Aristóteles tendrá una influencia directa en la formulación de leyes matemáticas que gobiernan los fenómenos físicos. Con Domingo de Soto, también en Salamanca, se pasó definitivamente de la lógica a la ciencia y se aplicaron las matemáticas a la física de la naturaleza, abonando la polémica sobre los orígenes de la dinámica moderna, con el llamado por Koyré enigma de Domingo de Soto (Koyré, 2000, Liso, 2000; Sols Lucía y Pérez Camacho, 1994; Flórez, 2002b, pp. 439 ss.). Esta época y temática han sido muy bien estudiadas por el equipo de investigación dirigido por el profesor Flórez, a cuyos estudios remito sin entrar más en ellas, narrando aquí ahora solamente algunas circunstancias orientadas a la explicación del contenido de los informes salmantinos sobre la reforma del calendario.

Como acabo de recordar, por lo que se refiere a Castilla en su conjunto, la plena incorporación del programa humanístico en el terreno científico puede personificarse en la actividad desplegada por Nebrija en los años de transición del siglo XV al XVI. Desde estas fechas y hasta mediados del Quinientos, esta mentalidad humanista renovada consiguió imponerse en muchas cátedras universitarias de artes y de medicina, y promovió la publicación de un notable número de textos. A pesar de ello, el escolasticismo arabizado conservó también una notable influencia y las iniciativas y tendencias renovadoras se repartieron entre ambas corrientes. Dice López Piñero que España participó plenamente en la primera fase del enfrentamiento entre las dos corrientes. A partir de la mitad del siglo XVI, en una segunda fase, ambas perdieron fuerza y adeptos: el programa humanístico dejó de tener, tanto en España como en Europa, el atractivo original que había tenido en el campo científico, en tanto que el escolasticismo arabizado quedó cada vez más reducido a un fenómeno residual.

Esta polémica ideológica asumió muy diversas formas, que esquemáticamente pueden reducirse a tres niveles. En el primero los intelectuales se limitaron a la reunión de observaciones y descripciones de datos nuevos, que desbordaban la capacidad interpretativa de las doctrinas tradicionales, aunque no llegara a formularse su crítica abierta, ni siquiera la necesidad de reformarlas; en esa situación se escribió el primer informe salmantino sobre la reforma del calendario. En el segundo se practicaron rectificaciones de detalle, que no significaron ruptura con las teorías o principios epistemológicos clásicos; en esa fase se redactó el segundo de nuestros informes. En el tercer nivel se produjeron crisis parciales que condujeron a renovaciones de fondo, aunque reducidas a sectores determinados de la actividad científica. No fueron más importantes los logros del humanismo científico que los del escolasticismo renacentista. Los debates y los descubrimientos fueron positivos en ambos casos. El humanismo perdió seguidores en la segunda mitad del siglo, de forma casi paralela a como los ganaron tanto el neoescolasticismo contrarreformista, como los criterios científicos de experiencia y razón frente al principio de autoridad de los clásicos y de la Biblia. Ello fue debido en parte al desarrollo de la cuantificación en las observaciones astronómicas, que abocó al cuestionamiento del principio de autoridad como norma de verdad. Hubo algunos que llegaron a concebir la razón y la experiencia como los cimientos del saber, utilizando la comprobación como criterio para invalidar teorías antiguas, oponiéndoles las nuevas, como lo hicieron José de Acosta, Diego Ufano, Juan de Valverde, etc. (López Piñero, 1999a, pp. 28-29).

Los intelectuales más lúcidos vieron frustradas las expectativas inicialmente volcadas en el renacimiento de la ciencia que el programa humanístico albergaba. De ahí deriva la ralentización de la ciencia académica del último tercio del siglo XVI y la atención que empezó a prestarse a la subcultura extra-académica y a la periferia de la técnica; lo que explica, por ejemplo, el desarrollo de la magia y la astrología en la segunda mitad del Quinientos.

Es decir, que el fracaso del humanismo indirectamente promovió el impulso de la magia, que supuestamente permitía un dominio directo del hombre sobre su entorno, basado precisamente en la idea de comunidad de naturaleza, de simpatía universal. Aunque desde la Antigüedad se dio gran importancia a la Luna y a su influencia sobre el hombre, a mediados del siglo XVI se avivó la reflexión y el estudio de esa fuerza común de origen ancestral, única, oculta y semejante, en la que el hombre podía introducirse y utilizar directamente para reconducir los hechos y sojuzgar. Fuerza que según algunos (por ejemplo Cornelio Agripa) penetra en el hombre y en el cosmos y permite a aquél controlar lo más secreto del mundo mediante lo que a veces se llama magia naturalista, otras magia celeste, otras magia religiosa y, otras —tras de Paracelso y Cardano— magia médica.

Dentro de este conocimiento se distinguieron dos vertientes distintas, aunque muy relacionadas entre sí: la que tenía como centro la alquimia y la constituida en torno a la astrología judiciaria y la magia negra. Aún no se había descubierto el concepto de lo imposible. Puesto que se creía en la posibilidad de comprender de forma directa los secretos más ocultos de la naturaleza, se inventaron fórmulas y procedimientos mágicos presuntamente eficaces para lograrlo. Pero esta sabiduría que propiciaba el control del futuro chocaba con el dogma, pues sólo a Dios le era dado conocer el porvenir, y algunas veces propiciaba procesos inquisitoriales, como el del molinero friulano que narra Carlo Ginzburg en El queso y los gusanos. San Agustín reconocía que las estrellas ejercían una influencia sobre el mundo, aunque rechazaba la predicción de la vida del hombre en función de ellas (San Agustín, De doctrina christiana, II, XXI, 32; XXIII, 36; Confessionum IV, III, 4-5). Desde finales del siglo XV se avivó el debate entre las dos caras de este saber, llegando a su culmen en la obra de Pico della Mirándola, Disputationes adversus Astrologiam divatricem (1494), sobre la que a su vez polemizó Sánchez Ciruelo en el prólogo de la Apostelesmata. Se andaba buscando un cierto equilibrio entre la astrología y el cristianismo: La astrología natural (con fines básicamente médicos), era respetada por la Iglesia y formaba parte del currículo académico universitario, junto a la astronomía y la medicina. De hecho, todos los tratados médicos de la época del Renacimiento incluyen el acceso a la astrología y a la magia como parte de los conocimientos imprescindibles (así se dice explícitamente) para el ejercicio de estas profesiones. Por ejemplo, Bartolomé Barrientos, en su Cometarum explicatio atque praedictio liberalium artium Magistro Barriento autore, humanarum literarum Salmanticae professore & cathedrario (Salmanticae: impensis Simonis Portanarii, 1574; BGH 36973 1) continúa la tradición astrológica que aconsejaba tener bien en cuenta las posiciones de los cuerpos celestes antes de rajar al paciente. En cambio la otra, la astrología judiciaria, la que permite conocer y predecir el destino de los hombres y pronosticar los sucesos terrestres, fue vista con recelo por las tres religiones reveladas y sería cada vez más perseguida en Castilla.

Esta tradición mágica fomentó una conocida leyenda según la cual el Marqués de Villena había estudiado artes nigrománticas con el Diablo en la Cueva de Salamanca. En ese enclave legendario que se dice estaba en lo que fue la cripta de la ya destruida iglesia de San Cebrián, el imaginario popular ubicaba una escuela de nigromancia, cuyas clases impartía el mismo Diablo (Villena, 1983; Marcos Celestino, 2004, pp. 155-186; Botello de Moraes, 1987; García Blanco, 1961; Egido, 1994). Así se explica que muchos profesores salmantinos de la segunda mitad del siglo XVI, se vieran tocados por estas creencias.

La vertiente práctica de la magia quedó a veces insensiblemente ligada a la alquimia. Se trataba de un conjunto de especulaciones y experiencias, generalmente de carácter esotérico, relacionadas con las transmutaciones de la materia, y cuyo objeto principal era la búsqueda de la piedra filosofal y de la panacea universal. El conocimiento de la alquimia se apoyaba en una triple base: la química de laboratorio, un proyecto espiritual y la promesa de fabricar oro (Esteva de Sagrera, 1993, p. 192). Había llegado a Europa con los árabes, a través de España. Carlos V se vio imbuido por ella: profesó gran admiración a Cornelio Agripa y tenía varias piedras filosofales. Cristianizada en el Escorial, la alquimia no sólo fue tolerada en principio, sino que incluso el rey Felipe II, junto con el grupo denominado círculo del Escorial, se interesó mucho por los temas herméticos y por el lulismo. Gracias a los esfuerzos de Juan de Herrera, este monarca se convirtió en ferviente admirador de este conocimiento hasta que fue para él evidente, desde 1567, la imposibilidad de conseguir oro mediante su práctica; a partir de ese momento el rey apuntó más hacia la técnica (García Tapia, 2003; Sánchez Ron, 1993, p. 43). Pero, a diferencia de la magia, la vertiente especialmente práctica de la alquimia no la había hecho proclive a ingresar en los programas universitarios ni medievales ni renacentistas.

Es decir, que, tras el cansancio o el desencanto del escolasticismo y del humanismo científico, se desarrollaron sobremanera y simultáneamente, tres formas de pensamiento y de acción: el neo-escolasticismo contrarreformista, la tradición mágica y el desarrollo práctico de la técnica.

Por lo que se refiere a la entonces llamada astrología, la situación cambió de forma notable en la segunda mitad del siglo XV. A partir de entonces, según Flórez-García-Albares (1998), Chaparro (2008) y Chabás (2006), la Universidad de Salamanca se convirtió en el centro más importante de conocimientos astrológicos de la Península Ibérica; como lugar no sólo de consumo, sino también de producción de astronomía. Flórez (Flórez-García-Albares, 1998, pp. 119 ss.) y otros hablan de tres generaciones o grupos de intelectuales de esta universidad en los que se reflejan tanto las citadas corrientes de pensamiento como este liderazgo, y que resumo sucintamente:

1. El primero de ellos, el de los astrólogos, que tendió a relacionar los contenidos teóricos con la observación de la realidad y con las nuevas evidencias. Con ellos se rompió el mito de la Antigüedad y se abrió el paso a la pluralidad de doctrinas (Chaparro, 2008, pp. 11-34). El interés por el conocimiento teórico y práctico influyó notablemente en el contenido de las obras astronómicas de los intelectuales de esa época, como Polonio, Zacut, Basurto (o Vasurto), y continuó más tarde en otros, como Sánchez Ciruelo y Gabriel Gómez. Este giro hacia el conocimiento astronómico práctico podría ejemplificarse tanto en las tablas astronómicas de Polonio conservadas en la Bodleian Library de Oxford —de las que ahora hablaremos—, como en las de Abraham Zacut (Almanach perpetuum, Salamanca: 1478), que aunque no llegó a ser profesor de astronomía en la Universidad, fue el gran maestro salmantino del último cuarto del siglo XV, con salario del obispo Vivero (Beltrán 1970b, p. 247). Práctica que se manifiesta en las traducciones de su obra de Juan de Salaya y Vizinho, en la investigación que realiza Basurto sobre instrumentos astronómicos, geográficos y de medida, en la intencionalidad práctica que conllevan los pronósticos o los eclipses de Diego de Torres, de quien los aprendió Pedro Sánchez Ciruelo, o en la ciencia desnuda de artificio de las obras de Gabriel Gómez... Después abundaremos en ello.

2. La segunda generación, en torno al año 1500, fue llamada por Flórez y otros la de los humanistas. Tuvo en Nebrija a su más afamado mentor, y como compañeros a Francisco Núñez de la Yerba y a Hernán Núñez, el Pinciano. Más que invenciones científicas, su relevancia radica en equiparar y subrayar la importancia del saber y del decir, y en escribir afilados comentarios sobre los autores grecolatinos que les interesaron. Según Rico, Ptolomeo sólo fue entendido en España desde la publicación Introductorium Cosmographicum de Nebrija (Rico, 1983, p. 15, nota; edición crítica con traducción en Bonmatí Sánchez, 2000), interesado en la posibilidad de establecer medidas precisas para cualquier lugar del globo terrestre y en la proyección que permite la representación de la Tierra en un plano (teniendo en cuenta la óptica).

3. La tercera generación, la de los físicos, fue contemporánea del surgimiento y consolidación del nominalismo y de la instauración del modo parisino de enseñanza (consistente en combinar la lección del profesor con preguntas y debates entre los alumnos sobre la materia explicada), que cristalizó en el proyecto de Estatutos de 1529. Sus principales representantes fueron Juan Martínez Silíceo, Pedro Margalho y Fernán Pérez de Oliva. En el ámbito de las cuestiones físicas la obra fundamental de ese movimiento es el Phisices compendium (Salmanticae: [s.n.], 1520) de Margalho.

A la vista de este esquema, se comprende que Salamanca se convirtiera en la segunda mitad del siglo XV y al menos hasta la fecha de redacción del primer informe salmantino sobre la reforma del calendario (año 1515) en el lugar más importante en producción y consumo de astronomía de la Península Ibérica. Dos hechos que suceden al mismo tiempo explican esta situación, según Chabás (2006, p. 35): La creación de la primera cátedra de astronomía-astrología en la Universidad y la presencia en la ciudad del mejor astrónomo del tiempo, Zacut. Con él la astronomía se convirtió en un punto de encuentro de los estudiosos judíos y cristianos, de otro modo claramente separados.

1.3.2.2. Los conocimientos y la enseñanza de la astronomía

1.3.2.2.1. La cuestión de los términos

Hasta bien avanzada la Edad Moderna existió una cierta indefinición de los conocimientos de cosmografía (incluyendo astronomía y geografía), matemáticas (aritmética, geometría y óptica), música, astrología judiciaria e incluso medicina. En las aulas universitarias europeas de comienzos del siglo XVI era frecuente que los conocimientos y la docencia de todas estas disciplinas estuvieran íntimamente ligados (Navarro Brotóns, 2006b, p. 217). Decía Isabel Vicente que la estrecha vinculación entre astronomía y geografía hizo necesario, especialmente a finales del siglo XV, incrementar en número y competencia la profesionalización de los estudiosos de los cielos (Vicente Maroto, 1993a, p. 583). Desde tiempo inmemorial, astrología, astronomía y medicina constituían un corpus unificado de conocimientos que servía tanto para predecir los fenómenos celestes como los avatares de la salud y de la vida cotidiana de los hombres. En DICTER (Diccionario de la ciencia y de la técnica del Renacimiento) se muestran las frecuentes imprecisiones terminológicas con las que se explicaban los hechos; por ejemplo, Diego Sagredo no discriminaba entre estas ciencias y decía en Medidas del Romano (1526):

...ca no ay ninguno tan osado que quiera escrevir en Filosofía sin tocar en Aristótil, ni en astrología sin tomar de Ptolomeo (p. 2; cf. DICTER).

En esta frase las palabras astrología y astronomía son sinónimas. Era algo normal en aquella época que los conocimientos y la docencia de estas materias estuvieran relacionados; explicándose muchas veces la astronomía en la cátedra de filosofía natural, junto a temas de botánica, zoología e incluso de filosofía y retórica. Íntima relación epistemológica patente asimismo entre la astronomía y la geografía, según se refleja en la Cosmographia de Pedro Apiano:

Antes que comencemos a tratar el arte de la Cosmographía, es menester tomar por fundamento los principios de la Astronomía, los quales dan noticia de los círculos de la sphera, porque el uso d’ellos es muy necessario para la Cosmographía (edición de 1575, p. 20; cf. DICTER).

Precisamente desde el siglo XVI, poco a poco, se fueron perfilando estos saberes y distribuyéndose en cátedras ad hoc. Pero todavía a mediados del siglo estos conocimientos aparecen frecuentemente entremezclados en los tratados que se intitulan bajo cualquiera de los citados términos y en el lenguaje cotidiano. Por ejemplo, en el Repertorio universal de todas las leyes destos reynos de Castilla, abreviadas y reduzidas en forma de repertorio, de Celso (año 1553), para diferenciar la astronomía de la astrología judiciaria, se dice:

ADEVINOS Y ADEVINANÇA. Dos maneras ay de adevinança: la una, que se haze por sciencia de astrología, la qual es una de las siete Artes Liberales, y la tal no es prohibida a los que son sabios en la dicha arte y sciencia; la otra es de los agoreros y de los hechizeros, que catan agüero de aves y de stornudos, o de palabras que llaman proverbios (f. IX v.). Y en después añade: La sciencia de astronomía es una de las siete Artes o Sciencias Liberales, y no es prohibida; antes, pueden usar d’ella, y aun para devinar, quando fueren en la tal arte sabidores (f. CCCII v.; cf. DICTER).

La inseparable relación de astrología y astronomía se aprecia también en la Instrución náuthica para el buen uso y regimiento de las naos..., de 1587, de Diego García de Palacio, cuando explica:

Y porque son muy pocos los marineros que entienden la astrología y muchos los que la ignoran, mal podrán sin ella pronosticar las mudanças de los tiempos, aunque sea por las estrellas segundas, por cuya causa me paresció llamarla astrología rústica, por ser mucha la differencia de la otra astronómica, que se haze teniendo qüenta con los movimientos celestes y las varias y differentes aplicaciones de unos planetas con otros (f. 66; cf. DICTER).

En cambio, hacia finales del siglo XVI, algunos escritos apuntaban claramente hacia una mayor precisión terminológica, como este texto recogido de El perfecto capitán, firmado por Diego de Álava y Viamont, año 1590, aunque en este caso pone en concomitancia astronomía y arte militar:

Si deve estimarse tanto la Teología, porque trata de Dios; la Jurisprudencia, de nuestra conservación; la Física, del conocimiento de la naturaleza; la Metafísica, del discurrir en las cosas; la Medicina, de nuestra salud; las Matemáticas, de las pruevas evidentes; la Astrología, del curso del cielo, hallo verdaderamente en esta arte militar todas las demás encerradas (cf. DICTER).

Esta precisión aparece poco a poco. Aquí la vemos implícita en el escrito de José Micón, titulado Diario y juizio del grande cometa que nuevamente nos ha aparecido hazia Occidente..., de 1578, en el que se lee:

Dígolo esto por algunos bachilleres, que no saben aún la distinción de la astrología real y judiciaria, y ya pretenden tratar de todos los acaecimientos del mundo y su fin, como si fuessen baxados del cielo hechos unos embaxadores del eterno Dios, como no haya cosa más ridiculosa que sus reglas y conclusiones, y más vana que sus presagios. Ni quiero dezir que los ingeniosos y estudiosos pierdan la confiança del todo, ni que estriban fuera de los fines legítimos, sino que procedan con cautela, con las alas del entendimiento estendidas ygualmente con la balança entre lo divino y humano, para que mal su grado no ayan de hazer experiencia de otro miserable caso de Phaetón y de Ícaro, hijo de Dédalo[46] (p. 81; cf. DICTER).

A pesar del avance en los matices, la imprecisión continúa durante mucho tiempo, porque incluso el Diccionario de la Lengua Española del año 1726, pretendiendo distinguir la astrología natural de la judiciaria, definía la palabra astronomía como:

...la ciencia que trata del movimiento de los Cielos y los Astros, prediciéndolos en el futuro, en que procede por cálculos arithméticos y trigonométricos, fundados en las repetidas observaciones de los phenómenos o apariencias que suceden siempre.

Explicación que apenas se diferencia de la que el mismo libro ofrece de la palabra astrología, definida como

...tratado o sermocinación [sic] de los Astros: la facultad que discurre y trata de sus influencias y predicciones de lo venidero…

En cambio en 1770, el mismo diccionario oficial de la Real Academia de la Lengua Española definió ya más acertadamente la astronomía como la:

...ciencia que trata de la grandeza, medida y movimiento de los astros y de los demás cuerpos celestes; reservando el término astrología para referirse a la ciencia congetural que enseña a juzgar de los efectos e influencias de los astros y a pronosticar los sucesos por la situación de los planetas y sus diferentes aspectos…

Quede claro, pues, que en el momento histórico aquí estudiado era habitual la falta de precisión en la denominación de estos conocimientos que hoy todos tenemos perfectamente delimitados. Ya vimos que algo similar ocurrió con la palabra tiempo. En el siglo XVI, lo que los documentos universitarios denominaban como astrología, comprendía astronomía, matemáticas (aritmética y geometría), óptica, música, astrología judiciaria, medicina, meteorología, agricultura, cómputo, filosofía natural y cosmografía (geografía matemática, cartografía y astronomía náutica) (Navarro Brotóns, 1992a, p. 188; 2006, p. 83). Chabás fecha en el siglo XV los inicios de un lenguaje de especialidad en castellano para la astronomía, pero, como acabamos de ver, no siempre fructificó en aquel tiempo (Chabás, 2002b).

1.3.2.2.2. Los planes de estudio, la enseñanza y la investigación

Este tema es hoy perfectamente conocido, pero en un estudio como éste parece razonable resumir su contenido.

En todas las universidades medievales hubo estudios de astronomía desde el momento de su fundación, porque esta materia era una de las siete artes liberales en las que se fundamentaba inicialmente la docencia universitaria. Yo observé en su día y otros lo han recogido sin citarme que en el tránsito del siglo XV al XVI se produjo una clara evolución del concepto de facultad de artes en España que se materializó en la secundarización de la materia universitaria de las artes, ante el mayor desarrollo de la teología, la medicina y los derechos (civil y canónico). Desde comienzos del siglo XVI, en casi todos los centros universitarios se constata la estandarización de la enseñanza universitaria en dos ciclos: uno introductorio, formado por las materias del trívium (gramática, retórica y dialéctica) y el quadrívium (aritmética, geometría música y astronomía), conformando la que desde entonces sería denominada como facultad menor de las artes, cuya enseñanza se convirtió en una especialidad en sí misma y, a su vez, en materia propedéutica o preparatoria especialmente para la teología. A su lado, por contraste, se reconocieron como facultades mayores todas las demás; o sea, teología, derecho civil, derecho canónico y medicina (Carabias Torres, 1986b).

En este sentido digo que la enseñanza de la astronomía necesariamente tuvo que existir en la Universidad de Salamanca desde 1218, fecha de su fundación. Lo mínimo que debía tener un estudio general para serlo era la docencia en artes y derechos. Recuérdese cómo la Partida II del rey Alfonso, decía que en un estudio general hay

...maestros de las artes, así como de la gramática e de lógica, e de retórica e de arismética e de geometría e de astronomía, e otrosí que ay maestros de decretos e señores de leyes... (García y García, 1989-1990, pp. 107-118).

Seguramente la astronomía fuera inicialmente una enseñanza sin cátedra propia, basada en la simple regencia de maestros que explicaban simultáneamente varias materias, porque años después sigue sin corroborarse la existencia de una cátedra específica para esta disciplina. Los primeros textos legislativos de esta Universidad, o no se han conservado o no aportan ninguna luz sobre el contenido de la docencia (constituciones de 1381 y de 1411). Sin embargo, según el Libro de Tercias de los años 1406-1408, en ese momento había varias cátedras de derecho, pero en él nada se dice de la de astronomía (Beltrán de Heredia, 1970a, I, n. 82).

Uno de los comisionados en Roma para la reforma del calendario, Pedro Chacón, que procedía de la Universidad de Salamanca y que redactó la primera historia de la institución que ha existido, se refería a la enseñanza en el año de 1411 de la siguiente forma:

...el papa Benedicto Decimotercio, siendo cardenal legado de España, visitó el Estudio salmantino e hizo unas constituciones por donde se gobernase. Y porque las rentas de las tercias habían ya crescido, añadió salarios a las cátedras de prima y vísperas de Theología y Medicina, y a las de vísperas de Cánones y a otras, ... e instituyó otras de nuevo... hasta veinte y cinco, conviene a saber: seis de Cánones, quatro de leyes, tres de Theología, dos de Medicina, dos de Philosophía Natural y Moral, dos de Lógica, una de Astrología, otra de Música, otra de Lenguas hebrea, caldea y arábica [sic] y otra de Retórica y dos de Gramática (Chacón, 1990, p. 80).

Conocemos bastante bien el carácter de Chacón, estudiado en la introducción a la edición de su Historia de la Universidad de Salamanca, y sabemos que era un intelectual extremadamente meticuloso en sus afirmaciones, de forma que, si dijo que en esa fecha se instituyó una cátedra de astrología, es porque lo había comprobado. De esa opinión también es Susana Burgueño en su trabajo sobre el saber astrológico en Salamanca a finales del siglo XV (2009b). Aun así, salvo la simple constatación de que en 1411 se instituyó dicha cátedra, nada sabemos del contenido institucional de esta enseñanza concreta antes de que se redactaran formalmente los planes de estudio para la salmantina. El cuerpo legislativo más importante de la institución de finales de la Edad Media, lejos aún de constituir un plan de estudios en forma, fueron las constituciones de 20 de febrero de 1422, otorgadas por el papa Martín V a esta Universidad. Están editadas en latín por Beltrán de Heredia (1966a, I, pp. 189-209) y en castellano por Valero-Pérez, en 1991 (Carabias Torres, 2010). Su mandato estuvo vigente hasta la reforma carolina de las universidades de 1771. Para completar, matizar y adecuar estas constituciones a lo largo de los tiempos se elaboraron sucesivos cuerpos de estatutos de los que sólo algunos se pusieron en vigor.

Antes hablamos de varias visitas a la Universidad que no derivaron en la aprobación de nuevas normas. La primera regulación estatutaria que recibió ratificación institucional fueron los estatutos del año 1538, elaborados a raíz de la inspección de don Juan de Córdoba. Un poco antes, en 1529, siendo rector Pérez de Oliva, se redactó un proyecto legislativo que no se sancionó en su día, pero que fue la base de los estatutos de 1538 (Fuertes Herreros, 1984; Valero García, 1986 y 1988). En 1529 se prescribía lo que iba a ser aprobado nueve años después, cundo se dice: El catedrático de matemáticas leherá arismética y jometría, astrología, perspectiva y cosmografía. En otros capítulos se indica como base documental a Aristóteles, Santo Tomás y Avicena: tres de los autores que constituían el fundamento del modelo científico básico en Salamanca, sin permitirse estudiar a ningún otro autor dentro de la temática astronómica (Fuertes Herreros, 1984, p. 124).

En la práctica, en 1538 el corpus normativo de la enseñanza de la astronomía quedaba repartido y diluido entre la cátedra de Físicos y la llamada cátedra de matemáticas. Por lo que se refiere a la primera, título XVIII, expresa De lo que han de leer los catedráticos de teología, medicina y filosophía natural y moral, y cómo han de oyr en estas facultades; y explica la actividad de los profesores artistas en los siguientes términos:

El catedrático de Filosofía Natural leerá texto de Aristóteles de la misma ciencia y de la metaphísica..., lo mismo hará el de moral el texto de philosophía.

Mientras el título XIX, denominado De los regentes en artes, establece que

...los regentes de filosophía lean quistiones de física sin texto hasta mediados de marzo, de lo natural lean texto De Caelo con glosa hasta fin de mayo, lean De Generatione, texto con glosa, y Metaurus [Meteoros] con texto y glosa hasta vacaciones; y cuando el catedrático de propiedad leyere De generatione, los regentes lean De Anima, texto y glosa. En la cátedra de Físicos de la una se lean Físicos, el texto de Aristóteles, los dos primeros libros hasta Navidad, tercero y quarto hasta medio marzo, quinto y sexto y séptimo hasta Sant Juan, octavo hasta vacaciones (Esperabé de Arteaga, 1914, I, pp. 139 ss.).

Es decir, que en la cátedra de físicos, en lo referente a astronomía, se estudiaba la Física de Aristóteles entre otras cosas, con algunos comentarios o glosas. Teniendo la tradición astronómica que hemos resumido y los fondos bibliotecarios de los que enseguida hablaré, cabe preguntarse si no se explicaría nada más.

En la aprobación definitiva de estatutos de 1538 el estudio de esta disciplina quedó regulado por el título XIX, de los regentes en artes: es decir, que aún se incluía parte de la enseñanza de esta materia dentro de la facultad de artes, que no debemos olvidar que se consideraba preparatoria o propedéutica para estudios superiores. La prescripción de la docencia es aquí muy escueta, pues sólo dice:

El catedrático de matemáticas leerá aritmética y jumetría y astrología, perspectiva y cosmographía, según los oyentes pidieran (Esperabé de Arteaga, 1914, I, pp. 158).

Fíjense en la coletilla según los oyentes pidieran, que no figuraba en el proyecto previo. La indefinición de estas normas no nos permite conocer el contenido específico de cada materia por esta vía. Ante ella, cabe suponer que son válidas para Salamanca las explicaciones de Navarro Brotóns (1992a, pp. 187-188) que dice que el profesor de astronomía no se ocupaba en general de la verdadera naturaleza de los cielos y sus auténticos movimientos, sino que presentaba los modelos planetarios como supuestos matemáticos. Los temas cosmológicos se discutían en otros contextos, tales como los comentarios a De Caelo y la Methaphysica de Aristóteles o al segundo libro de la Historia Natural de Plinio.

Hubo otras inspecciones a la Universidad de Salamanca, pero ninguna de ellas promovió la aprobación de un nuevo cuerpo estatutario hasta el año de 1561, redactado como consecuencia de la visita de Diego de Covarrubias. No obstante, cabe recordar el proyecto correctivo de Diego Enríquez de Almansa, que se llevó a cabo entre los años 1550 y 1555, cuya reforma estatutaria fue finalmente aprobada, con enorme retraso, en 1560, como puro trámite, y cuya vigencia no duró siquiera un año, al ser sustituidos por los de 1561 citados (Fernández Ugarte, 1989, p. 688; AUSA, 19, f. 83 ss.; Marcos Rodríguez, 1959).

En los estatutos de Covarrubias, la enseñanza de la astronomía se trata en el título XVIII, y —esto es muy importante— se plantea como una docencia desligada ya del grupo de las regencias de artes. Esto significa que entre 1538, fecha de los estatutos previos, y 1561, fecha de los actuales, se habían producido una evolución metodológica y epistemológica que permitió la revalorización de la materia; un ascenso cualitativo de su interés. En relación con este cambio, las prescripciones docentes son ahora algo más explícitas que en el estatuto anterior. Dice:

La cáthedra de Astrología el primer año se lea en los ocho meses Esphera y Theoricas de planetas, y unas tablas, en la substitución astrolabio.

El segundo año seys libros de Euclides y Artihmética hasta las raíces quadradas y cúbicas y el almagesto de Ptolomeo o su epítome de Monte Regio, Geber o Copérnico, al voto de los oyentes, en la sustitución la Esfera.

El tercero año Cosmographía o Geographía, un introductorio de iudiciaria y perspectiva o un instrumento, al voto de los oyentes, en la sustitución lo que pareciere al cathedrático comunicado con el Rector[47].

Obsérvese que ya no se habla, como en los anteriores, de la cátedra de matemáticas, sino de la de astrología; y que su docencia se desarrolla a lo largo de tres cursos del alumno, mientras que en los estatutos de 1538 este extremo no aparecía especificado. A partir de 1561, básicamente se sigue estudiando lo mismo que antes; es decir: aritmética y jumetría y astrología, perspectiva y cosmographía, pero ahora se introduce mucha mayor precisión en la distribución temporal de las materias y en los contenidos concretos de cada disciplina, en función de obras y autores especificados.

Por lo que se refiere al primer curso, el estatuto empieza diciendo que se ha de estudiar durante ocho meses, la esfera, Theoricas de planetas y unas tablas. Y en la sustitución el astrolabio. En 1538, para el estudio de la esfera podía utilizarse la Sphaera mundi de Johannes de Sacrobosco, de la que había varias ediciones, aunque el Brocense protestaba de que tenía mucha paja. La obra está formada por cuatro capítulos breves en los que Sacrobosco explica los conceptos fundamentales de la astronomía y de sus aplicaciones. El primero trata de la forma del universo, definición de esfera, eje y polos, estudio de las regiones sublunar y translunar, dimensiones y diámetro de la Tierra. El segundo recoge el tema de los diez círculos de la esfera, mayores y menores, los cuatro elementos heracliteanos, trópicos y polos, paralelos, longitud, latitud y la habitabilidad de la zona tórrida. El tercero alude a las opiniones sobre el nacimiento y ocaso de los signos, las teorías sobre la desigualdad de los días y las noches, las variaciones que experimentan los hombres según la zona que habiten y los siete climas. El cuarto resume los movimientos de los planetas y las causas de los eclipses (Chaparro, 2003, pp. 418-419).

La obra de Sacrobosco recibió una atención especial y proliferaron los comentarios sobre ella; dentro de los realizados por españoles, cabe recordar los de Pedro Ciruelo, Pedro de Espinosa, Pérez Oliva (dentro de su Cosmografía nueva), o El Brocense. Como ejemplo para mostrar he elegido el ejemplar Impressum Venetiis: per Iacobum Pentium de Leucho, 1519, die 24 decembris (véase la figura 6). Su portada contiene una carga didáctica impresionante, pues es una imagen estereotipada de la Tierra, mostrando a Adán y a Eva en el paraíso terrenal, con plantas y animales idealizados y la figura de Ptolomeo entronizada de modo casi divino, con una esfera en una mano y un instrumento astronómico en la otra, en actitud docente. Esa era la forma habitual de representar a los astrónomos o astrólogos desde la Edad Media. Francisco Rico (1983, pp. 157-186) observó que esta iconografía no cambió en siglos. Se usa en la portada de Sacrobosco, igual que la emplearon el astrónomo Oroncio Finé en 1532 o Sancho de Salaya en su Repertorio de los tiempos (Valladolid, Francisco Fernández, 1552); incluso en 1755, cuando se publica la obra de Diego de Torres y Villarroel, El gran Piscator de Salamanca, aparece el astrónomo caracterizado igualmente en este caso con esfera y compás. En la edición elegida de la Sphaera mundi la escena se cubre con la representación de las esferas homocéntricas, en las que van engastados el Sol, la Luna y los signos del zodiaco.

Fig. 6: SACRO BOSCO, Johannes de (1519). Sphaera mundi. Veneiis Iacobum Pentium de Leucho. Portada.

También dentro del primer curso se debía estudiar la Theoricas de planetas, refiriéndose el estatuto en este caso a una obra medieval anónima que después había sido completada y comentada en multitud de textos, constituyéndose en la base de la enseñanza de esta materia. En aquellos tiempos solían emplearse los comentarios realizados a la obra por otra homónima titulada Theoricae novae planetarum (Nuremberg, 1472), de Georgius Purbachius, más conocido en España como Peuerbach (1423-1461). Era éste uno de los tratados sobre el sistema ptolemaico más difundidos en la época del Renacimiento, llegándose a editar cincuenta y seis veces entre 1472 y 1653. Peuerbach inventó la vara de Jacob o ballastella, que permite medir alturas a distancia. Abundaron sus comentarios. En este caso he elegido uno de los posibles; el de Erasmus Oswald Schreckenfuchs, con un larguísimo título: Eras. Osuualdi Schrecsenfuchsii Commentaria in Nouas theoricas planetarum Georgii Purbachii: quas etiam breuibus tabulis pro eliciendis tùm mediis tùm ueris motibus omnium planetarum item tabulis coniunctionum & oppositionum ac eclipsium luminarium ad summum illustrauit lucemq[ue] maximam iis adiecit: his quoq[ue] accesserunt uaria exempla & demonstrationes, quibus astronomiae studiosus suo marte omnis generis tabulas secundorum mobilium facile conficiet & qua ratione ueteres confectae sint, uidebit: preaterea elegantes singulorum planetarum spherae. Philippi insuper Imsseri medici & mathematici in eiusdem Purbachii Theoricas, tabulis utilissimis adiectis. Basileae: per Henrichvm Petri, 1556. (véase la figura 7). Si comparamos la portada de este comentario de Schreckenfuchs con la de la Esfera de Sacrobosco anterior, observaremos el reflejo visual del avance en el camino de la geometrización del espacio, que será una de las claves científicas que explique este período.

En este mismo curso debían estudiarse también unas tablas, muy probablemente las de Alfonso X el Sabio, basadas en las tablas toledanas de Azarquiel (el inventor de la azafea), que fueron las que también se usaron en el Vaticano en los primeros momentos de la reforma del calendario. Una edición bastante conocida de este texto en las universidades fue Alfonsi Hispaniarum Regis Tabule [et] L. Gaurici... Theoremata quorum hic est index... In calce huius libri seorsum annexe sunt Tabule Elisabeth Regine nuper castigate & in ordinem redacte per L. Gauricum cum additionibus & nouis problematibus eiusdem Gaurici [Venetiis: in aedibus Lucae Antonii Juntae, c. 1524] (BGH 13020 1). El ejemplar que he elegido como representación había pertenecido a la biblioteca del Colegio Mayor del Arzobispo (véase figura 8). También pudieron usarse para la docencia las tablas de Polonio, Zacut, Alfonso de Córdoba, Francisco Sarzosa, Bernardo Granollach u otros, que estaban a su alcance.

El primer curso de astrología terminaba, según ley antigua, en la sustitución de junio: cuando un profesor había explicado durante ocho meses seguidos, tenía derecho a leer por sustituto durante lo que restaba de curso, de forma parecida a cuando se jubilaba, quedándose el titular de vacaciones. En este periodo la norma prescribe que, en esta sustitución, se estudie el astrolabio y para ello, los estudiantes de esta materia tuvieron a su alcance un astrolabio real. Lo digo porque, según veremos, la tradición didáctica de esta materia ya los usaba en el año 1461 y lo natural es pensar que siguieran usándose, aunque no se especifique en esta norma. En todo caso, es también natural que utilizaran textos teóricos sobre el uso de éste u otros instrumentos, como por ejemplo el de Jakob Koebel, Astrolabii declaratio: eiusdemque usus mire iucundus, non modo astrologis, medicis, geographis, caeterisque literarum cultorib. multum utilis ac necessarius, uerum etiam mechanicis quibusdam opificib. non parum commodus, à Iacobo Koebelio faciliorib. formulis nuper aucta longeque euidentior aedita; Cui accessit Isagogicon in astrologian iudiciariam. Moguntiae: Petrus Iordan, 1532 (BGH 45488 1), cuya tabla de contenidos se refleja en la figura 9. Obsérvese en ella el reflejo de la importancia contemporánea de los blasones, en relación al desarrollo del concepto de nación. Esta obra se imprimió en Maguncia y, en Alemania, durante todo el siglo XVI, los jefes de los principales estados que configuraban el Sacro Imperio Romano Germánico disputaban al Emperador el derecho a exhibir sus insignias y la importancia de éstas. Una portada como ésta hubiera sido impensable en aquellos territorios donde despuntaba el poder del nuevo Estado, como Francia, Inglaterra o Castilla.

El segundo curso, según estos estatutos, comenzaba por los seis libros de Euclides. La primera edición impresa de los Elementos de Euclides fue del año 1482. En la biblioteca de Salamanca tenían la edición de Joannes Voegelin, titulada Elementale Geometricum, ex Euclidis Geometria, à Ioanne Voegelin, Haylpronnensi; ad omnium mathematices studiosorum utilitatem decerptum. Parisiis: apud Christianum Wechelum sub scuto Basiliensi, 1534 (BGH 36894 1), que entremezclaba información teórica con las figuras geométicas correspondientes (véase la fig. 10). Este texto está en latín, pero en esta docencia y en la enseñanza de la astrología, estaba permitido el uso de la lengua castellana; por eso es más que probable que utilizaran para las clases uno de los manuales en este idioma, como el de Juan de Icíar, Libro intitulado Arithmetica practica: muy vtil y prouechoso para toda persona que quisiere exercitarse en aprender a contar, agora nueuamente hecho por Iuan de Yciar Vizcayno. 1 2 3 4 5 6 7 8 9 0. Çaragoça: en casa de Pedro Bernuz, a costa del autor y de Miguel de Çapila, mercader de libros, a 16 de febrero de 1549 (figura 11). Ésta era una de las materias más útiles para la vida cotidiana. Según el estatuto, debía estudiarse la aritmética hasta las raíces cuadradas y cúbicas.

Este segundo año el curso continuaba por el aprendizaje del Almagesto de Ptolomeo, o por uno de sus comentarios. El Almagesto contenía la más completa explicación estelar del sistema geocéntrico. Su contenido se divide en trece libros, dedicados: al sistema geocéntrico (el primero), la longitud del año y los equinoccios (segundo), los solsticios (el tercero), la Luna y su ciclo sinódico (el cuarto), la corrección de la paralaje del Sol y la Luna (el quinto), medidas del Sol y la Luna y eclipses (el sexto), las posiciones relativas de las estrellas (el séptimo) las estrellas australes (el octavo) y los cálculos de posición y trayectoria de los planetas con sus epiciclos (del noveno al decimotercero). Como dijimos, lo había traducido al latín Gerardo de Cremona en 1175. Su pretensión de salvar las apariencias y el éxito en hacerlo lo convirtió en la obra clave del conocimiento astronómico hasta el desarrollo del heliocentrismo. De hecho, la enseñanza de la astronomía se había basado en él a lo largo de las edades Antigua y Media. En Salamanca contaron con el ejemplar titulado Almagestum Cl. Ptolemei Pheludiensis Alexandrini astronomorum: opus ingens ac nobile omnes celorum motus continens. [Venetiis]: felicibus astris eat in lucem ductu Petri Liechtenstein Coloniensis Germani. Portada (BGH 36590) (figura 12).

Fig. 7: ...el primer año... Theoricas de planetas. SCHRECKENFUCHS, Erasmus Oswald (1556). …Commentaria in Nouas theoricas planetarum Georgii Purbachii… Basileae: per Henrichvm Petri.

Fig. 8: ...el primer año... Alfonsi Hispaniarum Regis Tabule [et] L. Gaurici... [Venetiis: in aedibus Lucae Antonii Juntae, ca. 1524].

Fig. 9: ...el primer año... sustitución... astrolabio. Tabla de instrumentos. KOEBEL, Jakob (1532). Astrolabii declaratio... Moguntiae: Petrus Iordan.

Fig. 10: El segundo año seys libros de Euclides... VOEGELIN, Joannes (1534). Elementale Geometricum, ex Euclidis Geometria... Parisiis: Christianum Wechelum sub scuto Basiliensi. fol. Aiii.

Fig. 11: El segundo año... Artihmética hasta las raíces quadradas y cúbicas. ICÍAR, Juan de (1549). Libro intitulado Arithmetica practica: muy vtil y prouechoso para toda persona que quisiere exercitarse en aprender a contar... Çaragoça: en casa de Pedro Bernuz... Portada.

Fig. 12: El segundo año... Almagestum Cl. Ptolemei Pheludiensis Alexandrini astronomorum: opus ingens ac nobile omnes celorum motus continens. [Venetiis]: felicibus astris eat in lucem ductu Petri Liechtenstein Coloniensis Germani. Portada.

Durante los siglos transcurridos hubo muchas oportunidades de corregir y matizar los contenidos de las obras clásicas y para eso se habían escrito los epítomes, resúmenes o compendios. El estatuto de Covarrubias sugiere usar o el original del Almagesto, o los epítomes de Monte Regio, Geber o Copérnico, al voto de los oyentes. En función de los ejemplares de estos comentarios que se han conservado en los registros sucesivos de los fondos de la biblioteca universitaria, cabe suponer que fue el comentario de Regiomontano el más empleado en Salamanca; por ejemplo In Ptolemaei Magnam compositionem, quam Almagestum vocant, libri tredecim, conscripti à Ioanne Regiomontano mathematico clarissimo. In quibus uniuersa doctrina de coelestibus motibus, magnitudinibus, eclipsibus &c. in epitomen redacta, proponitur. Noribergae: apud Ioan Montanum, & Vlricum Neuberum, 1550 (BGH 12914) (véase figura 13).

Por último, en el tercer año se prescribe el estudio de la cosmografía, una introducción a la astrología judiciaria y perspectiva, o un instrumento, a elección de los oyentes. En cuanto a la cosmografía, se utilizaba o la de Ptolomeo o la de Apiano (1495-1552). La de éste último, Cosmographia seu descriptio totius orbis (1524), era uno de los libros más comunes, con varias ediciones, una de ellas corregida y añadida por Gemma Frisio (1508-1555), como: Cosmographia Petri Apiani per Gemmam Frisium apud Louanienses medicum & mathematicum insignem, iam demum ab omnibus vindicata mendis, ac nonnullis quoque locis aucta. Additis eiusdem argumenti libellis ipsius Gemmae Frisii. Veneunt Antuerpiae: Gregorio Bontio, sub scuto Basiliensi, 1553 (BGH 32655). De este comentario se hicieron multitud de ediciones desde 1529: Yo conozco la de 1533 citada y las de 1535, 1539, 1540, 1544, 1545, 1548, 1550, 1551, 1553, 1564, 1574, 1575 y 1584. Hubo incluso traducciones al castellano; una publicada en Enveres [sic]: vendese casa de Gregorio Bontio en el escudo de Basilea, 1548; y otra, con el añadido El Sitio y Descripcion de las Indias y Mu[n]do Nueuo, sacada de la Historia de Francisco Lopez de Gomara, y de la Cosmographia de Ieronymo Giraua Tarragonez, en Anvers: por Juan Bellero al Águila de Oro, 1575. Obra que también se encontraba, en varias ediciones, en la mayoría de las bibliotecas científicas de la época.

Frisio añadió a la Cosmografía de Apiano un buen número de tablas de latitudes y cuadrados de números y raíces, explicando los procedimientos para varios tipos de mediciones (Vicente Maroto-Esteban Piñeiro, 1991, p. 251). Como ejemplo de la obra aquí muestro una Charta cosmographica con la representación geográfica de la Tierra rodeada por otra idealizada del cosmos. En mi opinión, puede ser un ejemplo del tránsito del antiguo paradigma cosmográfico, basado en la concepción ptolemaica del universo reflejado aquí en la plasmación idealizada de vientos y dioses, al nuevo paradigma, representado por la inclusión de la representación del continente americano (véase figura 14).

Respecto de la enseñanza de la astrología, en Salamanca se usaron desde el primer manual de astrología, el Tetrabiblos de Ptolomeo, hasta los textos de Alcabisio. El Liber quadipartitum (Tetrabiblos) y el Centiloquium se habían traducido del griego al árabe y de éste al latín. En Salamanca se usó en la edición titulada Hoc in libro nunquam ante typis aeneis in lucem edita haec insunt: Klaudiou Ptolemaeiou pelousieos Tetrabiblos syntaxis, pros Syron adelphon... (Norimbergae: apud Ioannem Petreium, 1535, BGH 13022 2), y en la versión de Aecio de Amida, titulada Aetii medici Graeci Contractae ex veteribus medicinae Tetrabiblos: hoc est, quaternio, siue libri uniuersales quatuor, singuli quatuor sermones complectentes... (Lugduni: ex officina Godefridi et Marcelli Beringorum fratrum, 1549, BGH 35564; también impresa en Lugduni: apud Sebastianum Honoratis, 1560, BGH 35945), de la que había en la biblioteca universitaria varios ejemplares.

Fig. 13: Prefacio del epítome de Monte Regio. REGIOMONTANUS, Johannes de (1550). In Ptolemaei Magnam compositionem, quam Almagestum vocant... Noribergae: apud Ioannem Montanum, & Vlricum Neuberum.

En la BGH de Salamanca se conservaban también otros manuscritos con textos del matemático, arquitecto y astrólogo Alcabitius o Al-Qabisi (Alcabisi según los estatutos) (?-967), que nació en Mosul y murió en Zaragoza. Alfonso X el Sabio contribuyó a la difusión de su obra astrológica por Castilla, promoviendo la traducción que de ella hizo Juan de Sevilla (Iohannes Hispalensis). En esta biblioteca se hallan varios ejemplares de ella; por ejemplo, dos copias del «Liber introductorius», traducido por Iohannes Hispalensis (BGH ms. 2051, ff. 14r.-25v.; ms. 2621) y un «Comentario al tratado de astrología de Alcabitius» realizado por Jerónimo Muñoz (BGH ms. 2320). La biblioteca albergaba también dos impresos referidos a él: Precla[rum] summi in astro[rum] scientia principis Alchabitii opus ad scrutanda stella[rum] Magisteria isagogicu[m] pristino ca[n]dori nup[er]rime restitutu[um] a... Antonio de Fantis Taruisino..., en la edición de Venecia de 1521 (BGH 10971 2) y Alkabitius astronomie iudiciarie principia tracta[n]s cu[m] Ioannis saxonii com[m]e[n]tario ordine textus nuperrime disti[n]cto. Additis annotatio[n]ibus et in margine & in textu atq[ue] glossa per magistrum Petru[m] turrellum... (c. 1520, BGH 32622).

Fig. 14: El tercero año Cosmographía... Cosmographia Petri Apiani per Gemmam Frisium apud Louanienses medicum & mathematicum insignem, iam demum ab omnibus vindicata mendis, ac nonnullis quoque locis aucta. Additis eiusdem argumenti libellis ipsius Gemmae Frisii. Veneunt Antuerpiae: Gregorio Bontio, sub scuto Basiliensi.

Según he comentado más arriba, precisamente en la época en la que se aprueban estos estatutos, se recrudece la lucha entre la astrología permitida y la judiciaria, inaugurándose una verdadera cruzada católica contra esta última, que empezó a ser mirada con recelo. En Salamanca se editaron varios trabajos contra ella, desde el famosísimo Reprovación de las supersticiones y hechizerías, de Pedro Ciruelo (1538), hasta un libro titulado Reprobacion de la astrologia judiciaria o diuinatoria sacada del toscano en lengua castellana (Salamanca: Juan de Junta, 1546, BGH 36975) (figura 15). Debido a este enfrentamiento, en la época del Renacimiento se fueron separando la astrología de la astronomía, al mismo ritmo que lo hicieron la alquimia de la química. A pesar de que algunas obras astrológicas entraron a formar parte del Índice de libros prohibidos de 1559 (el del inquisidor Fernando de Valdés), la Iglesia no condenó explícitamente su práctica hasta la bula Contra exercentes artem astrologiae..., de Sixto V, de 1586, pero la orden no tuvo un efecto coercitivo inmediato en Castilla (Boeglin, 2006, p. 180). Hasta 1631 en España no se condenó la astrología judiciaria como herética, y siguió estando autorizado su uso para la navegación, la agricultura o la medicina, de forma que durante los años en los que se elaboraron los informes salmantinos sobre el calendario, era una materia habitual del currículo universitario.

En conjunto, frente a la rudimentaria reglamentación docente de los estatutos de 1538, los del año 1561 aportan una importantísima diversificación y matización de los contenidos didácticos. Recordemos lo dicho en cuanto a que ya no se habla de la cátedra de matemáticas, como se hacía en los estatutos de 1538, sino de la cátedra de astrología. Éste era el corpus legal vigente cuando se hizo el segundo informe sobre la reforma del calendario en Salamanca.

Treinta y tres años después, cuando se aprobó la siguiente reforma estatutaria tras la inspección de Juan de Zúñiga (año 1594), se denominó a esta docencia como cáthedra de mathemáticas y astrología, conjuntamente (Alejo Montes, 1990a, 1990b, 1990c, 1991, 1993, 1998). Un proyecto de reforma intermedio, realizado por el visitador Velarde en 1575, nunca entró en vigor (Alejo Montes, 1999). En 1594, la estructura de la enseñanza de la cátedra de matemáticas y astrología siguió el proceso natural de diversificación y matización de los contenidos, pero, en este caso, con otro importantísimo cambio cualitativo a favor de la enseñanza de los conocimientos tanto clásicos como punteros. En los cuatro años que distribuía esta docencia Zúñiga ordenó estudiar lo siguiente[48]:

El primer año... la Geometría: los seis libros primeros de Euclides, y la perspectiva del mismo, y la aritmética con las raíces cuadradas, y cúbicas declarando la letra del séptimo, octavo y nono libro de Euclides, y la agrimensura, que es el arte de medir la área de qualquier figura plana. En la sustitución los tres libros de triangulis sfericis de Teodosio.

El segundo año, sólo la Astronomía, comenzando por el Almagesto de Ptolomeo, y habiendo leído el primer libro, léase el tratado de signis rectis, el de triangulis rectilineis, y sphereis de Christóforo Clavio u otro moderno; después de leído el libro segundo se han de enseñar a hacer las tablas del primer móvil, como son las de las direcciones de Juan de Monte Regio, o de Erasmo Reinoldo. Acabado el libro segundo con sus adherentes, léase la teórica del sol por Puerbachio, y luego todo el libro tercero del Almagesto, y luego el uso de esto por las tablas del rey don Alonso.

El segundo cuadrienio léase a Nicolás Copérnico, y las tablas Pruténicas en la forma dada, y en el tercer cuadrienio a Ptolomeo.

En la sustitución lea la Gnómica, que es el arte de hacer relojes solares.

El tercer año léase la Geografía de Ptolomeo, y la Cosmografía de Petro Apiano, y arte de hacer mapas, el Astrolabio, el Planisferio de don Juan de Rojas, el radio Astronómico, el arte de navegar.

En la sustitución el arte militar.

El cuarto año la esfera y la astrología judiciaria por el cuadripartito de Ptolomeo y Alcabisio corregidos. En la sustitución, teóricas de Planetas.

Obsérvese, pues, que en astronomía se mantuvieron el Almagesto, la Esfera, la astrología judiciaria, Peuerbach y las tablas alfonsíes como base del programa de estudios, ampliándose estos conocimientos clásicos con las tablas de Regiomontano, las de Copérnico o las Pruténicas de Reinhold (Reinoldo); con dos matices importantes: este estudio ya no era, como antes, al voto de los oyentes, sino obligatorio; y que se alude a las tablas Pruténicas, las más precisas en aquel momento. En la cátedra de sustitución (durante las vacaciones del profesor titular) se estudiaba algo eminentemente práctico que también se verá en otros apartados: el arte de hacer relojes de sol.

El aprendizaje de la geografía seguía basándose en la Geografía de Ptolomeo, añadiéndose el manual de cosmografía de Pedro Apiano, al astrolabio de Juan de Rojas (editados en 1551), la cartografía (el Planispherio de Juan de Rojas), el radio astronómico y el arte de navegar; en la cátedra de sustitución, el arte militar.

No fue profesor en Salamanca Juan de Rojas y Sarmiento, pero, como vemos, estos estatutos de la Universidad de Salamanca establecieron la obligatoriedad de utilizar sus libros sobre el astrolabio y la cartografía. En este caso el aprendizaje del astrolabio aparece especificado; se usaba para medir o localizar cuerpos celestes y observar su movimiento, determinar la hora a partir de la latitud o viceversa y para medir distancias por triangulación. Por su versatilidad, fue muy usado por ejemplo entre los árabes para calcular las horas de oración. Es bastante probable que, junto al astrolabio, se estudiaran también el cuadrante (cuarta parte del círculo dividido en grados) y su variante, el cuadrante geométrico; el anillo astronómico o sucinta esfera armilar, para el cálculo de la latitud; y la ballestilla o báculo de Jacob del que ya hablé (dos varas cruzadas perpendicularmente, útil para medir distancias y alturas). Rojas era hijo del marqués de Poza y acompañó a Carlos V en alguno de sus viajes, conociendo a los cosmógrafos relacionados con la corte, como a Hugo Helt, en cuyo planisferio se basó para crear el suyo. La obra sobre el astrolabio de Rojas que sabemos se usó en Salamanca se titulaba Illustris uiri D. Ioannis de Roias commentariorum in Astrolabium quod Planisphaerium uocant libri sex nunc primum in lucem editi... (Lutetiae: Apud Vascosanum, 1550; tuvo reedición en 1551, BGH 36638). En ella, con gran dominio de la geometría ptolemaica, dio a conocer la proyección ortográfica: sistema de representación de elementos geométricos o volúmenes en un plano, mediante la proyección ortogonal; de modo similar a como se obtiene la sombra generada por un lejano foco de luz. Este tipo de proyección, que lleva el nombre de astrolabio de Rojas, era fundamental para la construcción del plano del reloj de sol, que se basaba en el analema (la curva que describe por ejemplo el Sol observado todos los días del año desde la misma hora y posición).

Fig. 15: El tercero año... un introductorio de iudiciaria... Reprobacion de la astrologia judiciaria o diuinatoria sacada del toscano en lengua castellana. Salamanca: Juan de Junta, 1546. Portada.

Las matemáticas continuaron estudiándose por la Geometría de Euclides, aunque se añadieron también temas de agrimensura (considerada como el arte de medir la área de qualquier figura plana) y De signis rectis, de triangulis rectilineis y sphaereis de Christophoro Clavio, otro de los comisionados en Roma para la reforma del calendario, un gran matemático.

En conjunto, los estatutos de Zúñiga representaron un espléndido planteamiento docente en astronomía, que acogía novedades de gran calado científico, tanto teórico como práctico. Cabe suponer que tal reforma fuera quizá la culminación de un estado de cosas que se fraguara lentamente y estuviera en parte vigente en el momento de redacción del segundo informe salmantino, teniendo en cuenta la novedosa audacia para la época que había significado la introducción de Copérnico en los estatutos de 1561. El profesor Bustos (1973) explicó que esta inclusión de Copérnico no aparecía en la primera redacción que se hizo de ellos, del mismo modo que tampoco aparecía en los de Enríquez de Almansa, del año 1545, y que ésta se debió a la defensa de Copérnico que hizo en el claustro el profesor Hernando de Aguilera, catedrático de astronomía de 1561 a 1576. Fernández Álvarez (1974) estudió todos los libros de visita de cátedra de esos años y comprobó que en ninguno de los interrogatorios practicados a los estudiantes acerca de lo que se explicaba en clase se citó a Copérnico, concluyendo que, en la práctica, no debió de usarse la astronomía del De revolutionibus orbium coelestium para la docencia. Flórez (2006, p. 422) opina que quizá las ideas de Copérnico estuvieran presentes en las aulas salmantinas a partir de la llegada a la cátedra de Juan de Aguilera, en 1550, y conjetura que luego pudieron prohibirse. La polémica que supone el considerar o no la enseñanza de esta obra en las aulas salmantinas como un síntoma de modernidad y de avance, ha sido zanjada definitivamente por Mariano Esteban. Este investigador ha dicho que

...basta con examinar la cuantiosa documentación existente en la Biblioteca de la Universidad de Salamanca y en la Biblioteca Nacional para convencerse de que con toda seguridad se discutió [en Salamanca] el sistema heliocéntrico, aunque no parece por el contenido de esos manuscritos que llegara a aceptarse como realidad sino tan sólo como una ingeniosa hipótesis geométrica que servía para construir tablas más precisas con las posiciones de los seis planetas (Esteban Piñeiro, 2006, p. 370).

Bustos, Fernández Álvarez y los demás investigadores que han entrado en el debate han sido excelentes profesionales de la literatura o de la historia, pero no de la historia de las matemáticas. Por eso decía antes que la polémica está zanjada, porque el profesor Esteban es uno de los mejores (sino el mejor) de los conocedores de la realidad matemática de esa época y sus apreciaciones tienen un valor cualitativo indiscutible en este punto.

Se ha criticado mucho la falta de conocimiento de la lengua latina en la Universidad salmantina del Renacimiento, a pesar de ser de uso obligatorio reiterado en los estatutos de 1538, 1561, 1594 y 1625. Lucio Marineo Sículo hablaba de aversión de los españoles al latín (De las cosas memorables de España. Libri I-III). Abundan los datos que demuestran la falta de cumplimiento de esta norma, de lo que es ejemplo su misma reiteración. Gil Fernández recoge varios testimonios que así lo indican, como por ejemplo el del embajador de Venecia, Navagero (hacia 1524), quien afirmaba que en las universidades españolas, salvo en la de Alcalá, la docencia se realizaba en castellano (no en latín); que en la de Valladolid se explicaban en lengua vulgar hasta los textos latinos, y que cuando Diogo de Teive llegó a Salamanca para estudiar leyes en 1532, estimó que no había allí quien supiera latín (Gil Fernández, 2004, pp. 30-43). Ante la falta de cumplimiento de los estatutos en este punto, se crearon en Salamanca el Colegio Trilingüe (1550) y un colegio de gramática, pero incluso en ellos hubo problema en el uso de esta lengua culta. En los estatutos del Trilingüe se decía:

Tendrase especial y principal cuydado en los tales colegios de que hablen siempre latín los estudiantes en tanto grado que en ninguna manera se permita a ninguno, por nuevo o ydiota que sea hablar sino latín o griego, como mejor pudiere (estatuto 61, cf. Carabias Torres, 1983, p. 145 nota).

Sin embargo, en varias inspecciones a este colegio se sacó a relucir la continuada falta de cumplimiento de esta prescripción. Se observó incluso que el Brocense, profesor del mismo, contraviniendo todas las normas, llegó a prohibir a sus estudiantes hablar latín en la casa salvo en las horas de clase, argumentando ante los visitadores, que se lo recriminaron, la ineficacia de la práctica errónea de esa lengua. Yo he leído esto en una de las visitas realizadas al Colegio Trilingüe, pero lamento no recordar ahora en cuál.

Intentando obviar el examen de latinidad exigido en Salamanca para matricularse en cualquier facultad, los estudiantes se graduaban de bachilleres en Valladolid u otra. Pretendiendo evitarlo, Felipe II ordenó que nadie pudiera ordenarse de bachiller en ninguna universidad española sin presentar cédula y testimonio de examen en gramática latina (Esperabé de Arteaga, 1914, I, pp. 432, 486, 509; cf. Gil Fernández, 2004, p. 43).

Según se expresa textualmente en los estatutos universitarios salmantinos del siglo XVI, sólo hubo una excepción: la única enseñanza que se permitía en lengua vernácula era precisamente la de la cátedra de astronomía. Así se ordenó en función de los contenidos de esta materia de estudio. En este sentido, los profesores y estudiantes de esta cátedra fueron los únicos que se vieron libres del hándicap que podía suponer este desconocimiento políglota.

Tratando de comprender los informes salmantinos sobre la reforma del calendario, me ha parecido adecuado tener presente el paisaje científico contemporáneo en orden a interpretar su contenido. Sin embargo, sobrepasa a las posibilidades de este apartado un planteamiento global de las ciencias astronómicas y matemáticas en la Universidad de Salamanca a lo largo del siglo XVI. Por eso, me he decidido sólo a esbozar la forma de enseñar estas ciencias en la Universidad y el tipo de conocimientos que generaron los profesores salmantinos respecto de las materias relacionadas con esta reforma del calendario. No me parece fácil recordar en pocas líneas estas aportaciones sin caer en el simplismo; y, aun consciente de que se me podrá acusar de hacerlo, y de que todos los estudios que se publican sobre estos temas repitan machaconamente los datos, considero pertinente presentar el siguiente catálogo de información científica en astronomía y matemáticas. En él tendré en cuenta los datos de Esperabé de Arteaga, aunque no los cite pormenorizadamente.

Antes de la publicación del primer plan de estudios del año 1538 sólo podemos suponer la realidad didáctica de la astronomía en Salamanca a través de fuentes no legislativas y de los libros de cuentas que utilizó Esperabé de Arteaga para fijar la cronología, las materias y los profesores de este Estudio. Afortunadamente se han descubierto otros dos grupos de textos que permiten un acercamiento distinto, quizá más interesante, para el conocimiento de esta enseñanza en la segunda mitad del siglo XV: una especie de manual para clase elaborado, entre otros, por el catedrático de astronomía salmantino Nicolás Polonio, del año 1461, y unos apuntes de un bachiller en artes, quizá de Nebrija. Veámoslo.

1. El manual de Polonio

Cuando se produjo la primera solicitud a Salamanca de un informe sobre la reforma del calendario ya existía en ella cátedra constituida de astrología-matemáticas de cierta antigüedad; muy probablemente desde el año 1460, como hemos dicho. La primera noticia encontrada sobre esta cátedra se remonta a Nicolás Polonio (Nicholaus Polonius) —catedrático de astrología entre 1460-1464— (Chabás, 2002, pp. 59-94; Chabás 2006, pp. 29-36, Chaparro, 2002, p. 19), que según el avecindado en Salamanca, Pedro de Medina (1980, pp. 13 y 88), fue el autor de las Tabulae ad meridianum Salmantinum (figura 16), que forman parte hoy de un manuscrito muy complejo conservado en la Bodleain Library de Oxford (ms. Can. Misc. 27)[49]. Cabe la posibilidad de que su contenido no sea obra exclusiva de Polonio, y de que en estas tablas esté también la mano de Abraham Zacut y de Juan de Salaya (Burgueño, 2009a, p. 8), pero, en todo caso, este manuscrito iluminado contiene distintas obras que han sido estudiadas por varios profesores desde diferentes puntos de vista. Como dicen Chabás y Goldstein, constituye un conjunto desordenado de textos astronómicos en latín, tablas y representaciones zodiacales. El pasaje de Polonio (f. 122v.-129r.) fue transcrito por Porres y Chabás (1998) y sus 18 capítulos tratan sobre las Tabulae Resolutae, calculadas para Salamanca en el año 1460.

Fig. 16: Comienzo de las Tabulae ad meridianum Salmantinum (1461), de Nicolás Polonio.

Comienza diciendo que el documento se redactó como ayuda a la enseñanza de la astronomía en Salamanca en el año 1461 (facta ad Salmanticam anno currente 1461, tabla 2), como apoyo a la docencia de las tablas alfonsíes que eran excesivamente complejas para los estudiantes (véase la figura 17). Su contenido es un claro ejemplo de astronomía práctica, pues enseña a calcular las posiciones de los siete cuerpos celestes, sus ascendentes, la elaboración de almanaques, etc. La primera de las tablas asociadas a estos cánones de Polonio es la citada Tabulae ad meridianum Salmantinum, en las que se usan las tablas de ecuación del tiempo de las antedichas Tabulae Resolutatae, datos presentes en las tablas alfonsíes, con los signos zodiacales, que fueron publicadas por Johann Schöner (1477-1547), con prefacio de Melanchton, en Tabulae astronomicae: quas vulgo... resolutas vocant... per Ioannem Schonerum... correctae & locupletatae. Ratio... coeli, authore Ioanne de Monte regio... (Norimbergae: apud Io. Petreium, 1536). Sin duda son una simplificación de aquéllas. Se habla también de otras tablas de la misma fecha, igualmente basadas en las alfonsíes, llamadas Tabulae Verificate (elaboradas según dicen por algún otro profesor de astrología de Salamanca) y de otras en castellano que enseñaban la corrección de los eclipses, a hallar la paralaje en otras latitudes, las coordenadas geográficas y la entrada del Sol en los signos del zodiaco (Chabás-Goldstein, 2008, pp. 33 ss.).

Fig. 17: Detalle del comienzo del canon de las tablas astronómicas de Nicolás Polonio, donde se dice que se hicieron ante la dificultad que entrañaban las Tablas alfonsíes para los estudiantes de astronomía de Salamanca.

El ms. Can. Misc. 27 citado termina con unas ilustraciones que han sido analizadas de forma muy sugerente por García Avilés, quien las reproduce al final de su estudio, on line en <http://hdl.handle.net/10486/861>. Este profesor explica que son una versión gótica de la típica forma de representación islámica del zodiaco, con inscripciones en castellano de las correspondientes mansiones lunares, resaltando las estrellas que las señalan. Subraya también la diferencia existente entre las del ms. Can. Misc. 27 y las pinturas de Fernando Gallego en la bóveda de la Biblioteca de la Universidad de Salamanca (véase la fig. 3), rechazando que éstas se inspiraran en el Poeticon astronomicon de Higino (Venecia: Erhardt Ratdolt, 1482), como sugirió en su día Santiago Sebastián. Avilés opina que en dicha bóveda se aunaron la tradición florentina denominada Planetas Finiguerra y las ilustraciones del Liber introductorius de Miguel Escoto (García Avilés, 1994, pp. 39-60; 1997, pp. 135-172). Miguel Rodríguez Llopis (1997, pp. 161-162) ha analizado el aspecto científico de estas ilustraciones, lejos del carácter talismánico de las imágenes de las mansiones lunares antes frecuentes. Por eso tiene sentido la leyenda conservada en la bóveda que reproduce el Salmo 8, 3: Quoniam videbo celos tuos, et opera digitorum tuorum, lunam et stellas quas tu fundasti (cuando contemplo el cielo, obra de tus dedos; la luna y las estrellas que has creado); un recordatorio de que lo que vemos en el firmamento procede de Dios.

En conjunto, el manuscrito conservado en la Bodleian Library contiene lo más importante de la tradición astronómica del momento (representada en la Teorica planetarium, más elaborada que la Esfera de Sacrobosco) y las tendencias más novedosas en la astronomía contemporánea, como la estimación de las medidas del universo o las tablas de longitudes y latitudes realizadas para Lisboa. Es decir, que aunque no se pueda demostrar estatutariamente, en Salamanca hubo una importante tradición astrológica desde el último tercio del siglo XV; y casi todos los catedráticos de astronomía, y otros que enseñaban distintas materias, la practicaron (Rico, 1983, pp. 157-186).

Me he parado en esta documentación de época anterior a la cronología de mi trabajo por parecerme de especial importancia para demostrar que, aunque la base teórica de las explicaciones en las aulas salmantinas repitiera las obras clásicas, y aún cuando el contenido de los planes de estudio plasmado en los estatutos sea al principio tan parco, la información astronómica se contrastaba, matizaba y corregía con lecciones de astronomía práctica cuyo modelo de explicación de la realidad parecía haber abandonado tiempo atrás el sistema explicativo aristotélico-ptolemaico. De hecho, la crítica a la filosofía natural de Aristóteles había contribuido al desarrollo de las matemáticas y la astronomía desde el momento que se buscaron formulaciones de leyes que explicaran los fenómenos físicos. Pensemos, por ejemplo, en la tabla que permite averiguar la paralaje en otras latitudes, enunciado que ya estaba en la propia obra de Ptolomeo pero cuya explicación, por sí sola, choca con el sistema de las esferas homocéntricas que predominaba en los manuales clásicos de la disciplina en Salamanca[50]. Precisamente la medición de la paralaje nula de la nova de 1572 permitió después a Jerónimo Muñoz desmentir la incorruptibilidad de los cielos, antes de que esta afirmación la publicara Kepler. Lo sorprendente, en mi opinión, es que estas tablas salmantinas hablan de paralaje ciento once años antes, no ya del Harmonices mundi de Kepler, sino de la nova de 1572.

2. Los apuntes de clase de un aspirante al bachillerato en artes

Se ha hablado mucho y bien del ms. 98-27 de la Biblioteca de la Catedral de Toledo que en sus ciento treinta folios contiene una miscelánea incompleta de apuntes de un aspirante al bachillerato en artes de la época. El orden temático que ofrece comienza por las matemáticas, explicadas por el profesor de astrología, como era lo habitual; después lógica, retórica, gramática y filosofía natural, pero —como dice Rico— las reinas de esta miscelánea concreta son la elocuencia y las matemáticas, con muy especial énfasis en la astrología (Rico, 1983, p. 165 ss.; Chabás-Goldstein, 2008, p. 61).

Dentro de esta ciencia, en el manuscrito están la Theorica planetarum, Practica astrolabii, la Aritmetica speculativa de Bradwardine y el libro primero de los Elementos de Euclides. Entre sus novedades cabe citar los cánones explicativos de unas tablas calculadas para la longitud y la latitud de Lisboa (f. 123-124). En dos ocasiones se extracta la obra de Alfragano, ambas orientadas a precisar las medidas de la Tierra, en sí misma y en relación a las dimensiones del universo (f. 59r., 128r.-129r.). Quizá se discutieran las cifras dadas en De Caelo (II, 14), o las glosas de Santo Tomás al mismo texto, que se debatían en la clase de filosofía natural. Rico se pregunta si se contradecían o se apoyaban en Salamanca los datos de la Meteorologica (II, 5), de Alberto Magno y de Pierre d’Ailly, de cuyo comentario a los Meteorologica, figuran algunas páginas en este códice (f. 32r.-34v); y concluye afirmando que por lo menos esto indica que los salmantinos

...estaban perfectamente familiarizados con esos textos, con los problemas que planteaban, y que sus inquisiciones astrológicas se fundían con el empeño de aprehender una nueva imago mundi.

Y algo que cabe destacar: que este tipo de cuestiones entraban en los debates de quienes se iniciaban en el estudio universitario (Rico, 1983, pp. 190-191). Puesto que Nebrija estuvo en Salamanca hacia 1461[51] y dado que en la tabla de latitudes que incluye se ha añadido Lebrixa, 36º 40’, tanto Beaujouand (1971, pp. 12-13), como Rico o Chabás han interpretado que pudiera ser un manuscrito del propio Nebrija, considerando además una anotación exterior del libro también en este sentido.

Los textos didácticos de los que acabo de hablar son una prueba clara de lo que dicen Flórez-García-Albares, Chabás o Chaparro al hablar de las tres generaciones de intelectuales salmantinos: que, junto a la astrología teórica, se desarrolló en Salamanca la astrología tabular o calculadora, inquisidora de la medida de los fenómenos. Este tema está bien estudiado y sólo lo recuerdo en función de la necesidad de tenerlo presente para comprender el tipo de respuesta sobre el calendario que ofreció la Universidad de Salamanca.

La tendencia a la determinación matemática de lo observable es patente en las tablas astronómicas de Polonio. También lo es en las de Abraham Zacut, que —como dije— no llegó a ser profesor de astronomía en la Universidad, aunque fue el gran maestro salmantino del último cuarto del siglo XV, a instancias del obispo Vivero. A Zacut le interesaron especialmente los movimientos del Sol y de la Luna en orden a fijar las fiestas del calendario judío (Carrera de la Red, 2004). Sus tablas del Almanach perpetuum (Salamanca: 1478) corrigieron y mejoraron las de otros astrónomos judíos previos (Chabás-Goldstein, 2008, p. 63 ss.), y, junto a su trabajo Tratado breve de las influencias del cielo, se convirtieron en la nueva clave para la determinación de las posiciones planetarias (longitud del Sol, de la Luna, latitud en cualquier lugar de la Tierra, clima, pronósticos...), por ser las más precisas hasta entonces (véase la tabla titulada Residuum tabue differentiarum ascensionalium, figura 18). El obispo Gonzalo de Vivero tuvo una cuota importante de responsabilidad en este renacimiento de la astronomía salmantina, protegiendo y encargando estudios concretos a Zacut. Éste, habiéndose ido de Salamanca a Portugal por la expulsión de los judíos, trabajó también allí en la organización del viaje de Vasco de Gama, enseñando a los marineros a construir y manejar tablas náuticas, o calculando, por ejemplo, las latitudes por la altura meridiana del Sol.

Fig. 18: «Residuum tabue differentiarum ascensionalium». Fuente: ZACUT, A. (1502). Almanach perpetuu[m] exactissime nuper eme[n]datu[m] omniu[m] celi motuum...

La tradición que aúna teoría y práctica continuó en Salamanca en los sucesivos catedráticos de astronomía: El amigo de Zacut, Juan de Salaya (catedrático entre 1464-1469), comentó la Física y De Caelo de Aristóteles, tradujo al castellano el canon explicativo de Almanach perpetuum (1469) y escribió sobre el eclipse de Sol de 29 de julio de 1478, interpretándolo —esto es importante— como un signo astrológico; por eso decía: Aconteció un horrible eclipse de Sol en el que se vieron todas las estrellas y del que se seguirán, entre otros grandes males, pestes, muertes de pontífices y de príncipes, relacionando astronomía y astrología judiciaria.

Como ya sabemos, después siguieron Diego Ortiz de Calzadilla (catedrático de 1469 a 1475), Fernando de Fontiveros (de 1476-1480), Diego de Torres (catedrático entre c. 1481 y 1495) y Rodrigo Basurto (de 1495-1504), todos contemporáneos de Abraham Zacut. Diego Ortiz de Calzadilla llegó a Salamanca tras su paso por Bolonia y París. Mezcló los orbes celestes con la política y tomó partido por Juana la Beltraneja en la Guerra de Sucesión castellana a la muerte de Enrique IV, basándose en una predicción astrológica que aseguraba el triunfo militar portugués. Esta imprudencia le obligó a expatriarse, pasando a la corte de Juan II de Portugal y después de su sucesor. Allí intervino como cosmógrafo en dos negocios particularmente importantes: para refutar el plan colombino en 1483 y en la preparación de una carta de itinerario fija de Pedro de Covilhã (que debía atravesar el Mediterráneo y bajar al Mar Rojo en busca de las Indias y del reino de Preste Juan); misión terrestre que tuvo lugar en 1487. Acabó siendo obispo de Ceuta. Su cátedra se dio por vaca en Salamanca el 19 de abril de 1475 ante su ausencia. Como sabemos, le sucedió en la cátedra salmantina Fernando de Fontiveros, por poco tiempo, pues dejó todo para hacerse franciscano en 1481.

El siguiente catedrático predicho, Diego de Torres, fue también autor de libros teóricos y prácticos sobre predicción de eclipses, horóscopos, etc., como por ejemplo el Eclipse del Sol. Medicinas preseruativas y curatiuas y remedios contra la pestilencia que significa el eclipse del sol del año de mil cccc.lxxxv a xvi de março (Salamanca 1485), editado por Amasuno, que sigue la tradición de relacionar astrología y medicina, proponiendo prevención y remedios ante el acontecimiento. También el Pronostico o Juyzio nueua y sutilisimamete sacado por... fray Diego de tores... Sacado de lo mas cierto de toda la astrologia. Y ve hasta el año de veynte y cinco... (s.l.: s.i., s.a. 1520?); un Astrologicum commentarium (Salamanca, 1487) que citan Beltrán de Heredia y otros, difícil de identificar; o los cuatro tratados de su Opus Astrologicum (BNE, ms. 3385), que fue acabado el 25 de mayo de 1487 y publicado por Susana Burgueño, escrito en castellano, aunque con introducción y explicit en latín. En este último ofrecía al lector conocimientos para confeccionar un horóscopo, predecir eclipses, utilizar un astrolabio, usar tablas astronómicas, etc., y quizá fuera también el traductor de la Esfera de Sacrobosco, en 1484 (Burgueño, 2009a; 2009b; Chabás 2006, p. 34).

Como apunté antes, el sucesor de Torres en la cátedra de astrología fue Rodrigo Basurto, que también mantuvo esta tradición teórico-práctica en su Additamentum ad calendarium Johannis de Monteregio [Salmanticae: Leonardus Hutz et Lupus Sanz (c. 1497)]. Investigó sobre instrumentos astronómicos, geográficos y de medida, polemizando con la obra de Monterregio, o remitiendo a Juan Hispano para la construcción de relojes. En Salamanca, en 1494, había publicado el Tractatus de natura loci et temporis. De carácter eminentemente práctico fue también su De fabricandi unius tabulae generalis ad omnes partes terrae et usu eius ad facilem Astrolabii compositionem; hacia 1497 publica Praxis pronosticandi; y el Additio ad tractatum Astrolabii, que según Rezábal y Ugarte en su Biblioteca... (1804) empezaba: Utile et necessarium additamentum... ad Kalendarium Ioannis de Monte Regio, germani, de conficiendis horologiis aut instrumentis in eo contentis. En 1497 predijo la muerte del príncipe Don Juan, lo que le otorgó gran fama como astrólogo, pero también la desaprobación de los reyes y el abandono de la cátedra, declarada vacante el 12 de julio de 1504; por último los reyes ordenaron su rehabilitación. Según dice Beltrán de Heredia, él mismo volvió a opositar a dicha cátedra cuando se publicó esta vacatura, pero la sacó Sancho de Salaya (catedrático de 1504 a 1542).

Aunque los datos escasean hacia atrás, a mí me parece que hay indicios para afirmar que esta tradición astrológica de la denominada primera generación salmantina nació un poco antes; que progresó en parte relacionada con la llamada Escuela de medicina del último tercio del siglo XV y que estuvo ligada al Colegio Mayor de San Bartolomé de Salamanca. A propósito de su antigüedad, Hernando del Pulgar decía sobre Alfonso Fernández de Madrigal, el Tostado (1404-1455):

E así mismo en el arte de la astrología e astronomía no se vido en los reinos de España, ni en otros extraños se oyó haber otro en sus tiempos que con él se comparase. Estos y otros estudios los adquirió en la Universidad de Salamanca (Claros varones de Castilla, tit. 24).

El Tostado había sido colegial (desde 1433) y después rector de San Bartolomé, igual que el maestro en artes Pascual Ruiz de Aranda, colegial desde 1449 y catedrático de filosofía natural desde 1456 hasta 1476 en que se jubiló explicando la cosmología aristotélico-ptolemaica. Después hablaremos de cómo el maestro Juan de Ortega logró ser catedrático de filosofía natural entre la regencia de esta cátedra por parte de otros dos bartolomeos, Martín Navarro y Martínez Silíceo. Todo parece indicar que habría que adelantar el nacimiento del llamado por Flórez y Chaparro colegio invisible de astrólogos del Colegio Mayor de San Bartolomé, que según ellos comenzó poco después de la creación de la cátedra de astrología de la Universidad (1460-61). A partir de esta creación, el monopolio de los bartolomeos sobre esa cátedra es clarísimo, pues la ocuparon el arriba citado Juan de Salaya, colegial de 1459-1467, que tras la cátedra de astrología (1464-1469) pasó a la de lógica. Después, según he dicho, su sucesor en la vacante sería Diego Ortiz de Calzadilla, que había ingresado en San Bartolomé dos años antes, el 25 de noviembre de 1457. El sucesor de éste, Fernando de Fontiveros, también becario de San Bartolomé desde el 5 de mayo de 1472. Tras Diego de Torres, que no era colegial, siguió el bartolomeo Rodrigo Basurto, admitido en el colegio el 17 de julio de 1495. Como vemos y como ha sido repetido cien veces, esta cátedra de astronomía estuvo casi siempre ocupada por estos colegiales en la última parte del siglo XV.

Lo que yo no he visto escrito aún es que los colegiales del Colegio Mayor de San Bartolomé no sólo monopolizaron esta cátedra, sino todas las de prestigio, en la medida que pudieron. En este sentido opino que este colegio invisible no sólo fue de astrólogos, ni comenzó en 1464 (con Juan de Salaya), como se ha dicho, sino que el colegio visible de San Bartolomé amplió el monopolio sobre la astronomía universitaria al campo de otras ciencias y desde una cronología bastante más temprana. En mi opinión el peso colegial es notorio desde 1433 —quizá desde antes—, coincidiendo justamente con la época en la que empieza a haber más datos, con la entrada de el Tostado en la institución y con la ampliación de su biblioteca, y en cierta medida propiciado por ello. Contra esta afirmación mía escribió en su día Beltrán (1972b, p. 245) que el resplandor mortecino de estas luces a punto de extinguirse impresiona a veces los ojos del historiador con fulgores de pleno día. A mí me parece que esto es discutible. El ambiente cultural salmantino fue rico y diversificado en ciencias a lo largo de los siglos XV y XVI, no mortecino.

Marcelino V. Amasuno se ha referido a la Escuela de medicina en su obra La escuela de medicina del estudio salmantino: (siglos XIII-XV). A través de las recién creadas cátedras cursatorias (siglo XV), se formaron algunos de los astrólogos. Nicolás Polonio, titular de astrología, era médico de los Reyes Católicos. También Diego de Torres, antes de ser catedrático de astrología, fue sustituto de varios profesores de medicina hasta 1496 (Amasuno 1972, pp. 114 ss.; Burgueño 2009a). Recuérdese que Torres fue el autor del primer tratado de medicina astrológica (Eclipse de Sol...) y de la Obra astrológica.

En realidad, a pesar del recelo que generará la astrología judiciaria en la segunda mitad del Quinientos, la astrología siguió considerándose un conocimiento imprescindible para los médicos y de ahí obras como la titulada «Astrología judiciaria y Esfera para médicos. Valladolid 1599» (ed. Anastasio Rojo Vega, en 2010).

La riqueza del ambiente cultural del que hablo se reflejó en la contribución de docentes salmantinos a la resolución de problemas prácticos. Es seguro que varios profesores se entrevistaran con Cristóbal Colón en abril de 1486 —aunque fuera a nivel particular— sobre la viabilidad de su proyecto (Espinel-Hernández, 1988; Lorenzo Sanz, 2006; Rico, 1983; García Castillo, 2006). Entre ellos, seguramente su mentor, fray Diego de Deza, el catedrático de prima de teología en la salmantina en ese momento (1480-1486); o su sucesor, catedrático de 1487 y 1503, fray Juan de Santo Domingo; o fray Tomás Durán, que más tarde sería el primer catedrático de matemáticas de la Universidad de Valencia, en 1503 (Robles, 1976) y después de filosofía (1509 a 1512) en Salamanca (Beltrán de Heredia, 1970b, p. 277 ss.), colaborador en la edición de las obras del calculador Bradwardino (1290-1349) que salieron a la luz como Preclarissimum mathematicaru[m] opus..., en Venetie: Ioannem Iofre, 1503. Más tarde, en 1524, otros dos profesores salmantinos, Tomás Durán y Sancho de Salaya, fueron nombrados como comisionados para la Junta de Badajoz-Elvas, sobre la pertenencia de las islas Molucas. Durán ya había participado en la Junta de Burgos de 1512, que elaboró leyes para las Indias. O sea, que varios universitarios salmantinos fueron en esos momentos actores en el tránsito de la cartografía oficial a la cartografía jurídica (Sánchez Martín 2009).

Tras este grupo o primera generación de astrólogos, con fuerte impregnación del Colegio de San Bartolomé, la astronomía teórica y práctica dejó de ser casi monopolio de dicho colegio y se expresó en Salamanca en obras de profesores que no fueron catedráticos de la materia y con los que se inaugura un nuevo paradigma cosmográfico. Esta segunda generación de intelectuales humanistas trabajaron desligados de esta docencia de la astrología debido a que, de 1504 a 1542, dicha cátedra estuvo ocupada (pero casi nunca regida) por el hijo del antiguo catedrático Juan de Salaya, Sancho de Salaya, el que acabo de citar como comisario en las Juntas de Badajoz-Elvas (1524). Había sido colegial de Santa Cruz de Valladolid (desde 1500) y consiguió mantener la titularidad de la cátedra salmantina mientras él trabajaba como protomédico de la Inquisición y médico de la emperatriz. Esta ocupación de carácter semi-político no le dio opción de mantener el liderazgo investigador en la salmantina de sus antecesores en la cátedra, a pesar de que escribió un Repertorio de los tiempos nuevos muy del gusto académico de la época (Zaragoza, 1536).

A esta segunda generación desligada de la cátedra de astronomía pertenecieron, según Flórez y otros, Antonio de Nebrija, Hernán Núñez, el Pinciano —que no se dedicó a la astronomía ni sus adyacentes— y Núñez de la Yerba: grupo que se inclinó hacia la lectura y al fino comentario de los clásicos, aunque sus textos resultaron igualmente cercanos a la ciencia práctica. Su esfuerzo promovió una inflación de la cosmografía a partir de la nueva imagen del mundo que surge en las aulas universitarias salmantinas con la Cosmographia Pomponii de Núñez de la Yerba y el In cosmographiae libros Introductorium de Nebrija, llegando a su culminación, en la siguiente generación, con el Phisices Compendium de Margalho (Flórez-García-Albares, 1990a, p. 12).

De la misma forma que los médicos justificaban la necesidad del conocimiento de la astrología para el ejercicio de su trabajo, Núñez de la Yerba reclamará la formación en cosmografía tanto para médicos como para filósofos, físicos naturales, astrónomos o teólogos.

Este sentido guió algunos tratados de Antonio de Nebrija (1441-1522): había conocido en Bolonia la Geographia de Ptolomeo y, entusiasmado, escribió su In cosmographiae libros introductorium (sin indicaciones tipográficas, pero editado en Salamanca, 1498), dirigida a don Juan de Zúñiga; obra en la que —según María Fernanda Alegría (Las relaciones entre Portugal y Castilla..., 2006, pp. 117 ss.)— por primera vez se alude a los territorios descubiertos. Es un texto de carácter científico que aboga por la precisión y la cuantificación de los fenómenos físicos, así como por la posibilidad de representación de la Tierra en un plano, igual que la de Ptolomeo. Calcula la circunferencia terrestre, no el grado de meridiano como se dice, aunque en realidad, lo que recoge su capítulo VI es la tradición de equivalencias conocidas: 1 estadio = 125 pasos; 1 milla = 8 estadios = 1.000 pasos... (más sobre medidas en Szaszdi Nagy, 1991). Arrastrado por la moda de la precisión, desarrolló el problema en tres relecciones o repeticiones universitarias: La sexta sobre las medidas (De mensuris); la séptima sobre los pesos (De ponderibus), dictada en 1511; y la octava sobre los números (De numeris), expuesta en 1512 (BGH 33811; Flórez-García-Albares, 1990a). Desde nuestro punto de vista, la más interesante es la relección sexta, dictada el 11 de junio de 1510, mientras era catedrático de retórica; en ella ordena alfabéticamente las medidas extraídas de monumentos y caminos romanos (Mérida, Vía de la Plata...) y ha sido muy bien estudiada por Jenaro Costas (Salamanca, 1981) (véase la figura 19).

Llama la atención la importancia que Nebrija otorga a los saberes útiles basados en la observación y en la medición, frente a los enciclopédicos, aunque no estoy convencida de que los pusiera realmente en práctica; en la primera página de su repetición sexta dice:

Pues aunque en los autores antiguos leemos todos los días muchas cosas que nos son desconocidas del todo punto o en su mayor parte, el ignorar algunas de ellas no supondría, con todo, perjuicio alguno para nuestra vida. Hay otras, en cambio, que son muy distintas: sin ellas muchas cosas creadas por nuestros antepasados para utilidad pública no pueden llegar hasta nosotros y el mantenerse en su ignorancia es cosa no sólo desastrada sino también vergonzosa (cf. Carabias Torres 2000, p. 197).

Fig. 19: NEBRIJA, Antonio de. Repetitio sexta. De mensuris [Salmanticae: Joannes de Porras].

Después explica cómo averiguó la medida del pie romano a partir del intervalo entre los miliarios de la Vía de la Plata y de las proporciones del teatro de Mérida; para ello dice haber utilizado una cuerda que ni se encogía ni se estiraba... No es que yo quiera enmendar la plana a uno de los más grandes intelectuales de la historia, pero me pregunto si con esos medios se puede presumir de precisión, como él hizo: era la precisión posible en la época. En el capítulo VI de su cosmografía dijo:

Midiendo yo estos espacios con pasos ahora contraídos, ahora estirados, averigüé que tenía de los míos cerca de mil quinientos [pies].

Nebrija podía ser algo petulante, pero nada ingenuo, de modo que nunca se atrevió a poner este supuesto patrón del pie romano a la vista de todos, en la puerta de la biblioteca de la Universidad, como varias veces adelantó. A mí me cabe la sospecha de que nunca la supo con certeza.

Este tipo de estudios sobre magnitud, medida o proporción fueron incentivados por las necesidades políticas de determinación de la raya de los Tratados de Tordesillas (1494), la disputa hispano-portuguesa sobre las islas Molucas (1524) o el problema del calendario...; atraían a los humanistas y los tratados sobre esta temática fueron abundantísimos. Su moda se expandió geográfica y cronológicamente entre los intelectuales que se vieron tentados a intentar determinar tanto la dimensión del pie romano como la clave para la fijación de la longitud, que sólo logró Harrison (1693-1776), con la invención de su cronómetro, mucho después (Sobel, 1997).

En este sentido no debe ser una casualidad el que, dentro del mismo incunable de la Biblioteca Universitaria de Salamanca (BGH 184) se encuentren unidas la repetición sexta sobre las medidas de Nebrija con la obra de Núñez de la Yerba (c. 1464-después de 1504) Cosmographia pomponii cum figuris [per Fra[n]ciscu[m] nuñis de la yerua... (Impressu[m] uero Salma[n]tice: [s.n.], 1498), antes citada. En esta obra, que se edita el mismo año que la Cosmografía de Nebrija, se ofrece también un estudio de las medidas terrestres a través de una tabla de longitudes y latitudes de noventa y cuatro lugares de la Tierra. En su folio Aiiii establece las medidas del ecúmene en los siguientes términos:

De donde se colige que la longitud el orbe conocido sobre el arco del círculo equinoccial es de noventa mil estadios y sobre el paralelo más austral es de ochenta y seis mil trescientos treinta y tres aproximadamente. En cambio, en el paralelo más septentrional es de cuarenta mil ochocientos cincuenta y cuatro (Ed. Flórez-García-Alvares, 1990a, pp. 127-223).

La tercera generación, la de los físicos, fue contemporánea del surgimiento y consolidación del nominalismo, de la integración de tradición clásica con el Renacimiento, de la implantación en Salamanca de la moda didáctica parisina y del primer informe salmantino sobre la reforma del calendario (1515). Representantes indiscutibles fueron Juan de Oria, Pedro Margalho, Juan Martínez Silíceo, Fernán Pérez de Oliva, Miguel Carenas, Alonso de Córdoba y Pedro de Espinosa. Casi todos escribieron sus principales obras después de la redacción de este informe, pero sus publicaciones sobre esta temática pudieron haber sido aprovechadas por los redactores del informe sobre el calendario de 1578.

Juan de Oria era maestro en teología en la salmantina en 1510 y catedrático de Biblia más tarde, período en el que fue denunciado por los dominicos ante el papa por las proposiciones de dudosa ortodoxia que enseñaba.

Miguel Carenas vino de Alcalá a Salamanca en 1511 a explicar la cátedra de filosofía natural, y en ella enseñó la física de Buridán hasta abril, en que decidió marcharse (Fuertes Herreros, 2006, p. 550)

Pedro Margalho (1474-1556) era un teólogo humanista que también se sintió arrastrado por la moda computacional e imbuido por el pitagorismo, según García Castillo («La presencia del pitagorismo...», 1988, pp. 171-178). Su vida y su obra han sido muy bien estudiadas también por Flórez-García-Albares (1990a, pp. 67-122 y 238-371). Por eso sólo aludiré a la ya citada, Phisices Compendium como una síntesis de cosmografía, de base aristotélico-ptolemaica, influida por Arato, Proclo, Cleomedes, Higinio, Vitrubio y otros; autores relacionados con el neopitagorismo y con la antigua tradición de la geometrización del espacio.

No tenía toda la razón Cortesão cuando le acusaba de escasa originalidad y de desconocer los descubrimientos geográficos portugueses, habiendo quedado anclado en las teorías ptolemaicas. Como Margalho quería subrayar la conexión entre los fenómenos celestes y los terrestres, en relación con ellos puso toda una serie de mitos o fábulas que han pasado a formar parte de la tradición occidental (Chaparro, 2008, pp. 20-21; Flórez; García; Albares, 1988). Pero más allá de estos cuentos, a pesar de que la obra fue concebida como un manual y que, por tanto se supone que buscaba la simplicidad, introdujo datos novedosos derivados de la ciencia práctica, basados en la experiencia de los navegantes, como también lo haría después Pérez de Oliva en su Cosmografía nueva. Dice Margalho:

Supongamos nuevamente, según usanza astrológica, que el mapa se divide en trescientas sesenta miríadas, que los nuestros llaman grados..., según el cómputo de los modernos navegantes, se le echan en tierra dieciséis parasangas con media y un sexto (f. iiii col. a).

En función de ello, hay que recordar, como ejemplo, la correspondencia que Margalho estableció entre un grado y 16 leguas y 2/3 (que era la cifra más aceptada por los navegantes portugueses del momento). Al final del pasaje, Margalho subraya la diferencia de la medida del grado usada por Ptolomeo (15 leguas y 1/2) y por Waldseemüller (16 leguas). Aunque cabe reconocer también que algunas imprecisiones expresadas en los folios 3v.-4r. del libro serán el punto flaco que aprovechen los comisionados españoles de la Junta de Badajoz-Elvas en 1524 (entre los que dijimos estaban sus antiguos compañeros de universidad Sancho de Salaya y Tomás Durán) para reclamar a Portugal la posesión de las islas Molucas, a cuya comisión asistió también Margalho como uno de los representantes portugueses.

No hay solución de continuidad entre el siglo XV y el siglo XVI en materias astronómicas y matemáticas. El ambiente científico creado por los matemáticos es un elemento nada despreciable a la hora de comprender la precisión en el cálculo de la respuesta salmantina al papa sobre el calendario. Aunque algunos la critiquen, es clásica ya la explicación de la historia de las matemáticas en la España del siglo XVI hecha por Rey Pastor, dividiéndola en tres períodos: En los primeros veinte años del siglo XVI progresaron los aritméticos, algunos de los cuales habían enseñado en la Universidad de París, bastante maltratados en la exposición de Rey Pastor. Entre los de este grupo este autor destaca a Juan Martínez Silíceo, Pedro Sánchez Ciruelo, fray Juan de Ortega, Gaspar Lax, Álvaro Tomás... Tras ellos, y después de una laguna editorial en la que no aparecen más obras que la reedición de las previas, se recibió el impulso novedoso de los aritméticos algebraicos, especialmente desde Italia y Alemania, aunque también desde Inglaterra y Francia, desarrollándose esta faceta en nuestro territorio por Marco Aurel, Pérez de Moya, Antich Rocha y Pedro Núñez. A partir de mediados del siglo XVI, en una tercera fase, adquirieron el liderazgo los geómetras, con la fundación de la Academia de Matemáticas por Felipe II y las figuras de Andrés García de Céspedes, Rodrigo Zamorano, Molina Cano y Jaime Falcó. En esta última fase, pasaron al punto de mira del debate el cálculo de áreas, volúmenes y centros de gravedad, las asíntotas, la correlación de los poliedros, las propiedades de las cónicas, los sectores, la Trigonometría... (Rey Pastor, 1913, p. 126; Garma Pons 1998, pp. 155 ss.). Siguiendo este crecido interés por las matemáticas, el informe salmantino de 1515 (el primero de ellos), concluye añadiendo una disertación sobre el calendario hebreo con unas proposiciones —como dice— al estilo de los matemáticos. El hábito en el cálculo mental del redactor o redactores de este texto, quedó reflejado cuando se dice:

Intencionadamente nos abstenemos de poner ejemplos para asignarlos, puesto que esto lo escribimos para aquellos de quienes no dudamos que basta y sobra a su perspicacia haberlo indicado sumariamente, quienes con tan sólo oír lo primero, vuelan raudos a lo último de todo con increíble rapidez (Informe de 1515, canon tercero, p. 291 de este texto).

Este ambiente calculador se vio también reflejado en el surgimiento del pensamiento económico de la Escuela de Salamanca (Gómez Camacho-Robledo, 1988). Recordemos que el nacimiento y el desarrollo de esta Escuela matizó las bases del derecho y la justicia (de donde proceden la Declaración Universal de los Derechos Humanos, el derecho de gentes, el desarrollo del concepto de soberanía y el concepto de guerra justa), promovió el nacimiento de la ciencia económica, e impulsó notablemente la teología (acotando temas como la existencia del mal en el mundo o la polémica De auxiliis —gracia y predestinación—). Los escolásticos de la Escuela de Salamanca describieron la realidad económica, encauzando la explicación del florecimiento en España del capital mercantil. En esa evolución la teología y la economía entrecruzaron sus rutas en las obras de Vitoria, Soto, Azpilcueta, Mercado, Molina, Suárez... No se debe olvidar que «La Economía nació en Salamanca», según el título de un artículo de Rodríguez Suanzes publicado en El Mundo, el domingo 3 de enero de 2010; y nació cronológicamente entre los dos informes sobre el calendario. Gómez Camacho (1999, p. 129 ss.) explicó con claridad meridiana, que los doctores españoles, siguiendo la tradición escolástica que arranca del siglo XIV, razonaron sobre cuestiones económicas basándose en el lenguaje matemático; que al aplicar el razonamiento matemático al problema de la tasa del precio medio del trigo, Melchor de Soria usó el teorema del valor medio, ya empleado y aplicado por los calculadores de Oxford y por Domingo de Soto a la caída de los cuerpos. La interpretación de ese fenómeno ha sido bastante debatida y José Barrientos es partidario de restringir la denominación de Escuela de Salamanca al período de 1526 a 1629, aplicándola exclusivamente a los dominicos de San Esteban con actividad docente e investigadora (Barrientos 1998, p. 99; véase también Flórez, 1998). Pero incluso teniendo en cuenta esta restricción, no cabe duda de que la evolución de la ciencia económica en Salamanca pudo ensanchar el paisaje científico ambiental de los redactores del segundo informe sobre la reforma del calendario.

Si también queremos tener presente la producción en astronomía y matemáticas de quienes estuvieron de alguna manera ligados a la Universidad de Salamanca en los períodos en el que se debatió el tema del calendario, cabe recordar a quienes generaron conocimiento en estas materias y lo imprimieron; entre ellos no podemos olvidar a: Juan Martínez Silíceo, Fernán Pérez de Oliva, Pedro Sánchez Ciruelo, Diego del Castillo, Pedro López de Espinosa, Rodrigo Dosma Delgado, Alonso Pérez, Andrés Laguna, Gabriel Gómez, Bartolomé de Barrientos, Andrés de Poza, el Brocense, Juan de Aguilera, Juan Pérez de Moya, Pedro Núñez... Sin duda también otros pudieron influir en los intelectuales salmantinos, porque la comunicación científica era fluida. En este sentido habría también que recordar a Martín Cortés, Juan López de Velasco, Jerónimo Muñoz, Gaspar Lax, fray Juan de Ortega, Jerónimo Salvador, Juan Martínez Guijarro... pero ellos no tuvieron nada que ver con la Universidad de Salamanca durante la elaboración de esos informes y por eso no citaré aquí sus obras, aunque sean destacables. La mayoría de ellos estudiaron o enseñaron en varias universidades, españolas y foráneas, teniendo la posibilidad de contrastar y completar los saberes recibidos en Salamanca. Sin estos contactos probablemente no se hubiera producido en Salamanca el cúmulo de conocimientos que se produjo. A continuación, pues, aludo brevemente a los autores y textos de astronomía-matemáticas que se conocieron en Salamanca entre 1515 y 1578, fechas de los informes sobre el calendario.

El ambiente cultural de Salamanca en la época de Juan Martínez Silíceo (1477-1557) fue analizado específicamente por el profesor Cirilo Flórez en un estudio titulado Arzobispos de Toledo, mecenas universitarios (coord. por F. Llamazares y C. Vizuete, 2004, pp. 111-142), al que remito. Un somero balance sobre el personaje habla de una trayectoria vital verdaderamente movida, pues habiendo nacido de una familia humilde, logró salir de su Llerena natal y estudiar en Valencia y París, llegando a ser profesor de la Sorbona. Pasó de allí al Colegio Mayor de San Bartolomé de Salamanca, en 1517 (colegial n.º 245 de Roxas y Contreras), empezando a enseñar en su Universidad en un curso de artes (1517-1522), más tarde en la cátedra de lógica nominal (1518-1522) y por último en la de filosofía natural (1522-1525). Su objetivo en la salmantina fue instaurar el nominalismo en la Universidad (Flórez, 2006, p. 412). Coincidió con Margalho en Valladolid en la junta que examinó las obras de Erasmo (1527) y ofreció una respuesta a la consulta sobre el divorcio de Enrique VIII. Siendo canónigo magistral en Coria en 1525, recibió el nombramiento de preceptor del príncipe Felipe (II) en 1534. Después fue nombrado obispo de Cartagena (1541) y promovido al arzobispado de Toledo (1546), cargo en el que fallece como cardenal, el 31 de mayo de 1557.

Este científico de vida itinerante, coincidió con Pedro Ciruelo y fray Juan de Ortega en concebir las matemáticas como un camino de acceso a la verdad, al conocimiento divino. Su pericia en esta ciencia fue reconocida en su época y se sigue reconociendo hoy en día. El libro Ars arithmetica Ioannis Martini Silicei, in theoricen & praxim scissa, omni hominu[m] co[n]ditioni perq[uam] vtilis & necessaria (Paris, 1514; reimpreso en esa misma ciudad en 1518, 1519 y 1526 y luego en Valencia en 1544), ha sido estudiado y traducido al castellano en 1996 por Cobos Bueno y Sánchez Saler, quienes explican que el autor organizó su contenido en dos partes. En la primera expone la tradición grecolatina en aritmética pitagórica siguiendo a Moderato de Gades, Nicómaco de Gerasa y Boecio, tratando del concepto de número y sus propiedades, proporciones, representación gráfica de números planos y sólidos y los distintos tipos de media (aritmética, geométrica y armónica). En la segunda parte incluye las tradiciones árabe y la de los calculadores, como haría también Sánchez Ciruelo, y expone las operaciones elementales, el sistema de numeración decimal, la extracción de raíz cuadrada y cúbica, las pruebas para comprobar que las operaciones estaban bien hechas, uso del ábaco, fracciones físicas o astronómicas, la división de la esfera celeste en doce signos, sus grados, minutos, segundos..., quebrados y regla de tres. Esta Ars arithmetica ha sido considerada como una de las obras de matemáticas más importantes de los españoles del siglo XVI, en la que incardina la aritmética especulativa y la mercantil, aunque Rey Pastor le reproche la ausencia total de la notación algebraica, de la que tanto se sabía en Italia. Dice Flórez que su forma de expresar la aritmética está relacionada con los que pretendían articular la retórica y las matemáticas, convirtiendo éstas en un modelo de conocimiento cierto. Así lo estimó Fineo (1494-1555), que en 1531 decía que la excelencia de las matemáticas derivaba de su posición intermedia entre la ciencia natural y la divina (Flórez, 2006, p. 414). En la reedición parisina de esta obra realizada en 1526 con el título Arithmetica Ioannis Martini Silicei..., el autor incluyó un prólogo sobre las partes de las matemáticas. Con posterioridad, editó también Arithmetic Silicei nuper permultis mendis vindicata & comentariorum proxilitate. Valentiae: excudebat Ioannes Mey, 1544. Las obras de Silíceo constituían, pues, una importantísima aportación a los cálculos necesarios para diseñar una reforma del calendario en la segunda de las consultas papales, pues ya vimos que llegó a Salamanca cuando había pasado la primera.

Otro intelectual ligado a Salamanca que dejó poso científico en esta temática fue Fernán Pérez de Oliva (1494-1533), cuya actividad literaria ha sido estudiada por Pedro Ruiz Pérez en varios trabajos editados en 1987, 1988, 1993 y 1994; y por María Luisa Cerrón Puga (1991), J. M. Ansino Domínguez (1995), Eduardo Pérez Rasilla (1995), María Jesús Pérez Ibáñez (1996), Raúl Marrero-Fente (2001), María José Vega Ramos (2002 y 2009), etc. El humanista Pérez de Oliva se formó en la salmantina (tres cursos), en Alcalá (un curso) y en París (doce años, en alguno de los cuales tuvo por maestro a Martínez Silíceo) y vivió en Roma (tres años) bajo la protección de León X. Ya como profesor en Salamanca, desde 1525, sustituyó al maestro Margalho en la cátedra de filosofía moral y a Martínez Silíceo en la de filosofía natural en el verano de 1526. Su valía le hizo merecedor del nombramiento para asistir a la Junta de Valladolid de 1527 que evaluó las obras de Erasmo. Llegó a ser rector de la Universidad de Salamanca en el curso 1528-1529, en cuyo mandato se elaboró el proyecto de estatutos (1529) del que ya he hablado, y después regentó la cátedra de teología nominal (1530-1531). A pesar de su corta vida, su variada formación le permitió explicar y escribir sobre temas rigurosamente nuevos en su tiempo, que han sido tratados por Flórez-García-Fuertes en la edición bilingüe de su Cosmografía nueva (Salamanca, 1985) y por Pedro Ruiz Pérez en su tesis doctoral: «Fernán Pérez de Oliva y la crisis del Renaciento» (2008: <http://hdl.handle.net/10396/184>). Entre sus obras cabe citar la perdida biografía de Colón, sus adaptaciones del teatro clásico, su empeño en pro del castellano y los diálogos (sobre el uso de las riquezas, la dignidad del hombre, la castidad)... Dentro de sus escritos, los que interesan a la historia de la astronomía y las matemáticas fueron el Dialogus inter Siliceum, Arithmeticam et Famam que acompañó la publicación del Ars Arithmetica de su maestro Martínez Silíceo (París, 1518), el Razonamiento sobre la navegación por el Guadalquivir, escrito en 1524 y publicado por Ambrosio de Morales, la citada Cosmografía nueva, De lumine et specie y De magnete. En sus apuntes sobre luz y perspectiva, Pérez de Oliva, explicó la confluencia entre la teoría científica de la perspectiva y la práctica de los pintores (Flórez, 2006, p. 411); pero su verdadero valor para quienes tuvieron que elaborar el proyecto sobre el calendario fue su contribución a la revolución cosmográfica que fue previa a la revolución científica.

Su sobrino, Ambrosio de Morales, recopiló parte de sus trabajos que vieron la luz en dos publicaciones distintas casi simultáneas: Las obras del maestro Fernán Pérez de Oliva (Córdoba: Bejarano, 1582?) y Las obras del maestro Fernan Perez de Oliua natural de Cordoua...: con otras cosas que van añadidas, como se dara razon luego al principio (Córdoba: Bejarano, 1586).

Otro científico que contribuyó a la ampliación de los conocimientos astrónómico-matemáticos en la Salamanca del siglo XVI fue el matemático y teólogo Pedro Sánchez Ciruelo (c. 1491-1580). Su obra entendida como una enciclopedia del saber fue también estudiada por Flórez-García-Albares (1990b; Flórez 2006); su figura por Santiago Garma (1992), Ayala Martínez (1993), su humanismo científico por Jorge Manuel Ayala Martínez (1993; 2004) y la Reprobación de hechicerías por Herrero Ingelmo (2003). Había sido Sánchez Ciruelo antiguo alumno de Diego de Torres en Salamanca y uno de los escritores más prolíficos y completos de su tiempo. No llegó a ser profesor en la salmantina, aunque murió en esta ciudad, donde ejercía oficios eclesiásticos (de 1537 a 1548), pero sus obras matemáticas fueron tan difundidas entre sus colegas salmantinos, que parece razonable nombrarlas en este elenco, por la influencia que pudieron llegar a tener en los redactores del informe salmantino de 1578. Marchó a París en 1492, donde se doctoró en teología y convivió con el que después sería profesor en Salamanca y colaborador en el informe sobre la reforma del calendario, Miguel Francés, y con otros. Enseñó en la Sorbona y en París publicó sus cuatro primeras obras de matemáticas: en 1496, su Thomae Bradwardini Arithmetica speculativa ex libris Euclidis, Boehii et aliorum bene revisa et correcta a Petro Sanchez Arabonensi Mathematicas legente, reeditada después en 1503 y 1505; también en 1496, el Tractatus arithmethice practice qui dicitur algorismus [a Petro Sanchez Ciruelo nouiter compilatus], que asimismo sería reeditado en 1502 y 1513; en 1498, Uberrimum Sphere mundi commentum Johannis de Sacro Busto anglici..., reeditada en 1515; y en 1511, la Geometria speculatiua Thome brauardini recoligens omnes conclusiones geometricas studentibus artium & philosophie aristotelis valde necessarias, simul cum quodam tractatu de quadratura circuli nouiter ed editio [reuisa a Petro sanchez ciruelo], reeditada en 1516.

De regreso a España trabajó como catedrático de filosofía en el Colegio de Portaceli de Sigüenza (1502-1505); seguidamente enseñó en Zaragoza, hasta que Cisneros le invitó, en 1509, a regentar la cátedra de teología tomista de Alcalá, en la que permaneció hasta 1533. Recuérdese que, en 1508, no aceptó la invitación de la Salmantina para que regresara a ella a enseñar nominales, debido a la palabra que ya había dado a Cisneros para trabajar en Alcalá, ciudad en la que continuó su prolífica labor editorial. Dentro de la temática que estudiamos, una obra clave fue su Cursus quatuor Mathematicaru[m] Artiu[m] Liberaliu[m] quas recollegit atq[ue] correxit magister Petr[us] Ciruelus... ([S.l.: s.n.], 1516), que tuvo un impacto extraordinario, reeditándose en 1516, 1523, 1526 y 1528. La concibió como una recopilación científica, en la que resume las ideas de Bradwartine y de algunos matemáticos árabes, estructurándola en cuatro partes, como el quadrívium, siguiendo la tradición de las artes liberales. Después publicó el Opusculu[m] de sphera mu[n]di Ioannis de sacro busto cu[m] additionib[us] [et] familiarissimo comentario Petri Ciruelli Daroce[n]esis; nunc recenter correctis a suo autore; intersertis etia[m] egregiis questionib[us] d[ivi]ni Petri de Aliaco. Fuit excussum... (Alcalá: Miguel de Eguía), y de contenido similar su: Habes lector Iohannis de Sacro Busto sphere textum: una cum additionibus... Petri Ciruelli... intersertis p[rae]terea q[uae]stio[n]ib[us] d[omi]ni Petri de Aliaco..., en 1515. Estos comentarios a la Esfera de Sacrobosco han sido traducidos y estudiados por Flórez-García-Albares (1990b) y representaron un sincretismo de lo parisino y de lo castellano: de las ideas físicas de Aristóteles —matizadas por el averroísmo—, las de Ptolomeo, la tradición astrológica y del ejercicio matemático de los calculadores (Flórez-García-Albares, 1990b; Ayala, 1993; Ayala Martínez, 1993; Herrero Ingelmo, 2003). Siguiendo los debates del momento que también preocuparon a Lax y a otros contemporáneos, se preguntaba en ellas Ciruelo por la naturaleza de los números, concluyendo que eran conceptos abstractos; debates que derivaron en los problemas de notación y de fórmulas que preocupaban a los matemáticos prácticos.

Ya dije antes que para varios calculadores de su época, las matemáticas disponen lo homogéneo en el orden necesario hacia la verdad racional y proporcionan a las ciencias el lenguaje común que, mediante la dialéctica, permite la construcción de un método universal. Según Flórez (2006, pp. 141 ss.), Ciruelo dividía las matemáticas como lo hiciera Aristóteles en su Física: en puras (aritmética y geometría) y mixtas (música, perspectiva y astrología). Decía que las puras son absolutamente ciertas, porque se basan en la demostración científica; en cambio las mixtas son demostrativas y admiten opinión.

Algo que no se ha resaltado de su obra es que escribió precisamente un tratado titulado De correctione kalendarii, escrito para el V concilio de Letrán, o sea, entre 1515 y 1516, aunque publicado em 1528. Hablaré después de él entre los informes presentados a dicho concilio.

Luis de Lucena (1491-1552) ha llamado la atención de investigadores como José Ramón López de los Mozos (1980), Bienvenido Morros Mestres (2004), y varios historiadores del arte que han analizado su capilla en Guadalajara. Lucena estudió en Salamanca, Alcalá y Montpellier, graduándose allí de doctor en artes y medicina. En 1535 viajó a Roma, período en el que, según él mismo dijo, se dedicaba a leer obras de Vitrubio y Arquímedes con otros compañeros. A través del epistolario de Lucena con Juan Ginés de Sepúlveda, se aprecian las aficiones humanísticas de un nutrido grupo de castellanos formados en Salamanca y Alcalá en esos años (Beltrán de Heredia 1970b, II, p. 265).

De forma indirecta también pudo haber contribuido al poso científico matemático salmantino la obra de Diego del Castillo. Tras sus estudios en Italia, escribió un Tratado de cuentas... en el qual se contiene que cosa es cue[n]ta y a quie[n] y como ande dar la cuenta los tutores y otros administradores de bienes agenos; obra muy necessaria y prouechosa la qual el hizo en latin y assi la presento al Rey nuestro señor y porque parescio a su magestad que puesta en Roma[n]ce seria mas general por su mandado la traslado en nuestra lengua Castellana (Burgos: Alonso de Melgar, 1522). Aunque su contenido tiene una gran parte de carácter jurídico, representa el primer tratado de contabilidad en castellano, el más técnico desde un punto de vista jurídico, que analiza las relaciones contractuales entre administradores y propietarios y la medición y revisión de las cuentas hechas por estos administradores (ed. en DICTER, <http://dicter.usal.es/bios/CastilloDiego>). Cabe resaltar el primero de los catorce capítulos que la completan, donde describe las tres formas de llevar cuenta y razón de la época, que es el antecedente del Libro de Caxa:

E digo que la cuenta y razón, que tiene de dar el administrador, es una memoria de lo que da y rescibe. Porque de lo que rescibe, tiene de dar cuenta por memoria y ansí mismo de lo que da. En ansí los mercaderes y personas que tienen cuenta con otros, asientan en sus libros en una parte el rescibo, y en otra parte lo que dan. E cuando averiguan sus cuentas con otros, entran por data y rescibo (Tratado de cuentas..., f. IIIv., cf. Donoso Anes, 1996, p. 126).

Del Castillo no fue profesor en Salamanca, pero la influencia sobre esta Academia se justifica en el momento que sabemos que después de la edición príncipe de su obra en 1522, se reeditó otras tres veces en Salamanca, respectivamente en los años 1542, 1551 y 1589.

El salmantino Pedro López de Espinosa siguió los pasos científicos pautados por su maestro, Juan Martínez Silíceo, llegando a ocupar una cátedra de artes y a escribir tres trabajos, que sepamos: Philosophia naturalis (Salamana: 1535), Tractatus proportionum (Salamanca: 1545) y Sphaera Joannis de Sacrobusto cum commentariis Petri a Spinosa, artium magitriceleberrimique praeceptoris Salmanticensis gymnasii editis (Salamanca: 1550). Otro discípulo, en este caso de Domingo de Soto, fue Rodrigo Dosma Delgado, viajero impenitente y excelente políglota, contado entre los cien científicos españoles a los que según Picatoste habría que erigirles un monumento en función de la importancia de sus obras. Escribió sobre aritmética, perspectiva, la esfera, el cómputo eclesiástico, geometría, anotaciones a Euclides, Arquímedes y otros (Picatoste, 1891, p. 77; Beltrán de Heredia 1970b, p. 367), aunque sus textos más conocidos sean de carácter teológico y editados con posterioridad al segundo informe sobre la reforma del calendario. Juan García Blanco ha publicado un artículo sobre su intervención en la construcción de la muralla de Badajoz (en Arte, poder y sociedad y otros estudios sobre Extremadura. 2006, pp. 71-80).

La figura de Andrés Laguna (1499-1559) ha atraído la atención de muchos investigadores. Guillermo Folch Jou y otros (1983), Antonio Gamoneda (1997), Francisco García Jurado (1997), José Luis Frequet Febrer (1999), María Teresa Ancín Chandía y Francisco Javier González Echevarría (1999), Alberto Gomis Blanco (1999), M. A. González Manjarrés (2000; 2001; María Jesús Pérez Ibáñez, 2003, J. B. Riera Palmero (2000 y dos trabajos de 2001), Francisco López y Cecilio Álamo (2007) han analizado el humanismo médico de Laguna. Sobre su faceta como humanista se celebró un congreso en Segovia en 1999, cuyas actas se publicaron bajo la coordinación de Juan Luis García Hourcade y Juan Manuel Moreno Yuste (2002). Asimismo han analizado el humanismo de Laguna A. Pires de Lima (1946), José María López Piñero (1999), Francisco Calero Calero (1999), Ignacio López-Calvo (2001), José Luis Mora García (2001).

Su faceta salmantina ha sido explicada por M. A. González Manjarrés en un artículo titulado precisamente «Andrés Laguna y Salamanca» (Salamanca: Revista de Estudios, Nº 44, 2000, pp. 253-270). Estudió artes en la salmantina alrededor de 1525; de aquí marchó a París donde aprendió griego y se graduó de bachiller en medicina, en 1534. Regresó a España a finales de 1535 y viajó a Inglaterra, los Países Bajos e Italia (Bolonia), entablando amistad en Venecia con el embajador español Diego Hurtado de Mendoza. De regreso a España ejerció la medicina de Carlos V y Felipe II, trabajando para éste en el jardín botánico de Aranjuez. Entre sus muchos estudios, los que ahora nos interesan, son el editado en Alcalá: Aristotelis de mundo seu de Cosmographia liber unus ad Alexandrum (Juan de Brocar, 1538). B. Gutiérrez Rodilla y M. C. Vázquez de Benito (en 2006) han estudiado los remedios medicinales del Dioscórides traducidos por Laguna y su influencia. Aunque no vivía en esta ciudad, no olvidemos que Laguna publicó en Salamanca al menos cinco ediciones de Acerca de la materia medicinal y de los uenenos mortíferos Pedacio Dioscorides anazarbeo; traduzido de lengua griega en la vulgar castellana & illustrado con claras y substantiales annotationes... por el doctor Andres de Laguna medico... (En Salamanca: por Mathias Gast., 1563, con reedición en 1566, 1570, 1586...). También publicó en Salamanca su Discurso breue sobre la cura y preseruacion de la pestilencia hecho por Andres de Laguna (Salamanca: por Mathias Gast, 1566).

Laguna era compañero en Salamanca de Juan Rodríguez (?-1568), más conocido como Amato Lusitano, discípulo del médico Lorenzo de Alderete, que escribió otros comentarios al Dioscórides editados en Venecia en 1553, con reimpresión en distintos lugares de 1554, 1565, 1558, 1577...

Sobre Juan de Arfe y Villafañe (1535-1603), el que llegaría a ser gran orfebre de las custodias de las catedrales de Ávila, Burgos, Valladolid, San Martín de Madrid, León (perdida) y Sevilla, sabemos que estudió latín y matemáticas aplicando sus conocimientos al arte y la arquitectura. Movido de curiosidad anatómica dice

...nos pareció que era razonable cosa ver hacer anatomía de algunos cuerpos; y así fuimos a Salamanca [hacia 1555] donde a la sazón se hacía por un catedrático de aquella Universidad que se llamaba el doctor Cosme de Medina y vimos desollar algunos hombres y mujeres justiciados y pobres (Beltrán de Heredia, 1970b, II, p. 261).

Acabó siendo ensayador de la Casa de la Moneda de Segovia y encargado de la ejecución de algunas obras en El Escorial. Su obra más famosa fue Quilatador de oro y plata, publicada en 1572, que es un manual práctico cargado de experiencia previa, dividido en tres partes, dedicadas respectivamente al oro, la plata y las piedras preciosas (cf. DICTER). Su obra más importante fue Varia conmensuracion para la escultura y arquitectura por..., publicada en Sevilla en 1585, con posteriores reediciones; en ella critica los excesos decorativos de la arquitectura manierista y ejerció enorme influencia en esas artes hasta el siglo XVIII. De su mano saldría también el Manual para construir toda especie de relojes de sol por J. de Arfe; adicionado con un tratado de los relojes de sol horizontales, verticales, laterales, etc. (Barcelona: Manuel Sauri, 1882).

Gabriel Gómez fue uno de los comisionados del segundo informe salmantino sobre la reforma del calendario, por lo que después hablaremos más largamente sobre él. Como consecuencia de su interés por el tema, después de la publicación del calendario gregoriano escribió un Libro de la Sphera del Mundo, del que Chaparro dice que es un texto estrictamente científico, sin adornos, pensado para explicar la naturaleza del globo terráqueo. Esto es verdad, pero no lo es menos que en él no aportó ningún descubrimiento. Lo complementó con un Tratado de geografía y anunció que tenía escritos otros tratados sobre el astrolabio y el trinquete, pero que, por ser técnicos —según decía—, retrasaba su publicación (Chaparro, 2003, p. 413; 2008, p. 18).

Alonso Pérez (?-1596), natural de Don Benito (Badajoz), tras estudiar en Sigüenza, fue en Salamanca colegial del Colegio Mayor del Arzobispo, donde entró en 1562. Empezó su carrera docente como profesor con una regencia de artes en la que explicaba físicos, éticos y meteoros de Aristóteles, elaborando dos textos sobre la materia titulados: Summa totius meteorología facultatis et rerum copia ubérrima... cui etiam Aristotelei textus in fine Epitome appenditur (Salamanca, herederos de Juan de Cánova, 1576) y Epitome in libros Metheorologicos Aristotelis, que imprimió en 1576 (Salamanca: herederos de Juan de Cánova). Picatoste ensalzaba este trabajo en el que el autor examinaba hechos físicos, astronómicos y meteorológicos con gran erudición, llegando a explicar la caída del agua por su gravedad mayor que la del aire (cf. Beltrán de Heredia, 1970b, II, p. 257). A pesar de ello parece que en su época fue más famoso por su edición de la novela pastoril sobre la Diana (Avalle-Arce, 1974, p. 136-137).

Bartolomé de Barrientos era ya maestro en artes por Zaragoza cuando llegó a Salamanca. En esta Academia desempeñó un partido (contrato docente temporal) de gramática desde 1552 y una regencia de la misma disciplina, desde 1562 a 1574. Nicolás Antonio le atribuye también otra regencia de matemáticas en Salamanca, lo que es probable teniendo en cuenta que escribió obras que requerían conocimientos de esta disciplina, como De cometarum explicatione atque praedictione, artium magistro Barriento auctore, Salmanticae professore et cathedratico (Salmanticae: impensis Simonis Portonarii, 1574). Aunque ésta fuera la más importante de las de la temática, previamente editó otras, como: Opuscula liberalium artium Magistri Barrienti...; De Periodoru[m] siue ambituum distinctionibus; De Periodis ordinandis; De Monetis antiquis, ad Castellanas pecunias reductis; De Coloribus & eorum significatis; De Calendis (Salmanticae: excudebat Mathias Gastius, 1569; reeditada en la misma prensa en 1573); Annotationum sylua per liberalium artium magistrum Barrientum... (Salmanticae: Baptista à Terranova, 1570); Liberalivm artivm Magistri Barrienti... Partium orationis Syntaxeos liber: Accessit eodem libri Syntaxeos: Epitome, mira breuitate totius libri commoda amplectens (Salmanticae: in aedibus Dominici à Portonariis, 1571); y Annotationum sylva per liberalium artium matistrum Barrientum Salmanticae cathedrarium (Salamanca: 1570). Su biblioteca particular ha sido estudiada por Donatella Gagliardi en Studia Aurea, Nº 1, 2007.

Andrés de Poza (?-1595), tras su primera adolescencia formándose en Lovaina, vino a Salamanca en cuya Universidad estudió diez años hasta obtener la licenciatura en leyes, en 1570. Esa especialización jurídica no fue obstáculo para que desarrollara sus profundos conocimientos matemáticos y astronómicos. Picatoste (1981, p. 259) dice que recopiló lo más moderno escrito en Francia, Italia, Inglaterra y Alemania sobre astronomía y navegación. Conoció la variación de la aguja magnética y trabajó como catedrático de la Escuela Náutica de San Sebastián, donde explicaba en 1583. Su obra más importante es Hidrografía la más curiosa que hasta aquí ha salido a la luz (Bilbao: 1585); su derrotero ha sido analizado por Guillermo Herráez Cubino (en Caminería Hispánica, 2004, I, pp. 211-218), quien también investigó su listado de anemónimos (comentario en Res Diachronicae, Nº 2, 2003, pp. 183-189). La Hidrografía... dividida en dos partes: la primera es un tratado de náutica convencional y en la segunda presenta un derrotero general de los puertos y costas atlánticos de Europa, una descripción en detalle de la ruta a la China y proporciona la posición geográfica de multitud de ciudades y puertos. Fue traducida por William Bourne al inglés como A regiment of the sea (London: 1574). Su trayectoria vital ha sido investigada por Rosa Mirén Pagola (El licenciado Andrés de Poza. Bilbao: Bizkaia Kutxa, 1996); y Eugenio Coseriu estudió su lingüística. Su mayor influencia posible sobre los intelectuales salmantinos ocurrió probablemente después de entregado el segundo de los informes sobre el calendario.

Un caso singular que ha atraído enorme atención por parte de los historiadores lo representa Francisco Sánchez de las Brozas, el Brocense (1523-1600). Sobre su obra se han publicado cientos de estudios entre los que cabe recordar los de A. Martín Jiménez: Retórica y literatura en el siglo XVI, el Brocense (1997); el de Martínez Cuadrado: El Brocense: semblanza de un humanista (2003); los libros coordinados por Codoñer-Ureña-López, titulado El Brocense y las humanidades en el siglo XVI (2003), por Merino Jerez-Sánchez Salor, titulado La recepción de las artes clásicas en el siglo XVI (1996), por Chaparro-Mañas, titulado Nulla dies sine línea. Humanistas extremeños: de la fama al olvido (2009)...

Parece que el Brocense llegó a trabajar en materias astrológicas por la necesidad de apuntarse a cualquier plaza universitaria vacante, e incluso a trabajar en dos simultáneamente, en función de sacar adelante a su numerosa familia. Este curioso y pendenciero personaje estudió en Salamanca entre 1545 y 1554, y después fue docente en esta Universidad hasta su muerte: profesor de un partido de retórica entre 1554 y 1559, y de 1564 a 1573; sustitución de media multa en la cátedra de astrología entre principios de enero de 1577 y el 21 de mayo de 1578, justamente cuando se estuvo elaborando el segundo informe sobre la reforma del calendario (luego retomaré este punto); de un partido de gramática de 1593 a 1600; y catedrático de retórica de 1573 a 1600. A su vez, ocupó a veces un partido de griego y de latín, y era profesor en el Colegio Trilingüe de Salamanca. En 1584 fue procesado por la Inquisición, siendo exculpado al fin.

Resultó un escritor prolífico en distintas materias. Publicó varias ediciones y comentarios: del uso del reloj de Frisio (1549), de Ángelo Poliziano (1554), de los emblemas de Alciato (1573), de Garcilaso (1574), del De situ orbis de Pomponio Mela (1574), de la Sphera mundi (1579, editada por Chaparro en 2006), de Juan de Mena (1582), de las Bucólicas de Virgilio (1591), del arte poética de Horacio (1591), de Auli Persii Flacci Saturae sex (1599) y de la doctrina de Epicteto (1600). A ellos unió otros trabajos de creación, como De arte dicendi (1556), Arte para saber latín (1595), Organum dialectum et rethoricum cunctis discipulis utilissimum et necessarium (1579), Paradoxa (1581), Grammaticae graecae compendium (1581), Minerva sive de causis linguae latinae (1587), Verae brevesque latinae institutiones (1587), De nonnulis Porphyrii aliorumque in dialectica erroribus (1588)... Desde la perspectiva en la que nosotros miramos este elenco, cabe destacar dos textos:

1. Declaracion y vso del relox español entretexido en las armas de la muy antigua, y esclarescida casa de Rojas, con el mesmo relox agora nueuamente compuesto por Hugo Helt Frisio; Y romançado por Francisco Sanchez natural de las Broças; con algunas addiciones del mesmo. Salamanca: por Juan de Junta, 1549 (BGH 45488 2). Es una traducción adaptada de la obra de Frisio, que refleja la temprana curiosidad del autor por el uso del reloj.

2. Y la Sphaera mundi ex variis autoribus concinnata per Franciscum Sanctium Brocensem... Salmanticae: ex officina Ildefonsi à Terranoua, 1579, que tuvo una segunda edición también en Salamanca: Guillelmum Foquel, 1588.

Chaparro ha estudiado específicamente esta faceta científica de Sánchez de las Brozas y afirma que las obras de estas características se ciñen a la lectura, traducción y comentario de los textos necesarios para la enseñanza, sin aportaciones propias (Chaparro Gómez, 2008, pp. 17-18; Chaparro, 2003, pp. 418 ss.). Después diré más.

Los hermanos Hernando y Juan de Aguilera (?-1560) adquirieron renombre como astrónomos en su tiempo. De Hernando no se conservan escritos, pero sí de Juan: Entre 1540 y 1550 éste estuvo en Roma trabajando como médico de Pablo III y Julio II. Allí entabló una amistad de por vida con Juan Páez de Castro, con el que (según algunas cartas) debatía sobre matemáticas y realizaba instrumentos astronómicos, como un cuadrante general (Beltrán 1970b, II, 253). Según Flórez (2006, p. 421), en Roma perfeccionó su obra Canones astrolabii uniuersalis, secundo aediti autore Doctore Ioanne Aguilera, praefecto aerarii Salmantinae ecclesie & astrologie publico in eiusdem ciuitatis scholis professor... Salmanticae: excudebat Andreas à Portonariis, 1554. (BGH 4456; la primera edición es de 1530). Ya estaba de regreso en Salamanca el 23 de octubre de 1549 y obtuvo la cátedra de astrología, desde 1551 hasta su muerte, cuya vacatura se anunció en 2 de enero de 1561. Juan se hizo sacerdote y, como tal, llegó a ser tesorero de la catedral de Salamanca, en cuyo recinto se conserva el enterramiento de los tres hermanos Aguilera, que luce una iconografía astronómica. En él, los ángeles tenantes del escudo portan en sus manos instrumentos usados en la materia (Sánchez y Sánchez, 2002, p. 427). Entre tanto su hermano Hernando le sustituye en Roma en la atención médica al papa y le sucedió en esta cátedra del año 1571 a 1576. Hernando regresó de Roma entusiasmado con la obra de Copérnico que probablemente también había conocido allí su hermano e insistió en la inclusión de este autor en los estatutos que se estaban elaborando en ese momento mediante la visita de Covarrubias. Estos estatutos fueron aprobados por Felipe II (15-11-1561), y en ellos, como hemos visto, quedó reflejada la posibilidad de estudiar a Copérnico, al voto de los oyentes.

En este ambiente se comprende la apertura de mente e ideas en la Universidad que llevó Juan de Aguilera a proponer al claustro que contratara a Juanelo Turriano. Beltrán de Heredia recoge el resumen de varias actas de claustro que reflejan los trámites realizados para traerlo a la Universidad. En el claustro de 28 de noviembre de 1558, Aguilera:

...alabó mucho a un extranjero, que dijo llamarse Juanelo, relojero que era del emperador, el cual era tal persona que cumplia mucho a esta Universidad que estuviese e residiese en la dicha Universidad, porque era muy hábil y suficiente en el dicho oficio de relojero (AUSA, 27, f. 8r.).

Encargando el claustro al proponente que se encargara de escribirle y de traerle. Unos meses después, en el claustro de 12 de mayo de 1559

...se cometió al doctor Juan Muñoz para que, estando en Valladolid, hable a Juanelo, relojero del Emperador, para que si se viniese a esta Universidad le darían salario y le pagarían ciertos instrumentos que serían necesarios que se hiciesen de astrología... (AUSA, 27, f. 34r.; cf. Beltrán de Heredia 1970, II, doc. 285).

Una Universidad que busca atraer hacia su recinto a los mejores, es necesariamente un centro abierto y progresista.

En la parte en que resumo el plan de estudios aprobado por Zúñiga hablo de la obligación que el estatuto impone de estudiar el astrolabio y el planisferio de Juan de Rojas, resumiendo allí la relevancia que para Salamanca tuvo este sabio. Lo recuerdo ahora como parte del ambiente científico que se respiraba en la Salamanca de finales de siglo XVI.

A esta guisa es imprescindible recordar también los avances en la física de Domingo de Soto (1494-1570). La atención historiográfica que ha tenido este personaje es afortunadamente enorme, en consonancia con la gran importancia de su obra jurídica, teológica, lógica y física. La versatilidad de sus trabajos le ha hecho merecedor de estudios de distintas temáticas (Brufau Prats es el gran conocedor de su figura y de su obra, según se ha puesto de manifiesto en trabajos como: El pensamiento político de Domingo de Soto y su concepción del poder, 1966; Humanismo y derecho..., 1962; el texto sobre su visión renacentista del derecho, 1973; otro sobre la promoción humana del indio, 1988 y 1989; El derecho de libertad religiosa..., 1992; Brufau está actualmente al cuidado de la edición de sus obras. Le han dedicado también trabajos: Carro, 1943; José Barrientos, especialmente su trabajo de 1985; Santolaria, 2003, Garrán Martínez, 2004; Wallace, 2004; Cruz, 2007; y un largo etcétera).

Este dominico, profesor de teología de la salmantina, asistente al concilio de Trento y confesor de Carlos I, es conocido desde nuestro punto de vista por los comentarios a la física y lógica de Aristóteles. Esta faceta ha sido trabajada, por ejemplo, por J. J. Pérez Camacho y I. Sols Lucía, en «Domingo de Soto en el origen de la ciencia Moderna» (Revista de Filosofía, 3ª época, Vol. VII, 1994, Nº 12, pp. 27-49); y por Sols Lucía, en solitario, con su trabajo sobre «La Física de Domingo de Soto...» (Revista Española de Física, Vol. 9, Nº. 4, 1995, pp. 56-58). En estos estudios se analizan las quaestiones sobre el séptimo libro de la física, su cinemática y su dinámica (las leyes del movimiento y la formulación del movimiento uniformemente disforme), así como su herencia en el Colegio Romano de los Jesuitas. Sus descubrimientos en física han sido clave y por eso Soto es nombrado en casi todos los libros de historia de la ciencia moderna. Los comisionados de 1578 pudieron consultar en la Biblioteca de la Universidad de Salamanca su Reverendi patris Dominici Soto... Super octo libros Physicorum Aristotelis quaestiones, en la edición de Salamanca, Juan de Junta, c. 1545, de la que al menos había dos ejemplares.

El salmantino Diego de Zúñiga (1536-1597 o 1598), agustino y estudiante de artes en Salamanca y de teología en Alcalá, llegó a ocupar una cátedra en la Universidad de Osuna. Su trayectoria ha sido estudiada especialmente por Gerardo Bolado Ochoa, en la Revista Agustiniana (ejemplar del año 2000), que ha tratado de su vida, de su filosofía (ejemplares de 1985 y 1989), y de su dialéctica (en el de 2003); también trabajó su copernicanismo en Religión y cultura (1985, pp. 153-188). Asimismo tratan de sus obras Leticia Carrasco Reija (en «Lo anecdótico en la historia...», editado en La recepción de las artes clásicas en el siglo XVI, 1996, pp. 555-562), Javier San José Lera («fray Diego de Zúñiga y fray Luis de León frente al ‘Libro de Job’», en Fray Luis de León: el fraile, el humanista, el teólogo, 1991, pp. 967-984); y Domingo Natal Álvarez («Galileo y el copernicanismo español: el caso de Diego de Zúñiga», en La filosofía española en Castilla y León..., 1997, pp. 413-420).

Cabe recordarlo en este recuento debido al apoyo que ofreció a la teoría heliocéntrica, declarando que Terram moveri non est contra Scripturam Sanctam, en su comentario a Job, publicado en Toledo en 1584, después de que se enviara el segundo informe sobre la reforma del calendario. Justificaba el pasaje qui commovit terram de loco suo, diciendo que el movimiento de la Tierra

...puede ilustrarse con la sentencia de los pitagóricos que la Tierra se mueve naturalmente, pues de otro modo no es posible explicar el movimiento de las estrellas discordantes, ya por su velocidad, ya por su lentitud... En nuestros días Copérnico ha explicado de un modo semejante el curso de los planetas y sin ningún género de duda mejor que con la Sintaxis de Tolomeo se ha venido en conocimiento por medio de su doctrina de la posición que ocupan los planetas... (cf. Beltrán de Heredia 1970b, p. 260; Bolado 1985).

Fue, pues, uno de los primeros y más fervientes defensores iniciales del copernicanismo en España.

Hasta este momento hemos hablado sólo de científicos que contribuyeron al desarrollo de los métodos matemáticos de los calculadores. Aunque en Salamanca en el siglo XVI el peso de estos matemáticos fue mucho mayor que el de los algebristas, y a pesar de que Rey Pastor se quejara tanto de la falta de estos últimos en nuestro territorio, también esta línea matemática estuvo presente en la ciudad gracias a la Aritmética práctica y especulativa de Juan Pérez de Moya (c. 1512-1596), obra editada en Salamanca, en 1562, con otras reediciones (Alcalá: 1569; Alcalá: 1573; Granada: 1590; Madrid: 1598; Alcalá: 1619, Madrid: 1624, Barcelona: 1705, Madrid: 1745; editada por Rafael Rodríguez Vidal en 1987 y que actualmente tiene cuatro ediciones en versión electrónica). Pérez de Moya también ha atraído la atención de numerosos estudiosos. Específicamente sobre él han escrito en los últimos años: Miguel Ángel Coloma, «El bachiller Juan Pérez de Moya» (en Universitarios gienenses en la historia..., 2000, pp. 63-74); Sonia García Merino, «El ‘Tratado de mathemáticas’ de Juan Pérez de Moya en la imprenta» (en La memoria de los libros..., 2004, pp. 435-462); y José María Núñez Espallargas, en «Estructura i context en una col·lecció de problemes de geometria del segle XVI: les «demandas» de Juan Pérez de Moya» (en Actes d’Història de la Ciència i de la Tècnica, Vol. 2, Nº 1, 2009, pp. 419-426).

Parece que este matemático sólo fue alumno en el Estudio salmantino, aunque Beltrán dice que también fue en él profesor de matemáticas (Beltrán de Heredia 1970b, p. 262). Flórez (2006, p. 415) ha analizado profundamente su Aritmética... y ha destacado tres cosas de su teoría matemática: la distinción entre cantidad continua y cantidad directa, que permitirá independizar la aritmética de la geometría y avanzar por la vía del álgebra; la copia del camino, incluso errónea, del álgebra de Marco Aurel; y la distinción entre matemática antigua (de estilo figural) y moderna (de estilo algebraico). Aparte de este estudio, su producción científica en matemáticas y astronomía fue impresionante; cinco de sus trabajos los publicó en Salamanca: Libro de cuenta, que tracta de las quatro reglas generales de arithmetica practica por numeros enteros y quebrados y de reduciones de monedas destos reynos de Castilla... (Toledo: 1554). Obra intitulada fragmentos mathematicos: en que se tratan cosas de geometria y astronomia y geographia y philosophia natural y sphera y astrolabio y nauegacion y reloxes... (Toledo: 1554). Libro segundo de Arithmetica: que trata de proporcion y regla de tres y monedas, pesos antiguos... ordenado por... Iuan Perez de Moya... (Salamanca: 1557). Libro segundo trata de numeros auebrados y de sus diferencias y operaciones (Salamanca: 1562). Libro segundo, trata cosas de Astronomia, y Geographia, y Philosophia natural, y Sphera, y Astrolabio, y Nauegacion, y Relojes... (Salamanca: 1567). Tratado de cosas de Astronomia y Cosmographia y Philosophia Natural... (Alcalá: 1573). Tratado de Geometria practica y speculatiua... (Alcalá: 1573). Un Tratado de mathematicas en que se contienen cosas de arithmetica, geometria, cosmographia y philosophia natural, con otras varias materias, necessarias a todas artes liberales y mechanicas: puestas por la orden q[ue] a la buelta de la hoja veras, en tres tomos (Alcalá: 1573). Un texto añadido a la edición del Tractado subtilissimo d[e] arismetica y geometría... de Juan de Ortega (Granada: 1563; BGH 36733). Arithmetica de Moya intitulada manual de contadores... (Alcalá: 1582). Manual de contadores: en que se pone en suma lo que vn contador ha menester saber y vna orden para que los que no saben escriuir, con oyrlo leer, sepan co[n]tar, y conuertir de memoria vnas monedas en otras: con vnas tablas al fin en guarismo y castellano para aueriguar con facilidad las cuentas de los reditos de los censos y juros, segun vsança de España y otros Reynos... (Madrid: 1589). [Arithmetica practica. El Bachiller Iuan Perez de Moya] (Granada: 1590). Picatoste dijo de él que fue uno de los hombres que luchó tenazmente por vencer el odio, el desprecio o el temor al estudio de las ciencias.

Del portugués Pedro Núñez (conocido por su apellido latinizado Nonnius, 1492-1578) y su relación con la Universidad de Salamanca también hizo un buen estudio Flórez (2006, p. 418). Fue el gran tratadista de navegación lusitano del Renacimiento. Según sus datos, durante seis años fue profesor de matemáticas de esta Universidad, de 1538 a 1544, aunque era ya doctor por Lisboa, donde trabajaba como catedrático de filosofía en 1530. Desde 1544 fue catedrático de matemáticas en Coimbra, compatibilizando este puesto primero con el de cosmógrafo y después con el de cosmógrafo mayor (desde 1547) en Lisboa, hasta su muerte. Escribió De erratis Orontio Finei, cuyo propósito era demostrar los errores de Fineo, una de las figuras más representativas en Francia, dejando al descubierto el deficiente estado de la especulación matemática en ese país (está en DICTER). Dice Flórez que fue importante por tres aportaciones: Porque resolvió el problema del crepúsculo mínimo que Bernouilli presentó dos siglos después; por ser el inventor del nonius (instrumento de medida que aplicado a una regla graduada facilita la lectura de fracciones de la escala principal), y por haber aportado las curvas loxodrómicas: líneas de rumbos en su terminología, que son curvas irregulares que van haciendo ángulos iguales con los meridianos por los cuales pasan. Este invento fue utilizado por Mercator para la proyección de mapas. Por esos descubrimientos es considerado uno de los fundadores de la navegación científica. En el campo del álgebra escribió Libro de Álgebra en Arithmetica y Geometria (ed. en DICTER, <http://dicter.eusal.es/bios/NunezPedro>), publicado en Amberes en 1567, aunque escrito en español treinta años antes, durante su estancia en Salamanca (hacia 1538); en ella dedicó dos de sus tres partes al álgebra, peculiaridad nada frecuente en la Península Ibérica antes de él, y que le anticipa a Cardano, y realizó una crítica al álgebra de Lucas de Burgo y de Tartaglia. También fue obra suya el famoso Petri Nonii Salaciencis de arte atque ratione navigandi libri duo, publicado en Coimbra por Antonio Mariz.

Esta producción científica escrita, presente en Salamanca, de la que he hablado, sería sólo una parte de lo que presumiblemente pudo haber estado a disposición de los redactores de los informes sobre la reforma del calendario. Aún no había llegado a esta ciudad Jerónimo Muñoz, que vino cuando ya se había enviado el último de ellos; aunque quizá influyera en los comisionados de 1578 a través de su Libro del nueuo cometa y del lugar donde se haze[n] y como se vera por las Parallaxes quan lexos estan de tierra y del prognostico deste... (Valentia [sic]: ...Pedro de Huete..., 1573). Esta obra tuvo mucho mayor impacto en la época que sus Institutiones arithmeticae ad percipiendam astrologiam et mathematicas facultates necessariae... (Valentiae: ex typographia Ioannis Mey, 1566), textos ambos publicados antes de su traslado a la cátedra salmantina (sobre este autor es imprescindible citar a Navarro Brotóns 2001b, 2002, 2004, 2006; Navarro y otros 1998, 2007). Pero lo que sin ninguna duda también pudo influir sobre los comisionados fueron los libros de las bibliotecas, de los que paso a hablar.

1.3.2.2.3. Manuscritos, libros y bibliotecas

En los círculos intelectuales de la ciudad de Salamanca, desde el último cuarto del siglo XV, hubo gran interés por los temas astronómicos. Eso es lo que sugieren el número y el tipo de obras que se escribieron sobre la temática en ese tiempo y los fondos de sus bibliotecas. Para valorar adecuadamente esta importancia habría que conocer lo que se escribió antes de implantarse la imprenta (mucho presumiblemente perdido) y habría que ponerlo todo en relación con los conocimientos en otros lugares y en otras circunstancias. Haré lo que pueda y sepa.

En España y en la Baja Edad Media raros eran los individuos particulares que coleccionaban caros manuscritos y la novedad de los incunables. En general, el libro era un objeto infrecuente en el ajuar de la gente común (Chevalier, 1976, p. 21) y lo mismo cabe decir en aquellos tiempos de la propia Universidad de Salamanca; que adolecía de parecida falta de libros, como toda Castilla (Beltrán de Heredia, 1970b, II, p. 201).

A pesar de ello, había bastantes bibliotecas: en muchos monasterios (Silos, Guadalupe, la Rábida...), en las universidades (Salamanca, 1218; Lisboa, 1288; Valladolid, 1241; Lérida, 1300; Huesca, 1354; Barcelona, 1430; Sigüenza, 1485;...), en algunos los colegios universitarios, y comenzaron a tener un importante crecimiento las de los cabildos catedralicios. De estos últimos destacaban especialmente los de Santiago de Compostela y Toledo, con los restos del esplendor de las traducciones toledanas.

La concentración de comunidades eclesiásticas y seglares dedicadas a la formación universitaria de sus miembros, convirtió a Salamanca en un lugar idóneo para el trajín de la cultura académica escrita que circuló por Castilla (Carabias Torres 2007). Los eclesiásticos solían ser más proclives que los seglares a la acumulación documental, pero al morir, los colectores apostólicos normalmente se incautaban de los ejemplares en calidad de espolios, para remitirlos a Avignon, lo que explica, a pesar de todo, la pobreza de las primitivas bibliotecas eclesiásticas helmánticas.

En Salamanca casi todas las instituciones reservaban un lugar y unos recursos para los libros. En realidad no eran concebibles colegios, conventos, monasterios, cabildos catedralicios o universidades sin ellos. La librería de la Catedral de Salamanca recibió un empuje notable en su formación en el año 1480, con la donación de las obras del obispo Vivero (Marcos Rodríguez, 1991), amigo de Zacut; intelectual que se interesó en su testamento (publicado por Cantera Burgos) de que tanto los libros de Zacut como los suyos quedasen a buen recaudo en la iglesia, por ser provechosos —decía— para entender sus tablas, en orden a fijar con precisión la fecha de celebración de la Pascua (Beltrán de Heredia, 1970b, II, p. 248; Marcos Rodríguez, 1931). Sus últimas voluntades debieron cumplirse, según se desprende de la opinión del viajero Jerónimo Müntzer cuando refiriéndose a ella, en el año 1494, dijo que esta biblioteca tenía un excelente emplazamiento y una buena colección de libros de filosofía y teología:

...aedificio superbissimo... cum antiquissimis et optimis libris in pergameno in omni facultate praecipues in philosophia et teología (cf. Beltrán de Heredia, 1970b, II, p. 205).

Aunque estas palabras distan mucho de la precisión, en ellas se corrobora la tendencia general en Castilla a la creación o ampliación de las bibliotecas catedralicias de que habla Galende Díaz (1996, p. 103).

Tampoco se sabe demasiado de la biblioteca del convento dominico de San Esteban, pero M.ª Paz de Sena ensayó una aproximación al conocimiento de sus fondos, basándose en el análisis de los inventarios conservados: uno del siglo XVIII (BGH ms. 565) y otro del año 1836 (Archivo Histórico Nacional, Clero, 19707). Sus reflexiones son ilustrativas: aparte de títulos de carácter religioso, su librería contenía obras de cosmografía, astronomía y matemáticas, de interés muy restringido para el común de los intelectuales coetáneos. Entre ellos se encontraban los textos clásicos: la Geometría de Euclides en latín y romance, la Esfera de Sacrobosco, repertorios de los tiempos, dos geografías de Ptolomeo, la Nueva teoría de los planetas de Peuerbach, libros de astrología..., pero también obras de calculadores ingleses, como una de Juan Buridán (Sena, 1991 y 1993; agradezco a esta autora la información en este punto). Es decir, que a finales del siglo XV, los dominicos salmantinos poseían algunas obras poco frecuentes en los conventos coetáneos, aunque la dedicación de alguno de sus frailes a tareas docentes universitarias pueda justificar esta colección. También explica que Diego de Deza indujera a Cristóbal Colón a cambiar impresiones sobre su proyecto con sus compañeros salmantinos.

El resto de las bibliotecas conocidas de los demás conventos y monasterios, incluido el de los franciscanos, también poblada, reproducía el clásico modelo de librería filosófico-teológica, y todos estos materiales eran de uso restringido para sus respectivas comunidades.

La mayoría de los colegios universitarios de la ciudad abrirían sus puertas a lo largo del siglo XVI, pero las bibliotecas, siempre concebidas por sus fundadores, no fueron la primera de las necesidades a atender en las nuevas fundaciones. El llamado de Pan y Carbón fue el primero de los colegios universitarios salmantinos, fundado en 1386; pero no queda rastro de la posible librería que hubiera podido tener en los primeros tiempos. Una excepción a esta tónica general fue el caso del Colegio Mayor de San Bartolomé, que había sido fundado en 1401. Considerados los libros por su fundador, Diego de Anaya y Maldonado, como el tesoro más preciado, desde el año 1414 el centro contaba con una reglamentación pionera en cuanto a su ubicación, conservación, ampliación y posibilidades de consulta. Así el colegio fue una excepción, pues tuvo tempranamente biblioteca propia, estrenada con los libros donados por el propio fundador y, quizá por falta de datos más precisos de otras instituciones, de las más completas de su entorno a finales del siglo XV (Beaujouand, 1962; Marcos Rodríguez, 1960).

La conocemos por los asientos realizados en tres fechas distintas de la primera mitad del siglo XV, conservados dentro del «Inventario del Colegio de San Bartolomé de Salamanca» (Bibliothèque Nationel de France, ms. Espagne 524, ff. 1-103). Es éste un códice de temática miscelánea, que parece servía de libro de registro general de la institución, pues, agrupados por páginas (mediando algunas en blanco entre los grupos de información) recogía tanto estos listados de los ejemplares conservados, como el balance económico de las rentas, fechas de salidas temporales de los colegiales y la relación de los bienes de la capilla. Estas anotaciones comienzan precisamente por los registros bibliotecarios en los que algunos rectores del colegio certificaban los fondos existentes. El primer lote de libros que enumera es del año 1433, recoge 180 volúmenes, que fueron donación del fundador; el segundo lleva fecha de 1438, en que se recibieron 51 volúmenes a raíz de la muerte de éste, tal y como lo firmó el rector Rodrigo de Fontiveros el 1 de enero de dicho año; y el tercero es de 1440, y constituyó un grupo de 60 volúmenes de varias procedencias.

En los tres asientos se siguió el mismo orden expositivo: primero los libros de derecho canónico, siguiendo los de derecho civil y, por último, el conjunto los libri teologales et arçiales (de teología y artes); lo que muestra que era ya habitual el orden de los libros, que estudiara Chartier (Barcelona: Gedisa, 1994). El denominador común a todos es la falta de precisión de las anotaciones, que es el mal general de todos los inventarios bibliotecaros conservados de aquella época. Contienen bastantes glosas inscritas de forma muy imprecisa, como una glosa ordinaria Levitici, o la glosa ordinaria Johanis, sin especificar ni el autor ni de las características de la obra, que nos hubieran posibilitado precisar cuál es. Dentro del grupo de teología y artes —que es el que a nosotros ahora nos interesa— y contando con esta imprecisión de las inscripciones, podemos decir que la inmensa mayoría son obras de teología. Sólo hay una pequeña parte de ellas que responden a las necesidades de formación básica de los alumnos de la facultad de artes: lecturas De Caelo et Mundo, otros comentarios de la física y la metafísica de Aristóteles. El balance global de estos libros en enero de 1438 era de 37 obras de derecho canónico, 25 de derecho civil y 121 de teología y artes, mientras que en 1440 el conjunto ascendía a 298 volúmenes. Fijándonos en el grupo de obras que ingresaron en 1440, observamos una clara evolución hacia las ciencias astronómico-matemáticas; de hecho, desde ese año ingresaron en esta biblioteca textos de los lógicos y los científicos de Oxford: los manuscritos de Robert Alyngton «Super Predicamente y Claves terminorum», de Robert Stonham «Sophismata Willelmi Heytesbury recollecta» (actual BGH Ms. 1986), la «Lógica» de Juan Tardeys que incluye una «Summa Insolubilium» de Juan Wiclef (actual BGH Ms. 2358) o las Matemáticas de Felipe Elefant (siglo XIV) (Muñoz Delgado, 1983, p. 124; Beltrán, 1970b, p. 245).

Los becarios de San Bartolomé tenían libre acceso a estos materiales, además de poder consultar los libros de la biblioteca universitaria. En cambio, ningún miembro de la Universidad no bartolomeo podría acceder a estos ejemplares. Ya me referí a este códice en trabajos anteriores y debo reconocer que entonces confundí cantidad con calidad (Carabias Torres, 1986, pp. 736-760 y 1995). Me corrijo, pues, a mí misma y lamento no haberme dado cuenta antes de ello: A pesar de la predicha falta de precisión en las anotaciones, la lectura de esta documentación me permite afirmar que, en la primera mitad del siglo XV, el Colegio de San Bartolomé no tenía la riqueza documental manuscrita en astronomía que iba a tener cincuenta años después, y que ha quedado reflejada en los estudios de Beaujouand (editado en 1963) para finales del siglo XV, o los de Roxas y Contreras (Historia del Colegio Viejo..., 1766-1770) y Galende Díaz (2000) para el siglo XVIII. Es decir, que hubo una coincidencia cronológica evidente entre la presencia casi continuada de colegiales de San Bartolomé en la cátedra de astrología de Salamanca (la cual monopolizaron prácticamente desde 1467 hasta principios del siglo XVI) con el crecimiento de los fondos astronómicos de la biblioteca de dicho centro. Las holgadas posibilidades económicas del Colegio de San Bartolomé y el interés coyuntural por las cuestiones cosmológicas, matemáticas y cosmográficas, explica el crecimiento de su biblioteca en tales materias en la segunda mitad del siglo XV. A los ejemplares comprados se añadieron también los redactados o traducidos por los propios colegiales, algunos de los cuales tenían contenidos muy novedosos para la época. Estoy pensando en la traducción al castellano realizada por el colegial y catedrático Juan Salaya de los cánones de las tablas de su amigo Zacut.

Estos datos son bastante curiosos, sobre todo si tenemos en cuenta que San Bartolomé fue una institución creada sólo para quince becarios, de los cuales, por ley, diez debían estudiar derecho canónico y cinco teología. Analizando la matrícula universitaria desde el año 1546 —que es la fecha desde la que se conservan estos libros—, se comprueba que normalmente cursaban las materias prescritas en sus becas. Pero como al menos a los teólogos se les obligaba por ley a realizar primero los tres cursos de artes, y en ellos la astronomía se estudiaba como parte del quadrivium, se entiende que un buen porcentaje de estos becarios se dedicaran después a investigar y a enseñar la astronomía, materia bastante alejada de la especialidad de la beca colegial que habían disfrutado. Esta peculiar especialización científica de los bartolomeos en esta época explica que en el estudio que yo hice sobre los colegios mayores en el siglo XVI, el treinta y dos por ciento de sus estudiantes llegara a ocuparan una cátedra en esta facultad de artes (Carabias Torres, 1986, II, p. 903).

Por último hablaré de la biblioteca universitaria. Óscar Lilao y Marta de la Mano estudiaron su evolución a lo largo del Quinientos y comprobaron que el grueso de sus fondos derivaba de la donación de ochenta y ocho códices realizada a la Universidad por Juan de Segovia, en octubre de 1457: obras de derecho, medicina, filosofía, historia, gramática y retórica; mayoritariamente de carácter teológico; no astronómico (Hernández Montes, 1984; Beltrán de Heredia, 1970b, II, pp. 201 ss.).

Dicha biblioteca abrió sus puertas al público universitario en 1467, justo el año en que empezaron los bartolomeos a ocupar la cátedra de astrología, detectándose un considerable aumento de la adquisición de libros desde entonces. Pero la disponibilidad de consulta de sus fondos se vio interrumpida por varios cambios en la distribución del edificio, que afectaron a las posibilidades reales de uso de los libros. Se conserva una visita del año 1471, en la que se dice que en ella sólo se hallaron doscientos un volúmenes (Marcos Rodríguez, 1990, p. 270), en tanto que en 1610 sus fondos ascendían a mil cien títulos (Rodríguez-San Pedro, 1985, p. 108). En 1506 el claustro universitario decidió edificarla en la ubicación que tiene hoy en día, encima de las aulas (llamadas entonces generales) de leyes y filosofía, sobre la entrada y el general de medicina; obra que no terminó hasta 1526 (Lilao-De la Mano, 1999, p. 222). Luego quizá sus fondos no ayudaron mucho a los comisionados encargados de redactar el primero de los informes sobre reforma del calendario, en 1515, porque estaba cerrada; aunque muy probablemente la Universidad les permitió su consulta ante la solicitud papal del informe. En todo caso pudo ayudar mejor a los comisionados del año 1578. A pesar de todo, en 1548 Pedro de Medina se refería a ella como la mejor de España; y Jerónimo Müntzer lo corroboraba, comparándola en tamaño a la capilla de la Virgen de Nuremberg (Medina, 1944, p. 132; Münzer, 1951). Salvo este tipo de datos cualitativos que no sirven a nuestro objetivo, poco sé del ritmo y del tipo de las adquisiciones bibliográficas.

Los largos periodos de clausura forzosa determinada por los citados proyectos de edificación y reforma del edificio universitario; la modestia de una colección alimentada principalmente por las donaciones; la irremediable irregularidad en la compra de los libros, sometida a la disponibilidad presupuestaria; el abandono en el cumplimiento del horario de apertura y del cuidado del material;... parecen haber relegado la librería universitaria a una institución temporalmente inútil, que lejos de compartir, apoyar y recoger el brillante desarrollo de la docencia y la investigación que simultáneamente tenían lugar en las aulas salmantinas, se mantuvo al margen de los mismos.

Esta intermitente utilidad de la biblioteca universitaria, unida al crecimiento de la matrícula, puede explicar la proliferación de la oferta editorial fuera de las aulas. A esta guisa, Antonio Agustín —que cursó estudios en Salamanca antes de ingresar en el Colegio de Bolonia (en 1538)—, dijo que había más de cincuenta y dos imprentas y ochenta y cuatro tiendas de libros en la Salamanca que él conoció, ocupándose en esta industria más de tres mil seiscientas personas (Cuesta, 1981, p. 22). Si hacia 1535 Salamanca tenía tantas librerías como Agustín dice y Luisa Cuesta supone, se entiende que muchos universitarios tuvieran libros de su propiedad. En algún testamento de estudiante que he encontrado lo he podido comprobar: el familiar del Colegio Mayor de Cuenca Pedro de Moya dicta testamento a 25 de agosto de 1590 y en él se puede apreciar que tenía varios libros de su propiedad. Para valorar esta tenencia cabe recordar que los familiares eran los estudiantes más pobres, criados del colegio (fámulo), por cuyo trabajo recibían un sueldo miserable y aún así atesoraba libros (AHPS, 5643, f. 274r.-277v.)

También éste es el caso del actual ms. 2586 de la BGH: una copia espectacular de la Geographia de Ptolomeus, traducida por Jacobus d’Angelus, propiedad entonces de Diego Ramírez de Villaescusa, antiguo colegial de San Bartolomé y después visitador de la Universidad, que donó a la biblioteca del Colegio Mayor de Cuenca, que acababa de fundar. Sus mapas son de una belleza artística destacada, parangonable a otro ejemplar de la Biblioteca Vaticana. En este manuscrito aparece repetida la representación de la Península Ibérica; una de ellas, con sorprendente fiabilidad cartográfica. Villaescusa debió de adquirirlo bajo la influencia de la moda cosmográfica desarrollada intramuros del Colegio de San Bartolomé a finales del siglo XV. En este sentido, la ciudad y los ciudadanos de Salamanca se comportaron en estos tiempos como sus contemporáneos europeos: la época del Renacimiento se caracterizará por el crecimiento de las bibliotecas, tanto institucionales como particulares. Entre los humanistas se generalizó la costumbre de coleccionar libros particularmente; de formar bibliotecas para su uso privado y para el uso de sus colegas y amigos eruditos (Galende Díaz, 1996 y 2000).

Evaluando la información sobre astronomía que nos consta que estuvo a disposición de universitarios entre 1515 y 1578 (quizá hubiera otra que no me consta), procedente de las bibliotecas de la Universidad y del Colegio de San Bartolomé, podemos decir que los comisionados para la reforma del calendario tenían teóricamente a su alcance la práctica totalidad de la astronomía clásica (de origen griego y árabe) y bastantes libros recientes para su época:

1. Como poco, disponían de todos los manuscritos de carácter astronómico de la Universidad y los colegios mayores que catalogó Beaujouand (1962) en su día y, según este autor, la información con la que contaban era de las más precisas de Europa en aquellos momentos; grosso modo:

• Aristóteles era la base del plan de estudios y es natural que abunden sus obras y comentarios: La Phisica (ms. 68, siglo XV) y multitud de comentarios de ella en los manuscritos 2019, 1827, 1789, 1786, 2463 y 2535 de la actual BGH. El ms. 2256 (siglo XIV) incluye la Phisica y Meteora, en la traducción de Moerbeke. El ms. 2706 contiene Meteora, y una traducción de De Caelo et Mundo realizada por Gerardus Cremonienses.
• El ms. 111: Almanach coeleste cum figuris, que incluye: De Sphera (dos copias); Computus de Robertus Lincolniensis; Notas de astronomía; y Tabule astronomice novarienses. El ms. 189 (siglo XIV) el Tractatus quadrantis novi de Profatius Judeus (año 1301); y la traducción latina de otra arábiga del De infusione spermatis et cometis, etc.
• Varios trabajos de Sacrobosco en el ms. 2662: Algorismus, Sphera, Computus; y también «Tablas de longitudes solares»; Opus instrumenti declinationis solis; Gerardi: Theorica planetarum (de la que hay otra copia en el ms. 189); Thebit Ben Corat: De motu 8º sphere, De hiis que indigent expositione antequam legatur Almagesti, De recta imaginatione spere et circulorum eius diversorum y De quantitatibus stellarum et planetarum et proportione terre; y una obra de Azarchel [Tabulae astronomice cum canonibus], cuyos cálculos ya dijimos que fueron la base de las tablas alfonsíes. El ms. 1693 (principios del siglo XV) contiene: Robertus Anglicus, In tractatum de sphera [Joannis de Sacrobosco]; y Expositio Theorice planetarum [de Gerardi]. El ms. 221 (siglo XIV), recoge la Spherica de Theodosius, traducida por Gerardus Cremoniensis. El ms. 1693 (siglo XV): In tractatus de sphera de Robertus Anglicus, traducido por Sacrobosco; la Expositio Theorice planetarum de Gerardi; el Tractatus quadrantis veteris atribuido a Anglicus; y el Quadrans novs a Petro de Sancto Audemaro correctus, anno 1309, de Profatius Judeus. Y el ms. 2624: Euclides, Elementa geometrie [en la versión de Campani Novariensis].
• El ms. 2671 contiene la traducción de varias obras y comentarios de Averroes. El ms. 2241: Alpetragio, Theorica planetarum, con glosas marginales, del siglo XIII. El ms. 2051: Alfraganus, Liber de aggregationibus scientie stellarum [traducción de Gerardus Cremonensis]; Ptolomeus, Quadripartitum [traducción de Plato Tiburtinus]; Messahalla, De receptione planetarum [traducción Johannes Hispalensis]; y Abenragel, Capitulum de cometis ex libro de iudiciis astrorum. El ms. 2338, con el texto de Costa ben Luca (Quosti filius Luce), Tractatus sphere volubilis (traducida quizá por Stephanus Arlandi). El ms. 2353 conserva la Theorica planetarum de Campanus (de la que hay otra copia en el ms. 2621) y un comentario al tratado de la esfera de Sacrobosco.
• El ms. 2621 incluye: Compositio equatorii; Johannes Fusoris, Tabula 35 stellarum fisarum; [Confectio tabularum]; [Costa ben Luca, Practica sphere solide] traducido por Profatius Judeus y Stefanus Arlandi; Opus manuale in quo motus omnes longitudinales planetarum oculo discernantur; [Tabula 25 stellarum]; «Tabula [31] stellarum fixarum verificatarum Parisius per armillas»; y Alfraganus, [De scientia astrorum] traducido por Johannes Hispalensis, etc. El ms. 2495: Ptolomeus, Geographia (traducción Jacobus Angelus). El ms. 2138: Abraham Ibn Ezra, Libro del mundo; Messahalla, Libro de conjunctiones...

2. Además, en un caso excepcional como era una consulta papal sobre la reforma del calendario, los comisionados tendrían la posibilidad de usar la biblioteca del cabildo catedralicio, donde debían estar los libros de Abraham Zacut, y, en ellos, toda la tradición astronómica hebrea, porque Chabás y Goldstein (2008, pp. 63 ss.) han demostrado que Zacut conocía a fondo las obras astronómicas de sus predecesores judíos: Abraham Ibn Ezra, Maimónides, Jacob ben Tibbon, Isaac ben Sid, Isaac Israeli, Levi ben Gerson, Jacob ben David Bonjorn, Isaac-al-Habid... y, si las conocía tan bien, es porque las habría leído, dejándole estas obras a su amigo, el obispo Vivero, que ya he dicho que las depositó en la biblioteca de la catedral. La publicación on-line del Fondo Espinosa del Archivo de la Universidad de Salamanca, me ha permitido conocer un inventario de esta biblioteca realizado el 6 de junio de 1533 (pp. 21-28, <http://ausa.usal.es/imagen.php?serie=espinosamanuscritos&libros=AUSAA_RE%2C19%2C2&verPagina=21#estados>). Como era de esperar, en ese momento la mayoría de los fondos son de carácter teológico y jurídico, aunque hay también una buena colección de obras de astrología ubicadas dentro del llamado banco nono, entre ellas el Maleus maleficiorum [maleficarum] —de 1486, la obra clave para persecución de las brujas—, un Libro de Alquimia y una buena colección de libros de filosofía natural. Pero allí no he encontrado los libros de astronomía que pudieron haber pertenecido a Zacut y que fueron depositados en sus estantes cumpliendo el testamento del obispo Vivero, documento que por cierto también reproduce Espinosa en este fondo archivístico. Al no tener un inventario de los libros dejados por Zacut, no podemos saber con certeza si las obras hebreas que él conocía y citaba formaron parte de aquella donación al cabildo. Sólo corroboro que en 1533 allí no estaban.

3. Y, por último, dispusieron de un importante conjunto de manuscritos e impresos procedentes tanto de la compra directa en libreros, como de los estudios realizados por los propios profesores salmantinos a lo largo de los años. Este conjunto informativo era quizá el más abundante y también el más útil, porque una buena parte de él se había fundamentado en la observación y la medición continuada de los fenómenos astronómicos.

Según el balance editorial general de los reinos españoles firmado por Salabert (1999, pp. 233-252), el primer libro científico conocido en España es de 1471. Desde él y hasta la imposición de la primera censura de libros (1502), hubo una tasa de crecimiento decenal de primeras ediciones del 364 por ciento; desde 1502 hasta la pragmática de Felipe II de 1558 —que ampliaba notablemente los campos de prohibición—, la tasa de crecimiento decenal descendió al 34 por ciento; y entre 1558 y 1600, esta tasa es del 12 por ciento. Según su tabla 7, que distribuye por materias los impresos científico-técnicos españoles entre 1561-1600, hubo en esos años 32 nuevas ediciones de textos de astronomía o astrología, y 36 reimpresiones (un total de 68 ejemplares).

Los estudios de Ruiz Fidalgo (1994) han dado a conocer para el siglo XVI la publicación de 1.510 textos en las imprentas de Salamanca. Según sus estadísticas, la teología ocupa el 39,82% y el derecho el 14,03% del total; la filología sólo el 6,07% y la historia el 5,22%. Entre los autores con un número superior a diez ediciones estuvieron, en primer lugar Domingo de Soto, con 80 ediciones de 16 obras; el sexto El Brocense con 20 ediciones de 19 obras; el décimo nono Bartolomé de Barrientos, con 10 ediciones de 12 textos. Tres periodos establece Ruiz Fidalgo en la historia de la imprenta salmantina: de asentamiento de la imprenta (1501-1556), de auge y difusión de la industria editorial (1557-1582) y de estancamiento y decadencia (1583-1600) (Ruiz Fidalgo, 1994; Gil Fernández, 2004, p. 92). Por lo que se refiere a los libros sobre astronomía y astrología, Mariano Esteban Piñeiro (2002, nota 13) afirma que de más de doscientas obras publicadas en España entre 1481 y 1600, en Salamanca se imprimieron 38 libros del conjunto astronomía-astrología y 10 de cosmografía-náutica. Muchas de estas obras eran cosecha propia de los profesores salmantinos.

No se pueden obviar circunstancias como la de Cisneros, que queriendo erradicar de España la doctrina de Mahoma, mandó quemar los libros árabes, exceptuando los textos médicos y filosóficos, los cuales debían conservarse en la biblioteca de la Universidad de Alcalá de Henares recién creada por él en 1508 (Sánchez Ron, 1993, p. 49). Parece que estos ejemplos alarmistas fueron excepcionales, pero quizá expliquen la falta de obras hebreas (las de Zacut) en la biblioteca catedralicia de comienzos del siglo XVI. Mariano y José Luis Peset (1968), en cambio, corroboran que en relación a las ciencias del momento —salvo la teología—, los índices del inquisidor Quiroga de 1583 y 1584 no supusieron una grave cortapisa a la introducción y circulación de ideas científicas por España. Es decir, que a pesar de la censura de la que explicó Pardo Tomás, el llamado cierre ideológico de Felipe II no fue más que un gesto, según ha ratificado Goodman (1999). Todo corrobora que en Salamanca, por ejemplo, tanto en 1515 como en 1578 (fechas de los informes sobre la reforma del calendario), la información bibliográfica disponible para su consulta por los comisionados fue de las más completas de su tiempo.

Este paseo a vuelapluma sobre la atmósfera intelectual en la que se escribieron los informes salmantinos pretendía mostrar el saturado ambiente de ideas físico-matemáticas con que calificó Beltrán de Heredia a este largo periodo salmantino (1970b, II, p. 367). Como información de contraste presento ahora el análisis de las tablas publicadas por John Gascoigne que comparan el número de científicos citados en el Dictionary of Scientific Biography entre 1450 y 1650, atendiendo a sus naciones o a los países en los que enseñaron. Tomando como fronteras nacionales las actuales y teniendo en cuenta el lugar de nacimiento, en España y Portugal, conjuntamente, entre 1450 y 1550, hubo 18 científicos (el 10 por ciento), mientras que entre 1551-1600 sólo hubo 5 (el 2 por ciento). Según los campos cultivados: en matemáticas (incluyendo matemáticas, astronomía, mecánica y óptica), entre 1450 y 1550, hubo 66 científicos (el 38 por ciento); mientras que entre 1551-1600 hubo 159 científicos (el 49 por ciento); es decir, que en la Península Ibérica se constata un enorme incremento del interés por las matemáticas a lo largo del siglo XVI (cf. Sánchez Ron, 1993, p. 69 ss.), que corrobora la sensación de saturación que describía Beltrán de Heredia. Sin ninguna duda, Salamanca tenía medios humanos y bibliográficos para realizar adecuados informes sobre la reforma del calendario.

1.4. LA UNIVERSIDAD DE SALAMANCA Y EL PROBLEMA DEL CALENDARIO

1.4.1. Tiempo, ciencia y política

Éste es un estudio histórico de lo que en su día fue una cuestión a la vez histórica, científica, jurídica, política y religiosa. De ahí que tenga sentido aludir a la imbricación de esas circunstancias en los informes salmantinos, explicándolos en parte a través de ellas.

El hombre usó los números para poner orden en el cielo que veía al menos desde la época de los sumerios y los babilonios, dando origen a los calendarios. La configuración de un calendario requiere de muchísima observación y de la corrección de las desviaciones astronómicas observadas. Fue y sigue siendo un conocimiento alejado del talento del común de los mortales por su complejidad y por la necesidad de realizar gran cantidad de cálculos matemáticos y astronómicos; por eso sólo estuvo al alcance de algunos científicos y al servicio del poder.

La dificultad de la cronología y su accidentada historia radica en que el año no comprende un número íntegro de días o de meses lunares y los ciclos astronómicos no son ni constantes ni perfectamente medibles. Como muy bien dice el informe salmantino de 1578, el error se originó por la diversidad del movimiento del Sol y de la Luna. Diversidad que ha pretendido solucionarse mediante la fijación de un calendario civil, de validez universal, que es un calendario solar, basado en la progresión de las estaciones, o de las revoluciones de la Tierra alrededor del Sol. Pero los calendarios solares deben ajustarse con un algoritmo, método o regla matemática fija a la longitud de los meses y los años, porque sin ella las estaciones derivarían constantemente a lo largo de los meses.

Según el mismo informe, desechadas como método cronológico adecuado las imprecisas tablas previas de los antiguos romanos con las que trataban de ajustar las conjunciones del Sol y de la Luna, se tomó:

...de los caldeos el llamado ciclo lunar o decemnovenal; por ser un método más sencillo fácil y seguro lo acogieron con tanto entusiasmo que ordenaron escribirlo con letras de oro: de donde derivó el nombre de número áureo; con esto pensaron que ya tenían un sistema cierto, fijo y perpetuo para determinar estas conjunciones y oposiciones. Pues ellos creyeron que la Luna, pasados 19 años (que es el tiempo prefijado de este número, de donde vino a llamarse ciclo o número «decemnovenal»), volvía en el mismo punto y momento sin error alguno o diferencia a las mismas conjunciones (Informe de 1515 [3]).

El texto se refiere a Metón, que adoptó las reglas específicas para ajustar el tiempo adicional de estas conjunciones al estandarizar un ciclo de doscientos treinta y cinco meses lunares (el ciclo de Metón o ciclo decemnovenal) que equivale a diecinueve años, después del cual la Luna vuelve a repetir casi con exactitud su posición en el firmamento. El ciclo de Metón fue dado a conocer en los juegos olímpicos del año 453 a. C., y se dice que los atenienses, conscientes de la importancia de este descubrimiento para mejorar el cómputo del tiempo —como dice el texto—, lo grabaron en caracteres de oro en el templo de Minerva, diosa de la sabiduría. De ahí la expresión de número de oro o áureo número que en astronomía se refiere al rango que tiene un año específico en el ciclo de Metón, que se repite cada diecinueve años y que inicialmente, como digo, se creía que permitía hacer coincidir los ciclos de la Luna con los ciclos solares. Por tanto hay diecinueve números áureos (del 1 al 19) y cada año tiene su número áureo asociado; averiguación que ha servido hasta el presente para la elaboración de calendarios y almanaques.

En realidad la solución a los problemas cronológicos había sido ensayada desde las antiguas culturas de Oriente Próximo a través de tres modelos distintos de calendario (Vernet, 1946):

1. El calendario egipcio, que prescinde de las conjunciones del Sol y de la Luna y se basa en un año trópico de 365 días (el juliano tenía 365.25). Este calendario, con modificaciones, es el que a través de los griegos y los romanos utilizamos hoy en día.

2. El calendario babilónico, que intentó hacer del mes una unidad dependiente del movimiento de la Luna, obligándose, para evitar el corrimiento de los meses respecto de las estaciones, a introducir un mes de más cada dos o tres años (año con embolismo, después llamado bisiesto). Usa, por tanto, un sistema mixto, basado en los movimientos del Sol y de la Luna, y se mantiene actualmente en uso entre los judíos.

3. El calendario musulmán, que es lunar, sin concordancia con el año trópico y el ritmo solar, en el que el equinoccio de primavera puede coincidir con cualquiera de sus meses.

Es decir, que en función de los conocimientos y de las creencias ha habido distintos tipos de calendario a lo largo de la historia; unos basados en los ciclos del Sol, otros en los de la Luna y otros en ambos conjuntamente. Cuando el papado se planteaba la reforma evaluó las ventajas e inconvenientes de cada uno de ellos con miras a elegir el modelo computacional más adecuado a las celebraciones religiosas del calendario litúrgico; y lo hizo dentro de los siguientes modelos:

1. Los calendarios que se configuraron a partir de los ciclos del Sol se basaron en el año solar astronómico, que es el tiempo que invierte el Sol en recorrer con su movimiento propio aparente un signo del Zodiaco (RAE). Los más importantes calendarios solares de la historia han sido, sin duda, el calendario juliano y después el gregoriano, sirviendo el primero como referencia e inspiración del segundo. El calendario romano previo al juliano era luni-solar, pero con el tiempo sus diez meses dejaron de seguir las fases lunares y el ciclo de las estaciones (Michels, 1967; Bickerman, 1974). Por eso Julio César practicó una reforma en el año 46 d. C., siguiendo los consejos del alejandrino Sosígenes, estableciendo un año con doce meses de duración fija y la invención del año bisiesto: la intercalación de un día más al año común, añadido cada cuatro años al mes de febrero con el objeto de ajustar la duración de los años solares con el ritmo de las estaciones, que se habían desajustado ya en el mundo romano.

Como dice el informe salmantino,

Julio César fue el primero que le prefijó fecha al... número áureo, e hizo que comenzase a partir del primer día de enero, hace 1623 años, a saber el año 45 antes del nacimiento de Cristo (Informe de 1515 [3]. Dicen 45 y no 46 porque no cuentan el año cero).

Es decir, que 1578 (1623 - 45 = 1578) es el año en el que se escribieron estas palabras. Según se indica, estableció César el 1 de enero como comienzo del año y el 21 de marzo como fecha del equinoccio de primavera o equinoccio vernal, día que asumió después el calendario eclesiástico para fijar la celebración de la Pascua, y se consideraron años bisiestos los años divisibles por cuatro. Al año en el que César implantó su reforma se le llamó el año de confusión, porque se añadieron noventa días para devolver los meses del calendario romano a su lugar tradicional en lo que respecta a las estaciones. Finalmente, este modelo sirvió como estándar cronológico para la civilización europea hasta la reforma gregoriana del calendario.

La duración media del año calendario juliano fue fijada en 365.25 días, una medida razonable y aceptada por la comunidad científica de aquel momento, aunque ya advierte el informe salmantino que mide 365 días y cerca de 6 horas (Informe de 1515 [1]); no exactamente las 6 horas prescritas por César. De esta diferencia arrancaba la necesidad de reforma en la época de Gregorio XIII.

Los problemas comenzaron inmediatamente después de la muerte de César. Las autoridades romanas aplicaron erróneamente la regla del año bisiesto celebrándolo uno de cada tres años, en lugar de uno de cada cuatro. Se cree que el emperador Augusto corrigió esta situación al omitir las intercalaciones olvidadas de los 8 a. C. al 4 d. C., y que después de este ajuste, el calendario Juliano comenzó a funcionar como estaba previsto. Pero a lo largo de la Edad Media su uso adquirió peculiaridades locales que derivaron a veces de distintos criterios para la datación de los registros eclesiásticos, las transacciones fiscales y la correspondencia personal. Ya dije que César había designado el 1 de enero como comienzo del año, pero en la práctica esta determinación dependió de otros factores y las alternativas más populares fueron el 1 ó 25 de marzo y el 25 de diciembre, generando problemas de cronología a aquellos hombres y a los historiadores actuales que estudian aquellas sociedades. Afortunadamente ya contamos con trabajos que nos permiten conocer la clave de estos laberintos computacionales, como los libros de Cappelli (1930), Grotefend y Grotefend (1941) y Cheney (1945).

Recordemos que originalmente en el calendario juliano los días del mes fueron contados a partir de tres puntos de división del mismo: calendas, nonas e idus. Las calendas aluden al primer día del mes. Los idus al día 13, excepto en marzo, mayo, julio y octubre, que se referían al día 15. La nona era siempre ocho días antes de los idus. Las fechas comprendidas entre estos puntos de división eran designadas contando hacia atrás desde el punto de división más próximo y la intercalación se llevaba a cabo repitiendo el sexto día de las calendas de marzo; es decir insertando un día entre las VI calendas de marzo —por eso se llamó bisiesto— (24 de febrero) y las VII calendas de marzo (23 de febrero).

La posterior implantación del calendario gregoriano fue el resultado de la necesidad de reformar el método de cálculo de la fecha de la Pascua: está diseñado para mantener la sincronía con el año trópico (tiempo que transcurre entre dos pasos consecutivos y reales de la Tierra o aparentes del Sol por el mismo equinoccio o el mismo solsticio. RAE) y ha dado lugar a la adopción de una norma de la UNESCO para el registro de las fechas. A pesar de ello, a día de hoy existen trece calendarios en uso de los cuales los más importantes son el hebreo, el islámico, el indio, el chino, el juliano y el calendario gregoriano, siendo éste hoy en día el calendario civil internacional[52]. Se puso en vigor en octubre de 1582, tras varios siglos de debate científico y la bula Inter Gravissimas de Gregorio XIII, de 24 de febrero de 1582, y regula el ciclo ceremonial de la Iglesia Católica Romana y de las iglesias protestantes; de hecho, su propósito original era eclesiástico. Utiliza el 21 de marzo como fecha del equinoccio, el ciclo metónico como base para el cálculo de las fases lunares y continúa con la intercalación del año bisiesto juliano, pero de acuerdo a una regla diferente: el añadido de un día más al final del mes de febrero se practica cada cuatro años, a excepción del último de cada siglo cuyo número de centenas no sea múltiplo de cuatro. Las fechas gregorianas para la Pascua se fijan con un sistema de reglas eclesiásticas y de tablas preestablecidas.

2. Los calendarios lunares se apoyaban en el ciclo completo de las fases de la Luna o en las lunaciones de un mes lunar sinódico, que es el tiempo que tarda la Luna desde una conjunción con el Sol hasta la conjunción siguiente (RAE). Comienzan generalmente cada mes con una luna nueva o la primera luna creciente visible después de luna nueva. Entre los más importantes de este tipo está el calendario islámico, que sigue el ciclo de fases lunares sin tener en cuenta el año trópico y que comenzó el 16 de julio del 622 de la era cristiana, fecha de la Hégira o huida de Mahoma de la Meca a Medina. El calendario Islámico contempla ciclos lunares de 30 años (360 lunaciones): 19 años de 354 días (años simples de seis meses de 30 días y otros seis meses de 29 días) y 11 años de 355 días (llamados intercalares, divididos en siete meses de 30 días y cinco de 29 días). Dentro del ciclo son bisiestos los años 2, 5, 7, 10, 13, 16, 18, 21, 24, 26 y 29 de cada periodo de los 30 años. 33 años musulmanes equivalen a 32 años gregorianos.

3. Por último, un calendario luni-solar es el hebreo. El informe salmantino se refiere en más de una ocasión a él y, de hecho, por puro deleite, los informantes de 1515 añadieron una explicación minuciosa de su funcionamiento a pesar de que reconocían que no era necesaria para la idea reformadora que habían propuesto (comprende la última parte del ms. 97).

El calendario hebreo, como lo conocemos hoy, tuvo su origen en una fecha incierta, aunque se considera que se estableció en el año 359 de los gregorianos. Cada año está formado por doce meses lunares (año simple o común) o por trece meses lunares (cuando se agrega el mes Adar II y se le llama bisiesto, embolismal o preñado). Un año ordinario consta de 50 semanas y 3, 4 ó 5 días; uno bisiesto tiene 54 semanas y 5, 6, o 7 días. Los meses constan de 29 días (mes incompleto) o 30 días (mes completo). Como (6 x 30) + (6 x 29) = 354 días, de ahí la necesidad de introducir un año embolismal de 13 meses lunares, añadiendo el mes Adar II (Pedersen, 1983, p. 19).

Los nombres de los meses son:

1. Tishrei (30 días): entre septiembre u octubre.

2. Jeshvan (29 ó 30 días): entre octubre y noviembre.

3. Kislev (30 ó 29 días): entre noviembre y diciembre.

4. Tevet (29 días): entre diciembre y enero.

5. Shevat (30 días): entre enero y febrero.

6. Adar (29 días): entre febrero y marzo.

7. Nisán (30 días): entre marzo y abril.

8. Iyar (29 días): entre abril y mayo.

9. Siván (30 días): entre mayo y junio.

10. Tamuz (29 días): entre junio y julio.

11. Av (30 días): entre julio y agosto.

12. Elul (29 días): entre agosto y septiembre.

El mes Tishrei siempre es completo, Tevet siempre es incompleto, y de aquí en adelante se intercalan los meses completos con los incompletos. Fuera de la regla están los meses de Jeshvan y Kislev que a veces son incompletos, entonces el año es incompleto (353 días), a veces ambos son completos y el año es completo (355 días); aunque en algunos casos uno es completo y otro incompleto siendo el año regular (354 días). Esto con respecto al año simple, mientras que en el año bisiesto los números cambian: un año completo tiene 385 días, uno regular 384 días, y uno incompleto 383 días. Cada mes se determina por una tabla de luna nueva, que se basa en un valor medio. Para garantizar que las fiestas religiosas se produzcan en las estaciones apropiadas, se intercalan meses de acuerdo con el ciclo de Metón citado. Puesto que el año trópico equivale a 12.368 ciclos lunares —o vueltas de la Luna alrededor de la Tierra—, 19 años trópicos equivalen a 234.992 ciclos de la Luna. Desde esta base se establece que cada 19 años, habrá 12 años comunes (de doce meses) y 7 años embolismales con trece meses cada uno: los años número 3, 6, 8, 11, 14, 17 y 19 de cada ciclo decemnovenal.

Según lo explica el informe salmantino de 1515:

El cómputo judío divide todo el paso del tiempo desde la creación misma del mundo en revoluciones decemnovenales de las que la 277, que da origen al presente cómputo, comenzó en el año 1466 de la era cristiana, que los hebreos piensan que es el año 5226 desde el origen del mundo; pero la última revolución se termina el año 6000 de su cómputo.

Tales revoluciones decemnovenales no son todas iguales entre sí, pues aunque una cualquiera de ellas contenga 19 años, de los que son iguales doce comunes formados por sendos doce meses, y siete que crecen con la añadidura del embolismo, de los que cada uno comprende trece meses, es decir, el 3º, 6º, 8º, [11º], 14º, 16º [en lugar de 17º] y 19º de cada revolución, sin embargo se diferencian por el hecho de que los años de los hebreos son desiguales: unos de los ordinarios, y otros formados por años más largos.

El año del cómputo judío es de tres clases: igual, aumentado y disminuido. El igual o común es aquél cuyos cinco meses alternos se componen de 29 y 30 días. El aumentado es el que añade un día al número anterior, formando tres meses seguidos de 30 días. El disminuido, por el contrario, es el que otorga solamente 29 días a tres meses seguidos (Informe de 1515, proposiciones primera, segunda y tercera).

No sé de dónde tomaron los profesores salmantinos estos datos; lo único que puedo decir es que su cronología no coincide exactamente con la propuesta por Flavio Josefo en Antigüedades judías (Flavio Josefo, 2009, p. 7), que es una obra que citan y usan los salmantinos en otras partes de este informe sobre el calendario. En este punto los salmantinos se liaron.

El origen histórico de este calendario interesó especialmente a los informantes de Salamanca del año 1515, probablemente por la relación que tiene con el calendario litúrgico en función de la fijación de la fecha de Pascua. En principio, el ‘ibbur o intercalación se decidía empíricamente a propuesta del presidente del Sa‘ibbur nedrín, aconsejado por tres compañeros como mínimo y siete como máximo, teniendo en cuenta:

• Que el segundo día de Pascua cayese después del equinoccio de primavera.
• Que la vegetación estuviese lo suficientemente desarrollada para poder hacer las ofrendas señaladas en la Ley.
• Que en año sabático o jubilar no debía haber intercalación (Vernet 1954, p. 61).

Cuando estas normas quedaron fijadas matemáticamente, el calendario judío pasó —según Vernet— a ser uno de los más exactos del mundo, y aun hoy no ha perdido este carácter. Las reglas generales las fijó el patriarca Hil.lel II, que rompiendo con la tradición, difundió normas para el cálculo del calendario que hasta entonces se consideraban ciencia secreta de las autoridades religiosas. Los detalles exactos del calendario de Hil.lel no han llegado hasta nosotros, pero el principio básico consistió en adoptar el ciclo de Metón y fijar, dentro de él, los años que debían ser embolismales. Hasta el siglo X d. C. hubo desacuerdo sobre el año adecuado para la intercalación y para establecer el inicio del cómputo de los años. Dependía de una comisión del Sanedrín que evaluaba los informes observacionales de la Luna, y las decisiones sobre la intercalación estaban influenciadas, si no totalmente determinadas, por el estado de la vegetación (maduración) y de la vida animal.

En conjunto, este calendario se basa en complejos cálculos matemáticos y astronómicos del ciclo de la Tierra alrededor del Sol (año) y del de la Luna alrededor de la Tierra (mes), por imperativo de la Torá. Tiene una secuencia de meses basada en el ciclo de fases lunares, pero cada pocos años se intercala un mes para acompasarlo con el año trópico. En el calendario hebreo los años son contados a partir de la Era de la Creación del mundo, que creen que ocurrió hace más de 5000 años y que corresponde al 7 de octubre de 3760 del calendario juliano proléptico (así llamado cuando se utilizan sus normas para fechas anteriores al año de puesta en vigor de ese calendario) y de 3761 a. C. en el calendario gregoriano proléptico. El año del nacimiento de Jesús es el año 3760 del calendario hebreo.

Explicados sucintamente los tipos principales de calendario, pasaré a hablar de las circunstancias que condicionaron la elección papal de un modelo concreto, el desarrollo y la reforma que asumió el Vaticano y que se llamó calendario gregoriano.

Comenzaré por recordar algo obvio: que la reforma del calendario se promulgó en correspondencia con la jurisdicción coercitiva universal del papa. Las palabras lo que atares en la tierra será atado en el cielo, y lo que desatares en la tierra será también desatado en el cielo significan que Pedro y sus sucesores tienen el poder de imponer leyes preceptivas y prohibitivas, dispensar de esas mismas leyes y, cuando sea necesario, anularlas. En función del poder delegado de Cristo, a los papas corresponde juzgar las violaciones a esas leyes e imponer o condonar castigos; es decir, que el papa posee jurisdicción ordinaria, inmediata y episcopal sobre todos los fieles (igualmente sobre pastores y fieles). Como supremo maestro y guía de los cristianos tiene derecho a:

1. Determinar lo que debe ser creído por los fieles, pudiendo adoptar las medidas necesarias para la preservación y propagación de la fe.

2. Legislar con o sin asistencia del concilio general.

3. Total autoridad para interpretar, alterar y abrogar las leyes establecidas.

4. Dispensar y privilegiar, individual o colectivamente.

En consecuencia, para los cristianos de todos los tiempos el papa tiene plena autoridad legislativa y judicial (Riccardi, 1997) y, por tanto, tenía todo el derecho a imponer una reforma del calendario.

El problema de calendario en la Iglesia católica se creó en el mismo momento en que se asoció la fecha de celebración de la Pascua con el ritmo de los astros. El calendario eclesiástico se basaba en datos astronómicos con las siguientes constantes (Pedersen, 1983, p. 17):

1 año trópico = 365.2422 días medios solares.

1 mes sinódico = 29.53059 días medios solares.

Luego son ciclos no compaginables: 365.2422/29.53059 = 1.236826626220472 meses.

La fijación de la fecha de la Pascua fue el primer asunto que generó un conflicto computacional en el mundo cristiano. Recordemos que la Pascua era la fiesta principal de los judíos y el martirologio Romano la describe, como festum festorum y solemnitas solemnitatum. Conmemoraba la noche en que el ángel exterminador de los primogénitos de los egipcios pasó sin dañar a los hebreos liberados mediante el sacrificio y la sangre del cordero. Los hebreos la celebraban al anochecer del día 14 del mes de Nisán (entre marzo y abril), fecha en la que, según el Antiguo Testamento, será para vosotros el comienzo de los meses (Éxodo, 12; Números, 9; Deuteronomio, 16). Desde el siglo I, hubo acuerdo entre los cristianos en celebrar este aniversario de la muerte y Resurrección de Cristo, pero no en la fecha de la misma (Pérez Millán, 1956, pp. 99 ss.).

A medida que pasaba el tiempo, con una relación muy cercana a la festividad de la Pascua se fueron desarrollando gradualmente ciertas festividades que conocemos actualmente como fiestas móviles: la Cuaresma (que duraba 40 días desde los primeros años del siglo IV), el domingo de la Santísima Trinidad, el Corpus Christi, el día de la Ascensión (40 días después de la Pascua y 10 después de Pentecostés), la Septuagésima (domínica que celebraba la Iglesia tres semanas antes de la primera de Cuaresma)...

El primer canon conocido para la celebración de la Pascua fue la llamada octaëteris basada en la correspondencia entre 8 años y 99 meses: Después de 99 meses, la luna casi vuelve a estar llena. El casi se explica porque:

8 años alejandrinos = 8 x 365.25 = 2922.000 días

99 meses sinódicos = 99 x 29.53059 = 2923.528 días

Una buena aproximación, pero no perfecta. Cuando el cristianismo se extendió desde su lugar de nacimiento hacia Occidente, centrándose en Roma, comenzaron los problemas computacionales para la celebración de la Pascua. Los usos para realizarla se diversificaron en dos, el oriental y el occidental. Eusebio de Cesarea (c. 260-339) en su Historia eclesiástica (Eusebio, 2010) narra la llamada controversia de la Pascua en los primeros siglos de la Iglesia. Según este texto, en las comunidades orientales (Asia Menor), primaba la conmemoración de la Pasión y muerte de Cristo y la celebraban el 14 del mes de Nisán, como los judíos, independientemente del día de la semana en que cayese, concluyendo el ayuno preceptivo a esas fechas ese mismo día; quienes seguían este rito fueron llamados cuatrodecimanos. En cambio, en las iglesias occidentales (Roma, Alejandría...) se daba más importancia al hecho de la Resurrección y siguieron la costumbre romana de considerar el 14 de Nisán como fecha clave para la fijación de la Pasión, celebrando la Resurrección el domingo siguiente y manteniendo el ayuno hasta dicho día.

Los primeros conflictos derivados de estas diferencias trataron de solucionarse por la vía del consenso. Después de que el papa Pío I (142-155) emitiese un decreto obligando la celebración de la Pascua en domingo, el papa Aniceto (150) recibió la visita de San Policarpo de Esmirna que intentó persuadirle sin éxito de la necesidad de que toda la cristiandad se atuviera al criterio de los cuatrodecimanos. El primer acuerdo entre los discrepantes se logró hacia el 190, cuando el papa Víctor mandó reunir sínodos en las distintas provincias del Imperio para tratar el tema, pero en un primer momento los obispos de Asia se mantuvieron en la discrepancia. Los orientales defendían para mantener su costumbre que una cosa era la fe y otra la tradición apostólica, y se negaban a seguir los dictámenes de Roma. Cuando Víctor se disponía a separar a los asiáticos de la comunión eclesiástica alegando heterodoxia, la mediación del obispo galo San Ireneo (130-202), discípulo de San Policarpo, logró convencer a los asiáticos de adoptar el uso romano de celebrar la Pascua en domingo, y la controversia entró en una segunda fase en la que el problema fue acordar el domingo concreto de dicha conmemoración.

Así entendemos que en los primeros siglos de la era cristiana conviviesen fechas distintas para las celebraciones pascuales. La hilaridad de los judíos y de otros pueblos contra los cristianos por las contradicciones en torno a esta fiesta no terminó ahí. Las iglesias de Siria y algunos grupos occidentales (proto-pascuales) mantenían en cierta medida la costumbre hebrea eligiendo para la Pascua la dominica que seguía al 14 de Nisán; por lo que algunas veces la Pascua coincidía antes del equinoccio de primavera (21 de marzo). Roma y otras iglesias occidentales, como la de Alejandría, desarrollaron criterios propios distantes de la costumbre judía, pero preservando la peculiaridad de conmemorarla pasado el equinoccio. Incluso entre ellos se hacían notables las diferencias, pues los romanos fijaban el equinoccio el 18 de marzo, siguiendo la tabla pascual de Hipólito (c. 170-235), la primera conocida, en tanto que los alejandrinos lo fechaban el 21 de marzo, de acuerdo con el ciclo de los diecinueve años. El obispo Hipólito (que en realidad sólo fue presbítero, aunque el más importante teólogo de su tiempo), confeccionó un canon de la Pascua basado en un ciclo de 16 años; tras ellos la luna de Pascua volvía al mismo día del mes, pero no de la semana, para lo cual necesitaba un ciclo de ciento doce años. Ese canon se perdió y fue redescubierto durante las excavaciones en Roma de 1551. Se albergan muchas dudas acerca de por qué Hipólito eligió la cifra de 16 años (quizá fueran dos ciclos de 8), por qué eligió el 222 para comenzar ese ciclo, y sus criterios para introducir embolismos en el año lunar. En todo caso, un computista romano desconocido llamado el Pseudo-Cipriano, al revisar el ciclo de los 112 años en 243, introdujo un nuevo ciclo de la Pascua denominado Laterculus que igualaba 84 años julianos con 1039 meses sinódicos y 30682.3 días. Más tarde, los Cánones de Anatolio sobre la fecha de la Pascua, fijaron el equinoccio de primavera el 22 de marzo y adoptaron el ciclo lunar de los 19 años. Esta controversia de la Pascua afectó de forma importante a los dirigentes de la Iglesia y se escribieron bastantes tablas pascuales (por ejemplo la de Dionisio el Grande de Alejandría) que emplearon el equinoccio para la determinación de la luna pascual.

Orientales y occidentales trataron de solventar estas diferencias en el concilio de Arlés (314), en las Galias, al que acudieron delegados occidentales, y en el que acordaron veintidós cánones para dicha celebración que ratificaban la costumbre occidental y —esto es importante— que la Pascua se celebrara el mismo día en todo el mundo. Finalmente los orientales no acataron sus decisiones y convocaron poco después el concilio de Alejandría (324), que ratificó la costumbre judía. De ahí que haya sido tan importante el concilio de Nicea (en la actual Iznik —Turquía—, del 20 de mayo a 25 de julio del año 325), porque en él se resolvieron los problemas básicos que las investigaciones astronómicas habían supuesto para la praxis religiosa del cristianismo occidental, muy especialmente esta debatida fecha de la Pascua (Pedersen, 1983, pp. 67-71). Con la presencia de Constantino, en este concilio se ratificó que la Pascua debía celebrarse en un mismo día común para toda la cristiandad, y en fecha diferente de los judíos, después del 14 de Nisán y del equinoccio vernal (fijado el 21 de marzo), siempre en domingo: o sea, el domingo siguiente al 14 de Nisán y si ese día fuese domingo —celebrándola, pues, los judíos—, se pasaría al siguiente.

Un acuerdo teórico que fue un gran paso hacia la uniformización celebrativa entre los cristianos, pero no del todo resolutivo, pues al año siguiente, 326, occidentales y orientales la volvieron a conmemorar en distinto día debido a que ambos mantuvieron su cómputo previo. Así los intentos hacia el consenso siguieron sucediéndose. Los propósitos de acompasar las diferencias ensayadas por Victorio de Aquitania y por San León no resultaron suficientes. El concilio de Antioquía, del año 341, volvió a recordar la normativa de Nicea, también en presencia de Constantino. Allí se acordó elaborar un calendario perpetuo que aclarara con antelación la fecha pascual, basándose en el ciclo de Metón de los 19 años, que al menos hace casi concordar las lunas nuevas con las fechas del calendario solar. Es decir, que después del A.D. 341, Roma defendía el periodo de los 84 años de meses lunares para calcular la epacta o edad de la luna (de error de menor de un día y medio), mientras que los alejandrinos adoptaban el ciclo de Metón, el de los 19 años (también llamado enneakaidekaëteris o decemnovenal), que entonces se creía con esta equivalencia:

19 años trópicos = 235 meses sinódicos = 6939.75 días.

Este ciclo resultó fundamental para la determinación de la fecha de la Pascua ya que, conociendo el áureo número [áureo número = resto (n.º año+1) / 19] de cualquier año, la duración del mes sinódico y la fecha del equinoccio de primavera, se podía calcular la de la luna 14 y, con ella, la de la Pascua. Si dicho ciclo fuera exacto, sabiendo que cada 28 años se repetía la serie de los días de la semana (debido a los años bisiestos), cada 532 años (28 x 19 = 532) se repetiría la secuencia del mes y el día de la semana de la Pascua. La validez de este ciclo fue ratificada por Victorio de Aquitania (s. V), adoptada por el papa San Hilario († 29 de febrero de 468) e impuesta oficialmente en el sínodo de Orleans de 541.

Fig. 20: Primer punto de Aries, equinoccio de primavera.

Después, la verdadera cuestión fue que, con los siglos, la falta de perfecta coincidencia entre los movimientos del Sol y de la Luna había ido acumulando residuos de tiempo de tal modo que el equinoccio de primavera, fijado por Nicea el 21 de marzo, llegó a celebrarse el 11 del mismo mes. La Pascua, que conforme a los mismos decretos debía coincidir con el primer domingo tras la primera luna llena que siguiera al equinoccio de primavera (esto es, el plenilunio que cae en 21 de marzo, o el que se efectúa inmediatamente después), se iba alejando cada vez más del real plenilunio de marzo, con el peligro de coincidir con la Pascua judía.

Aunque su medida era bastante aproximada, el calendario juliano se retrasaba 11 minutos y 14 segundos por año respecto del año solar o trópico, de manera que el error era de un día completo cada 128 años. El Sol se adelantaba, y con él las estaciones y el equinoccio vernal o equinoccio de primavera, el del 21 de marzo, también llamado primer punto de Aries (véase la figura 20). Fallaba pues el ciclo de cuatro años para el bisiesto y fallaba también el ciclo decemnovenal, o la igualación de la duración de 19 años con 235 meses lunares.

El ciclo de Metón no era exacto. Se descubrió que tenía un desajuste, pues 19 años trópicos, equivalen, no a 235 meses sinódicos, sino a 234.992 ciclos de la Luna. Por tanto las 235 lunaciones del ciclo duran 1 hora y 29 minutos menos que los 19 años julianos, y por ello, con los siglos, se adelantaba también el plenilunio pascual, aunque no tanto como el equinoccio. Aún así el verdadero quebradero de cabeza era el adelanto de la Luna y el consiguiente crecimiento de la epacta (el número de días o edad que tiene la Luna de diciembre el día 1 de enero del año siguiente, contados desde el último novilunio) con respecto a los años julianos; porque al no poder utilizar el ciclo de Metón como base del acuerdo luni-solar, ya no servían los áureos números para señalar los novilunios en los calendarios, hasta que Lilio elaboró unas tablas epactales con una alternativa práctica para su fijación, ya en el umbral de la reforma gregoriana.

Los propios padres de Nicea tenían que conocer de antemano que el contenido de sus decretos sobre la Pascua eran necesariamente una solución temporal debido a la presunta precesión de los equinoccios (relacionada con la precesión de la Tierra): este movimiento lento del eje de rotación de la Tierra, que se creía la causa de las diferentes longitudes de los años sideral y trópico. La retrogradación de la fecha del equinoccio vernal (el de primavera) ocurría porque la duración media del año juliano era más larga que la del año trópico, ocurriendo un día antes cada 130 años julianos. Así en la práctica, en unos 308 años, las lunaciones se producen un día antes de lo calculado por el ciclo de Metón.

La precesión de los equinoccios fue descubierta por Hiparco alrededor del año 130 a. C. como un cambio lento del equinoccio de primavera a lo largo de la eclíptica (es decir, alrededor del zodíaco). Durante las edades Antigua y Media se concibió como un movimiento de las ocho esferas celestes (incluida la de las estrellas fijas) hacia el Este en relación con el punto equinoccial. Debido a esta circunstancia, en el siglo XVI el equinoccio no tenía lugar el día 21 de marzo, como se había fijado en Nicea, sino varios días antes, de modo que la prescripción nicénica no podía seguirse al pie de la letra. Aún así, el concilio de Nicea había proporcionado una solución computacional básica a la fijación de la fecha de la Pascua y después de este concilio la astronomía pasó a un plano muy secundario en los debates de los teólogos, quedando abierta en el ámbito de los científicos, que continuaron investigando.

El ciclo pascual fue ratificado de nuevo en el sínodo de Orleans (541), pero antes, en 525, el papa Juan I (470-526) había solicitado a Dionisio el Exiguo (c. 470-c. 544) un estudio que permitiera establecer como primer año de la Era cristiana el del nacimiento de Jesús, provocando sin querer un error que se arrastra desde entonces: Cristo vino al mundo varios años a. C. y el culpable de esta paradoja es Dionisio el Exiguo, este monje escita que en el año 532 puso fecha a su nacimiento (Carabias Torres 2000b). Según sus cálculos el hijo de Dios vino al mundo en el 753 ab urbe condita, o año de la fundación de Roma. Pero el monje no tuvo en cuenta el evangelio de San Lucas y San Mateo que declara: Nacido Jesús en los días de Herodes (Mateo, 2:1); y Herodes I el Grande había muerto en 750 ab urbe condita, cuando según Dionisio, Cristo aún no habría nacido. La estrella de Belén también contradice las tesis de Dionisio. Los evangelios son ambiguos, lo que ha dado lugar a varias teorías sobre el momento en el que la guía de los Reyes Magos cruzó el cielo de Judea. Algunos la identificaron con el cometa Halley, que aparece en el firmamento cada 76 años, lo que retrasaría la Natividad al 12 a. C.; Kepler propuso como explicación que la estrella de Belén fuera la conjunción de Júpiter y Saturno sobre la constelación de Piscis, un fenómeno muy luminoso que, según sus cálculos, tuvo lugar el año 7 a. C. Por tanto, Cristo nació entre el 7 y el 4 a.C.

Más allá de ello, lo que importa ahora es que, con estas estimaciones, en su De titulis paschalis Aegyptiorum, Dionisio inventó la era del Anno Domini Nostri Iesu Christi (llamada Anno Domini o simplemente A. D.). En su Tabla de Pascuas mantenía simultáneamente el ciclo decemnovenal de los alejandrinos y el canon de Victorio. Esta tabla fue de gran importancia y dejó en desuso otras muchas que circularon durante los siglos IV y V. Indicaban, en columnas, los siguientes datos: I: Anni Domini, II: Quae sint indictiones (ciclo de quince años introducido por Constantino en 312), III: Epactae i. e. Adiectiones Lunares (número de días que la luna de diciembre tiene al día primero de enero), IV: Concurrentes diez (día o días que sobran de las cincuenta y dos semanas de cada año), V: Quotus sit Lunae Circulus, VI: Quota sit Luna xiiii Paschalis, VII Dies Dominicae Festivitatis; VIII: Luna ipsius Diei Dominici (Pedersen, 1983, pp. 52-53). El conjunto de estos descubrimientos recibió el nombre de Argumenta Dionysii o procedimientos matemáticos para la determinación de los parámetros del calendario de un año dado, como el áureo número, concurrente, epacta, indicción, etc.

Esta tabla de Pascua enseguida fue aceptada por la cristiandad con pequeñas reticencias de bretones e irlandeses (aferrados a su ciclo de ochenta años) y finalmente la Pascua se fijaba por enésima vez el domingo siguiente al plenilunio posterior al equinoccio de primavera (determinado a su vez en el 21 de marzo); en una fecha, pues, que puede oscilar entre el 22 de marzo —cuando el plenilunio cae en sábado— y del 25 de abril —cuando cae en 18 de abril—.

Pero Dionisio no tuvo la precaución de comprobar la fiabilidad de su Tabla de Pascuas usándola para datar algún suceso histórico. Cuando inventó esta tabla, los años del calendario juliano se identificaban con los nombres de los cónsules que habían oficiado en ese año. Por ejemplo, declara Dionisio que el año actual es el consulado de Flavius Probus, el cual sucedió 525 años después de la Encarnación de Nuestro Señor Jesucristo. No se sabe cómo llegó a ese número. Lo que él ideó es un nuevo sistema de numeración de los años para reemplazar los años dioclecianos que se empleaban en las viejas tablas de Pascua, porque no quería continuar la memoria de un dictador que había perseguido a los cristianos. Pero en su cómputo faltó el número cero, que aún no se conocía, pues llegó a Occidente en el siglo VII procedente de la India. El propio calendario gregoriano no lo contempla (véase la tabla de la figura 21). Es decir, que Dionisio utilizó como base de la nueva era cristiana la numeración romana, en la que no existe esa cifra, según vemos en esta tabla.

Anno Domini y calendario gregoriano	3 a. C.	2 a. C.	1 a.C.	1 d. C.	2 d. C.
Calendario astronómico	-2	-1	0	+1	+2

Fig. 21: Tabla con la sucesión de los años según los distintos cómputos.

A pesar de la confusión cuando se trata de medir intervalos de tiempo que comienzan antes de la era cristiana, el Anno Domini se impuso en Europa Occidental cuando lo utilizó Beda el Venerable (c. 672-735) para fechar los sucesos en su Historia eclesiástica de los ingleses, que terminó en el 731. También Beda, en su obra De Temporum Rationale (725), a pesar de que conocía la inexactitud del ciclo de Metón, ratificó el periodo antedicho de 19 x 28 = 532 años (el llamado ciclo pascual) que garantizaba la repetición de la Pascua cada 28 años y aseguraba su celebración en Domingo. Esta obra de Beda se convirtió en un manual para la determinación de la fecha de la Pascua y zanjó la controversia durante la mayor parte de la Edad Media.

Pasados los siglos, el tema del calendario volvió a ser especialmente relevante por las múltiples implicaciones científicas, políticas y, sobre todo, religiosas que tenía. Resultaba tan urgente como difícil el encontrar una alternativa computacional que se atuviera al ritmo real de las constelaciones y evitara la coincidencia cronológica entre las pascuas judía y cristiana. Debido a la variación en la duración del año trópico, sabemos ahora que es imposible conseguir un ajuste perfecto del calendario, aunque esto no se conocía entonces. Por otro lado, y aunque se deseaba permanecer fiel a la filosofía aristotélico-ptolemaica cristianizada por Santo Tomás (que era la única verosímil durante la Edad Media europea), era imposible obviar sus fallos. Dice Alberto Elena que la sociedad medieval seguía necesitando el principio ptolemaico de salvar las apariencias, y no desde un punto de vista exclusivamente filosófico, sino con una finalidad práctica: para la navegación, para confeccionar almanaques… facetas para las que sólo la astronomía ptolemaica, con su insuperable aparato computacional, era satisfactoria. Este éxito predictivo no evitaba el cuestionamiento de su fundamento físico. De este modo, junto a una innegable fidelidad a los principios físico-cosmológicos de Aristóteles, se reconocía a la astronomía computacional el derecho a guiarse por un ideal puramente descriptivo y predictivo, y se buscaba en tal subdivisión tácita de la disciplina una coartada para poder aceptar las hasta entonces insuperables conclusiones ptolemaicas (Elena, 1985, pp. 77-78).

Teniendo en cuenta estas dificultades comprendemos que la reforma del calendario fuera el asunto científico más delicado de los tratados hasta ese momento y pronto se convirtió en el gozne de un abanico de investigaciones parciales llevadas a cabo en todos los ámbitos de la intelectualidad del mundo occidental. En él, la Europa cristiana se encontró por primera vez sola; no podía contar con la ayuda de los científicos orientales, como en otras ocasiones, porque a los árabes, por ejemplo, excelentes matemáticos y astrólogos, no les motivaba la fijación de la fecha de la Pascua; aparte de que la astrología había sido claramente condenada por el Corán (XXVII, 65), debido a la supuesta pretensión de conocer el futuro, que sólo a Alá le era dado conocer. Aunque, tanto entre los cristianos como entre los árabes, pronto se salvó este escollo anti-astrológico con la interpretación neoplatónica de los astros como signos y no como causas (Tester, 1990; Vickers, 1990; McDannell-Lang, 1990).

A partir del siglo XII, se reavivó de nuevo el debate sobre el desfase de la fecha de la Pascua y proliferaron los proyectos de reforma del calendario. Estos proyectos medievales han sido estudiados por varios investigadores; entre ellos por North (1983, pp. 74-113), Kaltenbrunner (1876, pp. 49-51), Hefele (1917, pp. 445-451), Mansi (1960, pp. 370-381) y Pastor (1935, pp. 261 ss.). Resumiendo sus exposiciones diré que Grosseteste (1170-1253) midió el desfase del ciclo metoniano y propuso el ciclo de 76 años (4 x 19), o 4 ciclos metonianos, o 940 lunaciones (North, 1983, p. 80; The Electronic Grosseteste, <http://www.grosseteste.com/>). Pero el verdadero debate se reavivó cuando Roger Bacon (c. 1214-1294), en 1267, escribió que el retraso del calendario est intolerabilis omni sapienti, et horribilis onmi astronomo et derisibilis ab omni computista (Opus Tertium, cap. 1, p. XXII, publicada por Brewer en Londres: 1859): o sea, intolerable, horrible y ridículo; era urgente su reforma. Bacón no había sido el único ni el primero en denunciar este problema, aunque sus alusiones a la perentoria necesidad de la reforma fueran entonces y sean ahora las más conocidas (North, 1983, p. 82; Bonnin Aguiló, 1999, pp. 27-42).

Así pues, el creciente desajuste cronológico, la necesidad de hacer coincidir las celebraciones religiosas con el ritmo real de las revoluciones astronómicas y el escándalo que tales diferencias provocaban, fueron los factores que contribuyeron decisivamente a cambiar con los años la actitud de la Iglesia, desde el desinterés inicial, hasta convertirla en la institución promotora de los estudios encaminados a ofrecer una solución métrica definitiva. Bacon trabajó en el tema a petición de Clemente IV (1291-1352) y se dio cuenta de que el verdadero problema era el continuo adelanto que experimentaba el equinoccio de primavera; por ello propuso la supresión de aproximadamente un día cada 125 años (1127/9, con un resto) en De computo naturali y De reformatione calendari; pero no se le hizo caso (North, 1983, p. 83). De forma simultánea, Giovanni Campano (1220-1296) se dirigió también a la Santa Sede para comunicar a Urbano IV (1195-1264) el resultado de sus investigaciones sobre el calendario, optando por esa supresión de un día cada 100 años.

La generación siguiente trajo un cambio en el estilo de las tablas astronómicas. John de Murs, en su Autores calendarii nostri duo principaliter tractaerun... declaró que las Tablas de Tolosa eran las más precisas (año 1317) y, junto con Fermín de Belleval, fue invitado a Avignon por Clemente VI (1291-1352) para trabajar en la reforma del calendario, en el año 1344. El resultado de estas investigaciones basadas en los datos de las tablas alfonsíes puso de relieve que el calendario juliano adelantaba un día cada 134 años, luego la solución era o suprimir 10 días en un mismo año, o anular todos los bisiestos en 40 años y, en adelante, suprimir un día cada 134 años. No quedaba ninguna duda de cuál era el error y esta respuesta será después repetida en multitud de informes hasta la reforma gregoriana (North, 1983, pp. 84-85), incluidos los dos redactados en Salamanca.

En el ámbito de las disertaciones del concilio de Pisa, en 1411, el cardenal Pierre d’Ailly (1350-1420) escribió otra propuesta sobre la reforma del calendario, que finalmente fue leída en el concilio de Constanza (1414-1418), en marzo de 1417, y aprobada parcialmente por el papa. D’Ailly explicaba en ella que el calendario no usaba la duración verdadera del año, que era algo menor que la considerada, y la causa de que los solsticios y los equinoccios se adelanten aproximadamente un día cada 134 años. Ofrece varios métodos para la reforma: o suprimir un año bisiesto cada 134 años (lo que sólo corrige el error del Sol), o suprimirlo cada 304 años (que sólo corrige el error de la Luna), o, desestimando el áureo número, generar tablas astronómicas para fijar las fiestas religiosas (North, 1983, pp. 86 ss.). Obsérvese, pues, que esta propuesta coincide plenamente con el informe de Lillo repartido por los comisionados vaticanos de 1577 para su consulta pública. Por tanto, más que llamarse al calendario gregoriano liliano, como proponía Herrera Armendía (2007), habría que llamarle calendario baconiano-aillyano-mursiano-bellevaliano, en función de los verdaderos descubridores de estas proporciones antes de que las defendiera Salamanca.

También se vio implicado en estos estudios Nicolás de Cusa (1401-1464), redactando su De reparatione calendarii, y presentándolo al concilio de Basilea-Ferrara-Florencia (1431-1445). En su planteamiento aconsejó que se efectuase la reforma en el año 1349, siguiente a un año bisiesto y de áureo número igual a 1; la supresión de una semana para ese año y la omisión de un año bisiesto cada 304 años, de forma que el cómputo sería correcto durante unos 1000 años. En ese mismo foro, en 1435, presentó Thomas Czempin otra alternativa consistente en la intercalación de un día cada 136 años y el retraso de 1 número áureo cada 237 (Dobrzycki 1983, p. 118). Pero las turbulencias en el seno de la Iglesia impidieron la materialización de la reforma.

Recordemos que en el concilio de Basilea participó una buena representación de la intelectualidad universitaria salmantina, entre los que cabe recordar a Gonzalo García de Santa María, Juan Díaz de Coca, Ibo Moro, Álvaro Núñez de Isorna, Pedro de Bocanegra, Juan Alfonso de Segovia, Rodrigo Sánchez de Arévalo, Martín de Galos, Fernando Díaz de Carrión y Alonso de Madrigal, llamado el Tostado (Beltrán de Heredia, 1966a, pp. 315 y 474; Fuertes Herreros, 2006, p. 518). E. Vallina y otros piensan que este último no asistió a este concilio, pero aún así, influenciado por los debates conciliares, el Tostado escribió una explicación del calendario juliano dentro de su trabajo Tostado sobre Eusebio (Salamanca: Hans Gysser, 1506), conservándose un ejemplar en la biblioteca universitaria que pudo también estar a disposición de los comisionados salmantinos, tanto de los de 1515 como de los de 1578.

No sé si lo leyeron o no los comisionados de 1578, pero en su informe se refieren al citado concilio, aconsejando que se quiten los días que sobran para regular el equinoccio de primavera de una sola vez, porque

...borrados de un plumazo, pasará este asunto al olvido más rápidamente, y nadie se preocupará o lo sentirá, y luego, como atestigua el concilio de Basilea, no habrá de cambiar o borrar nada (Informe de 1515 [2]).

La redacción y el debate de los proyectos sobre el calendario en Basilea derivó en el primer intento efectivo de solución del problema que se dictó en el año 1437. Se ordenó en él de nuevo una reforma para 1441, consistente en la omisión de una semana en el ciclo lunar, más el cambio del áureo número; pero dicha orden no fue ejecutada, probablemente por las disensiones internas de la Iglesia.

En torno a este mismo reto científico se unieron las universidades de Cracovia, Nuremberg, Praga y Viena al final de la Edad Media. En 1470 el Cardenal Besarión (1403-1472) escribió a Paulo II (1417-1471) explicándole que la inexactitud en el cálculo del equinoccio y de las lunaciones había llevado a un cómputo pascual enteramente erróneo, pero hasta Sixto IV (1414-184) no se volvió a tratar seriamente el tema del calendario. En 1475, Johann Müller de Königsberg (Regiomontano, 1436-1476) fue llamado a Roma por Pío IV para estudiar el tema. Era un hombre célebre por su ciencia astronómica y sus trabajos sobre el calendario, pero apenas pudo avanzar en este encargo debido a su repentina y misteriosa muerte al año siguiente (julio de 1476). Más tarde, Juan de Novara, presentó un libro a Julio II (1443-1513) con otra propuesta de reforma, recibiendo de este papa la invitación para permanecer en Roma y proseguir sus estudios con el fin de llegar a una solución positiva.

En conjunto se desarrolló un animado debate, como vemos, pero sin ningún proyecto que resultara sin inconveniente alguno. En aquellos momentos el tema correspondía a las matemáticas en virtud de los cálculos imprescindibles, a la filosofía natural en razón de las demostraciones físicas y filosóficas, y a la Iglesia en función de la fijación de la fecha de la Pascua. Se observó que la cuestión atañía también a interesados planteamientos ideológicos y que sobrepasaba las posibilidades de solución de un único estado-nación. En la época del Renacimiento la reforma del calendario sólo tenía posibilidades de fructificar si la promovía el papa y la apoyaban los príncipes cristianos. Era imprescindible sobrepasar el plano investigador estrictamente local o nacional y por eso la solución implicó a astrónomos, astrólogos, matemáticos, teólogos y políticos de todo el mundo occidental. A pesar de los esfuerzos, la cristiandad occidental llegaba a la Edad Moderna sin una solución al problema computacional y el papa decidió solicitar ayuda a la Universidad de Salamanca y otros sabios y centros de saber de la cristiandad.

1.4.2. El informe salmantino de 1515

La intervención de Salamanca en la reforma del calendario comenzó a raíz del V concilio de Letrán (celebrado entre el 3 de mayo de 1512 y el 16 de marzo de 1517). Recordemos que la Universidad de Salamanca, de forma institucional, redactó dos informes sobre de la reforma del calendario a lo largo del siglo XVI: uno en el año 1515 y otro en 1578. El informe de 1515 fue consecuencia de una solicitud realizada a esta Academia por el papa León X (1475-1521) y el rey Fernando el Católico (1452-1516), a propósito de los debates computacionales en el citado concilio. Así se reflejó claramente en el título que los salmantinos dieron a la respuesta:

Traslado de lo que la Universidad de Salamanca imbió a nuestro muy Sancto Padre León, papa X, y al rey don Fernando en el año 1515 acerca de la restitución del Calendario (BGH ms. 97).

El segundo informe, de 1578, se redactó sesenta y tres años después, a petición de Gregorio XIII (1502-1585) y de Felipe II (1527-1598).

1.4.2.1. Las solicitudes de informe

Hacia 1515 estaba asomando la modernidad. Plagas, guerras, persecuciones, magia, brujería, Humanismo y Renacimiento, ciencia, fe y progreso —como dice Fernández Armesto (2010)— completan el horizonte del paisaje histórico. Algunas naciones tendían a convertirse en estados, y el papado, apenas recuperado del Gran Cisma, buscaba caminos de reforma que se encontrarían sobre bases diferentes sólo después del nacimiento del protestantismo y de la celebración del Concilio de Trento. Julio II entraba en lucha con Luis XII intentando expulsar a los franceses de Italia, respondiendo éste con medidas militares y eclesiásticas entre las cuales estuvo la de convocar un concilio cismático en Pisa (1 de septiembre de 1511). El papa comprendió que la mejor arma que podía oponerle era la de asumir y realizar él mismo un concilio para reformar la Iglesia, y lo reunió en 1512. Así comenzó el V concilio de Letrán. Visto desde esta perspectiva, las circunstancias de la convocatoria conciliar distaban de un interés prioritario sobre la investigación computacional; la cuestión conciliar clave era entonces el problema de los neo-aristotélicos, pese a lo cual el tema de la reforma del calendario recibió en dicho cónclave un tratamiento muy cuidadoso.

Como he dicho, León X, tanto personalmente como a través de Fernando el Católico (1452-1516), solicitó la opinión de Salamanca, pero casi nada sabemos sobre la contestación de esta academia, salvo —eso sí— el contenido de la respuesta misma: la inexistencia de la documentación universitaria referida a esta época y asunto, sobre todo la pérdida de los libros de claustros de la Universidad entre los años 1512 y 1526, deja irremediablemente en la sombra el interesantísimo debate que forzosamente tuvo que suscitar la doble petición, papal y real, de un informe universitario acerca de la reducción del calendario. Ni siquiera se ha conservado el original de este documento papal en el Archivo Universitario de Salamanca, ni la provisión real que tuvo que venir en requerimiento del mismo. El contenido de este informe lo conocemos porque lo recogieron literalmente más tarde los comisionados del año 1578, que naturalmente trabajaron a partir de sus contenidos.

De forma paralela y distante de los problemas políticos, un matemático —en Padua— y obispo de Fossombrone, Paul von Middelburg (1446-1534), había reavivado los debates sobre el calendario y promovido las solicitudes de colaboración emitidas por León X a instituciones científicas de la cristiandad y, entre ellas, a la Universidad de Salamanca. Middelburg había sido llamado desde Lovaina a Padua como profesor de matemáticas, y trabajó como médico-astrólogo del duque de Urbino. Su interés por el tema tenía un origen dogmático; el mismo que le había llevado a escribir la Epistola ad Universitatem Lovaniensem de recte Paschate observando (1487) y, especialmente, su obra principal: Pavlina De recta paschale celebratione et de die passionis domini nostri Iesv Christi [prima-secunda pars] (Fossombrone: Octavianum Petrutium, 1513). Después publicaría otros trabajos.

La importantísima actuación de este personaje en lo que se refiere a la historia de la reforma del calendario ha sido objeto de un detenido análisis por Marzi (1869; 1906). Este investigador explica cómo Middelbourg envió a Julio II una propuesta de reforma (su Pavlina…, publicada con este fin), texto que se debatió en el concilio de Letrán y que le otorgó el nombramiento como presidente de una comisión nombrada para la reforma del calendario. En él defendía algo que después traería cola: que bastaría la sola autoridad del pontífice para llevar a cabo la reforma, sin necesidad de contar con el apoyo de un concilio general. Justificaba una opinión de este tipo en la necesidad de tomar decisiones urgentes en un punto que evitara la hilaridad de los judíos cuando los cristianos confundían la luna llena con la luna nueva en las sucesivas celebraciones de la Pascua. Allí propuso suprimir 14 días del calendario, tratando de volver a la situación astronómica del siglo VIII, fijando el equinoccio de primavera en su lugar natural, el 10 de marzo y estableciendo un nuevo ciclo lunar de invención propia, para el caso de que no se considerara oportuno reformar el ciclo de Metón. Sugería como comienzo del ciclo el año 1500 (en ese momento ya pasado), año de jubileo. Todo eso lo expuso en su gruesa obra que no se imprimió hasta 1513 y en la que criticaba audazmente las propuestas reformistas de sus predecesores.

Muerto Julio II su sucesor León X (papa de 1413 a 1421), es decir, Giovanni de Médicis, hijo de Lorenzo de Médicis, continuó al frente del concilio, manteniendo vivo el interés por la resolución de este problema (Pastor, 1950; Minnich, 1993). Acorde con el talante personal del pontífice y del ambiente cultural en el que se había formado, mostró gran interés por las ciencias e instituyó una cátedra de astrología en La Sapienza bajo la enseñanza de Pedro Aretino y otra de matemáticas regida por Luca Pacioli (García Castaño 2009, p. 77). Enseguida aseguró la obra de Middelbourg contra cualquier contra-opinión e incluyó el asunto de la reforma del calendario entre las materias a tratar en el concilio, concretamente en la décima sesión (fijada en principio para el 1 de diciembre de 1514), encargándoselo a la comisión nombrada por su antecesor, que presidía el propio Middelbourg, en función de la solicitud papal fechada el 16-02-1514. A esta comisión perteneció también Luca Gaurico, quien después de muerto Middelbourg le acusó de haber colocado erróneamente la fecha de la Crucifixión en la luna llena (Thorndkike, 1941, p. 257).

Dentro de estas tentativas, a través de Sculteti —representante de la Santa Sede en Ermland—, Middelbourg requirió también la colaboración de Copérnico en ese mismo año de 1513, encargándole algo que a todas luces era fundamental para la pretendida reforma: la determinación de la medida del año trópico. Pero Copérnico desestimó en ese momento la invitación a participar en las discusiones, porque con razón opinaba que aún no se poseían medidas lo bastante precisas del curso del Sol y de la Luna, y entendiendo que tal reforma sólo sería viable cuando se pudiera contar con un bagaje teórico más adecuado (Ravetz, 1966, pp. 88-89; Hefele, 1939, Vol. IX, p. 448; Kuhn, 1966, p. 174). Copérnico llegaría incluso a acusar después al Concilio de Letrán de haber torcido su ruta ocupándose de este tema.

El 24 de julio de 1514 envía León X un breve a las universidades y a algunos científicos particulares, solicitando sus opiniones sobre el problema, y recabando al mismo tiempo la mediación activa del emperador y de todos los monarcas cristianos en orden a consensuar la solución. Su contenido va dirigido también a los doctores y maestros que se dedican a la teología y a la astrología, de cualquier lugar de la Tierra adonde llegara esta noticia. En España, Fernando el Católico obedeció la consigna papal y envió también a Salamanca una solicitud de respuesta. El documento papal que se adjuntaba llevaba por título: Breue sanctissimi d[omi]ni nostri d[omi]ni Leonis diui[n]a prouidentia pape decimi ad doctores sup[er] correctione cale[n]darii pro recta pasche celebratione. [Roma: Marcello Silber, 1514] (Marzi, 1896, pp. 91-100). El ejemplar recibido en la Universidad de Salamanca aún se conserva en su Biblioteca (véase la figura 22). En él se argumentaba la necesidad de reforma del calendario en función del obligado aumento y perfección del culto divino y de la indignidad de la descolocación de la Pascua respecto del lugar en que ubicaron su celebración los padres de Nicea. Resume el problema astronómico explicando el desplazamiento del equinoccio hasta diez días y la corrección del ciclo de Metón adelantando los números cinco días y haciendo comenzar el nuevo ciclo el 1 de enero de 1500, año de jubileo; solicita también la presencia de los expertos en el concilio o el envío de sus informes escritos.

A este requerimiento responde el primero de los informes salmantinos sobre la reforma del calendario, fechado en 1515, que como vimos, sorprendentemente no fue recogido por Marzi en el libro en el que estudió, muy bien por cierto, la cuestión del calendario en este concilio. Él utilizó los fondos de la Biblioteca Vaticana y allí reposa aún, pero en la versión que recogieron los comisionados de 1578; no la copia original. ¿Por qué falta sólo ésta? Después veremos.

A este primer llamamiento respondieron también otras instituciones, pero la mayoría de los informes no llegaron a tiempo para la décima sesión en la que se preveía tratar el problema (diciembre de 1514), aunque ésta se retrasó hasta mayo de 1515. El 1 de julio de 1515 León X emitió un segundo breve reiterando la solicitud, pero en este caso pidiendo opinión sólo sobre propuestas científicas concretas: la fijación del nuevo ciclo decemnovenal el 1 de enero de 1500 y el traslado de la fecha del equinoccio; o sea, que —según este último breve— el papa ya había hecho suyas las propuestas de Middelbourg.

Desde Viena, André Stiborius y el rector Georges Stannstefter ofrecieron una solución casi calcada de la salmantina, como veremos, salvo en la consideración de la medida del año trópico, para la que ellos proponían el curso verdadero (real) y no el curso medio —el de las tablas alfonsíes—; asignaban también al equinoccio de primavera una fecha fija (10 ó 25 de marzo), abandonando el ciclo de 19 años y calculando la luna nueva desde tablas astronómicas prefijadas que tomaran como base el meridiano de Roma. Muy similar opinión emitió asimismo la Universidad de Tubinga, a través del profesor de matemáticas Juan Stoeffler de Justingen: aboga por la fijación del equinoccio en el calendario, por ejemplo el 10 ó 11 de marzo, omitiendo un día cada 134 años y el abandono del ciclo de los diecinueve años, creando en su lugar unas tablas astronómicas con el meridiano de Roma como regulador. De similar contenido fue también el proyecto de Gionanni Maier. Ingolstadt, por su parte, había recibido el escrito imperial solicitándoselo el 21 de octubre de 1514 y el sabio doctor Juan Eck (¿el que unos años después se enfrentaría dialécticamente con Lutero en la Dieta de Worms?) compuso su propuesta titulada De vera Paschae celebratione J. Eckii theol. Diorthosis ad Leon X (1515), que pronto se dio a la imprenta. En Italia, el cisterciense Basile Lapi de Florencia dedica una obra al papa sobre la cuestión (De aetatum computatione et dierum anticipatione); lo mismo hizo Antonio Dulciato, con otro informe de veinticinco proposiciones, compuesto en diciembre de 1514. También en parecidos términos respondió Giovannhi Tolosani. La Universidad de Lovaina encargó el trabajo a Albert Pighe, pero éste no lo concluyó a tiempo. En 1518 terminó la parte preparatoria y en 1520 envió al papa su trabajo. Éste tampoco consideraba oportuno hacer depender de un cálculo astronómico la luna llena de la Pascua; propuso la fijación del equinoccio en el 5 o el 6 de marzo y la supresión definitiva de 6 días del calendario. Una solución, pese al retraso, no tan consensuada como las anteriores (Hefele, 1917, pp. 446 ss.; Marzi, 1896, pp. 100-167).

El papa tenía prisa, pero un tiempo tan limitado presumiblemente no permitiría la realización más que de informes muy cortos. Por eso, en la apertura de la décima sesión del concilio que debía tratar el tema, y a pesar del retraso que sufrió su convocatoria, la propuesta no estaba aún madura y León X así tuvo que reconocerlo.

Fig. 22: Breue sanctissimi d[omi]ni nostri d[omi]ni Leonis diui[n]a prouidentia pape decimi ad doctores sup[er] correctione cale[n]darii pro recta pasche celebratione [Roma: Marcello Silber, 1514].

Concluido el periodo de recepción de respuestas, el 1 de junio de 1516 se reunieron los expertos con el papa y éste encargó a Middelburg la redacción de un resumen de las observaciones recibidas, que se tituló Secundum compendium correctionis calendarii, constinens et exponens diversos modos corrigendi calendarium pro recta Pasche celebratione. En él se habla de los informes ya recibidos: los de la Universidad de Viena, Universidad de Frigurbo, Universidad de Tubinga (de Stöffler), el obispo de Tolosa, Peregrino Priscianus (Ferrara) y Copérnico; curiosamente nada se dice del de Salamanca o del de Pedro Ciruelo. A renglón seguido se declaraban los problemas detectados: El error en el ciclo decemnovenal, el retraso del equinoccio de un día cada 134 años y su posible fijación el 21 de marzo cuando el real ocurría el 11 ó 12 de ese mes. Cirilo Flórez ha analizado escueta y claramente el tipo de soluciones que se ofrecieron, dividiendo las respuestas en tres posturas: Primero aquellos que consideraban que la Pascua debía celebrarse en el mismo día (opinión que rechazaba Middelbourg). En segundo lugar los que defendían la celebración de la Pascua como fiesta móvil en relación al Sol, fijándola en el primer domingo después del equinoccio de primavera (opción aceptable para la Iglesia). En tercer lugar, la mayoría, que consideraban que era mejor tener en cuenta los movimientos del Sol y de la Luna simultáneamente, pero a su vez con dos versiones:

1. Los que proponían suprimir 10 ó 11 días, fijar el equinoccio el 21 de marzo, introducir un bisiesto cada 134 años y crear una tabla de epactas para la fijación de la luna de la Pascua. Esta opinión era contraria al pensamiento de Middelburg y es justamente la que defiende el informe salmantino.

2. Los que sugieren fijar el equinoccio el 10 ó 11 de marzo, suprimir un bisiesto cada 134 años y usar la tabla de epactas para la fijación de la Pascua durante los siguientes mil años.

El profesor Flórez (1999, p. 445-446) se pregunta con fina agudeza si el olvido en la cita de otros informes, como por ejemplo el de la Universidad de Salamanca, no se debería a que defendían opiniones contrarias a las de Middleburg.

No hay ningún dato que nos haga sospechar que la Universidad de Salamanca respondiera a este segundo requerimiento, a pesar de que, el 10 de julio de 1516, el papa decidió remitir de nuevo este Secundum compendium… para un examen más profundo a los obispos, a las universidades y a los sabios, solicitándoles de nuevo sus impresiones. Seguramente Salamanca hizo caso omiso de esta segunda petición, respondiendo quizá que pocos meses antes había enviado el ya redactado. De hecho, si hubiera existido este texto, lo hubieran recogido o nombrado los comisionados de 1578, igual que recogieron el anterior.

Tras esta segunda solicitud, nuevos textos se unieron al desafío. Los criterios no eran unánimes entre los científicos católicos y algunos encontraban ridículo tanto esfuerzo. La comisión conciliar discutía tanto los informes escritos como los orales ante León X, pero la acción conciliar tuvo que limitarse a elaborar una memoria en trece proposiciones que se pensó serviría de base a los trabajos posteriores. Se tituló De correctione Kale[n]darii propositiones XIII recollectae ex multis disceptatio[n]ibus habitis per D ad hoc specialiter deputatos: ex parte S.D.N. Papae & sacrae deputationis fidei in Concilio Lateranensi (véase la figura 23). No contiene data, pero el ejemplar que he usado tiene una anotación manuscrita de Hernando Colón que dice: «Costo vn quatrin en Roma por Julio de 1516», luego fue editado antes de dicha fecha. Este nuevo documento recogía una buena parte de las propuestas salmantinas: Establecer el 21 de marzo como fecha del equinoccio de primavera, aunque debía trasladarse cuanto antes al 10 de marzo; corregir un día cada 134 años (puesto que el año solar sobrepasaba un poco más de 10 minutos y 4 segundos el año real); y como el ciclo lunar y el áureo número eran defectuosos, pero no parecía posible abandonar el ciclo lunar de los 19 años, se sugería fijarlo para los siguientes 304 años. Animaban a la confección de tablas astronómicas para mil años y se pensaba seguir solicitando de los matemáticos la determinación astronómica de la luna llena de Pascua, refutando enseguida diversas objeciones que se dieron y argumentando las razones que justificaban este proyecto. Se ratificaban asimismo los dos procedimientos de corrección que también proponía la Universidad de Salamanca: retrasar 11 días el calendario en un sólo mes o en varios, u omitir el día bisiesto durante 44 años (lo que suponía suprimir poco a poco esos 11 días, intercaladamente).

El de Salamanca no fue el único informe sobre la reforma del calendario elaborado en Castilla en ese tiempo. Nebrija escribió un ensayo sobre el tema, titulado De ratione calendarii que no imprimió; sí lo hizo después con Carmina ex diuersis auctoribus ab Antonio nebrissensi in calendarii ratione[m] collecta [Burgis: per Fredericum alemanum, c. 1512?] (BGH 17072 3), coincidiendo con la solicitud que hiciera León X a los científicos cristianos desde el V concilio de Letrán para colaborar en la reforma. Él estaba entonces en Alcalá, donde se debatió el problema con interés. La prueba de que no sabía mucho de este tema es el resultado

Fig. 23: De correctione Kale[n]darii propositiones XIII recollectae ex multis disceptatioibus habitis per D ad hoc specialiter deputatos: ex parte S.D.N. Papae & sacrae deputationis fidei in Concilio Lateranensi.

de este impreso: dos hojas en cuarto con veintiséis axiomas en verso latino sobre el mundo celeste. Con eso no se podía reformar el calendario. Me recuerda mucho el planteamiento y las propuestas del proyecto de reforma del calendario que redactó su alumno, Juan Ginés de Sepúlveda (1490-1573), un poco después, con intención de presentar la solución (según en él presumía) al concilio de Trento (Carabias Torres 2003). Se tituló De Correctione Anni Mensivmqve Romanorvm. Ioannis Genesii Sepvlvedae Cordvbensis Commentatio (Venetiis: Gabrielem Iolitum de Ferrariis, 1546). Llegó a decir en él que lo enviaba al concilio para que lo utilizaran como base del debate sobre la reforma del calendario, cuando leyéndolo se comprueba que, por ejemplo, sólo conocía las Pléyades por la bibliografía. Parece, pues, ser verdad la opinión tantas veces recordada de Juan Páez de Castro, en carta a Zurita, donde decía:

...En lo del doctor Sepúlveda no sé que me diga sino que lo tengo por hombre non sani capitis, que ni en sus cartas ni en su diálogo sabe lo que dice por falta de principios (cf. Carabias Torres, 2003, p. CCLXI).

Opino, en este caso, que ni Nebrija ni su discípulo Sepúlveda supieron en estos textos lo que se traían entre manos. Un caso distinto fue la Tabla de la diversidad de los dias y horas y partes de hora en las ciudades, villas y lugares de España y otros de Europa que les responden por sus paralelos compuesta por el Maestro Antonio de Nebrija, Madrid: [s.n., s.a.] (ed. DICTER, <http://dicter.usal.es/bios/Nebrija>). En ella no aportaba novedad, pero al menos ofrecía una forma cómoda de entretener la curiosidad de la gente común. En consecuencia, pues, este grupo de intelectuales son especialmente memorables por sus trabajos cosmográficos y por otros, pero no tanto por los matemáticos, aunque sea de justicia reconocer a Nebrija su contribución al desarrollo de un léxico científico en latín (Hinojo, 2005).

Bajo el mismo influjo del V concilio de Letrán, Pedro Ciruelo envió a León X (no al concilio) un texto titulado De vera Luna paschali et de correctione Kalendarii Scripserat. Ciruelus de hoc argumento ad Leonem X Concilium Lateranense, celebratur 1515, atque hic... a se conscripta in Epitomen redegit (Alcalá: Miguel de Eguía, 1528), que dedicó a la Iglesia de Toledo. Lo publicó años después, dentro de su obra Expositio libri missalis peregregia nuper edita ex officina sapientissimi viri tam humanarum q[uam] sacrarum litterarum professoris, diuiniq[ue] Verbi predicatoris zela[n]tissimi Petri Cirueli Darocensis in Complutensi Achademia... (Compluten: in aedibum Michaelis de Eguia..., 1528), f. CCLXXVIII ss., y se titula De correctione kalendarij (figura 24). Tampoco Marzi se hace eco en sus trabajos de este informe enviado a propósito del concilio de Letrán.

Ciruelo propone en él suprimir los días sobrantes, fijar el equinoccio el 21 de marzo y guiarse por unas tablas para la determinación de la fecha de la Pascua, solución que resultaba también coincidente con la propuesta de Salamanca, de la que después hablaré más despacio. Adjunta al texto varias tablas: en la primera calcula el día de esta celebración pascual desde el año 1500 a 1604 (f. 230 r.); otra contiene la corrección del equinoccio trasladado al 21 de marzo; en otra reproduce la tabla pascual de Dionisio el Exiguo; y en la última, una tabla de tres filas, con la indicación de los números áureos según el cómputo seguido hasta 1515, a un lado, y del que resultaría después de la supresión de los días correspondientes y la fijación del equinoccio, en el otro, colocando entre medias de ambos la letra correspondiente de los días de la semana. La tabla incluida por los comisionados salmantinos de 1515 tenía esa misma estructura (véanse las pp. 305 ss. de este trabajo y compárense con la tabla de la figura 24). Ninguno de estos informes resultó suficiente a los expertos reunidos en el concilio.

Tal y como lo había expresado antes Copérnico, finalmente el concilio consideró que la cuestión no estaba madura, y se pospuso la solución para más adelante. Lo positivo fue que los debates conciliares y su repercusión incentivaron las observaciones, dándose a la prensa en esos años multitud de estudios de cronología. Después de tantos esfuerzos, en 1517 seguía pareciendo una realidad la frase que había escrito Alessandro Achillini en su Sobre las esferas (Bolonia, 1494), cuando dijo: En realidad, la astronomía no existe actualmente; sólo sirve para el cálculo de efemérides. No era capaz aún de resolver el desajuste en el calendario; y en Roma la reforma del calendario quedaba otra vez pendiente.

1.4.2.2. Los redactores del informe de 1515

Como acabamos de ver, León X, tanto personalmente como a través de Fernando el Católico, solicitó la opinión de Salamanca, como una de las más importantes academias científicas de la cristiandad; pero ya hemos dicho que casi nada sabemos sobre la respuesta de esta academia, salvo el contenido de la respuesta misma: la inexistencia de la documentación universitaria referida a esta época y asunto, sobre todo la pérdida de los libros de claustros de la Universidad entre los años 1512 y 1526 y de la documentación papal y real, tanto en Salamanca, como en Simancas, tampoco encontrada en el Vaticano, dificulta el estudio de estos hechos. Así que el contenido de este informe lo conocemos porque está incluido en el del año 1578, cuyos autores naturalmente trabajaron a partir de sus contenidos.

Esta falta de datos institucionales de este período sobre la salmantina resulta desoladora. Con notable dificultad sabemos incluso quién podía ser el rector que recibió y asumió el encargo, pues no he encontrado ni un sólo dato de rectorías referido a este año. Afortunadamente, Vicente Beltrán de Heredia ofrece alguna pista dentro de esta generalizada ignorancia, averiguando que un tal Don Lorenzo era el rector salmantino en el curso de 1514 a 1515 (Beltrán de Heredia, 1966a, p. 219). No sé quién es, pero indudablemente éste es el personaje que asumió dicho cometido. Quiero advertir que tengo esta lejana pista gracias a que Beltrán de Heredia acostumbraba a hacer anotaciones manuscritas en los márgenes de los libros de su propiedad, tanto de los que él mismo había publicado como de otros que usaba, siendo por esta causa de interés para el investigador actual la consulta de estas obras que se conservan en la Biblioteca del Convento de San Esteban de Salamanca. El nombre de este rector lo anota al margen de la obra de Esperabé de Arteaga guardada en esa biblioteca, con la signatura «378.11 ESPE, hist. 2», p. 7. Considero también digna de interés al respecto la revisión de las notas marginales de este autor relativas a los profesores de la Universidad de Salamanca de los siglos XV y XVI, de las que me haré eco en este trabajo.

Fig. 24: CIRUELO, Pedro (1528). De correctione kalendarii. En Expositio libri missalis peregregia... Alcalá: Miguel de Eguía 1528, f. 281v.

La consulta papal era compleja y es de suponer que el claustro universitario encargara la respuesta a una comisión formada por los más eminentes teólogos, juristas y artistas del Estudio (puesto que la astronomía era materia de estudio de la facultad de artes). Siempre se había hecho así y así se hizo sesenta y tres años después, cuando se repitió prácticamente la misma circunstancia en la época de Gregorio XIII. La falta de documentación relativa al año de 1515, de la que hablo, dificulta incluso la reconstrucción del plantel de profesores con los que contaba la Academia en ese momento, cuya identificación podría aportarnos alguna luz acerca del informe emitido. Aprovechando la información de los escasos documentos encontrados, Esperabé de Arteaga (1917, II, pp. 285 ss.) esbozó el plantel del profesorado, trabajo que puede a veces matizarse a través de datos aparecidos y publicados con posterioridad. Basándome fundamentalmente en ellos, he intentado reconstruir este elenco del profesorado en el año 1515. La presencia de algunos queda asegurada, mientras que la de otros resulta sólo probable. Quizá hubiera algún docente más de los que a día de hoy conozco, pero sólo he encontrado datos de los que a continuación señalo.

En la facultad de cánones, había dos cátedras de prima, o quizá sea que se desdobló esa docencia en dos partes, porque en 1532 encontramos a Álvarez de Tapia ocupando una de ellas de la que no se sabía nada con anterioridad. La segunda estuvo ocupada por Pedro de la Puebla desde el 10 de mayo de 1512, y es razonable pensar que el catedrático de prima de cánones fuera designado para formar parte de la comisión del calendario. En 1503 Puebla era ya catedrático de vísperas de cánones y el 27 de julio de 1507 pasó a regentar otra cátedra de la misma titulación que había dejado vacante el doctor Olarte. No se sabe cuando murió, en todo caso antes de 1518, porque el doctor Juan de Olarte la ocupaba ya en octubre de 1518.

Juan de Monleón ocupó la cátedra de vísperas de cánones desde 1512 hasta una fecha que se desconoce. El 26 de mayo de 1506 se le había nombrado sustituto de la de prima de cánones del doctor Diego Alonso de Benavente y, pocos meses después, fue también sustituto de la de prima del doctor Villasandino. A primeros de febrero de 1507 obtuvo el grado de doctor en cánones y el 14 de junio de 1512 recibió el nombramiento de catedrático de vísperas de cánones. Presuntamente estaba en ella cuando se recibió la solicitud papal.

Fernando Yáñez de Frechilla aparece nombrado en los libros de claustros de la Universidad desde el 2 de agosto de 1504, en que fue nombrado sustituto del doctor Cubillas para la cátedra de Decreto. El 30 de enero de 1511 fue reelegido catedrático de una de las cursatorias de cánones. Ya como doctor, figura en los libros de cuentas como catedrático de una de estas cursatorias de vísperas de cánones en 1518, cargo en el que murió el 16 de marzo de 1522. Es decir, que era profesor en 1515.

Juan de Olarte (llamado también a veces doctor Loarte) era doctor en cánones. El 1 de mayo de 1503 se le cita como catedrático de una de las de vísperas de cánones, que quedó vacante el 26 de junio de 1507, pues en esta fecha fue nombrado catedrático de Decreto. En ese puesto figura en 1512. A comienzos del curso 1518-1519 era ya catedrático de prima de cánones y no he podido encontrar exactamente qué enseñaba en 1515, pero sin duda estaba en Salamanca en ese tiempo. Murió el 23 de febrero de 1530.

Antonio de Benavente era en 1515 profesor de una cátedra cursatoria de esta facultad, que regentó desde 1512 a 1522, pasando después a la de Sexto y Clementinas, desde 1526 hasta 1557.

El catedrático de Sexto y Clementinas en 1515 era el doctor en cánones Juan de Castro. Ocupó este puesto desde el 20 de agosto de 1506 hasta 1526; trabajo que compatibilizó desde 1522 con una cursatoria de cánones, sustituyendo a los doctores Diego Alonso de Benavente y Villasandino. A principios de 1526 fue nombrado catedrático de decreto, por muerte del doctor Castro, regentando esta cátedra hasta 1528. Había realizado el juramento para optar al grado de doctor el 1 de mayo de 1503.

En la facultad de leyes se encontraban dotadas dos cátedras de prima:

La primera adscrita a Lorenzo Galíndez de Carvajal: Vemos ya a este profesor en una cursatoria en 1497, pues así fue citado por Marineo Sículo, junto a Alonso de Zúñiga, como jóvenes promesas del derecho (Beltrán de Heredia 1971, pp. 283 ss.). Recién doctorado, sucedió a Diego de Segura en la cátedra de prima de leyes, a principio de 1504. Pronto el rey lo vinculó a su servicio con retención de la cátedra salmantina, encargándole primero la ordenación de las leyes anteriores a las promulgadas en Toro en 1505, y después la edición de las promulgadas en ese lugar y fecha, que no llegó a imprimir. Fue asesor jurídico del Consejo de Indias y del Consejo Real. Continuó después trabajando para Carlos V y dice Beltrán que los servicios que prestó a la monarquía se pueden comparar a los de Palacios Rubios. Sólo escribió crónicas reales: la del rey Enrique IV, colaborando también en la de Juan II de Gómez de Ciudad Real. De lo dicho se desprende que no estaba en Salamanca en 1515 y, por tanto, aún siendo el titular de la cátedra, no pudo haber sido comisionado para la reforma del calendario. El 5 de diciembre de 1542 se publicó la vacatura de esta cátedra como consecuencia de su muerte.

La segunda cátedra de prima de leyes estuvo ocupada en 1515 por el doctor Tomás de San Pedro, desde el 26 de enero de 1508 hasta su muerte: se anunció vacante el 26 de octubre de 1526.

En aquella época hubo también otras dos cátedras de vísperas de leyes: una regentada por Alonso de Zúñiga (a veces llamado doctor Stúñiga), que ya era doctor y catedrático de vísperas en 1505 y continuaba siéndolo el 25 de octubre de 1521, en que se anunció la vacatura por muerte. Participó en la revolución de las Comunidades como procurador de la junta por Salamanca y figura entre los exceptuados del perdón general de Carlos V. Probablemente muriera o huyera en la revuelta. Es decir, que en 1515 Zúñiga era el profesor de la cátedra de vísperas de leyes.

También estaba presente en 1515 el profesor de la segunda de estas cátedras, Fernando Rodríguez de San Isidro, hijo del doctor en leyes Diego Rodríguez de San Isidro. Primero fue el sustituto de su padre; después, el 9 de noviembre de 1504, fue designado sustituto del doctor Galíndez de Carvajal en la cátedra de prima de leyes. El 4 de mayo de 1507 es nombrado catedrático de vísperas de leyes, y el 12 de diciembre de 1526 catedrático de prima de leyes. El 20 de mayo de 1527 lo jubilaron y el 15 de septiembre de 1534 se declaró vacante su cátedra por su muerte. Sin ninguna duda presenció los debates sobre el calendario.

Algo más abundantes son los datos relativos a los docentes de la facultad de teología. En la cátedra de prima estaba el dominico fray Pedro de León, que la ocupó hacia 1503 (otras fuentes dicen que desde 1507) y la mantuvo hasta su jubilación, en 1526. Murió ese mismo año, anunciándose la vacatura el 2 de agosto. En función de este puesto, también es muy probable que León fuera nombrado comisario para la cuestión del calendario.

En 1503 ya era catedrático de Biblia Martín de Frías, también llamado Martín Sánchez de Frías; oficio en el que continuaba el 23 de junio de 1506. En 1507 dejó vacante la cátedra de Biblia para pasar a la de vísperas de teología, ocupándola hasta su muerte, el 24 de octubre de 1528. Su fama le llevó a ser uno de los elegidos para asistir al examen de las obras de Erasmo en la Junta de Valladolid de 1527. En 1515 Frías era el profesor de vísperas de teología.

El dominico fray Alonso de Peñafiel sucedió al Maestro Betoño en la cátedra de Biblia en 1483. En 1503 a 1508 fue catedrático de tres lenguas (hebreo, caldeo y arábigo). De 1508 a 1518 ocupó la cátedra de Biblia, debiendo haber muerto ese año.

He dicho antes que la cátedra cursatoria de Escoto fue regida por el maestro en artes Juan de Ortega desde el 20 de octubre de 1505 hasta el 10 de febrero de 1508. Según Esperabé, aunque en 1508 dejó la cátedra cursatoria de Escoto para regentar la de filosofía natural, la recuperó tras un período de regencia de la misma por Ginés de Hormaza y Juan de Oria, ocupándola desde una fecha que no conocemos hasta que murió el 14 de mayo de 1522. Es decir, que desempeñó las dos cátedras simultáneamente y murió dejando vacantes ambos puestos (Beltrán de Heredia, 1972c, I, p. 508). Ortega, como mínimo, era el profesor de filosofía natural en 1515; quizá también explicaba en la de Escoto.

La cátedra cursatoria de Santo Tomás la regentó fray Matías de Paz desde una fecha que no se ha podido determinar hasta 1518. En ese momento pasó a ocupar la de Biblia y murió desempeñando ese oficio, el 8 de junio de 1519.

El maestro Gonzalo (no Gregorio, como indica Esperabé de Arteaga, Vol. II, p. 299) Gil era entonces el catedrático de filosofía moral de 1513-1514, a cuyas clases asistió Pérez de Oliva; durante el curso 1518-1519 explicó en Salamanca teología nominal (también llamada cátedra de Gregorio de Arimino o Durando). Estaba en Salamanca en 1515.

En la facultad de medicina sólo conocemos el nombre de Alonso de la Parra, que en 1508, sustituyó al doctor Álvarez de la Reina, renombrado para dicho cargo el 31 de julio de aquel año, como sustituto por diez años, pero renunció a esa sustitución el 30 de octubre de 1512, probablemente para ocupar la cátedra de vísperas de medicina. Regentó este oficio hasta el 28 de junio de 1526, en que fue nombrado catedrático de prima. Después fue enviado por Carlos V a servir a la reina de Inglaterra (su tía Doña Catalina, esposa de Enrique VIII), con licencia de la Universidad, con gran resistencia del claustro (Beltrán de Heredia 1970b, II pp. 555 y 559). Vacó dicha cátedra, por muerte del titular, el 19 de octubre de 1528. De la Parra también estaba en Salamanca en 1515.

En la facultad de artes —la facultad que directamente explicaba la temática que se necesitaba evaluar para la reforma del calendario— recordemos lo que acabamos de ver: que Juan de Ortega compatibilizó la cátedra de Escoto, en teología, con la de filosofía natural, de esta facultad. Enseñó en ésta desde el 10 de febrero de 1508 hasta el 14 de mayo de 1522. Este mismo cometido dual cayó bajo la responsabilidad del benedictino aragonés fray Juan de Oria, antes catedrático de Escoto —desde el 20 de octubre de 1505— y de lógica nominal (el primero en Salamanca), que el 9 de diciembre de 1510 pasó de la ésta a la de físicos dentro de la misma facultad de artes, manteniendo simultáneamente de Escoto, hasta que el 10 de junio de 1519 en que fue nombrado catedrático de Biblia (Esperabé de Arteaga, 1917, II, pp. 307 y 379). Fue denunciado por los dominicos ante el papa por las proposiciones que enseñaba, siendo procesado por la Inquisición de Valladolid (1525) que le prohibió ciertas enseñanzas, restando prestigio al nominalismo en España.

La cátedra de filosofía moral estuvo ocupada por fray Alonso de Valdivielso O.F.M. probablemente desde antes de 1503 hasta su muerte, el 1 de julio de 1519. Estos tres profesores estaban presentes en el momento de la consulta sobre el calendario. Cabe pensar que también estuvieran el catedrático de lógica magna Andres de Carmona (Muñoz Delgado, 1983, p. 125) y los de súmulas: Martín de Espinosa y Martín Vázquez de Oropesa (Fuertes Herreros, 2006, p. 548).

Como vimos en el capítulo anterior, el doctor Sancho de Salaya ocupaba en 1504 la cátedra de astrología pero, de forma parecida a lo que pasaba con Galíndez de Carvajal, tampoco enseñó en ella durante mucho tiempo, en realidad sólo dos cursos, siendo reclamado por la monarquía de forma continuada. Por tanto, se equivoca Flórez en la creencia de que Salaya, como catedrático titular de astrología, fue al menos uno de los autores del informe sobre la reforma del calendario (Flórez, 1999, p. 453). En el claustro de 12 de septiembre de 1506 ya se trató de prorrogar por otros dos años la licencia que ya disfrutaba Salaya y allí se recordó que se le requería en la corte como protomédico del Consejo de la Inquisición. Beltrán de Heredia publica varios documentos (1970b, II, d. 246, 247, 248...) con sucesivas solicitudes al claustro y, en nota de la p. 269, resume la historia de las ausencias de este profesor de su cátedra. Según estos datos, Salaya faltó de esta cátedra mediante licencias concedidas por el claustro desde el año 1506 hasta su muerte, en 1542. Es decir, que no pudo ser ni autor ni inspirador del informe salmantino de 1515.

De todos los citados ¿Quién formarían parte de esta comisión? Según la costumbre universitaria, seguramente el claustro nombraría a los representantes más notables de cada facultad. Entre los elegibles estaban:

1. Los canonistas Pedro de la Puebla, catedrático de prima de cánones; Fernando Yáñez de Frechilla, en una cursatoria de cánones; Juan de Olarte y Antonio de Benavente en sendas cursatorias de cánones; y Juan de Castro, en la de sexto y clementinas. No tengo la seguridad plena de que estuviera en 1515 en vísperas de cánones Juan de Monleón.

2. Ante la ausencia del catedrático de prima de leyes, Galíndez de Carvajal, los legistas susceptibles de ser designados eran Tomás de San Pedro, catedrático de prima de leyes; y Alonso de Zúñiga y Fernando Rodríguez de San Isidro en sendas cátedras de vísperas de leyes.

3. Los teólogos Pedro de León, catedrático de prima; Martín de Frías en la de vísperas de teología; Matías de Paz en una cursatoria de Santo Tomás; Alonso de Peñafiel en la de Biblia; y Gonzalo Gil, en moral.

4. El médico Alonso de la Parra, daba clase en la cátedra de vísperas de medicina.

5. Ausente también el catedrático de astrología Sancho de Salaya, los artistas disponibles eran Juan de Ortega y Juan de Oria, catedráticos de filosofía natural, y fray Alonso de Valdivielso, de filosofía moral.

Intentando arrojar alguna luz sobre quiénes pudieron haber redactado el informe salmantino de 1515, en la medida que he podido, he seguido los currículos de cada uno de ellos, tratando de encontrar algún texto o dato que los pudiera relacionar con la destreza en matemáticas o astronomía, porque sin esos conocimientos, su posible participación en aquella comisión universitaria los hubiera convertido en convidados de piedra. El resultado ha sido que no he hallado ningún texto, manuscrito o impreso sobre cuestiones astronómicas o matemáticas firmado por los profesores coetáneos de medicina, leyes, cánones o teología; ninguno parece haberse dedicado a las matemáticas, aunque tres de ellos escribieron sobre otras materias:

1. El primero es el catedrático de vísperas de teología Martín Sánchez de Frías, que debía ser un buen profesional porque la Universidad le ofreció un sustancioso incremento de salario a cambio de que no aceptara la canonjía de Córdoba que le habían ofrecido mientras era profesor en Salamanca. Compatibilizó el trabajo de profesor con los de visitador diocesano y vicario del obispo Francisco de Bobadilla, ausente en Roma durante muchos años. Formando parte de esa labor pastoral, escribió textos estrictamente teológicos, como el Tractatus perutilis Martini de Frias theologie in Salmanticensi academia professoris [Burgis: in aedibus Ioannis Iuntae, 1529], reeditado en Salamanca, en Juan de Junta, 1555. De 1577 se conservaba otro, quizá manuscrito, que fue citado en el repertorio bibliográfico del Monasterio de Santa María de la Vega, de Salamanca, como libro del maestro Frías titulado De arte et modo audiendi confessiones[53]. Sabemos que Fernando de Roa le dedicó sus comentarios a la Política de Aristóteles (Salamanca, 1502). Como nota curiosa, ha quedado noticia de su extravagante solicitud de que una copia de su testamento fuera depositada en el arca de la Universidad (Vivas Moreno, 1999, p. 121).

2. El segundo es Gonzalo Gil, que acompañó a Cisneros en la empresa de Orán y después narró la hazaña tanto en prosa como en verso. Tras ella, fue catedrático de teología nominal en Alcalá, entre 1509-1511, con ausencias hasta 1513, en que durante al menos un curso enseñó en Salamanca filosofía moral.

3. El tercero es Lorenzo Galíndez de Carvajal, un personaje controvertido (por falsario) con importante proyección política, que ya he dicho que trabajó en la recopilación de leyes y en crónicas reales (más información en Soto Vázquez, 2009).

Ante la ausencia del titular de astrología, los únicos profesores que presumiblemente tenían por su especialidad una preparación científica específica para haber sido nombrados miembros de la comisión eran Juan de Oria y Juan de Ortega.

Me parece seguro que fray Juan de Oria colaboró en la redacción de este informe: Este maestro en teología fue quizá el primer profesor de lógica nominal que hubo en Salamanca traído de Alcalá, que ya había publicado en París la Expositio super libris Physicorum Aristotelis necnon totius Philosophiae naturalis (París, c. 1500) y que editaría después las Súmulas en Salamanca[54], aparte de otras obras de carácter teológico. Fuertes Herreros califica sus conocimientos en física y lógica como muy superiores a los de Vitoria y Cano (Fuertes Herreros, 2006, p. 549). Es decir, que su preparación previa y el contenido de estos escritos lo convierten en candidato competente para la elaboración del informe sobre el calendario.

Juan de Ortega era asimismo catedrático de filosofía natural en 1515, pero el azar es caprichoso ya que este profesor se llama igual que otros tantos y no resulta fácil distinguirlos. El problema de homonimia de los Juan de Ortega ya lo advirtió Rey Pastor (1913, p. 68). Entre los individuos que se sabe tenían el mismo nombre en la época, aparte del sacristán mayor de Isabel la Católica, de cronología ligeramente anterior, o del alférez del ejército que cita Rey Pastor, hubo un santo, uno obispo de Ciudad Rodrigo y Calahorra, uno de la orden de los Jerónimos que llegó a ser obispo de Chiapas, un gobernador de la provincia del Paraguay, el profesor salmantino citado y el famosísimo matemático, fray Juan de Ortega, dominico de la provincia de Aragón y que debía estar muerto ya en 1552 cuando Gonzalo de Busto reedita una de sus obras en Sevilla. Santiago Garma Pons (2008, p. 155) establece su producción bibliográfica entre 1515 y 1542; otras fuentes aseguran que muere en 1568. Quizá sea el opositor a la cátedra de nominales o de Gabriel de la Universidad de Alcalá frente a Andrés de la Cuesta, que la ganó, en octubre de 1545; o el profesor alcalaíno de Durando (Beltrán de Heredia, 1973, IV, pp. 134 y 142).

En función de los conocimientos científicos, hubiera sido comprensible que el informe salmantino lo hubiera redactado el Juan de Ortega fraile dominico, porque en el año 1515 (fecha del mismo), él ya había enviado a la imprenta varios trabajos matemáticos de peso:

1. Uno de los primeros libros españoles de cálculo mercantil: el Tratado subtilíssimo de Arismética y Geometría, 1512? editado en Sevilla, en casa de Juan Croberger en 1534, 1537, 1542, 1552, 1563... como se ve con varias ediciones. Pérez de Moya publicará después uno suyo comentando el de Ortega (Granada: 1563).

2. Sigue se vna conpusicion de la arte de la arismetica y juntamente de geometría fecha y ordenada por fray Juan de ortega de la orden de santo domingo de los predicadores. Leon [Lyon, Francia]: en casa de maistro Nicolau de Benedictis..., 1512, BGH 36568; edición on line en DICTER, <http://dicter.eusal.es/bios/OrtegaJuan>); obra que fue editada también en Barcelona, 1512 y Sevilla, 1534, 1542 y 1552. A los tres años de su publicación, se tradujo al italiano y al francés. A la vista de la iconografía de su portada, con un ribete de imágenes de profesores y alumnos, no cabe ninguna duda de que el autor era un maestro.

3. Geometria Pratica vtilissima... (Roma: Stephano Guilleri de Lorena, 1515).

4. Suma de arithmetica geometria pratica utilissima (Roma: Mastro Stephano Guilleri de Lorena, 1515).

Debido a su importancia excepcional, Rey Pastor (1913, pp. 67-81) lo dejó para tratarlo al final de su obra, junto a Álvaro Tomás, e hizo un detallado análisis de las novedades que introdujo Ortega en el tratamiento de esta disciplina: Defendió la aritmética como un sistema de descripción del mundo real, de todas las cosas criadas (Marqués de Almeida, 2006, p. 226), un camino hacia la verdad; mostró que esta parcela de las matemáticas no provenía del desarrollo de conocimientos teóricos, sino de la reflexión sobre ese tipo de prácticas, que según Flórez (2006, p. 419), exigía la evolución de una nueva sociedad; modificó las extracciones de las raíces cuadradas que figuraban en la primera edición (1534) para sustituirlas por valores que satisfacían a la ecuación de Pell. Según se dice en su portada, la edición de 1552 apareció con corrección de errores de imprenta, realizada por Gonzalo Busto, que, bajo ese pretexto, suprimió todas las aproximaciones de las raíces cuadradas que habían enriquecido las ediciones previas, sustituyéndolas por los valores que aparecían en la primera edición; cosa que probablemente el autor no hubiera autorizado (Rey Pastor, 1912, p. 69). La obra tuvo una acogida muy positiva en toda Europa, especialmente por su carácter práctico. Se convirtió en el primer texto de aritmética comercial publicado en Francia. Es decir, que fray Juan de Ortega estaba en condiciones de haber podido realizar un informe sobre la reforma del calendario, pero en Salamanca, en ese momento, no residía él, sino su homónimo.

He incluido estas reflexiones sobre el fraile en orden a recordar la importancia nuclear que adquirieron las matemáticas en la época del Renacimiento, siendo comprensible el que incluso profesores de otras materias escribieran sobre ellas, como por ejemplo Nebrija. El dominio de la aritmética era clave para el avance de las ciencias del cálculo y de la representación y, sin duda, para elaborar un informe sobre el calendario (Salabert: trabajos sobre Aragón de 1990 y 1997 no citados aquí; sobre Castilla: 1994; Armando Marques 2006; Sierra-Rico-Gómez 2007).

¿Participó también en la redacción del informe de 1515 el Juan Ortega, maestro en artes y profesor salmantino, distinto del matemático fray Juan de Ortega? Aunque no parece conservarse ningún texto de Ortega que pudiera ayudarnos a evaluar sus conocimientos en cuestiones cosmológicas, a mí me parece que sí.

En la documentación del Archivo de la Universidad de Salamanca no he encontrado ningún dato que contradiga esta hipótesis, sino al contrario, algunos que tiende a corroborarla. Explicaré mis argumentos: El contenido del informe de 1515 sobre la reforma del calendario fue científicamente impecable y estuvo en la línea de la ciencia europea. Considerando el conocimiento y la comprensión del tema que denota este primer informe salmantino, no podía haberlo redactado quien no conociera perfectamente el problema del calendario y dominara la aritmética. Lamentablemente yo no tengo ningún dato directo para demostrar que este Juan de Ortega estuviera en situación de colaborar en la redacción de un informe tan brillante, pero de lo que no me cabe ninguna duda es de que la cátedra de filosofía natural de la Universidad de Salamanca que él ocupó desde 1508 a 1522 no se la daban a cualquiera. Su antecesor en la misma había sido Martín Navarro, colegial de San Bartolomé desde 1500, que figura con el número 217 de los catalogados por Roxas y Contreras. Es un hecho que, en aquellas fechas, para entrar en ese colegio había que poseer unas condiciones intelectuales destacables. Pues bien, Martín Navarro tomó posesión de la cátedra de filosofía natural el 18 de noviembre de 1504, dejando para ello vacante (fíjense bien) la cátedra de Santo Tomás, cuando teóricamente era más prestigiosa una de la facultad de teología que la de filosofía natural en la facultad de artes. El 3 de enero de 1508, cuando este profesor la abandonó[55], se declaró la vacatura y pudo acceder a ella Juan de Ortega, lo cual no debió de ser fácil para él. Y digo que no debió de serlo, porque ese mismo mes de enero, el licenciado Ortega se había opuesto a la cátedra de hebraico, caldeo y arábigo de la Universidad y sus colegas opositores fueron también intelectuales de altura: el colegial de San Bartolomé licenciado Juan Rodríguez de Peralta, el religioso italiano Diego de Populeto, el dominico Juan de Vitoria, el cristiano nuevo Alonso de Arcos (el después llamado Alonso de Zamora) y el bachiller Parejas. Dice Beltrán de Heredia (1970b, II, p. 109) que, después de mucho debate en el claustro, ante la falta de acuerdo, quedó estancada aquella provisión durante más de dos años. Ante este intento frustrado, Ortega se presentó y obtuvo la cátedra de filosofía natural, que como he dicho antes después compatibilizó durante un tiempo con la de Escoto.

A la muerte de Ortega el 14 de mayo de 1522, su sucesor en la cátedra de filosofía natural fue el bartolomeo Juan Martínez Silíceo (Esperabé de Arteaga, 1917, II, p. 303), el gran matemático, del que ya he hablado, que llegó a Salamanca un año después de entregado el informe sobre el calendario. Para sopesar mejor lo que la tenencia de esta cátedra suponía en la época, hay que recordar la enorme presión que ofrecían los colegiales de San Bartolomé en su disfrute. Juan de Ortega la ocupó entre dos bartolomeos... tenía que ser intelectualmente muy bueno para que se le escapara temporalmente esta regencia a los del Colegio de San Bartolomé.

El talante de Ortega también apunta hacia esta co-autoría, porque se mostró en los claustros universitarios como hombre abierto a las novedades, curioso e interesado. Por eso formó parte de la junta de los nominales, creada a favor de esta doctrina filosófica implantada por Cisneros en la recién creada Universidad de Alcalá de Henares y cuyo éxito hacía peligrar la supervivencia de la teología salmantina. Porque, como dijo el dominico Peñafiel en el claustro de 2 de octubre de 1508, que había peligro de que Cisneros quedase como árbitro de la salmantina.

Este dato lo he tomado de Marcos Rodríguez, en sus Extractos de los libros de claustros...[56], quien también reproduce la sesión del claustro universitario salmantino de 1508 en la que

…acordaron que el Maestro Ortega vaya a Alcalá, adonde dicen que está el maestro Miguel Pardo, e a Zaragoza, adonde dicen que está Ciruelo, e vaya a costa de la Universidad, e los procure traer. E que si sino [sic] los pudiere traer por el dicho salario faciendo en ello su posibilidad, que les pueda prometer algo más. E que si no los podiere traer que busque otros que sean personas famosas e tales que fagan fructo en la Universidad.

Ortega hizo juramento de cumplir fielmente este encargo y de que no se quedará allá por ningún partido: es curioso que sus compañeros le hagan firmar este compromiso de fidelidad a la salmantina.

Quince días más tarde regresó Ortega a Salamanca y expuso en el claustro que se había entrevistado tanto con Miguel Pardo como con Pedro Ciruelo; que ambos habían declinado el generoso ofrecimiento de trasladarse a Salamanca porque ambos se habían comprometido antes con Cisneros para enseñar en Alcalá. La defensa de los nominales llevó incluso a Juan de Ortega a enzarzarse desaforadamente a la salida de esta reunión con el maestro León, que dijo algunas palabras contra los nominalistas, ante cuyo enfrentamiento, el Vicescolástico les conminó a que ninguno dijera descortesías en el claustro y les impuso el castigo de no salir de sus casas durante un año sin su licencia, so pena de excomunión e multa (2 de octubre de 1508).

Ante la imposibilidad de traer profesores españoles expertos en nominales, el 17 de octubre el claustro encomendó a Velarde (de quien no he encontrado ninguna noticia en el archivo universitario) que fuera a París a buscar a los mejores, con una previsión de fondos de 17.000 maravedíes que pareció un exceso al gestor económico de la Universidad. Como dice Beltrán, la Universidad andaba mendigando catedráticos de nominales. Después volvieron a encargar al doctor Talavera que escribiera a Miguel Pardo, a Alcalá, y al maestro Ortega que hiciera lo propio al doctor Pedro D [sic], a Burgos, aunque parecía poco decoroso después de que Pardo ya hubiera rechazado la invitación salmantina previa (Actas de Claustros y Juntas de la Universidad, 1507-1511, AUSA 5, f. 325r.).

¿Quiénes, pues formaron parte de aquella comisión sobre la reforma del calendario de 1515? Teniendo en cuenta lo que ocurrió sesenta y tres años después, lo razonable es pensar que estuviera formada por un catedrático de derecho canónico (¿Pedro de la Puebla?), otro de teología (¿Pedro de León?), quizá algún profesor de derecho civil (¿Tomás de San Pedro?) y de medicina (¿Alonso de la Parra?), y, a falta del titular de astrología —el más pertinente—, los catedráticos de filosofía natural Juan de Oria y Juan de Ortega. Desde el punto de vista de la capacitación científica para el tema, los más idóneos, sin duda, eran los dos últimos.

1.4.2.3. El contenido del informe de 1515

Dentro del ms. 97 de la Biblioteca Universitaria de Salamanca (BGH), con copia casi exacta en el códice Vat. Lat. 7049 de la Biblioteca Apostólica Vaticana y en el ms. 9-2073, ff. 89-119 de la Real Academia de la Historia de Madrid, se encuentra el informe salmantino sobre la reforma del calendario realizado en 1578, dentro del cual se reproduce el del año 1515.

Las características físicas de estas copias han sido tratadas en las pp. 243 ss. de este trabajo. Tomando el ejemplar de Salamanca como referencia, se observa que la mayor parte del códice está ocupada por la respuesta que envió la Universidad de Salamanca al papa León X y a Fernando el Católico; concretamente los folios 10r.-35v. (véase el comienzo del texto en la figura 25); así pues sólo nueve folios fueron redactados por la comisión salmantina de 1578 (ff. 1r.-9v.) frente a los veinticinco folios que corresponden al argumento de los comisionados de 1515. Es importante subrayar que la brevedad relativa del segundo informe se debe precisamente a que sus autores se identificaron con la propuesta ya ofrecida en 1515 y por eso remitieron a ella, incluyéndola como parte constitutiva de la contestación de 1578.

El informe de 1515 tiene, a su vez, varias partes:

La primera contiene una explicación del problema computacional (ff. 10r.-27v.). Como se verá (pp. 272 ss. de este trabajo), esta parte del documento se ha dividido en once puntos indicados con el número correspondiente entre corchetes, de acuerdo con el sentido del discurso, de forma que pueda ser más cómoda su lectura y la localización de las citas. La segunda es una tabla de números áureos y letras dominicales para todos los meses del año, con su canon explicativo (ff. 28r.-30v.; pp. 305 ss. de este trabajo). La tercera presenta el canon de otras tablas que no se han conservado en ninguna de las copias encontradas, probablemente porque estuvieran sueltas, en las que se exponían pormenorizadamente las características del calendario hebreo y su correspondencia con el juliano (ff. 31r.-35v.; véase la figura 26, pp. 311 de este trabajo). Debido a esta pérdida, lo que puedo decir del canon conservado es que denota una excelente capacidad de cálculo de su autor o autores y un preciso conocimiento del calendario judío, en los términos en que ha quedado expresado en este trabajo (p. 139).

Los comisionados de 1515 respondieron a León X y a Fernando el Católico con los argumentos que ahora resumo y comento en función de los once apartados predichos:

[1] La reforma del calendario eclesiástico es una cuestión de gran trascendencia y a la vez de gran dificultad. Debido a ella algunos dicen que es imposible e incluso inútil y, además, ajena a los criterios establecidos en el concilio de Nicea. La incapacidad de resolver el problema computacional deriva de que es imposible corregir las desviaciones de las revoluciones del Sol y de la Luna con una única suma o resta, debido a que, en los mismos años, el Sol se ha anticipado 11 días y la Luna sólo 4.

No sirve de nada basarse en el cálculo del ciclo solar (se refieren al ciclo de los 28 años determinado por Dionisio el Exiguo) y de la longitud del año trópico de Ptolomeo, que dicen es una tricentésima parte del día más breve que la del año eclesiástico; año que comprende 365 días y 6 horas exactamente, según afirman. O sea, que los comisionados opinan que Ptolomeo se equivocó en 4,8 minutos, o 288 segundos, en esta estimación, cuando hoy sabemos que su error era de 11 minutos y 12 segundos.

…la cual descontada en virtud de la disimulada intercalación bisextil cada 300 años, falta muy poco para que los ciclos de los novilunios vuelvan exactamente a los mismos sitios.

También son perfectamente conscientes de que la longitud del año aceptada es una convención:

…es algo que más bien se puede desear que creer en ella o llegar a probarla. Nadie hay tan ignorante en astrología, que no tenga por muy probado que este cómputo de Ptolomeo está manifiestamente en contra de aquella variación que llevamos desde el nacimiento de Cristo hasta esta nuestra época. De donde se deduce de nuevo la dificultad y aun la imposibilidad de solucionar la propuesta igualación.

Explica que ni los más eminentes astrólogos han logrado determinar exactamente la longitud del año solar, a pesar de la

…favorable superioridad de los instrumentos astronómicos, sobre todo porque la opinión de todos los eruditos sobre ese movimiento del cielo estelar, que llaman trepidación, sigue imprecisa hasta el día de hoy.

Por ello, el equinoccio de primavera no cae en el 10 ó 11 de marzo, como ordinariamente se admite, sino mucho antes, el 28 de febrero. Todos los astrólogos coinciden en que le falta una parte del día a la longitud del año solar establecida por la Iglesia, pero no hay acuerdo en determinar si esta carencia es una tricentésima parte [es decir, 288 segundos], o la centésima quincuagésima [576 segundos], o la centésima trigésima cuarta [644.776119 segundos], o la centésima sexta [815.094340 segundos], o la vigésima [4320 segundos], o la vigésima cuarta [3600 segundos].

Esta afirmación denota que conocen la medida del año trópico establecida por distintos astrónomos, que, expresada en días, era la siguiente (Proverbio 1983, p. 131):

Hiparco:	365.2500
Ptolomeo:	265.2466
Albategnius:	365.2403
Hispalensis:	365.2424
Tablas alfonsíes:	365.2425
Copérnico:	365.2427

Este cálculo cuidadoso dicen que depende tanto de la contemplación de los fenómenos celestes, como de la fiabilidad de los aparatos: Esta afirmación, junto a la estimación que ellos han hecho arriba del error ptolemaico en la medición del año trópico, es demostrativa de la dedicación a la astronomía práctica y a las matemáticas que tenían el autor o autores de este informe. En ella se expresa el trabajo cotidiano en astronomía, que ellos mismos cifran en el cálculo y la observación mediante instrumentos adecuados.

Ante el fracaso humano en esta determinación, esperaban que cierta ventura divina permitiera sacar a la luz pública argumentos segurísimos de cuestión tan abstrusa.

[2] Algunos opinan que no hay por qué aferrarse a una fecha o a unos cánones específicos para la celebración de la Pascua, porque ésta puede cambiarse, sin perjuicio de la religión, mediante una decisión positiva de la autoridad. En este sentido los comisionados salmantinos estaban apoyando la opinión defendida por Paul von Middelburg en el concilio de Letrán, relativa a que el papa, sin autorización del concilio, podía dictar la reforma. Los salmantinos tenían delante esta declaración de Middelburg, pues estaba entre la documentación que recibieron junto a la solicitud del informe. Son conscientes de que los padres de Nicea sabían que el Sol se había anticipado ya desde la muerte de Cristo.

Pues habían transcurrido, desde el comienzo de la Redención cristiana hasta el concilio niceno, más de trescientos años, que se comprueba han superado, por lo menos en un día entero, a otros tantos reales ciclos solares.

Los conciliares y cualquier astrónomo lo sabía. Dicen, que según las tablas del rey Alfonso, el equinoccio de primavera en el momento de la Redención cristiana tuvo lugar poco más o menos el día 21 de marzo, mientras que en tiempos del concilio de Nicea ocurría el 18 del mismo mes.

Aunque Nicea no pretendió que la celebración de la Pascua cambiase conforme a la variación de los equinoccios, sin embargo estableció unas fechas límite para su celebración, de modo que quien se atuviese a ellas, no la celebraría en la luna 15ª que sigue inmediatamente al equinoccio de primavera, ni el domingo siguiente. No se ha de acusar, pues, a Nicea, ya que

...en aquellos trescientos años que transcurrieron entre la Pasión del Señor y el concilio de Nicea no pudo producirse tanta anticipación del Sol, que hiciera trasladar el equinoccio primaveral desde el día 25 de marzo hasta el 21 del mismo mes, cuatro días justos de anticipación; pues de producirse el adelantamiento en esa proporción, dicho equinoccio caería en estos nuestros tiempos, no ya el 10 u 11 de marzo (como vulgarmente se piensa) sino más bien el 4 ó 5 del mismo mes, estableciéndose entonces una longitud real del año solar como jamás sospechó ninguno de los más insignes astrólogos.

Estos datos corroboran —según los autores—, que aquellos padres no se atuvieron a los verdaderos límites de los equinoccios de su tiempo, sino solamente a aquel al que correspondía el equinoccio en el tiempo de la Pasión del Señor.

[3] Doscientos años después de este concilio, Dionisio el Exiguo, conservó los mismos límites establecidos por Nicea para la celebración de la Pascua, aun conociendo que en ese período el equinoccio se había adelantado ya otro día entero en el calendario eclesiástico. Al advertir a los venideros que pusieran remedio a los anticipos del equinoccio omitiendo la intercalación bisextil, es claro que Dionisio y los demás computistas eclesiásticos pensaban que no se había que tener en cuenta el equinoccio real, pues de lo contrario hubieran cambiado lo que ellos mismos creían que era necesario mudar.

En esta alusión a Dionisio sorprende la precisión en la cronología vital que le atribuyen y se sobrentiende que conocían su tabla de pascuas, además del período de Dionisio, o ciclo solar de los 28 años, que antes han citado (producto de los ciclos solar y lunar 28 x 19 = 532 años: hay que esperar un ciclo de 28 años para que el año comience el mismo día de la semana). Recordemos que en esta tabla pascual Dionisio inventó un nuevo sistema de numeración de los años para reemplazar los años dioclecianos que se usaban en las anteriores tablas pascuales, con la intención de separar esta celebración de la memoria de un perseguidor de los cristianos.

Siguen los comisionados afirmando que en esto se apoyan quienes opinan que hicieron bien los padres antiguos en ordenar la Pascua conforme al calendario eclesiástico, aunque se aparte de la fecha real del equinoccio. Pero censuran la variación del Sol y de la conjunción lunar que descuidaron aquellos padres y que acaba por formar un día completo al cabo de 304 años, algo que hay que corregir con la omisión de una intercalación besextil durante ese mismo número de años.

Para restablecer ahora y conservarse para siempre correcto el calendario eclesiástico proponen dos soluciones:

…ya se quiera reponer a sus sitios reales los números del ciclo decemnovenal establecidos en el calendario que han de cambiarse a cinco fechas antes en razón de la ya antes de ahora observada anticipación lunar; ya se quiera, manteniendo invariables los números, anular todos los días de dicha anticipación por medio de algún sistema estable y perpetuo, partiendo de un año cualquiera, que hagamos cuatro días enteros más cortos y reducidos de lo ordinario, o quitando estos días todos juntos de un mismo mes, o uno por uno de meses diversos.

Por medio de algún disimulo estable; o sea, mediante la aplicación de un algoritmo. Cualquiera de estas soluciones mantendría en orden el cómputo eclesiástico,… si es que se establece la ley de quitar en el futuro el incremento de un año bisiesto cada 304 años.

La pequeña variación que todavía restaría, a pesar de esa anulación de la intercalación bisextil cada 304 años, no completaría un día entero en muchos miles de siglos, que es lo que interesa al computador eclesiástico: ….en una diferencia que no hay que esperar si no es después de muchas miríadas de años.

[4] Pero esta opinión tiene también sus dificultades; pues si queremos atenernos a las gesta conciliorum vemos que, siguiendo los límites del calendario como si fueran constantes e inmutables, nos desviamos de las determinaciones de los concilios sobre la celebración de la Pascua, que dicen no ha de celebrarse fuera de la semana de los ácimos hebreos. Pero debido a la anticipación del equinoccio, aún cuando se mantuviera constante el novilunio, a veces celebraríamos la Pascua casi un mes después de la semana de los ácimos y, de hecho, pensaban que ya se habían apartado de ella de una manera notable

…no es sólo por la variación de un irregular novilunio… sino que también proviene de la anticipación del equinoccio, aún cuando el novilunio se mantenga claramente constante.

Fig. 25: [Informe de 1515] «Traslado de lo que la Universidad de Salamanca imbió a nuestro muy Sancto Padre León, papa X, y al rey Don Fernando en el año 1515 acerca de la restitución del Calendario».

Fig. 26: Informe de 1515, tercera parte. Canon de unas tablas perdidas sobre el calendario hebreo.

Consideran además que esta desviación se hará cada vez mayor, llegando incluso al cambio estacional; y piensan que no hay que refugiarse en decir que ese distanciamiento no ocurrirá más que dentro de miles de años, porque a la autoridad eclesiástica toca regular el futuro de la cultura religiosa, corrigiendo estas previsiones.

[5] Aunque algunos opinan que no deben preocuparnos los cambios en la celebración de la Pascua, los comisionados piensan que hay que cortar de raíz las acusaciones de los judíos tal y como siempre han defendido los antiguos y modernos escritores eclesiásticos, los cuales añaden también la razón de la anagogía espiritual, del sentido místico de la Biblia, manifestado en el simbolismo de la luz y del calor que se da en la Resurrección de Cristo unida al equinoccio de primavera.

Con ello se refuta también a quienes dicen que debe establecerse como término pascual el día de la Pasión del Señor y celebrarse la Pascua al domingo siguiente, sin tener en cuenta ni el equinoccio ni el plenilunio, y sin importarles la hilaridad de los judíos, queriéndose liberar de este precepto positivo. Piensan los salmantinos que esta opción tiene los mismos inconvenientes que las anteriores, más uno añadido: el posible eclipse el día de Viernes Santo (parasceve), que sería aun más irrisorio para los judíos e incomprensible para la gente común.

[6] Aclaradas estas circunstancias, nosotros —dice— vamos a proponer al concilio lateranense nuestra solución para corregir el error originado en el Sol y en la Luna, procurando satisfacer tanto a los defensores de la libertad como a los deseosos de la exactitud matemática. La cuestión es remediar el pequeño exceso de la conjunción del calendario eclesiástico sobre la conjunción real.

La dificultad que tiene la supresión de la intercalación bisextil cada 304 años es ésta: si los términos pascuales quedan invariables, la anticipación del equinoccio de primavera perturbaría el sistema de las fiestas fijas y móviles, incluso con cambios estacionales. Y esto sucedería, a no ser que se recortasen los años eclesiásticos. Y con este recorte se restaurarían las conjunciones con mínimo perjuicio y se aminoraría mucho la variación del equinoccio, aunque no se eliminase del todo.

Casi los mismos inconvenientes se derivarían si regulásemos la Pascua por su inmediato plenilunio, mediante tablas o con ayuda del ciclo decemnovenal, sin tener en cuenta la fijación del equinoccio. Así también se trasladarían las fechas de los días festivos con la consiguiente confusión y escándalo, e incluso la Pascua llegaría a coincidir con la Epifanía, la Navidad, etc., cosa que trastocaría todo el oficio divino. Más aun —dicen— sería trastocar toda la historia. Obsérvese que aquí el discurso da un salto desde el centralismo del hombre típico del Renacimiento, al centralismo derivado de una concepción histórica global cristiana

[7] El mismo argumento vale contra los que quieren restituir el equinoccio al 10 u 11 de marzo y retrasar en 5 cifras los números del ciclo decemnovenal, suprimiendo la intercalación bisextil cada 304 años. También en esta hipótesis se montarían las fiestas con el correr de los años y se adelantaría el equinoccio de primavera. Por tanto, con este sistema o la Pascua se uniría inevitablemente con las fiestas fijas, o nos desviaríamos de lo determinado por Nicea, sin poder mantener largo tiempo los mismos términos pascuales.

En cambio, con la supresión de la intercalación bisextil se conseguiría que los novilunios se restituyeran a sus límites, y al cabo de 335 años el equinoccio de primavera habría pasado del 10 al 9 de marzo, lo que haría variar los términos pascuales y obligaría a celebrar a veces la Pascua contra lo mandado por Nicea.

[8] Continúan afirmando que algunos magnifican la conjunción que se produjo al mediodía del 1 de enero de 1500 y con ello se están refiriendo a la propuesta de Middelburg y a lo que después van a proponer también, en su contestación al concilio de Letrán, las universidades de Viena (con André Stiborius y Georges Stannstefter) y de Tubinga (con el profesor Juan Stoeffler de Justingen), recomendando que ese ajuste se fijara para el ya pasado mediodía del 1 de enero de 1500 en el meridiano de Roma. Curiosamente, a los comisionados salmantinos esto no les parece importante, pues piensan que para restaurar el ciclo decemnovenal es irrelevante señalar como inicial el año 1500 u otro cualquiera. Lo comparan, jocosamente, con esperar leche de la gallina, diciendo que ojalá fuera éste el único o el principal nudo de la dificultad planteada que hubiera que desatar. Piensan que lo que hay que hacer es velar a la vez por la estabilidad de los equinoccios y por su fijación en una fecha, y también por el regreso de las conjunciones del Sol y de la Luna a las mismas fechas, lo que representa una doble dificultad. Para lograrlo proponen prescindir de novilunios y de equinoccios y valerse del cálculo de tablas para hallar en el futuro los plenilunios, estableciendo un equinoccio fijo y, en función de él, el término pascual. La destreza en el cálculo de los redactores quedó reflejada en la opinión de que para confeccionar estas tablas bastaría el trabajo de 15 días de un mediano calculador astrológico. Después, dichas tablas se insertarían en los epítomes y breviarios, sin generar trabajo ni molestia a los sencillos sacerdotes que deban celebrar la liturgia.

Como he dicho, proponen asimismo fijar el equinoccio en una fecha del calendario. Tratando de determinar la longitud del año solar y omitiendo la intercalación bisextil en proporción igual a la diferencia entre el ciclo verdadero del Sol y el año eclesiástico, volverían el equinoccio de primavera y el término pascual al 10 o el 11 de marzo. Aunque esto tiene dos inconvenientes: Primero que la Septuagésima (dominica que se celebra tres semanas antes de la Cuaresma) se adelanta a la Octava de Epifanía y que se aumentan los domingos post Pentecostés (que debía ser el quincuagésimo día que sigue al de Pascua de Resurrección); segundo que nos apartaríamos de los términos pascuales de Nicea, debido a que los judíos retrasan varios días la semana de los ácimos.

[9] En función de los argumentos evaluados, procurando por una parte mantener los términos prefijados por los padres de Nicea y por la otra tener en cuenta la exactitud matemática, la solución propuesta por los salmantinos fue la siguiente:

Quitar de un mes cualquiera (cosa que les parece menos conveniente) los 11 días de adelanto solar, o quitar un día de cada mes durante un año cualquiera, menos de febrero. Así el equinoccio verdadero volverá al 21 de marzo, y se restablecerán los decretos de Nicea y la fijación del término pascual. El mejor año para realizarlo es el 1519, de manera que en el año 1520 quedará restablecido el equinoccio el 21 de marzo según el cómputo en uso y podrá también comenzarse el día primero de enero con el número 1 del ciclo decemnovenal. Mejor que si se hiciera retrospectivamente en el año 1500.

Incluso en el caso de que no se quisiera seguir este camino de anular los 11 días y se prefiera cambiar el equinoccio y los términos pascuales de Nicea, también en ese caso es mejor el año 1519 para iniciar el nuevo ciclo decemnovenal que el 1500 propuesto por Middelburg, por estar más cercano a nosotros —dicen—. Saben que esto disgustará a los aferrados al ciclo decemnovenal y al bisiesto, pero a estos se responde que basta con que en el futuro se aumente una unidad al número áureo seguido hasta ahora.

Los salmantinos expresan la preferencia por el cálculo de tablas, que después propondrá Lillo:

Aunque a nosotros nos convence sobre todo aquel sistema que rechaza absolutamente toda preocupación por establecer cualquier ciclo decemnovenal y aconseja se debe atender a hallar en el futuro los plenilunios pascuales tan sólo con el cálculo de tablas. Pues de este modo el cálculo podrá permanecer más exacto y parece se debe estimar mucho el que, rechazadas aquellas intrincadísimas ambigüedades del antiguo cómputo eclesiástico, se haya dado con un camino facilísimo por el que los fijados límites pascuales se mantengan con mucha más certeza, exactitud y claridad que hasta ahora, de modo que en adelante sea factible a los sacerdotes de la Iglesia, por más ignorantes que sean, echarse a dormir (es lo que se dice) y no inquietarse ya por preocupación alguna sobre las fiestas móviles, cuyo desconocimiento se solucionaría ampliamente tan sólo con que conociesen el día de Septuagésima, del cual, por más ineptos que se les suponga, no podrían menos que deducir la serie completa de los días siguientes, que aun los niños de cuatro años comprenden; y consiguientemente sería lícito aún a los sacerdotes mejores y más eruditos ignorar las epactas concurrentes, los embolismos regulares, los números áureos y todo ese género de variaciones tan fastidiosas y pesadas.

Es decir, que en la propuesta salmantina triunfa el cálculo matemático sobre el tradicional modelo de cómputo eclesiástico. En el informe se insiste en que mediante el cálculo de unas tablas podrán determinarse en el futuro los plenilunios pascuales y no preocuparse del ciclo decemnovenal. Afirman que es un método mucho más exacto, con el que se simplifica notablemente el cómputo eclesiástico y se fijan más claramente los límites pascuales. De este modo cualquiera, por inculto que sea, deducirá sin dificultad todas las fiestas con sólo conocer el día de Septuagésima.

[10] En el caso de que el papa y sus consejeros quisieran mantener el ciclo decemnovenal y los equinoccios en la situación del momento:

...que cada 152 años se obligue al equinoccio de primavera a fijarse siempre en la misma fecha del calendario, omitiendo una única intercalación bisextil. Y para determinar los novilunios, no les atribuyamos después de 304 años aquel sitio al que le corresponde el número áureo, sino el inmediatamente siguiente; de la misma forma, en los novilunios, cada 304 años se ha de tener en cuenta esta postposición o especie de retraso.

En esta duplicidad de opciones apreciamos la exacta comprensión del problema que manifiestan los comisionados salmantinos. Para poner en valor su preferencia por la primera de las opciones, acuden a la autoridad de San Agustín, argumentando su mayor simplicidad. Es curioso que en medio de tan aguda erudición, de tan exacto conocimiento del problema y de la versatilidad de las soluciones que ofrecen, los profesores salmantinos vuelvan a hacerse eco del concepto utilitarista que algunos padres de la Iglesia habían dado a la astronomía, pues aluden a San Agustín diciendo que:

[San Agustín] ordena en el libro De doctrina christiana que las disciplinas de humana erudición de tal modo deben admitirse al servicio de la sabiduría divina y cristiana, que la dialéctica y la aritmética la sirvan de modo general, si son requeridas de alguna parte, mientras que las demás sólo parcialmente y con ciertos pequeños fragmentos; piensa este santo que conviene que los más versados en las ciencias las desarrollen de tal manera que se recojan solamente de cada una de ellas aquellas cosas que creyeron ser necesarias para ilustrar algunos pasajes de la Sagrada Escritura. Y si San Agustín creyó que bastaba una elemental doctrina astrológica al cristiano incluso sabio, con cuanto mayor motivo nosotros, prescindiendo de los asuntos más sutiles de la ciencia astrológica, pedimos también con insistencia la fortificación del cálculo de tablas como defensa de la sencillez eclesiástica.

En efecto, en varias obras ha mostrado esta opinión San Agustín; por ejemplo en su Comentario sobre el Génesis (XVI, 34) decía:

Cuando lo que nos interesa es saber qué creemos en materia de religión, no hay motivo para indagar la naturaleza de las cosas… Al cristiano le basta con creer que la causa de todas las cosas creadas, celestes y terrestres, visibles e invisibles, es la bondad del Creador... Dedicarse a sutiles investigaciones acerca de las distancias y el tamaño de los astros... no nos parece ni provechoso ni conveniente.

San Agustín se refiere a que, desde tiempo inmemorial, los estudios astronómicos y computacionales fueron abordados por la Iglesia en función de la necesaria correspondencia entre el calendario y el dogma, pero institucionalmente no causaban mucho interés los descubrimientos que iban desvelándose.

Se ha tomado la actitud de San Agustín como ejemplo de la postura tradicional de la Iglesia ante la astronomía al poner de manifiesto que estos temas sólo debían interesar al cristiano en la medida en que las teorías pudieran hacerse concordar con las Sagradas Escrituras y, en particular, con el relato de la Creación expuesto en los primeros capítulos del Génesis. De ahí, por ejemplo, la importancia que adquirió el debate sobre la esfericidad de la Tierra a finales del siglo XV, porque la interpretación medieval de la Biblia mostraba que el cielo había sido tendido por encima de la Tierra plana (Isaías, 48, 13; Isaías 40, 22). El cambio epistemológico que supuso pasar del concepto de una Tierra plana, en forma de disco, a la idea de globo terrestre está perfectamente trazado por Randles (1990, p. 69): a finales del siglo XV, en los círculos cultos, era indiscutible la esfericidad de la Tierra que ya había sido proclamada por los científicos mucho antes, desde Pitágoras al catedrático salmantino Diego de Torres, pasando por Platón, Aristóteles, Ptolomeo, Isidoro de Sevilla, Sacrobosco, Roger Bacon o Tomás de Aquino; tanto en la cultura occidental como entre los árabes. Por eso, la cuestión de la esfericidad de la Tierra y el problema subsiguiente de la existencia y características de los antípodas eran temas habituales de estudio de las cátedras de astrología y de físicos de la Universidad salmantina.

La alusión del informe de 1515 al razonamiento de San Agustín, de que no debía interesar mucho la astronomía al cristiano, choca vivamente con la actitud de los informantes: contrasta con la fortificación del cálculo que proclaman, y con la profundidad y exactitud de la argumentación desarrollada. Éste es un ejemplo clarísimo del cambio epistemológico que se había operado en la cosmología. En este informe no hay rastro de la circularidad ni de la uniformidad del mundo supra-lunar; no importan tanto como la precisión en la medida de estos fenómenos. Pero también es un ejemplo de la actitud de los sabidores: se muestran sumisos en las palabras (...siguiendo a San Agustín), pero insumisos en la práctica y en las creencias (hablan —repito— de fortificación del cálculo; de no molestar al clero inculto, ni a la gente común). Como si fueran los herederos y mantenedores de una tradición hermética consciente de la importancia de preservar el verdadero conocimiento entre los elegidos, en este caso entre los matemáticos, cuya sabiduría se orienta, sin proclamas, al servicio de la Universitas Christiana. Con ello cumplen asimismo con los principios perseguidos por todos los conciliares desde Nicea, en orden a proponer una solución sencilla y práctica; características que también habían movido dos años antes a Copérnico a justificar el heliocentrismo en su Comentariolus.

[11] En la última parte del informe confirman que la interrupción bisextil que proponen no se corresponde del todo con el cómputo de las tablas del rey Alfonso X; pero dicen no haber encontrado otra satisfacción mejor. Esto es verdad: su cálculo era más preciso que el de las Tablas alfonsíes. Piensan que, con la primera solución propuesta, no habría error de un día completo en 1.000 años; y el que hubiera podría facilísimamente corregirse con una nueva anulación extraordinaria de la intercalación bisextil. Esto les parece suficiente:

...démonos entre tanto por contentos y bástenos con que hayamos restablecido el orden de nuestro calendario hasta dentro de mil años e incluso un poco más y... a ejemplo de aquel alabado pintor, cubramos con silencio lo que no somos capaces de expresar con el pincel.

Acabada esta argumentación, los comisionados incluyen una tabla con los doce meses del año, independiente para cada mes, con tres filas cada una (véase la figura 27), similar a la que elaboraría también Pedro Ciruelo. En la primera y la tercera de las filas escriben sendos números áureos; el primero siguiendo el orden que se ha venido haciendo hasta ahora; y anotando en el segundo, el que resultaría después de fijando el equinoccio (o el 10 o el 21 de marzo), tomando como punto de partida o el año 1520 (una vez hecha la anulación de los 11 días, más que 10, como ellos estiman), o el 1519 (sin hacerla previamente); descontando los 4 días que sobran en la conjunción lunar y teniendo en cuenta la omisión de la intercalación bisextil cada 304 años. En la fila del medio, apuntan las letras del calendario correspondientes a cada día de la semana. Con ellas se facilita mucho el cálculo de las conjunciones futuras.

Fig. 27: Informe de 1515, segunda parte. Tabla de números áureos y letras del calendario, y su canon explicativo.

El canon explicativo que las acompaña vuelve a denotar conocimientos precisos y diversificados de la tradición astronómica. Advierten que no están más acertados quienes defienden la longitud del año trópico dada por Albategni que quienes se conforman con la de las Tablas alfonsíes; esto significa que han leído y entendido los Cánones del sirio Albateni (también llamado Albategnius, Albategni, Albatenius o Al-Battani; c. 858–929), o su Libro del quadrante sennero. Tener posibilidad de entender estas obras necesariamente es producto de una larga y profunda preparación científica, pues las prolijas y complejas explicaciones matemáticas, astronómicas y técnicas que se derivan de ellas no se improvisan y no dejan de amedrentar, según afirma Jesús Fernández[57].

Albateni destacó en matemáticas por sus descubrimientos en trigonometría y geometría (tangentes y cotangentes). Como astrónomo —faceta en la que aquí se le recuerda— fue muy conocido por haber logrado una determinación precisa del año solar de 365 días, 5 horas, 46 minutos y 24 segundos [hoy se estima en 365 días, 5 horas 48 minutos y 45.16 segundos] y la fijación del momento del equinoccio con un error menor a las dos horas. Averiguó que el punto que Ptolomeo determinó como afelio se desplazaba, y calculó la velocidad de dicho movimiento con bastante exactitud. Logró además calcular con escaso error el ángulo que forma el eje de la Tierra con su plano de rotación. Según la cita previa del informe salmantino, los comisionados sabían que, a pesar de su mayor precisión, la medida del año trópico de Albateni tampoco era exacta.

Algo que me parece digno de comentario es que en esta explicación de las tablas, introduce un algoritmo que permite averiguar fácilmente la fecha de la Pascua, poniéndola al alcance de quienes ni siquiera tuvieran una formación básica en aritmética. Dice el informe:

...La regla para esto es muy breve. Determinada la conjunción pascual de un año cualquiera, conjunción que proporcionará, bien la segurísima fiabilidad del cálculo de tablas, bien el testimonio de la autoridad competente; deducirás de este modo la conjunción pascual del año siguiente: Resta de los días y horas de la conjunción conocida 10 días y 15 horas, si el año siguiente se considera año común...; y si ves que es año con embolismo, añade a los mismos días y horas de la conjunción conocida 18 días y 21 horas, y con esto te aparecerá el día y la hora de la conjunción pascual que buscabas... y cuantas luego quisieres en una sucesión sin fin, con tal de que te acuerdes de restar una unidad al número de días resultante de esa adición o sustracción, si el año cuya conjunción buscas se considera bisiesto. Y se sabrá que el año futuro es embolismal por el cálculo del número áureo, es decir, si se ve que es el 3º, 6º, 8º, 11º, 14º, 17º ó 19º del ciclo decemnovenal.

Después, tras aclarar las peculiaridades de esta fijación de la Pascua en el calendario hebreo, terminan aclarando que no han elaborado dichas tablas por no considerarlo necesario, debido a la facilidad de su confección:

Intencionadamente nos abstendremos de confeccionar esas tablas (que pensamos han de insertarse en los breviarios eclesiásticos), cosa sumamente útil, puesto que pueden deducirse de las anteriores reglitas con escaso trabajo, y nuestra intención por otra parte fue más bien hacer indicaciones por encima y superficialmente, exhortar a dar explicaciones despacio, expresarlo todo sin mucha distinción y esperar lo que hemos creído que habrá de ser útil para facilitar la reforma propuesta.

En conclusión: ¿Qué propuso la Universidad de Salamanca en 1515 para la reforma del calendario? Como hemos dicho, aunque ofrecen otras posibilidades, los informantes se decantan por la siguiente solución:

1. Como el año solar sobrepasaba un poco más de 10 minutos y 4 segundos al año eclesiástico, y puesto que los datos de las tablas alfonsíes ponían de relieve que el calendario juliano adelantaba un día cada 134 años, proponen quitar de un mes cualquiera los 11 días de adelanto solar, o suprimir un día de cada mes durante un año cualquiera, menos de febrero. Así el equinoccio verdadero volvería al 21 de marzo, y se restablecerían los decretos de Nicea y la fijación del término pascual.

2. Se continuaría estableciendo una anulación de la intercalación bisextil cada 304 años (en relación con lo que, finalmente, la reforma gregoriana, para evitar el lento adelanto, estableció que de los 4 años seculares, sólo uno fuera bisiesto: el múltiplo de 400).

3. En lugar de adelantar el ciclo decemnovenal a cinco fechas antes en función de la anticipación lunar, sustituir el ciclo de Metón por unas tablas (de epactas). Una solución más sencilla.

4. Establecer el mejor momento para realizar la reforma el año 1519 (mejor que aplicarla retrospectivamente al año 1500), de manera que en 1520 quedaría restablecido el equinoccio según el cómputo en uso y comenzaría el día 1 de enero con el número 1 del ciclo decemnovenal (a favor de los nostálgicos).

El razonamiento es impecable y su propuesta coincide con la opción ratificada finalmente por Gregorio XIII bastantes años después, en la que sólo se añadió un algoritmo corrector en la celebración del año bisiesto.

Como bien ha dicho Flórez, uno de los grandes aciertos del informe salmantino fue el gran equilibrio entre las ideas teológicas y las científicas presentes en la reforma propuesta (Flórez, 1999, p. 448). Este profesor argumenta que la base teórica y técnica del informe salmantino es la Compilación magna de Zacut y su Almanaque perpetuo en función de que en ese momento Sancho de Salaya era el catedrático de astrología, y era hijo de Juan de Salaya, el traductor del canon de las tablas de Zacut (Flórez, 1999, p. 453). Ya he comentado que Sancho de Salaya no estaba en aquellos años enseñando en su cátedra, luego no podemos atribuir al texto ni esta autoría ni el camino de esta influencia, aunque sí la influencia en sí misma. Es una demostración más de que la obra de Zacut representaba un poso de conocimiento común de la ciencia en Salamanca del momento.

1.4.3. El informe salmantino de 1578

El concilio de Trento tampoco pudo ofrecer a la cristiandad la reforma del calendario. En la última sesión del mismo, de 4 de diciembre de 1563, al tiempo que se hacía la modificación del breviario y del misal que se introducirían respectivamente en 1568 y 1570, se volvió a declarar la necesidad de elaborar un plan para corregir los desfases en el calendario restableciendo el equinoccio de primavera al lugar que tenía cuando se celebró el concilio de Nicea (21 de marzo), e introduciendo la corrección que evitara esta deriva en el futuro. Aparte de ello, se acordó una declaración en el sentido de lo que ya habían defendido Bacon y Middelburg hacía siglos: encomendar directamente la reforma al Santo Padre (Mansi, 1902, p. 194).

Este fracaso conciliar tenía que repercutir en la consideración global sobre la validez de la astronomía. Era difícil mantener el carácter científico de unos conocimientos que nadie había podido sistematizar y cuya investigación ponía en entredicho a la Biblia y los principios cosmológicos ptolemaicos: Las comprobaciones astronómicas que caminaron paralelas a los debates sobre la reforma del calendario finalmente acabarían por desbaratar la tradicional imagen del cosmos cerrado, ordenado y jerárquico aristotélico que nos explicara Koyré.

1.4.3.1. El copernicanismo y la reforma del calendario en Salamanca

Dije antes que Middelburg solicitó la ayuda de Copérnico (1473-1543) en el fragor de los debates del concilio de Letrán y que éste declinó el ofrecimiento de colaboración aduciendo que faltaban las mediciones precisas imprescindibles del año trópico. Cuando Copérnico escribió el prefacio al De Revolutionibus veintiocho años después, todavía consideraba insuficientes estas proporciones y dirigiéndose al papa, escribió:

No hace mucho tiempo, bajo León X, cuando en el concilio de Letrán se debatía la cuestión, este tema quedó sin solución únicamente porque las dimensiones del año y de los meses y los movimientos del Sol y de la Luna se estimó que no estaban suficientemente bien medidas. Desde entonces he tenido el cuidado de estudiar estas cosas de una forma más exacta, animado por el muy célebre Pablo [de Middelburg], obispo de Fossombrone, que entonces había presidido estas deliberaciones. En cuanto a lo que yo he aportado en este orden de estudios, lo someto al juicio de Tu Santidad, así como al de todos los otros sabios matemáticos (Copérnico 1982, pp. 23-24).

Es decir, que él mismo concebía su obra como una aportación al estudio de la reforma del calendario. En opinión de E. Proverbio, aunque no pueda ser considerada como la razón más importante que movió a Copérnico a concebir el De Revolutionibus, la cuestión del calendario jugó un papel no secundario en la evolución de las teorías planetarias descritas por Copérnico en su Comentariolus, tratado presumiblemente escrito entre 1512 y 1514 (Proverbio, 1984, pp. 129-130), coincidiendo precisamente con la solicitud de Middelburg y del concilio lateranense citada. El contenido matemático del estudio contribuía al cálculo las tablas y los almanaques tan necesarios a los astrónomos y astrólogos de su tiempo, independientemente de las disquisiciones de si Copérnico había expuesto una teoría o se trataba de simples hipótesis conforme se desprendía del prólogo de la obra que añadiera el editor Osiander (1498-1552), con la aquiescencia de su alumno Rheticus (1514-1576).

En este sentido se puede decir que la alternativa heliocéntrica había sido una consecuencia indirecta de la necesidad de reforma del calendario, pero implicaba una transformación de la forma en que el hombre concebía su relación con Dios y las bases de la moral: por eso el copernicanismo y la reducción del calendario se vieron indirectamente involucrados en la batalla religiosa y política que derivó de aquélla, debido sobre todo a la importancia de sus cálculos. La primera oposición teológica (no científica) les vino de parte de los protestantes, quizá porque Copérnico había comenzado a obtener sus conclusiones mientras trabajaba para los católicos (por encargo de Middelburg), lo que, unido al notorio disgusto de los protestantes, probablemente influyera en el silencio inicial de Roma hacia esa teoría. No podemos olvidar que estos hechos se enredan en el tiempo en otros tres procesos históricos claves: al problema político que derivó de la Reforma protestante, al comienzo del Concilio de Trento y a la ulterior claudicación del sueño imperial carolino de la Universitas Christiana en la Paz de Augsburgo (1555); paz que supuso el triunfo político protestante en Alemania, encarnado en la frase cuius regio, eius religio. Es decir, en el ambiente de una lucha político-religiosa.

Aparte de los cálculos astronómicos, el De revolutionibus... ofrecía la novedad de la teoría heliocéntrica y el guiño a la tradición hermética. Se ha escrito mucho acerca del famoso pasaje copernicano sobre la centralidad del Sol; o su afirmación de que la armonía y precisión de un sistema geométrico justificaba su verdad mejor que su adecuación con las apariencias. Un testimonio excepcional de esta realidad nos lo ofreció Rheticus, cuando relacionaba la resistencia de Copérnico a publicar su obra con su filiación pitagórica, en cuya tradición se reservaban los secretos para un corto número de elegidos instruidos en matemáticas. Es interesante comprobar que el primero de los informes salmantinos sobre la reforma del calendario va a contener los mismos elementos platónicos, pitagóricos y herméticos del De Revolutionibus, desde el mito de la centralidad solar (que en el informe salmantino es lunar) hasta la inconveniencia de quebrantar la paz del clero inculto con explicaciones computacionales que sobrepasaban su interés y capacidad de comprensión (en esto insistieron los dos informes salmantinos conjuntamente). Es una muestra de la importancia que había tenido esta tradición hermética en el Renacimiento (Beltrán, 1995, pp. 71 ss.), que tuvo un reflejo palmario en la configuración de la fachada de la Universidad de Salamanca, según investigó Pablo Andrés Bravo en una obra de fuerte impregnación cabalística publicada en 2007.

La publicación por Copérnico de su obra, en 1543, fue el acontecimiento científico que marcó la época y estas investigaciones. Decía Goethe:

De todas las opiniones y descubrimientos, ninguno debe haber ejercido mayor efecto sobre el espíritu humano que la doctrina copernicana. Apenas el mundo había sido considerado como redondo y completo en sí mismo, cuando se le pidió que renunciara al tremendo privilegio de ser el centro del universo... No sorprende que sus contemporáneos rehusaran perder todo esto y presentaran toda la resistencia posible a una doctrina que autorizaba y exigía de sus conversos una libertad de miras y una grandeza de pensamiento desconocidas, ni tan siquiera soñadas hasta entonces (Cf. Hawking, 2009, p. 21).

Quizá porque anidaba en el punto medio de estos debates, debates que a su vez eran el centro de la problemática astronómica y matemática, durante la segunda mitad del siglo XVI el De revolutionibus... fue de referencia obligada en astronomía. Ya hemos dicho que la Universidad de Salamanca tomó partido a favor de sus cálculos en la compleja trama de persecución ideológica a que fue sometido el trabajo; aunque la fe de la mayor parte de los científicos en la inmovilidad de la Tierra —incluso de los salmantinos— siguiera oficialmente inquebrantable. Por eso en el plan de estudios se seguía estudiando como base el modelo cosmológico aristotélico (véase la figura 28), no exento de representaciones semi-mitológicas (figura 29). Digo esto porque los informes salmantinos sobre el calendario tienen elementos que permiten cuestionar esta inquebrantabilidad: sin ir más lejos podemos fijarnos en el baile de cifras sobre la medida del año trópico del que hablan, que no encaja con los supuestos cosmológicos de movimientos circulares y uniformes.

Fueron los protestantes los primeros en lanzarse vehementemente contra el heliocentrismo y, quizá sólo salvo Brahe y Kepler, también lo serían en enfrentarse a la bula que reformaba el calendario. Se dice que los católicos comprendieron más tardíamente que ellos las implicaciones teológicas que conllevaba la idea del movimiento de la Tierra. Lo revolucionario, lo subversivo, no fue tanto contradecir las Sagradas Escrituras o destronar al hombre del centro del universo, cuanto proclamar públicamente un conocimiento que la tradición hermética hubiera reservado para los iniciados en matemáticas (Elena, 1985). Éste es un ejemplo de la implicación de la Iglesia en la historia de la ciencia, tema que ha sido sugerentemente tratado por Riaza Morales (1999) y Dampier (2008).

Mientras las universidades de Zurich (1553), Rostock (1573) y Tubinga (1582) condenaban el heliocentrismo, Pauden, en Wittemberg, sugería la prohibición de la enseñanza del heliocentrismo o la Sorbona declaraba en 1587 que tales enseñanzas deben ser extirpadas no menos que las de los herejes, en Salamanca los dos hermanos Aguilera (Juan y Hernando) volvieron sucesivamente de Roma entusiasmados con el De revolutionibus... y Hernando logró que se incluyera su opción de estudio en las clases universitarias de astronomía, desde la reforma de estatutos de 1561; mandato reiterado en los sucesivos cuerpos estatutarios de 1594 y 1625 (véase el apartado 1.3.2.2.2.). En el mismo período en que se estaba practicando el teatrero cierre ideológico en España, el De Revolutionibus fue un lugar común entre los astrónomos de esta Universidad y sus tablas tuvieron que estar necesariamente sobre la mesa de los redactores del segundo informe salmantino sobre la reforma del calendario.

Ha sido muchas veces repetido en la historiografía contemporánea el hecho de que Salamanca se adelantara incluso a Cracovia en este camino, pues desde 1582 se aplicaron las doctrinas copernicanas al cálculo de efemérides (Bustos Tovar, 1973; Fernández Álvarez, 1974). Diego de Zúñiga en sus comentarios al libro de Job (editados en 1579 y redactados de forma paralela a estos informes sobre la medición del tiempo) demostraba que sus teorías no se oponían a las de las Sagradas Escrituras (Bolado, 1985), aunque después cambió de opinión en su Philosophiae prima pars quae perfecte et eleganter quatuor scientiae Metaphysica, Dialectica, Rhetorica et Physica declarantur (Navarro Brotóns, 2005).

Las investigaciones y debates llevados a cabo en los dos ámbitos, en el del heliocentrismo y en el de la reforma del calendario, al menos habían traído consigo la invención de la astronomía sistemática. Antes hablé de la inflación de las matemáticas a lo largo del siglo XVI y no cabe duda de que esta inflación se produjo arrastrada por el tirón simultáneo de esos dos problemas. A las clases, a las tertulias y a las mesas de trabajo de los intelectuales llegó el interés por el cómputo en todos los sentidos. De forma paralela a la celebración del concilio de Trento se multiplicaron las ediciones de obras que trataban el problema del calendario. En España, al proyecto de Juan Ginés de Sepúlveda ya citado, siguieron los de Bernardo Pérez de Vargas (Repertorio perpetuo, 1563), Bartolomé Antist (Almanac o pronóstico de los efectos que se esperan según las configuraciones de los planetas y estrellas que han de suceder en diversas partes del mundo y particularmente en el horizonte de Valencia, 1580), Pedro de la Hera (cálculos de eclipses lunares con arreglo al meridiano de Madrid), fray Juan de la Barrera (Repertorio perpetuo de los tiempos, 1579), Jerónimo de Chaves (Cronografía o repertorio de los tiempos, el más copioso que hasta ahora ha salido a la luz, con quince ediciones en España desde 1554 a 1600), fray Diego Jiménez (Kalendarium perpetuum secundum institutum patrum predicatorum, 1563) y, sobre todo, una obra del franciscano valenciano Juan Salón, que se tituló De Romani Calendarii Nova Emendatione, ac Paschalis Solemnitatis Reductione (Florentiae: in officina Georgij Marescotti, 1576), y que obtuvo el aplauso papal. Hubo muchos más impresos sobre el tema, algunos de escaso valor en los círculos pontificios pero de gran interés en España en cuanto que ayudaron a popularizar el tema del calendario entre las gentes: me refiero por ejemplo a los de Juan Terréu, Agelasio Palmireno, Álvaro Piña, García de Lovas, y otros.

Fig. 28. Cosmología de Aristóteles. APIANUS, Petrus. Cosmographia Petri Apiani / per Gemmam Frisium… Veneunt Antuerpiae, 1545.

1.4.3.2. Las nuevas solicitudes de informe

Al ocupar Ugo Buocompagni la cátedra de Pedro, en 1572, y convertirse en Gregorio XIII (1502-1585), tomó como tarea propia la corrección del calendario, siguiendo el interés y las órdenes del concilio de Trento, concilio al que asistió. Kaltenbrunner (1876; 1877; 1881), Schmid (1882a; 1882b; 1884), Coyne (1983), así como todas las historias de los papas ofrecen los pormenores de la cuestión de la reforma tal y como se vivió en el Vaticano. Resumiré este tema antes de tratar del informe salmantino.

Tras el nombramiento del nuevo papa y basándose en el derecho que el propio concilio de Trento le había reconocido, Gregorio XIII promovió la investigación sobre la reforma del calendario comprometiendo en ella a cuantos matemáticos y astrónomos de prestigio se pudo convocar. En este sentido el pontífice continuó una tradición papal que se repitió pendularmente en todos los papados a lo largo de la Edad Media, salvo en tres: los de Nicolás V (papa entre 1447-1455), Calixto III (1455-1458) y Pio II (1458-1464).

Desde Trento el interés por el tema creció enormemente en los círculos cultos de Europa y ello condujo a una proliferación inusitada de nuevos estudios y proyectos de reforma que han sido estudiados particularmente por August Ziggelaar (1983, pp. 205 ss.). La Santa Sede coadyuvó directamente a la elaboración y a la edición de muchos de ellos, con el objetivo de recoger y difundir todo lo posible los avances que se iban realizando, tratando de promover un consenso tanto en la fijación de las medidas como en el conveniencia de la reforma. Con esta intención, en 1575 contrató a Carlos Octaviano Lauro, un gran matemático, solicitándole una propuesta al respecto; propuesta que sabemos terminó, pero de la que no se habló más, nombrando el pontífice una comisión con este cometido en el año 1577 (Fernández Collado, 1990, p. 151).

La reforma resultó finalmente ajena a la tradición local romana debido a la composición universal de la comisión nombrada al efecto, muy pensada por el pontífice con este fin. Los datos sobre ella no son siempre coincidentes, porque sus componentes variaron a lo largo del tiempo. Según Baldini (1983, pp. 137-138), inicialmente se organizó bajo la dirección de un paisano del papa, Tomás Lilio, obispo de Sora, que pronto —en el mismo 1577— fue sustituido por el cardenal Guglielmo Sirleto como coordinador de los trabajos, el más influyente en el tema según Ranke (Die Römischen Päpste, I, p. 428). A su alrededor convocó a dos prelados: el obispo de Mondovi (Italia), Vicencio Lauri, como asesor teólogo, y el patriarca de Antioquía, Ignatius, hombre muy versado en astronomía. En función de la operatividad, el papa buscó a especialistas en cronología eclesiástica, liturgia, historia del calendario, deliberaciones conciliares y ritos de las iglesias oriental y occidental: el maltés Leonardo Abel —por su conocimiento del mundo árabe—, el jurista francés Seraphinus Olivarius —auditor de la Rota y especialista en textos latinos—, el español Pedro Chacón —gran erudito en Patrística e historia de la Iglesia, muy hábil en cuestiones relativas al calendario litúrgico, martirologio e interpretaciones conciliares— y, finalmente, a conocidos científicos: Antonio Lilio —astrónomo, hermano de Luis Lilio—, y dos expertos matemáticos: el dominico Ignacio Danti y el jesuita Cristóbal Clavio. Schmid (Schmid, 1884, p. 58) añade a esta lista el nombre de Juan Bautista Gavio, poeta y profesor de griego de La Sapienza.

Fig. 29: APIANUS, Petrus. Astronomicum Caesareum. Ingolstadii: 1540.

Una comisión internacional e interdisciplinar en la que sólo hubo un español, formado precisamente en Salamanca: Pedro Chacón (1527-1581). Chacón nació en Toledo y estudió en la Universidad de Salamanca de 1555 a 1562, en la que se graduó de maestro (doctorado) en teología. Era muy aficionado a las matemáticas y al griego, materia ésta que dominó rápidamente aprendiéndola de forma autodidacta. Algunos dicen que fue catedrático de griego en la salmantina y que declinó varios ofrecimientos en la Universidad, marchando a Roma (en febrero de 1570), siguiendo los consejos de su amigo Francisco Salinas, el catedrático de Música. En los registros universitarios no figura que Chacón haya enseñado en esta Universidad y no me parece que se pueda declinar el ofrecimiento de ser catedrático en ella cuando, para serlo, era necesario presentarse voluntariamente a una oposición, cosa que de Chacón no consta.

Era de carácter retraído, modesto, solitario, sin ambición, obsesionado por el anonimato y poco amigo de editar sus obras; por eso la mayoría se publicaron después de su muerte. En Roma estuvo al servicio del papa, primero en la revisión de la Biblia, de varios textos de los Santos Padres y del decreto de Graciano. En reconocimiento a esta dedicación el papa le nombró canónigo de Sevilla, aunque continuó en la curia romana trabajando en la comisión para la reforma del calendario. Fruto de esta dedicación surgió su Kalendarii Romani veteris explanatio (Amberes: 1568), de cuya edición se encargó Arias Montano. Pero de su pluma salieron también otras obras, que han sido catalogadas en el Centro de Documentación Gonzalo Díaz y María Dolores Abad (Biblioteca Virtual de Pensamiento Político Hispánico), y cuyas primeras ediciones fueron: In Pomponium festum de verborum significatione. Venetiis, 1559. In Ioannis Cassiani Opera Annotationes (Roma: 1580). In Pomponium Mela Commentarium (Roma: 1582). In C. Julii Caesaris Commentarios Scholia Uberiora. In C. Crispum Sallustium Breviora. Impresas por Fulvio Orsini junto con su obra In historicos latinos (Roma: 1582). In Tertulliani Opera Coniecturae (Roma: 1584). In M. Terentii Varronis, libros de Lingua Latina, De Re Rustica Commentarium (Roma: 1587). In Arnobii Adversus Gentes libros octo, Minutti Foelices Octavium. Notae (Romae: 1582). De Nummis libri tres (Roma: 1586). De Triclinio romano libero Fulvi Ursinis Appendix (s.I.: In Officina Santandreana, 1590). Opuscula: In Columnae Rostratae inscriptionum. De ponderibus, De Mensuris, De Nummis (Lugduni Batavorum: Ex Off. Plantiniana apud Franciscum Raph, aelengium, 1597). De Accubitus in coena antiquorum origine (Amsterdam: Henricum Wetstemius, 1689). Historia de la Universidad de Salamanca que escribió... BNE, ms 7456 (hay otros ejemplares en distintas bibliotecas; se editó en Semanario Erudito. Madrid, 1789, Vol. 18, pp. 3-61; Chacón 1990). In S. Isidori Praesulis Hispalensis Etymologiarum Libros XX (según Juan Grial la obra debía imprimirse en Madrid a expensas de Felipe II; Grial la utilizó, pero no se sabe si la impresión se llevó a cabo). Quedan aún manuscritas las siguientes: Fragmento de Astrologia. Annotationes in Sphaeram Ioannis de Sacrobosco. In decretum Gratiani Correctiones. E In Plinium notae. Una copiosa producción literaria con comentarios a Pomponio Mela, Casiano, Sacrobosco, Julio César, Tertuliano, Terencio, Arnobio, San Isidoro y también sobre medidas, calendarios o el decreto de Graciano. Desafortunadamente, Chacón murió antes de ver culminado el trabajo del calendario y publicada la reforma gregoriana.

Después de muchos estudios y debates, la comisión romana, con Chacón incluido, decidió centrarse en el plan para la reforma ideado por el médico y matemático Luigi Giglio, más conocido como Aloisius (Luis) Lilio (c. 1510-1576), aspecto que ha sido irremediablemente mentado por todos los investigadores de la historia del calendario. Este proyecto lo presentó a la curia Antonio Lilio en el año 1577; había sido elaborado por su hermano, ya fallecido, bajo el título Compendium novae rationionis restituendi Kalendarii (figura 30). Conocemos muy poco de la biografía de su autor. Luis Lilio era de origen veronés, según el cardenal Noris (Tratato sopra il cicle Ravennate) y Ricciolis (Almagestum Novum); o calabrés, según Clavio (Romani Calendarii Explicatio) y Pietro Maffei (Annali di Gregorio XIII). Se creía su obra perdida, pero Swerdlow encontró un ejemplar impreso en la Biblioteca Nacional Central de Florencia y después Gordon Moyer y otros han descubierto más (Moyer, 1982, p. 91).

La comisión decidió enviar el Compendium de Lilio (fig. 30), refundido e impreso por Pedro Chacón (Roma: 1577), a los príncipes y expertos de la cristiandad recabando sus opiniones. Con estas miras se expidió un breve el 5 de enero de 1578 dirigido precisamente a estos príncipes, en el que se solicitaba su apoyo para la obra de reforma prevista (Moyer 1983, pp. 171-188).

Dentro de los reinos hispánicos, Gregorio XIII consultó a las universidades de Salamanca y Alcalá de Henares y a Juanelo Turriano. El recurso a Alcalá tenía sentido por ser la única universidad hispana especializada en estudios teológicos y por el hecho de referirse a un problema que afectaba directamente a la fijación de ciertas celebraciones religiosa. No sorprende tampoco el llamamiento a Turriano, dada la fama que había adquirido este peculiar personaje como inventor de sofisticados instrumentos mecánicos; fama que le propició el oficio de relojero imperial de Carlos V (Fernández Collado, 1989, pp. 151-161; Turriano, 1990). El llamamiento a la salmantina estaba también dentro del ámbito de lo esperado, pues se le había preguntado ya en 1515, mantenía el prestigio científico que se había hecho patente en la resolución de otros problemas científicos y en sus aulas se había formado uno de los comisionados, Chacón.

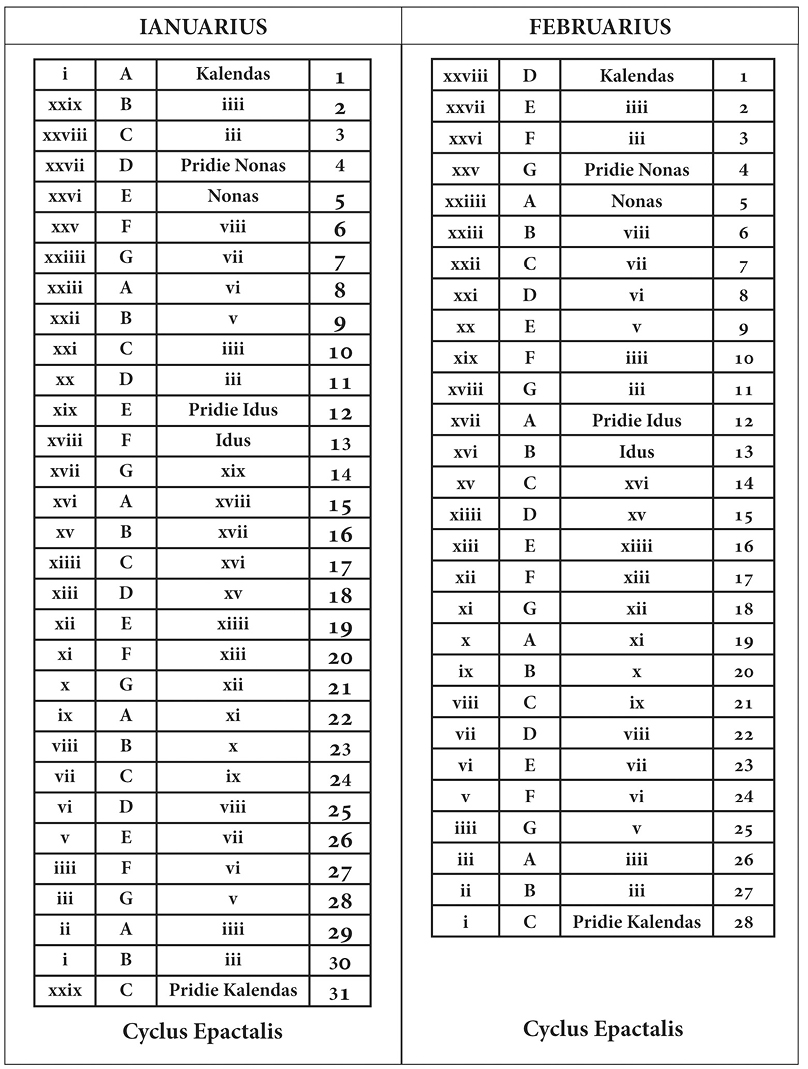
Fig. 30: Con la epacta y las letras dominicales se podían determinar los días de la semana y las fases de la Luna. Tabla con el ciclo de la epacta, letras dominicales, calendario romano y calendario juliano según Lilio [LILIO, Luigi (1577). Compendium novae rationis restituendi kalendarium. Biblioteca Nazionale Centrale di Roma, 68.13.C. 46, f. 5r.]. Obsérvese la similitud de esta tabla con la correspondiente del informe salmantino de 1515 (Fig. 27).

La comisión lo tenía muy claro. El desfase en el calendario provenía de un inexacto cómputo del número de días del año trópico. El calendario juliano, que había introducido un bisiesto cada cuatro años, fijaba el año trópico promedio en 365.25 días, en notación decimal (según la medida de Sosígenes), en tanto que la cifra más aproximada es de 365.242189, o lo que es lo mismo, 365 días 5 horas 48 minutos 45.16 segundos. Pero hace 2052 años la duración del año se fijó en 365.24232, es decir 11 minutos y 4 segundos más corto que el calendario Juliano. Este decremento daba por resultado el adelantarse un día solar medio aproximadamente cada 130 años (134 según la comisión de 1515), de donde proviene el anticipo gradual de la fecha del equinoccio de primavera. Además se sabe que la regresión de las fechas de los equinoccios y solsticios se ha acelerado, pues en 1577, el año solar medio sólo se desviaba un día por cada 128.5 años. Contados adicionalmente a cada año estos 11 minutos y 4 segundos, habrían supuesto un error acumulado de aproximadamente 10 días en los 1257 años que mediaban entre 325 —fecha del concilio de Nicea— y 1582. Al mismo tiempo, el cómputo de la Luna había acumulado un error de un día cada 310 años por lo que, en vísperas de la reforma, el calendario lunar iba con 4 días de adelanto (Kaltenbrunner 1887, pp. 16 y 498). A partir de estas estimaciones Lilio proponía en su compendio algo bastante sencillo y concordante con lo que había propuesto la Universidad de Salamanca:

1. La fijación de la fecha del equinoccio el 21 de marzo.

2. La supresión de 10 días del calendario civil, o de una sola vez, o quitando los bisiestos durante 40 años (el informe salmantino proponía suprimir 11 días).

3. Considerar bisiesto cada año divisible por 4, a excepción de los años de centuria que serían bisiestos sólo si eran divisibles por 400 (equivalente a la anulación extraordinaria de la intercalación bisextil cada 1000 años propuesta por los salmantinos). Esto conlleva la supresión de tres días intercalares en los años centenarios que no fueran exactamente divisibles por 400. Según sus cálculos (los mismos que los de la Universidad de Salamanca en 1515) se produce un error de un día cada 134 años, o lo que es lo mismo tres días cada 402 años. Había que suprimir tres días cada 402 años. El sistema liliano redujo, pues, a 97 el intercalado de días en un periodo de 400 años (en lugar de los 100 días intercalares en el mismo periodo del sistema juliano). De aquí que se hable del ciclo de los 400 años.

4. La corrección del calendario lunar: El ciclo de 19 años para el cálculo de la Luna era enmendado por medio de la eliminación de un día cada 300 ó 400 años (8 veces en 2500 años). Pero se introducía un nuevo método para el cálculo de la fecha de la Pascua que consistió en la sustitución del ciclo metónico y el áureo número por la tabla de epactas ya propuesta por la Universidad de Salamanca; tabla que no había presentado Salamanca a León X en su informe de 1515 porque, según expresaron, bastaría el trabajo de 15 días de un mediano calculador astrológico para elaborarlas. Lilio fue, pues, ese mediano calculador astrológico del que hablaron los salmantinos.

Pues bien, con este planteamiento, a la Universidad de Salamanca llegó una petición real de Felipe II, cuya data es en Madrid a 22 de abril de 1578, en la que manda atender al deseo papal sobre la reforma del calendario, a fin de que los oficios divinos —decía— se celebrasen a su tiempo, y disponiendo que se nombrase a las personas más convenientes para estudiar el problema. Esta carta fue leída y su contenido tratado en el claustro pleno de la Universidad, reunido a este fin, el domingo 27 de abril de 1578, a las tres de la tarde, en el que se informó de la llegada de las dos cartas sobredichas —una de Su Santidad y otra de Su Majestad—. El rector tomó la palabra y dijo:

Que de parte de Su Majestad y de Su Santidad y del reverendísimo Nuncio se le había enviado un envoltorio en el cual venía un breve de Su Santidad y una carta de Su Majestad y otra del Nuncio en las cuales se manda a esta universidad mande ver y vea el cómputo o calendario que por mandado de Su Santísima se ha hecho en Roma, para que, visto por la universidad y sus comisarios, en su nombre el dicho calendario, apunten y vean lo que vieren se les ofrece e conviene añadir o quitar de él.... (AUSA, 47, f. 55v.).

Efectivamente, a continuación se recoge el breve pontificio que instaba a la Universidad a estudiar el tema. Va dirigido al rector y a la Universidad de Salamanca, y dice que entre sus responsabilidades pastorales y en orden a la utilidad de la Iglesia, se envía un compendio elaborado por Lilio y analizado por expertos matemáticos, en orden a reformar el calendario... para el beneficio común de toda la cristiandad y la gloria divina (AUSA, 47, fol. 55v.; ed. Beltrán de Heredia, 1972a, IV, p. 317).

El acta de claustro reproduce a continuación el texto de la solicitud real y una carta del nuncio Felipe Sega, obispo de Ripa, en el mismo sentido; nuncio que se convertiría pronto en el intermediario para España en este asunto, desde el oficio que desempeñó entre 1577 y 1581. Es fácil seguir la cronología de estos hechos a través de su correspondencia (Olarra-Larramendi, 1948, I, pp. 13-15, 19, 27, 26, 27, 42, 44, 48, 59, 67, 73, 82, 87, 89).

La citada petición real explicaba el motivo de la misma, especialmente la utilidad de la Iglesia, encomendando muy encarecidamente a la Universidad una respuesta a la solicitud pontificia. Decía Felipe II:

Venerable Rector, consiliarios y diputados del Estudio y Universidad de Salamanca. Por el breve de Su Santidad y tratado que con él se os envía por parte de su nuncio que en mi corte reside, veréis lo que Su Beatitud, atendiendo a la común utilidad de la Iglesia, desea que los divinos oficios se celebren a sus tiempos y que para esto se enmiende el calendario, como me lo ha avisado por otro breve que de su parte me ha dado el dicho nuncio, encomendándome que mande hacer en mis reinos las diligencias necesarias a este propósito. Y por ser el que Su Santidad muestra tan justo, conveniente y necesario, y lo mucho que importa que obra en que Nuestro Señor, será tan servido se acierte y tenga el efecto que conviene, holgaremos mucho y así os lo encargamos, que haviendo visto el breve de Su Santidad y lo que en aquella conformidad el nuncio os escriviere, ordenéis cómo por las personas de esa Universidad que para este menester os parecieren más convenientes se mire muy bien lo que a esto toca y se apunte lo que en ello se les ofreciere y pareciere, con la más brevedad que se pueda, para que con la misma se responda a Su Santidad, que en ello me serviréis. De Madrid a veinte y dos de abril de mil y quinientos y setenta y ocho años. Yo el Rey. Por mandado de su Majestad, Mateo Vázquez (AUSA, 47, fol. 56r.).

El objetivo de la reforma es, pues, de carácter litúrgico. Tras la lectura de los textos, los asistentes celebraron ante ellos el ceremonial de acatamiento acostumbrado, tratando e votando acerca de ellos, y determinando nombrar una comisión de profesores para que se hiciera cargo de tan importante negocio.

Unos tres meses después se recibió la segunda carta real, fechada el 2 de julio de 1578 en San Lorenzo del Escorial, instando a la Universidad a responder con la mayor celeridad posible. Dado su interés, estas cartas han sido publicadas en varias ocasiones (Beltrán Llera et al., 1960, docs. 344 y 345, p. 24; Esperabé de Arteaga, 1914, docs. 171 y 172, p. 567).

1.4.3.3. La comisión salmantina de 1578

¿Quiénes podían ser designados para responder a esta solicitud? Dado el complejo talante científico de la consulta y el excepcional carácter de los peticionarios, era natural que el claustro seleccionara a los más prestigiosos y cualificados del Estudio, tanto desde el punto de vista institucional como científico. El número de profesores salmantinos entre los que se podía elegir a los comisarios era ahora mucho más amplio que en 1515. Según el listado de nombres y cronologías que ofrece Esperabé de Arteaga, los profesores más destacados en sus especialidades proclives a recibir este encargo, el 27 de abril de 1578, eran los siguientes (sigo a Esperabé de Arteaga 1914, I, y 1917, II, y completo sus datos con otras fuentes):

En la facultad de cánones, había dos cátedras de prima; una la ocupaba Antonio de Aguilera (la regentó entre 1549 y 1580) y la otra Cristóbal Gutiérrez de Moya (entre 1569 y 1591). Aunque Antonio Aguilera era el titular de la plaza, no estaba presente en la Universidad en 1578. Había sido colegial del Colegio Mayor de Oviedo y tenía una larga experiencia profesional. El 3 de junio de 1534 había recibido el grado de licenciado en cánones y el 30 de abril de 1535 el nombramiento como profesor de una de las cursatorias de esa facultad, regentándola hasta el 26 de enero de 1538. En ese tiempo hizo el juramento para recibir el grado de doctor. Ese 26 de enero pasó a ocupar la cátedra de decreto que dejó vacante Martín de Azpilcueta; después (octubre de 1549) ganó la de prima de cánones, de la que se jubiló el 21 de junio de 1557. En el momento en que se realiza el informe sobre el calendario él es miembro del Consejo Real. Era un anciano y no pisaba por la Universidad. La vacatura de su cátedra por muerte se anunció el 19 de octubre de 1580.

El otro titular de la cátedra de prima, Cristóbal Gutiérrez de Moya, sí tenía docencia activa en abril de 1578. Había hecho el juramento para recibir el grado de licenciado el 28 de febrero de 1549 y en el curso 1554-1555 fue sustituto de la cátedra de sexto y clementinas del doctor Benavente; sustitución que abandonó el 28 de junio de 1557 para pasar a serlo de la cátedra de prima de cánones del doctor Aguilera. El 14 de marzo de 1558 ocupó una cursatoria de cánones, ya como doctor (hizo este juramento el 1 de noviembre de 1556). El 15 de enero de 1560 recibió la designación como catedrático de vísperas y el 21 de julio de 1569 para la de prima de cánones, de la que se jubiló el 29 de julio de 1579. El 5 de enero de 1591 se anunciaría la vacatura de su plaza por muerte. Estaba, pues, presente en el Estudio en abril de 1578.

El doctor Diego de Vera fue una pieza clave en el informe salmantino de 1578 y por eso hablaremos después de él. Ocupaba en aquellos momentos la cátedra de decreto (de 1563 a 1580). En función de esta titularidad fue nombrado comisario para el calendario.

En 1578 había asimismo dos cátedras de vísperas de cánones, en las que en trabajaban Miguel Acosta (entre 1566-1584) y Martín Salvador de Azpilcueta (entre 1569-1581). Miguel de Acosta había sido ya en 1557 sustituto en la clase de sexto y clementinas del doctor Benavente; de ella pasó el 30 de octubre de ese mismo año a una cursatoria de cánones, en la que enseñó hasta 1566. En ese tiempo recibió los grados de licenciado y doctor en cánones (juramento el 31 de agosto de 1562 y 2 de mayo de 1563 respectivamente). Desde el 24 de diciembre de 1566 hasta su muerte regentó la cátedra de vísperas, anunciándose la vacatura de su cátedra ante su muerte el 14 de enero de 1584.

Martín Salvador de Azpilcueta (al que no hay que confundir con el homónimo, llamado doctor Navarro) había ingresado en el Colegio Mayor de Oviedo hacia el 10 de febrero de 1563 y su primera docencia la realizó a partir de marzo de 1566 como sustituto de sexto y clementinas en la cátedra del doctor Castrillo. Muerto éste, Azpilcueta pasó a enseñar en una catedrilla de cánones (8 de marzo de 1567), más tarde en la sustitución del doctor Aguilera en la de prima de cánones (10 de enero de 1568) y, desde el 5 de agosto de 1569 hasta el 3 de enero de 1581 —período de la consulta—, fue catedrático de propiedad de vísperas de cánones. Incorporó a Salamanca su grado de doctor sacado en Coimbra; y después llegaría a ocupar la cátedra de decreto, hasta el 21 de marzo de 1583, en que se le proveyó una canonjía doctoral de la iglesia de Toledo.

Martín de Busto era en ese tiempo el catedrático de sexto y clementinas. Se había graduado de licenciado y de doctor jurando para la adquisición de estos grados los días 12 de mayo de 1559 y 2 de mayo de 1562, respectivamente. Desde 1562 fue el titular en una cursatoria de cánones; del 9 de mayo de 1574 hasta el 30 de abril de 1583 ocupó la cátedra citada de sexto y clementinas, desde la que pasó a la de decreto hasta su jubilación (21 de junio de 1593). Desempeñó después el oficio de oidor de la Chancillería de Valladolid hasta su muerte, en los primeros días del curso 1601-1602.

En la facultad de leyes, el segoviano Antonio de Solís era el catedrático de prima de leyes en 1578 (desde el 8 de mayo de 1565 hasta el 18 de noviembre de 1592, en que murió). Antes de ello, había hecho el juramento para recibir el grado de licenciado en leyes el 28 de enero de 1555 y para doctor el 11 de junio de 1559. En noviembre de ese año, fue nombrado catedrático de instituta y, poco después (en 1559) de código, docencia que regentó hasta el 27 de marzo de 1561, en que pasó a la de digesto viejo durante un cuadrienio. Aparece ya como jubilado en el curso 1583-1584 y murió el 18 de noviembre de 1592. Este profesor sería el encargado por el claustro para responder por carta al papa y al rey sobre la consulta, como representante de la Universidad.

Desde 1540 el lisboeta Héctor Rodríguez era doctor en leyes por la Universidad de Coimbra y había sido ya catedrático de prima de leyes en aquella academia cuando vino a oponerse a la de prima de leyes de Salamanca, tras la muerte del doctor Pinel. Era el titular de esta cátedra en el momento de la consulta sobre el calendario (lo fue desde el 23 de febrero de 1563 hasta 1579). Los días 29 de marzo y 7 de abril de ese mismo año practicó los juramentos para recibir el grado de licenciado e incorporar el de doctor antedicho. Su cátedra se anunció como vacante por muerte el 19 de octubre de 1579.

Una de las dos cátedras de vísperas de dicha facultad estaba regentada en 1578 por Juan de Andrada (desde 1561 hasta 1586), que previamente había sido catedrático de volumen (1553-1554) y de digesto viejo (1560-1561). La segunda la ocupaba el zamorano Diego Enríquez, que antes había hecho los juramentos para recibir los grados de licenciado y doctor en leyes el 21 de junio de 1557 y el 28 de abril de 1560 respectivamente. También había sido catedrático de código (en 1565) y de volumen (1569-1572), y ganó esta de vísperas de cánones el 6 de junio de 1572, regentándola hasta el 21 de marzo de 1584, en que tomó posesión de la de prima de leyes; en esta última enseñó hasta su muerte, unos días antes del 26 de agosto de 1605.

Por lo que se refiere a la facultad de teología, fray Bartolomé de Medina era en 1578 el catedrático de prima (lo fue de 1576 a 1581) y, como era de esperar, fue nombrado para formar parte de la comisión. Luego hablaré más de él.

En aquel momento el agustino fray Juan de Guevara ocupaba la cátedra de vísperas (de 1565 a 1600); la compatibilizó con la de Santo Tomás desde principios de 1556 hasta el 14 de enero de ese año que ganó la cátedra de teología nominal. Estando en ella hizo los juramentos para recibir los grados de licenciado y maestro en teología el 20 y 30 de junio de 1560 respectivamente. Pasó de la cátedra de nominales a la de vísperas de teología el 6 de marzo de 1565, quedándose en este puesto hasta su jubilación. Posteriormente fue provincial de Castilla dentro de su orden (1582). Murió el 23 de agosto de 1600.

Aunque el maestro Gregorio Gallo era el titular de la cátedra de Biblia durante la redacción del informe sobre el calendario, no estaba presente en ese momento en la Universidad de Salamanca: Se había jubilado de ella el 9 de julio de 1560, y, siendo obispo electo de Segovia, pasaba temporadas en la corte. Esta cátedra de Biblia se anunció como vacante por muerte el 19 de octubre de 1579. Previamente había completado un brillante currículo: En 1534 el bachiller Gallo se encargó de la lectura de la cátedra de vísperas de teología por enfermedad de fray Domingo de Soto; después, el 4 de enero de 1536, ocupó la de media multa de Biblia por ausencia del maestro Ortiz, hasta el 27 de marzo de 1538, en que tomó posesión de la cátedra cursatoria de Santo Tomás. Al poco tiempo, el 9 de agosto de ese mismo año se le encargó la de teología nominal (Gregorio Arimino). Entre tanto, el 28 de mayo de 1537 hizo el juramento para el grado de licenciado en teología; el grado de maestro lo ganó en junio de 1538. El 19 de octubre de 1540 obtuvo el nombramiento para la cátedra de Biblia. En 26 de enero de 1551 se le dio licencia para marchar al concilio de Trento en representación de la Universidad, estando de regreso el 1 de marzo de 1557. El curso siguiente lo pasó en la corte y fue nombrado maestrescuela de Salamanca (16 de diciembre de 1559). Murió siendo obispo de Segovia, el 25 de septiembre de 1578, causando la vacante en la cátedra de Biblia de Salamanca.

Fray Luis de León era el titular de un partido de teología, aunque durante la redacción del informe pasó a ocupar la cátedra de filosofía moral (el día 14 de agosto de 1578). También volveremos enseguida sobre él.

Dentro de esta misma facultad, la cátedra cursatoria de Escoto estaba adscrita al salmantino fray Pedro de Aragón (1576-82). Era licenciado y maestro en las facultades de teología y artes, tras los juramentos previos de 6 de febrero y 4 de marzo de 1576 para los grados de teología, y el 10 y 16 de enero de 1583 para los de artes. El 7 de noviembre de 1576 fue nombrado catedrático de Escoto, y en ello trabajó hasta el 13 de diciembre de 1582, fecha en la que pasó a la de prima de lógica hasta su muerte, el 24 de noviembre de 1592.

En 1578 ocupaba la cátedra de Santo Tomás el maestro Diego Rodríguez Lencina, que la mantuvo desde 1557 a 1594. La de teología nominal (llamada de Gregorio de Arimino o Durando) estuvo regida por fray Domingo Báñez desde el 23 de abril de 1577 hasta el 18 de febrero de 1581, que fue otro de los comisionados.

Los partidos más importantes de la facultad de medicina los regentaban Cosme de Medina, otro de los comisionados por el claustro para el informe sobre el calendario, y el lisboeta Ambrosio Núñez: éste ya era doctor en medicina cuando fue nombrado catedrático de Articela, el 7 de febrero de 1559, pasando en 1560 a la de Avicena y, por último, a la cátedra de vísperas de medicina, el 4 de diciembre de 1563. Se jubiló de ella en 1583, aunque no se dio por vaca su cátedra hasta su muerte, en 1611.

En 1578 también estaba en Salamanca uno de los más importantes representantes del humanismo médico y buen comentador de Hipócrates, el catedrático de medicina Juan Bravo. Había hecho el juramento para recibir el grado de licenciado en medicina el 18 de diciembre de 1553. El 30 de marzo de 1560 era ya catedrático de Articela y el 16 de noviembre de 1561 juró para la toma de grado de doctor; el 4 de diciembre de 1563 fue nombrado catedrático de la de Avicena; en 29 de abril de 1577, fue elevado a una cátedra de propiedad, sin especificar cuál, de la que se jubiló en el curso 1596-1597. Se dio por vacante por muerte el 27 de julio de 1610.

En cuanto al plantel docente la facultad de artes en torno a 1578, la cátedra de filosofía moral era regentada por Francisco Sancho (a veces llamado Sánchez), pero no enseñaba en ella, porque ya estaba jubilado. Había sido colegial de San Bartolomé desde 1534, y enseñó también en una de las cátedras cursatorias de artes, de 1530 a 1536. El 21 de diciembre de 1535 hizo el juramento para recibir el grado de licenciado en teología; de 1536 a 1540 ocupó la cátedra de Escoto y después pasó a la de teología nominal. Hacia finales de 1541 obtuvo la cátedra de lógica magna, en la que permaneció hasta el 10 de mayo de 1549, en que se le otorga la citada de filosofía moral. El 7 de febrero de 1542 juró para el grado de licenciado en artes y seguidamente, el 15 de ese mes, incorporó su grado de maestro en artes. Pasó a su condición de jubilado el 25 de junio de 1561 y después ejerció como canónigo de la Iglesia de Salamanca y obispo de Segorbe (en 1577).

También estaba jubilado en 1578 el titular de la cátedra de prima de lógica Enrique Hernández. Siendo bachiller, desempeño la docencia cursatoria de artes de 1526 a 1532 y la catedrilla de físicos de 1533 a 1535. El 29 de julio de ese año accedió a cátedra de filosofía natural, manteniéndose en esa titularidad hasta la vacatura por muerte en 2 de enero de 1585, aunque se había jubilado mucho antes.

La de súmulas (lógica) pertenecía en ese momento a Martín de Peralta (desde 1561 a 1579). Había obtenido el grado de maestro en artes en la Universidad de Zaragoza y en 1549 figura como catedrático de una de las cursatorias de artes. Hacia 1551 fue encargado de la de Escoto y la desempeñó hasta el 21 de enero de 1557, en que tomó posesión de la de Santo Tomás. El 15 de diciembre de 1561 pasó a la de prima de lógica y, el 22 de enero siguiente, incorporó su grado de maestro. Por muerte se publicó la vacatura de su cátedra el 11 de agosto de 1579.

Miguel Francés enseñaba temporalmente en la sustitución de la cátedra de filosofía natural del maestro Enrique Hernández cuando llegó la consulta sobre el calendario. En principio no fue nombrado para esta comisión probablemente debido a su precario contrato laboral con la salmantina, pero sería finalmente uno de los redactores del informe de 1578, por lo que después volveremos sobre él.

Fray Gaspar de Torres había sido profesor en una de las cursatorias de artes, de 1542 a 23 de octubre de 1548, en que fue nombrado catedrático de físicos. El 17 de junio de 1549 ocupó la plaza de lógica magna, hasta 1584, en que murió. Desde su jubilación en la Universidad fue obispo de Medauro y visitador general del arzobispado de Sevilla.

De 1578 a 1592 la cátedra de astrología-matemáticas estuvo sin proveerse en propiedad y se leyó por sustituto (Rodríguez San Pedro, 2002, I, p. 124), justamente cuando más se hubiera necesitado a un buen astrónomo para la redacción del informe sobre la reforma del calendario. Ya vimos antes que en tiempos de la visita de Covarrubias se habían sucedido en ella los hermanos Juan (desde 1551 a su muerte en 1561) y Hernando de Aguilera (desde 1561 hasta el 1 de julio de 1576, en que murió) (Navarro Brotóns, 1992a, p. 192), quedando después ocupada la plaza en media multa (medio salario, por falta de graduación del candidato) por Álvaro González de Talavera. No debió de explicar mucho en ella este profesor, por no vivir en Salamanca. Solicitó que se le diera el sueldo completo a pesar de no tener el preceptivo magisterio en artes y este tema se trató en el claustro de 15 de enero de 1577, decidiéndose en él consultarlo al Consejo Real, que se lo reconoció un mes después. En el tiempo que tardó en llegar esta concesión, González de Talavera no asistía con regularidad a sus clases y, a principios de enero, el rector le encargó esta docencia a Sánchez de las Brozas, en calidad de sustituto. En ella enseñó como pudo el Brocense hasta la vacatura de la plaza el 21 de mayo de 1578, así que trabajó en ella un año y unos cuatro meses, pero dice Esperabé que no la debía de desempeñar de buena gana, pues sólo aparece en esta sustitución del 2 al 4 de enero de 1578 y fue multado por no cumplir su cometido. A mí no me parece que se pueda decir eso de alguien que escribió y publicó un manual para los alumnos de la cátedra de astronomía en ese tiempo, pues su Sphera mundi salió en 1579. Por mandato del rector, explicó en ella 75 lecciones de la materia astronómica (Esperabé de Arteaga, 1917, II, p. 393).

Es decir, que el Brocense era el improvisado invitado de la enseñanza de astronomía-matemáticas cuando se recibió la solicitud del informe sobre la reforma del calendario, el 27 de abril de 1578. En el momento en que él la dejó, la Universidad comenzó los trámites que concluyeron en la venida a Salamanca de Jerónimo Muñoz, que por fin ocupó el partido de astrología, creado para él, el 10 de enero de 1579. Luego veremos más del tema.

Pues bien, de entre todos ellos, el claustro salmantino nombró para resolver esta demanda a cinco profesores: los doctores Diego de Vera y Cosme de Medina, y a los maestros fray Luis de León, fray Bartolomé de Medina y fray Domingo Báñez. Recordemos que los títulos de doctor y de maestro representaban el mismo nivel académico, el más alto, recibiendo distinto nombre en función de la especialidad del mismo.

Lo primero que llama la atención es que no haya matemáticos o astrónomos entre los designados, seguramente por la falta de titular en la cátedra de astrología-matemáticas. Ya es casualidad que las dos veces que el papa pidió a la salmantina ayuda en materia astronómica coincidiera la ausencia de los titulares de esa cátedra. Veamos quiénes eran los comisionados y en concepto de qué se les designó.

1. Diego de Vera (¿-1598) ocupaba en aquellos momentos en la cátedra de decreto (de 1563 a 1580). Los juramentos para la recepción de sus grados de licenciado y doctor en cánones están fechados el 13 de febrero de 1548 y el 25 de octubre de 1550 respectivamente. Desde 1554 y hasta el 19 de febrero de 1563 enseñó en una cursatoria (con una sustitución intermedia en 1560), siendo designado ese día para la regencia de la cátedra de decreto citada; de ella se jubiló en el curso 1583-1584. Fue simultáneamente canónigo doctoral de la Catedral de Salamanca. Su cátedra se anunció vacante el 13 de marzo de 1598 por su muerte. Escribió un Tractatus de carácter religioso. Esta figura ha atraído poco la atención de los investigadores. Se le eligió para la comisión como máximo representante del derecho canónico en Salamanca.

2. Cosme de Medina (1522-1591?) era en 1578 catedrático de prima de medicina. Tiempo atrás había sido el que estrenó en Salamanca la recién creada cátedra cursatoria de anatomía en 1551. Siguió encargado de ella hasta que en noviembre de 1561 le nombraron catedrático de vísperas de medicina. En 1562, siendo ya licenciado, hizo el juramento para recibir el grado de doctor. En 1563 accedió a la cátedra de prima, pero según el Registro de la antigua Notaría de la Universidad de Salamanca, de 1859, la que verdaderamente ocupó en 1563 fue la de vísperas de medicina, tras la muerte de Antonio Parra. No sé si es un error, porque en el claustro de 4 de junio de 1578, se le comisionó para buscar sustitutos en la cátedra de astronomía y allí se dice que era catedrático de prima de medicina. En una carta real de 1572 se autoriza a la Universidad para aumentar el salario que le pagaba como médico del hospital del Estudio, en cuya regencia continuó después de jubilarse de la docencia en junio de 1581: aún se hablaba de él en mayo de 1591 como médico del Hospital del Estudio. Adquirió una gran reputación como galeno (Santander Rodríguez, 1984). Pardo Tomás hace un estudio profundo de su biografía que nos permite saber que descubrió, junto a su alumno Collado, el hueso estribo del oído (Pardo Tomás, 2006, pp. 22-40). Los fondos de su biblioteca fueron estudiados por Teresa Santander Rodríguez (Salamanca: Universidad Pontificia de Salamanca, 1999) y contenían un alto grado de contemporaneidad. De ellos, trescientos volúmenes habían sido adquiridos en su periodo de docencia, entre 1551 y 1589 y, en la materia médica lo tenía casi todo, incluso las obras de Andrés Alcázar (1575), que le sustituiría en cirugía, y la de Agustín Vázquez (1589) que le sucedería en anatomía. Su persona es el mejor ejemplo de la revalorización de las artes médicas en el Renacimiento, pues logró encumbrarse como tal en la ciudad de Salamanca, para lo que quizá influyera la posesión de una pequeña fortuna que le permitió comprar varias casas y disfrutar de una vida cómoda. El claustro lo elige para la comisión por sus conocimientos en astrología y por la posesión de la cátedra que detentaba.

3. Fray Luis de León (1527-1591) era el titular de un partido de teología (1577-1578), aunque durante la redacción del informe sobre el calendario pasó a la de filosofía moral (el 14 de agosto de 1578 hasta 1579). Su trayectoria académica como profesor había comenzado con los juramentos para los grados de licenciado y maestro en teología, el 7 de mayo y 30 de junio de 1560 respectivamente. En 24 de diciembre de 1561 figuraba como encargado de la clase de Santo Tomás, continuando así hasta el 16 de marzo de 1565 en que accedió a la cátedra de teología nominal o Durando. Al expirar el cuadrienio vacó esta cátedra, pero el claustro se la otorgó nuevamente el 22 de marzo de 1569 y en ella estuvo hasta ser preso por la Inquisición, el 24 de marzo de 1572. Tras el proceso inquisitorial, el 2 de marzo de 1577 empezó á enseñar en un partido de teología, hasta el 14 de agosto de 1578, en que —como acabo de decir— fue nombrado catedrático de filosofía moral. El 25 de octubre de ese mismo año incorporó su grado de maestro en artes. En 7 de diciembre de 1579 le encargan de la cátedra de Biblia, nombramiento sobre el que se siguió proceso en la Chancillería de Valladolid entre fray Luis y fray Domingo de Guzmán. El pleito se sentenció a favor de fray Luis, desempeñándola hasta su muerte, en agosto de 1591. Se anunció la vacatura de la misma el día 26 de dicho mes y año. Su vida y su obra son muy conocidas. La bibliografía sobre fray Luis es numerosísima. Rafael Lazcano González publicó un elenco de estudios, junto a un cronograma completo de su vida en Fray Luis de León: bibliografía (2004, pp. 21-32). Yo he aludido aquí al antiguo trabajo de Alonso Getino (1907) porque este autor transcribió parte de las actas de claustro en las que intervino el agustino. Cabe destacar también los trabajos de José Barrientos (especialmente el editado en 1996) quien ha estudiado muy bien la relación del fraile con la Universidad de Salamanca. El grueso de las obras de fray Luis son textos de carácter teológico o jurídico, aunque son también de destacar sus poesías y epistolario. Directamente no escribió nada relacionado con el calendario o el cómputo litúrgico. Quizá su afición a la astrología determinó su nombramiento para esta comisión.

4. Fray Bartolomé de Medina: (?-1581) este dominico y filósofo escolástico creador del probabilismo era en aquel momento el catedrático de prima de teología (lo fue de 1576 a 1581). Se enfrentó a Juan de Guevara por una cátedra (ejecutoria del pleito, el 28 de enero de 1568) y a fray Luis de León por la sustitución de otra en las vacaciones del curso de 1565-1566, y sucedió a dicho fraile en la cátedra de Durando el 7 de abril de 1573, desempeñándola hasta que el 21 de agosto de 1576; en esa fecha se le dio la posesión de la cátedra de prima de teología. Ya para entonces había recibido los grados de licenciado y maestro en teología, pues hizo los juramentos previos el 30 de enero y 22 de febrero de 1570. Por muerte del maestro se declaró vacante la cátedra de prima el 2 de enero de 1581. Ramón Vecino Merillas hizo una semblanza del dominico en 1997, dentro del libro La filosofía española en Castilla y León: de los orígenes al Siglo de Oro; antes se había hecho otra en la Historia de la filosofía española: Época del renacimiento. (Siglo XVI), Madrid: Real Academia de Ciencias Exactas, Físicas y Naturales, 1941, pp. 151 ss.; también se ha estudiado prolijamente su contribución a la moral económica dentro de la Escuela de Salamanca por parte de Jesús Canto del Cerro (2001); y abunda la información bibliográfica sobre su enfrentamiento y denuncia a fray Luis en el proceso inquisitorial. Se le nombró comisionado para el tema de la reforma del calendario porque, ante una consulta de Roma, el nombramiento del catedrático de prima de teología parece obligado.

5. Fray Domingo Báñez (1528-1604) es reconocido como uno de los grandes maestros de la Escuela de Salamanca. Recibió el encargo sobre el calendario siendo catedrático de de teología nominal (Gregorio de Arimino o Durando), en la que ejerció desde 23 de abril de 1577 hasta el 18 de febrero de 1581; ese día pasó a ser catedrático de prima de teología. Mientras era catedrático de Durando realizó los juramentos para la adquisición de los grados de licenciado y maestro en teología, el 21 de junio y el 7 de julio de 1577 respectivamente. Una real cédula de 4 de marzo de 1591 comunicó a la Universidad su nombramiento para otra comisión encargada por Felipe II. Se jubiló en el curso 1601-1602 y murió el 22 de octubre de 1604. Báñez publicó muchos trabajos a lo largo de su vida, especialmente sobre filosofía, moral y derecho: De fide, spe & charitate catholico Regi Philippo II... Scholastica commentaria in Secundam Secundae Angelici... (Salamanca: 1584); Serenissimo Principi Philippo III... De iure & iustitia decisiones... (Salamanca: 1594); Institutiones minoris Dialecticae... (Salamanca: 1599); Commentaria et quaestiones in duos Aristotelis... (Salamanca: 1585); ...Super primam partem diui Thomae... (Salamanca: 1588);... Decisiones de Iure & Iustitia... (Salamanca: 1995);... algunas con bastantes reediciones. A su vez se ha escribo mucho sobre la filosofía y la teología de Báñez[58]. Su designación como comisionado para la reforma del calendario derivó también de su peso intelectual en la Universidad y de la titularidad en la cátedra de teología nominal que poseía en ese momento.

He resumido los resúmenes de los currículos académicos de los profesores comisionados para que se adquiera perspectiva de la dificultad que podía entrañar para ellos una consulta como la del calendario. Los designados habrían recibido una preparación en materias astronómicas como parte de su formación académica previa, cuando eran estudiantes; pero era ésta una formación lejana y superficial. Un canonista, tres teólogos y un médico; ningún matemático. Bien es verdad que la entonces llamada astrología se consideraba un conocimiento imprescindible para el ejercicio de la medicina, y la comisión contaba con el médico Cosme de Medina; también sabemos que fray Luis estuvo muy interesado en ella, pero la consulta papal requería de una especialización y de un dominio en las matemáticas que en principio ninguno tenía. La formación académica y el día a día de su docencia estaban alejados de los conocimientos necesarios para redactar el informe solicitado. Todos los comisionados disfrutaban de enorme peso institucional en el Estudio y de un gran respeto académico en sus respectivas especialidades, pero no eran expertos en astronomía y matemáticas. Por eso, aún presuponiéndoseles la mejor de sus voluntades, como se apreció repetidamente en Vera a través de las actas de claustros, no podían resolver el reto sin ayuda.

Una de las cosas que más llama la atención es el nombramiento conjunto para esta comisión de fray Luis de León y fray Bartolomé de Medina, que eran enemigos reconocidos. Las manifestaciones de los testigos del proceso inquisitorial de fray Luis y sus mismas declaraciones son clarísimas al respecto (Continuación del proceso de fray Luis de León. CODOIN. Madrid: Imprenta de la viuda de Calero, 1847). Por ejemplo, el testigo Francisco de Almansa, a la pregunta 16 respondió:

...queste testigo por cosa pública oyó tratar en esta dicha ciudad entre estudiantes y otras gentes, quentre los dichos maestros Medina y fray Luis de León había malas voluntades sobre las pendencias de sus cátedras y que en conclusión había habido palabras entre ambos descometidas... porque había entrellos enemistad muy formada (p. 315).

Los testigos fray Juan de Guevara, fray Francisco de Figueroa, fray Diego López y don Pedro Portocarrero declararon

que los años pasados el dicho fray Bartolomé de Medina... pretendía leer las substituciones por el maestro Mancio; y que el dicho fray Luis de León no las obtase, y le puso pleito sobre ello y lo venció en corte y trujo provisión sobre ello, y así las leyó siempre y le quitó que no las leyese, lo cual él sintió mucho (p. 259).

En similar sentido respondió el secretario de la Universidad, Andrés de Guadalajara (p. 322), todo lo cual corroboran las declaraciones y alegaciones de fray Luis (de 4 de agosto de 1574, p. 22), acusando a Bartolomé de Medina de manifiesta malicia y de falso testimonio (p. 41), por ser fray Luis el mayor impedimento que tiene en sus pretensiones de cátedras (p. 42). Razón no debía faltarle al agustino, porque en abril de 1573, Medina había aprovechado la finalización del cuadrienio de la cátedra de Durando en la que enseñaba fray Luis antes de ser procesado y la reclamó; y en él se proveyó el 7 de abril. A la vuelta de la cárcel inquisitorial, cuando fue exculpado de sus cargos, fray Luis reclamó todo el salario de la misma (Vida de fray Luis de León, de J. González Tejada. Madrid: 1863, pp. 44-45). Mal podían trabajar juntos, según creo.

En el claustro que se les nombró comisarios para la reforma del calendario, a renglón seguido, se les ofreció la opción de llamar a cuantos expertos consideraran capaces de ayudarles. En el mismo claustro se repartió entre los comisionados el material de debate enviado por Roma (la impresión hecha por Pedro Chacón en Roma del Compendium de Lilio, que no he encontrado en la BGH) correspondiéndoles sendos ejemplares a Diego de Vera y al maestro Guevara, maestrescuela de la Universidad.

Del mismo modo, se encargó al catedrático de prima de leyes, Antonio de Solís, la redacción de las respuestas con el acuse de recibo para el rey y para el papa. Este hecho sugiere el deseo del claustro de implicar en el asunto a los más importantes profesores de cada facultad; señal —según pienso— de la importancia que la Universidad otorgaba a la consulta.

La importancia citada se aprecia también en la actitud de los claustrales de no escatimar esfuerzos ni dineros en orden a cumplir adecuadamente con el reto. No debemos olvidar que se trataba de algo verdaderamente excepcional para la época. No era frecuente una consulta dirigida a una Universidad en la que se conjugara una petición procedente al mismo tiempo de las autoridades civil y eclesiástica. Además no se había preguntado de forma generalizada a todas las universidades de la cristiandad, sino sólo a algunas, que presumiblemente eran las más prestigiosas. En España, a Salamanca y a Alcalá. El orgullo gremial coincidió en este caso con una época de relativa bonanza económica, según se desprende del análisis financiero de la Universidad realizado por Martín Lamouroux, (1990, p. 417, gráfico; Ídem, 1988); y ambas circunstancias se reflejaron en el encargo concreto que se hace a estos comisionados en ese mismo claustro:

...que se junten y, conforme a la cédula de Su Majestad y breve de Su Santidad, vean el calendario y entre sí lo traten y comuniquen, y visto y mirado y platicado, vean los convenientes o inconvenientes que en él hay o puede haber, y si fuere necesario llamar y juntar consigo alguna o algunas personas peritas en el arte de Matemáticas de este dicha Universidad, las llamen y junten consigo para tratar el dicho negocio; y si les pareciere que conviene llamar y traer persona alguna de fuera para el dicho efecto, den de ello relación a la universidad, para que provea en ello...

La alusión explicita a las matemáticas de esta encomienda da cuenta de que los claustrales habían captado el fondo del problema, pero el entusiasmo inicial se tornó pronto en zozobra entre los comisionados, porque el asunto era más complicado de lo que en principio quizá habían podido sospechar. En esta apreciación coincidieron todos los que trabajaron en aquellos tiempos para la reforma gregoriana, incluso Juanelo Turriano, que llegó a escribir en su propio informe:

Equilibrar el movimiento de los cuerpos celestes o la situación de las órbitas... con la paciencia de la computación, es en verdad un trabajo de Hércules o una obra de Atlas (Turriano, 1990, p. 21).

Aunque la comisión solicitó la opinión de sus colegas docentes en principio no designados para este trabajo, pronto se llegó al consenso de la necesidad de ayuda científica externa al Estudio. Con este convencimiento acudió el doctor Vera al claustro de diputados celebrado el día 31 de mayo de 1578, donde expuso estos argumentos y, sin ningún tipo de contradicción, todos los asistentes consintieron en contratar a una persona docta en astrología. Antes se había hablado de matemáticas; ahora se hablaba de astrología: parece como si antes estuvieran pensando en expertos adecuados al carácter del problema (un problema matemático) y ahora deliberaran sobre la denominación de la plaza que debería ocupar el presunto experto (cátedra de astronomía).

Como había ocurrido en otras circunstancias precedentes, no se debían escatimar dineros en cuestiones de las que dependía el prestigio del Estudio. Igual que en 1508 la Universidad formó una junta de nominales con el objetivo de implantar la enseñanza de esta nueva doctrina filosófica en Salamanca y se mandó a buscar expertos a Alcalá, Zaragoza y París; o de forma similar a como se intentó contratar a Juanelo Turriano en 1559, ahora se empezó a pensar en traer a un experto de donde hiciera falta.

Para concretar este trámite, la Universidad volvió a tratar el tema en el claustro pleno del día 4 de junio de 1578 en el que, primero se dio lectura a una carta del nuncio en la que agradecía la enviada por Solís comprometiéndose en nombre de la Academia a resolver el encargo; después se retoma la acuciante necesidad de especialistas concretos. El rector, licenciado Juan de Arana, recordó allí que se encontraba vacante la cátedra de astrología porque, a su parecer,

...hay muy pocas o casi ninguna [personas] en quien se pueda proveer, por haber pocas personas entregadas a las Matemáticas.

Es decir, que se ratificó el consenso entre los reunidos de la necesidad de ayuda experta y específica, que en ese momento no se tenía por estar vacante la citada cátedra. Ante esta eventualidad y la necesidad ya irrenunciable de otorgar un veredicto sobre la reforma del calendario, el rector era de la opinión de que se prorrogaran los edictos para la presentación de opositores a ella y que se incentivara a los posibles candidatos con un incremento salarial de 400 ducados. Sin duda se estaba produciendo la inflación de las matemáticas de la que he hablado. El objetivo, según allí se dijo, era el atraer personal de otras universidades. Con el fin de evitar estas carencias en el futuro, se propuso también la conveniencia de instituir una catedrilla menor, de quince a veinte mil maravedíes de salario, para que se fuera formando en ella algún matemático, atendiendo a que de ellos había grandísima necesidad.

La singularidad de la solicitud papal justifica el sostenido debate que el tema provocó entre los claustrales. El maestrescuela apoyaba la opinión del rector, en el sentido de la conveniencia de crear una catedrilla, en la que se fueran formando los futuros profesores, aunque aconsejaba que, dada la excepcionalidad, el aumento de salario de la cátedra principal se hiciera mediante una resolución real. ¿Qué quería decir con esta puntualización? Quizá que el incremento del gasto de la universidad por esta causa pudiera reclamársele al monarca, que lo estaba generando.

Todos iban votando a favor de esta propuesta rectoral hasta llegar a fray Bartolomé de Medina, quien aludió primero a la constitución universitaria, recordando que ella prohibía explícitamente la prórroga de los edictos para las plazas de profesor. Curiosamente olvidaba al punto estos escrúpulos defendiendo, que la provisión de la cátedra se hiciera por el claustro y no por votos de estudiantes —lo cual iba también contra derecho—, atenta la urgencia y necesidad de esta dotación, según decía; subrayando finalmente que el aumento del salario a 400 ducados le parecía muy excesivo.

Parte del malestar, la suspicacia y la protesta velada en el ambiente derivaba del hecho de que tradicionalmente las cátedras de las facultades llamadas «menores», sobre todo de artes y medicina, recibían entre un cincuenta y un setenta por ciento menos de salario que las equivalentes en las facultades mayores (leyes, cánones y teología). Al ser Bartolomé de Medina catedrático de teología, es comprensible que le resultara discriminatorio el que se aplicara al futuro nuevo catedrático de astrología (de la facultad de artes y de un nivel económico y científico teóricamente inferior al suyo) un salario equiparable al de los catedráticos de las facultades mayores, que era el que él disfrutaba.

La variedad económica entre los salarios de unas facultades y otras fue algo constitutivo de las universidades. De hecho, Alfonso X el Sabio, en su carta magna a la salmantina del año 1254 establecía esta diferencia en la siguiente proporción: Mientras que la cátedra de leyes tenía asignados 500 maravedíes anuales, las de decretos se pagaban a 300, las de lógica, gramática y doctor a 200 y la de órgano a 50 maravedíes (Carabias Torres 1986b, p. 324). Esta distancia se mantiene y agranda en 1401, según el libro de Tercias de la Universidad. En esa época: las cátedras de prima de cánones y leyes tenían asignados 7.250 maravedíes viejos, mientras que el catedrático de prima de medicina cobraba 2.200, el de vísperas de medicina 1.400; y los profesores de gramática, lógica y filosofía natural, 2.000 maravedíes viejos (Beltrán de Heredia, 1970b, p. 219). Esto no era privativo de Salamanca, pues en la de Zaragoza, en el año 1583, mientras que los titulares de teología, cánones y leyes de la primera cátedra (había establecidos cuatro grupos) cobraban 50 libras anuales, los de medicina, artes, retórica y gramática, sólo percibían 25 libras anuales (Cfr. Carabias Torres, 1986b, p. 325).

Pero la solución pasaba por la colaboración de un verdadero experto; por eso, inmediatamente después, en ese mismo claustro se empezó a debatir el tema de la cátedra de astrología, en la que tantas esperanzas habían depositado los comisionados. El calado científico de la reforma del calendario era muy hondo pero los candidatos que se presentaron a la vacante tras la marcha de el Brocense no lo eran tanto. Ante la falta de candidatos idóneos, el claustro celebrado el 4 de junio decidió prorrogar la convocatoria y buscar persona competente para regentarla, dado que a ella sólo se había presentado hasta entonces un estudiante salmantino, mancebo de poca edad, cuya inexperiencia en nada podía ayudar a resolver el problema.

Hacía falta —decían— un verdadero experto... acerca del compendio en que se trata de la reducción del año verdadera y reformación del calendario.

El doctor Medina explicó que había comunicado esta oferta laboral al doctor Jerónimo Muñoz, que estaba en Valencia, por ser uno de los mejores especialistas del reino. Diego de Vera, por su parte, manifiesta haber escrito a Sevilla al obispo D. Gaspar de Torres, con el ruego de que se informase de quiénes había allí hábiles en estas materias, habiendo respondido éste que en la Casa de Contratación había uno muy principal en astrología y matemáticas, llamado Rodrigo Zamorano, que era el encargado de examinar a todos los pilotos de las flotas de las Indias. Tanto Medina como Vera consideraban a ambos candidatos competentes en el tema y dispuestos a venir a Salamanca por un salario razonable. La importancia histórica de estos dos personajes justifica que este acta del claustro fuera publicada por Beltrán de Heredia (1972a, IV, pp. 320-323). En cambio Alonso Getino, centrado en la figura de fray Luis, transcribió con algunos errores que a veces atañen al sentido de los textos las sesiones de claustros universitarios en las que el fraile intervenía, dejando al margen estas otras, relativas a la dotación de la cátedra de astrología, cuya importancia él no relacionó con aquel problema.

Desde la perspectiva histórica actual, no cabe la menor duda de que Jerónimo Muñoz y Rodrigo Zamorano eran competentes; probablemente no existían entonces en España muchos científicos más preparados que ellos. Zamorano (1542-1623) estaba efectivamente ligado laboralmente a la Casa de Contratación, de la que sería más tarde piloto mayor (del 13 de abril de 1586 al 24 de julio de 1620), cosmógrafo oficial y colaborador en la reforma del Padrón Real. Aparte de ser autor de su conocidísimo Compendio de la arte de navegar, de Rodrigo Çamorano... (Sevilla: 1581), también era un reputado matemático, como se aprecia en Los seis libros primeros de la geometria de Euclides... (Sevilla: 1576), o en su Cronologia y reportorio [sic] de la razon de los tiempos (Sevilla: 1594), libro en el que dio a conocer una fórmula inventada por él para la averiguación del domingo de Resurrección a través de los dedos de la mano izquierda (algo parecido a lo que había diseñado Francisco Salinas, según veremos) y calculó los treinta y tres eclipses que habían de verificarse entre 1584 y 1606 —que resultó a la postre bastante complejo en su uso—, publicando las láminas de las vistas de todos ellos en función del meridiano de Sevilla y detallando la hora de los eclipses para las principales ciudades de Europa y América. Toda una proeza para la época.

El segundo candidato, Muñoz (1520-1591), nació en Valencia, en cuya Universidad estudió artes, graduándose de bachiller en 1537. Después, viajó por Europa para completar su formación, trabajando en actividades cartográficas. En sus manuscritos se declara discípulo de Oronce Finé y de Gemma Frisius, lo que indica que debió de residir en París y en Lovaina. Ocupó durante algunos años la cátedra de hebreo de la Universidad de Ancona y, antes de 1556, volvió a Valencia, donde ejerció de catedrático de hebreo y matemáticas entre 1563 y 1578 (Navarro Brotóns, 1992a, p. 193). De su obra cabe subrayar la observación del cometa que apareció el 11 de noviembre de 1572 en la constelación de Casiopea, publicando sus revolucionarias conclusiones antes que cualquier otro astrónomo en el Libro del nueuo cometa y del lugar donde se haze[n] y como se vera por las Parallaxes quan lexos estan de tierra y del prognostico deste (Valencia: 1573): O su Suma del pronostico del Cometa y de la Eclipse de la Luna... (Valencia: 1578)[59].

En el claustro se votaron estas propuestas y, cuando la mayoría se inclinaba por la opinión del maestrescuela sobre la opción de Jerónimo Muñoz, ofertándole 400 ducados por encima del salario que la cátedra tenía fijado, los maestros fray Luis de León y Guevara interponen una reflexión ética, aludiendo al agravio que esta decisión podía suponer para el único opositor que se había presentado y para la normativa estatutaria que desautorizaba una decisión de estas características. Pero de nada les sirvió, pues la mayoría (diecinueve en total) votaron a favor de que los edictos de la cátedra siguieran prorrogándose para poder buscar a persona capacitada; que se fijara el salario en la cantidad sobredicha y se solicitara la confirmación de estos acuerdos al rey. Requieren asimismo información de la suficiencia de Muñoz y acuerdan que se le propusiera un contrato de cuatro años por la cantidad antedicha, más otros treinta ducados para ayuda de la mudanza; si Muñoz no aceptaba, se buscaría a otro. Ante esta resolución tan contraria a derecho, un pequeño grupo de claustrales encabezados por Luis de León, Guevara y Arévalo Sedeño, no ratificaron el acuerdo. Lamentablemente para los comisionados, cuando quiso resolverse la dotación de la cátedra y Jerónimo Muñoz se presentó en Salamanca, ya corría el 10 de enero de 1579 (AUSA, 48, f. 16v.; Beltrán de Heredia, 1972a, IV, p. 324) de forma que no pudo ayudar al trabajo del calendario para el que en principio se pensó contratarle, y que originó el debate sobre su contratación.

La materialización de estos acuerdos llevaba tiempo y el retraso natural de la dotación de esta cátedra, por cuestiones procedimentales, iba en perjuicio de la comisión encargada del informe sobre el calendario que necesitaba ayuda urgente. A través de sus propias palabras sabemos que los comisionados continuaban trabajando intensamente en el proyecto, pero la conclusión se retrasaba, y a la Universidad siguieron llegando recordatorios sobre la urgencia del negocio, tanto por parte del nuncio, como por parte de Felipe II, que escribió de nuevo, diciendo:

...Aunque creo que en cumplimiento del breve de Su Santidad sobre lo que toca al calendario y lo que en aquel propósito nos ha escrito iréis entendiendo en ello con la atención, cuidado y diligencia que se requiere, deseo tanto que se pueda responder a Su Beatitud con brevedad, así por lo que conviene como por la instancia que de su parte se hace que por todo esto me ha parecido tornaros a encargar, como lo hacemos, que procuréis en ello toda la que sea posible y de manera que si lo fuere concluirse de aquí a las vacaciones se haga, que en ello me haréis mucho placer y servicio... (AUSA, 47, f. 89r.).

Estos apremios provocaron la explicación verbal del doctor Vera en el claustro pleno del día 2 de julio de 1578, en forma de autodefensa, que decía que:

…en el dicho negocio del calendario no había ningún descuido y se habían hecho ciertas juntas de personas que entendían en ello, y de fuera asimismo habían hecho venir al cura de Gatón, que es astrólogo y muy entendido en el arte. Y que en efecto estaba acordado que para el primer día de agosto se volviesen a juntar y cada uno trajese allí el parecer que acerca de ello tenían (claustro pleno de 22 de julio de 1578; doc. 1.629 del Cartulario..., II, de Beltrán de Heredia).

Un cura de Gatón de Campos, un pueblecito de Valladolid, tan entendido en el arte como para que fuera invitado por los científicos a participar en los debates... A través de fuentes indirectas sabemos que se trata de Juan Galván, un hombre culto, sin duda, que solía frecuentar la tertulia científica que reunía doña Cecilia de Morille en su casa de Valladolid, a la que asistía también el licenciado Andrés García de Céspedes, según los datos proporcionados por uno de los hijos de esta humanista, que escribió la «Relación de cosas memorables de la vida y muerte del señor D. Francisco Sobrino, obispo de Valladolid, y de sus padres y hermanos. Dedicada al mismo señor obispo por F. Diego de San Joseph, su hermano carmelita descalço» (Biblioteca de la Catedral de Valladolid, Ms. 98, f. 14r.). Si no hubiera sido por la colaboración de don Jonás Castro Toledo, archivero del Archivo de la Catedral de Valladolid, que me ayudó hace ya más de trece años en esta búsqueda, no hubiera podido matizar ni el nombre del cura ni esta información.

El ambiente cultural de la casa de la señora Morille, según la citada «Relación...» era tan excepcional como ella misma. Una salmantina que había estudiado con su padre las materias equivalentes a la facultad de artes y que se las enseñó a sus hijos; aparte de tener una apreciable habilidad para las manualidades, que la hizo famosa, tanto por las flores en papel que confeccionaba y regaló a Felipe II (acabando en El Escorial), como por el globo terráqueo que bordó sobre una esfera de corcho; o por los títulos universitarios que preparaba para ser después expedidos por la Universidad de Valladolid, en la que su esposo trabajaba.

El problema fue que, aunque Juan Galván —el cura de Gatón— fuera tan culto, sus conocimientos astronómicos resultaron científicamente irrelevantes para la hondura del problema científico de la reforma del calendario. Esta incapacidad que enseguida mostró devino en el olvido inmediato de este personaje por parte de los comisionados. Así lo juzgo yo y así se desprende del silencio sobre este personaje de Nicolás Antonio, Picatoste, Palau y Dulcet, Vindel y otros. Pero el hecho de haber sido requerido por la Universidad de Salamanca para colaborar en este asunto, sugiere, tanto la fama de Galván como astrólogo, como la profunda preocupación, rayana con la desesperación, de la comisión nombrada por el claustro salmantino, que acude a cualquiera que pudiera ayudarles a elaborar la respuesta.

El portavoz de la comisión en el claustro pleno de 22 de julio de 1578, el doctor Vera, volvió a justificar la tardanza diciendo que

...el negocio no era tan liviano y que era menester consultarlo e mirarlo con gran atención y cuidado.

Ya que la comisión era la única culpable del retraso, se encargó al propio Vera (no a Solís, como antes) la respuesta al papa, al rey y al nuncio, explicándoles los problemas que estaban ocasionando esta dilación.

En esos meses avanzó el tema de la dotación de la cátedra, pero no así el del informe. Una nueva carta del nuncio de 16 de agosto de 1578 recordando la premura fue leída en el claustro del día 20. Allí presente Diego de Vera, argumentó que la comisión se había

...juntado muchas veces a tratarlo, y que el tema requiere mucho más tiempo del que se les ha dado y da, a pesar de lo cual... tiene ya hecha la respuesta que se les pide, la cual se está sacando en limpio y se traerá a claustro dentro de dos o tres días, para que la universidad lo vea e provea acerca de ello lo que más viere que conviene.

Así lo comunica, pero no era verdad, pues los dos o tres días se dilataron en la práctica hasta casi los dos meses, aunque el esperado anuncio consiguió ilusionar a todos, incluso al nuncio Felipe Sega (Fernández Collado, 1991), que el 23 de agosto escribió al cardenal de Como, en Roma, comunicándole que ya tenía en su poder el informe emitido por la Universidad de Alcalá y que había recibido desde Salamanca una carta en la que se anunciaba el próximo envío del estudio realizado por sus profesores. A fin de cuentas Salamanca no era la última, pues todos se hacían eco del retraso de Juanelo Turriano en este asunto.

Felipe II dio una especie de ultimátum a Salamanca el día 11 de octubre: debían enviar el informe sin mayor dilación, tanto al papa como a él mismo. Este dirigismo político de rey estaba relacionado con el interés personal del monarca por la ciencia y el coleccionismo astronómico. En el propio Monasterio de El Escorial construyó en el suelo de una de las salas una especie de reloj de sol que indica el momento en que el astro rey pasa por el meridiano local a las doce horas del equinoccio. Como dice Isabel Moran, la afición por la astronomía del Rey Prudente va a manifestarse en cuatro vertientes: decorativa, bibliográfica, coleccionista y de pura investigación (Morán Suárez 1993, p. 503). Fue un coleccionismo de investigación, el de un rey entusiasta con todas las ciencias y patrono de científicos (Goodman, 1999, pp. 91-112). Conocimiento —como dice R[odríguez] de la Flor (1996, p. 92)— que no estuvo ajeno al sometimiento y al control, administrado por unas instituciones siempre vigilantes, prohibido o alentado también por unas leyes explícitas o implícitas.

El día 19 se anuncia este ultimátum en el claustro y Vera, notoriamente apurado, se defendió diciendo

...que tenía todo el cuidado posible en el despacho y expedición de la respuesta, e que ya la tenía casi acabada para la presentar en el claustro... e que en ello había trabajado todo lo posible en estas vacaciones.

Por fin, lo que Turriano apodara como la obra de Atlas, esto es, la respuesta al papa y al rey sobre el calendario, estuvo terminada y el contenido del manuscrito que aquí estudio fue elevado a la consideración de la Universidad: en latín se leyó en este dicho claustro el día 23 de octubre. No me parece aventurado imaginar la absoluta incomprensibilidad que tenía, para la mayor parte de los claustrales un texto de estas características: un documento tan largo, de temática tan abstrusa, tan alejado del tipo de conocimientos que conformaban los programas docentes, incluso de la propia facultad de artes, leído en latín, después de la comida del medio día... Ante la perplejidad por lo oído, que cada claustral debió interpretar para sus adentros como consecuencia de su particular e inconfesable ignorancia, impresionados por las conocidas fatigas de los comisionados y sus muchas consultas, creo entender la escueta sentencia con la que tranquilizaron el desasosiego de Vera frente a compañeros y demás autoridades, diciendo:

E por los señores del dicho claustro oída y entendida, dijeron estar muy bien hecha.

Y en el fondo no les faltaba razón en el juicio emitido, pues el informe otorgaba una solución computacional razonable; pero no exactamente el que había firmado Vera, sino el que Vera y los otros incluyeron dentro del suyo, realizado anteriormente por sus compañeros del año 1515. Después volveré sobre el tema.

Deciden enviar el documento a las autoridades solicitantes y piden

...que de la dicha respuesta quede traslado, el cual se ponga en el archivo de esta universidad.

Una de estas copias es muy probablemente el actual manuscrito 97 de la BGH que aquí estamos analizando. El claustro salmantino lo remitió al papa a principios de noviembre. Se ha publicado que el claustro remitió el informe al papa el 21 de octubre de 1578, y al rey el día 28 de ese mismo mes. Sin embargo, en el propio manuscrito se dice:

Este trasunto saqué yo, Juan Bautista de la Canal, notario vecino de la ciudad de Salamanca, el cual concuerda con otro del mismo tenor que la Universidad de Salamanca envió a Su Majestad y a Su Santidad por principio del mes de noviembre de 1578 (BGH ms. 97, f. 35v.).

Este retraso lo corrobora el hecho de que en el propio claustro pleno celebrado el 14 de noviembre se leyera otra carta del nuncio, datada el pasado día 6, en la que nuevamente se apremiaba la respuesta; puesto que entre las resoluciones del mismo claustro se deja de lado este asunto, es de suponer que el documento ya se hubiera mandado.

Como es natural, la comisión salmantina no cejó en el empeño de ofrecen el mejor informe que pudo; pero ¿quién o quienes lo redactaron realmente? Con afinada crítica reflexionaba Getino (1907, p. 249, nota) sobre la circunstancia de que las firmas que aparecen al final del texto son todas de mano del notario, apoyando la idea de que el maestrescuela y los demás profesores que figuran no tenían que ser necesariamente los verdaderos autores del texto, sino representantes de la Escuela ante el pontífice. Las firmas que transcribe el notario en su copia testifical son la del maestrescuela Guevara y los doctores Cristóbal Arias, Diego de Vera y Antonio de Solís. Es evidente que lo firman como representantes de la Universidad ante la Santa Sede y el Estado: Cristóbal Arias no había sido nombrado en los debates: era el síndico o gestor económico de la Universidad de Salamanca, que previamente había sido catedrático de volumen entre 1557 y 1564 (Barrientos García, 1996, p. 799). Los otros dos, ya conocidos, eran respectivamente catedráticos de decreto y de prima de leyes.

¿Quiénes fueron los autores? En teoría, al menos, los comisarios nombrados en su día al efecto; es decir los doctores Diego de Vera y Cosme de Medina, más los maestros fray Luis de León, fray Bartolomé de Medina y fray Domingo Báñez. Sin ningún género de dudas, todos ellos trabajaron en la respuesta (no me explico cómo saldaron sus diferencias León y Medina). Sin embargo, la autoría intelectual de su contenido científico no debió ser toda suya, porque ninguno de ellos tenía en aquel momento, ni tuvo después, demostración de conocimientos matemáticos suficientes para realizarla.

Me inclino a pensar que los verdaderos artífices fueron aquellos otros que, concluido el proceso, Diego de Vera propone como dignos de gratificación ante el claustro de la Universidad por el tiempo y el esfuerzo volcados en el asunto, cuyos nombres no habían salido a relucir antes en ninguno de los debates universitarios. Concretamente fray Francisco Alcocer, el licenciado Gabriel Gómez, y el maestro Miguel Francés. Ante la petición de Vera, el claustro determinó:

Iten se proveyó e mandó que, atento que algunos comisarios, como es el dicho doctor D. Diego de Vera y el padre Alcocer y maestro Francés, catedrático de sustitución de filosofía moral, el cual trabajando en la dicha obra enfermó reciamente, y el licenciado Grabriel Gómez, médico, y otros señores que han trabajado mucho con gran cuidado y asistencia, y perdiendo de sus casas por las muchas congregaciones, juntas y conferencias que en lo susodicho ha habido, la dicha universidad y claustro proveyó y mandó que el dicho señor doctor Diego de Vera tantee y mire con diligencia lo que se debe hacer con cada una de las dichas personas... y en el primer claustro dé su parecer para que la universidad provea y mande se remunere.

1. Fray Francisco de Alcocer era un franciscano de la provincia de Santiago, residente en el Colegio de San Francisco de Salamanca, que no era profesor de la Universidad y cuya trayectoria intelectual la había desarrollado alrededor de las ciencias sacras. He encontrado pocos datos sobre él y no me ha sido posible leer el texto de A. López titulado precisamente «Fr. Francisco de Alcocer» (en: El Eco Franciscano, Nº 33, 1916, pp. 104-107). Tenía entonces publicados tres libros de gran difusión y del gusto de la época, para ayuda de confesores:

• El Tratado del Juego, compuesto por fray Francisco de Alcoçer, de la orden del bienaventurado Sant Francisco, de la Provincia de Santiago, de la observancia, en el qual se trata copiosamente, quando los jugadores pecan y son obligados a restituyr assí de derecho divino como de derecho común, y del Reyno, y de las apuestas, suertes, torneos, justas, juegos de cañas, toros y truhanes, con otras cosas provechosas y dignas de saber (Salamanca: Andrea Portonaris, 1559, tuvo otras ediciones posteriores).
• Reglas de rezar el officio diuino, y como se ha de dezir la missa: segun la sancta yglesia romana, como lo rezan y dizen los frayles menores compuestas por fray Francisco de Alcocer... Salamanca: en casa de Iuan de Canoua, 1566.
• Confesionario breve y muy provechoso para los penitentes. Compuesto por fray Francisco de Alcocer, de la Orden de los Frayles menores de la Observancia de la Provincia de Santiago. En el qual, con toda brevedad y claridad se ponen todos los pecados ordinarios y comunes a ta [sic] dos..., Salamanca: Juan de Canova, 1568, fue reeditado también en Salamanca: 1572; Salamanca: 1587; Córdoba: 1592; Madrid, 1592; Barcelona: 1594; Madrid: 1598; Barcelona: 1994; Barcelona: 1615[60].

José Barrientos piensa que se le eligió en función de las tablas litúrgicas que introducía en su obra Reglas de rezar el officio diuino... (Barrientos, 1999, pp. 533 ss.).

2. En principio era aún más difícil discriminar a Gabriel Gómez entre los homónimos. En el año 1578 he encontrado cuatro individuos llamados Gabriel Gómez, matriculados en el Alma Mater salmantina[61], de los cuales dos eran sólo bachilleres médicos —y por tanto hay que excluirlos en la localización del nuestro, que ya era licenciado— y otros dos licenciados. Puesto que uno de los licenciados, el Gabriel Gómez, natural de Salamanca, continúa matriculándose para la consecución de este grado hasta el curso 1579-80, fecha en que el informe sobre la reforma del calendario ya está emitido, cabe concluir que el Gabriel Gómez al que se refiere el texto debe ser un médico de origen portugués. No lo recoge el índice de médicos Españoles, publicado por Luis S. Granjel y Teresa Santander Rodríguez (Salamanca: 1962), pero sí está catalogado entre los escolares médicos en Salamanca del siglo XVI de Teresa Santander Rodríguez (Salamanca: 1984, N. 1153, p. 177). Con seguridad habría que identificarlo con el estudiante portugués, natural de Santarén en la diócesis de Lisboa, que ya era licenciado en medicina por la Universidad de Coimbra cuando se matriculó en medicina en Salamanca. En esta Academia amplió sus estudios médicos durante por lo menos veinte años, de 1557 a 1577. Ya comenté que, según César Chaparro, escribió el Libro de la sphera del mundo en romance y por estilo muy claro y fácil a todos, con un tratado de Cosmograhía (manuscrito, 1585), en castellano, del que se ha eliminado todo lo que suponía adorno —como las referencias a los poetas—, para dejar un texto estrictamente científico que pretendía explicar la naturaleza del globo terrestre. Como complemento del libro añadió un Tratado de geografía y anunció otros sobre el astrolabio y el trinquete (Chaparro Gómez 2003, pp. 413). No he leído ese manuscrito, pero tengo noticias indirectas de que era un resumen escueto de lo conocido.

3. Miguel Francés era natural de Zaragoza, de la parroquia de San Pablo, en cuya Universidad cursó la licenciatura y el magisterio en artes, ampliando sus conocimientos posteriormente en la Sorbona. En París fue continuador de la tradición matemática aragonesa, y llegó a ser allí profesor junto a su antiguo compañero de estudios, Gaspar Lax y el también aragonés Pedro Ciruelo (Rey Pastor, 1913, p. 38). Según Latassa (Biblioteca nueva de los escritores aragoneses que florecieron... I, pp. 176-178) escribió una «Respuesta y solución de las dificultades propuestas a él por la Universidad de Bolonia sobre la reducción del calendario, después de celebrado el Santo General Concilio de Trento», que —según Picatoste— le dio gran renombre científico. Llegado a Salamanca, la Universidad lo contrató para impartir un curso de artes del año 1554 a 1559. El 1 de junio de ese año sustituyó al maestro Enrique Hernández en su cátedra de filosofía natural, permaneciendo en ella hasta el 25 de octubre de 1579 (AUSA, 965, f. 639 ss.). Estaba ocupando, pues, esta sustitución cuando formó parte de la comisión para la reforma del calendario. El 24 de octubre de 1579 fue nombrado catedrático de prima de lógica (Súmulas), tras una dura oposición en la que se enfrentó al maestro Francisco Zumel, plaza que ocupó hasta su muerte en marzo de 1582. A mí me parece que este nombramiento fue la forma de agradecerle la Universidad de Salamanca sus desvelos en los trabajos de la comisión del calendario. El 10 de diciembre de 1579 hizo el juramento para tomar el grado de licenciado —grado que era necesario para poder cobrar el salario entero— y, una vez recibido, se le incorporó el grado de maestro en artes por Zaragoza, previo el pago de unas tasas que se acordaron en claustro[62]. Se le hizo este beneficio por estar considerado como uno de los hombres más insignes de Europa (AUSA, 810, f. 90v.).

Miguel Francés había tenido una oportunidad excepcional de formación en matemáticas mientras estuvo en la Sorbona. En París entabló amistad también con otros excelentes intelectuales, muchos de ellos matemáticos: Juan de Celaya, Jerónimo Pardo y Diego Ramírez de Villaescusa[63]; también lo fue de Francisco M. Zarzoso y conoció a Álvaro Tomaz, asimismo profesor en el colegio de Coquerett de París (además de Ciruelo y Lax). Lo corrobora Latassa (p. 330). Es decir, que había hecho amistad con la mayor parte de los que serían los mejores matemáticos de la Península Ibérica. Ya hemos hablado del enorme peso específico de Ciruelo en la ciencia matemática de su época; también fue admirable la altura que alcanzó Juan de Celaya. Este profesor, en el comentario de la Física de Aristóteles (París: 1517) introdujo contribuciones de los mertonianos (Brardwardine, Heytesbury, Swineshead...), parisinos (Buridan, Sajonia...), italianos (Pablo de Venecia, Gaethano da Thiene, Bernardo Torni...) y de sus contemporáneos, como Álvaro Thomaz, autor del libro Liber de triplici motu (1509) (Navarro Brotons, 1999, p. 190). De altura científica similar eran, como sabemos Gaspar Lax, Ramírez de Villaescusa y Jerónimo Pardo. Esto permitió a Miguel Francés familiarizarse con las teorías científicas y con los últimos descubrimientos en matemáticas.

Durante casi toda su labor académica vivió Francés aquejado de dolencias y puesto que el salario que ganaba en la Universidad era corto al estar basado durante años en su cargo de sustituto, el claustro decidió ayudarle económicamente al menos en dos ocasiones. La primera vez fue el 9 de marzo de 1563, con 10 ducados:

...el maestro Francés dio una petición diciendo que ha más de once años que sirve a esta Universidad leyendo e trabajando; e de cuatro años a esta parte ha tenido e tiene grandes enfermedades por donde ha venido a gran necesidad. Por lo cual pidió... a sus mercedes le hagan merced de alguna ayuda de costa... le mandaron dar diez ducados atento a sus trabajos (AUSA, 31, f. 41v.).

La segunda vez fue el 1 de febrero de 1570. Ese día, el rector dijo en el claustro que Francés leía la sustitución de filosofía natural desde hacía tiempo, con muchos oyentes, con muy poco salario, y que sabe padece gran necesidad. El doctor Castro, que estaba presente, dijo que a él y a otro de la Universidad se le dieron ciertos dineros para que los repartiese en limosnas en esta ciudad; y que habiendo tenido noticia de la pobreza del maestro Francés,

...e de cómo era sacerdote e tan honrado se le habían dado ocho mil maravedís en limosna... todos comenzaron a tratar que hasta que mejorase en cátedra o en otras cosas se le diesen en cada un año sirviendo a la dicha Universidad veinte fanegas de trigo, demás del salario de su cátedra.

Se votó en secreto por agallas blancas y negras y todas salieron blancas, luego debía ser un buen hombre. Aprobaron, pues, darle 8.000 maravedíes de limosna, equivalentes a 21,33 ducados, más las 20 fanegas de trigo anuales (AUSA, 38, f. 48v; AUSA, 44, f. 114v.). La publicación del Fondo Espinosa del Archivo de la Universidad de Salamanca ha puesto a nuestra disposición una gran cantidad de documentación relevante en cada tema que este investigador copió despaciosamente a lo largo de los años. Entre ella, hay varios poderes notariales otorgados por Francés, de varios años distintos, normalmente a favor de un hermano suyo que vivía en Zaragoza, para que cobrara una renta de 200 ducados de pensión, que decía le había concedido Su Majestad, en el obispado de Huesca; luego quizá no fuera tan pobre como se decía en el claustro (véase por ejemplo: <http://ausa.usal.es/imagen.php?serie=espinosa_extractos&libros=ESPINOSA+8N.1D.36&verPagina=15#estados>). De hecho, en cuanto accedió a la cátedra en propiedad, se compró una casa en Salamanca, según se dice en esos mismos papeles.

José Barrientos otorgó gran protagonismo a fray Luis en la redacción del informe salmantino y a mí me parece que no le falta razón (Barrientos, 1996, pp. 533 ss.), aunque es evidente que fray Luis no hubiera podido hacerlo solo; porque de lo contrario no hubieran solicitado ayuda externa los comisionados. El propio fraile debió estar muy interesado en el tema, prueba de ello que una copia del informe salmantino estuviera en su poder, lo que indujo a Marcelino Gutiérrez a interpretarlo como obra suya (RAH 9/2073, ff. 89r.-119r.). Fray Luis se había visto muy atraído por la astrología y, para conocerla, es imprescindible saber astronomía y matemáticas. En varios libros se repite el lance que tuvo con la astrología judiciaria, que cuenta José González de Tejada en la Vida de fray Luis de León (Madrid: Fortanet, 1863). Según la propia declaración del fraile de 18 de abril de 1572, estudió el libro de Sigilos astrológicos que le proporcionó el licenciado Poza, pintando rayas con un cuchillo sobre una lámina de plomo y profiriendo palabras que eran santas, en el sentido que en ellas pretendió el Espíritu Santo, sólo por probar lo falso de tales cosas (p. 14). Según ha explicado últimamente L. M. Vicente García, fray Luis cristianizó la astrología en su idealización poética (2007, pp. 307-332; San José Lera, 1992). Pero no sólo fray Luis estuvo imbuido por la astrología, sino quizá todos los que vivieron aquel momento histórico como profesores de Salamanca. Por ejemplo fray Bartolomé de Medina enseñaba astrología en sus clases, según Julio Caro Baroja (Vidas mágicas e Inquisición. Madrid: Istmo, I, p. 304). En realidad todos los maestros de matemáticas anteriores se habían dedicado a ella: Polonio, Zacut, Salaya, Torres, Ortiz de Calzadilla... Aunque poco a poco se fue cerrando el círculo hasta ahogar estos conocimientos y sus ensoñadoras prácticas. El proceso en Salamanca contra Luis Rosicler y el catedrático de matemáticas Bartolomé González —encargado del partido de astrología en la Universidad—, iniciado en 1605 y suspendido después, agotó definitivamente este interés (Rico 1983b, pp. 157-186; Rico 1992, pp. 101-112).

Los datos expuestos indican que el informe que la Universidad de Salamanca firmó en 1578 no fue redactado por todos los comisionados, sino, sólo —en mi opinión— por Miguel Francés, fray Luis de León, Gabriel Gómez y fray Francisco Alcocer. Si Bartolomé de Medina y Luis de León se llevaban tan mal, y dado que Medina no era un experto en matemáticas, seguramente no participó demasiado en los trabajos. El resto de los comisarios nombrados inicialmente por el claustro quizá colaboró con su apoyo moral.

Evaluando el asunto de la gratificación a los tres personajes de la comisión antedichos, que no eran del cuerpo de la universidad, Vera presentó su propuesta en el claustro de diputados —el órgano que regía la vida económica de la Universidad— de 22 de noviembre. Según una costumbre que pervive en Salamanca, pretendían premiar económicamente a los profesores no ordinarios, puesto que los ordinarios debían y debemos considerarnos pagados con el sueldo habitual. Decía Vera:

...y así su parecer era que se debía gratificar al maestro Francés porque trabajó con gran cuidado y diligencia en él [el informe] hasta que cayó enfermo, y al padre Alcocer, religioso del Convento de San Francisco, y al licenciado Gabriel Gómez, los cuales habían hecho toda su diligencia, y ocupáronse mucho tiempo en ello, y que aunque otros muchos señores doctores y maestros de la universidad se habían ocupado y trabajado mucho en ello, como eran el padre fray Luis de León y maestro Medina, y fray Domingo Báñez, por ser personas de la universidad a quien no se podía pagar ni gratificar según la calidad de sus personas y lo mucho que en el dicho negocio habían hecho... le parecía que a las tres personas susodichas [Francés, Alcocer y Gómez], así por sus trabajos como por no ser del gremio de la universidad, se debía satisfacer como a la Universidad pareciese (AUSA, 47, f. 118r.; los errores de transcripción de este texto que publicó Alonso Getino trastocan parte del sentido del mismo. Un traslado más exacto en Beltrán de Heredia, 1972a, I, p. 323).

Obsérvese que los claustrales consideraron a los tres individuos ajenos al cuerpo de la Universidad, a pesar de que Miguel Francés era el profesor sustituto en la cátedra al maestro Enrique Hernández.

Los pagos se establecieron del siguiente modo: al maestro Francés y al licenciado Gómez sendos 24 ducados; al maestro Alcocer, atento que era fraile mendicante, lo que costare un hábito de buen paño frayleño con su capa. Aparte de esto se ordena remunerar también adecuadamente al escribano y encuadernador, Juan Bautista de la Canal, que lo pasó a limpio en sustitución del notario de la Universidad; ya hemos dicho que este escribano participó por aquellas fechas en otros encargos universitarios, pero no era titular de ninguna de las escribanías de número de la ciudad de Salamanca.

1.4.3.4. El contenido del informe de 1578

Las características del informe salmantino de 1578 son diferentes de las del previo, tanto desde el punto de vista estilístico, como desde el del contenido científico. Está escrito en un lenguaje más sencillo y es más breve. Además, es el único que era en parte conocido hasta que el profesor Flórez hizo un ensayo sobre el tema (Flórez, 1999). El texto de 1578 (véase la figura 31), como digo, era el único conocido por la transcripción latina que publicó Fernández Vallín, con las carencias que ya anuncié, y por el resumen de Schmid en «Zur Geschichte der Gregorianischen Kalenderreform», en 1882. Decía que:

Sopesadas, pues, todas estas dificultades e inconvenientes y considerando además que en tanta diversidad y dificultad de cosas, en las que no se puede hallar una proporción verdadera y exacta, es preciso que nos contentemos con lo que menos se aparte de la verdad misma y acarree los menores inconvenientes, juzgamos que aquella tabla desarrollada de epactas propuesta por Lilio es un descubrimiento docto e ingenioso. Y esto, por varias razones que esta Universidad expuso en otro tiempo más completa y abundantemente al santísimo Pontífice Leon X, en el año 1515, mientras se celebraba en Roma aquel santo concilio lateranense, razones que también ahora de intento pasamos por alto, puesto que han sido explicadas con diligencia por el mismo Lilio (subrayado nuestro).

En estas afirmaciones se expresa que el envío de la respuesta al papa del año 1515, que ellos incluyen dentro de la de 1578, no ha de entenderse como un simple anejo al informe propiamente dicho, sino como parte integrante del mismo, tal y como se deduce de este texto, donde se asumen como válidas las razones de la respuesta previa. Probablemente por esta razón resulte tan simple el informe de 1578 cuando se lee sin conocer el otro; sencillamente porque a sus autores no les pareció necesario abundar más en lo dicho y sólo lo ratificaron y adjuntaron.

En la carta enviada por los comisionados de 1578 al papa acompañando el informe redactado entonces, se decía que el texto elaborado en Salamanca en 1515 coincidía sorprendentemente con la propuesta redactada por Lilio, que fue distribuida en 1577 para su evaluación por los expertos de la cristiandad y de la que salió el contenido de la reforma finalmente aprobada por Gregorio XIII. Decía exactamente esta carta:

Después… de recordar y considerar atentamente todo lo que en otro tiempo [año 1515] respondió esta Universidad al Santísimo Sumo Pontífice León X, que la consultaba sobre este mismo asunto, respuesta que en todo o en su mayor parte coincidía maravillosamente con los escritos de Lilio... (subrayado nuestro).

Lilio tuvo oportunidad de inspirarse en la propuesta de Salamanca porque su hermano Antonio era uno de los comisionados por Gregorio XIII y tenía a su alcance el conjunto de la documentación vaticana sobre el calendario, que naturalmente incluiría el informe salmantino de 1515. ¿No será acaso que el informe salmantino de 1515 en su copia exenta falte del archivo de la Biblioteca Vaticana, donde tendría que estar, porque lo uso Lilio y al morir éste quedara traspapelado entre sus apuntes?

En tales circunstancias, es natural que los comisionados de 1578 expresaran escuetamente el acuerdo con la propuesta enviada ahora desde Roma, elaborada por Lilio, razonando que era casi idéntica a la suya previa.

Daban igualmente la plena aprobación a las restantes ecuaciones desarrolladas por Lilio, recomendando la tabla de las epactas como una solución sabia y aguda, además de ser la más exacta, sin error digno de consideración; atendía a los movimientos medios de las conjunciones y oposiciones del Sol y de la Luna, lo cual es suficiente... para el uso del calendario, que en ese momento era el verdadero objetivo: en aquella situación y momento, importaba menos la verdad que la liturgia.

Explicaban su acuerdo con el trabajo de Lilio propuesto porque, al calcular con los datos de su tabla las futuras conjunciones y oposiciones y compararlas con otras tablas más exactas, las han hallado sin error digno de consideración. Por consiguiente, el uso de la tabla de Lilio podría ser bueno y duradero. Son conscientes de que el resultado de su aplicación no sería válido en todos los tiempos y confían en que, con el tiempo, se descubran ecuaciones más precisas.

Probablemente con las tablas más exactas se refieran a las Pruténicas de Reinhold (Prutenicae Tabulae coelestium motuum; Tubingae: 1551), que son una versión crítica y corregida de las de Copérnico y no tan exactas como ellos suponían. Las tablas alfonsíes habían constituido la teoría astronómica dominante durante más de doscientos años. Su éxito se había debido a que combinaban dos antiguos modelos: uno, el ptolemaico, de movimiento uniforme de la esfera estelar a lo largo de la eclíptica; y otro imaginado, de oscilación periódica de la esfera alrededor de dos puntos fijos (llamado trepidación). Incluso en el siglo XVI era frecuente medir las posiciones estelares anotando al lado las mediciones de las tablas alfonsíes. Esta pervivencia en su uso se comprende cuando tenemos en cuenta que estas tablas recogieron en 1256 la tradición astronómica conocida, desde el primer catálogo de estrellas de Hiparco, matizado por Ptolomeo en el 140 d.C., hasta las correcciones de Abd ar-Rahman as-Sufi (903-986), en su Libro de las estrellas fijas.

A partir de 1551, las Tablas Pruténicas desplazaron a las alfonsíes entre los astrónomos profesionales, a pesar de que ambas poseen errores y valores similares, y fueron las que se usaron en el tramo final de la reforma del calendario (Dobrzycki 1983, pp. 117-123).

Quizá por no presentar una respuesta tan breve que podría haberse resumido en un folio, los comisionados recogieron de forma sintética lo principal de lo expresado por los informantes de 1515, recordando las dificultades de determinar la medida del año trópico, la adopción de la vía media por las tablas de Alfonso X, o la necesidad de fijar la celebración de la Pascua en el calendario eclesiástico, para lo cual:

...como atestigua Josefo en su libro De antiquitatibus, la Luna ha de estar opuesta al Sol y éste situado en Áries, y el domingo que sigue inmediatamente después de esta luna 14ª se ha de celebrar la santa Pascua de los cristianos.

Me llama la atención la imprecisión con la que citan este libro. La obra de Flavio Josefo se titulaba exactamente Antiquitates Iudaicae. De antiquitate Iudaeorum contra Appionem. De bello Iudaico Rufino Aquileiensi interprete; los universitarios salmantinos la tenían a su alcance en la biblioteca, en su edición de Venecia de 1499 (BGH I. 40 3). Probablemente les era tan familiar que la citaron (mal) de memoria. En aquellos momentos también tenían probablemente a mano su otro libro Flauii Iosephi Hebraei, historiographi clariss. Opera: ad multorum codicum Latinorum, eorundemque vetustissimorum fidem recognita & castigata, quorum catalogus est qui sequitur... (París: 1528; BGH 41925). Josefo (Yosef bar Mattityahu) fue el más afamado historiador judío, cuyos textos adquirieron gran difusión en Europa durante la Edad Media y en la España del Renacimiento, pues según De la Cuadra Blanco, sus descripciones probablemente fueron el modelo del monasterio de El Escorial. Las Antiquitates Iudaicae adquirieron una importancia notable para la historia del pueblo hebreo y de los primitivos cristianos y, naturalmente, en ellas se hace puntual explicación de la celebración de la Pascua (judía). Ha tenido multitud de ediciones, aunque ahora la hay también electrónica en la Biblioteca Valenciana Digital: <http://bivaldi.gva.es/es/consulta/registro.cmd?id=3197> [consulta 10 de agosto de 2010].

Ésta es la única cita bibliográfica concreta que contiene el informe salmantino de 1578, aunque también habla, como acabo de decir, de las tablas alfonsíes o de Dionisio el Exiguo; igual que el informe previo. El resto de la información cualitativa y cuantitativa que incluye se encontraba ya en la respuesta de 1515. Sólo añaden a ella una justificación de la opinión salmantina previa de suprimir 11 días del calendario en lugar de los 10 que proponía Lilio, diciendo:

...serán 11, más bien que 10, ya que a los 11 les faltan muy pocas horas, y en estos casos en que no debe hacerse igualación si no es de multitud de años pasados, lo que falta, que es ciertamente poco, puede ser muy bien añadido, puesto que eso con el correr del tiempo quedará compensado y enmendado.

Fig. 31: Informe de 1578.

La respuesta de 1578 es escueta, pero no simple. La alusión que hacen a la comprobación realizada entre la tabla de Lilio y las Pruténicas confirma que conocían perfectamente la astronomía computacional: sintiéndose de acuerdo con el veredicto de sus colegas de 1515, simplemente lo ratificaron. Ambos informes demuestran la existencia de una tradición astronómica puntera entre los profesores de esta universidad en esos dos momentos históricos, sin la cual no hubiera sido posible la precisión de sus cálculos y el tino de sus explicaciones.

Para valorar la respuesta salmantina en su conjunto (la respuesta de 1578 más la de 1515) es preciso ponerla en relación con otras, y es lo que haré a continuación sucintamente antes de comentar el resultado final de la reforma del calendario.

Pocos días después recibía el nuncio el parecer del Estudio salmantino y, junto al de la Universidad de Alcalá de Henares, lo envió a Felipe II para su conocimiento y visto bueno, que fue otorgado por el monarca. El informe de Alcalá lleva distinto título en el catálogo de la Biblioteca Vaticana (Tractatus Segurae Mathematicae Professoris in Universitate complutensi de nova restituendi Kaledarium tempore Gregorii XIII) que en el documento en sí mismo, actualmente conservado con la signatura Vat. Lat. 7048, f. 20r-36r, siendo el quinto de los documentos de ese códice. Comienza su portada con el título Pro nova ratione restituendi kalendarium y, como se ve por el número de folios, es sensiblemente más corto que el de Salamanca y el de Turriano, que enseguida comentaremos. Divide su exposición en varios apartados, dedicándole bastante espacio a la explicación histórica de los hechos, partiendo del Génesis, pasando por la historia de los israelitas, la controversia de la Pascua... Después alude a los movimientos desiguales del Sol y la Luna, las sedes de los equinoccios, el áureo número... y pasa después a temas de cómputo. Parte del valor medio del año trópico que fija en 365 días, 5 horas, 49 minutos y 16 segundos (fol. 26) —distanciándose de la tónica general de estos informes— y, tras el análisis laudatorio del documento de Lilio, se muestra conforme con su propuesta.

El último de los informes españoles en estar listo fue el parecer de Juanelo Turriano (c. 1500-1585). Recogidos ya los textos de Alcalá y Salamanca, el nuncio comunicaba al Santo Padre que el de Juanelo ya se estaba imprimiendo, pero que faltaban aún los instrumentos mecánicos que éste había prometido fabricar como fundamento explicativo de su propuesta, que no estuvieron terminados hasta diciembre. Juanelo se había hecho célebre en España como relojero del emperador y como creador de ingenios mecánicos. Un gran admirador suyo, Juan de Aguilera, el catedrático de astrología salmantino que quiso convertirlo en profesor de Salamanca, quizá fue el autor del Pseudo Juanelo Turriano y de la obra Los veintiún libros de los ingenios y de las máquinas[64]. Lo fuera o no, lo cierto es que en la Universidad de Salamanca Aguilera y otros le tuvieron en gran estima, consultándole y solicitándole la fabricación de instrumentos. Varias veces pidió el nuncio la benevolencia papal frente a este retraso, justificándolo —decía— en que Juanelo:

...es hombre que no hace las cosas sino cuando le viene en gana; es necesario se tenga un poco de paciencia (cf. Fernández Collado 1990, p. 154).

Este informe fue el que mayor expectativas y comentarios generó, entre otras cosas por su tardanza. En junio de 1579, bastante después que el resto de los proyectos, dirigió por fin Juanelo Turriano al rey Felipe II el estudio sobre el calendario, excusándose del retraso en función de su avanzada edad (tenía 78 años) y precaria salud. Su proyecto, completado por unos instrumentos astronómicos, no se aceptó en el Vaticano quizá porque distaba bastante de la media de las opiniones sobre el tema, y desde luego era de dificultosa aplicación y mantenimiento. Según González Aboín —que lo ha estudiado—, proponía, una vez fijado el equinoccio en cualquiera de los dos puntos (10 ó 21 de marzo), ir intercalando los años de 4 en 4 hasta el 33º, y éste hacerlo común. Después continuar la intercalación hasta el 34º bisiesto, que se hará común, y proceder así alternativamente. En resumen, Juanelo era partidario de fijar el equinoccio, corregir el movimiento lunar restando un día cada 304 años y otra corrección solar consistente en hacer comunes los años bisiestos cada 132 y 136 años alternativamente; o sea, un verdadero lío lejano a la simplicidad solicitada por el Vaticano. Para facilitar la comprensión de lo expuesto, Juanelo elaboró una serie de tablas: una esférica grande, una cuadrada y una pequeña redonda para cómoda consulta de la cuadrada (Turriano, 1990, pp. 43-44). Defraudaron las expectativas puestas en su trabajo. Su propuesta era enredada y extravagante.

Aún a comienzos del año 1580 el abad Briceño escribió repetidas veces a Felipe II desde Roma comunicándole que el papa tenía ya en sus manos todos los materiales españoles sobre la reforma del calendario, a excepción de los instrumentos mecánicos de Juanelo Turriano[65]. El 22 de febrero de 1580 la Secretaría de Estado de Roma ratificaba oficialmente a Felipe Sega que se habían recibido finalmente los documentos españoles y que los secretarios de la Congregación atendían a estudiarlos con diligencia. Habían llegado también otros textos de científicos franceses, húngaros, portugueses, italianos y de las universidades de Padua, Lovaina, París, Viena y Colonia, pero parece que no se han conservado todas las respuestas. En ellos se encontraban argumentadas todas las correcciones imaginables. Sólo el parecer de Alcalá aprobaba enteramente el proyecto presentado por Lilio con la invención de la epacta, mientras que en el extremo opuesto quedaba el elaborado por Alejandro Piccolomini desde París, que lo rechazaba completamente.

La Universidad de Viena no recibió directamente de Roma el compendio de Lilio, sino a través del emperador. El rector Petrus Muchitsch, el 26 de julio de 1578, presentó dos proyectos mucho menos elaborados que los de la Universidad de Salamanca. La comisión vienesa estuvo formada por el médico Andreas Dudius y el profesor de matemáticas Martin Bengel, junto al que sería el verdadero artífice de la propuesta, el matemático Paulus Fabricius, que se reducía a alabar la excelencia del trabajo de Lilio, especialmente su tabla de epactas, aun reconociendo que ésta podía no ser una solución absoluta. Abogaba, como Salamanca, porque la reforma se hiciera en 40 años y no de golpe, con la supresión de 13 días, no de 10 como se hizo, y recomendando emprenderla el año 1580, por ser bisiesto (Kaltembrunner, 1877, p. 492).

El matemático de Manuel Filiberto de Saboya, Juan Bautista Benedetti, era partidario de que la fecha de la Pascua se fijase de acuerdo a los movimientos del Sol y de la Luna, mejor que por el uso de los ciclos o de los valores medios. Fue el único que proponía suprimir, no 10, sino 24 días para hacer coincidir el 1 de enero con el solsticio de invierno; y la duración de los meses en relación con los signos del zodiaco. Con estos cambios, según Benedetti, el ajuste del calendario quedaría fijado durante 24.000 años. El teólogo francés Francisco Giuntini escribió Synopsis de Restitutione Calendarii, contando con que en 1580 caería el equinoccio en el 10 de marzo, proponiendo el 25 de marzo como fecha fija y midiendo la duración del año en 365 días 5 horas 47 minutos y 22 segundos: esta propuesta produciría el error de un día cada 114 años. Venecia preguntó al astrónomo de Padua José Moleto, quien fue también de la opinión de llevar el equinoccio al 25 de marzo, como estuvo en tiempos de Julio César, y basarse en los movimientos verdaderos de los astros, en lugar de en los movimientos medios (Turriano, 1990, pp. 41-42).

En esta misma época, en toda Europa se publicaron multitud de textos con propuestas de reforma: En 1579 el genovés Caretto aportó su opinión en un tratado titulado De cursu anni et calendario reformando. Ese mismo año Franciscus Junctinus escribe Synopsis de restitutione Kalendarii, publicado en Florencia; y Johann Bernhard Rastellius, desde París, elaboró su particular Correctio Calendarii. En 1580 aparecía en Venecia el texto de Lardinus, Tractatus de vera anni forma et de ejus emendatione, y el de Zarlinus, De vera anni forma sive de recta ejus emendatione ad S. Gregorium XIII. El obispo Hugolinus Martellus publicó dos textos sobre el tema en Lieja en 1580: De la integración anni in integrum unacum Apología restitución, quae est asaertio temporum sacrorum y Sacrorum Assertio temporum; en ellos opina que no era preciso mantener los decretos de Nicea y, por pura utilidad, que se tuviera en cuenta también la opinión de los que en su día fueron considerados herejes por no seguir los decretos conciliares. Otro estudio, del músico de San Marcos, Josefus Zarlinus, giraba en torno a la propuesta de Martellus, pero estas opiniones no fueron seguidas por la comisión romana. El número de informes enviados a Roma antes de 1582 debió de ser muy numeroso. Algunos llegaron como respuesta a la solicitud papal, pero otros fueron escritos por iniciativa particular de científicos de toda la cristiandad. Es llamativo que en los escritos de la comisión y en los de Clavio nunca se refieran a ellos.

Como todos sabemos, tras un proceso de estudio laborioso debido sobre todo a Clavio, pudo publicarse la bula Inter Gravisimas, 24 de febrero de 1582 (figura 32), por la que Gregorio XIII ordenaba la reforma del calendario que lleva su nombre. Es éste un documento que resume perfectamente el problema y sus circunstancias, por lo que paso a resumir su contenido.

Comienza Gregorio XIII expresando que con ella pretende completar los decretos del concilio de Trento, porque los padres conciliares, aplicados a la reforma del breviario, se vieron impelidos por la falta de tiempo para materializar la reforma del calendario. Dice que, dentro del breviario hay una parte dedicada a los rezos y otra al ciclo anual de la Pascua y al resto de festividades cuya celebración depende de la medida del movimiento del Sol y de la Luna. La reforma de la primera parte, la de los rezos, fue realizada por su predecesor, Pio V, en la bula Quod a nobis (09-07-1568). La reforma de la segunda parte requiere en primer lugar la restauración del calendario, reforma que no se ha podido hacer hasta ahora porque la multitud de propuestas presentadas al Vaticano sobre ello presentaban inmensas y casi inextricables dificultades, no proponían soluciones duraderas y, lo más importante, no mantenían intactos los antiguos ritos de la Iglesia, que era la principal preocupación papal.

Explica que esa tarea le había sido encomendada por el concilio y que para ello ha contado con el texto de Aloysius Lilio, entregado por su hermano Antonio, que propuso un nuevo ciclo de epactas, con unas reglas muy precisas para la determinación del número áureo que se adaptaba perfectamente a la duración del año solar, lo que había hecho derrumbarse todos los defectos del antiguo calendario, cuyas efemérides podrían ahora corregirse de forma coherente y duradera. Dicho texto fue enviado años atrás a los príncipes cristianos y a las grandes universidades, de manera que el resultado es el compromiso de todos y se ha realizado con la ayuda de todos.

Sigue diciendo que organizó una reunión en la Ciudad Santa para reformar el calendario, formada por los hombres calificados en la materia, elegidos entre los principales países del mundo cristiano. Estos, tras dedicar mucho tiempo y atención a este trabajo, y tras largas discusiones y estudio, se decantaron por este ciclo de las epactas de Lilio para la reforma, que pareció esencial para la realización de un calendario perfecto.

Tras su examen, se constató ser necesario establecer tres puntos para la restauración de la celebración de la Pascua, de acuerdo a las normas fijadas por los pontífices de otros tiempos, particularmente por Pío I (c. 140-154), Víctor I (c. 189-198 quien había estableció la celebración de la Pascua en domingo, después del 14 de Nisán) y por los padres del concilio de Nicea, a saber: En primer lugar la fecha concreta del equinoccio de primavera, o sea la fecha exacta del día decimocuarto de la luna que llega a esta edad el mismo día que el equinoccio, o inmediatamente después, y la fecha del domingo que sigue a este día decimocuarto de la luna. Por lo tanto se han ocupado no sólo del regreso del equinoccio de primavera a su primitiva fecha, de la que ya se ha desviado alrededor de diez días desde el Concilio de Nicea; y también para que se ponga el decimocuarto día de la luna en el lugar que le corresponde, del que se ha alejado algo más de cuatro días: instaurar, pues, un sistema metódico y racional que garantice en el futuro que el equinoccio y el decimocuarto día de la luna no se muevan de sus lugares adecuados.

Así pues, para que el equinoccio de primavera, que fue fijado por los padres del concilio de Nicea en las XII calendas de abril (o sea, el 21 de marzo), se restituya a esta fecha, el papa prescribe y ordena que, a partir de octubre del año 1582, se eliminen los diez días que van desde la tercera antes de las nonas (5 de octubre) hasta el día antes de los idus inclusive (14 de octubre), de manera que el día que seguirá a las IV nonas, que tradicionalmente celebraba la festividad de San Francisco de Asís, se celebre la fiesta de los santos mártires Ionisio, Rústico Eleuterio, así como la memoria de San Marcos (fiesta el 7 de octubre), papa y confesor de los santos mártires Sergio, Baco, Marcelo y Apuleyo. Después vendrían las XVI calendas de noviembre (17 de octubre). La letra dominical pasaría de G a C. En las decimoquintas calendas de noviembre se celebraría la fiesta de San Lucas, el Evangelista (18 de octubre), tras la cual se conmemorarían el resto de las fiestas móviles según se describe en el calendario.

A los jueces correspondía juzgar el retraso de los pagos mensuales y anuales con la consiguiente eliminación o aplazamiento de los días suprimidos.

A fin de que la fecha del equinoccio no se volviera a alejar de las XII calendas de abril (21 de marzo), se establece un año bisiesto cada cuatro años, salvo en los años centenarios, que siempre fueron bisiestos; ahora serán bisiestos, los tres primeros de cada cuatro años centenarios. 1600 será bisiesto, pero no lo serían los años 1700, 1800 y 1900. Lo sería el 2000. En estos años bisiestos se añadiría un día a febrero, el 29. Así a perpetuidad.

A fin de que el decimocuarto día de la luna pascual sea fijado con precisión y que la edad de la luna se establezca con exactitud, conforme al uso de la Iglesia antigua y la lectura del martirologio, el número áureo es retirado y es sustituido por un ciclo de epactas que, gracias a reglas muy precisas antes referidas al número áureo, permiten establecer con mucha precisión el día decimocuarto de la luna pascual, conforme con las antiguas costumbre de la Iglesia y para que sea más fácilmente fijada la fecha de la sagrada Pascua.

Por último, debido en parte a los diez días suprimidos en octubre de 1582 (año que desde ahora debe llamarse el año de la reforma), y en parte a los tres días que no se deberán intercalar durante cada período de cuatrocientos años, será necesario interrumpir el ciclo de los 28 años y usar el ciclo de Lilio de la intercalación bisextil en los últimos años del siglo, de manera que la letra dominical sea determinada fácilmente, como antes se hacía con la ayuda del ciclo solar.

Por lo tanto, con el atributo tradicional del soberano pontífice, éste dice aprobar el calendario reformado, gracias a la infinita benevolencia de Dios hacia su Iglesia, para que se imprima en Roma junto con el martirologio. A fin de mantener intactos y sin errores los calendarios. Finalmente el papa se atribuyó el monopolio e impresión de calendarios y martirologios. Nadie podría imprimirlos, bajo pena de cien mil ducados de oro para la Sede Apostólica.

Fig. 32: [Gregorio XIII] Bula Inter Gravissimas. CLAVIUS, Christoph. Romani calendarii a Gregorio XIII P. M. restituti explicatio S. D. N. Clementis VIII P. M. iussu edita. Roma: Aloysium Zannettum, 1603.

A aquellos que vivieran en lugares demasiado distantes para tener conocimiento de estos cambios a tiempo, se les permitía practicarlo en octubre de 1583 o en el siguiente, tan pronto como fuera posible.

En virtud de la autoridad divina que le compelía, Gregorio XIII exhortó a sus queridos hijos en Jesucristo, el emperador Rodolfo [II] y a los otros reyes y príncipes, igual que a las repúblicas, a adoptar este calendario y a cuidar de que todos sus súbditos lo aprobaran y respetaran, ajustándose escrupulosamente a él. Terminó prohibiendo cualquier conato de eliminación, supresión o alteración de este mandato, bajo la pena de incurrir en la cólera de Dios y de sus bienaventurados apóstoles Pedro y Pablo. Dicha bula fue otorgada en Tusculi [a 6 kms. de la actual Frascati], en el año de la Encarnación del Señor de 1581, sexto de las calendas de marzo (24 de febrero) de nuestro décimo año de pontificado. Tras ella, Felipe II publicó la Pragmatica sobre la orden que se ha de guardar, en la reformacion y cuenta del Año. [S.l.: s.n.], fechada en Lisboa, a 29 de septiembre de 1582 y pregonada en Madrid, a 3 de octubre del mismo año; y, más tarde, la Pragmática sobre los diez días del año (Aranjuez, 14-05-1583, on line en <http://www.wdl.org/es/item/2837/>) que cité al comienzo de este trabajo. En ambas ordenaba su puesta en vigor en España y en sus colonias.

Esquematizando lo que la propia bula explica y lo que la comisión romana decidió, diré que la reforma siguió las directrices marcadas por Lilio en el Compendium, que como hemos visto eran muy simples y básicamente coincidentes con las propuestas salmantinas. De hecho, ningún informe sobre el calendario que yo conozca tiene más coincidencias con el proyecto de Lilio y con el finalmente aprobado que el de la Universidad de Salamanca. Consistió en:

1. La fijación del equinoccio vernal del hemisferio norte el 21 de marzo (nadie habló nunca del otro hemisferio). Para ello fue necesario suprimir 10 días del calendario, los comprendidos entre el jueves 4 de octubre y el viernes 15 de octubre de 1582, sin alterarse, pues, los días de la semana; días elegidos —según Clavio— porque en ellos había una menor concentración de fiestas religiosas.

2. La modificación de la regla de los años bisiestos según la alternativa de Lilio, o sea, la salmantina de introducir una nueva anulación extraordinaria de la intercalación bixextil cada mil años. En el Compendium liliano se propuso la supresión de tres días intercalares en los años centenarios que no fueran exactamente divisibles por 400. Gregorio XIII ratificó que todos los años que no son fines de siglo pueden ser bisiestos si son divisibles entre cuatro, y duran 366 días; o comunes si no son divisibles entre cuatro, y duran 365 días. Los fines de siglo que son divisibles entre 400 son bisiestos mientras que los que no son divisibles entre 400 son comunes. O sea, que la intercalación gregoriana sigue el mismo sistema juliano con la única excepción de que los años centenarios, como 1700, 1800, 1900, 2100 ó 2200, que habrían sido bisiestos en el calendario juliano, se convirtieron en años comunes. La corrección lunar fue la más complicada. Como por último se estimó que se llevaba 3 días de retraso, se añadieron 3 unidades a la epacta y a continuación se restaron 10, para compensar los 10 días suprimidos; así pues la epacta quedó disminuida en 7 unidades. Para estabilizar en el futuro la concordancia de la Luna con los años solares, calcularon el adelanto de las 235 lunaciones sobre los 19 años julianos en una hora y 28 minutos; ello exigía aumentar un día a la epacta cada 312 años y medio, pero prefirieron también hacerlo en fin de siglo, incrementando esa unidad a la epacta cada 300 años (desde el año 1500; por tanto la primera adición se practicó en 1800), y después de 7 aumentos, el octavo se haría al cabo de 400 años: esto significa que se ordenaron un total de 8 días de aumento cada 2500 años.

En conjunto con la reforma gregoriana cada periodo de 400 años comprende:

• (400/4)-4 seculares = 96 años bisiestos (múltiplo de 4).
• De los 4 años seculares, sólo uno es bisiesto (múltiplo de 400).
• En el ciclo de los 400 años tenemos:

96 + 1 = 97 años bisiestos.

400 - 97 = 303 años comunes.

Es decir, que se establecieron 97 años bisiestos de cada 400 (en lugar de 100 cada 400 como se cumplía antes):

303 años comunes = 303 x 365 = 110.595 días

97 años bisiestos = 97 x 366 = 35.502 días

(110595 + 35502)/400 = 365.2425 días medios = 365d 5h 49m 12s

¡Tantos esfuerzos y cálculos para lograr la misma estimación media del año trópico que ofrecían las tablas alfonsíes: 365,2425 días! A pesar de que las tablas Pruténicas (1551) parecían haber desbancado a las alfonsíes en las investigaciones llevadas a cabo para la reforma del calendario, parece que no se equivocó del todo Pedro Chacón, en la previsión de perdurabilidad de éstas que hizo cuando escribió su Historia de la Universidad de Salamanca y dijo:

Juntados pues estos [científicos], con grande estudio, inmenso trabajo e increíble diligencia, compusieron aquellas tan celebradas tablas [astronómicas], que por haverse hecho por orden suya, se llamaron del rey Don Alonso, que durarán todo lo que el movimiento del cielo durare, pues no se espera que en aquel género pueda haver jamás tan perfecta obra (Chacón, 1990, p. 59).

A pesar del consenso, el calendario gregoriano tiene algunos defectos, los principales de ellos son:

1. La diferente duración de los meses.

2. Las semanas no se corresponden con los meses.

3. La variabilidad del día de Pascua en el calendario eclesiástico.

4. La diferencia con el año real de 24.192 segundos, por lo que desde 1582 se acumula un retraso que en el año 4909 sumará un día entero.

5. El tema del año cero, que al no existir obliga a comenzar los siglos en el 01 en lugar de en el doble cero. Aunque no es una cuestión fácil de resolver, ya que se necesitaría un año cero d. C., y un año cero a. C. Aunque desde el punto de vista matemático y cronológico los siglos comienzan en el 01, para la Historia los siglos van desde el 00 hasta el 99, de la misma manera que las décadas van desde el 0 hasta el 9 (años veinte: 1920-1929). Para la Historia no tiene mucha importancia que el siglo primero tenga 99 años.

Herrera Armendia, en su trabajo sobre el calendario liliano (2007), siguiendo la explicación de Moyer (1982, p. 92-93), ha resumido el cómputo de esta propuesta y reitera que el cambio fue pequeño pero muy importante porque con él se lograba acercar la duración del año calendárico a la del año trópico: la duración del primero se fijó, como acabamos de ver, en 365.2425 días, mientras que la duración del año trópico en 1582 se aproximaba a 365.24222 días (Moyer, 1982, p. 93), difiriendo de la duración del calendario gregoriano un poco más de 24 segundos por año. De hecho, si el tiempo que transcurre en un año no fuera disminuyendo gradualmente, el calendario gregoriano retendría la fecha del equinoccio de primavera en el 21 de marzo durante 3571.43 años. Esto se puede explicar así: La diferencia entre la duración del calendario gregoriano y la del año trópico es de 24.192 segundos:

365.24250 - 365.24222=0.00028 días

Expresado en segundos es: (0.00028) (86.400) = 24.192 segundos.

Si lo comparamos con la unidad para determinar el adelanto de un día en un período de tiempo, resulta:

1/ 0.2425 - 0.24222 = 1/ 0.00028 = 3571.43 años

Exactamente 3571.428571428571 años; lo que es lo mismo que 3571 años, 5 meses y 4 días (Herrera Armendia, 2007).

No sabemos por qué Lilio fijó sin explicación el año trópico en 365.2425, igual que lo hizo el informe de la Universidad de Salamanca. Algunos lo interpretaron como la adopción de la medida de las tablas alfonsíes (Moyer, 1983), pero tanto las tablas alfonsíes, el De Revolutionibus..., y las tablas Pruténicas dieron un valor aproximado al año de 365 días 5 horas 49 minutos y 16 segundos (o lo que es lo mismo a 365.2425463 días) difiriendo entre unas y otras estimaciones menos de un segundo y excediendo todas ellas aproximadamente en 4 segundos al 365.2425 propuesto por Lilio. La mejor hipótesis sobre el origen de la longitud del año de Lilio la ofreció Swerdlow (2001; cf. Herrera Armendia, 2007) que observó que la parte fraccionaria de la duración del año escrita en las obras mencionadas se expresan en el sistema sexagesimal: 365;14,33. Al convertir la fracción sexagesimal a común, se obtiene justamente la medida ofrecida por Lilio es

365 + 97/400 ; es decir: 365 + (14 x 60-1) + (33 x 60-2) = 365 + 14/60 + 33/3600 = 365 + (840 + 33)/3600 = 365 + 873/3600 = 365 + 97/400, , ó 365.2425 días

En este ciclo los días se repiten en periodos de 400 años. Es decir, que con esa propuesta sí se conseguía la mayor simplicidad buscada por la Iglesia, y en la que tanto había insistido el informe salmantino de 1515. Sin embargo, aunque se pretendió conservar la tradición de la Iglesia, la reforma constituyó una verdadera novedad en su forma de determinar la Pascua. Había que dar una explicación del contenido de la bula papal y de las tablas de epactas. Esta tarea se encomendó a Antonio Lilio quien en 1585 anunció haberla terminado tras un gran trabajo, pero nunca se publicó. Por fin fue Clavio, el último superviviente de la comisión, quien publicó en 1603 Romani calendarii a Gregorio XIII P. M. restituti explicatio, que es la obra fundamental en lo que se refiere al calendario gregoriano y su explicación.

Después de la puesta en vigor del nuevo calendario, otra procesión de textos se alinearon en dos sentidos: o criticándolo o explicándolo. En España, el navarro Francisco Vicente Tornamira sacó a la luz una Chronographia y Repertorio de los tiempos... y El Calendario Gregoriano, ambos en Pamplona, respectivamente en 1585 y 1591, pretendiendo —especialmente con el último— la divulgación de los nuevos criterios computacionales. Hubo varias obras, pero me quiero detener un momento en dos de ellas que yo no he visto citadas antes: La de García de Loaysa y la de Francisco Salinas.

1. Con una erudición sorprendente escribió un comentario al calendario gregoriano García Loaysa y Girón (1534-1599), capellán de Felipe II y arzobispo de Toledo de 1598 a 1599, titulado Parecer de D. García Loaisa y Girón sobre la reforma del calendario de intentaba Gregorio XIII (figura 33), del que he encontrado dos copias manuscritas en la BNE, ms. 13019. Es un memorial dirigido al rey cuyo objetivo expreso es hacer una recopilación del problema para mostrar la dificultad que había tenido la enmienda. Explica de forma sorprendentemente precisa la antigua controversia de la Pascua entre los occidentales y los cuatrodecimanos; recoge después las medidas del año trópico según diversos autores; resume la propuesta de Lilio y manifiesta conocer algunos de los proyectos enviados a Roma. En el f. 159v. se dice que este texto se sacó de un tomo de borradores de don García de Loaysa, Arzobispo de Toledo, de un borrador de su mano... y de la misma letra que éste, se conservan otras copias de documentación relativa a la reforma del calendario, como la de la carta de la Universidad de Salamanca a Gregorio XIII, de 12 de noviembre de 1578 (BNE ms. 10206).

2. Un compañero de los comisionados salmantinos, Francisco Salinas (1513-1590), tenía unos conocimientos astronómicos y matemáticos que me asombran, sobre todo teniendo en cuenta su ceguera. En la Biblioteca Nacional de Madrid se encuentran dos ejemplares manuscritos de sus «Anotaciones sobre el calendario gregoriano hechas por el maestro Francisco de Salinas, cathedrático de propiedad en la facultad de Música de la Universidad de Salamanca. 1983» (figura 34; BNE, ms. 23106). Esta portada tiene una línea manuscrita abajo, de otra letra, que dice «Es de la librería del Monasterio de Nuestra Señora de la Vid». Yo no he visto citada antes la referencia a este documento, y por eso hablaré algo más de él.

Evidentemente la música no era una facultad en sí misma, como dice aquí Salinas, sino una materia más de las que conformaban los estudios de la facultad de artes. La fecha, 1583, muestra un interés por comprender y explicar tempranamente la reforma gregoriana y la anotación final sugiere que esta copia quizá perteneció al monasterio que se encuentra a 18 Km. de Aranda de Duero (Burgos), entre Valladolid y Soria.

Fig. 33: LOAYSA Y GIRÓN, García. «Parecer de D. García Loaisa y Girón sobre la reforma del calendario de intentaba Gregorio XIII».

Fig. 34: SALINAS, Francisco. «Anotaciones sobre el calendario gregoriano hechas por el maestro Francisco de Salinas, cathedrático de propiedad en la facultad de Música de la Universidad de Salamanca.»

Tengo delante una copia del manuscrito y algo que no me explico es cómo no se nombró al maestro Francisco Salinas para la comisión universitaria del calendario en Salamanca. En la designación inicial era razonable que el claustro convocara a un representante de cada facultad, pero igual que después colaboraron Alcocer, Gómez y Francés, hubiera podido ayudar Salinas. Probablemente se debiera a que su interés por el tema derivó precisamente de los debates claustrales y de la amistad con fray Luis de León, y su texto pretendió a la vez explicar y criticar la reforma finalmente aprobada. Su discurso aparece dividido en 16 partes o reglas:

• «La primera regla que trata del áureo número o círculo lunar.
• Segunda regla del círculo solar y letra dominical.
• Tercera regla de las epactas y novilunios, que suceden en lugar de los áureos números.
• Quarta regla de las tablas de las equaciones para conformar los años solares con los lunares.
• Quinta regla de la tabla expansa de Lilio y cómo della se saca la perpetua del calendario y de la del calendario se puede también sacar la que hasta agora se usaba del cómputo de Dionisio.
• Sexta regla de la necesidad que hubo de hazer para la diversidad de los tiempos la tabla de la equación de los años solares con los lunares sin la qual ninguna cosa se hubiera hecho para la corrección del calendario.
• Séptima regla en que se muestra cómo se saca la tabla primera después de la corrección del calendario a la letra de la equación D de la tabla de las 30 epactas y de algunas cosas dignas de considerar en ella.
• Octava regla, en que se muestra el arte para sacar la segunda tabla después de la corrección del calendario a la letra de la equación C y cómo se reduce a la mano de la manera que la primera.
• Novena regla en que se muestra cómo se saca la tabla tercera para el año de 1900 hasta el 2200 exclusive de la tabla perpetua del calendario y de otras cosas tocantes a ella y a todas 30 tablas en universal.
• Dézima regla de la orden que llevan los áureos números en los principios y fines de todas las 30 tablas.
• Onzena regla que trata de los embolismos qué cosa sean y de cómo se arían variándose la letra de la equación en todas 30 tablas.
• Dozena regla de otra nueva consideración sobre la naturaleza de los embolismos muy digna de ser sabida.
• Dézima terzia regla de las 30 letras de la equazión que se hallan en la tabla expansa de Lilio y en la perpetua del calendario, como están en las 3 tablas y otras cosas.
• Catorzena regla que muestra a hallar los áureos números que responden en todos los tiempos a las 30 epactas por todas las 30 tablas por la qual se entiende también el verdadero modo de hallar las más baxas quartas déximas.
• Quinzena regla de lo que es necesario considerar para mejor entender el calendario del año y en qué año de círculo solar padeció Nuestro Señor Jesuchristo y los inconvenientes que parece averse seguido de la corrección del año y que han sido mayores los bienes que della han resultado.
• Dézima sexta regla de una tabla temporaria hasta el año de 1595 del año emendado, cotejada con la que fuera sino se emendara».

El conjunto resulta una curiosa explicación del nuevo calendario, con tablas y aclaraciones realizadas con cierto sentido irónico y descalificador, pero con sorprendente capacidad de cálculo mental. Buscando la vertiente práctica, dentro de la regla séptima (f. 29r.), propone una pauta nemotécnica basada en los nudillos de la mano para la averiguación de la epacta; y en la octava, hace lo mismo pero aplicándola a la fijación de la fecha de la Pascua, que se parece, en su concepción, al uso nemotécnico de la mano que diseñó Rodríguez Zamorano en su Cronologia y reportorio de la razon de los tiempos (Sevilla: 1594) ¿Copió Zamorano a Salinas en este uso? El escrito de Salinas es desde luego anterior.

Sus explicaciones son generalmente claras, pero no siempre precisas. Como ejemplo de esa imprecisión recojo parte de la regla onzena, en la que trata de explicar el ciclo del calendario hebreo; me parece que si no se conoce previamente su funcionamiento, no es de fácil comprensión a través de sus palabras; él dice:

Embolismo no es otra cosa sino una lunación que se añade unas vezes de tres en tres años y otras de dos en dos, siete vezes en los 19 años del círculo lunar de los días que sobran al año solar sobre el lunar quando pasan de 30 días hasta tres o quatro o faltan quatro o cinco para llegar a ellos y aquel año que precede al embolismal tiene 13 lunaciones y ay dos meses dozenos que entrambos se llaman de un nombre Adar, y éstas son 7 y las seys lunaciones son de 30 y la séptima de 29 como por exemplo... (f. 39r.).

Lo que trata de explicar es el criterio de los meses embolismales o añadidos al calendario hebreo según el ciclo de los 19 años que, como dijimos, tendrá 12 años comunes (de doce meses) y 7 años embolismales con trece meses cada uno: los años número 3, 6, 8, 11, 14, 17 y 19 de cada ciclo decemnovenal. La ironía de la que hablaba arriba se aprecia, por ejemplo, cuando dice:

Han de advertir los obispos y prelados de los monasterios, los unos quando ordenaren y los otros quando dieren las profesiones a los que entraren en religión, que los que antes de la corrección del calendario habían de tener 24 años y an de entrar en los 25 para ordenarse de Misa, después della no cumplen los 24 hasta 10 días después, ni tampoco 16 los que han de hazer profesión, porque es necesario esperar otros 10 días más (f. 61r.).

Salinas no participó en los trabajos para la reforma del calendario en Salamanca quizá porque era ciego y estudiar los cielos no parecía un encargo para invidentes, pero en el texto citado denota una capacidad de cálculo mental absolutamente excepcional.

En conjunto esta reforma consistió en hacer concordar los calendarios convencionales con las conjunciones astrales y en proponer un nuevo método para hallar el domingo pascual. La reforma del calendario gregoriano vino a ser un barómetro del alcance de la autoridad papal: los católicos de Italia, España, Francia y Polonia la acogieron inmediatamente, mientras que los protestantes, a pesar de las recomendaciones de Ticho Brahe o Johannes Kepler, tardaron más en empezar a aceptarla. La historia posterior de este tema puede seguirse a través de Coyne (1983, pp. 243 ss.).

1.5. CONCLUSIONES

La primera y más importante de las conclusiones a las que he llegado es que la Universidad de Salamanca inventó en 1515 un procedimiento matemático que permitía enlazar en un cómputo convergente el distinto ritmo del Sol y de la Luna; y que lo hizo de forma tan exitosa como para haber sido este procedimiento el que finalmente ratificaron los expertos vaticanos y el propio pontífice como base de la reforma gregoriana del calendario.

Considero éste un logro científicamente relevante e historiográficamente desconocido: A pesar de que la nueva forma de historiar la ciencia ha permitido un avance inusitado en esta disciplina, creciendo de forma logarítmica su producción editorial en los últimos veinticinco años, la reforma del calendario gregoriano ha pasado inadvertida, sin pena ni gloria, para los grandes investigadores actuales sobre la historia de la ciencia en España. Después de haber estudiado pausadamente este tema, creo que las investigaciones sobre la reforma del calendario corrieron parejas con el progreso de la ciencia astronómica, tanto en España como en toda Europa; pero mientras que varios investigadores alemanes, italianos e ingleses han realizado estudios concomitantes entre ciencia en general e historia del calendario en particular, en España este último aspecto quedó siempre como un apéndice insignificante, incómodo, desconocido y hasta pasado de moda. Ni Goodman, ni López Piñero y su espléndido equipo valenciano, ni Mariano Esteban Piñeiro y el otro gran equipo de historiadores de la ciencia de la Universidad de Valladolid, han deparado en la importancia nuclear del tema del calendario en astronomía y matemáticas, desde el siglo XIII al siglo XVII. Nadie parece haberse dado verdadera cuenta en España de que incluso el nacimiento del heliocentrismo copernicano fue una consecuencia directa de los estudios sobre la reforma del calendario.

Salamanca contribuyó a esta reforma con dos proyectos institucionales, uno redactado en el año 1515 y otro en 1578, ambos bajo la solicitud simultánea de papas (respectivamente León X y Gregorio XIII) y reyes (Fernando el Católico y Felipe II). En conjunto —como acabo de decir— representan una contribución muy significativa a la resolución del citado problema científico y no he encontrado ningún otro informe sobre esta reforma que sea tan coincidente como el salmantino de 1515 con el proyecto finalmente aprobado por el pontífice. A pesar de conservarse su referencia en los índices de la Biblioteca Apostólica Vaticana, este documento sólo se ha conservado por incluirse como una parte constitutiva y nuclear de la respuesta salmantina de 1578; circunstancia que me lleva a proponer la hipótesis de que quedara traspapelado entre los documentos personales del supuesto redactor del proyecto de reforma del calendario, Luigi Lilio, cuando murió, que muy probablemente lo usó para redactar su Compendium, prestado por su hermano Antonio, que era miembro de la comisión vaticana nombrada para estudiar este tema.

Al observar que el informe salmantino de 1515 se ajustaba maravillosamente —como decían los comisionados de 1578— con lo expresado posteriormente en el Compendium novae rationis restituendi kalendarium de Lilio, que fue enviado por el Vaticano para su evaluación por los expertos, también creo, como lo creyeron los comisarios salmantinos de 1578, que fue una coincidencia cercana al plagio. Es verdad que, analizando la tradición computista desde la Edad Media, cabe pensar que Lilio pudo no haber copiado específicamente el informe salmantino de 1515 —aunque a mí me parece seguro que lo conoció y que en parte copió—, sino que quizá recogió y expuso el contenido y las proposiciones de esta tradición que arranca de Roger Bacon y pasa por Pierre d’Ailly, John de Murs, Fermín de Belleval, Paul von Middelburg, la Universidad de Salamanca, Pedro Ciruelo y seguramente otros. Mi certeza deriva de que las cifras y proporciones concretas del informe salmantino de 1515, y no otras, fueron las que indiscutiblemente recogió y matizó Lilio en su Compendium.

También me parece destacable que el informe salmantino de 1515 ofreciera la solución precisa en un momento en que el V concilio de Letrán le había pedido pronunciarse sobre el proyecto de reforma realizado entonces por Middilburg, en el que no se defendían ni uno solo de los extremos que Salamanca propuso con este fin y que finalmente se aprobaron en la reforma gregoriana del calendario de 1582. Es verdad que también la Universidad de Viena envió al concilio en 1515 un informe de talante similar al salmantino, pero sus redactores se inclinaban a considerar el curso real del año trópico, mientras que la salmantina apoyaba el curso medio, que fue el finalmente aprobado por el pontífice.

Esta certeza demuestra, una vez más, la excepcionalidad de los conocimientos matemáticos y astronómicos existentes en el seno de la Universidad de Salamanca en torno al año 1515. Por eso opino que, quienes como Rey Pastor (Rey Pastor-Babini, 1997, cap. VII) lamentaron la poca altura científica de los textos matemáticos españoles del siglo XVI, deberían haber leído éste.

En los estudios encaminados a la realización de este trabajo me he encontrado con varios tratados sobre el calendario que no conocía y que no había visto citados antes. Especialmente los de la Universidad de Alcalá de Henares, el del matemático Pedro Ciruelo, el de Francisco Salinas —catedrático de Música de la Universidad de Salamanca— y el de García de Loaísa y Girón —arzobispo de Toledo—. Los cuatro contienen afiladas explicaciones computacionales que denotan una extraordinaria capacidad de cálculo mental, especialmente los dos últimos. En cambio, otros proyectos de reforma que son conocidos y aplaudidos, como los de Antonio de Nebrija y Juan Ginés de Sepúlveda, no fueron más que caprichos literarios sin ningún interés computacional.

No ha quedado rastro que permita atribuir una autoría cierta al informe salmantino del año 1515. Habiendo seguido la bibliografía de todos los profesores que entonces enseñaban en la Universidad de Salamanca y no habiendo encontrado manuscritos o impresos realizados por ellos en relación con la astronomía o las matemáticas, salvo en el caso de Juan de Oria, me cabe suponer que, formara quien formara aquella comisión en el año 1515, los autores intelectuales de aquel informe fueron los catedráticos de filosofía natural: sin duda Juan de Oria y muy probablemente Juan de Ortega (a quien no hay que confundir con fray Juan de Ortega).

Por lo que se refiere al segundo de los informes, el del año 1578, es de destacar el esfuerzo conjunto de varios intelectuales salmantinos contemporáneos convocados por el claustro para su redacción. Pero la búsqueda incesante de ayuda externa por parte de estos comisionados con este fin demuestra que Diego de Vera, Cosme de Medina, fray Luis de León, fray Bartolomé de Medina y fray Domingo Báñez —los cinco comisionados— no tenía conocimientos suficientes para redactar la respuesta. La colaboración que solicitaron y obtuvieron por parte de Juan Galván (el cura de Gatón de Campos), fray Francisco Alcocer, Gabriel Gómez y Miguel Francés no me parece a mí que resultara de un valor equiparable entre ellos. Los conocimientos matemáticos del cura de Gatón fueron desestimados por los salmantinos en cuanto le conocieron. Las obras escritas y publicadas por fray Francisco Alcocer y Gabriel Gómez no denotan profundidad alguna de entendimiento matemático y, sabiendo de la trayectoria intelectual de Miguel Francés y de su informe previo sobre el calendario, elaborado a petición de la Universidad de Bolonia, cabe concluir que fue éste el autor intelectual del segundo de los informes salmantinos.

En esta reforma gregoriana primaron los criterios teológicos sobre los científicos y con ella el papado domesticó el tiempo social en función de sus intereses dogmáticos. Sin embargo, la experiencia y la observación que este proceso de domesticación promovió apuntaron paradójicamente hacia la autonomía de la razón que —contra los intereses eclesiásticos— se fue imponiendo, frente a la autoridad de los clásicos y frente a las Sagradas Escrituras.

A pesar de todo, la reforma del calendario iniciada por el papado ha sido el gesto más importante en la historia de la globalización. Su imposición transformó el mundo, o al menos lo recondujo hacia un proyecto global, pues la historia del presente y la vida civil están hoy regidas por este calendario gregoriano.

Notas