2

Pares e impares

Los números pares son divisibles por 2; los números impares no lo son. Por lo tanto, 2 es el único número primo par. Es una suma de dos cuadrados: 2 = 12 + 12. Los otros primos con esta propiedad son precisamente aquellos cuyo resto es 1 al dividirlos por 4. Los números que son una suma de dos cuadrados pueden caracterizarse en términos de sus factores primos.

La aritmética binaria, usada en los ordenadores, está basada en potencias de 2 en lugar de en potencias de 10. Las ecuaciones cuadráticas, en las que está involucrada una potencia de dos de un número desconocido, pueden resolverse usando raíces cuadradas.

La distinción entre pares e impares se extiende a las permutaciones, que son modos de ordenar un conjunto de objetos. La mitad de las permutaciones son pares y la otra mitad impares. Te mostraré una aplicación clara: una prueba sencilla de que un famoso rompecabezas no puede resolverse.

PARIDAD (PARES/IMPARES)

Una de las distinciones más importante en todas las matemáticas es la que hay entre números pares e impares.

Empecemos con los números naturales 0, 1, 2, 3, ... Entre ellos, los números pares son:

0 2 4 6 8 10 12 14 16 18 20 ...

y los impares son:

1 3 5 7 9 11 13 15 17 19 21 ...

En general, cualquier número natural que es múltiplo de 2 es par y cualquier número natural que no es múltiplo de 2 es impar. En contra de lo que algunos profesores parecen creer, 0 es par, porque es múltiplo de 2, en concreto, 0 × 2.

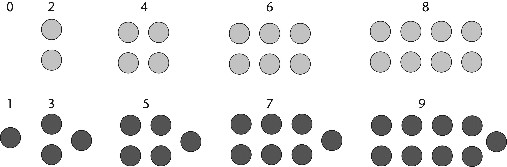
Figura 8. Números pares e impares.

Los números impares tienen resto igual a 1 cuando se dividen entre 2 (el resto es distinto de 0 y menor que 2, lo cual solo deja 1 como posibilidad). De modo que, algebraicamente, los números pares son de la forma 2n, donde n es un número natural, y los números impares son de la forma 2n + 1. (De nuevo, si tomamos n = 0, tenemos que 0 es par.) Para extender el concepto «par» e «impar» a los números negativos, permitimos que n sea negativo. Entonces –2, –4, –6, etcétera, son pares y –1, –3, –5, etcétera, son impares. Los números pares e impares se alternan a lo largo de la recta numérica.

Figura 9. Los números pares e impares se alternan a lo largo de la recta numérica.

Una característica agradable de los números pares e impares es que obedecen a reglas aritméticas sencillas:

par + par = par

impar + impar = par

par + impar = impar

impar + par = impar

par × par = par

impar × impar = impar

par × impar = par

impar × par = par

no importa el número en concreto de que se trate. De modo que si alguien afirma que 13 × 17 = 222, sabes que está equivocado sin hacer los cálculos: impar × impar = impar y 222 es par.

EL PRIMO MÁS PEQUEÑO Y EL ÚNICO PAR

La lista de números primos empieza con 2, de modo que 2 es el número primo más pequeño. También es el único número primo par, porque por definición todos los números pares son divisibles por 2. Si el número que nos ocupa es 4 o mayor, se expresa como el producto de dos números más pequeños, de modo que es compuesto. Estas propiedades, aunque sean sencillas y obvias, dan a 2 un estatus de unicidad entre todos los números.

TEOREMA DE LOS DOS CUADRADOS

En el día de Navidad de 1640, el brillante matemático aficionado Pierre de Fermat escribió al monje Marin Mersenne y le hizo una pregunta intrigante: ¿qué números pueden escribirse como una suma de dos cuadrados perfectos?

El cuadrado de un número es lo que obtienes cuando lo multiplicas por sí mismo. Así, el cuadrado de 1 es 1 × 1 = 1, el cuadrado de 2 es 2 × 2 = 4, el cuadrado de 3 es 3 × 3 = 9, etcétera. El símbolo para el cuadrado de un número n es n2. De modo que 02 = 0, 12 = 1, 22 = 4, 32 = 9, etcétera.

Los cuadrados de los números del 0 al 10 son:

0 1 4 9 16 25 36 49 64 81 100

Por lo tanto, 4 es el primer cuadrado perfecto después de los menos interesantes 0 y 1.

La palabra «cuadrado» se usa porque estos números surgen al colocar puntos juntos en cuadrados.

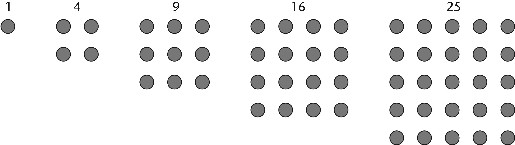
Figura 10. Cuadrados.

Cuando sumamos los cuadrados de dos en dos, obviamente podemos obtener los propios cuadrados; basta sumar 0 al cuadrado. Pero también obtenemos números como

1 + 1 = 2

4 + 1 = 5

4 + 4 = 8

9 + 1 = 10

9 + 4 = 13

16 + 1 = 17

que no son cuadrados. Aun así, muchos números no aparecen, por ejemplo, 3, 6, 7, 11.

A continuación hay una tabla que muestra todos los números del 0 al 100 que son suma de dos cuadrados. (Para obtener el número de las celdas que no están en negrita, suma el número en negrita en la parte superior de su columna con el número en negrita a la izquierda de su misma fila. Por ejemplo, 25 + 4 = 29. Se han omitido las sumas mayores que 100.)

 0149162536496481100
00149162536496481100
112510172637506582
445813202940536885
99101318253445587390
1616172025324152658097
25252629344150617489
363637404552617283
4949505358657498
64646568738089
818182859097
100100 

Tabla 2

A primera vista, es difícil encontrar un patrón, pero hay uno, que Fermat descubrió. El truco es escribir los factores primos de los números en la tabla. Dejando fuera el 0 y el 1, que son excepciones, tenemos:

2 = 2

4 = 22

5 = 5

8 = 23

9 = 32

10 = 2 × 5

13 = 13

16 = 24

17 = 17

18 = 2 × 32

20 = 22 × 5

25 = 52

26 = 2 × 13

29 = 29

34 = 2 × 17

36 = 22 × 32

37 = 37

40 = 23 × 5

41 = 41

45 = 32 × 5

49 = 72

50 = 2 × 52

53 = 53

58 = 2 × 29

61 = 61

64 = 26

65 = 5 × 13

68 = 22 × 17

72 = 23 × 32

73 = 73

74 = 2 × 37

80 = 24 × 5

81 = 32

82 = 2 × 41

85 = 5 × 17

89 = 89

90 = 2 × 32 × 5

97 = 97

100 = 22 × 52

He subrayado los números que son primos, porque son la clave para el problema.

Faltan algunos primos, en concreto: 3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79 y 83. ¿Puedes emular a Fermat y descubrir su característica común?

Cada uno de estos primos es un múltiplo de 4 menos 1. Por ejemplo, 23 = 24 – 1 y 24 = 6 × 4. El primo 2 aparece en mi lista, de nuevo, lo cual es excepcional en algunos aspectos. Todos los primos impares en mi tabla son un múltiplo de 4 más 1. Por ejemplo, 29 = 28 + 1 y 28 = 7 × 4. Los primeros primos de esta forma aparecen todos en mi lista y, es más, si la ampliase, parece que no faltaría ninguno.

Todo número impar es o bien un múltiplo de 4 menos 1 o bien un múltiplo de 4 más 1, esto es, es de la forma 4k – 1 o 4k + 1, para todo número natural k. El único primo par es 2. De modo que todo primo debe cumplir una de las siguientes condiciones:

• ser igual a 2

• ser de la forma 4k + 1

• ser de la forma 4k – 1

Los primos que faltan en mi lista de la suma de dos cuadrados son precisamente los primos de la forma 4k – 1.

Estos primos pueden aparecer como factores de los números en la lista. Observa al 3, por ejemplo, que es factor de 9, 18, 36, 45, 72, 81 y 90. No obstante, todos estos números son en realidad múltiplos de 9, esto es, de 32.

Si observas listas más largas desde el mismo punto de vista, aparece un patrón sencillo. En su carta, Fermat afirmaba haber probado que los números distintos de cero que son suma de dos cuadrados son precisamente aquellos para los que todo factor primo de la forma 4k – 1 aparece con una potencia par. La parte más difícil era probar que todo primo de la forma 4k + 1 es la suma de dos cuadrados. Albert Girard solo había llegado a hacer conjeturas en 1632, pero no había probado nada.

La tabla incluye algunos ejemplos, pero comprobemos el argumento de Fermat con algo un poco más ambicioso. El número 4.001 es claramente de la forma 4k + 1; basta tomar k igual a 1.000. Es también primo. Por el teorema de Fermat, debería ser una suma de dos cuadrados. ¿Cuáles?

En ausencia de un método más inteligente, podemos intentar sustraer 12, 22, 32, etcétera por turnos, y ver si obtenemos un cuadrado. Los cálculos empiezan así:

4.001 – 12 = 4.000: no es un cuadrado

4.001 – 22 = 3.997: no es un cuadrado

4.001 – 32 = 3.992: no es un cuadrado

...

Y finalmente llegamos a

4.001 – 402 = 2.401: es el cuadrado de 49

De modo que

4.001 = 402 + 492

y Fermat lo explica usando un ejemplo.

Esta es esencialmente la única solución, además de 492 + 402. Obtener un cuadrado restando un cuadrado de 4.001 es un resultado raro, casi parece que fortuito. Fermat explicó por qué no lo es. También sabía que cuando 4k + 1 es primo, hay solo un modo de dividirlo en dos cuadrados.

En general, no hay un camino sencillo y práctico de encontrar los números correctos. Gauss proporcionó una fórmula, pero no es muy práctica. La prueba tiene que demostrar que el cuadrado requerido existe, aunque sin proporcionar una manera rápida de encontrarlo, lo cual es algo técnico y requiere mucha preparación, por lo que no intentaré explicar la demostración aquí. Uno de los encantos de las matemáticas es que afirmaciones verdaderas y sencillas no siempre se demuestran fácilmente.

SISTEMA BINARIO

Nuestro sistema numérico tradicional se llama «decimal», porque usa 10 como su número base y en latín 10 es decem. Hay diez dígitos 0-9 y el valor de los dígitos se multiplica por 10 en cada posición que se avanza de derecha a izquierda. Así, 10 significa diez; 100, un centenar, 1.000, un millar; etcétera [véase 10].

Pueden establecerse sistemas de notación similares para números usando cualquier número como base. El más importante de estos sistemas de notación alternativos, llamado binario, usa base 2. Tiene solo dos dígitos, 0 y 1, y el valor de un dígito se dobla en cada posición que avanza de derecha a izquierda. En binario, 10 quiere decir 2 (usando nuestra notación decimal), 100 quiere decir 4, 1.000 quiere decir 8, 10.000 quiere decir 16, etcétera.

Para obtener números que no son potencias de 2, sumamos distintas potencias de 2. Por ejemplo, 23 en decimal es igual a

16 + 4 + 2 + 1

que usa un 16, ningún 8, un 4, un 2 y un 1. De modo que en notación binaria pasa a ser

10111

Los primeros números binarios y sus equivalentes decimales son:

decimal binario decimal binario
00111011
11121100
210131101
311141110
4100151111
51011610000
61101710001
71111810010
810001910011
910012010100
1010102110101

Tabla 3

Para «decodificar» los símbolos, por ejemplo, para el número 20, los escribimos como potencias de 2:

 1   0   1   0   0

16   8   4   2   1

Las potencias de 2 que se dan con el símbolo 1 son 16 y 4. Súmalas: el resultado es 20.

Historia

En algún momento entre 500 a. C. y 100 a. C., el académico hindú Pingala escribió un libro llamado Chandaḥśāstra sobre rimas en poesía y listó diferentes combinaciones para sílabas largas y breves. Clasificó esas combinaciones usando una tabla, la cual en su forma moderna usa 0 para una sílaba breve y 1 para una larga. Por ejemplo,

00 = breve-breve

01 = breve-larga

10 = larga-breve

11 = larga-larga

Los patrones aquí son los mismos que en la notación binaria, pero Pingala no hacía cálculos aritméticos con sus símbolos.

El antiguo libro chino de adivinación, el I Ching (Yì Jīng), usaba 64 conjuntos de seis líneas horizontales, bien completas (yang) o partidas en dos (yin), como un oráculo. Estos conjuntos se conocen como hexagramas. Cada hexagrama consiste en dos trigramas puestos uno sobre otro. Originariamente el hexagrama era usado para predecir el futuro, arrojando tallos de milenrama al suelo y aplicando unas reglas para determinar qué hexagrama deberías observar. Más tarde pasaron a usarse tres monedas.

Si usamos 1 para representar una línea completa (yang) y 0 para una partida (yin), cada hexagrama se corresponde a un número binario de seis dígitos. Por ejemplo, el hexagrama en la Figura es 010011. Según el método de adivinación, este es el hexagrama 60 (= jié), e indica «articulación», «limitación» o «moderación». Una interpretación típica (no me pidas que la explique porque no tengo ni idea) comienza:

Limitación Sobre: k’an lo catastrófico, agua. Bajo: tui la alegría, lago.

Juicio Limitación, éxito. Limitación irritante no debe ser perseverada.

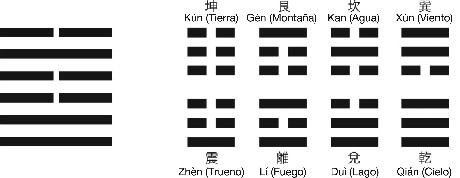
Figura 11. A la izquierda, un hexagrama. A la derecha, los ocho trigramas.

Image Agua sobre lago: la imagen de la limitación. Así el hombre superior crea números y medida, y examina la naturaleza de la virtud y la conducta correcta.

De nuevo, aunque los patrones binarios están presentes en el I Ching, la aritmética no lo está. En los escritos de Thomas Harriot (1560-1621) aparece más sobre la estructura matemática de los símbolos binarios, que dejó miles de páginas de manuscritos no publicados. Uno de ellos contiene una lista que empieza

1 1

2 2

3 2 + 1

4 4

5 4 + 1

6 4 + 2

7 4 + 2 + 1

y continúa hasta

30 = 16 + 8 + 4 + 2

31 = 16 + 8 + 4 + 2 + 1

Está claro que Harriot entendió el principio básico de la notación binaria. Sin embargo, el contexto de esta lista es una larga serie de tablas enumerando cómo varios objetos pueden combinarse de maneras diferentes, no aritmética.

En 1605, Francis Bacon explicó cómo codificar letras del alfabeto como secuencias de dígitos binarios, y se acercó mucho a usarlas como números. Los binarios finalmente llegaron como una notación aritmética en 1697, cuando Leibniz escribió al duque Rudolph de Brunswick proponiendo un «medallón o moneda conmemorativo».

Figura 12. Medallón binario de Leibniz.

El diseño muestra una tabla de las representaciones binarias de los números del 0 al 15, con la inscripción Omnibus ex nihilo ducendis sufficit unum («Para todo lo que surge de la nada, uno basta»). Matemáticamente, Leibniz está indicando que si tienes el símbolo 0 (nada) y añades el 1 (uno), entonces puedes obtener cualquier número (todo). Pero también estaba haciendo una afirmación religiosa simbólica: un único Dios puede crear todo de la nada.

La medalla nunca se acuñó, pero su solo diseño fue un paso significativo. En 1703, Leibniz estaba desarrollando las matemáticas binarias y publicó un artículo «Explication de l’arithmétique binaire» en Mémoires de l’Académie Royale des Sciences. Escribió: «En lugar de esta progresión por las decenas [notación decimal], durante muchos años he usado la más sencilla de todas, la que va de dos en dos». Indica que las reglas para la aritmética binaria son tan sencillas que nadie se puede olvidar de ellas, pero también dice que, debido a que la forma binaria de un número es alrededor de cuatro veces más larga que su forma decimal, el método no es práctico. En cierto modo profético, también dijo que «el cálculo de dos en dos es más fundamental para la ciencia y proporciona nuevos descubrimientos» y «estas expresiones de números facilitan mucho todo tipo de operaciones».

Esto es lo que tenía en mente. Para realizar cálculos aritméticos con números binarios, todo lo que necesitas saber es:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0 llevando 1

0 × 0 = 0

0 × 1 = 0

1 × 0 = 0

1 × 1 = 1

Una vez que conoces esta información sencilla, puedes sumar y multiplicar dos números binarios cualesquiera, usando métodos similares a los que usas en aritmética ordinaria. También puedes hacer restas y divisiones.

Computación digital

Ahora sabemos que Leibniz dio en el clavo cuando sugirió que el sistema binario sería «fundamental para la ciencia». El sistema binario fue originariamente una rareza matemática, pero la invención de ordenadores digitales ha cambiado esto. La electrónica digital está basada en una distinción simple entre presencia, o ausencia, de una señal eléctrica. Si simbolizamos estos dos estados con 1 y 0, la razón para trabajar con un sistema binario se hace evidente. En principio, podemos construir ordenadores usando el sistema decimal, por ejemplo, permitiendo que los dígitos 0-9 se correspondan con señales a 0 voltios, 1 voltio, 2 voltios, etcétera. Sin embargo, en cálculos complicados se darían imprecisiones y no estaría claro si una señal de, por ejemplo, 6,5 voltios es el símbolo 6 en un voltaje elevado, o el símbolo 7, en uno reducido. Usando solo dos niveles de voltaje, muy separados, las ambigüedades de este tipo pueden eliminarse asegurándose que el error es siempre mucho más pequeño que la diferencia entre los dos niveles.

Con los métodos de fabricación actuales, sería posible construir ordenadores fiables usando base 3, o bases mayores, en lugar de 2. Pero ya se ha fabricado una cantidad enorme de tecnología usando el sistema binario, y es fácil pasar de binario a decimal como parte de la computación, de modo que otras bases no proporcionan una ventaja lo suficientemente grande comparadas con el sistema binario estándar.

PARIDAD DE UNA PERMUTACIÓN

La distinción entre números pares e impares es especialmente importante en la teoría de permutaciones, la cuales son modos de reordenar un lista ordenada de números o letras u otros objetos matemáticos. Si la lista contiene n objetos, entonces el número total de permutaciones posibles es el factorial

n! = n × (n – 1) × (n – 2) × ... × 3 × 2 × 1

porque podemos escoger el primer número de n maneras, el segundo de n – 1, el tercero de n – 2, etcétera [véase 26!].

Hay dos tipos de permutaciones: pares e impares. Las permutaciones pares intercambian el orden de un número de pares de objetos par; las permutaciones impares intercambian el orden de un número de pares de objetos impar. Enseguida hablaré de esto con más detalle. A este «par» o «impar» se le conoce como la paridad de la permutación.

De las n! posibles permutaciones, exactamente la mitad son pares y la otra mitad impares (excepto n = 1, caso en el que hay una permutación par y ninguna impar). De modo que cuando n ≥ 2, hay 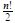permutaciones pares y n!

2 impares.

Podemos comprender la diferencia entre permutaciones pares e impares usando diagramas. Por ejemplo, piensa en la permutación (que llamaremos A) que empieza con la lista

1, 2, 3, 4, 5

y la reordena del siguiente modo:

2, 3, 4, 5, 1

Los números en la lista se mueven como ves en la Figura:

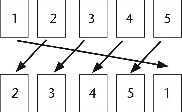
Figura 13. Diagrama para la permutación A.

De manera similar, si empezamos con la lista

2, 3, 4, 5, 1

y la reordenamos así:

4, 2, 3, 1, 5

entonces los símbolos se mueven como se indica en el siguiente diagrama:

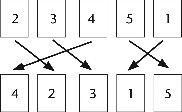
Figura 14. Diagrama para la permutación B.

Llama a esta permutación B. Observa que la lista en la que empezamos no necesita estar en un orden numérico habitual. Lo que cuenta no es el orden como tal, sino cómo este cambia.

Composición de permutaciones

Podemos componer (o combinar) dos permutaciones para crear otra. Al hacer esto, reordenamos la lista según la primera permutación y luego la reordenamos según la segunda. El proceso es más fácil de entender al poner los dos diagramas juntos.

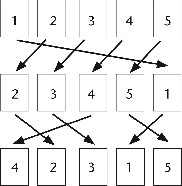
Figura 15. Diagrama de la permutación A seguida de la B.

Las dos permutaciones A y B se muestran con la fila superior de flechas y la fila inferior de flechas. Para componerlas (con lo que obtendremos una permutación que llamaré AB), seguimos pares de flechas que se correspondan y eliminamos la fila de números de en medio. Obtenemos esto:

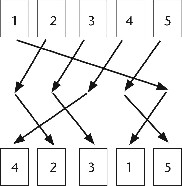
Figura 16. Diagrama para la permutación AB, antes de unificar las flechas.

Finalmente, unificamos las flechas para obtener:

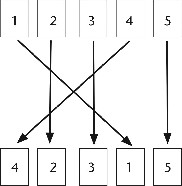
Figura 17. Diagrama para la permutación AB, después de unificar las flechas.

Esta es la permutación que convierte a la lista

1, 2, 3, 4, 5

en la lista

4, 2, 3, 1, 5.

Número de intersecciones y paridad

En la permutación A, la flecha más larga cruza las otras cuatro flechas. Decimos que esta permutación tiene un total de 4 intersecciones y lo escribimos como c(A) = 4. La permutación B tiene 3 intersecciones, c(B) = 3. Su composición AB tiene 5 intersecciones, c(AB) = 5.

Antes de que unificásemos las flechas, AB tenía 7 intersecciones. Es la suma del número de intersecciones de A y B: 4+3=7. Cuando unificamos las flechas, dos intersecciones desaparecieron, las dos en la parte de la derecha. Estas dos flechas se cruzaban la una con la otra, y luego se volvían a cruzar. De modo que la segunda intersección «anula» a la primera.

Esta observación es cierta en general. Si componemos dos permutaciones cualesquiera A y B para obtener AB, entonces, antes de que se unifiquen y enderecen las flechas, el número de intersecciones de AB es el número de A más el número de B. Cuando enderezamos las flechas, el número de intersecciones puede permanecer igual o se sustrae un número par. De modo que aunque c(AB) no necesariamente es igual a c(A) + c(B), su diferencia es siempre par. Y eso significa que la paridad de c(AB) es la suma de las paridades de c(A) y c(B).

Decimos que una permutación A es par si c(A) es par, e impar si c(A) es impar. Por consiguiente, la paridad de la permutación A es «par» o «impar».

Una permutación par intercambia el orden de un número de pares de símbolos par.

Una permutación impar intercambia el orden de un número de pares de símbolos impar.

Esto implica que cuando componemos permutaciones:

par compuesto con par da par

impar compuesto con impar da par

par compuesto con impar da impar

impar compuesto con par da impar

igual que cuando se suman números pares e impares. Estas propiedades se usan en todas partes en matemáticas.

JUEGO DEL 15

Las paridades de las permutaciones podrían parecer un tema bastante técnico, pero tienen muchas aplicaciones. Una de las más entretenidas es un juego inventado por un norteamericano llamado Noyes Chapman. Se hizo muy popular y se extendió a lo largo de Estados Unidos, Canadá y Europa. El empresario Matthias Rice lo fabricó como el Gem Puzzle y un dentista llamado Charles Pevey ofreció un premio a quien fuese capaz de resolverlo. Se le conoce también con otros nombres como Cuadrado místico o Puzle del 15.

El juego está formado por 15 piezas cuadradas corredizas, numeradas del 1 al 15; se empieza con los números ordenados excepto por el 14 y el 15 y una casilla vacía en la parte inferior a la derecha (véase la Figura de la izquierda). El objetivo del juego es deslizar piezas sucesivas en la casilla vacía (que se mueve a medida que las piezas se deslizan) y poner los cuadrados en el orden correcto (Figura de la derecha).

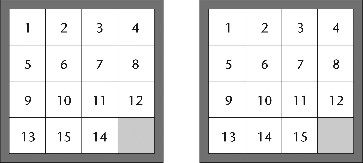
Figura 18. Se empieza esto... ... y se acaba con esto.

Este juego suele atribuirse al famoso autor de rompecabezas Sam Loyd, que reavivó el interés en él en 1886 ofreciendo un premio de mil libras. Sin embargo, Loyd estaba seguro de que el dinero no corría riesgo, porque en 1879, William Johnson y William Story habían probado que el Juego del 15 no tenía solución.

El punto fundamental es que cualquier posición en el juego puede pensarse como una permutación de la posición original, contando la casilla vacía como una «virtual» decimosexta pieza. La posición original, junto un par de piezas (14 y 15) intercambiadas, es una permutación impar de la posición final que se desea. Pero el requisito de que la casilla vacía acabe en el mismo sitio que empezó, implica que los movimientos permitidos solo llevan a permutaciones pares.

Por lo tanto, los movimientos permitidos, empezando por cualquier estado inicial, pueden llegar exactamente a la mitad de 16! reordenamientos posibles, que son 10.461.394.944.000 reordenamientos. Por ensayo y error es imposible explorar más de una fracción de estas posibles disposiciones, lo cual fácilmente puede convencer a la gente de que si lo siguen intentando, podrían dar con una solución.

ECUACIONES CUADRÁTICAS

Los matemáticos distinguen las ecuaciones algebraicas por su grado, que es la mayor potencia de la incógnita que aparece. El grado de la ecuación

5x – 10 = 0

es uno, porque solo aparece la potencia de uno de x. El grado de

x2 – 3x + 2 = 0

es dos, porque aparece el cuadrado (la potencia de 2) de x, pero no aparecen potencias mayores. El grado de

x3 – 6x2 + 11x – 6 = 0

es tres. Y así sucesivamente.

Hay nombres especiales para las ecuaciones de grados pequeños:

grado 1 = lineal

grado 2 = cuadrática

grado 3 = cúbica

grado 4 = cuártica

La principal tarea cuando aparece una ecuación es resolverla. Esto es, encontrar el valor (o valores) de la incógnita x que la verifiquen. La ecuación lineal 5x – 10 = 0 tiene la solución x = 2, porque 5 × 2 – 10 = 0. La ecuación cuadrática x2– 3x + 2 = 0 tiene la solución x = 1, porque 12 – 3 × 1 + 2 = 0, pero también tiene una segunda solución x = 2, porque 22 – 3 × 2 + 2 = 0. La ecuación cúbica x3 – 6x2 + 11x – 6 = 0 tiene tres soluciones, x = 1, 2 o 3. El número de soluciones (reales) es siempre menor o igual que el grado.

Las ecuaciones lineales son fáciles de resolver y se han conocido métodos generales durante miles de años, que se remontan a mucho antes de que se inventara el álgebra simbólica. No sabemos exactamente cuándo, porque no existen los registros adecuados.

Las ecuaciones cuadráticas, de grado dos, son más complicadas. Pero el modo de resolverlas era conocido en la antigua Babilonia, hace 4.000 años, y es lo que veremos a continuación. Me ocuparé de las ecuaciones cúbicas, cuárticas y de grado cinco en los capítulos 3, 4 y 5.

La solución babilónica

Figura 19. Dos tablas matemáticas babilónicas.

En 1930, el historiador matemático Otto Neugebauer identificó tablas de barro de la antigua Babilonia que explicaban cómo resolver ecuaciones cuadráticas.

Primero necesitamos saber un poco sobe la notación numérica de Babilonia. No usaban base 10, sino base 60. De modo que 2.015 en notación babilónica (usaban marcas con forma de cuña en el barro, en lugar de nuestros dígitos) significaba:

2 × 603 + 0 × 602 + 1 × 601 + 5 × 600

que es:

2 × 216.000 + 0 × 3.600 + 1 × 60 + 5 × 1 = 432.065

en base decimal. Tenían también una versión de nuestra coma decimal, sumando múltiplos de 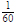, , 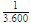etcétera.

Los historiadores reescriben los dígitos babilónicos así:

2,0,1,5

y usan un punto y coma en lugar de la coma decimal. Por ejemplo:

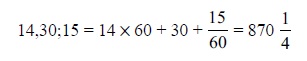
Figura 20. Símbolos cuneiformes babilónicos para los números 1-59.

Veamos ahora la ecuación cuadrática. Una tabla babilónica, que se remonta alrededor de 4.000 años, plantea: «Encuentra el lado de un cuadrado si el área menos el lado es 14,30». Este problema involucra al cuadrado de una incógnita (el área del cuadrado), así como a la propia incógnita, de modo que se reduce a una ecuación cuadrática. En la tabla siguiente se explica cómo obtener la respuesta:

Instrucciones babilónicas Nuestra notación
Toma la mitad de 1, la cual es 0;30
Multiplica 0;30 por 0;30, que da 0;15
Suma esto a 14,30 para obtener 14,30;15(14 × 60 + 3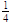0) + = 870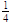
Esto es el cuadrado de 29;30870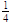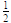 = (29) × (29)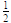
Ahora suma 0;30 a 29;3029 +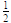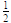
El resultado es 30, el lado del cuadrado30

Tabla 4

El paso más complicado es el cuarto, que haya un número (es 29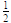) cuyo cuadrado es 870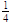. El número 29 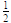es la raíz cuadrada de 870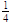. Las raíces cuadradas son la principal herramienta para resolver ecuaciones cuadráticas.

Esta presentación es típica de las matemáticas babilónicas. La descripción involucra a números específicos, pero el método es más general. Si cambias los números sistemáticamente y sigues el mismo procedimiento, puedes resolver otras ecuaciones cuadráticas. Si usas notación algebraica moderna, reemplazando los números con símbolos, y empiezas con una ecuación cuadrática general:

ax2 + bx + c = 0

entonces el método babilónico produce la respuesta

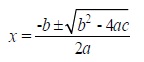
Puede que la reconozcas: en efecto, es la fórmula que nos enseñaron en la escuela.