Capítulo 2

La esencia de la simetría

Para la mayoría de la gente, la matemática trata sobre números. Imaginan a los matemáticos como personas que se pasan el día procesando números: números grandes y números más grandes aún, con nombres exóticos. Yo también lo pensaba..., al menos, hasta que Yevgueni Yevguénievich me presentó los conceptos e ideas de las matemáticas modernas. Uno de ellos resultó ser clave para el descubrimiento de los quarks: el concepto de simetría.

¿Qué es la simetría? Todos comprendemos intuitivamente qué es: la reconocemos cuando la vemos. Cuando pido a la gente que me dé un ejemplo de simetría, suelen mencionar mariposas, copos de nieve o el cuerpo humano.

Pero si les pregunto qué significa que un objeto determinado es simétrico, dudan.

Yevgueni Yevguénievich me la explicó así:

—Observemos esta mesa cuadrada y esta mesa redonda —dijo, señalándome las dos mesas de la oficina—. ¿Cuál es más simétrica?

—La redonda, claro, ¿no es obvio?

—Pero ¿por qué? Ser matemático significa que uno no da nada por obvio, sino que intenta razonarlo. Muy a menudo te darás cuenta de que la respuesta más obvia es errónea.

Al ver mi cara de confusión, Yevgueni Yevguénievich me dio una pista:

—¿Cuál es la propiedad de la mesa redonda que la hace más simétrica?

Pensé en el tema durante un rato y de repente me di cuenta:

—Supongo que la simetría de un objeto tiene que ver con que mantenga su forma y su posición cuando se le aplican cambios.

Yevgueni Yevguénievich asintió.

—Efectivamente. Veamos todas las posibles transformaciones de una mesa que conservan su forma y su posición —dijo—. En el caso de la mesa redonda...

Le interrumpí:

—Cualquier rotación en torno a su centro valdrá. Tendremos la misma mesa en la misma posición. Pero si aplicamos una rotación arbitraria a una mesa cuadrada, tendremos una mesa cambiada de posición. Solo las rotaciones de 90 grados y sus múltiplos la mantendrían sin cambios en su aspecto.

—¡Exacto! Si te fueras de la oficina durante un minuto y yo girara la mesa redonda en cualquier ángulo, no notarías la diferencia. Pero si hiciera lo mismo con la mesa cuadrada, lo verías, a menos que yo la girara 90, 180 o 270 grados.

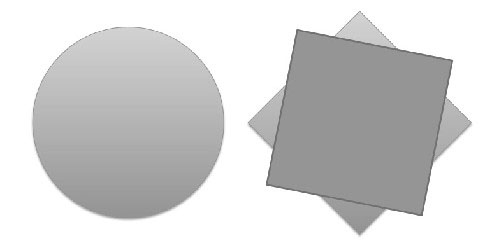
Si aplicamos a una mesa redonda una rotación de un ángulo cualquiera no cambia, pero si a una mesa cuadrada le aplicamos una rotación de un ángulo que no sea múltiplo de 90, sí cambia (ambas vistas desde arriba).

Continuó:

—A estas transformaciones se les denomina simetrías. De modo que, como ves, la mesa cuadrada tiene cuatro simetrías de rotación, mientras que la mesa redonda tiene muchas más: en realidad, infinitas más. Por eso decimos que la mesa redonda es más simétrica.

Tenía mucho sentido.

—Esta es una observación bastante directa —continuó Yevgueni Yevguénievich—. No es necesario ser matemático para ver esto. Pero si eres un matemático, te harás la siguiente pregunta: ¿cuáles son todas las posibles simetrías de un objeto?

—Examinemos el caso de la mesa cuadrada. Sus simetrías¹ son estas cuatro rotaciones alrededor del centro de la mesa: de 90 grados, de 180 grados, de 270 grados y de 360 grados, en el sentido contrario a las agujas del reloj.² Un matemático diría que el conjunto de simetrías de la mesa cuadrada consiste en cuatro elementos, que se corresponden a los ángulos 90, 180, 270 y 360. Cada rotación lleva a una de las esquinas (marcada con un círculo en la figura) a uno de los cuatro rincones.

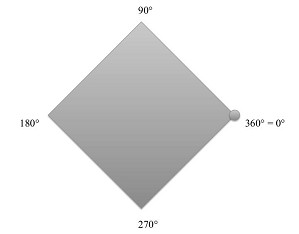
—Una de estas rotaciones es especial: la rotación a 360 grados es la misma que la rotación a 0 grados, es decir, que ninguna rotación. Se trata de una simetría especial porque, en realidad, no hace nada a nuestro objeto: cada punto de la mesa acaba exactamente en la misma posición en que estaba al principio. La llamamos identidad.³

Téngase en cuenta que una rotación en cualquier ángulo superior a 360 grados equivale a una rotación de un ángulo entre 0 y 360 grados. Por ejemplo, una rotación de 450 grados es lo mismo que una rotación de 90 grados, porque 450 = 360 + 90.

Es por eso por lo que solo tenemos en cuenta las rotaciones en ángulos de entre 0 y 360 grados.

Aquí llega la observación crucial: si aplicamos dos rotaciones de la lista (90, 180, 270, 360 grados) una después de la otra, obtendremos otra rotación de la misma lista. Llamamos a esta nueva simetría una composición de las dos.

Como es obvio, cualquiera de las dos simetrías conserva la mesa: por tanto, la composición de ambas también la conserva. Ergo, esta composición también ha de ser una simetría. Por ejemplo, si rotamos la mesa 90 grados y luego otros 180 grados, el resultado neto de la operación es una rotación de 270 grados.

Veamos qué ocurre con la mesa al aplicar estas simetrías. Tras la rotación de 90 grados en el sentido contrario a las agujas del reloj, la esquina de la derecha (la que está marcada con un punto en la imagen anterior) pasará a ser la esquina superior. Luego, aplicamos una rotación de 180 grados, de modo que la esquina superior pasa a ser la esquina de la parte inferior. El resultado final será que la esquina de la derecha pasará a ser la esquina de la parte inferior. Esto es el resultado de una rotación de 270 grados en sentido contrario a las agujas del reloj.

He aquí otro ejemplo:

90º + 270º = 0º

Al rotar 90 grados y luego 270 grados más, obtenemos una rotación total de 360 grados. Pero el efecto de una rotación de 360 grados es el mismo que el de una rotación de 0 grados, como hemos visto antes. Esta es la «identidad».

En otras palabras: la segunda rotación de 270 grados deshace la rotación inicial de 90 grados. Esta es, en realidad, una propiedad importante: toda simetría puede deshacerse, es decir: para toda simetría S existe otra simetría S' tal que su composición sea la identidad. A esta S' se le llama el inverso de la simetría S. De modo que vemos que la rotación de 270 grados es el inverso de la rotación de 90 grados. De igual manera, el inverso de una rotación de 180 grados es la misma rotación de 180 grados.

Ya vemos que lo que parecía una sencilla agrupación de simetrías de la mesa cuadrada (las rotaciones de 90, 180, 270 y 360 grados) en realidad tiene una enorme estructura interna, o reglas de cómo pueden interactuar los miembros del conjunto.

En primer lugar, podemos componer dos simetrías cualesquiera (es decir, aplicarlas una tras la otra).

En segundo lugar, existe una simetría especial, la identidad. En nuestro ejemplo, es la rotación de 0 grados. Si la componemos con cualquier otra simetría, obtenemos nuevamente esa simetría. Por ejemplo:

90º + 0º = 90º, 180º + 0º = 180º, etc.

En tercer lugar, para toda simetría S existe una simetría inversa S' tal que la composición de S y S' sea la identidad.

Y ahora llegamos al punto esencial: el conjunto de rotaciones, junto con estas tres estructuras, constituye un ejemplo de lo que los matemáticos denominan un grupo.

Las simetrías de cualquier otro objeto también constituyen un grupo, que en general tiene más elementos: posiblemente, infinitos.⁴

Veamos cómo funciona esto en el caso de la mesa redonda. Ahora que ya tenemos cierta experiencia, vemos fácilmente que el conjunto de todas las simetrías de la mesa redonda es el conjunto de todas sus posibles rotaciones (no solo los múltiplos de 90 grados) y podemos visualizarlo como el conjunto de todos los puntos de la circunferencia.

Cada punto de esta circunferencia corresponde a un ángulo de entre 0 y 360 grados, y que representa la rotación de la mesa en ese ángulo en sentido contrario a las agujas del reloj. Sobre todo, hay un punto especial que corresponde a una rotación de 0 grados. Está marcado en el diagrama de abajo, junto a otro punto correspondiente a una rotación de 30 grados.

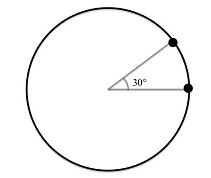
Pero no deberíamos pensar en los puntos de esta circunferencia como puntos de la mesa redonda. Más bien, cada punto de la circunferencia representa una rotación determinada de la mesa redonda. Fíjese en que la mesa no tiene un punto preferido, pero nuestro círculo sí: el que corresponde a una rotación de 0 grados.⁵

Veamos ahora si las tres estructuras antes mencionadas se pueden aplicar al conjunto de puntos de la circunferencia.

En primer lugar, la composición de dos rotaciones, en los ángulos φ₁ y φ₂, es la rotación de la suma de ángulos φ₁+φ₂. Si φ₁ +φ₂ es mayor que 360 grados, sencillamente restamos 360 grados. En matemáticas, a esto se le llama suma de módulo 360. Por ejemplo, si φ₁ = 195º y φ₂ = 250º, la suma de los dos ángulos es de 445º, y una rotación de 445º es igual que una rotación de 85º. De modo que en el grupo de rotaciones de la mesa redonda, tenemos que

195º + 250º = 85º.

En segundo lugar, hay en la circunferencia un punto especial que corresponde a una rotación de 0 grados. Es el elemento identidad de nuestro grupo.

En tercer lugar, el inverso de la rotación en sentido contrario a las agujas del reloj de φ grados es la rotación en sentido contrario a las agujas del reloj de (360−φ) grados, o, de manera equivalente, a la rotación en sentido de las agujas del reloj de φ grados (véase figura).

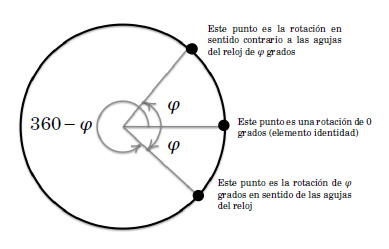
Así hemos descrito el grupo de rotaciones de la mesa redonda. Le llamaremos grupo circular. A diferencia del grupo de simetrías de la mesa cuadrada, que tiene cuatro elementos, este grupo tiene infinitos elementos más porque hay infinitos ángulos entre 0 y 360 grados.

Hemos puesto ahora nuestra intuición acerca de la simetría sobre bases sólidas: en efecto, la hemos convertido en un concepto matemático. En primer lugar, hemos postulado que la simetría de un objeto determinado es una transformación que conserva este objeto y sus propiedades. Y hemos dado un paso decisivo: nos hemos centrado en el conjunto de todas las simetrías posibles de este objeto. En el caso de la mesa cuadrada, este conjunto rotacional consiste en cuatro elementos (rotaciones de ángulos múltiplos de 90 grados); en el caso de una mesa redonda, es un conjunto infinito (todos los puntos de la circunferencia). Finalmente, hemos descrito las precisas estructuras que este conjunto de simetrías posee siempre: se pueden componer dos simetrías cualesquiera para obtener otra simetría; existe la simetría identidad y para toda simetría existe su simetría inversa. La composición de simetrías satisface también la propiedad de asociatividad (descrita en la nota 4). De este modo hemos llegado al concepto matemático de grupo.

Un grupo de simetrías es un objeto abstracto muy diferente del objeto concreto con el que comenzamos. No podemos tocar ni sostener el conjunto de simetrías de una mesa (a diferencia de la propia mesa) pero podemos imaginarlo, dibujar sus elementos, estudiarlo y hablar de él. Todos los elementos de este conjunto abstracto tienen un sentido concreto: representan una transformación puntual de un objeto concreto, su simetría.

Las matemáticas tratan del estudio de objetos abstractos y conceptos como estos.

La experiencia demuestra que la simetría es un principio básico que ejerce de guía para las leyes naturales. Por ejemplo, un copo de nieve tiene una forma hexagonal perfecta porque este es el estado de energía mínima en que las moléculas de agua pueden cristalizar. Las simetrías del copo de nieve son rotaciones en múltiplos de 60 grados, es decir, en 60, 120, 180, 240, 300 y 360 grados (que es la misma que a 0 grados). Además, podemos «voltear» el copo de nieve en torno a cualquiera de los seis ejes correspondientes a esos ángulos. Todas estas rotaciones y giros conservan la forma y posición del copo de nieve, y son, por tanto, sus simetrías.^*

En el caso de una mariposa, voltearla equivaldría a ponerla patas arriba. Dado que tiene patas en uno de sus lados, voltearla no sería una geometría, estrictamente hablando, de la mariposa. Cuando decimos que una mariposa es simétrica estamos hablando de una versión idealizada de la misma, en la que la parte frontal y la de atrás son idénticas, a diferencia de las de una mariposa real. En tal caso, el volteo, que intercambia las alas de derecha e izquierda, sí que se convierte en una simetría (también podríamos pensar en intercambiar las alas de la mariposa sin darle la vuelta).

Esto nos lleva a un punto importante: hay muchos objetos en la naturaleza cuyas simetrías son aproximadas. Una mesa real no es perfectamente redonda ni cuadrada; una mariposa presenta asimetría entre el lado delantero y el de atrás; un cuerpo humano no es completamente simétrico.

Sin embargo, en estos casos resulta útil pensar en versiones abstractas e idealizadas, o modelos: una mesa perfectamente redonda o cuadrada, o una imagen de una mariposa sin distinción entre ambas caras. Entonces exploramos simetrías de estos objetos idealizados y ajustamos las inferencias que hayamos podido extraer del análisis para que tenga en cuenta las diferencias entre el objeto real y el modelo.

Esto no significa que no apreciemos la asimetría: lo hacemos, y a menudo hallamos belleza en ella. Pero el objetivo principal de la teoría matemática de simetrías no es el estético. Es formular el concepto de simetría en los términos más generales y, por tanto, más abstractos, que se puedan aplicar de manera unificada en diferentes dominios como la geometría, la teoría de números, la física, la química, la biología, etcétera. Una vez enunciamos dicha teoría, podemos hablar de los mecanismos de ruptura de simetría, ver la asimetría emergente, en otras palabras. Por ejemplo, las partículas elementales adquieren masa porque la llamada simetría de gauge a que obedecen (que se tratará en el capítulo 16) se rompe. Esto lo facilita el bosón de Higgs, una escurridiza partícula recientemente descubierta en el Gran Colisionador de Hadrones que hay bajo la ciudad de Ginebra.⁶ El estudio de estos mecanismos de ruptura de simetría proporciona valiosísimas reflexiones acerca del comportamiento de los ladrillos fundamentales de la naturaleza.

Me gustaría señalar algunas de las cualidades básicas de la teoría abstracta de simetrías porque constituye un buen ejemplo de por qué las matemáticas son importantes.

La primera es la universalidad. El grupo circular no es tan solo el grupo de simetrías de una mesa redonda, sino también el de todos los demás objetos redondos, como un vaso, una botella, una columna, etcétera. En realidad, decir que un objeto es redondo es lo mismo que decir que su grupo de simetrías es el grupo circular. Es una frase poderosa: vemos que podemos describir un importante atributo de un objeto («que es redondo») describiendo su grupo de simetrías (el círculo). De igual manera, «ser cuadrado» significa que su grupo de simetrías de rotación es el grupo de cuatro elementos arriba descrito. En otras palabras, el mismo objeto abstracto matemático (por ejemplo, el grupo circular) sirve para muchos objetos concretos diferentes, y señala propiedades universales que todos tienen en común (como su cualidad de redondos).⁷

La segunda es la objetividad. El concepto de un grupo, por ejemplo, es independiente de nuestra interpretación. Significa lo mismo para todos aquellos que lo aprenden. Evidentemente, para comprenderlo, uno ha de conocer el lenguaje en que se expresa, es decir, el lenguaje matemático. Pero cualquiera puede aprender ese lenguaje. De igual manera, si uno quiere aprender el significado de la frase de René Descartes Je pense, donc je suis, necesitará saber francés (al menos, las palabras empleadas en la frase)... pero cualquiera puede aprenderlo. Sin embargo, en el caso de esta última frase, una vez la comprendamos, serán posibles distintas interpretaciones. Además, diferentes personas pueden estar de acuerdo o en desacuerdo con respecto a cualquier interpretación acerca de si la frase es cierta o no. Sin embargo, el significado de una frase matemática consistente no está sujeto a interpretaciones.⁸ Además, su verdad es objetiva. (Por norma general, la verdad de una determinada afirmación puede depender del sistema de axiomas dentro del cual se enmarque. Sin embargo, incluso en ese caso, la dependencia de esos axiomas es también objetiva.) Por ejemplo, la afirmación «el grupo de simetrías de una mesa redonda es el círculo» es verdadera para todo el mundo, en cualquier lugar, en cualquier momento. Dicho de otra manera: las verdades matemáticas son las verdades necesarias. Hablaremos más de esto en el capítulo 18.

La tercera cualidad, estrechamente relacionada, es la resistencia. No cabe duda de que el teorema de Pitágoras significaba lo mismo para los antiguos griegos que hoy en día para nosotros, y existen todas las razones del mundo para suponer que significará lo mismo para cualquiera en el futuro. De la misma manera, todas las afirmaciones matemáticas de las que hablaremos en este libro serán verdaderas para siempre.

El hecho de que exista un conocimiento objetivo y perdurable (y más aún, de que nos pertenezca a todos) es poco menos que un milagro. Sugiere que los conceptos matemáticos existen en un mundo separado de los mundos físico y mental, al que a veces se llama mundo platónico de las matemáticas: hablaremos de ello en el capítulo final. Aún no comprendemos exactamente qué es y qué impulsa el descubrimiento matemático. Pero es evidente que esta realidad oculta jugará un papel cada vez más grande en nuestras vidas, especialmente con el advenimiento de las nuevas tecnologías informáticas y de la impresión 3D.

La cuarta cualidad es la relevancia de las matemáticas con respecto al mundo físico. Por ejemplo, se han realizado grandes progresos en física cuántica en los últimos cincuenta años gracias a la aplicación del concepto de simetría a las partículas elementales y a la interacción entre ellas. Desde este punto de vista, una partícula, como un electrón o un quark, es como una mesa redonda o un copo de nieve, y su comportamiento está determinado en gran manera por sus simetrías. Algunas de esas simetrías son exactas y otras son aproximadas.

El descubrimiento de los quarks es un ejemplo perfecto de cómo funciona esto. Al leer los libros que Yevgueni Yevguénievich me prestó, aprendí que en la raíz de la clasificación de Gell-Mann y Ne’eman de los hadrones, de la que hablamos en el capítulo previo, había un grupo de simetrías. Este grupo ya había sido estudiado previamente por matemáticos, que, sin embargo, no habían previsto ninguna conexión con partículas subatómicas. El nombre matemático del grupo era SU(3). En este caso, «S» y «U» eran las iniciales de special unitary («unitario especial»). Este grupo es muy similar en sus propiedades al grupo de simetrías de la esfera, del que hablaremos en el capítulo 10.

Los matemáticos habían descrito las representaciones del grupo SU(3), es decir, las diferentes maneras en que el grupo SU(3) podía actuar como grupo de simetrías. Gell-Mann y Ne’eman notaron las similitudes entre la estructura de esas representaciones y los patrones de hadrones que habían hallado. Emplearon esa información para clasificar los hadrones.

En matemáticas, la palabra «representación» se emplea de una manera determinada, diferente de su uso tradicional. De modo que déjeme detenerme y explicar lo que significa la palabra en este contexto concreto. Posiblemente ayudaría que diera primero un ejemplo. Recuerde el grupo de rotaciones de una mesa redonda del que hablamos antes, el grupo circular. Ahora imagine que extendemos el plano de la mesa en todas las direcciones hasta el infinito. De esta manera obtenemos un objeto matemático abstracto: un plano. Cada rotación del plano de la mesa, en torno a su centro, da lugar a una rotación del plano en torno al mismo punto. De esta manera obtenemos una regla que asigna una simetría de este plano (una rotación) a cada elemento del grupo circular. En otras palabras: todos los elementos del grupo circular pueden representarse mediante una simetría del plano. Por ello, los matemáticos se refieren a este proceso como una representación del grupo circular.

El plano es bidimensional porque tiene dos ejes de coordenadas y, por tanto, todo punto tiene dos coordenadas.

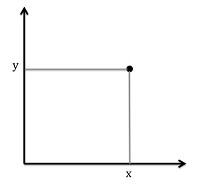
Por consiguiente, decimos que hemos construido una «representación bidimensional» del grupo de rotaciones. Significa sencillamente que todos y cada uno de los elementos del grupo de rotaciones se entienden como una simetría del plano.⁹

También hay espacios de más de dos dimensiones. Por ejemplo, el espacio que nos rodea es tridimensional, es decir, posee tres ejes de coordenadas, de modo que para especificar la posición de un punto, deberemos especificar sus tres coordenadas (x, y, z) tal y como se muestra en esta gráfica:

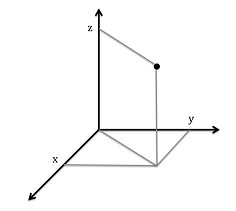
No somos capaces de imaginar un espacio tetradimensional, pero las matemáticas nos proporcionan un lenguaje universal que nos permite hablar de espacios con cualquier cantidad de dimensiones. Para ser exactos, representamos puntos del espacio tetradimensional mediante grupos de cuatro números (x, y, z, t) de la misma manera que representamos puntos del espacio tridimensional mediante tripletes de números (x, y, z). De igual manera, representamos los puntos de cualquier espacio n-dimensional, para cualquier número natural n, mediante grupos de n números. Si alguna vez ha empleado un programa de hoja de cálculo, se habrá encontrado con estos grupos de n números: aparecen como filas en la hoja, en la que cada uno de los n números corresponde a un atributo particular de los datos almacenados. Así, cada fila de una hoja de cálculo se refiere a un punto en un espacio n-dimensional. Hablaremos más de espacios de varias dimensiones en el capítulo 10.

Si todos los elementos de un grupo pueden generarse, de un modo consistente,¹⁰ como simetrías de un espacio n-dimensional, podemos decir que el grupo tiene «una representación n-dimensional».

Resulta que un grupo determinado puede tener representaciones de diferentes dimensiones. La razón por la que las partículas elementales se pueden ensamblar en grupos de a 8 y de a 10 es que el grupo SU(3) posee una representación 8-dimensional y una representación 10-dimensional. Las 8 partículas de cada octete construido por Gell-Mann y Ne’eman (como la del diagrama de la p. 26) están en correspondencia uno a uno con los 8 ejes coordenados de un espacio 8-dimensional que es una representación de SU(3). Lo mismo vale para el decuplete de partículas. Pero las partículas no pueden ensamblarse en, digamos, familias de 7 u 11, porque los matemáticos han demostrado que el grupo SU(3) no posee representaciones 7- u 11-dimensionales.

Al principio, esto era tan solo una manera cómoda de combinar partículas con propiedades similares. Pero después, Gell-Mann fue más allá. Postuló que había una razón profunda para este esquema de clasificación. En esencia, dijo que este esquema funciona tan bien porque los hadrones están hechos de partículas aún más pequeñas, a veces de dos y a veces de tres: los quarks. El físico George Zweig (que llamó a estas partículas «ases») hizo, de modo independiente, una propuesta similar.

Se trataba de una propuesta sorprendente. No solo atentaba contra la creencia común, en aquella época, de que protones, neutrones y otros hadrones eran partículas indivisibles, sino que se proponía que estas nuevas partículas poseían cargas que eran fracciones de la del electrón. Se trataba de una predicción sorprendente porque nadie había visto con anterioridad esas partículas. Sin embargo, pronto se comprobó experimentalmente la existencia de los quarks y, como se había predicho, ¡poseían cargas eléctricas fraccionales!

¿Qué había motivado a Gell-Man y Zweig a predecir la existencia de quarks? La teoría matemática de representaciones de SU(3). Para ser exactos, el hecho de que el grupo SU(3) tiene dos representaciones tridimensionales diferentes (en realidad, esa es la razón del «3» en su nombre). Gell-Man y Zweig sugirieron que esas dos representaciones describirían dos familias de partículas fundamentales: 3 quarks y 3 antiquarks. Resultaba que las representaciones 8- y 10-dimensionales de SU(3) se podían construir a partir de las 3-dimensionales. Y esto daba unas instrucciones precisas para construir hadrones a partir de quarks, como en un juego de Lego.

Gell-Man denominó a los 3 quarks up («arriba»), down («abajo») y strange («extraño»).¹¹ Un protón consiste en dos quarks arriba y uno abajo, mientras que un neutrón consiste en dos quarks abajo y uno arriba, como hemos visto en los gráficos de la p. 25. Ambas partículas pertenecen al octete mostrado en el diagrama de la p. 26. Otras partículas de este octete implican al quark extraño, así como a quarks arriba y abajo. Existen también octetes que consisten en partículas compuestas por un quark y un antiquark.

El descubrimiento de los quarks es un buen ejemplo de ese papel preponderante que desempeñan las matemáticas en la ciencia, del que hablábamos en el prefacio. Estas partículas se predijeron no fundamentándose en datos empíricos, sino a partir de patrones de simetría matemáticos. Fue una predicción puramente teórica, efectuada dentro del marco de una sofisticada teoría matemática de representaciones del grupo SU(3). Los físicos tardaron años en dominar esta teoría (e incluso hubo algunas resistencias a ella al principio) pero hoy en día forma parte básica de la teoría elemental de partículas. No solo proporcionó una clasificación de hadrones, sino que también llevó al descubrimiento de los quarks, lo que cambió para siempre nuestra comprensión de la realidad física.

Imagínelo: una teoría matemática aparentemente esotérica nos permitió llegar al corazón de los «ladrillos» básicos de la naturaleza. ¿Cómo no quedar fascinados ante la mágica armonía de esos diminutos trocitos de materia, o maravillarse ante la capacidad de las matemáticas para revelar los principios fundamentales que rigen el universo?

Dice una anécdota que Elsa, la mujer de Einstein, al oír que se necesitaba un telescopio en el Monte Wilson para determinar la forma del espacio-tiempo, dijo: «Oh, mi marido lo hace en el revés de un sobre».

Los físicos necesitan máquinas gigantescas y sofisticadas como el Gran Colisionador de Hadrones de Ginebra, pero lo asombroso es que científicos como Einstein y Gell-Man han empleado lo que parece ser el conocimiento matemático más puro y abstracto para desvelar los secretos más profundos del universo que nos rodea.

No importa quién sea o en qué crea, todos compartimos este conocimiento. Nos acerca unos a otros y proporciona un nuevo sentido a nuestro amor por el universo.