Capítulo 2

etnem al ed ojo le ne aírtemiS

Entre todos los sentidos humanos, la visión es, con mucho, el vehículo de percepción más importante. Sin embargo, los ojos no son más que mecanismos ópticos; la percepción requiere la participación del cerebro. La percepción visual es un complejo de procesos del cerebro en el cual combina sensaciones del mundo exterior para producir una imagen informativa. Nuestro entorno produce muchas más señales de las que posiblemente podemos analizar. En consecuencia, la percepción implica tamizar la riqueza de los datos y seleccionar los de mayor utilidad. Cuando los jugadores del ajedrez humano planifican su siguiente jugada, no examinan mentalmente todos los movimientos posibles dentro del tablero. Se centran en esos pocos movimientos que parecen ser más beneficiosos cuando se encuentran contra la línea de fondo de la información acumulada: lo que llamamos memoria. En la película de Woody Allen La maldición del escorpión de jade, Dan Aykroyd hace el papel de jefe de una compañía de seguros. En una escena dice a uno de sus investigadores, C. W. Briggs (interpretado por Woody Allen): «¿Sabes?, hay una palabra para la gente que cree que todo el mundo conspira contra ellos.» A lo cual Woody Allen responde: «Sí, ¡perceptivos!» En realidad, la paranoia representa, sin lugar a dudas, una distorsión de la percepción.

A primera vista, la percepción visual tiene que cumplir una misión imposible. Tiene que transformar el impacto físico de las unidades de energía luminosa (llamadas fotones) sobre los receptores de la parte posterior del ojo en representaciones mentales de objetos. Como veremos muy pronto, la simetría ofrece una ayuda importante para conseguir este objetivo.

Sin embargo, primero tenemos que apreciar qué tipo de dificultades hay que superar. La astronomía puede ayudar a ilustrar uno de los muchos obstáculos que acarrea este proceso: concretamente, la percepción de la distancia. La figura 17 muestra una foto tomada con el Telescopio Espacial Hubble, mirando a través del halo esférico de estrellas que rodean a la galaxia Andrómeda (conocida por los astrónomos como M31). Una galaxia es una vasta extensión de unos pocos cientos de miles de millones de estrellas parecidas al Sol. La M31, a una distancia aproximada de 2,5 millones de años luz, es una de las vecinas más próximas de nuestra galaxia, la Vía Láctea. (Un año luz equivale aproximadamente a 10 billones de kilómetros). La foto de la figura 17 contiene unas diez mil estrellas de M31 y alrededor de un centenar de galaxias que se aprecian en segundo plano (algunas parecen objetos borrosos de gran extensión). Sin embargo, aquí está el problema. Mirando simplemente la foto, no hay modo de saber si las estrellas están muy cerca relativamente hablando (a una distancia de 2,5 millones de años luz), mientras que algunas de las galaxias están ¡a más de 10 miles de millones de años luz de distancia! Del mismo modo, cuando contemplamos el mundo que nos rodea, los ojos sólo reconocen la dirección del rayo de luz en el que viaja un fotón. Como la imagen se proyecta en una superficie de dos dimensiones (la retina), sin alguna información adicional el cerebro no tiene idea de lo lejos que se originó el fotón. En el caso de una estrella relativamente cercana, los astrónomos resuelven el problema de la determinación de la distancia utilizando un método conocido como paralaje trigonométrico. Ven la estrella desde dos puntos diferentes de la órbita terrestre alrededor del Sol (figura 18). En el transcurso del año, la estrella cercana parece moverse adelante y atrás en relación con las estrellas más distantes (fijas) del fondo. Midiendo el ángulo asociado a este movimiento aparente podemos conocer el diámetro de la órbita terrestre y, utilizando la simple trigonometría escolar, se puede calcular la distancia a la estrella.

Figura 18

Los humanos utilizan los dos ojos exactamente de la misma forma para producir conciencia espacial. Se puede descubrir este mecanismo, llamado visión estereoscópica, siguiendo este sencillo experimento. Extienda su brazo, levante un dedo y mírese el dedo contra algún fondo. Si cierra alternativamente el ojo derecho y el izquierdo, su dedo parecerá moverse adelante y atrás en relación con los objetos del fondo. Acérquese el dedo a los ojos y notará que el salto entre ambas posiciones aumenta. Este desplazamiento aparente (paralaje) ocurre porque sus dos ojos ven el dedo desde dos puntos diferentes. Dado que el paralaje depende de la distancia del objeto, al medir el ángulos entre las posiciones aparentes y conociendo la separación entre los ojos, el cerebro «trigonometriza» la distancia al objeto. Si está familiarizado con la pérdida de percepción de la profundidad que se asocia a cerrar un ojo, quizá crea que el papel de los dos ojos en la visión estereoscópica se conoce desde la Antigüedad. Para nuestra sorpresa, incluso algunos de los mejores investigadores en el campo de la perspectiva pasaron completamente por alto el concepto de la visión estereoscópica. Matemáticos como Euclides en la antigua Grecia, los arquitectos renacentistas Brunelleschi y Alberti, los pintores Piero della Francesca, Paolo Ucello y Alberto Durero, e incluso el gran Isaac Newton, pensaron que los dos ojos constituían una simple manifestación de simetría bilateral, sin otra función especial. El primero en darse cuenta de que los dos ojos pueden proporcionar algo que uno solo no puede fue el hombre renacentista por excelencia: Leonardo da Vinci (1452-1519).

Leonardo observó que cuando miramos un objeto con los dos ojos, el derecho se las arregla para captar la parte del espacio que hay detrás del objeto a la derecha, mientras que el izquierdo se ocupa del entorno izquierdo del objeto. De esto, Leonardo concluyó: «el objeto... visto con ambos ojos parece convertirse en transparente... pero esto no ocurre cuando un objeto... se mira con un solo ojo». A pesar de su perspicacia, al limitar su atención únicamente a las esferas, Leonardo dejó escapar la oportunidad de descubrir que los dos ojos captaban dos perspectivas diferentes no sólo del fondo, sino también del propio objeto. La persona que estableció la importancia de mirar con ambos ojos para percibir la distancia fue el astrónomo alemán Johannes Kepler (1571-1630). En dos obras notables, Astronomiae Pars Optica (La parte óptica de la astronomía), publicada en 1604, y Dioptrice (Dioptrio, la parte de la óptica que trata de la refracción), publicada en 1611, Kepler ofreció una detallada descripción de la óptica del ojo, explicó el funcionamiento de las gafas y desarrolló la teoría de la visión estereoscópica. Sin embargo, en cierto modo, la obra de Kepler pasó relativamente inadvertida y ni siquiera Charles Wheatstone, que redescubrió el mecanismo de la percepción de la profundidad en 1838, la conocía.

Charles Wheatstone (1802-1875) nació en el seno de una familia de músicos y sus primeras investigaciones se referían al sonido, las vibraciones de diversos dispositivos como cuerdas y tubos, e instrumentos musicales. En 1822 realizó una demostración en la tienda de su padre, en Pall Mall, en Londres, que ofrecía música no sólo para los oídos, sino también para los ojos. Esta «Lira Encantada» estaba suspendida mediante un fino alambre que pasaba a través del techo hasta la habitación de encima e iba conectado a la caja de un piano, un arpa y un dulcimer. Mientras Wheatstone iba tocando los intrumentos de la habitación superior, la Lira Encantada parecía tocar sola. Experimentalista muy imaginativo, Wheatstone inventó la concertina (un instrumento musical parecido a un pequeño acordeón) y patentó el telégrafo eléctrico en Gran Bretaña.

Wheatstone inició sus experimentos sobre la visión estereoscópica en 1832 y presentó su teoría en un artículo publicado el 21 de junio de 1838. El título del artículo era «Contributions to the Physiology of Vision. Part the First. On some remarkable, and hitherto unobserved, Phenomena of Binocular Vision» (Contribuciones a la Fisiología de la Visión. Parte Primera. Sobre algunos fenómenos notables, hasta ahora no observados, de la visión binocular). El primer párrafo de este artículo describe la esencia del descubrimiento: que la incongruencia de las imágenes en las dos retinas y el subsiguiente proceso mental producen una percepción espacial. En palabras de Wheatstone:

Cuando se mira un objeto a una distancia tan grande que los ejes ópticos de ambos ojos son sensiblemente paralelos al dirigirse hacia él, las proyecciones de su perspectiva, vistas por cada ojo separadamente, son similares, y la apariencia es exactamente la misma para los dos ojos que cuando se mira el objeto con un solo ojo... Pero esta similitud ya no existe cuando se coloca el objeto tan cerca de los ojos que para verlo los ejes ópticos tienen que converger; en estas condiciones, cada ojo ve la proyección de una perspectiva diferente... Este hecho puede verificarse fácilmente colocando cualquier figura en tres dimensiones, por ejemplo, un cubo, a una distancia moderada de los ojos y, con la cabeza siempre perfectamente recta, mirarlo sucesivamente con cada ojo mientras se mantiene el otro cerrado.

He intentado explicar el descubrimiento de los procesos implicados en la percepción de algo tan elemental como la profundidad espacial porque esta historia ayuda a ejemplificar los inmensos obstáculos asociados con el desarrollo de una verdadera comprensión de la percepción. Las teorías de la percepción humana pueden llenar, como así ha sido, volúmenes enteros. Aquí me centraré tan sólo en la función de la simetría en este proceso.

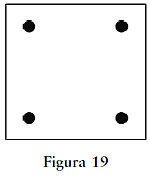
El papel de la simetría en la percepción saltó al centro del escenario gracias a la escuela de pensamiento conocida como la psicología de la Gestalt. Los psicólogos Max Wertheimer, Kurt Koffka e Ivo Kohler, iniciadores de esta doctrina, fundaron en 1912 un influyente laboratorio para la investigación en psicología en la Universidad de Frankfurt. Uno de los problemas clave que los psicólogos de la Gestalt se dispusieron a tratar fue el de la organización perceptual: cómo se organizan los pequeños bits de información que reciben los sentidos en estructuras perceptuales mayores. ¿Cómo sabemos qué segmentos encajan juntos para formar un objeto? ¿Cómo separamos unos objetos de otros y cómo distinguimos entre objeto y fondo? La «ley» central de la organización perceptual se conoce como principio de Prägnanz, habitualmente aludido como ley de la «buena figura» (Prägnanz significa «brevedad» en alemán). Esta ley dice: «De las numerosas disposiciones geométricas posibles, se adopta la que posee la mejor forma, la más simple y la más estable.» Por lo tanto, para los psicólogos de la Gestalt, la simetría era uno de los elementos clave que contribuían de forma significativa a la «bondad» de la figura. Una colocación de cuatro puntos como la que aparece en la figura 19 se percibe como un cuadrado, porque la «bondad» del cuadrado como una forma simétrica, cerrada y estable es mayor que la de un triángulo con un punto extra. Aunque los psicólogos de la Gestalt nunca lograron formular una teoría precisa de la percepción de la forma, los teóricos posteriores, como el psicólogo holandés Emanuel Leeuwenberg y los norteamericanos Wendell Garner y Stephen Palmer, ampliaron sus principios básicos. Garner y Palmer en especial reconocieron el importante papel de varios tipos de simetrías (como la simetría según rotaciones y reflejos) para la «bondad» de la figura.

Leeuwenberg y sus colaboradores desarrollaron una teoría de representación de las formas más conocida como teoría de la información estructural. Los dos conceptos fundamentales de esta teoría son los códigos y las cargas de información. Los códigos son simples descripciones perceptuales que pueden generar una figura observada. Por ejemplo, para describir un rectángulo podemos empezar por la esquina superior izquierda y dar la longitud del segmento que hay que dibujar (fig. 20), seguido del ajuste del ángulo que tiene que ser representado después. A continuación damos la siguiente longitud, nuevamente seguida por el ajuste angular. El código final para dibujar el rectángulo tomaría la forma a 90 b 90 a 90 b 90. Sin embargo, vemos que, como hay que repetir las mismas instrucciones dos veces, podemos simplificar este código escribiendo 2^* (a 90 b 90).

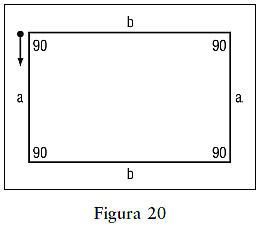
La carga de información mide la complejidad del código más simple que consigue realizar la tarea. En general, se puede proce>sar la carga de información simplemente contando el número de parámetros del código (como a, b, y 90 en el ejemplo anterior). La idea central de la teoría de la información estructural es que la «bondad» de la figura es mayor cuando menor es la carga de información. Las figuras simétricas contienen una carga de información menor y por lo tanto están más arriba en la escala de «bondad». Por ejemplo, para el código del rectángulo de más arriba, la carga de información es 4: el número de iteraciones (2); las dos longitudes (a, b); y el ángulo (90). Por otra parte, para una figura cuadrilátera arbitraria, la carga de información sería 8 (cuatro longitudes y cuatro ángulos).

Figura 21

Otros dos elementos importantes de los principios de la organización de la Gestalt son la proximidad y la semejanza. La «ley» de la proximidad expresa el hecho de que, en general, nuestra mente agrupa las formas que están próximas. En la figura 21a percibimos columnas porque el espaciado vertical de los puntos es menor que el horizontal. Lo contrario ocurre en la figura 21b, que resulta en una percepción de filas. Cuando los espaciados son iguales (como en la figura 21c), nos quedamos con una impresión ambigua.

Las formas semejantes también tienden a agruparse por asociación, y la similitud a veces puede constituir un elemento organizativo más poderoso que la proximidad. En la figura 22 tendemos a percibir columnas a causa de la semejanza de los círculos oscuros, aunque, sólo a causa de su proximidad, si todos los círculos hubieran sido oscuros habríamos visto filas.

La simetría desempeña un papel importante en el reconocimiento de la semejanza porque representa una verdadera invariante: una inmunidad al cambio. En consecuencia, la simetría es un rasgo de especial ayuda para que el sistema perceptual lo utilice para determinar si los patrones observados son efectivamente semejantes o diferentes.

Figura 23

Otro principio de la Gestalt es la buena continuidad: percibimos el símbolo X como dos líneas que se cruzan entre ellas, no como una V derecha y una V boca abajo que están conectadas por el vértice. El destino común es también una base para la agrupación. Tendemos a agrupar juntas cosas que se mueven a la misma velocidad en la misma dirección. El profeta bíblico Amós era totalmente consciente de este principio cuando preguntó: «¿Caminan juntas dos personas a menos que se hayan citado?».

El psicólogo de la Universidad de California-Berkeley Stephen Palmer y sus colaboradores añadieron a los principios de la organización los de la región común, la conectividad y la sincronía. La figura 23 muestra estos principios. La región común se refiere al hecho de que los elementos se agrupan cuando están circunscritos a una región espacial (23a). La conectividad significa que percibimos como unidades elementos que parecen estar físicamente conectados (23b). Finalmente, la sincronía refleja el hecho de que se perciban como asociados acontecimientos visuales simultáneos (23c).

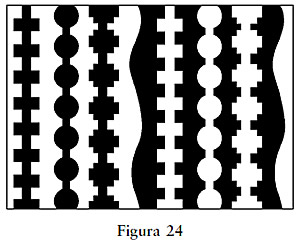
La simetría, y en especial la simetría bilateral, también es uno de los elementos clave en la segregación figura-fondo: la capacidad de ver objetos como figuras que destacan del fondo. Eche una ojeada a la figura 24, a derecha e izquierda, y decida de qué color es la figura y de qué color es el fondo. Las áreas bilateralmente simétricas tienden a ser percibidas como figuras contra los fondos asimétricos. En consecuencia, a la izquierda de la figura 24 nos inclinamos a identificar las zonas negras como figuras, mientras que a la derecha, las figuras son las blancas. También es más probable que las orientaciones horizontal y vertical sean vistas como figuras, más que cualquier otra orientación. Finalmente, las áreas más reducidas rodeadas de otras mayores tienden a ser identificadas como figuras, por ser significativas o familiares.

Probablemente habrá notado que las «leyes» originales de la Gestalt no eran más que heurísticas: principios-conjetura que funcionan la mayoría de las veces, pero no necesariamente siempre. Utilizan de forma bastante vaga conceptos definidos, como la «bondad» o la «semejanza». Cabe preguntarse por qué funcionan realmente esos principios. La respuesta es que, con toda probabilidad, representan una combinación de aprendizaje y evolución. Oscar Wilde dijo en una ocasión: «La experiencia es el nombre que todos dan a sus errores». Los humanos han estado «practicando» la percepción durante generaciones, y a lo largo de su interminable número de encuentros perceptuales han aprendido lo que se podía esperar. A pesar de sus defectos, los principios originales de la Gestalt fueron útiles porque ofrecieron una respuesta rápida. Cuando uno quiere encontrar sus llaves, primero se dirige a los dos sitios donde suele dejarlas y sólo cuando eso ha fallado se embarca en una búsqueda sistemática por toda la casa.

En general, las teorías psicológicas más recientes y los resultados experimentales confirman el importante papel de la simetría en la percepción. Muchos experimentos muestran que la simetría bilateral a lo largo de un eje vertical es lo más fácil de reconocer (es decir, es lo que se reconoce con mayor rapidez) y eso se explota como propiedad diagnóstica para el juicio «igual-diferente». Básicamente, la simetría es una propiedad que atrae la atención en las primeras etapas del proceso de la visión. La simetría también es muy útil para discriminar a los organismos vivientes (incluyendo a los potenciales depredadores) de los artículos inanimados y en la selección de la pareja deseada (volveré sobre estos temas en el capítulo 8). Otros experimentos han demostrado que las figuras simétricas se reproducen más fácilmente que las asimétricas. En un interesante estudio, los psicólogos de la Universidad de Stanford Jennifer Freyd y Barbara Tversky descubrieron que en una primera fase los sujetos determinaban con rapidez si la simetría global estaba presente o ausente. Después, si se percibía que la forma tenía simetría global, algunos individuos distorsionaban mentalmente la imagen y suponían (a veces incorrectamente) que también era simétrica en los detalles.

Una sugerencia intrigante de que la preferencia por varios tipos de simetrías puede ser una característica aprendida procede de los experimentos llevados a cabo en la Universidad de Illinois por el psicólogo Ioannis Paraskevopoulos. Sus sujetos fueron setenta y seis colegiales de la escuela elemental. Paraskevopoulos descubrió que la doble simetría (reflejo vertical y horizontal) era la preferida a la edad de seis años, la simetría bilateral (sólo reflejo vertical) a los siete y la simetría horizontal (reflejo horizontal) a los once.

Algunos de los estudios recientes más interesantes son los que tratan de utilizar la resonancia magnética nuclear (RMN) para estudiar las áreas del cerebro que responden a la simetría. El psicólogo Christopher W. Tyler del Smith-Kettlewell Eye Research Institute de San Francisco presentó sujetos con una variedad de patrones simétricos traslacionales (y de reflejo). Descubrió que esos estímulos producían la activación de una región del lóbulo occipital, cuya función por lo demás se desconoce. Sorprendentemente, en otras áreas con funciones visuales conocidas se detectó muy poca o ninguna activación. Tyler llegó a la conclusión de que esta región especializada probablemente codifica la presencia de la simetría en el campo visual.

La interrelación entre simetría y orientación también es fascinante. Las figuras simétricas no cambian cuando las hacemos rotar, reflejarse o trasladarse en ciertas formas. Sin embargo, muchas formas no son simétricas respecto a ninguna transformación (excepto la identidad, que deja la forma intacta), y la forma en que las percibimos definitivamente se ve afectada, por ejemplo, por su orientación. Vamos a echar una ojeada rápida a la figura 25. ¿Ha reconocido el mapa de África? O, sin darle la vuelta al libro, ¿reconoce al personaje de la figura 26?

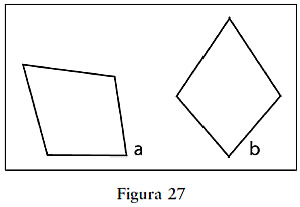
Incluso la percepción de la simetría puede ser engañosa. Una forma puede ser simétrica de reflejo respecto a un eje, como en la figura 27a, pero a menos que le dé la vuelta como en la figura 27b, de forma que el eje de la simetría sea vertical, no percibimos la simetría. El científico cognoscitivo Irvin Rock de la Universidad de Rutgers y sus colaboradores llevaron a cabo una serie de experimentos diseñados para comprobar la dependencia de la percepción de la forma sobre la orientación. En concreto, querían comprobar si la percepción de la simetría bilateral depende de si el eje de la simetría es verdaderamente vertical en la imagen de la retina o si sólo se percibe como algo vertical. Los investigadores utilizaron una forma como la que aparece en la figura 28a como forma estándar. Esta forma es simétrica tanto en su reflejo vertical como horizontal. Se pidió a los sujetos que indicaran cuál de las dos figuras, 28b o 28c, creían que se parecía más a 28a. Vemos que la figura 28b estaba ligeramente cambiada para que no fuera simétrica respecto al eje vertical, pero conservando todavía la simetría respecto al eje horizontal. En la figura 28c se realizó lo contrario. Cuando los sujetos observaron las figuras con la cabeza vertical, la mayoría escogía la figura 28c. Esto ya era de esperar; el físico y filósofo moravio-austríaco Ernst Mach (1838-1916) observó ya en 1914 que las figuras se perciben como algo básicamente simétrico como resultado de una simetría de reflejo a lo largo del eje vertical. Sin embargo, tuvieron una sorpresa. Cuando los observadores se inclinaron 45 grados, continuaron escogiendo la figura 28c como la más parecida a la 28a, a pesar del hecho de que con esta orientación, ni la 28b ni la 28c conservaban la simetría en la imagen de la retina. A partir de éste y otros experimentos, Rock concluyó que «para una figura novedosa no hay mucho cambio en la apariencia cuando sólo cambia la orientación de su imagen de la retina». Rock descubrió que lo que realmente importa no es tanto la orientación real de la figura en su entorno, como el hecho de que normalmente asignemos las direcciones arriba, abajo, izquierda y derecha a las figuras. Estas asignaciones dependen típicamente de otras indicaciones visuales, tales como la dirección de la gravedad o el marco de referencia del entorno. Las figuras que no están orientadas respecto a las direcciones asignadas no se reconocen fácilmente. Rock descubrió que el efecto de la forma percibida es mínimo cuando el único cambio efectuado es una inversión izquierda-derecha. Estos resultados confirman de nuevo la importancia capital de la simetría bilateral en la percepción. Sin embargo, Rock reconoció que algunas figuras, como las palabras escritas en cursiva o los retratos, son muy difíciles de reconocer incluso cuando sólo se altera la orientación de la imagen de la retina.

Aunque la simetría actúa en la mayoría de los casos para facilitar la percepción, hay un tipo de simetría que realmente puede atraer la vista hacia una mala interpretación de lo que ve. El médico escocés David Brewster (1781-1868), que también inventó el caleidoscopio en 1816, observó una cosa extraña cuando miraba un papel pintado de pared con patrones repetitivos de simetría traslacional. La fecundidad de Morris and Company y sus contemporáneos garantizó que esos patrones fueran ubicuos durante la era victoriana. Para su sorpresa, Brewster descubrió que algunos de esos diseños literalmente «brotaban» de la pared y se convertían en ilusiones en tres dimensiones, que hoy se conocen como ilusiones del papel pintado o de las escaleras mecánicas, ya que tanto los papeles pintados como las escaleras mecánicas poseen patrones repetitivos. Puede que ya esté familiarizado con el fenómeno de los múltiples libros y pósters del Ojo Mágico. La fascinación con estos autoestereogramas realizados con ordenador (patrones que saltan a la tridimensionalidad cuando se miran fijamente cruzando los ojos) alcanzó la magnitud de locura a principios de los noventa. La figura 29 muestra este sorprendente efecto. Si la mira fijamente durante un minuto como si estuviera fijando la vista en una imagen que hubiera detrás de la página, los surfistas se materializarán milagrosamente en tres dimensiones. Por razones que no están del todo claras, algunas personas no son capaces de percibir las ilusiones creadas por los autoestereogramas. O sea, que si no vieron que la figura 29 ganaba profundidad de repente, no se desesperen; pertenecen a un club exclusivo. La idea que hay detrás de las ilusiones del Ojo Mágico procede de la investigación realizada sobre la percepción de la profundidad de la psicóloga húngaro-americana Bella Julesz en 1959. El colaborador de Julesz, el psicólogo Christopher Tyler del Smith-Kettlewell Eye Research Institute, descubrió en 1979 que podía utilizar una técnica de impresora offset para generar estereogramas de una sola imagen. La explicación básica de la magia de los patrones de repetición es bastante simple. Con cada ojo fijo en un miembro diferente de un par adyacente del patrón repetitivo, el cerebro percibe erróneamente los dos objetos como uno solo a diferente distancia (fig. 30). La razón de este «fallo» del cerebro es, naturalmente, el hecho de que los motivos repetitivos crean imágenes idénticas en ambas retinas, dando la impresión de que está enfocado un solo objeto.

Figura 28

Cuando el patrón de repetición es muy próximo en el espacio y está formado por motivos de mucho contraste puede inducir una ilusión de movimiento muy poderosa. La artista británica de Op Art (Arte óptico) Bridget Riley deslumbró a numerosos observadores con patrones así de alucinantes en su obra Fall (fig. 31).

Figura 29

Con la excepción de las permutaciones y del principio de exclusión de Pauli, todas las simetrías descritas hasta ahora eran de siluetas, formas y configuraciones. Eran simetrías de objetos en el espacio, impuestas por la disposición de sistemas específicos y percibidas a través de los sentidos. Podemos ver que una catedral tiene una simetría bilateral, que el diseño de un papel pintado presenta simetría traslacional y que un círculo tiene simetría rotacional. Las simetrías que subyacen a las leyes fundamentales de la naturaleza son parientes cercanas de las simetrías de más arriba, pero en lugar de centrarse en la forma o figura exterior, se concentran en la cuestión: ¿qué operaciones se pueden realizar en el mundo que nos rodea que dejaría inalteradas las leyes que describen todos los fenómenos observados?

Las reglas del juego

¿Qué son las leyes de la naturaleza? El biólogo Thomas Henry Huxley (1825-1895), el defensor más apasionado de la teoría de la evolución y de la selección natural de Darwin, ofreció la siguiente explicación:

El tablero de ajedrez es el mundo, las piezas son los fenómenos del universo, las reglas del juego son lo que llamamos las leyes de la Naturaleza. El jugador contrario está oculto. Sabemos que su juego siempre es limpio, justo y paciente. Pero también sabemos, por experiencia, que nunca pasa por alto un error, ni hace la menor concesión a la ignorancia.

Esta definición, de un hombre que tenía por mote «el bulldog de Darwin», carecía de ambición según los estándares modernos. Los físicos actuales querrían que las leyes de la naturaleza no sólo representaran las reglas del juego, sino que también explicaran la existencia misma y las propiedades del tablero de ajedrez, e incluso de las propias piezas.

Hasta el siglo XVII los seres humanos no soñaron siquiera con la posibilidad de que existiera un conjunto de leyes que lo explicaran todo. Galileo Galilei (1564-1642), René Descartes (1596-1650) y especialmente Isaac Newton (1642-1727) demostraron por primera vez que un puñado de leyes (como las leyes del movimiento y de la gravedad) podían explicar una abundancia de fenómenos, que iban desde las manzanas que caían y las mareas en las playas hasta el movimiento de los planetas.

Otros siguieron estos pasos de gigante. En 1873, el físico escocés James Clerk Maxwell (1831-1879) publicó su Treatise on Electricity and Magnetism, un trabajo monumental que unificaba los fenómenos eléctricos, magnéticos y luminosos al amparo de tan sólo cuatro ecuaciones matemáticas. Apoyándose en los resultados experimentales del físico inglés Michael Faraday (1791-1867), Maxwell consiguió demostrar que la fuerza que mantiene a los planetas en sus órbitas y la que mantiene los objetos en la superficie de la Tierra son de hecho la misma: la electricidad y el magnetismo no son más que diferentes manifestaciones de una misma esencia física. El siglo XX fue testigo del nacimiento no de una, sino de dos revoluciones científicas de suma importancia. En primer lugar, las teorías especial y general de Einstein sobre la relatividad cambiaron para siempre el significado del espacio y el tiempo. Estos dos últimos conceptos han pasado a estar inextricablemente unidos en la entidad que hoy conocemos como espacio-tiempo. La relatividad general también sugería que la gravedad no es ninguna fuerza misteriosa que actúa a una cierta distancia, sino simplemente una manifestación del espacio-tiempo curvado por la materia, como una lona que se hunde bajo el peso de una pesada bala de cañón. Todo lo que se mueve a través de este espacio distorsionado (como los planetas en su trayectoria) viaja no sólo por líneas rectas, sino también por trayectorias curvas. En segundo lugar, y en otro frente, toda esperanza de un mundo totalmente determinista quedó hecha añicos con la introducción de la mecánica cuántica. En la mecánica newtoniana e incluso en la relatividad general, si se pudiera conocer la posición de cada partícula del universo en un momento determinado y la velocidad y dirección en que se movía en ese instante, se podría predecir de manera inequívoca el futuro del universo y también explicar con todo detalle toda la historia cósmica precedente. Las únicas limitaciones irían asociadas a extrañas circunstancias en las que la relatividad general se rompe, como en el caso de los objetos denominados agujeros negros. La mecánica cuántica cambió todo esto. Ni siquiera la posición y la velocidad de una sola partícula se pueden determinar con exactitud. Las únicas cosas deterministas en el universo son las probabilidades de diversos resultados, no los resultados en sí mismos. Aunque por razones bastante diferentes, el universo se parece un poco al tiempo: lo máximo que podemos hacer es predecir la probabilidad de que llueva mañana, no si lloverá o no de verdad. Desde luego, Dios juega a los dados.

Con cada paso hacia las revoluciones de la relatividad y la mecánica cuántica, el aprecio del papel de la simetría en las leyes de la naturaleza ha ido en aumento. Los físicos ya no se contentan con explicar los fenómenos individuales. Están convencidos más que nunca de que la naturaleza tiene un diseño subyacente en el que la simetría es el ingrediente clave. La simetría de las leyes significa que cuando observamos los fenómenos naturales desde diferentes perspectivas, descubrimos que están gobernados precisamente por las mismas leyes de la naturaleza. Por ejemplo, si realizamos experimentos en Nueva York, Tokio o en el otro extremo de la Vía Láctea, las leyes de la naturaleza que explican los resultados de esos experimentos tomarán la misma forma. Como vemos, la simetría de las leyes no implica que los resultados de los propios experimentos permanezcan necesariamente inalterados. La fuerza de la gravedad en la Luna es diferente de la que tiene en la Tierra y en consecuencia los astronautas en la Luna parecían dar saltos mucho más amplios de los que darían en la Tierra. Sin embargo, la dependencia de la fuerza de la atracción gravitatoria de la masa y el radio de la Luna es la misma que la dependencia de la gravedad terrestre sobre su propia masa y radio. Esta simetría de las leyes (la inmunidad a los cambios cuando se desplazan de un lugar a otro) es una simetría traslacional. Sin esta simetría acorde con la traslación habría resultado prácticamente imposible entender el universo. La razón principal por la que podemos interpretar con relativa facilidad la observación de galaxias que se encuentran a diez mil millones de años luz es que hemos descubierto que allí los átomos de hidrógeno obedecen exactamente a las mismas leyes mecánicas cuánticas que obedecen en la Tierra.

Las leyes de la naturaleza también son simétricas según la rotación. La física no tiene ninguna dirección preferida en el espacio: descubrimos las mismas leyes si realizamos el experimento estando de pie o inclinados hacia cualquier lado, o si medimos las direcciones respecto a arriba, abajo, norte o suroeste. Esto es menos intuitivo de lo que cabría pensar. Recordemos que para las criaturas que evolucionaron en la superficie de la Tierra hay una clara distinción entre arriba y abajo. Aristóteles y sus seguidores pensaban que los objetos caían hacia abajo porque es el lugar lógico para las cosas pesadas. Naturalmente, Newton dejó claro que arriba y abajo nos parecen diferentes no porque las leyes físicas dependan de esas direcciones, sino porque da la casualidad de que sentimos bajo nuestros pies el tirón gravitacional de esta masa tan grande que llamamos Tierra. Esto supone un cambio en el entorno, no en las leyes. En cierta forma, somos afortunados: las simetrías según la traslación y la rotación garantizan que independientemente de dónde nos encontremos en el espacio o cómo estemos orientados, encontraremos las mismas leyes.

Un ejemplo sencillo puede ayudar a esclarecer aún más la diferencia entre las simetrías de las formas y de las leyes. Los antiguos griegos pensaban que las órbitas de los planetas debían de ser circulares porque es una forma simétrica según las rotaciones en cualquier ángulo. En lugar de ello, la simetría de la ley de Newton de la gravitación según la rotación significa que las órbitas pueden tener cualquier orientación en el espacio (fig. 32). Las órbitas no tienen que ser circulares; pueden ser, y de hecho son, elípticas.

Existen otras simetrías más esotéricas que dejan intactas las leyes de la naturaleza y volveremos sobre algunas de ellas y de sus importantes implicaciones en el capítulo 7. Sin embargo, el punto clave que hay que recordar es que la simetría es una de las herramientas más importantes que poseemos para descifrar el diseño de la naturaleza.

Hasta el momento, nuestro rápido vistazo general a las simetrías, ya sea de objetos o de leyes naturales, ha sido como un viaje turístico por el extranjero. Hemos podido admirar el escenario, pero para adquirir un conocimiento más profundo de la cultura tenemos que aprender a hablar la lengua. Así que ya es hora de tomar un curso intensivo en la Berlitz.

La madre de todas las simetrías

Incluso con la breve ojeada que hemos dado al mundo de las simetrías, por el momento ha quedado claro que la simetría se encuentra en la intersección entre ciencia, arte y psicología perceptual. La simetría representa la esencia pertinaz de las formas, las leyes y los objetos matemáticos que permanecen inalterados bajo las transformaciones. El lenguaje que describe las simetrías tiene que identificar estas esencias invariadas cuando están enmascaradas con diferentes disfraces disciplinarios.

El lenguaje del mundo financiero, por ejemplo, es el lenguaje de las operaciones aritméticas. Si quiere comparar de inmediato la potencia económica de dos compañías, no necesita leerse volúmenes enteros de texto; bastará una comparación de algunos números clave. Cuando Isaac Newton formuló sus celebradas leyes del movimiento, también desarrolló el lenguaje de cálculo para que éste fuera capaz de expresarlas y manipularlas. Cabría decir que uno de los logros del arte abstracto y no objetivo del siglo XX fue la transformación del color en un lenguaje de significado y emoción. Algunos pintores abandonaron el uso de la forma y otros elementos visuales casi por completo en favor de la comunicación exclusiva a través del color.

Para explorar los laberintos de la simetría, los matemáticos, los científicos y los artistas iluminaron su camino con el lenguaje de la teoría de grupos. Como ocurre en algunos clubs exclusivos, un grupo matemático se caracteriza porque sus miembros tienen que obedecer ciertas normas. Un conjunto matemático es cualquier grupo de entidad, ya sean las piezas de un avión, las letras del alfabeto hebreo o una extraña colección compuesta por la oreja de van Gogh, el conejito de Pascua, todos los periódicos albanos y el tiempo de Marte. Un grupo, por otra parte, es un conjunto que tiene que obedecer ciertas reglas respecto a ciertas operaciones. Por ejemplo, uno de los grupos más comunes está formado por todos los números enteros (positivos, negativos y cero; es decir, ... –4, –3, –2, –1, 0, 1, 2, 3, 4, ...), conjuntamente con la simple operación aritmética de la suma.

Las propiedades que definen un grupo son:

1. Proximidad. El vástago de dos miembros cualesquiera combinados por la operación también tiene que ser miembro. En el grupo de los números enteros, la suma de dos enteros cualesquiera también da como resultado un número entero (p. ej., 3 + 5 = 8).

2. Propiedad asociativa. La operación tiene que ser asociativa: cuando se combinan tres elementos ordenados (según la operación), se pueden combinar dos de ellos primero y el resultado es el mismo, sin que le afecte la forma en que se encierran entre paréntesis. La suma, por ejemplo, es asociativa: (5 + 7) + 13 = 25 y 5 + (7 + 13) = 25, donde los paréntesis, los «signos de puntuación» matemáticos, indican qué par se suma primero.

3. Elemento neutro. El grupo debe contener un elemento neutro tal que cuando se combina con cualquier miembro, lo deja inalterado. En el grupo de los números enteros, el elemento neutro es el número cero. Por ejemplo: 0 + 3 = 3 + 0 = 3.

4. Elemento inverso. Para cada miembro del grupo tiene que existir un inverso. Cuando un miembro se combina con su inverso, da como resultado el elemento neutro. Para los números enteros, el inverso de cualquier número es el número del mismo valor absoluto, pero con el signo opuesto: por ejemplo, el inverso del 4 es –4 y el inverso de –4 es 4; 4 + (–4) = 0 y (–4) + 4 = 0.

El hecho de que esta simple definición pueda conducir a una teoría que abarca y unifica todas las simetrías de nuestro mundo continúa asombrando incluso a los matemáticos. Como dijo en una ocasión el gran geómetro británico Henry Frederick Baker (1866-1956): «Qué riqueza, qué grandeza de pensamiento puede brotar de unos modestos comienzos». La teoría de grupos ha sido bautizada por el célebre erudito matemático James R. Newman «el supremo arte de la abstracción matemática». Obtiene su increíble poder de la flexibilidad intelectual que le proporciona su definición. Como veremos más adelante, los miembros de un grupo pueden ser cualquier cosa, desde las simetrías de las partículas elementales del universo o las diferentes barajadas de un mazo de cartas hasta las simetrías del triángulo equilátero. La operación entre los miembros puede ser algo tan mundano como la suma aritmética (como en el ejemplo anterior) o más complicado, como el de «seguido de», para la operación de dos transformaciones simétricas (como en la rotación de un ángulo seguido de otra rotación de otro ángulo).

La teoría de grupos explica lo que ocurre cuando se aplican sucesivamente varias transformaciones, como la rotación o el reflejo, a un objeto determinado, o cuando una operación determinada (como la suma) mezcla diferentes objetos (como los números) todos juntos. Este tipo de análisis pone al descubierto las estructuras fundamentales de las matemáticas. En consecuencia, cuando los accionistas del mercado de valores o los físicos de las partículas elementales tropiezan con dificultades insuperables en el reconocimiento de patrones, en ocasiones pueden utilizar el formalismo de la teoría de grupos para cruzar a otras disciplinas y tomar prestadas herramientas desarrolladas en ellas para tratar problemas parecidos.

Para tener una idea de la relación entre teoría de grupos y simetrías, comencemos por el caso más simple de las simetrías de la figura humana. Los seres humanos quedan casi inalterados únicamente con dos transformaciones de simetría. Una es la identidad, que lo deja todo como está y, por lo tanto, es una simetría clara. La segunda es el reflejo a lo largo de un plano vertical: la simetría bilateral (aproximada). Utilicemos el símbolo I para indicar la operación de la transformación de la identidad y el símbolo r para indicar la reflexión. El conjunto de todas las transformaciones simétricas de la forma humana comprende, por tanto, sólo dos miembros: I y r. ¿Qué ocurre si aplicamos esas transformaciones sucesivamente? Un reflejo seguido de la identidad es lo mismo que realizar sólo el reflejo. Simbólicamente podemos expresar esto del siguiente modo: I ο r = r, donde el símbolo ο denota «seguido de». Vemos que el orden es siempre del siguiente modo: el primer símbolo a la derecha es la transformación que se aplica primero y después va la otra. Por lo tanto, a ο b ο c significa que c se aplicó primero, seguido de b y luego de a.

La aplicación de los dos reflejos sucesivamente retorna la figura humana al original, ya que el primer reflejo intercambia izquierda y derecha y el segundo las vuelve a intercambiar. Aplicar r seguido de r es, por tanto, lo mismo que aplicar la identidad I: r ο r = I.

Ahora podemos intentar construir una especie de tabla de multiplicar para las dos simetrías, donde la entrada en la fila I y en la columna r es I ο r, y así sucesivamente. La palabra multiplicar se utiliza aquí de forma aproximada para representar la operación entre las transformaciones (en este caso, «seguido de»).

La tabla de multiplicar revela una importante verdad: el conjunto de todas las transformaciones de simetría de la figura humana es un grupo. Vamos a comprobar que las propiedades definitorias de un grupo son efectivamente satisfechas:

1. Proximidad. La tabla de multiplicar demuestra que la combinación de dos transformaciones de simetría cualesquiera por la operación «seguido de» es también una transformación de simetría. Si se piensa bien, no debe sorprendernos. Como ninguna de las dos transformaciones deja la figura inalterada, tampoco debería hacerlo su aplicación combinada.

2. Propiedad asociativa. Ésta queda claramente satisfecha porque es cierta para tres transformaciones cualesquiera de este tipo combinadas por «seguido de». En efecto, cuando aplicamos, digamos, I ο r ο r, no hay diferencia alguna según dónde pongamos los paréntesis.

3. Elemento neutro. La identidad es una transformación de simetría.

4. Elemento inverso. La tabla de multiplicar muestra que cada una de las transformaciones de identidad y de reflexión sirve como su propio inverso: aplicando cualquiera de ellos dos veces da como resultado la identidad: I ο I = I y r ο r = I.

El grupo de simetrías del cuerpo humano sólo contiene dos elementos, pero la asociación que hemos descubierto entre simetrías y grupos es muy convincente. Para escoger un ejemplo un poco más fértil, vamos a examinar la silueta de tres piernas corriendo de la figura 33. Éste es el símbolo de la británica Isla de Man situada en el Mar de Irlanda.

Esta forma tiene precisamente tres transformaciones de simetría: 1) rotación de 120 grados alrededor del centro; 2) rotación de 240 grados, y 3) la identidad (o rotación de 360 grados). Vemos que la figura no es simétrica según ningún tipo de reflexión porque las reflexiones hacen que los pies señalen en la dirección equivocada. Podemos indicar la rotación de 120 grados con a, la rotación de 240 con b y la identidad con I, y examinar de nuevo lo que ocurre cuando combinamos varias transformaciones de simetría a través de la operación «seguido de» (indicada por el símbolo ο). Si la hacemos rotar 120 grados y luego nuevamente otros 120 grados, obtenemos una rotación de 240 grados; significa que a ο a = b. Igualmente, si la hacemos rotar dos veces 240 grados, el resultado es el mismo que si la hiciéramos rotar 120 grados porque 480 grados forman una revolución completa (360 grados = la identidad) más 120 grados. Por lo tanto, tenemos b ο b = a. Finalmente, si la hacemos rotar 120 grados seguido de una rotación de 240 grados (o al revés), el resultado es una rotación de 360 grados, o sea, la identidad: b ο a = a ο b = I. Ahora estamos en situación de completar la «tabla de multiplicar»:

Vemos que este conjunto de transformaciones de simetría de las tres piernas corriendo también forma un grupo. La tabla demuestra proximidad, y las transformaciones a y b son los inversos mutuos: si aplicamos uno tras otro volvemos a tener las cosas como estaban, obtenemos la identidad.

Quizá empecemos a darnos cuenta de que allá donde exista simetría habrá grupos. De hecho, la recopilación de todas las transformaciones de simetría de cualquier sistema siempre forma un grupo. Esto es fácil de entender. Si A es una transformación de simetría, es decir, su aplicación deja al sistema inalterado, y B es otra transformación de simetría, entonces también lo es A ο B (B seguido de A). Cada transformación tiene además un inverso, devolviendo las cosas al estado original. Como veremos a lo largo de este libro, la potencia unificadora de la teoría de grupos es tan colosal que el historiador de la matemática Eric Temple Bell (1883-1960) comentó una vez: «Siempre que aparecían los grupos, o bien los introducían, la simplicidad cristalizaba a partir del caos comparativo.»

Sin embargo, a diferencia de la mayor parte de los descubrimientos matemáticos, cuando se descubrió este concepto nadie estaba buscando una teoría de grupos, ni siquiera una teoría de las simetrías. Más bien al contrario; la teoría de grupos apareció de un modo bastante casual, a partir de la milenaria búsqueda de una solución para una ecuación algebraica. Haciendo honor a su descripción como concepto que cristalizó en simplicidad a partir del caos, la teoría de grupos nació propiamente de una de las anécdotas más tumultuosas de la historia de las matemáticas. Casi cuatro milenios de curiosidad y lucha, sazonadas con intrigas, miseria y persecución, culminaron con la creación de la teoría en el siglo XIX. Esta asombrosa historia, cuya crónica se recoge en los tres capítulos siguientes, comenzó con los albores de las matemáticas a orillas de los ríos Nilo y Éufrates.