Capítulo 2
Repaso de unidades físicas y rudimentos matemáticos
En este capítulo
Aprenderás a dominar las unidades (y a mantenerlas a raya al resolver ecuaciones)
Controlarás los dígitos significativos y posibles errores
Repasarás el álgebra elemental y unos cuantos conceptos de trigonometría
La física emplea la observación y los datos para desarrollar modelos mentales y matemáticos que explican cómo funciona el mundo (y todo lo que contiene). La mayoría de gente no está familiarizada con ese procedimiento; eso es lo que encontrarás en este capítulo.
Este capítulo trata sobre algunos conocimientos básicos necesarios para pasar a los capítulos siguientes. En él abordo las unidades y la notación científica, repaso el álgebra elemental y la trigonometría, e incido en los dígitos que debes tener más en cuenta y los que puedes ignorar. Ganarán así unos fundamentos científicos, sólidos e inquebrantables, en los que apoyarte a lo largo de todo este volumen.
Cómo medir el mundo que te rodea y realizar predicciones
La física destaca por medir y predecir el mundo físico; a fin de cuentas, esa es su razón de ser. Tomar medidas es el punto de partida, la parte que consiste en observar el mundo para poder elaborar modelos y definir qué ocurrirá en él. Para eso tienes unas cuantas varas de medir: unas son para la longitud, otras para la masa o el peso, varias son para medir el tiempo, etcétera. Dominar esas unidades es una parte importante de dominar la física.
Cómo emplear los distintos sistemas de unidades
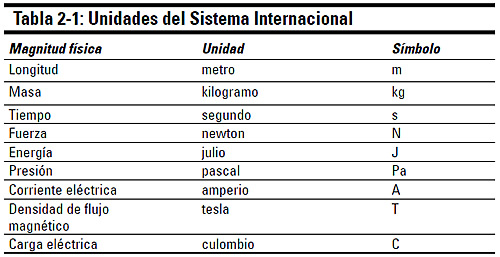
Los físicos y los matemáticos han agrupado las unidades semejantes en sistemas de unidades. De todos los que hay, el que se ve con más frecuencia al introducirse en la física es el sistema cuyas unidades fundamentales son el metro, el kilogramo y el segundo; se trata del Sistema Internacional de Unidades, que suele abreviarse por sus siglas: SI; pero también puedes encontrarte con el sistema sajón pie-libra-segundo. En la tabla 2-1 se relacionan algunas unidades del SI, junto con sus símbolos.
Como cada sistema de unidades usa distintos patrones de longitud, puedes encontrarte con cantidades numéricas distintas para una misma magnitud al resolver una parte de un problema, dependiendo de la unidad de medida que uses. Por ejemplo, para medir la profundidad del agua de una piscina puedes emplear el SI, que te dará la respuesta en metros, o recurrir al sistema sajón (menos habitual), y en ese caso hallarás la profundidad en pies. La cuestión es que al resolver un problema, uses el mismo sistema de unidades en todas las ecuaciones implicadas. Si no lo haces, obtendrás como resultado un batiburrillo carente de sentido porque estarás cambiando la vara de medir y, sin embargo, aspiras a obtener una sola respuesta. Mezclar unidades da problemas, imagina que la receta de un bizcocho requiere dos tazas de harina y, en lugar de eso, echas dos litros.
De metros a pulgadas y a la inversa: conversiónde unidades
Acabas de ver que hay diversos sistemas de medida para registrar los datos de las observaciones. Pero ¿qué sucede cuando hay que convertir las unidades de un sistema a las de otro? A veces, el principal escollo de un problema de física es que los datos que necesitas están en unidades mezcladas: un dato en centímetros y aquel otro en metros, y tal vez incluso algún otro en pulgadas. No te dejes engañar. Antes de empezar a operar hay que convertirlo todo al mismo sistema de unidades y, dentro de él, a las mismas unidades. ¿Cómo realizar esa conversión de la manera más fácil posible? Usa los factores de conversión que explico en este apartado.
Cómo emplear factores de conversión
Para realizar conversiones entre unidades de sistemas distintos hay que multiplicar por un factor de conversión. Un factor de conversión es una fracción que, al multiplicarla por el elemento que quieres convertir, anula las unidades que no quieres y conserva tan solo las que necesitas. Esa fracción que actúa de factor de conversión tiene que valer 1.
Mira cómo funciona. En toda relación entre unidades (por ejemplo, un día es lo mismo que veinticuatro horas) puedes formar una fracción que valga 1. Si, por ejemplo, divides por 1 ambos lados de la ecuación 24 h = 1 d, obtienes:
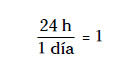
Supongamos que quieres convertir tres días en horas. Basta con multiplicar ese tiempo por la fracción anterior. Al hacerlo no alteras el valor temporal porque estás multiplicando por 1. Mira cómo se anula la unidad de los días para que quede tan solo una cantidad en horas:
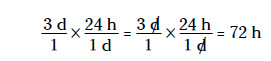
Las unidades, como días, segundos o metros, funcionan igual que las variables x e y en cuanto a que, si aparecen tanto en el numerador como en el denominador de la fracción, se anulan entre sí.
Para realizar la transformación a la inversa (de horas a días, en este caso) basta con partir de la misma relación original, 24 h = 1 d, pero esta vez habrá que dividir ambos lados de la igualdad entre 24 h para obtener:
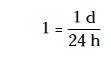
Después hay que multiplicar por esa fracción para anular las unidades de abajo y quedarte tan solo con las de arriba.
Veamos el siguiente problema. Tras cruzar una frontera te das cuenta de que has recorrido 4.680 km en tres días justos. Impresionante. Si has viajado con una velocidad constante, ¿cuál ha sido? La velocidad, tal como imaginarás, no es más que la distancia dividida entre el tiempo. Así que tendrás que calcularla de esta manera:
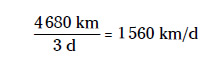
No obstante, la respuesta que has obtenido no es una unidad de medida estándar. Tienes el resultado en kilómetros por día, que se escribe como km/d. Para pasarlo a km/h necesitas un factor de conversión que elimine los días del denominador y los convierta en horas, así que multiplicarás por d/h y anularás los días:
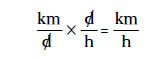
El factor de conversión que empleas es d/h. Al multiplicar por el factor de conversión tu obra tendrá este aspecto:
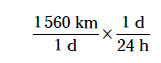
Conviene darse cuenta de que, como un día consta de 24 h, el factor de conversión vale exactamente 1, como debe ocurrir con cualquier factor de conversión. Así que al multiplicar 1.560 km/d por ese factor de conversión, no estás alterando nada, lo único que haces es multiplicar por 1. Cuando reduces los días y multiplicas las fracciones, hallas la respuesta que buscabas:
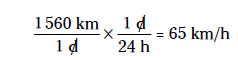
No es obligatorio que emplees un factor de conversión; si instintivamente ya sabes que hay que dividir entre 24 para convertir km/d en km/h, mejor que mejor. Pero siempre que te asalte la duda, usa un factor de conversión y anota los cálculos, porque seguir la ruta más larga es mucho mejor que cometer un fallo. Yo he visto a mucha gente hacerlo todo bien dentro de un problema, menos estas sencillas conversiones.
Si los números te marean, fíjate en las unidades
¿Quieres conocer un truco que los profesores usan para resolver problemas de física? Presta atención a las unidades con las que trabajes. Yo he hecho miles de tutorías con alumnos para resolver problemas de los que se llevaban a casa como deberes y puedo decirte que este es uno de los trucos que siempre usan los docentes.
Como ejemplo sencillo digamos que te dan una distancia y un tiempo, y tienes que hallar la velocidad. Puedes ir de inmediato a la esencia del enunciado del problema porque sabes que la distancia (expresada, por ejemplo, en metros) dividida por el tiempo (por ejemplo, en segundos) equivale a la velocidad (m/s). La multiplicación y la división se reflejan en las unidades. En efecto, como la velocidad se calcula dividiendo la distancia recorrida entre el tiempo que se ha tardado en recorrerla, la unidad que la expresará será metros por segundo (m/s). Por poner otro ejemplo, la cantidad denominada cantidad de movimiento (o momento) se calcula multiplicando la velocidad (metros/segundo) por la masa (kilogramos); así que se expresa en unidades de kg·m/s.
A medida que los problemas son más complejos, intervienen más elementos (digamos, por ejemplo, una masa, una distancia, un tiempo, etc.). Te verás leyendo el enunciado de un problema en diagonal para tomar nota de los valores numéricos y sus unidades. ¿Te piden que halles una cantidad de energía? La energía es la masa por la distancia elevada al cuadrado partida por el tiempo al cuadrado, así que, si eres capaz de identificar esos elementos en la pregunta, ya sabes cómo encajarán en la solución y no te perderás con los números.
La conclusión es que las unidades son buenas amigas. Te ofrecen una manera sencilla de asegurarte de que vas por buen camino para llegar a la respuesta deseada. Así que, cuando te hagas un lío con los números, revisa las unidades para comprobar si vas bien. Pero recuerda que también deberás cerciorarte de estar empleando las ecuaciones correctas.
Prescinde de algunos ceros: usa la notación científica
Los físicos se las apañan para meter la cabeza en los lugares más recónditos y esos parajes implican a menudo números realmente grandes o pequeños. La física ofrece un método para tratar con números muy grandes y muy pequeños; para reducir el embrollo y facilitar su digestión, recurre a la notación científica.
La notación científica consiste en escribir un número en forma decimal (con un solo dígito delante de la coma decimal) multiplicado por una potencia de diez. La potencia de diez (un 10 elevado a un exponente) expresa el número de ceros. Para hallar la potencia de diez correcta para un número muy grande, hay que contar todas las posiciones que hay antes de la coma decimal, de derecha a izquierda, hasta el lugar situado justo a la derecha del primer dígito (el primer dígito no se cuenta porque debe quedar delante de la coma decimal en el resultado).
Por ejemplo, imagina que te encuentras con la distancia promedio que separa el Sol de Plutón, que ronda los 5.890.000.000.000 metros. Manejas un montón de metros además de muchos ceros. Pues bien, puedes escribir la distancia que media entre el Sol y Plutón de este modo:
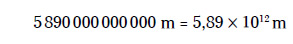
El exponente es 12 porque hay 12 posiciones entre el final de 5.890.000.000.000 (allí donde correspondería escribir un decimal en el número entero) y el lugar que ocupa ahora la marca decimal justo después del 5.
La notación científica también funciona con los números muy pequeños, como el que sigue, en el que la potencia de diez es negativa. Cuenta la cantidad de posiciones de izquierda a derecha desde la coma decimal hasta justo antes del primer dígito que no es un cero (dejando también ahora el resultado con un solo dígito delante de la marca decimal):
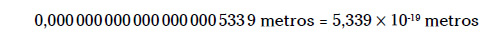
El empleo de prefijos de unidades
Los científicos han desarrollado una notación que ayuda a controlar las variables con valores muy elevados o muy bajos en sus unidades.
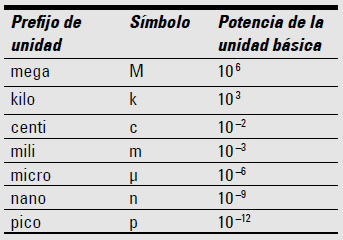
Imagina que estás midiendo el grosor de un cabello humano y concluyes que mide 0,00002 m. Podrías usar la notación científica para escribir esa cifra como 2 × 10–5 m (20 × 10–6 m), pero también podrías emplear el prefijo μ, que significa ‘micro’: 20 μm. Cuando μ aparece delante de cualquier unidad, significa 10–6 veces la unidad. Por ejemplo, el kilómetro, km, equivale a 103m, es decir, 1.000 m. La siguiente tabla contiene otros prefijos frecuentes de unidades.
Si el número que tienes que usar es mayor que diez, tienes un exponente positivo en notación científica; si es menor que diez, tienes un exponente negativo. Como ves, el empleo de números supergrandes o superpequeños con notación científica es más fácil que escribirlos enteros, por eso las calculadoras traen ya incorporada esta funcionalidad.
He aquí un ejemplo sencillo: ¿Qué aspecto tiene el número 1.000 escrito en notación científica? Podrías escribir 1.000 como 1,0 veces 10 elevado a una potencia, pero ¿a qué potencia? Habría que desplazar la coma decimal de 1,0 tres lugares hacia la derecha para obtener 1.000, así que la potencia es tres:
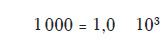
Comprueba la exactitud y la precisión de las medidas
La exactitud y la precisión son importantes cuando se toman (y analizan) medidas en física. No puedes dar a entender que tus medidas son más precisas de lo que sabes que son, añadiéndoles dígitos significativos; por otra parte, hay que tener en cuenta la posibilidad de que haya algún error en el sistema de medición utilizado y, para ello, se pone el símbolo ± cuando sea necesario. Este apartado profundiza en el tema de los dígitos significativos, la precisión y la exactitud.
Cómo saber qué dígitos son significativos
Aquí encontrarás cómo indicar de manera adecuada la precisión conocida de las medidas y usarla dentro de los cálculos, cómo representar números ajustados a su precisión conocida y cómo efectuar cálculos cuando intervienen medidas con distintos grados de precisión.
Cómo hallar la cantidad de dígitos significativos
Los dígitos significativos (o cifras significativas) de una medida son aquellos que se han registrado. Pongamos que mides una longitud con una regla en la que se leen los milímetros. La medida tomada podría ser 10,42 cm y ese resultado tendrá cuatro dígitos significativos (has calculado la distancia entre marcas para estimar el último dígito). Pero, si usaras un micrómetro muy preciso, podrías medir esa longitud hasta la centésima parte de la medida anterior, de modo que obtendrías que ese mismo objeto mide 10,4213 cm, un dato con seis dígitos significativos. Por convención los ceros que simplemente rellenan valores antes (o después) del punto decimal no se consideran significativos. Cuando te encuentras con un número como 3.600, sabes que el 3 y el 6 aparecen porque son significativos. Sin embargo, puede resultar espinoso saber qué ceros son significativos, si es que lo es alguno.
La mejor manera de escribir un número sin dejar lugar a dudas sobre cuántos dígitos significativos lo componen consiste en recurrir a la notación científica. Por ejemplo, si te encuentras con una medida de 1.000 m, no sabes si cuenta con una, dos, tres o cuatro cifras significativas. Pero si la vieras expresada como 1,0 × 103 m, sabrías que se compone de dos dígitos significativos. Si la vieras escrita como 1.000 × 103 m, entonces sabrías que tiene cuatro cifras significativas.
Cómo redondear las respuestas hasta el número adecuado de dígitos
Al realizar cálculos suele ser necesario redondear la respuesta hasta el número correcto de dígitos significativos. Si incluyes algún dígito más, entonces transmites una precisión que no es real y que no has medido.
Por ejemplo, si alguien te dice que un cohete recorrió 10,0 m en 7,0 s, te están comunicando que esa distancia se conoce hasta tres dígitos significativos, y que los segundos se conocen hasta dos dígitos significativos (la misma cantidad de dígitos de cada uno de esos datos numéricos). Para hallar la velocidad del cohete, puedes sacar la calculadora y dividir 10,0 metros (m) entre 7,0 segundos (s) y obtendrás como resultado 1,428.571.429 metros por segundo (m/s), lo que en efecto parece una medida muy precisa. Pero se trata de una precisión excesiva porque, si solo conoces los datos iniciales hasta dos o tres dígitos significativos, entonces no puedes decir que conoces la respuesta con diez dígitos significativos. Tal afirmación sería como medir algo con una regla hasta el milímetro más próximo, y después anotar una respuesta hasta la diezmillonésima de milímetro más próxima. Hay que redondear la respuesta.
Las reglas para decidir la cantidad correcta de dígitos significativos después de realizar los cálculos son:
Al multiplicar o dividir números. El resultado tiene la misma cantidad de dígitos significativos que el número de partida que tenga menos dígitos significativos. En el caso del cohete, en el que había que dividir, el resultado solo debe tener dos dígitos significativos (que son los que tiene 7,0). Lo mejor que puedes decir es que el cohete viaja a 1,4 m/s, que es el número 1,428.571.429 redondeado hasta una sola cifra decimal.
Al sumar o restar números. Alinea en vertical los puntos decimales; el último dígito significativo del resultado se corresponderá con la columna situada más a la derecha en la que todos los números empleados tengan dígitos significativos. Si tienes que sumar 3,6, 14 y 6,33, tendrías que escribir la respuesta con el número entero que más se acerque al resultado porque, como el 14 no tiene cifras significativas después del punto decimal, la respuesta tampoco debe tenerlas. Echa una ojeada para ver a qué me refiero:
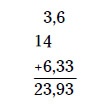
La respuesta redondeada hasta el número correcto de dígitos significativos es 24.
Para redondear un número hay que mirar el dígito situado a la derecha de la posición hasta la que redondeas. Si ese dígito situado a su derecha es 5 o mayor, redondea al alza. Si ese número es 4 o menos, redondea a la baja. Por ejemplo, 1,428 se redondea al alza y da 1,43; pero 1,42 se redondea a la baja y da 1,4.
Cómo estimar la exactitud
Los físicos no siempre recurrimos a los dígitos significativos para registrar medidas. A veces te encontrarás medidas con el signo más-menos para indicar posibles errores de medición, como en el siguiente caso:
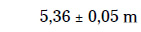
La parte que lleva el signo ± (0,5 m en el ejemplo anterior) es la estimación del posible error en la medida, así que nos están diciendo que el valor real se sitúa entre 5,36 + 0,05 (que es 5,41) m, y 5,36 – 0,05 (es decir, 5,31) m, ambos incluidos. Cuidado porque el posible error no radica en cuánto se aparta esa medida de la respuesta correcta, sino que indica la precisión del aparato empleado para efectuar esa medición; en otras palabras, indica la fiabilidad del resultado como medición.
Ármate del álgebra básica
La física conlleva un montón de ecuaciones y para poder manejarlas bien debes saber cómo mover las variables dentro de ellas. Fíjate que el álgebra no solo sirve para introducir números y hallar valores de distintas variables, sino que también te permite reorganizar las ecuaciones para realizar sustituciones en otras ecuaciones, las cuales, a su vez, pondrán de manifiesto conceptos físicos distintos. Si eres capaz de seguir la deducción de una fórmula en un libro de física, entenderás mejor por qué el mundo funciona tal como lo hace. ¡Esto es realmente importante! Ha llegado la hora de regresar al álgebra básica para refrescar la memoria.
Debes ser capaz de despejar distintas variables. Por ejemplo, la siguiente ecuación expresa la distancia, s, que recorre un objeto que parte de un estado de reposo y acelera a una tasa a durante un tiempo t:
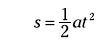
Supongamos ahora que en realidad el problema te da el tiempo que permanece el objeto en movimiento y la distancia que recorre, pero te pide que calcules la aceleración del objeto. La reordenación algebraica de la ecuación anterior te permitirá despejar la aceleración:
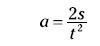
En este caso has multiplicado por dos ambos miembros de la ecuación y los has dividido entre t2 para dejar despejada la aceleración, a, en un lado de la igualdad.
¿Y si tuvieras que hallar el tiempo, t? Desplazando el número y las variables, se obtiene la siguiente ecuación:
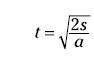
¿Hay que memorizar estas tres variantes de la misma ecuación? Desde luego que no. Basta con recordar una ecuación que relacione esos tres elementos (distancia, aceleración y tiempo) y después reordenarla según convenga en cada caso despejar una variable u otra.
Un poco de trigonometría
Debes saber algo de trigonometría, sobre todo las funciones seno, coseno y tangente, para resolver problemas de física. Para hallar esos valores, parte de un sencillo triángulo rectángulo. Echa una ojeada a la figura 2-1, en la que encontrarás un triángulo rectángulo espléndido para seguir la explicación. Fíjate sobre todo en el ángulo θ, situado entre uno de los catetos y la hipotenusa (la hipotenusa es el lado más largo, opuesto al ángulo recto). El lado y es opuesto a θ, y el lado x es adyacente a θ.
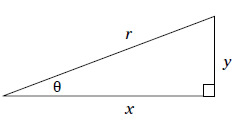
Figura 2-1.
Triángulo para hallar valores trigonométricos
Para hallar los valores trigonométricos del triángulo de la figura 2-1 hay que hacer divisiones de un lado entre otro (en diferentes combinaciones). He aquí la definición de seno, coseno y tangente:
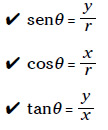
Si te dan el valor de un ángulo y un lado del triángulo, puedes calcular la longitud de los demás lados. Estas son otras formas de relaciones trigonométricas con las que sin duda te sentirás cómodamente familiarizado al acabar cualquier curso de física. Pero no tienes por qué memorizarlas. Si conoces las ecuaciones anteriores para seno, coseno y tangente, a partir de ellas deducirás estas otras según las vayas necesitando:
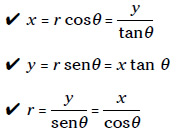
Para hallar el ángulo θ puedes proceder al revés con el arcoseno, el arcocoseno y la arcotangente, que en este libro se escriben como sen–1, cos–1 y tan–1. Básicamente, si introduces el seno de un ángulo en la fórmula del sen–1, obtienes el valor del ángulo en sí. He aquí las funciones trigonométricas inversas para el triángulo de la figura 2-1:
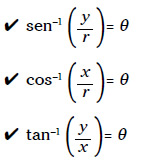
El mundo se expresa mediante ecuaciones
Tras enseñar física a universitarios durante muchos años, soy muy consciente de uno de los mayores problemas a los que se enfrentan: sentirse perdidos e intimidados por las matemáticas.
Sé un genio: no te centres en las matemáticas
Richard Feynman fue un científico famoso, que recibió el Premio Nobel de Física, muy conocido entre las décadas de 1950 y 1960 por su portentosa genialidad. Más tarde explicó su método: relacionaba el problema que tenía entre manos con una situación de la vida real y se hacía una imagen mental, mientras que otros se quedaban atascados en las matemáticas. Así, por ejemplo, cuando alguien le enseñaba una larga deducción matemática que salía mal, él pensaba en alguno de los fenómenos físicos que la deducción debía explicar. Procediendo de ese modo llegaba un momento en que las fórmulas dejaban de encajar con lo que sucedía en el mundo real; entonces señalaba dónde estaba el problema. Siempre daba en el clavo y desconcertaba a los demás, que, impresionados, lo tenían por un supergenio. ¿Quieres ser un supergenio? Haz lo mismo: no te dejes intimidar por las matemáticas.
Ten siempre presente que el mundo real va antes, y las matemáticas vienen después. Cuando te enfrentes a un problema de física, asegúrate de que no te pierdes en los entresijos matemáticos. Conserva una idea general de lo que sucede en el problema, porque eso te ayudará a mantener el control.
En física son importantes las ideas y las observaciones del mundo físico. En realidad, las operaciones matemáticas no son más que un lenguaje simplificado para describir con exactitud lo que está sucediendo. Por ejemplo, he aquí una ecuación sencilla para la velocidad:
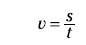
En esta ecuación, v es la velocidad, s es la distancia y t es el tiempo. Puedes analizar los términos de esta ecuación para comprobar que engloba simples conceptos de sentido común sobre la velocidad. Imagina que recorres una distancia mayor en el mismo tiempo. En ese caso, la parte derecha de la ecuación debe ser más grande, lo que significa que tu velocidad, en la parte izquierda, también es mayor. Si recorres igual distancia pero tardas más tiempo, entonces la parte derecha de esta ecuación se vuelve menor, lo que implica que tu velocidad es más baja. La relación entre los distintos elementos tiene sentido.
Puedes aplicar la misma lógica a todas las ecuaciones que te encuentres para asegurarte de que tienen sentido en el mundo real. Si ves que la ecuación no tiene sentido físico, entonces sabrás que algo tiene que estar mal en ella.
En resumen: en física, las matemáticas son buenas amigas. No debes perderte en ellas, sino usarlas para formular el problema y para guiarte mejor hacia su resolución. Cada una de esas operaciones matemáticas es muy simple por sí sola, pero al juntarlas todas, se vuelven muy poderosas.