1

Non omnis moriar^*

El autómata

La escena está dominada por un silencio absoluto, y se desarrolla en 1835 en Richmond, una próspera ciudad de la Costa Este de Estados Unidos. Podemos imaginar una sala de tamaño medio, en la que cabrían tal vez un centenar de personas, llena de sillas en las que se sientan los espectadores, completamente entregados a la partida de ajedrez bajo la luz de las velas. En el escenario, el aspecto de uno de los jugadores destaca sobre todo lo demás, con su rostro oscuro y expresión adusta, algo rígida y aparentemente concentrada, la cabeza coronada por un vistoso turbante y el cuerpo cubierto con un vestido de inspiración oriental. El jugador está sentado detrás de una mesa sobre la que vemos el tablero. Una mano sostiene una larga pipa, mientras el otro brazo está a un lado del tablero. El adversario observa las piezas febrilmente, intentando remontar una posición difícil. Al final, como le ocurrió a la inmensa mayoría de los oponentes que se enfrentaron a la figura del turbante, termina perdiendo.

La importancia de esta escena puede comprenderse con facilidad si tenemos en cuenta la fecha del acontecimiento y la naturaleza del exótico adversario. Se trata del autómata más famoso de la historia, bautizado como el Turco por sus peculiares indumentarias (figura 1.1). Construido en 1770 en Austria por el barón Wolfgang von Kempelen, este artefacto fue anunciado por su creador como el mayor invento de la historia de las máquinas. Un autómata que superaría todo lo visto hasta aquel momento, que contaba por entonces con todo un repertorio de aves, músicos o bailarines mecánicos de exquisita complejidad. Aquélla era la época dorada de los autómatas, las máquinas creadas por el hombre para imitar la naturaleza humana. No es extraño que la presentación en sociedad del Turco causara un revuelo de enormes dimensiones. Su existencia sugería posibilidades extraordinarias para una máquina, tal vez incluso la posesión de inteligencia. Como en todas las partidas, el autómata jugaba de forma sutil, para muchos demasiado humana. Y sin embargo, era a todas luces un artefacto: movía sus fichas de forma mecánica y, si se escuchaba con atención, se podían oír los engranajes en movimiento en el interior de la caja sobre la que se hallaba el tablero y dentro de la cual se encontraría, por así decirlo, el alma de la máquina. Cuando era preciso, un ingenioso sistema le permitía incluso pronunciar la palabra échec («jaque»).

Antes de llegar a Richmond, la fama del autómata había crecido hasta convertirlo en una verdadera leyenda. Jugó partidas no sólo con grandes maestros del tablero, sino también con personajes de la talla de Napoleón Bonaparte o Benjamin Franklin. A lo largo de sus ochenta y cuatro años de vida (sobrevivió a su inventor), el Turco se convirtió en una atracción de enorme magnetismo para una multitud de curiosos entre los que se encontraban numerosos científicos, escritores y magos. Sus proezas generaron una gran polémica. Es muy probable que el autómata tuviera una influencia importante en algunos pensadores clave, como el inglés Charles Babbage (1791-1871), considerado el padre del primer ordenador mecánico (figura 1.1). Después de ver jugar al Turco, Babbage consideró seriamente la posibilidad de construir un artefacto capaz de jugar al ajedrez y concluyó que sería de hecho más simple que la «máquina diferencial» que estaba construyendo, destinada a resolver cálculos complejos que hasta entonces se llevaban a cabo a mano. Babbage jugó con el autómata en 1820, perdió y señaló en su diario que su contrincante «jugaba de forma muy cauta». Y aunque no estaba convencido de que se tratara realmente de una máquina, aquel encuentro le llevó a iniciar una reflexión muy profunda acerca de la posibilidad de que una máquina pudiera llevar a cabo tareas intelectuales.

Figura 1.1. El Turco (izquierda) en un grabado de 1784, y uno de sus más famosos admiradores (y críticos): el matemático inglés Charles Babbage (1871), inventor de la primera calculadora mecánica. Ambas ilustraciones aparecieron en el Illustrated London Newspaper.

Desde la distancia que nos proporciona la época en que vivimos, parece claro que algo extraño ocurría con el Turco. El ajedrez es un juego de gran complejidad y sobre todo de una astronómica potencialidad. El poeta y novelista Pierre Mac Orlan sostenía: «Hay más aventuras en un tablero de ajedrez que en todos los mares del mundo». Cada partida representa un camino distinto y los posibles senderos que pueden recorrer los jugadores son prácticamente infinitos. No se trata de tocar una pieza de música (por hermosa y barroca que sea), sino de internarse en las posibilidades y compromisos que depara la estrategia de ambos jugadores, sus expectativas, sus trampas en las que espera que el adversario caiga sin darse cuenta. Una máquina capaz de manejar tanta diversidad de posibilidades no podía pasar desapercibida a las miradas escépticas.

Hay un segundo motivo por el que la partida de Richmond es de enorme interés. Si nos encontráramos sentados en la primera fila y observáramos a nuestro alrededor, es muy posible que nuestra mirada se detuviera sobre el rostro de un joven de aspecto cansado, ensimismado y se diría que hipnotizado por el autómata. Aunque su talento extraordinario ha empezado a ser apreciado por algunos de sus contemporáneos, nunca alcanzará el éxito en vida y años después agonizará en una callejuela de mala muerte de Nueva York, delirante y solo. Morirá al cabo de dos días en un hospital, rodeado de apenas un puñado de amigos; con el paso del tiempo se convertirá en una de las grandes figuras de la literatura norteamericana. El joven de tez pálida y ojos inescrutables no es otro que el gran Edgar Allan Poe, creador de algunos de los mejores relatos y poemas de la historia de la literatura universal. Poe ha sido atraído por los anuncios del actual propietario del Turco, que ahora viaja con su nuevo propietario, Johan von Maelzel, que en su momento compró la máquina a los herederos de Kempelen tras su muerte en 1804. Cuando Kempelen murió, el Turco era ya una leyenda, y aunque su creador nunca imaginó hasta qué punto llegaría la fama del ajedrecista mecánico, el epitafio de su tumba, «Non omnis moriar», parece más que apropiado. El encuentro con Poe será uno más de los muchos que han ocurrido y ocurrirán a lo largo de la vida del Turco, y cada uno de ellos contribuirá a su leyenda, aunque en esta ocasión sea para descubrir su secreto.

Como otros antes que él, Poe sospecha del Turco y decide llevar a cabo un examen a conciencia del desarrollo de la partida y también —muy especialmente— de la forma de actuar del autómata. El resultado de sus pesquisas es un ensayo demoledor titulado «El jugador de ajedrez de Maelzel», en el que el escritor y periodista (no en vano considerado precursor de las novelas de misterio y detectives) deconstruye minuciosamente cada detalle de la partida. Sin entrar en el análisis pormenorizado, baste decir que Poe encuentra algunos aspectos del «comportamiento» del autómata extremadamente difíciles de explicar como resultado de las acciones de una máquina. En particular, Poe hacía notar que el autómata necesitaba más tiempo en unas ocasiones que en otras para hacer sus movimientos, contrariamente a lo que se esperaría de una simple máquina, y también que sus movimientos eran demasiado rígidos. Aunque esta última afirmación pueda parecer un débil argumento, debemos mencionar que en aquella época ya era bien sabido cómo conferir suficiente elegancia a los movimientos mecánicos para que aquella maravilla tecnológica no se moviera con tanta rigidez. A juicio del escritor, aquél era uno de los muchos recursos empleados para distraer la atención y apoyar la sugestión de que el Turco no escondía nada. Poe estaba en lo cierto: la máquina escondía a un humano, un jugador de ajedrez de gran talento (se sucedieron varios) que prestaba su mente a un hermoso y sofisticado fraude.

El Turco tuvo una «vida» muy agitada y su desaparición (de alguna forma, su muerte) está a la altura de aquélla. El autómata terminó sus días exhibido en el Museo Chino de Filadelfia junto a otras muchas curiosidades, y aún «jugó» algunas partidas, aunque normalmente lo hacía frente a escolares. Su vejez, por así decirlo, transcurría tranquila hasta que un incendio destruyó el museo, en una noche de verano, en julio de 1854, y aunque se intentó por todos los medios rescatar al Turco de las llamas, resultó imposible. El doctor John Mitchell, un médico que había comprado el autómata de Maelzel a sus acreedores, fue el último en verlo. Al darse por vencido ante la magnitud del incendio, volvió la vista atrás, contemplando cómo las llamas prendían en la ropa del Turco. Mientras se quemaba, inalterable como siempre, el calor hacía que sus sistemas mecánicos de voz le hicieran repetir una y otra vez una extraña letanía: «jaque..., jaque...». Nada pudo recuperarse y aunque las leyendas hablaban de que el jugador había sido visto más tarde en diversos lugares, lo cierto es que aquélla fue su última partida.

Pocas historias pueden citarse acerca de un fraude que mantengan, nuestra atención en toda su intensidad. En esta extraña representación, llena de engaños, suspicacias, desafíos y hasta un final de película, el jugador mecánico como tal nunca existió. Detrás de las bambalinas nunca hubo un alma mecánica, una conciencia artificial capaz de contemplar el mundo y jugar partidas. El Turco fue un fraude de inmenso calado y de gran maestría. Y aun así, al juzgar desde nuestra perspectiva el impacto que tuvo sobre tantos científicos y pensadores, no podemos por menos de concluir que si el Turco encerraba o no una verdadera mente era lo de menos. Situado en los límites de lo que separaba lo vivo de lo mecánico, la misma idea que encerraba la simple posibilidad de que el autómata fuese real inspiró a muchas personas. De alguna forma encarna uno de los problemas más profundos de la ciencia: la creación de un ser inteligente, capaz de pensar.

Si no pienso... ¿no existo?

El Turco fue el heredero (fraudulento) de una larga tradición de autómatas mecánicos construidos a lo largo de los siglos y que alcanzaron su máximo esplendor en el siglo XVIII. El autómata, aun en nuestros días, descubre extraños sentimientos en nuestro interior. Las preguntas inevitables que surgen de la contemplación de uno de estos artefactos suelen ser universales: ¿qué define el límite entre un sistema mecánico y un sistema vivo?, o bien: ¿hasta qué punto se asemeja un autómata a un ser humano? Hay algunas líneas bien demarcadas que colocan al autómata muy lejos de nosotros. En particular, el paso del tiempo y su percepción. Como señala la escritora y periodista Gaby Wood: «El ser humano está sujeto al tiempo y su inevitable marcha hacia la muerte. El autómata, por el contrario, simplemente marca el paso del tiempo sin caer nunca en sus garras» (Wood 2002, 7-11).^* Para nosotros el tiempo es una certeza absoluta dentro de la cual navegamos sin cesar, siendo conscientes de su paso y su significado. Hay un pasado al que podemos remitirnos y un futuro para ser soñado o temido. Un tiempo para la nostalgia y un tiempo para morir. El autómata fluye a través del mismo tiempo que nosotros, pero para éste no hay presente, pasado ni futuro. En la obra teatral R.U.R., el texto visionario del checo Karel Čapek, en la que por primera vez se introduce el término «robot», una mujer pregunta a un robot femenino si tiene miedo a morir. Su respuesta es tan ignorante como contundente: «No puedo decirlo». Su antítesis nos la da el androide de Blade Runner que, al final de su existencia, se muestra más humano de lo que sus creadores habrían deseado. En la azotea del edificio Bradbury, Roy Batty rememora algunas de sus experiencias más valiosas en aquellas frases ya legendarias en la historia del cine: «Yo he visto cosas que vosotros no creeríais», y se lamenta por todo aquello que desaparece con él mismo: «Todos esos recuerdos se perderán en el tiempo como lágrimas en la lluvia».

Los inicios de los autómatas mecánicos marcan también el comienzo de una profunda reflexión acerca de la naturaleza del alma humana. Y, como intentos de simular a la que se consideraba la mayor creación de Dios, aquéllos eran vistos como amenazas e incluso herejías. Ya Descartes, en el siglo XVII, se encontró ante el dilema de dar a conocer sus ideas o enfrentarse a la todopoderosa Iglesia católica, con consecuencias impredecibles. En una carta a un amigo sugiere de hecho la posibilidad de «quemar todos mis escritos, o al menos no dejar que nadie los vea». El miedo a las represalias estaba más que justificado e influyó decisivamente en el resultado final de sus grandes obras. En su Tratado del hombre, considerado uno de los primeros textos de fisiología, el filósofo francés cruzaba una peligrosa frontera al comparar al ser humano con los mecanismos de una máquina. Pero Descartes, aunque era el ejemplo más visible, no fue ni mucho menos el único en sufrir el acoso (directo o potencial) de la Iglesia. Prácticamente todos aquellos que en su momento intentaron emular la vida mediante autómatas se vieron amenazados. Hay ejemplos tragicómicos, como el de Pierre JaquetDroz, inventor, en 1774, de un magnífico autómata escritor (aún en funcionamiento en el museo de Neuchatel, en Francia) que, no por casualidad, escribía con una caligrafía perfecta la célebre frase cartesiana «Pienso, luego existo». En una gira por España, Droz fue acusado de hereje y pasó, acompañado de su autómata, varios días en la cárcel. Algo parecido le ocurrió en 1738 a Jacques de Vaucanson, inventor de un famoso pato mecánico que simulaba la ingestión y expulsión de comida. El ingenioso y elegante ánade creó escuela, aunque pocos llegaron a aquel nivel de perfección. Ya de niño, Vaucanson se sintió fascinado por los relojes mecánicos y era capaz de trazar diseños muy complejos de sus mecanismos internos. Años más tarde, como novicio en un convento de Lyon, construyó unos delicados autómatas que servían y limpiaban la mesa con ocasión de la llegada al monasterio de un ilustre visitante que, aunque disfrutó de la novedad, ordenó su destrucción. Al parecer, el sugerente parecido entre los androides y los humanos a los que imitaban fue considerado una herejía. Con el tiempo, Vaucanson encontró el modo de abandonar el convento y llevar adelante su carrera como uno de los más grandes creadores de autómatas de la historia.

Los autómatas mecánicos sirvieron de plataforma para pensar acerca de la naturaleza del alma humana. En una forma hasta entonces desconocida, planteaban de forma inequívoca la necesidad de comprender las fronteras de aquello que separa la máquina de la vida, y lo hacían a través de preguntas difíciles: ¿cómo saber si una máquina está viva?, ¿tiene sentido la pregunta?, ¿hasta qué punto podemos decir que un sistema vivo es una clase de máquina? Desde entonces, ya fuera en la literatura de ficción o desde la ciencia y la ingeniería, el problema ha reaparecido continuamente. Pero no fue hasta la segunda mitad del siglo XX cuando las preguntas empezaron a obtener respuestas, a la vez que —como siempre ocurre en la ciencia— nuevas preguntas se abrían paso.

De entre los muertos

Estamos tan habituados a que los ordenadores formen parte de nuestras vidas que, incluso para quienes experimentamos la transición de la sociedad sin ordenadores a la actual, se hace difícil imaginar algo distinto. Sólo cuando vemos una vieja película en la que se muestra una oficina repleta de gente escribiendo a máquina acude a nuestra mente aquel mundo ya desaparecido en el que la información se almacenaba en fichas de cartón y las enciclopedias pesaban decenas de kilos, y ocupaban metros de estanterías en bibliotecas y salones. El desarrollo de los ordenadores tuvo consecuencias extraordinarias en nuestra civilización. En apenas unas décadas nuestra capacidad de procesar datos, almacenarlos y manipularlos aumentó con tal rapidez que literalmente entramos en una nueva era de la información. En los años cuarenta, el enorme tamaño de los ordenadores (figura 1.2) y sus elevados costes llevaron al entonces responsable de IBM, Thomas Watson, a pronunciar una frase que hoy nos hace sonreír: «Creo que existe un mercado mundial para unos cinco ordenadores». A medida que el hardware se hacía menos costoso y más compacto, los ordenadores redujeron rápidamente sus dimensiones y complejidad al tiempo que aumentaban su potencia a gran velocidad. Y en cierto momento ocurrió lo que ni siquiera la ciencia ficción había anticipado: los ordenadores, cientos de millones, entraron en nuestras casas y en nuestros lugares de trabajo para convertirse en piezas básicas de la vida cotidiana. Su uso se generalizó y dejó de ser la herramienta exclusiva de científicos o militares. El ordenador personal acercaría la capacidad de llevar a cabo cálculos precisos y complejos a cualquiera que deseara hacerlos y, lo que era aún más importante: creaba un nuevo escenario en el que la realidad tangible, los mecanismos y los autómatas podían ser reemplazados por simulaciones virtuales. En sus orígenes, la simulación estuvo directamente unida al desarrollo de armamento: desde el cálculo de trayectorias balísticas al estudio de la detonación de una bomba atómica. Aquellas enormes máquinas lograron por primera vez cubrir el terreno que las matemáticas solas no podían alcanzar. Con ello, dieron paso a una nueva vía para acceder a problemas hasta entonces inabordables. Hoy, gran parte de aquellas simulaciones se puede llevar a cabo mediante ordenadores personales. La simulación por ordenador, que había empezado su andadura a mediados del siglo XX, acabó convertida rápidamente en una herramienta accesible para una multitud de investigadores y aficionados científicos. En el camino, un joven inquieto y aún sin objetivos claros acerca de qué hacer con su vida iba a regresar a las viejas preguntas, esta vez armado con un nuevo artefacto que, en su interior, podía iluminar algunas de las dudas planteadas por el Turco y sus congéneres. Este joven investigador no era otro que Chris Langton, el padre de la vida artificial (figura 1.3).

Figura 1.2. Los primeros ordenadores capaces de llevar a cabo cálculos complejos, como el ENIAC (una parte del cual vemos en la imagen), ocupaban cientos de metros cuadrados, pesaban varias toneladas y aun así no podrían competir con una calculadora de bolsillo moderna. (Imagen cortesía de la Universidad de Pensilvania.)

Langton llegó al Hospital General de Massachusetts, en Boston, en 1971, tras declararse objetor de conciencia en la época de la guerra de Vietnam. Su imagen era la del hippy de cabello largo, motorista, algo descuidado y abstraído, pero en su caso también lleno de interés por comprender el universo. Había seguido cursos de astrofísica, ingeniería y antropología, pero también le atraían la biología y algunos de sus problemas de fondo. Sin embargo, sus múltiples intereses hacían difícil ver con claridad qué camino seguir. En el hospital desempeñó varios trabajos no cualificados, entre los que estuvo el de trasladar cadáveres a la morgue. Una noche en la que empujaba una camilla con un cadáver camino del depósito, el supuesto difunto despertó. Aquel episodio sucedió poco después de haber visto en el cine La noche de los muertos vivientes, y Langton solicitó un puesto de trabajo algo menos estresante. Al cabo de poco tiempo, empezó a trabajar como programador en los ordenadores del hospital, en el laboratorio de psiquiatría.

El lugar resultó más interesante de lo que Langton esperaba. Parte de su trabajo tenía que ver con el análisis de datos, en particular series provenientes de electroencefalogramas. Aquella labor no sólo era una forma de aprender más cosas sobre esas máquinas sino también emplearlas para explorar otras ideas. Langton disfrutaba de sus tareas como programador, a la vez que empleaba el ordenador para pensar, especialmente de madrugada, acerca de la información que entraba y salía de las máquinas. No debemos olvidar que, más allá de la materia y la energía que permite la existencia de la vida, es la información lo que nos hace distintos de los sistemas puramente físicos. Aquellos aparatos eran los nuevos autómatas del siglo XX, llenos de circuitos electrónicos en lugar de elementos mecánicos. Eran también la puerta de entrada a una revolución que aún estaba por llegar y era el caballo de batalla de nuevas formas de crear y explorar la información. Una de las novedades del momento era «el Juego de la Vida», un sencillo programa salido del legendario Instituto Tecnológico de Massachusetts, que creaba estructuras complejas que parpadeaban y evolucionaban en la pantalla.

Figura 1.3. Arriba, Christopher Langton, el padre de la vida artificial, en 1989. (Fotografía de Cary Herz, con permiso del Instituto de Santa Fe.) Su trabajo en este campo se basó fundamentalmente en el empleo de autómatas celulares, que podemos imaginar como sistemas simples de interacción entre elementos sobre un tablero, en el que las piezas (abajo) serían nuestros autómatas, que nacen, mueren o se mueven en función de reglas simples. (Fotografía de Anna Bozzano.)

El Juego de la Vida no es realmente un juego con jugadores, estrategias, vencedores ni vencidos. Es más bien una imitación simplificada de un sistema de elementos que se replican y mueren sobre un espacio bidimensional. En las noches de trabajo en el laboratorio de psiquiatría, el juego solía estar en funcionamiento y sus resultados aparecían y cambiaban constantemente. El juego manejaba también información y creaba nueva información que generaba una nueva estructura. Una de aquellas noches Langton cayó en la cuenta de que lo que el ordenador recreaba no era una simple forma cambiante. Langton quedó atrapado, como muchos otros antes y después, por el Juego de la Vida, un modelo extremadamente simple creado por un matemático americano que buscaba —y encontró— un sistema sorprendentemente simple que, sin embargo, es capaz de generar estructuras de complejidad casi infinita, como la vida misma. Para Langton, las luces parpadeantes que brillaban en la semioscuridad del laboratorio se convirtieron en una revelación acerca de la posibilidad de entender lo vivo desde una perspectiva nueva y revolucionaria: la vida podía existir en el mundo virtual, ser recreada en el interior de un ordenador. Aunque Langton no lo sabía entonces, su intuición y la de otros investigadores iba a desarrollarse en unos años, hasta dar a luz a un nuevo campo de conocimiento. Un campo en el que se cruzarían disciplinas y sistemas tan diversos como la virología, el estudio del cáncer, los mercados financieros, la cosmología y la historia.

Vivir al límite

John Conway tiene su despacho en la prestigiosa Universidad de Princeton, lleno de poliedros, puzles y dibujos que representan estrategias complejas asociadas a juegos de todo tipo. Ha resuelto multitud de problemas matemáticos relacionados con la resolución de juegos, pero su contribución más famosa es el Juego de la Vida, que creó en 1970. El juego se hizo famoso gracias a un artículo aparecido en Scientific American que escribió su amigo Martin Gardner, uno de los más grandes divulgadores de las matemáticas de todos los tiempos. El juego es extremadamente simple, y puede «jugarse», como hizo Conway al principio, en un tablero de damas. Imaginemos que en una casilla ponemos una ficha si está «viva» y la dejamos vacía en caso contrario. El juego permite que estas fichas se reproduzcan dependiendo de lo que rodea a la casilla en cuestión. Este entorno queda definido por el número de vecinos «vivos» que posee (con un máximo de ocho). Del mismo modo, una ficha puede desaparecer y de alguna forma «morir». Las reglas exactas del juego son fáciles de definir. Partiendo de un tablero con fichas distribuidas al azar repetimos una y otra vez las siguientes operaciones:

(1) Si una casilla está ocupada por una pieza, ésta sigue viva si posee dos o tres vecinos vivos. En caso contrario, muere (desaparece).

(2) Una casilla vacía puede ser colonizada si tiene exactamente tres vecinos vivos.

Las reglas son claramente arbitrarias, aunque poseen cierta lógica. La primera nos dice que la supervivencia depende de la presencia de otros individuos, como ocurre en algunos sistemas biológicos en los que se requiere cierto grado de coo peración para garantizar (o facilitar) su persistencia como población. La limitación impuesta por un número muy bajo o muy alto puede entenderse como una masa crítica de individuos que ayuden a la supervivencia o como un exceso de ellos que —tal vez— consuman demasiados recursos. La segunda regla es algo menos evidente, aunque nos dice que la reproducción requiere de varios individuos que se encuentren en cierta región. El número tres no se corresponde con la reproducción sexual que conocemos (cosa de dos), pero deja espacio a la imaginación. En cualquier caso, en el Juego de la Vida no se puede aplicar aquello de que «tres son multitud».

En lugar de hacer un experimento con un tablero de ajedrez, traslademos las reglas a nuestro ordenador (existen muchas páginas en internet que simulan el juego) y veamos qué ocurre. El lector estará de acuerdo con que las reglas son de una simplicidad ridícula. No resulta evidente qué puede ocurrir cuando dejamos que las reglas actúen y hagan su trabajo, cambiando nuestra configuración inicial. Pero se trata de un sistema que crea y destruye elementos, así que lo más probable es que acabemos obteniendo una población de piezas estable. Estas expectativas son correctas: el juego genera cambios que hacen que el número de elementos se reduzca al principio hasta alcanzar un treinta por ciento del total, aproximadamente. En la figura 1.4 vemos un ejemplo de los cambios que se dan en el sistema sobre un tablero en el que hemos colocado al azar cierto número de partículas vivas (casillas negras) y hemos seguido sus cambios en instantes sucesivos. Para visualizar mejor el comportamiento, hemos empleado una proyección del tablero sobre una esfera. La primera imagen (figura 1.4a) representa el momento inicial, en el que tenemos partículas vivas esparcidas al azar. Al poco tiempo (figura 1.4b) observamos una menor densidad y grupos de agregados de partículas que se definen cada vez más (figura 1.4c) y alcanzan un estado que, aunque variable en el tiempo, parece mantener cierta estructura básica. Si seguimos observando la evolución, después de un periodo más o menos largo se alcanza un estado en el que un conjunto de formas permanece estable. Algunos ejemplos de estas estructuras se muestran en la figura 1.5a-e. Entre las formas que genera el programa se encuentran algunas que son estáticas y no cambian una vez alcanzadas, mientras que otras siguen secuencias de cambios periódicos. Entre estas últimas tenemos varias formas que presentan dos estados alternativos mientras que otras, como los llamados «deslizadores», cambian regularmente mientras vuelan sobre el tablero, desplazándose a velocidad constante.

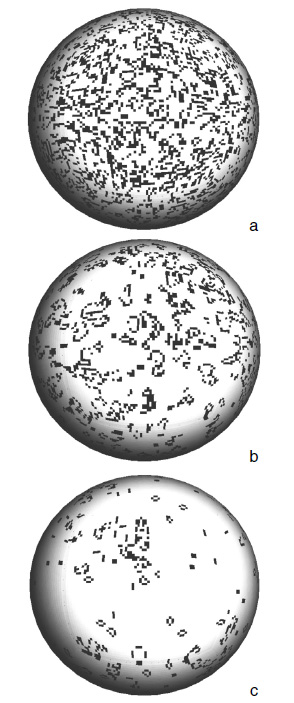
Figura 1.4. Ejemplo de evolución del sistema en el Juego de la Vida, en la que apreciamos multitud de estructuras complejas, muchas de las cuales cambian constantemente mientras otras se propagan sin cesar. Partimos de una situación inicial (a) generada al azar, que evoluciona rápidamente (b-c) a un estado de baja densidad dominado por estructuras complejas. Estas estructuras permanecen más o menos estables después de un tiempo. (Imágenes de Sergi Valverde.)

Pero hay mucho más. De hecho, el juego tiene unas posibilidades virtualmente infinitas de generar estructuras complejas. Todo depende de la condición inicial: de cómo estaban las piezas distribuidas al principio. Podemos «preparar» nuestro sistema de forma que, en lugar de poner nuestras piezas iniciales al azar sobre el tablero, las colocamos en lugares bien elegidos, como vemos en la figura 1.5f. A lo largo de los años, los científicos, informáticos o simples aficionados que se han sumergido en las complejidades del juego han descubierto todo tipo de estructuras complejas que éste puede formar. Es posible diseñar naves espaciales que se desplazan y cambian, fábricas de deslizadores, incluso un ordenador capaz de emular a cualquier otro que podamos imaginar. Este computador, que funciona con las reglas del Juego de la Vida, puede construirse diseñando adecuadamente la ordenación inicial de todos los componentes, y al igual que los ordenadores que empleamos a diario, posee una unidad de memoria, un sistema de procesamiento de información y es capaz de leer y procesar información externa. Sin embargo, y aquí tenemos una diferencia importante, la «máquina» es un sistema permanentemente activo: para mantener su estructura, debe estar constantemente cambiando. No es un sistema muy eficiente, dado que cualquier proceso que deseemos ejecutar será difícil de preparar. Pero aun así la posibilidad de poder construir una máquina de semejante potencia a partir de las reglas triviales del Juego de la Vida nos envía un mensaje de enorme importancia: reglas simples pueden dar lugar a comportamientos extremadamente complejos. Si le damos la vuelta a esta afirmación, podemos llegar a una conclusión no menos inesperada: tal vez el comportamiento complejo de muchos sistemas se deba a reglas simples, a leyes fundamentales comprensibles. De ser así, incluso aquellos fenómenos que consideraríamos tremendamente complicados por el número de variables implicadas podrían —tal vez, sólo tal vez— explicarse a partir de mecanismos simples. Los sistemas vivos, las sociedades o la mente no serían cajas negras inaccesibles a nuestra comprensión. Quizá no deba sorprendernos que este programa simple y a la vez complejo haya servido de inspiración para reflexionar sobre problemas de enorme calado, como el del propio origen del cosmos: en El gran diseño, los físicos Stephen Hawking y Leonard Mlodinow emplean el Juego de la Vida como metáfora de las reglas de «diseño» de nuestro universo. Tal y como señalan estos autores, si tuviéramos que estudiar el Juego de la Vida como las reglas de un universo, procederíamos de forma similar a lo que hacen los físicos en el nuestro. El comportamiento del sistema, en particular los cambios regulares observados en los bloques oscilantes o los deslizadores, serían explicables por medio de reglas físicas apropiadas, como las del movimiento o la colisión de estructuras, si bien estas leyes no se encuentran definidas en las reglas del juego, que sólo tienen que ver con nacimientos y muertes. Como apuntan Hawking y Mlodinow, el Juego de la Vida nos muestra de forma simple una lección que resulta difícil de asimilar (sobre la que volveremos más adelante): nuestra descripción de la realidad depende del modelo empleado.

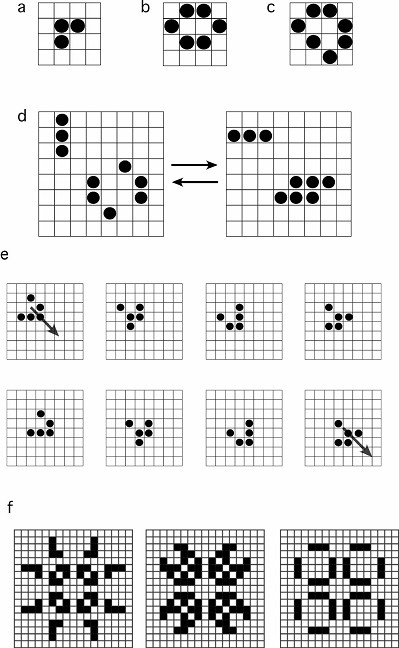
Figura 1.5. Diversos ejemplos de los cambios de estado de una pequeña parte de un tablero sobre el que evolucionan los autómatas celulares siguiendo las reglas del Juego de la Vida de Conway. Aquí las casillas «vivas» están ocupadas por círculos mientras que las «muertas» están vacías. Los ejemplos a-c son pequeñas estructuras estables, que no cambian con el tiempo. Las figuras (d) y (e) muestran secuencias de cambios oscilatorios (d) o de movimiento direccional (e) de un deslizador. En (f) se muestra un ejemplo de estructura oscilatoria de tres estados y mayor tamaño. (Gráficos de Ricard Solé)

Langton terminaría dedicando su carrera posterior al estudio de autómatas celulares, a cuya teoría y aplicaciones contribuyó de forma muy notable, pero el camino hasta el lugar adecuado en el que trabajar resultó ser muy tortuoso. Cuando el laboratorio de psiquiatría cerró, Langton quedó en un limbo intelectual. Después de una accidentada búsqueda de un lugar en el que estudiar y desarrollar una tesis, terminó investigando durante un tiempo en la Universidad de Michigan. Entre dichos accidentes se contaba uno totalmente real: una caída casi mortal mientras volaba en parapente que, entre otras cosas, le destrozó los huesos de la cara, en la que se clavaron sus rodillas, y que requirió numerosas intervenciones. Aquélla fue una época difícil, en la que Langton tuvo que acudir a sus clases en la universidad ayudándose de muletas, y con la cara llena de vendajes y grapas, en un homenaje indeseado al monstruo de Frankenstein.

En Michigan creó el primer programa simple en el que se demostraba cómo hacer un sistema virtual capaz de autorreplicarse y al que casi nadie prestó atención, aunque representaba ya entonces un enorme salto adelante en nuestra comprensión de un problema que no se había abordado seriamente desde los años cincuenta. También empezó a desarrollar la idea de que los sistemas vivos se encuentran situados en cierta frontera entre el orden y el desorden. El argumento de Langton puede expresarse brevemente así: para poder almacenar información de forma estable, es preciso disponer de cierto grado de organización interna (orden), pero a la vez, si queremos manipular y procesar esta información, hace falta que el sistema pueda crearla y destruirla (desorden). La conjetura de Langton, aún no demostrada, es que la vida se halla en la frontera que separa ambas fases. Al final, su talento llamó la atención del físico Doyne Farmer, que consiguió que lo contratara el prestigioso Laboratorio de los Álamos, en Nuevo México. Allí pudo cumplir uno de sus sueños: organizar, con un éxito sin precedentes, el Primer Congreso de Vida Artificial, que propició que el campo en el que había estado trabajando durante años se convirtiera en una realidad. Podríamos decir que lo demás es historia, pero no lo es. Esta disciplina ha crecido de distintas formas, y su filosofía ha invadido distintos campos, con lo que las fronteras entre lo que podemos o no llamar vida artificial son difíciles de establecer. En este libro adoptaremos como convenio aceptar como parte de esta disciplina aquellos sistemas que son estudiados bajo el prisma de la simulación por ordenador y que implican sistemas vivos, ya sean éstos células, tejidos, organismos, ecosistemas, sociedades humanas o mercados financieros. Antes de internarnos con mayor profundidad en cada clase de sistema, nos detendremos para definir uno de sus elementos más característicos y sorprendentes.

Autoorganización

El Juego de la Vida es un ejemplo (tal vez el más famoso) de los denominados autómatas celulares. Éstos representan la forma más simple de simular mediante el ordenador el comportamiento de muy diversos sistemas complejos en los que células, hormigas, individuos o sociedades se relacionan en un espacio dado. En algunos casos, con el objetivo de definir de forma general los objetos básicos que constituyen las unidades del sistema, se emplea el término «agente» para denotar cierto elemento más o menos complejo, ya se trate de una neurona o de un agente de Bolsa. Como veremos más adelante, y sin ánimo de ofender, los agentes de Bolsa (y me temo que algunos políticos) pueden ser en ocasiones reemplazados en un modelo económico por poco menos que una neurona, en el que la imitación suele ser un elemento clave del comportamiento de los individuos. Aquí emplearemos indistintamente el término autómata celular o agente para referirnos a estas unidades. El Juego de la Vida queda definido por el tablero de células (nuestros agentes) y las reglas de cambios. No es casualidad que aparezca el término «autómata» de nuevo, aparentemente muy lejos de los autómatas mecánicos de los que hablábamos al principio. Pero ambos comparten cierta simplicidad básica en la ejecución de unas reglas que les hacen responder de forma previsible. En el Juego de la Vida, por ejemplo, lo que suceda en el siguiente instante sólo depende del estado actual del sistema. Cualquier otro evento previo es ignorado.

Los autómatas (como el de Conway) se definen mediante reglas de interacción que suelen ser muy simples. En este sentido, los modelos que simulan un problema dado se basan en una simplificación extrema de las reglas reales (que pueden ser desconocidas). Los detalles, por lo tanto, se dejan de lado para quedarnos con lo esencial. He aquí una de las tareas más difíciles: ¿qué es importante y qué no lo es? Lamentablemente no hay una respuesta fácil. Einstein señaló en una ocasión que «los modelos deben ser tan simples como sea posible, pero no más simples». En otras palabras, la idea básica es que debemos renunciar a tantos detalles como podamos, pero no dejar de lado aquello que, de alguna forma, constituye la esencia del problema. Una de las grandes ventajas de la simulación por ordenador es que podemos probar un modelo y lo que aprendamos de su comportamiento y su similitud con la realidad nos permite corregirlo y modificarlo. Podemos no sólo recrear el comportamiento de un ecosistema, un tumor o el cerebro, sino también extraer aquellos factores que realmente explican su funcionamiento. La simulación es así una forma de acercarse a la realidad distinta de la observación y de la teoría pura. Permite hacer experimentos imposibles por su magnitud o singularidad, como recrear la explosión de estrellas, la formación de galaxias o de agujeros negros, pero también nos acerca a sistemas que, por sus propiedades especiales, no permiten observar lo que ocurre en las escalas más pequeñas. Un tumor en desarrollo representa un desafío para la observación directa: tenemos una masa de millones de células tumorales que interaccionan entre sí y con el tejido sano, mutando y adaptándose a los retos que encuentran y explotando recursos del organismo, como por ejemplo sus vasos sanguíneos. Sabemos que todo eso ocurre, pero es muy difícil saber de qué manera. Combinando lo que biólogos moleculares, oncólogos y patólogos han aprendido, y haciendo algunas hipótesis razonables (recordemos la advertencia de Einstein) sobre lo que es esencial, ha sido posible plantear modelos explicativos del crecimiento tumoral y sus respuestas a los tratamientos.

Los modelos de autómatas suelen definirse, como ocurría en el ejemplo del Juego de la Vida, sobre un tablero cuadrado. En general, el elemento que ocupa una casilla (si no está vacía) puede poseer varios «estados» distintos. Si tratamos con células, pueden ser, por ejemplo, cancerosas o sanas. Si se trata de especies en un ecosistema, pueden corresponder a individuos de distintas especies, como presas y depredadores. Por otra parte, necesitamos definir la forma en que estos elementos interaccionan entre sí. Las reglas son, de hecho, la parte fundamental del problema, ya que realmente recogen las leyes subyacentes. Algunas reglas pueden ser evidentes: un depredador se encuentra a una presa y la devora, con lo que ésta desaparece, o dos sustancias químicas entran en contacto y forman dos productos de reacción nuevos o se aniquilan entre sí.

Uno de los aspectos más interesantes de la complejidad, ya sea biológica o social, es la presencia de propiedades emergentes. Ésta es la característica definitoria de lo complejo: la existencia de propiedades nuevas a cierta escala que no son reducibles a las propiedades de los elementos (agentes) del nivel inferior. La vida, por ejemplo, no es simplemente el ADN de la célula, ni la lista de proteínas que hacen sus tareas de transporte o mantenimiento, ni tampoco la membrana que define la frontera con el mundo externo. La vida es el resultado emergente de la combinación e interacción entre estos tres componentes, ninguno de los cuales por sí solo puede explicar la naturaleza de lo vivo. Del mismo modo, nuestros pensamientos no son reducibles a lo que hacen las neuronas individuales ni la sociedad a sus individuos componentes. De hecho, una de las características más destacadas de la forma en la que se comportan los sistemas complejos, y que los modelos de simulación han podido explicar en muchos casos, es la presencia de autoorganización: la aparición de estructuras espaciales o temporales cuyo tamaño o duración es muy superior al de los elementos constituyentes. La autoorganización es por tanto la «explicación» dinámica de las propiedades emergentes.

Para ilustrar un proceso de creación de orden espontáneo a partir de las interacciones de autómatas, consideraremos un proceso biológico en el que células de distintos tipos dan lugar a un tejido complejo. Este ejemplo nos ayuda a comprender una serie de observaciones experimentales muy interesantes y proponer el mecanismo explicativo para éstas. Los experimentos originales que nos llevan a este problema revelan la existencia de una asombrosa capacidad para la regeneración por parte de algunas especies de organismos. El caso paradigmático es el desarrollo de embriones de erizo de mar. Éste es uno de los llamados «modelos animales», esto es, organismos muy bien conocidos y que, por sus propiedades especiales, permiten comprender y analizar en detalle los procesos que determinan su desarrollo. Puede resultar poco atractivo emplear un organismo aparentemente tan alejado de nosotros como punto de referencia, pero no debemos olvidar que compartimos con cualquier ser vivo una buena cantidad de material genético y de numerosos ejemplos de moléculas y mecanismos moleculares que se han conservado a lo largo de millones de años. Las lecciones que extraigamos del erizo nos pueden ser de enorme ayuda para comprendernos a nosotros mismos, nuestra evolución y la naturaleza de la enfermedad.

Este organismo en particular atraviesa diversas fases de desarrollo características a medida que crece, entre ellas, fases larvarias en las que miles de células forman un primer estado del futuro animal adulto. Imaginemos que tomamos esta larva y la disgregamos por completo, separando todas sus células, que colocaremos en una placa de Petri. Dado que la larva es el resultado de un proceso de divisiones sucesivas a partir de una única célula y de una historia de cambios en los estados de estas células, parece lógico esperar que el orden anterior se haya perdido por completo. Lo que muestra el experimento es algo totalmente inesperado: las células inician un lento pero inexorable proceso de reorganización que termina con la completa reconstrucción de la larva, que sigue entonces el desarrollo habitual hasta alcanzar el estado adulto. Esta observación nos habla de una extraordinaria plasticidad para regenerar información perdida, y se da en otros muchos casos.

En general, si mezclamos células previamente aisladas a partir de tejidos diversos y las colocamos en el mismo lugar, observaremos un proceso parecido, en el que las células se agrupan en formas bien organizadas, formando capas y tubos dentro de lo que algunos han llamado «microórganos». Estos órganos artificiales microscópicos son como pequeños agregados de tejidos ordenados según formas que recuerdan los tejidos dentro del organismo. Así, los tipos de células que suelen estar en la zona exterior o interior del órgano tienden a mantener esta posición, mientras que las que forman cavidades tienden a distribuirse juntas formando pequeñas cavidades. ¿De dónde surge este orden espontáneo?, ¿hay algún tipo de información compleja que permite a las células decidir de qué forma deben crear estructuras? Un modelo simple demuestra que la tendencia de cada tipo de célula a adherirse a los otros tipos explica lo que observamos.

Imaginemos que planteamos nuestro modelo considerando para empezar sólo dos tipos de células, que indicaremos por simplicidad como áreas blancas y negras (figura 1.6). Cada tipo de célula puede tener mayor o menor afinidad por las células de su mismo tipo o del otro. Asimismo, las células pueden encontrarse mejor o peor en contacto con el medio externo, con lo que pueden tender a evitar el contacto con éste. Al principio, igual que ocurre con los experimentos, nuestras células artificiales están distribuidas al azar. Dado que las células reales poseen una tendencia intrínseca a moverse alrededor cuando están aisladas, dejaremos que las células virtuales se desplacen al azar por el tablero. Tarde o temprano, entrarán en contacto con otras células iguales o distintas. Supongamos que hemos inventado una tabla de números que miden hasta qué punto nuestra célula se considera rodeada de los vecinos adecuados para dejar de moverse. Supongamos que las células blancas tienden a quedarse cerca de las de su mismo tipo y evitar las negras y la exposición al medio, mientras que las negras se agregan a la vez que pueden adherirse (con menor intensidad) a las blancas. ¿Cuál es el resultado de este escenario? Como muestra la figura 1.6, el agregado que se forma termina en una esfera en la que las células se distribuyen de forma concéntrica creando un objeto ordenado en el espacio. Si las intensidades relativas son distintas, obtendremos distintos tipos de complejos multicelulares. Estos microórganos pueden ser más complejos si incluimos más tipos celulares. Sin más información que las preferencias de cada célula por permanecer o no en un lugar, y basando estas preferencias en el estado de los vecinos más cercanos, podemos generar una estructura global ordenada a partir del desorden inicial. Como dijo Ilya Prigogine, el orden surge del caos microscópico. La forma esférica es el resultado de minimizar las interacciones indeseables y, con argumentos puramente físicos, puede demostrarse que es la forma estable.

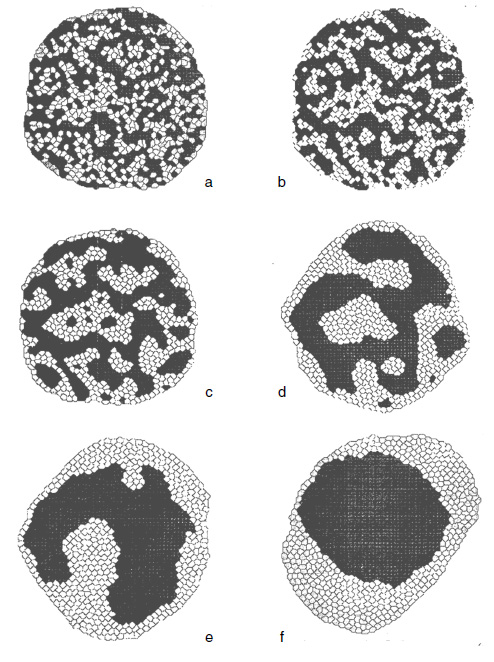
Figura 1.6. Autoorganización de tejidos virtuales. En esta secuencia vemos cómo una masa inicial (a) compuesta de dos tipos de células (indicadas por elementos blancos y negros) cambia en el tiempo (b-f) mostrando una segregación constante entre ambos tipos, que forman conjuntos separados, si bien al final uno engloba al otro (f). Este proceso es el resultado de interacciones celulares en las que los grupos homogéneos son más estables. (Imágenes de James Glazier.)

¿Dinosaurios sintéticos?

La capacidad de reconstruir tejidos a partir del intercambio de información entre células no se limita a la generación de estructuras más o menos ordenadas. En el ejemplo anterior, hemos visto cómo un conjunto de células ya diferenciadas se reorganizaban formando tejidos. Pero durante el desarrollo no sólo se dan estos procesos de redistribución en el espacio: el propio estado de las células cambia como resultado de sus interacciones, de modo que se produce un diálogo entre el proceso de construcción del tejido y su composición. Un experimento desarrollado en 1980 nos muestra de forma espectacular hasta qué punto es así. Una de las características de los vertebrados es la presencia de dientes. Los dientes son estructuras antiguas, que emergieron por primera vez hace millones de años y desaparecieron del programa de desarrollo de las aves hace al menos 70 u 80 millones de años. En el embrión en crecimiento, los dientes se forman y desarrollan a partir de la interacción entre distintas capas de tejido. Para que un embrión de ave «construya» un diente completo, basta con poner en contacto células del mesodermo de ratón (que están en zonas más profundas, debajo de la superficie) con células epiteliales del embrión de pollo en el momento adecuado de su desarrollo. En condiciones normales, el mesodermo y epitelio de ave interaccionan entre sí sin producir la formación de dientes. Pero al cambiar las señales reguladoras, podemos recuperar la capacidad de generar no sólo dentina (el material precursor de los dientes) sino incluso dientes completos. Reconocemos no sólo el tipo de células que los forman, sino pura y simplemente su aspecto, como si alguien los hubiera colocado allí. Estudios posteriores llevados a cabo por Matthew Harris en la Universidad de Wisconsin demostraron que es posible inducir la formación de dientes sin manipular tejidos, actuando directamente sobre las señales moleculares. Tras activar la llamada beta-catenina en los embriones, éstos desarrollaron dientes. Los dientes obtenidos eran inconfundiblemente reptilianos, con una forma característica de los arcosaurios (un grupo al que pertenecen los cocodrilos). El potencial para construir el diente se halla así presente, aunque podríamos decir que dormido.

Una de las historias más interesantes acerca de este potencial tiene que ver con la huella que la evolución ha dejado en nuestro genoma y que, a veces, nos permite rescatar fenómenos y estructuras que se dieron en un pasado muy remoto. Tomemos por ejemplo los dinosaurios. ¿Qué no daríamos por devolverlos a la vida? ¿Será capaz la biología, mediante la ingeniería genética, lograr algo así? Aunque el escenario de Parque Jurásico está muy lejos de ser real algún día, podemos recrear algunas piezas del puzle si somos lo bastante hábiles para unirlas. El ejemplo de los dientes no es una simple anécdota. En 1999, Neda Nikbakht y John McLachlan presentaron un estudio experimental en el que demostraban la posibilidad de inducir la formación de dedos en las alas de aves, empleando para ello factores de crecimiento. En este sentido, la observación de las fases iniciales del desarrollo de un embrión de ave nos da indicaciones del potencial dormido. El ala del embrión cambia con el desarrollo desde una estructura similar a la de Archaeopteryx, con los dedos separados, a la estructura adulta en la que éstos se han fusionado (figura 1.7). Los dedos adicionales formados en las alas de los embriones manipulados muestran rasgos que se han hallado en fósiles de dinosaurios y su estructura es la de un dedo anatómicamente distinguible.

Terminemos indicando que en otra serie de experimentos, Lars Larsson y sus colaboradores de la Universidad de McGill, en Canadá, han observado que un tercer ingrediente, común en los dinosaurios alados pero desaparecido en las aves modernas, parece estar también dormido: la cola de sus antecesores reptiles no existe en la contrapartida aviar, pero su breve aparición durante el crecimiento del embrión nos sugiere que esta propiedad también sería recuperable mediante una adecuada manipulación. La observación de estos investigadores es concluyente: al seguir con atención el crecimiento y desarrollo de embriones de ave, vieron que en la zona de la cola se muestra en cierto momento la formación de estructuras vertebrales que sin lugar a dudas son el remanente de las antiguas colas. Pero después de un breve periodo de desarrollo, estas estructuras son reabsorbidas y simplemente desaparecen. Su aparición momentánea es un recordatorio más del pasado evolutivo y de su marca. El poder evocativo de estos experimentos y observaciones ha llevado al famoso paleontólogo Jack Horner (que inspiró a Michael Crichton para su personaje de la novela Parque Jurásico) a sugerir la posibilidad real de crear un —llamémosle así— dinosaurio artificial. El libro de Horner, How to Build a Dynosaur, es sugerente. Horner es un entusiasta de esta posibilidad, como no podía ser de otra forma, aunque él mismo admite que será difícil conseguir que una institución financie un proyecto semejante. Y aunque es cierto que se necesitará de una buena cantidad de dinero, sospecho que, en el peor de los casos, aprenderíamos mucho de los mecanismos de construcción de organismos y su conservación a lo largo de eras geológicas. En el mejor (y apuesto a que posible) escenario, podríamos acercarnos tanto como podamos a recrear criaturas que fueron borradas de nuestra biosfera hace millones de años, antes de que el largo verano de los dinosaurios terminara. Pocos momentos serán tan excitantes para un científico como aquel en que el recién llegado desde el mundo de la vida sintética empiece a golpear con su pico (lleno de dientes) el cascarón del huevo en el que procesos de construcción hasta entonces dormidos habrán vuelto a la vida.

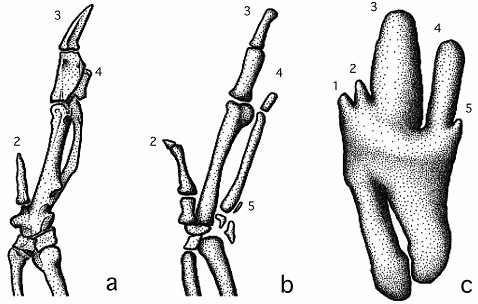
Figura 1.7. La presencia de los procesos de formación de una extremidad completa con cinco dedos, que se daba en los dinosaurios y que se transformó a lo largo de la evolución de las alas de las aves, se pone de manifiesto durante el desarrollo de un embrión de pollo. Los dibujos (adaptados de Nikbakht y McLachlan, 1999) presentan varios estados del desarrollo del ala de pollo. Aquí vemos: (a) el ala del adulto, que presenta tres dedos fusionados, (b) el ala del embrión a los ocho días, con cuatro dedos visibles y (c) el mismo sistema en etapas muy tempranas, en el que se aprecian cinco condensaciones óseas correspondientes a los cinco dígitos.

Memento mori

Los autómatas mecánicos siguen llamando a la puerta de nuestra imaginación. Ya en los inicios de la revolución industrial algunos pensadores, como Samuel Butler, reflexionaron acerca de lo que podría ocurrir en el futuro, cuando las máquinas pudieran imitar la evolución de la vida. Butler escribió un ensayo titulado Darwin entre las máquinas, en el que ya reflexionaba en profundidad sobre lo que cabía esperar si las máquinas terminaban por dominar el mundo. Estas ideas fueron precursoras de lo que la ciencia-ficción, siempre avanzada a lo que la tecnología podía generar, desarrollaría a lo largo del siglo XX. Butler escribía en 1863 acerca de nuestra subordinación a las máquinas, profetizando que, tarde o temprano, «tendrán la verdadera supremacía sobre el mundo y sus habitantes».

Butler estaba convencido de que los objetos tecnológicos, las máquinas en particular, formaban una especie de reino similar a los reinos animales y vegetales. En este dominio de lo no vivo, destacan los robots, que definen la fase última —aunque no el final— del árbol de la evolución artificial y a la que volveremos en el capítulo 3. Pero también las criaturas realmente vivas que se pueden diseñar y construir en un laboratorio. Con el comienzo del siglo XXI asistimos a la imparable emergencia de nuevas formas de retomar, probablemente con éxito, los sueños y esperanzas que los constructores de autómatas plantearon hace siglos. Desde la ciencia y la ingeniería más avanzadas, nuestra comprensión de la vida pero también de sus alternativas posibles, crecen a diario. Inspirados en el funcionamiento del cerebro, podemos desarrollar robots que aprenden a comunicarse, cooperar o mentir. Es posible construir bacterias que incorporan en su interior genes humanos y que llevan a cabo tareas que la evolución nunca planeó que fueran capaces de hacer. Mientras tanto, ya hay robots exploradores que recorren la superficie de Marte y sondas automáticas que trazan mapas de los confines de nuestro sistema solar, más allá de lo que incluso Galileo habría soñado jamás. En centros de investigación de todo el mundo se dan pasos pequeños, pero seguros, hacia nuevas formas de introducir comportamientos complejos en sistemas artificiales. Existen ya máquinas que simulan emociones y, aunque lejos de nuestra complejidad mental, empiezan a desafiar nuestra capacidad de discernir lo natural de lo artificial. A medida que sabemos más del funcionamiento de la mente y el potencial para simular su comportamiento crece con el avance de la tecnología, las fronteras se hacen más tenues. En este libro nos acercamos a esta zona aún por definir que separa lo real de lo artificial, lo biológico de lo sintético, la vida de la no vida.

La idea de crear vida artificial que traza la historia de los autómatas es sólo un hilo en una madeja mucho más compleja formada por distintos hilos a menudo entrelazados entre sí. El autómata es una representación de lo humano, y en ciertos aspectos manifiesta la esencia de lo que somos. Pero los autómatas son también simulacros de vida y como tales nos remiten al viejo problema de la posibilidad de crear vida. Y más profundamente, como simulacros de la realidad, los autómatas podrían considerarse las primeras simulaciones de sistemas vivos. Hoy en día, la simulación por ordenador representa —por paradójico que parezca— una de las más importantes formas de aproximarnos a la realidad. Con las máquinas que hemos inventado podemos recrear otras máquinas aún más fascinantes. En el interior de nuestros ordenadores yace el potencial para soñar realidades alternativas y mundos que no existen. Pero también el laboratorio esencial para ayudarnos a comprender el mundo y sus fragilidades. Son una herramienta imprescindible para predecir los cambios que experimenta nuestro clima y los posibles escenarios futuros, algunos de los cuales debemos evitar antes de que sea demasiado tarde. Nos permiten diseñar puentes, aviones u ordenadores. Nos asoman a la complejidad de enfermedades que aún no entendemos, capacitándonos para ver aquello que sólo podemos intuir. Al imitar la vida, nos acercamos a su esencia y a las preguntas que hasta hace apenas unas décadas formaban parte de la filosofía. Preguntas que a veces nos impiden dormir de noche y nos hacen soñar de día, navegando tal vez a través de la oscuridad de los museos de autómatas, donde los androides descansan en su noche sin sueños.