2
EL SECRETO DE LA CUCHARA
QUE SE DOBLA
Por qué los magos vigilan sus ángulos
Seis semanas después de hablar con Jamy, nos encontramos sentados en el patio del restaurante y tienda de vinos Cheuvront, situado en la Central Avenue de Phoenix, cada uno con su copa en la mano. El tren ligero que cruza el centro de la avenida va dejando sus chirridos metálicos mientras sigue su recorrido en dirección norte, y hace una parada a unos pocos cientos de metros de distancia. Sólo una persona se ha apeado del tren y ahora se dirige hacia nosotros desde el andén, llevando una bolsa negra que se balancea a cada paso que da. Se trata de Anthony Barnhart, más conocido por sus fans como Magic Tony, y lo que lleva en la bolsa son las herramientas de su oficio: barajas, monedas, unas pelotas de goma de color rojo y unas cuerdas convenientemente preparadas para sus trucos.
Magic Tony es nuestro instructor y mentor de magia, y vamos a reunirnos con él para tener otra de esas divertidas sesiones de «enseñemos a este par de científicos un poco de prestidigitación, o que al menos aprendan algún truco clásico de magia para que no se avergüencen a sí mismos cuando lo realicen en el Magic Castle». Tony es un tipo corpulento, con el pelo negro y muy corto, y aire jovial. Durante la semana, trabaja en su doctorado en psicología por la Universidad Estatal de Arizona, en Tempe. Pero los viernes por la noche se pone su corbata de color rojo fosforito («La llevo porque me da la gana») y sus zapatos de piel de leopardo («Hicieron falta dos leopardos para confeccionarlos, pero no pasa nada; eran cachorros») para actuar en el Dragonfly Café de North Scottsdale, donde va de mesa en mesa haciendo trucos de magia. La clientela se entusiasma con él. Y nosotros también.
Tony creció en Milledgeville, Illinois, donde su entrenador de natación le enseñaba además juegos de magia. Así, mientras aprendía el estilo crol, aquel niño de siete años tomó sus primeras lecciones de magia y acabó apasionándose. También aprendió una lección de vital importancia: la magia consiste en entretener al público. Los jóvenes magos no deberían centrarse tanto en la metodología a expensas de lo teatral.
Un día abrieron una tienda de magia, The Magic Manor, a una hora de su casa, en la vecina ciudad de Rockford. Como tantos jóvenes enamorados de la magia, Tony pasó innumerables tardes hurgando en la tienda y asistiendo a cursillos, donde siempre era el más joven de la clase (y también el más rápido en aprender). Durante dos años seguidos se apuntó a los campamentos de magia que la empresa Tannen organiza en Long Island. Aún recuerda lo alucinado que se quedó una noche en su dormitorio, aunque quizá no fuese más que una tomadura de pelo. Él y sus dos compañeros de habitación estaban durmiendo cuando, hacia las dos de la madrugada, el supervisor del campamento los despertó y le dijo a Tony: «Piensa en una carta». Así lo hizo, y a continuación el hombre le preguntó cuál era la carta en la que había pensado medio dormido (era el siete de tréboles). «Aún no sé cómo lo hizo —afirma Tony—. Quizá me predispuso de alguna manera, pero no puedo asegurarlo. Y casi prefiero no saberlo.»
Hoy Tony nos enseñará dos técnicas utilizadas para el número de la carta ambiciosa. Este célebre truco puede realizarse de infinitas maneras, pero las que vamos a aprender tienen una especial relación con el modo en que los magos engañan nuestro sistema visual. El mago nos pide que escojamos una carta, cualquiera, de la baraja. Lo hacemos y luego colocamos la carta en medio de la baraja. El mago chasquea los dedos sobre la baraja y… voilà: nuestra carta ha ascendido misteriosamente hasta la parte superior. Es sin duda una carta ambiciosa, siempre destaca por encima de las demás.
El número ha pasado a los anales de la magia como el célebre truco que engañó a Harry Houdini. En las primeras décadas del siglo XX, Houdini era el mago más famoso del mundo. Tan seguro estaba de su absoluto y espectacular dominio en escapismo que quizá pecó de un exceso de confianza en lo que a la magia de cerca se refiere. En un alarde de envalentonamiento, Houdini lanzó un desafío a todos los magos: «Hacedme un truco tres veces seguidas y os diré cómo lo habéis hecho».
En 1922, en el hotel Great Northern de Chicago, un mago de mucho talento llamado Dai Vernon aceptó el desafío haciendo una demostración de su versión del truco de la carta ambiciosa. Vernon, más conocido como «el Profesor», era algo más que un simple rival para Houdini. Se trataba de uno de los mejores artistas de entonces en juegos de manos y, junto con Ed Marlo, posiblemente el mago de cartas más influyente del siglo XX. Vernon era un brillante inventor de trucos de magia de cerca usando cartas, monedas, pelotas y otros objetos pequeños.
Vernon pidió a Houdini que escogiera una carta y escribiera en ella sus iniciales. A continuación, metió la carta en mitad de la baraja. Vernon chasqueó los dedos y la carta de Houdini había subido a lo más alto.
Houdini se quedó perplejo.
—Tienes una carta duplicada —le dijo.
—¿Con tus iniciales, Harry? —contestó Vernon.
Éste repitió el truco tres veces, usando una técnica diferente en cada ocasión. Houdini estaba furioso; era incapaz de averiguar cómo lo hacía. Vernon realizó el truco cuatro veces más y Houdini no logró adivinarlo, aunque jamás lo reconoció en público.
La prestidigitación, si se hace bien, es una maravilla digna de verse. (La palabra procede del latín praestus: rápido, y digitus: dedo, y se aplica desde el siglo XIX al escamoteador, al jugador de manos.) Habitualmente se realiza de cerca, a muy poca distancia del espectador. Hay cientos de trucos diferentes. Algunos se basan en distraer la atención del que mira (como veremos en el capítulo 4), y otros, en aprovechar las debilidades de nuestro sistema visual. En cualquier caso, la percepción visual desempeña un papel fundamental en la prestidigitación.

No es ninguna casualidad que los magos utilicen barajas para llevar a cabo sus trucos. Las cartas destacan porque son objetos rígidos pero a la vez muy finos. Caben perfectamente en la palma de la mano y pueden esconderse con facilidad. Pueden barajarse, abrirse en abanico, voltearse, escamotearse, cortarse, pegarse y guardarse en el bolsillo. Hoy nuestra primera lección será el doble volteo o doble lift, probablemente la prestidigitación básica del repertorio de un mago, y clave para cualquier número de la carta ambiciosa. El truco consiste en volver dos cartas cara arriba en lo alto de la baraja haciendo creer que se está volteando sólo una. Así de sencillo. Pero cuando se lleva a cabo midiendo bien el tiempo y en combinación con otros recursos de desvío de la atención, el resultado es increíble. Dai Vernon era todo un maestro en la ejecución del doble volteo. Imaginemos que nuestra carta es el as de trébol. El mago abre las cartas en abanico y colocamos el as en la baraja. Mientras cierra el abanico, coloca una carta encima del as y marca con disimulo el lugar, llamado en el argot «separación», con el dedo meñique. Corta rápidamente la baraja sabiendo que el as es ahora la segunda carta situada en la parte superior, y entonces realiza el doble volteo. Coge las dos primeras cartas de modo que sólo se vea la segunda, nuestro as. Es la carta ambiciosa.
El mago sonríe y dice: «Pues sí, es una carta muy ambiciosa». Vuelve a colocar las dos cartas boca abajo y coge la que está encima (la que creemos es el as, aunque no lo sea) y la mete en medio de la baraja. A continuación chasquea los dedos y pone boca arriba la carta que está en lo alto, y que resulta ser ¡nuestro as! Menuda ambición la suya, pensamos, y nos quedamos estupefactos.
Los magos necesitan entrenarse miles de horas en el doble volteo para que no se note que están «manipulando» las cartas. Tienen que ejercitar la habilidad de los dedos para poder levantar dos cartas y convencernos de que sólo levantan una. Además, deberán recurrir a diferentes técnicas, como plegar ligeramente las dos cartas de modo que cuando estén boca abajo el mago pueda sentirlas como una. Cuando les dé la vuelta, se deshará el pliegue y volverán a quedar lisas. Para llegar a dominar este truco de prestidigitación, los magos deben ser capaces de realizar todos los movimientos sin prestar atención a lo que hacen. En un libro que Vernon escribió en 1961 titulado Estrellas de la magia (Páginas Libros de Magia, 2000), advertía sobre el hecho de que muchos magos se equivocan en el doble volteo porque los aterra que las dos cartas se separen de repente. «Una carta —decía— es un objeto ligero y delicado y no se le debería dar la vuelta como si fuera un bloque de cemento.»
Pero ¿cómo es posible que el doble volteo nos engañe una y otra vez? ¿Por qué nuestro sistema visual no acierta a seguir correctamente la colocación de las cartas? La respuesta tiene que ver con el centro de nuestra visión. Si quisiéramos detectar las dos cartas que se mueven como una sola por estar bien sujetas la una a la otra, tendríamos que acercar los ojos a muy pocos centímetros de las manos del mago y observar las cartas como a través de una lupa. Incluso así, es muy probable que se nos escapara el truco.
La explicación de todo ello radica en que la resolución de nuestro sistema visual es muy pobre, excepto en el centro exacto de nuestra mirada. Las cartas son tan delgadas que nuestra visión es incapaz de distinguirlas, sobre todo si están en manos de un experto tramposo. El centro en cuestión se llama mácula, y es la zona más próxima a la retina dotada de fotorreceptores. Es, junto con la fóvea (el centro exacto de la mácula que goza de la mayor resolución), responsable de la agudeza visual. Se trata de una parte tan especializada de nuestra anatomía que padece sus propias enfermedades, como la degeneración macular asociada a la edad. De hecho, esta degeneración macular constituye la forma más común de ceguera en los ancianos, e implica que la mácula muere en el transcurso de unos pocos años. Sin máculas, sólo tenemos visión periférica, cuya resolución es muy baja y que hace que vayamos por el mundo viendo sólo lo que sucede a ambos lados de nuestra cabeza.
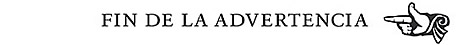
Tony nos enseña otra manera de realizar el número de la carta ambiciosa. Se trata de la Ilusión de Profundidad de Vernon (también conocida como Tilt de Marlo, porque los dos magos lo desarrollaron de forma independiente). Mucho después de que Houdini muriera, Vernon siguió perfeccionando el truco con una perspicacia diabólica en lo que a procesos visuales se refiere.*
En este pase de prestidigitación —extraído de un raro material de rodaje de la década de 1950—, Vernon pide al espectador que escoja una carta y la firme. Luego coge la carta y la introduce en mitad de la baraja, despacio y con decisión, para que no haya ninguna duda de que esa carta es la escogida. Finalmente, le da la vuelta a la carta que hay en lo alto de la baraja. Y, voilà!, aparece la carta firmada.

Es algo increíble, asombroso y también exasperante. He aquí cómo lo hizo.
En cuanto le dan la carta escogida, Vernon la tuerce apenas y la introduce parcialmente en el centro de la baraja, desde atrás. El ángulo de torsión asegura que la carta no se introducirá por completo en la baraja. En lugar de eso, hace que las otras cartas sobresalgan justo donde estamos mirando, la parte frontal de la baraja, ligeramente inclinada hacia abajo. Estas cartas que asoman refuerzan la impresión de que Vernon está empujando la carta hacia el centro de la baraja, pero no es más que una artimaña. Mientras vuelve a cuadrar la baraja (empujando las cartas con el dedo desde la parte frontal), como si estuviera corrigiendo una equivocación, Vernon inclina levemente hacia arriba el reverso de la carta que está en lo alto de la baraja. Desde nuestra perspectiva, no podemos ver esa inclinación, aunque, visto desde la parte posterior de la baraja, se ha producido un hueco de casi un centímetro entre la carta que está en lo alto y la que está inmediatamente debajo.
A continuación, Vernon coge la carta que hemos firmado y la desliza dentro de la baraja hacia el fondo de ese hueco que no vemos. Desde nuestra posición nos parece que está introduciéndola en mitad de la baraja, pero en realidad es la segunda contando desde arriba. Hay dos razones por las cuales no apreciamos la diferencia. En primer lugar, porque desde nuestra perspectiva no podemos ver la inclinación de la carta que está en lo alto, y además no se nos ocurre pensar que está deslizando nuestra carta para colocarla justo debajo de la primera.
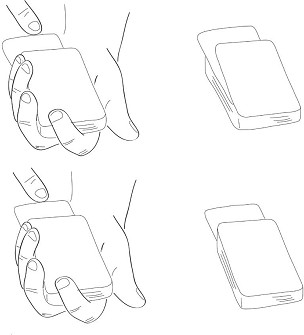
El mago puede empujar la carta en la parte central de la baraja (abajo derecha) o justo debajo de la carta superior inclinada (arriba derecha). En ambos casos, desde el punto de vista del espectador, parece que se está introduciendo la carta en mitad de la baraja (columna izquierda). (Dibujo de Jorge Otero Millán.)
En segundo lugar, nuestro sistema visual nos convence de que nuestra carta está muy alejada de la segunda posición dentro de la baraja. De hecho, parece que está en medio, más o menos en el mismo lugar que cuando Vernon ha empujado «accidentalmente» las cartas con la que estaba angulada. Hemos visto que algunas cartas sobresalían cuando se «insertaba» la otra. Pero ¿realmente hemos visto cómo la introducía?
Obviamente, no lo hemos visto, pero el sistema visual nos dice que nuestra carta está siendo ocultada por la parte superior de la baraja. Nuestro ángulo de perspectiva nos informa de que la carta se está insertando. Asimismo, nuestra visión tridimensional nos convence de que la carta debe de estar en medio de la baraja, unas veinticinco cartas por debajo de la que está en lo alto.
Huelga decir que esta lógica no funciona cuando la parte de atrás de la primera carta se inclina en el transcurso del segundo intento de inserción. Luego, un movimiento muy inocente de la mano de Vernon permite que la carta inclinada caiga y cierre así el hueco originado. Nuestra carta firmada se encuentra ahora en la posición perfecta para llevar a cabo un doble volteo. Vernon nos asegura que nuestra carta ambiciosa ha ascendido hasta arriba, y ahí es donde aparece. No contento con asombrarnos una vez, Vernon propone: «Hagámoslo otra vez». Vuelve a colocar las dos cartas boca abajo, retira la que está en lo alto (que no es nuestra carta firmada, aunque creamos lo contrario) y la introduce en mitad de la baraja. El resto ya lo sabemos. Nuestra carta está ahora en lo más alto.
Dos de las claves para la percepción de la profundidad —la oclusión y la perspectiva— han estado conspirando para engañarnos.1 Estos procesos son automáticos y tienen lugar sin que seamos conscientes de ellos, de ahí que el truco funcione. Como ya hemos dicho antes, es nuestro cerebro quien construye la realidad. En este caso, nuestro sistema visual nos está diciendo qué es «real», pero se ha convertido en una desdichada víctima en manos de un mago experto.
La oclusión se produce, por ejemplo, cuando una persona se encuentra parcialmente oculta detrás de otra, y damos por sentado que la que no está oculta se encuentra más cerca de nosotros. Con las cartas ocurre lo mismo. Se trata de una deducción lógica que el cerebro realiza de forma automática y casi instantánea, sin que medie el pensamiento consciente.
Así es como engaña Vernon a nuestro sistema visual. Al «ver» que nuestra carta se introduce en mitad de la baraja, damos por sentado que las demás se hallan encima de ella. Están ocultando nuestra carta, lo cual nos lleva a pensar que debe de encontrarse bastante más abajo.
Nadie sabe en qué lugar del cerebro se computa la oclusión, pero es probable que suceda a una altura de nuestro sistema visual donde las neuronas más adecuadas descifran las formas individuales. Las neuronas que se activan en un primer momento ante un campo visual sólo detectan rasgos menores del mundo, como los bordes, las esquinas y las curvas. Para constituir una forma completa y ver un objeto de interés (una persona, una carta), hacen falta neuronas que sepan discriminar las formas y combinen la información que envían los primeros detectores de rasgos. Siguiendo esta lógica, necesitamos un nivel de computación incluso más tardío que pueda determinar que se está ocluyendo la forma preferida de una neurona. De este modo, el sistema visual construye la percepción de la profundidad igual que un automóvil en una cadena de montaje, pieza a pieza, hasta obtener una percepción rica en profundidad.
Además, Vernon se aprovecha del deseo de nuestro cerebro de comprender el mundo en perspectiva. La perspectiva lineal se apoya en el hecho de que las líneas paralelas, como las de las vías del tren, parecen converger en la distancia (la ilusión de la torre inclinada del capítulo 3 se basa en este fenómeno). El sistema visual interpreta esta convergencia como profundidad porque da por sentado que las líneas paralelas se mantendrán en paralelo.
En el truco de cartas de Vernon entra en juego la perspectiva del tamaño. Si dos objetos similares aparecen con tamaños diferentes, nuestro sistema visual dará por hecho que el más pequeño está a más distancia. Aquí, la carta firmada es ligeramente más pequeña en nuestra retina, lo cual significa que debe de estar más lejos. Si nos basamos en los estímulos visuales que recibimos, debe de estar introduciéndose en mitad de la baraja.
A comienzos de la década de 1970, una nueva superestrella de la magia barrió los escenarios del mundo entero. Se llamaba Uri Geller y era un joven israelí alto y larguirucho, con una pelambrera negra a lo Beatle, cejas negras y mirada penetrante. Con un dominio carismático de la escena, Geller podía doblar cucharas y hacer que los relojes se detuvieran o funcionaran más deprisa, leía dibujos por telepatía y dejaba conmocionada a la gente con sus «poderes sobrenaturales».
Qué ingenuidad la de aquella época.
Quizá se debía a las drogas. Si uno se ponía una tira de gelatina de LSD en la lengua y veía cómo el mundo se transformaba en un paisaje digno de Salvador Dalí, con vivos colores, tenues formas geométricas y fantasmagorías cambiantes, a la vez que perdía la noción de sí mismo, ¿por qué no iba a ser alguien capaz de doblar una cuchara con el pensamiento?
O tal vez se debía a la paranoia de la Guerra Fría. La CIA estaba convencida de que el KGB sabía cómo utilizar la percepción extrasensorial o la visión remota. Los espías enemigos podían acceder a nuestros secretos más íntimos desde cualquier parte del mundo usando sus poderes telepáticos. Eran incluso capaces de escuchar los latidos de un corazón a gran distancia (para una visión divertida de esta época, véase la película Los hombres que miraban fijamente a las cabras),
Quizá se trate de uno de esos extraños momentos de la historia en que un número nada despreciable de personas que en otro momento se mostraría del todo racional se deja seducir por el pensamiento mágico. Las modas pasajeras típicas del New Age pregonaban las maravillas del tarot, del I Ching, de la cámara Kirlian, del poder de los cristales, la radiestesia, la astrología y las nuevas formas de crecimiento personal en armonía con la evolución del planeta.
A Geller, en primera línea de fuego de esta locura, se lo conoció sobre todo por su capacidad para doblar cucharas. «¿No es maravilloso?», se admiraba mientras sostenía una cuchara por el cuello del mango y la acariciaba con suavidad pero con rapidez con el dedo índice. Poco a poco, como un acróbata contorsionándose lánguidamente, la cuchara se doblaba cada vez más hasta que adquiría una curvatura insólita. Era la magia de la cuchara.
Millones de personas se quedaron ensimismadas ante la actuación de Geller. Al menos hasta que el célebre desenmascarador de supuestos casos paranormales, James Randi, conocido como el Asombroso Randi, salió a escena y echó un buen jarro de agua fría en la acalorada actuación de Geller.*
Éste llegó a afirmar en una ocasión que podía realizar aquellas proezas gracias a los poderes sobrenaturales que le habían dado unos extraterrestres. Sin embargo, Randi proclamó que las hazañas de Geller no eran más que trucos de salón. Él mismo las repitió una a una explicando su funcionamiento, desde la cuchara doblada hasta la radiestesia, pasando por la telepatía y el reloj parado. «El pensamiento mágico es un terreno muy resbaladizo —asegura Randi durante sus demostraciones—. A veces es inofensivo, pero puede resultar muy peligroso. Me opongo a los farsantes. Sólo pretendo poner al descubierto a determinadas personas y sus ilusiones mostrándolas tal cual son.»
Randi explica, por ejemplo, que los mentalistas reproducen desde hace años dibujos ocultos. Alguien dibuja algo en un trozo de papel y lo esconde, y a continuación el mago adivina qué ha dibujado. A veces el mago se da la vuelta y se tapa los ojos mientras la persona hace el dibujo. «¿Por qué se tapa los ojos si se ha dado la vuelta?», se pregunta Randi, y nos ofrece la explicación: porque lleva un pequeño espejo escondido en la palma de la mano que, al taparse los ojos, le muestra exactamente lo que la otra persona está dibujando.
A pesar de los esfuerzos de Randi por dejar claro que Geller era sólo un ilusionista, la gente siguió creyéndolo. De hecho, más de un científico cayó en la trampa. En 1975, dos investigadores expertos en psicología paranormal del Instituto de Investigación de Stanford, Russell Targ y Harold Puthoff, llevaron a cabo experimentos con Geller y concluyeron que los había superado satisfactoriamente, lo cual justificaba que se realizaran más estudios serios sobre él. Lo llamaban «el efecto Geller». Las ondas cerebrales, aseguraban, podían afectar los metales dúctiles.
Danny Hillis, científico de renombre en materia de computación y mago aficionado, explica por qué los científicos se muestran especialmente ingenuos ante los Gellers de este mundo. «Cuanto mejor es el científico, más fácil resulta engañarlo —afirma—. Los científicos son gente honrada. No tienen la menor idea de hasta dónde es capaz de llegar un mago, y además no están entrenados en el fraude.»
Hillis cuenta que una vez hizo un truco de magia ante Richard Feynman, el célebre físico del California Institute of Technology (Caltech), al que todo el mundo considera una de las personas más brillantes que han existido. «Se trataba de hacer un truco y desafiarlo a que lo adivinara. Al cabo de uno o dos días de pensarlo a fondo, volvió con la respuesta correcta —dice Hillis—. Entonces repetí el truco pero usando un método completamente diferente. Y se volvió loco. Jamás se le ocurrió el metaprincipio de que yo había cambiado el método. Esto puede deberse al hecho de que a los científicos se los prepara para que utilicen el método científico. Hay que seguir experimentando hasta que se da con la respuesta. La naturaleza es fiable. La idea de que alguien fuese capaz de cambiar de método era simplemente inconcebible para él.»

Una cuchara puede doblarse de muchas maneras. He aquí el método que nos enseñó Tony.*
Empieza mostrando tres cucharas y haciendo que alguien coja una y la examine. A continuación pide a esa persona que se coloque la cuchara en la frente —Tony lo ilustra poniéndose otra cuchara en su propia frente— y que le avise cuando note que se calienta.
Mientras Tony se quita la suya de la frente y la atención de todo el mundo se concentra en el pobre incauto de la cuchara, Tony dobla por el cuello simultáneamente las otras dos cucharas en noventa grados.
Así es como se dobla una cuchara. Y es que las cucharas se doblan antes de crear la ilusión. Los magos llaman a esto «doblamiento». Tony dobla la primera cuchara con la mano derecha presionando la cabeza con el pulgar y reteniendo el mango en el puño. Al mismo tiempo, dobla la segunda cuchara por el cuello presionando la cabeza pero contra el reverso de la muñeca de la mano derecha. La operación es limpia y natural; el objetivo, dar la sensación de que simplemente está juntando las cucharas en la mano derecha. En cualquier caso, la atención de todo el mundo está puesta en el tipo con la cuchara en la cabeza. Entretanto, Tony pasa rápidamente a la mano derecha la cuchara ya doblada de la mano izquierda y sostiene ambas entre el pulgar y el índice de la derecha de modo que se unan por la parte doblada de ambas. Parece que está sosteniendo dos cucharas sin doblar y cruzadas a la altura del cuello del mango.
Entonces Tony agita las cucharas y dice: «Vamos a ablandarlas». Con ese movimiento, parece que las cucharas realmente se están ablandando y que poco a poco se doblan por el cuello. En realidad, lo que hace es girar con suavidad las cucharas entre los dedos para que las partes dobladas queden en la misma dirección, hasta que las cabezas aparezcan de pronto colgando. Tony se toma un breve respiro y con la mano izquierda recupera la tercera cuchara del espectador. Reorienta la atención del público hacia las dos cucharas que está doblando diciendo que está concentrándose en ellas. Entretanto, dobla con disimulo la tercera cuchara presionándola contra la pierna y luego la sostiene en la mano de forma que sólo el mango sea visible.
Cuando las dos cucharas que se están «ablandando» se hallan completamente dobladas, Tony se las entrega al mismo espectador y dice: «Vamos a intentarlo de nuevo». Ahora sostiene la tercera cuchara con ambas manos de modo que el mango asoma en vertical desde atrás. De este modo, ni la parte cóncava de la cuchara ni el cuello doblado en un ángulo de noventa grados son visibles. El público da por sentado que la cuchara permanece recta, sobre todo porque el espectador ya la ha inspeccionado.
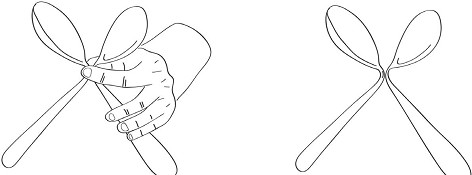
La ley de la buena continuidad hace que veamos las cucharas como si se cruzaran cuando el mago las sostiene (izquierda), a pesar del hecho de que ya están dobladas (derecha). (Dibujo de Jorge Otero Millán.)
Tony se concentra en la tercera cuchara, y, poco a poco, con mucha intensidad pero sin ejercer ninguna presión perceptible, el mango de la cuchara se dobla hasta que el cuello de la misma cae hacia él en un ángulo de noventa grados. Tony muestra la cuchara doblada al público, que aplaude. Fin del espectáculo.
Hay varios conceptos psicológicos importantes que contribuyen a que nos convenzamos falsamente de que las cucharas están rectas cuando en realidad ya se han doblado. El primero de ellos es lo que los científicos especializados en visión denominan «completado amodal», el proceso según el cual un objeto que aparece parcialmente escondido detrás de un segundo objeto se verá en su totalidad aunque se encuentre oculto. Ahora, querido lector, imagine que está usted aquí, en Phoenix, con nosotros y con Magic Tony, observando el desarrollo de nuestra lección de magia. Está sentado a nuestro lado frente a un plato de queso manchego y con una copa de Rioja en la mano, y entre truco y truco contempla ensimismado el vasto desierto de Sonora. De repente, ve una liebre que da tres saltos y aterriza justo detrás de un enorme cactus saguaro de cuatro brazos, de modo que sólo se le ven las patas traseras y la cola. ¿Podríamos afirmar que el animal tiene cabeza? Por supuesto que sí, me dirá. Ya, pero ¿cómo lo sabe si no puede verla? ¿Cómo es posible que el cerebro esté informándole sobre la forma de una parte de la liebre que se oculta detrás del cactus? ¿Y qué pasaría si, en lugar de la liebre, fuese una superficie rectangular la que asomara por el cactus? En ese caso, no podría recurrir a la experiencia para saber cómo es de grande la parte que no ve por la sencilla razón de que, a diferencia de las liebres, los rectángulos pueden tener cualquier tamaño. Imagine ahora que el rectángulo asoma por ambos lados de la planta, de modo que puede ver sus cuatro ángulos, aunque la parte central permanezca oculta. A pesar de que la mayor parte de su superficie no se ve, tendrá una impresión más clara del tamaño y de la forma del objeto, aunque no pueda saber realmente cómo es la porción de la superficie que se esconde detrás del cactus.
En el caso de la liebre, su cerebro ha dibujado un mapa en tres dimensiones del modelo biológico de la liebre, y ha supuesto, desde el punto de vista de la percepción, qué aspecto debe de tener la parte oculta del animal. Todo esto es de gran ayuda, sobre todo si uno caza liebres. En el caso del rectángulo, el cerebro puede llegar a realizar determinadas conjeturas de percepción, pero sólo en función de cuánta información contiene.
Tony se aprovecha de este completado amodal cuando con el pulgar y el índice sujeta en pinza las dos cucharas dobladas.2 Como el mango de la cuchara número uno está perfectamente alineado con la parte cóncava de la cuchara dos, y viceversa, ambas parecen rectas; el completado amodal ha completado ambos objetos de forma inadecuada bajo los dedos de Tony. Él mismo explica que este proceso obedece a la ley de la buena continuidad, descrita por los psicólogos de la Gestalt alemana a comienzos del siglo XX.
¿Se ha preguntado alguna vez cómo es posible que un mago corte en dos a una mujer con una sierra?3 La ilusión se basa en dos elementos: en una caja hueca y en el deseo de nuestro cerebro de lograr continuidad. Cuando la mujer en cuestión se introduce en la caja, vemos la cabeza en un extremo y los pies en el otro. El cerebro nos dice que está tumbada sobre la espalda y que está entera, pero en realidad no es así. La caja se ha construido para que la cabeza que asoma por un lado y los pies que sobresalen por el otro pertenezcan a dos mujeres diferentes. La ilusión se acentúa a menudo pintando en la caja su cuerpo en posición horizontal. ¡Cómo nos engañan!
POR QUÉ LA BUENA CONTINUIDAD ES GENIAL

La buena continuidad es el proceso mediante el cual nuestro cerebro hace que las cosas parezcan completas a partir de información escasa. El completado amodal es un buen ejemplo de buena continuidad, pero hay otros muchos. Ya hemos mencionado el filling-in, o proceso de relleno. En realidad, el mundo es demasiado grande y complejo para que seamos capaces de verlo todo. Cuando miramos una playa repleta de cantos rodados o una de esas alfombras persas tan elaboradas, nuestro cerebro no se dedica a analizar cada una de las piedrecitas o los nudos de hilo; no tenemos suficientes células en la retina para eso. Vemos una pequeña porción de playa o de alfombra y rellenamos el resto. La buena continuidad constituye una parte tan importante de toda una serie de mecanismos cerebrales, que, según Tony, es el recurso más explotado por toda la magia en general.4
Para comprobar hasta qué punto es inteligente nuestro cerebro a la hora de realizar estos rellenos, el lector puede tratar de llevar a cabo el experimento Ganzfeld. (En alemán, Ganzfeld significa «campo homogeneizado».) En primer lugar, corte una pelota de ping-pong por la mitad. A continuación, sintonice la radio hasta que sólo se escuche la estática. Túmbese, coloque las mitades de la pelota sobre cada ojo sujetas con cinta adhesiva, y espere. Al cabo de unos minutos empezará a experimentar un auténtico aluvión de sensaciones muy raras, como ver osos polares haciendo cabriolas con elefantes o a aquel tío suyo que murió hace tiempo. Cualquier cosa. El cerebro no sabe cómo comportarse cuando el nivel de información que recibe es cero, y por eso inventa su propia realidad. Lo importante de este experimento es que el cerebro crea su propia realidad tanto si recibe información real como si no. En ausencia de entrada de información sensorial, las maquinaciones que realiza nuestro cerebro continúan a pesar de todo. He aquí por qué el confinamiento en soledad se considera un castigo en nuestro sistema penitenciario. Podría pensarse que la incomunicación constituye un alivio si tenemos en cuenta los peligros y las penalidades de la vida en prisión. Sin embargo, es lo peor que se le puede hacer a un preso, porque pierde el contacto con la realidad. Muchos consideran esta práctica una forma de tortura y, de hecho, se han escrito muchos libros sobre los efectos psicológicos negativos del confinamiento en soledad. Los presos acaban sufriendo alucinaciones y otros tipos de reacciones psicóticas.
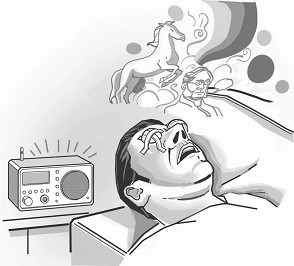
Cómo alucinar usando una pelota de ping-pong y una radio. (Hack Your Brain, publicado con autorización de Globe Newspaper Company, Inc., de una edición de 2010 del Boston Globe © 2010.)
Hay algunos mecanismos de buena continuidad que comprendemos cada vez mejor. En el sistema visual, por ejemplo, la buena continuidad depende de la orientación y de la posición espacial de las líneas que estemos mirando. Cuando la posición relativa y la orientación de dos o más segmentos se encuentran alineadas podremos ver un contorno. Cuando dos o más líneas con similares orientaciones se colocan muy cerca de sus extremos alineados, podremos advertir que los segmentos individuales destacan visualmente mucho más: sobresalen con respecto al fondo. Pero si la separación entre segmentos, o las diferencias en sus orientaciones, es demasiado grande, la buena continuidad falla y los segmentos resultan más difíciles de discriminar con respecto al fondo.
Charles Gilbert y sus colaboradores en el laboratorio de la Universidad Rockefeller han descubierto la base fisiológica del funcionamiento de la buena continuidad en el sistema visual.5 Recordemos que las neuronas de la corteza visual primaria se ajustan a determinadas orientaciones; prefieren, por poner un ejemplo, los segmentos de líneas horizontales o verticales. Estas neuronas especializadas se encuentran en diferentes partes de la corteza visual primaria, de forma que el cerebro pueda integrar información más allá de los límites de cada neurona. Resulta entonces que las neuronas con atributos similares están conectadas por medio de fibras horizontales que atraviesan una larga distancia en la corteza visual primaria. El ojo de la mente puede «ver» la liebre escondida detrás del cactus gracias a las conexiones de largo alcance existentes en la corteza entre neuronas de tipos parecidos. Los mismos procesos podrían desempeñar un papel similar en otros tipos cognitivos de percepción visual, algo que trataremos en próximos capítulos con mayor profundidad.
Hay un segundo concepto que también se ha documentado con respecto a la ilusión de la cuchara.6 Cuando las cucharas se agitan entre los dedos del mago, parece que pierdan su rigidez. La ilusión se debe a que nuestro sistema visual tiene dos mecanismos distintos para ver las líneas: uno especializado en los bordes, y otro en el final de las líneas. Para detectar el borde de una línea, recurrimos a las neuronas de nuestra corteza visual primaria. Sin embargo, para localizar los extremos de una línea, tenemos las llamadas células con inhibición final, las cuales se ajustan para reaccionar ante el final de largos contornos.7
Algunas neuronas selectivas a la orientación y con inhibición final reaccionan de manera especial ante un estímulo móvil, como es el caso del mango de una cuchara si la agitamos entre los dedos. Pero el tiempo de sus reacciones es diferente. El cerebro percibe las líneas de orientación mucho más deprisa que el final de las líneas. De ahí que parezca que el mango de una cuchara que se agite se mueva antes de que se muevan los extremos, lo que origina la ilusión de que la cuchara se está doblando.
Por muy romántico que parezca llegar a la conclusión de que los pensamientos pueden doblar cucharas o levitar mesas, o que los poderes psíquicos, la clarividencia y el poder de la mente sobre la materia son fenómenos reales, las consecuencias de tales creencias a menudo resultan dolorosas o, por lo menos, muy bochornosas. Cuando Susana tenía ocho años, se empeñó en que era capaz de atravesar cualquier barrera sólo con el poder de su mente. La pesada puerta de hierro forjado que daba entrada al edificio donde vivían sus abuelos en Santander, parecía ideal para llevar a cabo el experimento. Cuando los adultos se retiraron para dormir la siesta, salió del piso a escondidas y bajó corriendo los tres tramos de escaleras que llevaban a la entrada del edificio. Con gran decisión, se arrojó de cabeza contra la puerta a toda velocidad. Por sorprendente que parezca, la puerta de hierro forjado no se movió de su sitio, como lo demuestra la pequeña cicatriz que aún luce en la sien izquierda. Tardó más de diez años en confesar a su familia que lo de aquel día no había sido un tropezón accidental.
Los charlatanes y embaucadores campan a sus anchas aprovechándose de clientes desesperados o incautos que creen sinceramente en las aptitudes psíquicas. A estos clientes siempre se los engaña por dinero, o peor todavía: a veces se los convence para que rechacen tratamientos médicos de probada eficacia en favor de todo tipo de intervenciones psíquicas. Cuando un parapsicólogo, un sanador espiritual, un médium o un charlatán aseguran poder desafiar las leyes de la naturaleza, detrás siempre se esconde una ilusión. Nuestro objetivo no es otro que el de descubrir cómo lo hacen. Y de eso trata en gran medida este libro.