Notación

(No lo lea antes de que se haya familiarizado con los conceptos, ¡aunque quizá encuentre los tipos de letra confusos!)

He tratado de ser razonablemente coherente en el uso de tipos de letra especiales a lo largo de todo el libro. Pero puesto que no todo esto es estándar, puede resultar útil para el lector que haga explícitos los usos que he adoptado.

Las letras itálicas (griegas o latinas), tales como en w², pn, log z, cos u, e^iθ, o ex se utilizan de la manera convencional para variables matemáticas que son cantidades numéricas o escalares; pero las constantes numéricas establecidas, tales como e, i, o π o las funciones establecidas tales como sen, cos o log se denotan mediante redondas. Sin embargo, las constantes físicas estándar tales como c, G, h, 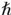, g o k son itálicas.

Una cantidad vectorial o tensorial, cuando se considera en su totalidad (abstracta), se denota por una letra itálica negrilla, tal como R para el tensor de curvatura de Riemann, mientras que su conjunto de componentes podría escribirse con itálicas (tanto para el núcleo como para sus índices), como R_abcd. De acuerdo con la notación de índices abstractos, introducida aquí en §12.8, la cantidad R_abcd puede representar alternativamente el tensor entero R, si esta interpretación es apropiada, y esto debería hacerse claro en el texto. Las transformaciones lineales abstractas son tipos de tensores, y letras itálicas negrillas tales como T se utilizan también para tales entidades. También se utiliza aquí, cuando es apropiado, la forma de índices abstractos T^a_b para una transformación lineal abstracta, donde el escalonamiento de índices hace clara la conexión precisa con el ordenamiento de la multiplicación de matrices. Así, la expresión de índices abstractos S^a_bT^b_c representa el producto ST de transformaciones lineales. Como sucede con los tensores generales, los símbolos S^a_b y T^b_c pueden representar alternativamente (según el contexto o la especificación explícita en el texto) los correspondientes conjuntos de componentes —que son matrices— para los que también pueden utilizarse letras redondas negrillas S y T. En ese caso, ST denota el correspondiente producto matricial. Esta interpretación «ambivalente» de símbolos tales como R_abcd o S^a_b (ya representen el conjunto de componentes o el propio tensor abstracto) no debería causar confusión, pues las relaciones algebraicas (o diferenciales) a las que están sujetos estos símbolos son idénticas para ambas interpretaciones. A veces se utiliza también aquí una tercera notación para dichas cantidades —la notación diagramática— que se describe en las Figs. 12.17, 12.18, 14,6, 14.7, 14.21, 19.1 y otros lugares en el libro.

Hay lugares en este libro donde necesito distinguir las entidades espaciotemporales 4-dimensionales de la teoría de la relatividad de las correspondientes entidades espaciales ordinarias puramente 3-dimensionales. Así, aunque podría utilizarse una notación itálica negrilla, como antes, tal como p o x, para el 4-momento o la 4-posición, respectivamente, las correspondientes entidades puramente espaciales 3-dimensionales se denotarán por las correspondientes letras negrillas p o x. Por analogía con la notación T para una matriz, en oposición a T para una transformación lineal abstracta, se considera que las cantidades p y x «representan» las tres componentes espaciales, en cada caso, mientras que p y x podrían verse como una interpretación más abstracta libre de componentes (aunque yo no seré especialmente estricto en esto). La «longitud» euclídea de una cantidad 3-vectorial a = (a₁, a₂, a₃) puede escribirse a, donde a² = a₁² + a²₂ + a₃², y el producto escalar de a por b = (b₁, b₂, b₃), se escribe a • b = a₁b₁ + a₂b₂ + a₃b₃. Esta notación «punto» para productos escalares se aplica también, en el contexto n-dimensional general, para el producto escalar (o interno) α • ξ de un covector abstracto α por un vector ξ.

Sin embargo, surge una complicación notacional con la mecánica cuántica, puesto que las magnitudes físicas, en esta disciplina, suelen representarse como operadores lineales. No adopto el procedimiento totalmente estándar en este contexto de colocar «sombreros» (circunflejos) sobre las letras que representan las versiones como operadores cuánticos de las familiares magnitudes clásicas, pues creo que esto conduce a una innecesaria acumulación de signos. (En su lugar, tenderé a adoptar un punto de vista filosófico según el cual las magnitudes clásicas y cuánticas son realmente las «mismas» —y por ello es justo utilizar los mismos símbolos para ambas—, excepto que en el caso clásico uno está justificado al ignorar cantidades del orden de , de modo que las propiedades de conmutación clásica ab = ba pueden ser válidas, mientras que en mecánica cuántica ab podría diferir de ba en algo del orden de .) Por consistencia con lo anterior, parecería que tales operadores lineales tienen que ser denotados por letras itálicas negrillas (como T), pero eso anularía la filosofía y las distinciones invocadas en el párrafo anterior. Por consiguiente, con respecto a magnitudes específicas, tal como el momento p o p, o la posición x o x, tenderé a utilizar la misma notación que en el caso clásico, en la misma línea con lo que se ha dicho antes en este párrafo. Pero para operadores cuánticos menos específicos se utilizarán letras itálicas negrillas tales como Q.

Las letras N, Z, R, C y F_q, respectivamente, para el sistema de los números naturales (i.e., enteros no negativos), los enteros, los números reales, los números complejos y el campo finito con q elementos (siendo q una potencia de un número primo, véase §16.1), son ahora estándares en matemáticas, como lo son los correspondientes Nⁿ, Zⁿ, Rⁿ, Cⁿ y Fⁿ_q, para los sistemas de n-tuplas ordenadas de tales números. Estas son entidades matemáticas canónicas de uso estándar. En este libro, esta notación se extiende a otras estructuras matemáticas estándar tales como un 3-espacio euclídeo E³ o, con más generalidad, un n-espacio euclídeo Eⁿ. En este libro aparece con frecuencia el espaciotiempo de Minkowski plano 4-dimensional estándar, que es en sí mismo un tipo de espacio «pseudo»-euclídeo, de modo que utilizo la letra M para este espacio (con Mⁿ para denotar la versión n-dimensional, un espaciotiempo «lorentziano» con 1 tiempo y (n – 1) dimensiones espaciales). A veces utilizo C como un adjetivo, para denotar «complexificado», de modo que podríamos considerar el 4-espacio euclídeo complejo, por ejemplo, denotado por CEⁿ. La letra P puede utilizarse también como un adjetivo, para denotar «proyectivo» (véase §15.6), o como un sustantivo, cuando Pⁿ denota el n-espacio proyectivo (utilizo RPⁿ o CPⁿ si hay que dejar claro que estamos interesados en un n-espacio proyectivo real o complejo, respectivamente). En teoría de twistores (capítulo 33), existe el 4-espacio complejo T, que está relacionado con M (o su complexificación CM) de una manera canónica, y existe también la versión proyectiva PT. En esta teoría existe también un espacio N de twistores nulos (el doble papel que tiene esta letra no causa aquí conflicto), y su versión proyectiva PN.

El papel adjetivo de la letra C no debería confundirse con el del tipo C, que aquí representa «conjugado complejo de» (como se utiliza en §§13.1,2). Esto es básicamente similar a otro uso de C en física de partículas, a saber la conjugación de carga, que es la operación que intercambia cada partícula con su antipartícula (véanse los capítulos 24 y 25). Esta operación se considera habitualmente junto con otras dos operaciones básicas en física de partículas, a saber, P para paridad, que se refiere a la operación de reflexión en un espejo, y T, que se refiere a la inversión temporal. Las letras sans serif que son negrillas sirven aquí para un objetivo diferente, el de etiquetar espacios vectoriales, siendo las letras V, W y H las utilizadas con más frecuencia con este objetivo. El uso de H es específico para los espacios de Hilbert de la mecánica cuántica, y Hn representaría un espacio de Hilbert de n dimensiones complejas. Los espacios vectoriales son, en un sentido claro, planos. Los espacios que son (o podrían ser) curvos se denotan por letras script, tales como M, S o T, donde hay un uso especial para el tipo concreto I que denota el infinito nulo. Además, sigo el convenio común que utiliza letras script para lagrangianos (L) y hamiltonianos (H), en vista de su estatus muy especial en la teoría física.