7
Cálculo infinitesimal con números complejos
7.1. SUAVIDAD COMPLEJA; FUNCIONES HOLOMORFAS
¿Cómo debemos entender la noción de diferenciación cuando se aplica a una función compleja f(z)? Ciertamente, no sería oportuno que intentara abordar tal cuestión con todo detalle en este libro.[1] Ni siquiera he abordado de manera adecuada en §6.2 todos estos detalles para una función real. Pero al menos puedo intentar transmitir las ideas básicas. Lo que sigue es un rápido esbozo del argumento esencial para mostrar qué es lo que consigue la diferenciabilidad compleja. Después de esto, seré un poco más explícito acerca de alguno de sus sorprendentes ingredientes.
Básicamente, para la diferenciación compleja exigimos que exista una noción de «pendiente» de la curva compleja w = f(z) en cualquier punto z en el dominio de la función. (Ahora se permite que tanto la función f(z) como la variable z tomen valores complejos.) Para que esta noción de «pendiente» tenga un sentido consistente, cuando movemos ligeramente la variable z en diferentes direcciones en el plano complejo de la z, es necesario que f(z) satisfaga un par de ecuaciones llamadas ecuaciones de Cauchy-Riemann[2] (que incluyen las derivadas de las partes real e imaginaria de f(z), tomadas con respecto a las partes real e imaginaria de z; véase §10.5). Estas ecuaciones nos dicen algo bastante notable acerca de la integración compleja —algo que hace posible definir una nueva noción de integración, llamada integración de contorno—. Entonces puede darse una bonita fórmula para la n-ésima derivada de f(z) en términos de dicha integración de contorno. Así pues, una vez que tenemos la derivada primera, obtenemos gratis todas las derivadas superiores.
A continuación utilizamos esta fórmula para que nos dé los coeficientes de una serie de Taylor que se propone para f(z), y que tenemos que demostrar que converge realmente a f(z). Al haber conseguido esto, tenemos una expresión en serie de Taylor para f(z) que funciona dentro de cualquier círculo en el z-plano complejo en el que f(z) está definida y es diferenciable. Se da así el hecho mágico de que cualquier función compleja que sea suave-compleja ¡es necesariamente analítica!
En consecuencia, en el análisis complejo no hay ningún problema en reconocer las limitaciones de los «trabajos de pegado» en ciertas C∞-funciones tales como la «h(x)» definida en el capítulo anterior. Con seguridad, a Euler le hubiera encantado la potencia de la suavidad compleja. (Por desgracia para el Leonhard Euler real, la sorprendente potencia de esta «suavidad compleja» fue apreciada demasiado tarde para él, ya que fue descubierta por primera vez por Augustin Cauchy en 1821, unos treinta y ocho años después de la muerte de Euler.) Vemos así que la suavidad compleja proporciona una vía para expresar lo que se necesita para nuestra noción «euleriana» de función de una forma mucho más económica que la que ofrece la existencia de un desarrollo en serie de potencias. Pero hay también otra ventaja en considerar tales funciones desde el punto de vista complejo. Recordemos nuestra incómoda «1/x» que parecía ser «una sola función», pese al hecho de que la curva real y = 1/x consta de dos fragmentos separados que no están empalmados «analíticamente» a través de valores reales de x. Desde la perspectiva compleja, vemos con claridad que 1/z es realmente una sola función. El único lugar donde la función «no funciona» en el plano complejo es el origen z = 0. Si eliminamos este punto del plano complejo, seguimos teniendo una región conexa. La parte de la recta real para la que x < 0 está conectada a la parte para la que x > 0 a través del plano complejo. Así pues, 1/z es realmente una función compleja conexa, siendo esto completamente diferente de la situación que teníamos con números reales.
Las funciones que son suave-complejas (analítico-complejas) en este sentido se denominan holomorfas. Las funciones holomorfas desempeñarán un papel importante en muchas de nuestras discusiones posteriores. Veremos su importancia en relación con las aplicaciones conformes y las superficies de Riemann en el capítulo 8, y con las series de Fourier (fundamentales para la teoría de vibraciones) en el capítulo 9. Tienen papeles importantes que desempeñar en la teoría cuántica y en la teoría cuántica de campos (como veremos en §24.3 y §26.3). Son asimismo fundamentales en diversos enfoques para el desarrollo de nuevas teorías físicas (en particular, la teoría de twistores —véase el capítulo 33—, y también desempeñan un papel importante en la teoría de cuerdas; véanse §§31.5,13,14).
7.2. INTEGRACIÓN DE CONTORNO
Aunque no es este el lugar para desgranar los detalles de los argumentos matemáticos indicados en §7.1, en cualquier caso será ilustrativo desarrollar el esbozo anterior. En particular, será conveniente dar aquí una explicación de la integración de contorno que proporcione al lector una idea de cómo puede utilizarse la integración de contorno para establecer lo que se necesita para los requisitos de §7.1. Recordemos, en primer lugar, la notación que se ha introducido en el capítulo anterior para una integral definida con una variable real x, y consideremos ahora que se aplica a una variable compleja z:
 f(z) dz = g(b) – g(a),
f(z) dz = g(b) – g(a),
donde g′(z) = f(z). En el caso real, la integral se toma entre un punto a de la recta real y otro punto b en dicha recta. Hay solo un camino para ir de a a b a lo largo de la recta real. Ahora la consideraremos como una fórmula compleja. Aquí tenemos a y b como dos puntos en el plano complejo. Ahora ya no solo tenemos un camino para ir de a a b, sino que podemos dibujar montones de caminos diferentes que conectan a y b. Lo que nos dicen las ecuaciones de Cauchy-Riemann es que si hacemos nuestra integración a lo largo de uno de estos caminos,[3] obtenemos la misma respuesta que si la hacemos a lo largo de cualquier otro camino que pueda obtenerse a partir del primero por una deformación continua dentro del dominio de la función. (Véase la Fig. 7.1.) Esta propiedad es una consecuencia de un simple caso del «teorema fundamental del cálculo exterior», descrito en §12.6. Para algunas funciones, entre las que se cuenta 1/z, el dominio tiene un «agujero» (en el caso 1/z, el agujero está en z = 0), de modo que puede haber varias formas esencialmente diferentes para ir de a a b. Aquí, «esencialmente diferente» se refiere al hecho de que un camino no puede ser deformado de forma continua hasta el otro sin dejar de permanecer en el dominio de la función. En tales casos, el valor de la integral entre a y b puede dar una respuesta diferente para los dos caminos.

Fig. 7.1. Diferentes caminos de a a b. Integrando una función holomorfa f a lo largo de un camino se obtiene la misma respuesta que a lo largo de cualquier otro camino que pueda obtenerse a partir del primero por una deformación continua dentro del dominio de la f. Para algunas funciones, el dominio tiene un «agujero» dentro (por ejemplo, z = 0, para 1/z) que impide ciertas deformaciones, de modo que pueden obtenerse respuestas diferentes.
En este punto habría que introducir una nota de aclaración (o más bien de corrección). Cuando hablo de un camino que es deformado de forma continua hasta otro, me refiero a lo que los matemáticos llaman deformaciones homólogas, y no a las homotópicas. En el caso de una deformación homóloga, es legítimo que partes de los caminos se cancelen mutuamente, con tal de que dichas porciones se recorran en sentidos opuestos. Véase la Fig. 7.2 para un ejemplo de este tipo de deformaciones permitido. De dos caminos que son deformables uno hasta otro en este sentido se dice que pertenecen a la misma clase de homología. Por el contrario, las deformaciones homotópicas no permiten este tipo de cancelación. Caminos deformables hasta coincidir uno con otro donde no está permitida tal cancelación, pertenecen a la misma clase de homotopía. Las curvas homotópicas son siempre homólogas, pero la inversa no es necesariamente cierta. Tanto la homotopía como la homología tienen que ver con la equivalencia bajo movimientos continuos. Así pues, forman parte de la disciplina de la topología. Más tarde veremos diferentes aspectos de la topología que desempeñan papeles importantes en otras áreas.
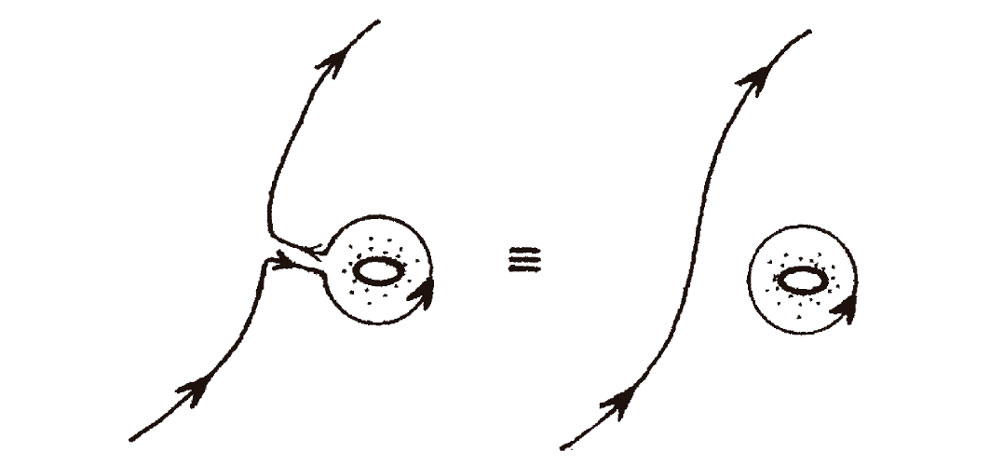
Fig. 7.2. Con una deformación homóloga, partes de los caminos se cancelan mutuamente, si se recorren en sentidos opuestos. A veces esto da lugar a lazos separados.
La función f(z) = 1/z es, de hecho, una función para la que se obtienen diferentes respuestas cuando los caminos no son homólogos. Podemos ver por qué debe ser así a partir de lo que ya sabemos sobre los logaritmos. Hacia el final de la sección anterior se advirtió que log z es una integral indefinida de 1/z. (De hecho, esto solo se estableció para una variable real x, pero el mismo razonamiento por el que se llega a la respuesta real sirve, asimismo, para llegar a la correspondiente respuesta compleja. Este es básicamente un principio general que se aplica también a cualesquiera otras fórmulas explícitas.) Tenemos así

Pero recordemos de §5.3 que existen diferentes «respuestas» alternativas a un logaritmo complejo. Más pertinente es que podemos pasar de forma continua de una respuesta a otra. Para ilustrarlo, mantengamos a fijo y dejemos que b varíe. De hecho, vamos a permitir que b describa de forma continua un círculo alrededor del origen en sentido positivo (i.e., contrario a las agujas del reloj), que lo lleva de nuevo a su posición original (véase la Fig. 7.3a). Recordemos de §5.3 que la parte imaginaria de log b es simplemente su argumento (i.e., el ángulo que forma b con el eje real positivo, medido en el sentido positivo; véase la Fig. 5.4b). Este argumento se incrementa precisamente en 2π en el curso de este movimiento, de modo que encontramos que log b ha aumentado en 2πi (véase la Fig. 7.3b). Así pues, el valor de nuestra integral aumenta en 2πi por cada nueva vuelta alrededor del origen (en sentido positivo) que da el camino a lo largo del cual se realiza la integral.

Fig. 7.3. (a) La integración de z–1 dz de a a b da log b – log a. (b) Mantener a fijo, y permitir que b dé una vuelta en el sentido contrario a las agujas del reloj alrededor del origen, incrementa log b en la respuesta en 2πi. (c) Luego volvemos a a hacia atrás a lo largo de la ruta original. (d) Cuando la parte del camino se cancela desde a, nos quedamos con una integral de contorno cerrada en sentido contrario a las agujas del reloj  z–1 dz = 2πi.
z–1 dz = 2πi.
Podemos reexpresar este resultado en términos de contornos cerrados, cuya existencia es un rasgo característico y poderoso del análisis complejo. Consideremos la diferencia entre el segundo y el primero de nuestros dos caminos, es decir, recorramos primero el segundo camino y luego recorramos el primero en sentido contrario (Fig. 7.3c). Consideramos esta diferencia en el sentido homólogo, de modo que podemos cancelar porciones que «vuelven sobre sus pasos» y resolver las demás de una forma continua. El resultado es un camino —o contorno— cerrado que forma un solo lazo alrededor del origen (véase la Fig. 7.3d), y no se interesa por la elección de a ni de b. Esto proporciona un ejemplo de una integral de contorno (cerrado), que normalmente se escribe con el símbolo « », y encontramos, en este ejemplo,[7.1]
», y encontramos, en este ejemplo,[7.1]

Por supuesto, cuando utilizamos este símbolo debemos tener cuidado en dejar claro qué contorno real se está utilizando, o más bien qué clase de homología de contorno se está utilizando. Si nuestro contorno hubiera dado dos vueltas (en el sentido positivo), entonces habríamos obtenido la respuesta 4πi. Si hubiera dado una vuelta alrededor del origen en el sentido opuesto (i.e., en el de las agujas del reloj), entonces la respuesta habría sido –2πi.
Resulta interesante que esta propiedad de obtener una respuesta no trivial con semejante contorno cerrado dependa críticamente de la multivaluación del logaritmo complejo, una característica que podría haber parecido ser solo una complicación en la definición de un logaritmo. Más adelante veremos que esto no es una simple curiosidad. De hecho, la potencia del análisis complejo depende de ello de forma crucial. En las dos secciones siguientes esbozaré algunas de las consecuencias de este tipo de cosas. Espero que los lectores no matemáticos puedan sacar algún provecho de la exposición. Creo que transmite algo a la vez genuino y sorprendente en la naturaleza del razonamiento matemático.
7.3. SERIES DE POTENCIAS A PARTIR DE LA SUAVIDAD COMPLEJA
La expresión mostrada antes es un caso particular (para la función constante f(z) = 2πi) de la famosa fórmula de Cauchy que expresa el valor de una función holomorfa en el origen en términos de una integral de contorno alrededor del origen:[4]
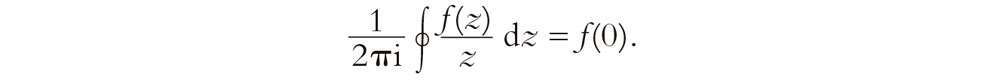
Aquí f(z) es holomorfa en el origen (i.e., suave-compleja en una región que contiene el origen), y el contorno es cierto lazo que precisamente rodea el origen, o podría ser cualquier lazo homólogo a aquel, en el dominio de la función del que se ha eliminado el origen. Así pues, tenemos el hecho notable de que lo que la función está haciendo en el origen está completamente determinado por lo que está haciendo en un conjunto de puntos alrededor del origen. (La fórmula de Cauchy es básicamente una consecuencia de las ecuaciones de Cauchy-Riemann, junto con la expresión anterior  z–1 dz = 2πi, tomada en el límite de lazos pequeños; pero no sería oportuno que entrara aquí en estos detalles.)
z–1 dz = 2πi, tomada en el límite de lazos pequeños; pero no sería oportuno que entrara aquí en estos detalles.)
Si en lugar de utilizar 1/z en la fórmula de Cauchy utilizamos 1/zn + 1, donde n es algún entero positivo, obtenemos una versión de «orden superior» de la fórmula de Cauchy que da lo que resulta ser la n-ésima derivada f(n)(z) de f(z) en el origen:
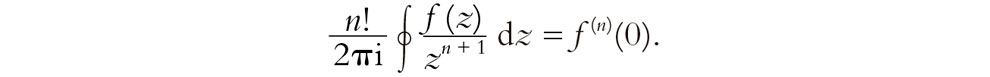
(Recordemos n! de §5.3.) Podemos ver que esta fórmula «tiene que ser la respuesta correcta» examinando la serie de potencias para f(z),[7.2] pero utilizar este hecho sería una petición de principio, puesto que aún no sabemos si existe el desarrollo en serie de potencias, y ni siquiera si existe la n-ésima derivada de f. Todo lo que sabemos por ahora es que f(z) es suave-compleja, sin saber si puede diferenciarse más de una vez. Sin embargo, utilizamos simplemente esta fórmula como algo que nos proporciona la definición de la derivada n-ésima en el origen. Podemos entonces incorporar esta «definición» en la fórmula de Taylor an = f(n)(0)/n! para los coeficientes en la serie de potencias (véase §6.4)
a0 + a1z + a2z2 + a3z3 + a4z4 + …,
y con un poco de trabajo podemos demostrar que la suma de esta serie es realmente f(z) en cierta región que comprende el origen. En consecuencia, la función tiene una derivada n-ésima en el origen dada por la fórmula.[7.3] Esto contiene la esencia del argumento que demuestra que la suavidad compleja en una región que rodea el origen implica, de hecho, que la función es realmente analítica (-compleja) en el origen (i.e., holomorfa).
Por supuesto, en todo esto no hay nada de especial en el origen. Igualmente podemos hablar de series de potencias en torno a cualquier otro punto p en el plano complejo y utilizar la serie de Taylor, como hemos hecho en §6.4. Para esto, simplemente desplazamos el origen al punto p para obtener la fórmula de Cauchy en la forma con «origen desplazado»
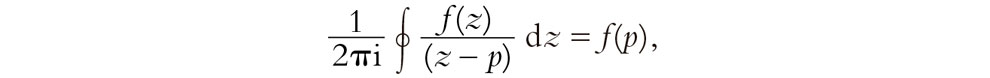
y también la expresión para la derivada n-ésima
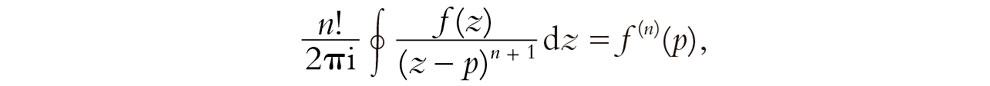
donde ahora el contorno rodea al punto p en el plano complejo. Así pues, la suavidad compleja implica la analiticidad (holomorficidad) en todo punto del dominio.
He preferido mostrar la esencia del argumento por el que, localmente, la suavidad compleja implica analiticidad, en lugar de exigir que el lector acepte el resultado como cierto, porque es un ejemplo maravilloso del modo en que los matemáticos pueden obtener a veces sus resultados. Ni la premisa (f(z) es suave-compleja) ni la conclusión (f(z) es analítica) contienen ningún indicio de la noción de integración de contorno o de la multivaluación de un logaritmo complejo. Pese a todo, estos ingredientes proporcionan las claves esenciales hacia la verdadera ruta para encontrar la respuesta. Es difícil ver cómo podría haberlo logrado un argumento «directo» (cualquiera que pudiera ser). La clave es el juego matemático. La naturaleza tentadora del propio logaritmo complejo es lo que nos seduce para estudiar sus propiedades. Este atractivo intrínseco es en apariencia independiente de cualquier aplicación que pudiera tener el logaritmo en otras áreas. Lo mismo se puede decir, incluso en mayor medida, de la integración de contorno. Hay una extraordinaria elegancia en la idea base, donde la libertad topológica se combina con las expresiones explícitas con exquisita precisión.[7.4] Pero no se trata meramente de elegancia; la integración de contorno proporciona también una técnica matemática muy poderosa y útil en muchas áreas diferentes, que contiene bastante de la magia de los números complejos. En particular, conduce a formas sorprendentes de evaluar integrales definidas y sumar explícitamente diversas series infinitas.[7.5],[7.6] Asimismo, encuentra muchas otras aplicaciones en física e ingeniería, así como en otras áreas de las matemáticas. ¡Euler hubiera disfrutado con todo esto!
7.4. PROLONGACIÓN ANALÍTICA
Tenemos ahora el extraordinario resultado de que la suavidad-compleja en cierta región es equivalente a la existencia de un desarrollo en serie de potencias en torno a cualquier punto en dicha región. Sin embargo, debería aclarar un poco más lo que significa «región» en este contexto. En términos técnicos, entiendo por ello lo que los matemáticos llaman una región abierta. Podemos expresarlo diciendo que si un punto a está en la región, entonces hay un círculo centrado en a cuyo interior está también contenido en la región. Quizá esto no sea muy intuitivo, así que permítanme poner algunos ejemplos. Un único punto no es una región abierta, ni lo es una curva ordinaria. Pero el interior del círculo unidad en el plano complejo, es decir, el conjunto de puntos cuya distancia al origen es estrictamente menor que la unidad, es una región abierta. Esto se debe a que cualquier punto que esté estrictamente en el interior del círculo, por muy próximo que se halle a la circunferencia que lo limita, está rodeado por un círculo mucho más pequeño que aún yace estrictamente dentro del círculo unidad (véase la Fig. 7.4). Por el contrario, el disco cerrado, que consiste en los puntos cuya distancia al origen es menor o igual que la unidad, no es una región abierta porque ahora está incluida la circunferencia, y un punto de la circunferencia no tiene la propiedad de que existe un círculo centrado en dicho punto que esté contenido dentro de la región.
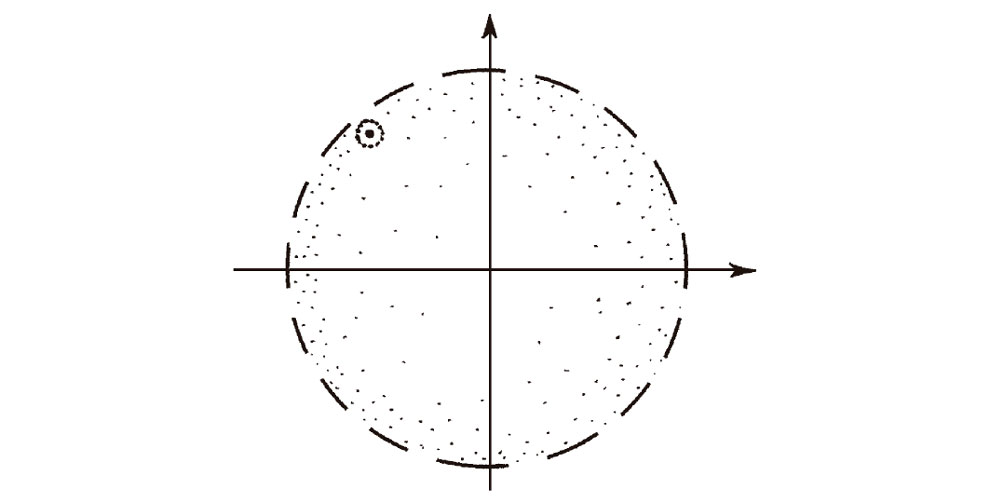
Fig. 7.4. El disco unidad abierto |x| < 1. Cualquier punto estrictamente interior, por muy próximo que esté a la circunferencia, está rodeado por muchos círculos más pequeños cuyo interior sigue yaciendo estrictamente dentro del círculo cerrado |x| ≤ 1, lo que no ocurre para puntos en la frontera.
Consideremos ahora el dominio[5] D de cierta función holomorfa f(z), donde tomamos D como una región abierta. En todo punto de D la función f(z) será suave-compleja. Así pues, de acuerdo con lo anterior, si seleccionamos un punto cualquiera p en D, tenemos una serie de potencias convergente en torno a p que representa a f(z) en una región apropiada que contiene a p. ¿Qué tamaño tiene esta «región apropiada»? Tenderá a darse el caso de que para un p concreto, la serie de potencias no funcionará para la totalidad de D. Recordemos el círculo de convergencia descrito en §4.4. Este sería algún círculo centrado en p (se admite un radio infinito) tal que para puntos estrictamente dentro de ese círculo la serie de potencias convergerá, pero no lo hará para puntos z estrictamente fuera del círculo. Supongamos que f(z) tiene una singularidad en algún punto q, a saber, un punto en el que la función f(z) no puede extenderse y seguir siendo suave-compleja. (Por ejemplo, el origen q = 0 es una singularidad de la función f(z) = 1/z; véase §7.1. Una singularidad se conoce a veces como un «punto singular» de la función. Un punto regular es simplemente un lugar donde la función es no singular, y con ello holomorfa.) Entonces, el círculo de convergencia no puede ser tan grande que contenga a q en su interior. Tenemos así un mosaico de círculos de convergencia (normalmente en número infinito) que, en conjunto, recubren la totalidad de D, aunque en general uno solo de dichos círculos no lo hará. El caso f(z) = 1/z ilustra este punto (véase la Fig. 7.5). Aquí, el dominio D es el plano complejo del que se ha eliminado el origen. Si seleccionamos un punto p en D, encontramos que el círculo de convergencia es el círculo centrado en p y que pasa por el origen.[7.7] Necesitamos un número infinito de tales círculos para recubrir la región entera D.
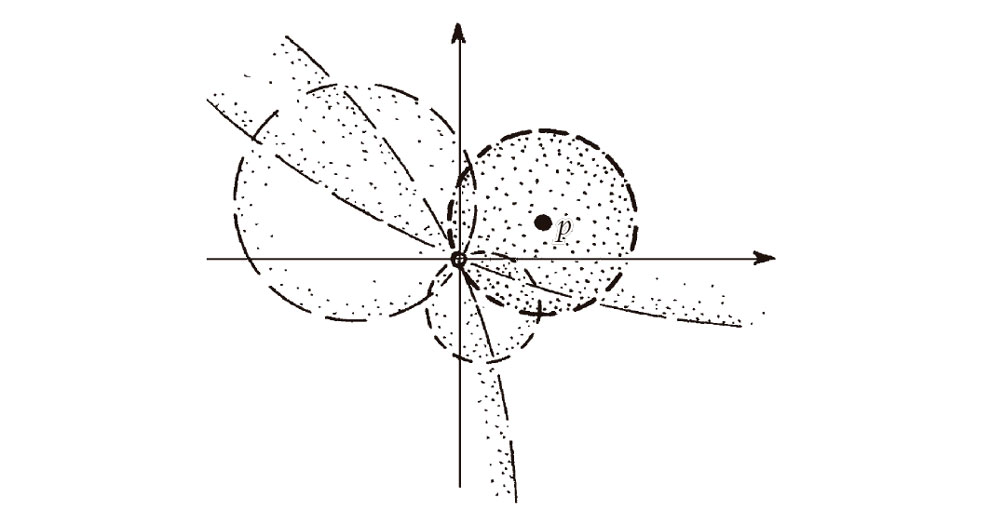
Fig. 7.5. Para f(z) = 1/z, el dominio D es el plano complejo con el origen eliminado. El círculo de convergencia alrededor de cualquier punto p en D está centrado en p y pasa por el origen. Para cubrir D por entero, necesitamos un atlas (infinito) de círculos semejantes.
Esto nos lleva a la importante cuestión de la prolongación analítica. Supongamos que se nos da cierta función f(z), holomorfa en cierto dominio D, y consideremos la pregunta: «¿Podemos extender D a una región mayor D′, de modo que f(z) también se extienda de forma holomorfa a D′?». Por ejemplo, se nos podría haber dado f(z) en forma de una serie de potencias, convergente dentro de su círculo de convergencia específico, y podríamos desear extender f(z) fuera de este círculo. Con frecuencia esto es posible. En §4.4 hemos considerado la serie 1 – z2 + z4 – z6 + …, que tiene al círculo unidad como círculo de convergencia; pese a todo, tiene la extensión natural a la función (1 + z2)–1, que es holomorfa en todo el plano complejo del que solo se han eliminado los dos puntos +i y –i. Así pues, en este caso la función puede ser extendida analíticamente mucho más allá del dominio sobre el que estaba dada inicialmente.
Aquí hemos sido capaces de escribir una fórmula explícita para la función, pero en otros casos puede no ser tan fácil. De todas formas, existe un procedimiento general según el cual puede llevarse a cabo frecuentemente la prolongación analítica. Podemos imaginar que partimos de alguna pequeña región en la que se conoce una expresión en serie de potencias válida localmente para la función f(z). Entonces podemos movernos a lo largo de cierto camino, prolongando la función mediante el uso repetido de series de potencias basadas en puntos diferentes. Para esto utilizaríamos una secuencia de puntos a lo largo del camino y tomaríamos una sucesión de desarrollos en serie de potencias en torno a cada uno de estos puntos. Esto determinará la prolongación con tal de que puedan solaparse los interiores de los sucesivos círculos de convergencia (véase la Fig. 7.6). Cuando puede llevarse a cabo este procedimiento de forma consistente, la función resultante está unívocamente determinada por el valor de la función en la región inicial y en el camino a lo largo del cual esta siendo prolongada.
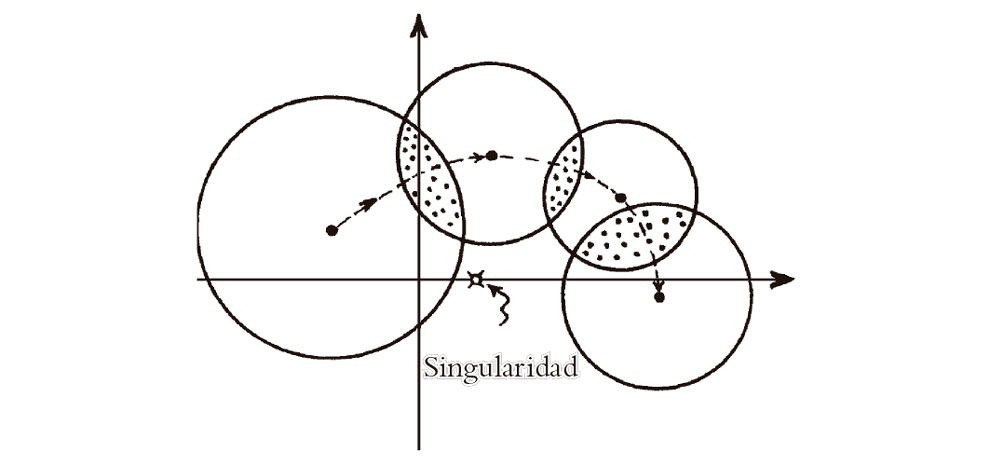
Fig. 7.6. Una función holomorfa puede ser prolongada analíticamente, utilizando una sucesión de expresiones en serie de potencias en torno a una secuencia de puntos. Esto procede unívocamente a lo largo del camino que los conecta, suponiendo que se solapan los sucesivos círculos de convergencia.
Existe así una notable «rigidez» en las funciones holomorfas, como se manifiesta en este proceso de prolongación analítica. En el caso de C∞-funciones reales, por el contrario, era posible «ir cambiando de idea» acerca de lo que tenía que hacer la función (como con la h(x) suavemente parcheada de §6.3, Fig. 6.7, que repentinamente «despega» después de haber sido nula para todos los valores negativos de x). Esto no puede suceder con las funciones holomorfas. Una vez que la función está determinada en su región original y se fija el camino, no hay elección sobre la forma de extender la función. De hecho, lo mismo es cierto para funciones analítico-reales de una variable real. También estas tienen una «rigidez» similar, pero ahora tampoco hay mucha elección sobre el camino. Solo puede ser en un sentido o en el otro a lo largo de la recta real. Con las funciones complejas, la prolongación analítica puede ser más interesante debido a esta libertad del camino dentro de un plano bidimensional.
Para ilustrarlo, consideremos a nuestra vieja amiga log z. Ciertamente, no tiene un desarrollo en serie de potencias en torno al origen, puesto que tiene una singularidad allí. Pero, si queremos, podemos desarrollarla en torno al punto p = 1, por ejemplo, para obtener la serie[7.8]

El círculo de convergencia es el círculo de radio unidad centrado en z = 1. Imaginemos que se realiza una prolongación analítica a lo largo de un camino que describe un círculo alrededor del origen en el sentido contrario a las agujas del reloj. Si quisiéramos, podríamos utilizar, series de potencias tomadas en torno a los puntos sucesivos 1, ω, ω2, y vuelta a 1, regresando así a nuestro punto de partida después de haber dado una vuelta alrededor del origen (Fig. 7.7). Aquí he utilizado las tres raíces cúbicas de la unidad, situadas regularmente a lo largo del círculo unidad, a saber, 1, ω = e2πi/3 y ω2 = e4pi/3, como se ha expuesto al final de la sección §5.4, y la ruta alrededor del origen es un triángulo equilátero. Alternativamente, podría haber utilizado 1, i, –1, –i, 1, que es ligeramente menos económico. En cualquier caso, no hay necesidad de calcular la serie de potencias, puesto que ya conocemos la respuesta explícita para la propia función, a saber, log z. El problema, por supuesto, es que cuando hemos dado una vuelta alrededor del origen, siguiendo unívocamente la función, encontramos que la hemos extendido unívocamente a un valor diferente de aquel del que hemos partido. De algún modo, se ha sumado 2πi a la función cuando giramos una vuelta. Si hubiésemos decidido proceder alrededor del origen en sentido contrario, entonces habríamos encontrado que se había restado 2πi de la función de la que hemos partido. Así pues, la unicidad de la prolongación analítica puede ser algo muy sutil, y puede depender decididamente del camino tomado. Para funciones «multivaluadas» más complicadas que log z, podemos obtener algo mucho más elaborado que el mero añadido de una constante (como 2πi) a la función.
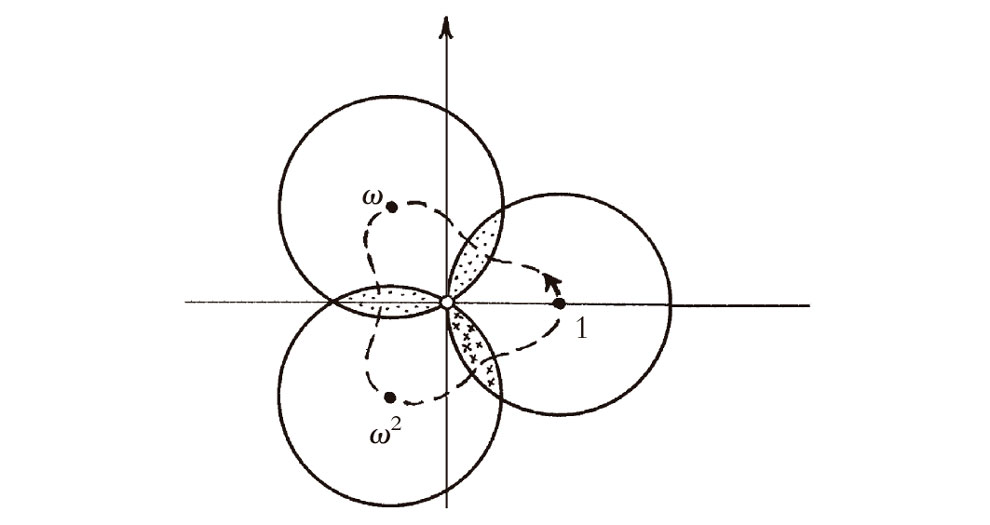
Fig. 7.7. Partimos de z = 1, prolongando analíticamente f(z) = log z a lo largo de un camino que rodea al origen en el sentido contrario a las agujas del reloj (desarrollando en torno a los puntos sucesivos 1, ω, ω2, 1; ω = e2πi/3. Encontramos que 2πi se suma a f.
Como un aparte, vale la pena señalar que la noción de prolongación analítica no necesita referirse concretamente a series de potencias, pese al hecho de que he encontrado útil emplearlas en algunas de mis descripciones. Por ejemplo, hay otra clase de series que tienen gran importancia en la teoría de números, a saber, las denominadas series de Dirichlet. La más importante de estas es la función zeta de (Euler-)Riemann,[6] definida por la suma infinita[7]
ζ(z) = 1–z + 2–z + 3–z + 4–z + 5–z + …,
que converge con la función holomorfa denotada por ζ(z) cuando la parte real de z es mayor que 1. La prolongación analítica de esta función la define unívocamente (y «univaluadamente») en la totalidad del plano complejo, pero del que se ha eliminado el punto z = 1. Quizá el más importante de los problemas matemáticos no resueltos hoy es la hipótesis de Riemann, que concierne a los ceros de dicha función zeta extendida analíticamente, es decir, las soluciones de ζ(z) = 0. Es relativamente fácil demostrar que ζ(z) se anula para z = –2, –4, –6, … La hipótesis de Riemann afirma que todos los ceros restantes yacen en la recta Re(z) = 1/2, es decir, ζ(z) se anula (a menos que z sea un número entero par) solo cuando la parte real de z es igual a 1/2. Toda la evidencia numérica hasta la fecha apoya esta hipótesis, pero su verdad real es una incógnita. Tiene implicaciones fundamentales para la teoría de los números primos.[8]
Notas
Sección 7.1
7.1. A aquellos lectores que quieran explorar estas fascinantes cuestiones con un mayor detalle geométrico, les recomiendo Needham (1997).
7.2. Las daré en §10.5, cuando se haya introducido la idea de derivada parcial.
Sección 7.2
7.3. De forma más explícita, la integración de f «a lo largo» de un camino dado por z = p(t) (donde p es una función suave de valor complejo de un parámetro real t) puede expresarse como la integral definida  uv f(p(t))p′(t) dt =
uv f(p(t))p′(t) dt =  f(z)dz, donde p(u) es el punto inicial a del camino y p(v) es el punto final b.
f(z)dz, donde p(u) es el punto inicial a del camino y p(v) es el punto final b.
Sección 7.3
7.4. Una «razón» por la que la fórmula de Cauchy debe ser verdadera es que para un lazo pequeño alrededor del origen, f(z) debe ser tratada realmente como el valor constante f(0), y entonces la situación se reduce a la estudiada en §7.2.
Sección 7.4
7.5. Una de las cosas irritantes de la terminología de este tema es que el término «dominio» tiene dos significados distintos. Uno, que no es el que se pretende aquí, es simplemente cualquier «región abierta conexa en el plano complejo». Aquí, como antes (véase §6.1), entiendo por región la que se da en el plano complejo en la que está definida la función f, que en general no tiene por qué ser necesariamente abierta no conexa (aunque aquí se toma abierta).
7.6. La función zeta fue considerada por primera vez por Euler, pero normalmente se le da el nombre de Riemann, en vista de su fundamental trabajo, que incluye la extensión de esta función al plano complejo.
7.7. Nótese la curiosa relación «al revés» entre esta serie y una serie de potencias ordinaria, a saber, (– z) + (– z)2 + (– z)3 + … = –z(1 + z)–1.
7.8. Para más información sobre la función ζ y la hipótesis de Riemann, véanse Apostol (1976) y Priestley (2003). Para exposiciones de divulgación, véanse Derbyshire (2003), Du Sautoy (2003), Sabbagh (2002) y Devlin (1988, 2002).