6
Cálculo infinitesimal con números reales
6.1. ¿QUÉ HACE RESPETABLE A UNA FUNCIÓN?
El cálculo infinitesimal —o, según su nombre más sofisticado, análisis matemático— está construido a partir de dos ingredientes básicos: diferenciación e integración. La diferenciación está relacionada con velocidades y aceleraciones, con pendientes y curvaturas de curvas y superficies, y cosas similares. Estas son tasas de cambio de las cosas, y son cantidades definidas localmente, en términos de estructura o comportamiento en los entornos más minúsculos de puntos simples. La integración, por el contrario, está relacionada con áreas y volúmenes, con centros de gravedad y con muchas otras cosas de esa misma naturaleza general. Estas son cosas que implican de una u otra forma medidas de totalidad, y no están definidas meramente por lo que pasa en los entornos locales o infinitesimales de puntos individuales. El hecho notable, conocido como teorema fundamental del cálculo infinitesimal, es que cada uno de estos ingredientes es, en esencia, justo el inverso del otro. Básicamente es esto lo que posibilita que estos dos importantes dominios de estudio matemático se combinen y proporcionen un poderoso cuerpo de conocimiento y de técnica de cálculo.
Esta disciplina del análisis matemático, tal como se originó en el siglo XVII en la obra de Fermat, Newton y Leibniz, con ideas que se remontan hasta Arquímedes en el siglo III a.C., se denomina «cálculo infinitesimal» porque proporciona un cuerpo de técnica de cálculo mediante el que algunos problemas que, de otro modo, serían conceptualmente difíciles de manejar, pueden ser resueltos con frecuencia «de forma automática», siguiendo unas pocas reglas relativamente sencillas que a menudo pueden aplicarse sin necesidad de hacer un gran esfuerzo mental. Pese a todo, en este cálculo hay un contraste sorprendente entre las operaciones de diferenciación e integración atendiendo a lo que es lo «fácil» y lo que es lo «difícil». Cuando se trata de aplicar las operaciones a fórmulas explícitas que implican funciones conocidas, la diferenciación es la «fácil» y la integración la «difícil», y en muchos casos la última puede ser imposible de llevar a cabo de una manera explícita. Por el contrario, cuando las funciones no están dadas en términos de fórmulas, sino que vienen dadas en forma de listas tabuladas de datos numéricos, entonces la integración es la «fácil» y la diferenciación la «difícil» y la que, estrictamente hablando, quizá no sea posible en la forma usual. Las técnicas numéricas están relacionadas generalmente con aproximaciones, pero también en la teoría exacta hay una analogía muy estrecha con este aspecto de las cosas, y de nuevo es la integración la que puede realizarse en circunstancias en las que la diferenciación no puede hacerse. Tratemos de entender algo de esto. Estas cuestiones tienen que ver, de hecho, con lo que realmente se entiende por una «función».
Para Euler y los demás matemáticos de los siglos XVII y XVIII, una «función» significaría algo que se podría escribir explícitamente, como x2 o sen x o log(3 – x + ex), o quizá algo definido por cierta fórmula que incluye una integración o tal vez por una serie de potencias dada explícitamente. En la actualidad, se prefiere pensar en términos de «aplicaciones», mediante las que cierta colección A de números (o entes más generales) llamada dominio de la función se «aplica» en cierta colección B, llamada imagen de la función (véase la Fig. 6.1). El punto esencial de esto es que la función asignará un miembro de la imagen B a cada miembro del dominio A. (Podemos pensar que la función «examina» un número que pertenece a A y, entonces, dependiendo solo de qué número encuentre, produce un número definido perteneciente a B.) Una función de este tipo puede ser simplemente una «tabla de búsqueda». No es necesario que haya una «fórmula» de apariencia razonable que exprese la acción de la función de una manera manifiestamente explícita.
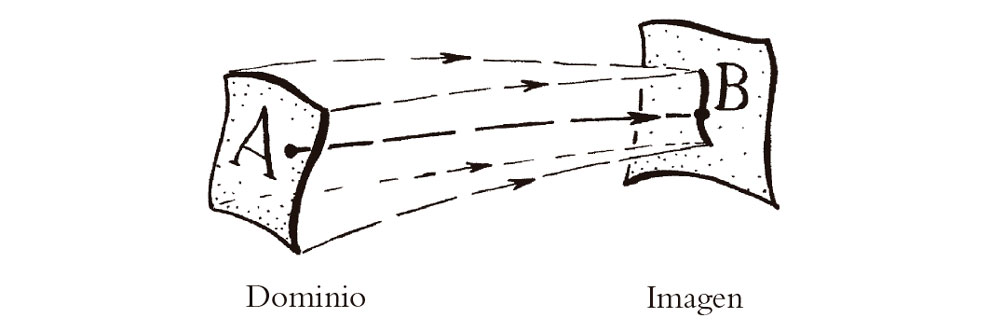
Fig. 6.1. Una función como «aplicación», en donde su dominio (una colección A de números o de otras entidades) se «aplica» en su imagen (otra colección B). A cada elemento de A se le asigna un valor particular en B, aunque diferentes elementos de A pueden alcanzar el mismo valor y algunos valores de B pueden no ser alcanzados.
Consideremos algunos ejemplos. En la Fig. 6.2 he dibujado las gráficas de tres funciones[1] sencillas, a saber, las dadas por x2, |x| y θ(x). En cada caso, los espacios dominio e imagen son ambos la totalidad de los números reales, que suelen representarse mediante el símbolo R. La función que estoy denotando por «x[2]» da simplemente el cuadrado del número real que está examinando. La función denotada por «|x|» (llamada valor absoluto) da simplemente x si x es no negativo, pero da –x si x es negativo; así pues, el propio valor |x| no es nunca negativo. La función θ(x) es 0 si x es negativo y 1 si x es positivo; también es habitual definir θ(0) = 1/2. (Esta función se denomina función escalón de Heaviside; véase §21.1 para otra importante influencia matemática de Oliver Heaviside, quizá más conocido por haber postulado por primera vez la «capa de Heaviside» en la atmósfera terrestre, tan importante para las transmisiones por radio.) Cada una de estas es una función perfectamente buena en el sentido moderno del término, pero Euler2 habría tenido dificultad en aceptar que |x| o θ(x) fueran realmente una «función» en su sentido del término.
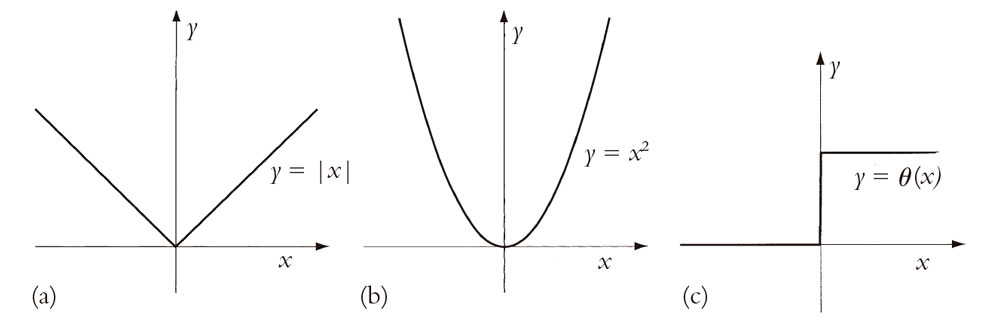
Fig. 6.2. Gráficas de (a) |x|, (b) x2, y (c) θ (x); en cada caso el dominio y la imagen son el sistema de los números reales.
¿Por qué podría ser así? Una posibilidad es pensar que la dificultad con |x| y θ(x) es que hay demasiadas cosas del tipo: «si x es tal y cual, entonces tomemos esto y aquello, mientras que si x es …», y no hay una «fórmula bonita» para la función. Sin embargo, esto es un poco vago, y en cualquier caso podríamos preguntarnos qué hay realmente erróneo en que |x| cuente como una «fórmula». Además, una vez que hemos aceptado |x|, podríamos escribir[6.1] una fórmula para θ(x)

(aunque podríamos preguntarnos si hay un sentido aceptable en el que esto da el valor correcto para θ(0), puesto que la fórmula da simplemente 0/0). Una objeción más pertinente es decir que la dificultad con |x| consiste en que no es «suave», y no en que su expresión explícita no sea «bonita». Vemos esto en el «ángulo» en el centro de la Fig. 6.2a. La presencia de este ángulo es lo que impide que |x| tenga una pendiente bien definida en x = 0. Tratemos ahora de entender esta idea.
6.2. PENDIENTES DE FUNCIONES
Como se ha comentado antes, una de las cosas con las que tiene que ver el cálculo diferencial es con hallar «pendientes». Vemos claramente en la gráfica de |x|, tal como se muestra en la Fig. 6.2a, que no tiene una pendiente única en el origen, donde está nuestro molesto ángulo. En cualquier otro lugar, la pendiente está bien definida, pero no en el origen. Debido a esta dificultad en el origen, decimos que |x| no es diferenciable en el origen o, de forma equivalente, que no es suave allí. Por el contrario, la función x2 tiene una pendiente perfectamente buena definida unívocamente en todo lugar, como se ilustra en la Fig. 6.2b. De hecho, la función x2 es diferenciable en todo lugar.
La situación con θ(x), tal como se ilustra en la Fig. 6.2c, es incluso peor que para |x|. Nótese que θ(x) da un «salto» desagradable en el origen (x = 0). Decimos que θ(x) es discontinua en el origen. Por el contrario, las dos funciones x2 y |x| son continuas en todo lugar. La dificultad de |x| en el origen no es una solución de continuidad, sino de diferenciabilidad. (Aunque la solución de continuidad y de suavidad son cosas diferentes, son realmente conceptos interrelacionados, como veremos en breve.)
Ninguno de estos fallos hubiera agradado, presumiblemente, a Euler, y parecen proporcionar razones por las que |x| y θ(x) podrían no ser consideradas como funciones «propiamente dichas». Pero consideremos ahora las dos funciones ilustradas en la Fig. 6.3. La primera, x3, sería aceptable para el criterio de cualquiera; pero ¿qué pasa con la segunda, que puede definirse mediante la expresión x|x|, y que ilustra la función que es x2 cuando x es no negativo y –x2 cuando x es negativo? A simple vista, las dos gráficas parecen muy similares y ciertamente «suaves». De hecho, ambas tienen un valor perfectamente bueno para la «pendiente» en el origen, a saber, «cero» (lo que significa que las curvas tienen allí una pendiente horizontal) y son en realidad «diferenciables» en todo lugar, en el sentido más directo de dicha palabra. Pese a todo, x|x| no parece ser ciertamente el tipo «bonito» de función que hubiera satisfecho a Euler.
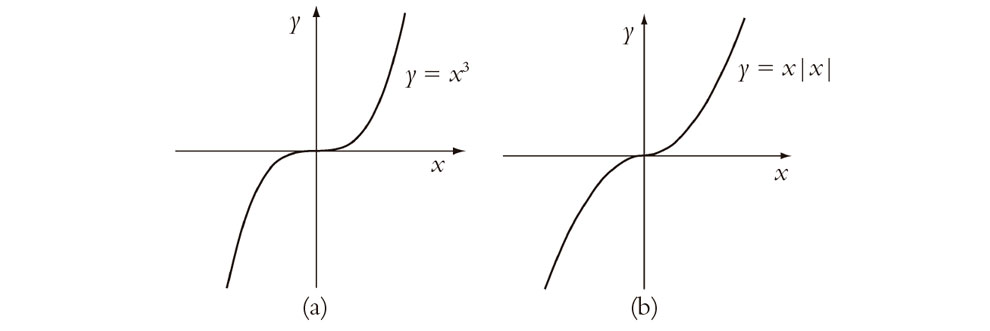
Fig. 6.3. Gráficas de (a) x3 y (b) x|x| (i.e., x2 si x ≥ 0 y –x2 si x < 0).
Lo que «falla» con x|x| es que no tiene una curvatura bien definida en el origen, y la noción de curvatura es ciertamente algo que concierne al cálculo diferencial. De hecho, la «curvatura» es algo que incluye lo que se denominan «derivadas segundas», que significa hacer la «diferenciación» dos veces. En efecto, decimos que la función x|x| no es dos veces diferenciable en el origen. Llegaremos a las derivadas segundas y superiores en §6.3.
Para empezar a entender todo esto, necesitaremos ver qué es lo que hace realmente la operación de diferenciación. Para ello tenemos que saber cómo se mide una pendiente. Esto se ilustra en la Fig. 6.4. He mostrado una función de apariencia bastante representativa que llamaré f(x). La curva de la Fig. 6.4a muestra la relación y = f(x), donde el valor de la coordenada y mide la altura, mientras que x mide el desplazamiento horizontal, como es habitual en una descripción cartesiana. He indicado la pendiente de la curva en un punto particular p, como el incremento en la coordenada y dividido por el incremento en la coordenada x, cuando procedemos a lo largo de la línea tangente a la curva en el punto p. (La definición técnica de «línea tangente» depende de los procedimientos adecuados de paso al límite, pero no es mi propósito ahora el discutir estos tecnicismos. Espero que el lector encontrará mis descripciones intuitivas adecuadas para nuestros propósitos inmediatos.)[3] La notación estándar para el valor de dicha pendiente es dy/dx. Podemos considerar «dy» como un incremento muy pequeño en el valor de y a lo largo de la curva y dx como el correspondiente incremento minúsculo en el valor de x. (Aquí, la corrección técnica nos exigiría un paso al «límite», a medida que cada uno de estos minúsculos incrementos se reducen a cero.)
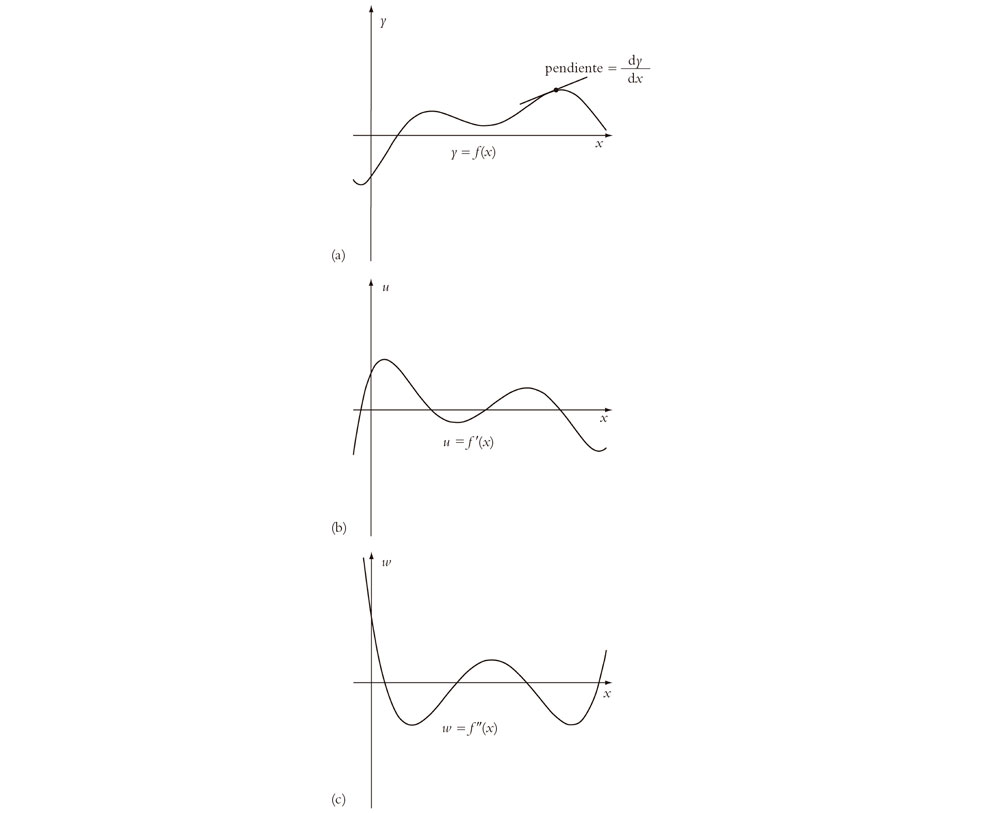
Fig. 6.4. Representación cartesiana de (a) y = f(x); (b) la derivada u = f′(x) (= dy/dx), y (c) la segunda derivada f″(x) = d2y/dx2. (Nótese que f(x) tiene pendiente horizontal solamente donde f′(x) corta al eje x, y tiene un punto de inflexión donde f″(x) corta al eje x.)
Ahora podemos considerar otra curva, que representa (frente a x) dicha pendiente en cada punto p, para las diversas elecciones posibles de la coordenada x; véase la Fig. 6.4b. De nuevo, estoy utilizando una descripción cartesiana, pero ahora es dy/dx, en lugar de y, lo que se representa en vertical. El desplazamiento horizontal sigue estando medido por x. La función que se está representando aquí se denomina normalmente f′(x), y podemos escribir dy/dx = f′(x). Llamamos a dy/dx la derivada de y con respecto a x, y decimos que la función f′(x) es la derivada[4] de f(x).
6.3. DERIVADAS DE ORDEN SUPERIOR; FUNCIONES C∞-SUAVES
Veamos ahora lo que sucede cuando tomamos una derivada segunda. Esto significa que ahora estamos considerando la función-pendiente para la nueva curva de la Fig. 6.4b, que muestra u = f′(x), donde ahora u representa a dy/dx. En la Fig. 6.4c he mostrado esta función-pendiente de «segundo orden», que es la gráfica de du/dx frente a x, de la misma forma que lo hemos hecho antes para dy/dx, de modo que el valor du/dx nos da ahora la pendiente de la segunda curva u = f′(x). Esto nos da lo que se denomina derivada segunda de la función original f(x), y se escribe normalmente f″(x). Cuando sustituimos u por dy/dx en la cantidad du/dx obtenemos la derivada segunda de y con respecto a x, que se escribe (con no mucha lógica) d2y/dx2.
Nótese que los valores de x donde la función original f(x) tiene pendiente horizontal son precisamente los valores de x donde f′(x) corta al eje x (de modo que dy/dx se anula para dichos valores de x). Los lugares donde f(x) alcanza un máximo o un mínimo (local) se dan en tales posiciones, lo que es importante cuando estamos interesados en encontrar los valores máximos y mínimos (localmente) de una función. ¿Qué pasa con los lugares donde la derivada segunda f″(x) corta al eje x? Estos se dan donde la curvatura de f(x) se anula. En general, estos puntos son aquellos donde la dirección en que se «dobla» la curva y = f(x) cambia de un lado de la curva a otro, en un lugar llamado punto de inflexión. (De hecho, no sería correcto decir que f″(x) «mide» realmente la curvatura de la curva definida por y = f(x), en general; la curvatura real viene dada por una expresión más complicada[5] que f″(x), pero que incluye a f″(x), y la curvatura se anula cuando f″(x) se anula.
Consideremos a continuación nuestras dos funciones x3 y |x|x de apariencia (superficialmente) similar consideradas más arriba. En la Fig. 6.5 a, b, c, he representado x3 y sus derivadas primera y segunda, como he hecho con la función f(x) en la Fig. 6.4, y en la Fig. 6.5 d, e, f he hecho lo mismo con |x|x. En el caso de x3 vemos que no hay ningún problema con la continuidad o la suavidad ni en la primera ni en la segunda derivada. De hecho, la primera derivada es 3x2 y la segunda es 6x, ninguna de las cuales hubiese dado ningún momento de preocupación a Euler. (Veremos dentro de poco cómo obtener estas expresiones explícitas.) Sin embargo, en el caso de |x|x encontramos algo muy parecido al «ángulo» de la Fig. 6.2a para la derivada primera, y un comportamiento de «función-escalón» para la derivada segunda, muy similar a la Fig. 6.2c. Tenemos una solución de suavidad para la derivada primera y una solución de continuidad para la segunda. A Euler no le hubiera gustado nada. La derivada primera es realmente 2|x| y la derivada segunda es –2 + 4θ|x|. (Mis lectores más escrupulosos podrían quejarse y aducir que yo no debería escribir tan alegremente una «derivada» para 2|x|, que no es realmente diferenciable en el origen. Cierto, pero no vamos a discutir por eso: puede conseguirse una justificación completa para esto utilizando las nociones que se introducirán al final del capítulo 9.)
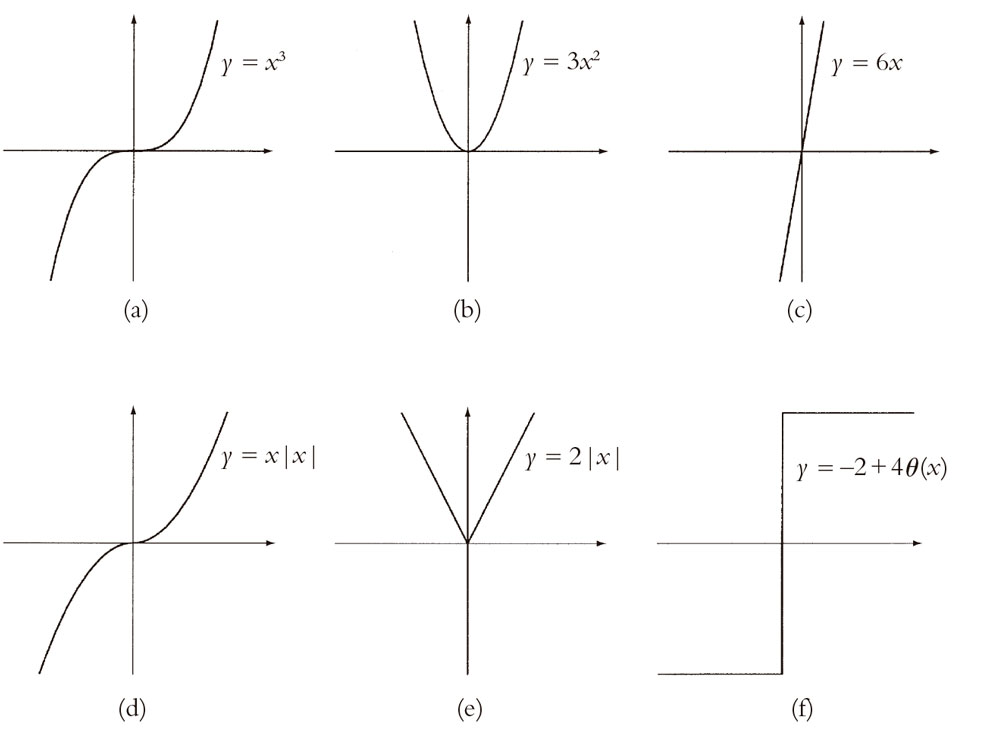
Fig. 6.5. (a) (b), (c) Representaciones de x3, su primera derivada 3x2 y su segunda derivada 6x, respectivamente. (d), (e), (f) Representaciones de x|x|, su primera derivada 2|x| y la segunda derivada –2 + 4θ(x), respectivamente.
Es fácil imaginar que se pueden construir funciones para las que tales soluciones de suavidad o de continuidad no se manifiestan hasta que no se han llevado a cabo un gran número de derivadas. Lo cierto es que bastará con funciones de la forma xn|x|, donde podemos tomar n como un número entero positivo tan grande como queramos. La terminología matemática para este tipo de cosas es decir que la función f(x) es Cn-suave si puede ser diferenciada n veces (en cada punto de su dominio) y la n-ésima derivada es continua.[6] La función xn|x| es, de hecho, Cn-suave pero no es Cn + 1-suave en el origen.
¿Qué valor de n satisfaría a Euler? Parece claro que él no se hubiera contentado con detenerse en cualquier valor particular de n. Con seguridad, el tipo de función autorrespetable que Euler hubiera aprobado sería una que se pudiera diferenciar tantas veces como queramos. Para cubrir esta situación, los matemáticos denominan a una función C∞-suave si es Cn-suave para todo entero positivo n. Para decirlo de otra forma, una función C∞-suave debe ser diferenciable tantas veces como queramos.
Podemos presumir que la idea de Euler de una función hubiera exigido algo parecido a la C∞-suavidad. Al menos podríamos imaginar que él hubiera esperado que su función fuera C∞-suave en la mayoría de los lugares de su dominio. Pero ¿qué pasa con la función 1/x? (véase la Fig. 6.6.) Ciertamente, esta no es C∞-suave en el origen. Ni siquiera está definida en el origen en el sentido moderno de una función. A pesar de este problema, nuestro Euler hubiera aceptado ciertamente 1/x como una «función» decente. Después de todo, existe para ella una sencilla fórmula de apariencia natural. Cabe imaginar que Euler no se hubiera interesado tanto en que sus funciones fueran C∞-suaves en todos los puntos de su dominio (suponiendo que él se hubiera preocupado siquiera de «dominios».) Quizá el que las cosas no funcionasen en el punto singular no importaría. Pero |x| y θ(x) solo fallaban en el mismo «punto singular» en que lo hacía 1/x. Parece que, a pesar de nuestros esfuerzos, aún no hemos captado la noción «euleriana» de función por la que nos estamos esforzando.
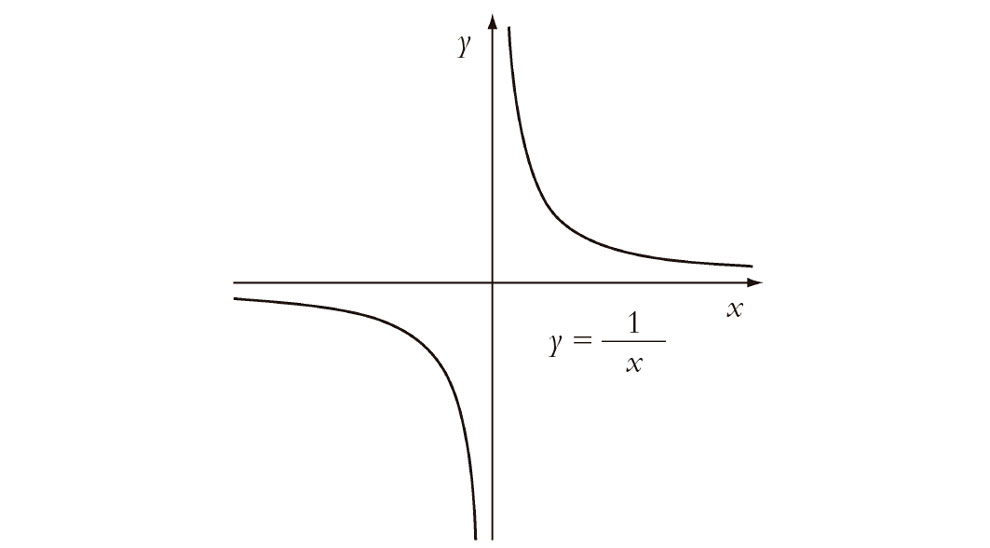
Fig. 6.6. Representación de 1/x.
Tomemos otro ejemplo. Consideremos la función h(x) definida por las reglas

La gráfica de esta función se muestra en la Fig. 6.7. Ciertamente, tiene el aspecto de una función suave. De hecho, es muy suave. Es C∞-suave sobre todo el dominio de los números reales. (Probar esto es el tipo de cosas que uno hace en un curso de la licenciatura en matemáticas. Recuerdo cómo tuve que enfrentarme personalmente a ello cuando era estudiante.)[6.2] A pesar de su absoluta suavidad, uno puede imaginar a Euler mirando por encima del hombro a una función definida de esta manera. Claramente no es «una sola función» en el sentido de Euler. Son «dos funciones pegadas», con independencia de lo suave que sea el trabajo de pegado hecho para empalmar la «falla» en el origen. En contraste, para Euler 1/x es una sola función, pese al hecho de que está separada en dos piezas por una «punta» muy desagradable en el origen, donde no es ni siquiera continua, y mucho menos suave (Fig. 6.6). Para nuestro Euler, la función h(x) no es realmente mejor que |x| o θ(x). En estos casos teníamos claramente «dos funciones pegadas», aunque con trabajos de pegado mucho más chapuceros (y con θ(x), el pegado parece haberse separado por completo).
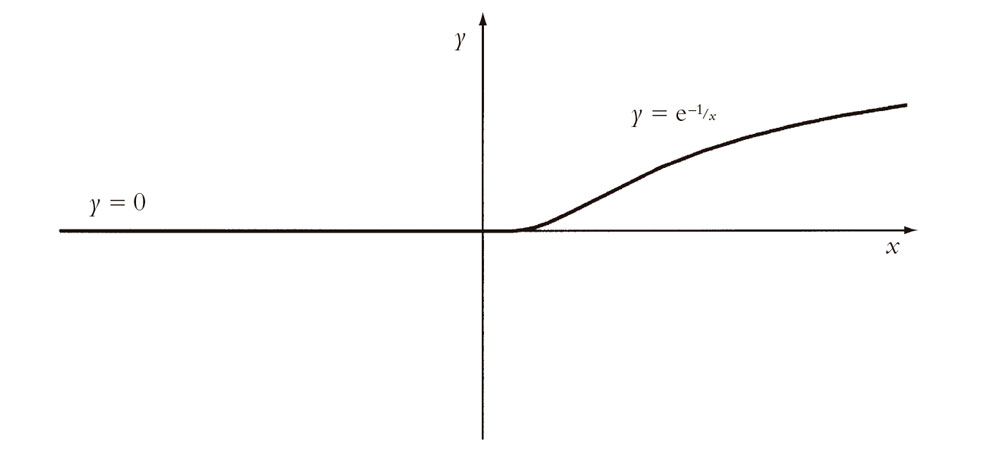
Fig. 6.7. Representación de y = h(x) (= 0 si x ≤ 0 y = e–1/x si x > 0), que es C∞-suave.
6.4. ¿LA NOCIÓN «EULERIANA» DE FUNCIÓN?
¿Cómo hay que entender esta noción «euleriana» de tener solo una única función y no una colección de funciones separadas? Como el ejemplo de h(x) muestra con claridad, la C∞-suavidad no es suficiente. Resulta que hay dos enfoques de apariencia completamente diferente para resolver esta cuestión. Uno de ellos utiliza los números complejos, y es engañosamente sencillo de enunciar, aunque trascendental en sus consecuencias. Exigimos que nuestra función f(x) se pueda extender a una función f(z) de la variable compleja z, de modo que f(z) sea suave en el sentido de que meramente se requiere que sea una vez diferenciable con respecto a la variable compleja z. (Así pues, f(z) es, en el sentido complejo, un tipo de C1-función.) El hecho de que sea esto todo lo que necesitamos es una muestra extraordinaria de auténtica magia. Si f(z) puede ser diferenciada una vez con respecto a la variable compleja z, ¡entonces puede ser diferenciada tantas veces como queramos!
Volveré al tema del cálculo infinitesimal complejo en la próxima sección. Pero hay otro enfoque para la solución de este problema de la «noción euleriana de función» que utiliza solo números reales, y este enfoque implica el concepto de serie de potencias que encontramos en §2.5. (Una de las cosas en las que Euler era un auténtico maestro en manipular series de potencias.) Será útil considerar la cuestión de las series de potencias, en esta sección, antes de volver al tema de la diferenciabilidad compleja. El hecho de que, localmente, la diferenciabilidad compleja resulta ser equivalente a la validez del desarrollo en serie de potencias es una de las piezas verdaderamente grandes de la magia de los números complejos.
Llegaré a todo esto a su debido tiempo, pero por el momento quedémonos en las funciones reales. Supongamos que cierta función f(x) tiene realmente una representación en serie de potencias:
f(x) = a0 + a1x + a2x2 + a3x3 + a4x4 + …
Ahora bien, existen métodos para encontrar, a partir de f(x), cuáles deben ser los coeficientes a0, a1, a2, a3, a4, … Para que exista tal desarrollo, es necesario (aunque no suficiente, como veremos de inmediato) que f(x) sea C∞-suave, de modo que tendremos nuevas funciones f′(x), f″(x), f″′(x), f″″(x), …, etc., que son las derivadas primera, segunda, tercera, cuarta, etc., de f(x), respectivamente. De hecho, nos interesaremos en los valores de dichas funciones solo en el origen (x = 0), y solo allí necesitamos la C∞-suavidad de f(x). El resultado (a veces denominado serie de Maclaurin)[7] es que si f(x) tiene un desarrollo tal en serie de potencias, entonces[6.3]
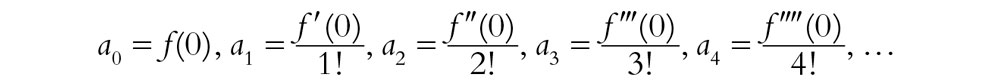
(Recordemos, de §5.3, que n! = 1 × 2 × … × n.) Pero ¿qué pasa a la inversa? Si se dan las an de este modo, ¿se sigue de ello que la suma realmente nos da f(x) (en un intervalo que incluye al origen)?
Volvamos a nuestra h(x) aparentemente sin fisuras. Quizá podamos detectar un fallo en el punto de unión (x = 0) utilizando esta idea. Tratemos de ver si h(x) tiene realmente un desarrollo en serie de potencias. Haciendo f(x) = h(x) en lo que precede, consideremos los diferentes coeficientes a0, a1, a2, a3, a4, … notando que todos ellos tienen que anularse siempre que x esté a la izquierda del origen, puesto que la serie tiene que coincidir con el valor h(x) = 0. De hecho, encontramos que todos ellos se anulan también para e–1/x, que es básicamente la razón por la que h(x) es C∞-suave en el origen, pues empalman todas las derivadas que vienen de los dos lados. Pero esto nos dice también que no hay forma de que la serie de potencias pueda funcionar, puesto que todos los términos son cero (véase el ejercicio [6.1]) y por consiguiente no pueden sumar e–1/x. Así pues, hay un fallo en la unión en x = 0; la función h(x) no puede expresarse como una serie de potencias. Decimos que h(x) no es analítica en x = 0.
En la exposición anterior me he estado refiriendo realmente a lo que se denominaría un desarrollo en serie de potencias en torno al origen. Un análisis similar se aplicaría a cualquier otro punto del dominio real de la función. La diferencia está entonces en que tenemos que «desplazar el origen» a algún otro punto particular, definido por el número real p en el dominio, lo que significa reemplazar x por x – p en el anterior desarrollo en serie de potencias, para obtener:
f(x) = a0 + a1(x – p) + a2(x – p)2 + a3(x – p)3+ …,
donde ahora
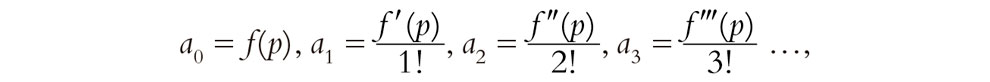
Esto se denomina un desarrollo en serie de potencias en torno a p. La función f(x) se llama analítica en p si puede expresarse como un desarrollo semejante en serie de potencias en algún intervalo que englobe a x = p. Si f(x) es analítica en todos los puntos de su dominio, la llamamos simplemente función analítica o, lo que es equivalente, una función Cω-suave. Las funciones analíticas son, en un sentido claro, incluso «más suaves» que las funciones C∞-suaves. Además, tienen la propiedad de que no es posible salir del paso pegando dos funciones analíticas «diferentes», a la manera de los ejemplos θ(x), |x|, x|x|, xn|x|, o h(x), que se han dado antes. Euler se habría mostrado feliz con las funciones analíticas. ¡Son funciones realmente «respetables»!
Sin embargo, resulta complicado seguir estas series de potencias, aunque solo sea en la imaginación. La forma «compleja» de considerarlas es más económica, e incluso nos ofrece una comprensión más profunda. Por ejemplo, la función 1/x no es analítica en x = 0, pero sigue siendo «una función».[6.4] La «filosofía de la serie de potencias» no nos dice esto directamente. Pero desde el punto de vista de los números complejos, 1/x es claramente una sola función, como veremos.
6.5. LAS REGLAS DE DIFERENCIACIÓN
Antes de examinar estas materias será útil decir algo acerca de las maravillosas reglas que nos proporciona el cálculo diferencial; reglas que nos permiten diferenciar funciones casi sin pensar, ¡aunque, por supuesto, solo tras meses de práctica! Estas reglas nos permiten ver la forma de escribir directamente la derivada de muchas funciones, en especial cuando se representan como series de potencias.
Recordemos, de paso, que antes he comentado que la derivada de x3 es 3x2. Este es un caso particular de una fórmula sencilla pero importante: la derivada de xn es nxn – 1, que podemos escribir
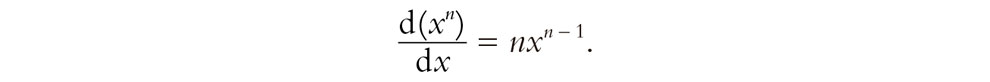
(Nos distraeríamos demasiado si intentara explicar por qué es válida esta fórmula. No es realmente difícil demostrarlo, y el lector interesado puede encontrar todo lo que se necesita en cualquier libro de texto elemental sobre cálculo infinitesimal.[8] Dicho sea de paso, n no tiene por qué ser entero.) También podemos expresar[9] esta ecuación («multiplicando por dx») mediante la fórmula conveniente
d(xn) = nxn – 1dx.
No necesitamos saber mucho más por lo que respecta a la diferenciación de series de potencias. Hay básicamente otras dos cosas. En primer lugar, la derivada de una suma de funciones es la suma de las derivadas de las funciones:
d[f(x) + g(x)] = df(x) + dg(x).
Esto se extiende a una suma de cualquier número finito de funciones.[10] En segundo lugar, la derivada del producto de una función por una constante es el producto de la constante por la derivada de la función:
d{a f(x)} = a df(x).
Por una «constante» entiendo un número que no varía con x. Los coeficientes a0, a1, a2, a3, … en la serie de potencias son constantes. Con estas reglas podemos diferenciar directamente cualquier serie de potencias.[6.5]
Otra manera de expresar la constancia de a es
da = 0.
Teniendo esto en cuenta, encontramos que la regla inmediatamente anterior a esta es realmente un caso especial (con g(x) = a) de la «ley de Leibniz»:
d{f(x) g(x)} = f(x) dg(x) + g(x) df(x)
(y d(xn)/dx = nxn – 1, para cualquier número natural n, también puede obtenerse de la ley de Leibniz).[6.6] Otra ley útil es
d{f(g(x))} = f′(g(x))g′(x)dx.
A partir de las dos últimas y de la primera, poniendo f(x)[g(x)]–1 en la ley de Leibniz, podemos deducir[6.7]
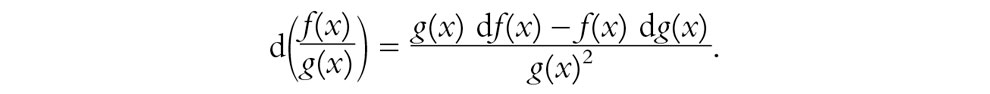
Provisto de estas pocas reglas (y muchísima práctica), uno puede convertirse en un «experto en diferenciación» sin necesidad de tener mucho conocimiento real de por qué funcionan las reglas. Esta es la potencia que tiene un buen cálculo.[6.8] Además, con el conocimiento de las derivadas de tan solo algunas funciones especiales,[6.9] uno puede convertirse en un experto aún mayor. Solo para que el lector no iniciado pueda convertirse en un «miembro al instante» del club de diferenciadores expertos, permítanme dar los ejemplos principales:[11],[6.10]

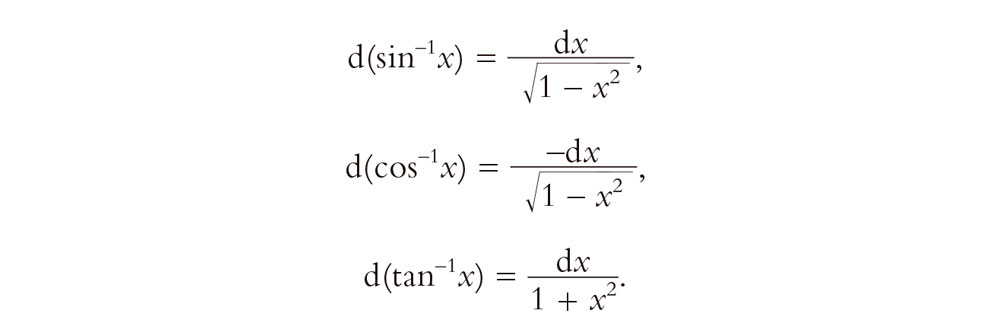
Esto ilustra el punto mencionado al principio de esta sección según el cual, cuando se nos dan fórmulas explícitas, la operación de diferenciación es «fácil». Por supuesto, con ello no quiero decir que sea algo que uno pueda hacer mientras duerme. De hecho, en ejemplos concretos, puede darse el caso de que se obtengan expresiones realmente muy complicadas. Cuando digo «fácil», quiero decir que hay un procedimiento computacional explícito para llevar a cabo la diferenciación. Si sabemos cómo diferenciar cada uno de los ingredientes de una expresión, entonces los procedimientos del cálculo, como los dados antes, nos dicen cómo llegar a diferenciar la expresión completa. «Fácil», aquí significa en realidad algo que podría ser programado directamente en un computador. Pero las cosas son muy diferentes si tratamos de ir en dirección inversa.
6.6. INTEGRACIÓN
Como se ha afirmado al principio de esta sección, la integración es la operación inversa de la diferenciación. Esto equivale a tratar de encontrar una función g(x) para la que g′(x) = f(x), i.e., encontrar una solución y = g(x) a la ecuación dy/dx = f(x). Otra forma de decirlo es que en lugar de bajar de una imagen a otra en la Fig. 6.4 (o 6.5), tratamos de hacer nuestro camino hacia arriba. La belleza del «teorema fundamental del cálculo infinitesimal» reside en que este procedimiento nos está diciendo cómo calcular las áreas bajo cada curva sucesiva. Echemos una ojeada a la Fig. 6.8. Recordemos que la curva inferior u = f(x) puede obtenerse a partir de la curva superior y = g(x) porque representa las pendientes de esta curva, al ser f(x) la derivada de g(x). Esto es precisamente lo que teníamos antes. Pero empecemos ahora con la curva inferior. Encontramos que la curva superior simplemente expresa las áreas que hay bajo la curva inferior. De forma un poco más explícita: si en la imagen inferior tomamos dos rectas verticales dadas por x = a y x = b, respectivamente, entonces el área limitada por estas dos rectas, el eje x y la propia curva, será la diferencia entre las alturas de la curva superior en esos dos valores de x. Por supuesto, en cuestiones como estas debemos tener cuidado con los «signos». En las regiones donde la curva inferior está por debajo del eje x, las áreas cuentan negativamente. Además, en la imagen he tomado a < b y la «diferencia entre las alturas» de la curva superior en la forma g(b) – g(a). Los signos se invertirían si a > b.
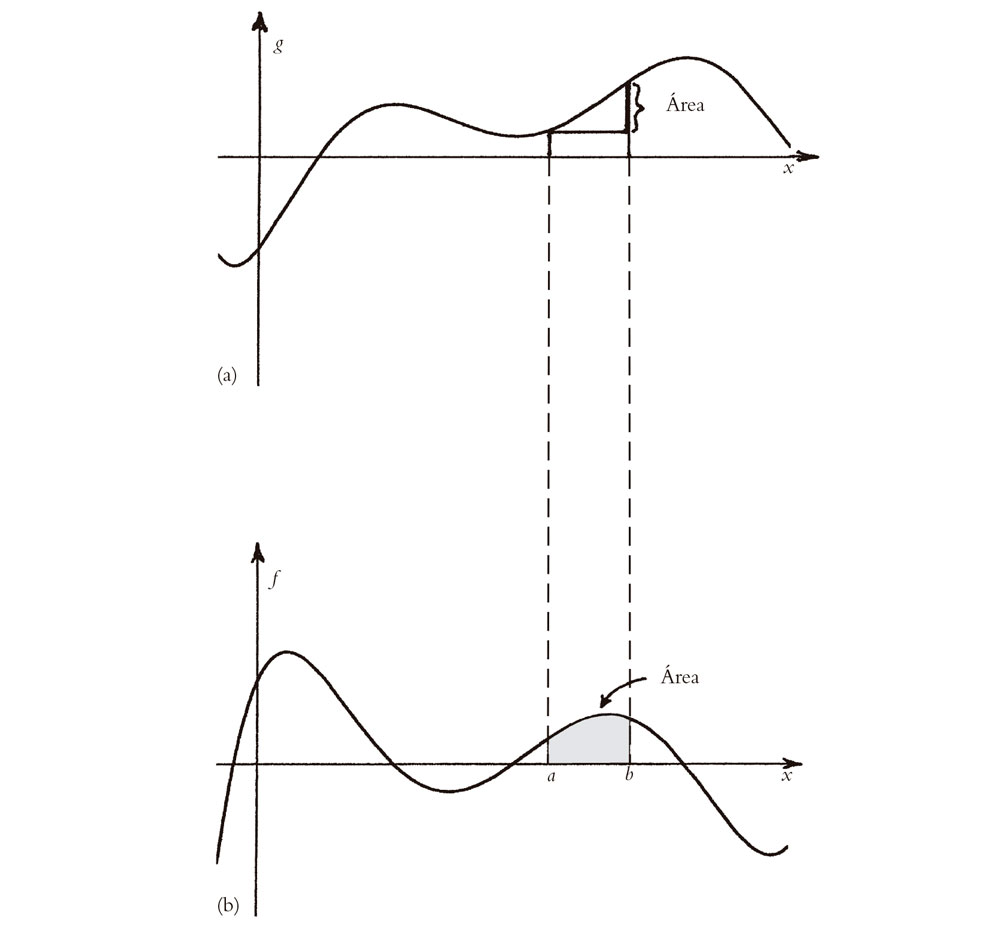
Fig. 6.8. Teorema fundamental del cálculo: reinterpretamos la Fig. 6.4a,b, procediendo hacia arriba y no hacia abajo. La curva superior (a) representa las áreas bajo la curva inferior (b), donde el área limitada por dos líneas verticales x = a y x = b, el eje x y la curva inferior es la diferencia g(b) – g(a) de alturas de la curva superior en esos dos valores de x (teniendo en cuenta los signos).
En la Fig. 6.9 he tratado de hacer intuitivamente creíble por qué existe esta relación inversa entre pendientes y áreas. Imaginemos que b sea mayor que a tan solo en una minúscula cantidad. Entonces, el área a considerar, en la imagen inferior, es el área de la franja muy estrecha limitada por las rectas vecinas x = a y x = b. La medida de esta área es esencialmente el producto de la anchura minúscula de la franja (i.e., b – a) por su altura (desde el eje x a la curva). Pero se supone que la altura de la franja está midiendo la pendiente de la curva superior en dicho punto. Por lo tanto, el área de la franja es esta pendiente multiplicada por la anchura de la franja. Pero la pendiente de la curva superior multiplicada por la anchura de la franja es la cantidad en que aumenta la curva superior desde a a b, es decir, la diferencia g(b) – g(a). Así pues, para franjas muy estrechas, el área está medida realmente por esta diferencia. Las franjas más anchas se consideran construidas a partir de grandes números de franjas estrechas, y obtenemos el área total midiendo cuánto aumenta la curva superior en el intervalo completo.
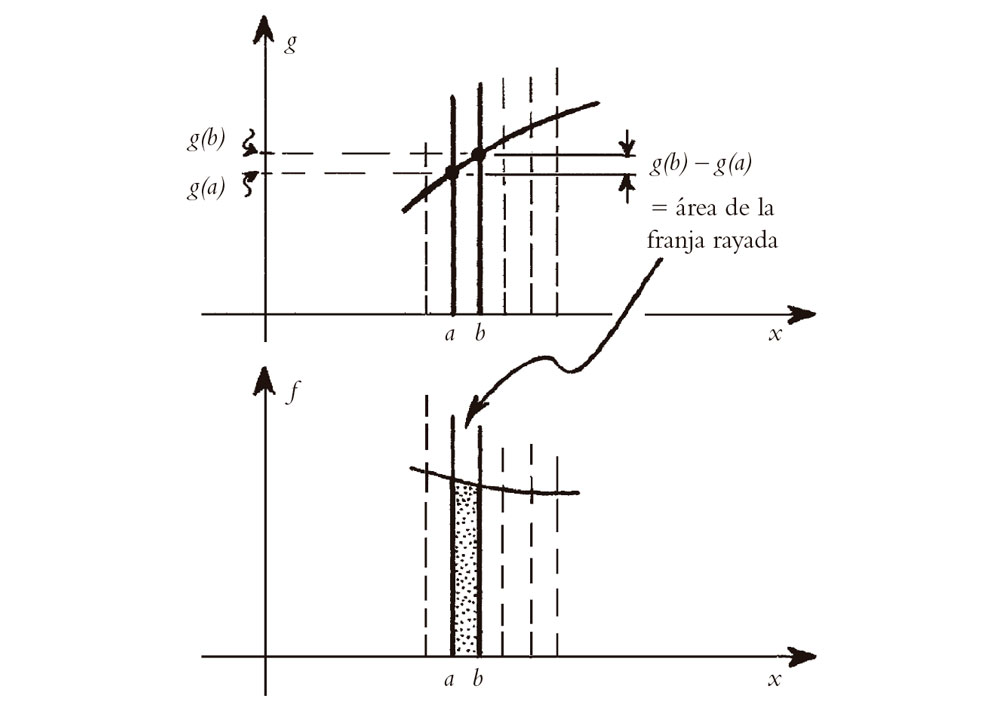
Fig. 6.9. Tómese b > a en una cantidad minúscula. En la imagen inferior, el área de una franja muy estrecha entre líneas vecinas x = a, x = b es esencialmente el producto de la anchura de la franja b – a por su altura (del eje x a la curva). Esta altura es la pendiente de la curva superior, de donde el área de la franja es esta pendiente × la anchura de la franja, que es la cantidad en que crece la curva superior de a a b, i.e., g(b) – g(a). Sumando muchas franjas estrechas, encontramos que el área de una franja ancha bajo la curva inferior es la cantidad correspondiente en que aumenta la curva superior.
Aquí hay un punto importante que debería sacar a colación. En el paso desde la curva inferior a la curva superior hay una no unicidad en lo que respecta a la altura a que debe situarse globalmente la curva superior. Solo estamos interesados en diferencias entre alturas en la curva superior, de modo que desplazar la curva hacia arriba o hacia abajo en una cantidad constante no supone ninguna diferencia. Esto también queda claro por la interpretación de la «pendiente», puesto que la pendiente en puntos diferentes de la curva superior será exactamente la misma si la desplazamos hacia arriba o hacia abajo. Esto equivale, en nuestro cálculo, a que si sumamos una constante C a g(x), entonces la diferenciación de la función resultante sigue dando f(x):
d(g(x) + C) = dg(x) + dC = f(x) dx + 0 = f(x) dx.
Una función semejante g(x), o equivalentemente g(x) + C para una constante arbitraria C, se denomina integral indefinida de f(x), y escribimos
 f(x) dx = g(x) + const.
f(x) dx = g(x) + const.
Esta es solo otra forma de expresar la relación d[g(x) + const.] = f(x) dx, de modo que simplemente consideramos el signo «∫» como el inverso del símbolo «d». Si queremos especificar el área entre x = a y x = b, entonces queremos lo que se denomina la integral definida, y escribimos
 f(x) dx = g(b) – g(a).
f(x) dx = g(b) – g(a).
Si conocemos la función f(x) y queremos obtener su integral g(x), apenas tenemos reglas tan directas para obtenerla como las teníamos para la diferenciación. Se conocen muchos trucos, varios de los cuales pueden hallarse en los libros de texto estándar y en los paquetes informáticos, pero no bastan para tratar todos los casos. De hecho, con frecuencia encontramos que hay que ampliar la familia de funciones estándar explícitas que habíamos estado utilizando previamente, e «inventar» nuevas funciones para expresar los resultados de la integración. En efecto, ya hemos visto esto en los ejemplos especiales que se han dado antes. Supongamos que estuviéramos familiarizados solo con funciones construidas a partir de combinaciones de potencias de x. En el caso de una potencia general xn, podemos integrarla para obtener xn + 1/(n + 1). (Esto es simplemente utilizar nuestra fórmula anterior, en §6.5, con n + 1 en lugar de n: d(xn + 1)/dx = (n + 1)xn.) Todo va bien hasta que nos preocupamos por lo que hay que hacer en el caso n = –1. Entonces, la supuesta respuesta xn + 1/(n + 1) tiene un cero en el denominador, de modo que esto no funciona. ¿Cómo integramos entonces x–1? Bien, notemos que, por la mayor de las fortunas, en nuestra lista existe la fórmula d(log x) = x–1 dx. De modo que la respuesta es log x + const.
¡Esta vez hemos tenido suerte! Sencillamente, ya habíamos estudiado antes la función logaritmo por una razón diferente, y conocíamos algunas de sus propiedades. Pero en otras ocasiones bien podríamos encontrarnos con que no hay ninguna función previamente conocida y en cuyos términos pudiéramos expresar nuestra respuesta. En realidad, a menudo las integrales proporcionan los medios adecuados por los que se definen nuevas funciones. En este sentido, dicha integración explícita es «difícil».
Por el contrario, si no estamos tan interesados en expresiones explícitas sino más bien en cuestiones de existencia de funciones que son las derivadas o integrales de funciones dadas, entonces las cosas cambian. La integración es ahora la operación que funciona suavemente y la diferenciación la que causa problemas. Lo mismo es válido cuando se realizan estas operaciones con datos numéricos. Básicamente, el problema con la diferenciación reside en que depende de forma muy crítica de los detalles finos de la función que va a ser diferenciada. Esto puede presentar un problema si no tenemos una expresión explícita para la función que tiene que ser diferenciada. La integración, por el contrario, es relativamente insensible a tales cuestiones, al estar interesada en la naturaleza global de la función que va a integrar. De hecho, cualquier función continua (una C0-función) cuyo dominio es un intervalo «cerrado» a ≤ x ≥ b puede ser integrada,[12] y el resultado es una función C1 (i.e., C1-suave). Esta puede ser integrada de nuevo, siendo el resultado C2, y luego una vez más, dando una función C3-suave, y así sucesivamente. La integración hace las funciones cada vez más suaves, y podemos continuar así indefinidamente. La diferenciación, por el contrario, solo empeora las cosas, y puede llegar a un final en cierto punto, donde la función se hace «no diferenciable».
Pese a todo, existen enfoques de estas cuestiones que hacen posible que el proceso de diferenciación se continúe también indefinidamente. Ya he insinuado esto cuando me he permitido diferenciar la función |x| para obtener θ(x), incluso si |x| es «no diferenciable». Podríamos intentar ir más lejos y diferenciar también θ(x), pese al hecho de que tiene una pendiente infinita en el origen. La «respuesta» es lo que se denomina una función delta de Dirac:[13] una entidad de enorme importancia en las matemáticas de la mecánica cuántica. En realidad, la función delta no es una función en absoluto, en el sentido ordinario (moderno) de «función» que aplica espacios dominio en espacios imagen. No hay ningún «valor» para la función delta en el origen (donde solo podría haber sido infinita) y es cero en los demás lugares. Pese a todo, la función delta encuentra una definición matemática clara dentro de varias clases más amplias de entidades matemáticas, de las que las distribuciones son las mejor conocidas.
Para esto tenemos que extender nuestra noción de Cn-funciones a casos en los que n puede ser un entero negativo. La función θ(x) es entonces una C–1-función y la función delta es C–2. Cada vez que diferenciamos, debemos disminuir en una unidad la clase de diferenciabilidad (i.e., la clase se hace más negativa en una unidad). Parecería que con todo esto nos estamos alejando cada vez más de la noción de Euler de una «función decente», y que él se negaría a tener ningún trato con cosas semejantes si no fuera por el hecho de que parecen ser útiles. Pese a todo, encontraremos, a su debido tiempo, que es aquí donde los números complejos nos sorprenden con una ironía, ¡una ironía que se expresa en una de sus mayores hazañas mágicas! Tendremos que esperar hasta el final del capítulo 9 para ser testigos de esta hazaña, pues no es algo que pueda describirse ahora adecuadamente. El lector debe seguir conmigo durante un rato, pues primero hay que preparar el terreno, pavimentado con otros ingredientes de soberbia magia.
Notas
Sección 6.1
6.1. Aquí estoy cometiendo un pequeño «abuso de notación», pues técnicamente x2, por ejemplo, denota el valor de la función más que la función. La propia función aplica x en x2 y podría denotarse por x  x2, o por λx[x2], según el cálculo lambda de Alonzo Church (1941); véase el capítulo 2 de Penrose (1989).
x2, o por λx[x2], según el cálculo lambda de Alonzo Church (1941); véase el capítulo 2 de Penrose (1989).
6.2. En esta sección me referiré a menudo a las opiniones que Euler podría haber tenido con respecto a la idea de función. Sin embargo, debería dejar claro que el «Euler» al que me estoy refiriendo es en realidad un individuo hipotético o idealizado. No tengo ninguna información directa acerca de cuáles podrían haber sido los puntos de vista del Leonhard Euler real en cualquier caso concreto. Pero las opiniones que estoy atribuyendo a mi «Euler» no parecen estar muy alejadas del tipo de opiniones que el Euler real podría haber expresado. Para más información sobre Euler, véanse Boyer (1968), Thiele (1982) y Dunham (1999).
Sección 6.2
6.3. Para más detalles, véase Burkill (1962).
6.4. Estrictamente hablando, es la función f′ la que es la derivada de la función f; no podemos obtener el valor de f′ en x simplemente a partir del valor de f en x. Véase la nota 6.1.
Sección 6.3
6.5. Viz., f″(x)/[1 + f′(x)2]3/2.
6.6. De hecho, esto implica que todas las derivadas hasta la n-ésima, esta incluida, deben ser continuas, porque la definición técnica de diferenciabilidad requiere continuidad.
Sección 6.4
6.7. Tradicionalmente, este desarrollo en serie de potencias en torno al origen se conoce (con poca justificación histórica) como serie de Maclaurin; el resultado más general en torno al punto p (véase más adelante en la sección) se atribuye a Brook Taylor (1685-1731).
Sección 6.5
6.8. Véase Edwards y Penney (2002).
6.9. Por el momento, trate solo formalmente las siguientes expresiones, o si no «divida por dx» mentalmente si eso le hace más feliz. La notación que estoy utilizando aquí es compatible con la de las formas diferenciales, que se discutirán en §§12.3-6.
6.10. Sin embargo, hay una sutileza técnica en la aplicación de esta ley a la suma del número infinito de términos que necesitamos para una serie de potencias. Esta sutileza puede ignorarse para valores de x estrictamente dentro del círculo de convergencia; véase §4.4. Véase también Priestley (2003).
6.11. Recordemos de §5.1 que sen–1, cos–1 y tan–1 son las funciones inversas de sen, cos y tan, respectivamente. Así, sen (sen–1 x) = x, etc. No obstante, debemos tener en cuenta que estas funciones inversas son «funciones multivaluadas», y es habitual seleccionar los valores para los cuales
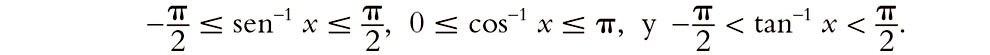
Sección 6.6
6.12. El requisito importante sobre el dominio es que sea lo que se denomina compacto; véase §12.6. Los intervalos finitos de la recta real que incluyen sus puntos extremos son, de hecho, compactos.
6.13. Al parecer, Oliver Heaviside también había concebido la «función delta» muchos años antes que Dirac.