5
Geometría de logaritmos, potencias y raíces
5.1. LA GEOMETRÍA DEL ÁLGEBRA COMPLEJA
Los aspectos de la magia de los números complejos discutidos al final del capítulo anterior implican muchas sutilezas, de modo que retrocedamos un poco y consideremos algunos otros fragmentos de magia más elementales aunque igualmente enigmáticos e importantes. En primer lugar, veamos cómo se representan geométricamente en el plano complejo las reglas para la suma y la multiplicación que encontramos en §4.1. Podemos presentarlas como la ley del paralelogramo y la ley del triángulo semejante, respectivamente, que se muestran en la Fig. 5.1a,b. En concreto, para dos números complejos generales w y z, los puntos que representan w + z y wz vienen determinados por las afirmaciones respectivas:
los puntos 0, w, w + z, z son los vértices de un paralelogramo
y
los triángulos con vértices 0, 1, w y 0 z, wz son semejantes.
(Aquí se han adoptado los convenios usuales sobre ordenamientos y orientaciones. Por eso, entiendo que recorremos el paralelogramo cíclicamente, de modo que el segmento de recta que va de w a w + z es paralelo al que va de 0 a z, etc.; más aún, la relación de semejanza entre los dos triángulos no incluye «reflexión». Además, hay casos especiales en que los triángulos y el paralelogramo degeneran de varias maneras.)[5.1] El lector interesado puede comprobar estas reglas por trigonometría y cálculo directo.[5.2] Sin embargo, hay otra manera de considerar estas cosas que evita el cálculo detallado y proporciona intuiciones mayores.
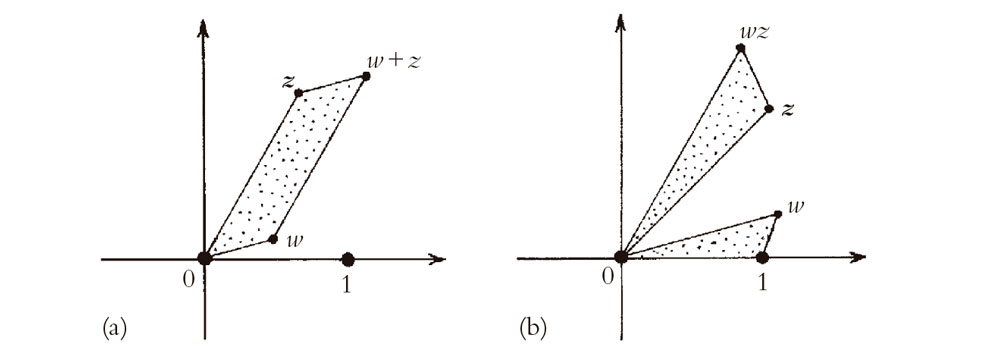
Fig. 5.1. Descripción geométrica de las leyes básicas del álgebra de los números complejos. (a) Ley del paralelogramo de la adición: 0, w, w + z, z dan los vértices de un paralelogramo. (b) Ley del triángulo semejante de la multiplicación: los triángulos con vértices 0, 1, w y 0, z, wz son semejantes.
Consideremos la suma y la multiplicación en términos de diferentes aplicaciones (o «transformaciones») que aplican el plano complejo entero en sí mismo. Cualquier número complejo w dado define una «aplicación suma» y una «aplicación multiplicación», que son las operaciones que, cuando se aplican a un número complejo arbitrario z, sumarán w a z y harán el producto de w por z, respectivamente, i.e.,
z  w + z y z
w + z y z  wz.
wz.
Es fácil ver que la aplicación suma desliza simplemente el plano complejo sin rotación ni cambio de tamaño o forma —un ejemplo de una traslación (véase §2.1)— desplazando el origen 0 al punto w; véase la Fig. 5.2a. La ley del paralelogramo es básicamente una reformulación de esto. Pero ¿qué pasa con la aplicación multiplicación? Esta proporciona una transformación que deja el origen fijo y conserva las formas —y que envía 1 al punto w—. En el caso general combina una rotación con una dilatación (o contracción) uniforme; véase la Fig. 5.2b.[5.3] La ley del triángulo semejante muestra esto de modo efectivo. Esta aplicación tendrá una especial importancia para nosotros en §8.2.
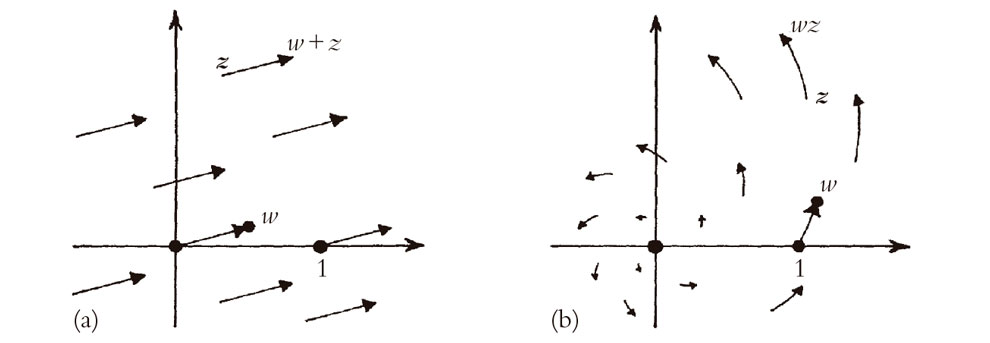
Fig. 5.2. (a) La aplicación suma «+w» proporciona una traslación del plano complejo, que envía 0 a w. (b) La aplicación multiplicación «×w» proporciona una rotación y dilatación (o contracción) del plano complejo en torno a 0, que envía 1 a w.
En el caso particular w = i, la aplicación multiplicación es simplemente una rotación a izquierdas (i.e., en sentido contrario a las agujas del reloj) de un ángulo recto  . Si aplicamos esta operación dos veces, obtenemos una rotación de π, que es simplemente una reflexión respecto al origen; en otras palabras, es la aplicación multiplicación que hace corresponder a cada número complejo z su negativo. Esto nos proporciona una realización gráfica de la «misteriosa» ecuación i2 = –1 (Fig. 5.3). La operación «multiplicar por i» queda realizada como la transformación geométrica «rotar un ángulo recto». Visto de este modo, no parece tan misterioso que el «cuadrado» de esta operación (i.e., hacerla dos veces) produzca el mismo efecto que la operación de «tomar el negativo». Por supuesto, esto no elimina la magia y el misterio de por qué el álgebra compleja funciona tan bien, ni nos habla de un papel físico claro para estos números. Podríamos preguntarnos, por ejemplo: ¿por qué rotar solo en un plano? ¿Qué pasa en tres dimensiones? Más adelante abordaré diferentes aspectos de esta cuestión, especialmente en §§11.2,3, §18.5, §§21.6,9, §§22.2,3,8-10, §33.2 y §34.8.
. Si aplicamos esta operación dos veces, obtenemos una rotación de π, que es simplemente una reflexión respecto al origen; en otras palabras, es la aplicación multiplicación que hace corresponder a cada número complejo z su negativo. Esto nos proporciona una realización gráfica de la «misteriosa» ecuación i2 = –1 (Fig. 5.3). La operación «multiplicar por i» queda realizada como la transformación geométrica «rotar un ángulo recto». Visto de este modo, no parece tan misterioso que el «cuadrado» de esta operación (i.e., hacerla dos veces) produzca el mismo efecto que la operación de «tomar el negativo». Por supuesto, esto no elimina la magia y el misterio de por qué el álgebra compleja funciona tan bien, ni nos habla de un papel físico claro para estos números. Podríamos preguntarnos, por ejemplo: ¿por qué rotar solo en un plano? ¿Qué pasa en tres dimensiones? Más adelante abordaré diferentes aspectos de esta cuestión, especialmente en §§11.2,3, §18.5, §§21.6,9, §§22.2,3,8-10, §33.2 y §34.8.
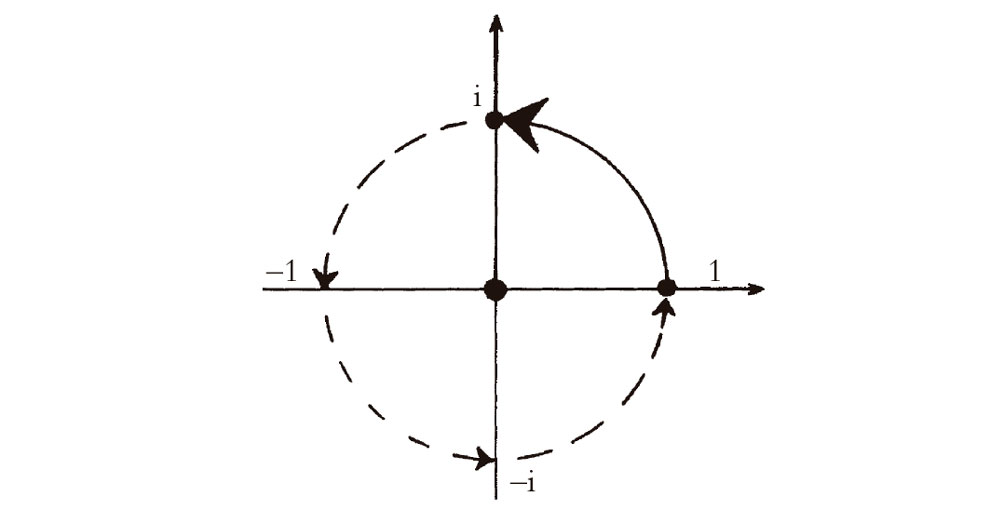
Fig. 5.3. La operación concreta «multiplicar por i» se realiza, en el plano complejo, como la transformación geométrica «rotar un ángulo recto». Se visualiza la «misteriosa» ecuación i2 = –1.
En nuestra descripción de un número complejo en el plano utilizábamos las coordenadas cartesianas estándar (x, y) para un punto en el plano, pero alternativamente podríamos utilizar las coordenadas polares [r, θ]. Aquí, el número real positivo r mide la distancia al origen y θ mide el ángulo que forma la recta que une el origen y el punto z con el eje real, medido dicho ángulo en sentido contrario a las agujas del reloj; véase la Fig. 5.4a. La cantidad r se conoce como el módulo del número complejo z, que solemos escribir como
r = |z|,
y θ como su argumento (o, en teoría cuántica, se conoce a veces como su fase). En el caso z = 0, no tenemos que preocuparnos por θ, pero podemos seguir definiendo r como la distancia al origen, que en este caso da simplemente r = 0.
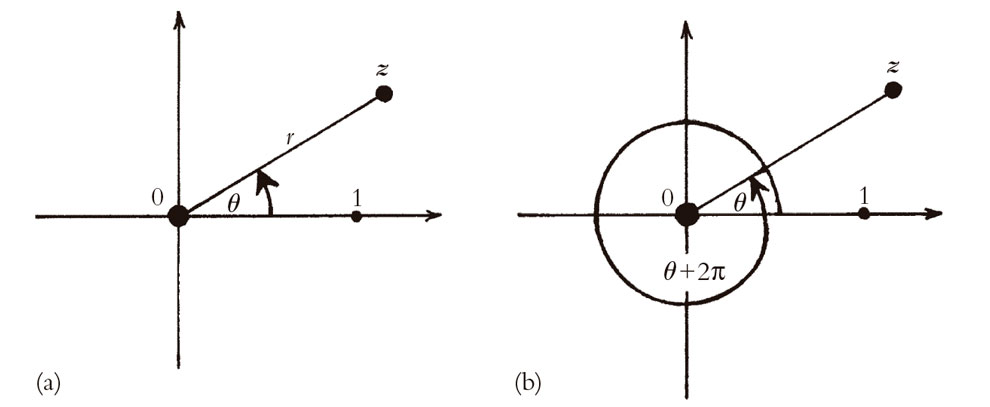
Fig. 5.4. (a) Al pasar de cartesianas (x, y) a polares [r,θ], tenemos z = x + iy = reiθ, el módulo r = |z| es la distancia al origen y el argumento θ es el ángulo que forma la recta que va del origen a z con el eje real, medido en sentido contrario a las agujas del reloj. (b) Si no insistimos en –π > θ ≤ π, podemos permitir que z dé muchas vueltas alrededor del origen, sumando cualquier múltiplo entero de 2π a θ.
Para ser más precisos, podríamos insistir en que θ esté comprendido en un intervalo concreto, tal como –π < θ ≤ π (que es el convenio estándar). Alternativamente, podemos considerar simplemente el argumento como algo con la ambigüedad de que está permitido añadirle múltiplos enteros de 2π sin que nada se vea afectado. Se trata solo de que, cuando medimos el ángulo, podemos dar tantas vueltas alrededor del origen como queramos y en cualquier sentido (véase la Fig. 5.4b). (Este segundo punto de vista es en realidad el más profundo, y enseguida tendrá algunas implicaciones para nosotros.) A partir de la Fig. 5.5 y la trigonometría elemental, vemos que
x = r cos θ e y = r sen θ,
y recíprocamente que

donde θ = tan–1(y/x) significa un valor concreto de la función multivaluada tan–1. (Para aquellos lectores que han olvidado la trigonometría, las dos primeras fórmulas simplemente reexpresan las definiciones del seno y el coseno de un ángulo en términos de un triángulo rectángulo: «el coseno de un ángulo es igual al lado adyacente dividido por la hipotenusa» y «el seno de un ángulo es igual al lado opuesto dividido por la hipotenusa», siendo r la hipotenusa; las dos siguientes expresan el teorema de Pitágoras y, en forma inversa, «la tangente de un ángulo es igual al lado opuesto dividido por el lado adyacente». Asimismo, habría que advertir que «tan–1» es la función inversa de «tan», y no el recíproco, de modo que la ecuación anterior θ = tan–1(y/x) representa tan θ = y/x. Finalmente, existe una ambigüedad en tan–1, pues puede añadirse a θ cualquier múltiplo entero de 2π y la relación seguirá siendo válida.)[1]
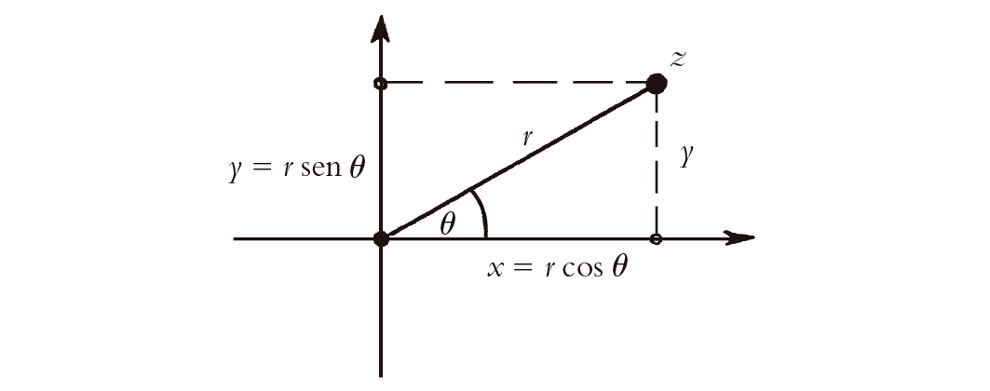
Fig. 5.5. Relación entre las formas cartesiana
y polar de un número complejo: x = r cos θ, e y = r sen θ, donde recíprocamente r = 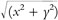 y θ = tan–1(y/x).
y θ = tan–1(y/x).
5.2. LA IDEA DEL LOGARITMO COMPLEJO
Ahora, la «ley del triángulo semejante» de la multiplicación de dos números complejos, que se ilustra en la Fig. 5.1b, puede reexpresarse en términos del hecho de que cuando multiplicamos dos números complejos sumamos sus argumentos y multiplicamos sus módulos.[5.4] Adviértase aquí el hecho notable de que, por lo que respecta a la regla para los argumentos, hemos convertido la multiplicación en suma. En esto se basa el uso de los logaritmos (el logaritmo del producto de dos números es igual a la suma de sus logaritmos: log ab = log a + log b), como se manifiesta en la regla de cálculo (Fig. 5.6), y esta propiedad fue de fundamental importancia para la práctica del cálculo en épocas anteriores.[2] Ahora utilizamos calculadoras electrónicas que hacen las multiplicaciones por nosotros. Aunque esto es mucho más rápido y más exacto que el uso de una regla de cálculo o de unas tablas de logaritmos, perdemos algo muy importante para nuestra comprensión si no extraemos ninguna experiencia directa de la bella y muy importante operación logarítmica. Veremos que los logaritmos desempeñan un papel profundo en relación con los números complejos. De hecho, el argumento de un número complejo es realmente un logaritmo, en un sentido muy claro. Trataremos de entender cómo se produce esto.
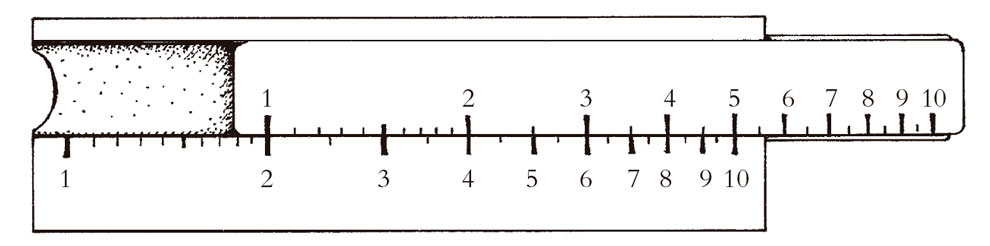
Fig. 5.6. Las reglas de cálculo muestran números en una escala logarítmica, posibilitando con ello que la multiplicación se exprese por la suma de distancias, de acuerdo con la fórmula logb(p × q) = logb p + logbq. (Se ilustra la multiplicación por 2.)
Recordemos también que en §4.2 he afirmado que tomar raíces de números complejos es básicamente una cuestión de comprender los logaritmos complejos. Encontraremos que existen algunas relaciones sorprendentes entre logaritmos complejos y trigonometría. Tratemos de ver cómo se combinan todas estas cosas.
En primer lugar, recordemos algo sobre los logaritmos ordinarios. Tomar un logaritmo es la operación inversa de «elevar un número a una potencia», o de la exponenciación. «Elevar a una potencia» es una operación que convierte suma en multiplicación. ¿Por qué es esto? Tomemos cualquier número b. Notemos entonces la fórmula (que convierte suma en multiplicación)
bm + n = bm × bn,
que es obvia si m y n son enteros positivos, porque cada miembro representa simplemente m + n copias del número b, todas ellas multiplicadas. Lo que tenemos que hacer es encontrar una manera de generalizar esto de modo que m y n no tengan que ser enteros positivos, sino que puedan ser números complejos cualesquiera. Para ello necesitamos encontrar la definición correcta de «b elevado a la potencia z», para z complejo, y queremos que la misma fórmula anterior, a saber b(w + z) = bw × bz, sea válida cuando los exponentes w y z son complejos.
De hecho, el procedimiento para hacer esto refleja, en cierta medida, la historia misma de generalizar, paso a paso, desde los enteros positivos a los números complejos, como se hizo, partiendo de Pitágoras, por la obra de Eudoxo, pasando por Brahmagupta, hasta llegar a la época de Cardano y Bombelli (y más tarde), tal como se ha indicado en §3.4 y §4.1. Primero, la noción de «bz» es inicialmente entendida cuando z es un número positivo, simplemente como b × b × b × … × b, con z b’s multiplicadas; en particular, b1 = b. Luego (siguiendo a Brahmagupta, permitimos que z sea cero, advirtiendo que para conservar b(w + z) = = bw × bz tenemos que definir b0 = 1. A continuación permitimos que z sea negativo, y advertimos, por la misma razón, que para el caso z = –1 debemos definir b–1 como el recíproco de b (i.e., 1/b), y que b–n para un número natural n debe ser la n-ésima potencia de b–1. Luego tratamos de generalizar a situaciones en que z es una fracción, empezando con el caso z = 1/n, donde z es un entero positivo. La aplicación repetida de bw × bz = b(w + z) nos lleva a concluir que (bz)n = bzn; así pues, haciendo z = 1/n, llegamos a que b1/n es una raíz n-ésima de b.
Podemos hacer esto dentro del dominio de los números reales, con tal de que el número b se haya tomado positivo. Entonces podemos tomar b1/n como la única raíz n-ésima positiva de b (cuando n es un entero positivo) y podemos continuar definiendo unívocamente bz para cualquier número racional z = m/n como la m-ésima potencia de la raíz n-ésima de b y de aquí pasar (utilizando un proceso de paso al límite) a cualquier número real z. Pero si se permite que b sea negativo, entonces tropezamos con una pega en z = 1/2, puesto que Œ„b requiere entonces la introducción de i y caemos en la pendiente resbaladiza hacia los números complejos. En el fondo de dicha pendiente encontramos nuestro mágico mundo complejo, de modo que agarrémonos y sigamos hasta abajo.
Necesitamos una definición de bp tal que para todos los números complejos p, q y b (con b ≠ 0), tengamos:
bp + q = bp × bq.
Podríamos confiar entonces en definir el logaritmo en base b (la operación denotada por «logb») como la inversa de la función definida por f(z) = bz, es decir,
z = logb w si w = bz.
Entonces esperaríamos
logb(p × q) = logb p + logb q,
de modo que esta noción de logaritmo convertiría realmente la multiplicación en suma.
5.3. MULTIVALUACIÓN, LOGARITMOS NATURALES
Aunque esto es básicamente correcto, hay ciertas dificultades técnicas en hacerlo (y dentro de poco veremos cómo tratarlas). En primer lugar, bz es «multivaluada». Es decir, existen, en general, muchas respuestas diferentes para el significado de «bz». Hay también una multivaluación adicional para logb w. Hemos visto ya la multivaluación de bz con valores fraccionarios de z. Por ejemplo, si z = 1/2, entonces «bz» debería significar «cierta cantidad t cuyo cuadrado es b», puesto que exigimos que t2 = t × t = b × b
× b = b
= b +b
+b = b1 = b. Si un número t satisface esta propiedad, entonces –t también lo hará (puesto que (–t) × (–t) = t2 = b). Suponiendo que b ≠ 0, tenemos dos respuestas distintas para b1/2 (normalmente escritas ±
= b1 = b. Si un número t satisface esta propiedad, entonces –t también lo hará (puesto que (–t) × (–t) = t2 = b). Suponiendo que b ≠ 0, tenemos dos respuestas distintas para b1/2 (normalmente escritas ± 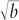 ). Con más generalidad, tenemos n respuestas complejas distintas para b1/n, cuando n es un entero positivo: 1, 2, 3, 4, 5, … De hecho, tenemos un número finito de respuestas cuando quiera que n sea un número racional (no nulo). Si n es irracional, entonces tenemos un número infinito de respuestas, como veremos enseguida.
). Con más generalidad, tenemos n respuestas complejas distintas para b1/n, cuando n es un entero positivo: 1, 2, 3, 4, 5, … De hecho, tenemos un número finito de respuestas cuando quiera que n sea un número racional (no nulo). Si n es irracional, entonces tenemos un número infinito de respuestas, como veremos enseguida.
Tratemos de ver cómo podemos hacer frente a estas ambigüedades. Empezaremos haciendo una elección concreta de b, a saber, el número fundamental «e», conocido como la base de los logaritmos naturales. Esto reducirá nuestro problema de ambigüedad. Tenemos, como definición de e:
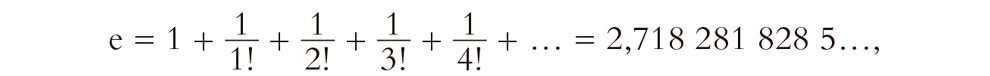
donde los signos de admiración denotan factoriales, i.e.,
n! = 1 × 2 × 3 × 4 × … × n,
de modo que 1! = 1, 2! = 2, 3! = 6, etc. La función definida por f(z) = ez se conoce como función exponencial, y a veces se escribe «exp»; puede considerarse como «e elevado a la potencia z» y esta potencia se define mediante la siguiente modificación sencilla de la serie anterior para e:

Esta importante serie de potencias converge realmente para todos los valores de z (de modo que tiene un círculo de convergencia infinito; véase §4.4). La suma infinita hace una elección particular para la ambigüedad en «bz» cuando b = e. Por ejemplo, si z = 1/2, entonces la serie nos da la cantidad concreta positiva +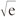 y no –
y no –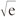 . El hecho de que z = 1/2 dé realmente una cantidad e1/2 cuyo cuadrado es e se sigue del hecho de que ez, definida por esta serie,[5.5] siempre tiene la propiedad requerida «de suma a multiplicación»
. El hecho de que z = 1/2 dé realmente una cantidad e1/2 cuyo cuadrado es e se sigue del hecho de que ez, definida por esta serie,[5.5] siempre tiene la propiedad requerida «de suma a multiplicación»
ea + b = eaeb,
de modo que (e )2 = e
)2 = e e
e = e
= e +
+  = e1 = e.
= e1 = e.
Tratemos de utilizar esta definición de ez para darnos un logaritmo inambiguo, definido como la inversa de la función exponencial:
z = log w si w = ez.
Esto se conoce como el logaritmo natural (y escribiré la función simplemente como «log», sin un símbolo para la base).[3] De la anterior propiedad «de suma a multiplicación», esperamos una regla «de multiplicación a suma»:
log ab = log a + log b.
No es inmediatamente obvio que tal inverso de ez exista necesariamente. Sin embargo, resulta en efecto que para cualquier número complejo w, distinto de 0, siempre existe z tal que w = ez, de modo que podemos definir log w = z. Pero aquí hay una trampa: hay más de una respuesta.
¿Cómo expresamos estas respuestas? Si [r, θ] es la representación polar de w, entonces podemos escribir su logaritmo z en la forma cartesiana habitual (z = x + iy) como
z = log r + iθ,
donde log r es el logaritmo natural ordinario de un número real positivo —la inversa de la exponencial real—. Resulta intuitivamente claro de la Fig. 5.7 que semejante función logarítmica real existe. En la Fig. 5.7a tenemos la gráfica de r = ex. Simplemente intercambiamos los ejes para obtener la gráfica de la función inversa x = log r, como en la Fig. 5.7b. No es tan sorprendente que la parte real de z = log w sea simplemente un logaritmo real ordinario. Lo que es algo más notable[4] es que la parte imaginaria de z es simplemente el ángulo θ, que es el argumento del número complejo w. Este hecho hace explícito mi anterior comentario acerca de que el argumento de un número complejo es realmente una forma de logaritmo.
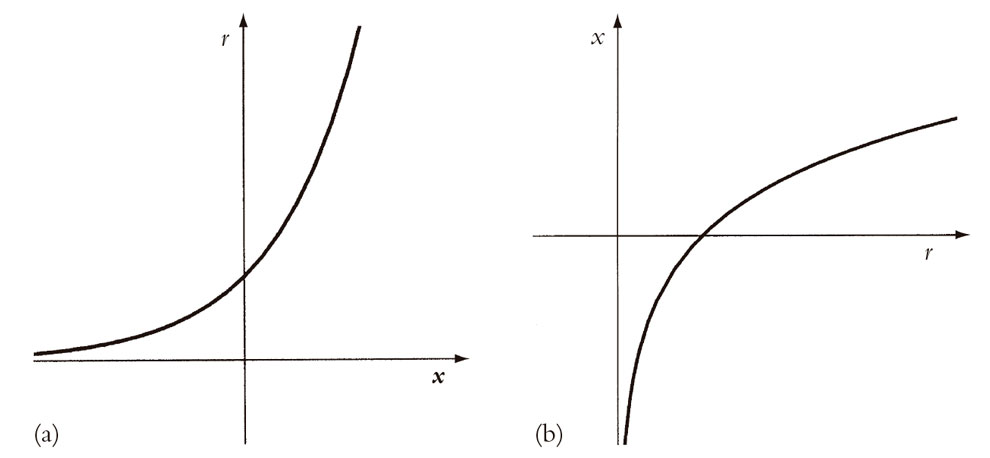
Fig. 5.7. Para obtener el logaritmo de un número real positivo r, consideremos la gráfica (a) de r = ex. Se alcanzan todos los valores positivos de r, de modo que invirtiendo la figura, obtenemos la gráfica (b) de la función inversa x = log r para r positivo.
Recordemos que existe una ambigüedad en la definición del argumento de un número complejo. Podemos añadir a θ cualquier múltiplo entero de 2π, y esto también servirá (recordemos la Fig. 5.4b). En consecuencia, hay muchas soluciones z diferentes para una elección dada de w en la relación w = ez. Si tomamos uno de estos z, entonces z + 2πin es otra posible solución, donde n es cualquier entero que queramos escoger. Así pues, el logaritmo de w es ambiguo en cuanto que está definido salvo la suma de cualquier múltiplo entero de 2πi. Debemos tener esto en cuenta con expresiones tales como log ab = = log a + log b, asegurándonos de que se hacen las correspondientes y adecuadas elecciones de logaritmo.
En esta etapa, esta característica de los logaritmos complejos parece ser solo una incomodidad. Sin embargo, veremos en §7.2 que es absolutamente capital para algunas de las más poderosas, útiles y mágicas propiedades de los números complejos. El análisis complejo depende de ello de forma crucial. Por el momento, tratemos solo de apreciar la naturaleza de la ambigüedad.
Otra forma de entender esta ambigüedad en log w consiste en advertir la sorprendente fórmula
e2πi = 1,
de donde ez + 2πi = ez = w, etc., lo que demuestra que z + 2πi es un logaritmo de w tan bueno como lo es z (y entonces podemos repetir esto tantas veces como queramos). La fórmula anterior está estrechamente relacionada con la famosa fórmula de Euler
eπi + 1 = 0
(que relaciona los cinco números fundamentales 0, 1, i, π y e en una expresión casi mística).[5.6]
Podemos entender mejor estas propiedades si tomamos la exponencial de la expresión z = log r + iθ para obtener
w = ez = elog r + iθ = elog reiθ = reiθ.
Esto demuestra que la forma polar de cualquier número complejo w, que yo había estado denotando hasta ahora por [r, θ], puede escribirse de forma más reveladora como
w = reiθ.
De esta forma, es evidente que si multiplicamos dos números complejos, tomamos el producto de sus módulos y la suma de sus argumentos (reiθseiΦ = rsei(θ +Φ), de modo que r y s se multiplican, mientras que θ y Φ se suman, teniendo en cuenta que restar 2πi de θ + Φ no supone ninguna diferencia), como está implícito en la «ley del triángulo semejante» de la Fig. 5.1b. En lo sucesivo abandonaré la notación [r, θ] y utilizaré en su lugar la expresión mostrada más arriba. Nótese que si r = 1 y θ = π, obtenemos –1 y recuperamos la famosa fórmula de Euler anterior eπi + 1 = 0, utilizando la geometría de la Fig. 5.4a; si r = 1 y θ = 2π, obtenemos +1 y recuperamos eπi = 1.
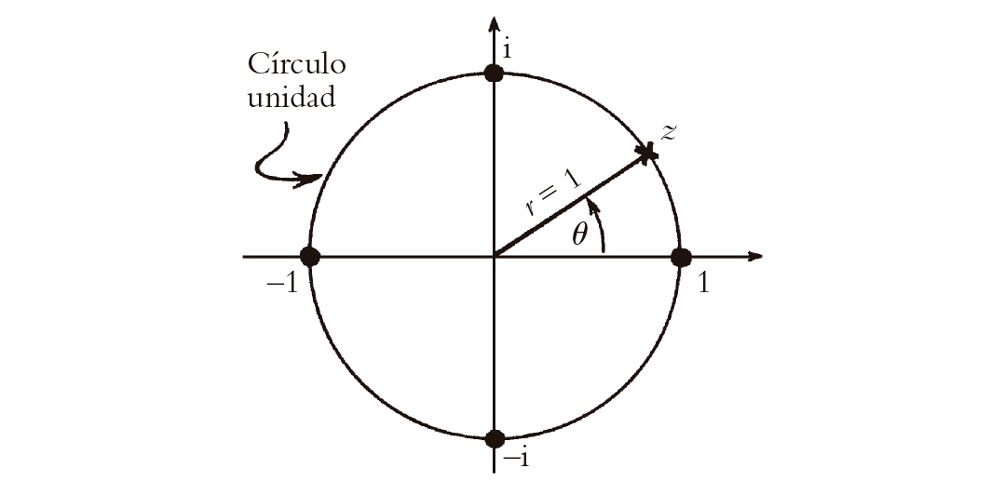
Fig. 5.8. El círculo unidad, que consiste en números complejos de módulo unidad. La fórmula de Cotes-Euler los da como eiθ = cos θ + i sen θ para θ real.
El círculo con r = 1 se denomina el círculo unidad en el plano complejo (véase la Fig. 5.8). Este está dado por w = eiθ para θ real, según la expresión de arriba. Comparando esta expresión con las anteriores x = r cos θ e y = r sen θ dadas arriba para las partes real e imaginaria de lo que ahora es la cantidad w = x + iy, obtenemos la prolífica «fórmula de (Cotes-)Euler»[5]
eiθ = cos θ + i sen θ,
que básicamente engloba los elementos esenciales de la trigonometría en las propiedades mucho más simples de las funciones exponenciales complejas.
Veamos ahora cómo funciona esto en casos elementales. En particular, la relación básica ea + b = eaeb, cuando se desarrolla en términos de partes real e imaginaria, da inmediatamente[5.7] las expresiones de apariencia mucho más complicada (sin duda tristemente familiares para algunos lectores):
cos (a + b) = cos a cos b – sen a sen b,
sen (a + b) = sen a cos b + cos a sen b.
Análogamente, el desarrollo de e3iθ = (eiθ)3, por ejemplo, da rápidamente[6],[5.8]
cos 3θ = cos3 θ – 3 cos θ sen2 θ,
sen 3θ = 3 sen θ cos2 θ – sen3 θ.
Hay realmente magia en la forma directa en que tales fórmulas algo complicadas surgen de sencillas expresiones con números complejos.
5.4. POTENCIAS COMPLEJAS
Volvamos ahora a la cuestión de definir wz (o bz, como hemos escrito previamente). Podemos conseguir esto escribiendo
wz = ez log w
(puesto que esperamos que ez log w = (elog w)z y elog w = w). Pero notemos que, debido a la ambigüedad en log w, podemos añadir a log z cualquier múltiplo entero de 2πi para obtener otra respuesta admisible. Esto significa que podemos multiplicar o dividir cualquier elección particular de wz por ez • 2pi cualquier número de veces y seguimos teniendo un «wz» admisible. Resulta divertido ver la configuración de puntos en el plano complejo que da esto en el caso general. Esto se ilustra en la Fig. 5.9. Los puntos están en las intersecciones de dos espirales equiangulares. (Una espiral equiangular —o logarítmica— es una curva en el plano que forma un ángulo constante con las líneas rectas que irradian de un punto en el plano.)[5.9]
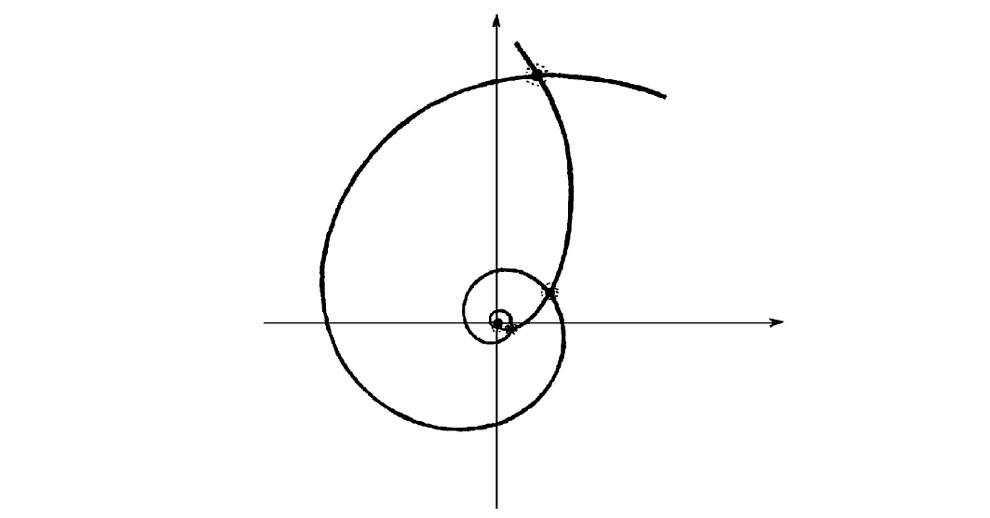
Esta ambigüedad nos lleva a todo tipo de problemas si no tenemos cuidado.[5.10] La mejor forma de evitar tales problemas parece consistir en adoptar la regla de que la notación wz se utilice solo cuando se ha especificado una elección particular de log w. (En el caso especial de ez, el convenio tácito es hacer siempre la elección particular log e = 1. Entonces, la notación estándar ez es consistente con nuestra más general wz.) Una vez que se ha hecho esta elección de log w, entonces wz está definida inequívocamente para todos los valores de z.
Puede comentarse en este punto que también necesitamos una especificación de log b si queremos definir el «logaritmo en base b» mencionado antes en esta sección (la función denotada por «logb»), porque necesitamos un w = bz inequívoco para definir z = logb w. Aun así, logb w será por supuesto multivaluada (como lo era log w), donde podemos sumar a logb w cualquier múltiplo entero de 2πi/log b.[5.11]
Una curiosidad que ha intrigado enormemente a algunos matemáticos en el pasado es la cantidad ii. Podría parecer que «no puede haber nada más imaginario que esto». Sin embargo, encontramos la respuesta real
ii = ei log i = ei •  πi = e–π/2 = 0,207 879 576…,
πi = e–π/2 = 0,207 879 576…,
especificando log i = 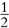 πi.[5.12] Hay también muchas otras respuestas,
πi.[5.12] Hay también muchas otras respuestas,
dadas por las otras especificaciones de log i. Estas se obtienen multiplicando la cantidad anterior por e2πn, donde n es un entero (o, de forma equivalente, elevando la cantidad anterior a cualquier potencia de la forma 4n + 1, donde n es un entero positivo o negativo).[5.13] Es sorprendente que todos los valores de ii son, de hecho, números reales.
Veamos cómo funciona la notación wz para z = 1/2. Esperamos ser capaces de representar las dos cantidades ±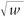 como «w1/2» en algún sentido. De hecho, para obtener estas dos cantidades basta con especificar primero un valor para log w y especificar luego otro, donde sumamos 2πi al primero para obtener el segundo. Esto da lugar a un cambio de signo en w1/2 (debido a la fórmula de Euler eπi = –1). De modo análogo, podemos generar todas las n soluciones zn = w cuando n es 3, 4, 5, … como la cantidad w1/n, cuando se especifican sucesivamente diferentes valores de log w.[5.14] Con más generalidad, podemos volver a la cuestión de las raíces z-ésimas de un número complejo w no nulo que he mencionado en §4.2. Podemos expresar esta raíz z-ésima como la expresión w1/z, y generalmente obtenemos un número infinito de valores alternativos para esto, dependiendo de qué elección de log w se especifique. Con la elección específica correcta para log (w1/z), a saber, la dada por (log w)/z, obtenemos realmente (w1/z)z = w. Notamos, con más generalidad, que
como «w1/2» en algún sentido. De hecho, para obtener estas dos cantidades basta con especificar primero un valor para log w y especificar luego otro, donde sumamos 2πi al primero para obtener el segundo. Esto da lugar a un cambio de signo en w1/2 (debido a la fórmula de Euler eπi = –1). De modo análogo, podemos generar todas las n soluciones zn = w cuando n es 3, 4, 5, … como la cantidad w1/n, cuando se especifican sucesivamente diferentes valores de log w.[5.14] Con más generalidad, podemos volver a la cuestión de las raíces z-ésimas de un número complejo w no nulo que he mencionado en §4.2. Podemos expresar esta raíz z-ésima como la expresión w1/z, y generalmente obtenemos un número infinito de valores alternativos para esto, dependiendo de qué elección de log w se especifique. Con la elección específica correcta para log (w1/z), a saber, la dada por (log w)/z, obtenemos realmente (w1/z)z = w. Notamos, con más generalidad, que
(wa)b = wab,
donde una vez que hemos hecho una especificación de log w (para el segundo miembro), debemos especificar (para el primer miembro) que log (wa) sea a log w.[5.15]
Cuando z = n es un entero positivo, entonces las cosas son mucho más simples, y obtenemos precisamente n raíces. En este caso se da una situación de interés particular cuando w = 1. Entonces, especificando sucesivamente posibles valores de log 1, a saber, 0, 2πi, 4πi, 6πi, … obtenemos 1 = e0, e2πi/n, e4πi/n, e6πi/n, … para los posibles valores de 11/n. Podemos escribirlos como 1, ε, ε2, ε3, … donde ε = e2πi/n. En términos del plano complejo, obtenemos n puntos igualmente espaciados alrededor del círculo unidad, llamados raíces n-ésimas de la unidad. Estos puntos constituyen los vértices de un n-ágono regular (véase la Fig. 5.10). (Nótese que las elecciones –2πi, –4πi, –6πi, etc., para log 1 darían meramente las mismas raíces n-ésimas, en orden inverso.)
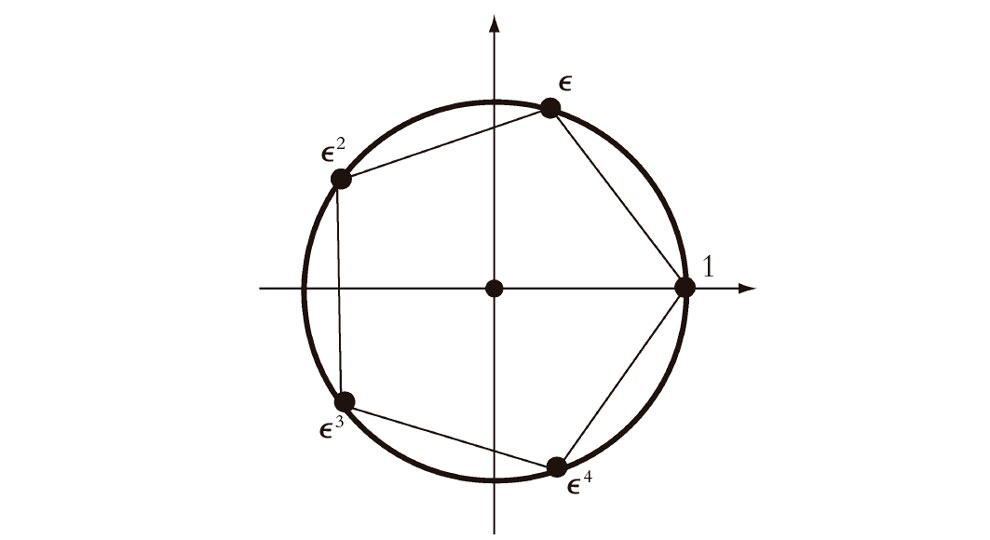
Fig. 5.10. Las raíces n-ésimas de la unidad e2 π ri/n(r = 1, 2, …, n), igualmente espaciadas alrededor del círculo unidad, proporcionan los vértices de un n-ágono regular. Aquí n = 5.
Resulta interesante observar que, para un n dado, las raíces n-ésimas de la unidad constituyen lo que se denomina un grupo multiplicativo finito, más concretamente, el grupo cíclico Zn (véase §13.1). Tenemos n cantidades con la propiedad de que podemos multiplicar dos cualesquiera de ellas y obtener otra. También podemos dividir una por otra para obtener una tercera. Como ejemplo, consideremos el caso n = 3. Ahora obtenemos tres elementos 1, ω y ω2, donde ω = e2πi/3 (de modo que ω3 = 1 y ω–1 = ω2). Tenemos las siguientes tablas simples de multiplicación y división para estos números:
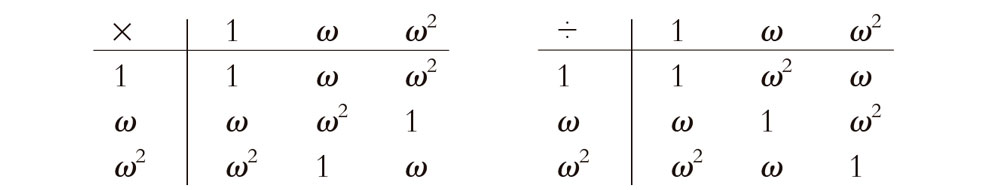
En el plano complejo, estos números concretos están representados como los vértices de un triángulo equilátero. La multiplicación por ω rota el triángulo 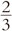 π (i.e., 120°) en sentido contrario a las agujas del reloj, y la multiplicación por ω2 lo rota
π (i.e., 120°) en sentido contrario a las agujas del reloj, y la multiplicación por ω2 lo rota  π en el sentido de las agujas; para la división, la rotación es en sentido opuesto (véase la Fig. 5.11).
π en el sentido de las agujas; para la división, la rotación es en sentido opuesto (véase la Fig. 5.11).
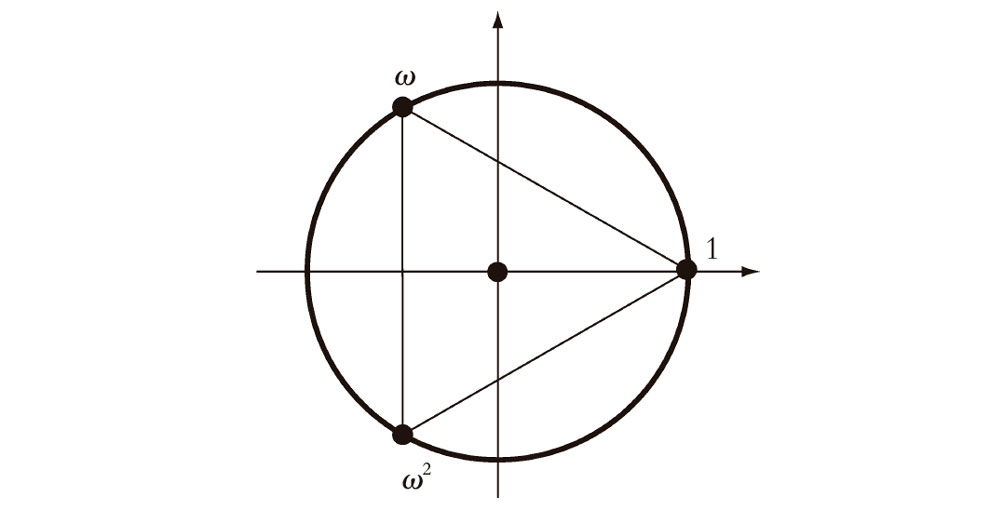
Fig. 5.11. Triángulo equilátero de raíces cúbicas 1, ω y ω2 de la unidad. La multiplicación por ω rota 120° en sentido contrario a las agujas del reloj, y la multiplicación por ω2, en el sentido de las agujas del reloj.
5.5. ALGUNAS RELACIONES CON LA FÍSICA DE PARTÍCULAS MODERNA
Números como estos tienen interés en la moderna física de partículas, pues proporcionan los casos posibles de un número cuántico multiplicativo. En §3.5 he comentado el hecho de que los números cuánticos (escalares) aditivos de la física de partículas están invariablemente cuantificados, hasta donde conocemos, por enteros. Existen también unos pocos ejemplos de números cuánticos multiplicativos, y estos parecen estar cuantificados en términos de las raíces n-ésimas de la unidad. Solo conozco unos pocos ejemplos de tales cantidades en la física de partículas convencional, y en la mayoría de estos la situación es el caso relativamente sin interés n = 2. Hay un caso claro en que n = 3 y posiblemente un caso para el que n = 4. Por desgracia, en la mayoría de los casos el número cuántico no es universal, i.e., no puede aplicarse de forma consistente a todas las partículas. En tales situaciones, me referiré al número cuántico como solo aproximado.
La magnitud física denominada paridad es un número cuántico multiplicativo (aproximado) con n = 2. (Hay también otras magnitudes aproximadas n = 2, similares en muchos aspectos a la paridad, tal como la g-paridad. No las discutiré aquí.) La noción de paridad para un sistema compuesto se construye (multiplicativamente) a partir de las paridades de sus partículas constituyentes básicas. Para una de tales partículas constituyentes, su paridad puede ser par, en cuyo caso la reflexión especular de la partícula es igual que la propia partícula (en un sentido apropiado); alternativamente, su paridad puede ser impar, en cuyo caso su reflexión especular es lo que se denomina su antipartícula (véanse §3.5, §§24.1-3,8 y §26.4). Puesto que la noción de reflexión especular, o de tomar la antipartícula, es algo «cuyo cuadrado es la unidad», i.e., hacerla dos veces nos devuelve al punto de partida, el número cuántico —llamémoslo ε— tiene que tener la propiedad ε2 = 1, de modo que debe ser una «raíz n-ésima de la unidad» con n = 2, i.e., ε = 1 o ε = –1). Esta noción es solo aproximada porque la paridad es una magnitud que no se conserva en las denominadas «interacciones débiles» y, en realidad, quizá no haya una paridad bien definida para ciertas partículas a causa de ello (véanse §§25.3,4).
Además, la noción de paridad se aplica, en las descripciones normales, solo a la familia de partículas conocidas como bosones. Las demás partículas pertenecen a otra familia y se conocen como fermiones. La distinción entre bosones y fermiones es muy importante aunque algo sofisticada, y llegaremos a ella más adelante, en §§23.7,8. (En una de sus manifestaciones, tiene que ver con lo que sucede cuando rotamos de forma continua el estado de la partícula hasta completar un giro de 2π (i.e., 360°). Solo los bosones quedan completamente restaurados en sus estados originales tras una rotación semejante. En el caso de los fermiones habría que hacer dos veces esta rotación. (Véanse §11.3 y §22.8.) Hay un sentido en el que «dos fermiones hacen un bosón», mientras que «dos bosones hacen también un bosón» y «un bosón y un fermión hacen un fermión». Así pues, podemos asignar el número cuántico multiplicativo –1 a un fermión y +1 a un bosón para describir su naturaleza fermión/bosón, y tenemos otro número cuántico multiplicativo con n = 2. Hasta donde se sabe, esta magnitud es un número cuántico multiplicativo exacto.
En mi opinión, hay también una noción de paridad que puede aplicarse a fermiones, aunque no parece que esta sea una terminología convencional. Esta debe combinarse con el número cuántico fermión/bosón para dar un número cuántico combinado multiplicativo con n = 4. Para un fermión, el valor de la paridad tendría que ser +i o –i, y su doble reflexión especular tendría el efecto de una rotación de 2π. Para un bosón, el valor de la paridad sería ±1, como antes.
El número cuántico multiplicativo con n = 3 que he mencionado es a lo que me referiré como quarkedad. (Esta no es una terminología estándar, ni es habitual referirse a este concepto como número cuántico, pero recoge un aspecto importante de nuestro conocimiento actual de la física de partículas.) En §3.5 he mencionado el moderno punto de vista según el cual se supone que las partículas que «interaccionan fuertemente» conocidas como hadrones (protones, neutrones, mesones-π, etc.) están compuestas de quarks (véase §25.6). Estos quarks tienen valores para su carga eléctrica que no son múltiplos enteros de la carga del electrón, sino múltiplos enteros de un tercio de dicha carga. Sin embargo, los quarks no pueden existir como partículas individuales independientes, y sus compuestos solo pueden existir como individuos independientes si la suma de sus cargas es un número entero, en unidades de la carga del electrón. Sea q el valor de la carga eléctrica medida en unidades negativas de la carga del electrón (de modo que para el propio electrón tenemos q = –1, ya que la carga del electrón se cuenta como negativa según el convenio usual). Para los quarks, tenemos q = 2/3 o –1/3; para los antiquarks, q = 1/3 o –2/3. Así pues, si tomamos para la quarkedad el número cuántico multiplicativo e–2qπi, encontramos que toma valores 1, ω y ω2. Para un quark, la quarkedad es ω, y para un antiquark es ω2. Una partícula puede existir independientemente solo si su quarkedad es 1. De acuerdo con §5.4, los grados de quarkedad constituyen el grupo cíclico Z3. (En §16.1 veremos cómo, con un elemento «0» adicional y una noción de suma, este grupo puede extenderse al campo finito F4.)
Tanto en esta sección como en la anterior, he presentado algunos de los aspectos de la magia de los números complejos y he sugerido tan solo algunas de sus aplicaciones. Pero no he mencionado todavía aquellos aspectos de los números complejos (que se verán en el capítulo 7) que a mí personalmente me parecieron los más mágicos de todos cuando los aprendí siendo estudiante de licenciatura en matemáticas. En años posteriores he encontrado aspectos aún más sorprendentes de dicha magia, y uno de estos (descrito al final del capítulo 9) es extrañamente complementario del que más me impresionó siendo estudiante. Estas cosas, sin embargo, dependen de las nociones básicas del cálculo infinitesimal, de modo que para transmitir algo de esto al lector será necesario decir algo sobre ciertas nociones básicas del cálculo. Hay, por supuesto, una razón adicional para hacerlo. ¡El cálculo infinitesimal es esencial para un conocimiento adecuado de la física!
Notas
Sección 5.1
5.1. También deberían señalarse las funciones trigonométricas cot θ = = cos θ/sen θ = (tan θ)–1, sec θ = (cos θ)–1 y cosec θ = (sen θ)–1, así como las versiones «hiperbólicas» de las funciones trigonométricas, senh t =  (et + e–t), cosh t =
(et + e–t), cosh t =  (et – e–t), tanh t = senh t/cosh t, etc. Nótese también que las inversas de estas operaciones se denotan por cot–1, senh–1, etc., como sucede con la «tan–1(y/x)» de §5.1.
(et – e–t), tanh t = senh t/cosh t, etc. Nótese también que las inversas de estas operaciones se denotan por cot–1, senh–1, etc., como sucede con la «tan–1(y/x)» de §5.1.
Sección 5.2
5.2. Los logaritmos fueron introducidos en 1614 por John Neper (Napier) y utilizados con fines prácticos por Henri Briggs en 1624.
Sección 5.3
5.3. Los logaritmos naturales también se escriben habitualmente como «ln».
5.4. De lo que hemos establecido hasta aquí, no podemos inferir que «iθ» en la fórmula z = log r + iθ no debería ser un múltiplo real de iθ. Esto requiere cálculo infinitesimal.
5.5. Roger Cotes (1714) tenía la fórmula equivalente log (cos θ + i sen θ) = = iθ. La eiθ = cos θ + i sen θ de Euler parece haber aparecido por primera vez treinta años más tarde (véase Euler, 1748).
5.6. Aquí estoy utilizando la notación conveniente (aunque no muy lógica) cos3 θ para (cos θ)3, etc. Debería advertirse la inconsistencia notacional con la (más lógica) cos–1 θ, que también se denota habitualmente como arc cosθ. La fórmula sen nθ + i cos nθ = (sen θ + i cos θ)n se suele conocer como «teorema de De Moivre». Parece que también Abraham de Moivre, un contemporáneo de Roger Cotes (véase la nota anterior), ha sido codescubridor de eiθ = cos θ + i sen θ.