4
Los mágicos números complejos
4.1. EL MÁGICO NÚMERO «i»
¿Cómo es posible que –1 tenga una raíz cuadrada? El cuadrado de un número positivo es siempre positivo, y el cuadrado de un número negativo es también positivo (y el cuadrado de 0 es simplemente 0, de modo que de poco nos sirve aquí). Parece imposible que podamos encontrar un número cuyo cuadrado sea realmente negativo. Sin embargo, esta es una situación similar a la que hemos visto antes, cuando hemos establecido que 2 no tiene una raíz cuadrada dentro del sistema de los números racionales. En ese caso hemos resuelto la situación ampliando nuestro sistema de números desde los racionales a un sistema mayor, y hemos establecido el sistema de los reales. Tal vez el mismo truco funcione de nuevo.
Realmente lo hace. De hecho, lo que tenemos que hacer es algo mucho más fácil y menos drástico que el paso de los racionales a los reales. (Raphael Bombelli introdujo el procedimiento en 1572 en su obra L’Algebra, siguiendo los encuentros originales de Girolamo Cardano con los números complejos en su Ars magna de 1545.) Todo lo que tenemos que hacer es introducir una simple cantidad, llamada «i» cuyo cuadrado sea –1, y añadirla al sistema de los reales, permitiendo combinaciones de i con números reales para formar expresiones de la forma
a + ib,
donde a y b son números reales arbitrarios. Cualquiera de estas combinaciones se denomina un número complejo. Es fácil ver cómo se suman los números complejos:
(a + ib) + (c + id) = (a + c) + i(b + d),
que es de la misma forma que antes (pero ahora los números reales a + + c y b + d toman el lugar de los «a» y «b» que teníamos en nuestra expresión original). ¿Qué pasa con la multiplicación? Es casi igual de fácil. Vamos a encontrar el producto de a + ib por c + id. En primer lugar, multiplicamos simplemente estos factores, desarrollando la expresión mediante el uso de las reglas ordinarias del álgebra:[1]
(a + ib)(c + id) = ac + ibc + aid + ibid
= ac + i(bc + ad) + i2bd.
Pero i2 = –1, de modo que podemos reescribir esto como
(a + ib)(c + id) = (ac – bd) + i(bc + ad),
que de nuevo tiene la misma forma que nuestro a + ib original, pero donde ac – bd toma el lugar de a y bc + ad toma el lugar de b.
Es bastante fácil restar dos números complejos, pero ¿qué pasa con la división? Recordemos que en la aritmética ordinaria nos está permitido dividir por cualquier número real distinto de cero. Tratemos ahora de dividir el número complejo a + ib por el número complejo c + id. Debemos tomar este último distinto de cero, lo que significa que los números reales c y d no pueden ambos ser cero. Entonces, c2 + d2 > 0, y por consiguiente c2 + d2 ≠ 0, de modo que podemos dividir por c2 + d2. Es un ejercicio directo[4.1] comprobar (multiplicando ambos miembros de la expresión por c + id) que
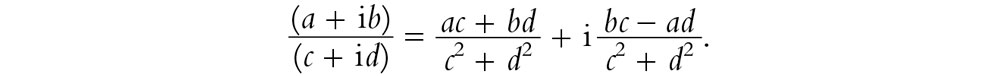
Esta expresión es de la misma forma que antes, de modo que es de nuevo un número complejo.
Cuando nos acostumbramos a jugar con estos números complejos, dejamos de pensar en a + ib como un «par» de objetos, a saber, los dos números reales a y b; ahora pensamos en a + ib como un «objeto» completo autónomo, de modo que podríamos utilizar una sola letra, digamos z, para denotar el número complejo global z = a + ib. Puede comprobarse que todas las reglas usuales del álgebra son satisfechas por los números complejos.[4.2] De hecho, todo esto es mucho más sencillo que comprobar cada una de estas cosas para los números reales. (Para esa comprobación, suponemos que ya estábamos convencidos de que las reglas del álgebra son satisfechas por las fracciones, y luego tenemos que utilizar «cortaduras» de Dedekind para demostrar que las reglas siguen funcionando para los números reales.) Desde este punto de vista, resulta bastante extraño que los números complejos se vieran con recelo durante mucho tiempo, mientras que la mucho más complicada ampliación de las racionales a los reales había sido aceptada sin problemas después de la época de la Grecia antigua.
Presumiblemente, el motivo de este recelo era que la gente no podía «ver» que los números complejos se les presentasen de un modo obvio en el mundo físico. En el caso de los números reales existía la sensación de que las distancias, los tiempos y otras magnitudes físicas proporcionaban la realidad que tales números requerían; pero los números complejos parecían ser entidades meramente «inventadas», sacadas de la imaginación de los matemáticos que deseaban números con un alcance mayor que los que ya conocían. Pero habría que recordar de §3.3 que la conexión que tienen los números reales matemáticos con aquellos conceptos físicos de longitud o tiempo no es tan clara como habíamos imaginado. No podemos ver directamente los mínimos detalles de una cortadura de Dedekind, ni está claro que realmente existan en la naturaleza longitudes o tiempos arbitrariamente grandes o arbitrariamente pequeños. Se podría decir que los denominados «números reales» son tan producto de la imaginación de los matemáticos como lo son los números complejos. Pese a todo, encontraremos que los números complejos, tanto como los reales, y quizá más incluso, componen una notable unidad con la naturaleza. Es como si la propia naturaleza estuviera tan impresionada por el alcance y consistencia del sistema de los números complejos como lo estamos nosotros, y hubiera confiado a estos números las operaciones detalladas de su mundo en sus escalas más minúsculas. En los capítulos 21-23 veremos en detalle cómo funciona esto.
Además, mencionar solo el alcance y la consistencia de los números complejos no hace justicia a este sistema. Hay algo más que, en mi opinión, solo puede ser calificado de «mágico». En lo que queda de este capítulo y en el siguiente, me propongo transmitir al lector algo del sabor de esta magia. Más adelante, en los capítulos 7-9, seremos testigos de nuevo de esta magia de los números complejos en algunas de sus más sorprendentes e inesperadas manifestaciones.
Durante los cuatro siglos que hace que se conoce el sistema de los números complejos, muchas cualidades mágicas se han ido revelando poco a poco. Pero esta es una magia que se percibía dentro de las matemáticas, y ofrecía realmente una utilidad y una profundidad de intuición matemática que no podía conseguirse solo con el uso de los reales. No había ninguna razón para esperar que el mundo físico estuviera interesado en ello. Y durante los aproximadamente trescientos cincuenta años transcurridos desde la época en que dichos números fueron introducidos en las obras de Cardano y Bombelli, la magia del sistema de los números complejos solo fue percibida a través de su papel matemático. Para todos aquellos que se habían mostrado recelosos de los números complejos habría sido sin duda una sorpresa encontrar que, según la física de los últimos tres cuartos del siglo XX, las leyes que gobiernan el comportamiento del mundo en sus escalas más minúsculas dependen fundamentalmente del sistema de los números complejos.
Estos temas serán capitales para algunas de las secciones posteriores de este libro (especialmente en los capítulos 21-23, 26 y 31-33). Por el momento nos concentraremos en una parte de la magia matemática de los números complejos y dejaremos su magia física para más adelante. Recordemos que todo lo que hemos hecho es exigir que –1 tenga una raíz cuadrada, además de exigir que se mantengan las leyes usuales de la aritmética, y hemos descubierto que dichas exigencias pueden satisfacerse de forma consistente. Esto parece algo bastante simple de hacer. ¡Pero pasemos a la magia!
4.2. RESOLVIENDO ECUACIONES CON NÚMEROS COMPLEJOS
En lo que sigue, será necesario introducir una notación algo más matemática que la utilizada hasta ahora. Pido disculpas por ello. Sin embargo, difícilmente pueden transmitirse ideas matemáticas serias sin cierta cantidad de notación. Soy consciente de que habrá muchos lectores que se sientan incómodos con ello. Mi consejo para tales lectores es que tan solo lean el texto y no se preocupen demasiado por tratar de entender las ecuaciones. Cuando menos, lean por encima las diversas fórmulas y sigan adelante. De hecho, habrá numerosas expresiones matemáticas serias desperdigadas a lo largo de este libro, especialmente en algunos de los últimos capítulos. Creo que, con el tiempo, empezarán a calar ciertas dosis de conocimiento si se hace un pequeño intento por entender lo que todas las expresiones significan realmente. Así lo espero, porque la magia de los números complejos es un milagro que vale la pena apreciar. Si usted puede entender la notación matemática, entonces mucho mejor.
Antes de nada, podemos preguntarnos si otros números tienen raíces cuadradas. ¿Qué pasa, por ejemplo, con –2? Esto es fácil. El número complejo i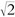 ciertamente tiene –2 como cuadrado, y también lo tiene –i
ciertamente tiene –2 como cuadrado, y también lo tiene –i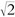 . Más aún, para cualquier número real positivo a, el número complejo i
. Más aún, para cualquier número real positivo a, el número complejo i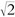 tiene como cuadrado –a, y lo mismo sucede con –i
tiene como cuadrado –a, y lo mismo sucede con –i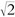 . No hay aquí ninguna magia. Pero ¿qué pasa con el número complejo más general a + ib (donde a y b son reales)? Encontramos que el número complejo
. No hay aquí ninguna magia. Pero ¿qué pasa con el número complejo más general a + ib (donde a y b son reales)? Encontramos que el número complejo
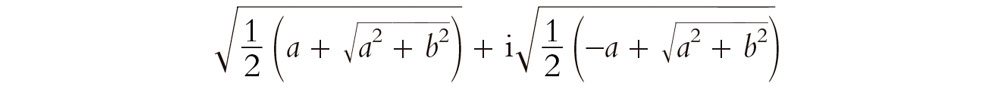
tiene como cuadrado a + ib (y lo mismo sucede con su negativo).[4.3] Así pues, vemos que incluso si solo añadimos una raíz cuadrada para una cantidad (a saber –1), ¡encontramos que todos los números del sistema resultante tienen ahora automáticamente una raíz cuadrada! Esto es muy diferente de lo que sucedía al pasar de los racionales a los reales. En este caso, la mera introducción de la cantidad 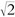 en el sistema de los racionales no nos hubiera llevado casi a ninguna parte.
en el sistema de los racionales no nos hubiera llevado casi a ninguna parte.
Pero esto es solo el principio. Podemos preguntarnos sobre raíces cúbicas, raíces quintas, raíces 999-ésimas, raíces π-ésimas —e incluso raíces i-ésimas—. Milagrosamente, encontramos que para cualquier raíz compleja que escojamos y cualquier número complejo al que la apliquemos (excluyendo el 0), hay siempre una solución compleja a este problema. (De hecho, normalmente habrá varias soluciones diferentes al problema, como veremos dentro de poco. Antes he señalado que para raíces cuadradas teníamos dos soluciones, pues el negativo de la raíz cuadrada de un número complejo z es también una raíz cuadrada de z. Para raíces más altas hay más soluciones; véase §5.4.)
Apenas estamos arañando todavía en la superficie de la magia de los números complejos. Lo que acabo de afirmar es realmente muy fácil de establecer (una vez que tengamos la noción del logaritmo de un número complejo, como veremos en el capítulo 5). Algo más notable es el denominado «teorema fundamental del álgebra», que afirma que cualquier ecuación polinómica, tal como
1 – z + z4 = 0
o
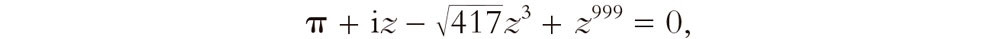
debe tener soluciones con números complejos. Dicho de forma más explícita, siempre habrá una solución (y normalmente varias diferentes) para cualquier ecuación de la forma
a0 + a1z + a2z2 + a3z3 + … + anzn = 0,
donde a0, a1, a2, a3, …, an son números complejos dados, con el an tomado no nulo.[2] (Aquí n puede ser cualquier entero positivo que escojamos, tan grande como queramos.) Deberíamos recordar, por comparación, que «i» fue introducida simplemente para proporcionar una solución a la ecuación particular
1 + z2 = 0.
¡Todo lo demás lo obtenemos gratis!
Antes de seguir adelante vale la pena mencionar el problema que interesaba a Cardano, aproximadamente en 1539, cuando encontró por primera vez los números complejos y captó un indicio de otro aspecto de sus propiedades mágicas inherentes. Dicho problema era, en efecto, encontrar una expresión para la solución general de una ecuación (real) cúbica (i.e., n = 3, en el caso anterior). Cardano encontró que la cúbica general podía reducirse mediante una sencilla transformación a la forma
x3 = 3px + 2q
Aquí p y q son números reales (y he vuelto a utilizar x en la ecuación, en lugar de z, para indicar que ahora estamos interesados en soluciones reales en lugar de complejas). La solución completa de Cardano (tal como la publicó en 1545 en su libro Ars magna) parece haber sido desarrollada a partir de una solución parcial anterior que había aprendido en 1539 de Niccolò Fontana («Tartaglia»), aunque esta solución parcial (y quizá incluso la solución completa) había sido encontrada previamente (antes de 1526) por Scipione del Ferro.[3] La solución de (Del Ferro-)Cardano era en esencia la siguiente (escrita en notación moderna):
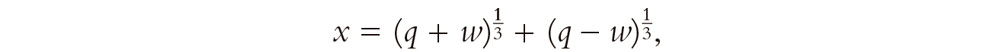
donde
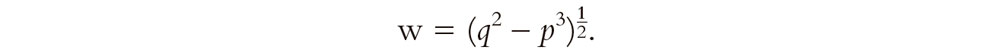
Esta ecuación no plantea ningún problema fundamental dentro del sistema de los números reales si
q2 ≥ p3.
En este caso solo hay una solución real x a la ecuación, y viene dada correctamente por la fórmula de (Del Ferro-)Cardano expuesta antes. Pero si
q2 < p3,
el denominado caso irreducible, entonces, aunque ahora hay tres soluciones reales, la fórmula incluye la raíz cuadrada del número negativo q2 – p3 y por ello no puede ser utilizada sin introducir los números complejos. De hecho, como Bombelli demostró más tarde (en el capítulo 2 de L’Algebra de 1572), si admitimos los números complejos, entonces las tres soluciones reales están correctamente expresadas por la fórmula.[4] (Esto tiene sentido porque la expresión nos proporciona dos números complejos sumados, y las partes que contienen «i» se cancelan en la suma para dar una respuesta real.)[5] Lo que hay de misterioso en esto es que, aunque pudiera parecer que el problema no tiene nada que ver con los números complejos —pues la ecuación tiene coeficientes reales y todas sus soluciones son reales (en este caso, «irreducible»)—, tenemos que viajar por este territorio en apariencia ajeno del mundo de los números complejos para que la fórmula nos permita regresar con nuestras soluciones puramente reales. Si nos hubiéramos restringido al recto y estrecho camino «real», habríamos vuelto con las manos vacías. (Resulta irónico que solo puede haber soluciones complejas a la ecuación original en aquellos casos en que la fórmula no implica necesariamente este viaje por los complejos.)
4.3. CONVERGENCIA DE SERIES DE POTENCIAS
A pesar de estos hechos notables, aún no hemos ido muy lejos en la magia de los números complejos. ¡Queda mucho más por venir! Por ejemplo, algo en que los números complejos resultan verdaderamente inestimables es en ofrecer una comprensión del comportamiento de lo que se denominan series de potencias. Una serie de potencias es una suma infinita de la forma
a0 + a1x + a2x2 + a3x3 + …
Puesto que esta suma implica un número infinito de términos, puede darse el caso de que la serie diverja, lo que significa que no se asienta en un valor particular finito a medida que se suman más términos. Por ejemplo, consideremos la serie
1 + x2 + x4 + x6 + x8 + …
(donde he tomado a0 = 1, a1 = 0, a2 = 1, a3 = 0, a4 = 1, a5 = 0, a6 = = 1, …). Si hacemos x = 1, entonces, sumando los términos sucesivamente, obtenemos
1, 1 + 1 = 2, 1 + 1 + 1 = 3,
1 + 1 + 1 + 1 = 4, 1 + 1 + 1 + 1 + 1 = 5, etc.,
y vemos que la serie no tiene posibilidad de asentarse en un valor particular finito, es decir, es divergente. Las cosas son aún peores si probamos con x = 2, por ejemplo, puesto que ahora los términos individuales son más grandes, y sumando términos sucesivamente obtenemos
1, 1 + 4 = 5, 1 + 4 + 16 = 21, 1 + 4 + 16 + 64 = 85, etc.,
que claramente diverge. Por el contrario, si hacemos x = 1/2, obtenemos
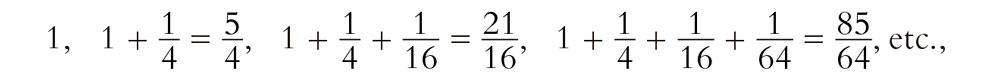
y resulta que estos números se acercan cada vez más al valor límite 4/3, de modo que la serie es ahora convergente.
Con esta serie no es difícil darse cuenta de que, en cierto sentido, hay una razón subyacente por la que la serie no puede sino divergir para x = 1 y x = 2, mientras que converge para x = 1/2 para dar la respuesta 4/3. En efecto, podemos escribir explícitamente la «respuesta» a la suma de toda la serie, encontrando[4.4]
1 + x2 + x4 + x6 + x8 + … = (1 – x2)–1.
Cuando sustituimos x = 1, encontramos que esta respuesta es (1 – 12)–1 = 0–1, que es «infinito»,[6] y esto nos permite entender por qué la serie tiene que divergir para ese valor de x. Cuando sustituimos x = 1/2, la respuesta es (1 – 1/4)–1 = 4/3, y la serie converge realmente a este valor concreto, tal como se ha establecido antes.
Todo esto parece muy razonable. Pero ¿qué pasa con x = 2? Ahora hay una «respuesta» dada por la fórmula explícita, a saber, (1 – 4)–1 = = –1/3, aunque no parece que obtengamos dicho valor sumando simplemente los términos de la serie. Difícilmente podríamos obtener esta respuesta porque estamos sumando cantidades positivas, mientras que –1/3 es negativo. La razón de que la serie diverja es que, cuando x = 2, cada término es mayor que el término correspondiente para x = 1, de modo que la divergencia para x = 2 se sigue lógicamente de la divergencia para x = 1. En el caso x = 2 no se trata de que la «respuesta» sea realmente infinita, sino de que no podemos llegar a esta respuesta intentando sumar la serie directamente. En la Fig. 4.1 he representado las sumas parciales de la serie (i.e., las sumas hasta cierto número finito de términos), sucesivamente hasta cuatro términos, al lado de la «respuesta» (1 – x2)–1 y podemos ver que, con tal de que x esté comprendida estrictamente[7]> entre los valores –1 y +1, las curvas que muestran estas sumas parciales convergen realmente a esta respuesta, a saber (1 – x2)–1, como cabía esperar. Pero fuera de este intervalo, la serie simplemente diverge y no llega realmente a ningún valor finito.
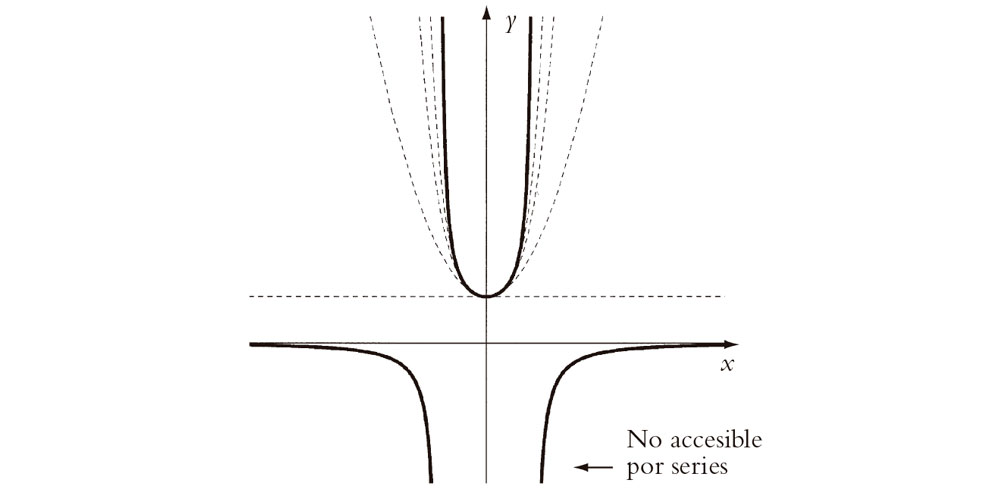
Fig. 4.1. Se representan las respectivas sumas parciales 1, 1 + x2, 1 + x2 + x4, 1 + x2 + + x4 + x6 (líneas de trazos) de la serie para (1 – x2)–1, que ilustran la convergencia de la serie para (1 – x2)–1 para |x| < 1 y la divergencia para |x| > 1.
A modo de pequeña digresión, será útil abordar aquí una cuestión que tendrá importancia para nosotros más adelante. Planteemos la siguiente pregunta: la ecuación que obtenemos haciendo x = 2 en la expresión anterior, es decir,

¿tiene sentido realmente? El gran matemático del siglo XVIII Leonhard Euler solía escribir ecuaciones como esta, y llegó a ser una moda hacer bromas a su costa por sostener tales absurdos, aunque se le podrían perdonar sobre la base de que en aquellos primeros días no se entendía adecuadamente nada relativo a la «convergencia» de series y cosas similares. De hecho, lo cierto es que el tratamiento matemático riguroso de las series no llegó hasta finales del siglo XVIII y principios del XIX, con la obra de Augustin Cauchy y otros. Además, según este tratamiento riguroso, la ecuación anterior sería clasificada oficialmente como «sin sentido». Pese a todo, creo que es importante darse cuenta de que, en el sentido adecuado, Euler sabía bien lo que estaba haciendo cuando escribía absurdos aparentes de esta naturaleza, y que hay sentidos en los que la ecuación anterior debe considerarse «correcta».
En matemáticas es realmente imperativo dejar absolutamente claro que las ecuaciones que se obtienen tienen un sentido estricto y preciso. Sin embargo, es asimismo importante no ser insensible a «lo que sucede fuera de escena», que puede, en última instancia, llevar a intuiciones más profundas. Es fácil perder de vista tales cosas si nos atenemos de forma demasiado rígida a lo que parece ser estrictamente lógico, como es el hecho de que la suma de los términos positivos 1 + 4 + 16 + 64 + 256 + … no puede ser –1/3 de ningún modo. Como ejemplo pertinente, recordemos el absurdo lógico de encontrar una solución real a la ecuación x2 + 1 = 0. No hay solución; pero si nos quedamos en esto, perderemos todas las intuiciones profundas que proporciona la introducción de los números complejos. Un comentario similar es aplicable a lo absurdo de una solución racional a x2 = 2. De hecho, es perfectamente posible dar un sentido matemático a la respuesta «–1/3» a la serie infinita anterior, pero hay que tener cuidado con las reglas que nos dicen lo que está permitido y lo que no está permitido. No es mi intención discutir aquí estas cuestiones en detalle,[8] pero habría que señalar que en la física moderna, especialmente en el área de la teoría cuántica de campos, es frecuente encontrar series divergentes de este tipo (véanse especialmente §§26.7,9 y §§31.2,13). Es una cuestión muy delicada la de decidir si las «respuestas» que se obtienen de este modo son realmente significativas y, además, realmente correctas. A veces se obtienen respuestas muy precisas manipulando tales expresiones divergentes, y en ocasiones son sorprendentemente confirmadas al compararlas con experimentos físicos reales. Otras veces, por el contrario, no se tiene tanta suerte. Estas delicadas cuestiones desempeñan papeles importantes en las teorías físicas actuales y son muy relevantes en nuestros intentos de evaluarlas. El punto de relevancia inmediata para nosotros aquí es que el «sentido» que podemos ser capaces de atribuir a semejantes expresiones aparentemente sin significado depende con frecuencia, y de un modo esencial, de las propiedades de los números complejos.
Volvamos ahora a la cuestión de la convergencia de series, y tratemos de ver cómo encajan los números complejos en la imagen. Para ello, consideremos una función tan solo ligeramente diferente de (1 – x2)–1, a saber (1 + x2)–1, y tratemos de ver si tiene un desarrollo en serie de potencias razonable. Ahora parece haber una mejor oportunidad de convergencia completa, puesto que (1 + x2)–1 se mantiene suave y finita sobre todo el intervalo de los números reales. Existe, de hecho, una serie de potencias de apariencia sencilla para (1 + x2)–1, tan solo ligeramente diferente de la que teníamos antes, a saber
1 – x2 + x4 – x6 + x8 – … = (1 + x2)–1,
donde la diferencia es meramente un cambio de signo en términos alternos.[4.5] En la Fig. 4.2 he representado las sumas parciales de la serie, sucesivamente hasta cinco términos, de modo similar a lo que hemos hecho antes, junto con esta respuesta (1 + x2)–1. Lo que parece sorprendente es que las sumas parciales siguen convergiendo a la respuesta solo en el intervalo estricto entre los valores –1 y +1 . Parece que vamos a obtener una divergencia fuera de este intervalo, incluso si la respuesta no tiende ni mucho menos a infinito, a diferencia de nuestro caso anterior. Podemos comprobar esto de forma explícita utilizando los mismos tres valores x = 1, x = 2, x = 1/2 que hemos utilizado antes, encontrando que, como antes, la convergencia ocurre solo en el caso x = 1/2, para el que la respuesta da correctamente el valor límite 4/5 para la suma de la serie entera:

Advertimos que la «divergencia» en el primer caso consiste simplemente en que las sumas parciales de la serie no llegan nunca a asentarse, aunque no divergen realmente a infinito.
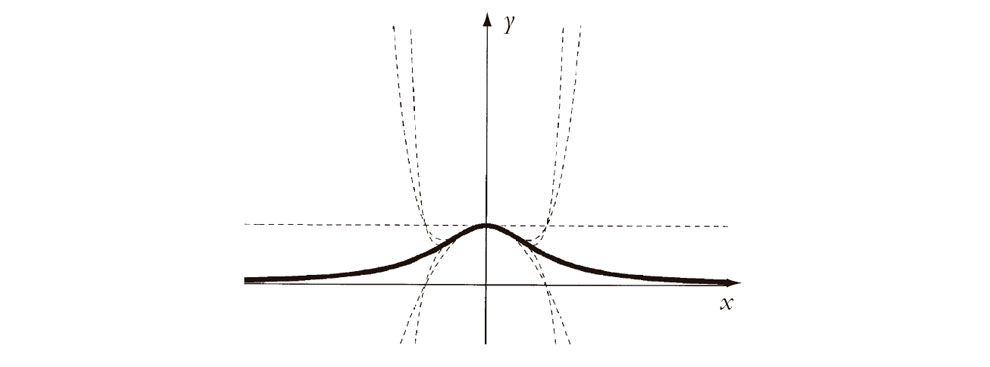
Fig. 4.2. Del mismo modo se representan las sumas parciales 1, 1 – x2, 1 – x2 + x4, 1 – x2 + x4 – x6, 1 – x2 + x4 – x6 + x8, de la serie para (1 + x2)–1, y de nuevo hay convergencia para |x| < 1 y divergencia para |x| > 1, pese al hecho de que la función tiene un comportamiento perfectamente bueno en x = ±1.
Así pues, si solo se consideran números reales, hay una discrepancia enigmática entre sumar realmente la serie y pasar directamente a la «respuesta» que se supone que representa la suma infinita de la serie. Las sumas parciales simplemente «despegan» (o más bien oscilan incontroladamente arriba y abajo) precisamente en los mismos lugares (a saber, x = ±1) donde surgían problemas en el caso anterior, aunque ahora la supuesta respuesta a la suma infinita, a saber (1 + x2)–1, no muestra ninguna característica notable en dichos lugares. Encontraremos la solución a este misterio si examinamos valores complejos de esta función en lugar de restringir nuestra atención a los reales.
4.4. EL PLANO COMPLEJO DE CASPAR WESSEL
Para ver lo que está pasando aquí, será importante utilizar la ahora estándar representación geométrica de los números complejos en el plano euclídeo. Caspar Wessel en 1797, Jean Robert Argand en 1806, John Warren en 1828 y Carl Friedrich Gauss mucho antes de 1831 dieron todos ellos, de forma independiente, con la idea del plano complejo (véase la Fig. 4.3), en el que ofrecieron interpretaciones geométricas claras de las operaciones de adición y multiplicación de números complejos. En la Fig. 4.3 he utilizado ejes cartesianos estándar, con el eje x apuntando horizontalmente hacia la derecha y el eje y apuntando verticalmente hacia arriba. El número complejo
z = x + iy
viene representado como el punto del plano con coordenadas cartesianas (x, y).
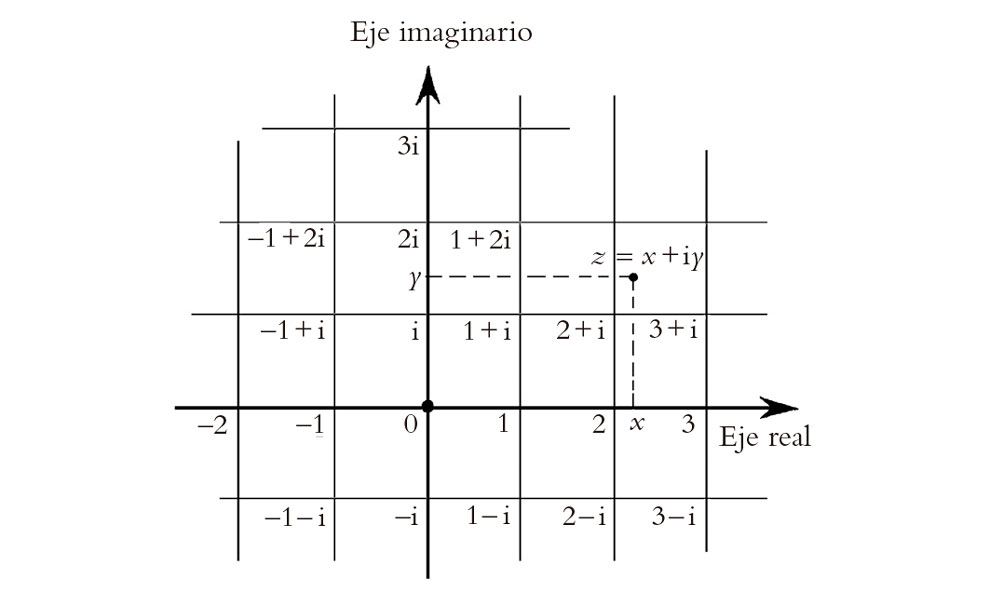
Fig. 4.3. El plano complejo de z = x + iy. En coordenadas cartesianas (x, y), el eje x dirigido horizontalmente hacia la derecha es el eje real; el eje y dirigido verticalmente hacia arriba es el eje imaginario.
Ahora tenemos que considerar un número real x como un caso particular del número complejo z = x + iy en el que y = 0. Así pues, tenemos que considerar que el eje x de nuestro diagrama representa la recta real (i.e., la totalidad de los números reales, ordenados linealmente a lo largo de una recta). El plano complejo nos da así una representación gráfica directa de cómo se amplía el sistema de los números reales para convertirse en el sistema completo de los números complejos. Esta recta real se suele conocer como el «eje real» en el plano complejo. En correspondencia, el eje y se conoce como el «eje imaginario». Consiste en todos los múltiplos de i por un número real.
Volvamos ahora a nuestras dos funciones que hemos estado tratando de representar en términos de series de potencias. Tomábamos estas como funciones de la variable real x, a saber (1 – x2)–1 y (1 + x2)–1, pero ahora vamos a extender dichas funciones de modo que se aplican a una variable compleja z. No hay ningún problema en hacer esto: simplemente escribimos estas funciones ampliadas como (1 – z2)–1 y (1 + z2)–1, respectivamente. En el caso de la primera función real (1 – x2)–1 éramos capaces de reconocer dónde empezaban los problemas de «divergencia», puesto que la función es singular (en el sentido de que se hace infinita) en los dos lugares x = –1 y x = +1; pero con (1 + x2)–1 no veíamos ninguna singularidad en estos lugares y, de hecho, ninguna singularidad real en absoluto. Sin embargo, en términos de la variable compleja z, vemos que estas dos funciones son mucho más parecidas. Hemos advertido las singularidades de (1 – z2)–1 en dos puntos z = ±1 a distancia unidad del origen a lo largo del eje real; pero ahora vemos que (1 + z2)–1 tiene también singularidades, a saber, en los dos lugares z = ±i (puesto que entonces 1 + z2 = 0), siendo estos los dos puntos situados a distancia unidad del origen en el eje imaginario.
Pero ¿qué tienen que ver estas singularidades complejas con la cuestión de la convergencia o divergencia de la serie de potencias correspondiente? Hay una respuesta sorprendente a esta pregunta. Ahora debemos considerar nuestras series de potencias como funciones de la variable compleja z, en lugar de la variable real x, y podemos preguntar por aquellas localizaciones de z en el plano complejo para las que la serie converge y aquellas para las que diverge. La notable respuesta general[9] para cualquier serie de potencias
a0 + a1z + a2z2 + a3z3 + …,
es que existe un círculo en el plano complejo, centrado en 0, llamado círculo de convergencia, con la propiedad de que si el número complejo z está estrictamente dentro del círculo, entonces la serie converge para dicho valor de z, mientras que si z está estrictamente fuera del círculo, entonces la serie diverge para dicho valor de z. (Si la serie converge o no cuando z está exactamente sobre el círculo es realmente una cuestión algo delicada en la que no entraremos aquí, aunque tiene cierta relevancia para las cuestiones a las que llegaremos en §§9.6,7.) En este enunciado estoy incluyendo las dos situaciones límite: aquella para la que la serie diverge para todos los valores no nulos de z, cuando el círculo de convergencia se ha contraído hasta un radio cero, y aquella en que converge para todo z, en cuyo caso el círculo se ha dilatado hasta un radio infinito. Para encontrar dónde está realmente el círculo de convergencia para una función dada, miramos en qué parte del plano complejo están localizadas las singularidades, y dibujamos el círculo más grande con centro en el origen z = 0 y que no contenga ninguna singularidad en su interior (i.e., lo dibujamos de forma que pase por la singularidad más próxima al origen).
En los casos particulares (1 – z2)–1 y (1 + z2)–1 que hemos estado considerando, las singularidades son de un tipo simple denominado polos (que surgen donde se anula un polinomio que aparece como divisor en una expresión). Aquí todos estos polos están a distancia unidad del origen, y vemos que el círculo de convergencia es, en ambos casos, el círculo unidad alrededor del origen. Los lugares donde dicho círculo corta al eje real son los mismos en ambos casos, a saber, los dos puntos z = ±1 (véase la Fig. 4.4). Esto explica por qué las dos funciones convergen y divergen en las mismas regiones, un hecho que no era manifiesto simplemente a partir de sus propiedades como funciones de variables reales. Así pues, los números complejos nos ofrecen ideas profundas sobre el comportamiento de series de potencias, ideas que sencillamente no están disponibles a partir de la consideración de su estructura en variable real.
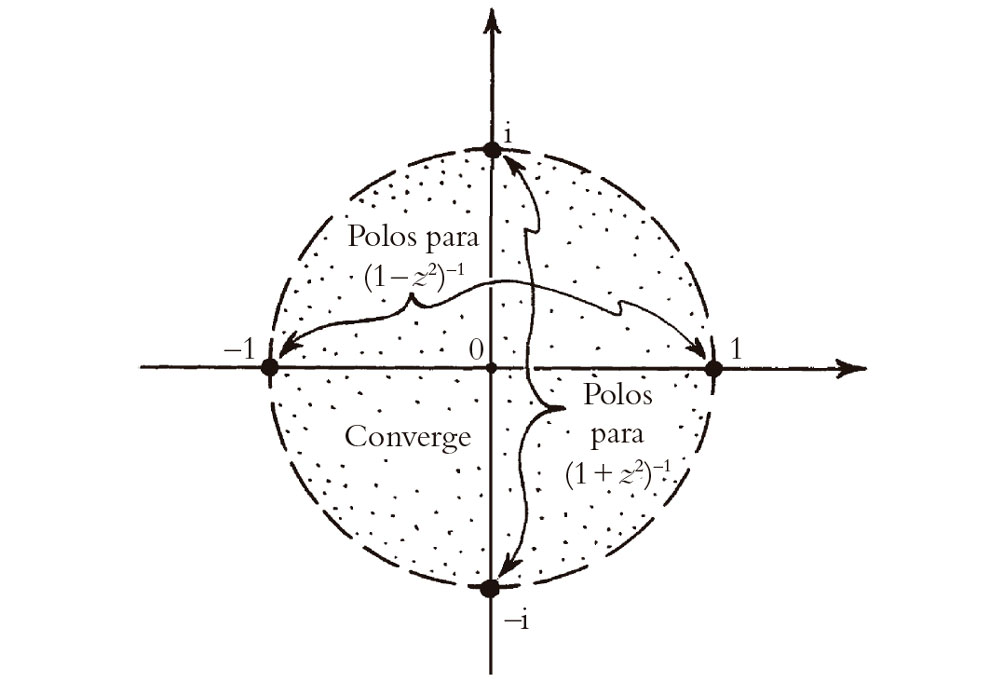
Fig. 4.4. En el plano complejo, las funciones (1 – z2)–1 y (1 + z2)–1 tienen el mismo círculo de convergencia, habiendo polos para la primera en z = ±1 y polos para la segunda en z = ±i, todos ellos a la misma distancia (unidad) del origen.
4.5. CÓMO SE CONSTRUYE EL CONJUNTO DE MANDELBROT
Para terminar este capítulo, consideremos otro tipo de cuestión convergencia/divergencia. Es la que subyace en la construcción de esa configuración extraordinaria, mencionada en §1.3 y mostrada en la Fig. 1.2, conocida como el conjunto de Mandelbrot. De hecho, este es solo un subconjunto del plano complejo de Wessel que puede definirse de un modo notablemente simple, si lo comparamos con la extrema complicación de dicho conjunto. Todo lo que tenemos que hacer es examinar las aplicaciones repetidas del reemplazamiento
z  z2 + c,
z2 + c,
donde c es un número complejo escogido. Consideremos c como un punto en el plano complejo y empecemos con z = 0. Entonces iteramos esta transformación (i.e., la aplicamos repetidamente una y otra vez) y vemos cómo se comporta el punto z en el plano complejo. Si escapa al infinito, entonces el punto c se marca en color blanco. Si z se mueve por cierta región restringida sin llegar nunca al infinito, entonces c se marca en color negro. ¡La región negra nos da el conjunto de Mandelbrot!
Describamos este procedimiento con un poco más de detalle. ¿Cómo procede la iteración? En primer lugar, fijamos c. Luego tomamos algún punto z y aplicamos la transformación, de modo que z se convierte en z2 + c. Después la aplicamos otra vez, de modo que ahora reemplazamos la «z» en z2 + c por z2 + c y obtenemos (z2 + c)2 + c. A continuación reemplazamos la «z» en z2 + c por (z2 + c)2 + c, de modo que nuestra expresión se convierte en ((z2 + c)2 + c)2 + c. Luego continuamos reemplazando la «z» en z2 + c por ((z2 + c)2 + c)2 + c, y obtenemos (((z2 + c)2 + c)2 + c)2 + c, y así sucesivamente.
Veamos ahora qué sucede si empezamos en z = 0 e iteramos de esta manera. (Simplemente ponemos z = 0 en las expresiones anteriores.) Obtenemos la secuencia
0, c, c2 + c, (c2 + c)2 + c, ((c2 + c)2 + c)2 + c, …
Esto nos da una sucesión de puntos en el plano complejo. (Si trabajáramos con un computador, no utilizaríamos las expresiones algebraicas anteriores, sino que procederíamos de forma puramente numérica para cada elección individual del número complejo c. Resulta mucho más «barato» computacionalmente hacer la aritmética desde el principio cada vez.) Ahora, para cualquier valor dado de c, puede suceder una de dos cosas: (i) los puntos de la secuencia se alejan a distancias cada vez mayores, i.e., la secuencia no está acotada, o (ii) cada uno de los puntos yace a una distancia del origen menor que cierto valor dado (es decir, dentro de cierto círculo alrededor del origen) en el plano complejo, i.e., la secuencia está acotada. Las regiones blancas de la Fig. 1.2 son las localizaciones de c que dan una secuencia no acotada (i), mientras que las regiones negras son las localizaciones de c para las que se da el caso (ii); el conjunto de Mandelbrot propiamente dicho es la totalidad de la región negra.[10]
La complejidad del conjunto de Mandelbrot surge del hecho de que la secuencia iterada puede permanecer acotada de muchas maneras diferentes, y a veces muy complicadas. Puede haber combinaciones de ciclos y «casi» ciclos de varios tipos, que puntean el plano de diversas formas complicadas, pero nos llevaría demasiado lejos tratar de entender en detalle cómo surge la extraordinaria complejidad de este conjunto, donde están implicadas cuestiones sutiles de análisis complejo y teoría de números. El lector interesado puede consultar Peitgen y Reichter (1986) y Peitgen y Saupe (1988) para más información e imágenes (véase también Douady y Hubbard, 1985).
Notas
Sección 4.1
4.1. Véase el ejercicio [4.2] para estas reglas.
Sección 4.2
4.2. Una consecuencia directa[4.6] es que cualquier polinomio complejo de la sola variable z factoriza en factores lineales,
a0 + a1z + a2z2 + … + anzn = an(z – b1)(z – b2)…(z – bn)
y es a este enunciado al que normalmente se llama «el teorema fundamental del álgebra».
4.3. La historia es que Tartaglia había revelado su solución parcial a Cardano solo después de que este hubiera jurado guardar el secreto. Por lo tanto, Cardano no podía publicar su solución más general sin romper su juramento. Sin embargo, en un viaje posterior a Bolonia, en 1543, Cardano examinó los papeles póstumos de Del Ferro y se convenció de la prioridad real de Del Ferro. Consideró que esto le dejaba libre para publicar todos estos resultados (con los debidos reconocimientos a Tartaglia y Del Ferro) en Ars magna en 1545. Tartaglia discrepó, y la disputa tuvo consecuencias muy amargas (véase Wykes, 1969).
4.4. Para más información, véase Van der Waerden (1985).
4.5. La razón para esto es que estamos sumando dos números que son mutuamente complejos conjugados (véase §10.1), y una suma semejante es siempre un número real.
Sección 4.3
4.6. Recordemos de la nota 2.4 que 0–1 debería significar 1/0, i.e., «uno dividido por cero». Una abreviatura conveniente para expresar el «resultado» de esta operación ilegal es «0–1 = ∞».
4.7. «Estrictamente»: significa que los valores extremos no están incluidos en el intervalo.
4.8. Para más información, véase, por ejemplo, Hardy (1949).
Sección 4.4
4.9. Véanse, por ejemplo, Priestley (2003), p. 71, en lo referente a «radio de convergencia», y Needham (1967), pp. 67 y 264.
Sección 4.5
4.10. En las imágenes del conjunto de Mandelbrot generadas por ordenador (tales como la Fig. 1.2), uno no puede, por supuesto, computar indefinidamente para asegurar que una secuencia en apariencia acotada está realmente acotada. Es habitual «cortar» la iteración al cabo de un número apropiado de pasos. Sin embargo, retrasar simplemente el corte no mejora necesariamente la apariencia exacta de una imagen, porque los filamentos tienden a desaparecer.