3
Tipos de números en el mundo físico
3.1. ¿UNA CATÁSTROFE PITAGÓRICA?
Volvamos ahora a la cuestión de la demostración por contradicción, el principio que Saccheri trató inútilmente de utilizar en su intento de demostración del quinto postulado de Euclides. Hay muchos casos en las matemáticas clásicas en los que el principio ha sido aplicado con éxito. Uno de los más famosos se remonta a los pitagóricos, y zanjó una cuestión matemática en un sentido que les iba a causar grandes problemas. La cuestión era la siguiente: ¿es posible encontrar un número racional (i.e., una fracción) cuyo cuadrado sea exactamente el número 2? Resulta que la respuesta es no, y la afirmación matemática que voy a demostrar dentro de poco es, en efecto, que no existe tal número racional.
¿Por qué estaban los pitagóricos tan molestos por este descubrimiento? Recordemos que una fracción —es decir, un número racional— es algo que puede expresarse como la razón a/b de dos enteros a y b, siendo b distinto de cero. (Véase el prefacio para una discusión de la definición de una fracción.) Los pitagóricos tenían al principio la esperanza de que toda su geometría podría expresarse en términos de longitudes que podrían medirse en términos de números racionales. Los números racionales son cantidades bastante simples, pues son descriptibles y comprensibles en términos finitos simples; pese a todo, pueden utilizarse para especificar distancias tan pequeñas o tan grandes como queramos. Si pudiera hacerse toda la geometría con los racionales, esto haría las cosas relativamente sencillas y fácilmente comprensibles. La noción de un número «irracional», por el contrario, requiere procesos infinitos, y esto hubiera planteado dificultades considerables a los antiguos (y con toda la razón). ¿Qué dificultad plantea el hecho de que no exista un número racional cuyo cuadrado sea 2? Esta procede del propio teorema de Pitágoras. Si en la geometría euclídea tenemos un cuadrado con lados de longitud unidad, entonces la longitud de su diagonal es un número cuyo cuadrado es 12 + 12 = 2 (véase la Fig. 3.1). Sería realmente catastrófico para la geometría que no hubiera ningún número que pudiera describir la longitud de la diagonal de un cuadrado. Al principio, los pitagóricos trataron de arreglárselas con una noción de «número en acto» que pudiera describirse simplemente en términos de razones de números enteros. Veamos por qué esto no puede funcionar.
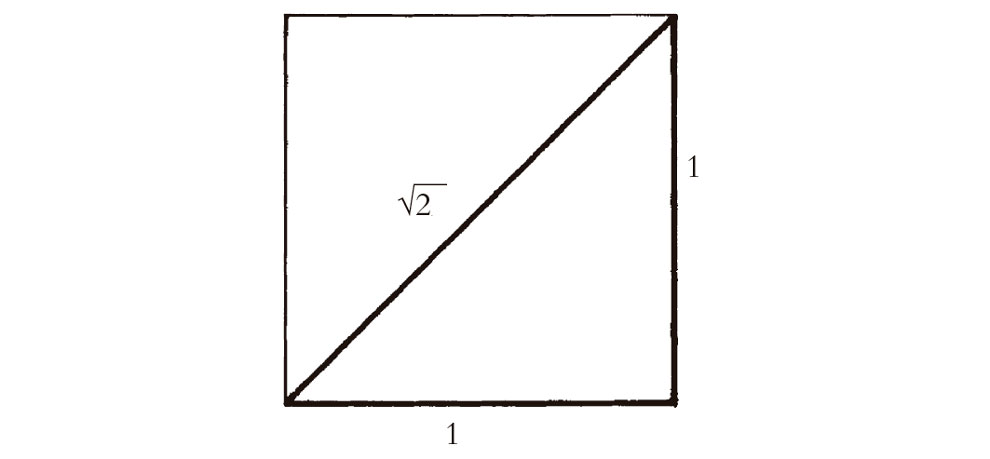
Fig. 3.1. Un cuadrado de lado longitud unidad tiene diagonal 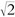 , por el teorema de Pitágoras
, por el teorema de Pitágoras
La cuestión consiste en ver por qué la ecuación
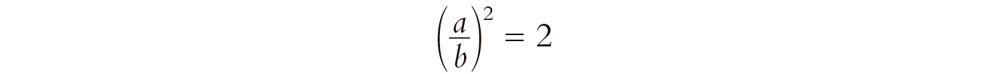
no tiene solución para enteros a y b, donde estos enteros se consideran positivos. Utilizaremos las demostración por contradicción para demostrar que no pueden existir tales a y b. Supongamos, por lo tanto, que sí existen tales a y b. Multiplicando ambos miembros de la ecuación anterior por b2, encontramos que se convierte en
a2 = 2b2
y concluimos[1] claramente que a2 > b2 > 0. Ahora, el segundo miembro, 2b2, de la ecuación anterior es par, de donde se sigue que a debe ser par (y no impar, puesto que el cuadrado de cualquier número impar es impar). Así pues, existe un entero positivo c tal que a = 2c. Sustituyendo a por 2c en la ecuación anterior, y elevando al cuadrado, obtenemos
4c2 = 2b2,
es decir, dividiendo ambos miembros por 2,
b2 = 2c2,
y concluimos que b2 > c2 > 0. Ahora bien, esta es precisamente la misma ecuación que teníamos antes, excepto que b reemplaza ahora a a y c reemplaza a b. Nótese que los enteros correspondientes son ahora más pequeños que antes. Podemos repetir el argumento una y otra vez, obteniendo una secuencia interminable de ecuaciones
a2 = 2b2, b2 = 2c2, c2 = 2d2, d2 = 2e2…,
donde
a2 > b2 > c2 > d2 > e2 > … ,
siendo todos estos enteros positivos. Pero cualquier secuencia decreciente de enteros positivos debe llegar a un final, lo que contradice el hecho de que esta secuencia es interminable. Esto nos da una contradicción con lo que se había supuesto, a saber, que existe un número racional cuyo cuadrado es 2. De ello se sigue que no existe tal número racional, como queríamos demostrar.[2]
Algunos puntos del argumento anterior merecen un comentario. En primer lugar, de acuerdo con los procedimientos normales de la demostración matemática, en el argumento se ha apelado a ciertas propiedades de los números que se tomaban como «obvias» o como previamente establecidas. Por ejemplo, hemos utilizado el hecho de que el cuadrado de un número impar es siempre impar y, además, que si un entero no es impar, entonces es par. También utilizamos el hecho fundamental de que cada secuencia estrictamente decreciente de números enteros positivos debe llegar a un final.
Una razón por la que puede ser importante identificar las hipótesis precisas que entran en una demostración —incluso si algunas de estas hipótesis pudieran ser cosas perfectamente «obvias»— es que los matemáticos están a menudo interesados en otros tipos de entidades distintas de aquellas a las que originalmente concernía la demostración. Si estas otras entidades satisfacen las mismas hipótesis, entonces la demostración será extrapolable y se verá que la afirmación que ha sido demostrada tiene una generalidad mayor que la originalmente percibida, puesto que se aplicará también a estas otras entidades. Por el contrario, si alguna de las hipótesis necesarias deja de ser válida para estas entidades alternativas, entonces la afirmación en cuestión puede resultar falsa para dichas entidades. (Por ejemplo, es importante darse cuenta de que en las demostraciones del teorema de Pitágoras dadas en §2.2 se utilizaba el postulado de las paralelas, por lo que el teorema es realmente falso en la geometría hiperbólica.)
En el argumento anterior, las entidades originales son números enteros y estamos interesados en aquellos números —los números racionales— que se construyen como cocientes de enteros. Con tales números se da realmente el caso de que ninguno de ellos tiene 2 como cuadrado. Pero hay otros tipos de números además de los simples enteros y racionales. En realidad, la necesidad para una raíz cuadrada de 2 obligó a los antiguos griegos, muy en contra de su voluntad en aquel tiempo, a salir de los confines de los números enteros y los racionales, los únicos tipos de números que previamente habían estado dispuestos a aceptar. El tipo de número al que se vieron llevados fue el que hoy día llamamos un «número real»: un número que ahora expresamos mediante un desarrollo decimal interminable (aunque una representación semejante no estaba disponible para los antiguos griegos). De hecho, 2 tiene una raíz cuadrada dentro de los números reales, a saber (como ahora la escribiríamos):
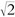 = 1,414 213 562 373 095 048 801 688 72 …
= 1,414 213 562 373 095 048 801 688 72 …
En la próxima sección consideraremos con más detalle el estatus físico de tales números «reales».
Como curiosidad, podemos preguntar por qué la demostración anterior de la no existencia de una raíz cuadrada de 2 falla para números reales (o para razones de números reales, lo que es equivalente). ¿Qué sucede si reemplazamos «entero» por «número real» en todo el argumento? La diferencia básica es que no es cierto que cualquier sucesión estrictamente decreciente de reales positivos (o incluso de fracciones) debe llegar a un final, y el argumento se viene abajo en ese punto.[3] (Consideremos, por ejemplo, la secuencia interminable 1, 1/2, 1/4, 1/8, 1/16, 1/32, …, .) A uno podría preocuparle qué sería un número real «impar» y «par» en este contexto. De hecho, el argumento no encuentra ninguna dificultad en este punto porque todos los números reales tendrían que contar como «pares», puesto que para cualquier real a hay siempre un real c tal que a = 2c, al ser siempre posible la división por 2 para los reales.
3.2. EL SISTEMA DE LOS NÚMEROS REALES
Así fue como los griegos se vieron obligados a admitir que los números racionales no son suficientes para desarrollar adecuadamente las ideas de la geometría (de Euclides). Hoy día no nos preocupa excesivamente que cierta cantidad geométrica no pueda ser medida en términos de números racionales simplemente. Esto se debe a que la noción de un «número real» resulta muy familiar para nosotros. Aunque nuestras calculadoras de bolsillo expresan los números mediante un número finito de dígitos, aceptamos que esta es una aproximación a la que nos obliga el hecho de que la calculadora es un objeto finito. Estamos dispuestos a admitir que el número matemático ideal (platónico) podría requerir que el desarrollo decimal se prolongue indefinidamente. Esto se aplica, por supuesto, incluso a la representación decimal de la mayoría de las fracciones, tales como
 = 0,333 333 333 …,
= 0,333 333 333 …,
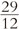 = 2,416 666 666 …,
= 2,416 666 666 …,
 = 1,285 714 285 714 285 …,
= 1,285 714 285 714 285 …,
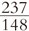 = 1,601 351 351 35 … .
= 1,601 351 351 35 … .
En el caso de una fracción, el desarrollo decimal siempre acaba siendo periódico, lo que quiere decir que llega un momento en que la secuencia infinita de dígitos consiste en una secuencia finita que se repite indefinidamente. En los ejemplos anteriores, las secuencias repetidas son 3, 6, 285714 y 135, respectivamente.
Los desarrollos decimales no estaban disponibles para los antiguos griegos, pero ellos tenían sus propios modos de entender los números irracionales. En efecto, lo que adoptaron era un sistema de representación de números en términos de lo que ahora llamamos fracciones continuas. No hay necesidad de entrar aquí en detalles, pero es apropiado hacer algunos breves comentarios. Una fracción continua[4] es una expresión finita o infinita a + (b + (c + (d + …)–1)–1)–1, donde a, b, c, d, … son enteros positivos:

Cualquier número racional mayor que 1 puede escribirse como una de estas expresiones terminada (donde, para evitar ambigüedades, exigimos normalmente que el último entero sea mayor que 1), por ejemplo, 52/9 = 5 + (1 + (3 + (2)–1)–1)–1:
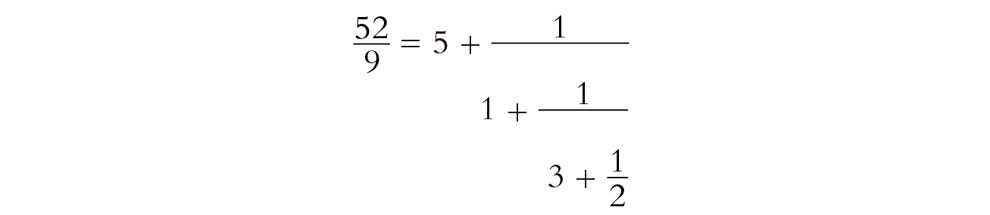
y, para representar un racional positivo menor que 1, simplemente admitimos que el primer entero en la expresión sea cero. Para expresar un número real, que no es racional, simplemente[3.1] permitimos que la expresión de la fracción continua siga de manera indefinida, siendo algunos ejemplos[5]
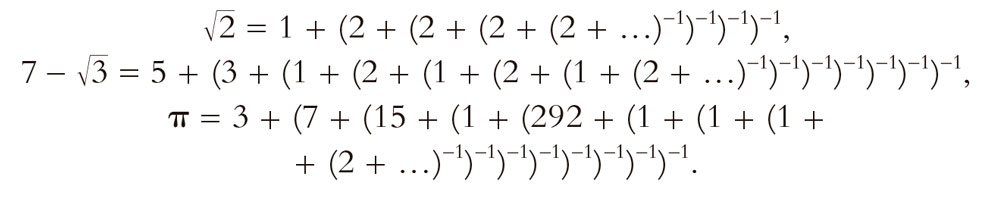
En los dos primeros de estos ejemplos infinitos, las secuencias de números naturales que aparecen —a saber, 1, 2, 2, 2, 2, … en el primer caso y 5, 3, 1, 2, 1, 2, 1, 2, … en el segundo— tienen la propiedad de que son finalmente periódicas (repitiéndose indefinidamente el 2 en el primer caso y repitiéndose indefinidamente la secuencia 1, 2 en el segundo).[3.2] Recordemos que, como ya se ha advertido antes, en la notación decimal familiar, son los números racionales los que tienen expresiones (finitas o) finalmente periódicas. Por otra parte, podemos considerar que una virtud de la representación de «fracción continua» griega es que los números racionales tienen ahora siempre una descripción finita. Una pregunta natural que se puede plantear en este contexto es: ¿qué números tienen una representación en forma de fracción continua finalmente periódica? Un teorema notable, demostrado por primera vez que sepamos por el gran matemático del siglo XVIII Joseph L. Lagrange (cuyas otras ideas más importantes encontraremos más adelante, en particular en el capítulo 20), dice que los números cuyas representaciones en términos de fracciones continuas son finalmente periódicas son los denominados irracionales cuadráticos.[6]
¿Qué es un irracional cuadrático y qué importancia tiene para la geometría griega? Es un número que puede escribirse en la forma
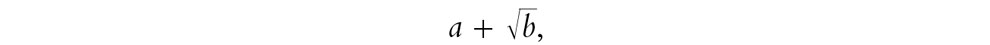
donde a y b son fracciones, y donde b no es un cuadrado perfecto. Estos números son importantes en geometría euclídea porque son los números irracionales más inmediatos que se encuentran en las construcciones con regla y compás. (Recordemos el teorema de Pitágoras, que en §3.1 nos ha llevado por primera vez a considerar el problema de 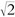 , y otras construcciones sencillas de longitudes euclídeas nos llevaron directamente a otros números de la forma anterior.)
, y otras construcciones sencillas de longitudes euclídeas nos llevaron directamente a otros números de la forma anterior.)
Ejemplos concretos de irracionales cuadráticos son aquellos casos donde a = 0 y b es un número natural (no cuadrado) o racional mayor que 1, por ejemplo:

La representación de fracción continua de un número semejante es especialmente sorprendente. La secuencia de números naturales que la define como una fracción continua tiene una curiosa propiedad característica. Empieza con cierto número A, que luego es seguido inmediatamente por una secuencia «palindrómica» (i.e., una que se lee igual hacia atrás), B, C, D, …, D, C, B, seguida por 2A, tras el cual la propia secuencia B, C, D, …, D, C, B, 2A se repite indefinidamente. El número ŒW14 es un buen ejemplo, para el que la secuencia es
3, 1, 2, 1, 6, 1, 2, 1, 6, 1, 2, 1, 6, 1, 2, 1, 6, …
Aquí A = 3 y la secuencia palindrómica B, C, D, …, D, C, B es simplemente la secuencia de tres términos 1, 2, 1.
¿Cuánto de esto era conocido por los antiguos griegos? Parece probable que conocían mucho —muy posiblemente todas las cosas que he descrito antes (incluido el teorema de Lagrange)—, aunque quizá carecieran de demostraciones rigurosas para todo. Al parecer, gran parte de esto fue establecido por Teeteto, contemporáneo de Platón. Parece incluso que hay alguna evidencia de este conocimiento (incluidas las secuencias palindrómicas repetidas antes mencionadas) manifiesta en la dialéctica de Platón.[7]
Aunque la incorporación de los irracionales cuadráticos nos acerca algo hacia los números adecuados para la geometría euclídea, no hace todo lo que se necesita. En el décimo (y más difícil) libro de Euclides se consideran números como 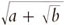 (con a y b racionales positivos). Estos no son generalmente irracionales cuadráticos, pero se dan, de todas formas, en construcciones de regla y compás. Números suficientes para tales construcciones geométricas serían aquellos que pueden formarse a partir de números naturales por uso repetido de las operaciones de adición, sustracción, multiplicación, división, y toma de la raíz cuadrada. Pero operar exclusivamente con tales números se hace muy complicado, y estos números son todavía demasiado limitados para consideraciones de geometría euclídea que van más allá de las construcciones de regla y compás. Es mucho más satisfactorio dar el paso capital —y hasta qué punto es capital se indicará en §§16.3-5— de permitir expresiones de fracciones continuas infinitas que son completamente generales. Esto proporcionó a los griegos una forma de describir números que resulta adecuada para la geometría euclídea.
(con a y b racionales positivos). Estos no son generalmente irracionales cuadráticos, pero se dan, de todas formas, en construcciones de regla y compás. Números suficientes para tales construcciones geométricas serían aquellos que pueden formarse a partir de números naturales por uso repetido de las operaciones de adición, sustracción, multiplicación, división, y toma de la raíz cuadrada. Pero operar exclusivamente con tales números se hace muy complicado, y estos números son todavía demasiado limitados para consideraciones de geometría euclídea que van más allá de las construcciones de regla y compás. Es mucho más satisfactorio dar el paso capital —y hasta qué punto es capital se indicará en §§16.3-5— de permitir expresiones de fracciones continuas infinitas que son completamente generales. Esto proporcionó a los griegos una forma de describir números que resulta adecuada para la geometría euclídea.
Estos números son en realidad, en terminología moderna, los denominados «números reales». Aunque se considera que una definición completamente satisfactoria de tales números no fue encontrada hasta el siglo XIX (con el trabajo de Dedekind, Cantor y otros), el gran matemático y astrónomo griego Eudoxo, que había sido uno de los discípulos de Platón, había obtenido las ideas esenciales ya en el siglo IV a.C. Aquí resulta apropiado comentar las ideas de Eudoxo.
En primer lugar, notemos que los números en geometría euclídea pueden expresarse en términos de razones de longitudes, más que directamente en términos de longitudes. De esta forma, no se necesitaba ninguna unidad específica de longitud (tal como la «pulgada» o el «dactylos» griego). Además, con razones de longitudes no habría restricciones en cuanto al número de tales razones que podían multiplicarse (obviando la aparente necesidad de «hipervolúmenes» en dimensiones más altas cuando se multiplican más de tres longitudes). El primer paso en la teoría de Eudoxo consistía en proporcionar un criterio acerca de cuándo una razón de longitudes a : b sería mayor que otra razón semejante c : d. Este criterio es que existen ciertos enteros positivos M y N tales que la longitud a sumada a sí misma M veces supera a b sumada a sí misma N veces, mientras que también d sumada a sí misma N veces supera a c sumada a sí misma M veces.[3.3] Un criterio correspondiente es válido para expresar la condición de que la razón a : b es menor que la razón c : d. La condición para la igualdad de ambas razones sería que no se cumpla ninguno de estos criterios. Con esta ingeniosa noción de «igualdad» de tales razones, Eudoxo tenía, en efecto, un concepto abstracto de «número real» en términos de razones de longitudes. Él también proporcionó reglas para la suma y el producto de tales números reales.[3.4]
Sin embargo, había una diferencia básica en el punto de vista entre la noción griega de número real y la moderna, porque los griegos creían que el sistema de números nos estaba básicamente «dado» en términos de la noción de distancia en el espacio físico, de modo que el problema consistía en tratar de establecer cómo se comportaban realmente estos números «distancia»; pues el propio «espacio» podría haber parecido un absoluto platónico incluso si los objetos físicos reales existentes en dicho espacio estuvieran inevitablemente muy lejos del ideal platónico.[8] (Sin embargo, en §17.9 y §§19.6,8 veremos que la teoría de la relatividad general de Einstein ha cambiado ahora esta perspectiva del espacio y la materia de un modo fundamental.)
Un objeto físico tal como un cuadrado dibujado en la arena o un cubo esculpido en mármol podría haber sido considerado por los antiguos griegos como una razonable o a veces una excelente aproximación al ideal geométrico platónico. Pese a todo, cualquier objeto semejante proporcionaría en cualquier caso una mera aproximación. Detrás de tales aproximaciones a las formas platónicas —así hubiera parecido— estaría el propio espacio: una entidad de existencia tan abstracta o conceptual que muy bien podría haber sido considerada como una realización directa de una realidad platónica. La medida de distancia en esta geometría ideal sería algo a determinar; en consecuencia, sería apropiado tratar de extraer esta noción ideal de número real de una geometría del espacio que se suponía dada. De hecho, esto es lo que Eudoxo consiguió hacer.
No obstante, en los siglos XIX y XX había surgido la idea de que la noción matemática de número debería presentarse con independencia de la naturaleza del espacio físico. Puesto que se había demostrado que existían geometrías matemáticamente consistentes diferentes de la de Euclides, resultaba inoportuno insistir en que la noción matemática de «geometría» debería ser extraída necesariamente de la naturaleza supuesta del espacio físico «real». Además, podría ser muy difícil, si no imposible, establecer la naturaleza detallada de esta supuesta «geometría física platónica» subyacente en términos del comportamiento de objetos físicos imperfectos. Para conocer la naturaleza de los números de acuerdo con los cuales debe definirse la «distancia geométrica», por ejemplo, sería necesario saber qué sucede tanto a distancias infinitamente minúsculas como infinitamente grandes. Incluso hoy, estas cuestiones no tienen una clara respuesta (y las abordaré de nuevo en capítulos posteriores). Así pues, era mucho más oportuno establecer la naturaleza del número de un modo que no remitiera directamente a medidas físicas. En consecuencia, Richard Dedekind y Georg Cantor elaboraron sus ideas de lo que «son» los números reales mediante el uso de nociones que no se refieren directamente a la geometría.
Dedekind define un número real a partir de conjuntos infinitos de números racionales. Lo que se hace, básicamente, es considerar que los números racionales, tanto positivos como negativos (y el cero), están dispuestos en orden de tamaño. Podemos imaginar que este ordenamiento tiene lugar de izquierda a derecha, considerando que los racionales negativos se extienden indefinidamente hacia la izquierda, y los racionales positivos se extienden indefinidamente hacia la derecha, estando 0 en el centro. (Esto es solo para propósitos de visualización; de hecho, el procedimiento de Dedekind es completamente abstracto.) Dedekind imagina un «corte» que divide esta disposición claramente en dos, de modo que aquellos números que están a la izquierda del corte son más pequeños que los que están a la derecha. Cuando el «filo del cuchillo» que hace el corte no «incide» sobre un número racional sino que cae entre ellos, entonces decimos que define un número real irracional. Dicho de forma más correcta, esto ocurre cuando los que están a la izquierda no tienen un miembro máximo, y los que están a la derecha no tienen un miembro mínimo. Cuando se añade el sistema de los «irracionales», definidos en términos de tales «cortes», al sistema de los números racionales que ya teníamos, se obtiene la familia completa de los números reales.
El procedimiento de Dedekind conduce directamente, por medio de simples definiciones, a las leyes de adición, sustracción, multiplicación y división de números reales. Además, permite ir más allá y definir límites, mediante los cuales pueden asignarse significados en números reales a cosas tales como la fracción continua infinita que hemos visto antes
1 + (2 + (2 + (2 + (2 + …)–1)–1)–1)–1
o la suma infinita
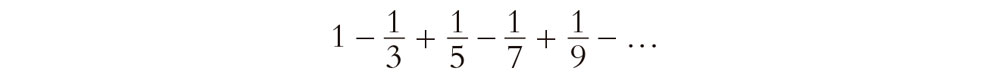
De hecho, la primera nos da el número irracional 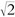 y la segunda,
y la segunda,  π. La capacidad de tomar límites es fundamental para muchas nociones matemáticas, y es esto lo que da a los números reales su fuerza especial.[9] (Quizá el lector recuerde que la necesidad de «procedimientos de paso al límite» era un requisito para la definición general de áreas, como se ha indicado en §2.3).
π. La capacidad de tomar límites es fundamental para muchas nociones matemáticas, y es esto lo que da a los números reales su fuerza especial.[9] (Quizá el lector recuerde que la necesidad de «procedimientos de paso al límite» era un requisito para la definición general de áreas, como se ha indicado en §2.3).
3.3. LOS NÚMEROS REALES EN EL MUNDO FÍSICO
Aquí estamos tocando una cuestión profunda. Una fuerza impulsora inicial en el desarrollo de las ideas matemáticas ha sido siempre el intento de encontrar estructuras matemáticas que reflejen de forma precisa el comportamiento del mundo físico. Pero normalmente no es posible examinar el propio mundo físico con un detalle tan preciso que de él puedan extraerse directamente nociones matemáticas de la claridad adecuada. El progreso se produce más bien debido a que las nociones matemáticas tienden a tener un «impulso» propio que parece brotar casi por entero del interior de la propia disciplina. Las ideas matemáticas evolucionan, y varios tipos de problemas parecen surgir de forma natural. Algunos de estos (como sucedió con el problema de encontrar la longitud de la diagonal de un cuadrado) pueden llevar a una ampliación esencial de los propios conceptos matemáticos en cuyos términos se había formulado originalmente el problema. Puede parecer que tales ampliaciones nos vienen obligadas, o también pueden surgir de maneras que parecen ser cuestiones de conveniencia, consistencia o elegancia matemática. En consecuencia, podría parecer que el desarrollo de las matemáticas se aleja de lo que se habían propuesto conseguir, a saber: reflejar el comportamiento físico. Pero, en muchos casos, este mismo impulso hacia la consistencia y elegancia matemáticas nos lleva a estructuras y conceptos matemáticos que resultan reflejar el mundo físico de una forma mucho más profunda y de mayor alcance que aquellas de las que partimos. Es como si la propia naturaleza se guiara por el mismo tipo de criterios de consistencia y elegancia que guían al pensamiento matemático humano.
Un ejemplo de esto es el propio sistema de los números reales. No tenemos ninguna evidencia directa en la naturaleza de que haya una noción física de «distancia» que se extienda hasta escalas arbitrariamente grandes; menos evidencia hay aún de que semejante noción sea aplicable en el nivel infinitamente minúsculo. En realidad, no hay evidencia de que existan «puntos en el espacio» de acuerdo con una geometría que haga uso precisamente de distancias en números reales. En la época de Euclides había escasa evidencia para apoyar siquiera la pretensión de que tales «distancias» euclídeas se extendían hacia fuera hasta más allá de, digamos, unos 1012 metros,[10] o hacia dentro, hasta algo tan pequeño como 10–5 metros. Pero, al haber sido impulsadas matemáticamente por la consistencia y elegancia del sistema de los números reales, todas nuestras teorías físicas satisfactorias y de más amplio alcance hasta la fecha han seguido ateniéndose, sin excepción, a esta antigua noción de «número real». Aunque podría parecer que ha habido muy poca justificación para hacer esto a partir de la evidencia de que se disponía en la época de Euclides, nuestra fe en el sistema de los números reales parece haberse visto recompensada. En efecto, nuestras modernas y satisfactorias teorías cosmológicas nos permiten ahora ampliar el rango de nuestras distancias en números reales hasta aproximadamente 1026 metros o más, mientras que la precisión de nuestras teorías de la física de partículas extiende este rango hacia dentro, hasta 10–17 metros o menos. (La única escala para la que se ha propuesto con seriedad que podría llegar un cambio es de unos dieciocho órdenes de magnitud inferior a esta, a saber 10–35 metros, que es la «escala de Planck» de la gravitación cuántica que cobrará una importancia especial en nuestras discusiones posteriores; por ejemplo, §§31.1,6-12,14 y §32.7.) Puede considerarse una notable justificación de nuestro uso de idealizaciones matemáticas el hecho de que el rango de validez del sistema de los números reales se ha ampliado desde un total de aproximadamente 1017, desde lo más pequeño a lo más grande, que parecía adecuado en la época de Euclides, hasta al menos los 1043 que nuestras teorías actuales utilizan directamente, lo que supone un extraordinario incremento en un factor de 1026.
Hay mucho más a favor de la validez física del sistema de los números reales. En primer lugar, debemos considerar que también las áreas y los volúmenes son magnitudes para las que convienen medidas muy precisas en números reales. Una medida de volumen es el cubo de una medida de distancia (y un área es el cuadrado de una distancia). En consecuencia, en el caso de los volúmenes podemos considerar que el intervalo relevante es el cubo del anterior. Así, para la época de Euclides esto nos daría un rango de aproximadamente (1017)3 = 1051; para las teorías actuales, el intervalo es al menos (1043)3 = 10129. Además, existen otras medidas físicas que requieren descripciones en números reales, según las teorías que hoy día resultan satisfactorias. La más digna de mención de estas es el tiempo. Según la teoría de la relatividad, este tiene que añadirse al espacio para que nos proporcione el espaciotiempo (que será objeto de nuestro estudio en el capítulo 17). Los volúmenes espaciotemporales son tetradimensionales, y muy bien podría considerarse que el rango temporal (de nuevo de aproximadamente 1043 o más en rango total, en nuestras teorías mejor comprobadas) debería ser incorporado también en nuestras consideraciones, dando así un total del orden de 10172. Veremos algunos números reales todavía mucho mayores que este cuando lleguemos a nuestras consideraciones posteriores (véanse §27.13 y §28.7), aunque en algunos casos no esté realmente claro que sea esencial el uso de números reales (antes que, por ejemplo, enteros).
Más importante para la teoría física es el hecho de que, desde Arquímedes hasta Maxwell, Einstein, Schrödinger, Dirac y otros, pasando por Galileo y Newton, un papel crucial del sistema de los números reales ha consistido en proporcionar un marco necesario para la formulación estándar del cálculo infinitesimal (véase el capítulo 6). Todas las teorías dinámicas satisfactorias han requerido para su formulación las nociones del cálculo. Ahora bien, el enfoque convencional del cálculo requiere que la naturaleza infinitesimal de los reales sea la que es. Es decir, en el extremo inferior de la escala es el rango entero de los números reales el que está siendo utilizado. Las ideas del cálculo infinitesimal subyacen en otras nociones físicas, tales como velocidad, momento o energía. En consecuencia, el sistema de los números reales entra en nuestras teorías físicas satisfactorias de una manera fundamental para nuestra descripción de todas aquellas magnitudes. Aquí, como se ha mencionado antes en relación con las áreas, en §2.3 y §3.2, se está invocando el límite infinitesimal de la estructura a pequeña escala del sistema de los números reales.
Pese a todo, podemos seguir preguntándonos si el sistema de los números reales es realmente «correcto» para la descripción de la realidad física en sus niveles más profundos. Cuando empezaron a introducirse las ideas mecanocuánticas a comienzos del siglo XX, existía la sensación de que quizá entonces empezábamos a ser testigos de una naturaleza discreta o granular del mundo físico en sus escalas más pequeñas.[11] Aparentemente, la energía solo podía existir en paquetes discretos —o «cuantos»— y las magnitudes físicas de «acción» y «espín» parecen darse solo en múltiplos discretos de una unidad fundamental (véanse §§20.1,5 para el concepto clásico de acción y §26.6 para su contrapartida cuántica; véanse §§22.8-12 para el espín). Por ello, varios físicos intentaron construir una imagen alternativa del mundo en la que procesos discretos gobernaban todas las acciones en los niveles más ínfimos.
Sin embargo, y tal como ahora entendemos la mecánica cuántica, esta teoría no nos obliga (ni siquiera nos lleva) a la idea de que hay una naturaleza discreta o granular para el espacio, el tiempo o la energía en sus niveles más ínfimos (véanse los capítulos 21 y 22, en particular la última frase de §22.13). En cualquier caso, nos ha quedado la idea de que quizá haya realmente una discretización tal en la naturaleza, pese al hecho de que la mecánica cuántica, en su formulación estándar, no implica esto ni mucho menos. Por ejemplo, el gran físico cuántico Erwin Schrödinger fue uno de los primeros en sugerir que podría ser necesario un cambio hacia alguna forma de discretización espacial fundamental:[12]
La idea de un rango continuo, tan familiar para los matemáticos de nuestros días, es algo bastante exorbitante, una enorme extrapolación de lo que es accesible para nosotros.
Relacionó dichas propuestas con algunas ideas griegas antiguas relativas a la discretización de la naturaleza. También Einstein sugirió, en sus últimas palabras publicadas, que una teoría («algebraica») basada en la discretización podría ser el camino hacia la física futura:[13]
Se pueden dar buenas razones por las que la realidad no puede representarse como un campo continuo … Los fenómenos cuánticos … deben llevar a un intento de encontrar una teoría puramente algebraica para la descripción de la realidad. Pero nadie sabe cómo obtener la base de una teoría semejante.[14]
Otros[15] también han perseguido ideas de este tipo (véase §33.1). A finales de la década de 1950, yo mismo ensayé algo parecido, llegando a un esquema al que denominé teoría de «redes de espín», en la que la naturaleza discreta del espín mecanocuántico se toma como el bloque constituyente fundamental para un enfoque combinatorio (i.e., discreto en lugar de basado en números reales) de la física (este esquema se describirá brevemente en §32.6). Aunque mis propias ideas en esta dirección no se desarrollaron hasta convertirse en una teoría global (si bien en cierto sentido se metamorfosearon más tarde en la «teoría de twistores»; véase §33.2), la teoría de redes de espín ha sido ahora importada, por otros, en uno de los programas principales para atacar el problema fundamental de la gravitación cuántica.[16] Daré breves descripciones de estas ideas en el capítulo 32. En cualquier caso, tal como hoy se ensaya y pone a prueba la teoría física —y como lo ha sido durante los veinticuatro siglos pasados—, los números reales siguen constituyendo un ingrediente esencial en nuestra comprensión del mundo físico.
3.4. ¿NECESITAN LOS NÚMEROS NATURALES AL MUNDO FÍSICO?
En la descripción anterior, en §3.2, de la aproximación de Dedekind al sistema de los números reales, he supuesto que los números racionales se daban por «entendidos». De hecho, no es difícil pasar de los enteros a los racionales. Los racionales son simplemente razones de enteros (véase el prefacio). ¿Qué pasa entonces con los enteros propiamente dichos? ¿Están enraizados en ideas físicas? Incluso los enfoques discretos de la física, que se mencionaron en los dos párrafos anteriores, dependen de nuestra noción de número natural (i.e., «número para recuento») y su extensión, mediante la inclusión de los números negativos, a los enteros. Los griegos no consideraban los números negativos como «números» en acto, así que continuemos nuestras consideraciones preguntando primero por el estatus físico de los propios números naturales.
Los números naturales son las cantidades que ahora denotamos por 0, 1, 2, 3, 4, etc., i.e., son los números enteros no negativos. (Hoy se incluye al 0 en esta lista, lo que es apropiado desde el punto de vista matemático, aunque parece que los antiguos griegos no reconocieron el «cero» como un número en acto. Esto tuvo que esperar hasta los matemáticos hindúes de la India, empezando con Brahmagupta en el siglo VII y seguido de Mahavira y Bhaskara en los siglos IX y XII, respectivamente.) El papel de los números naturales es claro e inequívoco. Son los «números para recuento» más elementales, y tienen un papel básico, cualesquiera que puedan ser las leyes de la geometría o de la física. Los números naturales están sujetos a ciertas operaciones familiares, muy en especial las operaciones de adición (tal como 37 + 79 = 116) y multiplicación (por ejemplo, 37 × 79 = 2.923), que permiten combinar pares de números naturales para producir nuevos números naturales. Estas operaciones son independientes de la geometría del mundo.
No obstante, podemos plantear la cuestión de si los propios números naturales tienen un significado o existencia con independencia de la naturaleza real del mundo físico. Quizá nuestra noción de los números naturales depende de que en nuestro universo haya objetos discretos razonablemente bien definidos y que persisten en el tiempo. Después de todo, los números naturales aparecen inicialmente cuando queremos contar cosas. Pero esto parece depender de que existan realmente «cosas» persistentes y distinguibles en el universo que estén disponibles para ser «contadas». Supongamos, por el contrario, que nuestro universo fuera tal que el número de los objetos tuviese tendencia a variar. ¿Realmente serían los números naturales conceptos «naturales» en un universo semejante? Más aún, quizá el universo contenga solo un número finito de «objetos», en cuyo caso ¡los propios números «naturales» podrían terminar en algún punto! Podemos concebir incluso un universo que consista solo en una sustancia amorfa e indiferenciada, para la cual la noción misma de cuantificación numérica podría parecer intrínsecamente inadecuada. ¿Tendría la noción de «número natural» la más mínima relevancia para la descripción de universos de este tipo?
Aunque muy bien pudiera darse el caso de que los habitantes de un universo semejante encontraran difícil de captar nuestro concepto matemático presente de «número natural», es difícil imaginar que no siguiera habiendo un papel importante para entidades tan fundamentales. Hay varias formas de introducir los números naturales en las matemáticas puras, y estas no parecen depender en absoluto de la naturaleza real del mundo físico. Básicamente, es la noción de un «conjunto» la que necesita ser invocada, siendo esta una noción abstracta que no parece estar relacionada de ninguna manera esencial con la estructura específica del universo físico. De hecho, existen ciertas sutilezas, concernientes a esta cuestión, y volveré a ello más adelante (en §16.5). Por el momento, será conveniente ignorar tales sutilezas.
Consideremos un modo (anticipado por Cantor y defendido por el destacado matemático John von Neumann) de introducir los números naturales utilizando simplemente la noción abstracta de conjunto. Este procedimiento permite definir lo que se denominan «números ordinales». Al conjunto más simple de todos se le llama «conjunto nulo» o «conjunto vacío», y está caracterizado por el hecho de que ¡no contiene ningún miembro! El conjunto vacío se suele denotar por el símbolo Ø, y podemos escribir esta definición
Ø = { },
donde los corchetes delimitan un conjunto, el conjunto específico bajo consideración, que tiene como miembros las cantidades indicadas dentro de los corchetes. En este caso, no hay nada dentro de los corchetes, de modo que el conjunto descrito es realmente el conjunto vacío. Asociemos Ø con el número natural 0. Ahora podemos continuar y definir el conjunto cuyo único miembro es Ø; i.e., el conjunto {Ø}. Es importante darse cuenta de que {Ø} no es el mismo conjunto que el conjunto vacío Ø. El conjunto {Ø} tiene un miembro (a saber, Ø), mientras que el propio Ø no tiene ninguno. Asociemos {Ø} con el número natural 1. A continuación definimos el conjunto cuyos dos miembros son los dos conjuntos que ya hemos encontrado, a saber Ø y {Ø}, de modo que este nuevo conjunto es {Ø, {Ø}}, que será asociado con el número natural 2. Luego asociamos con 3 la colección de las tres entidades que hemos encontrado hasta ahora, a saber, el conjunto {Ø, {Ø}, {Ø, {Ø}}}, y con 4 el conjunto {Ø, {Ø}, {Ø, {Ø}}, {Ø, {Ø}, {Ø, {Ø}}}}, cuyos miembros son de nuevo los conjuntos que hemos encontrado previamente, y así sucesivamente. Quizá no sea así como se consideran normalmente los números naturales, en cuanto a su definición, pero es una de las formas en que los matemáticos pueden llegar al concepto. (Compárese esto con la exposición del prefacio.) Más aún, nos muestra, al menos, que cosas como los números naturales[17] pueden ser extraídas literalmente de la nada, empleando solo la noción abstracta de «conjunto». Obtenemos una secuencia infinita de entidades matemáticas abstractas («platónicas»): conjuntos que contienen, respectivamente, cero, uno, dos, tres, etc., elementos, un conjunto por cada uno de los números naturales, de forma completamente independiente de la naturaleza física real del universo. En la Fig. 1.3 imaginábamos un tipo de «existencia» independiente para las nociones matemáticas platónicas —en este caso, los propios números naturales—, pero esta «existencia» puede ser extraída en apariencia, y ciertamente puede accederse a ella, por el mero ejercicio de nuestra imaginación, sin ninguna referencia a los detalles de la naturaleza del universo físico. Además, la construcción de Dedekind muestra cómo puede llevarse más lejos este tipo de procedimiento «puramente mental», lo que nos permite «construir» el sistema entero de los números reales,[18] sin ninguna referencia tampoco a la naturaleza física real del mundo. Pese a todo, y como se ha señalado antes, los «números reales» parecen tener realmente una relevancia directa para la estructura real del mundo, lo que ilustra la muy misteriosa naturaleza del «primer misterio» representado en la Fig. 1.3.
3.5. NÚMEROS DISCRETOS EN EL MUNDO FÍSICO
Pero me estoy adelantando un poco a mis propósitos. Podemos recordar que la construcción de Dedekind utilizaba realmente conjuntos de números racionales, y no directamente de números naturales. Como se ha mencionado antes, no es difícil «definir» lo que entendemos por número racional una vez que tenemos la noción de número natural. Pero, como paso intermedio, es oportuno definir la noción de entero, que es un número natural o el negativo de un número natural (siendo el número cero su propio negativo). En un sentido formal, no hay ninguna dificultad para dar una definición matemática de «negativo»: dicho de forma muy tosca, simplemente añadimos un «signo», escrito como «–», a cada número natural (excepto el 0) y definimos consistentemente todas las reglas aritméticas de adición, sustracción, multiplicación y división (excepto por cero). Sin embargo, esto no aborda la cuestión del «significado físico» de un número negativo. ¿Qué podría significar, por ejemplo, decir que hay menos tres vacas en un campo?
Creo que está claro que, a diferencia de los propios números naturales, no hay contenido físico evidente para la noción de un número negativo de objetos físicos. Ciertamente, los enteros negativos tienen un papel organizador extraordinariamente valioso, como se ve en los balances bancarios y otras transacciones financieras. Pero ¿tienen relevancia directa para el mundo físico? Cuando digo «relevancia directa», no me estoy refiriendo a circunstancias donde podría parecer que son los números reales negativos los que constituyen las medidas relevantes, como sucede cuando una distancia medida en una dirección cuenta como positiva mientras que medida en dirección contraria contaría como negativa (o lo mismo con respecto al tiempo, en cuyo caso el tiempo que se extiende hacia el pasado cuenta como negativo). Me estoy refiriendo más bien a números que son cantidades escalares, en el sentido de que no hay un aspecto direccional (o temporal) en la magnitud en cuestión. En estas circunstancias, parece ser que es el sistema de los enteros, tanto positivos como negativos, el que tiene relevancia física directa.
Resulta notable que solo en los últimos cien años aproximadamente se ha hecho manifiesto que el sistema de los enteros parece tener realmente una relevancia física directa. El primer ejemplo de una magnitud física que parece estar cuantificada apropiadamente por enteros es la carga eléctrica.[19] Hasta donde sabemos (aunque todavía no hay una completa justificación teórica para ello), la carga eléctrica de cualquier cuerpo discreto aislado está realmente cuantificada en términos de múltiplos enteros, positivos, negativos o nulos, de un valor concreto, a saber, la carga del protón (o del electrón, que es la negativa de la del protón).[20] Ahora pensamos que los protones son objetos compuestos construidos a partir de entidades más pequeñas conocidas como «quarks» (y otras entidades sin carga denominadas «gluones»). Hay tres quarks en cada protón, que tienen cargas eléctricas con valores respectivos de 2/3, 2/3, –1/3. La suma de estas cargas constituyentes da un valor total de 1 para el protón. Si los quarks son entidades fundamentales, entonces la unidad básica de carga es un tercio de la que parecíamos tener antes. En cualquier caso, sigue siendo cierto que la carga eléctrica se mide en términos de enteros, aunque ahora son múltiplos enteros de un tercio de la carga del protón. (El papel de los quarks y los gluones en la moderna física de partículas se discutirá en §§25.3-7.)
La carga eléctrica es solo un ejemplo de lo que se denomina un número cuántico aditivo. Los números cuánticos son cantidades que sirven para caracterizar a las partículas de la naturaleza. Un número cuántico semejante, que consideraré aquí que es un número real de algún tipo, es «aditivo» si para obtener su valor para una entidad compuesta sumamos simplemente los valores individuales de las partículas constituyentes —teniendo en cuenta debidamente, por supuesto, los signos, como en el caso del protón y sus quarks constituyentes que se ha señalado antes—. Es un hecho muy sorprendente, de acuerdo con el estado actual de nuestro conocimiento físico, que todos los números cuánticos aditivos conocidos[21] estén cuantificados realmente en términos del sistema de los enteros, no en términos de números reales en general, ni tampoco de simples números naturales, de modo que realmente se dan los valores negativos.
De hecho, según la física del siglo XX, ahora hay un sentido en el que tiene significado referirse a un número negativo de entidades físicas. El gran físico Paul Dirac propuso, en 1929-1931, su teoría de las antipartículas, según la cual (tal como se entendió posteriormente) por cada tipo de partícula existe también su correspondiente antipartícula para la que cada número cuántico aditivo tiene exactamente el negativo del valor que tiene para la partícula original (véanse §§24.2,8). Así pues, el sistema de los enteros (incluidos los negativos) parece tener realmente una clara relevancia para el universo físico, una relevancia física que se ha hecho manifiesta solo en el siglo XX, a pesar de los muchos siglos durante los cuales los enteros han encontrado gran valor en las matemáticas, el comercio y muchas otras actividades humanas.
Llegados a este punto, habría que hacer una matización importante. Aunque es verdad que, en cierto sentido, un antiprotón es un protón negativo, no es realmente «menos un protón». La razón está en que la inversión de signo se refiere solo a los números cuánticos aditivos, mientras que la noción de masa no es aditiva en la teoría física moderna. Esta cuestión será explicada de manera más detallada en §18.7. «Menos un protón» tendría que ser un antiprotón cuya masa fuera el negativo del valor de la masa de un protón ordinario. Pero la masa de una partícula física real no puede ser negativa. Un antiprotón tiene la misma masa que un protón ordinario, que es una masa positiva. Veremos más adelante que, según las ideas de la teoría cuántica de campos, existen objetos denominados partículas «virtuales» para los que la masa (o, más correctamente, la energía) puede ser negativa. «Menos un protón» sería realmente un antiprotón virtual. Pero una partícula virtual no tiene una existencia independiente como la de una «partícula real».
Ahora nos haremos la correspondiente pregunta acerca de los números racionales. ¿Ha encontrado este sistema de números cualquier relevancia directa para el universo físico? Hasta donde sabemos, no parece que sea así, al menos en lo que respecta a la teoría convencional. Existen algunas curiosidades físicas[22] en las que la familia de los números racionales desempeña su papel, pero sería difícil sostener que esto revela algún papel físico fundamental para los números racionales. Por otra parte, pudiera ser que hubiera un papel especial para los racionales en las probabilidades mecanocuánticas fundamentales (donde una probabilidad racional representa una elección entre alternativas, cada una de las cuales implica solo un número finito de posibilidades). Este tipo de cosas desempeña un papel en la teoría de las redes de espín, como se describirá brevemente en §32.6. De momento, el estatus adecuado de estas ideas no está claro.
Pese a todo, existen otros tipos de números que, según la teoría aceptada, sí parecen desempeñar un papel fundamental en la marcha del universo. Los más importantes y sorprendentes de estos son los números complejos, en los que se introduce la cantidad aparentemente mística 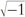 , normalmente denotada por «i», y se añade al sistema de los números reales. Encontrados por primera vez en el siglo XVI, pero tratados con desconfianza durante cientos de años, la utilidad matemática de los números complejos impresionó poco a poco a la comunidad matemática en un grado cada vez mayor, hasta que los números complejos se convirtieron en un ingrediente indispensable y casi mágico de nuestro pensamiento matemático. Y ahora encontramos que no solo son fundamentales para las matemáticas: estos extraños números desempeñan también un papel extraordinario y muy básico en el funcionamiento del universo físico en sus escalas más ínfimas. Esto produce asombro, y como ejemplo de la convergencia entre ideas matemáticas y los mecanismos más profundos del universo físico es más sorprendente incluso que el sistema de números reales que hemos estado considerando en esta sección. Vayamos ahora a estos números notables.
, normalmente denotada por «i», y se añade al sistema de los números reales. Encontrados por primera vez en el siglo XVI, pero tratados con desconfianza durante cientos de años, la utilidad matemática de los números complejos impresionó poco a poco a la comunidad matemática en un grado cada vez mayor, hasta que los números complejos se convirtieron en un ingrediente indispensable y casi mágico de nuestro pensamiento matemático. Y ahora encontramos que no solo son fundamentales para las matemáticas: estos extraños números desempeñan también un papel extraordinario y muy básico en el funcionamiento del universo físico en sus escalas más ínfimas. Esto produce asombro, y como ejemplo de la convergencia entre ideas matemáticas y los mecanismos más profundos del universo físico es más sorprendente incluso que el sistema de números reales que hemos estado considerando en esta sección. Vayamos ahora a estos números notables.
Notas
Sección 3.1
3.1.Las notaciones >, <, ≥, ≤, frecuentemente utilizadas en este libro, representan, respectivamente, «es mayor que», «es menor que», «es mayor o igual que» y «es menor o igual que».
3.2.Algunos lectores quizá conozcan un argumento aparentemente más corto que empieza exigiendo que a/b esté «en sus menores términos» (i.e., que a y b no tengan factores comunes). Sin embargo, esto supone que esta expresión en términos menores existe siempre, lo que, aunque sea completamente cierto, necesita ser demostrado. Encontrar una expresión en términos menores para una fracción dada A/B (implícita o explícitamente, utilizando el algoritmo de Euclides, pongamos por caso; véanse, por ejemplo, Hardy y Wright, 1945, p. 134; Davenport, 1952, p. 26; Littlewood, 1949, cap. 4, y Penrose, 1989, cap. 2) implica un razonamiento similar al dado en el texto, aunque más complicado.
3.3.Podría objetarse que resulta algo curioso utilizar números reales en la demostración anterior, puesto que los «racionales reales» (i.e., cocientes de reales) serían de nuevo números reales simplemente. Esto no invalida, sin embargo, lo que se acaba de decir. Puede señalarse que, en el argumento original, a y b se tomaban además enteros, y no racionales en sí mismos. En efecto, si a y b fueran meramente racionales, el argumento fallaría en la parte de la «secuencia decreciente», incluso si el propio resultado siguiera siendo cierto.
Sección 3.2
3.4.En una ojeada informal, expresiones como a + (b + (c + (d + …)–1)–1)–1 pueden parecer bastante extrañas. Sin embargo, son muy naturales en el contexto del pensamiento griego antiguo (aunque los griegos no utilizaban esta notación concreta). El algoritmo de Euclides se ha mencionado en la nota 3.2 en el contexto de encontrar la forma en términos más sencillos de una fracción. El algoritmo de Euclides (cuando se desenmaraña) lleva precisamente a dicha expresión como fracción continua. Los griegos aplicarían este mismo procedimiento a la razón de dos longitudes geométricas. En el caso más general, el resultado sería una fracción continua infinita, del tipo considerado aquí.
3.5.Para más información (con demostraciones) sobre fracciones continuas, véase la elegante exposición dada en el capítulo 4 de Davenport (1952). Puede señalarse que en ciertos aspectos la representación como fracciones continuas de los números reales es más profunda e interesante que la normal en términos de desarrollos decimales, y encuentra aplicaciones en muchas áreas diferentes de las matemáticas modernas, incluida la geometría hiperbólica examinada en §§2.4,5. Por otra parte, las fracciones continuas no son en absoluto apropiadas para (la mayor parte de) los cálculos prácticos, pues la representación decimal convencional es mucho más fácil de utilizar.
3.6.Los irracionales cuadráticos se denominan así porque aparecen en la solución de una ecuación cuadrática general
Ax2 + Bx + C = 0,
con A distinto de cero, cuya solución es
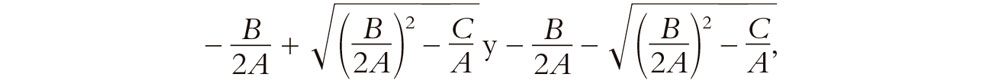
donde, para permanecer dentro del dominio de los números reales, debemos tener B2 mayor que 4AC. Cuando A, B y C son números enteros o racionales, y no hay solución racional para la ecuación, las soluciones son irracionales cuadráticos.
3.7.El profesor Stelios Negrepontis me informa de que esta evidencia se encuentra en el diálogo platónico El político, el tercero en la «trilogía» Teeteto-El sofista-El político. Véase Negrepontis (2000).
3.8.Para una exposición del pensamiento griego antiguo sobre la naturaleza del espacio, véase Sorabji (1983, 1988).
3.9.Véanse Hardy (1914), Conway (1976) y Burkill (1962).
Sección 3.3
3.10.La notación científica «1012» para «un millón de millones» hace uso de exponentes, como se describe en las notas 1.2 y 2.4. En este libro tenderé a evitar términos verbales tales como «millón», y en especial «billón», dando preferencia a esta notación científica mucho más clara. La palabra «billón» es particularmente confusa, pues en su uso estadounidense —ahora comúnmente adoptado también en el Reino Unido— «billón» se refiere a 109, mientras que en el uso más antiguo (y más lógico) en el Reino Unido, de acuerdo con la mayoría de las restantes lenguas europeas, se refiere a 1012. Los exponentes negativos, tales como en 10–6 (que se refiere a una «millonésima»), se utilizan también aquí de acuerdo con la notación científica normal.
La distancia 1012 metros es aproximadamente 7 veces la separación entre la Tierra y el Sol. Esta es aproximadamente la distancia al planeta Júpiter, aunque no era conocida en tiempos de Euclides y se hubiera conjeturado mucho menor.
3.11.Véase, por ejemplo, Russell (1903), cap. 4.
3.12.Schrödinger (1952), pp. 30-31.
3.13.Véase Stachel (1995).
3.14.Einstein (1955), p. 166.
3.15.Véanse, por ejemplo, Snyder (1947), Schild (1949) y Ahmavaara (1965).
3.16.Véanse Ashtekar (1986), Ashtekar y Lewandowski (2004), Smolin (1998, 2001) y Rovelli (1998, 2003).
Sección 3.4
3.17.La noción de «número ordinal», proporcionada aquí en el caso finito, se extiende también a números ordinales infinitos, de los que el menor es el «ω» de Cantor, que es la colección ordenada de todos los ordinales finitos.
3.18.No obstante, esta noción de «constructo» no debería tomarse en un sentido demasiado fuerte. En §16.6 encontraremos que hay ciertos números reales (de hecho, la mayoría de ellos) que son inaccesibles mediante cualquier procedimiento computacional.
Sección 3.5
3.19.El físico irlandés George Johnstone Stoney fue el primero, en 1874, en dar una (cruda) estimación de la carga eléctrica básica y, en 1891, acuñó el término «electrón» para esta unidad fundamental. En 1909, el físico estadounidense Robert Andrews Millikan diseñó su famoso experimento de la «gota de aceite», que demostró de forma precisa que la carga en cuerpos eléctricamente cargados (las gotas de aceite en su experimento) se da en múltiplos enteros de un valor bien definido: la carga del electrón.
3.20.En 1959, R.A. Lyttleton y H. Bondi propusieron que una ligerísima diferencia entre la carga del protón y (menos) la del electrón, del orden de una parte en 1018, podría explicar la expansión del universo (para la cual, véanse §§27.11,13, y el capítulo 28). Véase Lyttleton y Bondi (1959). Por desgracia para esta teoría, semejante discrepancia fue pronto refutada en varios experimentos. De todas formas, esta idea proporcionó un excelente ejemplo de pensamiento creativo.
3.21.Aquí estoy distinguiendo los números cuánticos «aditivos» de los números que los físicos llaman «multiplicativos», a los que llegaremos en §5.5.
3.22.Por ejemplo, en el «efecto Hall cuántico fraccionario» se observa que los números fraccionarios desempeñan un papel clave; véase, por ejemplo, Fröhlich y Pedrini (2000).