2
Un teorema antiguo y una pregunta moderna
2.1. EL TEOREMA DE PITÁGORAS
Consideremos la cuestión de la geometría. ¿Cuáles son, realmente, los diferentes «tipos de geometría» a los que he aludido en el capítulo anterior? Para abordar esta cuestión, volveremos a nuestro encuentro con Pitágoras y consideraremos el famoso teorema que lleva su nombre:[1] para cualquier triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados (Fig. 2.1). ¿Qué razones tenemos para creer que esta afirmación es cierta? ¿Cómo podemos «demostrar» realmente el teorema de Pitágoras? Se conocen muchos argumentos. Quiero considerar dos de ellos, elegidos por su especial transparencia, que ponen el acento en puntos diferentes.
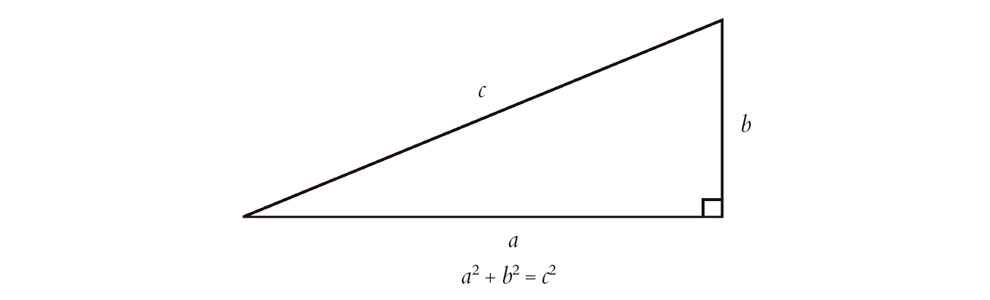
Fig. 2.1. El teorema de Pitágoras: para cualquier triángulo rectángulo, el cuadrado de la hipotenusa c es la suma de los cuadrados de los otros dos lados a y b.
En cuanto al primero, consideremos la estructura que se ilustra en la Fig. 2.2. Está compuesta enteramente por cuadrados de dos tamaños diferentes. Puede considerarse «obvio» que esta estructura puede prolongarse indefinidamente y que el plano entero queda así recubierto de forma regular y repetitiva, sin huecos ni solapamientos, por cuadrados de estos dos tamaños. La naturaleza repetitiva de esta estructura se hace manifiesta por el hecho de que si marcamos los centros de los cuadrados más grandes, dichos centros constituyen los vértices de otro sistema de cuadrados, de un tamaño algo mayor que cualquiera de los otros, pero inclinados en un cierto ángulo respecto a los originales (Fig. 2.3) y que por sí solos recubrirán el plano entero. Cada uno de estos cuadrados inclinados tiene exactamente las mismas marcas, de modo que las líneas interiores de estos cuadrados encajan para formar la estructura de dos cuadrados original. Lo mismo se aplicaría si, en lugar de tomar los centros de los cuadrados más grandes de entre los dos tipos de cuadrados de la estructura original, elegimos cualquier otro punto, junto con su conjunto de puntos correspondientes a lo largo de toda la estructura. La nueva estructura de cuadrados inclinados es exactamente la misma que antes pero desplazada sin rotación —i.e., mediante un movimiento que se conoce como una traslación—. Por simplicidad, podemos escoger ahora nuestro punto de partida en una de las esquinas de la estructura original (véase la Fig. 2.4).

Fig. 2.2. Una teselación del plano por cuadrados de dos tamaños diferentes.
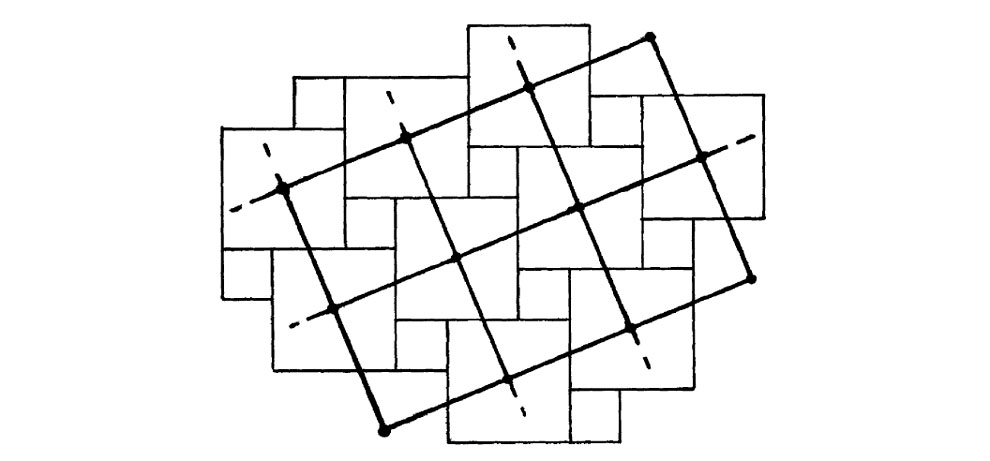
Fig. 2.3. Los centros de los (por ejemplo) cuadrados mayores forman los vértices de un retículo de cuadrados aún mayores, inclinados en un determinado ángulo.
Debería quedar claro que el área del cuadrado inclinado debe ser igual a la suma de las áreas de los dos triángulos más pequeños: de hecho, para cualquier punto de partida de los cuadrados inclinados, las piezas en que el cuadrado mayor queda subdividido por las líneas interiores pueden ser desplazadas sin rotación hasta que encajen para formar los dos cuadrados más pequeños (por ejemplo, la Fig. 2.5). Además, resulta evidente de la Fig. 2.4 que la longitud del lado del cuadrado inclinado grande es la hipotenusa de un triángulo rectángulo cuyos otros dos lados tienen longitudes iguales a los lados de los dos cuadrados más pequeños. Hemos establecido así el teorema de Pitágoras: el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.

Fig. 2.4. El retículo de cuadrados inclinados puede desplazarse por una traslación, de modo que los vértices del retículo inclinado están sobre los vértices del retículo de dos cuadrados original, lo que muestra que el lado de un cuadrado inclinado es la hipotenusa de un triángulo rectángulo (sombreado) cuyos otros dos lados son los de los dos cuadrados originales.
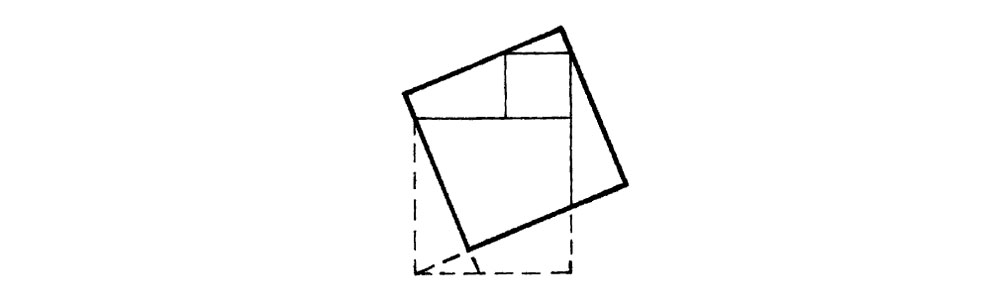
Fig. 2.5. Para cualquier punto de partida particular en el cuadrado inclinado, como el que se muestra, el cuadrado inclinado queda dividido en piezas que encajan para formar los dos cuadrados más pequeños.
El argumento anterior proporciona los elementos esenciales de una demostración sencilla de este teorema y, además, nos ofrece una «razón» para creer que el teorema tiene que ser verdadero, lo que quizá no fuera tan obvio en el caso de un argumento más formal construido mediante una sucesión de pasos lógicos sin un motivo claro. Sin embargo, habría que señalar que en este argumento han intervenido varias hipótesis implícitas. Una de ellas, y no la menos importante, es la hipótesis de que la estructura en apariencia obvia de cuadrados repetidos que se muestra en la Fig. 2.2 o incluso en la Fig. 2.6 es geométricamente posible —o incluso, y más críticamente, ¡que un cuadrado es algo geométricamente posible!—. Después de todo, ¿qué entendemos por un «cuadrado»? Normalmente pensamos en un cuadrado como una figura plana cuyos lados son todos iguales y cuyos ángulos son todos rectos. ¿Qué es un ángulo recto? Bien, podemos imaginar dos líneas rectas que se cortan en un punto formando cuatro ángulos que son todos iguales. Cada uno de estos ángulos iguales es entonces un ángulo recto.

Fig. 2.6. El retículo familiar de cuadrados iguales. ¿Cómo sabemos que existe?
Tratemos ahora de construir un cuadrado. Tomemos tres segmentos de recta iguales AB, BC y CD, donde ABC y BCD son ángulos rectos, y D y A están en el mismo lado de la línea BC, como en la Fig. 2.7. Surge la pregunta: ¿tiene AD la misma longitud que los otros tres segmentos? Más aún: ¿son los ángulos DAB y CDA también ángulos rectos? Estos ángulos deberían ser iguales entre sí por la simetría izquierda-derecha de la figura, pero ¿son realmente ángulos rectos? El hecho de que lo sean solo parece obvio a causa de nuestra familiaridad con los cuadrados, o quizá porque podemos recordar de nuestros días escolares alguna proposición de Euclides que puede ser utilizada para deducir que los lados BA y CD tendrían que ser «paralelos» entre sí, y alguna proposición acerca de que cualquier recta «transversal» a un par de paralelas tiene que formar ángulos correspondientes iguales allí donde corta a las dos paralelas. De esto se sigue que el ángulo DAB tendría que ser igual al ángulo complementario de ADC (i.e., al ángulo EDC, en la Fig. 2.7, siendo ADE una recta) además de ser, como se ha señalado antes, igual al ángulo ADC. Un ángulo (ADC) solo puede ser igual a su complementario (EDC) si es un ángulo recto. Debemos demostrar también que el lado AD tiene la misma longitud que BC, pero ahora esto se sigue también, por ejemplo, de las propiedades de las rectas transversales a las paralelas BA y CD. Por lo tanto, es cierto que a partir de un argumento euclídeo de este tipo podemos demostrar que realmente sí existen cuadrados hechos de ángulos rectos. Pero aquí se esconde una cuestión profunda.

Fig. 2.7. Tratemos de construir un cuadrado. Tomemos ABC y BCD como ángulos rectos, con AB = BC = CD. ¿Se sigue de esto que DA es también igual a estas longitudes y que DAB y CDA son también ángulos rectos?
2.2. LOS POSTULADOS DE EUCLIDES
Al construir su noción de geometría, Euclides puso mucho cuidado en ver de qué hipótesis dependía su demostración.[2] En particular, tuvo cuidado en hacer una distinción entre ciertas afirmaciones llamadas axiomas —que se tomaban como verdades autoevidentes, y que básicamente eran definiciones de lo que él entendía por puntos, líneas, etc.— y los cinco postulados, que eran hipótesis cuya validez parecía menos segura, pero que parecían ser ciertas para la geometría de nuestro mundo. La última de estas hipótesis, conocida como el quinto postulado de Euclides, se consideraba menos obvia que las otras, y durante varios siglos se tuvo la sensación de que debería ser posible encontrar una forma de demostrarla a partir de los otros postulados más evidentes. El quinto postulado de Euclides se conoce habitualmente como el postulado de las paralelas, y yo seguiré esta práctica aquí.
Antes de discutir el postulado de las paralelas, vale la pena señalar la naturaleza de los otros cuatro postulados de Euclides. Los postulados conciernen a la geometría del plano (euclídeo), aunque Euclides también consideró el espacio tridimensional en sus obras posteriores. Los elementos básicos de su geometría plana son puntos, líneas rectas y círculos. Aquí consideraré que una «línea recta» (o simplemente una «recta») se extiende indefinida en ambas direcciones; si no es así, me referiré a un «segmento de recta». El primer postulado de Euclides afirma, en efecto, que existe un (único) segmento de recta que conecta dos puntos cualesquiera. Su segundo postulado afirma la prolongabilidad ilimitada de cualquier segmento de recta. Su tercer postulado afirma la existencia de un círculo con un centro cualquiera y con cualquier valor para su radio. Finalmente, su cuarto postulado afirma la igualdad de todos los ángulos rectos.[3]
Desde una perspectiva moderna, algunos de estos postulados parecen un poco extraños, en particular el cuarto, pero debemos tener en cuenta el origen de las ideas que subyacen en la geometría de Euclides. Él estaba interesado básicamente en el movimiento de cuerpos rígidos idealizados y la noción de congruencia que se manifestaba cuando uno de tales cuerpos rígidos idealizados se movía hasta coincidir con otro. La igualdad entre un ángulo recto en un cuerpo y un ángulo en otro cuerpo tenía que ver con la posibilidad de mover un cuerpo de modo que las líneas que formaban su ángulo recto coincidieran con las líneas que formaban el ángulo recto en el otro. De hecho, el cuarto postulado está afirmando la isotropía y la homogeneidad del espacio, de modo que una figura en un lugar podría tener la «misma» (i.e., congruente) forma geométrica que una figura en otro lugar. Los postulados segundo y tercero expresan la idea de que el espacio es indefinidamente prolongable y sin «huecos» en su interior, mientras que el primero expresa la naturaleza básica de un segmento de línea recta. Aunque Euclides consideraba la geometría de un modo bastante diferente de como la consideramos hoy, sus cuatro primeros postulados recogen básicamente nuestra noción actual de un espacio métrico (bidimensional) con completa homogeneidad e isotropía, e infinito en extensión. De hecho, semejante imagen parece estar en estrecho acuerdo con la naturaleza espacial a muy gran escala del universo real, de acuerdo con la cosmología moderna, como veremos en §27.11 y §28.10.
¿Cuál es, entonces, la naturaleza del quinto postulado de Euclides, el postulado de las paralelas? Tal como Euclides formulaba esencialmente dicho postulado, este afirma que si dos segmentos de recta a y b en un plano cortan a otra línea recta c (de modo que c es lo que se denomina transversal a a y b) de tal forma que la suma de los ángulos interiores en el mismo lado de c es menor que dos ángulos rectos, entonces a y b, cuando se prolongan a suficiente distancia en ese lado de c, se cortarán en alguna parte (véase la Fig. 2.8a). Una forma equivalente de este postulado (a veces conocida como axioma de Playfair) afirma que, para cualquier línea recta y para cualquier punto que no esté en dicha línea, existe una única línea recta que pasa por dicho punto y es paralela a la primera recta (véase la Fig. 2.8b). Aquí, rectas «paralelas» serían dos líneas rectas coplanares que no se cortan (y recordemos que mis «rectas» son entidades completamente prolongadas, y no los «segmentos de línea recta» de Euclides.[2.1]
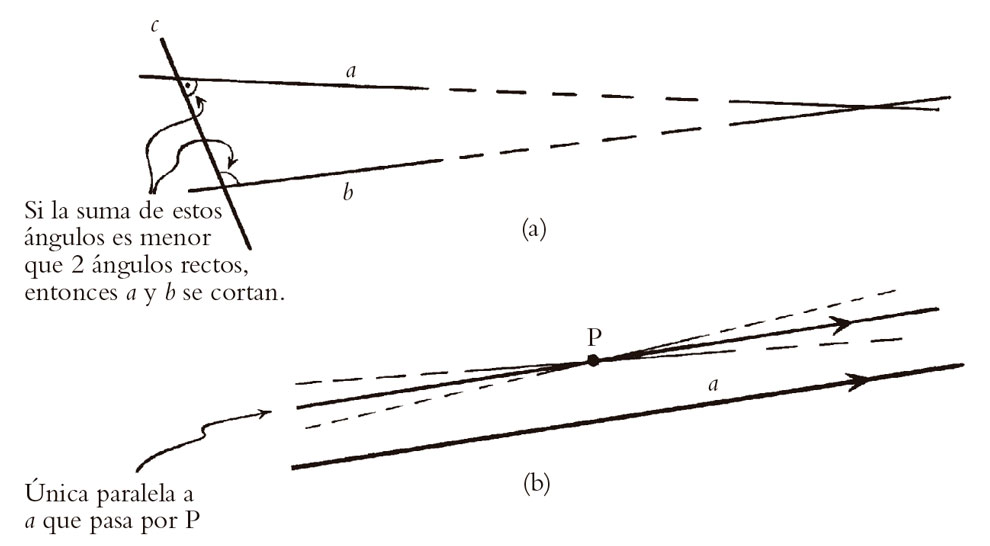
Fig. 2.8. (a) Postulado de las paralelas de Euclides. Las líneas a y b son trasversales a una tercera línea c, tal que los ángulos interiores donde a y b cortan a c suman menos que dos ángulos rectos. Entonces a y b (suponiendo que se prolongan lo suficiente) se cortarán en última instancia. (b) Axioma (equivalente) de Playfair: si a es una línea en un plano y P un punto del plano que no está en a, entonces hay solo una línea paralela a a que pasa por P en el plano.
Una vez que tenemos el postulado de las paralelas, podemos proceder a establecer la propiedad necesaria para la existencia de un cuadrado. Si una recta transversal a un par de líneas rectas corta a estas de modo que los ángulos internos a un lado de la transversal suman dos ángulos rectos, entonces se puede demostrar que las líneas que forman el par son realmente paralelas. Además, se sigue inmediatamente que cualquier otra transversal al par tiene exactamente la misma propiedad angular. Esto es lo que necesitábamos para el argumento dado antes para la construcción de nuestro cuadrado. Vemos que es precisamente el postulado de las paralelas el que debemos utilizar para demostrar que nuestra construcción da realmente un cuadrado, con todos sus ángulos rectos y todos sus lados iguales. Sin el postulado de las paralelas no podemos establecer que existen realmente los cuadrados (en el sentido habitual de tener todos sus ángulos rectos).
Puede parecer que es una mera cuestión de pedantería matemática el preocuparse por cuáles son exactamente las hipótesis necesarias para proporcionar una «prueba rigurosa» de la existencia de un objeto tan obvio como un cuadrado. ¿Por qué deberíamos interesarnos en cuestiones tan pedantes, cuando un «cuadrado» es simplemente esa figura familiar que todos conocemos? Bien, pronto veremos que Euclides dio realmente pruebas de una extraordinaria perspicacia al preocuparse por tales cuestiones. La pedantería de Euclides está relacionada con una cuestión profunda que tiene mucho que decir sobre la geometría real del universo, y en más de una forma. En particular, no es en absoluto obvio que existan «cuadrados» físicos a una escala cosmológica en el universo real. Esta es una cuestión que se tiene que resolver mediante la observación, y por el momento la evidencia parece contradictoria (véanse §2.7 y §28.10).
2.3. LA DEMOSTRACIÓN DEL TEOREMA DE PITÁGORAS POR ÁREAS SEMEJANTES
En la próxima sección volveré a la trascendencia matemática que tiene el no dar por supuesto el postulado de las paralelas. Las cuestiones físicas relevantes serán examinadas en §18.4, §27.11, §28.10 y §34.4. Pero antes de discutir tales cuestiones, será instructivo dirigir nuestra atención a la otra demostración del teorema de Pitágoras que ya había prometido con anterioridad.
Una de las formas más sencillas de ver que la afirmación de Pitágoras es cierta en la geometría euclídea es considerar la configuración consistente en el triángulo rectángulo dado subdividido en dos triángulos más pequeños por una recta perpendicular a la hipotenusa trazada desde el ángulo recto (Fig. 2.9). Ahora tenemos tres triángulos: el original y los dos en que este ha sido subdividido. Evidentemente, el área del triángulo original es la suma de las áreas de los dos más pequeños.

Fig. 2.9. Demostración del teorema de Pitágoras utilizando triángulos semejantes. Tómese un triángulo rectángulo y trácese una perpendicular desde su ángulo recto a su hipotenusa. Los dos triángulos en el que ahora está dividido el triángulo original tienen áreas cuya suma es la del triángulo original. Los tres triángulos son semejantes, de modo que sus áreas son proporcionales a los cuadrados de sus hipotenusas respectivas. De ello se sigue el teorema de Pitágoras.
Ahora es sencillo ver que estos tres triángulos son semejantes entre sí. Esto significa que todos ellos tienen la misma forma (aunque diferentes tamaños), i.e., se obtienen unos a partir de otros mediante una dilatación o contracción uniforme, junto con un movimiento rígido. Esto se sigue porque cada uno de los tres triángulos posee exactamente los mismos ángulos, en cierto orden. Cada uno de los dos triángulos más pequeños tiene un ángulo en común con el más grande, y uno de los ángulos de cada triángulo es un ángulo recto. El tercer ángulo también debe coincidir porque la suma de los ángulos de cualquier triángulo es siempre la misma. Ahora bien, una propiedad general de las figuras planas semejantes es que sus áreas son proporcionales a los cuadrados de sus correspondientes dimensiones lineales. Para cada triángulo, podemos considerar que esta dimensión lineal es el lado más largo, i.e., su hipotenusa. Notemos que la hipotenusa de cada uno de los triángulos más pequeños coincide con uno de los lados (no hipotenusa) del triángulo original. Así pues, se sigue al mismo tiempo (del hecho de que el área del triángulo original es la suma de las áreas de los otros dos) que el cuadrado de la hipotenusa del triángulo original es realmente la suma de los cuadrados de los otros dos lados: ¡el teorema de Pitágoras!
Una vez más, tendremos que examinar algunas hipótesis concretas que intervienen en este argumento. Un ingrediente importante del argumento es el hecho de que la suma de los ángulos de un triángulo tiene siempre el mismo valor. (Este valor de la suma es, por supuesto, 180°, pero Euclides hubiera dicho «dos ángulos rectos». La descripción matemática «natural» y más moderna consiste en decir que los ángulos de un rectángulo, en la geometría de Euclides, suman π. Esto supone utilizar radianes para la medida absoluta de un ángulo, donde el símbolo para el grado «°» cuenta como π/180, de modo que podemos escribir 180° = π.) La demostración habitual se representa en la Fig. 2.10. Prolonguemos CA hasta E y tracemos una recta AD que pasa por A y es paralela a CB. Entonces (como se sigue del postulado de las paralelas), los ángulos EAD y ACB son iguales, y también DAB y CBA son iguales. Puesto que los ángulos EAD, DAB y BAC suman π (o 180°, o dos ángulos rectos), así deben hacerlo también los tres ángulos ACB, CBA y BAC del triángulo, tal como queríamos demostrar. Pero nótese que aquí se ha utilizado el postulado de las paralelas.
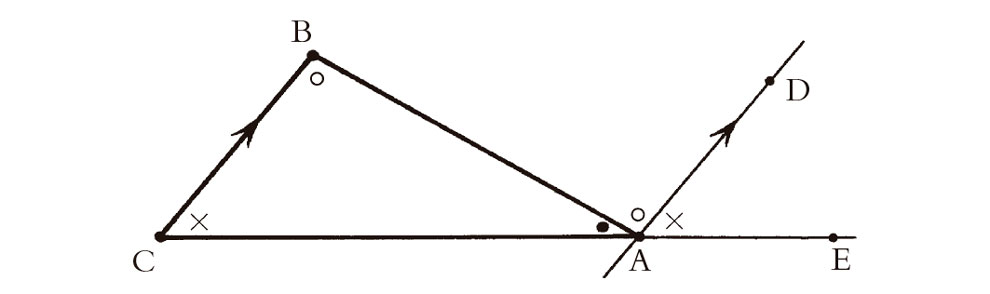
Fig. 2.10. Demostración de que la suma de los ángulos de un triángulo ABC es (= 180° = dos ángulos rectos). Prolónguese CA hasta E; dibújese AD paralela a CB. Se sigue del postulado de las paralelas que los ángulos EAD y ACB son iguales y que los ángulos Puesto que los ángulos EAD, DAB y BAC suman π, también lo hacen los ángulos ACB, CBA y BAC.
Esta demostración del teorema de Pitágoras también hace uso del hecho de que las áreas de figuras semejantes son proporcionales a los cuadrados de cualquier medida lineal de sus tamaños. (Aquí escogemos la hipotenusa de cada triángulo como representación de su medida lineal.) Este hecho no solo depende de la existencia misma de figuras semejantes de diferentes tamaños —que en el caso de los triángulos de la Fig. 2.9 se han establecido utilizando el postulado de las paralelas—, sino también de algunas cuestiones más sofisticadas que se relacionan con el modo en que definimos realmente el «área» para formas no rectangulares. Estas cuestiones generales se abordan en términos de procedimientos de paso al límite y no quiero entrar por el momento en esta clase de discusión. Nos llevará a cuestiones más profundas relacionadas con el tipo de números que se utilizan en geometría. Volveremos a la cuestión en §§3.1-3.
Un mensaje importante de la discusión de las secciones precedentes es que el teorema de Pitágoras parece depender del postulado de las paralelas. ¿Es así realmente? Supongamos que el postulado de las paralelas fuera falso. ¿Significa eso que el propio teorema de Pitágoras podría ser falso? ¿Tiene sentido semejante posibilidad? Tratemos de abordar la cuestión de lo que sucedería si se admite que el postulado de las paralelas sea considerado falso. Parecerá que estemos entrando en un mundo de fantasía, en el que la geometría que aprendimos en la escuela se pone patas arriba. Así es, pero también encontraremos que aquí hay un objetivo más profundo.
2.4. GEOMETRÍA HIPERBÓLICA: IMAGEN CONFORME
Echemos una ojeada a la imagen de la Fig. 2.11. Es una reproducción de uno de los grabados en madera de M. C. Escher, llamado Límite circular I. En realidad, nos proporciona una representación muy aproximada de un tipo de geometría —llamada geometría hiperbólica (o a veces lobachevskiana)— en la que el postulado de las paralelas es falso, el teorema de Pitágoras deja de ser válido y los ángulos de un triángulo no suman π. Además, para una figura de un tamaño dado no existe, en general, una figura semejante de tamaño mayor.

Fig. 2.11. Límite circular I, grabado en madera de M.C. Escher, que ilustra la representación conforme del plano hiperbólico.
En la Fig. 2.11, Escher ha utilizado una representación concreta de la geometría hiperbólica en la que el «universo» entero del plano hiperbólico está «comprimido» en el interior de un círculo en un plano euclídeo ordinario. La circunferencia que limita al círculo representa el «infinito» para este universo hiperbólico. Podemos ver que, en la imagen de Escher, los peces parecen apretarse mucho a medida que se acercan a dicha frontera. Pero debemos considerar esto como una ilusión. Imagínese que usted es uno de los peces. Entonces, ya esté situado próximo al borde de la imagen de Escher o próximo a su centro, el universo (hiperbólico) entero tendrá la misma apariencia para usted. La noción de «distancia» en esta geometría no coincide con la del plano euclídeo en cuyos términos ha sido representada. Cuando miramos la imagen de Escher desde nuestra perspectiva euclídea, los peces próximos a la frontera parecen hacérsenos minúsculos. Pero desde su propia perspectiva «hiperbólica», los peces blancos o negros piensan que tienen exactamente la misma forma y tamaño que los que están próximos al centro. Más aún, aunque desde nuestra perspectiva euclídea exterior ellos parecen acercarse cada vez más a la propia frontera, desde su propia perspectiva hiperbólica dicha frontera siempre queda infinitamente lejos. Ni el círculo frontera ni nada del espacio «euclídeo» exterior tiene existencia para ellos. Su universo entero consiste en lo que para nosotros parece estar estrictamente dentro del círculo.
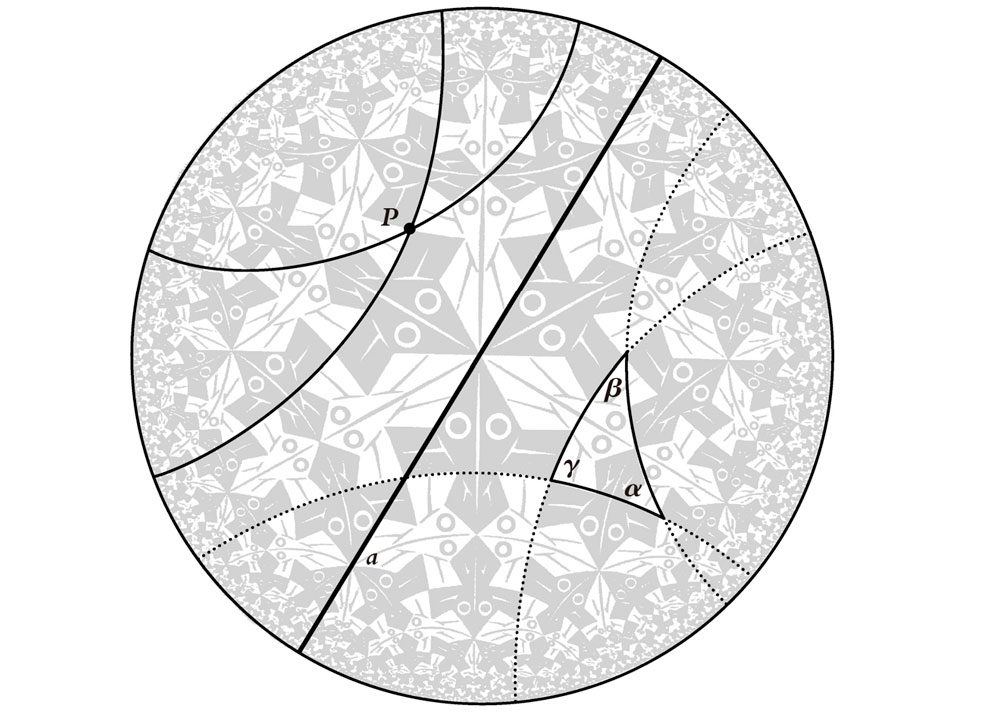
Fig. 2.12. La misma imagen de Escher que en la Fig. 2.11, pero con líneas rectas hiperbólicas (círculos euclídeos o líneas que cortan ortogonalmente al círculo frontera) y un triángulo hiperbólico. Los ángulos hiperbólicos coinciden con los euclídeos. Evidentemente se viola el postulado de las paralelas y los ángulos de un triángulo suman menos que π.
En términos más matemáticos, ¿cómo está construida esta imagen de la geometría hiperbólica? Consideremos un círculo cualquiera en el plano euclídeo. El conjunto de puntos interiores a este círculo va a representar el conjunto de puntos en el plano hiperbólico entero. Las líneas rectas se representan, de acuerdo con la geometría hiperbólica, como círculos euclídeos que cortan ortogonalmente —lo que significa a ángulos rectos— al círculo frontera. Ahora resulta que la noción hiperbólica de ángulo entre dos curvas cualesquiera, en su punto de intersección, es exactamente la misma que la medida euclídea del ángulo entre las dos curvas en el punto de intersección. Una representación de esta naturaleza se denomina representación conforme. Por esta razón, a la representación concreta de la geometría hiperbólica que utilizó Escher se le llama a veces el modelo conforme del plano hiperbólico. (También suele llamársele disco de Poincaré. La dudosa justificación histórica de esta terminología será examinada en §2.6.)
Estamos ahora en situación de ver si los ángulos de un triángulo, en la geometría hiperbólica, suman o no π. Una rápida ojeada a la Fig. 2.12 nos lleva a creer que no lo hacen y que suman algo menos. De hecho, la suma de los ángulos de un triángulo en la geometría hiperbólica es siempre menor que π. Podríamos considerar esto como una característica desagradable de la geometría hiperbólica, ya que parece que no tenemos una respuesta «clara» para la suma de los ángulos de un triángulo. Sin embargo, cuando sumamos los ángulos de un triángulo hiperbólico sucede algo extraordinario y particularmente elegante: el déficit es siempre proporcional al área del triángulo. De forma más explícita, si los tres ángulos del triángulo son π, β y γ, entonces tenemos la fórmula (descubierta por Johann Heinrich Lambert, 1728-1777)
π – (α + β + γ) = CΔ,
donde Δ es el área del triángulo y C es una constante. Esta constante depende de las «unidades» que se escojan para medir longitudes y áreas. Siempre podemos fijar la escala de modo que C = 1. Es un hecho realmente notable que el área de un triángulo pueda expresarse de una forma tan simple en la geometría hiperbólica. En la geometría euclídea no hay modo de expresar el área de un triángulo simplemente en función de sus ángulos, y la expresión para el área de un triángulo en función de las longitudes de sus lados es bastante más complicada.
De hecho, aún no he acabado mi descripción de la geometría hiperbólica en términos de esta representación conforme, puesto que todavía no he descrito cómo va a definirse la distancia hiperbólica entre dos puntos (y convendría saber qué es «distancia» antes de que podamos hablar realmente de áreas). Permítaseme dar una expresión para la distancia hiperbólica entre dos puntos A y B interiores al círculo. Esta expresión es
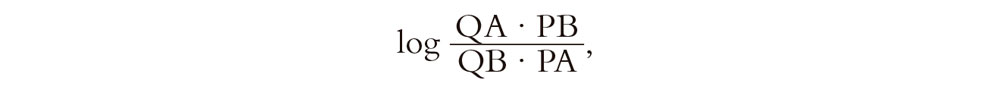
donde P y Q son los puntos donde el círculo euclídeo (i.e., la línea recta hiperbólica) que pasa por A y B y es ortogonal al círculo frontera corta a dicho círculo frontera, y donde «QA», etc., se refieren a distancias euclídeas (véase la Fig. 2.13). Si se quiere incluir la «C» de la fórmula del área de Lambert (con C ≠ 1), solo hay que multiplicar la expresión anterior para la distancia por C–1/2 (el recíproco de la raíz cuadrada de C).[4][2.2] Por razones que espero que se aclaren más adelante, me referiré a la cantidad C–1/2 como el pseudorradio de la geometría.
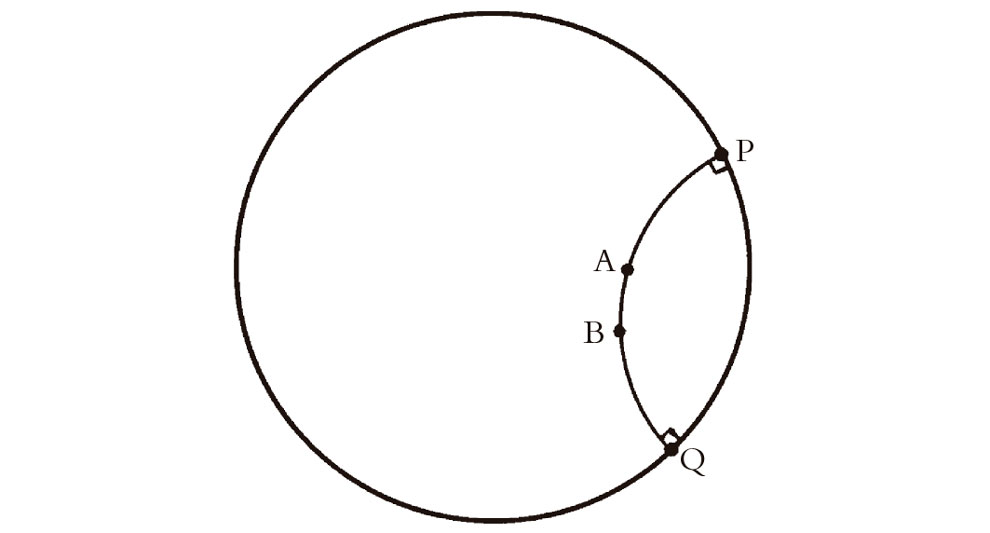
Fig. 2.13. En la representación conforme, la distancia hiperbólica entre A y B es log {QA.PB/QB.PA}, donde QA, etc., son distancias euclídeas, y P y Q son los puntos donde el círculo euclídeo que pasa por A y B y es ortogonal al círculo frontera (línea hiperbólica) corta a este círculo.
Si expresiones matemáticas como la fórmula «log» anterior le parecen disuasorias, por favor, no se preocupe. Solo la doy para aquellos a quienes les gusta ver las cosas explícitamente. En cualquier caso, no voy a explicar por qué funciona la expresión (por ejemplo, por qué la distancia hiperbólica más corta entre dos puntos, así definida, se mide realmente a lo largo de una línea recta hiperbólica, o por qué las distancias a lo largo de una línea recta hiperbólica «se suman» de la forma adecuada).[2.3] También pido disculpas por el «log» (logaritmo), pero así son las cosas. De hecho, este es un logaritmo natural («log en base e») y tendré mucho que decir sobre ello en §§5.2,3. Veremos que los logaritmos son entidades realmente muy bellas y misteriosas, además de ser importantes en muchos contextos diferentes.
La geometría hiperbólica, con esta definición de distancia, resulta tener todas las propiedades de la geometría euclídea salvo aquellas que necesitan el postulado de las paralelas. Podemos construir triángulos, y otras figuras planas, de diferentes formas y tamaños, y podemos desplazarlos «rígidamente» (manteniendo invariables sus formas y tamaños hiperbólicos) con la misma libertad con que podemos hacerlo en la geometría euclídea, de modo que, igual que en la geometría euclídea, surge una noción natural de cuándo son «congruentes» dos figuras (donde «congruente» significa «que pueden desplazarse rígidamente hasta que llegan a coincidir»). De hecho, todos los peces blancos del grabado de Escher son mutuamente congruentes, según esta geometría hiperbólica, y también lo son todos los peces negros.
2.5. OTRAS REPRESENTACIONES DE LA GEOMETRÍA HIPERBÓLICA
Por supuesto, no todos los peces blancos parecen de la misma forma y tamaño, pero ello se debe a que los estamos viendo desde una perspectiva euclídea en lugar de una hiperbólica. La imagen de Escher hace uso simplemente de una representación euclídea concreta de la geometría hiperbólica. La propia geometría hiperbólica es algo más abstracto que no depende de ninguna representación euclídea en particular. Sin embargo, tales representaciones son muy útiles para nosotros, pues proporcionan un modo de visualizar la geometría hiperbólica refiriéndola a algo que es más familiar y en apariencia más «concreto» para nosotros, a saber, la geometría euclídea. Además, tales representaciones dejan claro que la geometría hiperbólica es una estructura consistente, y que, en consecuencia, el postulado de las paralelas no puede demostrarse a partir de las otras leyes de la geometría euclídea.
Hay, de hecho, otras representaciones de la geometría hiperbólica en términos de geometría euclídea que son diferentes de la representación conforme que utilizó Escher. Una de ellas es la que se conoce como el modelo proyectivo. Aquí, el plano hiperbólico entero es de nuevo representado como el interior de un círculo en un plano euclídeo, pero las líneas rectas hiperbólicas están ahora representadas como líneas rectas euclídeas (y no como arcos de círculo). Hay, sin embargo, un precio a pagar por esta aparente simplificación, puesto que los ángulos hiperbólicos no son ahora iguales a los ángulos euclídeos, y muchos considerarían que este es un precio demasiado alto. Para aquellos lectores que estén interesados, la distancia hiperbólica entre dos puntos A y B en esta representación está dada por la fórmula (véase la Fig. 2.14).
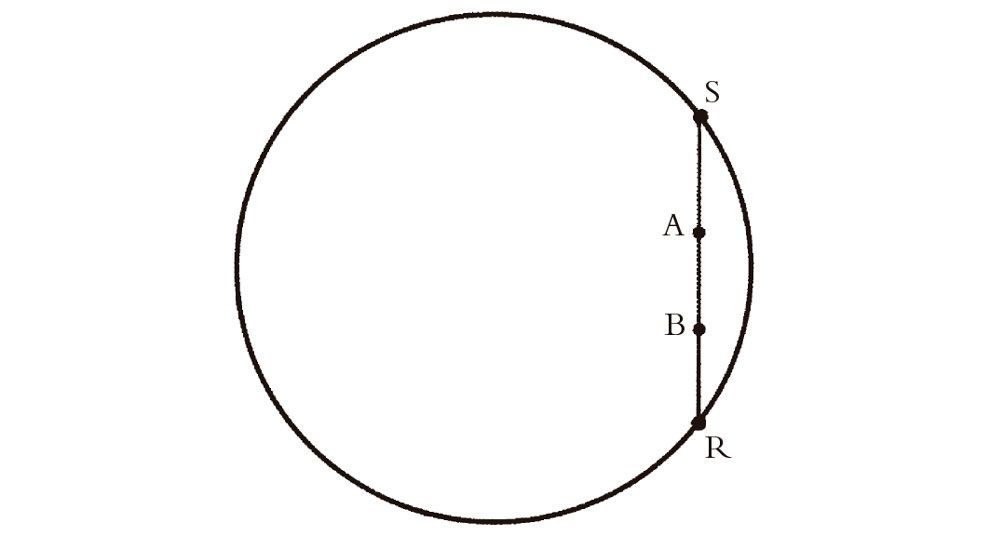
Fig. 2.14. En la representación proyectiva, la fórmula para la distancia hiperbólica es ahora 1/2 log {RA.SB/RB.SA}, donde R y S son las intersecciones de la línea recta euclídea (i.e., hiperbólica) AB con el círculo frontera.
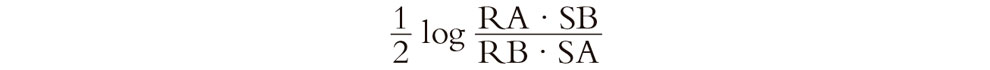
(tomando C = 1, que es casi igual que la expresión que teníamos antes para la representación conforme), donde R y S son las intersecciones de la línea recta prolongada AB con el círculo frontera. Esta representación de la geometría hiperbólica puede obtenerse a partir de la conforme por medio de una dilatación radial a partir del centro en una cantidad dada por
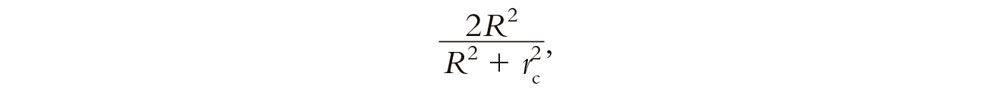
donde R es el radio del círculo frontera y rc es la distancia euclídea de un punto al centro (euclídeo) del círculo frontera en la representación conforme (véase la Fig. 2.15).[2.4] En la Fig. 2.16 la imagen de Escher de la Fig. 2.11 ha sido transformada del modelo conforme al modelo proyectivo utilizando esta fórmula. (Pese a la pérdida de detalle, el arte preciso de Escher sigue siendo evidente.) Aunque resulta menos atractiva de esta manera, ¡presenta un nuevo punto de vista!
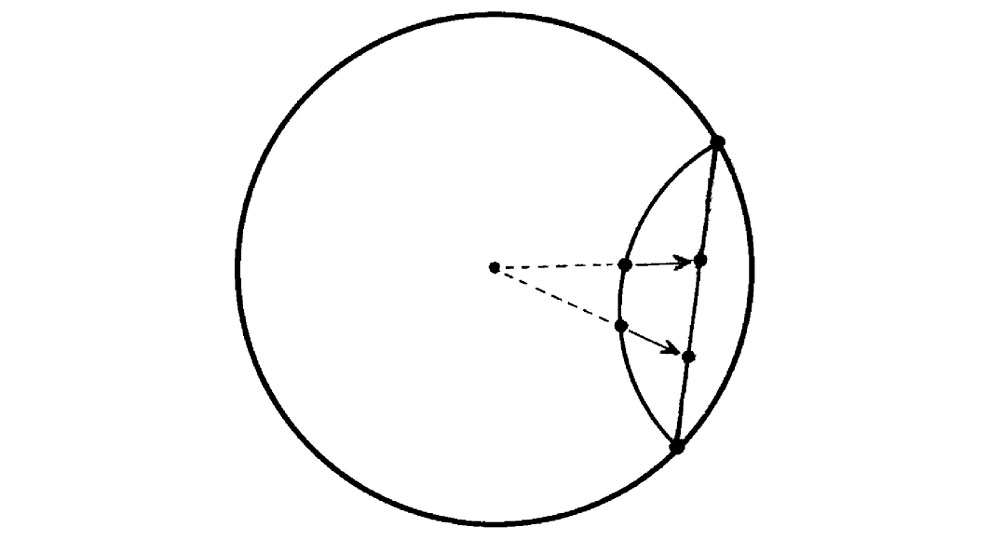
Fig. 2.15. Para pasar de la representación conforme a la proyectiva, se expande a partir del centro en un factor 2R2/(R2 + r2c), donde R es el radio del círculo frontera y rc es la distancia euclídea al punto en la representación conforme.

Fig. 2.16. La imagen de Escher de la Fig. 2.11 transformada desde la representación conforme a la proyectiva.
Existe una forma más directamente geométrica de relacionar las imágenes conforme y proyectiva, a través de otra representación aún más ingeniosa de la misma geometría. Las tres representaciones se deben al ingenioso geómetra italiano Eugenio Beltrami (1835-1900). Consideremos una esfera S, cuyo ecuador coincide con el círculo frontera de la representación proyectiva de la geometría hiperbólica que se ha dado antes. Ahora vamos a encontrar una representación de la geometría hiperbólica en el hemisferio norte S+ de S, que llamaré representación hemisférica. Véase la Fig. 2.17. Para pasar de la representación proyectiva en el plano (considerado horizontal) a la nueva representación en la esfera, simplemente proyectamos verticalmente hacia arriba (Fig. 2.17a). Las líneas rectas en el plano, que representan líneas rectas hiperbólicas, se representan en S+ por semicírculos que cortan ortogonalmente al ecuador. Ahora, para ir de la representación en S+ a la representación conforme en el plano proyectamos desde el polo sur (Fig. 2.17b). Esta es la que se denomina proyección estereográfica, y más adelante desempeñará un papel importante en este libro (cf. §8.3, §18.4, §22.9 y §33.6). Dos propiedades importantes de la representación estereográfica a la que llegaremos en §8.3 son que es conforme, de modo que conserva los ángulos, y que hace corresponder círculos en la esfera a círculos (o, excepcionalmente, a líneas rectas) en el plano.[2.5][2.6]
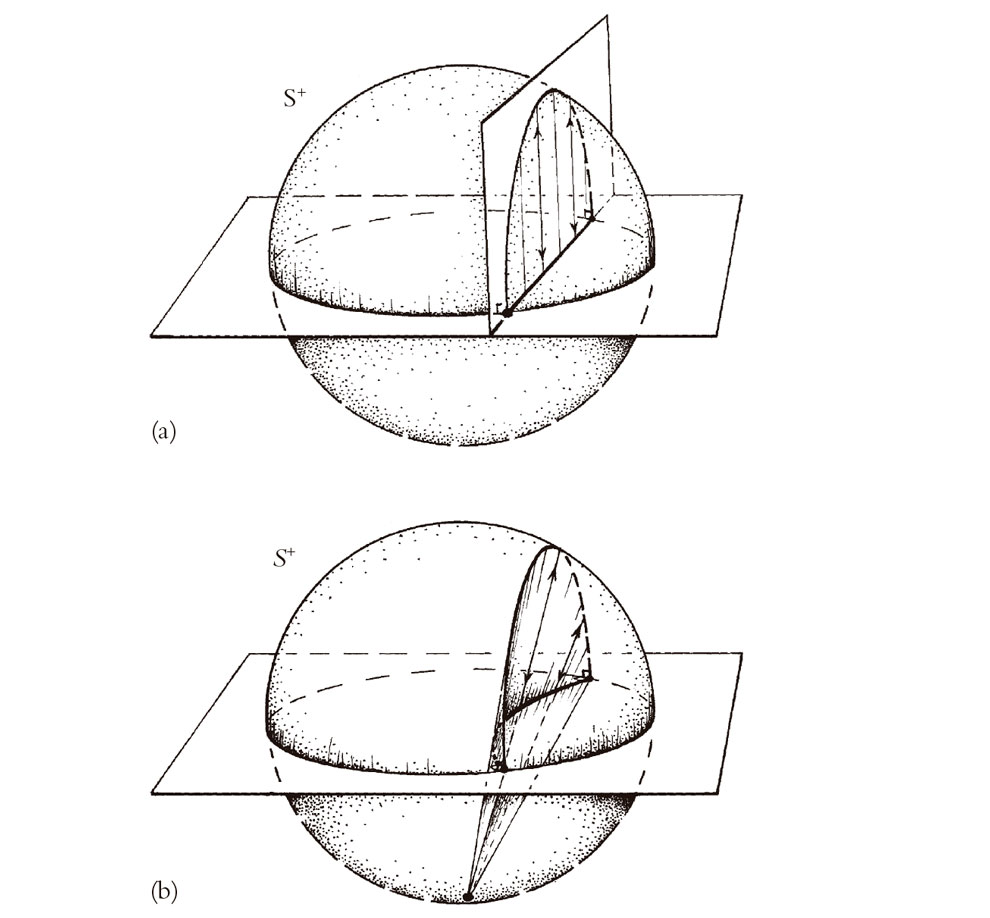
Fig. 2.17. Geometría de Beltrami, que relaciona tres de sus representaciones de la geometría hiperbólica. (a) La representación hemisférica (conforme en el hemisferio norte S+) se proyecta verticalmente en la representación proyectiva sobre el disco ecuatorial. (b) La representación hemisférica proyecta estereográficamente desde el polo sur a la representación conforme sobre el disco ecuatorial.
La existencia de varios modelos diferentes de geometría hiperbólica, expresados en términos de espacio euclídeo, sirve para acentuar el hecho de que en realidad estos son meramente «modelos euclídeos» de geometría hiperbólica y no debemos considerar que nos estén diciendo qué es realmente la geometría hiperbólica. La geometría hiperbólica tiene su propia «existencia platónica», igual que la tiene la geometría euclídea (véanse §1.3 y el prefacio). Ninguno de estos modelos debe tomarse como la «representación» correcta de la geometría hiperbólica, en detrimento de los otros. Las representaciones de la misma que hemos estado considerando son muy valiosas como ayudas para nuestra comprensión, pero solo porque el marco euclídeo es aquel al que estamos más acostumbrados. Para una criatura sintiente que haya crecido con una experiencia directa de la geometría hiperbólica (antes que de la euclídea), un modelo de geometría euclídea en términos hiperbólicos parecería la vía más natural. En §18.4 encontraremos aún otro modelo de geometría hiperbólica, esta vez en términos de la geometría minkowskiana de la relatividad especial.
Para terminar esta sección, volvamos a la cuestión de la existencia de cuadrados en la geometría hiperbólica. Aunque en la geometría hiperbólica no existen cuadrados cuyos ángulos sean ángulos rectos, sí existen «cuadrados» de un tipo más general cuyos ángulos son menores que los ángulos rectos. La forma más fácil de construir un cuadrado de este tipo es trazar dos líneas rectas que se cortan a ángulos rectos en un punto O. Nuestro «cuadrado» es ahora el cuadrilátero cuyos cuatro vértices son las intersecciones A, B, C, D (tomadas cíclicamente) de estas dos líneas con un círculo con centro O. Véase la Fig. 2.18. Debido a la simetría de la figura, los cuatro lados del cuadrilátero resultante ABCD son iguales y los cuatro ángulos también deben ser iguales. Pero ¿son rectos estos ángulos? No en la geometría hiperbólica. De hecho, pueden ser cualquier ángulo (positivo) que queramos que sea menor que un ángulo recto, pero no igual a un ángulo recto. Cuanto más grande es el cuadrado (hiperbólico), es decir, cuanto mayor es el círculo en la construcción anterior, menores serán sus ángulos. En la Fig. 2.19a he representado un retículo de cuadrados hiperbólicos, utilizando el modelo conforme, donde hay cinco cuadrados en cada vértice (en lugar de los cuatro euclídeos), de modo que el ángulo es 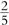 π, o 72°. En la Fig. 2.19b he dibujado el mismo retículo utilizando el modelo proyectivo. Se verá que este no permite las modificaciones que serían necesarias para el retículo de dos cuadrados de la Fig. 2.2.[2.7]
π, o 72°. En la Fig. 2.19b he dibujado el mismo retículo utilizando el modelo proyectivo. Se verá que este no permite las modificaciones que serían necesarias para el retículo de dos cuadrados de la Fig. 2.2.[2.7]
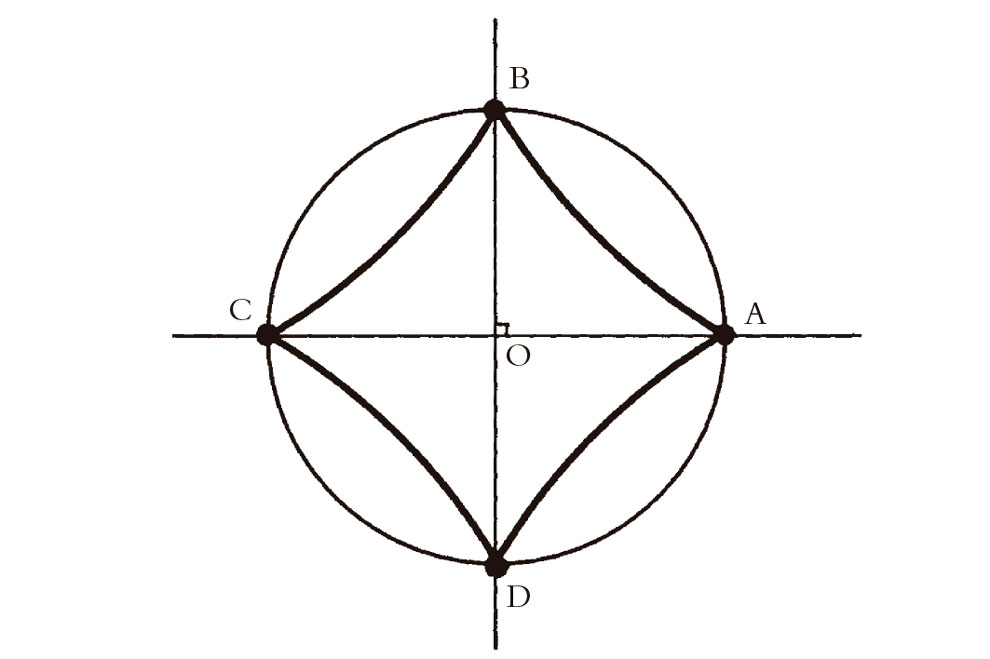
Fig. 2.18. Un «cuadrado» hiperbólico es un cuadrilátero hiperbólico, cuyos vértices son las intersecciones A, B, C, D
(tomadas cíclicamente) de dos rectas hiperbólicas perpendiculares que pasan por un punto O con un círculo centrado en O. Debido a la simetría, los cuatro lados de ABCD, así como los cuatro ángulos son iguales. Estos ángulos, no son
rectos, pero pueden ser iguales a cualquier ángulo positivo dado menor que  π.
π.
Fig. 2.19. Un retículo de cuadrados, en el espacio hiperbólico, en el que cinco cuadrados se encuentran en cada vértice, de modo que los ángulos del cuadrado son 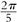 , o 72°. (a) Representación conforme. (b) Representación proyectiva.
, o 72°. (a) Representación conforme. (b) Representación proyectiva.
2.6. ASPECTOS HISTÓRICOS DE LA GEOMETRÍA HIPERBÓLICA
Aquí es oportuno hacer algunos comentarios históricos concernientes al descubrimiento de la geometría hiperbólica. Durante los siglos siguientes a la publicación de los elementos de Euclides, aproximadamente en el año 300 a.C., varios matemáticos intentaron demostrar el quinto postulado a partir de los otros axiomas y postulados. Estos esfuerzos alcanzaron su culminación con el heroico trabajo del jesuita Girolamo Saccheri, en 1773. Podría parecer que el propio Saccheri debió de pensar que la obra de su vida era, en definitiva, un fracaso, pues se reducía a un intento insatisfactorio de demostrar el postulado de las paralelas mostrando que la hipótesis de que la suma de los ángulos de todo triángulo es menor que dos ángulos rectos lleva a una contradicción. Incapaz de hacer esto de forma lógica tras tremendos esfuerzos, concluyó, más bien débilmente:
La hipótesis del ángulo agudo es absolutamente falsa, porque repugna a la naturaleza de la línea recta.[5]
La hipótesis del «ángulo agudo» afirma que las líneas a y b de la Fig. 2.8 a veces no se cortan. Es realmente viable, ¡y, de hecho, da la geometría hiperbólica!
¿Cómo puede ser que Saccheri descubriera efectivamente algo que él estaba tratando de demostrar que era imposible? La propuesta de Saccheri para demostrar el quinto postulado de Euclides consistía en formular la hipótesis de que el quinto postulado era falso y obtener entonces una contradicción a partir de dicha hipótesis. De este modo, él proponía hacer uso de uno de los principios más tradicionales y fructíferos que han sido propuestos en matemáticas —muy posiblemente introducido por primera vez por los pitagóricos— llamado demostración por contradicción (o reductio ad absurdum, para darle su nombre latino). Según este procedimiento, para probar que una afirmación es cierta se formula primero la hipótesis de que la afirmación en cuestión es falsa, y luego se argumenta que de ello se sigue una contradicción. Si se llega a encontrar tal contradicción, se deduce que la afirmación debe ser, después de todo, verdadera.[6] La demostración por contradicción proporciona un método muy potente de razonamiento en matemáticas, hoy aplicado con frecuencia. Aquí es apropiada una cita del distinguido matemático G. H. Hardy:
La reductio ad absurdum, que tanto amaba Euclides, es una de las armas matemáticas más valiosas. Es un gambito mucho más fino que cualquier gambito de ajedrez: un jugador de ajedrez puede ofrecer el sacrificio de un peón o incluso una pieza, pero un matemático ofrece el juego.[7]
Veremos otros usos de este importante principio más adelante (véanse §3.1 y §§16.4,6).
Sin embargo, Saccheri fracasó en su intento de encontrar una contradicción. Por consiguiente, no pudo obtener una demostración del quinto postulado. Pero al esforzarse en ello, descubrió algo mucho más grande: una nueva geometría, diferente de la de Euclides —la geometría discutida en §§2.4,5 que ahora llamamos geometría hiperbólica—. A partir de la hipótesis de que el quinto postulado de Euclides era falso, obtuvo, en lugar de una contradicción real, un montón de teoremas de apariencia extraña y apenas creíble, pero muy interesantes. No obstante, por extraños que parecieran tales resultados, ninguno de ellos era realmente una contradicción. Como sabemos ahora, no había ninguna posibilidad de que Saccheri encontrara de esta manera una contradicción genuina, por la sencilla razón de que la geometría hiperbólica existe realmente, en el sentido matemático de que existe una estructura semejante consistente. En la terminología de §1.3 la geometría hiperbólica habita en el mundo platónico de las formas matemáticas. (La cuestión de la realidad física de la geometría hiperbólica se tocará en §2.7 y §28.10.)
Poco tiempo después de Saccheri, el muy perspicaz matemático Johann Heinrich Lambert (1728-1777) obtuvo también numerosos y fascinantes resultados geométricos a partir de la hipótesis de que el quinto postulado de Euclides es falso, incluyendo el bello resultado mencionado en §2.4 que da el área de un triángulo hiperbólico en función de la suma de sus ángulos. Parece que Lambert pudo haberse formado la opinión, al menos en alguna etapa de su vida, de que realmente podía obtenerse una geometría consistente a partir de la negación del quinto postulado de Euclides. Al parecer, la razón tentativa de Lambert era que podía contemplar la posibilidad teórica de la geometría en una «esfera de radio imaginario», i.e., en una esfera cuyo «radio al cuadrado» es negativo. La fórmula de Lambert π – (α + β + γ) = = CΔ da el área, Δ, de un triángulo hiperbólico, donde α, β, γ son los ángulos del triángulo y C es una constante (siendo –C lo que ahora llamaríamos la «curvatura gaussiana» del plano hiperbólico). Esta fórmula tiene básicamente la misma apariencia que una previamente conocida debida a Thomas Hariot (1560-1621), Δ = R2(α + β + γ – π), para el área Δ de un triángulo esférico, dibujado con arcos de círculo máximo[8] en una esfera de radio R (véase la Fig. 2.20).[2.8] Para recuperar la fórmula de Lambert, tenemos que poner
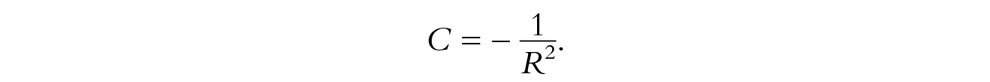
Pero, para dar el valor positivo de C, como sería necesario en la geometría hiperbólica, necesitamos que el radio de la esfera sea «imaginario» (i.e., que sea la raíz cuadrada de un número negativo). Nótese que el radio R está dado por la cantidad imaginaria (–C)–1/2. Esto explica el término «pseudorradio», introducido en §2.4, para la cantidad real C–1/2. De hecho, el procedimiento de Lambert está perfectamente justificado desde nuestra perspectiva más moderna (véanse el capítulo 4 y §18.4), y el hecho de haberlo previsto revela una gran intuición por su parte.

Fig. 2.20. La fórmula de Hariot para el área de un triángulo esférico, con ángulos α, β y γ es Δ = R2 (α + β + γ – π). La fórmula de Lambert, para un triángulo hiperbólico, tiene C = –1/R2.
Sin embargo, el punto de vista convencional (algo injusto, en mi opinión) niega a Lambert el honor de haber construido por primera vez una geometría no euclídea, y considera que (aproximadamente medio siglo más tarde) la primera persona que llegó a una aceptación clara de una geometría completamente consistente, distinta de la de Euclides, en la que el postulado de las paralelas es falso, fue el gran matemático Carl Friedrich Gauss. Al ser un hombre muy cauteloso, y temiendo la controversia que semejante revelación pudiera causar, Gauss no publicó sus hallazgos y se los reservó para sí.[9] Unos treinta años después de que Gauss hubiera empezado a trabajar en ello, la geometría hiperbólica fue redescubierta de forma independiente por otros, entre ellos el húngaro János Bolyai (en 1829) y, muy en especial, el geómetra ruso Nicolái Ivánovich Lobachevski hacia 1826 (de ahí que la geometría hiperbólica sea denominada con frecuencia geometría lobachevskiana).
Las realizaciones concretas proyectiva y conforme de la geometría hiperbólica que he descrito antes fueron encontradas por Eugenio Beltrami, y publicadas en 1868, junto con algunas otras elegantes representaciones que incluyen la hemisférica mencionada en §2.5. No obstante, la representación conforme se conoce normalmente como el «modelo de Poincaré», porque el redescubrimiento de esta representación que hizo Poincaré en 1882 es mejor conocido que la obra original de Beltrami (básicamente debido al importante uso que hizo Poincaré de este modelo).[10] Análogamente, la representación proyectiva del pobre Beltrami se denomina a veces «representación de Klein». No es infrecuente en matemáticas que el nombre habitualmente asociado a un concepto matemático no sea el de su descubridor original. Al menos, en este caso, Poincaré sí redescubrió la representación conforme (como hizo Klein con la proyectiva en 1871). Hay otros ejemplos en matemáticas en los que el (los) matemático(s) cuyo nombre (o nombres) está asociado a un resultado ¡ni siquiera conocía el resultado en cuestión![11]
La representación de la geometría hiperbólica por la que Beltrami es más conocido es otra que él también encontró en 1868. Esta representa la geometría sobre cierta superficie conocida como una pseudoesfera (véase la Fig. 2.21). Dicha superficie se obtiene rotando una tractriz, una curva investigada por primera vez por Isaac Newton en 1676, alrededor de su «asíntota». La asíntota es una línea recta a la que se aproxima la curva, haciéndose asintóticamente tangente a ella cuando la curva se extiende al infinito. Aquí vamos a imaginar la asíntota dibujada en un plano horizontal de textura rugosa. Imaginemos ahora una varilla ligera, recta y rígida, uno de cuyos extremos, P, lleva unida una masa puntual pesada, y el otro extremo R se mueve a lo largo de la asíntota. El punto P describe entonces una tractriz. Ferdinand Minding descubrió, en 1839, que la pseudoesfera tiene una geometría intrínseca negativa constante, y Beltrami utilizó esto para construir el primer modelo de geometría hiperbólica. Parece que el modelo de la pseudoesfera de Beltrami fue el que convenció a los matemáticos de la consistencia de la geometría hiperbólica plana, puesto que la medida de la distancia hiperbólica coincide con la distancia euclídea a lo largo de la superficie. Sin embargo, es un modelo algo complicado porque representa a la geometría hiperbólica solo localmente, en lugar de presentar toda la geometría de una vez, como hacen los otros modelos de Beltrami.
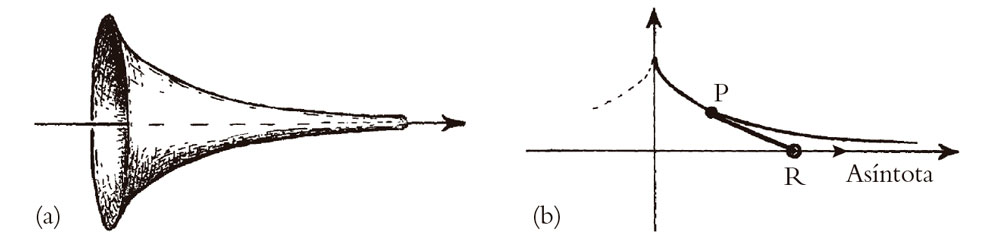
Fig. 2.21. (a) Una pseudoesfera. Esta se obtiene rotando una tractriz (b) alrededor de su asíntota. Para construir una tractriz, imaginemos que su plano es horizontal, sobre el que se arrastra una varilla ligera, rígida y sin fricción. Un extremo de la varilla es un peso puntual P con fricción, y el otro extremo R se mueve a lo largo de la asíntota (recta).
2.7. ¿RELACIÓN CON EL ESPACIO FÍSICO?
La geometría hiperbólica también funciona perfectamente en dimensiones más altas. Más aún, existen versiones de dimensión superior de los modelos conforme y proyectivo. En el caso de la geometría hiperbólica tridimensional, tenemos una esfera frontera en lugar de un círculo frontera. Toda la geometría hiperbólica tridimensional infinita está representada por el interior de esta esfera euclídea finita. El resto es básicamente igual que lo que teníamos antes. En el modelo conforme, las líneas rectas en esta geometría hiperbólica tridimensional se representan como círculos euclídeos que cortan ortogonalmente a la esfera frontera; los ángulos vienen dados por las medidas euclídeas, y las distancias vienen dadas por la misma fórmula que en el caso bidimensional. En el modelo proyectivo, las líneas rectas hiperbólicas son líneas rectas euclídeas, y las distancias vienen dadas de nuevo por la misma fórmula que en el caso bidimensional.
¿Qué pasa con nuestro universo real a escalas cosmológicas? ¿Esperamos que su geometría espacial sea euclídea, o podría estar en mejor acuerdo con alguna otra geometría, tal como la extraordinaria geometría hiperbólica (aunque en tres dimensiones) que hemos estado examinando en §§2.4-6? Esta es una cuestión realmente importante. Sabemos por la relatividad general de Einstein (a la que llegaremos en §17.9 y §19.6) que la geometría euclídea es solo una aproximación (extraordinariamente precisa) a la geometría real del espacio físico. Dicha geometría no es ni siquiera exactamente uniforme, al tener pequeños rizos de irregularidad debidos a la presencia de densidad de materia. Pese a todo, y de forma notable, de acuerdo con la mejor evidencia observacional de que hoy disponen los cosmólogos, estos rizos parecen promediarse, en escalas cosmológicas, hasta un grado extraordinariamente preciso (véanse §27.13 y §§28.4-10), y la geometría espacial de nuestro universo real parece concordar extraordinariamente bien con una geometría uniforme (homogénea e isótropa; véase §27.11). Parece que al menos los cuatro primeros postulados de Euclides han superado de forma impresionante la prueba del tiempo.
Aquí es necesario hacer un comentario aclaratorio. Básicamente existen tres tipos de geometría que satisfarían las condiciones de homogeneidad (todos los puntos son iguales) e isotropía (todas las direcciones son iguales), que se conocen como euclídea, hiperbólica y elíptica. La geometría euclídea nos es familiar (y lo ha sido durante unos veintitrés siglos). La geometría hiperbólica ha constituido nuestro interés principal en este capítulo. Pero ¿cuál es la geometría elíptica? Esencialmente, la geometría elíptica plana es la satisfecha por figuras dibujadas en la superficie de una esfera. Apareció en la discusión de la aproximación de Lambert a la geometría hiperbólica, en §2.6. Véanse las Figs. 2.22 a, b, c, para la interpretación de Escher de los casos elíptico, euclídeo e hiperbólico, respectivamente, utilizando en los tres casos una teselación similar de ángeles y demonios, la tercera de las cuales ofrece una alternativa interesante a la Fig. 2.11. (Existe también una versión tridimensional de la geometría elíptica, y hay versiones en las que se considera que puntos diametralmente opuestos de la esfera representan el mismo punto. Estas cuestiones se examinarán con algo más de detalle en §27.11.) Sin embargo, podría decirse que el caso elíptico viola los postulados segundo y tercero de Euclides (además del primero). En efecto, se trata de una geometría que es finita en extensión (y en la que más de un segmento de línea une un par de puntos).
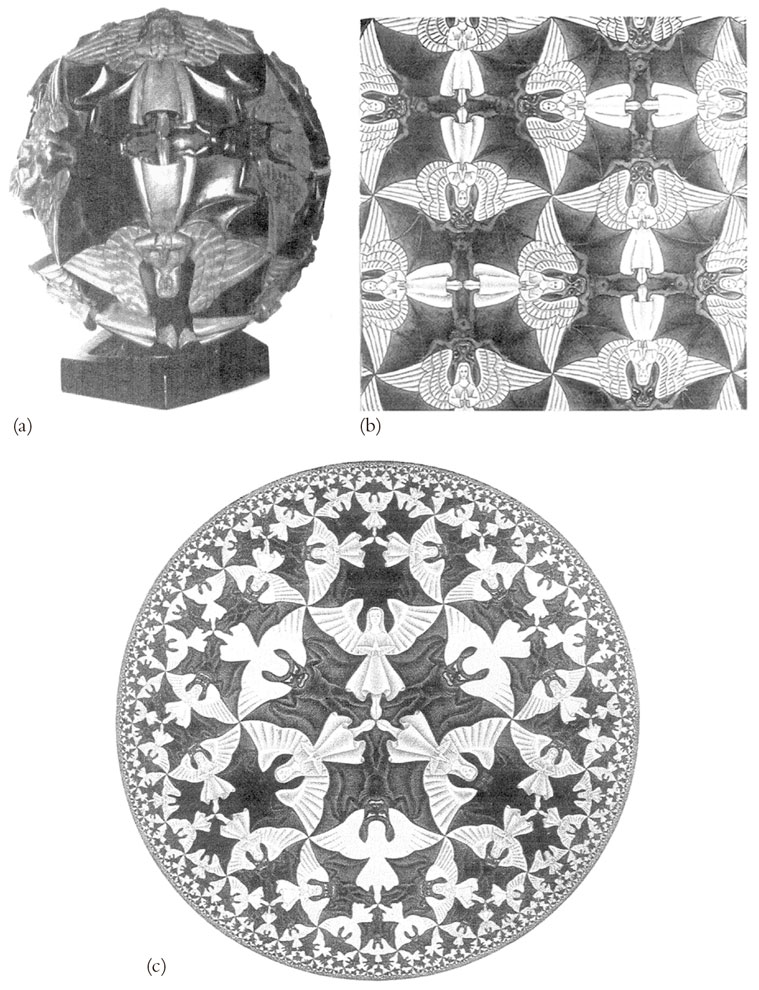
Fig. 2.22. Los tres tipos básicos de geometría plana uniforme, tal como son ilustrados por Escher utilizando teselaciones de ángeles y demonios. (a) Caso elíptico (curvatura positiva); (b) Caso euclídeo (curvatura cero), y (c) Caso hiperbólico (curvatura negativa), en la representación conforme (Límite circular IV de Escher, que debe compararse con la Fig. 2.17).
¿Cuál es, entonces, el estatus observacional de la geometría espacial a gran escala del universo? Solo se puede decir que todavía no lo sabemos, aunque recientemente se ha dado gran publicidad a afirmaciones de que la geometría de Euclides era correcta en todos los niveles, y que su quinto postulado también se cumple, de modo que la geometría espacial promediada es lo que llamamos «euclídea».[12] Por otra parte, existe también evidencia (parte de la cual procede de los mismos experimentos) que parece apuntar firmemente a una geometría global hiperbólica para el universo espacial.[13] Además, algunos teóricos han argumentado hace tiempo a favor del caso elíptico, y este no está desde luego descartado por la propia evidencia que se aporta en apoyo del caso euclídeo (véanse las últimas partes de §34.4). Como percibirá el lector, la cuestión está todavía llena de controversia y, como cabría esperar, de discusiones con frecuencia acaloradas. En posteriores capítulos de este libro, trataré de presentar muchas de las ideas que se han propuesto en relación con esto (y no intento ocultar mi propia opinión a favor del caso hiperbólico, aunque tratando de ser tan justo respecto a los otros como sea posible).
Por fortuna para aquellos, como yo mismo, que se sienten atraídos por las bellezas de la geometría hiperbólica, y también por la magnificencia de la física moderna, existe otro papel para esta soberbia geometría que es indiscutiblemente fundamental para nuestra moderna comprensión del universo físico. En efecto, según la moderna teoría de la relatividad, el espacio de velocidades es ciertamente una geometría hiperbólica tridimensional (véase §18.4), en lugar de la euclídea que sería válida en la más antigua teoría newtoniana. Esto nos ayuda a entender algunos de los enigmas de la relatividad. Imaginemos, por ejemplo, un proyectil lanzado hacia delante, con velocidad cercana a la de la luz, desde un vehículo que también se mueve hacia delante con una velocidad comparable y pasa frente a un edificio. Pese a todo, con relación a dicho edificio, el proyectil nunca puede superar la velocidad de la luz. Aunque esto parece imposible, veremos en §18.4 que encuentra una explicación directa en términos de geometría hiperbólica. Pero estas materias fascinantes deben esperar hasta capítulos posteriores.
¿Qué pasa con el teorema de Pitágoras, cuyo fallo hemos visto en la geometría hiperbólica? ¿Debemos abandonar el mayor de los regalos concretos que hicieron los pitagóricos a la posteridad? En absoluto, pues la geometría hiperbólica —y, de hecho, todas las geometrías «riemannianas» que generalizan la geometría hiperbólica de una manera irregularmente curvada (que forma el marco esencial de la teoría de la relatividad general de Einstein; véanse §13.8, §14.7, §18.1 y §19.6)— depende vitalmente de la validez del teorema de Pitágoras en el límite de pequeñas distancias. Además, su enorme influencia impregna otras vastas áreas de las matemáticas y la física (por ejemplo, la estructura métrica «unitaria» de la mecánica cuántica; véase §22.3). A pesar de que este teorema es, en cierto sentido, reemplazado para «grandes» distancias, sigue siendo central para la estructura a pequeña escala de la geometría, encontrando un rango de aplicación que supera muchísimo a aquel para el que fue propuesto originalmente.
Notas
Sección 2.1
2.1. No está muy claro históricamente quién demostró realmente por primera vez lo que ahora conocemos como «teorema de Pitágoras»; véase la nota 1.1. Parece que los antiguos egipcios y babilonios conocían al menos muchos ejemplos de este teorema. El verdadero papel desempeñado por Pitágoras o sus seguidores es básicamente supuesto.
Sección 2.2
2.2. No obstante, incluso con todo este cuidado en la obra de Euclides quedaron varias hipótesis ocultas, que tienen que ver básicamente con lo que ahora llamaríamos cuestiones «topológicas» que habrían parecido «intuitivamente obvias» para Euclides y sus contemporáneos. Estas hipótesis no mencionadas solo fueron advertidas siglos después, en particular por Hilbert a finales del siglo XIX. Las ignoraré en lo que sigue.
2.3. Véase, por ejemplo, Thomas (1939). Compárese también con Schulz (1997), que da una bella exposición axiomática de la geometría espaciotemporal 4-dimensional de Minkowski (§17.8, §18.1).
Sección 2.4
2.4. La notación «exponencial» tal como C–1/2 se utiliza con frecuencia en este libro. Como ya se ha dicho en la nota 1.1, a5 significa a × a × a × a × a; por consiguiente, para un entero positivo n, el producto de a consigo mismo un total de n veces se escribe an. Esta notación se extiende a exponentes negativos, de modo que a–1 es el recíproco 1/a de a, y a–n es el recíproco 1/an de an, o de forma equivalente (a–1)n. De acuerdo con la discusión más general de §5.2, a1/n, para un número positivo a, es la «raíz n-ésima de a», que es el número (positivo) que satisface (aa1/n)n = a (véase la nota 1.1). Además, am/n es la potencia m-ésima de a1/n.
Sección 2.6
2.5. Saccheri (1733), Prop. XXXIII.
2.6. Existe un punto de vista conocido como intuicionismo, mantenido por una minoría (bastante pequeña) de matemáticos, en el que no se acepta el principio de «demostración por contradicción». La objeción consiste en que este principio puede ser no constructivo en cuanto que a veces lleva a una afirmación de la existencia de cierta entidad matemática, sin que se ofrezca ninguna construcción real de la misma. Esto tiene cierta relevancia para las cuestiones discutidas en §16.6. Véase Heyting (1956).
2.7. Hardy (1940), p. 34.
2.8. Los arcos de círculo máximo son las curvas «más cortas» (geodésicas) sobre la superficie de una esfera; yacen en planos que pasan por el centro de la esfera.
2.9. Es un tema de discusión si Gauss, que estaba profesionalmente interesado en asuntos de geodesia, podría haber tratado de averiguar realmente si hay desviaciones medibles de la geometría euclídea en el espacio físico. Debido a su bien conocida reticencia en cuestiones de geometría no euclídea, es poco probable que lo diera a conocer si en efecto estuviera tratando de hacerlo, especialmente porque (como ahora sabemos) estaba abocado al fracaso, debido a la pequeñez del efecto, según la teoría moderna. Parece que hoy día hay consenso en que él «solo estaba haciendo geodesia», al estar interesado en la curvatura de la Tierra, y no del espacio. Pero encuentro algo difícil creer que él no anduviera también buscando cualquier discrepancia importante con la geometría euclídea; véanse Fauvel y Gray (1987) y Gray (1979).
2.10. La representación denominada «semiplano de Poincaré» (con forma métrica (dx2 + dy2)/y2; véase §14.7) se debe también a Beltrami (1868). La curvatura negativa constante de la «métrica de Poincaré» 4(dx2 + + dy2)/(1 – x2 – y2)2 de las Figs. 2.11-13 fue advertida realmente por Riemann.
2.11. Esto parece aplicarse incluso al propio Gauss (que, por otra parte, había anticipado con mucha frecuencia el trabajo de otros matemáticos). Existe un importante teorema matemático topológico conocido como «teorema de Gauss-Bonnet», que puede demostrarse elegantemente mediante el uso de la denominada «aplicación de Gauss», pero el propio teorema parece deberse en realidad a Blaschke y el elegante método de demostración citado fue encontrado por Olinde Rodrigues. Parece que Gauss y Bonnet no conocieron jamás ni el resultado ni el método de demostración. Existe un teorema de «Gauss-Bonnet» más elemental, correctamente citado en varios textos; véanse Willmore (1959) y Rindler (2001).
Sección 2.7
2.12. La evidencia principal respecto a la estructura global del universo como un todo procede de un análisis detallado de la radiación cósmica de fondo de microondas (CMB) que se discutirá en §§27.7,10,11,13, §§28.5,10 y §30.14. Una referencia básica es de Bernardis et al. (2000); para datos más recientes y más precisos, véase Netterfield et al. (2001) (concernientes a BOOMERanG). Véanse también Hanany et al. (2000) (concernientes a MAXIMA), Halverson et al. (2001) (concernientes a DASI), y Bennet et al. (2003).
2.13. Véanse Gurzadyan y Torres (1997) y Gurzadyan y Kocharyan (1994) para los soportes teóricos, y Gurzadyan y Kocharyan (1992) (para los datos de COBE) y Gurzadyan et al. (2002, 2003) (para los datos de BOOMERanG y (2004) para los datos de WMAP) para los correspondientes análisis de los datos CMB reales.