1
Las raíces de la ciencia
1.1. LA BÚSQUEDA DE LAS FUERZAS QUE CONFIGURAN EL MUNDO
¿Qué leyes rigen nuestro universo? ¿Cómo las conoceremos? ¿Cómo puede servirnos este conocimiento para comprender el mundo y con ello orientar sus acciones en nuestro provecho?
Desde los albores de la humanidad, los hombres se han sentido profundamente intrigados por preguntas como estas. Al principio trataron de dar sentido a las fuerzas que controlan el mundo aferrándose al tipo de conocimiento que les era accesible a partir de sus propias vidas. Imaginaban que cualquier cosa o quienquiera que fuera lo que controlaba su entorno lo haría de la misma forma en que ellos se esforzaban para controlar las cosas: originalmente habían creído que su destino estaba bajo la influencia de seres que actuaban de acuerdo con sus propios y variados impulsos humanos. Tales fuerzas impulsoras podían ser el orgullo, el amor, la ambición, la rabia, el miedo, la venganza, la pasión, el castigo, la lealtad o el arte. Por consiguiente, el curso de los fenómenos naturales —como el Sol, la lluvia, las tormentas, el hambre, la enfermedad o la pestilencia— se entendía como el capricho de dioses o diosas motivados por tales impulsos humanos. Y lo único que se podía hacer para influir en estos acontecimientos era apaciguar a las figuras divinas.
Pero poco a poco se empezó a establecer la fiabilidad de otro tipo de pautas. La precisión del movimiento del Sol en el cielo y su evidente relación con la alternancia del día y la noche ofrecía el ejemplo más obvio; pero también la posición del Sol respecto a las estrellas del orbe celeste aparecía estrechamente asociada al cambio y a la implacable regularidad de las estaciones, y a la clara influencia en el clima que la acompañaba y, en consecuencia, en la vegetación y el comportamiento animal. También el movimiento de la Luna parecía firmemente regulado, y sus fases determinadas por su relación geométrica con el Sol. Se advirtió que en aquellos lugares de la Tierra en los que los océanos abiertos se encuentran con la tierra, las mareas tenían una regularidad rígidamente gobernada por la posición (y la fase) de la Luna. Por último, incluso los mucho más complicados movimientos aparentes de los planetas empezaron a ceder sus secretos, revelando una regularidad y una inmensa precisión subyacente. Si los cielos estaban realmente controlados por los caprichos de los dioses, entonces estos mismos dioses parecían estar bajo el hechizo de leyes matemáticas exactas.
Del mismo modo, las leyes que controlaban algunos fenómenos terrestres —tales como los cambios diarios y anuales de temperatura, el flujo y reflujo de los océanos, y el crecimiento de las plantas— que, al menos en ese aspecto, se veían influidos por los cielos, compartían esa misma regularidad matemática que parecía guiar a los dioses. Pero este tipo de relación entre el comportamiento de los cuerpos celestes y los terrestres iba a ser a veces exagerado o mal entendido, e iba a cobrar una importancia desmesurada, que llevaría a las connotaciones ocultas y místicas de la astrología. Pasaron muchos siglos antes de que el rigor del conocimiento científico hiciera posible desenredar las verdaderas influencias de los cielos de las puramente hipotéticas y místicas. Pese a todo, desde los tiempos más remotos había estado claro que aquellas influencias existían realmente y que, en consecuencia, las leyes matemáticas de los cielos debían tener relevancia también aquí en la Tierra.
De forma en apariencia independiente se percibieron otras regularidades en el comportamiento de los objetos terrestres. Una de ellas era la tendencia de todas las cosas en una vecindad a moverse en la misma dirección hacia abajo, bajo la influencia de lo que ahora llamamos gravedad. Se observó que a veces la materia se transformaba de una forma en otra, tal como ocurría en la fusión del hielo o la disolución de la sal, aunque la cantidad total de materia nunca parecía cambiar, lo que refleja la ley que ahora conocemos como conservación de la masa. Además, se advirtió que hay muchos cuerpos materiales con la importante propiedad de que conservan su forma, de donde surgió el concepto de movimiento espacial rígido; y se hizo posible comprender las relaciones espaciales en términos de una geometría precisa y bien definida: la geometría tridimensional que ahora denominamos euclídea. Más aún, la noción de «línea recta» en esta geometría resultó ser la misma que la que proporcionaban los rayos luminosos (o las líneas visuales). Sin duda, había una extraordinaria precisión y belleza en estas ideas, que despertaban una gran fascinación en los antiguos, igual que la despiertan hoy en nosotros.
Sin embargo, y en relación con nuestras vidas cotidianas, las implicaciones de esta precisión matemática para las acciones del mundo parecían con frecuencia poco excitantes y limitadas, pese al hecho de que las propias matemáticas parecían representar una verdad profunda. En consecuencia, en tiempos antiguos muchas personas iban a permitir que su imaginación se dejara llevar por su fascinación por el tema y les condujese mucho más allá de lo que era adecuado. En astrología, por ejemplo, las figuras geométricas también solían generar connotaciones místicas y ocultas, como era el caso de las supuestas potencias mágicas de pentagramas y heptagramas. Y había una supuesta asociación completamente hipotética entre los sólidos platónicos y los estados elementales de la materia (véase la Fig. 1.1). Tardarían muchos siglos en llegar los conocimientos más profundos que tenemos en la actualidad, concernientes a las relaciones reales entre la masa, la gravedad, la geometría, el movimiento planetario y el comportamiento de la luz.
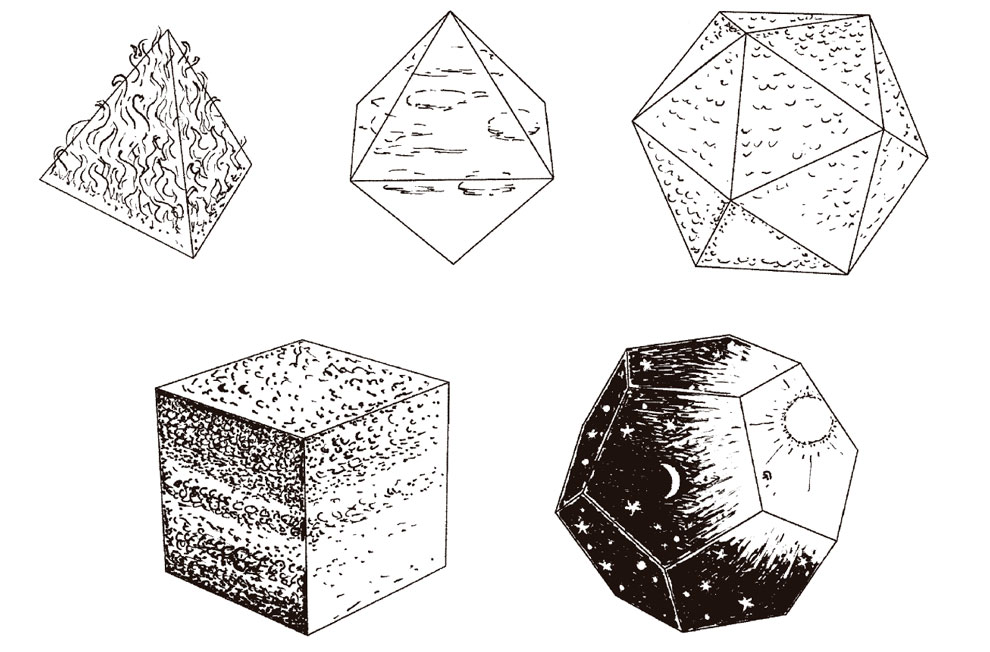
Fig. 1.1. Una asociación fantástica, hecha por los antiguos griegos, entre los cinco sólidos platónicos y los cuatro «elementos» (fuego, aire, agua y tierra), junto con el firmamento celeste representado por el dodecaedro.
1.2. LA VERDAD MATEMÁTICA
Los primeros pasos hacia una comprensión de las influencias reales que controlan la naturaleza requerían desenredar lo verdadero de lo puramente hipotético. Pero antes de que estuvieran en situación de hacer esto de forma fiable para su conocimiento de la naturaleza, los antiguos necesitaban algo más. Lo primero que tenían que hacer era descubrir la forma de desenredar lo verdadero de lo hipotético en matemáticas. Se necesitaba un procedimiento para decir si se puede confiar o no en la verdad de una afirmación matemática dada. Hasta que no quedara establecida de forma razonable esta cuestión preliminar, habría pocas esperanzas de abordar con seriedad aquellos problemas más difíciles concernientes a las fuerzas que controlan el comportamiento del mundo y cualesquiera que pudieran ser sus relaciones con la verdad matemática. Esta comprensión de que la clave para entender la naturaleza reside en unas matemáticas incuestionables fue quizá el primer avance trascendental en la ciencia.
Aunque ya desde los tiempos antiguos de Egipto y Babilonia se habían supuesto todo tipo de verdades matemáticas, solo cuando los filósofos griegos Tales (c. 625-547 a.C.) y Pitágoras[1][*] de Samos (c. 572-497 a.C.) empezaron a introducir la idea de demostración matemática se colocó la primera piedra fundacional firme del conocimiento matemático —y, por consiguiente, de la propia ciencia—. Quizá fuera Tales el primero en introducir esta idea de demostración, pero parece que fueron los pitagóricos quienes hicieron por primera vez un uso importante de la misma para establecer cosas que, de otro modo, no eran obvias. Parece que Pitágoras también tuvo una fuerte intuición de la importancia del número, y de los conceptos aritméticos, en el gobierno de las acciones del mundo físico. Se dice que un factor importante en esta comprensión fue el darse cuenta de que las armonías más bellas producidas por liras o flautas correspondían a las razones más simples entre las longitudes de las cuerdas vibrantes o los tubos. También se dice que él introdujo la «escala pitagórica», cuyas razones numéricas sabemos ahora que son las frecuencias que determinan los intervalos principales en los que se basa esencialmente la música occidental.[2] El famoso teorema de Pitágoras, que afirma que el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los otros dos lados, mostró, quizá más que cualquier otra cosa, que existe una relación precisa entre la aritmética de los números y la geometría del espacio físico (véase el capítulo 2).
Pitágoras tuvo un número considerable de seguidores —los pitagóricos— establecidos en la ciudad de Crotona, en lo que hoy es el sur de Italia, pero su influencia en el mundo exterior se vio dificultada por el hecho de que todos los miembros de la fraternidad pitagórica hacían un juramento de secreto. Por ello, casi todas sus conclusiones detalladas se han perdido. De todas formas, algunas de estas conclusiones se filtraron, con consecuencias desafortunadas para los «topos», que, al menos en una ocasión, ¡sufrieron el castigo de morir ahogados!
A la larga, la influencia de los pitagóricos sobre el progreso del pensamiento humano ha sido enorme. Por primera vez, con demostración matemática, era posible hacer afirmaciones significativas de un carácter incuestionable, de modo que seguirían siendo tan verdaderas hoy como en la época en que se hicieron, con independencia de cuánto haya progresado nuestro conocimiento del mundo desde entonces. Empezaba a revelarse la naturaleza verdaderamente intemporal de las matemáticas.
Pero ¿qué es una demostración matemática? En matemáticas, una demostración es un argumento impecable, basado solo en los métodos del razonamiento puramente lógico, que permite inferir la validez de una afirmación matemática dada a partir de la validez preestablecida de otras afirmaciones matemáticas, o de ciertas afirmaciones concretas primitivas —los axiomas— cuya validez se considera evidente. Una vez que tal afirmación matemática ha quedado establecida de esta forma, se conoce como un teorema.
Muchos de los teoremas que interesaban a los pitagóricos eran de naturaleza geométrica; otros eran solo afirmaciones sobre números. Aquellos que concernían puramente a los números tienen hoy una validez inequívoca, igual que la tenían en los tiempos de Pitágoras. ¿Qué ocurre con los teoremas geométricos que los pitagóricos habían obtenido utilizando sus procedimientos de demostración matemática? También estos tienen hoy una clara validez, pero ahora surge una cuestión que complica las cosas. Se trata de una cuestión cuya naturaleza es más obvia para nosotros desde nuestro punto de vista moderno que lo era en el tiempo de Pitágoras. Los antiguos solo conocían un tipo de geometría, a saber, la que ahora llamamos geometría euclídea, pero ahora conocemos otros muchos tipos. Así pues, al considerar los teoremas geométricos de la época griega antigua es importante especificar que la noción de geometría a la que nos referimos es en realidad la geometría de Euclides. (Seré más explícito sobre estas cuestiones en §2.4, donde se dará un ejemplo importante de geometría no euclídea.)
La geometría euclídea es una estructura matemática específica, con sus propios axiomas específicos (incluidas algunas afirmaciones menos seguras conocidas como postulados), que proporciona una excelente aproximación a un aspecto concreto del mundo físico. Este era el aspecto de realidad, muy familiar para los antiguos griegos, que remitía a las leyes que gobiernan la geometría de los objetos rígidos y sus relaciones con otros objetos rígidos cuando se movían en el espacio tridimensional. Algunas de estas propiedades eran tan familiares y autoconsistentes que tendían a ser consideradas como verdades matemáticas «evidentes» y se tomaban como axiomas (o postulados). Como veremos en los capítulos 17-19 y en §§27.8,11, la relatividad general de Einstein —e incluso el espaciotiempo minkowskiano de la relatividad especial— proporciona geometrías para el universo físico que son diferentes de, e incluso más precisas que, la geometría de Euclides, pese al hecho de que la geometría euclídea de los antiguos era ya extraordinariamente precisa. Así pues, a la hora de considerar afirmaciones geométricas debemos tener cuidado si confiamos en los «axiomas» como si fueran, en cualquier sentido, realmente verdaderos.
Pero ¿qué significa «verdadero» en este contexto? La dificultad fue apreciada por el gran filósofo griego Platón, que vivió en Atenas desde c. 429 hasta 347 a.C., aproximadamente un siglo y medio después de Pitágoras. Platón dejó claro que las proposiciones matemáticas —las cosas que podían considerarse como incuestionablemente verdaderas— no se refieren a objetos físicos reales (como los cuadrados, triángulos, círculos, esferas y cubos aproximados que podrían construirse con marcas en la arena, o con piedra o madera), sino a ciertas entidades idealizadas. Él imaginaba que esas entidades ideales habitaban en un mundo diferente, distinto del mundo físico. Hoy día podríamos llamar a este mundo el mundo platónico de las formas matemáticas. Las estructuras físicas, tales como los cuadrados, los círculos o los triángulos recortados en papiro, o marcados en una superficie plana, o quizá los cubos, los tetraedros o las esferas esculpidas en mármol, podrían ajustarse estrechamente a estos ideales, pero solo de forma aproximada. Los cuadrados, cubos, círculos, esferas, triángulos, etc., matemáticos reales no serían parte del mundo físico, sino que serían habitantes del mundo platónico de las formas matemáticas idealizadas.
1.3. ¿ES «REAL» EL MUNDO MATEMÁTICO DE PLATÓN?
Esta era una idea extraordinaria para su época, y ha resultado ser una idea muy fecunda. Pero ¿existe realmente el mundo matemático platónico, en cualquier sentido significativo? Muchas personas, incluidos los filósofos, podrían considerar que un «mundo» semejante es una completa ficción, un mero producto de nuestra imaginación desbordante. Pese a todo, el punto de vista platónico es inmensamente valioso. Nos dice que debemos ser cuidadosos en distinguir las entidades matemáticas precisas de las aproximaciones que vemos a nuestro alrededor en el mundo de los objetos físicos. Más aún, nos proporciona el esquema con el que ha procedido la ciencia desde entonces. Los científicos propondrán modelos del mundo —o, mejor, de ciertos aspectos del mundo— y estos modelos pueden ser puestos a prueba frente a observaciones previas y frente a los resultados de experimentos cuidadosamente diseñados. Los modelos se juzgan apropiados si sobreviven a este examen riguroso y si, además, son estructuras con consistencia interna. Para nuestra discusión actual, el punto importante en estos modelos es que son básicamente modelos matemáticos puramente abstractos. En particular, la cuestión misma de la consistencia interna de un modelo científico requiere que el modelo esté especificado de forma precisa. La precisión requerida exige que el modelo sea matemático, pues de lo contrario no se puede estar seguro de que estas preguntas tengan respuestas bien definidas.
Si hay que atribuir algún tipo de «existencia» al propio modelo, entonces dicha existencia está localizada dentro del mundo platónico de las formas matemáticas. Por supuesto, se podría adoptar un punto de vista opuesto: que el modelo va a tener existencia solo dentro de nuestras diversas mentes, antes que aceptar que el mundo de Platón sea en algún sentido absoluto y «real». Pese a todo, se gana algo importante al considerar que las estructuras matemáticas poseen una realidad por sí mismas. En efecto, nuestras mentes individuales son notoriamente imprecisas, poco fiables e inconsistentes en sus juicios. La precisión, fiabilidad y consistencia que requieren nuestras teorías científicas exige algo más allá de cualquiera de nuestras mentes individuales (poco dignas de confianza). En las matemáticas encontramos una solidez mucho mayor que la que puede localizarse en cualquier mente concreta. ¿No apunta esto a algo exterior a nosotros mismos, con una realidad que está más allá de lo que cada individuo puede alcanzar?
De todas formas, aún se podría adoptar el punto de vista alternativo según el cual el mundo matemático no tiene existencia independiente y consiste meramente en algunas ideas que han sido destiladas de nuestras diversas mentes, que se han mostrado totalmente dignas de confianza y en las que todos coinciden. Pero incluso este punto de vista parece dejarnos muy lejos de lo que se necesita. ¿Queremos decir «en las que todos coinciden», por ejemplo, o «en las que coinciden quienes están en su sano juicio», o «en las que coinciden todos aquellos que tienen un doctorado en matemáticas (poco frecuente en la época de Platón) y que tienen derecho a aventurar una opinión autorizada»? Parece que aquí hay un peligro de circularidad; pues juzgar si alguien está o no «en su sano juicio» requiere algún patrón externo. Lo mismo sucede con el significado de «autorizada», a menos que se adoptara algún canon de naturaleza acientífica tal como la «opinión de la mayoría» (y debería quedar claro que la opinión de la mayoría, por importante que pueda ser para un gobierno democrático, no debería ser utilizada en modo alguno como criterio de aceptabilidad científica). Las propias matemáticas parecen tener realmente una solidez que va mucho más allá de lo que cualquier matemático individual es capaz de percibir. Aquellos que trabajan en esta disciplina, ya estén implicados activamente en la investigación matemática o bien utilicen resultados que han sido obtenidos por otros, sienten normalmente que son meros exploradores de un mundo que está mucho más allá de ellos mismos, un mundo que posee una objetividad que trasciende la mera opinión, ya sea dicha opinión la suya propia o la propuesta de otros, con independencia de cuán expertos pudieran ser esos otros.
Quizá pueda ayudar el que yo plantee de una forma diferente el caso de la existencia real del mundo platónico. Lo que entiendo por esta «existencia» es tan solo la objetividad de la verdad matemática. La existencia platónica, tal como yo la veo, se refiere a la existencia de un canon externo objetivo que no depende de nuestras opiniones individuales ni de nuestra cultura concreta. Tal «existencia» podría también referirse a objetos distintos de las matemáticas, tales como la moralidad o la estética (cf. §1.5), pero aquí estoy interesado solo en la objetividad matemática, que parece ser una cuestión mucho más clara.
Permítaseme ilustrar este punto considerando un ejemplo famoso de verdad matemática, y relacionarlo con la cuestión de la «objetividad». En 1637, Pierre de Fermat hizo su famosa afirmación conocida hoy día como el «último teorema de Fermat» (que ninguna potencia n-ésima[3] positiva de un número entero puede ser la suma de otras dos potencias n-ésimas positivas si n es un número entero mayor que 2), que él escribió en un margen de su copia de la Arithmetica, libro escrito en el siglo III por el matemático griego Diofanto. En este margen, Fermat anotó también: «He encontrado una demostración de esto verdaderamente maravillosa, que no cabe en este estrecho margen». La afirmación matemática de Fermat quedó sin confirmar durante más de trescientos cincuenta años, pese a que aunó los esfuerzos de muchos matemáticos destacados. Finalmente, Andrew Wiles publicó una demostración en 1995 (que se basaba en el trabajo previo de otros matemáticos), y esta demostración ha sido ahora aceptada como un argumento válido por la comunidad matemática.
Ahora bien, ¿aceptamos el punto de vista de que la afirmación de Fermat fue siempre verdadera, mucho antes de que este la hiciera en realidad, o es su validez una cuestión puramente cultural, dependiente de cuáles pudieran ser los cánones subjetivos de la comunidad de matemáticos humanos? Supongamos que la validez de la afirmación de Fermat es, de hecho, una cuestión subjetiva. Entonces no sería un absurdo que un matemático X hubiera dado con un contraejemplo real y concreto de la afirmación de Fermat, siempre que X lo hubiera hecho antes de 1995.[4] En tal caso, la comunidad matemática tendría que aceptar la corrección del contraejemplo de X. A partir de entonces, cualquier esfuerzo por parte de Wiles de demostrar la afirmación de Fermat tendría que ser infructuoso, por la sencilla razón de que X había obtenido su argumento primero y, en vista de ello, ¡la afirmación de Fermat sería ahora falsa! Más aún, podríamos plantear la pregunta adicional acerca de si, de acuerdo con la corrección del contraejemplo que iba a dar X, el propio Fermat habría estado necesariamente equivocado al creer en la validez de su «demostración verdaderamente maravillosa», en el instante en que escribió su nota en el margen. En el punto de vista subjetivo de la verdad matemática hubiera podido darse el caso de que Fermat tuviera una demostración válida (que habría sido aceptada como tal por sus pares en la época, si él la hubiera revelado), ¡y que fue el secretismo de Fermat el que permitió la posibilidad de que X obtuviese más tarde un contraejemplo! Creo que prácticamente todos los matemáticos, con independencia de las actitudes que profesen hacia el «platonismo», considerarán que tales posibilidades son manifiestamente absurdas.
Por supuesto, aún podría darse el caso de que el argumento de Wiles contenga un error y que la afirmación de Fermat fuera en realidad falsa. O que pudiera haber un error fundamental en el argumento de Wiles, pero que la afirmación de Fermat sea en cualquier caso verdadera. O podría ser que el argumento de Wiles sea correcto en sus líneas esenciales aunque contenga «pasos no rigurosos» que no superarían el canon de algunas reglas futuras de aceptabilidad matemática. Pero estas cuestiones no abordan el punto que estoy señalando aquí. La cuestión es la objetividad de la propia afirmación de Fermat, y no si la demostración (o la negación) particular de la misma que hiciera alguien podría resultar convincente para la comunidad matemática de cualquier época concreta.
Quizá habría que mencionar que, desde el punto de vista de la lógica matemática, la afirmación de Fermat es en realidad un enunciado matemático de un tipo particularmente simple,[5] cuya objetividad es especialmente evidente. Solo una pequeñísima minoría de matemáticos[6] consideraría que la verdad de tales afirmaciones es de algún modo «subjetiva» —aunque podría haber cierta subjetividad acerca de los tipos de argumentos que se considerarían convincentes—. Sin embargo, hay otros tipos de afirmaciones matemáticas cuya verdad podría considerarse plausiblemente como una «cuestión de opinión». Tal vez la más conocida de dichas afirmaciones sea el axioma de elección. No es importante, por el momento, que sepamos qué es el axioma de elección. (Lo describiré en §16.3.) Aquí se cita solo como ejemplo. Probablemente la mayoría de los matemáticos considerarán que el axioma de elección es «obviamente verdadero», mientras que otros pueden considerarlo una afirmación algo cuestionable que incluso podría ser falsa (y yo mismo me inclino, en cierta medida, hacia este segundo punto de vista). Otros aún podrían tomarlo como una afirmación cuya «verdad» es una mera cuestión de opinión o, más bien, como algo que puede tomarse de un modo o de otro, dependiendo de a qué sistemas de axiomas y reglas de inferencia (un «sistema formal»; véase §16.6) decida uno adherirse. Los matemáticos que defienden este último punto de vista (pero aceptan la objetividad de la verdad de enunciados matemáticos particularmente nítidos, como la afirmación de Fermat que he mencionado antes) serían platonistas relativamente débiles. Aquellos que se adhieren a la objetividad con respecto a la verdad del axioma de elección serían platonistas más fuertes.
Volveré al axioma de elección en §16.3, pues tiene cierta relevancia para las matemáticas subyacentes en el comportamiento del mundo físico, pese al hecho de que no se aborda mucho en la teoría física. Por el momento será mejor que no nos preocupemos demasiado por esta cuestión. Si el axioma de elección puede ser dilucidado en un sentido u otro mediante alguna forma apropiada de razonamiento matemático incuestionable,[7] entonces su verdad es en realidad una cuestión totalmente objetiva, y o bien el axioma pertenece al mundo platónico o bien lo hace su negación, en el sentido en que estoy interpretando este «mundo platónico». Si, por el contrario, el axioma de elección es una simple cuestión de opinión o de decisión arbitraria, entonces el mundo platónico de las formas matemáticas absolutas no contiene axioma de elección ni su negación (aunque podría contener afirmaciones de la forma «tal y cual se sigue del axioma de elección», o «el axioma de elección es un teorema de acuerdo con las reglas de tal y cual sistema matemático»).
Los enunciados matemáticos que pueden pertenecer al mundo de Platón son precisamente aquellos que son objetivamente verdaderos. De hecho, yo consideraría que la objetividad matemática es realmente el objeto del platonismo matemático. Decir que una afirmación matemática tiene una existencia platónica es sencillamente decir que es verdadera en un sentido objetivo. Un comentario similar es aplicable a las nociones matemáticas —tales como el concepto del número 7, por ejemplo, o la regla para la multiplicación de números enteros, o la idea de que cierto conjunto contiene infinitos elementos—, todas las cuales tienen una existencia platónica porque son nociones objetivas. En mi opinión, la existencia platónica es simplemente una cuestión de objetividad y, en consecuencia, no debería verse como algo «místico» o «acientífico», pese a que así la consideran algunos.
No obstante, como sucede con el axioma de elección, las preguntas acerca de si debe considerarse o no que cierta propuesta concreta de una entidad matemática tiene una existencia objetiva pueden ser delicadas y a veces muy técnicas. Pese a ello, ciertamente no necesitamos ser matemáticos para apreciar la solidez general de muchos conceptos matemáticos. En la Fig. 1.2 he representado varias porciones pequeñas de esa famosa entidad matemática conocida como el conjunto de Mandelbrot. El conjunto tiene una estructura extraordinariamente complicada, pero no se debe a ningún diseño humano. Lo realmente notable es que esta estructura está definida por una regla matemática particularmente simple. Llegaremos a ella explícitamente en §4.5, pues nos distraeríamos de nuestros propósitos actuales si tratase ahora de ofrecer esta regla en detalle.

Fig. 1.2. (a) El conjunto de Mandelbrot. (b), (c) y (d) Algunos detalles que ilustran ampliaciones de las regiones correspondientemente marcadas en la Fig. 1.2a, aumentadas por factores lineales respectivos 11,6, 168,9 y 1.042.
El punto que deseo señalar es que nadie, ni siquiera el propio Mandelbrot cuando vio por primera vez las increíbles complicaciones en los detalles finos del conjunto, tuvo ninguna preconcepción real de la extraordinaria riqueza del conjunto. El conjunto de Mandelbrot no fue invención de ninguna mente humana: sencillamente, está ahí de manera objetiva, en las propias matemáticas. Si tiene significado atribuir una existencia real al conjunto de Mandelbrot, entonces dicha existencia no está dentro de nuestras mentes, pues nadie puede abarcar por completo la inacabable variedad y la ilimitada complejidad del conjunto. Y su existencia tampoco puede residir dentro de la multitud de representaciones gráficas impresas por un computador que empiezan a captar algo de su increíble sofisticación y detalle, pues, en el mejor de los casos, tales representaciones gráficas recogen tan solo una sombra de una aproximación al propio conjunto. Pese a todo, tiene una solidez que está más allá de cualquier duda, pues la misma estructura se revela —en todos sus detalles perceptibles, con finura cada vez mayor cuanto más de cerca se examina— independientemente del matemático o computador que la examine. Su existencia solo puede estar dentro del mundo platónico de las formas matemáticas.
Soy consciente de que aún habrá muchos lectores que encuentren difícil atribuir cualquier tipo de existencia real a las estructuras matemáticas. Rogaría a tales lectores que amplíen su idea de lo que la palabra «existencia» puede significar para ellos. Las formas matemáticas del mundo de Platón no tienen evidentemente el mismo tipo de existencia que los objetos físicos ordinarios tales como las mesas y las sillas. No tienen localización espacial; no existen en el tiempo. Hay que pensar en las nociones matemáticas objetivas como entidades intemporales, y no debe considerarse que nacieron en el instante en que fueron humanamente percibidas por primera vez. Las espirales concretas del conjunto de Mandelbrot que se muestran en las Figs. 1.2c o 1.2d no alcanzaron su existencia en el instante en que se vieron por primera vez en la pantalla o la impresora de un computador. Ni surgieron cuando la idea general que hay tras el conjunto de Mandelbrot fue propuesta por primera vez por un ser humano —no por Mandelbrot, tal como sucedió, sino por R. Brooks y J. P. Matelski, en 1981, o quizá antes—. Pues ciertamente ni Brooks ni Matelski, ni siquiera al principio el propio Mandelbrot, tenían ninguna concepción real de los diseños detallados y complicados que vemos en las Figs. 1.2c y 1.2d. Dichos diseños ya «existían» desde el principio de los tiempos, en el sentido potencial e intemporal con que necesariamente se iban a revelar en la forma exacta en que hoy los percibimos, con independencia de qué momento o qué lugar eligiera cualquier ser perceptivo para examinarlos.
1.4. TRES MUNDOS Y TRES PROFUNDOS MISTERIOS
Así pues, la existencia matemática es diferente no solo de la existencia física, sino también de una existencia que es atribuida por nuestras percepciones mentales. Pese a todo, hay una conexión misteriosa y profunda con cada una de esas otras dos formas de existencia: la física y la mental. En la Fig. 1.3 he mostrado de manera esquemática estas tres formas de existencia —la física, la mental y la matemático-platónica— como entidades que pertenecen a tres «mundos» separados, representados esquemáticamente como esferas. También están indicadas las misteriosas conexiones entre los mundos, y al dibujar el diagrama he impuesto al lector algunas de mis creencias, o prejuicios, acerca de tales misterios.
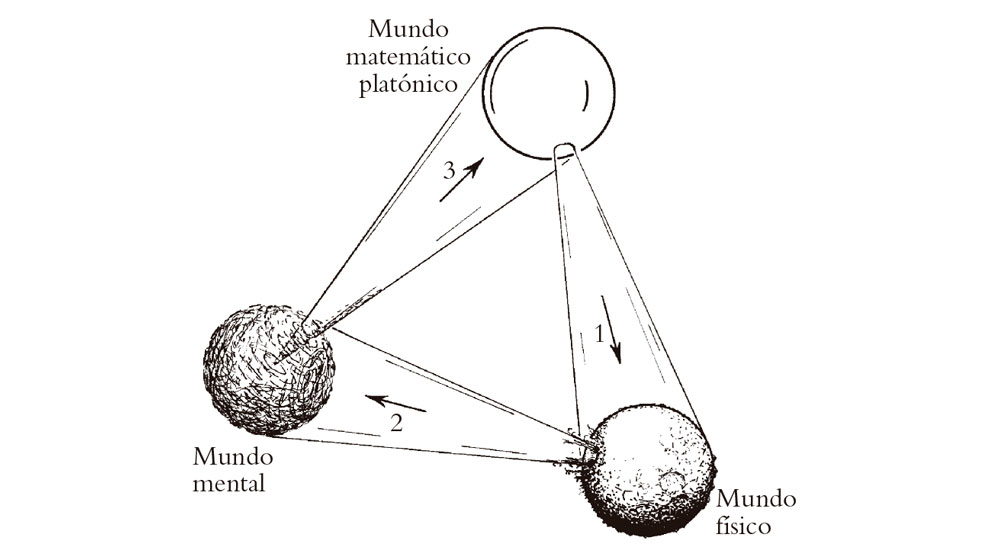
Fig. 1.3. Tres «mundos» —el matemático-platónico, el físico y el mental— y los tres profundos misterios en las conexiones entre ellos.
Con respecto al primero de esos misterios —que relaciona el mundo matemático-platónico con el mundo físico—, puede advertirse que estoy admitiendo que solo una pequeña parte del conjunto de las matemáticas tiene que tener relevancia para el funcionamiento del mundo físico. Sucede ciertamente que la gran mayoría de las actividades actuales de los matemáticos puros no tienen una conexión obvia con la física, ni con ninguna otra ciencia (cf. §34.9), aunque con frecuencia nos veamos sorprendidos por aplicaciones importantes e inesperadas. Análogamente, en relación con el segundo misterio, por el que la mentalidad entra en asociación con ciertas estructuras físicas (más concretamente, los cerebros humanos vivos, sanos y despiertos), no estoy insistiendo en que la mayoría de las estructuras físicas tengan que inducir mentalidad. Aunque el cerebro de un gato puede evocar realmente cualidades mentales, no estoy exigiendo lo mismo de una piedra. Por último, respecto al tercer misterio, ¡considero evidente que solo una pequeña fracción de nuestra actividad mental tiene que estar interesada en la verdad matemática absoluta! (Es más probable que estemos interesados en las múltiples irritaciones, placeres, preocupaciones, emociones y sensaciones por el estilo que llenan nuestras vidas cotidianas.) Estos tres hechos están representados en el pequeño tamaño de la base de la conexión de cada mundo con el siguiente, tomando los mundos del diagrama en el sentido de las agujas del reloj. Sin embargo, es en el hecho de englobar cada mundo entero dentro del ámbito de su conexión con el mundo que le precede donde estoy mostrando mis propios prejuicios.
Así pues, según la Fig. 1.3, todo el mundo físico se representa gobernado de acuerdo con leyes matemáticas. En capítulos posteriores veremos que hay una evidencia muy fuerte (aunque incompleta) que apoya esta opinión. Desde este punto de vista, todo lo que hay en el universo físico está realmente gobernado en todos sus detalles por principios matemáticos, quizá por ecuaciones, tales como las que trataremos en los capítulos que siguen, o quizá por algunas nociones matemáticas futuras fundamentalmente diferentes de aquellas que hoy etiquetamos con el término «ecuaciones». Si esto es así, entonces incluso nuestras propias acciones físicas estarían enteramente sujetas a semejante control matemático último, donde «control» podría admitir todavía cierto comportamiento aleatorio gobernado por principios probabilistas estrictos.
Muchas personas se sienten incómodas con este tipo de ideas, y debo confesar que a mí también me producen cierta desazón. De todas formas, mis prejuicios personales están realmente a favor de un punto de vista de este carácter general, puesto que es difícil ver cómo podría trazarse una línea que separe las acciones físicas bajo control matemático de aquellas que pudieran estar más allá de él. A mi modo de ver, la desazón que muchos lectores puedan compartir conmigo acerca de esta cuestión surge en parte de una noción muy limitada de lo que pudiera entrañar el «control matemático». Parte del objetivo de este libro es señalar, y revelar al lector, algo de la extraordinaria riqueza, poder y belleza que pueden brotar una vez que se ha dado con las nociones matemáticas correctas.
Ya en el conjunto de Mandelbrot, tal como se ilustra en la Fig. 1.2, podemos empezar a vislumbrar el alcance y la belleza inherentes en tales objetos. Pero incluso estas estructuras habitan en un rincón muy limitado del conjunto de las matemáticas, donde el comportamiento está gobernado por un control computacional estricto. Más allá de este rincón, hay una increíble riqueza potencial. ¿Cómo me siento realmente al considerar la posibilidad de que todas mis acciones, y las de mis amigos, estén gobernadas, en última instancia, por principios matemáticos de este tipo? Puedo aceptarlo. De hecho, preferiría que estas acciones estuviesen controladas por algo que residiera en algún aspecto semejante del fabuloso mundo matemático de Platón a que estuvieran sujetas al tipo de motivos primarios simples, tales como la búsqueda del placer, la codicia personal o la violencia agresiva, que muchos argumentarán que son las consecuencias de una posición estrictamente científica.
Pese a todo, imagino que muchos lectores seguirán teniendo dificultades para aceptar que tales acciones en el universo puedan estar enteramente sujetas a leyes matemáticas. Análogamente, muchos podrán poner objeciones a otros dos de mis prejuicios que están implícitos en la Fig. 1.3. Podrían pensar, por ejemplo, que estoy adoptando una actitud científica demasiado fría al dibujar mi diagrama de una forma que implica que toda mentalidad tiene sus raíces en la fisicidad. Esto es en realidad un prejuicio, pues aunque es cierto que no tenemos evidencia científica razonable de la existencia de «mentes» que no tengan una base física, no podemos estar completamente seguros de ello. Más aún, muchas personas con convicciones religiosas defenderán con vehemencia la posibilidad de mentes independientes de lo físico, y podrían apelar a lo que ellos consideran evidencia poderosa de un tipo diferente de la que se revela por la ciencia ordinaria.
Otro de mis prejuicios se refleja en el hecho de que en la Fig. 1.3 he representado todo el mundo platónico dentro del ámbito de la mentalidad. Con esto pretendo indicar que, al menos en principio, no hay verdades matemáticas que estén más allá del alcance de la razón. Por supuesto, hay enunciados matemáticos (incluso simples sumas aritméticas) que son tan enormemente complicados que nadie podría tener la fortaleza mental para llevar a cabo el razonamiento necesario. Sin embargo, tales objetos estarían potencialmente dentro del alcance de la mentalidad (humana), y serían compatibles con el significado de la Fig. 1.3, tal y como he pretendido representar. En cualquier caso, uno debe considerar que podría haber otros enunciados matemáticos que están incluso fuera del alcance potencial de la razón, y estos violarían la pretensión que hay tras la Fig. 1.3. (Esta cuestión será considerada más extensamente en §16.6, donde se examinará su relación con el famoso teorema de la incompletitud de Gödel.)[8]
En la Fig. 1.4, y como concesión a aquellos que no comparten todos mis prejuicios personales sobre estas cuestiones, he vuelto a dibujar las conexiones entre los tres mundos para admitir las tres posibles violaciones de mis prejuicios. En consecuencia, ahora se tiene en cuenta la posibilidad de acción física más allá del alcance del control matemático. El diagrama admite también la creencia de que pudiera haber mentalidad que no estuviera enraizada en estructuras físicas. Finalmente, permite la existencia de enunciados matemáticos verdaderos cuya verdad es en principio inaccesible mediante la razón y la intuición.
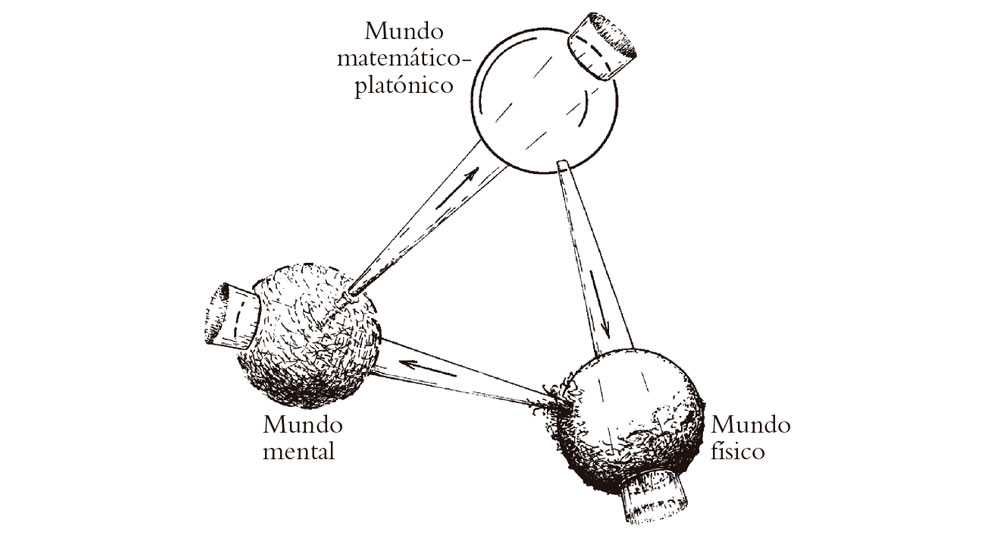
Fig. 1.4. Un nuevo dibujo de la Fig. 1.3 en el que se admiten violaciones de tres de los prejuicios del autor.
Esta imagen ampliada presenta otros misterios potenciales que van incluso más allá de aquellos que he admitido en mi imagen favorita del mundo, como se representa en la Fig. 1.3. En mi opinión, el punto de vista científico más firmemente organizado de la Fig. 1.3 tiene suficientes misterios. Estos misterios no desaparecen al pasar al esquema más relajado de la Fig. 1.4, pues sigue siendo un profundo enigma por qué tendrían que aplicarse las leyes matemáticas al mundo físico con tan extraordinaria precisión. (Vislumbraremos algo de la extraordinaria exactitud de las teorías físicas básicas en §19.8, §26.7 y §27.13.) Además, no es solo la precisión, sino también la sofisticación sutil y la belleza matemática de estas acertadas teorías lo que es profundamente misterioso. Hay asimismo un profundo e indudable misterio en cómo puede llegar a suceder que la materia física adecuadamente organizada —y aquí me refiero en concreto a cerebros humanos (o animales) vivos— pueda evocar de algún modo la cualidad mental del conocimiento consciente. Por último, hay también un misterio en cómo percibimos la verdad matemática. No se trata solamente de que nuestros cerebros estén programados para «calcular» de manera fiable. Hay algo mucho más profundo que eso en las intuiciones que incluso los más humildes de entre nosotros tenemos cuando apreciamos, por ejemplo, los significados reales de los términos «cero», «uno», «dos», «tres», «cuatro», etc.[9]
Algunas de las cuestiones que surgen en conexión con este tercer misterio serán objeto de nuestro interés en el capítulo siguiente (y más explícitamente en §§16.5,6) en relación con la noción de demostración matemática. Pero el impulso principal de este libro tiene que ver con el primero de estos misterios: la notable relación entre las matemáticas y el comportamiento real del mundo físico. No se puede alcanzar una apreciación adecuada del extraordinario poder de la ciencia moderna sin al menos cierta familiaridad con estas ideas matemáticas. Sin duda, muchos lectores pueden asustarse ante la perspectiva de tener que entender semejantes matemáticas para llegar a esta apreciación. Pese a todo, soy optimista, y creo que quizá se darán cuenta de que estas cosas no son tan terribles como ellos temen. Más aún, espero poder persuadir a muchos lectores de que, pese a lo que hayan podido creer previamente, ¡las matemáticas pueden ser divertidas!
Aquí no me interesaré especialmente por el segundo de los misterios mostrados en las Figs. 1.3 y 1.4, a saber, la cuestión de cómo la mentalidad —más en concreto, el conocimiento consciente— puede darse en asociación con estructuras físicas apropiadas (aunque tocaré esta profunda cuestión en §34.7). Tendremos ocupación más que suficiente en la exploración del universo físico y sus leyes matemáticas asociadas. Además, las cuestiones concernientes a la mentalidad son profundamente controvertidas, y si nos concentráramos en ellas nos distraería del objetivo de este libro. Sin embargo, quizá no esté de más hacer algún comentario. En mi opinión, se trata de que hay pocas posibilidades de que podamos tener una profunda comprensión de la naturaleza de la mente sin que antes aprendamos mucho más sobre las bases mismas de la realidad física. Como quedará claro en las discusiones que presentaré en capítulos posteriores, creo que se requieren revoluciones importantes en nuestra comprensión física. Hasta que no se hayan producido tales revoluciones, es muy optimista esperar que puedan hacerse demasiados progresos reales en la comprensión de la naturaleza real de los procesos mentales.[10]
1.5. LO BUENO, LO VERDADERO Y LO BELLO
En relación con esto, hay otra serie de cuestiones planteadas por las Figs. 1.3 y 1.4. He tomado la noción de Platón de un «mundo de formas ideales» solo en el sentido limitado de formas matemáticas. Las matemáticas se interesan crucialmente en el ideal concreto de verdad. El propio Platón habría insistido en que hay otros dos ideales fundamentales y absolutos, a saber, los de lo bello y lo bueno. No me niego ni mucho menos a admitir la existencia de tales ideales y a permitir que se amplíe el mundo platónico para contener absolutos de esta naturaleza.
De hecho, más adelante encontraremos algunas notables interrelaciones entre verdad y belleza que iluminan y confunden a la vez las cuestiones del descubrimiento y la aceptación de las teorías físicas (véase §§34.2, 3,9 en particular; véase también la Fig. 34.1). Más aún, aparte del indudable (aunque a menudo ambiguo) papel de la belleza en las matemáticas subyacentes en las acciones del mundo físico, los criterios estéticos son fundamentales para el desarrollo de ideas matemáticas por sí mismas, al aportar tanto el impulso hacia el descubrimiento como una poderosa guía a la verdad. Incluso conjeturaría que un elemento importante en la convicción común que tienen los matemáticos en que un mundo platónico externo tiene una existencia independiente de nosotros mismos procede de la extraordinaria e inesperada belleza oculta que tan a menudo revelan las ideas mismas.
De relevancia menos obvia aquí —pero de evidente importancia en un contexto más amplio— es la cuestión de un ideal absoluto de moralidad: ¿qué es bueno y qué es malo, y cómo perciben nuestras mentes dichos valores? La moralidad tiene una profunda conexión con el mundo mental, puesto que está íntimamente relacionada con los valores asignados por seres conscientes y, lo que es más importante, con la presencia misma de la propia consciencia. Es difícil ver qué podría significar la moralidad en ausencia de seres conscientes. A medida que progresan la ciencia y la tecnología, se hace cada vez más relevante una comprensión de las circunstancias físicas bajo las que se manifiesta la mentalidad. Creo que, en la cultura tecnológica de hoy día, es más importante que nunca que las cuestiones científicas no se separen de sus implicaciones morales. Pero estas cuestiones nos alejarían demasiado del alcance inmediato de este libro. Necesitamos abordar la cuestión de separar lo verdadero de lo falso antes de que podamos intentar de forma adecuada una aplicación de tal comprensión a separar el bien del mal.
Por último, hay otro misterio concerniente a la Fig. 1.3 que he dejado para el final. He dibujado deliberadamente la figura para ilustrar una paradoja. ¿Cómo es posible que, de acuerdo con mis prejuicios, cada mundo parezca englobar al siguiente en su totalidad? No creo que esto sea una razón para abandonar mis prejuicios, sino meramente para demostrar la presencia de un misterio aún más profundo que trasciende a aquellos que he señalado antes. Quizá haya un sentido en el que los tres mundos no sean en absoluto independientes, sino que meramente reflejen, individualmente, aspectos de una verdad más profunda sobre el mundo como un todo de la que tenemos muy poca idea en el momento presente. Tenemos un largo camino que recorrer antes de que tales cuestiones puedan ser iluminadas adecuadamente.
Me he permitido alejarme demasiado de las cuestiones centrales que nos interesarán en este libro. El objetivo principal de esta sección ha sido el de acentuar la importancia capital que tienen las matemáticas en la ciencia, tanto antigua como moderna. Echemos ahora una ojeada al mundo de Platón, al menos a una parte relativamente pequeña pero importante de dicho mundo, de especial relevancia para la naturaleza de la realidad física.
Notas
Sección 1.2
1.1. Por desgracia, no se conoce casi nada fiable sobre Pitágoras, su vida, sus seguidores o su trabajo, aparte de su existencia misma y el reconocimiento por parte de Pitágoras del papel de las razones simples en la armonía musical. Véase Burkert (1972). Pese a todo, muchas cosas de gran importancia se atribuyen habitualmente a los pitagóricos. En consecuencia, utilizaré el término «pitagórico» solo como una etiqueta, sin ninguna pretensión de exactitud histórica.
1.2. Esta es la «escala diatónica» pura en la que las frecuencias (inversamente proporcionales a las longitudes de los elementos vibrantes) están en las razones 24 : 27 : 30 : 32 : 36 : 40 : 45 : 48, que presentan muchos casos de razones simples, que subyacen a las armonías que resultan agradables al oído. Las «teclas blancas» de un piano moderno están afinadas (siguiendo un compromiso entre la pureza pitagórica de la armonía y la facilidad de los cambios de clave) como aproximaciones a estas razones pitagóricas, según la escala uniformemente temperada, con frecuencias relativas 1 : α2 : α4 : α5 : α7 : α9 : α11 : α12, donde α = 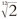 = 1,05946… (Nota: α5 significa la quinta potencia de α, i. e. α × α × α × α × α. La cantidad
= 1,05946… (Nota: α5 significa la quinta potencia de α, i. e. α × α × α × α × α. La cantidad 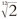 es la raíz duodécima de 2, que es el número cuya duodécima potencia es 2, i. e. 21/12, de modo que α12 = 2. Véanse la nota 1.3 y §5.2.)
es la raíz duodécima de 2, que es el número cuya duodécima potencia es 2, i. e. 21/12, de modo que α12 = 2. Véanse la nota 1.3 y §5.2.)
Sección 1.3
1.3. Recuérdese de la nota 1.2 que la potencia n-ésima de un número es dicho número multiplicado por sí mismo n veces. Así, la tercera potencia de 5 es 125, y se escribe 53 = 125; la cuarta potencia de 3 es 81, escrito 34 = 81; etc.
1.4. De hecho, mientras Wiles estaba tratando de corregir una «laguna» en su demostración del último teorema de Fermat que se había hecho evidente tras su presentación inicial en Cambridge en junio de 1993, se extendió por la comunidad matemática el rumor de que el matemático Noam Elkies había encontrado un contraejemplo de la afirmación de Fermat. Previamente, en 1988, Elkies había hallado un contraejemplo de la conjetura de Euler —que no hay soluciones enteras de la ecuación x4 + y4 + z4 = w4—, demostrando con ello que era falsa. No era inverosímil, por consiguiente, que él hubiera demostrado que la afirmación también fuera falsa. Sin embargo, el correo electrónico que inició el rumor tenía fecha de 1 de abril y se descubrió que era una broma de Henri Darmon; véase Singh (1997), p. 293.[*]
1.5. Técnicamente es una ∏1-sentencia; véase §16.6.
1.6. Me doy cuenta de que, en cierto sentido, estoy cayendo en mi propia trampa al hacer una afirmación semejante. No se trata en realidad de si los matemáticos que adoptan un punto de vista tan extremadamente subjetivo constituyen una pequeñísima minoría o no (y la verdad es que no he realizado una encuesta fiable entre los matemáticos sobre este punto); de lo que se trata es de si una posición tan extrema debe tomarse realmente en serio. Dejo esto a juicio del lector.
1.7. Quizá algunos lectores conozcan los resultados de Gödel y Cohen, según los cuales el axioma de elección es independiente de los axiomas más básicos de la teoría de conjuntos estándar (el sistema axiomático de Zermelo-Frankel). Debería quedar claro que el argumento de Gödel-Cohen no establece por sí mismo que el axioma de elección nunca será dilucidado en un sentido o en otro. Este punto es resaltado, por ejemplo, en la sección final del libro de Paul Cohen (Cohen, 1966, cap. 14, §13), salvo que Cohen está más interesado de forma explícita en la hipótesis del continuo que en el axioma de elección; véase §16.5.
Sección 1.4
1.8. Quizá se da aquí la ironía de que un antiplatónico hecho y derecho, que crea que las matemáticas están «todas en la mente», también debe creer —así parece— que no hay enunciados matemáticos verdaderos que estén en principio más allá de la razón. Por ejemplo, si el último teorema de Fermat hubiera sido inaccesible (en principio) a la razón, entonces esta visión antiplatónica no admitiría la validez de su verdad ni de su falsedad, ya que tal validez solamente viene del acto mental de percibir una demostración o una refutación.
1.9. Véase, por ejemplo, Penrose (1997b).
1.10. Mis propias ideas sobre el tipo de cambio que será necesario en nuestra visión del mundo física para que pueda acomodarse la mentalidad consciente se exponen en Penrose (1989, 1994, 1997a, 1997b).