I. El mundo de las ideas
HACE MÁS DE 100 AÑOS
Hace poco más de 100 años la física vivió una gran crisis, quizá la más grande de cuantas ha padecido. Durante casi todo el siglo XIX la física newtoniana había sido válida y constituía un baluarte del pensamiento científico. Según muchos, la física del siglo siguiente, es decir, del XX, sería asunto de refinamientos teóricos y experimentales que permitirían llegar a valores cada vez más precisos de las cantidades medidas. El futuro no ofrecía nada nuevo, sólo dificultades técnicas. Para mucha gente, describir el mundo era describir sistemas de muchas partículas, y la posibilidad de describir un conjunto de muchas partículas no estaba en los principios que subyacen a su comportamiento —que ya eran conocidos—, sino en el laborioso trabajo de cálculo para analizar cada una de las componentes.
Puede parecer paradójico, pero el mismo Michelson, de quien hablaremos más en este capítulo, escribía en 1899:
Las leyes más fundamentales y los hechos de la realidad física han sido descubiertos y ahora están tan firmemente establecidos que la posibilidad de ser suplantados como consecuencia de nuevos descubrimientos es muy remota. Los futuros descubrimientos se deben buscar ahora en la sexta posición de los decimales.1
No obstante, físicos notables como Lord Kelvin veían nubes en el horizonte. En un seminario impartido por él mismo en 1900, dijo:
La belleza y la claridad de la teoría dinámica según la cual el calor y la luz son un tipo de movimiento mecánico están hoy oscurecidas por dos nubes. La primera gran cuestión está relacionada con la manera como la tierra se mueve a través de un cuerpo elástico sólido como el éter que se supone sustenta a la luz al propagarse, y la segunda, con la doctrina de Maxwell-Boltzmann de distribución de la energía.2
James Clerk Maxwell había obtenido la ecuación que describe las velocidades de las moléculas en un gas. Ludwig Boltzmann, de manera independiente, desarrolló la teoría que permitía entender en la escala microscópica las propiedades termodinámicas que vemos en el nivel macroscópico. Sin embargo, cuando la gente trató de usar las ideas clásicas de estos modelos para describir la radiación de un cuerpo negro, el fracaso fue tan grande que se le llamó “catástrofe ultravioleta”.
Por otro lado, el éter del que habla Kelvin era una sustancia hipotética que lo llenaba todo y que permitía que por él viajase la luz, como sosteniéndola. Era así un marco de referencia con respecto al cual los demás objetos se movían. La palabra éter viene del griego y significa cielo o firmamento, y en la mitología helénica era la sustancia brillante que respiraban los dioses, en contraposición con el aire que respiran los mortales. Si bien para los físicos del siglo XIX la idea de un éter no era precisamente el de una sustancia brillante, sí se la pensaba como sustancia real. La idea fue puesta a prueba experimental y no pudo ser validada. El éter desapareció y con su desaparición llegó la teoría de la relatividad.
La primera revolución
En 1900 Max Planck propuso una solución a uno de los dos grandes problemas señalados arriba. Con la solución planteada no sólo resolvió el problema de la “catástrofe ultravioleta”, creó también una nueva física.
Veamos muy brevemente cómo se generó la revolución científica que dio origen a la mecánica cuántica: cuando uno calienta un cuerpo, por ejemplo, un bloque de metal como hierro o cobre, notará que cuando éste alcanza los 1 000 grados, aproximadamente, se pone incandescente. A esta temperatura el cuerpo emite un resplandor al que llamamos rojo vivo. Si seguimos calentando, el color irá cambiando poco a poco a anaranjado, luego a amarillo y finalmente a blanco. Si observamos esta luz a través de un prisma, veremos algo interesante. El prisma descompone la luz permitiendo que veamos qué colores se combinan para formarlo.
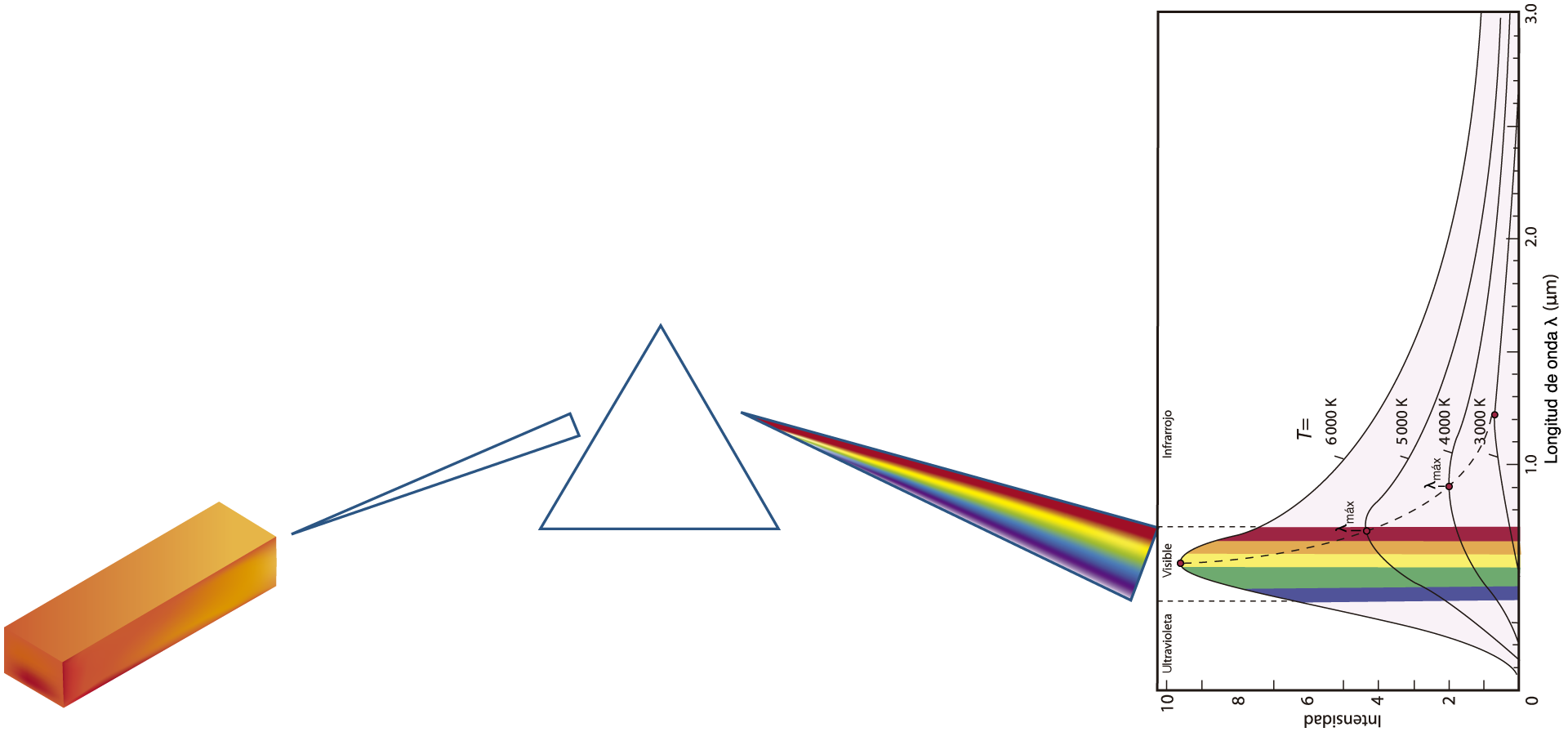
FIGURA I.1. Las curvas muestran la intensidad de cada color que compone la luz emitida a diferentes temperaturas. Nuestros ojos sólo son sensibles al intervalo de longitudes de onda que se muestra en colores.
Cuando tenemos el metal a 1 000 grados vemos un rojo intenso; cuando llega a 1 500 grados se ve anaranjado. En este punto el prisma nos revela que la luz que vemos está compuesta de rojo, anaranjado y amarillo. Si la temperatura del cuerpo llega a 2 000 grados lo vemos amarillo y el prisma nos revela que aparece un color verde entre las componentes. Cuando conseguimos poner el metal a 3 000 grados lo vemos blanco, y al llegar a este punto, con ayuda del prisma, nos percatamos de que la luz contiene todos los colores. Al seguir aumentando la temperatura, el color ya no cambia, aunque aumente la intensidad de cada color que compone el blanco.
Cuando a principios del siglo pasado se intentó calcular la intensidad de la radiación que emite el cuerpo caliente, el resultado no tuvo ningún sentido. Los cálculos decían que el cuerpo emitiría una cantidad infinita de radiación en el ultravioleta —esto es, abajo del violeta en la figura I.1—. Si bien el violeta es visible, el ultravioleta no lo es.
Lo que uno observa en el laboratorio es que la intensidad aumenta y luego disminuye nuevamente para longitudes de onda mayores, es decir, para luz roja y más allá del rojo. El infrarrojo tiene una longitud de onda tan larga que desaparece en la sensibilidad de nuestros ojos.
En esta discusión hemos usado metales para mostrar las ideas de emisión de radiación cuando son calentados. Los físicos discuten estos fenómenos con un objeto ideal al que se llama cuerpo negro, y por consiguiente se habla de “radiación de cuerpo negro”. Todos los cuerpos emiten y absorben radiación y el cómo lo hacen no sólo depende de la temperatura; también depende del tipo de superficie expuesta. Un cuerpo al que se pinta de negro será un excelente emisor, y como en general los buenos emisores son también buenos absorbentes de radiación, el cuerpo negro resulta ser muy eficiente al absorber radiación. Si al mismo cuerpo se le pinta de blanco, se convertirá en pésimo emisor y también en un muy mal absorbente de radiación. Si la taza de café es negra, el café en ella se enfriará más rápido que si la taza es blanca. Todos sabemos que la ropa negra no es muy conveniente en un día caluroso porque el color negro absorbe de manera eficiente el calor, aunque uno podría pensar que también es un buen emisor, y es cierto, sólo que si la temperatura externa es mayor que la de la piel, la ropa dará calor al cuerpo. En cambio, la ropa blanca es un buen reflector y por consiguiente un pobre absorbente de calor.
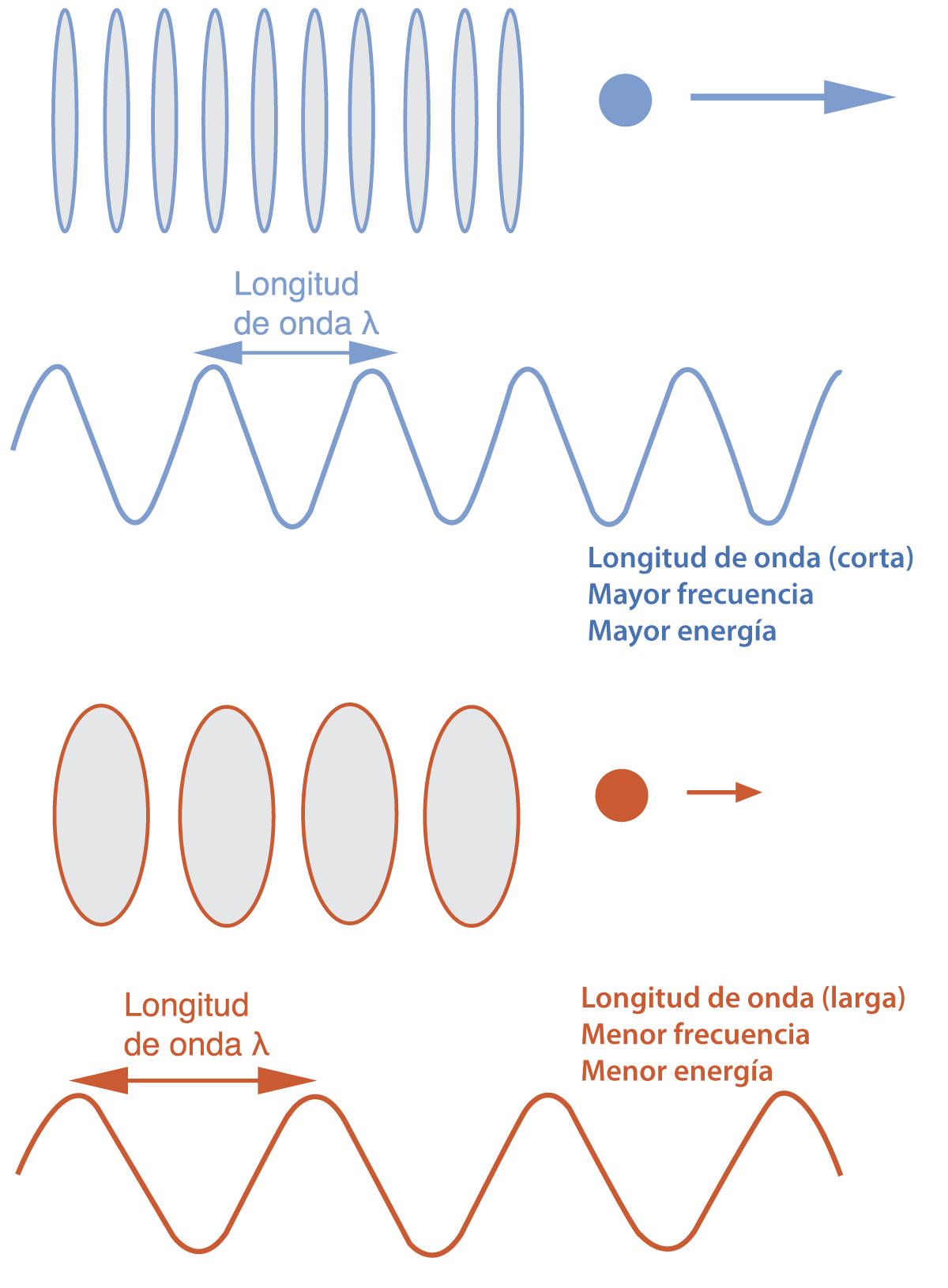
FIGURA I.2. Las partículas están asociadas a ondas. A aquellas partículas con mayor energía —como la que se muestra arriba, donde hemos representado la cantidad de movimiento con una flecha— se les asocian ondas que oscilan con mayor rapidez que a aquellas que tienen menor energía, como la de abajo.
Para los propósitos de estudio que hemos esbozado antes es bueno usar un cuerpo negro que sea lo más próximo posible al ideal. Una superficie de terciopelo negro absorbe cerca de 97% del calor que le llega, y para muchos propósitos se le puede considerar un cuerpo negro. Los metales pulidos de los que hablamos anteriormente sólo absorben 6% del calor que les llega, y por eso mismo están lejos de ser un cuerpo negro ideal. Antes usamos el metal como ejemplo porque resulta más intuitivo para el lector imaginar las ideas, pero la verdad es que está lejos de ser un buen cuerpo negro.
Ante la catástrofe ultravioleta, el físico alemán Max Planck propuso describir la emisión de radiación del cuerpo negro como si fuera discontinua. Él se imaginó que el cuerpo estaba compuesto de partículas que oscilaban a una cierta frecuencia. A estas pequeñas unidades o paquetes de energía los denominó quantum. Estableció además que la cantidad de energía de un quantum depende de la longitud de onda de la radiación, es decir, del color de la emisión: cuanto menor fuera esa longitud, mayor sería la fuerza energética del paquete.
La ecuación que Max Planck propuso es:
E = h v,
donde E es la energía del paquete y v su frecuencia. La letra h es una nueva constante de la naturaleza a la que se llama hoy la constante de Planck. El valor de esta constante es muy pequeño:
h = 6.6 × 10–34 J . s
Con estas ideas Planck pudo describir la emisión de cuerpo negro, que, como dijimos, era uno de los problemas abiertos cuando el siglo XX comenzaba.
En su momento la teoría de los paquetes de radiación tuvo poca repercusión por ser demasiado revolucionaria. A nadie se le hubiese ocurrido pensar que el cuerpo negro emitiría de manera discontinua. La teoría de Planck, sin embargo, sirvió más adelante para explicar otros fenómenos. Fue así como nació la cuantización de la energía, que en los años siguientes vendría a formalizarse y a adoptar una forma más completa. Éste es el origen de la mecánica cuántica.
La segunda revolución
A fines del siglo XIX se aceptaba ya que los planetas y las estrellas se movían. La pregunta crucial, no obstante, era: ¿con respecto a qué se mueven los astros?
La física newtoniana afirmaba que todo se movía en una sustancia incorpórea denominada éter. Si el éter permanecía inmóvil, entonces el movimiento de los cuerpos se podría determinar usándolo como marco de referencia. Sin embargo, en 1887 el físico estadunidense Albert Michelson, junto con Edward W. Morley, realizó varios experimentos que mostraron la inexistencia del éter. Ya antes, en 1881, Michelson había construido un interferómetro que perfeccionó en 1887. Con este aparato se podía medir la diferencia de velocidades de la luz en direcciones perpendiculares. Si la luz viaja más rápidamente en la dirección de movimiento del planeta que en la perpendicular, se debería ver un corrimiento en el patrón de interferencia. Si el éter se opone al movimiento de la luz —como el viento lo hace cuando viajamos en un auto a una velocidad considerable—, esta oposición del viento será menor en la dirección perpendicular y aun favorable en la dirección opuesta. La diferencia se puede apreciar con cambios en el patrón de interferencia de la luz.
Una manera sencilla de explicarlo es en términos de dos nadadores que compiten en tiempo de nado de la misma distancia. La competencia consiste en salir de un punto, llegar a una cierta marca y regresar. Si la competencia se realiza en una piscina donde el agua no corre, la carrera terminará en empate, porque —pensémoslo así— los dos nadadores son igualmente veloces. Sin embargo, si existe una corriente que va en contra del nadador 1, mientras que el nadador 2 avanza en la dirección perpendicular a la corriente, no es difícil saber que el nadador 2 ganará la competencia.
En la figura I.3 hemos dibujado el interferómetro de Michelson de manera muy sencilla. Ahí se puede identificar al rayo de luz 1 y al rayo de luz 2 como los dos nadadores de los que hablamos.
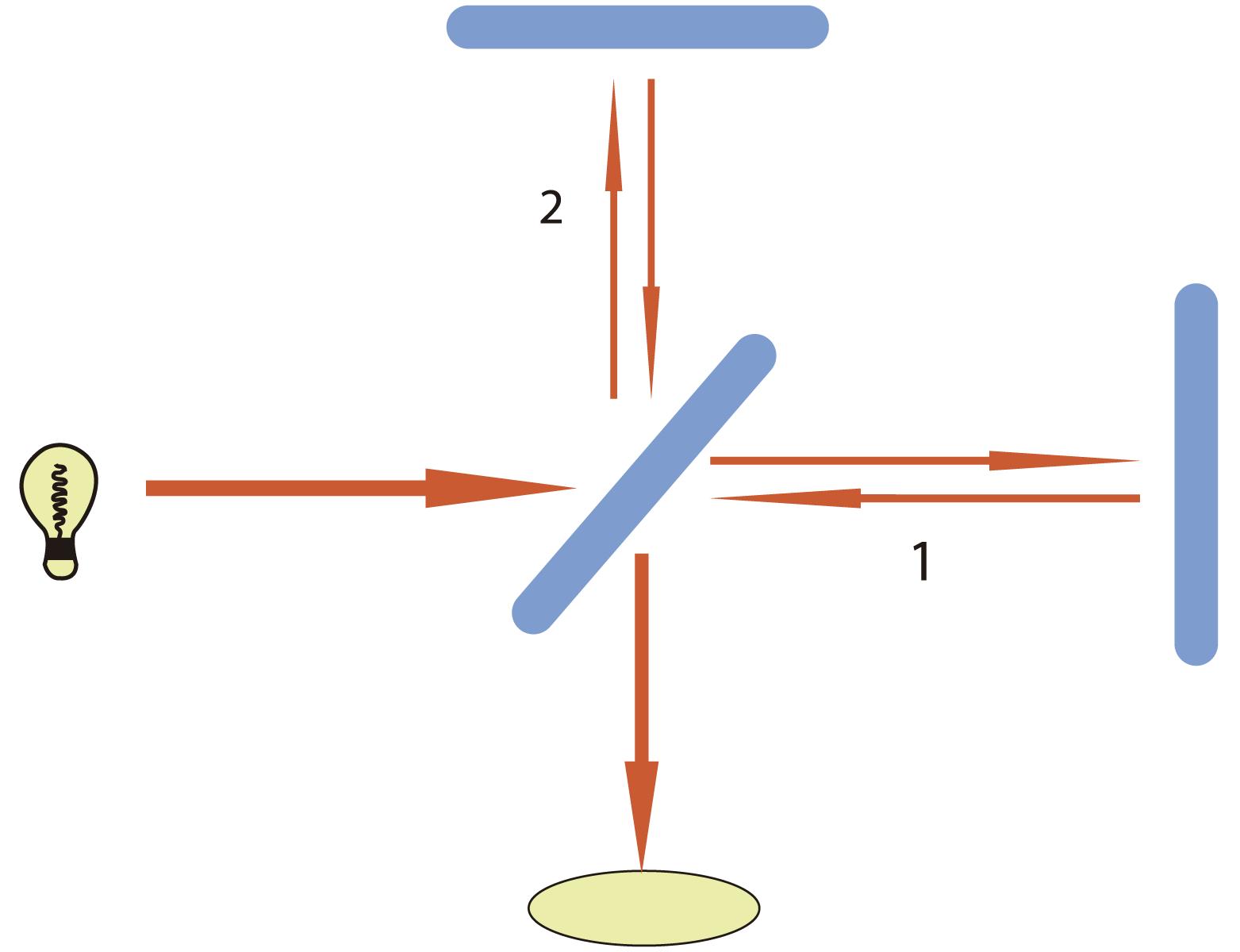
FIGURA I.3. En la imagen, la fuente de luz produce un haz que incide en un espejo medianamente plateado, es decir, que deja pasar la mitad de la luz y refleja la otra mitad. De esta manera hemos construido dos nadadores: (1) y (2). Los rectángulos azules son espejos que reflejan la luz. Cuando la luz regresa de los espejos normales al espejo medio plateado dejará pasar la mitad de uno y reflejará la mitad del otro para que éstos formen un patrón de interferencia en el punto amarillo (nótese que la mitad del rayo 1 que pasa de vuelta hacia la fuente, así como la mitad del 2 que se refleja hacia la fuente, no están dibujados).
Las distancias entre los espejos son tales que las distancias a las que los rayos 1 y 2 viajan serán las mismas, de tal manera que los dos rayos llegarán “en fase”, es decir, que, siendo ondas, los máximos y mínimos de ambos rayos deberán coincidir, produciendo un patrón constructivo que se verá en la pantalla amarilla con un brillo mayor. Si por alguna razón un haz viaja a mayor velocidad que el otro, entonces la interferencia entre ambos “producirá anillos de interferencia”. Si este aparato está montado en nuestro planeta, que se mueve a 29 000 metros sobre segundo alrededor del Sol, es decir, que se mueve a esta velocidad con respecto al éter, entonces tendremos el escenario de los nadadores en dirección contraria al viento del éter o en dirección perpendicular. Esto hará que uno de los haces esté en ventaja con respecto al otro. Al llegar antes producirá una interferencia que podemos medir en la pantalla amarilla.
Los brazos del interferómetro de Michelson medían 1.2 metros y todo el arreglo de espejos estaba montado en un bloque de mármol que flotaba sobre mercurio líquido para reducir el efecto de las vibraciones. Una vez ajustado el interferómetro podía ser girado en diferentes direcciones. Considerando la velocidad de la luz y la velocidad de la Tierra, podían haber visto con facilidad el cambio en el patrón de interferencia que se induciría como resultado del efecto que el éter tendría sobre uno y no sobre el otro de los haces; ¡sólo que esto nunca fue observado!
Pensaron que quizá la rotación de la Tierra cancelaba el efecto del movimiento del planeta alrededor del Sol, por lo que esperaron 12 horas para repetir el experimento. Pero esto no cambió las cosas y en la pantalla no observaron efecto alguno. Creyeron luego que quizá el movimiento de la Tierra alrededor del Sol era cancelado de alguna manera por la posición del planeta en su órbita, por lo que esperaron seis meses para rehacer el experimento y, de nuevo, no se observó cambio. Entonces se pensó que tal vez la Tierra arrastraba al éter consigo misma en su movimiento, por lo que buscaron una montaña en California con la idea de que, en la altura, el efecto de arrastre sería menor, pero nuevamente no se observó una interferencia.
Hendrick Lorentz interpretó el resultado del experimento de Michelson y Morley en 1892, con la hipótesis de contracción de la longitud. Explicó el resultado con la posibilidad de que los objetos sufriesen una contracción a lo largo de la dirección de movimiento. La contracción debía ser tal que permitía ajustar el resultado experimental.
En 1899, sobre la misma línea de trabajo, Lorentz llegó a las reglas de transformación entre marcos de referencia que vendrían a formar la parte medular de la teoría de la relatividad. Por su parte, Henri Poincaré en 1904 hablaba ya del principio de relatividad y trabajó la parte temporal de las transformaciones relativistas. Con estos antecedentes, Einstein publicó su famoso trabajo en 1905, y habría de quedar como el creador de la teoría de la relatividad. Al respecto, E. Whittaker escribió en un artículo lo siguiente:
[…] en el otoño del mismo año [1905] y en el mismo volumen de la revista Annalen der Physik en el que se había publicado su artículo acerca del movimiento browniano, Einstein escribió un artículo en el que exponía la teoría de la relatividad de Poincaré y Lorentz con algunos complementos, el cual llamó mucho la atención.3
Einstein partió de la hipótesis crucial: “la velocidad de la luz es una constante que no dependerá de ningún marco de referencia”. Para mantener esto fue necesario cambiar la mecánica conocida, dando origen a la teoría de la relatividad. La solución propuesta fue tal que no se necesitó más un marco de referencia absoluto y que las leyes y fenómenos que estudiamos no dependen de ningún marco en especial.
La teoría de la relatividad tiene dos versiones: la teoría especial, que se limita a la descripción de objetos en movimiento con velocidades constantes, y la teoría de la relatividad generalizada, que describe la fuerza gravitacional y la aceleración en los objetos.
La teoría general de la relatividad tuvo que esperar varios años. No fue sino hasta 1915 que David Hilbert, matemático alemán, presentó la ecuación que describe a la fuerza gravitatoria ante la Real Academia en Gotinga, Alemania. El 25 de noviembre de ese mismo año, es decir, cinco días más tarde, Albert Einstein presentó la misma ecuación en una reunión de la Academia de Prusia.
¿Por qué se ignora hoy la participación de más gente en la construcción de la teoría especial y general de la relatividad? ¿Por qué se atribuye todo a Albert Einstein? Muy probablemente hay aspectos sociológicos y de carácter histórico que acabaron por imponer la figura de Einstein como único autor, pero la verdad es que todas estas ideas estaban en el aire y mucha gente contribuyó a la construcción de lo que sería la nueva física.
La teoría general de la relatividad establece una relación estrecha entre la geometría del espacio-tiempo y la fuerza gravitacional. Según la teoría, los cuerpos con masa deforman el espacio y el tiempo curvándolo. La fuerza que ejercen sobre los otros cuerpos con masa es pues el efecto de esta deformación.
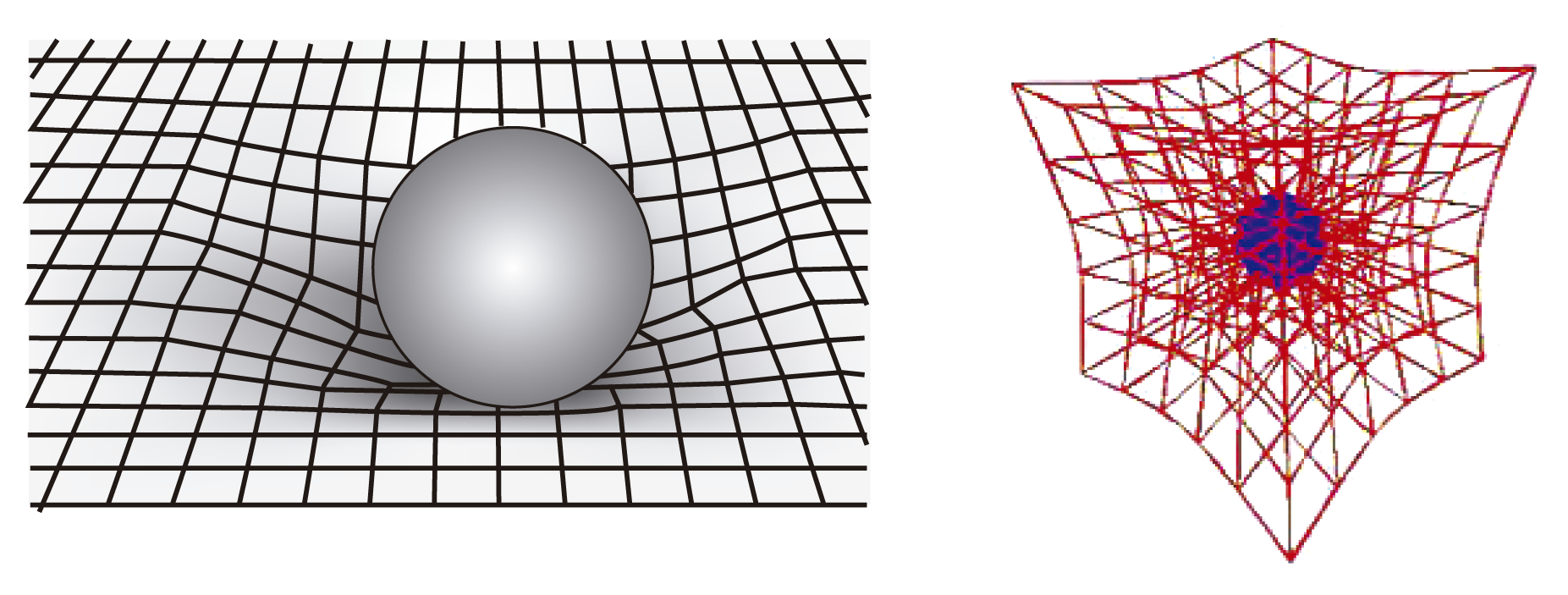
FIGURA I.4. Deformación del espacio-tiempo por la presencia de un cuerpo con masa. A la izquierda se ilustra en dos dimensiones, pero en realidad esta deformación actúa en tres dimensiones, como se muestra a la derecha.
La ecuación de la relatividad general tiene varias soluciones que dependen de la distribución de masa del universo. Una solución que fue encontrada por el mismo Albert Einstein se conoce como universo esférico de Einstein. Según éste, el universo es como una esfera. En este modelo, las coordenadas espaciales están curvadas con la forma esférica, pero el tiempo corre de manera lineal y recta, de tal manera que en el espacio-tiempo el universo es una especie de cilindro con el eje tiempo paralelo al eje del cilindro.
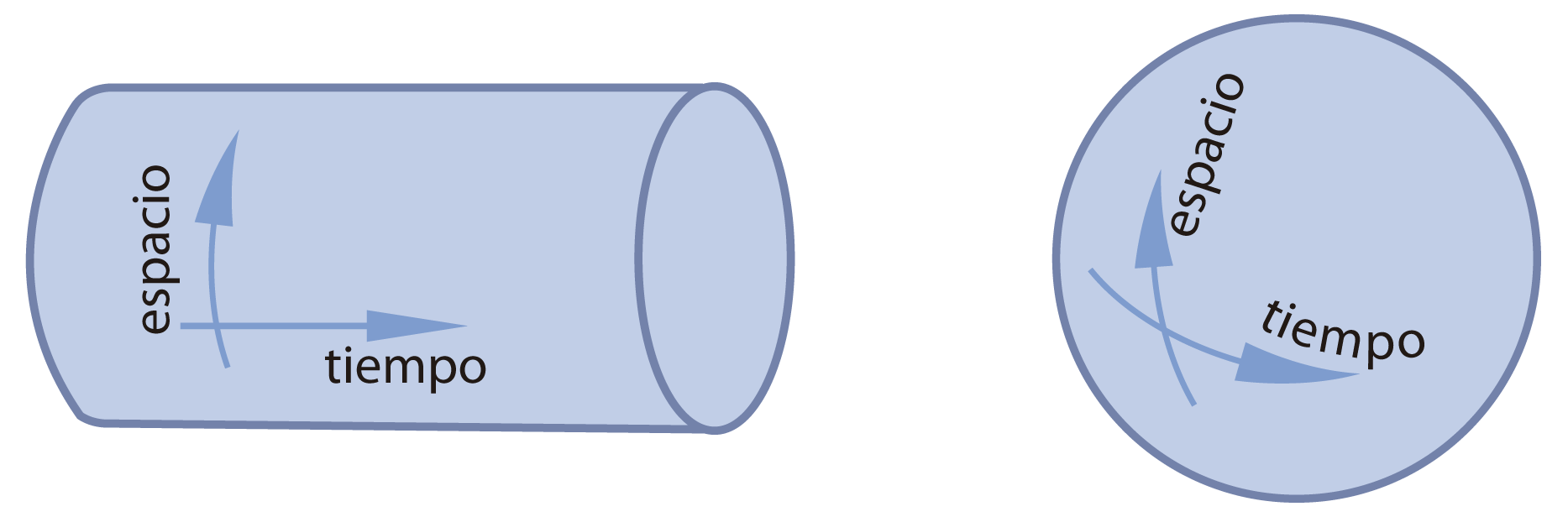
FIGURA I.5. El universo de Einstein (izquierda) y el universo de Willem de Sitter (derecha).
Otra solución a las ecuaciones de Einstein fue propuesta por Willem de Sitter. En el modelo de Sitter, tanto el espacio como el tiempo son curvos como una esfera donde la latitud es el espacio y la longitud es el tiempo. Ninguno de los dos modelos estuvo de acuerdo con el universo que observamos en expansión, porque ambos modelos consideraban un universo estático. No obstante, siguen siendo referentes y el universo de Sitter sigue siendo un modelo útil para describir la gravedad cuántica en un agujero negro. De esto hablaremos de nuevo un poco más adelante.
La teoría de la relatividad general tiene varias confirmaciones experimentales. Una de ellas es el corrimiento al rojo de las líneas espectrales en la presencia de un campo gravitacional fuerte.
El corrimiento al rojo es un resultado de la deformación del tiempo cerca de un objeto con masa considerable. Este efecto fue medido por primera vez en 1959 por Robert Pound y Glen Rebka. El experimento se llevó a cabo en la Universidad de Harvard usando fuentes radiactivas de fierro.
El fierro emite luz que lleva una energía de 14 kiloelectronvoltios. Los átomos pueden también absorberla si es que la luz le llega con la misma energía, porque de esa manera excita los mismos niveles atómicos que están en juego en la emisión.
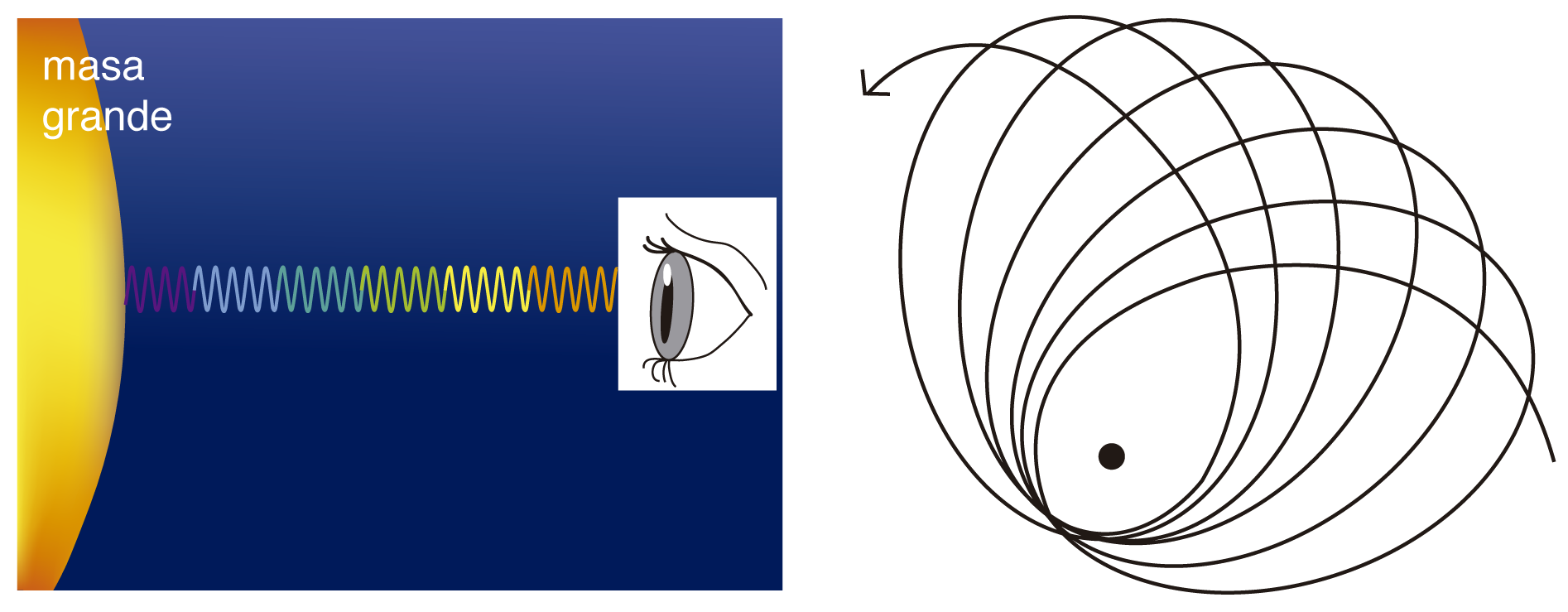
FIGURA I.6. A la izquierda, corrimiento al rojo que sufre la luz en la presencia de un campo gravitacional fuerte. A la derecha, precesión de Mercurio.
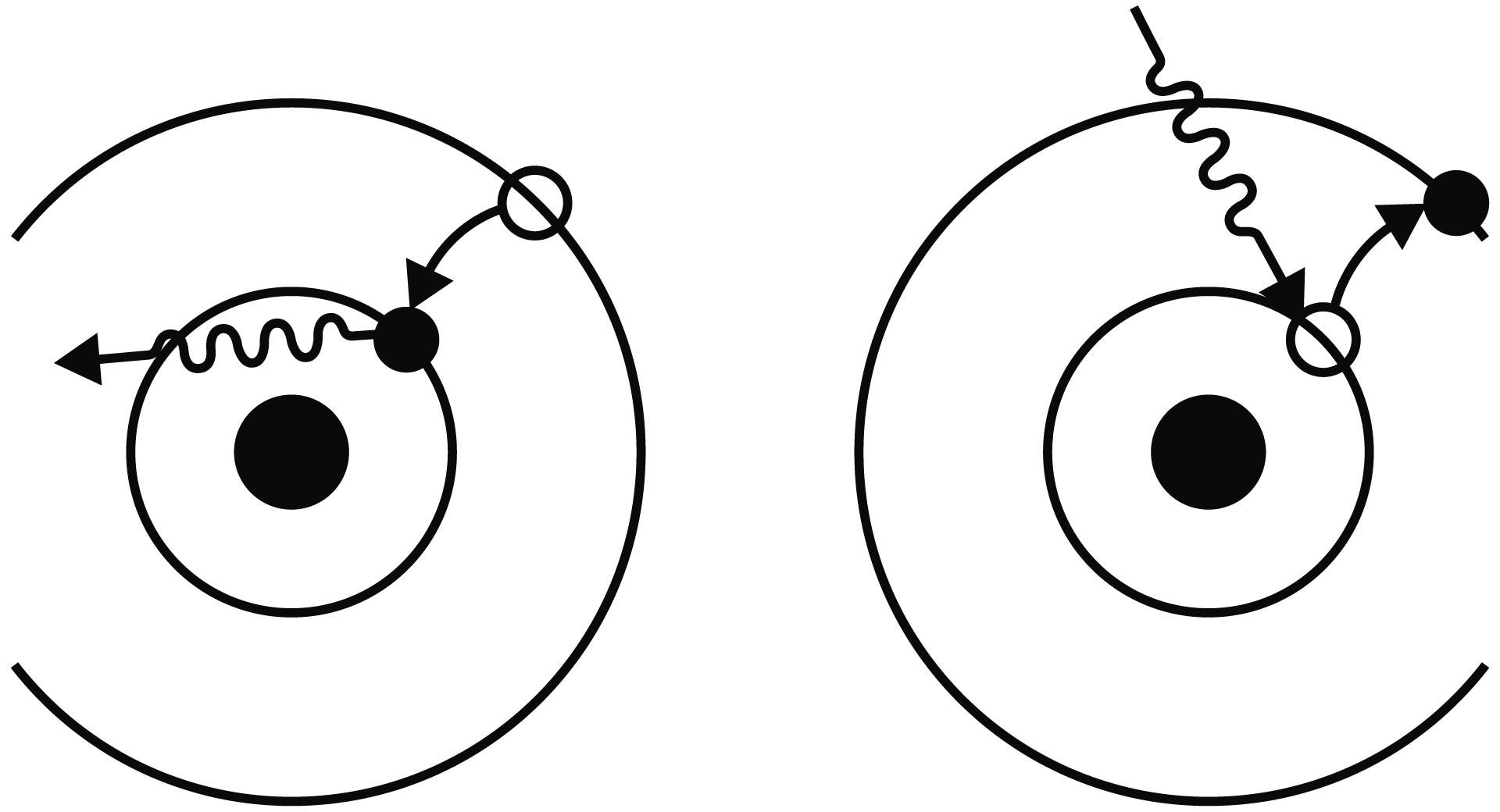
FIGURA I.7. Cuando el fierro 57 pasa de un estado excitado al estado base, emite luz (izquierda). De la misma forma cuando hasta él llega un fotón con la energía igual a la diferencia de energía entre el estado excitado y el estado base (derecha), éste será absorbido. Si la energía no es igual, el fotón no será absorbido.
Pound y Rebka pudieron medir el efecto tan pequeño que el campo gravitacional de la Tierra induce en la frecuencia de la luz emitida por átomos de fierro colocados en la base de una torre de la universidad. En la parte alta de la torre, a 22.5 metros de altura, se colocó fierro que debía absorber la radiación en caso de que su frecuencia no hubiese cambiado.
Resulta que debido al corrimiento que sufre la luz emitida por efecto del campo gravitacional de la Tierra, la frecuencia habrá cambiado al llegar arriba y no será absorbida más por los átomos de fierro, que sólo la absorben si es exactamente igual que la frecuencia de emisión. Se hizo necesario mover los átomos de fierro arriba para que el efecto Doppler compensase el corrimiento y entonces absorbiese la radiación. La cantidad de movimiento necesaria para que el fierro absorba la luz nos da una buena idea del corrimiento que sufrió por causa del campo gravitacional. La confirmación de la teoría general de la relatividad con este experimento llegó cuatro años después de la muerte de Albert Einstein.
Aunque aquí no expondremos con detalle este experimento, sí queremos mencionar que la relevancia no se quedó en la comprobación de la teoría de la relatividad, sino que además permitió pensar en aplicaciones. La precisión alcanzada fue el resultado de un ingenioso sistema de medición y de control de muchas variables en el montaje.
Actualmente el sistema global de posicionamiento, o Global Positioning System (GPS), que nos es muy familiar, debe considerar el corrimiento al rojo inducido por la gravedad del planeta para ofrecer la precisión de 10 metros en la posición de un objeto. Los satélites que envían continuamente señales a la Tierra para que los sistemas GPS calculen sus posiciones llevan consigo relojes atómicos muy precisos. Estos relojes van más rápido que los relojes en la Tierra por causa de un campo gravitacional más débil a la altura a la que se encuentran los satélites. Como resultado de esta diferencia en la gravedad, los relojes en estos satélites se adelantan tres microsegundos por día.
Sin embargo, si se quiere tener la posición de un objeto con precisión de 10 metros, es necesario que las señales de radio estén sincronizadas con gran precisión. Las señales de radio tardan 0.03 microsegundos en recorrer 10 metros. De manera tal que la sincronización debe ser mejor que eso.
En términos sencillos, si usted busca su posición en este momento con los relojes sincronizados, cuando lo haga nuevamente una hora más tarde, por efectos de la gravedad, el satélite estará adelantado 0.25 microsegundos. Esta diferencia en tiempo con el reloj en Tierra es mucho mayor que los 0.03 microsegundos que se requieren para una precisión de 10 metros. Por esto es que el GPS debe corregir estos efectos.
El GPS que usted tiene instalado en su carro o en su celular confirma el corrimiento gravitacional predicho por Einstein en 1911 con una precisión mejor que la del experimento de Pound y Rebka. ¡La física teórica más sofisticada y los experimentos sorprendentes por su alcance y precisión son una realidad en su bolsillo!
Otra verificación experimental de la teoría de la gravitación es la debida al fenómeno de precesión de Mercurio. Por precesión del planeta Mercurio nos referimos al movimiento del perihelio que se ilustra en la figura I.6. Este movimiento de Mercurio era ya conocido antes de la formulación de la teoría de la gravedad general. Se había observado que, cada 100 años, la órbita del planeta se recorre en 43 segundos de arco. Este movimiento se le atribuía a la fuerza que los otros planetas ejercen sobre Mercurio, sólo que, al calcular con la teoría de la gravitación de Newton, el resultado teórico difería de lo observado. Este hecho fue de particular impacto porque la medición de los astrónomos estaba muy bien establecida y con una precisión que rebasaba la discrepancia entre la teoría de Newton y la de la relatividad general. Además, la precesión de otros planetas sí concordaba con los cálculos de la teoría de Newton, lo que ponía a Mercurio en una situación especial y cada vez más preocupante para esos tiempos. Cuando los cálculos de la nueva teoría pudieron explicar esta diferencia, el terreno para la recepción de las nuevas ideas quedó preparado.
Éstas no fueron las únicas verificaciones experimentales. Aún hoy se siguen confirmando las ideas en observaciones y experimentos. La teoría de la relatividad es la segunda columna de la física moderna.
Dicotomía secular
El siglo XIX terminó con dos grandes enigmas que se resolvieron planteando la inexistencia de un marco de referencia absoluto, por un lado, y la cuantificación de la energía, por el otro. Estas dos grandes vertientes dieron origen a dos grandes teorías: la mecánica cuántica y la teoría de la relatividad. Ambas marcaron no sólo la física del siglo XX, cambiaron además nuestra concepción del espacio, el tiempo y hasta nuestra manera de entender el principio de causa y efecto.
La relatividad general y la mecánica cuántica describen nuestro universo a escalas muy distintas. La relatividad describe el universo macroscópico de galaxias y planetas, mientras que la mecánica cuántica lo hace para el mundo microscópico de las partículas subatómicas.
Sin embargo, y por consistencia, aspiramos a tener un solo esquema que las haga compatibles. Si bien la gravitación es muy débil como para ser relevante en el mundo microscópico de las partículas elementales, y los cúmulos de galaxias son tan grandes como para que los efectos cuánticos tengan alguna consecuencia, sí sabemos de por lo menos dos eventos universales que deben ser descritos por una teoría que los concilie, es decir, por una teoría cuántica de la gravedad, éstos son la Gran Explosión y los agujeros negros.
Los agujeros negros son probablemente el resultado de estrellas muy grandes que, al agotar su combustible, se colapsan produciendo un campo gravitacional del cual nada puede escapar, ni siquiera la luz. Deben ser muy pequeños y con una gravedad muy intensa.
La Gran Explosión es el mejor modelo que tenemos del origen del universo. Implica que una gran cantidad de energía se encontraba concentrada en un volumen microscópico donde la mecánica cuántica debe tener validez al mismo tiempo que los efectos gravitacionales.
Ambos, los agujeros negros y la Gran Explosión, involucran fuertemente a la gravedad porque las concentraciones de masa presentes son tan grandes que su interacción no puede ser ignorada. Por otro lado, los efectos de la mecánica cuántica deben estar presentes, ya que, como hemos visto, la concentración es tal que todos los fenómenos se desarrollan en la escala microscópica. Es pues en estos dos objetos que de forma irremediable se deben juntar las descripciones para explicar los fenómenos cuánticos y gravitacionales. Es aquí donde la teoría de la relatividad general y la mecánica cuántica deben unirse en un solo esquema que sea consistente.
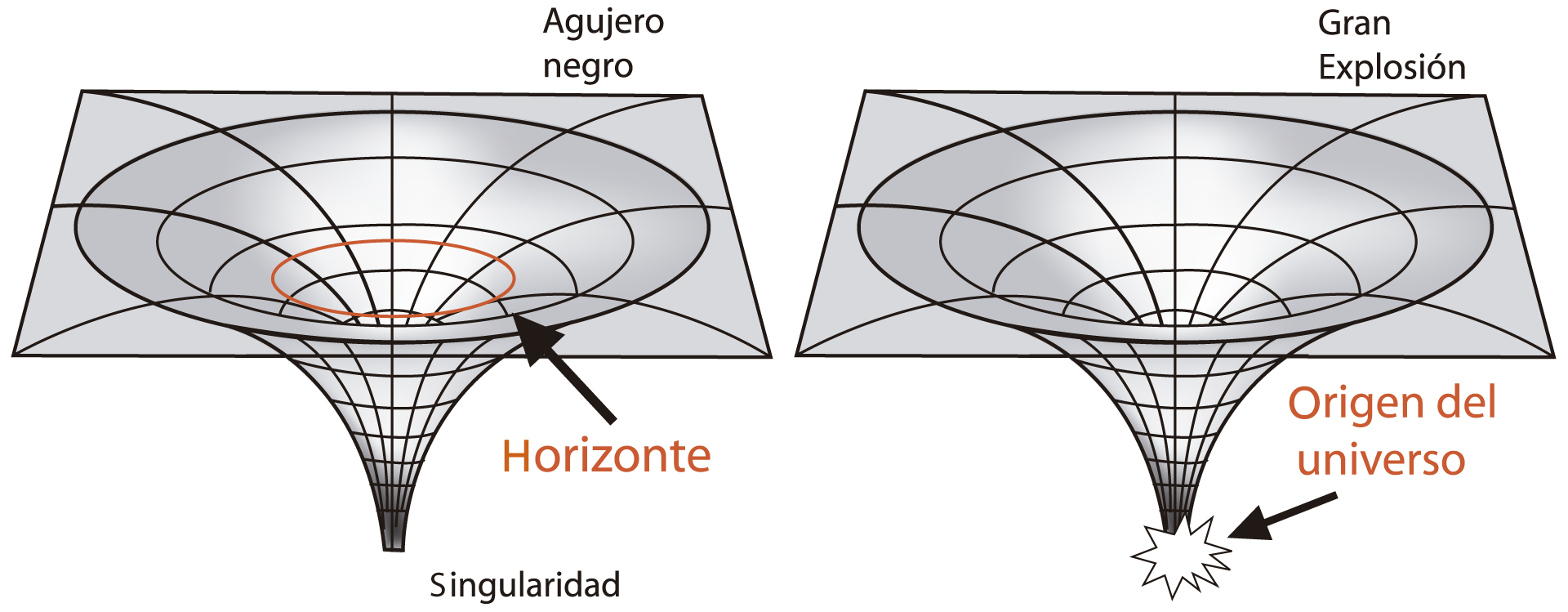
FIGURA I.8. La imagen de la izquierda muestra cómo se deforma el espacio en dos dimensiones. En la realidad esta curvatura se da en las tres dimensiones espaciales y la temporal. El círculo rojo muestra el horizonte, más allá del cual no existe retorno para la luz. A la derecha, la similitud con la Gran Explosión, en la que también debió existir una singularidad.
Los agujeros negros son parte de la teoría de la relatividad que predice su existencia. Según la teoría, es posible que el espacio-tiempo se curve en una cantidad infinita creando una singularidad. Esta singularidad es parecida a la que existió en el momento de la Gran Explosión. Como ya decíamos arriba, la curvatura del espacio-tiempo es la naturaleza real de la fuerza de gravedad, así que tener una singularidad en el espacio-tiempo es tener una fuerza de gravedad infinita. En un agujero negro el “horizonte” es la línea donde los eventos fuera y dentro del agujero se separan. Más allá del horizonte, la luz no puede escapar, y por eso los mundos se incomunican. El horizonte es el punto de no retorno. Más allá de éste, no habrá nada capaz de evitar la caída.
Es conocido desde hace un siglo el problema de unir la mecánica cuántica con la relatividad general en una sola teoría que pueda describir lo que ocurre en la Gran Explosión y en la cercanía de la singularidad de un agujero negro. Sin embargo, los esfuerzos encaminados a la construcción de una teoría cuántica de la gravedad siguen vivos.
La Gran Explosión es un evento único y la evidencia de su existencia parece ser sólida. En cambio, los agujeros negros podrían estar poblando el universo, pero no existen muestras contundentes de que así sea. Podría ser que las galaxias espirales como la nuestra tengan un agujero negro en su centro. Los astrónomos han encontrado sistemas binarios, es decir, dos estrellas orbitando entre sí, en los que una de las dos no es visible. Por la manera como la estrella visible rota, se puede pensar que el objeto que la acompaña tiene una masa enorme. Existen otros candidatos en los centros de muchas galaxias que son considerados como tales por la manera como se comporta la materia a su alrededor. Sin embargo, no existen objetos de los que podamos decir que cumplen con las características predichas por la teoría general de la relatividad para ser catalogados como agujeros negros y no otra cosa. Las observables que ahora hacen pensar en algunos objetos astronómicos como si fueran agujeros negros son tales que se darían de igual forma para estrellas de neutrones con campos gravitacionales grandes. Para confirmar su existencia y probar la teoría general de relatividad es necesario desarrollar técnicas de observación que sean sensibles a la curvatura del espacio-tiempo cerca del horizonte. Esto llegará en algún momento. Por ahora resulta difícil decir si lo que vemos es un agujero negro, una estrella de neutrones o algún otro objeto muy masivo.
EL MODELO ESTÁNDAR
El modelo estándar de las partículas elementales es sin duda uno de los grandes logros científicos del siglo XX. Describe la estructura elemental de la materia y sus interacciones y puede hacer predicciones cuantitativas con enorme precisión. Está basado en la mecánica cuántica y la teoría especial de la relatividad, de tal forma que su descripción de las partículas elementales y sus interacciones se lleva a cabo en términos de funciones de onda.
El modelo estándar ofrece una descripción de las interacciones o, mejor dicho, de tres de las cuatro interacciones presentes en la naturaleza. Curiosamente, la más familiar de las cuatro fuerzas, la gravitacional, ha eludido todo intento por enmarcarla en un esquema que las englobe a todas.
Uno podría pensar que existen muchas fuerzas en la naturaleza. Además de la fuerza gravitacional, también nos son familiares otras, como la fricción que todos percibimos cuando empujamos un bulto pesado en el suelo o la tensión que experimenta una cuerda que sostiene a la piñata, etc. Sin embargo, todas estas fuerzas surgen de cuatro que los físicos consideran fundamentales. Los físicos de partículas sólo se ocupan de las cuatro fuerzas fundamentales, puesto que éstas dan origen a todas las otras que nos acompañan en las actividades diarias.
Así, por ejemplo, la fricción que surge cuando tratamos de deslizar un objeto sobre la superficie de otro puede ser complicada de describir en detalle, pero sabemos que no es otra cosa que la fuerza electromagnética entre los átomos de un objeto y el otro. Si no existiese electromagnetismo no tendríamos fricción. De manera similar, la tensión que existe en un alambre que sostiene a un cuerpo se debe a la atracción electromagnética entre los átomos que forman la estructura del alambre. De nuevo, sin electromagnetismo no tendríamos tensión. En estos dos ejemplos la fuerza fundamental es el electromagnetismo y es una de las cuatro que existen en la naturaleza.
El modelo estándar es una descripción del mundo microscópico en el que la atracción gravitacional no representa un papel importante. La gravitación se manifiesta visiblemente en el macrocosmos en el que planetas, estrellas y galaxias se atraen entre sí por el hecho de tener masa.
Para tener una idea del papel que desempeña la atracción gravitacional en diferentes escalas veamos los escenarios macroscópico, mesoscópico y microscópico:
La fuerza que el Sol ejerce sobre la Tierra es una manifestación macroscópica de la interacción gravitacional. Esta fuerza hace que la Tierra se desvíe tres milímetros cada segundo, lo que ocasiona que ésta, y nosotros con ella, se mueva alrededor del Sol. En el libro clásico Física recreativa, Yakov Perelman habla sobre lo que sería necesario hacer si por alguna misteriosa razón la atracción del Sol desapareciera un día y nuestros ingenieros trataran de evitar que nos alejáramos para siempre en las frías profundidades del universo. Si la solución estuviera en tender cables de acero para mantenernos ligados al Sol, entonces sería necesario un millón de millones de cables con una sección transversal de 20 metros cuadrados cada uno. Para darse una idea de lo que esto significa, nos dice Perelman, si las columnas estuvieran distribuidas por todo el hemisferio terrestre que daría su cara al Sol, el espacio entre columnas sería un poco más ancho que ellas mismas. Este ejemplo imaginativo y ficticio nos da una idea de lo poderosa que es la invisible fuerza de atracción entre el Sol y la Tierra. Por supuesto que la solución no serían cables de acero, porque éste se funde a 1 535 grados y el Sol se encuentra a una temperatura sustancialmente mayor, por sólo mencionar una de las dificultades que se presentarían si tal cosa ocurriese en verdad.
En la escala media en la que vivimos, la atracción gravitacional es ya de efectos insignificantes. Con esto no nos referimos al efecto de la Tierra sobre nosotros y los objetos que nos rodean, sino a la atracción de tipo gravitatorio que objetos de nuestra escala ejercen sobre otros similares. Así, por ejemplo, dos personas de peso medio y separadas por dos metros de distancia se atraen mutuamente con una fuerza de 0.01 miligramos. Esta fuerza es completamente imperceptible, como ya todos sabemos. Si por alguna razón nos sentimos atraídos hacia otra persona, esto será seguramente por efectos diferentes a los gravitatorios. La química podría ser la responsable, y entonces estamos de nuevo ante la interacción electromagnética.
La interacción electromagnética es considerablemente mayor que la gravitacional. Para darse una idea de esto, es suficiente notar que la atracción gravitacional entre dos electrones es aproximadamente 0.24 × 10−42 veces menor que la atracción eléctrica que uno ejerce en el otro. Este número:
0.00000000000000000000000000000000000000000024
es extremadamente pequeño, como puede verse. Al respecto, Richard Feynman decía que en la magnitud de este número “yace un misterio muy profundo. ¿De dónde sale un número tan monstruoso? Si en algún momento consiguiéramos una teoría de la que pudieran derivarse ambas fuerzas, ¿cómo podrían hacerlo de forma tan desproporcionada?”4
La interacción eléctrica hace que los protones en un átomo se aparten mutuamente por el hecho de tener la misma carga. Dos protones a una distancia típica del orden de un diámetro nuclear se rechazan con una fuerza de aproximadamente 2.3 newtons. Aunque esta fuerza no parece ser grande, produciría a un objeto tan pequeño como el protón una aceleración enorme de 1.4 × 1027 metros sobre segundos cuadrados. Como ya vimos, la fuerza gravitacional es muy pequeña comparada con la eléctrica, ¿cómo es entonces que los núcleos atómicos se mantienen unidos si están hechos de protones?
En la naturaleza existen, además de la fuerza gravitacional y electromagnética, dos interacciones con las que estamos poco familiarizados. Éstas son la fuerza débil y la fuerza fuerte.
Estas dos interacciones son de alcance tan corto que les llevó a los físicos mucho tiempo descubrir su existencia. El primer contacto que los físicos tuvieron con la interacción débil fue hace 100 años, cuando se observó en sales de radio un resplandor inusual. Al estudiar con más detenimiento el fenómeno se pudo entender que esta luz procedía de partículas originadas en la desintegración de los núcleos de algunos átomos inestables. El fenómeno se conoce hoy como radiactividad y se ha establecido que ésta es debida a la interacción débil. La fuerza débil tiene una influencia sólo a distancias de 10−15 centímetros, es decir, a una centésima del tamaño de un protón. Es débil precisamente porque el tramo de influencia es muy pequeño y las partículas no se acercan tanto muy a menudo.
La interacción débil, a diferencia de la electromagnética y la gravitacional, hace que las partículas cambien de naturaleza. Un ejemplo de esto es que los neutrones se transforman en protones emitiendo un electrón y un neutrino. Hasta hace poco pensábamos que existían en el universo unas partículas que sólo son sensibles a esta fuerza. Los llamados neutrinos no tienen carga eléctrica, tampoco tienen la carga de color responsable de la interacción fuerte —como veremos— y no parecían tener masa. Ahora todo parece indicar que sí tienen masa, por lo que, además de la fuerza débil, deben experimentar la fuerza gravitacional.
Como su nombre lo indica, la fuerza es muy débil, y como consecuencia los neutrinos —que tienen una masa muy pequeña, aún desconocida, pero pequeña— son difíciles de observar. Sólo en raras ocasiones logramos que interactúen con un detector que nos diga que por ahí pasó un débil neutrino.
La relación entre la fuerza débil y la electromagnética fue entendida en los años setenta en el marco del modelo estándar, que ofrece una prescripción que permite ver a las dos interacciones como aspectos de la misma cosa.
Por otra parte, la interacción fuerte hace posible la existencia de núcleos en los átomos, pues, como ya comentamos anteriormente, los protones se apartan por tener la misma carga, y la atracción gravitacional entre ellos es muy débil como para mantenerlos unidos. La fuerza fuerte se encarga de esto. La distancia en que actúa es tan pequeña como el tamaño de los protones mismos, así que al alejarse un poco dejará de percibirse por completo.
Como su nombre lo indica, la interacción es muy fuerte, de tal manera que si dos partículas se aproximan a una distancia corta del orden del tamaño de un protón quedarán bajo el efecto de la interacción recíproca y después será muy difícil separarlas.
El modelo estándar parte del hecho de que la materia está formada por partículas a las que se denomina elementales y las cuales interactúan entre sí para formar todo lo que vemos a nuestro derredor.
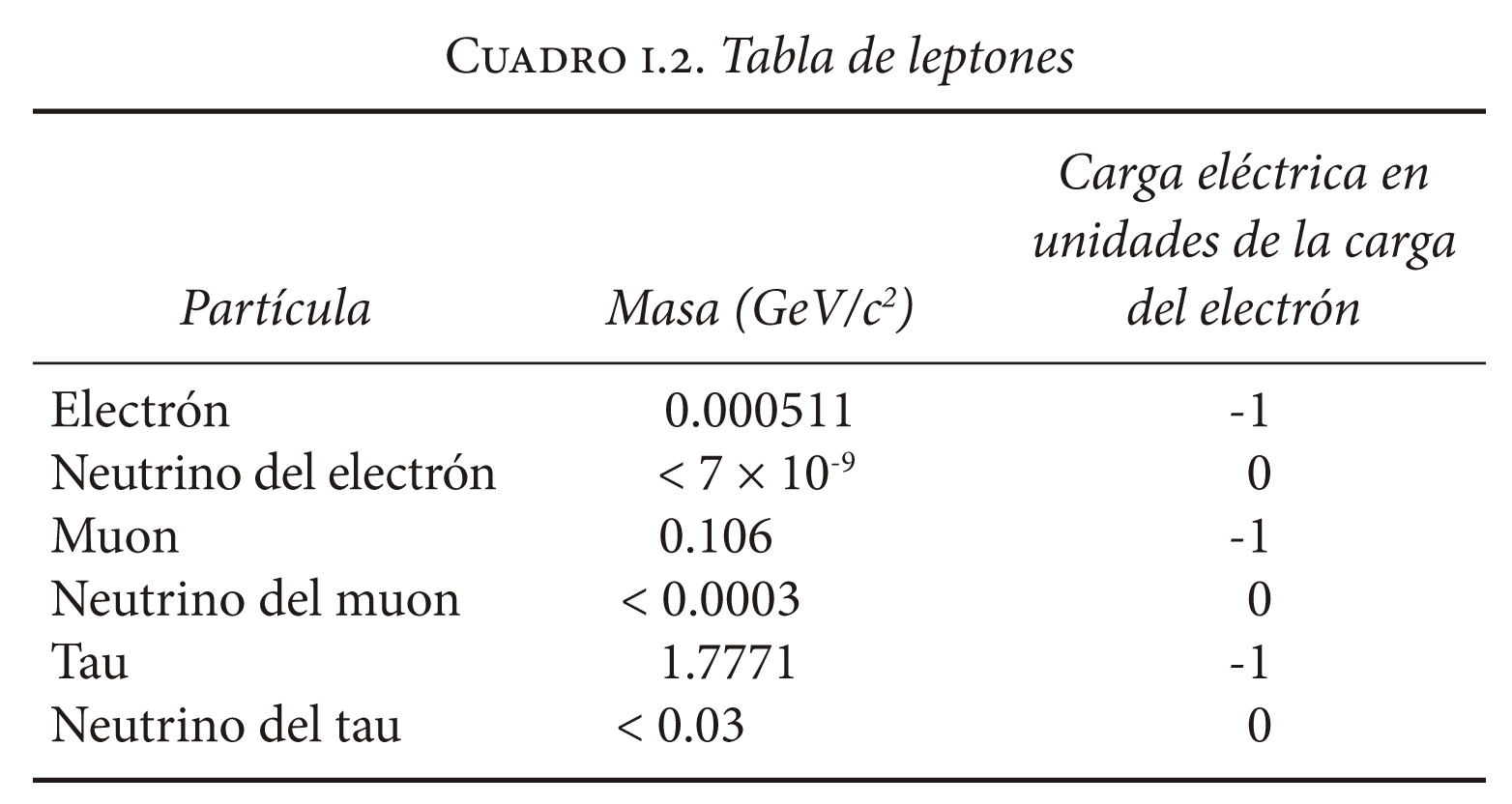
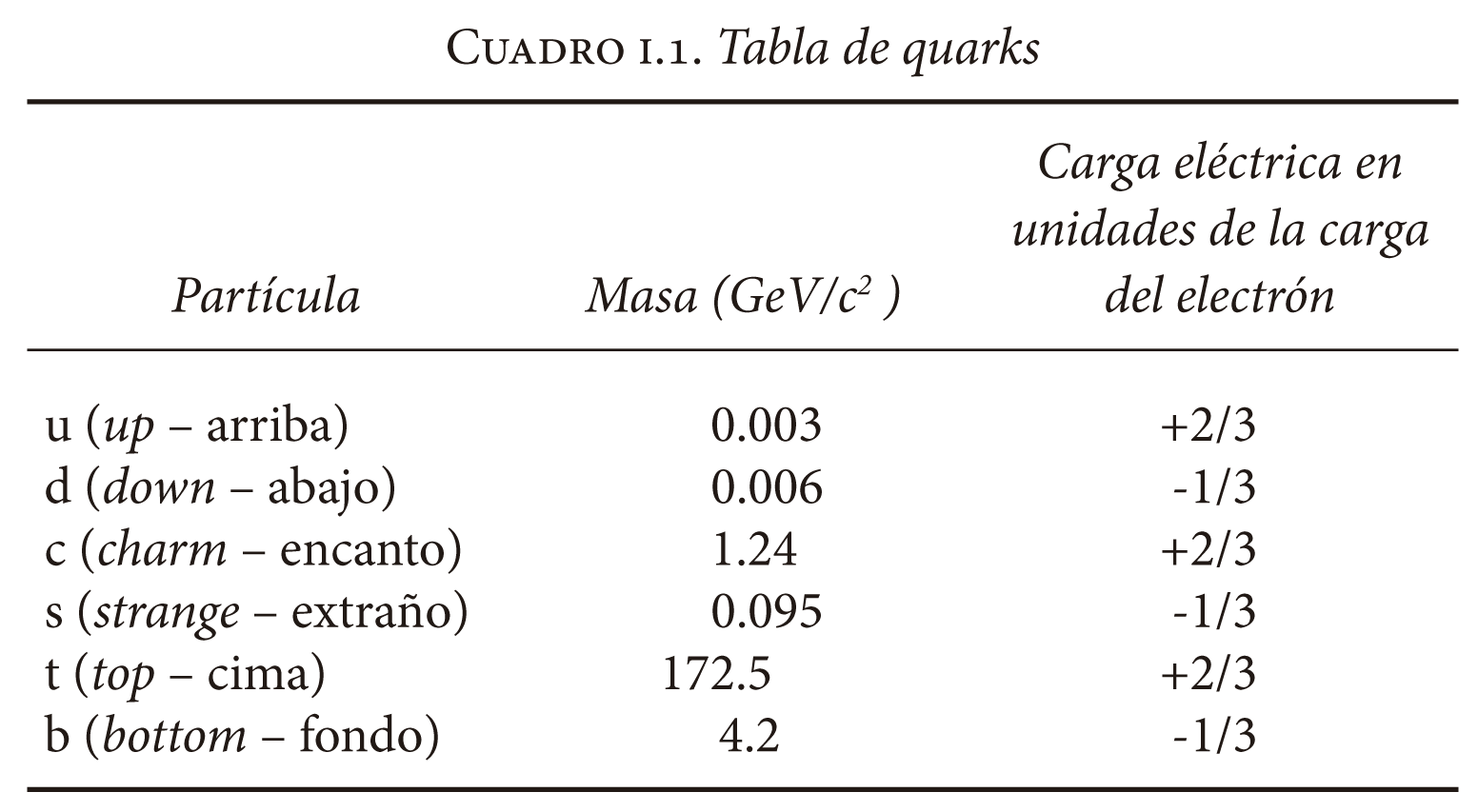
Como vimos, las interacciones no actúan de igual forma en todas las partículas, y esto permite clasificarlas. Existen dos grupos: el de los llamados leptones y el de los quarks. Sólo las primeras dos partículas de ambas listas forman la materia que nos rodea. Las otras pueden ser creadas en laboratorio o en la colisión de rayos cósmicos con átomos en la atmósfera, pero desaparecen muy pronto sin llegar a formar conglomerados que se integren con el entorno observable. Los quarks u y d de la lista de quarks y los electrones de la lista de leptones son suficientes para formar los átomos.
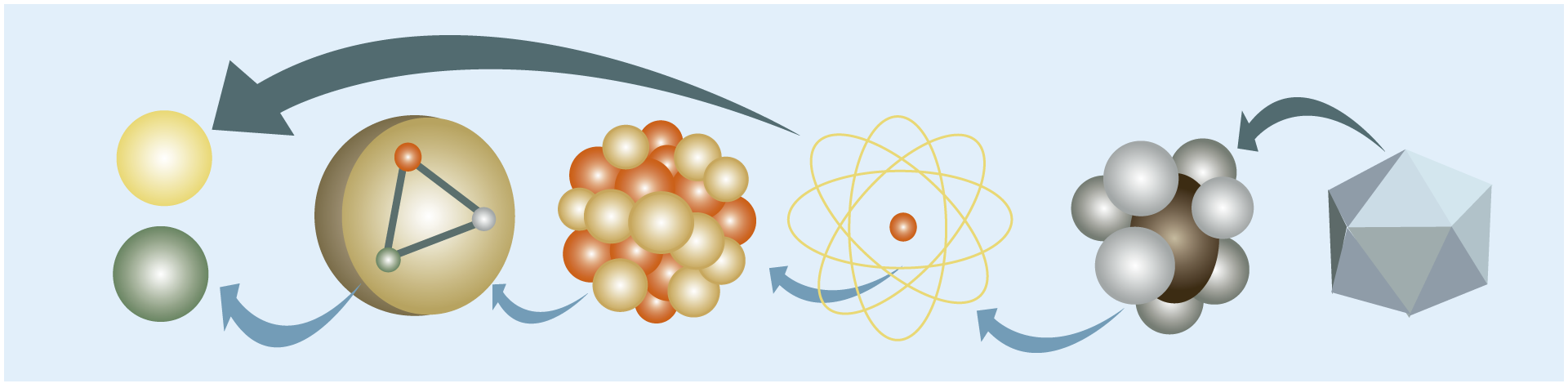
FIGURA I.9. Los objetos macroscópicos están hechos de moléculas que a su vez están formadas por átomos. El núcleo de estos átomos está hecho de protones y neutrones, y éstos a su vez están formados por quarks.
La palabra leptón proviene del griego y significa “ligero”. En contraposición, la palabra griega de “pesado” es barión. Los protones y los neutrones son ejemplos de bariones. Como bien sabemos, el protón tiene una masa 1 800 veces mayor que la del electrón.
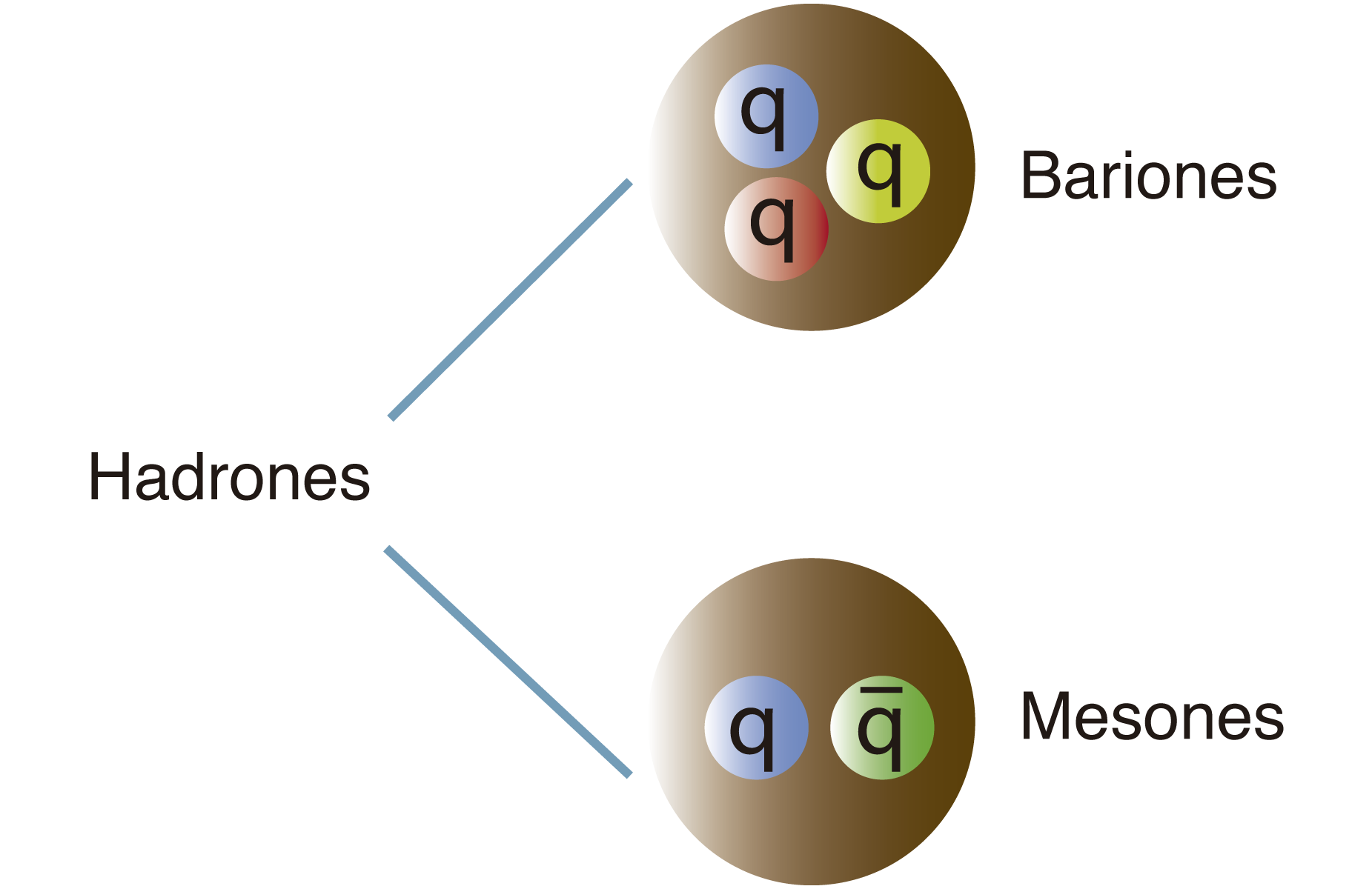
FIGURA I.10. Clasificación de hadrones en mesones y bariones.
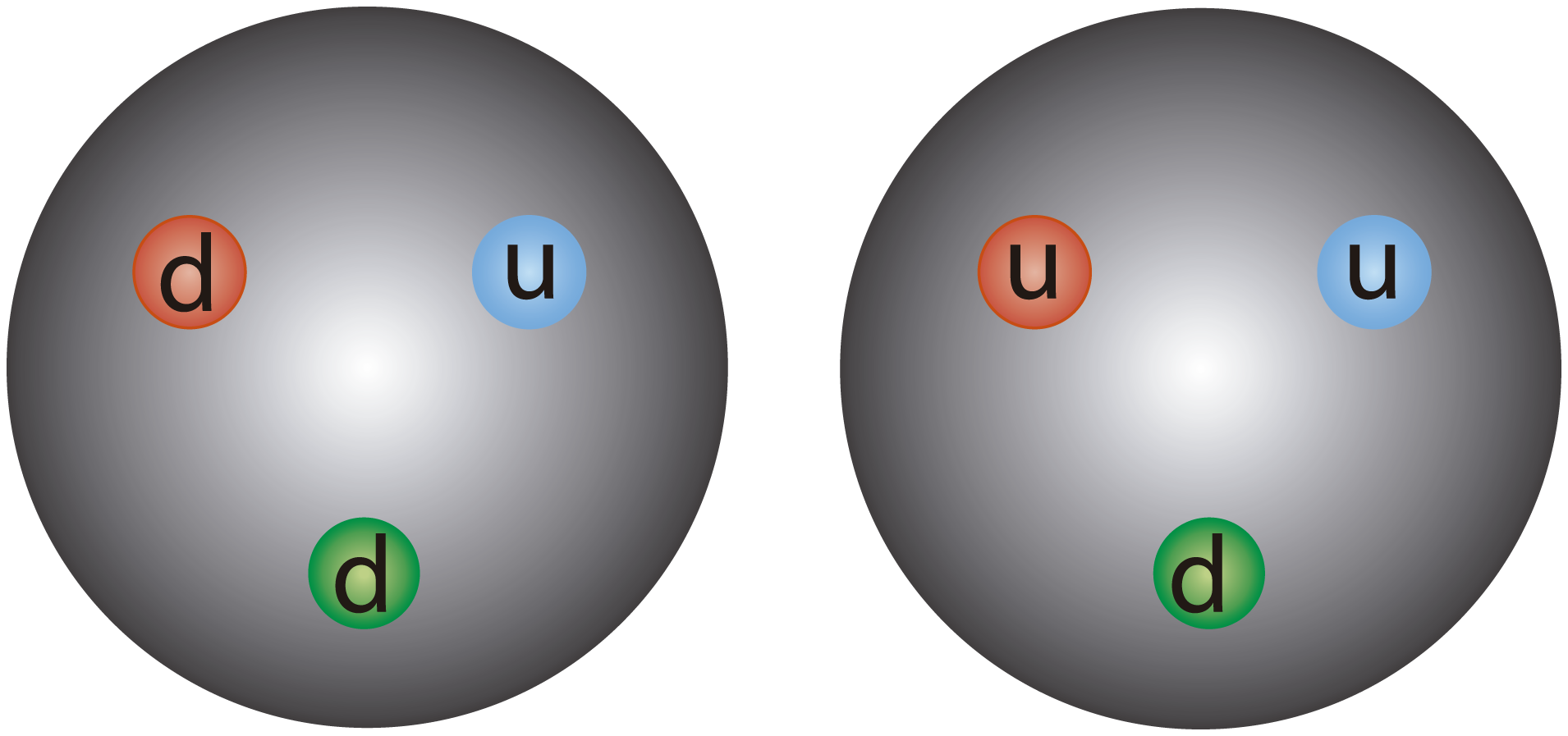
FIGURA I.11. Estructura de quarks del neutrón (izquierda) y el protón (derecha).
Entre las partículas pesadas llamadas bariones y las partículas ligeras llamadas leptones están las partículas medias llamadas mesones. Un ejemplo de mesón es la partícula π o pion, que tiene una masa 270 mayor a la del electrón, pero que es un séptimo de la del protón.
Sin embargo, la clasificación de las partículas por su masa no es muy buena. Ahora se conocen leptones con masas comparables a las de algunos bariones y tenemos al leptón muon, que tiene una masa parecida a la del mesón llamado pion, etcétera.
A los mesones y bariones se los llama en conjunto hadrones. En griego, hadrón significa “partícula fuerte”. Estas partículas, como su nombre lo indica, interactúan fuertemente.
Los mesones están hechos de dos quarks (de la tabla de quarks) y los bariones de tres. Para ser más precisos, los mesones están hechos de un quark y un antiquark, mientras que los bariones de un conjunto de tres quarks o de tres antiquarks.
Un aspecto del modelo estándar es que las interacciones se dan por medio del intercambio de partículas a las que se denominan bosones de norma. Así, por ejemplo, la partícula mediadora de las interacciones electromagnéticas es el fotón, mientras que las interacciones débiles se transmiten con los bosones W± y Z0, que fueron detectados en 1983 en el CERN de Ginebra, Suiza. Las interacciones fuertes, por su parte, se dan mediante el intercambio de gluones, que fueron detectados experimentalmente en 1979 en el laboratorio Desy de Hamburgo, Alemania.
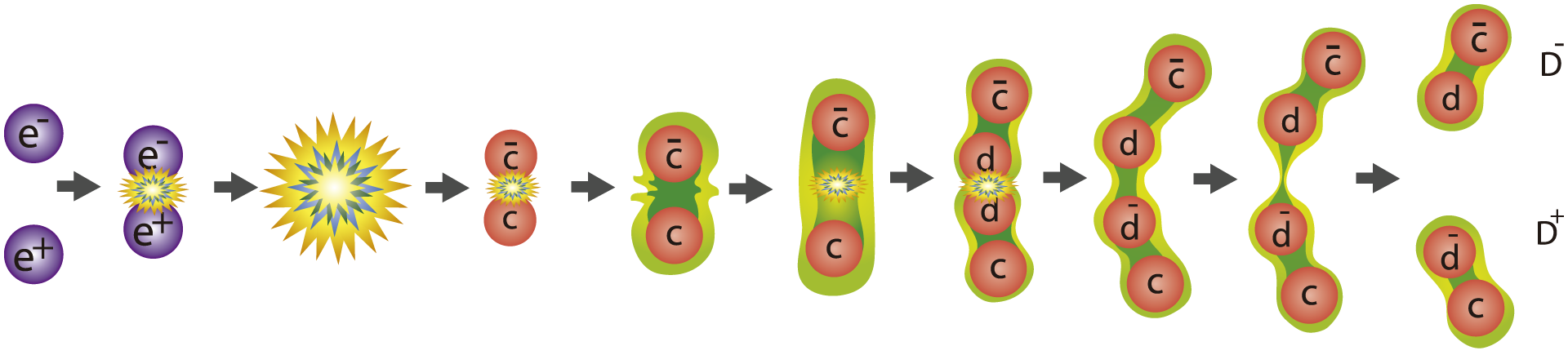
FIGURA I.12. La aniquilación de un electrón y un positrón produce un fotón que después puede producir un par de quark antiquark (quarks encanto).
En la figura I.12 se muestra la aniquilación de un electrón y un positrón, de la cual se produce un fotón que luego puede producir un par de quark-antiquark (en la figura, quarks encanto). Éstos permanecen ligados por una cuerda que al romperse produce otro par quark-antiquark (en el caso que se muestra, un d y su anti-d). Si la energía que llevan consigo ya no es suficiente para seguir rompiendo la cuerda que los une, terminarán confinados en un mesón D– y su antipartícula, el mesón D+. El lector notará que usamos ū para denotar el antiquark u.
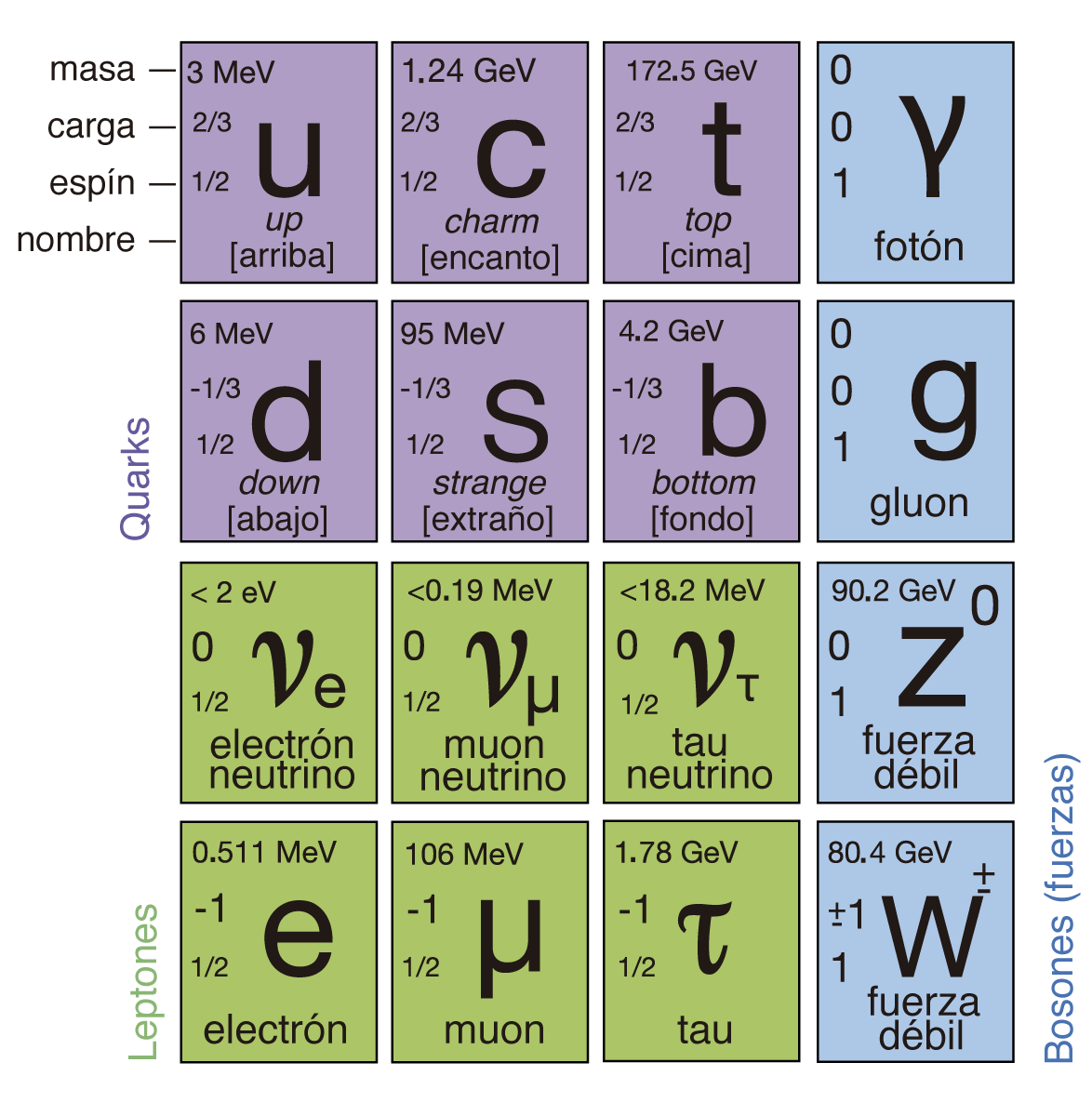
FIGURA I.13. Tabla de los elementos con las tres familias en arreglo vertical cada una de ellas. En la cuarta columna se muestran las partículas que median las interacciones.
La formulación electrodébil del modelo estándar tiene, sin embargo, un grave problema. El modelo pone en el mismo plano el fotón y los bosones W± y Z0. Sin embargo, el fotón no tiene masa, mientras que W± y Z0 son extremadamente pesados. Para resolver este problema se inventó el llamado mecanismo de Higgs. Este ingenioso artificio permite que los bosones de norma W± y Z0 tengan masa y que el fotón permanezca sin ella representando aspectos de la misma cosa, que es la interacción electrodébil. Sobre este mecanismo hablaremos más en el siguiente capítulo. La representación matemática involucra un campo nuevo al que se ha denominado campo de Higgs. El campo de Higgs a su vez se manifiesta como una partícula a la que se llama Higgs y que fue recientemente observada en el Gran Colisionador de Hadrones.
En los años sesenta Gabriele Veneziano, Leonard Susskind, Holger Nielsen, entre otros, inspirados por la idea de hadrones como cuerdas en cuyos extremos se encontraban los quarks, sentaron las bases para una teoría de cuerdas, y sugirieron que se podría describir el mundo microscópico de las partículas elementales como si éstas fueran cuerdas más que partículas puntuales. Durante los setenta, se desarrolló formalmente la teoría explorando la posibilidad de que las partículas elementales en realidad fueran sólo distintos tonos de vibración de una sola cuerda. La primera sorpresa de estas ideas fue que la teoría de cuerdas resultó ser una teoría cuántica de la gravedad.
Aún no sabemos si esta teoría es correcta o no. Como todas las ideas en la física, deberá someterse a la prueba de los experimentos y, aunque aún parece lejano el día en que esto ocurrirá, los desarrollos recientes parecen mostrar que algo interesante se esconde en los conceptos.
LA TEORÍA DE CUERDAS
Y EL UNIVERSO HOLOGRÁFICO
La teoría de cuerdas parte de la idea de que los electrones y los quarks no son partículas puntuales como planteamos arriba. Según esto, lejos de ser elementales, los quarks y los electrones están hechos de cuerdas que vibran para darles las propiedades que conocemos como carga, color, masa, espín, etc. Las cuerdas serían, pues, una escala menor en la estructura que observamos actualmente; de hecho, sería la escala más pequeña posible, que está definida como escala de Planck. De acuerdo con esta teoría, sólo existe un elemento fundamental que forma todo lo demás con su manera de vibrar, moverse, agruparse e interactuar con otras cuerdas, aunque también existen en la teoría de cuerdas otros objetos llamados branas —derivado de membrana—, en las que las cuerdas pueden unirse, deslizarse e interactuar de diferentes maneras.
Se usa la palabra brana para denotar algo más general que la membrana, que sería una 2-brana, es decir, una brana en dos dimensiones. Las branas en general pueden ser multidimensionales, pero serán siempre un subespacio de un espacio más grande. Las branas son generalizaciones de campos como el electromagnético.
De acuerdo con la teoría, las cuerdas tienen un tamaño del orden de la longitud de Planck, que es 1.6 × 10−35 metros. La escala de Planck se define en términos de tres constantes naturales: la velocidad de la luz en el vacío, la constante de Planck y la constante gravitacional. En la ecuación:
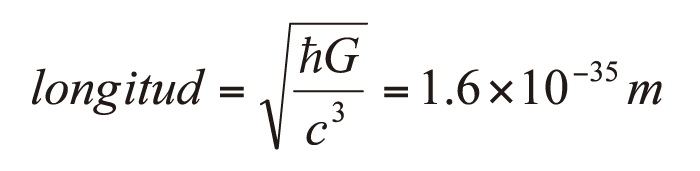
puede verse que es una escala de longitud extremadamente pequeña.
La longitud de Planck es la longitud más pequeña que se puede construir con constantes naturales y que involucra a la mecánica cuántica a través de ħ, constante que como vimos está asociada a los cuantos de luz que propuso Planck para el mundo microscópico, a la relatividad especial por medio de la velocidad de la luz c y a la gravitación por medio de G, constante de la gravitación universal. Por las constantes involucradas, resulta claro que, cuando uno se encuentre a esta escala, los valores de las constantes garantizan que los efectos cuánticos de la gravedad serán importantes.
Para darse una idea de la magnitud de la que se habla, considere las mediciones del radio del electrón, que muestran que, en caso de que éste tuviese estructura, ésta debe ser menor a 10−20 metros, que está aún muy lejos de la escala que propone la teoría para el tamaño hipotético de la cuerda elemental.
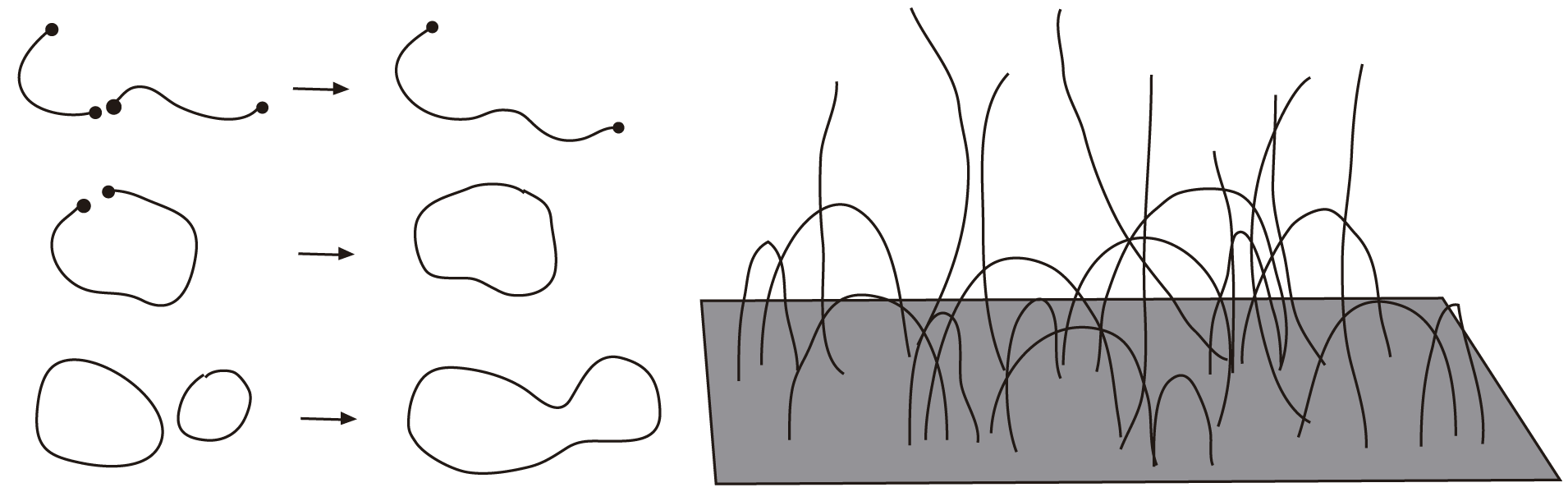
FIGURA I.14. Las cuerdas interaccionan de varias maneras: uniéndose o dividiéndose (izquierda). Además de cuerdas, existen en la teoría membranas o branas como la que se muestra (derecha).
Los físicos piensan que hay algo fundamental en este número tan diminuto, y que en algún momento esto se hará evidente en la teoría misma.
El origen de la teoría de cuerdas tiene que ver con la manera como los quarks interaccionan. Como hemos mencionado anteriormente, en los años sesenta algunas personas comenzaron a describir a los hadrones como cuerdas en cuyos extremos se encontraban los quarks, como se ilustra en la figura I.15. La cuerda, así, está formada por un tubo de gluones que mantiene unido al sistema. Esta manera de describir a los mesones y bariones permite también detallar la manera como se producen las partículas en interacciones de altas energías.
Cuando la cromodinámica cuántica apareció y comenzó a describir de manera exitosa al sector de quarks y gluones, la teoría original que modelaba a los hadrones con cuerdas perdió fuerza. Surgieron además dificultades para explicar algunos fenómenos en términos de los tubos que se forman entre los quarks, y la gente dejó de pensar en este modelo como algo más profundo. Aun así, la manera de describir a los hadrones mediante cuerdas sigue siendo usada como modelo de juguete con el que se puede describir muy bien la producción de partículas con programas computacionales que simulan las cuerdas y modelan su rompimiento, etc. Sin embargo, alguna gente tomó la idea y comenzó a desarrollarla a un nivel más profundo en su alcance y consecuencias. El concepto se desarrolló matemáticamente para llegar a ser una teoría distinta con dominio en una escala espacial considerablemente menor, y se delineó, con el paso del tiempo, como una de las teorías posibles que explicarían todas las interacciones y el comportamiento general de la naturaleza, es decir, una teoría del todo.
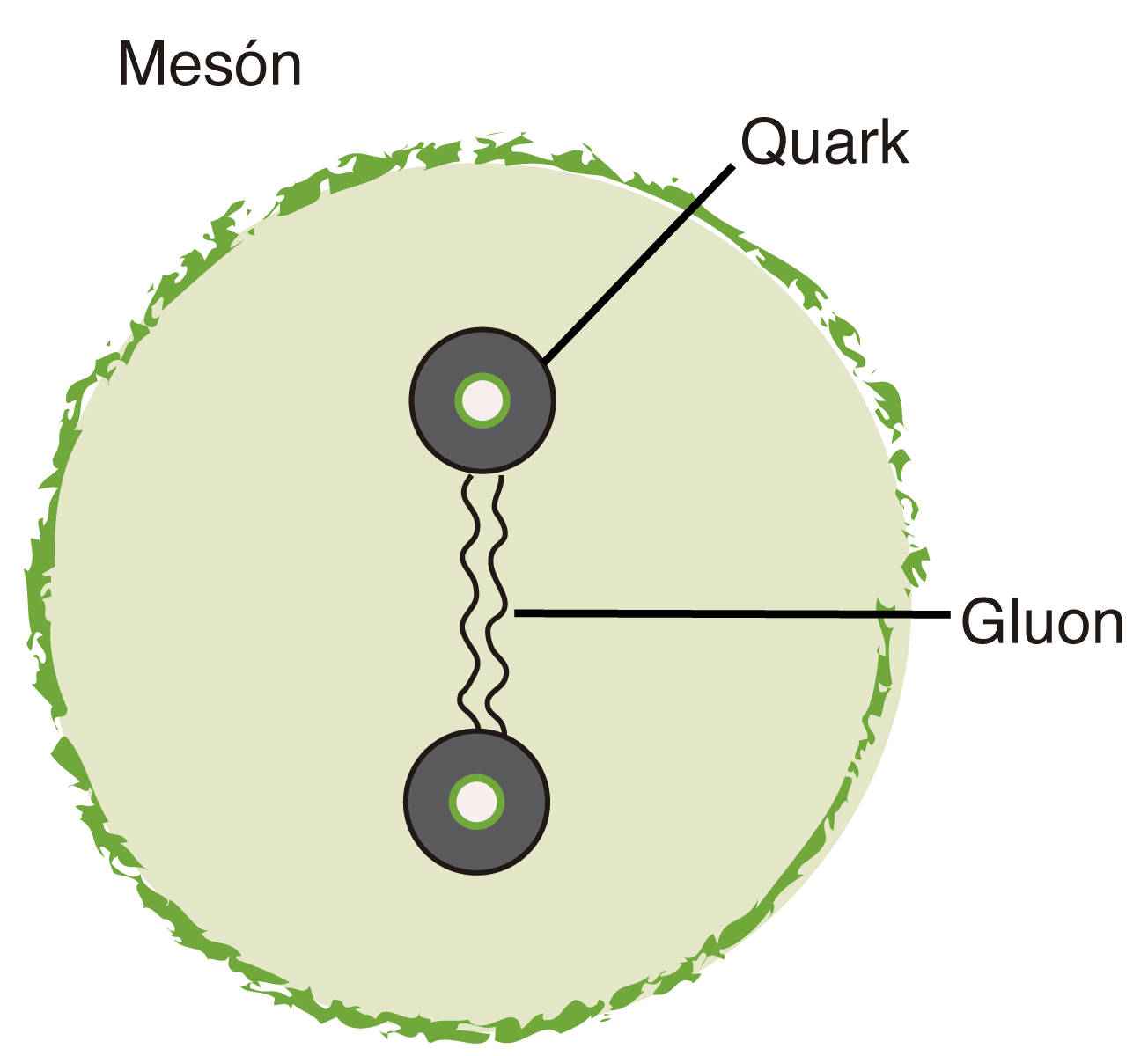
FIGURA I.15. La idea original de la teoría de cuerdas está en la descripción que en los sesenta se hacía de la interacción fuerte en los hadrones.
La teoría de cuerdas requiere la existencia de más dimensiones que las cuatro que nos son familiares. Todos percibimos tres dimensiones a nuestro derredor porque los objetos que nos rodean poseen un ancho, un largo y un fondo. Si a esto añadimos que los objetos cambian con el transcurrir del tiempo, podemos incorporar este cambio a las dimensiones para sumar espacio-tiempo en cuatro dimensiones. No obstante, para la teoría de cuerdas, el mundo que percibimos no es todo lo que hay y, como veremos, es posible pensar en un mundo con más dimensiones.
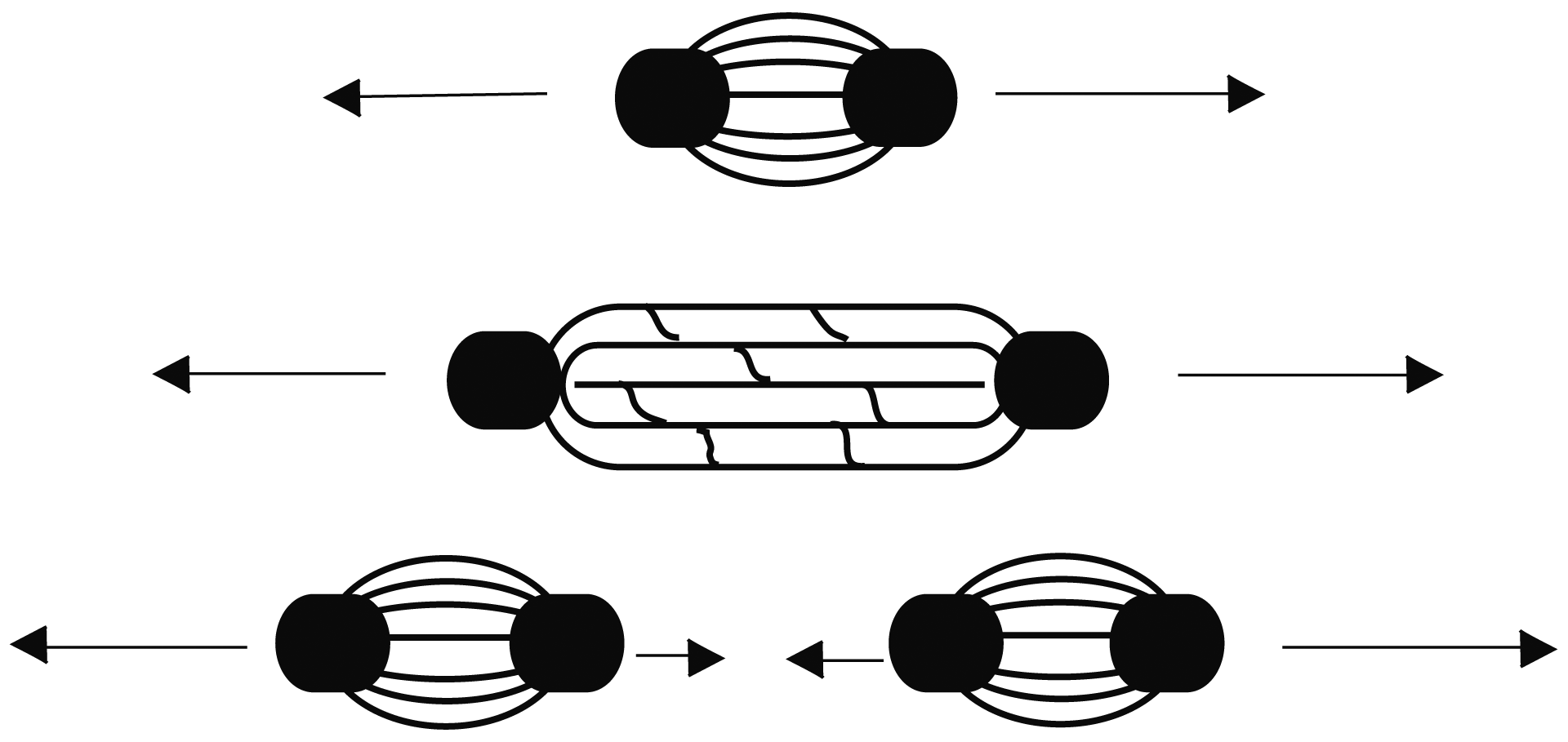
FIGURA I.16. Producción de partículas por el proceso de fragmentación. La interacción entre quarks se da a través de gluones que forman un tubo. Al romperse se forman un par quark-antiquark, y así sucesivamente, hasta que la energía ya no es suficiente para seguir produciendo pares.
Por otro lado, pero en el marco de los conceptos que han surgido alrededor de la teoría de cuerdas donde se trabaja con muchas dimensiones, Gerard t’ Hooft y Leonard Susskind comenzaron a pensar en la posibilidad de que las dimensiones en la naturaleza se comportasen como un holograma.
Los hologramas, que hoy son muy comunes porque van impresos incluso en el papel moneda y en las tarjetas de crédito, son objetos de dos dimensiones, pero que con la luz adecuada producen una imagen de tres. Esto quiere decir que toda la información necesaria para describir a un objeto de tres dimensiones está codificada en dos dimensiones, que es el holograma.
Más que una curiosidad, la idea que subyace al holograma se ha convertido en una manera muy seria de ver al universo. El principio holográfico nos dice cómo modelar todos los eventos que ocurren en una habitación con una teoría que sólo toma en cuenta lo que sucede en las paredes que la forman.
Uno podría ver al universo como un gran holograma donde una de las dimensiones es realmente sólo una ilusión. Las teorías holográficas del universo han tomado forma en la teoría de cuerdas y ahora son un muy activo campo de investigación. Según esto, nuestra experiencia cotidiana podría ser una proyección holográfica de procesos físicos que tienen lugar en una superficie de dos dimensiones. La tercera dimensión sería sólo un espejismo. Esta teoría holográfica del universo se ha desarrollado en espacios con curvatura negativa conocidos como anti-de Sitter.
En 1997 el físico argentino Juan Maldacena propuso una conjetura que hoy es conocida como la dualidad AdS/CFT. Esta dualidad establece una correspondencia exacta y uno a uno entre la teoría en cinco dimensiones de un espacio anti-de Sitter (AdS) y una teoría de campo conforme (Conformal Field Theory, en inglés, y de ahí CFT). Suena intimidante, pero en realidad el planteamiento es sencillo, como veremos.
Para entender qué significa todo esto, veamos primero que el mundo que nos rodea puede ser muy bien descrito con la geometría euclidiana que aprendemos en la escuela. Esta geometría es plana, no curva, y las figuras se pueden describir en una hoja plana de papel. En este espacio euclidiano las líneas paralelas nunca se juntan. También nos resulta familiar la geometría de espacios curvos como la que se puede construir en una esfera. En el caso de estas geometrías hablamos de la curvatura del espacio como algo que la caracteriza. Así, por ejemplo, el más simple de los espacios curvados es la esfera que tiene una curvatura positiva y constante. Esto quiere decir que en todas partes tiene el mismo grado de curvatura, a diferencia de lo que ocurre con un huevo, que es más curvado en el extremo más puntiagudo. Existen también espacios curvos con curvatura negativa. El más simple de éstos es el espacio hiperbólico, que en cierta forma es el equivalente de la esfera en el sentido de que en todas partes tiene la misma curvatura, sólo que ahora es negativa. Decimos que la esfera con curvatura positiva es cerrada, mientras que la “silla de montar”, o espacio hiperbólico, es abierta.
Los geógrafos a menudo usan esta geometría para proyectar los países del mundo de manera que sean apreciables ciertos detalles cuando se los dibuja en una plana de papel. Esto es la proyección de una geometría hiperbólica en dos dimensiones.
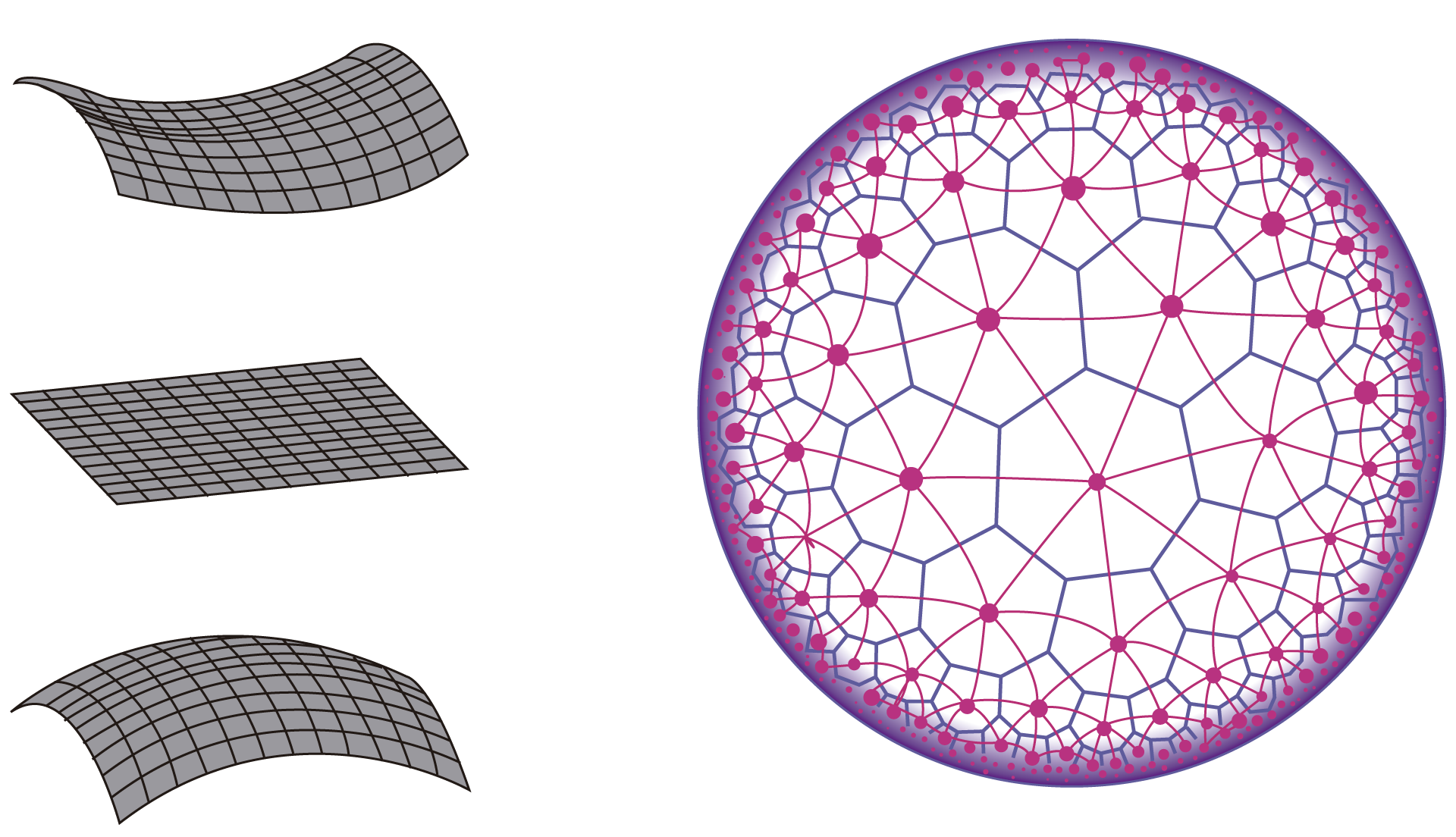
FIGURA I.17. A la izquierda vemos tres curvas: abajo con curvatura positiva, en el centro plana y arriba con curvatura negativa; a la derecha, una proyección en dos dimensiones del espacio hiperbólico de curvatura negativa. Las figuras geométricas (hexágonos y triángulos) parecen más pequeñas al borde sólo por la proyección a dos dimensiones que hacemos a la página plana.
En todo esto podemos ahora incluir al tiempo para hablar de espacio-tiempo, y continuar con la idea de espacio-tiempo con curvatura positiva o negativa. El más simple de los espacios-tiempo con curvatura positiva es el espacio de Sitter. De manera equivalente, el espacio-tiempo más simple de curvatura negativa es el espacio anti-de Sitter.
El nombre proviene de Willem de Sitter, quien, como vimos anteriormente, propuso uno de los primeros universos a partir de la teoría de la relatividad general. El modelo era simple y se trataba de una esfera espacio-temporal. Como decíamos, una esfera tiene curvatura positiva; de manera equivalente, el espacio anti-de Sitter es un espacio de curvatura negativa —como si se tratase de una antiesfera—, sólo que en cinco dimensiones.
En un espacio anti-de Sitter ocurren cosas interesantes. Por ejemplo, si usted lanza una pelota, ésta regresará después de un cierto tiempo. No importa con qué fuerza la aviente, regresará a usted siempre después del mismo tiempo. La única diferencia será que, cuanto más fuerza ponga usted en el lanzamiento, el objeto llegará más lejos. Si usted envía un pulso de luz en cualquier dirección, ésta llegará hasta el fin del universo y regresará a usted después de un tiempo finito. No es necesario esperar por siempre.
En la figura I.18 mostramos un espacio anti-de Sitter en dos dimensiones espaciales y una temporal que forma un cilindro tridimensional en el que la altura del cilindro es el tiempo. Sin embargo, para un espacio de cuatro dimensiones, con tres espaciales y una temporal, como el nuestro, no tendremos un círculo como límite de la parte espacial, que es la sección transversal del cilindro, sino una esfera en todo momento.
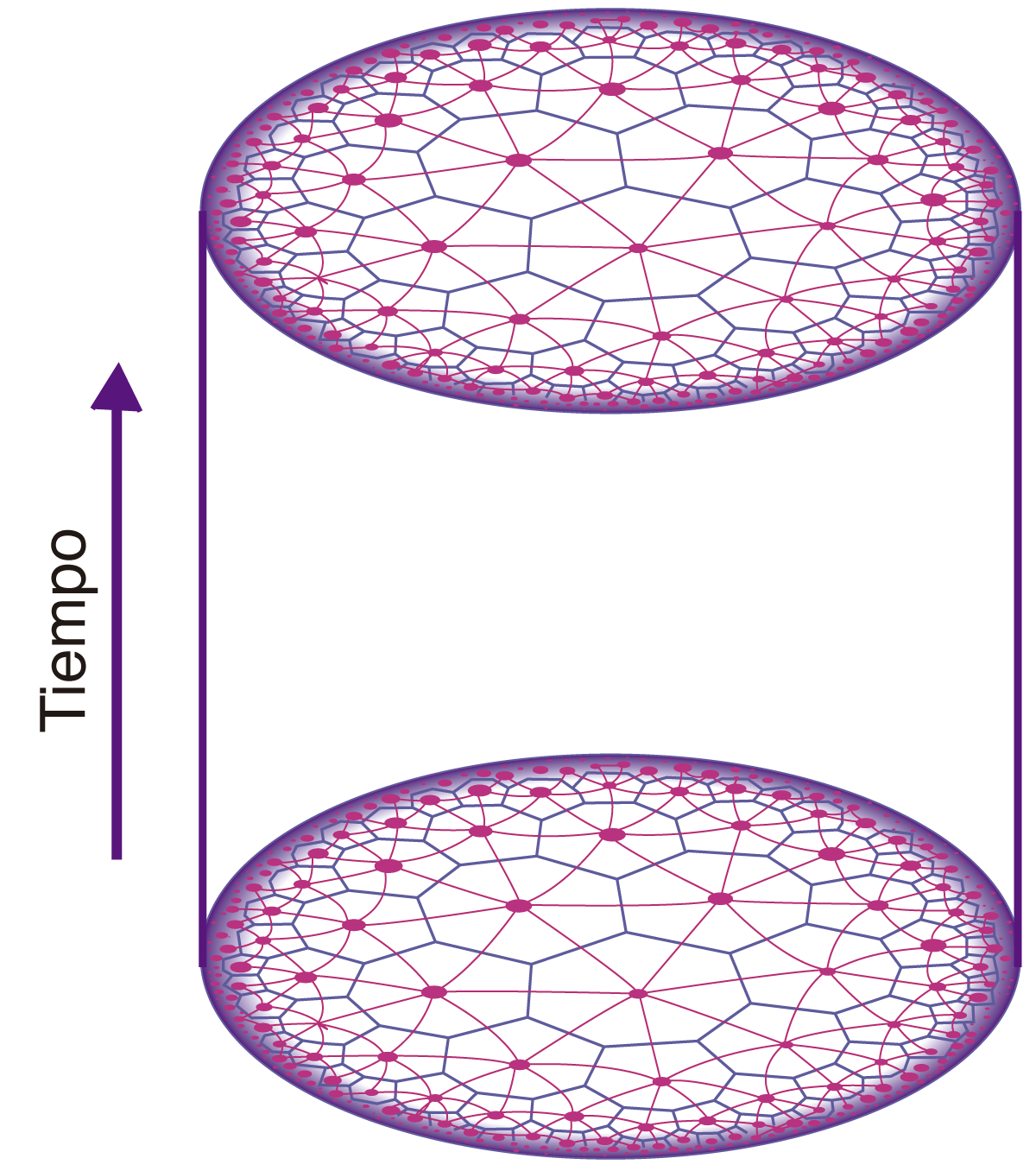
FIGURA I.18. Espacio-tiempo anti-de Sitter en dos dimensiones espaciales y una temporal.
En este contexto de espacios anti-de Sitter es que surgió la idea interesante que, en caso de llegar a corroborarse, representará el avance más significativo de los últimos años. La conjetura AdS/CFT dice que, en el interior de esta esfera espacio-tiempo anti-de Sitter, la teoría de gravedad cuántica es equivalente a una teoría cuántica de partículas elementales más o menos tradicional que vive en el borde de este espacio, es decir, a una teoría conforme de campos, expresada aquí como CFT. A esta relación se le conoce en matemáticas como dualidad y establece una correspondencia uno a uno entre lo que ocurre en ambas teorías.
De ser cierto lo anterior, significaría que podemos usar la teoría cuántica relativamente bien entendida de partículas para definir una teoría cuántica de la gravedad, o al revés, hacer uso de las técnicas matemáticas de un agujero negro donde la gravedad cuántica existe, para describir hechos de la vida diaria que un físico estudia en lugares como el Gran Colisionador de Hadrones del CERN, a saber, el comportamiento de quarks y gluones.
Podemos pues tener en la superficie del espacio anti-de Sitter al plasma de quarks y gluones descrito por una teoría tradicional cuántica de las partículas elementales que corresponde a la descripción en el interior de este espacio de objetos que están sujetos a la gravedad cuántica.
Lo maravilloso de estas ideas es que exista una correspondencia entre algo que tiene gravedad y mecánica cuántica con lo que es un plasma de quarks y gluones, que podemos crear en el laboratorio, y que no experimenta interacción gravitacional.
La termodinámica y las propiedades de transporte de un sistema fuertemente acoplado como el plasma de quarks y gluones están relacionadas con las propiedades geométricas de un agujero negro de tal manera que el cálculo de la viscosidad se vuelve un problema gravitacional. Ya se han llevado a cabo cálculos con la intención de ir entendiendo la relación entre un sistema de quarks y gluones, que puede ser producido experimentalmente.
Uno puede estudiar también otras cantidades tales como la pérdida de energía de un quark en un medio como el plasma de quarks y gluones. Este y otros fenómenos que pueden ser medidos experimentalmente nos podrían mostrar que tan correctas son las ideas que subyacen a la teoría de cuerdas.
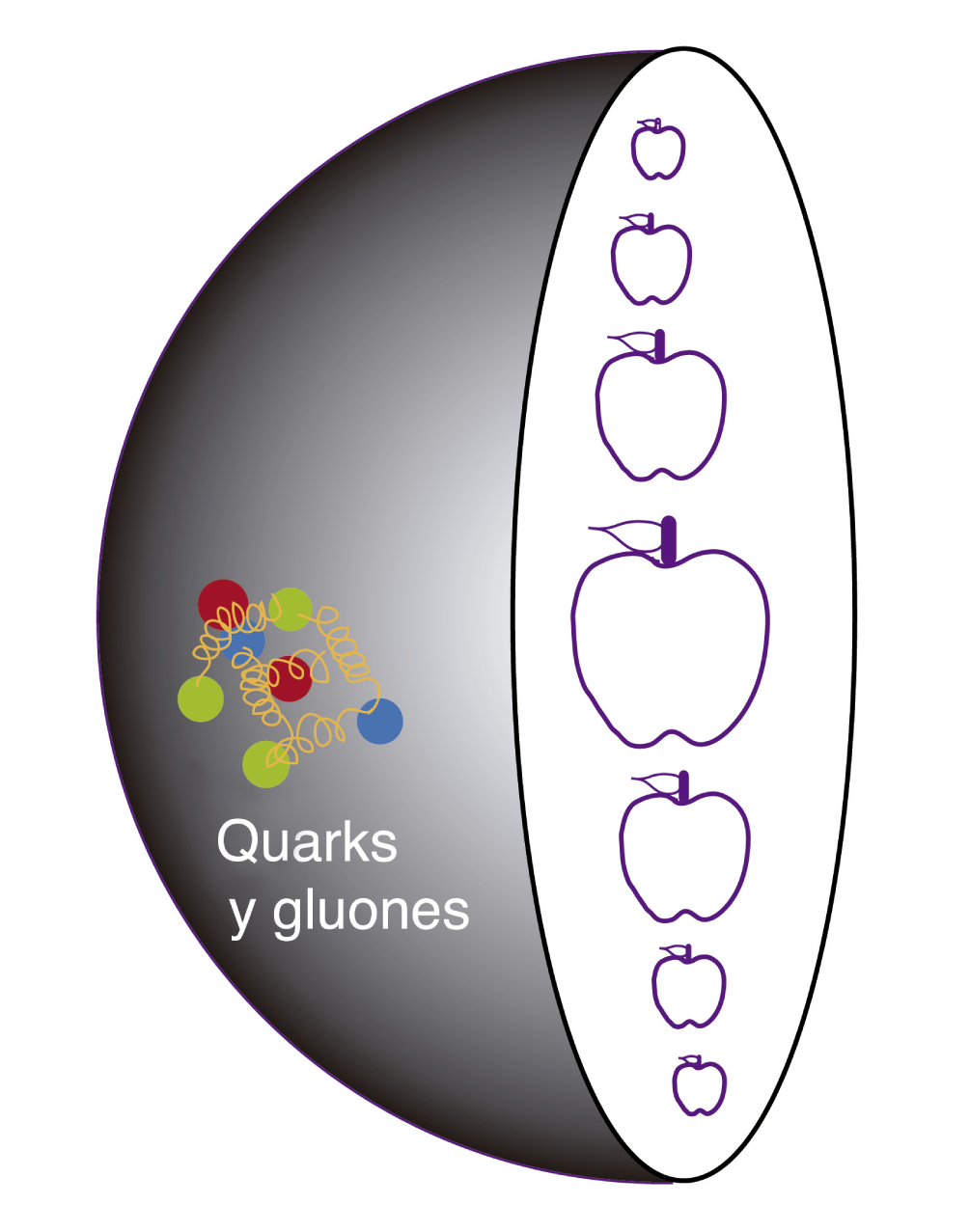
FIGURA I.19. Interior del espacio anti-de Sitter donde viven los objetos bajo las leyes de la gravedad cuántica. En la superficie del espacio el plasma de quarks y gluones puede ser descrito con una teoría tradicional que guarda correspondencia con el interior del espacio.
Hemos dicho anteriormente que la relación conocida como dualidad entre el mundo de la gravedad cuántica en un espacio anti-de Sitter con una teoría de campo conforme es tal que la correspondencia uno a uno entre los teoremas y las estructuras de un marco de conceptos con el otro es exacta. Esto podría significar que la aparición misma del plasma de quarks y gluones corresponderá a la aparición de un agujero negro en el espacio matemático. Sin embargo, es importante recordar que esta relación se da con una teoría conforme que en realidad es solamente una caricatura de la verdadera teoría que describe a los quarks y los gluones, que, como hemos dicho, es la cromodinámica cuántica.
Ya hemos comentado lo que significa pensar en un espacio anti-de Sitter; ¿por qué hablamos de teoría conforme de campos y no de teoría de quarks y gluones?, ¿qué es una teoría conforme de campos?
Una teoría de campos es aquella en la que los objetos de estudio son precisamente campos. Las teorías que describen el mundo microscópico hacen uso de este concepto matemático llamado campo, que asigna a cada punto del espacio una cantidad o valor. Si el campo es vectorial le asigna también una dirección y un sentido. Si el campo es escalar le asigna sólo un valor numérico.
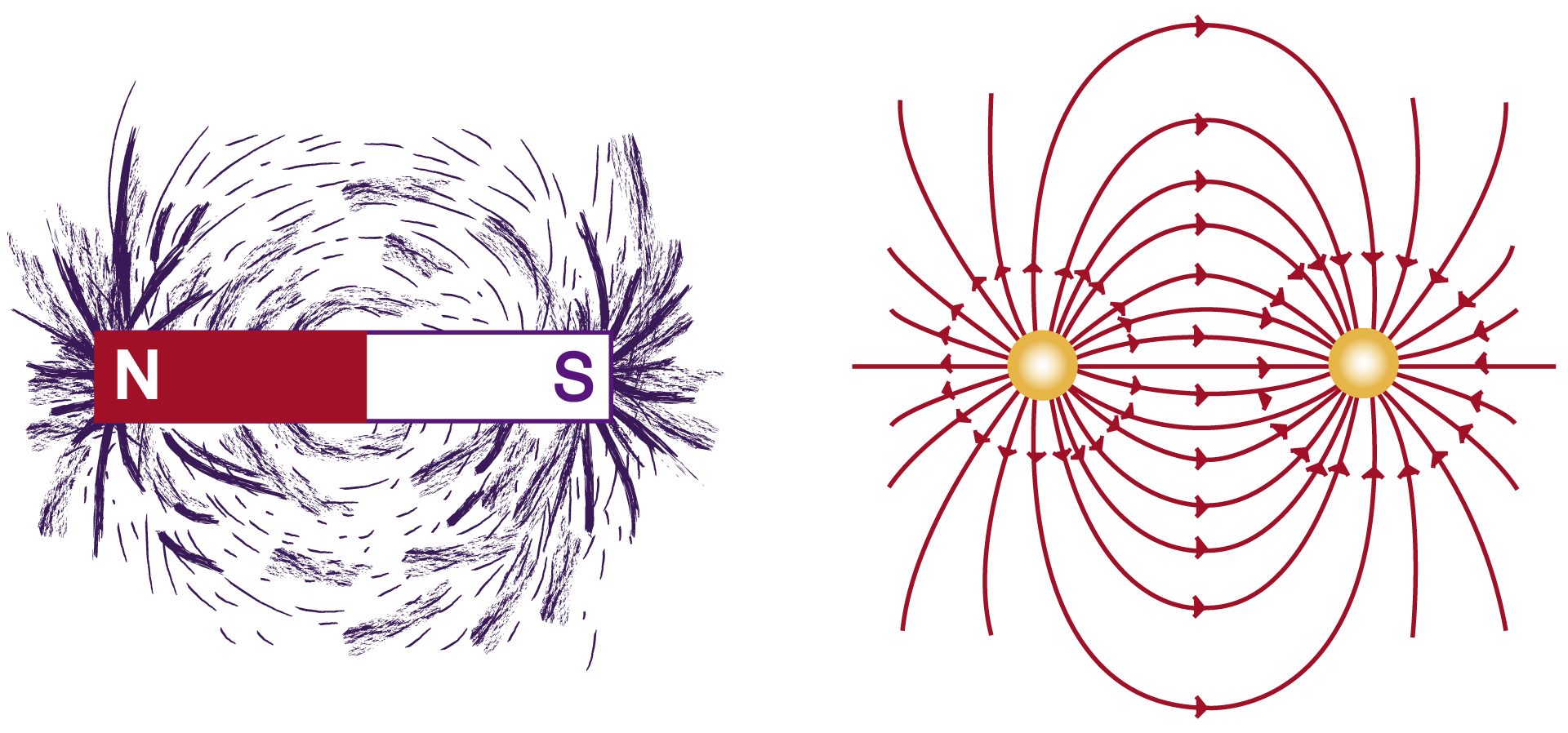
Los campos vectoriales pueden representar al campo magnético entre los polos de un imán o la intensidad, la dirección y el sentido de las fuerzas entre dos cargas eléctricas. En la figura I.20, las limaduras de hierro permiten visualizar el campo magnético que tiene, en cada punto, un valor de intensidad, una dirección y un sentido. También se muestra el campo vectorial entre dos cargas de signos opuestos que usualmente no vemos, pero que podemos imaginar.
Un campo escalar puede ser la distribución de temperaturas en un país como México, donde cada punto del espacio tiene asignado un número, que es la temperatura. Este número sólo tienen una magnitud y carece de dirección y de sentido. El equivalente meteorológico de un campo vectorial sería el mapa de vientos de la República. En un mapa así es necesario denotar no sólo la velocidad de los vientos con un número en cada punto del mapa, sino además el sentido norte-sur así como la dirección del viento.
Una teoría de campos que además es conforme es aquella en la que, cuando uno hace transformaciones de escala, los elementos de la teoría preservan los ángulos, pero no las longitudes.
Una manera de ilustrar esto con algo a lo que todos estamos acostumbrados es el de las proyecciones de mapas del planeta en una hoja plana. Para poder ver el mundo en una hoja plana es necesario desfigurar los países. Llevar una esfera a un rectángulo implica cambiar el tamaño de todo. Así, por ejemplo, Groenlandia aparece muchas veces como algo enorme o muy pequeño, como consecuencia de la proyección que estemos usando. Existen muchas maneras de hacer la proyección de una esfera en un rectángulo. Algunas de ellas tratan de preservar el área de los países, otras la forma o las distancias, dependiendo de cual será el uso que se le quiera dar al mapa que resulte de la transformación.
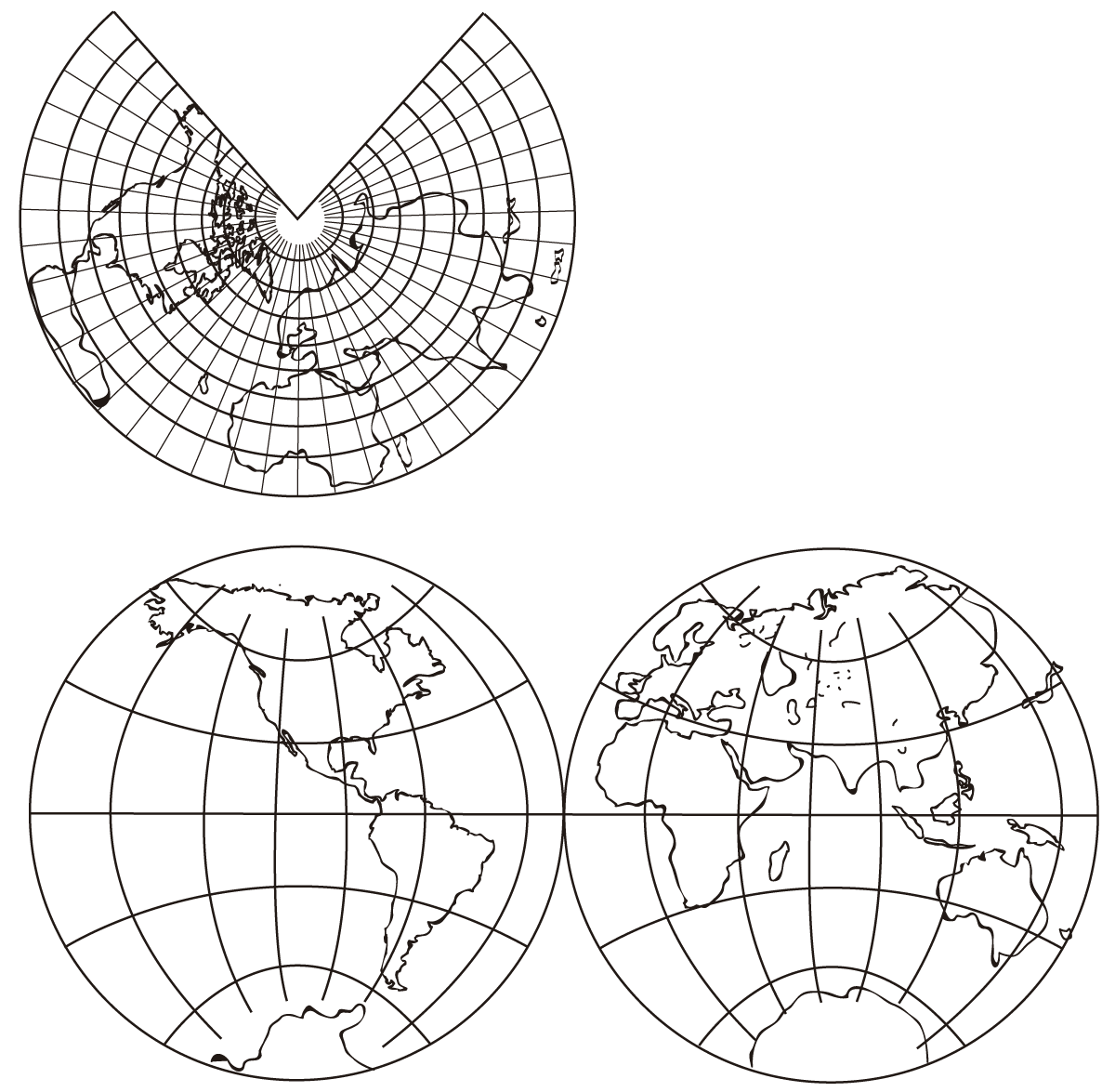
FIGURA I.21. Transformación conforme de una esfera a un plano. Los ángulos entre las líneas de latitud y de longitud permanecen en 90 grados.
La transformación conforme es aquella que preserva el ángulo. Un ejemplo de lo que esto significa con el planeta proyectado en una hoja plana se puede ver en la figura I.21. Uno puede notar que aunque los mapas se han deformado, los ángulos entre las líneas de latitud y las líneas de longitud permanecen igual en 90 grados. Justo como ocurría con la esfera original. Éstas son transformaciones conformes.
La teoría que describe a los quarks, la llamada cromodinámica cuántica, no es una teoría conforme. Éste es el primer pero de muchos que vendrán con la dualidad AdS/CFT. La conjetura no aplica. Al respecto, los entusiastas de la conjetura AdS/CFT argumentan que, si bien la teoría de los quarks y los gluones no es conforme, sí está muy cerca de serlo. La argumentación empieza a ser muy técnica y no la discutiremos aquí. No obstante, diremos que la teoría que describe a los quarks, llamada cromodinámica cuántica, se convierte en una teoría conforme cuando la masa de los quarks se hace cero. Una aproximación así no está nada mal. El modelo no sería ni el primero ni el único en partir de esta aproximación y es justamente este aspecto de viabilidad lo que estimula a la comunidad de investigadores que buscan algo más profundo en la relación AdS/CFT.
Por otro lado, la teoría que describe a los quarks tampoco es supersimétrica, mientras que la teoría conforme a la que se hará referencia como analogía sí lo es. Que una teoría sea supersimétrica quiere decir que en la descripción no se hace diferencia entre partículas con espín entero y semientero —en términos más sencillos, las partículas elementales que vimos arriba—, es decir, leptones y quarks, que forman todo lo que observamos, se pueden intercambiar con partículas que transportan las interacciones —también mostradas en la tabla de todos los componentes—. Además, como veremos, en los quarks y gluones que conocemos hemos identificado tres colores como cargas de interacción, mientras que la dualidad establece un número muy grande de colores para la teoría que es paralela a la del espacio anti-de Sitter.
Con todo esto, las estimaciones que se han obtenido a partir de AdS para los fenómenos presentes en el mundo de quarks y gluones son muy razonables, y existe la idea general de que esta correspondencia va en la dirección correcta.
Existen hoy cálculos que pueden ya ser comparados con los que se observan en los experimentos. Las estimaciones que se obtienen pueden no ser muy precisas, pero se acercan a la realidad.
Regresaremos a esto en el capítulo V, donde discutiremos algunos resultados recientes de los experimentos de iones pesados en los que se crea un sistema de quarks y gluones que podría ser descrito, de manera aproximada, por esta dualidad.
1 Albert A. Michelson, Light Waves and Their Uses, 2ª ed., The University of Chicago Press, Chicago, 1903, p. 23.
2 William Thomson (Lord Kelvin), “Nineteenth Century Clouds Over the Dynamical Theory of Heat and Light”, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 2 (6): 1-40, 1901.
3 Edmund Whittaker, History of Aether and Electricity. The Modern Theories 1900-1926, vol. 2, Thomas Nelson & Sons Ltd., Londres/ Edimburgo/ Nueva York, 1953, p. 40.
4 Richard Feynman, El carácter de la ley física, Antoni Bosch, Barcelona, 1983, p. 21.