4

EL FUNDAMENTO DE LA TEORÍA DE LA RELATIVIDAD GENERAL^*

A. CONSIDERACIONES FUNDAMENTALES SOBRE EL POSTULADO DE RELATIVIDAD

1. OBSERVACIONES SOBRE LA TEORÍA DE LA RELATIVIDAD ESPECIAL

La teoría de la relatividad especial se basa en el siguiente postulado, que también es satisfecho por la mecánica de Galileo y Newton.

Si se escoge un sistema de coordenadas K con relación al cual son válidas las leyes físicas en su forma más simple, las mismas leyes son también válidas con relación a cualquier otro sistema de coordenadas K’ que se mueve con movimiento de traslación uniforme con respecto a K. Llamamos a este postulado el «principio de relatividad especial». La palabra «especial» quiere dar a entender que el principio está restringido al caso en que K’ tiene un movimiento de traslación uniforme con respecto a K, pero que la equivalencia de K’ y K no se extiende al caso de movimiento no uniforme de K’ con respecto a K.

Así pues, la teoría de la relatividad especial no se aparta de la mecánica clásica por el postulado de relatividad, sino por el postulado de la constancia de la velocidad de la luz in vacuo, a partir del cual, en combinación con el principio de relatividad especial, se sigue, en la forma bien conocida, la relatividad de la simultaneidad, la transformación lorentziana y las leyes relacionadas para el comportamiento de cuerpos y relojes en movimiento.

La modificación a la que la teoría de la relatividad especial ha sometido a la teoría del espacio y el tiempo es realmente de largo alcance, pero hay un punto importante que ha permanecido inalterado. Pues las leyes de la geometría, incluso según la teoría de la relatividad especial, tienen que ser interpretadas directamente como leyes relacionadas con las posibles posiciones relativas de cuerpos sólidos en reposo; y, de una manera más general, las leyes de la cinemática deben interpretarse como leyes que describen las relaciones de medida de cuerpos y relojes. A dos puntos materiales seleccionados de un cuerpo rígido estacionario corresponde siempre una distancia de longitud bien definida, que es independiente de la localización y orientación del cuerpo, y es también independiente del tiempo. A dos posiciones seleccionadas de las manecillas de un reloj en reposo con respecto a un sistema de referencia privilegiado, corresponde siempre un intervalo de tiempo de longitud definida, que es independiente del lugar y el tiempo. Pronto veremos que la teoría de la relatividad especial no puede adherirse a esta interpretación física sencilla del espacio y el tiempo.

2. LA NECESIDAD DE UNA EXTENSIÓN DEL POSTULADO DE RELATIVIDAD

En mecánica clásica, y no menos en la teoría de la relatividad especial, existe un defecto epistemológico inherente que fue señalado claramente, quizá por primera vez, por Ernst Mach. Lo discutiremos mediante el siguiente ejemplo: dos cuerpos fluidos del mismo tamaño y naturaleza se mantienen libremente en el espacio a una distancia tan grande uno de otro y de todas las demás masas que sólo hay que tener en cuenta aquellas fuerzas gravitatorias que aparecen a partir de la interacción de diferentes partes del mismo cuerpo. Sea invariable la distancia entre los dos cuerpos, y supongamos que en ninguno de los dos cuerpos hay movimientos relativos de unas partes con respecto a otras. Pero supongamos que una de las dos masas, juzgada por un observador en reposo con respecto a la otra masa, rota con velocidad angular constante alrededor de la línea que une ambas masas. Éste es un movimiento relativo verificable de los dos cuerpos. Imaginemos ahora que cada uno de los cuerpos ha sido examinado por medio de instrumentos de medida en reposo con respecto al mismo, y que se muestra que la superficie de S₁ es una esfera y la de S₂ es un elipsoide de revolución. Acto seguido planteamos la pregunta: ¿cuál es la razón de esta diferencia entre los dos cuerpos? Ninguna respuesta puede admitirse como epistemológica satisfactoria,¹ a menos que la razón dada sea un hecho de experiencia observable. La ley de causalidad no tiene el significado de un enunciado acerca del mundo de la experiencia, excepto cuando hechos observables aparecen en última instancia como causas y efectos.

La mecánica newtoniana no da una respuesta satisfactoria a esta pregunta. Se pronuncia como sigue: las leyes de la mecánica se aplican al espacio R₁, con respecto al cual el cuerpo S₁ está en reposo, pero no al espacio R₂ con respecto al cual el cuerpo S₂ está en reposo. Pero el espacio privilegiado R₁ de Galileo, así introducido, es una causa meramente facticia, y no algo que pueda ser observado. Es evidente, por lo tanto, que la mecánica de Newton no satisface realmente el requisito de causalidad en el caso bajo consideración, sino que lo hace sólo aparentemente, puesto que hace a la causa facticia R₁ responsable de la diferencia observable en los cuerpos S₁ y S₂.

La única respuesta satisfactoria debe ser que el sistema físico consistente en S₁ y S₂ no revela dentro de sí mismo ninguna causa imaginable a la que pueda remitirse el diferente comportamiento de S₁ y S₂. Por consiguiente, la causa debe estar fuera de este sistema. Tenemos que asumir que las leyes generales de movimiento, que en particular determinan las formas de S₁ y S₂, deben ser tales que el comportamiento mecánico de S₁ y S₂ está condicionado en parte, y en aspectos muy esenciales, por masas distantes que no han sido incluidas en el sistema bajo consideración. Estas masas distantes y sus movimientos con respecto a S₁ y S₂ deben considerarse entonces como la sede de las causas (que deben ser susceptibles de observación) del diferente comportamiento de nuestros dos cuerpos S₁ y S₂. Ellas asumen el papel de la causa facticia R₁. De todos los espacios imaginables R₁, R₂, etc., en cualquier tipo de movimiento relativo mutuo, no existe ninguno que podamos considerar privilegiado a priori sin reavivar la objeción epistemológica antes mencionada. Las leyes de la física deben ser de tal naturaleza que se aplican a sistemas de referencia en cualquier tipo de movimiento. Por este camino llegamos a una extensión del postulado de relatividad.

Además de este poderoso argumento de la teoría del conocimiento, existe un hecho físico bien conocido en favor de una extensión de la teoría de la relatividad. Sea K un sistema de referencia galileano, i. e. un sistema con respecto al cual (al menos en la región tetradimensional en consideración) una masa, suficientemente distante de otras masas, se mueve con movimiento uniforme en línea recta. Sea K’ un segundo sistema de referencia que se mueve con respecto a K con traslación uniformemente acelerada. Entonces, con respecto a K’, una masa suficientemente distante de otras masas tendría un movimiento acelerado tal que la magnitud y dirección de su aceleración son independientes de la composición material y estado físico de la masa.

¿Permite esto a un observador en reposo con respecto a K’ inferir que él está en un sistema de referencia «realmente» acelerado? La respuesta es negativa; pues la relación antes mencionada de masas libremente movibles respecto a K’ puede interpretarse igualmente bien de la siguiente manera. El sistema de referencia K’ no está acelerado, pero el territorio espacio-temporal en cuestión está bajo el dominio de un campo gravitatorio que genera el movimiento acelerado de los cuerpos con respecto a K’.

Esta visión se hace posible para nosotros por la enseñanza de la experiencia acerca de la existencia de un campo de fuerzas, a saber, el campo gravitatorio, que posee la extraordinaria propiedad de impartir la misma aceleración a todos los cuerpos.² El comportamiento mecánico de los cuerpos con respecto a K’ es el mismo que se presenta a la experiencia en el caso de sistemas que solemos considerar como «estacionarios» o como «privilegiados». Por consiguiente, desde el punto de vista físico, se sugiere inmediatamente la hipótesis de que los sistemas K y K’ deben ser ambos considerados con igual derecho como «estacionarios», es decir, tienen el mismo título como sistemas de referencia para la descripción física de los fenómenos.

Se verá a partir de estas reflexiones que al seguir la teoría de la relatividad general nos veremos llevados a una teoría de la gravitación, puesto que podemos «producir» un campo gravitatorio cambiando meramente el sistema de coordenadas. También será obvio que el principio de la constancia de la velocidad de la luz in vacuo debe ser modificado, puesto que fácilmente reconocemos que la trayectoria de un rayo luminoso con respecto a K’ debe ser en general curvilínea, si con respecto a K la luz se propaga en línea recta con una velocidad constante definida.

3. EL CONTINUO ESPACIO-TEMPORAL. REQUISITO DE COVARIANCIA GENERAL PARA LAS ECUACIONES QUE EXPRESAN LAS LEYES GENERALES DE LA NATURALEZA

En mecánica clásica, así como en la teoría de la relatividad especial, las coordenadas de espacio y tiempo tienen un significado físico directo. Decir que un suceso tiene x₁ como coordenada X₁ significa que la proyección del suceso sobre el eje de X₁, determinada por reglas de medir rígidas y de acuerdo con las reglas de la geometría euclidiana, se obtiene colocando una regla de medir dada (la unidad de longitud) x₁ veces a partir del origen de coordenadas a lo largo del eje de X₁. Decir que un suceso puntual tiene x₄ = t como coordenada X₄ significa que un reloj estándar, construido para medir el tiempo con un período unidad definido, y que es estacionario con respecto al sistema de coordenadas y prácticamente coincidente en el espacio con el suceso puntual,³ habrá medido x₄ = t períodos en la ocurrencia del suceso.

Esta idea del espacio y el tiempo ha estado siempre en la mente de los físicos, incluso si, como regla, no han sido conscientes de ella. Está claro a partir del papel que estos conceptos desempeñan en las medidas físicas; también debe subyacer a las reflexiones del lector sobre la sección precedente (2) para conectar cualquier significado con lo que allí ha leído. Pero ahora demostraremos que debemos dejarla de lado y reemplazarla por una visión más general para poder completar el postulado de relatividad general, si la teoría de la relatividad especial se aplica al caso especial de ausencia de un campo gravitatorio.

En un espacio que está libre de campos gravitatorios introducimos un sistema de referencia galileano K (x, y, z, t), y también un sistema de coordenadas K’ (x’, y’, z’, t’) en rotación uniforme con respecto a K. Consideramos que los orígenes de ambos sistemas así como sus ejes Z coinciden en todo momento. Demostraremos que para una medida espacio-temporal en el sistema K’ no puede mantenerse la definición anterior del significado físico de longitudes y tiempos. Por razones de simetría es evidente que un círculo alrededor del origen en el plano X, Y de K puede considerarse al mismo tiempo como un círculo en el plano X’, Y’ de K’. Supongamos que la circunferencia y el diámetro de este círculo han sido medidos con una medida unidad infinitamente pequeña comparada con el radio, y que tenemos el cociente de ambos resultados. Si este experimento se realizara con una regla de medir en reposo con respecto al sistema galileano K, el cociente sería π. Con una regla de medir en reposo con respecto a K’, el cociente sería mayor que π. Esto se entiende inmediatamente si concebimos el proceso global de medir desde el sistema «estacionario» K, y tenemos en consideración que la regla de medir aplicada a la periferia sufre una contracción lorentziana, mientras que la aplicada a lo largo del radio no la sufre. Por lo tanto, la geometría euclidiana no se aplica a K’. La noción de coordenadas definida más arriba, que presupone la validez de la geometría euclidiana, deja de ser válida por consiguiente en relación al sistema K’. Así, también, somos incapaces de introducir un tiempo correspondiente a los requisitos físicos en K’, indicado por relojes en reposo con respecto a K’. Para convencernos de esta imposibilidad, imaginemos dos relojes de idéntica constitución colocados uno en el origen de coordenadas y el otro en la circunferencia del círculo, y ambos concebidos desde el sistema «estacionario» K. Por un resultado familiar de la teoría de la relatividad especial, el reloj en la circunferencia —juzgado desde K— marcha más lento que el otro, porque el primero está en movimiento y el último en reposo. Un observador en el origen común de coordenadas, capaz de observar el reloj en la circunferencia por medio de luz, vería por consiguiente que se retrasa respecto al reloj que tiene ante él. Puesto que él no estará preparado para admitir que la velocidad de la luz a lo largo del camino en cuestión dependa explícitamente del tiempo, interpretará sus observaciones como algo que demuestra que el reloj en la circunferencia «realmente» marcha más lento que el reloj en el origen. Por lo tanto, se verá obligado a definir el tiempo de tal manera que la marcha de un reloj depende de dónde pueda estar el reloj.

Por consiguiente, llegamos a este resultado: en la teoría de la relatividad general, el espacio y el tiempo no pueden definirse de manera tal que las diferencias de las coordenadas espaciales puedan medirse directamente por la regla de medir unidad, ni las diferencias en la coordenada temporal por un reloj estándar.

El método empleado hasta ahora para tender coordenadas en el continuo espacio-temporal de una manera definida deja así de ser válido, y parece que no haya otra forma que nos permitiera adaptar sistemas de coordenadas al universo tetradimensional, de modo que pudiéramos esperar de su aplicación una formulación particularmente simple de las leyes de la naturaleza. De modo que no hay nada sino considerar todos los sistemas de coordenadas imaginables, en principio, como igualmente adecuados para la descripción de la naturaleza. Esto viene a exigir que:

Las leyes generales de la naturaleza deben expresarse por ecuaciones que sean válidas para todos los sistemas de coordenadas. Es decir, sean covariantes con respecto a cualesquiera sustituciones (generalmente covariantes).

Es evidente que una teoría física que satisfaga este postulado también será adecuada para el postulado de relatividad general. Pues la suma de todas las sustituciones incluye, en cualquier caso, a aquellas que corresponden a todos los movimientos relativos de sistemas de coordenadas tridimensionales. Que este requisito de covariancia general, que despoja al espacio y el tiempo del último residuo de objetividad física, es un requisito general, se verá a partir de la siguiente reflexión. Todas nuestras verificaciones espacio-temporales equivalen invariablemente a una determinación de coincidencias espacio-temporales. Si, por ejemplo, los sucesos consistieran meramente en el movimiento de puntos materiales, entonces nada sería observable en definitiva salvo los encuentros de dos o más de dichos puntos. Además, los resultados de nuestras medidas no son nada más que verificaciones de tales encuentros de los puntos materiales de nuestros instrumentos de medida con otros puntos materiales, coincidencias entre las manecillas de un reloj y puntos en la esfera de un reloj, y sucesos puntuales observados que suceden en el mismo lugar y al mismo tiempo.

La introducción de un sistema de referencia no tiene otro propósito que facilitar la descripción de la totalidad de tales coincidencias. Asignamos al universo cuatro variables espacio-temporales x₁, x₂, x₃, x₄, de tal manera que para todo suceso puntual existe un correspondiente sistema de valores de las variables x₁.... x₄. A dos sucesos puntuales coincidentes corresponde un sistema de valores de las variables x₁ ... x₄, i. e. la coincidencia se caracteriza por la identidad de las coordenadas. Si, en lugar de las variables x₁ ... x₄, introducimos funciones de ellas, x’₁, x’₂, x’₃, x’₄, como un nuevo sistema de coordenadas, de modo que los sistemas de valores se hacen corresponder uno a otro sin ambigüedad, la igualdad de las cuatro coordenadas en el nuevo sistema servirá también como una expresión de la coincidencia espacio-temporal de los dos sucesos puntuales. Puesto que toda nuestra experiencia física puede reducirse en última instancia a tales coincidencias, no hay ninguna razón inmediata para preferir ciertos sistemas de coordenadas a otros. Es decir, llegamos al requisito de covariancia general.

4. LA RELACIÓN DE LAS CUATRO COORDENADAS CON LA MEDIDA EN EL ESPACIO Y EL TIEMPO

No es mi propósito en esta discusión presentar la teoría de la relatividad general como un sistema tan sencillo y lógico como sea posible, y con el mínimo número de axiomas; sino que mi principal objetivo es desarrollar esta teoría de tal manera que el lector sienta que el camino en el que hemos entrado es el natural desde un punto de vista psicológico, y que las hipótesis subyacentes parecerán tener el máximo grado de seguridad posible. Con este objetivo a la vista garanticemos ahora que:

Para regiones tetradimensionales infinitamente pequeñas es apropiada la teoría de la relatividad en el sentido restringido, si las coordenadas se escogen adecuadamente.

Para este fin debemos escoger la aceleración del sistema de coordenadas («local») infinitamente pequeño de modo que no haya ningún campo gravitatorio; esto es posible para una región infinitamente pequeña. Sean X₁, X₂, X₃ las coordenadas espaciales, y X₄ la correspondiente coordenada temporal medida en la unidad apropiada.⁴ Si se imagina dada una regla rígida como unidad de medida, las coordenadas, con una orientación dada del sistema de coordenadas, tienen un significado físico directo en el sentido de la teoría de la relatividad especial. Por la teoría de la relatividad especial la expresión

(1)

tiene entonces un valor que es independiente de la orientación del sistema de coordenadas local, y que se puede determinar mediante medidas de espacio y tiempo. Llamamos ds a la magnitud del elemento de línea perteneciente a puntos del continuo tetradimensional infinitamente próximos. Siguiendo a Minkowski, si el ds perteneciente a los elementos dX₁ ... dX₄ es positivo, le llamamos de tipo tiempo; si es negativo, le llamamos de tipo espacio.

Al «elemento de línea» en cuestión, o a los dos sucesos puntuales infinitamente próximos, corresponderán también diferenciales definidas dx₁ ... dx₄ de las coordenadas tetradimensionales de cualquier sistema de referencia escogido. Si este sistema, así como el sistema «local», está dado para la región en consideración, las dX_ν podrán representarse aquí por expresiones homogéneas lineales definidas de las dx_σ:

(2)

Insertando estas expresiones en (1), obtenemos

(3)

donde las g_στ serán funciones de las x_σ. Éstas ya no pueden ser dependientes de la orientación y el estado de movimiento del sistema de coordenadas «local», pues ds² es una magnitud que se puede establecer por medidas de regla-y-reloj de sucesos puntuales infinitamente próximos en el espacio-tiempo, y definida independientemente de cualquier elección de coordenadas concreta. Las g_στ deben escogerse aquí de modo que g_στ = g_τσ; la suma se extiende sobre todos los valores de σ y τ, de modo que la suma consta de 4 X 4 términos, de los cuales 12 se agrupan en pares iguales.

El caso de la teoría de la relatividad ordinaria aparece a partir del caso aquí considerado, si es posible escoger, por razón de las relaciones particulares de las g_στ en una región finita, el sistema de referencia en la región finita de tal manera que las g_στ toman los valores constantes

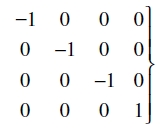
(4)

Encontraremos en adelante que la elección de tales coordenadas no es posible, en general, para una región finita.

De las consideraciones desarrolladas en los enunciados 2 y 3 se sigue que las cantidades g_τσ deben considerarse desde el punto de vista físico como las cantidades que describen el campo gravitatorio en relación con el sistema de referencia escogido. Pues si ahora suponemos que la teoría de la relatividad especial se aplica a una cierta región tetradimensional con las coordenadas adecuadamente escogidas, entonces las g_οτ tienen los valores dados en (4). Un punto material libre se mueve entonces, con respecto a este sistema, con movimiento uniforme en línea recta. Entonces, si introducimos nuevas coordenadas espacio-temporales x₁, x₂, x₃, x₄ por medio de cualquier sustitución que escojamos, las g^οτ en este nuevo sistema ya no serán constantes, sino funciones del espacio y el tiempo. Al mismo tiempo, el movimiento del punto lateral libre se presentará en las nuevas coordenadas como un movimiento no-uniforme curvilíneo, y la ley de este movimiento será independiente de la naturaleza de la partícula que se mueve. Por consiguiente, interpretaremos este movimiento como un movimiento bajo la influencia de un campo gravitatorio. Encontramos así la presencia de un campo gravitatorio conectada con una variabilidad espacio-temporal de las g_σ. Así también, en el caso general, cuando ya no podemos mediante una adecuada elección de coordenadas aplicar la teoría de la relatividad especial a una región finita, nos atendremos a la idea de que las g_στ describen el campo gravitatorio.

Por lo tanto, según la teoría de la relatividad general la gravitación ocupa una posición excepcional con respecto a otras fuerzas, en particular las fuerzas electromagnéticas, puesto que las diez funciones g_στ que representan al campo gravitatorio definen al mismo tiempo las propiedades métricas del espacio medido.

B. HERRAMIENTAS MATEMÁTICAS PARA LA FORMULACIÓN DE ECUACIONES GENERALMENTE COVARIANTES

Habiendo visto en lo que precede que el postulado de relatividad general conduce al requisito de que las ecuaciones de la física sean covariantes frente a cualquier sustitución de las coordenadas x₁ ... x₄, tenemos que considerar cómo pueden encontrarse tales ecuaciones generalmente covariantes. Ahora nos dirigimos hacia esta tarea puramente matemática, y encontraremos que en su solución juega un papel fundamental el invariante ds dado en la ecuación (3), que, tomándolo prestado de la teoría de superficies de Gauss, hemos llamado el «elemento de línea».

La idea fundamental de esta teoría general de covariantes es la siguiente: Definamos ciertos objetos («tensores») con respecto a cualquier sistema de coordenadas mediante un número de funciones de las coordenadas, llamadas «componentes» del tensor. Existen entonces ciertas reglas mediante las cuales pueden calcularse dichas componentes para un nuevo sistema de coordenadas, si se conocen para el sistema de coordenadas original. Estos objetos, en lo sucesivo llamados tensores, están además caracterizados por el hecho de que las ecuaciones de transformación para sus componentes son lineales y homogéneas. En consecuencia, todas las componentes en el nuevo sistema se anulan si todas se anulan en el sistema original. Si, por lo tanto, una ley de la naturaleza se expresa igualando a cero todas las componentes de un tensor, dicha ley es generalmente covariante. Examinando las leyes de formación de tensores adquirimos los medios de formular leyes generalmente covariantes.

5. CUADRIVECTORES CONTRAVARIANTES Y COVARIANTES

Cuadrivectores contravariantes. El elemento de línea está definido por las cuatro «componentes» dx_ν, para los que la ley de transformación se expresa por la ecuación

(5)

Las dx’_σ se expresan como funciones lineales y homogéneas de las dx_ν. De aquí podemos considerar estas diferenciales de coordenadas como las componentes de un «tensor» del tipo particular que llamamos cuadrivector contravariante. Cualquier objeto que está definido con relación al sistema de coordenadas por cuatro cantidades A^ν, y que se transforma por la misma ley

(5a)

se llama también un cuadrivector contravariante. De (5a) se sigue inmediatamente que las sumas (A^σ ± B^σ) son también componentes de un cuadrivector, si A^σ y B^σ lo son. Relaciones correspondientes válidas para todos los «tensores» deben introducirse posteriormente. (Regla para la adición y sustracción de tensores).

Cuadrivectores covariantes. Llamamos a cuatro cantidades A_ν componentes de un cuadrivector covariante si para cualquier elección arbitraria del cuadrivector contravariante B_ν

Σ_ν A_ν B^ν = Invariante.

(6)

La ley de transformación de un cuadrivector covariante se sigue de esta definición. En efecto, si sustituimos B^ν en el segundo miembro de la ecuación

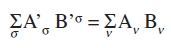
por la expresión resultante de la inversión de (5a),

obtenemos

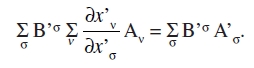
Puesto que esta ecuación es verdadera para valores arbitrarios de las B’^σ, se sigue que la ley de transformación es

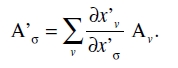
(7)

Nota sobre una forma simplificada de escribir las expresiones. Una ojeada a las ecuaciones de esta sección muestra que siempre hay una suma con respecto a los índices que aparecen dos veces bajo un signo de suma (e. g. el índice ν en (5)), y sólo con respecto a índices que aparecen dos veces. Por lo tanto, es posible, sin pérdida de claridad, omitir el signo de suma. En su lugar introducimos el siguiente convenio: si un índice aparece dos veces en un término de una expresión, siempre debe sumarse sobre el mismo a menos que se afirme expresamente lo contrario.

La diferencia entre cuadrivectores covariantes y contravariantes reside en la ley de transformación ((7) o (5) respectivamente). Ambas forma son tensores en el sentido del comentario general anterior. Ahí reside su importancia. Siguiendo a Ricci y Levi-Civita denotamos el carácter contravariante colocando el índice arriba, y el carácter covariante colocándolo abajo.

6. TENSORES DE SEGUNDO RANGO Y SUPERIORES

Tensores contravariantes. Si formamos los dieciséis productos A^µν de las componentes A^µ y B^ν de dos cuadrivectores contravariantes

A^µν = A^µ B^ν.

(8)

entonces por (8) y (5a) A^µν satisface la ley de transformación

(9)

Llamamos tensor contravariente de segundo rango a un objeto que está descrito con relación a cualquier sistema de referencia por dieciséis cantidades que satisfacen la ley de transformación (9). No todos los tensores semejantes pueden formarse de acuerdo con (8) a partir de dos cuadrivectores, pero se demuestra fácilmente que cualesquiera dieciséis A^µν dados pueden representarse como sumas de los A^µB^ν de cuatro pares de cuadrivectores adecuadamente seleccionados. De aquí podemos probar casi todas las leyes que se aplican al tensor de segundo rango definido por (9) de la forma más simple demostrándolas para los tensores especiales del tipo (8).

Tensores contravariantes de cualquier rango. Es evidente que, en línea con (8) y (9), también pueden definirse tensores contravariantes de tercer rango y superiores con 4³ componentes, y así sucesivamente. De la misma forma, se sigue de (8) y (9) que el cuadrivector contravariante puede tomarse en este sentido como un tensor contravariante de primer rango.

Tensores covariantes. Por otra parte, si tomamos los dieciséis productos A_µν de dos cuadrivectores covariantes A_µ y B_ν

A_µν = A_µ B_ν,

(10)

la ley de transformación para éstos es

(11)

Esta ley de transformación define el tensor covariante de segundo rango. Todos nuestros comentarios previos sobre tensores contravariantes se aplican igualmente a tensores covariantes.

NOTA. Es conveniente tratar los escalares (o invariantes) como tensores contravariantes o tensores covariantes de rango cero.

Tensores mixtos. También podemos definir un tensor de segundo rango del tipo

A^ν_µ = A_µ B^ν.

(12)

que es covariante con respecto al índice µ y contravariante con respecto al índice ν. Su ley de transformación es

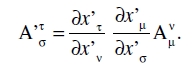
(13)

Naturalmente, existen tensores mixtos con cualquier número de índices de carácter covariante y cualquier número de índices de carácter contravariante. Los tensores covariantes y contravariantes pueden considerarse como casos especiales de tensores mixtos.

Tensores simétricos. Un tensor contravariante, o un tensor covariante, de segundo rango o superior se llama simétrico si dos componentes, que se obtienen una de otra por el intercambio de dos índices, son iguales. El tensor A^µν, o el tensor A_µν, son así simétricos si para cualquier combinación de los índices µ, ν,

A^µν = A^νµ,

(14)

o respectivamente,

A_µν = A_νµ.

(14a)

Hay que demostrar que la simetría así definida es una propiedad independiente del sistema de referencia. De hecho, se sigue de (9), cuando se tiene en cuenta (14), que

La penúltima ecuación depende del intercambio de los índices de suma µ y ν, i. e. meramente de un cambio de notación.

Tensores antisimétricos. Un tensor contravariante o un tensor covariante de segundo, tercero o cuarto rango se llama antisimétrico si dos componentes, que se obtienen una de otra por el intercambio de dos índices, son iguales y de signo opuesto. El tensor A^µν, o el tensor A_µν, es, por lo tanto, antisimétrico si siempre

A^µν = –A^νµ,

(15)

o respectivamente,

A_µν = –A_νµ.

(15a)

De las dieciséis componentes A^µν, las cuatro componentes A^µµ se anulan; el resto son iguales y de signo opuesto por pares, de modo que existen sólo seis componentes numéricamente diferentes (un seis-vector). Análogamente vemos que el tensor antisimétrico de tercer rango A^µνσ tiene sólo cuatro componentes numéricamente diferentes, mientras que el tensor antisimétrico A^µνστ tiene sólo una. No existen tensores antisimétricos de rango mayor que el cuarto en un continuo de cuatro dimensiones.

7. PRODUCTO DE TENSORES

Producto exterior de tensores. A partir de las componentes de un tensor de rango n y de un tensor de rango m, obtenemos las componentes de un tensor de rango n + m multiplicando cada componente de un tensor por cada componente del otro. Así, por ejemplo, los tensores T aparecen a partir de los tensores A y B de diferentes tipos

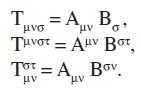
La demostración del carácter tensorial de T está dada directamente por las representaciones (8), (10), (12), o por las leyes de transformación (9), (11), (13). Las propias ecuaciones (8), (10), (12) son ejemplos de producto exterior de tensores de primer rango.

«Contracción» de un tensor mixto. A partir de cualquier tensor mixto podemos formar un tensor cuyo rango es menor en dos unidades, igualando un índice de carácter covariante con uno de carácter contravariante, y sumando con respecto a dicho índice («contracción»). Así, por ejemplo, a partir del tensor mixto de cuarto rango 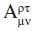, obtenemos el tensor mixto de segundo rango

y a partir de éste, por una segunda contracción, el tensor de rango cero

La demostración de que el resultado de la contracción posee realmente el carácter tensorial está dada o bien por la representación de un tensor de acuerdo con la generalización de (12) en combinación con (6), o bien por la generalización de (13).

Productos interior y mixto de tensores. Éstos consisten en una combinación de producto exterior con contracción.

Ejemplos. A partir del tensor covariante de segundo rango A_µν y el tensor contravariante de primer rango B^σ formamos por producto exterior el tensor mixto

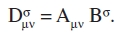
Por contracción con respecto a los índices ν y σ, obtenemos el cuadrivector covariante

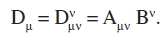
Llamamos a esto el producto interno de los tensores A_µν y B^σ. Análogamente, a partir de los tensores A_µν y B^στ, formamos por producto exterior y doble contracción el producto interior A_µν B^µν. Por producto exterior y una contracción, obtenemos a partir de A_µν y B^στ el tensor mixto de segundo rango D^τ_µ = A_µν B^ντ. Esta operación puede caracterizarse apropiadamente como una operación mixta, siendo «exterior» con respecto a los índices µ y τ, e «interior» con respecto a los índices ν y σ.

Ahora demostramos una proposición que suele ser útil como evidencia del carácter tensorial. A partir de lo que se acaba de explicar, A_µν B^µν es un escalar si A_µν y B^στ son tensores. Pero también podemos hacer la siguiente afirmación: si A_µν B^µν es un escalar para cualquier elección del tensor B^µν, entonces A_µν tiene carácter tensorial. En efecto, por hipótesis, para cualquier sustitución

A’_στ B’^στ = A_µν B^µν.

pero por una inversión de (9)

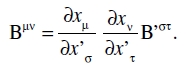
Esto, insertado en la ecuación anterior, da

Esto sólo puede satisfacerse para valores arbitrarios B’^στ si se anula el paréntesis. El resultado se sigue entonces por la ecuación (11). Esta regla se aplica correspondientemente a tensores de cualquier rango y carácter, y la demostración es análoga en todos los casos.

La regla también puede demostrarse de esta forma: si B^µ y C^ν son vectores cualesquiera, y si, para todos los valores de éstos, el producto interior A_µν B^µ C^ν es un escalar, entonces A_µν es un tensor covariante. Esta última proposición también es válida incluso si sólo es correcta la afirmación más especial: que con cualquier elección del cuadrivector B^µ, el producto interior A_µν B^µ C^ν es un escalar, si además se sabe que A_µν satisface la condición de simetría A_µν = A_νµ. En efecto, por el método dado antes demostramos el carácter tensorial de (A_µν + A_νµ), y de esto se sigue el carácter tensorial de A_µν debido a la simetría. Esto también puede generalizarse fácilmente al caso de tensores covariantes y contravariantes de cualquier rango.

Finalmente, a partir de lo que se ha demostrado se sigue la siguiente ley que también puede generalizarse para tensores cualesquiera: si para cualquier elección del cuadrivector B^ν las cantidades A_µν B^ν forman un tensor de primer rango, entonces A_µν es un tensor de segundo rango. En efecto, si C^µ es cualquier cuadrivector, entonces, debido al carácter tensorial de A_µν B^ν, el producto interior A_µν B^ν C^µ es un escalar para cualquier elección de los dos cuadrivectores B^ν y C^µ. De lo cual se sigue la proposición.

8. ALGUNOS ASPECTOS DEL TENSOR FUNDAMENTAL g_µν

El tensor fundamental covariante. En la expresión invariante para el cuadrado del elemento de línea

ds² = g_µνdx_µdx_ν ,

la parte que desempeñan las dx_µ es la de un vector contravariante que puede escogerse a voluntad. Puesto que además g_µν = g_νµ, de las consideraciones de la sección precedente se sigue que g_µν es un tensor covariante de segundo rango. Le llamamos «tensor fundamental». En lo que sigue deducimos algunas propiedades de este tensor que, es cierto, se aplican a cualquier vector de segundo rango. Pero puesto que el tensor fundamental desempeña un papel especial en nuestra teoría, que tiene su base física en el efecto peculiar de la gravitación, sucede que las relaciones que se van a desarrollar son de importancia para nosotros sólo en el caso del tensor fundamental.

El tensor fundamental contravariante. Si en el determinante formado por los elementos g_µν tomamos el cofactor de cada uno de los g_µν y lo dividimos por el determinante g = |g_µν|, obtenemos ciertas cantidades g^µν(= g^νµ) que, como demostraremos, forman un tensor contravariante.

Por una conocida propiedad de los determinantes

g_µσ g^νσ = δ^ν_µ ,

(16)

donde el símbolo δ_µ^ν denota 1 o 0, según µ = ν o µ≠ν.

En lugar de la expresión anterior para ds² podemos escribir

g_µσ δ^σ_ν dx_µ dx_ν

o, por (16)

g_µσ g_ντ g^στ dx_µ dx_ν .

Pero, por las reglas del producto de la sección precedente, las cantidades

dξ_σ = g_µσ dx_µ

forman un cuadrivector covariante, y de hecho un vector arbitrario, puesto que las dx_µ son arbitrarias. Introduciendo esto en nuestra expresión obtenemos

ds² = g^στ dξ_σ dξ_τ .

Puesto que esto, con la elección arbitraria del vector dξ_σ es un escalar, y g^στ por definición es simétrico en los índices σ y τ, se sigue de los resultados de la sección precedente que g^στ es un tensor contravariante.

Se sigue además de (16) que δ^ν_µ es también un tensor, al que podemos llamar el tensor fundamental mixto.

El determinante del tensor fundamental. Por la regla de multiplicación de determinantes

|g_µα g^αν| = |g_µα| X |g^αν|.

Por otra parte

|g_µα g^αν| = |δ_µ^ν| = 1.

Se sigue por consiguiente que

|g_µν| X |g^µν| = 1.

(17)

El volumen escalar. Buscamos primero la ley de transformación del determinante g = |g_µν|. De acuerdo con (11)

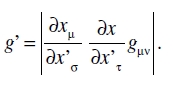
De aquí, por una doble aplicación de la regla para la multiplicación de determinantes se sigue que

o

Por otra parte, la ley de transformación del elemento de volumen

dτ = ∫ dx₁ dx₂ dx₃ dx₄

es, de acuerdo con el teorema de Jacobi

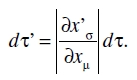
Multiplicando las dos últimas ecuaciones obtenemos

(18)

En lugar de √g , en lo que sigue introducimos la cantidad √–g, que es siempre real debido al carácter hiperbólico del continuo espacio-temporal. El invariante √–gdτ es igual a la magnitud del elemento de volumen tetradimensional en el sistema de referencia «local», medido con reglas rígidas y relojes en el sentido de la teoría de la relatividad especial.

Nota sobre el carácter del continuo espacio-temporal. Nuestra hipótesis de que la teoría de la relatividad especial siempre puede aplicarse a una región infinitamente pequeña, implica que ds² siempre puede expresarse de acuerdo con (1) por medio de cantidades reales dX₁ ... dX₄. Si denotamos por dt₀ el elemento de volumen «natural» dX₁, dX₂, dX₃, dX₄, entonces

dτ₀ = √–g dτ.

(18a)

Si √–g fuera a anularse en un punto del continuo tetradimensional, ello significaría que en este punto un volumen «natural» infinitamente pequeño correspondería a un volumen finito en las coordenadas. Supongamos que nunca es así. Entonces g no puede cambiar de signo. Supondremos que en el sentido de la teoría de la relatividad especial, g tiene siempre un valor negativo finito. Ésta es una hipótesis respecto a la naturaleza física del continuo en consideración, y al mismo tiempo un convenio sobre la elección de coordenadas.

Pero si –g es siempre finito y positivo, es natural establecer la elección de coordenadas a posteriori de tal manera que esta cantidad sea siempre igual a la unidad. Veremos más adelante que mediante una restricción semejante de la elección de coordenadas es posible conseguir una simplificación importante de las leyes de la naturaleza.

En lugar de (18), tenemos entonces simplemente dτ’=dτ, de lo cual, en vista del teorema de Jacobi, se sigue que

(19)

Así pues, con esta elección de coordenadas, sólo son permisibles sustituciones para las que el determinante es la unidad.

Pero sería erróneo creer que este paso indica un abandono parcial del postulado de relatividad general. No preguntamos: «¿Cuáles son las leyes de la naturaleza que son covariantes frente a todas las sustituciones para las que el determinante es la unidad?», sino que nuestra pregunta es: «¿Cuáles son las leyes de la naturaleza generalmente covariantes?». Hasta que no las hayamos formulado no podemos simplificar su expresión mediante una elección particular del sistema de referencia.

La formación de nuevos tensores por medio del tensor fundamental. El producto interior, exterior y mixto de un tensor por el tensor fundamental da tensores de diferente carácter y rango. Por ejemplo,

A^µ = g^µσ A_σ ,

A = g_µν A^µν.

Pueden señalarse especialmente las siguientes formas:

A^µν = g^µα g^νβ A_αβ ,

A_µν = g_µα g_νβ A^αβ.

(los «complementos» de tensores covariantes y contravariantes respectivamente), y

B_µν = g_µν g^αβ A_αβ .

Llamamos B_µν al tensor reducido asociado con A_µν. Análogamente,

B^µν = g^µν g_αβ A^αβ.

Puede notarse que g^µν no es entonces otra cosa que el complemento de g_µν, puesto que

g^µα g^νβ g_αβ = g^µα δ^ν_α = g^µν.

9. LA ECUACIÓN DE LA LÍNEA GEODÉSICA. EL MOVIMIENTO DE UNA PARTÍCULA

Puesto que el elemento de línea ds está definido independientemente del sistema de coordenadas, la línea trazada entre dos puntos P y P’ del continuo tetradimensional de tal manera que ∫ds es estacionario —una línea geodésica— tiene un significado que también es independiente de la elección de coordenadas. Su ecuación es

(20)

Realizando la variación de la manera habitual, obtenemos a partir de esta ecuación cuatro ecuaciones diferenciales que definen la línea geodésica; esta operación se insertará por compleción. Sea λ una función de las coordenadas x_ν, y defina ésta una familia de superficies que intersectan a la línea geodésica requerida así como a todas las líneas en la inmediata vecindad de ella que pasan por los puntos P y P’. Cualquiera de esta líneas puede suponerse entonces dada expresando sus coordenadas x_ν como funciones de λ. Indiquemos con el símbolo δ la transición de un punto de la geodésica requerida al punto correspondiente a la misma λ en una línea vecina. Entonces para (20) podemos sustituir

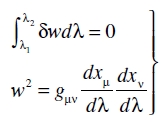
(20a)

Pero puesto que

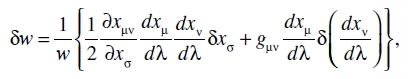
y

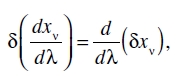
obtenemos a partir de (20a), tras una integración parcial,

donde

(20b)

Puesto que los valores de δx_σ son arbitrarios, se sigue de ello que

κ_σ = 0

(20c)

son las ecuaciones de la línea geodésica.

Si ds no se anula a lo largo de la línea geodésica podemos escoger la «longitud del arco» s, medida a lo largo de la línea geodésica, como parámetro λ. Entonces w = 1, y en lugar de (20c) obtenemos

o, por un mero cambio de notación,

(20d)

donde, siguiendo a Christoffel, hemos escrito

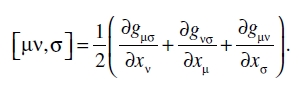
(21)

Finalmente, si multiplicamos (20d) por g^στ (producto exterior con respecto a τ, interior con respecto a σ), obtenemos las ecuaciones de la línea geodésica en la forma

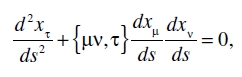
(22)

donde, siguiendo a Christoffel, hemos hecho

{µν, τ} = g^τα [µν, α].

(23)

10. LA FORMACIÓN DE TENSORES POR DIFERENCIACIÓN

Con la ayuda de la ecuación de la línea geodésica podemos ahora deducir fácilmente las leyes mediante las cuales pueden formarse nuevos tensores a partir de los viejos por diferenciación. Por este medio somos capaces de formular por primera vez ecuaciones diferenciales generalmente covariantes. Alcanzamos este objetivo por aplicación repetida de la siguiente ley simple:

Si en nuestro continuo tenemos una curva dada, cuyos puntos están especificados por la distancia de arco s medida a partir de un punto fijo sobre la curva, y si, además, φ es una función invariante del espacio, entonces dφ/ds también es un invariante. La demostración descansa en esto, que ds es un invariante tanto como dφ.

Puesto que

y por consiguiente

es también un invariante, y un invariante para todas las curvas que parten de un punto del continuo, es decir, para cualquier elección del vector dx_µ. De aquí se sigue inmediatamente que

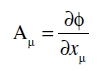
(24)

es un cuadrivector covariante: el «gradiente» de φ.

De acuerdo con nuestra regla, el cociente de diferenciales

tomado sobre una curva es análogamente un invariante. Insertando el valor de ψ, obtenemos en primer lugar

La existencia de un tensor no puede deducirse inmediatamente a partir de esto. Pero si podemos tomar la curva a lo largo de la cual hemos diferenciado como una geodésica, obtenemos al sustituir d²x_ν/ds² a partir de (22),

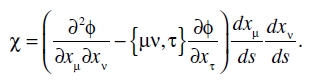
Puesto que podemos intercambiar el orden de las diferenciaciones, y puesto que por (23) y (21) {µν, τ} es simétrico en µ y ν, se sigue que la expresión entre paréntesis es simétrica en µ y ν. Puesto que una línea geodésica puede trazarse en cualquier dirección a partir de un punto del continuo, y por consiguiente dx_µ/ds es un cuadrivector con la razón de sus componentes arbitraria, se sigue de los resultados del enunciado 7 que

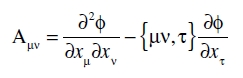
(25)

es un tensor covariante de segundo rango. Por lo tanto, hemos llegado a este resultado: a partir del tensor covariante de primer rango

podemos formar, por diferenciación, un tensor covariante de segundo rango

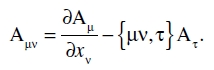
(26)

Llamamos al tensor A_µν la «extensión» (derivada covariante) del tensor A_µ. En primer lugar podemos demostrar inmediatamente que la operación conduce a un tensor, incluso si el vector A_µ no puede representarse como un gradiente. Para verlo, observamos en primer lugar que

es un vector covariante, si ψ y φ son escalares. La suma de cuatro de estos términos

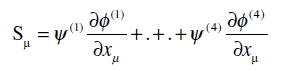
es también un vector covariante, si ψ⁽¹⁾, φ⁽¹⁾.... ψ⁽⁴⁾, φ⁽⁴⁾ son escalares. Pero es evidente que cualquier vector covariante puede representarse en la forma S_µ. Pues, si A_µ es un vector cuyas componentes son cualesquiera funciones dadas de las x_ν, sólo tenemos que poner (en términos del sistema de coordenadas seleccionado)

ψ⁽¹⁾ = A₁, φ⁽¹⁾ = x₁,

ψ ⁽²⁾ = A₂, φ⁽²⁾ = x₂,

ψ ⁽³⁾ = A₃, φ⁽³⁾ = x₃,

ψ⁽⁴⁾ = A₄, φ⁽⁴⁾ = x₄,

para asegurar que S_µ será igual a A_µ.

Por consiguiente, para demostrar que A_µν es un tensor si se inserta cualquier vector covariante en el segundo miembro de A_µ, sólo tenemos que demostrar que esto es así para el vector S_µ. Pero para este último propósito es suficiente, como nos enseña si damos una ojeada al segundo miembro de (26), ofrecer la demostración para el caso

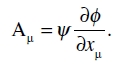
Ahora el segundo miembro de (25) multiplicado por ψ,

es un tensor. Análogamente

siendo el producto exterior de dos vectores, es un tensor. Mediante suma, se sigue el carácter tensorial de

Como mostrará una ojeada a (26), esto completa la demostración para el vector

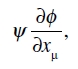
y en consecuencia, a partir de lo que ya se ha demostrado, para cualquier vector A_µ.

Mediante la extensión del vector, podemos definir fácilmente la «extensión» de un tensor covariante de cualquier rango. Esta operación es una generalización de la extensión de un vector. Nos restringimos al caso de un tensor de segundo rango, puesto que esto basta para dar una idea clara de la ley de formación.

Como ya se ha observado, cualquier tensor covariante de segundo rango puede representarse⁵ como suma de tensores del tipo A_µ B_ν. Por lo tanto, será suficiente con deducir la expresión para la extensión de un tensor de este tipo especial. Por (26) las expresiones son tensores. Por producto exterior de la primera por B_ν, y de la segunda por A_µ, obtenemos en cada caso un tensor de tercer rango. Sumándolos, tenemos el tensor de tercer rango

(27)

donde hemos puesto A_µν = A_µ B_ν. Puesto que el segundo miembro de (27) es lineal y homogéneo en las A_µν y sus primeras derivadas, esta ley de formación lleva a un tensor, no sólo en el caso de un tensor del tipo A_µ B_ν sino también en el caso de una suma de tales tensores, i. e., en el caso de cualquier tensor covariante de segundo rango. Llamamos a A_µνσ la extensión del tensor A_µν.

Es evidente que (26) y (24) conciernen sólo a casos especiales de extensión (la extensión de los tensores de rango uno y cero respectivamente).

En general, todas las leyes especiales de formación de tensores están incluidas en (27) en combinación con el producto de tensores.

11. ALGUNOS CASOS DE ESPECIAL IMPORTANCIA

El tensor fundamental. Demostraremos primero algunos lemas que serán útiles en lo sucesivo. Por la regla para la diferenciación de determinantes

dg = g^µν gdg_µν = –g_µν gdg^µν.

(28)

El último miembro se obtiene del penúltimo si se tiene en cuenta que g_µνdg^µ’^ν= δ^µ’_µ de modo que g_µν g^µν = 4, y en consecuencia

g_µν dg^µν + g^µν gdg_µν = 0.

De (28) se sigue que

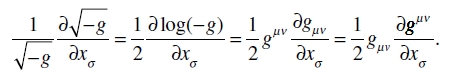
(29)

Además, de g_µσg^νσ= δ_µ^ν, se sigue por diferenciación que

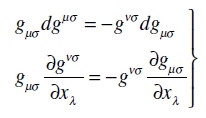
(30)

De éstos, por producto mixto por g^στ y g_νλ respectivamente, y un cambio de notación para los índices, tenemos

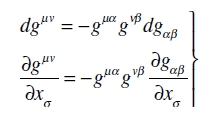
(31)

y

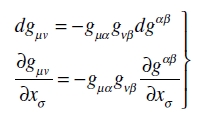
(32)

La relación (31) admite una transformación, de la que también haremos uso con frecuencia. De (21)

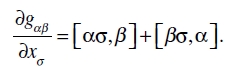
(33)

Insertando esto en la segunda fórmula de (31), obtenemos, en vista de (23)

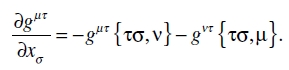
(34)

Sustituyendo el segundo miembro de (34) en (29) tenemos

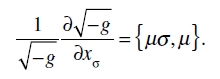
(29a)

La «divergencia» de un vector contravariante. Si tomamos el producto interior de (26) por el tensor fundamental contravariante g^µν, el segundo miembro, después de una transformación del primer término, toma la forma

De acuerdo con (31) y (29), el último término de esta expresión puede escribirse

Puesto que los símbolos de los índices de suma son mudos, los primeros dos términos de esta expresión cancelan el segundo de la expresión inmediatamente anterior. Si entonces escribimos g^µνA_µ = A^ν, de modo que A^ν, como A_µ, es un vector arbitrario, obtenemos finalmente

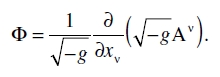
(35)

Este escalar es la divergencia del vector contravariante A^ν.

El «rotacional» de un vector covariante. El segundo término en (26) es simétrico en los índices µ y ν. Por lo tanto A_µν – A_νµ es un tensor antisimétrico construido de forma particularmente simple. Obtenemos

(36)

Extensión antisimétrica de un seis-vector. Aplicando (27) a un tensor antisimétrico de segundo rango A_µν, formando además las dos ecuaciones que aparecen mediante permutaciones cíclicas de los índices y sumando estas tres ecuaciones, obtenemos el tensor de tercer rango

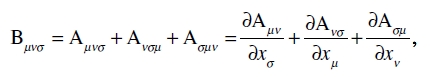
(37)

que es fácil probar que es antisimétrico.

La divergencia de un seis-vector. Tomando el producto mixto de (27) por g^µαg^νβ, obtenemos también un tensor. El primer término del segundo miembro de (27) puede escribirse en la forma

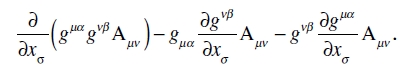
Si escribimos A_σ^αβ para g^µαg^νβ A_µνσ y A^αβ para g^µα g^νβ A^µν, y en el primer término transformado sustituimos

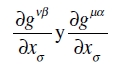
por sus valores dados por (34), resulta del segundo miembro de (27) una expresión consistente en siete términos, cuatro de los cuales se cancelan, y queda

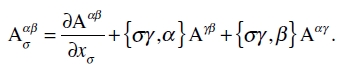
(38)

Ésta es la expresión para la extensión de un tensor contravariante de segundo rango, y también pueden formarse expresiones correspondientes para la extensión de tensores contravariantes de rango superior e inferior.

Notemos que de forma análoga también podemos formar la extensión de un tensor mixto:

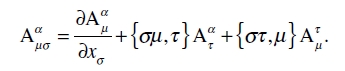
(39)

Contrayendo (38) con respecto a los índices β y σ (producto interior por δ^σ_µ), obtenemos el vector

Debido a la simetría de {βγ, α} con respecto a los índices β y γ, el tercer término del segundo miembro se anula, si A^αβ es, como supondremos, un tensor antisimétrico. El segundo término admite ser transformado de acuerdo con (29a). Así obtenemos

(40)

Ésta es la expresión para la divergencia de un seis-vector contravariante.

La divergencia de un tensor mixto de segundo rango. Contrayendo (39) con respecto a los índices α y σ, y teniendo en consideración (29a), obtenemos

(41)

Si introducimos en el último término el tensor contravariante A^ρσ = g^ρτ A_τ^σ, toma la forma

Si, además, el tensor A^ρσ es simétrico, esto se reduce a

Si en lugar de A^ρσ hubiéramos introducido el tensor covariante A_ρσ = g_ρα g_σβ A^αβ, que es también simétrico, el último término, en virtud de (31), tomaría la forma

En el caso de simetría en cuestión, (41) puede por lo tanto ser reemplazado por las dos formas

(41a)

(41b)

que tenemos que emplear más adelante.

12. EL TENSOR DE RIEMANN-CHRISTOFFEL

Buscamos ahora el tensor que puede obtenerse a partir del tensor fundamental solamente, por diferenciación. A primera vista, la solución parece obvia. Coloquemos el tensor fundamental de las g_µν en (27) en lugar de cualquier tensor dado A_µν, y así tenemos un nuevo tensor, a saber, la extensión del tensor fundamental. Pero fácilmente nos convencemos de que esta extensión es idénticamente nula. Alcanzamos nuestro objetivo, sin embargo, de la siguiente manera. En (27) colocamos

i. e. la extensión del cuadrivector A_µ. Entonces (nombrando los índices de forma algo diferente) tenemos el tensor de tercer rango

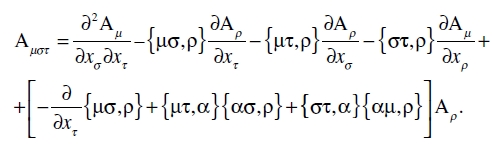
Esta expresión sugiere formar el tensor A_µστ – A_µτσ. Pues, si lo hacemos, los términos siguientes de la expresión para A_µστ cancelan a los de A_µτσ, el primero, el cuarto y el miembro correspondiente al último término entre paréntesis cuadrados; puesto que todos estos son simétricos en σ y τ. Lo mismo es válido para la suma del segundo y tercer términos. Así obtenemos

A_µστ – A_µτσ = B^ρ_µστ A_ρ,

(42)

donde

(43)

La característica esencial del resultado es que en el segundo miembro de (42) las A_ρ aparecen solas, sin sus derivadas. Del carácter tensorial de A_µστ – A_µτσ junto con el hecho de que A_ρ es un vector arbitrario, se sigue, por el enunciado 7, que B^σ_µστ es un tensor (el tensor de Riemann-Christoffel).

La importancia matemática de este vector es la siguiente: Si el continuo es de naturaleza tal que existe un sistema de coordenadas con referencia al cual las g_µν son constantes, entonces todas las B^ρ_µστ se anulan. Si escogemos cualquier nuevo sistema de coordenadas en lugar de las originales, las g_µν allí referidas no serán constantes, pero a consecuencia de su carácter tensorial las componentes transformadas de B^ρ_µστ seguirán siendo nulas en el nuevo sistema. Así, la anulación del tensor de Riemann es una condición necesaria para que, por una elección apropiada del sistema de referencia, las g_µν puedan ser constantes. En nuestro problema esto corresponde al caso en el que,⁶ con una elección adecuada del sistema de referencia, la teoría de la relatividad especial es válida para una región finita del continuo.

Contrayendo (43) con respecto a los índices τ y ρ obtenemos el tensor covariante de segundo rango

G_µν = B^ρ_µνρ = R_µν + S_µν

donde

(44)

Nota sobre la elección de coordenadas. Ya se ha observado en el enunciado 8, en conexión con la ecuación (18a), que la elección de las coordenadas puede hacerse ventajosamente de modo que √−g = 1. Una ojeada a las ecuaciones obtenidas en las dos últimas secciones muestra que con tal elección las leyes de formación de tensores experimentan una importante simplificación. Esto se aplica en particular a G_µν, el tensor que acabamos de desarrollar, que desempeña un papel fundamental en la teoría a establecer. Pues esta particularización de la elección de coordenadas produce la anulación de S_µν, de modo que el tensor G_µν se reduce a R_µν.

Debido a esto, en lo sucesivo daré todas las relaciones en la forma simplificada que trae consigo esta particularización de la elección de coordenadas. Será entonces fácil volver a las ecuaciones generalmente covariantes si en un caso especial parece deseable.

C. TEORÍA DEL CAMPO GRAVITATORIO

13. ECUACIONES DE MOVIMIENTO DE UN PUNTO MATERIAL EN EL CAMPO GRAVITATORIO. EXPRESIÓN PARA LAS COMPONENTES DE CAMPO DE LA GRAVITACIÓN

Un cuerpo libremente movible no sometido a fuerzas externas se mueve, según la teoría de la relatividad especial, uniformemente y en línea recta. Éste es también el caso, según la teoría de la relatividad general, para una parte de un espacio tetradimensional en la que el sistema de coordenadas K₀, puede ser, y lo es, escogido de modo que ellas tienen los valores constantes especiales dados en (4).

Si consideramos precisamente este movimiento desde cualquier sistema de coordenadas escogido K₁, el cuerpo, observado desde K₁, se mueve, según las consideraciones de 2, en un campo gravitatorio. La ley de movimiento con respecto a K₁ resulta sin dificultad de la siguiente consideración. Con respecto a K₀ la ley de movimiento corresponde a una línea recta tetradimensional, i. e. a una línea geodésica. Ahora bien, puesto que la línea geodésica está definida independientemente del sistema de referencia, su ecuación será también la ecuación de movimiento del punto material con respecto a K₁. Si hacemos

Γ^τ_µν = –{µν, τ}

(45)

la ecuación de movimiento del punto con respecto a K₁ se convierte en

(46)

Planteamos ahora la hipótesis, que se sugiere inmediatamente, de que este sistema de coordenadas covariante define también el movimiento del punto en el campo gravitatorio en el caso en que no hay ningún sistema de referencia K₀ con respecto al cual la teoría de la relatividad especial es válida en una región finita. Tenemos más justificación para esta hipótesis por cuanto (46) contiene sólo derivadas primeras de las g_µν, entre las cuales no subsisten relaciones ni siquiera en el caso especial de la existencia de K₀.⁷

Si las Γ^τ_µν se anulan, entonces el punto se mueve uniformemente en una línea recta. Por lo tanto, estas cantidades condicionan la desviación del movimiento respecto de la uniformidad. Son las componentes del campo gravitatorio.

14. LAS ECUACIONES DE CAMPO DE LA GRAVITACIÓN EN AUSENCIA DE MATERIA

En lo sucesivo hacemos una distinción entre «campo gravitatorio» y «materia» de esta manera: denotamos todo salvo el campo gravitatorio como «materia». Por lo tanto, nuestro uso de la palabra incluye no sólo la materia en el sentido ordinario, sino también el campo electromagnético.

Nuestra próxima tarea es encontrar las ecuaciones de campo de la gravitación en ausencia de materia. Aquí aplicamos de nuevo el método empleado en la sección precedente al formular las ecuaciones de movimiento del punto material. Un caso especial en el que las ecuaciones requeridas deben ser satisfechas en cualquier caso es el de la teoría de la relatividad especial, en el que las g_µν tienen ciertos valores constantes. Sea éste el caso en un cierto espacio finito en relación con un sistema de coordenadas definido K₀. Con respecto a este sistema todas las componentes del tensor de Riemann B^ρ_µστ, definido en (43), se anulan. Para el espacio en consideración se anulan entonces también en cualquier otro sistema de coordenadas.

Así pues, las ecuaciones requeridas del campo gravitatorio libre de materia deben ser satisfechas en cualquier caso si todas las B^ρ_µστ se anulan. Pero esta condición va demasiado lejos. En efecto, es evidente que, e. g., el campo gravitatorio generado por un punto material en su entorno no puede ciertamente ser «eliminado» por ninguna elección del sistema de coordenadas, i. e. no puede transformarse en el caso de g_µν constante.

Esto nos impulsa a exigir para el campo gravitatorio libre de energía que el tensor simétrico G_µν, derivado del tensor B^ρ_µστ, se anulará. Así, obtenemos diez ecuaciones para las diez cantidades g_µν, que se satisfacen en el caso especial de la anulación de todas la B^ρ_µστ. Con la elección que hemos hecho de un sistema de coordenadas, y teniendo en cuenta (44), las ecuaciones para el campo libre de materia son

(47)

Debe señalarse que existe sólo un mínimo de arbitrariedad en la elección de estas ecuaciones. Pues aparte de G_µν no hay ningún tensor de segundo rango que esté formado a partir de las g_µν y sus derivadas, no contenga derivaciones más altas que la segunda y sea lineal en dichas derivadas.⁸

Estas ecuaciones, que proceden, por el método de las puras matemáticas, del requisito de la teoría de la relatividad general, nos dan, en combinación con las ecuaciones de movimiento (46), en primera aproximación la ley de atracción de Newton, y en segunda aproximación la explicación del movimiento del perihelio del planeta Mercurio descubierto por Leverrier (tal como queda una vez que se han hecho correcciones para la perturbación). En mi opinión, estos hechos deben tomarse como una prueba convincente de la corrección de la teoría.

15. LA FUNCIÓN HAMILTONIANA PARA EL CAMPO GRAVITATORIO. LEYES DEL MOMENTO Y LA ENERGÍA

Para demostrar que las ecuaciones de campo corresponden a las leyes del momento y la energía, es más conveniente escribirlas en la siguiente forma hamiltoniana:

(47a)

donde, en la frontera de la región de integración tetradimensional finita que tenemos a la vista, las variaciones se anulan.

Primero tenemos que demostrar que la forma (47a) es equivalente a las ecuaciones (47). Para este fin consideramos H como una función de las g^µν y las g_ρ^µν (= δg^µν / δx_σ)

Entonces, en primer lugar

Pero

Los términos que aparecen de los dos últimos términos entre paréntesis redondos son de signo diferente, y resultan uno de otro (puesto que la denominación de los índices de suma carece de importancia) a través del intercambio de los índices µ y β. Se cancelan mutuamente en la expresión para δH, porque están multiplicados por la cantidad Γ^α_µβ que es simétrica respecto a los índices µ y β. Así pues, sólo queda por considerar el primer término entre paréntesis redondos, de modo que, teniendo en cuenta (31), obtenemos

Así pues

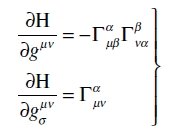
(48)

Realizando la variación en (47a), obtenemos en primer lugar

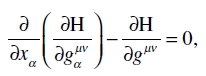
(47b)

que, debido a (48), coincide con (47), como había que demostrar.

Si multiplicamos (47b) por g_σ^µν, entonces, puesto que,

y, en consecuencia,

obtenemos la ecuación

o⁹

(49)

donde, debido a (48), la segunda ecuación de (47), y (34)

(50)

Hay que notar que t^α_σ no es un tensor; por otra parte (49) se aplica a todos los sistemas de coordenadas para los que √–g = 1. Esta ecuación expresa la ley de conservación del momento y de la energía para el campo gravitatorio. Realmente la integración de esta ecuación sobre un volumen tridimensional V da las cuatro ecuaciones

(49a)

donde l, m, n denotan los cosenos directores de la dirección de la normal interior en el elemento dS de la superficie frontera (en el sentido de la geometría euclidiana). Reconocemos en esto la expresión de las leyes de conservación en su forma habitual. A las cantidades t^α_σ las llamamos las «componentes de energía» del campo gravitatorio.

Ahora daré las ecuaciones (47) en una tercera forma, que es particularmente útil para una vívida comprensión de nuestro tema. Multiplicando las ecuaciones de campo (47) por g^νσ, éstas se obtienen en la forma «mixta». Notemos que

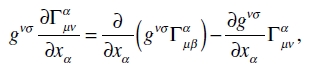
cuya magnitud, debido a (34), es igual a

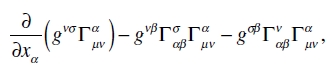
o (con símbolos diferentes para los índices de suma)

El tercer término de esta expresión se cancela con el que aparece del segundo término de las ecuaciones de campo (47); utilizando la relación (50), el segundo término puede escribirse

donde t = t^α_α. Así pues, en lugar de las ecuaciones (47) obtenemos

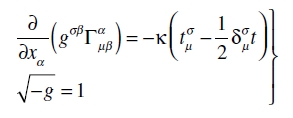
(51)

16. LA FORMA GENERAL DE LAS ECUACIONES DE CAMPO DE LA GRAVITACIÓN

Las ecuaciones de campo para el espacio libre de materia en el epígrafe 15 deben compararse con la ecuación de campo

∇²φ = 0

de la teoría de Newton. Exigimos que la ecuación correspondiente a la ecuación de Poisson

∇²φ = 4πλρ,

donde ρ denota la densidad de materia.

La teoría de la relatividad especial ha llevado a la conclusión de que la masa inerte no es ni más ni menos que energía, que encuentra su completa expresión matemática en un tensor simétrico de segundo rango, el tensor-energía. Así, en la teoría de la relatividad general debemos introducir un correspondiente tensor-energía de materia T^α_σ, que, como las componentes de energía t^α_σ [ecuaciones (49) y (50)] del campo gravitatorio, tendrán carácter mixto, pero pertenecerán a un tensor covariante simétrico.¹⁰

El sistema de ecuaciones (51) muestra cómo este tensor-energía (correspondiente a la densidad ρ en la ecuación de Poisson) debe introducirse en las ecuaciones de campo de la gravitación. Pues si consideramos un sistema completo (e. g. el sistema solar), la masa total del sistema, y por lo tanto también su acción gravitatoria total, dependerá de la energía total del sistema, y por lo tanto de la energía ponderable junto con la energía gravitatoria. Esto admitirá ser expresado introduciendo en (51), en lugar de las componentes de energía del campo gravitatorio solo, las sumas t_µ^σ + T_µ^σ de las componentes de energía de materia y de campo gravitatorio. Así, en lugar de (51) obtenemos la ecuación tensorial

(52)

donde hemos hecho T = T_µ^µ (escalar de Laue). Éstas son las requeridas ecuaciones generales de campo de gravitación en forma mixta. Trabajando hacia atrás a partir de ellas, tenemos en lugar de (47)

(53)

Hay que admitir que esta introducción del tensor-energía de materia no está justificada solamente por el postulado de relatividad. Por esta razón la hemos deducido aquí del requisito de que la energía del campo gravitatorio actuará gravitatoriamente de la misma manera que cualquier otro tipo de energía. Pero la razón más fuerte para la elección de estas ecuaciones reside en su consecuencia: que las ecuaciones de conservación del momento y la energía, correspondientes exactamente a las ecuaciones (49) y (49a), son válidas para las componentes de la energía total. Esto se demostrará en el epígrafe 17.

17. LAS LEYES DE CONSERVACIÓN EN EL CASO GENERAL

La ecuación (52) puede transformarse fácilmente de modo que el segundo término del segundo miembro se anule. Contraemos (52) con respecto a los índices µ y σ, y después de multiplicar la ecuación resultante por ¹⁄₂ δ_µ^σ, la restamos de (52). Esto da

(52a)

Sobre esta ecuación realizamos la operación δ/δx_σ. Tenemos

El primero y el tercer término de los paréntesis redondos producen contribuciones que se cancelan mutuamente, como puede verse intercambiando, en la contribución del tercer término, los índices de suma α y σ por una parte, y β y λ por otra. El segundo término puede remodelarse por (31), de modo que tenemos

(54)

El segundo término del primer miembro de (52a) da en primer lugar

o

Con la elección de coordenadas que hemos hecho, el término que se deriva del último término entre paréntesis redondos desaparece debido a (29). Los otros dos pueden combinarse, y juntos, por (31), dan

de modo que considerando (54) tenemos la identidad

(55)

De (55) y (52a), se sigue que

(56)

Así pues, resulta de nuestras ecuaciones de campo de gravitación que se satisfacen las leyes de conservación de momento y energía. Esto puede verse más fácilmente a partir de la consideración que lleva a la ecuación (49a); salvo que aquí, en lugar de las componentes de energía t^σ del campo gravitatorio, tenemos que introducir la totalidad de las componentes de energía de materia y campo gravitatorio.

18. LAS LEYES DE MOMENTO Y ENERGÍA PARA MATERIA, COMO CONSECUENCIA DE LAS ECUACIONES DE CAMPO

Multiplicando (53) por dg^µν/dx_σ obtenemos, por el método adoptado en el epígrafe 15, a la vista de la anulación de

la ecuación

o, en vista de (56),

(57)

La comparación con (41b) muestra que, con la elección del sistema de coordenadas que hemos hecho, esta ecuación afirma ni más ni menos que la anulación de la divergencia del tensor-energía material. Físicamente, la aparición del segundo término en el primer miembro muestra que las leyes de conservación de momento y energía no se aplican en sentido estricto para la materia solamente, o que se aplican sólo cuando las g^µν son constantes, i. e. cuando se anulan las intensidades de campo de gravitación. Este segundo término es una expresión para el momento, y para la energía, transferidos por unidad de volumen y unidad de tiempo desde el campo gravitatorio a la materia. Esto se manifiesta aún más claramente reescribiendo (57) en el sentido de (41) como

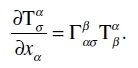
(57a)

El miembro derecho expresa el efecto energético del campo gravitatorio sobre la materia.

Así pues, las ecuaciones de campo de gravitación contienen cuatro condiciones que gobiernan el curso de los fenómenos materiales. Dan por completo las ecuaciones de los fenómenos materiales, si las últimas pueden caracterizarse por cuatro ecuaciones diferenciales mutuamente independientes.¹¹

D. FENÓMENOS MATERIALES

Las herramientas matemáticas desarrolladas en la parte B nos permiten generalizar inmediatamente las leyes físicas de la materia (hidrodinámica, electrodinámica de Maxwell), tal como están formuladas en la teoría de la relatividad especial, de modo que encajen en la teoría de la relatividad general. Cuando se hace así, el principio de relatividad general no nos ofrece una limitación adicional de posibilidades; pero nos familiariza con la influencia del campo gravitatorio sobre todos los procesos, sin que tengamos que introducir ninguna hipótesis nueva.

De aquí resulta que no es necesario introducir hipótesis definidas respecto a la naturaleza física de la materia (en el sentido más restringido). En particular sigue siendo una cuestión abierta si la teoría del campo electromagnético en conjunción con la del campo gravitatorio proporciona o no una base suficiente para la teoría de la materia. El postulado de relatividad general es incapaz en principio de decirnos nada sobre ello. Debe quedar por ver, durante la elaboración de la teoría, si la teoría electromagnética y la doctrina de la gravitación en colaboración pueden realizar lo que la primera es incapaz de hacer por sí sola.

19. ECUACIONES DE EULER PARA UN FLUIDO ADIABÁTICO SIN FRICCIÓN

Sean p y ρ dos escalares, al primero de los cuales llamamos «presión» y al segundo «densidad» de un fluido; y haya una ecuación que los relaciona. Sea el tensor simétrico contravariante

(58)

el tensor-energía contravariante del fluido. A él pertenece el tensor covariante

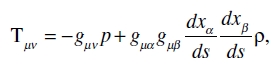
(58a)

así como el tensor mixto¹²

(58b)

Insertando el segundo miembro de (58b) en (57a) obtenemos las ecuaciones hidrodinámicas eulerianas de la teoría de la relatividad general. Éstas dan, en teoría, una solución completa al problema de movimiento, puesto que las cuatro ecuaciones (57a), junto con la ecuación dada entre p y ρ, y la ecuación

son suficientes, estando dadas las g_αβ, para definir las seis incógnitas

Si se desconocen también las g_µν, intervienen las ecuaciones (53). Hay once ecuaciones para definir las diez funciones g_µν, de modo que dichas funciones aparecen sobredeterminadas. Debemos recordar, sin embargo, que las ecuaciones (57a) ya están contenidas en las ecuaciones (53), de modo que las últimas representan sólo siete ecuaciones independientes. Hay una buena razón para esta falta de determinación, en cuanto que la amplia libertad de elección de coordenadas hace que el problema quede matemáticamente indeterminado en tal grado que tres de las funciones del espacio pueden ser escogidas a voluntad.¹³

20. ECUACIONES DEL CAMPO ELECTROMAGNÉTICO DE MAXWELL PARA EL ESPACIO LIBRE

Sean φ_ν las componentes de un vector covariante: el vector potencial electromagnético. A partir de ellas formamos, de acuerdo con (36) las componentes F_ρσ del seis-vector covariante del campo electromagnético, de acuerdo con el sistema de ecuaciones

(59)

Se sigue de (59) que el sistema de ecuaciones

(60)

es satisfecho, siendo su miembro izquierdo, por (37), un tensor antisimétrico de tercer rango. El sistema (60) contiene así esencialmente cuatro ecuaciones que se escriben como sigue

(60a)

Este sistema corresponde al segundo sistema de ecuaciones de Maxwell. Reconocemos esto inmediatamente haciendo

(61)

Entonces, en lugar de (60a) podemos poner, en la notación usual del análisis vectorial tridimensional

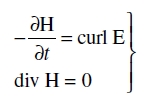
(60b)

Obtenemos el primer sistema de Maxwell generalizando la forma dada por Minkowski. Introducimos el seis-vector contravariante asociado con F^αβ

F^µν = g^µα g^νβ F_αβ ,

(62)

y también el vector contravariante J^µ de la densidad de corriente eléctrica. Entonces, teniendo en cuenta (40), las siguientes ecuaciones serán invariantes para cualquier sustitución cuyo invariante sea la unidad (en acuerdo con las coordenadas escogidas):

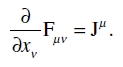
(63)

Sean

(64)

cuyas cantidades son iguales a las cantidades H_x ... E_z en el caso especial de la teoría de la relatividad restringida; si además

J¹ = j_x, J² = j_y, J³ = j_z, J⁴ = ρ,

obtenemos en lugar de (63)

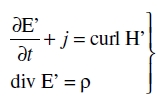
(63a)

Las ecuaciones (60), (62) y (63) constituyen así la generalización de las ecuaciones de campo de Maxwell para el espacio libre, con el convenio que hemos establecido con respecto a la elección de coordenadas.

Las componentes-de-energía del campo electromagnético. Formemos el producto interior

κ_σ = F_σµ J^µ.

(65)

Por (61) sus componentes, escritas a la manera tridimensional, son

(65a)

κ_σ es un vector covariante cuyas componentes son iguales al momento negativo, o, respectivamente, la energía, que se transfiera desde las masas eléctricas al campo electromagnético por unidad de tiempo y volumen. Si las masas eléctricas son libres, es decir, están bajo la sola influencia del campo electromagnético, el vector covariante κ_σ se anulará.

Para obtener las componentes de energía T^ν_σ del campo electromagnético, sólo tenemos que dar a la ecuación κ_σ = 0 la forma de la ecuación (57). A partir de (63) y (65) tenemos en primer lugar

El segundo término del segundo miembro, en virtud de (60), permite la transformación

cuya última expresión puede, por razones de simetría, escribirse también en la forma

Pero para esto podemos hacer

El primero de estos términos se escribe de forma más breve

el segundo, una vez llevada a cabo la diferenciación, y tras alguna simplificación, resulta

Juntando los tres términos obtenemos la relación

(66)

donde

La ecuación (66), si se anula κ_σ, es, debido a (30), equivalente a (57) o (57a) respectivamente. Por consiguiente, las T^ν_σ son las componentes de energía del campo electromagnético. Con la ayuda de (61) y (64) es fácil demostrar que estas componentes de energía del campo electromagnético en el caso de la teoría de la relatividad especial dan las bien conocidas expresiones de Maxwell-Poynting.

Ahora hemos deducido las leyes generales que son satisfechas por el campo gravitatorio y la materia, utilizando de manera consistente un sistema de coordenadas para el que √–g = 1. Con ello hemos conseguido una considerable simplificación de fórmulas y cálculos, sin dejar de satisfacer el requisito de covariancia general; pues hemos extraído nuestras ecuaciones de ecuaciones generalmente covariantes particularizando el sistema de coordenadas.

Aún queda la cuestión, no carente de interés formal, de si con una definición correspondientemente generalizada de las componentes de energía del campo gravitatorio y la materia, incluso sin particularizar el sistema de coordenadas, es posible formular leyes de conservación en forma de ecuación (56), y ecuaciones de campo de la gravitación de la misma naturaleza que (52) o (52a), de tal manera que a la izquierda tengamos una divergencia (en el sentido ordinario) y a la derecha la suma de las componentes de energía de materia y gravitación. He encontrado que en ambos casos es realmente así. Pero no creo que la comunicación de mis algo extensas reflexiones sobre este tema merezcan la pena, porque después de todo no nos dan nada que sea materialmente nuevo.

21. LA TEORÍA DE NEWTON COMO PRIMERA APROXIMACIÓN

Como ya ha sido mencionado más de una vez, la teoría de la relatividad especial como un caso especial de la teoría general se caracteriza porque las g_µν tienen los valores constantes (4). Por lo que ya se ha dicho, esto significa despreciar por completo los efectos de la gravitación. Llegamos a una aproximación más cercana a la realidad considerando el caso en donde las g_µν difieren de los valores de (4) en cantidades que son pequeñas comparadas con 1, y despreciando pequeñas cantidades de segundo orden y superiores. (Primer punto de vista de aproximación).

Hay que suponer, además, que en el territorio espacio-temporal en consideración las g_µν en el infinito espacial, con una elección de coordenadas adecuada, tienden hacia los valores (4); i. e. estamos considerando campos gravitatorios que pueden considerarse generados exclusivamente por materia en la región finita.

Podría pensarse que estas aproximaciones deben llevarnos a la teoría de Newton. Pero para este fin aún necesitamos aproximar las ecuaciones fundamentales desde un segundo punto de vista. Prestemos atención al movimiento de un punto material de acuerdo con las ecuaciones (16). En el caso de la teoría de la relatividad especial las componentes

pueden tomar cualquier valor. Esto significa que puede aparecer cualquier velocidad

que sea menor que la velocidad de la luz in vacuo. Si nos restringimos al caso que casi exclusivamente se ofrece a nuestra experiencia, de que v sea pequeña comparada con la velocidad de la luz, esto denota que las componentes

deben ser tratadas como cantidades pequeñas, mientras que dx₄/ds, a segundo orden de cantidades pequeñas, es igual a 1. (Segundo punto de vista de aproximación).

Notemos ahora que desde el primer punto de vista de aproximación las magnitudes Γ^τ_µν son todas pequeñas magnitudes de al menos primer orden. Una ojeada a (46) muestra así que en esta ecuación, desde el segundo punto de vista de aproximación, tenemos que considerar solamente términos para los que µ = ν = 4. Restringiéndonos a términos de orden más bajo obtenemos primero en lugar de (46) las ecuaciones

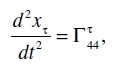
donde hemos hecho ds = dx₄ = dt; o con restricción a términos que desde el primer punto de vista de aproximación son de primer orden

Si además suponemos que el campo gravitatorio es un campo cuasi estático, limitándonos al caso en donde el movimiento de la materia que genera el campo gravitatorio es lento (en comparación con la velocidad de propagación de la luz), podemos despreciar en el segundo miembro las derivadas con respecto al tiempo en comparación con las derivadas con respecto a las coordenadas espaciales, de modo que tenemos

(67)

Ésta es la ecuación de movimiento del punto material según la teoría de Newton, en la que g₄₄ desempeña el papel del potencial gravitatorio. Lo que es notable en este resultado es que la componente g₄₄ del tensor fundamental define por sí sola, en primera aproximación, el movimiento del punto material.

Volvamos ahora a las ecuaciones de campo (53). Aquí debemos tener en cuenta que el tensor-energía de «materia» está definido casi exclusivamente por la densidad de materia en el sentido más estrecho, i. e. por el segundo término del segundo miembro de (58) [o, respectivamente (58a) o (58b)]. Si formamos la aproximación en cuestión, todas las componentes se anulan con la única excepción de T₄₄ = ρ = T. En el primer miembro de (53) el segundo término es una cantidad pequeña de segundo orden; el primero da, en la aproximación en cuestión,

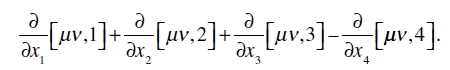
Para µ = ν = 4, esto da, con la omisión de los términos derivados con respecto al tiempo

La última de las ecuaciones (53) da así

(68)

Las ecuaciones (67) y (68) juntas son equivalentes a la ley de gravitación de Newton.

Por (67) y (68) la expresión para el potencial gravitatorio se convierte en

(68a)

mientras que la teoría de Newton, con la unidad de tiempo que hemos escogido, da

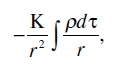
en donde K denota la constante 6,7 X 10^–8, normalmente llamada constante de gravitación. Por comparación obtenemos

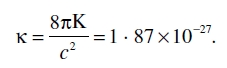
(69)

22. COMPORTAMIENTO DE REGLAS Y RELOJES EN EL CAMPO GRAVITATORIO ESTÁTICO. CURVATURA DE RAYOS LUMINOSOS. MOVIMIENTO DEL PERIHELIO DE UNA ÓRBITA PLANETARIA

Para llegar a la teoría de Newton como una primera aproximación tuvimos que calcular solamente una componente, g₄₄, de las diez g_µν del campo gravitatorio, puesto que sólo esta componente entra en la primera aproximación, (67), de la ecuación para el movimiento del punto material en el campo gravitatorio. A partir de esto, sin embargo, es ya evidente que otras componentes de las g_µν deben diferir de los valores dados en (4) en pequeñas cantidades de primer orden. Esto es exigido por la condición g = –1.

Para una masa puntual productora de campo en el origen de coordenadas, obtenemos, en primera aproximación, la solución con simetría radial

(70)

donde δ_ρσ es 1 ó 0, respectivamente, según sea ρ = σ ó ρ≠σ, y r es la cantidad 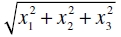debido a (68a)

(70a)

si M denota la masa productora de campo. Es fácil verificar que las ecuaciones de campo (fuera de la masa) resultan satisfechas en primer orden de pequeñas cantidades.

Examinemos ahora la influencia ejercida por el campo de la masa M sobre las propiedades métricas del espacio. La relación

ds² = g_µν dx_µ dx_ν

es válida siempre entre las longitudes «localmente» medidas (4) y tiempos ds por una parte, y las diferencias de coordenadas dx_ν por otra.

Para una unidad de medida de longitud tendida «paralela» al eje de las x, por ejemplo, tendríamos que hacer ds² = –1; dx₂ = dx₃ = dx₄ = 0. Por consiguiente, –1 = g₁₁dx₁². Si además la unidad de medida reposa sobre el eje de las x, la primera de las ecuaciones (70) da

De estas dos relaciones se sigue que, hasta primer orden de pequeñas cantidades,

(71)

La regla de medir unidad aparece así un poco acortada con relación al sistema de coordenadas por la presencia del campo gravitatorio, si la regla está tendida a lo largo de un radio.

De manera análoga obtenemos la longitud de coordenadas en dirección tangencial si, por ejemplo, hacemos

ds² = –1; dx₁ = dx₃ = dx₄ = 0; x₁ = r; x₂ = x₃ = 0.

El resultado es

–1 = g₂₂ dx²² = –dx²₂.

(71a)

Con la posición tangencial, por lo tanto, el campo gravitatorio del punto de masa no tiene influencia sobre la longitud de la regla.

Así pues, la geometría euclidiana no es válida ni siquiera en primera aproximación en el campo gravitatorio, si queremos tomar una y la misma regla independientemente de su lugar y orientación como una realización del mismo intervalo; aunque, por supuesto, una ojeada a (70a) y (69) muestra que las desviaciones que se pueden esperar son demasiado pequeñas para que sea posible advertirlas en medidas de la superficie de la Tierra.

Examinemos también la marcha de un reloj unidad, que está preparado para estar en reposo en un campo gravitatorio estático. Aquí tenemos para un período de reloj ds = 1; dx₁ = dx₂ = dx₃ = 0. Por consiguiente

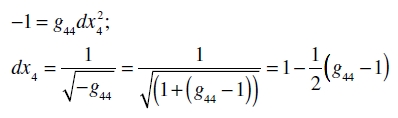
o

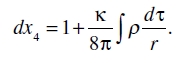
(72)

Así pues, el reloj marcha más despacio si se encuentra en la vecindad de masas ponderables. De esto se sigue que las líneas espectrales de la luz que nos llega desde la superficie de grandes estrellas debe aparecer desplazada hacia el extremo rojo del espectro.¹⁴

Examinemos ahora el curso de los rayos luminosos en el campo gravitatorio estático. Por la teoría de la relatividad especial la velocidad de la luz viene dada por la ecuación

– dx²₁ – dx₂ – dx²₃ – dx²₄ = 0

y, por lo tanto, por la teoría de la relatividad general viene dada por la ecuación

ds² = g_µν dx_µ dx_ν = 0.

(73)

Si la dirección, i. e. la razón dx₁ : dx₂ : dx₃ es dada, la ecuación (73) da las cantidades

y en consecuencia la velocidad

definida en el sentido de la geometría euclidiana. Reconocemos fácilmente que el curso de los rayos luminosos debe estar curvado con respecto al sistema de coordenadas, si las g_µν no son constantes. Si n es una dirección perpendicular a la propagación de la luz, el principio de Huyghens muestra que el rayo luminoso, imaginado en el plano (γ,n), tiene la curvatura –δγ/δn.

Examinemos la curvatura sufrida por un rayo luminoso que pasa frente a una masa M a una distancia ∆. Si escogemos el sistema de coordenadas de acuerdo con el diagrama que se acompaña, la curvatura total del rayo (calculada positivamente si es cóncava hacia el origen) viene dada con suficiente aproximación por

mientras que (73) y (70) dan

Haciendo el cálculo, esto da

(74)

Según esto, un rayo luminoso que pasa cerca del Sol sufre una desviación de 1.7’’; y un rayo que pasa cerca del planeta Júpiter sufre una desviación de aproximadamente 0.02’’.

Si calculamos el campo gravitatorio en un grado de aproximación superior, y con una precisión correspondiente al movimiento orbital de un punto material de masa relativa infinitamente pequeña, encontramos una desviación del siguiente tipo de las leyes de Kepler-Newton del movimiento planetario. La elipse orbital de un planeta experimenta una lenta rotación en la dirección de movimiento, de valor

(75)

por revolución. En esta fórmula a denota el semieje mayor, c la velocidad de la luz en la medida normal, e la excentricidad, T el tiempo de revolución en segundos.¹⁵

El cálculo da para el planeta Mercurio una rotación de la órbita de 43’’ por siglo, que corresponde exactamente a la observación astronómica (Leverrier); pues los astrónomos han descubierto en el movimiento del perihelio de este planeta, una vez consideradas las perturbaciones debidas a otros planetas, un residuo inexplicable de esta magnitud.