1

SOBRE LA ELECTRODINÁMICA DE LOS CUERPOS EN MOVIMIENTO^*

Es bien sabido que, cuando se aplica a cuerpos en movimiento, la electrodinámica de Maxwell tal como hoy se entiende normalmente conduce a asimetrías que no parecen ser inherentes a los fenómenos. Tomemos, por ejemplo, la interacción electrodinámica entre un imán y un conductor. Aquí los fenómenos observables dependen sólo del movimiento relativo del conductor y el imán, mientras que la visión habitual traza una nítida distinción entre los dos casos, en donde o bien uno u otro de los dos cuerpos está en movimiento. Pues, en efecto, si el imán está en movimiento y el conductor está en reposo, en la vecindad del imán aparece un campo electromagnético con una energía definida que produce una corriente dondequiera que haya localizados elementos del conductor. Pero si el imán está en reposo mientras que el conductor está en movimiento, no hay ningún campo eléctrico en la vecindad del imán, sino más bien una fuerza electromotriz en el conductor a la que no corresponde ninguna energía per se, sino que, suponiendo una igualdad del movimiento relativo en los dos casos, da lugar a corrientes eléctricas de la misma magnitud y el mismo curso que las producidas por las fuerzas eléctricas en el primer caso.

Ejemplos de este tipo, junto con los infructuosos intentos de detectar un movimiento de la Tierra con relación al «medio lumínico», llevan a la conjetura de que ni los fenómenos de la mecánica, ni tampoco los de la electrodinámica tienen propiedades que correspondan al concepto de reposo absoluto. Más bien, las mismas leyes de la electrodinámica y la óptica serán válidas para todos los sistemas de coordenadas en los que rigen las ecuaciones de la mecánica, como ya se ha demostrado para cantidades de primer orden. Elevaremos esta conjetura (cuyo contenido será denominado en adelante «el principio de relatividad») al estatus de un postulado e introduciremos también otro postulado, que es sólo aparentemente incompatible con él, a saber, que la luz se propaga siempre en el espacio vacío con una velocidad definida V que es independiente del estado de movimiento del cuerpo emisor. Estos dos postulados bastan para conseguir una electrodinámica de cuerpos en movimiento simple y consistente basada en la teoría de Maxwell para cuerpos en reposo. La introducción de un «éter lumínico» se mostrará superflua, puesto que la idea que se va a desarrollar aquí no requerirá un «espacio en reposo absoluto» dotado de propiedades especiales, ni asigna un vector velocidad a un punto del espacio vacío donde están teniendo lugar procesos electromagnéticos.

Como toda la electrodinámica, la teoría que va a desarrollarse aquí está basada en la cinemática de un cuerpo rígido, puesto que las afirmaciones de una teoría semejante tienen que ver con las relaciones entre cuerpos rígidos (sistemas de coordenadas), relojes y procesos electromagnéticos. Una consideración insuficiente de esta circunstancia está en la raíz de las dificultades con las que debe enfrentarse actualmente la electrodinámica de los cuerpos en movimiento.

A. PARTE CINEMÁTICA

1. DEFINICIÓN DE SIMULTANEIDAD

Consideremos un sistema de coordenadas en el que son válidas las ecuaciones mecánicas de Newton. Para distinguir nominalmente dicho sistema de aquellos que van a introducirse más tarde, y para hacer esta presentación más precisa, le llamaremos «sistema de reposo».

Si una partícula está en reposo con respecto a este sistema de coordenadas, su posición relativa al último puede determinarse por medio de varas de medir rígidas utilizando los métodos de la geometría euclidiana y expresarse en coordenadas cartesianas.

Si queremos describir el movimiento de una partícula, damos los valores de sus coordenadas como funciones del tiempo. Sin embargo, debemos tener en cuenta que una descripción matemática de este tipo sólo tiene sentido físico si tenemos ya claro lo que entendemos aquí por «tiempo». Debemos tener en cuenta que todos nuestros juicios que implican al tiempo son siempre juicios sobre sucesos simultáneos. Si, por ejemplo, yo digo que «El tren llega aquí a las 7 en punto», eso significa, más o menos, «La manecilla pequeña de mi reloj apuntando a las 7 y la llegada del tren son sucesos simultáneos».¹

Podría parecer que todas las dificultades implicadas en la definición de «tiempo» podrían superarse si sustituyo «posición de la manecilla pequeña de mi reloj» por «tiempo». Semejante definición es suficiente si va a definirse un tiempo exclusivamente para el lugar en el que está localizado el reloj; pero la definición ya no es satisfactoria cuando tienen que enlazarse temporalmente series de sucesos que ocurren en localizaciones diferentes, o —lo que es equivalente— cuando hay que evaluar temporalmente sucesos que ocurren en lugares remotos del reloj.

Por supuesto, podríamos contentarnos con evaluar el tiempo de los sucesos estacionando en el origen de las coordenadas a un observador con un reloj; este observador asigna a cada suceso a evaluar la posición correspondiente de las manecillas del reloj cuando a través del espacio vacío le llega una señal luminosa procedente de dicho suceso. Sin embargo, sabemos por experiencia que una coordinación semejante tiene el inconveniente de que no es independiente de la posición del observador con el reloj. Llegamos a un arreglo más práctico mediante el siguiente argumento.

Si existe un reloj en el punto A en el espacio, entonces un observador situado en A puede evaluar el tiempo de los sucesos en la inmediata vecindad de A hallando las posiciones de las manecillas del reloj que son simultáneas con dichos sucesos. Si existe otro reloj en el punto B que se asemeja en todos los aspectos al que hay en A, entonces el tiempo de los sucesos en la inmediata vecindad de B puede ser evaluado por un observador en B. Pero no es posible comparar el tiempo de un suceso en A con uno en B sin una estipulación adicional. Hasta aquí hemos definido sólo un «tiempo-A» y un «tiempo-B», pero no un «tiempo» común para A y B. El último puede ahora determinarse estableciendo por definición que el «tiempo» requerido por la luz para viajar de A a B es igual al «tiempo» que requiere para viajar de B a A. En efecto, supongamos que un rayo de luz parte de A hacia B en un «tiempo-A» t_A, es reflejado desde B hacia A en un «tiempo-B» t_B, y llega de nuevo a A en un «tiempo-A» t’_A. Los dos relojes son síncronos por definición si

t_B – t_A = t’_A – t_B.

Suponemos que es posible que esta definición de sincronicidad esté libre de contradicciones, y que lo esté para puntos en número arbitrario, y por consiguiente son válidas en general las relaciones siguientes:

1. Si el reloj en B marcha de forma síncrona con el reloj en A, el reloj en A marcha de forma síncrona con el reloj en B.

2. Si el reloj en A marcha de forma síncrona con el reloj en B así como con el reloj en C, entonces los relojes en B y C también marchan de forma síncrona uno con relación al otro.

Por medio de ciertos experimentos (mentales) físicos hemos establecido lo que debe entenderse por relojes síncronos en reposo relativo y situados en diferentes lugares, y con ello hemos llegado obviamente a definiciones de «síncrono» y «tiempo». El «tiempo» de un suceso es la lectura obtenida simultáneamente de un reloj en reposo situado en el lugar del suceso, que para todas las determinaciones temporales marcha de forma síncrona con un reloj especificado en reposo y, por supuesto, con el reloj especificado.

Basados en la experiencia, estipulamos además que la cantidad

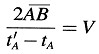
es una constante universal (la velocidad de la luz en el espacio vacío).

Es esencial que hayamos definido el tiempo por medio de relojes en reposo en el sistema de reposo; puesto que el tiempo recién definido está relacionado con el sistema en reposo, le llamaremos «el tiempo del sistema de reposo».

2. SOBRE LA RELATIVIDAD DE LONGITUDES Y TIEMPOS

Las consideraciones siguientes están basadas en el principio de relatividad y el principio de constancia de la velocidad de la luz. Definimos estos dos principios como sigue:

1. Si los dos sistemas de coordenadas están en movimiento relativo de traslación, paralela uniforme, las leyes de acuerdo con las cuales cambian los estados de un sistema físico no dependen de con cuál de los dos sistemas están relacionados dichos cambios.

2. Todo rayo luminoso se mueve en el sistema de coordenadas «de reposo» con una velocidad fija V, independientemente de si este rayo luminoso es emitido por un cuerpo en reposo o en movimiento. Por lo tanto, recorrido de la luz intervalo de tiempo

donde «intervalo de tiempo» debería entenderse en el sentido de la definición dada en la sección 1.

Tomemos una vara rígida en reposo; sea l su longitud, medida por una vara de medir que está también en reposo. Imaginemos ahora que se coloca el eje de la vara a lo largo del eje X del sistema de coordenadas en reposo, y que la vara es puesta entonces en movimiento de traslación paralela uniforme (con velocidad ν) a lo largo del eje X en la dirección de las x crecientes. Preguntamos sobre la longitud de la vara de medir, que imaginamos debe establecerse por las dos operaciones siguientes:

a) El observador se mueve junto con la mencionada vara de medir y la vara rígida susceptible de ser medida, y mide la longitud de esta vara tendiendo la vara de medir de la misma manera que si la vara susceptible de ser medida, el observador y la vara de medir estuvieran en reposo.

b) Utilizando relojes en reposo y síncronos en el sistema de reposo como se esbozó en la sección 1, el observador determina en qué puntos del sistema de reposo están situados el principio y el final de la vara susceptible de ser medida en algún tiempo t dado. La distancia entre estos dos puntos, medida con la vara utilizada antes —pero no en reposo—, es también una longitud que podemos llamar la «longitud de la vara».

De acuerdo con el principio de relatividad, la longitud determinada por la operación (a), que llamaremos «la longitud de la vara en el sistema en movimiento», debe ser igual a la longitud l de la vara en reposo.

La longitud determinada utilizando la operación (b), que llamaremos «la longitud de la vara (en movimiento) en el sistema de reposo», será determinada sobre la base de nuestros dos principios, y encontraremos que difiere de l.

La cinemática actual supone implícitamente que las longitudes determinadas por las dos operaciones anteriores son exactamente iguales entre sí, o, en otras palabras, que en el tiempo t un cuerpo rígido en movimiento es totalmente reemplazable, en cuanto a su geometría, por el mismo cuerpo cuando está en reposo en una posición concreta.

Además, imaginamos los dos extremos (A y B) de la vara provistos de relojes que son síncronos con los relojes del sistema de reposo, i. e., cuyas lecturas corresponden siempre al «tiempo del sistema de reposo» en las localizaciones que los relojes resultan ocupar; por lo tanto, estos relojes son «síncronos en el sistema de reposo».

Imaginemos además que cada reloj tiene un observador que se mueve con él, y que estos observadores aplican a los dos relojes el criterio para el ritmo síncrono de dos relojes formulado en la sección 1. Sea un rayo de luz que parte de A en el tiempo² t_A, es reflejado en B en el tiempo t_B, y llega de nuevo a A en el tiempo t’_A. Teniendo en cuenta el principio de relatividad de la velocidad de la luz, encontramos que

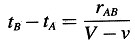
y

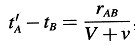
donde r_AB denota la longitud de la vara en movimiento, medida en el sistema de reposo. Los observadores que se mueven conjuntamente con la vara encontrarían así que los dos relojes no marchan de forma síncrona, mientras que los observadores en el sistema de reposo les dirían que están marchando de forma síncrona.

Vemos así que no podemos atribuir significado absoluto al concepto de simultaneidad; en su lugar, dos sucesos que son simultáneos cuando son observados desde algún sistema de coordenadas concreto ya no pueden considerarse simultáneos cuando son observados desde un sistema que está en movimiento relativo a dicho sistema.

3. TEORÍA DE LAS TRANSFORMACIONES DE COORDENADAS Y TIEMPO DESDE EL SISTEMA DE REPOSO A UN SISTEMA EN MOVIMIENTO DE TRASLACIÓN UNIFORME RELATIVO A AQUÉL

Sean dos sistemas de coordenadas en el espacio en «reposo», i.e., dos sistemas de tres líneas rectas materiales rígidas mutuamente perpendiculares con origen en un punto. Sean coincidentes los ejes X de los dos sistemas, y sean sus ejes Y y Z respectivamente paralelos. Cada sistema estará provisto de una vara de medir rígida y un número de relojes, y sean exactamente iguales las dos varas de medir y todos los relojes de los dos sistemas.

Ahora, pongamos el origen de uno de los dos sistemas, digamos k, en un estado de movimiento con velocidad (constante) ν en la dirección de las x crecientes del otro sistema (K), que permanece en reposo; e impartamos esta nueva velocidad a los ejes coordenados de k, su correspondiente vara de medir y sus relojes. A cada tiempo t del sistema de reposo K corresponde una localización definida de los ejes del sistema en movimiento. Por razones de simetría tenemos justificación para suponer que el movimiento de k puede ser tal que en el tiempo t («t» siempre denota un tiempo del sistema de reposo) los ejes del sistema en movimiento son paralelos a los ejes del sistema de reposo.

Imaginemos ahora el espacio a ser medido tanto desde el sistema de reposo K, utilizando la vara de medir en reposo, como desde el sistema k, utilizando la vara de medir en movimiento junto con él, y que de este modo se obtienen las coordenadas x, y, z y ξ, η, ζ, respectivamente. Además, por medio de los relojes en reposo en el sistema de reposo, y utilizando rayos luminosos como se describe en la sección 1, determinamos el tiempo t del sistema de reposo para todos los puntos donde hay relojes. De manera similar, aplicando de nuevo el método de señales luminosas descrito en la sección 1, determinamos el tiempo t del sistema en movimiento para todos los puntos de este sistema en movimiento en los que hay relojes en reposo relativo a este sistema.

A cada conjunto de valores x, y, z, t que determina por completo el lugar y tiempo de un suceso en el sistema de reposo le corresponde un conjunto de valores ξ, η, ζ, τ que fija el suceso relativo al sistema k, y el problema que hay que resolver ahora es encontrar el sistema de ecuaciones que conecta dichas cantidades.

En primer lugar, es evidente que estas ecuaciones deben ser lineales debido a las propiedades de homogeneidad que atribuimos al espacio y el tiempo.

Si hacemos x’=x – vt, entonces es evidente que a un punto en reposo en el sistema k le pertenece un conjunto de valores x’, y, z definido e independiente del tiempo. Determinamos primero τ como una función de x’, y, z y t. Para esto, debemos expresar en ecuaciones que τ es de hecho el agregado de lecturas de relojes en reposo en el sistema k, sincronizados de acuerdo con la regla dada en la sección 1.

Supongamos que en el instante τ₀ se envía un rayo luminoso a lo largo del eje X desde el origen del sistema k a x’, y que este rayo es reflejado en el instante τ₁ desde allí hacia el origen, adonde llega en el instante τ₂: entonces debemos tener

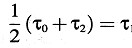
o, incluyendo los argumentos de la función τ y aplicando el principio de la constancia de la velocidad de la luz en el sistema de reposo,

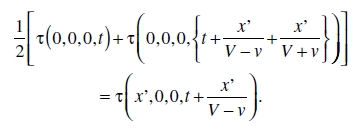
De esto obtenemos, haciendo x infinitesimalmente pequeño,

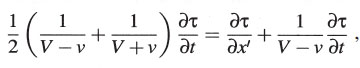
o

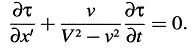
Habría que señalar que, en lugar del origen de coordenadas, podríamos haber escogido cualquier otro punto como origen del rayo luminoso y, por consiguiente, la ecuación recién obtenida es válida para todos los valores de x’, y, z.

Un razonamiento análogo —aplicado a los ejes Y y Z— da, recordando que la luz se propaga siempre a lo largo de estos ejes con la velocidad 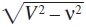cuando se observa desde el sistema de reposo,

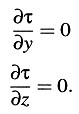
Estas ecuaciones dan, puesto que τ es una función lineal,

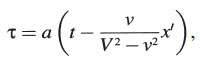
donde a es una función ϕ(ν) todavía desconocida, y donde suponemos por brevedad que en el origen de k tenemos t = 0 cuando τ = 0.

Utilizando este resultado, podemos determinar fácilmente las cantidades ξ, η, ζ si expresamos en ecuaciones que (como exige el principio de la constancia de la velocidad de la luz en unión con el principio de relatividad) la luz se propaga también con velocidad V cuando se mide en el sistema en movimiento. Para un rayo luminoso emitido en el instante t = 0 en la dirección de las ξ crecientes, tenemos

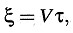
o

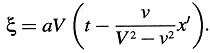
Pero medido en el sistema de reposo, el rayo luminoso se propaga con velocidad V – ν relativa al origen de k, de modo que

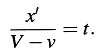
Sustituyendo este valor de t en la ecuación para ξ, obtenemos

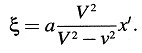
Análogamente, considerando rayos luminosos que se mueven a lo largo de los otros dos ejes, obtenemos

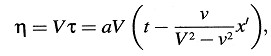
donde

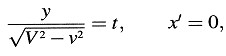
por lo tanto

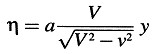
y

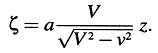
Si sustituimos el valor para x’, obtenemos

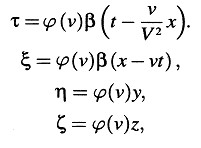
donde

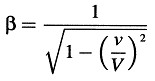
y ϕ es una función de v desconocida por el momento. Si no se hace ninguna hipótesis con respecto a la posición inicial del sistema en movimiento y el punto cero de τ, entonces debe sumarse una constante a los segundos miembros de estas ecuaciones.

Ahora tenemos que demostrar que, medido en el sistema en movimiento, todo rayo luminoso se propaga con la velocidad V si así lo hace, como hemos supuesto, en el sistema de reposo; pues no hemos demostrado todavía que el principio de la constancia de la velocidad de la luz es compatible con el principio de relatividad.

Supongamos que en el tiempo t = τ = 0 se quite una onda esférica desde el origen de coordenadas, que en dicho instante es común a ambos sistemas, y que esta onda se propaga en el sistema K con velocidad V. Por lo tanto, si (x, y, z) es un punto alcanzado por esta onda, tenemos

x² + y² + z² = V²t²

Transformamos esta ecuación utilizando nuestras ecuaciones de transformación y, tras un sencillo cálculo, obtenemos

ξ² + η² + ζ² = V²τ²

Así pues, nuestra onda es también una onda esférica con velocidad de propagación V cuando se observa en el sistema en movimiento. Esto demuestra que nuestros dos principios fundamentales son compatibles.

Las ecuaciones de transformación que hemos obtenido contienen también una función desconocida ϕ de ν, que queremos determinar ahora.

Para esto introducimos un tercer sistema de coordenadas K’ que, con relación al sistema k, está en movimiento de traslación paralelo al eje χ, y tal que su origen se mueve a lo largo del eje χ con velocidad –ν. Sean coincidentes los tres orígenes de coordenadas en el tiempo t = 0, y sea el tiempo t’ del sistema K igual a cero en t = x = y = z = 0. Denotamos por x’, y’, z’ las coordenadas medidas en el sistema K’, y por una doble aplicación de nuestras ecuaciones de transformación, obtenemos

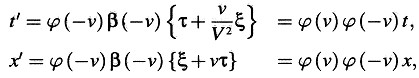
Puesto que las relaciones entre x’, y’, z’yx, y, z no contienen el tiempo t, los sistemas K y K’ no están en reposo relativo mutuo, y es evidente que la transformación de K a K’ debe ser la transformación identidad. Por lo tanto,

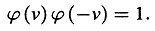
Exploremos ahora el significado de ϕ (ν). Nos centraremos en la porción del eje-Y del sistema k que se halla entre ξ = 0, η = 0, ζ = 0 y ξ = 0, η = l, ζ = 0. Esta porción del eje-Y es una vara que, con relación al sistema K, se mueve perpendicularmente a su eje con una velocidad v y cuyos extremos tienen coordenadas en K:

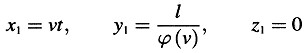
y

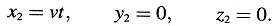
La longitud de la vara, medida en K es así l/ϕ(ν); esto nos da el significado de la función ϕ. Por razones de simetría, es ahora evidente que la longitud de una vara medida en el sistema de reposo y que se mueve perpendicularmente a su eje sólo puede depender de su velocidad y no de la dirección y sentido de su movimiento. Así pues, la longitud de la vara en movimiento medida en el sistema de reposo no cambia si se reemplaza ν por –ν. De esto concluimos

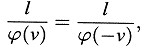
o

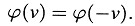
De esta relación y la encontrada antes se sigue que ϕ(ν) = 1, de modo que las ecuaciones de transformación obtenidas se convierten en

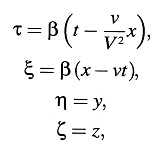
donde

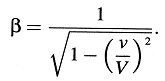
4. EL SIGNIFICADO FÍSICO DE LAS ECUACIONES OBTENIDAS EN LO QUE CONCIERNE A CUERPOS RÍGIDOS Y RELOJES EN MOVIMIENTO

Consideremos una esfera rígida³ de radio R que está en reposo relativo al sistema en movimiento k y cuyo centro yace en el origen de k. La ecuación de la superficie de esta esfera, que se mueve con velocidad ν relativa a k, es

ξ² + η² + ζ² = R²

Expresada en términos de X, y, z la ecuación de esta superficie en el tiempo t = 0 es

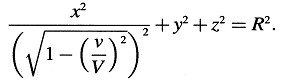
Un cuerpo rígido que tiene una forma esférica cuando se mide en reposo tiene, cuando se mide en movimiento —considerado desde el sistema de reposo—, la forma de un elipsoide de revolución con ejes

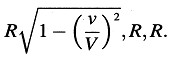
Así pues, mientras que las dimensiones Y y Z de la esfera (y, por lo tanto, también de todo cuerpo rígido, cualquiera que sea su forma) no parecen ser alteradas por el movimiento, la dimensión X parece estar contraída en la fracción 1: 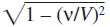, de modo que cuanto mayor es el valor de ν, mayor es la contracción. Para ν = V todos los objetos en movimiento considerados desde el sistema de «reposo» se contraen en estructuras planas. Para velocidades superlumínicas nuestras consideraciones dejan de tener significado; como veremos a partir de consideraciones posteriores, en nuestra teoría la velocidad de la luz representa físicamente el papel de velocidades infinitamente grandes.

Es evidente que los mismos resultados se aplican a cuerpos en reposo en el sistema de «reposo» cuando se consideran desde un sistema en movimiento uniforme.

Imaginemos además que uno de los relojes que puede indicar el tiempo t cuando está en reposo relativo al sistema de reposo y el tiempo τ cuando está en reposo relativo al sistema en movimiento, se coloca en el origen de k y se pone en marcha de tal forma que indica el tiempo τ. ¿Cuál es el ritmo de este reloj cuando se considera desde el sistema de reposo?

Las cantidades x, t y τ que hacen referencia a la posición de dicho reloj satisfacen obviamente las ecuaciones:

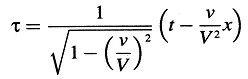
y

x = νt.

Así pues, tenemos

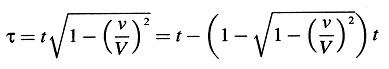
de lo que se sigue que la lectura del reloj considerado desde el sistema de reposo se retrasa cada segundo en (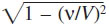) segundos, o, salvo cantidades de cuarto orden y superiores, en ¹⁄₂ (ν/V)² segundos.

Esto da lugar a la siguiente consecuencia peculiar: si en los puntos A y B de K hay relojes en reposo que, considerados desde el sistema de reposo, marchan de forma síncrona, y si el reloj de A es transportado a B a lo largo de la línea que los conecta con velocidad ν, entonces a la llegada de dicho reloj a B los dos relojes ya no marcharán de forma síncrona; en su lugar, el reloj que ha sido transportado de A a B se habrá retrasado ¹⁄₂ tν²/V² segundos (salvo cantidades de cuarto orden y superiores) respecto al reloj que ha estado en B desde el principio, donde t es el tiempo necesario para que el reloj viaje de A a B.

Vemos así que este resultado es válido incluso cuando el reloj se mueve de A a B a lo largo de cualquier línea poligonal arbitraria, e incluso cuando los puntos A y B coinciden.

Si suponemos que el resultado demostrado para una línea poligonal es también válido para una línea continuamente curvada, entonces llegamos al siguiente resultado: si existen en A dos relojes que marchan de forma síncrona, y uno de ellos se lleva a lo largo de una curva cerrada con velocidad constante hasta que haya vuelto a A, lo que necesita, digamos, t segundos, entonces, a su llegada a A se habrá retrasado ¹⁄₂ t(ν/V)² respecto al reloj que no se ha movido. De esto concluimos que un reloj de volantes situado en el ecuador debe, en circunstancias por lo demás iguales, marchar ligeramente más lento que un reloj absolutamente idéntico situado en uno de los polos terrestres.

5. EL TEOREMA DE ADICIÓN DE VELOCIDADES

En el sistema k en movimiento con velocidad ν a lo largo del eje X del sistema K, sea un punto que se mueve de acuerdo con las ecuaciones

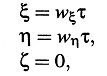
donde w_ξ y w_η denotan constantes.

Buscamos el movimiento del punto relativo al sistema K. Introduciendo las cantidades X, y, z, t en las ecuaciones de movimiento del punto por medio de las ecuaciones de transformación deducidas en la sección 3, obtenemos

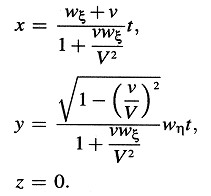
Así pues, de acuerdo con nuestra teoría, la suma vectorial de velocidades sólo es válida en primera aproximación. Sea

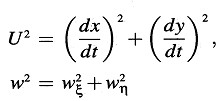
y

α debe considerarse entonces como el ángulo entre las velocidades ν y w. Después de un cálculo sencillo obtenemos

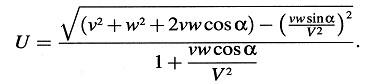
Vale la pena señalar que ν y w entran en la expresión para la velocidad resultante de una forma simétrica. Si w tiene también la dirección del eje X (eje χ), obtenemos

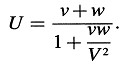
Se sigue de esta ecuación que la composición de dos velocidades que son menores que V da siempre como resultado una velocidad que es menor que ν. Pues si hacemos ν = V – κ, y w = V – λ, donde κ y λ son positivas y menores que V, entonces

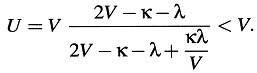
Se sigue también que la velocidad de la luz V no puede alterarse al componerla con una «velocidad sublumínica». Pues en este caso obtenemos

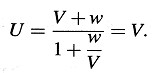
En el caso en que ν y w tienen la misma dirección, la fórmula para U podría haberse obtenido también componiendo dos transformaciones de acuerdo con la sección 3. Si además de los sistemas K y k, que aparecen en la sección 3, introducimos un tercer sistema de coordenadas K’, que se mueve paralelo a k y cuyo origen se mueve con velocidad w a lo largo del eje χ, obtenemos ecuaciones entre las cantidades X, y, z, t y las correspondientes cantidades de k’ que sólo difieren de las encontradas en la sección 3 en que «ν» es reemplazada por la cantidad

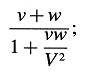
de esto vemos que tales transformaciones paralelas constituyen un grupo —como debe ser en realidad.

Hemos deducido ahora las leyes requeridas de la cinemática correspondiente a nuestros dos principios, y procedemos a su aplicación a la electrodinámica.

B. PARTE ELECTRODINÁMICA

6. TRANSFORMACIÓN DE LAS ECUACIONES DE MAXWELL-HERTZ PARA EL ESPACIO VACÍO. SOBRE LA NATURALEZA DE LAS FUERZAS ELECTROMOTRICES DEBIDAS AL MOVIMIENTO EN UN CAMPO MAGNÉTICO

Sean las ecuaciones de Maxwell-Hertz para el espacio vacío válidas para el sistema de reposo K, de modo que tenemos

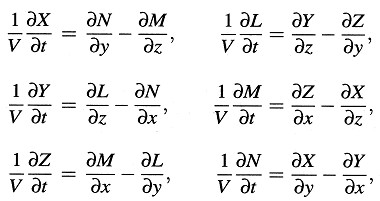
donde (X, Y, Z) denota el vector fuerza eléctrica y (L, M, N), el vector fuerza magnética.

Si aplicamos a estas ecuaciones las transformaciones deducidas en la sección 3, para relacionar los procesos electromagnéticos con el sistema de coordenadas en movimiento con velocidad v allí introducido, obtenemos las siguientes ecuaciones:

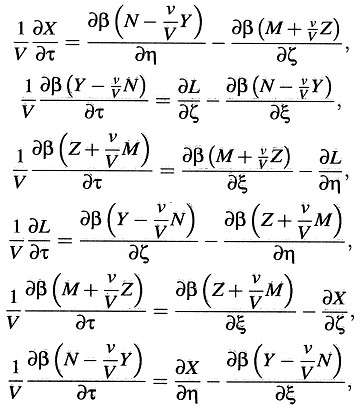
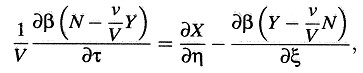
donde

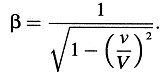
El principio de relatividad requiere que las ecuaciones de Maxwell-Hertz para el espacio vacío sean válidas también en el sistema k si son válidas en el sistema K, i. e., que los vectores de las fuerzas eléctrica y magnética —(X’, Y’, Z’) y (L’, M’, N’)— del sistema en movimiento k, que están definidos en dicho sistema por sus efectos ponderomotrices sobre cargas eléctricas y magnéticas, respectivamente, satisfagan las ecuaciones

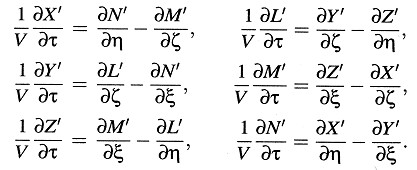
Obviamente, los dos sistemas de ecuaciones encontrados para el sistema k deben expresar exactamente lo mismo, puesto que ambos sistemas de ecuaciones son equivalentes a las ecuaciones de Maxwell-Hertz para el sistema K. Además, puesto que las ecuaciones para ambos sistemas están en acuerdo aparte de los símbolos que representan a los vectores, se sigue que las funciones que figuran en los sistemas de ecuaciones en lugares correspondientes deben coincidir salvo un factor ψ(ν), común a todas las funciones de uno de los sistemas de ecuaciones e independiente de ξ, η, ζ y τ, aunque posiblemente dependiente de ν. Así pues, tenemos las relaciones:

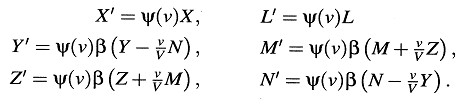
Si ahora invertimos este sistema de ecuaciones, resolviendo primero las ecuaciones recién obtenidas, y aplicando en segundo lugar a las ecuaciones la transformación inversa (desde k a K), que está caracterizada por la velocidad –ν, obtenemos, teniendo en cuenta que ambos sistemas de ecuaciones así obtenidos deben ser idénticos,

ψ(ν) · ψ(–ν) = 1.

Además, se sigue por razones de simetría⁴ que

ψ(ν) = ψ(–ν);

de modo que

ψ(ν) = 1.

y nuestras ecuaciones toman la forma

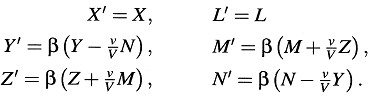
Para interpretar estas ecuaciones, apuntemos los siguientes comentarios: imaginemos una carga eléctrica puntual, cuya magnitud medida en el sistema de reposo es la «unidad», i. e., que cuando está en reposo en el sistema de reposo ejerce una fuerza de 1 dina sobre una carga igual situada a una distancia de 1 cm. De acuerdo con el principio de relatividad, esta carga eléctrica es también de magnitud «unidad» si se mide en el sistema en movimiento. Si esta carga eléctrica está en reposo relativo al sistema de reposo, entonces, por definición el vector (X, Y, Z) iguala a la fuerza que actúa sobre ella. Si, por el contrario, esta carga actuante está en reposo relativo al sistema en movimiento (al menos en el instante relevante), entonces la fuerza que actúa sobre ella medida en el sistema en movimiento es igual al vector (X’, Y’, Z’). Por lo tanto, las tres primeras de las ecuaciones anteriores pueden expresarse en palabras de las dos formas siguientes:

1. Si una carga eléctrica puntual unidad se mueve en un campo electromagnético, sobre ella actúa, además de la fuerza eléctrica, una «fuerza electromotriz» que, despreciando términos multiplicados por las potencias segunda y superiores de v/V, es igual al producto vectorial de la velocidad de la carga y la fuerza magnética, dividido por la velocidad de la luz. (Antiguo modo de expresión.)

2. Si una carga eléctrica puntual unidad se mueve en un campo electromagnético, la fuerza que actúa sobre ella iguala a la fuerza eléctrica en la localización de la carga unidad que se obtiene transformando el campo a un sistema de coordenadas en reposo relativo a la carga unidad. (Nuevo modo de expresión.)

Comentarios análogos son válidos para las «fuerzas magnetomotrices». Podemos ver que en la teoría aquí desarrollada, la fuerza electromotriz sólo representa el papel de un concepto auxiliar, que debe su introducción a la circunstancia de que las fuerzas eléctrica y magnética no tienen una existencia independiente del estado de movimiento del sistema de coordenadas.

Es además evidente que la asimetría en el tratamiento de las corrientes producidas por el movimiento relativo de un imán y un conductor, mencionada en la introducción, desaparece. Más aún, dejan de tener sentido las cuestiones acerca de la «sede» de las fuerzas electromotrices electrodinámicas (máquinas unipolares).

7. TEORÍA DEL PRINCIPIO DE DOPPLER Y DE LA ABERRACIÓN

Sea una fuente de ondas electromagnéticas en el sistema K y muy lejos del origen de coordenadas; en una región del espacio que contiene el origen de coordenadas, dichas ondas están representadas con precisión suficiente por las ecuaciones

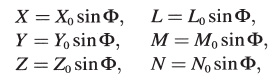
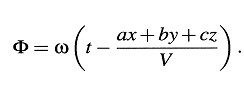
Aquí (X₀, Y₀, Z₀) y (L₀, M₀, N₀) son los vectores que determinan la amplitud del tren de ondas, y a, b, c son los cosenos directores de la normal a las ondas.

Queremos saber el carácter de dichas ondas cuando son investigadas por un observador en reposo en el sistema en movimiento. Aplicando las ecuaciones de transformación para las fuerzas eléctrica y magnética encontradas en la sección 6 y aquéllas para las coordenadas y el tiempo encontradas en la sección 3, obtenemos inmediatamente:

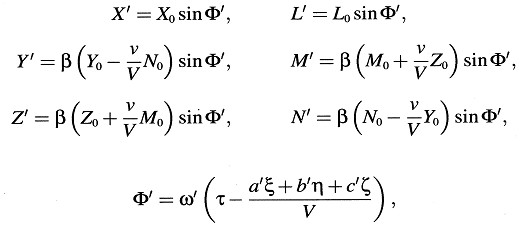
donde hemos hecho

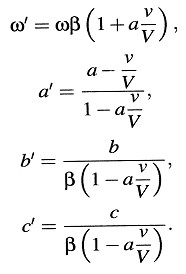
De la ecuación para ω’ se sigue que si un observador se mueve con velocidad ν relativa a una fuente de luz de frecuencia ν infinitamente lejana, de tal modo que la línea de unión «fuente de luz-observador» forma un ángulo ϕ con la velocidad del observador, siendo esta velocidad relativa a un sistema de coordenadas en reposo relativo a la fuente de luz, entonces ν’, la frecuencia de la luz percibida por el observador viene dada por la ecuación

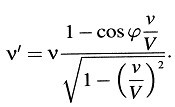
Éste es el principio de Doppler para velocidades arbitrarias. Para ϕ = 0, la ecuación toma la forma sencilla

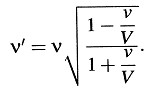
Vemos que, contrariamente a la concepción habitual, cuando ν = –∞, entonces ν = ∞.

Si ϕ’ denota el ángulo entre la normal a la onda (la dirección del rayo) en el sistema en movimiento y la línea de unión «fuente de luz-observador», la ecuación para α’ toma la forma

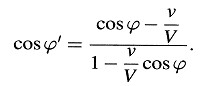
Esta ecuación expresa la ley de aberración en su forma más general. Si ϕ = π/2, la ecuación toma la forma simple

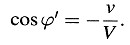
Aún tenemos que encontrar la amplitud de las ondas tal como aparece en el sistema en movimiento. Si A y A’ denotan la amplitud de la fuerza eléctrica y magnética en el sistema en reposo y el sistema en movimiento, respectivamente, obtenemos

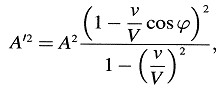
que para ϕ = 0 toma la forma más simple:

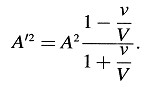
Se sigue de estos resultados que para un observador que se aproxima a una fuente luminosa a velocidad V, dicha fuente debería aparecer de intensidad infinita.

8. TRANSFORMACIÓN DE LA ENERGÍA DE RAYOS LUMINOSOS. TEORÍA DE LA PRESIÓN DE RADIACIÓN EJERCIDA SOBRE ESPEJOS PERFECTOS

Puesto que A²/8π es igual a la energía luminosa por unidad de volumen, de acuerdo con el principio de relatividad tenemos que considerar A’²/8π como la energía luminosa en el sistema en movimiento. Por lo tanto, A’²/A² sería la razón entre la energía de un complejo luminoso dado «medido en movimiento» y «medido en reposo» si el volumen de un complejo luminoso fuera el mismo medido en K y en k. Sin embargo, éste no es el caso. Si a, b, c son los cosenos directores de la normal a la onda luminosa en el sistema de reposo, entonces ninguna energía atraviesa los elementos de superficie de la superficie esférica

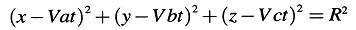
que se mueve con la velocidad de la luz; podemos decir por consiguiente que dicha superficie encierra permanentemente el mismo complejo luminoso. Investiguemos la cantidad de energía encerrada por dicha superficie considerada desde el sistema k, i. e., la energía del complejo luminoso relativa al sistema k.

Considerada en el sistema en movimiento, la superficie esférica es una superficie elipsoidal cuya ecuación en el instante τ = 0 es

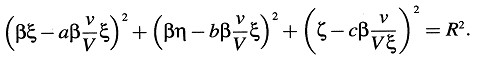
Si S denota el volumen de la esfera y S’ el del elipsoide, entonces un simple cálculo muestra que

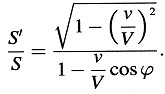
Si llamamos E a la energía de la luz encerrada por esta superficie cuando es medida en el sistema de reposo y E’ cuando es medida en el sistema en movimiento, obtenemos

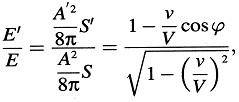
que, para ϕ = 0, se simplifica en

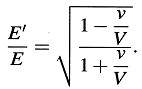
Es digno de mención que la energía y la frecuencia de un complejo luminoso varían con el estado de movimiento del observador de acuerdo con la misma ley.

Sea el plano de coordenadas ξ = 0 una superficie completamente reflectante en la que se reflejan las ondas planas consideradas en la sección 7. Investiguemos la presión de luz ejercida sobre la superficie reflectante, y la dirección, frecuencia e intensidad de la luz después de la reflexión.

Sea la luz incidente definida por las cantidades A, cosϕ y ν (relativas al sistema K). Consideradas desde k, las cantidades correspondientes son

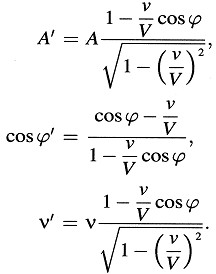
Refiriendo los procesos al sistema k, obtenemos para la luz reflejada

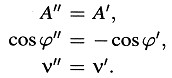
Finalmente, transformando de nuevo al sistema de reposo K, obtenemos para la luz reflejada

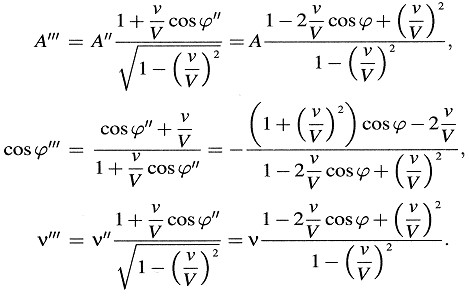
La energía (medida en el sistema de reposo) que incide sobre una superficie unidad del espejo por unidad de tiempo es obviamente A²/8π (V cosϕ – ν). La energía que deja una superficie unidad del espejo por unidad de tiempo es A’’²/8π (– V cos ϕ’’’ + ν). De acuerdo con el principio de la conservación de la energía, la diferencia entre estas dos expresiones es el trabajo realizado por la presión de luz por unidad de tiempo. Igualando este trabajo a P · ν, donde P es la presión de luz, obtenemos

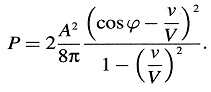
En primera aproximación, en acuerdo con el experimento y con otras teorías, obtenemos

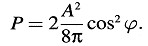
Todos los problemas de la óptica de cuerpos en movimiento pueden resolverse mediante el método aquí utilizado. El punto esencial es que los campos eléctrico y magnético de la luz que recibe la influencia de un cuerpo en movimiento se transforman a un sistema de coordenadas que está en reposo relativo a dicho cuerpo. De esta manera, todos los problemas de la óptica de cuerpos en movimiento se reducen a una serie de problemas de la óptica de cuerpos en reposo.

9. TRANSFORMACIÓN DE LAS ECUACIONES DE MAXWELL-HERTZ CUANDO SE TIENEN EN CUENTA CORRIENTES DE CONVECCIÓN

Partimos de las ecuaciones

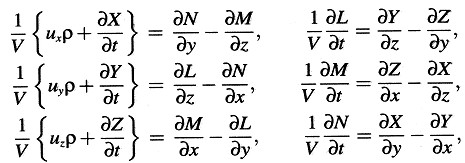
donde

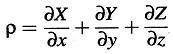
denota 4π veces la densidad de carga, y (u_x, u_y, u_z) el vector velocidad de la carga. Si se conciben las cargas eléctricas ligadas permanentemente a cuerpos rígidos y pequeños (iones, electrones), entonces estas ecuaciones constituyen el fundamento electromagnético de la electrodinámica y la óptica de Lorentz para cuerpos en movimiento.

Si, utilizando las ecuaciones de transformación presentadas en las secciones 3 y 6, transformamos estas ecuaciones, que se suponen válidas en el sistema K, al sistema k, obtenemos las ecuaciones

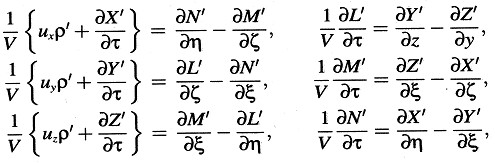
donde

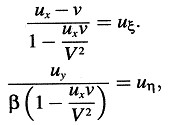
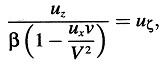
y

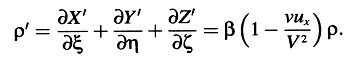
Puesto que —como se sigue del teorema de adición de velocidades (sección 5)— el vector (u_x, u_y, u_z) es en realidad la velocidad de las cargas eléctricas medida en el sistema k, hemos demostrado así que, sobre la base de nuestros principios cinemáticos, el fundamento electrodinámico de la teoría de Lorentz de la electrodinámica de cuerpos en movimiento está en acuerdo con el principio de relatividad.

Permítaseme también añadir brevemente que la siguiente proposición importante puede ser deducida fácilmente a partir de las ecuaciones que hemos obtenido. Si un cuerpo eléctricamente cargado se mueve arbitrariamente en el espacio sin alterar su carga cuando se observa desde un sistema de coordenadas que se mueve con el cuerpo, entonces su carga también permanece constante cuando se observa desde el sistema «de reposo» K.

10. DINÁMICA DEL ELECTRÓN (LENTAMENTE ACELERADO)

Sea una partícula eléctricamente cargada con carga e (en adelante llamada un «electrón») que se mueve en un campo electromagnético; sobre su ley de movimiento hacemos solamente la siguiente hipótesis:

Si el electrón está en reposo en un instante particular, su movimiento durante el siguiente instante de tiempo tendrá lugar de acuerdo con las ecuaciones

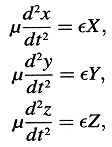
donde X, y, z denotan las coordenadas del electrón y µ su masa, siempre que el electrón se mueva lentamente.

Además, sea ν la velocidad del electrón en un cierto instante. Investiguemos la ley de movimiento del electrón durante el instante de tiempo inmediatamente posterior.

Sin pérdida de generalidad, podemos suponer, y así lo haremos, que el electrón está en el origen de coordenadas y se mueve con velocidad ν a lo largo del eje X del sistema K en el momento que nos interesa. Es entonces obvio que en el momento dado (t = 0), el electrón está en reposo relativo a un sistema de coordenadas k que se mueve con velocidad constante ν paralelo al eje X.

A partir de la hipótesis anterior, combinada con el principio de relatividad, es evidente que, considerado desde el sistema k, el electrón se moverá durante el período de tiempo inmediatamente siguiente (para pequeños valores de t) de acuerdo con las ecuaciones

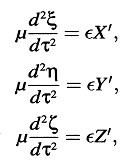
donde todos los símbolos ξ, η, ζ, τ, X’, Y’, Z’ se refieren al sistema k. Si estipulamos también que, para t = X = y = z = 0, también será válido τ = ξ = η = ζ = 0, entonces son aplicables las ecuaciones de transformación de las secciones 3 y 6, de modo que obtenemos

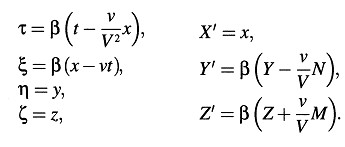
Con ayuda de estas ecuaciones transformamos las ecuaciones de movimiento anteriores desde el sistema k al sistema K, obteniendo

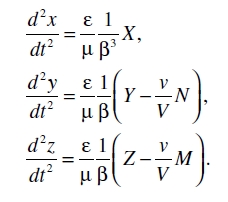
(A)

Siguiendo el enfoque habitual, investiguemos ahora la masa «longitudinal» y «transversal» del electrón en movimiento. Escribamos las ecuaciones (A) en la forma

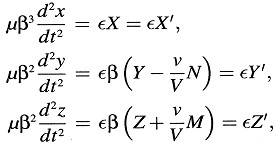
y notemos en primer lugar que ∈X’, ∈Y’, ∈Z’ son las componentes de la fuerza ponderomotriz que actúa sobre el electrón, considerado en un sistema en movimiento que, en dicho instante, se está moviendo con la misma velocidad que el electrón. (Esta fuerza podría medirse, por ejemplo, mediante una balanza de resorte en reposo en el último sistema.) Si simplemente llamamos a esta fuerza «la fuerza que actúa sobre el electrón», y mantenemos la ecuación

Masa X Aceleración = Fuerza,

estipulando, además, que las aceleraciones sean medidas en el sistema en reposo K, entonces las ecuaciones anteriores conducen a la definición:

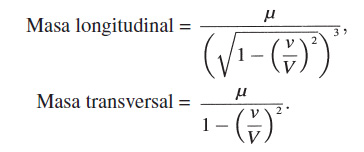
Por supuesto, con una definición diferente de fuerza y aceleración obtendríamos valores diferentes para estas masas; esto muestra que debemos proceder con mucha precaución cuando comparemos diversas teorías del movimiento del electrón.

Debería advertirse que estos resultados acerca de la masa son también válidos para puntos materiales ponderables, porque de un punto material ponderable puede hacerse un electrón (en nuestro sentido de la palabra) añadiéndole una carga eléctrica arbitrariamente pequeña.

Determinemos ahora la energía cinética de un electrón. Si un electrón parte del origen del sistema K con una velocidad inicial 0 y continúa moviéndose a lo largo del eje X bajo la influencia de una fuerza electrostática X, es evidente que la energía que toma del campo electrostático tiene el valor ∫ ∈Xdx. Puesto que se supone que el electrón se acelera lentamente y, en consecuencia, no puede emitir ninguna energía en forma de radiación, la energía tomada del campo electrostático debe ser igualada a la energía cinética W del electrón. Teniendo en cuenta que la primera de las ecuaciones (A) es válida durante todo el proceso del movimiento, obtenemos

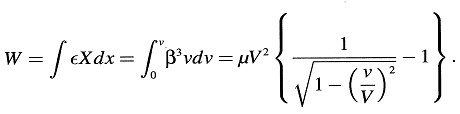
Así pues, W se hace infinitamente grande cuando ν = V. Igual que sucede con nuestros resultados anteriores, las velocidades superlumínicas no son posibles.

En virtud del argumento presentado antes, esta expresión para la energía cinética debe ser también válida para masas ponderables.

Enumeremos ahora las propiedades del movimiento del electrón resultante del sistema de ecuaciones (A) que son accesibles al experimento.

1. De la segunda ecuación del sistema (A) se sigue que una fuerza eléctrica Y y una fuerza magnética N tienen un efecto deflector igualmente intenso sobre un electrón que se mueve con velocidad ν si Y = Nν/V. Vemos así que, utilizando nuestra teoría, es posible determinar la velocidad del electrón a partir del cociente entre la deflexión magnética A_m y la deflexión eléctrica A_e para velocidades arbitrarias, aplicando la ley

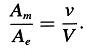
Esta relación puede ser comprobada experimentalmente, puesto que la velocidad del electrón también puede medirse directamente, por ejemplo, utilizando campos eléctricos y magnéticos rápidamente oscilantes.

2. A partir de la deducción de la energía cinética de un electrón se sigue que la diferencia de potencial atravesada por el electrón y la velocidad v que adquiere el electrón deben estar relacionadas por la ecuación

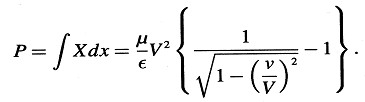
3. Calculamos el radio de curvatura R de la trayectoria del electrón si hay presente (como única fuerza deflectante) una fuerza magnética N que actúa perpendicularmente a su velocidad. De la segunda de las ecuaciones (A) obtenemos:

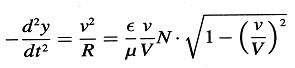
o

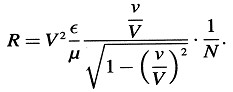
Estas tres relaciones constituyen una expresión completa de las leyes según las cuales, de acuerdo con la teoría aquí presentada, debe moverse el electrón.

Para concluir, permítaseme señalar que mi amigo y colega M. Besso me apoyó incondicionalmente en mi trabajo sobre el problema aquí discutido, y que estoy en deuda con él por varias sugerencias valiosas.