[ 1 ]
Estadística descriptiva
1.1 Introducción
La estadística es la ciencia que estudia la recolección, organización, análisis e interpretación de un conjunto de datos, y sus conceptos generales pueden aplicarse a distintas disciplinas como la ingeniería, la agricultura, la economía (donde se denomina econometría) o la psicología (donde se denomina biometría). Cuando la estadística se aplica en las ciencias de la salud, se utiliza el término bioestadística.
En términos globales, la estadística puede dividirse en descriptiva y analítica. La estadística descriptiva, como su nombre lo indica, solo pretende describir o caracterizar un conjunto de datos. La estadística analítica, en cambio, plantea hipótesis respecto a una población, usando un subconjunto de datos disponible de esta.
Para llevar a cabo un estudio descriptivo, es necesario conocer los conceptos de población y muestra (aleatoria) y sus propiedades, los tipos de variables aleatorias posibles de encontrar en la práctica y la forma como se describen: tablas de frecuencias, medidas de tendencia central y de dispersión y percentiles. Todos estos conceptos los encontrará definidos en este capítulo.
Los conceptos necesarios para hacer un estudio analítico los hallará en el capítulo de Asociación de variables.
1.2 Población y muestra
Población
La población (también llamada universo) se define como el conjunto total de objetos o personas de interés en un estudio. Una característica relevante de la población es que todos sus elementos deben cumplir con un conjunto predefinido de características.

Lo habitual es que la población esté constituida por un gran número de personas u objetos, por lo que normalmente se hace inviable acceder a todos ellos. El proceso de recopilación de datos de toda la población se denomina censo. Aunque sería atractivo acceder a toda la población, existen varios problemas para llevar a cabo esta idea:
• Un censo usualmente requiere invertir mucho tiempo y recursos, mientras que los estudios en salud se hacen cumpliendo ciertos plazos y con recursos limitados.
• Como las poblaciones son dinámicas, el objeto en estudio puede ser distinto en los primeros individuos estudiados que en los últimos, sobre todo si estos son vistos mucho tiempo después que los primeros. Por ejemplo, si un investigador quiere determinar la prevalencia de estrés en la Octava Región, y recopila los datos entre enero y marzo de 2010, sus resultados se verán afectados por la ocurrencia del terremoto del 27 de febrero de ese año.
• En ocasiones no es posible identificar con facilidad a los sujetos que componen la población. Por ejemplo, la población de personas que viven con VIH, o el número de aves acuáticas que existen en una reserva ecológica.
Muestra (aleatoria)
Dados los inconvenientes que se presentan al estudiar una población, lo habitual es que las investigaciones científicas se basen en una muestra de la población de interés, es decir, en un subconjunto de los elementos de la población.
Para que lo averiguado en la muestra sea cierto para la población en su conjunto, la muestra debe cumplir con los siguientes requisitos:
• La muestra debe ser aleatoria. Esto es, los sujetos en la muestra deben ser escogidos al azar (mediante un sorteo), de modo que todas las personas u objetos de la población tengan una probabilidad mayor que cero de estar presentes en la muestra.
• La muestra debe ser de un tamaño mínimo adecuado. Se entenderá por “adecuado” que el número de individuos seleccionados al azar de la población (el tamaño de la muestra) permita obtener estimaciones con un margen de error acotado.
Ejemplo 1.1 Supongamos que es de interés estimar el porcentaje de fumadores en cierta población, y que el porcentaje real de fumadores es de alrededor de 40%. Luego, si se quiere estimar con un margen de error de 5 puntos porcentuales, entonces el tamaño de la muestra debiera permitir obtener entre 35% y 45% de fumadores en la muestra.
• La muestra debe ser representativa de la población de la que procede. Esto se cumple cuando las características de la población relevantes para la investigación, están presentes en la misma proporción o promedio en la muestra. Por ejemplo, si la población tiene 30% de hombres, esta proporción se mantiene en la muestra estudiada. Si la edad promedio poblacional es 50 años, en la muestra se observa aproximadamente lo mismo, etc.
Sin embargo, es imposible determinar si efectivamente cada una de las características poblacionales está presente en la misma proporción o promedio en la muestra. En consecuencia, se asume que si una muestra es aleatoria y de tamaño mínimo adecuado, entonces esta es representativa de la población de interés.
La aleatoriedad y el tamaño de una muestra son características que podemos controlar (el tamaño muestral se puede calcular y el investigador suele escoger, entre varios métodos de selección al azar, el que se adecúe mejor a su estudio). La representatividad, en cambio, es una cualidad de la muestra.
1.3 Parámetros y estimadores
Llamaremos inferencia estadística a las deducciones que hacemos acerca de una población de interés, a partir de los resultados obtenidos mediante una muestra aleatoria de dicha población.
Por ejemplo, si en una muestra aleatoria se calcula que el promedio de edad es de 20 años, entonces se inferirá que el promedio de edad de la población de la cual procede la muestra debiera ser de aproximadamente 20 años, con un margen de error dado por el tamaño de la muestra. O bien, si se calcula que 38% de los individuos en la muestra es fumador, entonces se deducirá que el porcentaje de fumadores poblacional debiera ser aproximadamente 38%.
El promedio de edad y el porcentaje de fumadores poblacionales se denominan parámetros poblacionales (o simplemente parámetros). En general, un parámetro es cualquier función de los datos calculada en la población.
El promedio de edad y el porcentaje de fumadores calculados en la muestra, y utilizados para aproximar el verdadero valor poblacional, se denominan estimadores muestrales o estadísticos. Por lo común, un estimador puede ser cualquier función calculada con los datos muestrales y, como es un valor que representa a la muestra completa, suele llamarse también medida resumen.
[ Figura 1.1 ]
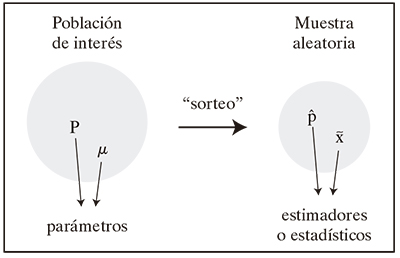
Parámetros poblacionales y estimadores muestrales. P: proporción poblacional de individuos con alguna característica de interés; µ: promedio poblacional de una variable de interés.
La muestra debiera ser un buen reflejo de la población. De esta forma, el objetivo cuando se estiman parámetros poblacionales es que:
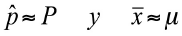
Esto solo es posible si la muestra escogida es representativa de la población de interés.
Un promedio o una proporción poblacional no es el único parámetro de interés en un estudio. Como puede ser cualquier función de los datos, podría interesar la mediana, varianza, desviación estándar, percentiles u otras funciones menos conocidas.
Por ejemplo, si se asume que la edad fértil es entre los 15 y 49 años, según el censo de 2002, el porcentaje de mujeres en edad fértil es 52%. Si se quiere hacer un estudio sobre el número de hijos promedio por mujer, en base a una muestra de 400 mujeres de Puente Alto, y se observan 190 mujeres en edad fértil, entonces 52% es el parámetro poblacional y 47,5% (190 mujeres de un total de 400) es el estimador de ese parámetro.
1.4 Variables aleatorias
Una vez que seleccionamos un conjunto de individuos de la población para que formen parte de la muestra aleatoria, cada uno de estos individuos es caracterizado por un conjunto de variables de interés en el estudio.
[ Figura 1.2 ]

Población, muestra, unidad muestral y variables que pueden determinarse a partir de esta.
Se denomina unidad muestral a cada elemento susceptible de ser seleccionado. Habitualmente la unidad muestral corresponde a un individuo, aunque no siempre es así. Por ejemplo, en un estudio de contaminación intradomiciliaria la unidad muestral podría ser un hogar (y no los sujetos que viven en ella). En un estudio en que interesa analizar el cambio a través de los años en el número de aves acuáticas en una reserva ecológica, la unidad muestral será un número de aves en cada momento del tiempo.
Llamaremos variable a cualquier característica que tome dos o más valores en una población. Por ejemplo, edad, sexo, hábito tabáquico, presencia o ausencia de una patología, valores de colesterol total, HDL y triglicéridos en un examen de lípidos, etc. Nosotros estudiaremos variables aleatorias, para las cuales no es posible anticipar su resultado, aun cuando se intente controlar los factores que puedan afectarlas. Visto de otra forma, si al mantener constantes las condiciones experimentales no es posible predecir el valor de una variable, entonces se está frente a una variable aleatoria.
Nótese que si la característica toma solo un valor, entonces es una constante y no es de interés estadístico. Por ejemplo, en el estudio de las dueñas de casa que usan Detergente X, la ciudad de residencia es constante, por lo que no es útil para discriminar entre las mujeres que usan el detergente de las que no lo hacen.
Determinar cuáles variables aleatorias deben ser medidas a cada unidad muestral es de vital importancia para el estudio. Por ejemplo, si interesa investigar factores de riesgo de infarto al miocardio, no puede dejar de medirse la edad, el hábito tabáquico o el consumo de alcohol, ya que todos son factores que se asocian con el fenómeno en estudio.
1.5 Variabilidad muestral
Cuando tomamos una muestra aleatoria de una población, lo que hacemos es observar una de muchas posibles muestras aleatorias de la población de interés.
Por ejemplo, si la población está compuesta de N = 50 individuos y decidimos tomar una muestra de n = 5 de ellos, entonces el número de muestras posibles de obtener es 2.118.760. Aunque el número de muestras posibles puede ser muy grande, en la práctica nosotros solo tenemos acceso a una de ellas.
En consecuencia, si es de interés calcular el promedio muestral, lo que obtenemos es uno de muchos promedios muestrales posibles de conseguir.
[ Figura 1.3 ]

De una población se pueden extraer muchas muestras diferentes de tamaño n. A partir de cada muestra se obtiene un promedio muestral distinto.
Claramente, si tomamos distintas muestras, el estimador será siempre diferente. Esto es conocido como variabilidad muestral.
Luego, ¿cómo podemos saber si nuestro promedio muestral es un buen estimador de µ?
La respuesta a esta pregunta está dada por el tamaño de la muestra y el método de selección. Para ilustrarlo, consideremos el siguiente ejemplo.
Ejemplo 1.2. (Se agradece la colaboración del Dr. Guillermo Marshall R., Profesor Titular de la Facultad de Matemáticas, por su aporte de este ejemplo). La siguiente hoja muestra las edades en que 350 personas enfermaron de cáncer al pulmón en cierta comunidad (asumamos que esta es la población completa). La edad media de los 350 pacientes de cáncer al pulmón es µ = 61.9 años.
[ Tabla 1.1 ]

Planilla con edad de 350 personas. En el recuadro se observa una muestra de n = 10 casos.
Para observar el efecto del tamaño muestral en la estimación de µ (es decir, en el cálculo de —x), consideremos muestras de n = 10 casos consecutivos, como la que se observa en el recuadro de la Tabla 1.1. Se obtuvieron 40 muestras de 10 casos, y se calculó la edad promedio para cada muestra, obteniéndose los siguientes resultados:
[ Figura 1.4 ]

Promedios obtenidos al repetir 40 veces el experimento de tomar una muestra n = 10.
Posteriormente, se seleccionaron n = 30 casos consecutivos y se calculó la edad media, y esta operación se realizó 40 veces. El mismo procedimiento se siguió con muestras de n = 100 casos consecutivos.
En las figuras siguientes se observan los promedios muestrales obtenidos en cada grupo de experimentos (Figura 1.5). La línea horizontal representa el promedio poblacional (61,9 años). En estas se observa que la variabilidad muestral es menor en la medida en que el tamaño muestral aumenta. Después, para obtener un buen estimador de un parámetro poblacional, lo recomendable es tomar una muestra lo más grande posible.
[ Figura 1.5 ]

Promedios de edad obtenidos al extraer 40 muestras de distintos tamaños de una población
de 350 (se observa que a medida que el tamaño de la muestra es mayor, los promedios obtenidos se aproximan más al promedio poblacional).
1.6 Tipos de muestreo
La selección de una muestra de la población de interés es de vital importancia para la obtención de resultados válidos. Si la muestra no es representativa de la población de la que procede, todos los cálculos que se hagan serán válidos solo para la muestra, sin posibilidad de extrapolar estos resultados a los individuos que no fueron incluidos en ella.
En general, estaremos interesados en muestras aleatorias, las cuales implican una selección al azar (mediante un sorteo) de los individuos que componen la muestra, en alguna etapa del proceso de muestreo. Este tipo de muestreo se denomina muestreo probabilístico.
Los principales tipos de muestreo aleatorio son el muestreo aleatorio simple, el muestreo estratificado y el muestreo sistemático. Además, actualmente adquieren mayor importancia tipos de muestreo más complejos, como el muestreo por conglomerados.
1.6.1 Muestreo aleatorio simple
Es un método de selección en que todos los elementos de la población tienen la misma probabilidad de ser elegidos en la muestra. En este tipo de muestreo se asume que la población en estudio es homogénea respecto a las variables que afectan al fenómeno estudiado.
Para aplicar este método es necesario tener un registro de todos los sujetos poblacionales (por ejemplo, un listado de los RUT, del número de ficha clínica, etc.).
La selección de los individuos muestrales podría hacerse con métodos tan simples como una bolsa con papeles numerados o con una tómbola (si la población fuera muy pequeña), hasta el uso de tablas de números aleatorios o la generación de números aleatorios mediante un computador.
Ejemplo 1.3. Supongamos que se quiere seleccionar 10 individuos de una población de 1.000. Para obtener esta muestra con Excel, podemos usar la función Aleatorio(), que genera números al azar entre 0 y 1. Por lo tanto, si la función se multiplica por 1.000 (que corresponde al tamaño de la población), se generan números entre 0 y 1.000.
Realizando lo anterior diez veces, se obtuvieron los siguientes números:
317,8 957,4 143,6 132,8 720,8 948,6 152,6 421,4 316,8 5,0
Luego, la muestra aleatoria simple está compuesta por los individuos:
5, 133, 144, 153, 317, 318, 421, 721, 949 y 957.
No obstante, si se hiciera nuevamente el proceso de usar la función Aleatorio(), se obtendrá una muestra distinta a la descrita.
1.6.2 Muestreo estratificado
Cuando la población es heterogénea respecto a una o más variables que afecten al fenómeno estudiado, seleccionar los datos mediante muestreo aleatorio simple podría resultar en una muestra no representativa de la población. En este caso, las conclusiones derivadas del análisis de los datos serían inválidas.
Por ejemplo, si las variables de interés tienen un comportamiento distinto según nivel socioeconómico (NSE), un muestreo aleatorio simple podría resultar en una proporción de individuos en cada NSE distinta a la observada en la población y por lo tanto los estimadores serían incorrectos.
Por ello, el investigador puede segmentar la población en estratos, los que corresponden a subconjuntos heterogéneos entre sí, pero que agrupan unidades homogéneas.
El muestreo estratificado es un método de selección en que se obtiene una muestra aleatoria simple de cada estrato por separado y se calculan los estimadores de parámetros (medias, proporciones, etc.) para cada estrato. Finalmente, se calcula un promedio ponderado de los estimadores de los estratos para obtener la medida resumen de interés.
Algunos problemas de investigación en los que podría ser útil usar muestreo estratificado son los siguientes:
• Interesa determinar el gasto promedio en alimentación de los hogares de cierta ciudad. Como el nivel de gasto es una característica que depende fuertemente del nivel socioeconómico familiar (NSE), conviene hacer estratos de la ciudad agrupando los hogares con niveles socioeconómicos semejantes. Así, la ciudad se podría dividir en zonas de NSE bajo, medio y alto, formando tres estratos. Al interior de cada estrato se toma una muestra aleatoria simple de hogares y se cuantifica el gasto en alimentación de cada hogar.
• En un muestreo para estimar la cosecha total de café en un país centroamericano, se sabe que la región ecológica donde se ubican los árboles influye mucho en su productividad. Después, sería conveniente estratificar las regiones según altura sobre el nivel del mar, nivel de vientos y temperatura antes de seleccionar los predios y determinar la productividad.
Respecto al número de individuos por seleccionar de cada estrato, existen dos criterios principales:
• Asignación proporcional. El número de individuos por seleccionar de cada estrato es proporcional al tamaño poblacional del estrato. Por ejemplo, si 25% de los habitantes de cierta ciudad son de nivel socioeconómico bajo, 65% de nivel medio y 10% de nivel alto, y se quiere una muestra estratificada de n = 120 casos, entonces, usando asignación proporcional, se debieran muestrear 30, 78 y 12 casos de cada NSE, respectivamente.
• Asignación óptima. El número de individuos por seleccionar de cada estrato es proporcional a la variabilidad de la característica en estudio al interior del estrato. Por ejemplo, si el gasto en alimentación presenta el doble de variación en el NSE alto que en los niveles medio y bajo, entonces se podría muestrear el doble de casos del NSE alto que de los otros dos niveles.
1.6.3 Muestreo sistemático
Este método de selección aleatoria es aplicable cuando los elementos de la población están ordenados físicamente y no existe un registro escrito o computacional, que permita hacer una selección por muestreo aleatorio simple. Por ejemplo, las fichas clínicas de un hospital, ordenadas según fecha de hospitalización en un estante, sería una situación adecuada para usar este tipo de muestreo.
Si la población tiene N elementos y se quiere una muestra aleatoria sistemática de n elementos, el procedimiento es el siguiente:
i) Calcule el tamaño del salto sistemático k = N/n. Si k tiene decimal, use la parte entera del número.
ii) Elegir un número entero al azar, r, entre 1 y k.
iii) Seleccionar de la población ordenada los elementos en la posición
r, r + k, r + 2k,…, r + (n-1)k
Al final del proceso, se tendrá una muestra de n elementos seleccionados sistemáticamente.
Ejemplo 1.4. Si tenemos 478 fichas clínicas y necesitamos seleccionar 55 para una encuesta de calidad de atención, tenemos:
N = 478 (tamaño de la población)
n = 55 (tamaño de la muestra)
k = 478 / 55 = 8.69. Usaremos saltos de 8 unidades.
Puede usar la función Aleatorio() de Excel para elegir un número al azar entre 1 y 8 (“= aleatorio()*8”). Supongamos que se obtiene r = 7.
Los números seleccionados serán 7, 15, 23, 31,…, 439 y 447.
Este método tiene la ventaja de que es fácil de aplicar. Sin embargo, se asume que el orden de los elementos de la población no afectará la estimación del parámetro de interés. Una desventaja importante es que este método es cada vez menos aceptado en publicaciones científicas.
1.6.4 Muestreo por conglomerados
Cuando es de alto costo realizar un muestreo aleatorio simple o cuando este último es inaplicable debido a que los individuos que componen la población no están identificados, un muestreo por conglomerados puede ser un método de selección adecuado.
Los conglomerados son divisiones de la población en que los elementos al interior de cada uno son heterogéneos, pero existe homogeneidad entre estas agrupaciones. Es decir, se quiere que haya “diversidad” al interior de cada conglomerado, pero que no importe cuáles conglomerados están presentes en la muestra, ya que entre ellos no hay mucha diferencia.
Esto es opuesto a lo que ocurre con los estratos, ya que aquí interesa que los individuos al interior de cada uno sean homogéneos entre sí y haya heterogeneidad entre los estratos.
El muestreo por conglomerados es un sistema de selección al azar que consta de dos fases principales: primero se eligen conglomerados al azar y luego se seleccionan elementos al interior de estos mediante un muestreo aleatorio simple.
Ejemplo 1.5. Si se quiere una muestra de 600 viviendas de una ciudad, podría ser de alto costo hacer muestreo aleatorio simple, ya que con seguridad se tendría que recorrer toda la ciudad. Si se toma una muestra por conglomerados, se podrían seleccionar al azar 20 zonas de la ciudad (entendiendo por zona un conjunto de varias manzanas), luego seleccionar 10 manzanas de cada zona y por último 3 viviendas de cada manzana, teniéndose una muestra total de 600 viviendas.
1.6.5 Selección con y sin reposición
Se asume en los tipos de muestreo anteriores que estos se realizan sin reposición. Es decir, sin devolver el elemento seleccionado a la población, después de ser observado. En este caso, la probabilidad de observar nuevamente el mismo elemento es cero, y la probabilidad de observar cualquier otro elemento se ve afectado por las observaciones anteriores.
Un muestreo es con reposición cuando cada elemento seleccionado es devuelto a la población de la cual procede después de ser observado. En este caso, la población siempre contiene los mismos elementos, por lo que todos conservan su probabilidad inicial de ser observados.
Nótese que, aunque en el muestreo sin reposición se altera la probabilidad de seleccionar un elemento, cuando ya han sido seleccionados otros previamente, si la población es lo suficientemente grande, esta probabilidad se puede considerar constante.
1.7 Tipos de variables
Como se mencionó antes (ver punto 1.4) cada uno de los individuos seleccionado en la muestra es caracterizado por un conjunto de variables de interés en el estudio. Estas variables podrían ser registradas, por ejemplo, en una planilla Excel. La planilla siguiente muestra el sexo, edad, nivel socioeconómico (NSE), estado civil y peso de seis individuos:
[ Tabla 1.2 ]
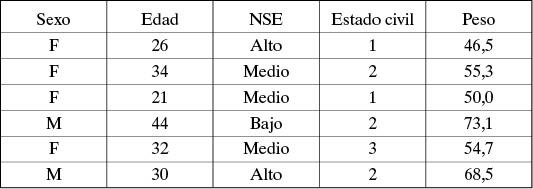
Segmento de una base de datos con cinco variables (sexo, edad, NSE, estado civil y peso)
para seis casos.
Cada variable registrada se puede clasificar en uno de los siguientes tipos:
• Variable nominal. Es aquella en que podemos clasificar sus valores en clases o categorías, sin establecer un ordenamiento sugerido por la magnitud de sus valores.
Esto significa que los valores con que se identifica cada nivel de la variable son arbitrarios. Por ejemplo, la variable sexo es nominal, ya que podemos identificar sus niveles mediante M (Masculino) y F (Femenino); o bien H (Hombre) y M (Mujer); o mediante 1 (Mujer) y 2 (Hombre), etc.
Otras variables nominales son: estado civil, causa de muerte, ciudad de residencia, tipo de parto, etc.
• Variable ordinal. Es un tipo de variables en la que sus valores o clases se pueden ordenar. Incluye variables con categorías (como gravedad de una enfermedad definida como leve, moderada o severa) y scores (como el test de Apgar del recién nacido).
En las ciencias de la salud, se generan muchas variables ordinales que intentan cuantificar características difíciles o imposibles de medir directamente, como la gravedad cardiaca medida usando scores como APACHE o TISS; el desarrollo puberal medido con escala de Tanner; el estado nutricional que se puede definir como bajo peso, normal, sobrepeso y obeso, etc.
Como se observa, las variables ordinales no tienen unidad de medida. Tampoco tiene sentido cuantificar la diferencia o la razón entre dos valores ordinales. Por ejemplo, si una persona tiene un puntaje de gravedad igual a 30 y otra tiene un puntaje de gravedad igual a 60 (asumiendo que mayor puntaje significa mayor gravedad), no podemos decir que la segunda tenga el doble de gravedad que la primera; solo podemos decir que la segunda está más grave.
• Variable intervalar. Es una variable cuantificable de manera objetiva, por lo que posee un orden natural en sus valores y es posible medir la diferencia entre dos valores. Generalmente tiene unidad de medida.
Una variable intervalar se denomina discreta cuando no puede tomar decimales, como en las variables de conteo (número de hijos, número de caries, días de hospitalización, etc.). Se denomina continua cuando toma cualquier valor en un intervalo (como el peso, talla, índice de masa corporal, triglicéridos, etc.).
El esquema siguiente resume los tipos de variables:
[ Figura 1.6 ]
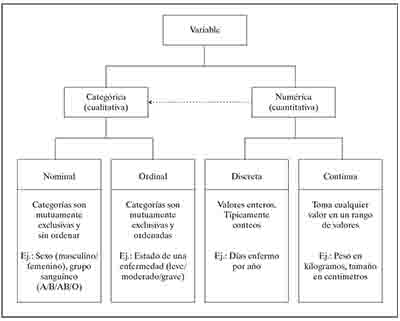
Clasificación de tipos de variables.
Los dos tipos de variable de interés estadístico
Para la mayoría de las descripciones y análisis estadísticos basta con identificar dos tipos de variables:
• Variables categóricas. Son aquellas para las cuales no es posible y no tiene sentido obtener su promedio. Incluye las nominales (como sexo o estado civil), las ordinales con pocos niveles (como nivel socioeconómico o severidad de una enfermedad) y las intervalares en rangos (como grupos etarios o peso de recién nacido en rangos).
• Variables numéricas. Son aquellas para las cuales tiene sentido obtener su promedio. Incluye las intervalares (como peso o número de hijos) y las ordinales que toman un rango amplio de valores (como puntaje Apgar o score Apache de gravedad cardiaca).
Nótese que una variable numérica puede transformarse en categórica construyendo rangos. Asimismo un conjunto de variables categóricas puede transformarse en una variable numérica construyendo scores.
1.8 Notación para variables aleatorias y sus mediciones
Por lo general se utiliza la letra N mayúscula para referirse al tamaño de una población (asumiendo que es una población finita) y la letra n minúscula para referirse al tamaño de una muestra.
Cuando nos referimos a una variable aleatoria en forma genérica (la variable Sexo, la variable Peso, etc.), usaremos letras X, Y o Z mayúsculas.
Al referirnos a los valores que toma una variable aleatoria X en una muestra de tamaño n, usaremos la letra x minúscula con subíndices: x1, x2,…, xn. Donde x1 es el valor de X en el primer sujeto muestral, x2 el valor en el segundo sujeto y así sucesivamente.
Cuando aludimos a los valores muestrales ordenados de la variable aleatoria X, usaremos la notación: x(1), x(2),…, x(n). De modo que x(1) ≤ x(2) ≤ … ≤ x(n). Nótese que x(1) es el mínimo valor muestral de X y x(n) es el máximo.
Usaremos el símbolo Σ para referirnos a la suma de un conjunto de valores. Por ejemplo:


Ejemplo 1.6. Consideremos la Tabla 1.2, que muestra los datos de algunas variables para n = 6 individuos.
Sea X la variable Edad. Luego, los valores muestrales de X son:
x1 = 26, x2 = 34, x3 = 21, x4 = 44, x5 = 32 y x6 = 30.
Los valores muestrales ordenados son:
x(1) = 21, x(2) = 26, x(3) = 30, x(4) = 32, x(5) = 34 y x(6) = 44.
La suma de los n valores muestrales es:
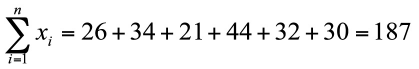
El producto de los n valores muestrales es:
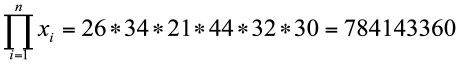
1.9 Descripción de variables categóricas
Las variables categóricas se describen principalmente mediante dos medidas resumen: el número y el porcentaje de casos en cada nivel de la variable. Como veremos más adelante, la proporción de casos en cada categoría también es una medida resumen de interés, ya que estima la probabilidad de ocurrencia de un evento en la población.
Los resultados obtenidos para una variable categórica se muestran en una tabla de frecuencias, que es la forma en que habitualmente los programas estadísticos entregan el resumen de una variable categórica.
Verbigracia, la tabla siguiente resume los resultados obtenidos para la edad en que enferman de cáncer al pulmón los 350 casos descritos en el Ejemplo 1.2.
[ Tabla 1.3 ]
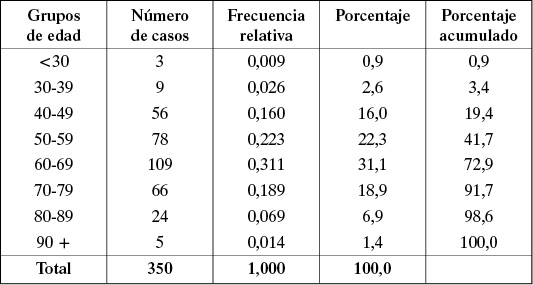
Tabla de frecuencias de 350 casos según el grupo de edad al cual pertenecen.
La interpretación de las columnas de la tabla de frecuencias es la siguiente:
• La primera columna da cuenta de los niveles observados en la muestra para la variable tabulada.
• La segunda columna indica el número de individuos en cada nivel de la variable. La última fila de esta columna presenta el total de casos.
• La tercera columna indica la proporción de sujetos en cada nivel (número de casos en el nivel dividido por el total de casos tabulados). La suma de estas siempre debe ser 1.
• La cuarta columna indica el porcentaje de casos en cada nivel (frecuencia relativa * 100). El total siempre debe sumar 100%.
• La última columna indica el porcentaje de casos hasta el nivel que se esté observando (por ejemplo, el porcentaje de casos que tiene menos de 80 años es 91,7%).
Por ejemplo, de la tabla de frecuencias podemos observar que:
• El 22,3% de la muestra tiene edad entre 50 y 59 años.
• El 41,7% tiene menos de 60 años.
• Si suponemos que los datos tabulados provienen de una población de tamaño 10.000, entonces podemos decir que existen aproximadamente 2.230 sujetos en la población con edad entre 50 y 59 años.
• El porcentaje de personas con 60 o más años es 100-41,7 = 58,3%.
1.10 Presentación gráfica de variables categóricas
Generalmente las variables categóricas se representan mediante gráficos de barras y gráficos circulares (también llamados tortas o pies).
Gráfico de barras
Un gráfico de barras es aquel en que los niveles de la variable se representan por barras verticales, cuya altura indica el número de casos, el porcentaje o la proporción de individuos en cada nivel.
[ Figura 1.7 ]

Gráfico de barras de datos en Tabla 1.3.
La figura anterior muestra el número de casos en cada nivel de la variable, por lo que es adecuado para hacer comparaciones entre los grupos graficados. Sin embargo, si se grafica el porcentaje es posible, además, hacer estimaciones a la población (los porcentajes muestrales estiman a los poblacionales). Igualmente, cuando se grafica más de una población solo es adecuado hacer gráficos de porcentajes, si el interés es comparar entre estas.
Este gráfico también se puede hacer con barras horizontales (de preferencia cuando la variable tiene muchos niveles), tener profundidad (gráfico 3D), y reemplazar las barras por conos, pirámides o cilindros, entre otras opciones.
Gráfico circular
Un gráfico circular es aquel en que el total de individuos es representado por un círculo (torta) y cada nivel de la variable corresponde a una porción del círculo, proporcional a su frecuencia relativa. De este modo, el producto de los 360° del círculo y la frecuencia relativa entrega los grados que corresponden a cada nivel de la variable.
[ Figura 1.8 ]

Gráfico circular de datos en Tabla 1.3.
Para resaltar algún nivel de la variable en particular, la porción de torta correspondiente puede mostrarse separada del resto, como en el gráfico anterior.
Los gráficos circulares no son buenos para comparar dos o más porciones, a menos que estas sean muy distintas. En este caso, es preferible hacer gráficos de barras.
1.11 Descripción de variables numéricas
Las variables numéricas se describen mediante el uso de una gran variedad de medidas resumen, las cuales se clasifican en dos grandes grupos: las medidas de posición y las de dispersión. Las medidas de posición, a su vez, se dividen en medidas de tendencia central y percentiles.
1.11.1 Medidas de tendencia central
Las medidas de tendencia central son aquellas que resumen en un solo valor el centro de los datos. Las más comunes son el promedio aritmético, la media geométrica y la mediana.
[ Figura 1.9 ]

Medida de tendencia central (la figura muestra dos conjuntos de datos, donde la primera curva tiene una medida de tendencia central menor que la segunda).
Promedio aritmético
También llamado media o simplemente promedio, es la medida de tendencia central utilizada con más frecuencia en la investigación científica. Se calcula como la suma de los valores dividido por el número de datos sumados.
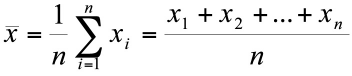
En general, n se refiere al tamaño de la muestra, pero si hay individuos para los cuales se desconoce su valor de X, entonces n será menor que el tamaño muestral. En cualquier caso, siempre se debe usar como denominador el número de valores consignados.
Ejemplo 1.7. La media de la muestra tamaño 10 con datos: 73, 68, 59, 40, 81, 72, 40, 70, 59 y 72 es:
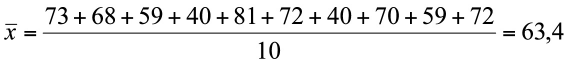
Si no se hubiera consignado la edad para uno de estos 10 individuos, entonces habría un valor menos en el numerador y sería necesario dividir por 9.
El promedio aritmético es un buen indicador del centro de los datos cuando su distribución es simétrica con respecto a esta medida de posición.
Ejemplo 1.8. En el gráfico de barras de la edad en que se enferma de cáncer al pulmón (Figura 1.7), se observa que hay cierta simetría en la distribución de los datos en torno al promedio (que es 61,9 años y está en la barra central). Podemos concluir entonces que, en este caso, la media aritmética es un buen indicador del centro de los datos.
Las ventajas del promedio aritmético son su facilidad de cálculo y de interpretación. Su principal desventaja es que se ve afectado por valores extremos u outliers que influyen la simetría de la distribución de los datos.

Media geométrica
Es una medida de posición que se usa cuando existe la necesidad de resumir datos que presentan valores extremos o cuya distribución sea muy asimétrica. A pesar de ser menos empleada que la media aritmética, es útil en algunas áreas específicas de la medicina, como en hematología.
Se calcula como la raíz enésima del producto de las n observaciones muestrales consignadas:
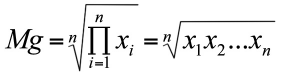
Ejemplo 1.9. La media geométrica de los valores 73, 68, 59, 40, 81, 72, 40, 70, 59 y 72 es:
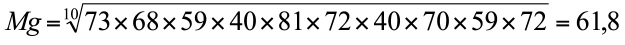
Una característica importante de la media geométrica es su poca sensibilidad a la presencia de valores extremos. Su desventaja es que es poco intuitiva como medida del centro de los datos.
Mediana
La mediana es el valor que ocupa la posición central cuando estos se ordenan de menor a mayor, de modo que 50% de los datos es menor o igual a la mediana y el resto es mayor, formándose dos grupos de igual tamaño.
Para ilustrar el cálculo de la mediana, consideremos nuevamente las 10 edades muestrales al momento de enfermar de cáncer al pulmón: 73, 68, 59, 40, 81, 72, 40, 70, 59, 72. Luego se realiza el siguiente procedimiento:
• Se ordenan los datos de menor a mayor: 40, 40, 59, 59, 68, 70, 72, 72, 73, 81.
• Se determina el dato que está en la mitad de la muestra ordenada. Si el tamaño muestral es impar, entonces existe un valor que está en la mitad de la muestra y corresponde a la mediana. Si el tamaño muestral es par, se calcula el promedio de los dos valores centrales.
Para los datos del ejemplo, como el n es par, la mediana es:
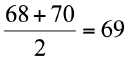
La principal ventaja de la mediana es que es muy poco sensible a la presencia de valores extremos en los datos.
[ Figura 1.10 ]

Diagrama que representa la relación entre la media y la mediana
En la figura anterior se observa que, al haber un valor extremo (arriba), el promedio aritmético se ve “atraído” en la misma dirección del valor extremo. Al eliminar el outlier (abajo) el promedio retorna a una posición más centrada. Asimismo, la mediana se ve poco afectada por la presencia o la ausencia del outlier, al encontrarse en el centro de la muestra ordenada.
1.11.2 Percentiles
Un percentil de orden p (0 < p < 100) es un valor que se obtiene en la muestra ordenada, de modo que el p% de los datos muestrales es menor o igual al valor del percentil y el (100-p)% restante queda sobre el percentil.
Dado que los percentiles se calculan en la muestra ordenada, también se les denomina estadísticos de orden.
Para ilustrar lo anterior, observe la siguiente figura. En la abscisa se indica el valor que debiera corresponder al percentil 10, ya que acumula 10% de los datos muestrales y deja sobre el percentil al 90% restante.
[ Figura 1.11 ]
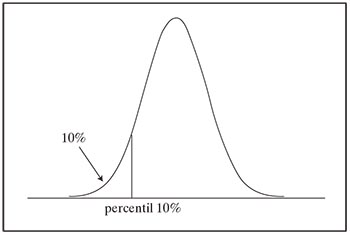
Representación gráfica del percentil 10% en datos con distribución simétrica.
Por ejemplo, si se sabe que un recién nacido que mide 47 cm está en el percentil 15, entonces 15% de los recién nacidos mide lo mismo o menos que él y 85% restante mide más.
Hay varias formas de calcular un percentil y no todas entregan exactamente el mismo resultado. En este texto presentaremos una de las formas más sencillas de cálculo de un percentil de orden p:
• Primero se ordenan los datos de menor a mayor. De este modo, si la muestra es de tamaño n, los datos muestrales ordenados son x(1), x(2),…, x(n).
• Se determina la posición, dentro de la muestra, en que se encuentra el percentil de orden p. Esta posición, que llamaremos k y que varía entre 1 y n, se calcula mediante la siguiente expresión:
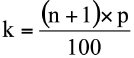
• Si k resulta ser un número con decimales, se aproxima al entero más cercano. Luego, el percentil de orden p buscado corresponde a la observación x(k).
• Si el decimal es .5 se promedian las dos observaciones adyacentes. Luego, el percentil de orden p buscado corresponde a la observación (x(k-0.5)+ x(k+0.5))/2.
Algunos percentiles importantes
Aunque se puede calcular cualquier percentil entre 0 y 100, algunos son utilizados con más frecuencia en investigación biomédica. Estos son:
• Cuartiles. Llamados así porque dividen la muestra en cuatro partes. Corresponden a los percentiles 25, 50 y 75. Estos se denominan como Q1, Q2 y Q3, respectivamente.
• Deciles. Dividen a la muestra en 10 partes. Corresponden a los percentiles múltiplos de 10, desde el percentil 10 hasta el 90.
• Percentiles 1, 5, 10, 90, 95 y 99. Se usan habitualmente para establecer criterios de “normalidad”.
Por ejemplo, en una muestra de recién nacidos sanos, los niños con peso inferior al percentil 10 podrían considerarse con bajo peso y aquellos sobre el percentil 90 se considerarían con sobrepeso. Igual criterio puede establecerse con los percentiles 5 y 95 o 1 y 99.
Ejemplo 1.10. Consideremos los primeros 25 datos de edad al momento de enfermar de cáncer al pulmón (ver Ejemplo 1.2). Para calcular los percentiles 25, 50 y 75 (es decir, los cuartiles), es necesario ordenar los datos de menor a mayor. Las edades ordenadas son:
[ Tabla 1.4 ]
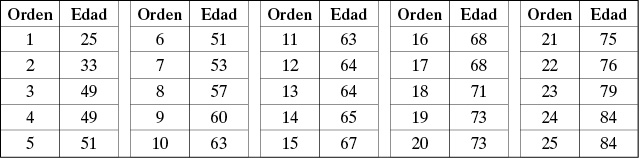
Datos ordenados de primeros 25 individuos en Tabla 1.1
Luego, los percentiles estimados son:
[ Tabla 1.5 ]

Percentiles 25, 50 y 75 de los datos en Tabla 1.4.
Interpretación. El 25% de los datos muestrales tiene hasta 52 años. El 50% tiene hasta 64 años y 75% tiene hasta 73 años.
1.11.3 Medidas de dispersión
Las medidas de dispersión son aquellas que miden la variabilidad de un conjunto de datos. Al analizar un conjunto de datos, no basta con calcular una medida de tendencia central, ya que esta no nos indica qué tan concentrados o dispersos se encuentran los datos en torno a este valor. Para obtener esta última información, es necesario calcular una medida de dispersión.
[ Figura 1.12 ]

Medida de dispersión (la figura muestra dos grupos de datos con distinto grado de variabilidad: la curva más alta muestra una variabilidad menor que la curva más baja).
Ejemplo 1.11. Consideremos las variables X = Edad en que se enferma de influenza e Y = Edad de primer diagnóstico de presbicia.
Si tomamos muestras de ambas poblaciones, el promedio muestral de las dos variables podría ser similar: alrededor de 40 años. Con solo esta información, podríamos pensar que las distribuciones de X e Y son similares.
Sin embargo, si nos informan que la influenza puede afectar desde niños hasta adultos mayores, mientras que la presbicia afecta principalmente la visión de los adultos, entonces nuestra percepción de las distribuciones cambia: esperaríamos que la variable X tenga mayor dispersión que la variable Y.
Según la figura anterior (Figura 1.12), la distribución de la presbicia tomaría una forma similar a la curva más alta y la influenza similar a la más baja.
Para cuantificar la variabilidad de los datos, se puede calcular la diferencia entre cada dato y el promedio muestral y luego resumir estos resultados en un solo valor. Aunque una manera intuitiva de resumir los datos es la suma de las diferencias, esta siempre es igual a cero. Dos modos de no considerar el signo de las diferencias, son calcular la suma de sus valores absolutos o de sus valores al cuadrado.
La medida que se basa en las diferencias absolutas se denomina desviación absoluta, que no es tratada en este texto debido a su poco uso en las ciencias de la salud. Las medidas basadas en las diferencias cuadráticas son la varianza y la desviación estándar.
Una medida que no se basa en estas diferencias es el rango, que se describe más adelante.
Varianza
La varianza es similar a un promedio de las desviaciones cuadráticas de cada dato respecto a la media aritmética. La varianza muestral se simboliza s2 y se calcula como:
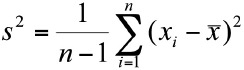
Ejemplo 1.12. En la muestra de edades: 73, 68, 59, 40, 81, 72, 40, 70, 59, 72, que tiene promedio muestral igual a 63,5 años, la varianza muestral es:
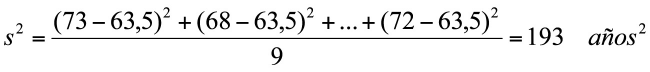
En el ejemplo anterior, los datos y el promedio están expresados en años, pero la varianza está expresada en años2, lo cual hace difícil determinar cuándo una varianza es “grande” o “pequeña”. Por estar en una escala distinta, es que la varianza no se usa habitualmente como medida de dispersión.
Desviación estándar
La desviación estándar es la medida de dispersión más utilizada, ya que está en la misma unidad de medida de los datos y el promedio. Se simboliza con la letra s, y se calcula como la raíz cuadrada de la varianza.
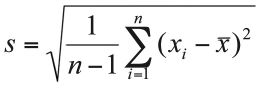
Ejemplo 1.13. Para la muestra de edades usada en el ejemplo previo, la desviación estándar es:
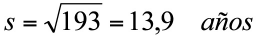
Una importante debilidad de la desviación estándar es que es sensible a la presencia de valores extremos: primero porque se basa en desviaciones respecto a la media aritmética (que es sensible a valores extremos) y además porque los sumandos que involucren a estos valores serán muy grandes, haciendo aumentar aún más la dispersión.
Relación entre el promedio aritmético y la desviación estándar
Sin importar la distribución de una variable numérica, al menos 75% de los datos muestrales se sitúa entre x− – 2s y x− + 2s .
Las relaciones más importantes entre la media y la desviación estándar surgen cuando la distribución de los datos es simétrica y en forma de campana, como en el caso de la distribución normal (que veremos en el capítulo 3). En este caso se cumple:
• Aproximadamente 68% de los datos muestrales se sitúa entre x− ± s.
• Aproximadamente 95% de los datos muestrales se sitúa entre x− ± 2s.
• Aproximadamente 99% de los datos muestrales se sitúa entre x− ± 3s.
El intervalo más utilizado de los anteriores es el que permite acotar a 95% de los datos muestrales.
Uno de los motivos es por su uso en la construcción de patrones de comportamiento normal de una variable, en el cual se considera que 95% de los datos centrales son el comportamiento “normal” y el 5% restante, ubicado por fuera del rango x− ± 2s, presenta alguna anomalía o patología respecto a la variable estudiada.
Otro motivo es por el uso habitual en bioestadística de medir variables con un margen de error de 5%. Esto se verá en detalle en el capítulo 3.
[ Figura 1.13 ]

Representación gráfica de una variable con forma de campana. El 95% de los datos se encuentra dentro del rango x− ± 2s.
Rango
El rango es la diferencia entre el valor máximo y el valor mínimo de la variable.
Ejemplo 1.14. Para los datos de edad 73, 68, 59, 40, 81, 72, 40, 70, 59, 72, el rango muestral es 81-40 = 41 años. Es decir, la diferencia entre las edades mínima y máxima es de 41 años.
Actualmente se prefiere presentar los valores mínimo y máximo en vez del rango, ya que aportan más información sobre la dispersión de los datos y permite calcular el rango fácilmente.
La desventaja del rango como medida de dispersión es su obvia sensibilidad a la presencia de valores extremos, porque se construye justamente con el mayor y el menor valor muestral.
Además, casi con seguridad en la población existe un valor menor que el mínimo observado en la muestra y un valor mayor que el máximo muestral. En consecuencia, el rango muestral muy probablemente subestima al rango poblacional.
1.11.4 Selección de medidas resumen de una variable numérica
Cuando se resumen y reportan los resultados de una variable numérica, siempre se presentará el número de casos, una medida de tendencia central y una medida de dispersión.
Entre las medidas disponibles, ¿cuáles son las más adecuadas para elegir? La regla general es la siguiente:
• Cuando los datos tienen distribución simétrica o, al menos, si existe poca dispersión (no hay valores extremos), lo habitual es presentar el número de casos, la media aritmética y la desviación estándar.
Ejemplo 1.15. Para los datos de edad 73, 68, 59, 40, 81, 72, 40, 70, 59, 72, la edad media de la muestra es 63,5 ± 13,9 años (n = 10).
• Cuando los datos exhiben mucha variabilidad o ante la existencia de valores extremos, se presenta el número de casos, la mediana como medida de tendencia central y el rango como medida de dispersión.
Ejemplo 1.16. Para la muestra de 10 edades, la mediana muestral es 69 años, con un rango de entre 40 y 81 años (n = 10).
• Cuando hay mucha variabilidad, en ocasiones se presenta el número de casos, la media geométrica y el rango. Esta opción es poco usada, pero podría ser útil cuando se quieran comparar los resultados de un estudio con otros ya publicados.
Ejemplo 1.17. Para la muestra de 10 edades, la media geométrica es 61,8 años, con un rango de entre 40 y 81 años (n = 10).
1.12 Propiedades de la media y la varianza
Si X es una variable aleatoria con media poblacional µ y varianza σ2, y a y b son constantes, entonces se cumplen las siguientes propiedades:
a) La variable X + b tiene media µ + b y varianza σ2. Es decir, si los datos tienen media µ, entonces al sumar b a cada valor de X, la nueva variable tiene media µ + b, pero no se modifica su varianza (solo se desplaza la curva en b unidades).
[ Figura 1.14 ]

Distribuciones con media µ (a la izquierda) y µ + b (a la derecha).
b) La variable aX tiene media am y varianza a2σ2. Al multiplicar cada valor de X por a, la nueva variable tiene media aµ y su varianza se amplifica por a2. Si a > 1, la varianza de la nueva variable será mayor que la varianza de X (a2 efectivamente amplifica la varianza σ2); y si a < 1, entonces la varianza será menor que la varianza de X (ya que a2σ2 < σ2, cuando a < 1).
[ Figura 1.15 ]

Cambio en la varianza de X al multiplicar los datos por una constante.
c) La variable aX + b tiene media aµ + b y varianza a2σ2. Esto es consecuencia directa de las propiedades 1 y 2.
1.13 Medidas de variabilidad de los estimadores muestrales
Cualquiera sea la medida resumen que se calcule en una muestra, lo que se obtiene es uno de muchos posibles estimadores de un parámetro poblacional, ya que la muestra es, a su vez, una de varias que es posible tomar de la población.
Lo que debiéramos esperar, es que cualquiera sea la muestra que tomemos, no exista mucha diferencia en la estimación del parámetro. Es decir, que no haya mucha dispersión entre los estimadores.
Esta dispersión entre las medidas calculadas con distintas muestras, se denomina error estándar.
Error estándar del promedio
Para comprender el concepto de error estándar, debemos recordar el de variabilidad muestral (ver punto 1.5): al calcular un promedio muestral se obtiene uno de los muchos promedios posibles de estimar, ya que la muestra con que contamos es una de las tantas que se podría haber tomado.
Luego, si tenemos una muestra de tamaño n, y dado que no es la única de ese tamaño que podemos obtener, ¿cuánta dispersión se debiera esperar entre los promedios muestrales? (ver esquema abajo).
El estimador de la dispersión de la media aritmética se denomina error estándar.
[ Figura 1.16 ]

Promedios calculados a partir de las posibles muestras de una población (se espera que la gráfica de los promedios sea una curva simétrica en forma de campana).
El error estándar mide la variabilidad esperada del promedio muestral como estimador de la media poblacional. Se simboliza “e.s.” o SEM (por la abreviación de standard error of mean) y se calcula como:
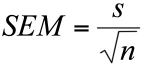
Donde s es la desviación estándar muestral y n, el tamaño de la muestra.
Ejemplo 1.18. Para los 10 datos de edad: 73, 68, 59, 40, 81, 72, 40, 70, 59, 72, el error estándar estimado es:
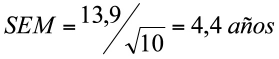
Nótese que el error estándar es menor en la medida en que el tamaño de la muestra aumenta. Más allá de que la fórmula refleja esto, debido a que el n está en el denominador, intuitivamente no se espera mucha dispersión entre promedios de muestras aleatorias de tamaño muy grande.
Ejemplo 1.19. Considere los datos de edad en que 350 personas se enferman de cáncer al pulmón y el experimento de tomar 40 muestras de distintos tamaños, descrito en el Ejemplo 1.2.
[ Figura 1.17 ]

La dispersión de los promedios muestrales es evidencia del error estándar para cada tamaño muestral.
En el gráfico anterior, se observa que la variabilidad de los promedios es menor a medida que el tamaño de las muestras es mayor. La dispersión que estamos observando es el error estándar.
Relación entre el promedio aritmético y el error estándar
El promedio aritmético ± dos errores estándar cubre aproximadamente 95% de los promedios de muestras de tamaño n, así como el promedio aritmético ± dos desviaciones estándar cubre aproximadamente 95% de los datos muestrales.
Como veremos más adelante, el rango de valores entre la media ± dos errores estándar es denominado un intervalo de confianza, y se probará que, bajo ciertas condiciones, con una probabilidad de 95%, la media poblacional se encontrará en el intervalo construido.

1.14 Presentación gráfica de variables numéricas
Histograma
El histograma es un gráfico que permite observar la distribución de un conjunto de datos. Aporta información sobre la tendencia central y dispersión, el grado de simetría, presencia de valores extremos, etc. A pesar de servir como guía para decidir el tipo de medidas resumen que se reportarán, y su importancia para el análisis de un conjunto de datos, rara vez se da cuenta de él en la literatura científica.
El gráfico muestra los valores de la variable de interés en el eje horizontal y en el eje vertical el número de casos o proporción para cada valor específico. Si la variable que se graficará toma un rango amplio de valores, se puede agrupar en intervalos.
Ejemplo 1.20. El siguiente es el histograma de la edad al momento de enfermar de cáncer al pulmón para los 350 casos, usando el programa estadístico SPSS. Se observa que los datos son simétricos, las medidas de tendencia central (promedio y mediana) debieran estar alrededor de los 60 años y no se aprecian valores extremos.
[ Figura 1.18 ]

Histograma de las edades en que 350 personas enfermaron de cáncer al pulmón.
Cajón con bigotes (Box-plot)
Es un gráfico que muestra medidas de posición y dispersión de un conjunto de datos. Aporta información sobre la distribución de la variable y sobre los valores extremos.
Está conformado por un rectángulo (cajón) y líneas verticales a él (bigotes). Los bordes inferior y superior del cajón representan el primer y tercer cuartil, respectivamente, y los extremos de los bigotes, los valores mínimo y máximo de la variable. Una línea horizontal dentro del cajón indica el valor de la mediana (segundo cuartil).
Otra variante del box-plot, menos usada, reemplaza la mediana por el promedio y el primer y tercer cuartil por el promedio menos una desviación estándar y el promedio más una desviación estándar, respectivamente.
[ Figura 1.19 ]

Box-plot de las edades en que 350 personas enfermaron de cáncer al pulmón.
La mayor utilidad del cajón con bigotes aparece cuando se quiere comparar dos o más grupos, ya que se ven reflejadas gráficamente las diferencias entre sus distribuciones.
Ejemplo 1.21. Si se sabe que dentro del grupo de 350 personas que enfermaron de cáncer al pulmón, las primeras 175 edades son de hombres y las siguientes 175 son de mujeres, el box-plot comparativo para la edad sería:
[ Figura 1.20 ]

Box-plot para comparar la distribución de las edades en que enfermaron de cáncer al pulmón, para una muestra de 350 personas según sexo.
Gráfico de promedio ± Desviación estándar (DS) o Error estándar (ES)
Estos gráficos son similares en apariencia, pero distintos en objetivo. El gráfico de media ± DS se usa para mostrar la distribución de los datos y es una alternativa al box-plot, aunque menos utilizada. El gráfico de media ± ES muestra la precisión del promedio y se usa habitualmente cuando se comparan dos o más grupos.
En ambos tipos de gráfico, la media está representada por un punto unido por líneas verticales al promedio ± DS o promedio ± ES, según corresponda.
De acuerdo a lo descrito en la relación entre el promedio y el error estándar (punto 1.13), una variante muy práctica es el gráfico de media ± 2*ES, que permite al observador determinar si existen diferencias importantes en la variable en estudio entre los grupos comparados.
[ Figura 1.21 ]

Gráfico de promedio ± ES de las edades en que enfermaron de cáncer al pulmón según sexo.
Gráfico de tallo y hoja (Stem-and-Leaf)
Al igual que el histograma, es un gráfico que permite observar la distribución de un conjunto de datos, por lo que aporta información sobre la tendencia central y dispersión, el grado de simetría, presencia de valores extremos, entre otros, y adicionalmente presenta los valores que componen la muestra.
Para ilustrar la forma como se construye un gráfico de tallo y hoja, considere el siguiente caso:
Ejemplo 1.22. El gráfico siguiente muestra la distribución de la edad para los 350 casos de personas que enfermaron de cáncer al pulmón.
La primera columna indica el número de observaciones acumulativo hasta la mitad del gráfico y el número acumulativo desde abajo hacia arriba, también hasta la mitad del gráfico; el número de casos entre paréntesis indica la fila donde se sitúa la edad mediana. La segunda columna muestra las decenas de la edad y finalmente cada barra muestra las unidades. Al unir cada decena con una unidad, se obtiene un valor de la edad graficada. Así, la primera fila muestra que hay una persona que enfermó a los 24, la segunda muestra que hay una persona que enfermó a los 27 y otra a los 28, etc.
[ Figura 1.22 ]

Gráfico de tallo de las edades en que 350 personas enfermaron de cáncer al pulmón
Ejercicios
1.1 La tabla siguiente muestra los pesos de nacimiento de 15 niños cuyas madres aumentaron más de 12 kilos de peso durante su embarazo. Los datos se muestran ordenados de menor a mayor:
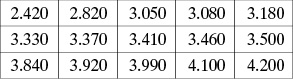
i) Obtenga una estadística descriptiva de los datos anteriores, asumiendo que la distribución es simétrica, sin valores extremos.
ii) Calcule una estadística descriptiva asumiendo que hay asimetría y/o valores extremos.
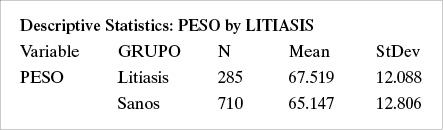
1.2 Para una muestra de 995 personas incluidas en un estudio de litiasis vesicular, se obtuvo la siguiente descripción del peso (en kilos) usando Minitab:
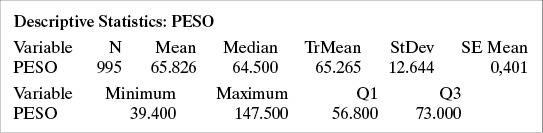
i) Interprete los resultados obtenidos. ¿Qué significa que SE Mean (el error estándar) sea igual a 0,401?
ii) ¿Cómo describiría la muestra? ¿Usando número de casos, promedio y desviación estándar o usando número de casos, mediana y rango?
iii) De acuerdo al siguiente histograma de los datos de peso, ¿considera usted que entre x–2s y x+2s se encuentra 95% de las observaciones? ¿Por qué?
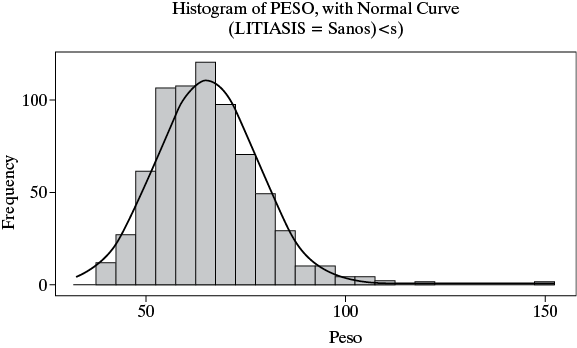
iv) Si la población bajo estudio tiene un total de 150.000 individuos y suponiendo que los datos de peso tiene distribución en forma de campana de Gauss, ¿cuántos de ellos se espera que tengan un peso inferior a x– - s?
v) ¿Le parece razonable pensar que si tomáramos varias muestras de tamaño 995, un histograma de estas medias tendría forma de campana de Gauss?
vi) ¿Entre qué valores se debiera situar 95% de los promedios de peso para muestras de tamaño 995?
vii) ¿Cuál es la probabilidad (aproximada) de obtener un promedio muestral superior a 67 kilos, en una muestra de tamaño 995?
viii) Responda sin hacer cálculos: la probabilidad de encontrar un individuo con peso superior a 67 kilos, ¿es mayor o menor que la probabilidad calculada en el punto anterior?
ix) ¿Qué tipo de gráfico le parece más adecuado para mostrar los siguientes resultados?
1.3 Para las siguientes encuestas, describa la población en estudio, la o las posibles fuentes de imprecisión de las respuestas y limitaciones en la representatividad de las muestras.
i) Una empresa de estudios agropecuarios realiza una encuesta para determinar el peso promedio de las vacas de una región. De una lista de las granjas disponibles en esa zona, se eligen al azar 50 de ellas. Luego se registra el peso de cada vaca de las 50 granjas elegidas.
ii) Aproximadamente 16.500 mujeres regresaron la Healthy Women Survey (la Encuesta de Salud de las Mujeres) que apareció en el ejemplar de septiembre de 1992 de la revista Prevention. El ejemplar de mayo de 1993, donde se informó de la encuesta, estableció que “92% de nuestras lectoras calificaron su salud como excelente, muy buena o buena”.
iii) Para estudiar el contenido nutricional de los menús en pensiones para ancianos en el estado de Washington, en Estados Unidos (estudio realizado en 1993), se enviaron encuestas a las 184 pensiones autorizadas en el estado, dirigidas al administrador y al gerente de servicios alimenticios. Un total de 43 cuestionarios fueron regresados antes de la fecha límite, incluyendo los menús.
1.4 En una muestra aleatoria de cierta población, se determinó que el peso promedio de nacimiento fue x– = 3200 grs, s2 = 250000 grs2. Asuma que la distribución de los pesos de nacimiento tiene forma de campana de Gauss.
i) Determine un rango aproximado de valores de peso de nacimiento que detecte a 2,5% de los niños con peso más bajo y a 2,5% de los niños con peso más alto.
ii) Determine el tamaño muestral mínimo necesario, de modo que aproximadamente 95% de los promedios muestrales de ese tamaño no se diferencien del peso promedio de la muestra descrita en el enunciado, en más de 50 gramos.
1.5 Observe la figura siguiente:
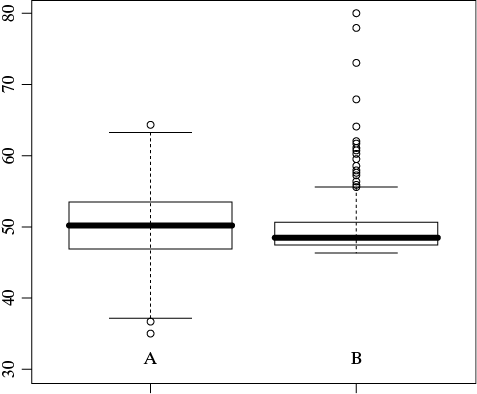
Conteste las siguientes afirmaciones con una V si considera que es Verdadera o con una F si considera que es Falsa. Justifique sus respuestas.
__ Asumiendo que en ambos box-plot se utilizaron el mismo tipo de medidas resumen, se puede deducir que ambos se hicieron usando promedio y desviación estándar.
__ En el box-plot B, es probable que la mediana subestime al promedio.
__ El box-plot A sugiere una variable con distribución relativamente simétrica.
__ Suponga que la variable en estudio es la edad. Si fuera de interés determinar cuál de las dos muestras (A o B) es más joven, la figura muestra resultados contradictorios para la mediana y el promedio muestrales.