Capítulo I

Una introducción a la argumentación

Este capítulo tiene la intención de proporcionar una serie de nociones básicas en referencia a la argumentación en general. Todos estamos acostumbrados a decir cosas como “éste es un buen argumento”, o “éste es un argumento falaz”, o frases similares. Sin embargo, ¿qué es lo que hace que un argumento sea un buen argumento? Desde un punto de vista tradicional, la idea de argumento se ha vinculado a la lógica, y ésta, a su vez, ha sido entendida como la ciencia o el arte del pensamiento. La influyente obra, conocida como lógica de Port Royal (1662), de Antoine Arnauld y Pierre Nicole se titulaba, precisamente, La logique ou l’art de penser.^[8]

Antiguamente se acostumbraba a tener una concepción psicologista de la lógica, que se concebía como la descripción de los procesos psicológicos de los seres humanos; sin embargo, hoy día esta concepción ha quedado totalmente abandonada.^[9] Por otra parte, la idea de la lógica como arte del pensar es más plausible. Podemos concebir la lógica como una disciplina normativa destinada a ordenarnos cómo tenemos que pensar (argumentar, inferir) para hacerlo de manera correcta. Como dice uno de los lógicos y filósofos vivos más importantes, W. V. Quine, “la lógica es la tecnología de la deducción”.^[10]

La lógica muestra cómo podemos derivar o inferir una conclusión^[11] a partir de un conjunto de enunciados denominados premisas. Asimismo, la lógica garantiza que si las premisas son verdaderas, la conclusión también será necesariamente verdadera o, dicho de otro modo, que no es posible que las premisas sean verdaderas y la conclusión sea falsa.

Este capítulo contiene una noción precisa de argumento, algunas consideraciones sobre el lenguaje en el que se expresan los argumentos (que nos van a ser útiles también más adelante) y algunas de las formas más habituales de argumentos falaces, junto con una presentación más sistemática de algunas nociones muy rudimentarias de lógica y de las reglas lógicas de los cálculos denominados de deducción natural.

No obstante, no podemos dejar de tener presente que el derecho se expresa en un lenguaje que no podemos considerar verdadero o falso; el lenguaje de las normas es, básicamente, un lenguaje prescriptivo. ¿Sirve la lógica, también, para controlar la calidad de los argumentos que contienen prescripciones?

1. Supongamos el siguiente argumento, que sólo contiene enunciados asertivos:

   

   Éste es un argumento correcto desde el punto de vista lógico; y, si las premisas son verdaderas, la conclusión será necesariamente verdadera. El conocimiento que tenemos de la naturaleza de los seres humanos puede garantizarnos la verdad de la primera premisa. La segunda premisa, no debemos olvidarlo, también tiene que ser verdadera –y lo es por lo que sabemos del filósofo griego llamado Sócrates–. Ahora bien, si Sócrates fuese, por ejemplo, el nombre de mi ordenador, la segunda premisa sería falsa.

2. De manera parecida, consideramos correcto el siguiente argumento, en el que la primera premisa tiene carácter prescriptivo:

   

   Ahora bien, ¿qué quiere decir que éste es un argumento correcto? En este caso no podemos decir que si las premisas son verdaderas la conclusión también lo será necesariamente. Y no lo podemos hacer, porque ni “Devuélveme todos los libros que te he dejado”, ni “Devuélveme este libro” son vehículos adecuados de la verdad o falsedad. Si un amigo nos dijera “¡Devuélveme el libro de Miguel Hernández!”, no sería una respuesta adecuada: “Eso es falso”. Nos encontramos ante un problema grave para la lógica aplicada a las normas: o bien las argumentaciones que contienen órdenes y normas no están controladas por la lógica, o bien la lógica va más allá de la verdad.

   En este capítulo también se trata esta cuestión y se analizan algunas de las propuestas que intentan fundamentar el discurso práctico (contraponiéndolo al discurso teórico, el discurso que puede ser verdadero o falso), en el que no disponemos, en un sentido estricto, de las nociones de verdad o falsedad.

1. ¿Qué es argumentar?

1.1. Noción de argumento: premisas y conclusión

Argumentar es inferir o derivar, a partir de un conjunto de enunciados llamados premisas, otro enunciado denominado conclusión. Así, podemos decir que la conclusión se sigue o es deducible de las premisas; o también podemos decir, usando la relación inversa a seguirse de o deducirse de, que las premisas implican la conclusión.

G. E. Moore (1873-1958) fue probablemente la primera persona que introdujo la noción de implicación: “Necesitamos, en primer lugar, algún término para expresar la inversa de la relación que afirmamos que se da entre una proposición determinada p y otra proposición q, cuando afirmamos que q se sigue de o es deducible de p. Utilizaremos el término implica (‘entails’) para expresar la inversa de esta relación” (G. E. Moore, 1922).^[12]

El término argumentar sufre la ambigüedad proceso/producto: puede hacer referencia tanto al proceso, de carácter psicológico, por el que inferimos una conclusión de un conjunto de premisas, como al producto o resultado de esta actividad, formado únicamente por el punto de partida del proceso, las premisas, y el punto de llegada, la conclusión. En estos dos primeros capítulos estudiamos la argumentación desde el punto de vista del resultado, del producto que nos ofrece. Y lo hacemos para averiguar cómo podemos distinguir los razonamientos correctos de los razonamientos incorrectos. Ésta es la función de la lógica.

La lógica, por tanto, es el estudio de los métodos y principios utilizados para distinguir los razonamientos correctos de los incorrectos. De este modo, la lógica no es una explicación de cómo pensamos, sino un modelo de cómo tenemos que pensar para hacerlo correctamente. La lógica es una especie de aparato para controlar la calidad de nuestros argumentos.

Hasta ahora hemos dicho que las premisas y la conclusión de los argumentos o de los razonamientos son enunciados; una distinción ulterior nos permitirá precisar esta caracterización. Hay que distinguir, en cualquier caso, entre oraciones y proposiciones:

1) Las oraciones

Una oración es un conjunto de símbolos lingüísticos con sentido completo. No todos los conjuntos de símbolos lingüísticos tienen sentido. Por ejemplo: “Mañana luna no sabemos” es un conjunto de símbolos lingüísticos del castellano que carece de sentido: es una expresión lingüística mal formada según las reglas gramaticales del castellano. En cambio, “La luna de Júpiter” es una expresión bien formada, a pesar de que no tiene un sentido completo, no es una oración. Un ejemplo de oración como “La Luna gira alrededor de la Tierra” es un conjunto de símbolos con sentido completo.

Entre las oraciones, debemos distinguir, también, las oraciones asertivas, que afirman o niegan algo y, por tanto, son susceptibles de verdad o falsedad, de otras oraciones que no afirman ni niegan nada, que no son susceptibles de verdad o falsedad.^[13]

2) Las proposiciones

Las proposiciones son el significado de las oraciones asertivas. Dos oraciones pueden expresar una sola proposición. Por ejemplo, las dos oraciones siguientes expresan una sola proposición:

• Alfonso quiere a Carmen.
• Carmen es querida por Alfonso.

La diferencia entre oraciones y proposiciones se ve claramente si tenemos en cuenta que las oraciones siempre forman parte de un lenguaje determinado, pero que oraciones expresadas en diferentes lenguajes pueden expresar la misma proposición. Por ejemplo: las cuatro oraciones siguientes expresan la misma proposición:

• Llueve.
• It is raining.
• Es regnet.
• Plou.

También es posible que la misma oración exprese, en diferentes contextos, diferentes proposiciones. Por ejemplo, la oración “El presidente de la Generalitat catalana es calvo” expresaba en 1979 una proposición referida a Josep Tarradellas, mientras que en 1996 expresa una proposición referida a Jordi Pujol.

Aunque ésta es una cuestión controvertida entre los mismos lógicos, suponemos, en principio, que los razonamientos se dan entre proposiciones, es decir, que las premisas de los razonamientos son proposiciones de las que se infiere otra proposición, que es la conclusión. Tenemos que observar que las nociones de premisa y conclusión hacen referencia a un razonamiento determinado. Es obvio que una misma proposición puede ser una conclusión en un razonamiento y una premisa en otro. Por ejemplo, supongamos el siguiente razonamiento:

Todas las palomas son pájaros

Todos los pájaros son vertebrados

 

Todas las palomas son vertebrados

La conclusión de este argumento puede llegar a ser premisa de otro:

Todas las palomas son vertebrados

Todos los vertebrados son animales

 

Todas las palomas son animales

Estos dos últimos argumentos parecen buenos ejemplos de argumentos correctos, pero, ¿qué significa que son correctos? Un argumento es correcto si, y sólo si, no es posible que sus premisas sean verdaderas y que la conclusión sea falsa; dicho de otra manera, si sus premisas son verdaderas, su conclusión tendrá que ser necesariamente verdadera. Como veremos más adelante, la lógica nos proporciona reglas y métodos para saber si un argumento es correcto.

1.2. Verdad y validez

Los argumentos correctos, desde el punto de vista de la lógica, son argumentos formalmente válidos. Hay que tener en cuenta la relación que existe entre los argumentos formalmente válidos y la verdad de las premisas y de la conclusión. ¿Qué relaciones se dan entre estos aspectos? Existen tres factores que deberemos considerar: la corrección formal del argumento, la verdad de las premisas y la verdad de la conclusión.

Tenemos, por tanto, ocho posibles tipos de razonamientos:

1. Razonamientos formalmente inválidos con premisas falsas^[14] y conclusión verdadera.
2. Razonamientos formalmente inválidos con premisas falsas y conclusión falsa.
3. Razonamientos formalmente inválidos con premisas verdaderas y conclusión verdadera.
4. Razonamientos formalmente inválidos con premisas verdaderas y conclusión falsa.
5. Razonamientos formalmente válidos con premisas falsas y conclusión verdadera.
6. Razonamientos formalmente válidos con premisas falsas y conclusión falsa.
7. Razonamientos formalmente válidos con premisas verdaderas y conclusión verdadera.
8. Razonamientos formalmente válidos con premisas verdaderas y conclusión falsa.

Pues bien, lo único que nos garantiza la lógica es que los argumentos válidos desde un punto de vista formal no pueden tener premisas verdaderas y conclusión falsa, por lo que los razonamientos de tipo 8) quedan excluidos. No es posible construir un argumento formalmente válido con premisas verdaderas y conclusión falsa. A continuación, mostramos algunos posibles ejemplos^[15] de los otros siete tipos de argumento:

1. Todos los personajes de ficción son mortales.

   Madame Bovary es mortal.

    

   Madame Bovary es un personaje de ficción.

2. Todos los mortales son personajes de ficción.

   Madame Bovary es mortal.

    

   Madame Bovary no es un personaje de ficción.

3. Todos los personajes de ficción son inmortales.

   Madame Bovary es inmortal.

    

   Madame Bovary es un personaje de ficción.

4. Todos los personajes de ficción son inmortales.

   Madame Bovary es inmortal.

    

   Madame Bovary no es un personaje de ficción.

5. Todos los mortales son personajes de ficción.

   Madame Bovary es mortal.

    

   Madame Bovary es un personaje de ficción.

6. Todos los personajes de ficción son mortales.

   Madame Bovary es un personaje de ficción.

    

   Madame Bovary es mortal.

7. Todos los personajes de ficción son inmortales.

   Madame Bovary es un personaje de ficción.

    

   Madame Bovary es inmortal.

• Hay varias maneras de demostrar que los cuatro primeros tipos de razonamientos –1), 2), 3) y 4)– incumplen algunas de las reglas lógicas (lo veremos más adelante). La lógica sólo se refiere a los argumentos válidos desde un punto de vista formal; es precisamente aquello que sirve para distinguir los razonamientos formalmente válidos de los razonamientos formalmente inválidos.

• Ahora bien, hay que distinguir la idea de razonamiento válido de la idea de verdad de las premisas o de la conclusión. Existen razonamientos formalmente válidos que tienen premisas falsas –con conclusiones verdaderas o falsas, como son el 5) y el 6).

• Nos interesan, sin embargo, de una manera especial los argumentos –como el 7)– que son formalmente válidos y que tienen premisas verdaderas, ya que éstos son los únicos que necesariamente tienen conclusiones verdaderas. A veces, estos razonamientos se llaman razonamientos materialmente válidos o, también, razonamientos sólidos. ^[16]

En cualquier caso, que un razonamiento sea sólido ya no depende de forma exclusiva de la lógica, sino de cómo es el mundo; y el mundo es como es, pero podría ser de otra manera. Los filósofos han construido la noción de mundo posible para expresar esta idea: existe un mundo posible donde Madame Bovary nace, se casa, tiene varios amantes y, al final, se suicida. Pues bien, haciendo referencia a este mundo, Madame Bovary no es inmortal. Ahora bien, existe un límite en la construcción de mundos posibles: en todos los mundos posibles son válidas las reglas de la lógica.^[17] Dicho de otra manera, todos los argumentos formalmente válidos serían sólidos en algunos mundos posibles, aunque sólo algunos de los argumentos formalmente válidos son sólidos en nuestro mundo.

Como vemos, la validez lógica es independiente de la verdad. La validez lógica sólo es, por decirlo de algún modo, un transmisor fiel de la verdad. Todavía nos podríamos preguntar: “Pero, ¿qué es la verdad?”. Se ha dedicado una gran cantidad de esfuerzos filosóficos para contestar a esta pregunta. Aquí no estudiamos esta cuestión con detenimiento. Suponemos que la verdad se predica de las proposiciones y que una proposición es verdadera si, y sólo si, se da el estado de cosas al que hace referencia. Por ejemplo, la proposición según la que Picasso pintó el Guernica es verdadera porque describe un hecho que ocurrió en realidad. En cambio, la proposición según la que Picasso pintó El nacimiento de Venus es falsa porque describe un hecho que no ocurrió en nuestro mundo (el cuadro que lleva este nombre fue pintado por Botticelli).

Esta noción de verdad tiene raíces aristotélicas. Aristóteles escribió: “La falsedad consiste en decir de lo que es que no es y de lo que no es que es, y la verdad consiste en decir de lo que es que es y de lo que no es que no es”[Metafísica, Γ, 7 (1011 b26-27)]. Esta idea de Aristóteles se ha desarrollado formalmente en el siglo xx por el importante lógico y filósofo polaco Alfred Tarski (1902-1983).^[18]

1.3. El lenguaje en acción

Dado que la mayoría de los argumentos producidos por los seres humanos lo son por medio de los lenguajes naturales (como el catalán, el castellano, el inglés, el ruso, etc.), y que la argumentación jurídica siempre se produce mediante algún lenguaje natural (oral o escrito), es importante que nos detengamos y estudiemos determinados aspectos centrales de estos lenguajes naturales que tienen mucho que ver con la argumentación.

Los lenguajes son los instrumentos de comunicación más importantes con que contamos los seres humanos. Son herramientas complejas y, al mismo tiempo, sutiles. A menudo nos encontramos con problemas de comunicación que no provienen del hecho que no hayamos entendido bien las palabras que nos han dicho, y tampoco del hecho de que no conozcamos bien aquel idioma, sino de otras fuentes.

Dos preguntas son ahora relevantes:

1. ¿Qué quiso decir X cuando emitió una expresión lingüística determinada?
2. ¿Qué hizo X al emitir una expresión lingüística determinada?

La primera cuestión tiene que ver con el contenido significativo de las expresiones lingüísticas, es decir, con su sentido. La segunda cuestión tiene que ver con la dimensión de acción que todo acto lingüístico tiene. El lenguaje sirve para muchas cosas: con el lenguaje podemos informar, pedir, prometer, dar miedo, elogiar, insultar, prohibir, sugerir, etc.; este aspecto de las expresiones lingüísticas constituye su fuerza. Así pues, una teoría completa del significado lingüístico tiene que contar con dos partes: una dedicada al sentido y otra, a la fuerza.^[19]

Estos dos aspectos ocupan los dos subapartados siguientes; además, a esto se añade una distinción ulterior entre el uso y la mención de las expresiones lingüísticas.

1.3.1. El sentido de las expresiones lingüísticas

No indagaremos aquí con detenimiento sobre cómo las expresiones lingüísticas llegan a ser significativas. Ésta es una cuestión filosófica muy importante, pero podemos prescindir de ella para nuestros intereses, que son más limitados. Vamos a tener suficiente, por ahora, con recordar que el sentido de una expresión lingüística es aquello que la conecta con su referencia. La referencia de un nombre propio, como puede ser “Hans Kelsen”, es el individuo Hans Kelsen. La referencia de un predicado como “ser filósofo” está constituida por la clase de los filósofos. La referencia de una oración como “Hans Kelsen es filósofo” está constituida por el estado de cosas del mundo que hacen verdadera la proposición que expresa la oración.

Es habitual que comprendamos las expresiones lingüísticas que leemos o escuchamos, puesto que captamos sin demasiadas dificultades su sentido. A pesar de todo, a veces nos encontramos con algunos problemas. En este subapartado analizamos dos de los problemas de comprensión adecuada más usuales de los lenguajes naturales: la vaguedad y la ambigüedad de las expresiones lingüísticas.

Para ser exactos, y como quedará claro después de la exposición, mientras que la ambigüedad es una propiedad de las expresiones lingüísticas (de los términos, de las oraciones), la vaguedad es una propiedad del sentido de estas expresiones lingüísticas (de los conceptos y de las proposiciones).

1) La vaguedad

El sentido de una expresión lingüística E es vaga si, y sólo si, en algunos casos se nos plantea el problema de si un determinado objeto pertenece o no a la referencia de E. Por ejemplo, hay términos genéricos, como bosque, calvo o montón, que plantean rápidamente esta cuestión. ¿Cuántos árboles tiene que tener una arboleda para ser un bosque? ¿Cuántos pelos tiene que tener una persona para no ser calva? Y, ¿cuántos granos de arena forman un montón de arena?

La paradoja de sorites

De hecho, este problema ya lo detectaron los estoicos; Eubúlides, en concreto, ya planteaba el problema de saber cuándo una persona llega a ser calva, o cuándo un grupo de granos de arena son un montón. Es más, se debe a los estoicos el planteamiento de una paradoja producida por la vaguedad, conocida como la paradoja de sorites.^[20]

La paradoja se puede plantear del siguiente modo: n (póngase el número que se quiera; por ejemplo, cien mil) granos de arena son un montón de arena. Si n granos de arena son un montón de arena, también lo son n - 1 granos de arena. Y, por aplicación de esta premisa tan plausible (un montón de arena no deja de serlo porque se le quite sólo un grano) un determinado número de veces (noventa y nueve mil novecientos noventa y nueve veces, en nuestro ejemplo), obtenemos que un grano de arena también es un montón de arena.

Modernicemos el ejemplo: Bill Gates (que tiene un buen montón de miles de millones de dólares, pongamos por ejemplo n$) es rico. Si Bill Gates, que tiene n$, es rico, también lo es alguien que tenga n – 1$. Por lo tanto, una persona que sólo tiene 1$ es rica.

Pongamos un ejemplo referido al derecho: la reclusión en una celda aislada durante diez años es un trato degradante.^[21] Si la reclusión en una celda aislada durante diez años es degradante, también lo es la reclusión en una celda aislada durante un minuto menos. En consecuencia, tras la aplicación de esta premisa el número adecuado de veces, la reclusión en una celda aislada durante un minuto es un trato degradante.

La paradoja plantea un desafío muy grave a algunas de nuestras intuiciones conceptuales. No es fácil escapar de los efectos devastadores de la paradoja de sorites.^[22]

En el lenguaje del derecho encontramos, también, la presencia de términos genéricos que plantean dudas a la hora de su aplicación: en el anterior Código penal -para poner un ejemplo conocido- había una circunstancia agravante de la responsabilidad penal conocida con el nombre de nocturnidad; sin embargo, ¿cuándo empieza a ser de noche? ¿Qué se puede decir de un delito cometido al anochecer? El artículo 153 del Código penal vigente castiga a la persona que habitualmente ejerza violencia física sobre su cónyuge, pareja de hecho o hijos. Sin embargo, ¿cuántas veces se tiene que repetir el comportamiento violento para que sea habitual?

De hecho, el problema es más grave porque no únicamente sufren vaguedad algunos términos genéricos. Como se ha mostrado en repetidas ocasiones, todos los términos genéricos expresan conceptos que pueden ser vagos; todos los términos genéricos son potencialmente vagos. Esta propiedad de los conceptos es conocida como textura abierta del lenguaje: siempre es posible imaginar un objeto del que dudemos que pertenezca o no a la referencia de la expresión. Por ejemplo, en principio parece que mesa es un término con una referencia clara; sin embargo, aunque una piedra en medio del bosque no parezca una mesa, ¿qué diríamos si le ponemos un mantel encima y una botella de Rioja y se oye: “¡A la mesa!”?

Algo parecido pasa con el término gato (en los contextos en que nos referimos a un animal doméstico). ¿Seguiríamos usando la palabra gato para hacer referencia a un animal con forma de gato, pero que midiese 1,80 metros, caminase de pie, fuese con un traje gris y corbata y se dirigiese a nosotros diciendo: “Nice to meet you”?^[23]

De manera similar, como el derecho utiliza reglas que contienen términos genéricos (dispuestos a ser aplicados a un número amplio de casos), existen muchos casos dudosos o difíciles a causa de la vaguedad de los conceptos utilizados por la regla. Por ejemplo, ¿cuán precioso ha de ser un objeto oculto e ignorado para que se lo considere un tesoro a efectos civiles?^[24] O, por ejemplo, cuando el nuevo Código penal vigente introduce^[25] la circunstancia agravante de ejecutar el hecho delictivo utilizando un disfraz, ¿cómo de escondido hay que llevar el rostro para que a efectos penales se considere que se va disfrazado? En palabras, ya célebres, de H. L. A. Hart:

“Todas las reglas importan reconocer o clasificar casos particulares como ejemplos de términos generales, y frente a cualquier regla es posible distinguir casos centrales claros, a los que ella, sin duda, se aplica y otros casos en los que hay tantas razones para afirmar como para negar que se aplica. Es imposible eliminar esta dualidad de un núcleo de certeza y una penumbra de duda, cuando se trata de colocar situaciones particulares bajo reglas generales.”^[26]

La vaguedad potencial se conoce, también, como vaguedad intensional,^[27] es decir, el supuesto en el que es posible que haya objetos que susciten dudas relativas a su pertenencia a la referencia del predicado en cuestión. Si, además, existen estos objetos, la vaguedad también es extensional. Si un predicado es vago de manera extensional, también lo es de manera intensional, pero la conversación no es necesariamente verdadera.^[28]

La cuestión de la determinación de los conceptos resulta grave en especial en el caso de términos como razonable, justo, bello, etc., puesto que son conceptos densos, valorativos, cuyo contenido es extremadamente controvertido. Se los llama conceptos esencialmente controvertidos, una idea que procede de W. B. Gallie y que ha sido muy utilizada por Ronald Dworkin^[29] en el ámbito de la filosofía del derecho. Dworkin distingue entre concepto y concepciones:

• El concepto hace referencia al núcleo común de significado que nos permite identificar los casos paradigmáticos.

• Las diferentes concepciones están constituidas por un conjunto de criterios, reconstruidos por una teoría, que permiten explicar la aplicación del concepto a determinados casos, así como resolver los casos controvertidos. Ahora bien, estos criterios son esencialmente controvertidos.

Veamos unos ejemplos de conceptos especialmente controvertidos: pensemos en expresiones como “buen equipo de fútbol”, “pintura excelente” o “poema profundo”. Todos somos capaces de identificar algunos casos como ejemplos de estos conceptos: el Barça de Cruyff (el dream team), los frescos de la Capilla Sixtina de Miguel Ángel, algunos de los sonetos de Shakespeare.

Ahora bien, esto no significa que usemos los mismos criterios para identificarlos. Podemos comprobar este extremo tratando de averiguar, por ejemplo, si el Barça de Cruyff entrenador era mejor que el Ajax del Cruyff jugador, o si los frescos de la Capilla Sixtina son mejores que los frescos de Santa María de Taüll, o cuál de los sonetos de Shakespeare es más profundo. El hecho de que sean controvertidos forma parte del significado de estos conceptos y nuestras teorías (estéticas, literarias, “futbolísticas”, etc.) tratan de ofrecer criterios que nos permitan averiguar estas cuestiones.

Pues bien, en el ámbito de la moral y en el del derecho también nos encontramos con muchos casos de conceptos esencialmente controvertidos. La dogmática administrativista española los denomina conceptos jurídicos indeterminados; son, por ejemplo, los casos de “razonable”, “diligencia de un buen padre de familia”, “interés público”, etc. La presencia de estos conceptos en el lenguaje del derecho hace que, en algunas ocasiones, las disputas jurídicas tengan un ineludible trasfondo moral.

Supongamos el ejemplo al que nos referíamos anteriormente de la prohibición establecida en la Constitución^[30] de los tratos inhumanos o degradantes. Seguro que en algunos casos estamos de acuerdo, como, por ejemplo, en considerar que la tortura es un trato inhumano o degradante; sin embargo, puede que haya otros casos en los que tengamos más dudas. El Reglamento penitenciario entonces vigente, por ejemplo, preveía la sanción de reclusión en celda aislada por un máximo de catorce días. ¿Esta sanción es un trato inhumano o degradante? El Tribunal Constitucional^[31] se pronunció sobre esta cuestión y resolvió que no se trata de un caso de trato inhumano ni degradante. Sea como sea, es obvio que los criterios utilizados por el Tribunal se podrían desafiar si fuéramos capaces de construir una concepción diferente de este concepto.

A modo de conclusión con respecto a la vaguedad, debemos señalar que todos los términos generales (que tienen una referencia empírica) expresan o significan conceptos vagos, real o potencialmente. Entre estos conceptos, vale la pena destacar los conceptos esencialmente controvertidos, en los que la disputa en referencia al significado del concepto es central y forma parte del mismo significado del término; por otro lado, los desacuerdos con respecto a la aplicación del concepto enriquecen nuestro debate en torno a cuestiones que para nosotros son importantes.

2) La ambigüedad

Una expresión lingüística E es ambigua si, y sólo si, tiene varios sentidos E₁, E₂, ..., En. Podemos distinguir dos tipos de ambigüedad:

1. Ambigüedad extracontextual. Una expresión lingüística es E-ambigua si, y sólo si, tiene varios significados al margen de cualquier contexto, pero dispone de un significado unívoco cuando se sitúa en un contexto determinado.

   Por ejemplo, la expresión luna posee este tipo de ambigüedad, ya que puede expresar varios significados. Sin embargo, esta ambigüedad desaparece cuando la expresión se incluye en un contexto, tal y como los siguientes ejemplos ponen de manifiesto:

   • Esta noche hay luna llena.
   • Rompieron la luna del espejo.

   Algunas expresiones del lenguaje legal tienen este tipo de ambigüedad que el contexto elimina. Esto es lo que ocurre con el término grado. En el contexto del Código civil significa el número de generaciones que determina la proximidad del parentesco, mientras que en el contexto del Código penal, en cambio, hace referencia a la clasificación de las penas según su gravedad. La E-ambigüedad no constituye un problema serio porque el contexto determina el sentido de la expresión.^[32]

2. Ambigüedad contextual. Una expresión lingüística es C-ambigua si, y sólo si, tiene varios significados en un contexto determinado. Entre las expresiones lingüísticas C-ambiguas aún podemos distinguir las que tienen varios significados de los cuales sólo uno prevalece alternativamente en un contexto determinado, como las expresiones CA-ambiguas, de las expresiones que tienen varios significados que se presentan simultáneamente en un contexto determinado, y que son las expresiones CS-ambiguas:

   La CA-ambigüedad es típica de muchas frases adjetivas o de relativo. Así, por ejemplo, a veces surgen dudas acerca de cuál es exactamente el antecedente de una cláusula de relativo. La frase “Vendió los cuadros y las joyas que le regaló su abuela” se puede entender como “Vendió los cuadros que le regaló la abuela y las joyas que le regaló la abuela” o, alternativamente, como “Vendió las joyas que le regaló la abuela y los cuadros”. En algunas ocasiones hallamos casos de este tipo de CA-ambigüedad en el lenguaje del derecho; el Código civil, por ejemplo, establece:

   Artículo 1346, 7.

   “Son bienes privativos de cada uno de los cónyuges la ropa y objetos de uso personal que no tengan un valor extraordinario.”

   ¿Se debe entender que la cláusula de relativo “que no tengan un valor extraordinario” se refiere sólo a los objetos de uso personal, o también a la ropa?

   Otro tipo de CA-ambigüedad se da en este ejemplo: “Pedro y María están casados”, que puede significar “Pedro está casado con X y María está casada con Y”, o bien, “Pedro está casado con María”. Una CA-ambigüedad parecida a ésta se produce con el texto del artículo 32.1 de la Constitución, que establece: “El hombre y la mujer tienen derecho a contraer matrimonio con plena igualdad jurídica”, lo cual puede significar que los hombres tienen derecho a contraer matrimonio con las mujeres y las mujeres con los hombres o bien, alternativamente, que el derecho se confiere a hombres y mujeres para contraer matrimonio tanto un hombre con una mujer, como una mujer con una mujer o un hombre con un hombre.

   La estructura sintáctica de estas oraciones no permite averiguar qué sentido tienen. Es posible que el contexto, a veces, elimine la ambigüedad, pero también es posible que el contexto permita, de manera alternativa, ambas lecturas.^[33]

   Un ejemplo de CA-ambigüedad se encuentra en la Constitución danesa de 1920, que establecía:

   Artículo 71

   “En el ejercicio de sus funciones los jueces están limitados por el derecho. Los jueces no serán separados de sus cargos si no es mediante juicio, ni serán trasladados en contra de su voluntad, excepto en aquellos casos en los que tenga lugar una reorganización de los tribunales.”

   En este caso, no queda claro si la excepción relativa a la reorganización de los tribunales se aplica sólo a los traslados, o también a la regla de acuerdo con la que no pueden ser separados sin juicio.

Como decíamos, cuando una expresión es CS-ambigua, dicha expresión tiene, en un contexto determinado, varios significados de manera simultánea. Con el fin de captar el sentido completo de una expresión CS-ambigua en un contexto determinado, tenemos que comprender sus múltiples significados.

He leído en algún lugar el siguiente ejemplo de CS-ambigüedad de una expresión lingüística oral: supongamos que un alemán está hablando por teléfono con su amante, que es de lengua inglesa, y en un momento determinado su esposa le pregunta en alemán “¿Te quedarás a cenar?”. Él contesta a ambas con una sola palabra, “Nain”. De este modo, a la vez, le contesta a su esposa que no se quedará a cenar (nein en alemán significa ‘no’) y queda a las nueve con su amante (dado que nine significa ‘nueve’ en inglés).

También he oído decir que, hacia finales de la Segunda Guerra Mundial, un oficial de las SS que huía envenenó unos bombones y escribió Gift en la caja, con la esperanza de que si la encontraban los aliados entendieran ‘regalo’ (que es lo que gift significa en inglés), y si la encontraban otros soldados del ejército alemán quedaran advertidos del envenenamiento de los bombones (dado que gift en alemán significa ‘veneno’).

Algunos tipos de metáfora son ejemplos de CS-ambigüedad. Para comprender el sentido de la metáfora debemos entender, y relacionar, dos o más sentidos. Así, cuando Jorge Luis Borges escribe el siguiente verso: “De hierro, no de oro, fue la aurora” (en el libro La moneda de hierro, del año 1976), se nos sugiere un amanecer gris más que resplandeciente; pero, simultáneamente, el lector, que sabe que lee un verso de un poema titulado “Elegía a la patria”, piensa en un comienzo de la patria situado más bien en la violencia que en la riqueza... Tan sólo la conjunción de los dos significados permite comprender el sentido de este verso de Borges.

Con el lenguaje del derecho pasa lo mismo. Algunos textos legales tienen varios significados de manera simultánea. Así, el Código civil establece: “Los menores de edad no emancipados no pueden contraer matrimonio”.^[34] Podemos entender esta frase, al mismo tiempo, como que los menores de edad no emancipados tienen prohibido contraer matrimonio, como que el matrimonio entre menores de edad no emancipados es nulo, o como que las autoridades competentes tienen prohibida la celebración del matrimonio entre los menores no emancipados.

1.3.2. La fuerza de las expresiones lingüísticas

Como ya hemos dicho, el lenguaje cumple una gran cantidad de funciones: existen usos del lenguaje muy diferentes. Además de determinar el significado de las palabras que hemos escuchado o leído, debemos ser capaces de saber qué tipo de acto llevamos a cabo al emitir una expresión lingüística determinada.

A veces, en filosofía del lenguaje, este aspecto se llama la dimensión ilocutiva del lenguaje, para diferenciarla de la dimensión locutiva, distinguiendo lo que se dice al emitir una expresión lingüística, de lo que se hace por el hecho de emitirla. Los dos filósofos del lenguaje más destacados en este tema son John L. Austin y John Searle.

Tanto Austin como Searle han intentado construir una clasificación, una taxonomía de los actos de habla satisfactoria; una empresa muy difícil, que parece condenada al fracaso ya desde el principio.^[35] Dada la multiplicidad de funciones que uno puede otorgar al lenguaje, hay que ser muy prudente a la hora de clasificar los usos del lenguaje. Con todo, y sólo con finalidades heurísticas, como una especie de orientación en este terreno difícil, proponemos una clasificación de los usos del lenguaje, divididos en cuatro tipos:

1. El uso asertivo o descriptivo.
2. El uso prescriptivo o directivo.
3. El uso emotivo.
4. El uso operativo o realizativo.^[36]

Si bien estos usos no son, en conjunto, exhaustivos, y ni siquiera, quizá, mutuamente excluyentes, son una clasificación de los casos más paradigmáticos y pueden representar un buen punto de partida para la construcción de análisis más detallados. A menudo se dice que esta clasificación entre usos del lenguaje está formulada desde el punto de vista pragmático. Esta afirmación evoca una distinción formulada por Rudolf Carnap y Charles Morris, según la que la semiótica^[37] se puede dividir en tres partes:

1. La sintaxis, que estudia la estructura de los símbolos y sus relaciones.
2. La semántica, que estudia la relación entre los símbolos y su significado.
3. La pragmática, que estudia la relación entre los símbolos y su uso.

1) El uso asertivo

A veces usamos el lenguaje con un propósito descriptivo de manera primordial para informar de ciertos fenómenos o estados de cosas. En tal caso, las oraciones que usamos expresan proposiciones, susceptibles de verdad o falsedad. Éste es el uso del lenguaje de muchas emisiones de nuestro lenguaje ordinario^[38]. El lenguaje científico es, quizá, el paradigma de este uso descriptivo. Es decir, para expresar proposiciones, susceptibles de verdad o falsedad, utilizamos un tipo especial de actos de habla: las aserciones.

2) El uso prescritivo

Este tipo de discurso se utiliza cuando el propósito principal es influir en el comportamiento de otras personas. El caso paradigmático de este uso lingüístico es ordenar, dado que las órdenes de los que tienen autoridad sobre otras personas^[39] son un buen ejemplo de esto. Sin embargo, también debemos incluir dentro de este uso del lenguaje las súplicas, las solicitudes y, quizá, los consejos.^[40]

El lenguaje del derecho es, de manera primordial, prescriptivo. Cuando el Código civil establece que “quien por acción u omisión causa daño a otros, mediante culpa o negligencia, está obligado a reparar el daño causado” (Artículo 1902.), no trata de informarnos, sino de prescribirnos un comportamiento determinado, el de reparar el daño causado en determinadas circunstancias. En este caso, estas emisiones lingüísticas no se utilizan para expresar nada susceptible de verdad o falsedad. Ni las órdenes, ni las súplicas, ni los consejos expresan proposiciones.

Ahora bien, podemos decir que las órdenes expresan normas. De la misma manera que las aserciones son el vehículo lingüístico de las proposiciones, las prescripciones (las órdenes) son el vehículo lingüístico de las normas. Podemos considerar las normas como el sentido de determinadas formulaciones normativas.

3) El uso emotivo

En determinadas ocasiones, el lenguaje se utiliza para expresar emociones o sentimientos determinados, pero no en el sentido de describir estos sentimientos o emociones, sino en el de exteriorizarlos. Uno de los paradigmas del lenguaje emotivo es la poesía.

Así, cuando Pablo Neruda escribe los primeros versos de su conocida canción desesperada (en su libro Veinte poemas de amor y una canción desesperada): “Emerge tu recuerdo de la noche en que estoy,/el río anuda al mar su lamento obstinado./Abandonado como los muelles en el alba/Es la hora de partir, ¡oh abandonado!”, no pretende darnos ninguna información, sino exteriorizar unos sentimientos determinados que pueden producir en el lector admiración, tristeza, complicidad o, sencillamente, goce estético. Como podemos apreciar, este uso del lenguaje tampoco es susceptible de verdad o falsedad. Hay que tener en cuenta que muchas expresiones lingüísticas de apariencia descriptiva tienen un contenido emotivo.

Supongamos las tres expresiones siguientes:

• El Parlamento ha despenalizado el aborto.
• El Parlamento ha permitido el asesinato de las criaturas más inocentes: los niños que todavía no han nacido.
• El Parlamento ha aumentado la capacidad de elegir de las mujeres despenalizando el aborto.

El contenido informativo de estas tres oraciones es, básicamente, el mismo; ahora bien, la primera oración utiliza un lenguaje neutro, mientras que las otras dos usan un lenguaje con una gran carga emotiva. En algunas ocasiones, el lenguaje del derecho también incorpora expresiones con carga emotiva. La Constitución de Cádiz de 1812 decía:

Artículo 6

“El amor de la Patria es una de las principales obligaciones de todos los españoles y, asimismo, el ser justos y benéficos.”

Decir que hay que ser justo y benéfico es más una carga emotiva que un contenido prescriptivo. Debemos ser conscientes de que la forma gramatical del discurso es, a veces, engañosa, para averiguar qué tipo de uso del lenguaje se utiliza.

4) El uso operativo o realizativo

Hay otro tipo de emisiones lingüísticas que no se pueden clasificar en ninguno de los tipos anteriores y que también tienen importancia. Cuando le decimos a otra persona “Os saludo” o “Te prometo que vendré a cenar” no le estamos informando de nada, ni prescribiendo nada, y tampoco expresamos de manera primordial nuestras emociones; lo que hacemos es, precisamente, saludarle o hacerle una promesa. Algunas expresiones lingüísticas sirven para hacer determinadas cosas.^[41] Este tipo de acto de habla presupone la existencia de un contexto institucional determinado, de un contexto en el que hay reglas.

Un buen ejemplo de contexto institucional es el de los juegos: en determinados juegos de cartas hay unas palabras concretas que sirven para adquirir una posición institucional determinada en el juego. Ocurre lo mismo, por ejemplo, en las promesas. El hecho de decir “prometo” en determinadas condiciones de sinceridad (no en una obra de teatro, o en broma –como si le decimos a una amiga “Te prometo que te haré emperatriz de China”–) equivale a prometer. Así, en el contexto de las promesas, decir “prometo” quiere decir prometer, y, en el contexto de la religión católica, decir “Bautizo a este niño con el nombre de Guillermo” quiere decir bautizar.

La forma canónica de estas reglas institucionales es la siguiente:

“En el contexto C, X cuenta por Y”

En el derecho, este uso del lenguaje es muy importante, ya que hay una gran cantidad de reglas que no son prescriptivas –no obligan, no prohíben ni permiten nada–, sino que son constitutivas; mediante su uso, en el contexto adecuado, se pueden hacer cosas: como, por ejemplo, adquirir o perder posiciones institucionales.^[42]

Existen muchas dimensiones significativas para mostrar cómo los actos ilocucionarios difieren entre sí;^[43] pero hay una dimensión relevante que nos permitirá distinguir con claridad el uso asertivo del lenguaje de su uso prescriptivo. Nos referimos a lo que John Searle denomina la dirección de ajuste^[44] (‘direction of fit’) entre las palabras y el mundo. Algunas expresiones lingüísticas tienen como parte de su dimensión ilocucionaria conseguir que las palabras (más estrictamente, su contenido proposicional) encajen en el mundo, mientras que la de otras es conseguir que el mundo encaje en las palabras. Las aserciones pertenecen a la primera categoría y las prescripciones, a la segunda. Searle adopta la ilustración de esta idea de la filósofa G. E. M. Anscombe.^[45]

Supongamos que un hombre va al supermercado con una lista que le ha dado su mujer en la que se halla escrito: “Pan, jamón, mantequilla y garbanzos”. Supongamos, también, que, mientras él camina por el supermercado, le sigue un detective que anota todas las cosas que coge de las estanterías. Cuando salen del supermercado, el marido y el detective deberían (si han hecho bien su trabajo) tener dos listas idénticas. Sin embargo, la función de las dos listas es totalmente diferente:

• En el caso del marido, el propósito de la lista, por decirlo de algún modo, es conseguir que el mundo encaje en las palabras: se supone que el comprador, al llevar a cabo sus acciones, se adecua a la lista.

• En el caso del detective, el propósito de la lista es hacer que las palabras encajen en el mundo: se supone que la persona, al hacer la lista, se adecua a las acciones del comprador.

Esto se puede mostrar si observamos el papel diferente del error en ambos casos:

• Si el detective vuelve a casa y se da cuenta de que el comprador adquirió habas en lugar de garbanzos, puede, sencillamente, borrar la palabra garbanzos de la lista y sustituirla por la palabra habas.

• En cambio, si cuando el comprador vuelve a casa ve que ha comprado habas en lugar de garbanzos, no puede corregir el error borrando la palabra garbanzos de la lista, sino que tendrá que volver al supermercado y cambiar las habas por los garbanzos.

Pues bien, la lista del detective se parece a las aserciones y tiene la dirección de encaje palabra-a-mundo, mientras que la lista del comprador se parece a las prescripciones y tiene la dirección de encaje mundo-a-palabra.

Mientras que las proposiciones son verdaderas si, y sólo si, encajan en el mundo, las normas son eficaces (u obedecidas, o seguidas) si, y sólo si, encaja el mundo en ellas. Creemos que este aspecto de la dimensión ilocucionaria capta a la perfección la diferencia entre proposiciones y normas. Pero, ¿qué sucede con los realizativos? ¿Qué ocurre con una expresión como “Te nombro Ministro de Cultura”? Pues, según Searle, la realización con éxito de este acto de nombramiento comporta el cambio de posición institucional, ahora eres Ministro de Cultura. Por esta razón, los realizativos tienen una doble dirección de encaje: por un lado palabra-a-mundo y, por otra, mundo-a-palabra.

La peculiaridad de los realizativos proviene del hecho de que, dadas ciertas reglas institucionales,^[46] por el hecho de decir ciertas palabras se “cambia el mundo” (se cambia el mundo institucional, no el mundo fáctico) y, por eso, tan cierto es que el mundo encaja en las palabras como que las palabras encajan en el mundo.

1.3.3. Uso y mención. Lenguaje objeto y metalenguaje

Por norma general utilizamos el lenguaje para referirnos a entidades extralingüísticas. Así, decimos “Kelsen^[47] nació en Praga”, pero también decimos “Kelsen tiene seis letras”. Obviamente, en la primera oración la palabra Kelsen es utilizada para hacer referencia a la persona Hans Kelsen; en la segunda, en cambio, la palabra Kelsen sólo se menciona y no se refiere al individuo Kelsen, sino a la palabra misma.

Para distinguir estos supuestos, cuando queremos mencionar una expresión lingüística la ponemos en cursiva o bien entre comillas y no usamos la expresión para referirnos a un objeto extralingüístico, sino que la mencionamos para hacer referencia a la misma expresión. En nuestro ejemplo, la diferencia es trivial: nadie confundiría la persona de Kelsen con su nombre; sin embargo, la diferencia, en otros contextos, es muy importante.

Esta diferencia nos permite distinguir entre lenguaje objeto, el lenguaje al que nos referimos, y metalenguaje, el lenguaje que usamos para hablar del lenguaje objeto.^[48] Obviamente, un metalenguaje puede ser, a su vez, lenguaje objeto de otro. Es decir, podemos construir todos los niveles lingüísticos que queramos o podamos.

Esta distinción es importante para ser conscientes de la ambigüedad que se da en la expresión lenguaje jurídico, que se refiere al mismo tiempo al lenguaje en que se expresan las normas, el lenguaje del derecho (principalmente, el lenguaje legal), y al lenguaje en que se expresan los juristas, el lenguaje de los juristas (el lenguaje de la ciencia o dogmática jurídica).

El lenguaje de los juristas es un metalenguaje del lenguaje del derecho, que es su lenguaje objeto. Las denominadas oraciones deónticas poseen la misma ambigüedad. Supongamos que un profesor dice en clase: “Está prohibido fumar”: es posible que esta oración sea una orden y, por tanto, que exprese una norma que el profesor, haciendo uso de su autoridad, impone a los estudiantes. Pero también es posible que esta oración sea una aserción: el profesor sólo informa a los estudiantes de la existencia de una norma, dictada quizá por las autoridades académicas, que prohíbe fumar. En este segundo caso la oración expresa una proposición normativa.^[49]

Si la oración “Está prohibido fumar en clase” es una prescripción y, en consecuencia, expresa una norma, que no es susceptible de verdad o falsedad, su dirección de encaje es mundo-a-palabra. Si la oración es una aserción y, por tanto, expresa una proposición normativa, susceptible de verdad o falsedad, su dirección de encaje es palabra-a-mundo. La proposición normativa es verdadera si, y sólo si, la norma que prohíbe fumar existe -es decir, si las autoridades académicas promulgaron una formulación normativa en este sentido.

Es importante que seamos conscientes de esta distinción: es posible que un libro de derecho civil contenga una expresión equivalente a la del primer párrafo del artículo 1.500 del Código civil:

Artículo 1.500

“El comprador está obligado a pagar el precio de la cosa vendida en el tiempo y lugar fijados en el contrato.”

Ahora bien, mientras que este texto del Código civil establece una obligación para los compradores e intenta guiar su comportamiento, el mismo texto en un libro de derecho civil sólo informa acerca de la existencia de esta norma en nuestro ordenamiento civil. Si el Código civil cambia, también cambian los libros de derecho civil. Así se entiende la famosa frase del jurista Julius H. von Kirchmann, quien en una conferencia de 1847 titulada Die Wertlosigkeit der Jurisprudenz als Wissenschaft (‘La falta de valor de la jurisprudencia como ciencia’)^[50] dijo: “Tres palabras rectificadoras del legislador, y bibliotecas enteras se convierten en basura”

1.4. Las definiciones

Una manera de disminuir algunos de los problemas que hemos visto, planteados por el uso de los lenguajes naturales, como la ambigüedad y la vaguedad, es recurrir a definir los términos que utilizamos. Por otro lado, las definiciones nos permiten aumentar el vocabulario con términos nuevos.

Tradicionalmente se solía distinguir entre dos tipos de definiciones:

• Definiciones reales, que captaban la esencia de una entidad mostrando su género y su diferencia específica.^[51]
• Definiciones nominales, que estipulaban la forma de entender un término o un símbolo nuevo.^[52]

Ahora bien, si no compartimos las dudosas premisas metafísicas que configuran el trasfondo de la idea “captar la esencia de algo”, esta distinción resulta muy cuestionable. Por ahora es suficiente con decir que una definición es un enunciado que establece el significado de una expresión, algo que se consigue relacionando la expresión que se define, el definiendum, con otras expresiones de las que ya disponemos, el definiens.

Una distinción más adecuada entre tipos de definiciones es la que distingue las definiciones lexicográficas de las definiciones estipulativas:

• Una definición lexicográfica nos informa del significado de una expresión lingüística determinada. Muchas de las entradas de un diccionario son definiciones lexicográficas; éstas son susceptibles de verdad o falsedad: son verdaderas si recogen el uso del término y son falsas si no lo hacen. Así pues, el Diccionario de la Lengua Española de la RAE define montaña de esta manera: ‘Gran elevación natural del terreno’. Como vemos, esta definición recoge el uso habitual de la expresión montaña.

• Una definición estipulativa es la que atribuye un nuevo significado a un término, que puede ser un término nuevo o un término ya existente al que asignamos un nuevo significado. Como es obvio, las definiciones estipulativas no son susceptibles de verdad o falsedad. Cuando, en este capítulo, al hablar de la ambigüedad que se da en un contexto de manera alternativa, la hemos llamado CA-ambigüedad, hemos introducido un término absolutamente nuevo. Ahora bien, en algunas ocasiones las definiciones estipulativas definen términos que ya poseemos, pero a los que queremos dar un sentido más preciso (evitando posibles ambigüedades y vaguedades). Esto es lo que sucede con el término anillo, redefinido por el álgebra, o con el término fuerza, redefinido por la física. Estos términos son ambiguos y vagos en el lenguaje ordinario, pero llegan a ser más precisos en el contexto del álgebra o de la física.

Algo similar sucede en el lenguaje del derecho. A veces tenemos términos que sólo se utilizan en contextos jurídicos y que los textos legales acostumbran a definir. Así, el artículo 1881 del Código civil define el término antincresis de la siguiente manera: “Por la anticresis el acreedor adquiere el derecho de percibir los frutos de un inmueble de su deudor, con la obligación de aplicarlos al pago de los intereses, si se debieren, y después al del capital de su crédito”. A pesar de que el término anticresis no fue creado por el legislador del Código civil, su origen fue también un contexto jurídico.

En algunas ocasiones, el legislador utiliza definiciones que ponen de manifiesto una cierta concepción esencialista del lenguaje.

El trasfondo de algunas disputas jurídicas

Algunas disputas jurídicas sólo son desacuerdos con respecto a determinadas definiciones estipulativas que se presentan como desacuerdos referentes a la esencia de algunos institutos jurídicos. Esta posición, conocida como conceptualismo o jurisprudencia de conceptos, fue criticada de manera inteligente y divertida por Rudolf von Ihering (1818-1892),^[53] quien había sido uno de los máximos representantes de la jurisprudencia de conceptos y que es uno de los juristas más importantes de todos los tiempos.

Es importante que seamos conscientes del tipo de desacuerdo que se produce en una controversia jurídica, y que no nos dejemos engañar por la apariencia metafísica de muchas disputas. Así, por ejemplo, el Código civil, después de definir el comodato como un préstamo de algo no fungible, añade: “El comodato es esencialmente gratuito” (artículo 1740). De este modo, los juristas afirman, a menudo, cosas como: “En la naturaleza jurídica del comodato se encuentra su carácter gratuito”.

Otras veces, el derecho usa términos que sí que se utilizan en el lenguaje ordinario, pero precisando su sentido. Así pues, el artículo 139 del Código penal usa el término asesinato, pero definido como: “Quien mate a otra persona concurriendo alguna de las circunstancias siguientes: con traición; por dinero, recompensa o promesa; con ensañamiento, aumentando deliberada e inhumanamente el dolor de la víctima.”

De este modo, el lenguaje del derecho es, parcialmente, un lenguaje técnico o especializado, ya que hace uso de términos que, o bien sólo se utilizan en ese ámbito y, por tanto, están rigurosamente definidos, o bien se extraen del lenguaje ordinario, pero se redefinen con la finalidad de que su uso llegue a ser más preciso.

Como vemos, el hecho de definir los términos de manera estipulativa tiene muchas ventajas: delimita el sentido del definiendum, precisándolo, aclarándolo, eliminando ambigüedades y reduciendo su vaguedad. Ahora bien, ¿hay reglas para conseguir buenas definiciones? Existen algunas reglas, pero su utilidad tan sólo es indicativa. Tradicionalmente se postulaban estas cuatro reglas:^[54]

1. Una definición debe dar la esencia de aquello que se define.
2. Una definición no tiene que caer en un círculo vicioso.
3. Una definición no debe ser negativa cuando puede ser positiva.
4. Una definición no se tiene que expresar en un lenguaje figurado u oscuro.

A estas reglas tradicionales, les podemos añadir dos^[55] más, imprescindibles si queremos que las definiciones posean relevancia teórica:

1. Un término definido tiene que ser eliminable del resto de enunciados de la teoría.
2. Una definición no debe permitir demostrar la existencia de relaciones entre los antiguos términos de la teoría que hasta entonces no se hayan podido demostrar. Es decir, una definición no debe ser creativa.

No obstante, podemos respetar estos seis criterios y no producir buenas definiciones. Las definiciones incorporadas en una teoría^[56] corren la suerte de las teorías a las que pertenecen. Una definición es, por tanto, más o menos adecuada en la medida en que lo sea la teoría que la formula. Como decían los antiguos, termini sine theoria nihil valent.^[57]

La ciencia jurídica también elabora definiciones de algunos términos que el legislador no define; tal es el caso de las definiciones de dolo, en el ámbito de la dogmática penal, o de empresa, en el ámbito de la dogmática mercantil. La suerte de estas definiciones va unida a la capacidad explicativa de las teorías que las definen; por ejemplo, la adecuación de la definición de dolo depende, básicamente, de la capacidad reconstructora de la teoría del delito que la incorpora. Ahora bien, la manera habitual en que los juristas usan los términos está de acuerdo con el sentido que tienen en el lenguaje del derecho. Los juristas utilizan el lenguaje, para decirlo como lo haría Carnap, de una manera traspuesta, es decir, poseen una manera material de hablar. Según Carnap, este uso del lenguaje se caracteriza por el hecho de decir algo de un objeto a, diciendo otra cosa de un objeto b, que tiene una determinada relación con el objeto a. Y añade:

“De acuerdo con el uso común del lenguaje, una acción a de una determinada persona se llama delito si el derecho penal del país en que vive esta persona coloca la descripción de la clase de acción a la que a pertenece en la lista de delitos.”^[58]

Cuando un jurista dice, por ejemplo, “Claudia es mayor de edad”, utiliza el lenguaje de esta manera y quiere decir algo como: “De acuerdo con el derecho español, los mayores de dieciocho años son mayores de edad^[59] y Claudia es mayor de dieciocho años”.

No queremos acabar sin una advertencia y una conjetura:

1. Es necesario advertir que las definiciones, además de servir para informar del uso de un término, como las definiciones lexicográficas, y para estipular uno nuevo, como las definiciones estipulativas, también se pueden utilizar para persuadir a una audiencia de algo. Si queremos usar el lenguaje de una manera rigurosa y que la fuerza de nuestros argumentos se base en la razón, tenemos que huir de las definiciones persuasivas, así como del uso expresivo o emotivo del lenguaje. El uso emotivo del lenguaje es muy apropiado para la poesía, pero muy poco para construir buenos argumentos.
2. La conjetura intenta responder a la siguiente pregunta: ¿qué tipo de discurso usamos cuando definimos de manera estipulativa? No utilizamos el discurso asertivo,^[60] ni tampoco el discurso prescriptivo.^[61] La conjetura consiste en sugerir que las definiciones estipulativas son un tipo de emisiones lingüísticas operativas o realizativas.

Al decir que A significa B, constituimos A como B, hacemos que A sea B. Si esta conjetura fuese sólida, entonces las definiciones jurídicas serían otro tipo de reglas constitutivas. Al definir “mayoría de edad” como “mayor de dieciocho años”, el derecho constituiría a los mayores de dieciocho como mayores de edad. Al decir: “La bandera de Cataluña es la tradicional de cuatro barras rojas en fondo amarillo”^[62] se constituye la bandera con cuatro barras rojas en fondo amarillo como bandera de Cataluña.

En algunas ocasiones, los juristas desconfían de las definiciones legales y también de las doctrinales,^[63] seguramente por una desconfianza histórica hacia las generalizaciones y por una tradición casuística que huye del pensamiento generalizador. A pesar de todo, sin definiciones no tenemos conceptos precisos y sin conceptos precisos nuestra capacidad cognitiva es mucho más débil de lo que podría ser.

2. La lógica como modelo de la argumentación correcta

Hemos dicho que la lógica es un tipo de control de calidad de nuestras argumentaciones. También hemos señalado que la validez lógica es independiente de la verdad o falsedad de las premisas. Un argumento es lógicamente válido si, y sólo si, entre las premisas y la conclusión existe una relación de implicación, lo cual hace posible que para realizar un análisis más profundo de esta relación podamos prescindir de la semántica, del significado de las expresiones lingüísticas, y quedarnos sólo con la sintaxis. Nos importa la forma y la conclusión de las premisas, no el contenido.

Por esta razón, en lógica se han construido determinados lenguajes artificiales que son muy aptos para el análisis de la relación de implicación, pero que son muy distintos de los lenguajes naturales en los que, de manera habitual, nos expresamos los seres humanos.

2.1. Lenguajes artificiales y sistemas formales

Los lenguajes artificiales son lenguajes que cuentan con un vocabulario básico, un alfabeto, rigurosamente establecido. En este aspecto ya se diferencian de los lenguajes naturales, si tomamos las palabras como las unidades mínimas del vocabulario de un idioma.^[64] También hay reglas sintácticas de formación de las expresiones bien formadas del lenguaje. Estas expresiones bien formadas se llaman fórmulas, y están rigurosamente definidas. Además, disponemos de reglas de transformación o reglas lógicas, que nos muestran cómo podemos pasar de unas fórmulas a otras, cómo podemos obtener determinadas conclusiones a partir de ciertas premisas.

Un sistema formal es un conjunto de símbolos primitivos, que constituyen el vocabulario básico, más un conjunto de reglas de formación y un conjunto de reglas de transformación o reglas lógicas. Es posible construir infinitos sistemas formales. Douglas R. Hofdstadter, en un libro bastante interesante^[65], propone el siguiente ejemplo (como un tipo de juego) de sistema formal, llamado sistema MIU:

1) Vocabulario básico

Símbolos primitivos: M, I, U.

2) Reglas de formación

1. Cualquier cadena que esté formada por los símbolos primitivos es una fórmula de MIU.
2. Sólo son fórmulas de MIU las cadenas integradas por los símbolos primitivos.
   Los siguientes ejemplos son ejemplos de fórmulas de MIU: MU, UIM, UI, MUUUU, UIIUMIUMUUIIIMM.

3) Reglas de transformación o reglas lógicas

Regla 1. Si tenemos una cadena cuya última letra es I, podemos agregarle una U al final. Así, por ejemplo, si tenemos MUUUI, podemos obtener: MUUUIU.

Regla 2. Supongamos que tenemos una fórmula de la forma Mx; entonces podemos obtener Mxx. Es obvio que x se encuentra en el lugar de cualquier conjunto de símbolos de MIU. Esta regla permite derivaciones como las siguientes:

• Si tenemos MU, podemos obtener MUU.
• Si tenemos MUI, podemos obtener MUIUI.
• Si tenemos MMU, podemos obtener MMUMU.

Regla 3. Si en una de las fórmulas aparece la secuencia III, podemos obtener una nueva fórmula sustituyendo III por U. Así, por ejemplo:

• Si tenemos MIII, podemos obtener MU.
• Si tenemos MIIII, podemos obtener tanto MIU como MUI.
• Si tenemos UMIIIMU, podemos obtener UMUMU.

Regla 4. Si la secuencia UU aparece en alguna fórmula, podemos obtener otra fórmula en la que la secuencia UU es eliminada. Así, por ejemplo:

• Si tenemos UUU, podemos obtener U.
• Si tenemos MIIIUUU, podemos obtener MIIIU.

Hofdstadter configura su sistema formal como un sistema axiomático. Un sistema axiomático es un sistema en el que algunas de las fórmulas son como los puntos de partida, indemostrables en el mismo sistema. Las otras fórmulas que, mediante las reglas de transformación, se obtienen de los axiomas reciben el nombre de teoremas.

Hofdstadter construye MIU, de manera que sólo tiene un axioma:

Axioma de MIU: MI.

Ejemplo de supuesto de demostración formal. Tratamos de probar el siguiente teorema: MUIIU

(1) MI (2) MII (3) MIIII (4) MIIIIU (5) MUIU (6) MUIUUIU (7) MUIIU

Axioma de (1), aplicando la regla 2. de (2), aplicando la regla 2. de (3), aplicando la regla 1. de (4), aplicando la regla 3. de (5), aplicando la regla 2. de (6), aplicando la regla 4.

Estamos, pues, ante un supuesto de demostración formal. Éste es un argumento lógicamente válido en MIU, porque la conclusión, MUIIU, se ha obtenido a partir de las premisas (en este caso el axioma MI) y sólo a partir de las reglas lógicas.

2.2. La lógica elemental

Con estas ideas estamos en condiciones de presentar algunos sistemas formales de la lógica elemental, que es, de hecho, la parte más elemental de esta rama de la lógica. Hoy día la lógica es una disciplina muy extensa y compleja, y aquí sólo nos interesa una pequeña parte de ésta, la que pensamos aplicar para controlar la validez de nuestros argumentos en el lenguaje ordinario.

Queremos presentar dos sistemas formales, el de la lógica proposicional (Lp) y el de la lógica de predicados (LP), y lo hacemos en lo que se llama cálculos de la deducción natural. Es decir, no presentamos los sistemas como sistemas axiomáticos, sino como sistemas que, a partir de determinadas premisas, permiten obtener determinadas conclusiones. Es habitual que en las argumentaciones ordinarias no razonemos de manera axiomática, sino que supongamos la verdad de las premisas y tratemos de ver las conclusiones que se derivan de éstas.

2.2.1. La lógica proposicional

1) Símbolos primitivos de Lp

El sistema Lp es un lenguaje con el siguiente vocabulario básico:

• Variables proposicionales: p, q, r, s, p’, q’, r’, s’, p’’, etc.

• Conectivas: ¬, ∧, ∨, → , ↔ .

• Paréntesis: ( ).

A continuación haremos algunos comentarios con respecto al vocabulario de Lp:

1. Variables proposicionales: las variables proposicionales representan proposiciones (el significado de las oraciones asertivas). En general, tendremos suficiente con las variables p, q, r y s, pero, como vemos, podemos conseguir un número infinito de variables mediante la añadidura de comillas a las letras iniciales.
2. Conectivas: presentamos ahora el significado de las conectivas.

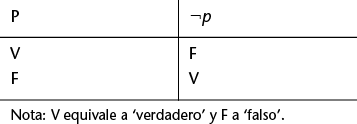
   • El signo ¬ es el signo de la negación.^[66] Aunque ahora no estamos interesados por la verdad de nuestras premisas, vale la pena realizar algunos comentarios con respecto a la semántica de las conectivas, ya que no podemos olvidar que un argumento es válido si, y sólo si, no es posible que las premisas sean verdaderas y la conclusión, falsa. Una variable proposicional, como p, puede ser verdadera o falsa. Entonces, si p es verdadera, ¬p es falsa, y si ¬p es falsa, p es verdadera. Podemos expresar esta idea con lo que se denomina una tabla de verdad. Ésta es la tabla de verdad de la negación:

     

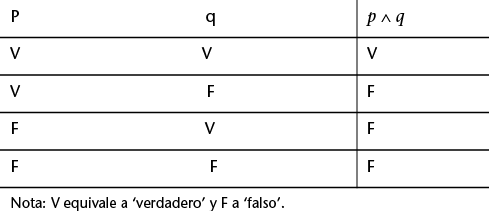
   • El símbolo ∧ es el símbolo de la conjunción.^[67] Se considera que una conjunción es verdadera sólo cuando lo son los dos miembros que la componen; en el resto de casos es falsa. Esta asignación de la verdad a las fórmulas conjuntivas se adecua bastante bien a nuestro uso ordinario. La tabla de la verdad de la conjunción es la siguiente:

     

   • El símbolo ∨ representa la disyunción.^[68] Es necesario aclarar que el significado de esta conectiva se adecua al que en algunas ocasiones se conoce como disyunción inclusiva, es decir, la disyunción sólo es falsa cuando lo son los dos miembros que la componen. Como dice W. V. Quine,^[69] mientras que en la conjunción la verdad es recesiva y la falsedad, dominante, en la disyunción es al revés: la verdad es dominante y la falsedad, recesiva. Ésta es la tabla de verdad para la disyunción:

     

   • El símbolo → es el del condicional.^[70] El símbolo que se encuentra a la izquierda del condicional recibe el nombre de antecedente, y el de la derecha, el de consecuente. De acuerdo con nuestras intuiciones previas, un condicional se considera verdadero cuando el antecedente es verdadero y el consecuente también lo es, y es falso cuando el antecedente es verdadero y el consecuente es falso. Ahora bien, ¿qué pasa cuando el antecedente es falso? En tal caso, la asignación es más arbitraria; no obstante, se considera que un condicional con antecedente falso es siempre verdadero.

   Los condicionales contrafácticos

   Existen expresiones que tienen forma condicional y que no se pueden analizar con este esquema, como es el caso de los denominados condicionales contrafácticos, que están en el modo subjuntivo, como, por ejemplo, la que tenemos a continuación: si Borrell hubiera sido candidato a la presidencia del gobierno en las elecciones generales de 2000, Aznar habría perdido las elecciones. Dado que el antecedente es falso, éste sería un condicional verdadero.

   Sin embargo, también lo sería este otro: Si Borrell hubiera sido candidato a la presidencia del gobierno en las elecciones generales de 2000, Aznar habría ganado las elecciones.

   Queda claro que los condicionales contrafácticos se tienen que analizar de otra manera. Los condicionales contrafácticos se deben analizar con otros elementos además de los valores de verdad de sus componentes, como, por ejemplo, mediante las relaciones causales entre antecedente y consecuente. Esta cuestión se escapa de la lógica en sentido estricto, motivo por el que no la desarrollaremos aquí.

   Por otro lado, a veces el símbolo → se lee como ‘implica’. Éste es un hábito que puede llevar a considerables malentendidos. La implicación tiene, obviamente, mucho que ver con el condicional, pero la relación de implicación es más “fuerte” que la del condicional: la implicación es, como sabemos, la validez lógica del condicional.^[71]

   La tabla de verdad del condicional es la siguiente:

   

   • El símbolo ↔  es el de bicondicional. Un bicondicional es la conjunción de dos condicionales: uno que va de izquierda a derecha y otro que va de derecha a izquierda. De este modo, si p y q significan lo mismo que en los ejemplos anteriores, p ↔ q significará ‘si, y sólo si llueve, hace sol’. El bicondicional es verdadero cuando sus dos componentes son verdaderos o falsos; si uno de ellos es falso y el otro verdadero, entonces es falso. A continuación podemos ver su tabla de verdad:

   • 
     
3. Paréntesis: los paréntesis se usan, como es habitual, en los sistemas formales. La comprensión de su uso es muy intuitiva, por lo que no es necesario que la explicitemos.

2) Las reglas de formación de Lp

Son las siguientes:

1. (1) Todas las variables proposicionales son fórmulas de Lp.
2. (2) Si A es una fórmula de Lp, entonces ¬A también lo es.
3. (3) Si A y B son fórmulas de Lp, A ∧ B, A ∨ B, A→B y A↔B también lo son.
4. (4) Sólo son fórmulas de Lp las que se forman mediante las reglas de formación:

A continuación, realizaremos algunos comentarios sobre las reglas de formación:

1. En primer lugar, las letras A y B no son fórmulas de Lp. Ni A ni B integran el vocabulario básico. Son esquemas de fórmulas, se encuentran en el lugar de determinadas fórmulas de Lp.
2. En segundo lugar, podemos considerar estas reglas como una definición recursiva de Lp. Un tipo de definición recursiva es la definición aritmética de número natural, que se corresponde con los dos primeros axiomas de la aritmética elemental (consta de cinco axiomas en total), formulados por Giuseppe Peano (1858-1932):
   1. El 0 es un número natural.
   2. Todo sucesor de un número natural es un número natural.

Este tipo de definiciones resultan especialmente adecuadas en el ámbito de los sistemas formales.^[72] Por norma general, la noción de norma válida no se ha definido, en teoría del derecho, mediante una definición recursiva; sin embargo, los filósofos del derecho argentinos Carlos E. Alchourrón (1931-1996) y Eugenio Bulygin (1931-)^[73] han presentado una definición recursiva de norma válida, en el sentido de norma que pertenece al derecho y, por tanto, de una definición de derecho. Tiene las tres cláusulas que anotamos a continuación:

1. Todas las normas que pertenecen al conjunto C (por ejemplo, una Constitución) son normas válidas.
2. Si hay una norma válida que autoriza a una autoridad normativa X a promulgar la norma N’, y X promulga N’, entonces N’ también es válida.
3. Todas las normas que son consecuencia lógica de las normas válidas también son válidas.

Una definición como ésta permite resolver algunos de los problemas que plantean concepciones como la de Hans Kelsen y la norma básica. Como es sabido, Kelsen establece que es una condición necesaria para la validez de cualquier norma que haya otra norma que autorice su creación. Entonces, una de las cuestiones con respecto a la norma básica es: ¿la norma básica es válida o no?

Si lo es, debe haber otra norma que autorice su creación; si no lo es, no puede transmitir la validez al resto de normas.

Si, en cambio, definimos la norma válida con una definición recursiva, podemos prescindir de la norma básica. Eso sí, debemos atribuir validez a las normas de la Constitución.

En tercer lugar, con las reglas de formación podemos averiguar si una determinada expresión es una fórmula de Lp o no lo es. Pensemos en la siguiente expresión:

(p ∧ ¬q) → (r ∨ s)

Ésta es una fórmula de Lp. ¿Por qué?

• p y q son fórmulas por la regla (1).
• ¬q es una fórmula por la regla (2).
• (p ∧ ¬q) es una fórmula por la regla (3).
• r y s son fórmulas por la regla (1).
• (r ∨ s) es una fórmula por la regla (3).
• (p ∧ ¬q) → (r ∨ s) también es una fórmula por la regla (3).

3) Reglas de transformación o reglas lógicas de Lp

Éstas son las reglas que nos garantizan que nuestros argumentos son válidos. Supongamos el siguiente argumento:

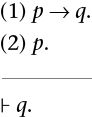
que podría ser una formalización de:

El signo├ es el signo de la implicación. Quiere decir que lo que hay a la derecha del símbolo (la conclusión) se deduce lógicamente de lo que hay a la izquierda del símbolo (las premisas) –o en la parte de arriba de la línea separadora. Éste parece un argumento correcto y, de hecho, lo es. ¿Cómo podemos probarlo? Antes de mostrar las reglas que nos permitirán demostrarlo, indicaremos de forma sumaria cómo se puede controlar la validez lógica de los argumentos mediante las tablas de verdad.

Método de las tablas de verdad

Construimos la tabla de verdad para esta deducción:

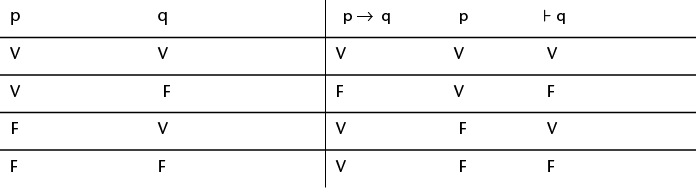
1. En primer lugar, vemos cuáles son las variables proposicionales que hay en el argumento y les asignamos todas las combinaciones posibles de valores de verdad. Las combinaciones son el resultado de 2ⁿ donde n es el número de variables proposicionales del argumento. Como en este caso tenemos dos, resulta que obtendremos cuatro combinaciones posibles, es decir, cuatro filas en la tabla de verdad.
2. Después construimos la tabla de las premisas y de la conclusión. El argumento es válido si, y sólo si, siempre que las premisas tienen el valor V, la conclusión también tiene el valor V. Es lo que pasa en nuestro ejemplo en la primera fila. Ergo, el argumento es válido.

Como se puede ver, el método de las tablas de verdad es muy intuitivo, ya que se corresponde con la definición de argumento correcto: no es posible que las premisas sean verdaderas y la conclusión sea falsa.

Tabla de verdad de un argumento con tres variables proposicionales

Vemos, ahora, que la tabla de verdad de otro argumento con tres variables proposicionales tiene ocho filas (resultado de elevar 2 a la tercera potencia, 23):

Veamos, ahora, la tabla de verdad de este argumento:

Una vez construida la combinación de valores de verdad entre p, q y r (las tres primeras columnas), sólo nos tenemos que fijar en las cuatro últimas columnas, que atribuyen valores de verdad tanto a las premisas como a la conclusión. Como se puede apreciar, las tres premisas sólo son verdaderas en la primera fila y, por tanto, ésta es la única fila que nos interesa; así pues, en la primera fila la conclusión también es verdadera. Ergo, el argumento es válido. La idea es simple: si no es posible que todas las premisas sean verdaderas y que la conclusión sea falsa, entonces el argumento es necesariamente válido.

El problema del sistema de las tablas de verdad radica en el hecho de que si tenemos más variables proposicionales en el argumento, el método se vuelve un poco pesado.^[74] No obstante, observad que es un método mecánico y seguro.

Método del cálculo de la deducción natural

Desarrollaremos ahora un método distinto: el cálculo de la deducción natural, que mediante determinadas reglas de transformación garantiza la validez de los argumentos. El método que presentamos es, con pequeñas variaciones, el método construido por el lógico Gerahrd Gentzen, que mediante unas reglas muy básicas de introducción y eliminación de las conectivas, contiene una gran fuerza deductiva:

1. Regla 1.ª: introducción de premisa (IP). Esta regla nos permite introducir cualquier fórmula en una derivación, siempre que a su izquierda escribamos el número que introducimos de la siguiente manera:

   n     ( n ) A     IP

   Ésta parece una regla muy liberal, pero, como tendremos ocasión de comprobar, debemos ser capaces de cancelar las líneas de la derivación que hemos supuesto.

2. Regla 2.ª: introducción de la conjunción (I∧). Esta regla nos permite introducir la conjunción de la siguiente manera:

   

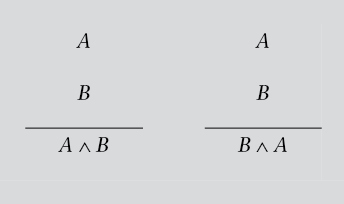
   Es decir, si tenemos dos fórmulas cualesquiera, en tal caso podemos obtener la conjunción entre ellas.

3. Regla 3.ª: eliminación de la conjunción (E∧). Esta regla nos permite eliminar la conjunción del siguiente modo:

   

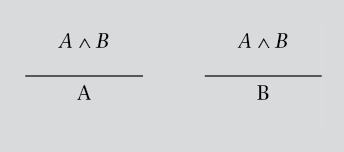
   Si tenemos dos fórmulas unidas por la conjunción, podemos obtener cualquiera de éstas por separado.

4. Regla 4.ª: introducción de la disyunción (I∨). Esta regla nos permite introducir la disyunción de esta manera tan sencilla:

   

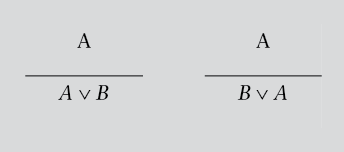
   La justificación intuitiva de esta regla es la siguiente: como para que una disyunción sea verdadera es suficiente con que lo sea uno de sus componentes, si una fórmula es verdadera, también lo será esta fórmula unida por la disyunción con otra cualquiera.

5. Regla 5.ª: eliminación de la disyunción (E∨). Esta regla es más complicada y la usaremos poco por las razones que veremos más adelante. De todos modos, aquí tenemos su formulación:

   

   Esta regla significa lo siguiente: si tenemos una disyunción en una premisa en la línea (n), y de cada uno de sus componentes (A y B) podemos derivar otra fórmula C (basada en las líneas de A y B que hemos supuesto), entonces podemos obtener C y cancelar los números (representados por las letras m y o que aparecen tachados) donde hemos introducido las premisas que hemos supuesto. Más adelante mostraremos con detenimiento cómo funciona esta regla.

6. Regla 6.ª: introducción del condicional (I →). Esta regla autoriza a poner el condicional entre dos fórmulas, siempre que demostremos que el consecuente se puede derivar del antecedente:

   

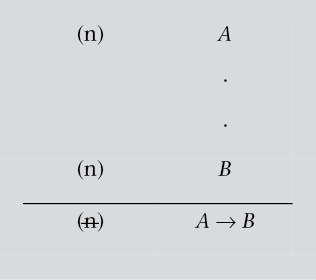
   Si podemos demostrar que B se deduce de A, entonces podemos eliminar la línea en que se basa A para obtener A → B. Muy pronto veremos cómo funciona esta regla.

7. Regla 7.ª: eliminación del condicional o modus ponendo ponens (E →). Esta regla permite separar un condicional siempre que tengamos su antecedente, obteniendo, así, su consecuente:

   

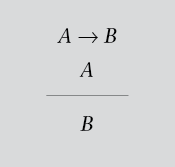
   Con esta regla nos encontramos en condiciones de ver, también, cómo funciona la regla de introducción del condicional. Veamos, ahora, una derivación de las premisas “Si se comete asesinato, también se comete homicidio” y “Si se comete homicidio, se comete un delito”; en la conclusión “Si se comete asesinato, se comete un delito”, p representa “se comete asesinato”, q “se comete homicidio” y r “se comete un delito”.

   

   Vemos, de este modo, cómo funciona la regla de la introducción del condicional: en la premisa (3) hemos introducido p y en la premisa (5) hemos demostrado r, basados en (3); entonces podemos obtener p → r y cancelar (3), que por eso aparece tachado a la izquierda de (6).

   Una derivación es correcta si, y sólo si, a la izquierda de la última línea sólo aparecen los números que corresponden a las premisas. La diferencia entre los números que aparecen a la izquierda del número de la línea y los que aparecen al lado del nombre de la regla que hemos aplicado es la siguiente: los números que acompañan al nombre de la regla (en la línea 5, por ejemplo, al lado de E → aparecen 2, 4) son los números de las líneas donde aplicamos la regla; los números de la izquierda de (5) (donde aparece 1, 2, 3) son los números en que se justifica esta derivación: 2 hace referencia al uso de la premisa (2) y 1, 3, hacen referencia a las premisas que justifican (4), que son precisamente 1, 3.

8. Regla 8.ª: introducción de la negación o reducción al absurdo (I¬). Esta regla nos permite lo siguiente: si suponemos una fórmula y, a partir de ella, derivamos otra fórmula y su negación (una contradicción), entonces podemos derivar la negación de la premisa supuesta y cancelar la suposición:

   

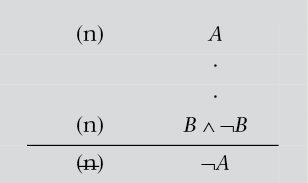
   La justificación intuitiva de esta regla se basa en el hecho de que, si suponiendo algo derivamos una contradicción, es un buen indicador de que lo supuesto sea falso. En no pocas ocasiones utilizamos este tipo de argumentos en la argumentación ordinaria:

   Ejemplo de argumentación

   Argumento: todos hemos oído alguna vez un argumento como el siguiente: supongamos que Dios existe. Si Dios existe, entonces es totalmente bondadoso y omnipotente. Si Dios es totalmente bondadoso y omnipotente, entonces Auschwitz no habría sucedido.^[75] Sin embargo, Auschwitz sucedió. Por tanto, Dios no existe.

   Formulación del argumento:

   “Dios existe” se representa por p.
   “Dios es totalmente bondadoso y omnipotente” se representa por q ∧ r.
   “Auschwitz sucedió”, por s.

   

   Debe quedar claro que esta conclusión sólo es verdadera si las premisas son verdaderas. Creemos que nadie mínimamente sensato desafiaría las premisas (1) y (3) –es obvio que la premisa 3 se ha desafiado, pero lo ha hecho gente carente de cordura o, todavía peor, con mala fe.

   Seguramente, los que están dispuestos a creer en la existencia de Dios desafiarían la premisa (2) diciendo que Auschwitz es compatible con un Dios omnipotente y bondadoso. No conozco ningún argumento que me haya convencido a abandonar la premisa (2); pero esto -obviamente- no quiere decir que no lo haya.

9. Regla 9.ª: regla de la eliminación de la negación o de la doble negación (E¬). Esta regla permite eliminar las negaciones cuando encontramos dos seguidas ante una fórmula. Es una regla muy fácil de aplicar:

   
   

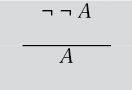
Las reglas derivadas

Las reglas que acabamos de ver nos permiten demostrar la validez de determinadas reglas derivadas que son muy útiles en el cálculo. De hecho, con las reglas básicas sería suficiente para demostrar todo lo que es posible con el sistema de la lógica proposicional. Pero las reglas derivadas hacen más ligero el trabajo de deducir, como se demuestra en los ejemplos siguientes:

1. Las dos reglas de introducción y eliminación de la negación, junto con la regla de la introducción de la conjunción, nos permiten obtener la regla derivada de la doble negación (DN), de acuerdo con la cual no sólo cuando tenemos ¬¬p pueden obtener p (de acuerdo con E¬), sino que también a partir de p podemos obtener ¬¬p de la siguiente forma:

   

2. Otro caso de regla derivada: la regla de la reducción al absurdo nos permite mostrar cómo funciona la regla de la eliminación de la disyunción (la regla 5.ª). Mostraremos cómo funciona esta regla con la finalidad de demostrar otra regla derivada, pero muy útil, denominada regla del silogismo disyuntivo (SD) o, también, modus tollendo ponens.^[76] Esta regla nos permite obtener, de las premisas “Llueve o hace sol” (p ∨ q) y “no llueve” (¬p), la conclusión “hace sol” (q). Ésta es su demostración:

   

3. Otra regla derivada muy útil es la que recibe el nombre de modus tollendo tollens (MT): permite obtener la negación del antecedente de un condicional a partir del condicional y de la negación de su consecuente. De esta manera:

   

   Como podemos apreciar, las reglas derivadas nos permiten obtener conclusiones ahorrándonos muchos pasos intermedios. A continuación, mostramos otras reglas derivadas que también tienen importancia, pero sin la intención de ser exhaustivos.

4. Tenemos, por ejemplo, la regla según la cual a partir de una contradicción se sigue cualquier conclusión, llamada por los antiguos ex falso quodlibet. Es una regla muy fácil de probar haciendo uso de alguna de las reglas derivadas, en concreto del silogismo disyuntivo (SD):

   

   Ésta es una demostración elegante y simple de un teorema importante de la lógica: introducir una contradicción en un sistema tiene consecuencias fatales porque entonces cualquier fórmula es demostrable en el sistema. Y un sistema que lo prueba todo, obviamente, no sirve para nada.

   Una contradicción en el sistema formal de Gottlob Frege

   La honestidad intelectual del lógico Gottlob Frege se puso de manifiesto cuando otro gran lógico y filósofo, Bertrand Russell (1872-1970)^[77] le escribió una carta en la que le mostraba que el sistema formal que había creado, y al que había dedicado buena parte de su vida, contenía una contradicción.

   Frege, consciente de la importancia del problema, abandonó el sistema e intentó, sin demasiado éxito, poner remedio al problema.

5. También son muy importantes las reglas derivadas que permiten la interdefinición de las conectivas. Así, tenemos las denominadas leyes de De Morgan,^[78] que permiten interdefinir la conjunción y la disyunción:

   

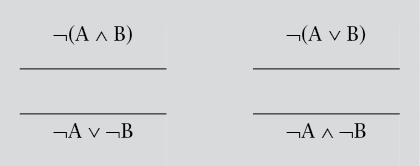
   Utilizamos dos rayas para representar que las dos fórmulas que hay encima y abajo de las dos rayas son equivalentes y que la derivación es válida en ambos sentidos.

6. También tenemos las reglas que interdefinen el condicional con la conjunción (Df. → , ∧) y el condicional con la disyunción (Df. → ,∨):

   

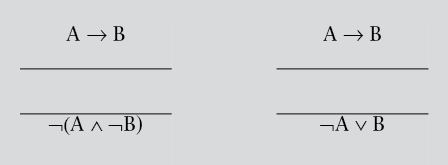
   Demostraremos sólo una de las direcciones de la definición del condicional con la conjunción: a partir de p → q demostraremos ¬(p ∧ ¬q).

   

   Estrategias para obtener la conclusión

   Cuando uno empieza a familiarizarse con la lógica, es usual que se pregunte: pero, ¿qué reglas tenemos que usar para obtener la conclusión? Esta pregunta no tiene una respuesta unívoca. Es como cuando, al aprender a jugar al ajedrez, nos preguntamos: ¿qué estrategia tenemos que seguir para ganar la partida? La respuesta es: “Depende”. Depende de la estrategia del adversario, en el caso del ajedrez; y depende de la composición de las premisas y de la conclusión, en el caso de la lógica.

   A pesar de todo, podemos facilitar algunas estrategias que aseguran el éxito:

   a) Intentad utilizar las reglas que conocéis para conseguir tantas variables proposicionales como podáis (o sus negaciones) operando en las premisas.

   b) Si la conclusión tiene forma condicional, introducid el antecedente por medio de la regla IP y tratad de probar su consecuente. Si lo conseguís, podéis aplicar la regla de introducción del condicional I → y así habréis demostrado la conclusión.

   c) En caso de que ninguna de estas estrategias tenga éxito, introducid la negación de la conclusión (o si la conclusión tiene forma condicional, la negación del consecuente de la conclusión) por medio de IP e intentad probar una contradicción (una fórmula y su negación); entonces podréis usar la regla de la introducción de la negación (la regla de la reducción al absurdo) I¬, y así probaréis la conclusión (bien directamente, bien por eliminación de la negación E¬).

Nos quedan dos reglas muy sencillas (las reglas 10.ª y 11.ª) que hacen referencia a la introducción y eliminación del bicondicional, y que son las siguientes:

1. Regla 10.ª: introducción del bicondicional (I↔). Esta regla nos permite introducir el bicondicional siempre que tengamos dos condicionales que unan dos fórmulas de izquierda a derecha y de derecha a izquierda:

   

2. Regla 11.ª: eliminación del bicondicional (E↔). Esta regla nos permite obtener dos condicionales –de izquierda a derecha y de derecha a izquierda– a partir de un bicondicional:

   

4) Los teoremas de Lp

Otra propiedad importante del sistema formal Lp es que existen fórmulas que se pueden demostrar sin premisas. Estas fórmulas son los teoremas de Lp. Los teoremas de Lp tienen la peculiaridad de ser fórmulas siempre verdaderas, algo que se puede comprobar elaborando su tabla de verdad y mostrando que cualquier distribución de los valores de verdad preserva la verdad de la fórmula. Una fórmula siempre verdadera es una tautología. En lógica proposicional, todos los teoremas son tautologías (el sistema Lp es consistente) y todas las tautologías son teoremas (el sistema Lp es completo).

La noción de tautología y su opuesta, la contradicción (cuando todas las distribuciones de verdad de la fórmula tienen como resultado la falsedad), fueron introducidas por Ludwig Wittgenstein en una obra capital para la historia de la lógica de la que reproducimos algunos párrafos:

“4.46. Entre los posibles grupos de condiciones de verdad existen dos casos extremos.

En el primer caso, la proposición es verdadera para todas las posibilidades de verdad de las proposiciones elementales. Decimos que las condiciones de verdad son tautológicas.

En el segundo caso, la proposición es falsa para todas las posibilidades de verdad: las condiciones de verdad son contradictorias.

En el primer caso decimos que la proposición es una tautología; en el segundo, que es una contradicción.”

“4.61. La proposición muestra aquello que dice; la tautología y la contradicción muestran que no dicen nada.

La tautología no tiene ninguna condición de verdad, ya que es verdadera sin condiciones; y la contradicción no es verdadera bajo ninguna condición. La tautología y la contradicción están vacías de sentido.

(Como el punto del que se separan dos flechas en direcciones opuestas.)

(No sé nada sobre el tiempo, por ejemplo, cuando sé que llueve o que no llueve.)”^[79]

Vamos a demostrar que una fórmula conocida como la ley del tercer excluido (p ∨ ¬p, tertium non datur) es una tautología mediante las tablas de verdad, y que es una fórmula que se puede demostrar sin premisas (mediante las reglas lógicas del cálculo de la deducción natural). Empecemos por la tabla de verdad, que bajo la fórmula p ∨ ¬p sólo tiene el valor V:

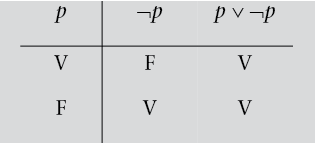
Probemos, ahora, que p ∨ ¬p se puede demostrar sin premisas:

Como se puede apreciar, en la última línea –la línea (9)– hemos probado que p ∨ ¬p se ha derivado sin premisas, ya que a la izquierda de (9) no hay escrito ningún número: no necesitamos premisas para demostrar su validez.

El método axiomático

Existe una forma más económica, aunque también más pesada, de hacer la derivación o de presentar los sistemas de lógica proposicional. Se trata de una presentación axiomática:

1. Podemos reducir nuestro vocabulario hasta quedarnos sólo con dos conectivas:

   ¬, →.

2. Y podemos reducir nuestras reglas lógicas hasta quedarnos con una sola regla: la regla de la eliminación del condicional (E→) o modus ponens.
3. Con tan poco utillaje y los tres axiomas siguientes^[80] es posible derivar todos los teoremas de la lógica proposicional:

   

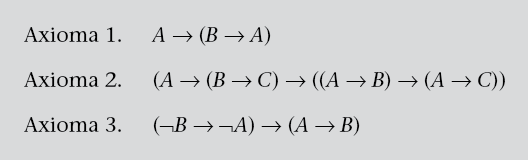
   Un teorema como puede ser p → p, que es muy fácil de demostrar en el cálculo de la deducción natural, se convierte en una prueba pesada con el método o sistema axiomático:

   

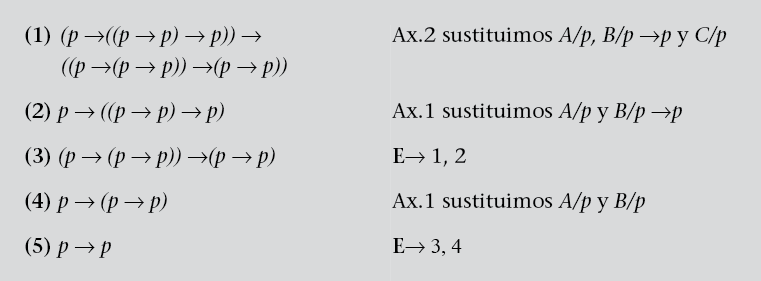
Como se puede ver, el método axiomático resulta mucho menos manejable que el método del cálculo de la deducción natural, aunque tiene otras finalidades. Por ejemplo, es más fácil probar la consistencia (que el sistema no tiene contradicciones) con el sistema axiomático, porque sólo tenemos que probar que los axiomas son consistentes y que la regla de eliminación del condicional preserva su consistencia.

2.2.2. La lógica de predicados

La lógica proposicional, sin embargo, no permite saber si algunos argumentos muy simples son válidos o no. Por ejemplo:

(1) Todos los edificios son bienes inmuebles.

(2) La Sagrada Familia es un edificio.

 

Ergo, la Sagrada Familia es un bien inmueble.

En lógica proposicional, tendríamos que:

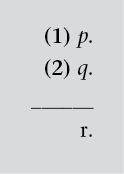
Éste no es un argumento válido en lógica proposicional. No es posible mostrar que la conclusión se deriva de las premisas. Para formalizar estos argumentos necesitamos, por decirlo de algún modo, una lógica más potente. Esta lógica es el sistema formal LP o lógica de predicados.

1) Símbolos primitivos de LP

El vocabulario de LP es más extenso que el de Lp. Éstos son sus símbolos primitivos:

1. Constantes: a, b, c, a’, b’, c’, a’’...

   Las constantes denominan a un único individuo (funcionan como los nombres propios de los lenguajes naturales).

2. Predicados: F, G, H, F’, G’, H’, F’’...

   Los predicados son como los verbos del lenguaje natural. Pueden ser los que denominamos a continuación:

   • Monádicos. Cuando van seguidos de una única constante (como los verbos intransitivos de los lenguajes naturales, corre, camina, y también ser filósofo, ser bien inmueble).
   • Diádicos. Cuando van seguidos de dos constantes (como, por ejemplo, lee, es mayor que, etc.).
   • Triádicos (como, por ejemplo, estar entre: “a está entre b y c”; o comprar: “(la persona) a compra (la cosa) b a (la persona) c”.
   • Y, en general, predicados n-ádicos.

3. Conectivas: ¬, ∧, ∨, →, ↔.

   Ya los conocemos: son los mismos que los del sistema Lp.

4. Paréntesis: ( ).

5. Variables: x, y, z, x’, y’, z’, x’’...

   Funcionan de manera similar a los pronombres de los lenguajes naturales.

6. Cuantificadores: ∀, ∃.

   ∀ es el cuantificador universal y se lee: “para todo”. ∃ es el cuantificador existencial y se lee: “hay algún” o “hay por lo menos uno”.

Fórmula atómica de LP

Veamos ahora las reglas de formación de LP. Con esta finalidad, es muy conveniente definir antes la expresión fórmula atómica de LP. Una fórmula atómica de LP es un predicado n-ádico seguido de n constantes, donde n es mayor o igual que 1.

La definición sólo señala que un predicado seguido de n constantes es una fórmula atómica. Supongamos que queremos representar “Kelsen es filósofo”; pues si a significa ‘Kelsen’ y F significa ‘ser filósofo’, escribiremos Fa. Supongamos que queremos representar “Kelsen escribió la teoría pura del derecho y que representamos ‘escribir’ por G y la ‘teoría pura del derecho’ por b; en tal caso, dado que éste es un predicado diádico, escribiremos Gab.

2) Las reglas de formación de LP

Ahora estamos en condiciones de presentar las reglas de formación de LP:

1. Las fórmulas atómicas de LP son fórmulas.
2. Si A es una fórmula de LP, entonces ¬A también lo es.
3. Si A y B son fórmulas de LP, A ∧ B, A ∨ B, A → B y A ↔ B también lo son.
4. Si A es una fórmula de LP y A* es la expresión resultante de sustituir en A una constante por una variable, entonces la expresión formada por el cuantificador universal ∀ seguido de la misma variable y seguido de A* también es una fórmula.
5. Si A es una fórmula de LP, y A* es la expresión resultante de sustituir en A una constante por una variable, entonces la expresión formada por el cuantificador existencial ∃ seguido de la misma variable y seguido de A* también es una fórmula.
6. Sólo son fórmulas de LP las formadas mediante las reglas a), b), c), d) y e).

Debemos hacer algunos comentarios referidos a las cláusulas d) y e):

• Supongamos que tenemos una fórmula atómica tal como:

  Fa

• Si sustituimos a por la variable x, entonces obtenemos una expresión del tipo A*:

  Fx

• Si le ponemos delante el cuantificador universal seguido de la variable y seguido de A*, obtenemos:

  ∀x(Fx),

  que se lee: “Para todo x: x es un F”.

• Si tuviéramos una expresión como puede ser:

  ∃x(Fx),

  se leería: “Hay algún x tal que x es un F”.

• Esto nos permite formalizar algunos enunciados como “Todos los edificios son bienes inmuebles”. Si “ser edificio” lo representamos por F y “ser bien inmueble” por G, entonces tendremos:

  ∀x(Fx →  Gx),

  que se lee: “Para todo x, si x es un F (un edificio), entonces también es un G (un bien inmueble)” o, lo que es lo mismo: “Todos los edificios son bienes inmuebles”.

• Si queremos representar “Algunos edificios son bienes inmuebles”, lo hacemos así:

  ∃x(Fx ∧ Gx),

  que se lee: “Hay algún x tal que x es F (edificio) y x es G (bien inmueble)”, o

  lo que es lo mismo: “Algunos edificios son bienes inmuebles”.

• Esta formalización tiene la ventaja de evitar algunos problemas de ambigüedad que ya hemos tratado. Hemos dicho que la oración “Pedro y María están casados” es ambigua: puede significar ‘Pedro está casado con x y María están casada con y’, o bien, ‘Pedro está casado con María’. Estas dos expresiones son muy diferentes en el lenguaje de LP. Respectivamente –y suponiendo que a significa ‘Pedro’, b significa ‘María’ y F , ‘está casado con’– la representación sería:

  ∃x ∃y (Fax ∧ Fby), Fab

En la primera oración tenemos: “Existe alguna x y algún y, tales que Pedro está casado con x y María está casada con y”. En la segunda tenemos: “Pedro está casado con María”.

Reglas básicas de transformación o reglas lógicas de LP

Las reglas básicas de transformación o reglas lógicas de LP son las once mismas que las de Lp, más las cuatro particulares siguientes de LP (que llamaremos reglas duodécima, decimotercera, decimocuarta y decimoquinta), que permiten introducir y eliminar los cuantificadores: ^[81]

1. Regla 12.ª: introducción del cuantificador universal (I∀)

   

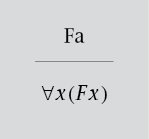
   Esta regla sólo vale con dos reservas:

   • Cuando se usa la regla es necesario que la constante sea sustituida por la variable en todas las ocasiones en que figura en la fórmula.

   • La constante a no debe figurar en ningún supuesto previo no cancelado.

2. Regla 13.ª: eliminación del cuantificador universal (E∀). Ésta es una regla muy fácil de utilizar:

   

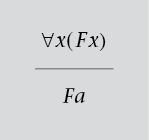
   La justificación intuitiva es la siguiente: si una propiedad vale para todos, también vale para un individuo cualquiera.

   Con esta regla ya podemos representar el argumento con que iniciábamos el apartado, según el cual de las oraciones “Todos los edificios son bienes inmuebles” y “La Sagrada Familia es un edificio”, podemos deducir que “La Sagrada Familia es un bien inmueble”.

   Supongamos que F significa ‘edificio’, G ‘bien inmueble’ y a ‘la Sagrada Familia’. Entonces tendremos:

   

   Veamos, ahora, las reglas del cuantificador existencial.

3. Regla 14.ª: introducción del cuantificador existencial (I∃)

   

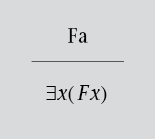
   La justificación también es muy intuitiva: lo que vale de un individuo a, también vale al menos de un individuo cualquiera. Si la Sagrada Familia es un edificio, entonces existe al menos un edificio.

4. Regla 15.ª: eliminación del cuantificador existencial (E∃). Esta regla resulta más difícil de aplicar. Veámosla:

   

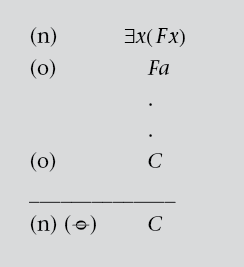
   Asimismo, es necesario que utilicemos esta regla con dos reservas:

   • La constante a no debe figurar en las premisas.

   • La constante a no debe figurar tampoco en la conclusión C, ni en ningún supuesto previo no cancelado.

   El sistema formal LP tiene una gran fuerza deductiva (que aquí sólo podemos sugerir). De hecho, toda la silogística aristotélica,^[82] que constituyó prácticamente toda la lógica hasta G. Frege, es sólo una parte de nuestro sistema formal LP. La teoría del silogismo se ocupaba sólo de las proposiciones categóricas, es decir, las que ponen en relación a un sujeto con un predicado. Pero, de hecho, con la terminología de LP, y como es obvio, ponen en relación dos predicados.

   La teoría del silogismo parte de la siguiente clasificación de las proposiciones (de acuerdo con la división entre proposiciones), según la cantidad -si son universales o particulares- y según la calidad -si son afirmativas o negativas:

1. i) Proposiciones universales afirmativas (A),^[83] que en LP, como ya sabemos, podemos representar por:

   ∀x (Fx →  Gx)

2. ii) Proposiciones universales negativas (E), como, por ejemplo, “Ningún edificio es un bien inmueble” –para todo x: si x es un edificio, entonces no es un bien inmueble–”, que podemos representar por:

   ∀x (Fx → ¬Gx)

3. iii) Proposiciones particulares afirmativas (I),^[84] que podemos representar por:

   ∃x (Fx ∧ Gx)

4. iv) Proposiciones particulares negativas (O),^[85] que podemos representar por:

   ∃x (Fx ∧ ¬Gx)

La teoría del silogismo muestra cómo a partir de dos premisas de este tipo (A, E, I u O) es posible, en algunas ocasiones, llegar a algunas conclusiones. Lo muestra señalando las relaciones que existen entre este tipo de proposiciones y construyendo cuatro figuras según cómo estén ordenadas las premisas y la conclusión. Se conoce como término medio del silogismo el predicado que figura en las dos premisas, pero no en la conclusión.

He aquí un ejemplo de silogismo:

El término medio de este silogismo es “ser bien inmueble”, y la forma, según la teoría del silogismo, es la siguiente:

S designa el sujeto de la conclusión y P, el predicado de la conclusión. La primera premisa siempre contiene el predicado y la segunda, el sujeto. M es el término medio:

En la primera figura tenemos el término medio como sujeto de la premisa mayor (la primera premisa) y como predicado de la menor (la segunda premisa) –como en nuestro ejemplo, en el que “bien inmueble” es sujeto de la premisa mayor y predicado de la premisa menor. En la segunda figura tenemos el término medio como predicado en ambas premisas. En la tercera figura el término medio es sujeto de las dos premisas. Y en la cuarta figura, el término medio es predicado de la premisa mayor y sujeto de la segunda premisa.

Hay 256 tipos de silogismos distintos, pero sólo un número muy reducido, en concreto veinticuatro, constituyen modos válidos desde un punto de vista lógico. Estos modos válidos tienen nombres nemotécnicos^[86] que expresan qué tipo de proposición tienen las premisas y la conclusión, y cómo se pueden transformar en otras figuras.

El silogismo de nuestro ejemplo es un silogismo en BARBARA, el primer modo de la primera figura: las tres proposiciones son de tipo A –universales afirmativas–; hecho que indica la repetición de la vocal A tres veces en BARBARA.^[87] Ahora bien, todos los modos válidos de silogismo se pueden probar como argumentos correctos de LP:

Así, por ejemplo, la validez del silogismo en BARBARA mencionado se puede probar en LP de la siguiente forma (supongamos que F significa ‘bien inmueble’, G significa ‘cosa’ y H significa ‘edificio’):

Por otro lado, la teoría tradicional del silogismo era incapaz de explicar las fórmulas que contienen predicados poliádicos (predicados acompañados por más de una constante), como, por ejemplo, “Todo el mundo quiere a alguien”, que se representaría en LP (suponiendo que F significa ‘querer’) por:

∀x ∃y (Fxy)

que se lee así : “Para todo x: x quiere a algún y”.

Por ejemplo, como De Morgan puso de manifiesto, la teoría tradicional del silogismo es incapaz de mostrar la corrección de un razonamiento simple como éste:

La razón de esto es precisamente la falta de capacidad para representar predicados poliádicos. Demostraremos este razonamiento utilizando LP y suponiendo que F representa ‘caballo’, G significa ‘animal’ y H, ‘ser cabeza de’ (un predicado diádico). Este hecho nos permite representar la premisa del argumento por ∀x (Fx → Gx) y la conclusión por ∀x ∀y (Fx ∧ Hyx → Gx ∧ Hyx):

El sistema formal LP permite explicar la lógica de las relaciones, algo que no podía hacer la lógica tradicional. Más adelante veremos que la lógica de relaciones (de predicados poliádicos) es importante para representar algunos argumentos jurídicos muy célebres (por ejemplo, el argumento por analogía).

2.3. Normas y lógica

Hemos dicho hasta ahora que las relaciones lógicas tienen lugar entre proposiciones, entre el significado de oraciones asertivas. Pero ¿no existen relaciones lógicas entre normas, entre el significado de oraciones prescriptivas?

Nuestra intuición nos dice que entre las normas también existen relaciones lógicas, que es contradictorio ordenar y prohibir el mismo comportamiento a los mismos destinatarios, que si alguien prohíbe fumar en todas las habitaciones de su casa, también prohíbe fumar en el dormitorio de su casa, etc. Sin embargo, esto nos plantea un dilema. Un dilema es un argumento que tiene la siguiente forma:

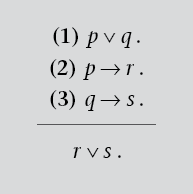
Pues bien, el dilema se puede presentar de la siguiente forma:^[88]

1. O bien mantenemos la noción de lógica de acuerdo con la cual las inferencias lógicas sólo tienen lugar entre enunciados susceptibles de verdad o falsedad y, entonces, a pesar de las apariencias, no existen inferencias entre enunciados prescriptivos.
2. O bien modificamos la noción de lógica de manera que haya relaciones de inferencia entre enunciados prescriptivos y, por lo tanto, argumentos válidos de lógica de normas, pero entonces la lógica va más allá de la verdad.

El dilema se conoce con el nombre de dilema de Jörgensen, porque fue planteado por Jörgen Jörgensen. El nombre de dilema de Jörgensen lo puso el filósofo del derecho Alf Ross.^[89] Existe una forma de rechazar el planteamiento del dilema, que consiste en afirmar que las normas son susceptibles de verdad o falsedad. Sin embargo, para defender esta posición debemos suponer que existe un mundo normativo con relación al cual las normas son verdaderas o falsas y que, al lado de los hechos empíricos, existe un tipo de hechos normativos. No consideraremos, aquí, esta posibilidad, ya que comporta un fuerte compromiso ontológico.

También podríamos abandonar nuestras firmes intuiciones y suponer que no existen relaciones lógicas entre las normas, lo cual nos conduciría a una situación difícil en una materia dedicada, básicamente, a la argumentación jurídica, que muy a menudo es una aumentación entre normas. Tampoco seguiremos esta vía, que aún dejaría abierta la posibilidad de que haya relaciones lógicas entre proposiciones normativas que, como sabemos, sí que son portadoras de verdad o falsedad.

Aceptaremos, en cambio, que existen relaciones lógicas entre normas y que, por tanto, la lógica va más allá de la verdad:

1. Quizá podríamos encontrar una contrapartida a la verdad para las normas. La eficacia podría serlo. Entonces, el hecho de decir que una norma implica otra norma, que la norma expresada por “Es obligatorio fumar” implica la norma expresada por “Prohibido no fumar”, por ejemplo, querría decir que si la primera es eficaz la segunda también lo es necesariamente.
2. También podríamos presentar una noción abstracta de consecuencia lógica, que no la hiciera depender de la verdad o la falsedad, como hacen C. E. Alchourrón y A. A. Martino en el artículo anteriormente mencionado.^[90] El intento de articular esta noción de eficacia para las normas tiene una gran tradición filosófica.
3. Sin embargo, para nuestra finalidad (la argumentación en el ámbito del derecho) podemos dejar esta polémica sólo planteada y confiar en que habrá alguna manera de justificar las relaciones lógicas entre normas.^[91]

La lógica de normas o lógica deóntica nació con un artículo, ahora ya famoso, del filósofo finlandés Georg Henrik von Wright (1917).^[92] La idea básica es que las variables proposicionales se pueden enfocar por medio de los denominados operadores deónticos, que son los siguientes:

• O, que se lee “Obligatorio”.
• Ph, que se lee “Prohibido”.
• P, que se lee “Permitido”.
• F, que se lee “Facultativo”.

Estos operadores se pueden interdefinir de la siguiente forma:

O = Ph¬ = ¬P¬ Ph = O¬ = ¬P P = ¬O¬ = ¬Ph

Y nos queda el último. “Facultativo p” se considera equivalente a “Permitido p y permitido no p”. Es decir:

F = P ∧ P¬

Hay muchos sistemas de lógica de normas y mucha discusión con respecto a cuáles son las inferencias válidas en lógica de normas. También se discute acerca de cuáles son las expresiones bien formadas de la lógica de normas. Sin embargo, para las finalidades de nuestra materia tenemos suficiente con añadir unas cuantas consideraciones a los sistemas Lp y LP:

1. i) Sólo utilizaremos operadores normativos en los siguientes casos:

   • Ante variables proposicionales aisladas, como, por ejemplo:

     Op

   • Ante variables proposicionales negadas, como, por ejemplo:

     O ¬p

   • Ante estas expresiones, cuando sean el consecuente de un esquema condicional, como por ejemplo:

     p →  Op

   • O bien:

     p →  O¬q

2. ii) Con respecto a LP, actuaremos de la misma manera.

   • Ante una fórmula atómica de LP podemos poner un operador normativo:

   O (Fa)

   • Y también ante una fórmula atómica negada:

     O(¬Fa)

     Y también ante el consecuente de una fórmula condicional. De esta manera:

     Fa → OGa

   • Y también:

     ∀x (Fx → OGx)

3. iii) Confiemos en que con estas fórmulas tengamos suficiente para simbolizar los argumentos jurídicos más habituales. Así,

   ∀x (Fx → OGx)

   podría simbolizar, por ejemplo, la prescripción que establece que “Todas las personas que tienen unos ingresos superiores a dieciocho mil euros anuales deben presentar la declaración de la renta”. Si F significa ‘tener unos ingresos superiores a dieciocho mil anuales’ y G, ‘presentar la declaración de la renta’, la lectura más literal sería: “Para todo x, suponiendo que x tiene unos ingresos superiores a dieciocho mil euros, entonces es obligatorio que x presente la declaración de la renta”.

4. iv) Sólo precisamos una regla para la lógica de normas. La regla según la cual, cuando un comportamiento es obligatorio, esto quiere decir que éste está permitido; por otro lado, parece una regla bastante intuitiva. Podríamos expresarla así para Lp:

   

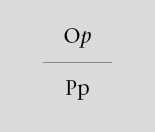
   Y para LP:

   

5. v) Además de esta regla, es necesario introducir algunas restricciones a las inferencias válidas en lógica de normas, que impidan derivaciones como ésta:

   

Recordemos que la premisa (2) es equivalente a P¬ p, es decir, “Permitido no coger el paraguas”. Entonces, de dos normas deduciríamos una conclusión que es una proposición, el significado de una oración asertiva. Esto nos llevaría a cometer una violación de la ley de Hume, formulada por el gran filósofo inglés David Hume (1711-1776), que veda la posibilidad de obtener conclusiones normativas de premisas asertivas, y al revés. La importancia de la ley de Hume no puede pasar desapercibida: la lógica deóntica no puede autorizar a deducir proposiciones fácticas a partir de normas, ni normas a partir de proposiciones fácticas.

Podemos formular estas restricciones en la validez de nuestros argumentos deónticos de la siguiente forma:

• De premisas asertivas sólo se puede derivar una conclusión asertiva.

• Si entre nuestras premisas hay alguna premisa prescriptiva (alguna fórmula que contiene un operador normativo), entonces sólo podemos derivar una conclusión que también sea prescriptiva (que contenga un operador normativo).

Obviamente, ésta es sólo una parte muy pequeña de la lógica de las normas. En la bibliografía de este capítulo se encuentra una serie de textos donde se pueden ampliar los conocimientos sobre esta rama de la lógica. Pero las nociones que aquí hemos introducido deben ser suficientes para simbolizar la mayoría de textos legales que contienen formulaciones normativas.

Nuestras fórmulas captan, en concreto, el esquema tradicional de norma jurídica como el compuesto formado por un supuesto de hecho y una consecuencia jurídica.

Si p (supuesto de hecho), entonces Oq (consecuencia jurídica).

3. Falacias y argumentación

La finalidad de este capítulo es suministrar un conjunto de técnicas para construir argumentos correctos, lo que comporta una cierta capacidad de detectar los argumentos incorrectos. Una falacia, en sentido amplio, es precisamente un error en la argumentación. Ahora bien, mientras que el conjunto de reglas básicas del razonamiento correcto –desde el punto de vista de la lógica– se puede definir claramente, el conjunto de errores posibles, como hemos visto, no puede ser definido. Existen infinitas maneras de razonar incorrectamente. Por esta razón, aunque la mayoría de libros de introducción a la lógica acostumbra a contener un capítulo dedicado a las falacias, existen tantas clasificaciones de falacias como autores que las han propuesto.

De todas maneras, no estamos interesados en todos los errores de argumentación posibles, sino sólo por los que tienen una cierta fuerza de convicción, por los argumentos que, a pesar de ser incorrectos, son persuasivos.^[93] De esta manera, podemos definir falacia de una manera más concreta como la forma de argumentación que parece correcta, pero que nos damos cuenta de que no lo es al analizarla de forma más minuciosa. Podemos dividir las falacias en dos grandes tipos:

1. Las falacias formales. Son errores de aplicación de las reglas lógicas y producen argumentos inválidos desde el punto de vista de la lógica.
2. Las falacias no formales. Son producidas por argumentos que son incapaces de establecer la verdad de las premisas y que no son sólidos, independientemente de su corrección lógica.^[94]

Es muy importante distinguir las dos clases de falacias: la lógica sólo es un control de la calidad de los argumentos capaz de ahuyentar el primer tipo de falacia; las falacias no formales son modos incorrectos de argumentar que la lógica no puede remediar.

3.1. Las falacias formales

Según la definición que hemos ofrecido, cualquier mal uso de una regla lógica provoca que el argumento sea incorrecto. Ahora bien, existen algunos malos usos de las reglas lógicas que son más corrientes y que merecen ser destacados. Presentaremos dos de ellos muy habituales:

1. La falacia de la afirmación del consecuente. Esta falacia se da en argumentos como éste:

   (1) Si un matrimonio m se celebra por error en la identidad de la persona,
   m entonces es nulo.

   (2) El matrimonio m es nulo.

    

   Ergo, el matrimonio m se celebra por error en la identidad de la persona.

   La forma lógica de este argumento es la siguiente:

   

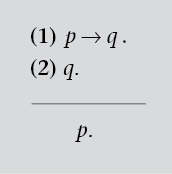
   No existe ninguna regla lógica que nos habilite para hacer esta deducción. Recordad que hay una regla derivada, el modus tollendo tollens (MTT), que nos garantiza el hecho de pasar de la negación del consecuente de un condicional a la negación de su antecedente. Sin embargo, no tenemos ninguna garantía lógica si pasamos de la afirmación del consecuente a la afirmación del antecedente.

   En concreto, en nuestro argumento las premisas podrían ser verdaderas y la conclusión falsa. Por ejemplo, supongamos que el matrimonio m sea nulo, pero no por haberse producido por error, sino por haber sido prestado el consentimiento mediante coacción; entonces, las dos premisas del argumento serían verdaderas, pero la conclusión sería falsa. Ésta es una prueba clara de que se trata de un argumento lógicamente inválido.

2. La falacia de la negación del antecedente. Esta falacia se da en argumentos de este tipo:

   (1) Si x obra en legítima defensa, entonces x obra de manera justificada.

   (2) x no obra en legítima defensa.

    

   Ergo, x no obra de manera justificada.

   Ésta es claramente una manera falaz de razonar. El esquema formal que reconstruye este argumento es el siguiente:

   

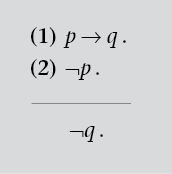
   No existe ninguna regla lógica que autorice esta inferencia. Recordad que hay una regla, la regla de eliminación del condicional o modus ponendo ponens (E→), que nos permite, a partir de un esquema condicional y la afirmación del antecedente, obtener la afirmación del consecuente; sin embargo, con la negación del antecedente no podemos obtener la negación del consecuente.

   En concreto, sería posible que las premisas del argumento fueran verdaderas y la conclusión falsa: podría ser que x no actuara en defensa legítima, sino en estado de necesidad (o en cumplimiento de un deber o en el ejercicio legítimo de un derecho, oficio o cargo); entonces las dos premisas serían verdaderas y la conclusión falsa, dado que x actuaría de manera justificada.

3.1.1. Remedios para las falacias formales

Las falacias formales sólo tienen un remedio: el control de las inferencias por medio de las reglas lógicas. Una falacia formal es como un movimiento incorrecto de las piezas del ajedrez. Dado que las reglas del ajedrez definen claramente el número de movimientos correctos, la única manera de jugar correctamente al ajedrez es siguiendo sus reglas. De manera similar, seguir las reglas de la lógica es la única manera de evitar las falacias formales.

3.2. Las falacias no formales

En las falacias no formales se acostumbra a distinguir entre las falacias materiales y las falacias verbales:

1. Las falacias materiales son conocidas como falacias de la presunción, porque las premisas “presumen” demasiadas cosas, sin probarlas.
2. Las falacias verbales son, generalmente, falacias de la ambigüedad, porque la conclusión se obtiene mediante un uso impropio de las palabras.

3.2.1. Las falacias materiales

En esta presentación seguimos aproximadamente la clasificación de Aristóteles en Sophistici Elenchi. Distinguiremos seis tipos, en algunos casos con subtipos, de falacias materiales:

1) La falacia del accidente

La falacia del accidente consiste en aplicar una regla general a un caso particular, cuyas circunstancias accidentales hacen que la regla sea inaplicable. Las reglas generales acostumbran a tener excepciones, lo que es habitual en derecho. Éste es un ejemplo de falacia del accidente:

(1) Todos los que matan a otro cometen un delito punible.

(2) x mató a y en defensa legítima.

 

Ergo, x ha cometido un delito punible.

Éste es un argumento falaz porque no presta atención al hecho de que la defensa legítima es una causa de justificación que exime de responsabilidad criminal.

2) La falacia del accidente inverso

Esta falacia se comete cuando se realiza una generalización de manera inadecuada. Del hecho de que el contrato de compraventa sea un contrato a título oneroso, no podemos derivar que todos los contratos sean a título oneroso: existen contratos a título gratuito.

3) La falacia de la conclusión irrelevante

Se comete cuando la conclusión hace referencia a un aspecto que las premisas no tienen en cuenta ni pueden fundamentar. Existen muchas subclases de esta falacia. Podemos mencionar las siguientes:

1. El argumentum ad hominem. Se trata de descalificar las opiniones de alguien descalificando algunas de sus circunstancias personales o de sus acciones. No hay ninguna relación entre las opiniones de alguien y sus circunstancias o acciones personales que justifique esta desacreditación.^[95]

2. El argumentum ad populum. Es un argumento dirigido a los sentimientos más que a la razón de la audiencia. La publicidad y la propaganda son una forma refinada de argumento ad populum. En el proceso judicial se usa con abundancia en los procesos con tribunal del jurado.

3. El argumentum ad misericordiam. Es una apelación a la piedad. Acostumbran a usarlo los abogados penalistas cuando defienden a una persona a la que todas las pruebas incriminan.

4. El argumentum ad verecundiam. Es una apelación a la autoridad, al respeto que nos merecen determinadas personas por su capacidad personal en una materia. Este argumento no es siempre un argumento falaz.

   Nadie lo puede saber todo y es normal que nos fiemos del juicio de nuestro médico, que es un experto, por lo que se refiere a determinados problemas de salud, o de nuestro mecánico cuando tenemos una avería en el coche, etc. Ahora bien, a veces el prestigio personal de alguien se utiliza para avalar su opinión en una materia en la que no es experto, o bien para tergiversar un poco su sentido. Cuando se usa este argumento, y los abogados lo hacen con las opiniones doctrinales, es necesario comprobar las fuentes y su viabilidad, citarlas adecuadamente, etc.

   Sin embargo, en derecho, el argumento de autoridad tiene otra dimensión, una dimensión práctica (ya no teórica): cuando se apela a la ley o a la jurisprudencia, se apela a opiniones revestidas de autoridad; pero no de autoridad teórica, sino práctica. Eso plantea un problema que veremos más adelante, como, por ejemplo, qué grado de deferencia se debe tener con respecto a las intenciones de los legisladores.

5. El argumentum ad ignorantiam. Es un argumento que trata de probar la verdad de una opinión porque nadie ha podido probar, hasta ahora, su falsedad.^[96]
6. El argumentum ad baculum. Se comete cuando se apela a la fuerza o la amenaza de la fuerza para hacer que se acepte una conclusión. No es necesario decir nada más sobre esta falacia.^[97]

4) La falacia del argumento circular o petito principii

En este caso, la conclusión ya se presupone en una de las premisas. Y es verdadera o falsa independientemente de las premisas. Es necesario recordar que aquí no hay ningún problema de validez lógica del argumento: toda premisa se implica a sí misma y, por tanto, es una conclusión de sí misma; el problema es de fuerza de convicción del argumento.

Un ejemplo de argumento circular es el siguiente: “x siempre vota de manera sabia”; si preguntamos “¿Cómo lo sabes?” y nos contestan “Siempre vota por el partido A”, entonces se argumenta en círculo porque se presupone que vota de manera sabia quien vota por el partido A.

5) La falacia de la causa falsa

Consiste en tomar por la causa de alguna cosa otra cosa que realmente no lo es. El más conocido de estos argumentos es el de post hoc ergo propter hoc (‘después de esto, por tanto a causa de esto’).

De todos modos, esta falacia nos llevaría a estudiar la cuestión de la inducción, es decir, la relación causal entre los fenómenos –un aspecto central del método científico–, lo que no haremos aquí. Será suficiente recordar que la sucesión de fenómenos no equivale a la causalidad. Sin embargo, esta falacia se comete a veces en el ámbito del proceso judicial, cuando se argumenta sobre la prueba.

Por ejemplo, del hecho de que se haya pasado algunas veces por delante de una determinada tienda y después hayamos tenido dolor de cabeza, no se deriva que la causa de nuestro dolor de cabeza sea el hecho de haber pasado por delante de aquella tienda.

6) La falacia de la pregunta compleja o pluribus interrogationum

Se trata de formular una pregunta que tiene varias respuestas posibles como si sólo se pudiera contestar sí o no. Los abogados, en sus interrogatorios con los testimonios, utilizan a menudo este tipo de falacia.

Así, por ejemplo, “Los que asistieron a la fiesta vieron a la señora X. ¿Asistió usted a la fiesta?” La respuesta “Sí” parece comportar que Y vio a la señora X, aunque es posible que asistiera a la fiesta y no viera a la señora X.

3.2.2. Las falacias verbales

Muchas falacias verbales tienen que ver con el tema de la ambigüedad de las expresiones lingüísticas, que ya hemos estudiado. Nos referiremos a cinco de estas falacias:

1) La falacia del equívoco

Hemos visto que algunas expresiones lingüísticas tienen más de un sentido. Si usamos la misma expresión, con significados diferentes, dentro de un mismo contexto cometemos esta falacia. Eso se puede dar en casos de E-ambigüedad.

Supongamos que una persona quiere cambiar la rueda del coche y le dice a un amigo suyo que se encuentra dentro de casa: “¿Has visto el gato?”. El amigo, creyendo que se refiere al gato Katze que tienen en casa, le contesta: “Está en el jardín, al lado de los rosales”.

La conclusión de que el gato para elevar el coche se encuentra en el jardín es, obviamente, inválida.

2) La falacia de la anfibología

Se da cuando se argumenta a partir de premisas cuya formulación es ambigua a causa de su estructura gramatical, y que son CA-ambiguas.

Por ejemplo, hasta ahora sólo ha habido una reforma de la constitución de 1978, la referida al artículo 13.2. Antes decía: “Sólo los españoles serán titulares de los derechos reconocidos en el artículo 23, salvo que, de acuerdo con criterios de reciprocidad, pueda establecerse por tratado o por ley para el derecho de sufragio activo en las elecciones municipales”. Por otro lado, el Tratado de Maastricht exigía conceder, en las elecciones municipales, el derecho de sufragio activo y pasivo a los extranjeros naturales de otros estados de la Unión Europea.

De este hecho, algunos juristas concluyeron que había que reformar el artículo 13.2; otros, que se tenía que reformar también el 23, y otros, que la Constitución no se tenía que reformar para cumplir con el Tratado de Maastricht. Olvidemos por un momento la posición según la cual era necesario reformar también el artículo 23.^[98]

Los que consideraban que se tenía que reformar el artículo 13.2 lo interpretaban de manera que la cláusula “para el derecho de sufragio activo pasivo” afectaba a los sustantivos tratado y ley. Los que consideraban que no hacía falta reformar la Constitución interpretaban que la cláusula sólo se refería al sustantivo ley. Es decir, la excepción incluía lo que se estableciera por ley para el derecho de sufragio activo en las elecciones municipales y lo que se estableciera por tratado. Finalmente, el artículo 13.2 fue reformado para incluir después de la palabra activo la expresión y pasivo. Sin embargo, las diferentes opiniones provenían del hecho de que la formulación normativa era anfibológica.

3) La falacia del énfasis

En este caso, una determinada expresión lingüística es ambigua dependiendo de dónde ponemos el acento en la expresión.

Por ejemplo, eso es lo que hace una prensa determinada con los titulares sensacionalistas, así sale un gran titular de la portada que dice “La actriz X se divorcia” y, después, con letra muy pequeña, pone “en la serie de TV que protagoniza”.

4) La falacia de la composición

Tiene dos versiones:

1. Una versión de la premisa que atribuye una propiedad a las partes de un todo concluye de manera falaz la atribución de la propiedad al todo.
2. La otra versión parte del hecho de que la atribución de cierta propiedad a los miembros de un conjunto depende de la atribución de esta propiedad al conjunto.

Del hecho de que los suecos sean altos no se puede deducir que Suecia sea alta. Suecia no es un individuo y, por tanto, no es ni alta ni baja. A veces se usan expresiones así, como un tipo de paráfrasis. Cuando decimos que Suecia es un país rico, queremos decir que la renta per cápita de Suecia es de las más elevadas del mundo.

Otras veces no está tan claro: cuando se dice que la lengua de Irlanda es el irlandés, no quiere decir que la mayoría de los irlandeses hablen el irlandés (sólo lo hace el 2% de la población total), sino otra cosa, que no siempre está clara. Del hecho de que las hojas de un libro sean muy finas no podemos concluir que el libro es muy fino (puede ser que el libro sea muy grueso y sus páginas sean de papel biblia).

5) La falacia de la división

Es la opuesta a la anterior. Se argumenta, de una propiedad que se aplica a un conjunto, la aplicación de la misma propiedad a los individuos que son miembros del conjunto. Aunque es verdad que los socios del Barça son numerosos, de eso no se puede deducir que el presidente del Barça sea numeroso. La calidad de la “numerosidad” es predicable de conjuntos, no de individuos.

3.2.3. Las paradojas

En sentido estricto, una paradoja es la formulación de un argumento que en principio parece plausible, pero que, mirándolo bien, lleva a una contradicción o, en un sentido más amplio, a una conclusión bastante censurable. Si el argumento es lógicamente correcto, debería haber algún problema en las premisas. La singularidad de las paradojas es que no sabemos detectar dónde está el problema en las premisas.

La paradoja del mentiroso

La más famosa de todas las paradojas es la del mentiroso, que en sus formulaciones más simples dice “Estoy mintiendo” o bien “Este enunciado es falso”, de manera que si el enunciado es verdadero (si estoy diciendo la verdad), entonces es falso, y si es falso (si estoy mintiendo), entonces es verdadero.

Una de las expresiones más famosas de esta paradoja (atribuida a Epiménides de Creta) se encuentra en una carta de san Pablo:

“Uno de ellos, su propio profeta, dijo: «Cretenses, siempre mentirosos, malas bestias, vientres perezosos». Este dicho es verdad.”

Carta de san Pablo a Tito (1:12).

Si el autor de Creta decía la verdad cuando decía que los cretenses siempre mentían, entonces él no mentía y los cretenses no mentirían siempre y el dicho no sería verdadero (si el dicho no era verdadero, es decir, mentía; no hay paradoja y por eso la paradoja no está en estado puro en la formulación paulina). Parece que san Pablo no se percató del problema.

La paradoja del barbero

Se han planteado muchas paradojas de este tipo; por ejemplo, la paradoja del barbero: en una ciudad, pongamos Sevilla, hay un barbero que sólo afeita a todos los que no se afeitan a sí mismos. ¿Se afeita a sí mismo el barbero de Sevilla?

La paradoja de Russell

Una paradoja con más “pedigrí” filosófico es la paradoja de Russell (una paradoja de la teoría de conjuntos): ¿pertenece a sí misma la clase de todas las clases que no pertenecen a sí mismas? Si pertenece, entonces no pertenece y si no pertenece, entonces pertenece.

La paradoja de Sancho Panza

En el capítulo LI de la segunda parte del Quijote se puede leer una divertida paradoja que Cervantes hace plantear a Sancho Panza, cuando era gobernador de la isla de Barataria:

“–Señor, un caudaloso río dividía dos términos de un mismo señorío... Y esté vuesa merced atento, porque el caso es de importancia y dificultoso. Digo, pues, que sobre este río estaba un puente, y al cabo de ella, una horca y una como casa de audencia, en la cual de ordinario había como cuatro jueces que juzgaban la ley que puso el dueño del río, de la puente y del señorío, que era en esta forma: «Si alguna pasare por este puente de una parte a otra, ha de jurar primero adónde va y a qué va; y si jurare verdad, dejénle pasar; y si dijere mentira, muera por ello, ahorcado en la horca que allí se muestra, sin remisión alguna». Sabida esta ley y la rigurosa condición della, pasaban muchos, y luego en lo que juraban se echaba de ver que decían verdad, y los jueces lo dejaban pasar libremente. Sucedió, pues, que tomando juramento a un hombre, juró y dijo que para el juramento que hacía, que iba a morir en aquella horca que allí estaba, y no a otra cosa. Repararon los jueces en el juramento, y dijeron: ‘Si a este hombre le dejamos pasar libremente, mintió en su juramento, y, conforme a la ley debe morir; y si le ahorcamos, él juró que iba a morir en aquella horca, y, habiendo jurado verdad, por la misma ley debe ser libre’.”

Ni Sancho ni nadie podía resolver el caso. Sancho, siguiendo un recordado consejo del Quijote, decide que cuando la justicia está en duda, se debe resolver de acuerdo con la misericordia (el argumentum ad misericordiam).

Una paradoja jurídica

Para finalizar el tema de las paradojas, veremos una paradoja jurídica de la Antigüedad griega. Euatlo quería aprender a hacer de abogado y por eso se dirigió al maestro Protágoras, para que le impartiera clases. Sin embargo, Euatlo no tenía con qué pagar a Protágoras y éste le propuso el siguiente trato: yo te doy clases de retórica de forma gratuita y tú me pagas con los honorarios del primer caso que ganes. Euatlo aceptó.

Al pasar el tiempo, Protágoras le dijo a su discípulo que creía que ya estaba preparado para hacer de abogado. Sin embargo, el tiempo pasaba y Euatlo no defendía ningún caso. Al final, Protágoras decidió demandar a Euatlo.

Comparecieron ante el juez y éste les indicó que formularan sus alegaciones. Protágoras habló así: “Tanto si mi demanda se estima como si se desestima, Euatlo deberá pagar. Si se estima, porque he ganado este litigio. Si se desestima, porque él ha ganado su primer litigio y de acuerdo con el contrato que celebramos, me debía pagar los honorarios obtenidos en el primer litigio”.

Ahora bien, Euatlo contestó: “Tanto si gano como si pierdo el litigio, no tengo que pagar nada a Protágoras. Si gano, porque he resultado absuelto. Si pierdo, porque aún no he ganado ningún litigio”.

3.3. Remedios contra las falacias no formales

No existe ningún remedio totalmente seguro para escapar a las falacias no formales. El lenguaje es un instrumento con muchas trampas, y un instrumento, como hemos dicho, sutil y complejo. Hay que estar atentos y quizá las falacias hasta ahora explicadas puedan servir como una especie de indicadores de los caminos que debemos evitar si queremos razonar correctamente. Sin embargo, hay indicaciones generales para que nuestras argumentaciones sean más fiables.

Algunos de los filósofos que han trabajado en el ámbito de la argumentación y en el ámbito de la filosofía del lenguaje se han ocupado de dar algunas reglas generales. En este apartado seleccionamos dos contribuciones, una procedente de la filosofía del lenguaje (de Paul Grice) y otra de la teoría de la argumentación (de Robert Alexy), que pueden ser útiles por lo que respecta al caso.^[99]

3.3.1. El principio de cooperación de Paul Grice

Una manera de asegurar que nuestras argumentaciones asertivas son adecuadas, no sólo por la validez lógica, sino también por la solidez de argumentos, es maximizar la posibilidad de que las premisas sean verdaderas. Sin embargo, también nos interesa que los demás entiendan adecuadamente nuestros argumentos, es decir, estamos interesados en maximizar la comunicación. La argumentación es, a menudo, una práctica comunicativa^[100] y, por eso, es necesario que cuidemos algunos de sus aspectos.^[101]

Paul Grice presenta unas máximas que quieren aumentar la verdad de nuestras contribuciones a la conversación y su capacidad comunicativa. Grice afirma con razón que cuando conversamos o argumentamos no sólo queremos decir lo que explícitamente decimos y lo que es consecuencia de lo que decimos, sino otras cosas que están presupuestas en nuestro discurso. Cuando le decimos a un amigo “Hoy llegas puntual”, aunque no lo decimos, presuponemos que habitualmente no llega puntual. Grice^[102] denomina a este tipo de presuposiciones implicaturas.

Entre ellas, Grice distingue lo que denomina implicaturas conversacionales, que son las implicaturas que están vinculadas a ciertas propiedades generales del discurso. Nuestras conversaciones y nuestras argumentaciones están guiadas habitualmente por un objetivo común que las partes, cooperando entre ellas, tratan de obtener. Grice lo llama el principio cooperativo y lo define así: “Haced que vuestra contribución a la conversación sea tal como exige, en el estado en que tenga lugar, el propósito o la dirección del intercambio que mantengáis”.

Haciéndose eco de Kant, Grice articula un conjunto de máximas que explicitan este principio general, y las agrupa en cuatro categorías:^[103]

1. La categoría de cantidad tiene que ver con la cantidad de información que se debe proporcionar y pertenecen a ella las dos máximas siguientes:
   1. “a) Haced que vuestra contribución sea tan informativa como sea necesario (de acuerdo con los objetivos de la comunicación).”
   2. “b) No hagáis que vuestra información sea más informativa de lo necesario.”
2. A la categoría de calidad pertenece un principio general, “Tratad de que vuestra contribución sea verdadera”, y dos máximas más específicas:
   1. “a) No digáis lo que creáis que es falso.”
   2. “b) No digáis cosas de las cuales no tenéis pruebas adecuadas.”
3. Dentro de la categoría de relación hay una sola máxima:
   1. “a) Sed relevantes.”

      Esta máxima tan lacónica es todo lo que Grice nos dejó de la categoría de relación.

4. La categoría de modo no tiene que ver con lo que se dice, sino con cómo se dice lo que se dice. El principio general de esta categoría es “Sed perspicuos”. Esta cláusula se desglosa en cuatro máximas:
   1. “a) Evitad la oscuridad en la expresión.”
   2. “b) Evitad la ambigüedad.”
   3. “c) Sed breves (evitad ser innecesariamente prolijos).”
   4. “d) Proceded con orden.”

Si una persona sigue estas máximas de Grice, es obvio que sus argumentaciones serán más adecuadas y evitarán muchas posibilidades de cometer falacias. ¿No creéis que serían unas máximas muy adecuadas para algunos de nuestros tribunales?

3.3.2. La teoría del discurso práctico de Robert Alexy

Como sabemos, en el ámbito de las prescripciones -el ámbito del discurso práctico y no del teórico- no tenemos verdad ni falsedad. Eso nos plantea algunas dificultades importantes: algunas de las máximas de Grice aquí no nos sirven, en especial las máximas de calidad: “No digáis lo que creáis que es falso” y “No digáis lo que no podéis probar”.

Por eso, ¿cómo podemos maximizar la cooperación en el ámbito del discurso práctico? ¿Qué hace que nuestros argumentos prácticos sean argumentos no sólo lógicamente correctos, sino también sólidos?

Robert Alexy (1989) ha construido una teoría del discurso práctico (para después aplicarla a la argumentación jurídica, como veremos más adelante), que trata de contestar a esta pregunta. La idea básica que forma el trasfondo de la concepción de Alexy es que también las cuestiones prácticas (que tienen que ver con normas, con guías del comportamiento humano) están sujetas a la razón humana.

Alexy toma la idea, sobre todo, de la filosofía del pensador alemán Jürgen Habermas. Según Habermas -y simplificando ahora un pensamiento profundo, extenso y complejo-, mientras que las aserciones son susceptibles de verdad o falsedad, las prescripciones y los juicios de valor^[104] serían susceptibles de corrección^[105] o incorrección.

Habermas^[106] pretende construir una pragmática universal en la que se reconstruyen los presupuestos de racionalidad implícitos en el uso del lenguaje. Estos presupuestos definen lo que Habermas denomina una situación ideal de diálogo. A la persona que usa el lenguaje se le tiene que suponer una pretensión de validez en su uso del lenguaje.^[107] Ahora bien, según el tipo de discurso que se emplea, la pretensión de validez cambia:

• Si se emplea el lenguaje asertivo, se pretende que las proposiciones que se afirman sean verdaderas y verídicamente afirmadas para que el auditorio pueda compartir lo que el usuario del lenguaje comunica.

• Si se emplea el lenguaje prescriptivo, se pretende que las normas formuladas sean correctas para que el auditorio pueda coincidir con quien las formula.

En los dos casos se pretende la inteligibilidad de lo que se dice, ya que si no la comunicación no sería posible. Para justificar las pretensiones de validez –de verdad o corrección– cuando son problemáticas, el usuario del lenguaje debe dar razones que justifiquen sus emisiones lingüísticas.

Robert Alexy^[108] ha tratado de articular los principios racionales que existen en el trasfondo del discurso práctico, con la convicción de que la corrección del discurso práctico es un tipo de corrección -como también piensa Habermas- de carácter procedimental. Eso significa que un enunciado normativo o una proposición normativa (y por proposición normativa Alexy no entiende una proposición que describe la existencia de normas, sino una norma o un juicio de valor) es correcta si, y sólo si, puede ser el resultado de un determinado procedimiento. El procedimiento adecuado para el discurso práctico se expresa en las siguientes reglas y formas de argumentos:

1) Las reglas básicas

Son reglas que se aplican tanto a la verdad como a la corrección: son válidas para el discurso teórico y para el discurso práctico. Incluyen los principios de no-contradicción, de sinceridad y de universalidad^[109] del uso común del lenguaje. Son las siguientes:

“(1.1.) Ningún usuario del lenguaje se puede contradecir.”

“(1.2.) Todo usuario del lenguaje puede afirmar sólo lo que él mismo cree.”

“(1.3.) Todo usuario del lenguaje que aplique el predicado F a un objeto a debe estar dispuesto a aplicarlo también a cualquier otro objeto igual a a en todos los aspectos relevantes.”

“(1.4.) Todo usuario del lenguaje sólo puede afirmar aquellos juicios de valor y aquellos juicios de deber que también afirmaría en todas las situaciones en las que afirmase que son iguales en todos los aspectos relevantes.”

“(1.5.) Diferentes usuarios del lenguaje no pueden usar la misma expresión con significados diferentes.”

2) Las reglas de racionalidad

Son las reglas que definen las condiciones más importantes de la racionalidad del discurso. La primera es como una regla general, que se hace explícita en igualdad de derechos, universalidad y no-coerción.

“(2) Todo usuario del lenguaje debe fundamentar lo que afirma cuando se le pide, a excepción del caso de que pueda dar razones que justifiquen la negativa de la fundamentación.”

“(2.1.) Todos los que pueden hablar deben poder tomar partido en el discurso.”

“(2.2.) a) Todos pueden cuestionar cualquier aserción.”

“(2.3.) No se puede impedir a ningún usuario del lenguaje que ejerza sus derechos fijados en (2.1.) y (2.2.), mediante coerción interna o externa al discurso.”

3) Las reglas sobre la carga de la argumentación

Son un tipo de reglas técnicas destinadas a facilitar la comunicación y a impedir situaciones de bloqueo:

“(3.1) Quien propone tratar a una persona A de manera diferente que a una persona B, está obligado a fundamentarlo.”

“(3.2) Quien ataca una proposición o una norma que no es objeto de discusión, debe dar sus razones para ello.”

“(3.3) Quien ha aducido un argumento sólo está obligado a añadir otros en caso de contraargumentos.”

“(3.4.) Quien introduce en el discurso una aserción o una emisión lingüística sobre sus opiniones, deseos o necesidades que no se refieran como argumento a una anterior emisión lingüística tiene que justificar la introducción de esta emisión lingüística si se le pide.”

4) Las formas de los argumentos

Según Alexy, existen dos maneras de justificar una norma singular o individual N: por referencia a una regla general R o bien por referencia a las consecuencias F (del alemán Folge, que significa ‘consecuencia’) que tiene seguir N.

1. En el primer caso, además de la regla general necesitamos un enunciado descriptivo de las condiciones de aplicación de la regla T (del alemán Tatsache, que significa ‘supuesto de hecho’).
2. En el segundo caso, además de las consecuencias, se debe suponer una regla que diga que la producción de determinadas consecuencias es un estado de cosas obligatorio.

Dos ejemplos de razonamiento de este tipo podrían ser los siguientes:

Alexy añade que se puede solicitar una justificación de la regla R; entonces será posible justificarla mediante reglas de nivel superior que muestren que los estados de cosas producidos por el mantenimiento de R son justificables.

5) Las reglas de fundamentación

Sirven para justificar el uso de los argumentos anteriores, sobre todo mediante el principio de universalización^[110] . Se agrupan en tres categorías:

“(5.1.1) Quien afirma una proposición normativa que presupone una regla para la satisfacción de los intereses de otras personas debe poder aceptar las consecuencias de esta regla también en el caso hipotético de que se encontrase en las circunstancias de aquellas personas.”

“(5.1.2) Las consecuencias de cada regla para la satisfacción de los intereses de cada uno deben poder ser aceptadas por todos.”

“(5.1.3) Toda regla debe poder enseñarse de forma abierta y general.”

“(5.2.1) Las reglas morales que sirven de base a las concepciones morales del usuario del lenguaje deben poder pasar la prueba de su génesis historicocrítica. Una regla no pasa esta prueba: a) si, aunque originariamente se podía justificar de manera racional, después ha perdido su justificación; b) si originariamente no se podía justificar de manera racional y después tampoco se han podido aducir nuevas razones que sean suficientes.”

“(5.2.2.) Las reglas morales que sirven de base a las concepciones morales del usuario del lenguaje deben poder pasar la prueba de su formación histórico-individual. Una regla moral no pasa esta prueba si se ha establecido sólo sobre la base de condiciones de socialización no justificables.”

“(5.3.) Es necesario respetar los límites de realizabilidad que ya vienen dados.”

6) Las reglas de transición

En último lugar, existe un conjunto de reglas que autorizan a los usuarios del lenguaje a cambiar de un tipo de discurso a otro:

“(6.1) Es posible para cualquier usuario del lenguaje y en cualquier momento pasar a un discurso teórico (empírico).”

“(6.2) Es posible para cualquier usuario del lenguaje y en cualquier momento pasar a un discurso de análisis del lenguaje.”

“(6.3) Es posible para cualquier usuario del lenguaje y en cualquier momento pasar a un discurso de teoría del discurso.”

Es obvio que estas reglas tienen limitaciones; en particular -como Alexy acepta-, no es seguro que siempre nos lleven a juicios normativos individuales indiscutibles y unívocos. Sin embargo, no son malas guías para fundamentar nuestros juicios prácticos: la corrección de las normas (el acuerdo con determinados procedimientos) es diferente de la verdad (la correspondencia con el estado de cosas del mundo); sin embargo, no lo es tanto de la asertabilidad, las condiciones en las cuales estamos justificados a mantener una creencia porque creemos que es verdadera. Sea como sea, la teoría de Alexy^[111] es una manera de controlar la solidez de nuestros juicios normativos: no queremos decir que así es como se razona realmente sobre cuestiones prácticas, sino como se debería razonar. Es un tipo de control de calidad de nuestro discurso práctico, de control de calidad no sólo de la validez lógica de los argumentos prácticos,^[112] sino también de su solidez.

Conclusiones

Este primer capítulo contiene una introducción a la argumentación. Es, como ya hemos dicho, un tipo de “gramática de la argumentación”. Contiene una noción precisa de argumento, algunas consideraciones sobre el lenguaje en que se expresan los argumentos -referidas a la cuestión de cómo las expresiones lingüísticas llegan a ser significativas y los problemas que eso plantea-, algunas de las formas más habituales de argumentos falaces, junto con una presentación más sistemática de algunas nociones muy rudimentarias de lógica y de las reglas lógicas de los cálculos denominados de deducción natural, a las cuales se tienen que añadir algunas consideraciones sobre la lógica de normas.

El capítulo está dividido en tres partes:

1. En la primera parte se presenta la noción de argumento lógicamente válido y la de argumento materialmente válido o sólido, junto con una presentación de los problemas de vaguedad y ambigüedad que los lenguajes naturales suscitan, como también de los diferentes usos del lenguaje. Esta primera parte acaba con unas consideraciones sobre las definiciones.
2. En la segunda parte se presentan la lógica proposicional y la lógica de predicados de manera introductoria, mediante el método de las tablas de verdad y de la deducción natural. Se acaba con una presentación del núcleo de la lógica de normas.
3. En la tercera parte se introduce la noción de falacia (de falacia formal y de falacia material), junto con algunos remedios para evitar razonar falazmente. Con esta finalidad, se expone un conjunto de reglas que, tanto en la argumentación teórica como en la argumentación práctica, pueden evitar las falacias materiales.