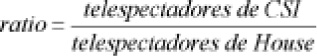
“Las matemáticas son el alfabeto con el cual
Dios ha escrito el Universo” (Galileo Galilei)
Cuando se manejan cifras o datos numéricos, es habitual efectuar comparaciones o relaciones entre ellos con el fin de obtener determinadas conclusiones.
Las operaciones con porcentajes constituyen una de las partes más elementales del álgebra básica y tienen muchas aplicaciones prácticas en la vida diaria. A pesar de su sencillez, en ocasiones se producen confusiones que pueden dar lugar a errores importantes.
Repasaremos en este capítulo las nociones básicas de los porcentajes y, a través de diversos ejemplos, se comentarán algunas de las aplicaciones más destacables en los campos del periodismo, publicidad y comunicación.
Una fracción es el cociente de dos cantidades denominadas numerador (dividendo) y denominador (divisor). Si el denominador es superior al numerador, el resultado es inferior a la unidad y la fracción se llama “propia”.
Uno de los casos de fracción propia es aquél en el que se relaciona una parte (numerador) con un total (denominador). El resultado siempre es inferior a la unidad, y se dice que el resultado está expresado en tantos por uno.
Un ratio es la relación o cociente entre dos cantidades que corresponden a dos partes o a dos conjuntos distintos. Según sean sus valores, el resultado puede ser mayor, menor o igual a la unidad.
Algebraicamente, el ratio es una fracción que puede ser propia o impropia, según sean las cantidades que se comparen o relacionen.
Supongamos, por ejemplo, que estoy interesado en conocer el ratio de los telespectadores de dos programas de televisión, CSI y House, que se emiten en distintos días. El ratio se obtendría dividiendo el número de telespectadores de ambos programas:
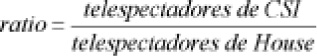
Ambas cifras de audiencia absoluta (número estimado de telespectadores) corresponden a cadenas distintas, de diferentes días, y, por tanto, no están relacionadas entre sí, pues pertenecen a grupos distintos.
Un porcentaje es una forma de expresar una fracción cuyo denominador es 100 y se indica con el símbolo %. Por ejemplo:
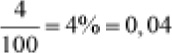
Es importante remarcar que el símbolo “%” significa que la cifra que lo acompaña está dividida por 100. Es un error común operar únicamente con dicha cifra sin tener en cuenta que, en realidad, es la centésima parte de ella.
Para expresar una fracción en porcentajes, se multiplica por 100 y al resultado se le añade el símbolo %. Ejemplo:
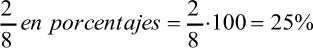
El resultado puede interpretarse así: 2 es a 8 como 25 es a 100, o lo que es lo mismo, 2 es la cuarta parte de 8 (igual que 25 lo es de 100).
En realidad, la conversión a porcentajes no es más que un cambio de referencia. A veces resulta más fácil o intuitivo plantearlo como una simple regla de tres (directa):
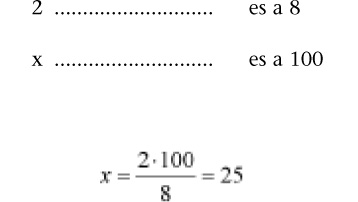
De donde,
Se ha hallado una cantidad, 25, que respecto a su total, 100, guarda la misma proporción que 2 a 8.
Veamos con mayor detalle algunas aplicaciones simples y útiles del cálculo con porcentajes:
• Conversión de una cantidad en un porcentaje
• Cálculo del porcentaje de una cantidad
• Variaciones porcentuales
- Cálculo del valor inicial, conocido el incremento porcentual y el valor final.
- Cálculo del valor final, conocido el incremento porcentual y el valor inicial.
Se trata de expresar una cantidad P, que representa una parte de un total T, en un porcentaje. Para ello necesito conocer dos cifras: la que voy a convertir en un porcentaje (P) y la que nos indica la cantidad total (T). Es el caso ya comentado anteriormente, y que puede resolverse con una simple regla de tres simple directa:

de donde
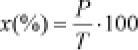
Ejemplo
En una determinada ciudad, de 42.000 habitantes, se estima que existen 3.000 lectores diarios de una publicación local. ¿Cuál es el porcentaje de lectores diarios?
En este caso, P = 3.000 y T = 42.000. El porcentaje de lectores diarios será:
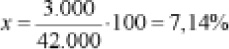
Si lo planteamos con una regla de tres:

O bien,

En ambos casos, aislando la incógnita, resulta el mismo valor:
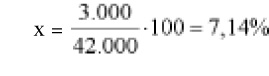
En este caso, pretendemos conocer a cuánto asciende el porcentaje de una cantidad, que llamaremos base o referencia (T).
Por ejemplo, deseo conocer el 24% de 2.000. Algebraicamente se trata de calcular 24 centésimas de 2.000. Ello significa dividir la cantidad total (2.000) en centésimas y sumar 24 de ellas. Por tanto,
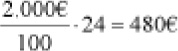
Si planteo una regla de tres:
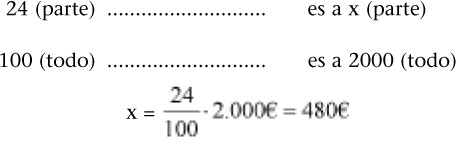
Ejemplo
De los 3.000 lectores del ejemplo anterior, un 20% son jóvenes entre 23 y 28 años. ¿Cuántos jóvenes, de dicha edad, son lectores?
Según los planteamientos anteriores:
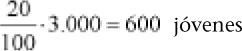
Mediante la regla de tres:

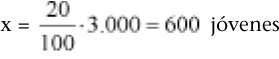
En la prensa económica y, en general, la relacionada con el mundo publicitario, es habitual el manejo de porcentajes y de incrementos o variaciones porcentuales. Por ejemplo:1

Los incrementos o decrementos de determinadas cantidades producidas en distintos periodos de tiempo, suelen expresarse en porcentajes. Si nos detenemos unos instantes en reflexionar acerca de su planteamiento, resulta muy sencillo deducir como se calculan.
En general, intervienen tres variables:
Vi = valor inicial Vf = valor final Δ=incremento en %
Cuando una cantidad varía con el tiempo, y deseamos cuantificar de alguna manera su evolución en dos periodos determinados, hay dos opciones:
• De forma absoluta: mediante su diferencia algebraica.
• De forma relativa: expresando, la diferencia anterior con relación a su valor inicial. Dicho cociente, como ya hemos comentando anteriormente, puede multiplicarse por 100 y expresarse en porcentajes. Si el resultado es positivo, indicará un incremento (Δ), o sea, una tendencia creciente. Por el contrario, si es negativo, se ha producido un decremento (∇) o bien, un incremento negativo (-Δ).
¿Cuál sería el incremento obtenido, en cantidades absolutas? Sencillamente, la diferencia algebraica entre ambas cantidades (final e inicial):
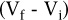
Si en vez de la diferencia en unidades absolutas, deseo calcular dicha diferencia en unidades relativas, el resultado anterior se divide por el valor inicial:
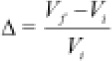
Si quiero expresar el resultado en porcentajes, hay que multiplicar por 100 y, no nos olvidemos, añadir el símbolo %:
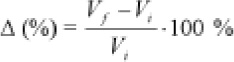
Ejemplo
¿Qué variación se requiere para pasar de 5 a 15?
En unidades absolutas, es la diferencia:
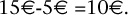
En unidades relativas, se divide dicha cantidad absoluta por la inicial (5€),
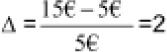
El incremento resulta igual a 2. Significa dos veces el valor inicial, o lo que es lo mismo, expresado en porcentajes,
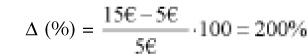
El valor final se ha obtenido al incrementar un 200% el valor inicial.
Comprobémoslo:
• Un 200% del valor inicial es igual a: 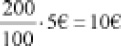
• Si sumamos 10€ a los 5€ iniciales, efectivamente obtenemos los 15€ finales. Luego el cálculo es correcto.
Es fácil deducir que, por ejemplo, cuando se produce un incremento del 100% (incremento igual al valor inicial), la cantidad final es el doble de la inicial.
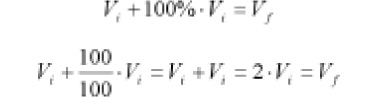
A veces, se confunde un valor doble final como un incremento del 200%. Para evitarlo conviene diferenciar entre el incremento y la relación entre la cantidad final respecto a la inicial. Recordar que el valor final se obtiene sumando al valor inicial el incremento que se produce sobre dicha cantidad.
De forma similar, un incremento del 200% (es decir un aumento de una cantidad doble a la del valor inicial) añadido al valor inicial da lugar a una cantidad final que es el triple de la inicial. Ello no significa que se haya producido un incremento del 300%, sino que la cantidad final resultante es el triple de la inicial.
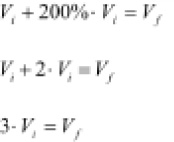
A veces, aunque se tenga claro el concepto, se utilizan términos inapropiados creándose confusiones y malentendidos.
Planteamiento general
Tal como hemos comentado, si partimos de una cantidad o valor inicial y ésta resulta incrementada en un porcentaje (aplicación de un porcentaje a una cantidad), se obtiene el valor final. Podemos plantear que:
valor inicial + variación producida sobre el valor inicial = valor final
Algebraicamente,
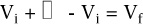
A partir de esta sencilla ecuación en la que intervienen tres variables (Vi,  , Vf ) puede obtenerse cualquiera de ellas, conociendo las restantes. Veamos las distintas posibilidades que tenemos:
, Vf ) puede obtenerse cualquiera de ellas, conociendo las restantes. Veamos las distintas posibilidades que tenemos:
a) Se conoce el valor inicial y el final. El incremento será:
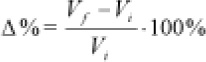
b) Se conoce el valor inicial y el incremento. El valor final será:
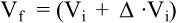
c) Se conoce el valor final y el incremento. El valor inicial se obtiene:
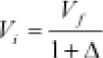
Hay multitud de ocasiones en la práctica profesional (y también en la personal) en las que tendremos que operar con las anteriores fórmulas: conocer el presupuesto antes de IVA a partir del presupuesto global (con IVA), calcular comisiones de agencia, descuentos de negociación, repartir presupuestos por medios, etc. Son cálculos sencillos que, si no son correctos, pueden suponer pérdidas importantes para la empresa. Las cifras presupuestarias que se manejan, por ejemplo en concursos públicos de contratación de medios, son realmente importantes y, en determinados casos, de millones de euros. Un porcentaje o un descuento mal aplicado, por pequeño que sea, como la base es elevada, supone una cantidad económica importante.
Observación: recordar que cuando se manejan porcentajes hay que operar, algebraicamente, con dichos valores divididos por 100. En las dos fórmulas anteriores los valores de los Δ hay que expresarlos en tantos por uno. Por ejemplo, si el incremento producido es del 6%, debe sustituirse Δ por 0,06 y no por 6.
Suele decirse que las prisas son malas consejeras. Ya sea por ello o por falta de conocimientos, en ocasiones se cometen errores cuando se opera con porcentajes. Citemos algunas de las precauciones que hay que tener en cuenta para no incurrir en ellos:
• No se pueden sumar, restar o promediar directamente porcentajes, a no ser que tengan la misma base (ver ejercicio comentado al respecto).
• Cuando la base es pequeña, cualquier cambio (variación o porcentaje) puede producir un incremento grande y si la base es grande, un pequeño porcentaje puede dar lugar a una cantidad importante. Así pues, si me interesa que una cantidad parezca pequeña, la expresaré como un porcentaje de algo grande. Si lo que quiero es que parezca grande, la expresaré como un porcentaje de algo pequeño. Las propiedades anteriores pueden utilizarse para producir un mayor o menor impacto (sin falsedades) en aquello que desee comunicarse.
• Un porcentaje siempre debe considerarse como una fracción dividida por 100 ó por su equivalente en centésimas. Es fuente de numerosos errores, utilizar simplemente el numerador, es decir, la cantidad que acompaña al símbolo %. Por ejemplo, un 2%, representa 2 centésimas partes que es muy distinto a 2 unidades (cantidad 100 veces superior). Recordar que el símbolo % equivale a 1/100.
• Es necesario saber cuál es la referencia o base a la cual está referido el porcentaje. Cuando se cita que ha habido una disminución del 5% o un aumento del 42% es con relación a una determinada cantidad. Si ésta es desconocida, difícilmente puede obtenerse una interpretación correcta.
Ejemplo
En la revista Science Digest2, se publicó un resumen acerca de un debate real en el Parlamento británico acerca de la esterilización de los desequilibrados mentales.
En él, se cita que tanto el proponente como el opositor de la tesis habían aceptado que en Gran Bretaña había aproximadamente 400.000 desequilibrados mentales y que si se adoptara la política de la esterilización su número se reduciría a la mitad más o menos en medio siglo.
Los argumentos que el proponente y opositor utilizaron en el debate fueron los siguientes:
Proponente: hay casi 400.000 desequilibrados mentales en el país, lo que equivale a un 25% de toda la población de Gales. La esterilización reduciría esa cifra a la mitad en aproximadamente 50 años.
Opositor: hoy el número de desequilibrados no llega al 1% de la población. Cincuenta años de esterilización probablemente reducirían esa proporción al 0,5%, pero ¿vale la pena hacerlo?
Observar que se alude a las mismas cifras pero la percepción es totalmente distinta por el hecho de utilizar bases o referencias diferentes (población de Gales y/o población de Gran Bretaña).
1.- De un grupo de 500 personas, 100 escuchan diariamente la radio y el resto, ocasionalmente. Calcular e interpretar los siguientes ratios:
1.- Oyentes diarios / oyentes ocasionales
2.- Oyentes ocasionales / oyentes diarios
Solución
Datos iniciales
Total personas: 500
Oyentes diarios de radio: 100
Oyentes de radio ocasionales: 500-100 = 400
Resolución
1) El ratio oyentes diarios/ oyentes ocasionales es:
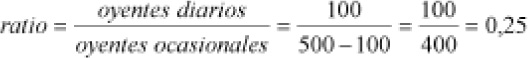
2) El ratio oyentes ocasionales/ oyentes diarios es, según lo anterior, el cociente entre las cantidades 400 y 100. Es decir,
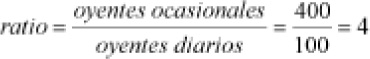
Como el ratio solicitado es el inverso del calculado, también podría obtenerse así:
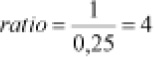
Observaciones
Los resultados indican que hay un oyente diario por cada cuatro ocasionales y cuatro oyentes ocasionales por cada oyente diario.
2.- A partir del ejercicio anterior, calcular la proporción de personas que escucha diariamente la radio.
Solución
Datos iniciales
Total personas: 500
Oyentes diarios de radio: 100
Consideraciones
• Como se pide una proporción, se halla la relación entre aquellos que escuchan diariamente la radio y el total de personas del grupo.
Resolución
Hay 100 personas que escuchan diariamente la radio de un total de 500. Por tanto la proporción será:

Observaciones
El resultado indica que de cada cinco personas del grupo, tan solo una escucha diariamente la radio.
3.- Con los datos del primer ejercicio, obtener los siguientes porcentajes:
a) Oyentes diarios
b) Oyentes ocasionales
Solución
Datos iniciales
Total personas: 500
Oyentes diarios de radio: 100
Oyentes de radio ocasionales: 500-100 = 400
Consideraciones
• A partir de las correspondientes fracciones, se calculan los porcentajes multiplicando por 100 y añadiendo el símbolo correspondiente (%).
Resolución
a) Del total de 500 personas, solamente 100 son oyentes diarios. El porcentaje es dicha proporción multiplicada por 100.
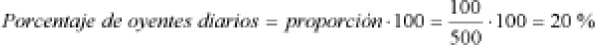
b) Hay 400 personas que escuchan ocasionalmente la radio, por tanto, el porcentaje sería el siguiente:
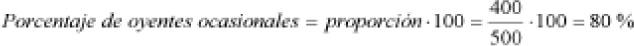
Observaciones
Las interpretaciones de los resultados serían las siguientes:
a) De cada 100 personas del grupo, 20 son oyentes diarios.
b) 80 de cada 100 personas del grupo, son oyentes ocasionales.
4.- Lucía ha visto un precioso vestido en las rebajas. Llega a la tienda y comprueba que el establecimiento ha añadido un 40 por ciento de descuento sobre la rebaja del 40 por ciento que ya tenía la prenda. Lucía entra contenta en el local pensando que comprará el vestido con una rebaja del 80 por ciento, pero al ir a pagar, comprueba que no es así. ¿Cuál es el descuento real?3
Solución
Datos iniciales
Precio del vestido: x
Descuento de la primera rebaja: 40% sobre x
Descuento de la segunda rebaja: 40% sobre el precio de la primera rebaja
Consideraciones
• El segundo descuento se aplica al precio ya rebajado, que es distinto del precio inicial. Por tanto, no pueden sumarse ambos porcentajes ya que las bases o referencias son distintas.
Resolución
El precio del vestido en la primera rebaja es:
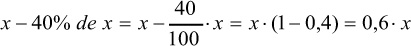
En la segunda rebaja, hay que aplicar el descuento del 40% a este nuevo precio:
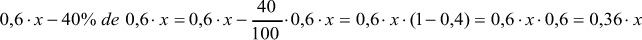
Si el precio inicial del vestido era x, en la segunda rebaja es de 0,36 · x. La diferencia es (x − 0,36 x) = 0,64 · x, por lo que el descuento, con relación al precio original, es el 64% y no el 80%.
El descuento real es del 64 por ciento.
Observaciones
No es posible sumar ambos descuentos porque las bases a las que se aplican son distintas. El primer descuento está relacionado con el precio inicial del vestido (x), y el segundo con el precio ya rebajado, que es 0,6 · x.
5.- Elisa, Tomás y Vanesa ocupan los cargos de presidenta (120.000 € anuales), vicepresidente (100.000 € anuales) y secretaria-tesorera (50.000 € anuales) de una compañía cuyo consejo de administración ha aprobado aumentar sus salarios, respectivamente en un 8%, 10% y 12%. ¿Cuál ha sido el incremento medio de aumento?
Solución
Datos iniciales
Sueldo anual presidenta: 120.000 €. Incremento del 8%
Sueldo anual vicepresidente: 100.000 €. Incremento del 10%
Sueldo anual secretaria-tesorera: 50.000 €. Incremento del 12%
Consideraciones
• Cada sueldo tiene un incremento distinto y, por tanto, las bases o referencias son diferentes. No sería correcto, pues, calcular el incremento medio como un promedio aritmético simple de los tres anteriores.
Resolución
Se calculan los sueldos finales con los incrementos correspondientes y se halla el incremento total comparando las cantidades totales final e inicial.
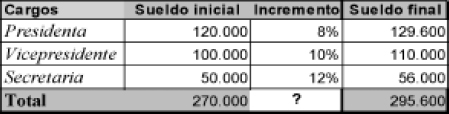
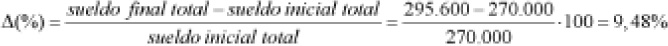
El incremento medio ha sido del 9,48 por ciento.
Observaciones
Si se efectúa el promedio simple de los tres incrementos, resultaría un 10%. Esta solución sería correcta si todos los sueldos fuera idénticos, pero éste no es el caso planteado.
6.- ¿Qué te sugiere el siguiente titular: “Los homicidios han aumentado un 60% respecto al año anterior”?
Solución
Datos iniciales
Incremento de los homicidios: 60%
Consideraciones
• No tenemos información acerca de cuál es la referencia o base y es difícil conocer el significado real de dicho incremento, en términos absolutos.
Resolución
La primera sensación que se tiene es como si la calle estuviera llena de asesinos… Sin embargo hay que ser prudentes en su interpretación ya que desconocemos el número de homicidios del año anterior (cantidad base). Si ésta es pequeña, apenas me preocuparé. Si, por el contrario, es una cifra elevada, ¡¡¡mejor sería no salir de casa!!!
Observaciones
Otro periódico aclaró que los homicidios habían aumentado de 5 a 8 a lo largo de un año. Por lo tanto, el porcentaje era correcto pero daba lugar a una posible interpretación fuera de lugar, al no indicar las cifras absolutas que habían originado el porcentaje citado.
7.- Verificar que los datos que aparecen en el anuncio son correctos.

Solución
Datos iniciales
Precio inicial: 384,67 €
Precio final: 284,67 €
Ahorro: 100 €, 26%
Consideraciones
• Como se conoce el precio inicial y final, es posible calcular el incremento producido (en este caso sería un incremento negativo o decremento) y compararlo con el anunciado.
Resolución
El incremento es:
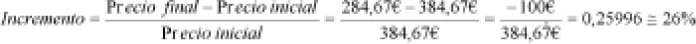
El resultado coincide con lo expuesto en el anuncio.
Observaciones
También puede resolverse directamente a partir del incremento dado (en este caso decremento), relacionándolo respecto al precio inicial.
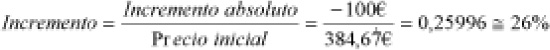
8.- El Heraldo de Aragón publicó en primera página, el 18 de diciembre de 1991, el siguiente titular: “El precio de los coches se reducirá un 5% en enero”, aludiendo al cambio en los tipos impositivos del Impuesto sobre el Valor Añadido. Comprobar su veracidad.
Solución
Datos iniciales
IVA de los coches en el año 1991: 33%
IVA de los coches en el año 1992: 28%
Precio del coche sin IVA: Pc
Precio del coche con IVA en el año 1991: Vi
Precio del coche con IVA en el año 1992: Vf
Consideraciones
• Hay que comprobar el incremento real que se ha producido al variar el porcentaje del impuesto que se aplica al precio de coste del vehículo, considerando los valores iniciales y finales correspondientes.
Resolución
Teniendo en cuenta los datos anteriores, los valores iniciales y finales (con el IVA) son:
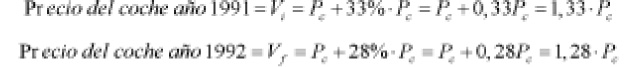
El incremento producido ha sido:
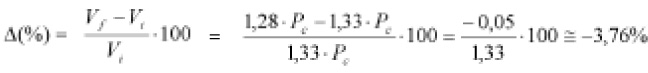
Se ha producido un incremento de -3,76% o, lo que es lo mismo, un decremento del 3,76%. Por tanto, el titular publicado era incorrecto.
Observaciones
El titular quería dar a entender la “rebaja” como simple diferencia entre los porcentajes aplicados al precio de coste del vehículo, pero no tenía en cuenta la comparativa o relación con el precio inicial del mismo.
9.- Los ingresos publicitarios de TVE en 1994 fueron de 75.100 millones de pesetas, y en 1.993 de 72.565 millones de pesetas. Calcular el incremento que se obtuvo en dicho periodo.
Solución
Datos iniciales
Ingresos publicitarios en 1993: 72.565 millones de ptas.
Ingresos publicitarios en 1994: 75.100 millones de ptas.
Consideraciones
• Conocidos los valores iniciales y finales se aplica la fórmula para calcular el incremento (en %).
Resolución
El incremento es:

El incremento producido es del 3,49 por ciento.
Observaciones
Si queremos estar seguros del resultado, podemos comprobarlo. Para ello aplicamos el incremento obtenido a la cantidad inicial y vemos si resulta la cantidad final:
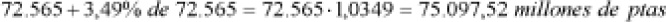
Observamos que existe una diferencia entre el resultado comprobado y el proporcionado en el ejercicio. Dicha diferencia proviene del redondeo a dos decimales en el cálculo del incremento. Si en vez de dos decimales se utilizan cinco (3,49342%), resultaría:
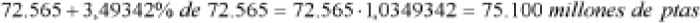
10.- Según una noticia difundida por la prensa, la cadena de televisión Tele 5 ganó 12.107 millones de pesetas netos en 1998, que supuso un 34,5% más que en 1997. Calcular el beneficio obtenido en dicho año.
Solución
Datos iniciales
Beneficio en 1998: 12.107 millones ptas.
Incremento producido: 34,5%
Consideraciones
• Conocemos el valor final (beneficio en 1998), la variación experimentada (incremento del 34,5% ) y hay que calcular el valor inicial (beneficio en 1997). Utilizaremos la expresión algebraica para el cálculo del valor inicial.
Resolución
El valor inicial es:
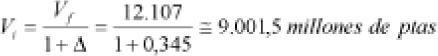
El beneficio en el año 1997 fue de 9.001,5 millones de pesetas.
Observaciones
Si comprobamos el resultado, se obtiene:
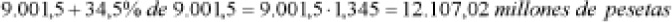
En este caso, la cifra es bastante aproximada a la indicada, lo cual sugiere que el error de redondeo en el incremento, ha sido menor que en el caso anterior.
11.- En base a las mediciones efectuadas por Sofres, la cadena de televisión Antena 3 obtuvo, un determinado día, unas audiencias de 388.341 y 734.861 individuos a las 21:00 y 21:30 horas respectivamente. Calcular la variación relativa de audiencia en dicho periodo de tiempo.
Solución
Datos iniciales
Audiencia estimada a las 21:00 = 388.341 individuos
Audiencia estimada a las 21:30 = 734.861 individuos
Consideraciones
• Es un problema típico de cálculo de un incremento. Se procede de forma similar a los casos anteriores.
Resolución
El incremento es:

El incremento de audiencia fue del 89,24 por ciento.
12- A partir de la información del artículo El número de ricos se estanca pese al espectacular crecimiento de la economía4, y con relación al gráfico “Vivienda”, comprobar los siguientes resultados:
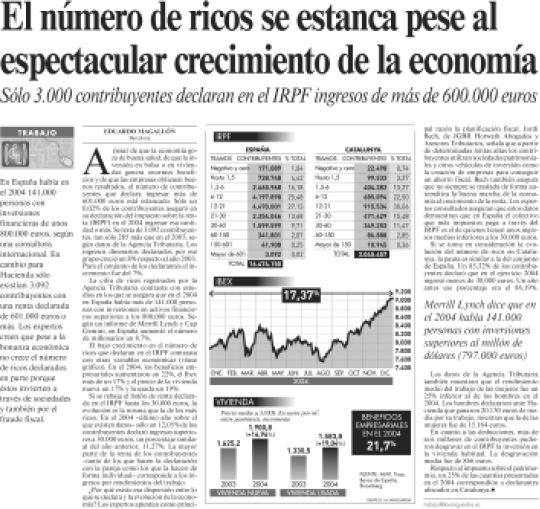
1. El incremento, en porcentaje, de la vivienda usada en el periodo 2003-04.
2. El precio medio a 31/XII de la vivienda nueva en el año 2003.
Solución
Datos iniciales
Vivienda usada
Valor inicial año 2003 = 1.330,5 €/m2
Valor final año 2004 = 1.583,8 €/m2
Vivienda nueva
Precio medio año 2004 = 1.900,8 €/m2
Incremento periodo 2003-2004 = 16,96%
Consideraciones
• Aplicaremos las fórmulas del incremento y del valor inicial, para la primera y segunda cuestión, respectivamente.
Resolución
1) 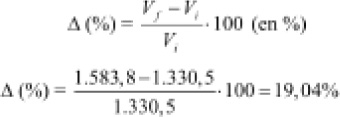
El incremento de la vivienda usada en el periodo 2003-2004 fue del 19,04 por ciento.
2) El valor inicial, es igual a:
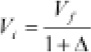
Sustituyendo,
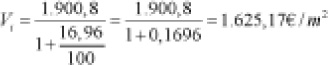
El precio medio a 31/XII de la vivienda nueva en el año 2003 fue de 1.625,17€/m2
Observaciones
A veces, se observan pequeñas diferencias entre los valores calculados (comprobados) y los que constan o aparecen publicados. Exceptuando los errores involuntarios, lo más probable es que se deban a los redondeos o aproximaciones de las cantidades que se citan.
13.- Según la información reflejada en el artículo sobre los presupuestos generales del 2003,5 averiguar:

1. ¿Cuál era el sueldo del Presidente del Gobierno en el año 2002?
2. ¿Cuál es el incremento medio de variación del sueldo del presidente del Gobierno, presidente del Tribunal Constitucional y del fiscal general del Estado, entre los años 2002/03?
Solución
Datos iniciales
Sueldo del presidente del Gobierno en el año 2003 = 81.661€/año
Incremento con relación al sueldo del año 2002 = 2,00%
Incremento del sueldo del presidente del Tribunal Constitucional = 3,35%
Incremento del sueldo del fiscal general del Estado = 57,00%
Consideraciones
• En el primer caso se trata de averiguar el sueldo del año 2002, es decir, el valor inicial, ya que conocemos el sueldo previsto (valor final) así como el incremento contemplado.
• Con relación a la segunda cuestión, tendremos que averiguar los sueldos iniciales de los cargos citados y calcular el incremento producido a partir de los sueldos totales final e inicial.
Resolución
1) El valor inicial es,
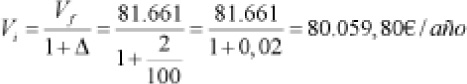
El sueldo anual del presidente del Gobierno, en el año 2002, fue de 80.059,80€
2) En el año 2002, los sueldos de los cargos citados eran:
- Presidente del Tribunal Constitucional:
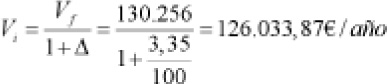
- Fiscal general del Estado:
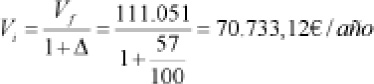
En el año 2002, el valor total de los sueldos, incluyendo al del presidente del Gobierno fue:
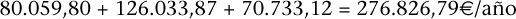
En el año 2003, el valor final previsto de dichos sueldos fue:
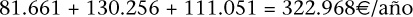
Por tanto, se produjo el siguiente incremento:

En el periodo 2002-03, el incremento medio de los sueldos de los cargos citados fue del 16,67 por ciento.
Observaciones
No es posible calcular el incremento medio mediante un simple promedio aritmético ya que cada uno de ellos se refiere a una base distinta. Si lo hiciéramos así, resultaría un incremento medio, no correcto, del 20,78 por ciento.
14.- Dada la información que aparece en el artículo Piqué lanza al PP hacia el pospujolismo6, responder a las siguientes preguntas:
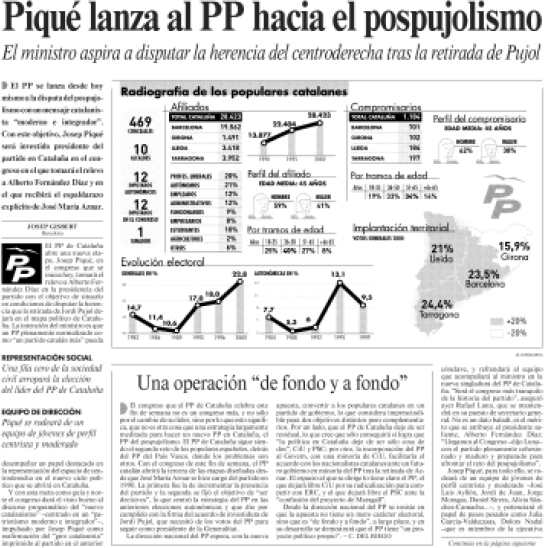
1. ¿Cuándo se produce un incremento mayor de afiliados de PP en Cataluña, en el periodo 1990-1995 o en 1995-2002?
2. Calcula el número de autónomos afiliados al PP en Cataluña (año 2002).
3. ¿A cuanto asciende y cuál es el significado del ratio concejales/diputados autonómicos del PP en Cataluña?
Solución
Datos iniciales (referidos al PP y a Cataluña)
Afiliados en el año 1990 = 13.877
Afiliados en el año 1995 = 22.404
Afiliados en el año 2002 = 28.423
Porcentaje de autónomos afiliados = 21%
Número de concejales = 469
Número de diputados autonómicos = 12
Consideraciones
• Es un sencillo ejemplo a partir del cual podrían plantearse bastantes cuestiones relativas a cálculos de porcentajes. En el caso que nos ocupa, el ejercicio se reduce a comparar dos incrementos, calcular el porcentaje de una cantidad y plantear e interpretar un ratio.
Resolución
1) Los incrementos son los siguientes:
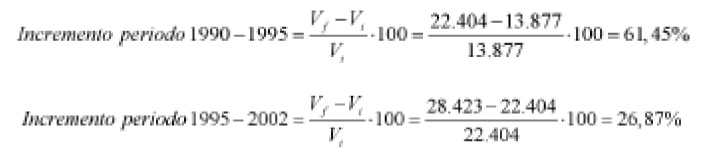
El incremento mayor se produce en el periodo 1990-1995.
2) Aplicamos el 21% al total de afiliados de Cataluña (28.423):
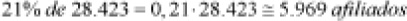
En el año 2002 había 5.969 afiliados al PP en Cataluña.
3) El ratio solicitado es el siguiente:

En el año 2002, el Partido Popular tenía en Cataluña 39 concejales por cada diputado autonómico.
15) Un organismo público saca a concurso la contratación de publicidad en distintos medios, por un presupuesto total de licitación de 6.000.000 € (incluido IVA). En este presupuesto se incluyen las siguientes partidas:
• Coste de la adquisición de espacios publicitarios en todos los medios/soportes que se determinen.
• Comisiones y/o impuestos que se deriven de la ejecución del mismo (gastos de producción que gravan ciertos soportes a la hora de contratar determinadas acciones).
• Honorarios: comisión de agencia en concepto de servicio de elaboración estratégico-táctica de la campaña publicitaria y de intermediación en la contratación de los medios/soportes correspondientes. En cualquier caso, dicha comisión se fijará en un porcentaje máximo del 2,5% y mínimo del 0,75% para cualquiera de los planes y acciones que se lleven a efecto. Este porcentaje se aplicará a la cantidad resultante antes de IVA, una vez aplicados los correspondientes descuentos de negociación sobre tarifa y descuentos de Agencia.
La distribución estimada del citado presupuesto de licitación es la siguiente:
• Año 2007: 3.480.000 € IVA incluido.
• Año 2008: 2.520.000 € IVA incluido.
La estimación de reparto del presupuesto por medios (basado en el importe total neto, una vez aplicados descuentos de negociación y descuentos de agencia), se realizará en base a la siguiente tabla:
MEDIOS |
% Inversión |
TELEVISIÓN |
50 |
PRENSA |
13 |
REVISTAS y SUPLEMENTOS DOMINICALES |
10 |
RADIO |
5 |
EXTERIOR |
9 |
INTERNET |
4 |
CINE |
4 |
OTROS NO CONVENCIONALES |
5 |
Se pide calcular:
a) ¿Cuál es el presupuesto neto, antes IVA, para el año 2007?
b) ¿Qué cantidad hay que destinar a internet, antes de comisión de agencia e IVA? Suponer que la agencia trabaja con un 0,75% sobre neto.
c) ¿Qué ingreso tendría la agencia si aplicara un 2,5% de comisión de agencia? Indicar la cantidad antes de IVA.
d) ¿Cuál sería el presupuesto a tarifa en TV si el descuento de negociación fuera un 70%, el descuento de agencia un 0% y antes de la comisión de agencia?
Solución
Datos iniciales
Presupuesto total (licitación) con IVA: 6.000.000 €
Presupuesto año 2007: 3.480.000 €
Presupuesto año 2006: 2.520.000 €
Comisión agencia: 0,75% a 2,50%
Reparto presupuesto según medios: tabla adjunta
Presupuesto destinado a internet: 4% del importe total neto (aplicados los descuentos de negociación y de agencia)
Consideraciones
• Es un ejercicio práctico de aplicación de cálculos con porcentajes. La única dificultad del ejercicio consiste en distinguir correctamente entre los distintos conceptos que aparecen, en particular, los referentes a los importes netos y/o a los importes antes o con IVA incluido.
Resolución
a) En el año 2007 el presupuesto destinado, con IVA, es: 3.480.000 €. Para conocer el presupuesto sin la afectación del IVA, hay que dividir por 1,16:
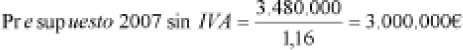
Equivale al cálculo de un valor inicial, considerando que el valor final es 3.480.000 € y el incremento es el 16%:
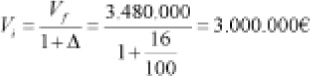
El presupuesto neto, antes IVA, para el año 2007 es de 3 millones de euros.
b) La pregunta hace relación al presupuesto global para internet, sin tener en cuenta el IVA y la comisión de la agencia.
En este caso conocemos cuál es el valor final (6.000.000 €) que está afectado del IVA (incremento del 16%) y de la comisión de la agencia (incremento del 0,75%). Operando por partes, calculo los correspondientes valores iniciales (o netos), tal como se ha indicado antes:

Observemos que en el denominador debe constar: 1 + incremento en tanto por uno = 1 + 0,75% = 1 + 0,75/100 = 1 + 0,0075 = 1,0075
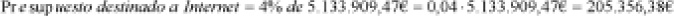
La cantidad destinada a internet, antes de la comisión de la agencia y del IVA es de 205.356,38 €
c) Según se cita en el enunciado, la comisión de agencia se aplicará a la cantidad resultante antes de IVA, una vez aplicados los correspondientes descuentos de negociación sobre tarifa y descuentos de agencia. Por tanto, de nuevo, el cálculo es pasar de valores finales (con impuestos y/o comisiones) al valor inicial (neto).
En el presupuesto global sin IVA (valor final) obtenido anteriormente está incluida (sumada) la comisión de la agencia. Por tanto, debe eliminarse o sustraerse dicho incremento (comisión del 2,5%). Nuevamente, hay que calcular un valor inicial:
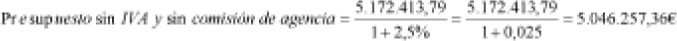
El ingreso de la agencia sería la diferencia entre ambas cantidades:
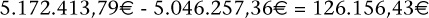
La agencia ingresaría la cantidad de 126.156,43 €
d) Los cálculos serían los siguientes:
El presupuesto global sin IVA y antes de la comisión de agencia (0,75%) es: 5.133.909,47 € (calculado en el apartado b).
La inversión en TV debe ser del 50% según se indica, por tanto,

Este sería el presupuesto neto, es decir, con los precios negociados y descontados todos los descuentos de agencias si los hubiera.
Si se ha conseguido un 70% de descuento significa que la cantidad anterior es equivalente al 30%, es decir,
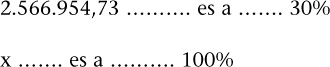
Resolviendo esta regla de tres simple:
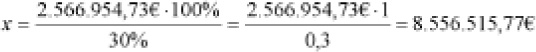
El presupuesto a tarifa de TV con un descuento de negociación del 70%, descuento de agencia del 0% y antes comisión agencia, es de 8.556.515,77 €
Observaciones
A veces se cometen errores en los cálculos anteriores por no tener claros los conceptos relativos a cuáles son los importes brutos, netos, antes de IVA, antes de comisión agencia, descuentos, etc.
Por ejemplo, en el apartado c) un error frecuente es aplicar el 2,5% a la cantidad global sin IVA, es decir, a 5.162.413,79 €. Si lo hiciera así, resultarían 129.060,34 € que sumados a 5.162.413,79 € serían 5.291.474,13 €. Aplicando el IVA a esta cantidad, resulta la cantidad final de 6.138.110 €, que es superior a la indicada como presupuesto total (6.000.000 €) y, por tanto, no es posible.
Estos errores, que algunos estudiantes consideran como simples equivocaciones, no pueden admitirse en la práctica profesional, pues supone un desconocimiento de los procedimientos básicos algebraicos que redundan negativamente en la imagen, profesionalidad, y en el correspondiente balance o resultados económicos de la empresa.
1.- Se adjunta información relativa a las ventas de pantallas electrónicas durante los años 2002 y 2003. Completar las cifras correspondientes a los espacios indicados (a, b, c, d, e y f).
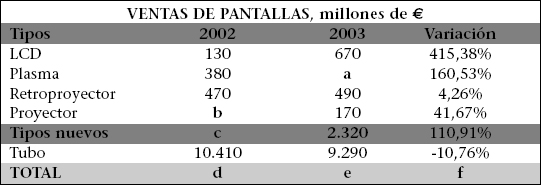
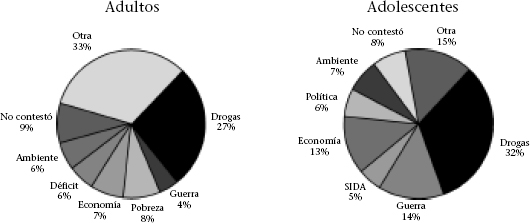
2.- En el año 1989 se llevó a cabo, en EE.UU., una encuesta a 1.005 adultos y 500 adolescentes sobre ¿Cuál es el problema principal de los Estados Unidos? Los resultados se muestran en los gráficos de sectores circulares adjuntos. Se propone la resolución de las siguientes cuestiones:
a) ¿Cuál es el porcentaje de personas que respondió que el problema principal eran las drogas?
b) ¿Cuál es el porcentaje de personas seleccionadas que son adolescentes?
c) ¿Qué porcentaje de adolescentes, sobre el total de personas, contestó que el principal problema eran las drogas?
d) Cuántos adolescentes señalaron la “Economía” como principal problema?
e) Un 7% de los adultos respondió que la “Economía” era el principal problema frente a un 13% de los adolescentes. Por tanto, el número de adolescentes que mantiene esta opinión es mayor que el número de adultos. ¿Es cierto o falso? ¿Por qué?
f) ¿Cuántas personas no contestaron a la encuesta?
g) En total, un 27% más un 32%, es decir, un 59% de las personas encuestadas (1.505) aludieron a las “drogas” como principal problema. ¿Es cierto? ¿Por qué?
3.- Con relación al artículo La Vanguardia aumenta su difusión y consolida su hegemonía en Cataluña,7 responder a las siguientes preguntas:

a) ¿Cuál fue el decremento de ventas de La Vanguardia en el periodo 1999-2000?
b) En el año 2001 el promedio de difusión de La Vanguardia fue superior al conseguido por El Periódico. Calcular el incremento en porcentaje.
c) Indicar si es correcta la conclusión obtenida a partir de lo expresado en el artículo: “…la variación experimentada por El País en el año 2001 con relación al 2000 fue de un -0,62% y la Razón de un 80,41%…” Conclusión: en promedio, la variación media de ambos periódicos fue de un 39,90%.
4.- En el año 1993, los tipos impositivos (IVA) de los hoteles disminuyeron del 15% al 6%, es decir, disminuyendo los precios un 9%. ¿Es correcta esta afirmación?
5.- ¿Qué te sugiere el siguiente titular? “La tasa de desempleo aumentó un 30%”
6.- En base a la información suministrada en el artículo Las adopciones internacionales aumentan un 40% en un solo año en España8 responder a las siguientes cuestiones:
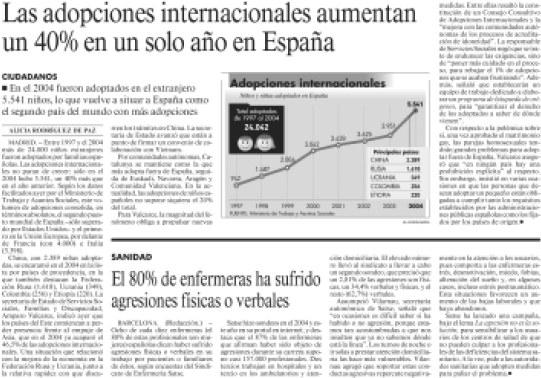
a) ¿Cuál fue el incremento de adopciones en el periodo 2003-04?
b) ¿Cómo se denomina, algebraicamente, la relación “volumen de adopciones de Francia respecto a las de Italia”?
7.- A partir de los datos reflejados en el artículo La universidad se globaliza,9 contestar a las siguientes preguntas:

a) ¿Cómo se denomina la relación “total Erasmus Catalunya/Madrid”?
b) ¿Cuántos estudiantes Erasmus llegaron a España en el curso 2004-05?
8.- Una vez leído y analizado el artículo Caffarel anuncia el fin de un ciclo en la memoria de RTVE,10 responde a las siguientes cuestiones:

a) ¿Cómo se denomina la relación “empleados fijos RTVE/contratados”?
b) ¿Qué incremento porcentual de contratados se produjo en el periodo 2004-05?
9.- Con relación al artículo La escuela crece gracias a los extranjeros, se proponen los siguientes cálculos:11
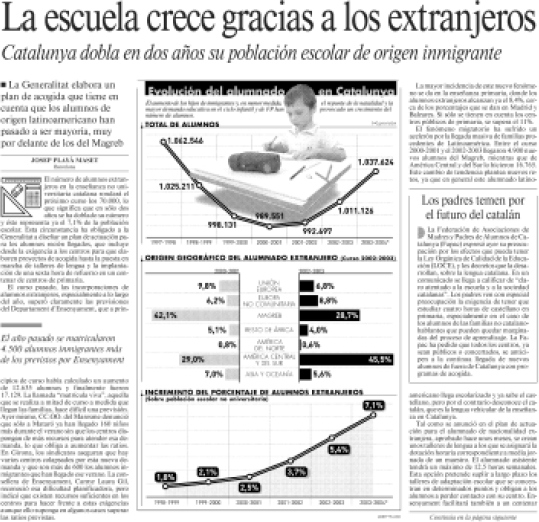
a) Los siguientes ratios (curso 2000-01):
1. “Alumnos UE/Asia-Oceanía”
2. “Alumnos UE/resto de África”
b) Teniendo en cuenta la información recogida en el primer párrafo del artículo, calcula a cuánto asciende la población escolar.
10.- En base a la información aparecida en el artículo sobre los presupuestos generales del Estado para el año 2003 (ver ejercicio comentado número 13), calcular:
a) El sueldo del presidente del Tribunal Supremo en el año 2002
b) El incremento medio de variación, en los años 2002-03, de los sueldos de los presidentes del Tribunal de Cuentas, Tribunal Constitucional y fiscal general del Estado.
11.- En el mes de abril del 2003 apareció publicado en La Vanguardia, el artículo adjunto Objetivo: evitar guetos en la escuela.12 Responder a las siguientes preguntas:

a) ¿Qué incremento de alumnos extranjeros de “Educación primaria” se produjo en los cursos 2001-02 y 2002-03?
b) ¿Es correcta la siguiente afirmación? “…En la ESO, el número de alumnos extranjeros en los últimos cuatro años, ha sido de 40.620, lo cual equivale a un 15,84%…”:
c) ¿Qué presupuesto se destinó, en el año 2002, a los cursos intensivos de catalán para hispanoparlantes?
12.- Con relación al artículo La inversión publicitaria creció sólo un 0,2% en el 2002 por la crisis económica,13 responder a las siguientes preguntas:

a) ¿Cuál fue la inversión publicitaria en medios convencionales en el año 2002?
b) ¿Cuál fue la inversión publicitaria en medios no convencionales en el año 2001?
c) ¿Cuál fue la inversión publicitaria total en el año 2002?
d) ¿Cuál fue la cadena de TV con un crecimiento mayor?
e) ¿Cuál fue el medio convencional que tuvo un mayor incremento de publicidad en relación al año 2001?
f) ¿Qué cadena de TV sufrió un decremento mayor en relación al 2001?
g) ¿Qué cantidad se invirtió en publicidad en TV en el año 2001?
h) Considerando la televisión, internet y revistas, ¿cuál fue el incremento medio de variación?
i) Calcular la cantidad que se invirtió en los diarios deportivos en el año 2001
j) Los medios convencionales han invertido, en el año 2002, un 46,16% de la cantidad total. ¿Qué porcentaje, respecto al total de la inversión publicitaria, supone para el medio “radio”?
13.- Dada la tabla adjunta, Audiencia de las cadenas de radio en Catalunya (2000-2001) (en miles), comprobar, considerando los valores iniciales, finales e incrementos, los siguientes datos:14
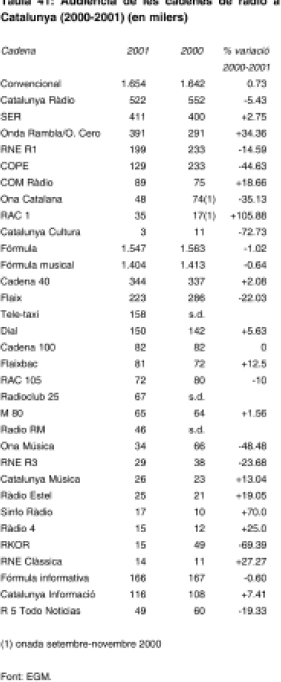
a) El incremento de audiencia de COM Ràdio fue del 18,67%.
b) La audiencia de Catalunya Ràdio en el año 2000 era de 552 miles.
c) La audiencia en el año 2001 de Ràdio 4 fue de 15 miles.
Soluciones
1.- a) 990 millones de euros
b) 120 millones de euros
c) 1.100 millones de euros
d) 11.510 millones de euros
e) 11.610 millones de euros
f) 0,87%
2.- a) 28,64%
b) 33,22%
c) 10,63%
d) 65 adolescentes
e) Falso. Aunque el valor relativo es superior, en cifras absolutas es menor.
f) 130 personas
g) No. No es posible sumar los porcentajes porque las bases son distintas.
3.- a) 6,56% (como se indica decremento, no hace falta poner el signo -).
b) 19%
c) No. Las bases son distintas y no pueden promediarse.
4.- Falso. El ahorro real fue del 7,83% y no el 9%.
5.- La sensación inicial es que se producirá una recesión económica importante. Sin embargo, si sabemos que la tasa de desempleo actual es del 3%, un aumento del 30% significaría pasar al 3,9%, es decir apenas un incremento de un punto porcentual. Aunque es un incremento relativo importante, es mayor la sensación inicial que la que realmente es. En función de lo que desee comunicarse, producirá mayor impacto decir que el aumento de la tasa de desempleo es un 30% que citar que ha aumentado del 3% al 3,9%, cuando ambas afirmaciones son idénticas.
6.- a) 40,24%
b) Ratio
7.- a) Ratio
b) 25.241 estudiantes Erasmus
8.- a) Ratio
b) −7,18%
9.- a) 1,4 y 1,9
b) 985.915 alumnos
10.- a) 127.701,96 euros
b) 17,01%
11.- a) 54,43%
b) No es correcto, ya que los % corresponden a bases distintas
c) 8.533.846,15 €
12.- a) 5.403,8 millones (dato)
b) 6.211,7 millones (dato)
c) 11.707,7 millones (dato)
d) TVE, con un 12,8%
e) El cine (1,7%)
f) Resto autonómicas (-5,6%)
g) 2.150,19 millones
h) 0,185%. Se calcula el incremento teniendo en cuenta los valores totales finales e iniciales en los distintos años.
i) 54,89 millones €. Se conoce la cantidad total invertida en “Diarios” (1.531,2 millones €) y la parte relativa a los “deportivos” en el año 2002 (3,7%). Con dichos datos y conociendo la variación relativa (3,2%) es fácil obtener el resultado indicado.
j) 4,14%. Es el porcentaje correspondiente a 484,9 millones € con relación al total invertido en publicidad (11.707,7 millones €).
13.- a) La audiencia inicial (año 2000) fue de 75 miles y la final (año 2001) de 89 miles. Calculando el incremento, con relación al valor inicial, resulta el 18,67%.
b) En este caso la incógnita es el valor inicial (año 2000). Los datos son el valor final (522 miles) y el incremento del -5,43%. A partir de la expresión que nos calcula el valor inicial resulta la cantidad aproximada de 552 miles.
c) Ahora la incógnita es el valor final. Los datos son los valores iniciales (12 miles) y el incremento (25%). Aplicando la fórmula correspondiente, se obtiene el resultado indicado.
1. Estudio Infoadex de la inversión publicitaria en España 2007
2. Septiembre de 1952
3. PUNSET, E. (2006, 262) El alma está en el cerebro. Madrid, Santillana Ediciones Generales.
4. MAGALLÓN, E. La Vanguardia [Barcelona] (18 octubre 2006), Economía, p. 70.
5. La Vanguardia [Barcelona] (26 septiembre 2002), p. 75.
6. GISBERT, J. La Vanguardia [Barcelona] (19 octubre 2002), Política, p.17.
7. La Vanguardia [Barcelona] (9 junio 2002), Sociedad, p. 41.
8. Rodríguez de Paz, A. La Vanguardia [Barcelona] (29 abril 2005), Sociedad, p. 36.
9. Gutiérrez, M. La Vanguardia [Barcelona] (15 mayo 2006), Sociedad, p. 31.
10. Orta, J.M. La Vanguardia [Barcelona] (27 junio 2006), Vivir, p. 11.
11. Playa, J. La Vanguardia [Barcelona] (13 septiembre 2003), Sociedad, p. 31.
12. Chavarría, M. La Vanguardia [Barcelona] (15 abril 2003), Sociedad, p. 25
13. Rodríguez de Paz, A. La Vanguardia [Barcelona] (28 febrero 2003), Vivir, p. 11.
14. Informe de l’Audiovisual a Catalunya 2001: La ràdio a Catalunya. CAC, p. 55.