Recomendadores y agrupamientos
Actualmente la gran mayoría de instrumentos de medida de cualquier tipo de magnitud (desde magnitudes físicas como longitud, temperatura, tiempo hasta magnitudes de comportamiento como patrones de búsqueda y navegación en la web y preferencias de compra online, pasando por herramientas comunes como las cámaras digitales) son capaces de volcar sus mediciones a algún formato digital; de esa forma todos esos datos pueden estar fácilmente disponibles para su tratamiento.
En este momento el problema no es disponer de datos, pues se dispone en gran abundancia de ellos; el reto es conseguir extraer información a partir de los datos, o sea, darles un sentido y extraer conclusiones útiles de ellos. Esta tarea se conoce por el nombre de minería de datos (data mining).
Uno de los principales retos en el procesamiento de datos es el de integrarlos procedentes de múltiples fuentes, para así dotar de diferentes perspectivas al conjunto de estos, lo que permite extraer información más rica. Esta tendencia se da en casi todas las áreas: recopilación de la actividad de los usuarios en un sitio web; integración de sensores de temperatura, presión atmosférica y viento en el análisis meteorológico; uso de diferentes datos financieros y bursátiles en la previsión de inversiones; entre otros ejemplos.
La tarea de integración de múltiples fuentes de datos recibe el nombre de filtrado colaborativo (collaborative filtering).
De la misma forma que en las ciencias experimentales es fundamental utilizar un instrumental adecuado y unas unidades consistentes, un aspecto clave en cualquier tarea de procesamiento de datos es el uso de métricas, o sea medidas de distancia, adecuadas para el tipo de datos que se está tratando.1
Una de las aplicaciones en las que se centra este capítulo es la de los recomendadores. Un recomendador es un sistema que recoge y analiza las preferencias de los usuarios, generalmente en algún sitio web (comercios, redes sociales, sitios de emisión o selección de música o películas, etc.). La premisa básica de los recomendadores es que usuarios con actividad o gustos similares continuarán compartiendo preferencias en el futuro. Al recomendar a un usuario productos o actividades que otros usuarios con gustos similares han elegido previamente el grado de acierto acostumbra a ser más elevado que si las recomendaciones se basan en tendencias generales, sin personalizar.1
La tarea de encontrar a los usuarios más afines y utilizar esta información para predecir sus preferencias puede inscribirse en una tarea más general que recibe el nombre de agru-pamiento (clustering), y que consiste en encontrar la subdivisión óptima de un conjunto de datos, de forma que los datos similares pertenezcan al mismo grupo.2
1. Métricas y medidas de similitud
Una métrica es una función que calcula la distancia entre dos elementos y que por tanto se utiliza para medir cuán diferentes son. Existen varias formas de medir la distancia entre dos elementos, y elegir la métrica adecuada para cada problema es un paso crucial para obtener buenos resultados en cualquier aplicación de minería de datos. A menudo se utilizan funciones que miden la similitud entre dos elementos en lugar de su distancia.
En este apartado utilizaremos la distancia euclídea y estudiaremos una medida de similitud habitual, la correlación de Pearson.3
Por último, una forma habitual y segura4 de convertir una función de distancia d en una función de similitud s es la siguiente:
En un sitio web de visualización de películas a la carta se recoge la valoración de cada usuario sobre las películas que va viendo, con el objetivo de poder proponer a los usuarios las películas que más se adapten a sus gustos. Tras ver una película, un usuario ha de dar una valoración entre 1 y 5, donde las valoraciones más bajas corresponden a películas que han disgustado al usuario, y las más alta a las que le han gustado más. Se desea descubrir similitudes entre usuarios de manera que a cada usuario se le propongan las películas que más han gustado a los usuarios con gustos más parecidos al suyo.
Para poner en práctica estas pruebas se utilizarán los conjuntos de datos disponibles en http://www.grouplens.org/node/73, concretamente el conjunto de 100k valoraciones (fichero ml-data_0.zip), que contiene 100.000 valoraciones (del 1 al 5) de 1.682 películas realizadas por 943 usuarios. Si bien el conjunto de datos contiene 23 ficheros, en este capítulo sólo se utilizará el fichero u.data, que es el que contiene las valoraciones de los usuarios. En la tabla 4 se muestra un ejemplo meramente ilustrativo de valoraciones.5
Tabla 4. Valoraciones de 8 películas (ejemplo)
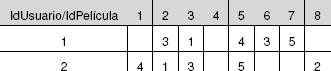
Los datos se presentan en forma matricial por legibilidad y concisión.
El fichero u.item contiene información sobre cada película, y el fichero u.user contiene información genérica sobre cada usuario (edad, sexo, etc.). Como se puede observar, los usuarios no tienen por qué valorar todas las películas, sino sólo las que han visto. La información de la tabla puede expresarse en Python mediante un diccionario en el que cada identificador de usuario es una clave, y el valor asociado a dicha clave es otro diccionario que asocia cada identificador de película a la puntuación asignada por ese usuario. El fragmento de código 1 muestra la representación correspondiente a la tabla 4.
Código 1: Diccionario de valoración de películas
La distancia euclídea de dos puntos P = (p1, p2, …, pn) y Q = (q1, q2, …, qn) en el espacio n-dimensional Rn viene dada por la fórmula:
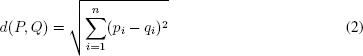
La distancia euclídea no es más que la generalización a n dimensiones del teorema de Pitágoras. Si las distancias en sí no son importantes, sino sólo su comparación, a menudo se utiliza la distancia euclídea cuadrada, es decir, sin la raíz cuadrada, pues la comparación entre distancias euclídeas cuadradas da los mismos resultados que entre las distancias euclídeas y puede resultar mucho más rápida de calcular, ya que la raíz cuadrada es una operación computacionalmente costosa.
La función que calcula la distancia euclídea entre las valoraciones de dos usuarios (según el formato visto en el fragmento de programa 1) en Python se muestra en el fragmento de programa 2, así como la función necesaria para convertir la distancia en una similitud.
Código 2: Distancia euclídea entre dos diccionarios
En la tabla 5 se muestran las similitudes entre las valoraciones de los usuarios utilizando la distancia euclídea. Como se puede comprobar, s(P,P) = 1 (ya que d(P,P) = 0) y s(P, Q) = s(P, Q), o sea, la matriz de similitudes es simétrica.
Tabla 5. Similitud euclídea de las valoraciones
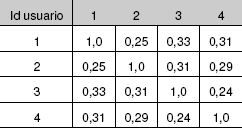
Supongamos que el usuario 4 desea que se le recomiende alguna película; el sistema, de momento, puede sugerirle que vea las películas que han gustado al usuario 1 (y no ha visto el 4), ya que es el usuario con mayor similitud; en el ejemplo, el usuario 4 podría elegir las películas 5 y 7, que son las que más han gustado al usuario 1 y aún no ha visto el 4.
Una limitación de la similitud (y la distancia) euclídea6 es que es muy sensible a la escala: si un usuario tiende a puntuar las películas que le gustan con un 4 y otro con un 5, habrá una cierta distancia entre ellos, en especial si el número de valoraciones es alto, aunque en el fondo ambos usuarios comparten gustos a pesar de utilizar las puntuaciones de formas diferentes.
Además, a mayor número de dimensiones (valoraciones, en este caso), la distancia eu-clídea tiende a ser mayor, lo que puede distorsionar los resultados. Por ejemplo, si dos usuarios comparten 2 valoraciones y hay una diferencia de 1 entre cada una de ellas, su distancia será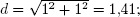 
sin embargo, si comparten 5 valoraciones con una diferencia de 1 entre ellas, su distancia será 
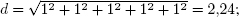una distancia bastante mayor para unas valoraciones en apariencia similares. Cuantas más valoraciones compartan dos usuarios (aunque no sean muy diferentes), más alejados estarán, lo que parece contrario a la lógica.
El coeficiente de correlación de Pearson es una medida de similitud entre dos variables que resuelve los problemas de la similitud euclídea. Se trata de una medida de cómo las dos variables, una frente a otra, se organizan en torno a una línea recta (línea de mejor ajuste), tal y como se puede ver en la figura 1. Cuanto más similares son las valoraciones de dos usuarios, más se parecerá su recta a la recta y = x, ya que las valoraciones serán de la forma (1, 1), (3, 3), (4, 4), etc.
Figura 1. Correlación entre las valoraciones los usuarios 1 y 2 de la tabla 4
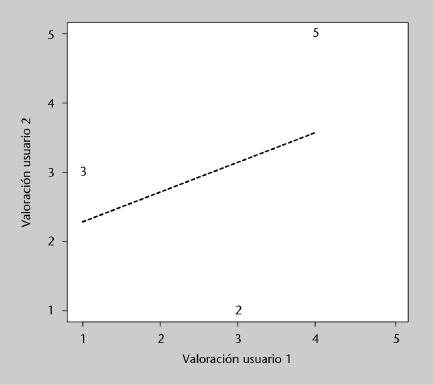
Diagrama de dispersión (scatter plot) de las valoraciones de dos usuarios: se representa la valoración de cada película en común tomando el eje x como la valoración de un usuario, y el eje y como la valoración del otro usuario. Los números en el diagrama corresponden a los identificadores de las películas comunes.
El coeficiente de correlación de Pearson (en este subapartado, simplemente correlación) está relacionado con la pendiente de la recta representada en la figura 1, y puede tomar un valor en el rango [-1, 1]. Si su valor es 1 indica que las dos variables están perfectamente relacionadas; si es 0, no hay relación lineal entre ellas7; si es negativo es que existe una correlación negativa, en este caso que las valoraciones de un usuario son opuestas a las del otro.
El cálculo del coeficiente de correlación de Pearson sobre dos muestras de datos alineados (valoraciones de usuarios, en nuestro caso) xi e yi viene dado por la fórmula:
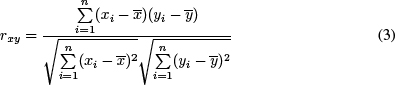
donde x es la media de los valores de x y y la media de los valores de y.
Nótese que para efectuar el cálculo los datos deben estar alineados: en nuestro caso, sólo se deben tomar las valoraciones comunes a los dos usuarios. También hay que prever que el denominador pueda valer cero. Con todas esas consideraciones, en el código 3 se muestra la función en Python que calcula el coeficiente de correlación de Pearson de dos diccionarios de valoraciones.
código 3: Coeficiente de Pearson entre dos diccionarios
Como se deduce de su definición, el coeficiente de correlación de Pearson es simétrico y vale 1 al calcularlo respecto a la misma variable. En la tabla 6 puede verse los valores correspondientes a las valoraciones de los usuarios de la tabla 4. En este ejemplo la correlación entre los usuarios 1 y 3 es 0 porque sólo tienen una película en común, con lo que la recta de ajuste no se puede definir.
Tabla 6. Coeficiente de Pearson de las valoraciones
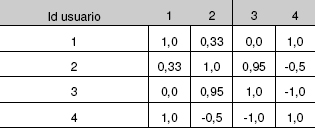
También se observa que los usuarios 1 y 4 tienen una correlación de 1,0; eso es debido a que, independientemente de factores de escala, su tendencia a valorar las películas es igual. Nótese la diferencia con la similitud euclídea mostrada en la tabla 5, si bien el usuario más similar al 4 sigue siendo el 1 y por lo tanto las películas que podría elegir serían las mismas. Por otra parte, los usuarios 3 y 4 hacen valoraciones contrarias, por lo que su coeficiente es -1,0. No obstante, sería conveniente disponer de más datos para obtener medidas más realistas.
El coeficiente de correlación de Pearson resulta útil como medida de similitud porque es independiente de los desplazamientos y escalas de los valores estudiados; para conseguir estas propiedades utilizando la similitud euclídea sería necesario normalizar los datos previa-menente a su análisis. Uno de sus principales inconvenientes en su uso en filtrado colabo-rativo es que requiere que haya al menos dos valores comunes para poder dar un resultado significativo; eso limita su aplicación en aquellos casos en que se desea sugerir productos similares a un cliente que ha hecho una única elección.
1.4. Procesamiento de datos reales
Hasta ahora se han utilizado las funciones de similitud sobre datos de prueba introducidos manualmente; sin embargo, es interesante probarlas con un volumen de datos apreciable para poder valorar mejor su comportamiento.
En el fragmento de código 4 se leen los datos del fichero u.data de la base de datos de valoraciones de películas Movielens utilizada en este subapartado, y se produce como resultado un diccionario con la misma estructura que el dado como ejemplo en el código de programa 1.
Para utilizarlo basta con aplicar alguna de las funciones de similitud descritas anteriormente a cualquier par de usuarios (claves del diccionario principal), o bien escribir un programa que genere una tabla o diccionario con todas las correlaciones.
código 4: Función que lee un fichero de valoraciones de MovieLens
Las principales limitaciones de los procedimientos explicados en este apartado son dos: primera, que no permiten sugerir productos directamente, sino sólo usuarios afines; esta limitación se resolverá en el siguiente apartado. La segunda limitación estriba en que es necesario almacenar en memoria todas las valoraciones de los usuarios y recalcularlas todas cada vez que se incorpora una nueva valoración o usuario, lo que puede suponer un coste computacional alto en aplicaciones grandes; visto de otra manera, no se genera ninguna abstracción o modelo de los datos que permita trabajar con una versión reducida de los datos. Esta limitación se resolverá en el apartado 3, que trata sobre los algoritmos de agrupamiento.
2.Recomendadores basadosenmemoria
En este apartado se mejorará el sistema de recomendación de películas visto en el apartado 1 para que, en lugar de sugerir usuarios con gustos similares, sugiera directamente las películas que pueden ser más interesantes para el usuario.
Se habla de recomendadores basados en memoria porque requieren mantener todos los datos disponibles para poder realizar una recomendación; además, cada vez que se introduce un nuevo dato o que se solicita una recomendación estos recomendadores han de efectuar sus operaciones sobre el conjunto completo de datos, lo que provoca que sean relativamente ineficientes, especialmente en aplicaciones con volúmenes de datos grandes. No obstante, tienen interés porque son muy sencillos conceptualmente y su programación es relativamente rápida.
Estos recomendadores están estrechamente relacionados con los clasificadores basados en distancias estudiados en el apartado 3, pues emplean una metodología similar (por ejemplo buscar el elemento más cercano al que se está evaluando); la diferencia radica en el uso que se hace de esta información, pues en el caso de los clasificadores se toma un nuevo elemento y se decide a qué clase debe pertenecer, mientras que en el caso de los recomendadores se toma un elemento y se sugieren los elementos más semejantes, sin necesidad de realizar una clasificación.
En la práctica se trata de generar una valoración (ranking) de todos los datos o preferencias registradas y que tenga en cuenta las particularidades del solicitante (gustos del usuario, etc.).
La forma más sencilla de generar una valoración global de un conjunto de elementos es promediar su grado de valoración. En el ejemplo de las películas, si una película tiene cuatro valoraciones (3, 5, 4, 3), su valoración media será 3,75; las películas con mayor valoración global serán las sugeridas al usuario. En el código 5 se muestra la función que devuelve una lista ordenada (de mayor a menor valoración) de películas, a partir del diccionario de valoraciones de los usuarios.
código 5: Función de recomendación media global de películas
Obviamente es posible añadir un if para omitir de la lista las películas que ya ha visto el usuario, aunque no se ha incluido esa operación para simplificar el código fuente mostrado.
La principal limitación de este método radica en que no tiene en cuenta las preferencias individuales de cada usuario. No obstante, esta estrategia puede ser útil con usuarios nuevos, sde los que no se conoce sus gustos. Una ventaja es que no depende de ninguna métrica para efectuar sus recomendaciones.
Una estrategia sencilla que tiene en cuenta las preferencias del usuario consiste en seleccionar las películas favoritas del usuario más semejante, que era lo que se dejaba hacer manualmente en el apartado 1 tras sugerir el usuario más cercano. La desventaja de esta estrategia consiste en que está limitada a las películas que ha visto el usuario más cercano. Si no ha visto una película que muchos otros usuarios relativamente afines han visto y valorado positivamente, el sistema nunca sugerirá esa película a pesar de que podría tratarse de una buena recomendación. Esta estrategia es similar al método de clasificación del vecino más cercano (1-Nearest-Neighbour) que se estudia en el subapartado 3.1.
Es posible utilizar un método que reúna las ventajas de los dos métodos de recomendación simples que se acaban de exponer. La idea es sencilla: se trata de obtener una valoración global del conjunto de elementos (productos) pero en lugar de calcular la media aritmética de las valoraciones, hay que calcular la media de las valoraciones ponderada por la afinidad del usuario correspondiente. De esa manera, la valoración global de los productos está personalizada para cada usuario y, por tanto, debería resultar más útil y acertada. En el programa 6 se muestra una función que calcula la valoración media de todas las películas ponderada por la afinidad de los usuarios con el usuario actual. vpj(x) es la valoración ponderada de una película x para el usuario j, y viene dada por la expresión:
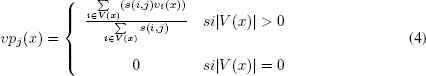
donde vi (x) es la valoración de la película x por el usuario i y s (i, j) es la similitud entre los usuarios i y j. Por último, V(x) es el conjunto de usuarios que han valorado la película x.
código 6: Función de recomendación media ponderada de películas
Los recomendadores vistos en este apartado permiten mejorar de una forma muy sencilla sitios web y otras aplicaciones similares para sintonizar mejor con los usuarios y sugerirles productos que les puedan interesar, mejorando así tanto su satisfacción con la aplicación como los éxitos potenciales de venta o acceso.
Las limitaciones de los métodos vistos hasta ahora son que, como se ha explicado, son métodos basados en memoria: requieren almacenar y procesar todos los datos cada vez que se realiza una consulta. De este modo, una operación sencilla no resulta excesivamente costosa, pero como se tiene que repetir completamente en cada consulta puede dar lugar a una carga computacional y de memoria desmesurada en aplicaciones medianas y grandes.
Otra limitación fundamental es que los métodos de recomendación que se acaban de estudiar no abstraen los datos de ninguna forma, es decir, no proporcionan información global acerca de los datos de los que se dispone, con lo que su uso está limitado a producir recomendaciones de productos, pero no pueden utilizarse para abordar estudios más complejos sobre los tipos de usuarios o productos de que se dispone, estudios que son esenciales para analizar el funcionamiento de la aplicación y diseñar su futuro. A continuación se estudiarán métodos que sí abstraen y producen información de alto nivel a partir de los datos disponibles.
3. Algoritmosdeagrupamiento(clustering)
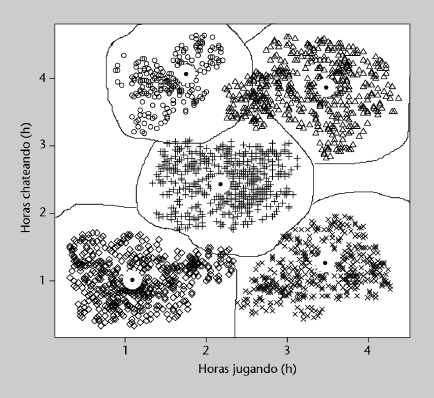
Una empresa de juegos en línea está analizando el comportamiento de sus clientes con el fin de ofrecerles los productos y características más adecuados a sus intereses. En este estudio se miden dos características: número de horas diarias jugando y número de horas diarias charlando (chateando) con otros jugadores, ambas en valor promedio para cada jugador. Los objetivos son dos: el primero, determinar qué tipos o clases de jugadores existen, según su actividad; el segundo, clasificar a los nuevos jugadores en alguna de esas clases para poder ofrecerles las condiciones y productos más adecuados. El segundo objetivo se trata extensamente en el apartado 3 dedicado a la clasificación, mientras que en este subapartado nos centraremos en cómo organizar un conjunto de datos extenso en unas cuantas clases o grupos, desconocidos a priori.
En la figura 2 se muestran los datos recogidos de 2.084 jugadores. Se trata de datos sintéticos (generados artificialmente) con el propósito de que ilustren más claramente los métodos que se expondrán a continuación. Concretamente, se pueden observar cinco clases o grupos claramente diferenciados, cada uno marcado con un símbolo diferente. En los datos reales no suele observarse una separación tan clara, y por consiguiente la ejecución de los métodos de agrupamiento no produce resultados tan definidos.
Figura 2. Actividad de los jugadores en línea
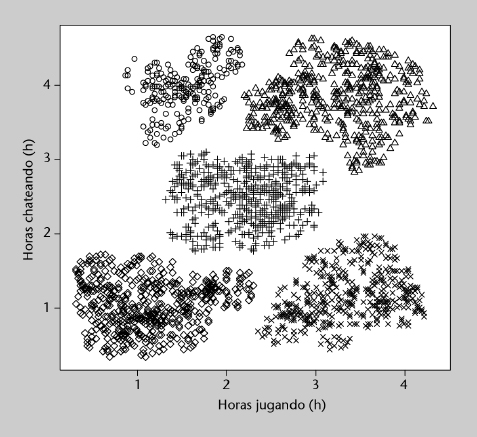
Las dos variables utilizan las mismas unidades (horas) y magnitudes similares y por tanto pueden utilizarse directamente para agrupar; en un caso más general, en el que las variables tengan magnitudes diferentes, suele ser necesario normalizarlas para que su magnitud se equipare y no tengan más influencia unas que otras (salvo que se pretenda justamente eso por la naturaleza del problema).
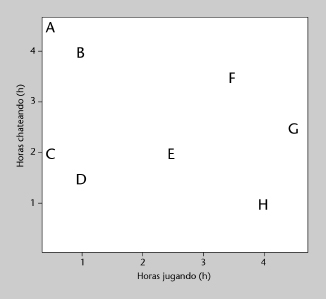
De hecho, para mostrar la ejecución paso a paso de algunos algoritmos de agrupamiento es necesario utilizar muchos menos datos, que en este caso son los que se muestran en la tabla 7 y en la figura 3.
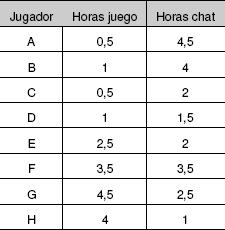
Figura 3. Actividad de 8 jugadores de ejemplo
La tarea de agrupamiento de datos es una tarea no supervisada, ya que los datos que se le proporcionan al sistema no llevan asociada ninguna etiqueta o información añadida por un revisor humano; por el contrario, es el propio método de agrupamiento el que debe descubrir las nuevas clases o grupos a partir de los datos recibidos. Si bien los algoritmos de agrupamiento se han introducido en el subapartado anterior como herramienta para crear recomendadores, sus aplicaciones van mucho más allá y se emplean en numerosos ámbitos, como por ejemplo:
• Procesamiento de imagen, para separar unas zonas de otras (típicamente con imágenes de satélite).
• Agrupamiento de genes relacionados con una determinada característica o patología.
• Agrupamiento automático de textos por temas.
• Definir tipos de clientes y orientar las estrategias comerciales en función de esos grupos.
• En general, definir grupos en conjuntos de datos de los que no se conoce una subdivisión previa: astronomía, física, química, biología, medicina, farmacología, economía, sociología, psicología, etc.
A menudo el agrupamiento de los datos precede a la clasificación de nuevos datos en alguno de los grupos obtenidos en el agrupamiento; por esa razón, el agrupamiento y la clasificación de datos están estrechamente relacionados, como se podrá observar en este subapartado, que comparte algunas técnicas con el subapartado 3.
Los algoritmos de agrupamiento se pueden clasificar en dos tipos: los jerárquicos con progresivos, es decir que van formando grupos progresivamente, y se estudiarán en primer lugar; los particionales sólo calculan una partición de los datos: los restantes algoritmos estudiados en este subapartado pertenecen a esta categoría. Utilizando algoritmos de agru-pamiento es posible construir recomendadores basados en modelos, llamados así porque a diferencia de los recomendadores basados en datos no necesitan almacenar todos los datos de que se dispone, sino que producen una abstracción de los datos dividiéndolos en grupos; para producir una recomendación sólo es necesario asociar un usuario o producto a un grupo existente, por lo que la información a almacenar se reduce a la descripción de los grupos obtenidos previamente. De esta forma la generación de una recomendación se simplifica notablemente, y por tanto los recursos requeridos para generarla.
Más allá de los recomendadores, una de las características más importantes de los algoritmos de agrupamiento es que permiten organizar datos que en principio no se sabe o puede clasificar, evitando criterios subjetivos de clasificación, lo que produce una información muy valiosa a partir de datos desorganizados.
Una característica común a casi todos los algoritmos de agrupamiento es que son capaces de determinar por sí mismos el número de grupos idóneo, sino que hay que fijarlo de antemano o bien utilizar algún criterio de cohesión para saber cuándo detenerse (en el caso de los jerárquicos). En general ello requiere probar con diferentes números de grupos hasta obtener unos resultados adecuados.
3.3. Agrupamiento jerárquico. Dendrogramas
Hay dos tipos de algoritmos de agrupamiento jerárquicos. El algoritmo aglomerativo parte de una fragmentación completa de los datos (cada dato tiene su propio grupo) y fusiona grupos progresivamente hasta alcanzar la situación contraria: todos los datos están reunidos en un único grupo. El algoritmo divisivo, por su parte, procede de la forma opuesta: parte de un único grupo que contiene todos los datos y lo va dividiendo progresivamente hasta tener un grupo para cada dato.
El dendrogram8 es un diagrama que muestra las sucesivas agrupaciones que genera (o deshace) un algoritmo de agrupamiento jerárquico. En la figura 4 puede verse el dendro-grama resultante de aplicar agrupamiento aglomerativo a los datos mostrados en la tabla 7.
Figura 4. Dendrograma de los 8 jugadores de ejemplo de la tabla 7
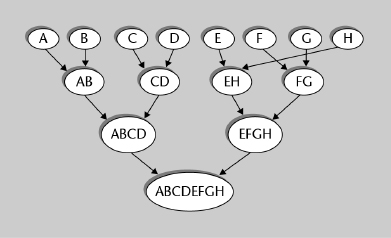
En los algoritmos jerárquicos de agrupamiento, se parte del estado inicial y se aplica un criterio para decidir qué grupos unir o separar en cada paso, hasta que se alcance el estado final. Si bien conceptualmente ambos tipos de algoritmos jerárquicos (aglomerativo y divisivo) son equivalentes, en la práctica el algoritmo aglomerativo es más sencillo de diseñar por la razón de que sólo hay una forma de unir dos conjuntos, pero hay muchas formas de dividir un conjunto de más de dos elementos.
Criterios de enlace
En cada paso de un algoritmo de agrupamiento jerárquico hay que decidir qué grupos unir (o dividir). Para ello hay que determinar qué grupos están más cercanos, o bien qué grupo está menos cohesionado. Supongamos que estamos programando un algoritmo aglomerativo; la distancia entre dos grupos puede determinarse según diferentes expresiones, que reciben el nombre de criterios de enlace. Algunos de los criterios más utilizados para medir la distancia entre dos grupos A y B son los siguientes:
• Distancia máxima entre elementos de los grupos (enlace completo):
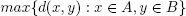
• Distancia mínima entre elementos de los grupos (enlace simple):
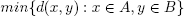
• Distancia media entre elementos de los grupos (enlace medio):
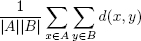
Una desventaja del criterio de enlace simple es que puede provocar que un único elemento fuerce la unión de todo su conjunto con otro conjunto que, por lo demás, no sea especialmente cercano. Por esa razón en general se preferirán otros criterios (completo, medio u otros).
Código del algoritmo aglomerativo
En el siguiente programa se definen las funciones necesarias para calcular el agrupamien-to aglomerativo sobre conjunto de datos utilizando distancia euclídea (podría utilizarse otra distancia) y criterios de enlace completo o mínimo. La función fusionaGrupos toma un agru-pamiento, selecciona los dos grupos más cercanos según el criterio indicado y los fusiona; la función agrupamientoAglomerativo inicialmente genera un grupo para cada dato y los va fusionando hasta que sólo queda un grupo; en cada fusión muestra el agrupamiento resultante. Finalmente se incluye una función leeJugadores que lee un fichero con los datos de los jugadores en formato “horasJuego horasChat clase” (se incluye la clase para evaluar el rendimiento del programa).
código 7: Agrupamiento aglomerativo
Conclusiones
El principal interés de los algoritmos jerárquicos radica en que generan diferentes grados de agrupamiento, y su evolución, lo que puede ser tan útil como la obtención de un agru-pamiento definitivo. Además son sencillos conceptualmente y desde el punto de vista de la programación. Por otra parte, los algoritmos jerárquicos de agrupamiento actúan de forma voraz (greedy), ya que en cada paso toman la mejor decisión en ese momento, sin tener en cuenta la futura conveniencia de tal decisión. Por ese motivo, en general dan peor resultado que otros algoritmos de agrupamiento.
El algoritmo de agrupamiento k-medios busca una partición de los datos tal que cada punto esté asignado al grupo cuyo centro (llamado centroide, pues no tiene por qué ser un punto de los datos) sea más cercano. Se le debe indicar el número k de clusters deseado, pues por sí mismo no es capaz de determinarlo.
A grandes rasgos el algoritmo es el siguiente:
1) Elegir k puntos al azar como centroides iniciales. No tienen por qué pertenecer al conjunto de datos, aunque sus coordenadas deben estar en el mismo intervalo.
2) Asignar cada punto del conjunto de datos al centroide más cercano, formándose así k grupos.
3) Recalcular los nuevos centroides de los k grupos, que estarán en el centro geométrico del conjunto de puntos del grupo.
4) Volver al paso 2 hasta que las asignaciones a grupos no varíen o se hayan superado las iteraciones previstas.
El programa de k-medios está escrito en el código 33. Si bien se trata de un algoritmo sencillo y rápido, al tener en cuenta sólo la distancia a los centroides puede fallar en algunos casos (nubes de puntos de diferentes formas o densidades), ya que por lo general tiende a crear esferas de tamaño similar que particionen el espacio. Así, para los datos mostrados en la figura 2, la partición en grupos aproximada es la mostrada en la figura 5, en la que se ve que, por ejemplo, algunos puntos del grupo superior derecho (triángulos) se han asignado al superior izquierdo (círculos) por estar más cercanos al centroide, sin tener en cuenta el espacio que los separa. El mismo problema se da en otros puntos. Además, su resultado puede variar de una ejecución a otra, pues depende de los centroides generados aleatoriamente en el primer paso del algoritmo.
Figura 5. K-medios ejecutado sobre los datos de la figura 2
Los puntos negros rodeados de una zona blanca representan los centroides de los grupos obtenidos.
3.5. c-medios difuso (Fuzzy c-means)
Resulta lógico pensar que, en k-medios, un punto que esté junto al centroide estará más fuertemente asociado a su grupo que un punto que esté en el límite con el grupo vecino. El agrupamiento difuso (fuzzy clustering) representa ese diferente grado de vinculación haciendo que cada dato tenga un grado de pertenencia a cada grupo, de manera que un punto junto al centroide puede tener 0,99 de pertenencia a su grupo y 0,01 al vecino, mientras que un punto junto al límite puede tener 0,55 de pertenencia a su grupo y 0,45 al vecino. Esto es extensible a más de dos grupos, entre los que se repartirá la pertenencia de los datos. Se puede decir que el agrupamiento discreto (no difuso) es un caso particular del difuso en el que los grados de pertenencia son 1 para el grupo principal y 0 para los restantes.
El algoritmo de c-medios difuso es prácticamente idéntico al algoritmo k-medios visto anteriormente, las principales diferencias son:
• En lugar de crear k centroides aleatoriamente, se asigna el grado de pertenencia de cada punto a cada grupo aleatoriamente y después se calculan los centroides a partir de esa información.
• El cálculo de los centroides está ponderado por el grado de pertenencia de cada punto al grupo correspondiente mx(k).
A grandes rasgos las ventajas e inconvenientes de c-medios difuso son las mismas que las de k-medios: simplicidad, rapidez, pero no determinismo y excesiva dependencia de la distancia de los puntos a los centroides, sin tener en cuenta la densidad de puntos de cada zona (por ejemplo, espacios vacíos). Se trata de un algoritmo especialmente utilizado en procesamiento de imágenes.
3.6. Agrupamiento espectral (spectral clustering)
El espectro de una matriz es el conjunto de sus valores propios9. La técnica de análisis de componentes principales descrita en el subapartado 1.2 está estrechamente relacionada con el agrupamiento espectral, pues determina los ejes en los que los datos ofrecen mayor variabilidad tomando los vectores asociados a valores propios mayores; en la técnica que aquí nos ocupa, por el contrario, se buscan los valores propios menores, pues indican escasa variabilidad y por tanto pertenencia a un mismo grupo (Luxburg, 2007).
1) Calcular la matriz de distancias W de los datos que se desea agrupar.
2) Calcular la laplaciana10 de la matriz de distancias mediante la fórmula Lrw = D - W, donde I es la matriz identidad y D es una matriz en la que los elementos de la diagonal son la suma de cada fila de W.
3) Calcular los valores y vectores propios de Lrw.
4) Ordenar los valores propios de menor a mayor; reordenar las columnas de la matriz de vectores propios según ese mismo orden.
5) El número de grupos k sugerido por el algoritmo es el número de valores propios muy pequeños (menores que 10-10 si los grupos están realmente separados).
El código 8 muestra el programa correspondiente a la descripción anterior, en la que faltaría la llamada a uno de los métodos de agrupamiento vistos anteriormente, como k-medios, para completar el proceso.
código 8: Agrupamiento espectral
El agrupamiento espectral es un método de agrupamiento muy potente, pues es capaz de agrupar datos teniendo en cuenta las diferencias de densidad, datos convexos (por ejemplo un círculo rodeando a otro), etc. Además indica el número de grupos que deben formarse.
Habitualmente se aplica un núcleo gaussiano11 al calcular la matriz de distancias para mejorar su rendimiento.
3.7. Recomendadores basados en modelos
La aplicación de algoritmos de agrupamiento para la construcción de recomendadores se basa, por lo general, en utilizar los grupos obtenidos para decidir qué recomendar a un usuario, en lugar de utilizar todos los datos disponibles. Esto agiliza enormemente el proceso de decisión y permite disponer de varias “vistas” de los datos: grupos de usuarios, de productos, etc. De esta manera, en cada circunstancia se puede encontrar una recomendación adecuada de forma rápida.
1 En el subapartado 1 de este capítulo se estudian algunas de las métricas más habituales.
1 En el subapartado 2 se describen algunas estrategias sencillas para construir recomendadores.
2 En el subapartado 3 se presentan los métodos de agrupamiento más importantes.
3 Las distancias y similitudes se utilizan en gran cantidad de métodos, por lo que en este capítulo se presentan
otras métricas como la distancia de Hamming en el subapartado 3.1 y la información mutua en el subapartado 1.3.
4 Segura porque no incurre en divisiones por cero si la distancia es cero.
5 En el fichero u.data cada valoración aparece en una fila, y las columnas son IdUsuario IdPelícula Valoración Fecha.
6 La distancia euclídea es una métrica útil en numerosas aplicaciones, en especial si las magnitudes son lineales y su escala es uniforme; además, es sencilla y rápida de calcular.
7 El coeficiente de correlación de Pearson sólo mide relaciones lineales; aunque valga 0, puede haber relaciones no lineales entre las dos variables.
8 O diagrama de árbol, del griego dendron, árbol, y gramma, dibujo.
9 Los valores y vectores propios de una matriz y su obtención con Python están explicados en el subapartado 1.1.
10 La laplaciana calculada en el algoritmo de agrupamiento espectral se trata de la laplaciana no normalizada.
Existen otras dos laplacianas aplicables en agrupamiento espectral, la simétrica y la de recorrido aleatorio; en muchos casos su comportamiento es equivalente.
11 Véase el apartado 2 del capítulo V en adelante.