Fins aquest moment s’ha estudiat essencialment una sola forma de programar una sèrie de càlculs repetitius de forma mecànica: els algorismes iteratius. Aquests sóon els algorismes que, en llenguatge de programacioó C, escrivim fent servir les instruccions while, for, i do−while.
En aquest tema es veurá una nova forma de programar cálculs repetitius, els anomenats algorismes recursius. D’aquesta forma disposarem de diferents técniques d’on escollir quan vulguem escriure un algorisme. Hi ha casos en que és més apropiat fer servir una técnica, però n’hi ha d’altres en que òs millor fer servir l’altre. És per aquesta raó que cal entendre ambdues técniques de programació de forma que es pugui escollir la més adient per a cada cas.
La referéncia bibliogràfica bàsica per preparar aquest tema la podeu trobar a [Wir80], capÍtol 3.
En general, es diu que un objecte és recursiu quan es defineix en funcioó de si mateix. El concepte de recursivitat es fa servir amb molta frequüència en el camp de les matemàtiques. Vegem uns quants exemples.
Exemple 1.1.1. Els números naturals es defineixen de la seguüent forma: (1) 1 és un número natural; i (2) el seguüent d’un número natural és també un número natural. Vegem com aquesta definició és, efectivament, recursiva, ja que per tal de definir el que és un número natural estem fent servir, de fet, el concepte de número natural.
Exemple 1.1.2. La funció n! per calcular el factorial d’un nómero natural n qualsevol es defineix
Aquest exemple és també clarament recursiu, ja que la definició del factorial fa servir la pròpia funció factorial.
Exemple 1.1.3. La suma de dos números naturals també es pot definir de forma recursiva. Suposem, igual que hem fet a l’Exemple 1.1.1, que disposem d’alguna forma de saber quin és el següent i també el predecessor d’un natural n. Sota aquestes condicions, la suma de dos naturals, a i b, es pot definir recursivament:
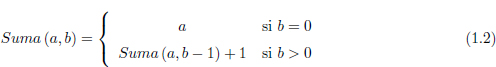
Vegem també com la suma ve definida en funció d’ella mateixa.
És important observar com en tots els exemples anteriors les definicions recursives sempre presenten dues parts clarament diferenciades. Per una banda tenim un cas trivial o elemental del càlcul, com per exemple el factorial de 0 (que ßs 1), o la suma de a+0 = a. Desprßs tenim la part pròpiament recursiva de la definició. És important veure com en aquesta segona part es defineix el problema inicial, per exemple Suma(a, b), en funció d’una versió més ‘senzilla’ del mateix problema. En aquesta cas, és més senzill calcular Suma(a, b − 1) que no pas Suma(a, b). Per aquest motiu Suma(a, b) es defineix en funció de Suma(a, b − 1). A més a més, cal veure que si seguim aplicant reiteradament aquesta segona part de la definició el valor del segon paràmetre b pren cada cop un valor menor. És a dir, si en aquest exemple apliquéssim la definició recursiva diversos cops obtindríem:
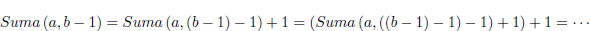
D’aquesta forma ens assegurem que en algun moment haurem de calcular Suma(a, 0), el qual és, precisament, el cas trivial de la definició. Per tant en algun moment arribarem a fer servir la part trivial del càlcul, la qual no requereix la utilització de recursivitat. Podem estar segurs, doncs, que no estarem aplicant la definició recursiva de forma indefinida.
1.2 Principis dels algorismes recursius
Per tal d’escriure problemes recursius correctament cal raonar d’una forma anàloga a com es fa quan s’aplica el Principi d’Inducció per demostrar una determinada propietat sobre els naturals. Recordem que el principi d’inducció ens permet demostrar una propietat P sobre els números naturals de la següent forma:
Base d’Inducció Cal demostrar que la propietat és vàlida per a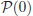 
.
Pas d’Induccioó Si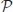 
és vàlida per a un natural, també ho és pel següent.
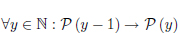
• Si es demostren aquests dos passos, llavors sabem que la propietat 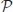és certa per a qualsevol natural, 
.
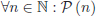Recordem amb un exemple senzill com s’aplica aquest principi.
Exemple 1.2.1. Demostrar per inducció que
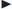Solució.
Aixíí doncs, la propietat que volem demostrar és
Comencem per la base d’inducció:
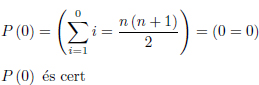
Ara, pel que fa al pas d’inducció, suposem que és cert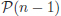 
, és a dir, suposem que efectivament
i volem demostrar que també és cert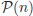 
. La suposició de que 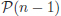és cert s’anomena Hipòtesi d’Inducció.
Així doncs tenim:
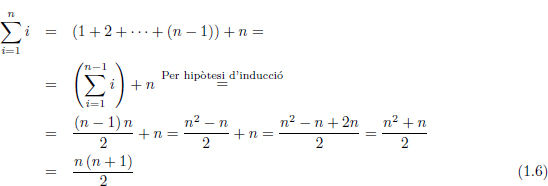
Algorisme 1.1: Funció Factorial(n) - versió recursiva
tal i com volíem demostrar. Hem satisfet les dues parts de la demostració pel Principi d’Inducció. Per tant podem estar segurs que, per a qualsevol número n natural, sempre és certa l’Equació 1.3.
Pels objectius d’aquest tema, el més important d’aquesta demostració és el fet que hem suposat que la propietat era certa per a un determinat valor, i hem demostrat que si es així també ha de ser cert pel següent valor.
Resumint, quan fem servir el Principi d’Inducció ens cal:
1. Un cas base, o trivial de comprovar.
2. Demostrar que si la propietat és certa per un cas concret també ho és pel següent.
És interessant veure la semblança d’aquests dos casos amb el que s’ha explicat a la secció anterior, quan s’han donat uns quants exemples de definicions recursives (suma, factorial). En tota definició recursiva, també, ha d’haver-hi un cas elemental de càlcul, juntament amb la definició pròpiament recursiva. A més, la definició recursiva es realitza en funció d’una versió més ‘senzilla’ del problema (que en aquest context equival, d’alguna forma, al seu valor anterior ).
1.3 Programació amb recursivitat
A programació també es fan servir definicions recursives. Diem que una funció o una acció és recursiva quan conté una crida a si mateixa. Vegem l’exemple prototípic que es fa servir amb frequüència per explicar la recursivitat: el càlcul del factorial d’n.
Exemple 1.3.1. Escriure una funció que pren com a paràmetre d’entrada un número natural n qualsevol, i retorna el valor del factorial d’n (n!).
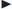Solució.
L’algorisme 1.1 mostra una possible solució a aquest exemple. Aquesta funció s’ha escrit directament a partir de la definició recursiva donada anteriorment pel factorial (Exemple 1.1.2, pàgina 9). El funcionament d’un algorisme recursiu es pot entendre seguint, pas a pas, la seva execució. Per exemple, si es vol calcular el factorial de zero (0), i per tant es crida a Factorial (0), la funció avaluarà la senténcia condicional (línia 2). El resultat serà cert, i per tant senzillament es retornará 1. Així doncs, per aquest algorisme, Factorial (0)=1, la qual cosa és consistent amb la definició del factorial donada a l’Exemple 1.1.2.
Per altre banda, si es volgués calcular el factorial d’algun altre número, per exemple n = 1, es cridaria inicialment a Factorial (1). La comparació d’n amb 0 retornaria fals, i per tant s’executaria la segona branca del condicional (línia 5). Per tal d’avaluar l’expressió n∗Factorial(n–1) caldria fer una crida a Factorial (0), es a dir, que la funció es crida a si mateixa, però amb un valor del paràmetre n (en aquesta cas 0) més petit que el valor d’entrada (en aquest cas 1). Sabem pel paràgraf anterior que Factorial (0) retorna 1. Així doncs quan es retorna es pot avaluar n∗Factorial(n–1). En aquesta cas cal avaluar 1∗Factorial(0), que es equivalent a 1∗1=1. Aquest serà el valor retornat. Per tant Factorial (1) també retorna el valor 1.
El mateix raonament es pot fer per altres valors d’n. Si, per exemple, es fes la crida Factorial (2), caldria avaluar 2∗Factorial(1). En aquest cas es farien dues crides recursives, primer Factorial (1) i després Factorial (0). Sabem pel paràgraf anterior que Factorial (1)=1, i per tant es pot veure com Factorial (2)=2. Tots aquesta valors sòn consistents amb el que sabem d’n!.
Amb raonaments anàlegs als que s’han fet més amunt es podria veure l’execució d’aquest algorisme per a qualsevol n.
El més important a notar en aquest primer exemple d’algorisme recursiu és que està format per les dues mateixes parts amb que construïm les demostracions quan fem servir el Principi d’Inducció (veure Exemple 1.2.1). És a dir, en aquesta algorisme recursiu també podem identificar:
1. Un cas base o trivial de calcular, que en aquest cas és el càlcul 0! = 1.
2. Suposar que la funció fa el càlcul correctament per a n– 1, és a dir, que la crida recursiva retorna el valor correcte pel seu paràmetre. després l’algorisme ha de fer les operacions apropiades sobre el resultat de la crida recursiva ( Factorial (n–1)) per tal de obtenir el resultat correcte pel parámetre n. En aquest cas l’operaciò necessária (multiplicar per n) s’ha deduït a partir de la definició del factorial, Exemple 1.1.2.
Al cas base l’anomenarem Base de Recursivitat i, en general, podrem tenir més d’una base de recursivitat per a un algorisme concret.
Però, per què serveix la recursivitat, al cap i a la fi l’algorisme pel factorial, per exemple, també es pot escriure de forma iterativa? Com veurem a la Secció 1.7, tot algorisme recursiu es pot escriure de forma iterativa, i tot algorisme iteratiu es pot escriure de forma recursiva. La principal justificació per l’estudi de la recursivitat és el fet de que alguns algorismes sòn més clars i intuïtius si s’escriuen recursivament. Per aquesta raó és necessari saber aplicar aquesta tècnica de programació, i també quan és apropiat aplicar-la. El principal inconvenient de la recursivitat és que les successives crides recursives consumeixen més recursos, com per exemple temps d’execució i memòria, que quan s’implementa el mateix algorisme de forma iterativa.
1.3.1 Model de les Còpies d’un programa recursiu
L’estudi dels algorismes recursius produeix una certa confusió quan s’estudia per primer cop. El seu funcionament, amb molta frequüència, és un poc obscur fins que no s’han estudiat, i intentat d’escriure, diversos algorismes d’aquest tipus [DCP01, Geo02, Geo00, AVI00]. La seva comprensió mitjançant el Principi d’Inducció, tal i com s’ha presentat abans, no és de gaire ajut si no es té una intuïció matemàtica sòlida sobre el funcionament d’aquest principi. Tot i que per escriure un algorisme recursiu el més adient és aplicar un raonament anàleg al que es fa servir quan s’aplica el Principi d’Inducció, aquest no sempre és el mecanisme més apropiat per entendre el funcionament de la recursivitat.
Aquesta Secció descriu breument una forma alternativa d’interpretar una funció (o acció) recursiva, l’anomenat Model de les Còpies. Amb aquest es pretén contribuir a la creació del model mental apropiat que faciliti la comprensió inicial de la recursivitat.
Prenguem un altre cop l’exemple de la funció del factorial donada a l’Exemple 1.3.1, pàgina 12. És útil imaginar-se que, internament, cada cop que es fa una crida recursiva es crea automàticament una còpia de la funció recursiva, però amb el paràmetre apropiat. Vegem un exemple concret del model de les Còpies.
Suposem que es vol calcular Factorial (4). Podem imaginar que, internament, un computador hauria de crear algun tipus d’informació com el que es veu a la Figura 1.1.
Per tal de calcular el factorial de 4, però abans s’ha de calcular el factorial de 3. Això requereix doncs una crida recursiva, però aquest cop amb valor del paràmetre n = 3. Quan es fa una crida recursiva es pot pensar com si es creés una nova còpia de la funció amb un valor diferent pel paràmetre, tal i com es mostra a la Figura 1.2. De forma similar es pot pensar com si es creessin una sequüència de Còpies de la funció, una per a cada crida recursiva. La Figura 1.3 mostra totes les Còpies per aquest exemple concret. Ja que el paràmetre n de la funció decreix a cada crida recursiva, podem estar segurs que en algun moment el paràmetre serà n = 0 i per tant en lloc d’entrar per la part “sino” del condicional l’execució passará per la part “si”, en la qual no es fa crida recursiva, i per tant la cadena de crides recursives s’acabará. És en aquest punt quan la sequüència comença a retornar el resultat de cada una de les Còpies. Al final de tot la primera de les Còpies, Factorial (4), també retornará el seu resultat final. Aquest fet es mostra a la Figura 1.4.
Figura 1.1: còpia de la funció Factorial(n) per a n = 4
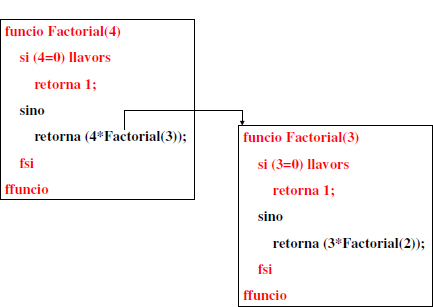
Figura 1.2: sequüència de Còpies de la funció Factorial(n) per a n = 4 i n = 3
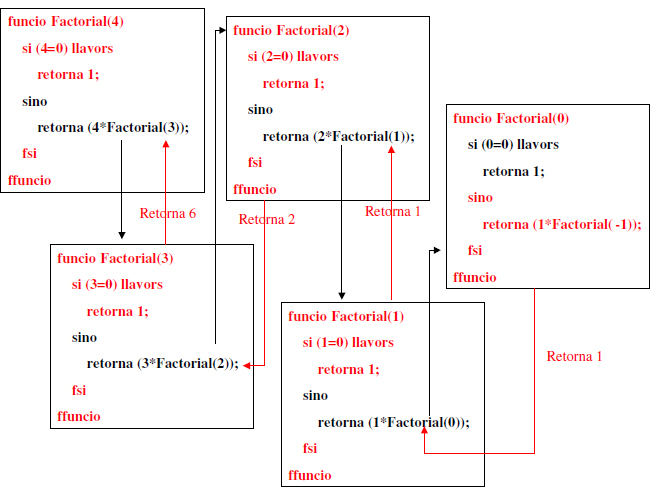
Figura 1.3: sequüència de Còpies de la funció Factorial(n) per a n = 4, 3, 2, 1, 0
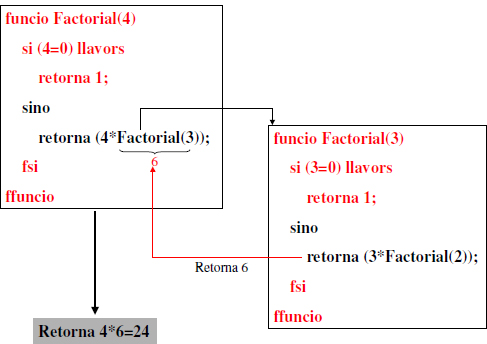
Figura 1.4: Resultat final de la sequüència de Còpies generada per Factorial(n) per a n = 4
És important entendre que, en realitat, internament en el computador no es generen noves Còpies d’un algorisme recursiu cada cop que es fa una crida recursiva. El model de les Còpies pretén ser, únicament, un instrument que faciliti la comprensió del concepte de la recursivitat. L’execució real d’un algorisme recursiu en un computador s’estudiará en altres assignatures d’aquests estudis (Computadors II).
1.4 Exemples d’algorismes recursius
Vegem uns quan exemples més d’algorismes recursius.
Exemple 1.4.1. Escriure una funció recursiva per calcular la suma de dos números naturals, suposant que només sabem com calcular el successor (+1) i el predecessor (-1) d’un número, tal i com s’ha definit a l’Exemple 1.1.3.
Solució.
L’algorisme següent mostra una possible solució a aquest problema, fent servir la definició recursiva de la suma que s’ha donat a l’Exemple 1.1.3.
Aquesta algorisme resulta de la transformació directe de la definició de l’Exercici 1.1.3, escrita en forma algorísmica.
Exemple 1.4.2. Escriure una funció recursiva per calcular el producte de dos números naturals, fent servir la funció suma de l’Exemple 1.4.1.
Solució.
L’algorisme següent mostra una possible solució a aquest problema.
Exemple 1.4.3. La successió de Fibonacci es defineix de la següent forma:
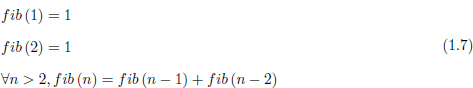
Algorisme 1.2: Funció Fibonacci(n)
Fent servir aquesta definició, escriviu una funció recursiva que, donat un número n natural, calculi el terme n-èssim de la successió.
Solució.
L’algorisme 1.2 mostra una possible solució a aquest problema, aplicant directament la definició de la funció que s’ha donat a l’enunciat.
Aquest exemple presenta una característica que no hem vist fins ara. Apart de les dues bases de recurrència que presenta (per n = 1 i n = 2), cal observar que es fan dues crides recursives a dintre la funció (per n – 1 i n – 2), i no només una com fins ara. Quan un algorisme fa només una crida recursiva, s’anomena algorisme amb recursivitat simple. En canvi, quan es fa més d’una crida, com es el cas d’aquest algorisme Fibonacci(n), s’anomena recursivitat múltiple.
Exemple 1.4.4. Escriure una funció recursiva per calcular la suma dels elements d’una vector de naturals de mida donada.
Solució.
Els paràmetres d’aquesta funció han de ser el vector que conté els elements a sumar, i la mida d’aquest vector, tal i com es mostra a l’Algorisme 1.3. Per conveniència, també es crea una funció auxiliar (SumaVectorRecursiva()) amb un paràmetre addicional, el qual representará la posició de l’element del vector que s’ha d’afegir a la suma total. Aquest paràmetre prendrá els valors des d’1 fins a midaV ector. Per tal de poder donar el valor inicial, 1, a aquest paràmetre s’ha creat aquesta funció auxiliar.
La funció auxiliar utilitzada en aquest exemple s’ha fet servir únicament per raons, diguem-ne, estètiques. És raonable esperar que si volem escriure aquesta funció per a un ‘client’, el més normal és que amaguem certs detalls de implementació. El fet que la funció sigui recursiva és certament un detall de implementació. Concretament, el segon paràmetre de SumaVectorRecursiva(), anomenat posicio, és necessari només perquè estem realitzant una implementació recursiva. Una forma de amagar aquesta fet consisteix en oferir la funció SumaVector() al ‘client’, la qual no requereix aquest paràmetre i senzillament realitza la crida inicial a SumaVectorRecursiva().
Algorisme 1.3: Suma del elements d’un vector - versió recursiva
Com en qualsevol algorisme recursiu, és necessari fer la crida recursiva amb paràmetres que representin un versió ‘més senzilla’ del mateix problema. És més senzill sumar n – 1 elements del vector, que no pas n elements. Aquesta idea és precisament la que s’ha aplicat en la crida recursiva d’aquest algorisme (línia 13).
Exemple 1.4.5. Escriure una acció recursiva per mostrar la representació binària d’un número natural.
Solució.
El mecanisme de canvi de base ja el coneixeu. El que cal fer és anar prenent els restes de la divisió entera del número entre 2. L’Algorisme 1.4 mostra una possible solució. En aquest cas, l’operaciò n mod 2 representa el reste de la divisió entera d’n entre 2. El quocient d’aquest reste es representa com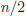 
. també s’ha fet servir una nova funció, Mostrar(), únicament per indicar el fet de mostrar alguna informació per pantalla.
Igual que en els exemples anteriors, en aquest cas també s’ha escrit la funció fent una crida recursiva amb paràmetres que representen una versió ‘més senzilla’ del problema. Concretament s’ha fet servir un valor d’n menor, el resultat de calcular 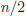. A més a més, la base de recursivitat es dóna quan el parámetre pren el valor més petit dins del conjunt dels naturals: 0.
Es pot observar que aquest algorisme s’ha escrit com a una acció, i no com a una funció. Aquest algorisme no ha de retornar cap valor, senzillament mostrar el resultat per pantalla. Amb conseqüéncia s’ha fet servir una acció.
Algorisme 1.4: Presentació binària d’un natural
1.5 Finalització de la sequüència de crides recursives
Com ja s’ha il·lustrat repetidament en els exemples anteriors, per tal de escriure apropiadament un algorisme recursiu el raonament necessari és anàleg al que es fa servir en el Principi d’Inducció. Així, sempre cal tenir una o més Bases de Recursivitat, o casos trivials, en els quals no hi ha crida recursiva. Pel que fa a la part de l’algorisme que realitza les crides recursives sempre s’escriu suposant que l’algorisme és correcte per un valor dels paràmetres anterior, i es programa el que calgui fer per tal que també sigui correcte pel valor actual dels paràmetres.
Un algorisme recursiu genera una sequüència de crides recursives les quals acaben únicament si en algun moment es satisfá alguna base de recursivitat. Per tant, per tal d’escriure un algorisme recursiu correcte, cal assegurar-se que sempre s’arriba a alguna de les bases de recursivitat de l’algorisme.
Exemple 1.5.1. Vegem com el programa mostrat a l’Algorisme 1.5 per a tot n > 0 genera una seqüència de crides recursives infinites, i per tant el programa mai no acaba. Aquest pseudocodi no representa un algorisme correcte.
Imaginem-nos que podem establir algun tipus d’ordre entre els paràmetres de la crides recursives, de forma que a cada crida els paràmetres prenguin valors menors dins d’aquest ordre. Imaginemnos, també, que les bases de recursivitat representen els valors més petits dins d’aquest ordre. Sota aquestes suposicions, podem estar segurs que l’algorisme recursiu sempre acaba, ja que siguin quin siguin els valors dels seus paràmetres inicialment, aquests aniran reduint-se fins arribar a alguna base de recursivitat.
Algorisme 1.5: Funció Factorial Incorrecte
Per exemple, en el cas de la crida Factorial (5) a l’algorisme mostrat a l’Exemple 1.3.1, el paràmetre és n = 5 i per tant els valors que pren a cada crida recursiva sòn, respectivament, n = 5, 4, 3, 2, 1, 0. És trivial veure que, efectivament, aquests valors estan ordenats 0 ≤ 1 ≤ 2 ≤ 3 ≤ 4 ≤ 5. A més, la base de recursivitat d’aquest algorisme és, precisament, n = 0, el qual representa el número més petit dins d’aquest ordre. Per aquesta raó sabem que aquest algorisme sempre acaba.
Alternativament, considerem l’Exemple 1.5.1. En aquest cas FactIncorrecte(5) genera la seqüència de crides recursives amb valors pel seu paràmetre n = 5, 6, 7, 8, 9, . … És clar que en aquest cas els valors no tendeixen cap a la base de recursivitat. Per aquest motiu, aquest ‘algorisme’ (de fet, com que no acaba, no es pot anomenar algorisme) genera una seqüència infinita de crides recursives. Aquest programa, doncs, mai no acaba si n > 0. El problema en aquest cas és que les crides recursives no es realitzen amb valors ‘menors’ del paràmetre dintre de l’ordre definit entre els valors del paràmetre de les crides.
Sabem com interpretar l’ordre entre els paràmetres en el cas més senzill: quan tenim només un parámetre de tipus natural. Pero, què passa en el cas general, en que podem tenir qualsevol nombre de paràmetres de qualsevol tipus de dades? En aquests casos hem de ser capaços de establir, també, una relació d’ordre entre els paràmetres. Concretament, hem de poder definir el que s’anomena una Relació de Pre-Ordre. Com recordareu, una relació R entre elements d’un conjunt A és de pre-ordre si és:
Reflexiva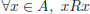 
Transitiva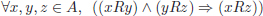 
Una relació R que és de pre-ordre es denota normalment fent servir el símbol ‘≤’.
En el cas de l’algorisme del factorial és trivial comprovar que la relació entre els valors del paràmetre de les successives crides recursives és de pre-ordre. En aquest cas es tracta de l’ordenació entre números natural, que ja sabem que és de pre-odre. Vegem ara uns exemples un poc més complexos.
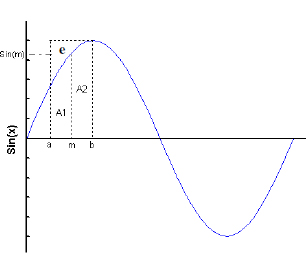
Figura 1.5: Integració numèrica pel Mètode del Trapezi
Exemple 1.5.2. Escriure una funció que calculi l’integral entre a i b del sin(x), fent servir l’anomenat Mètode del Trapezi.
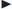Solució.
El Mètode del Trapezi és únicament una forma de dividir en subproblemes més senzills el problema de calcular una integral definida. Si [a, b] és l’interval d’integració, l’integral entre a i b també es pot calcular com la suma de la integral a [a, m] més la integral a [m, b], on m és el punt mig entre a i b.
És a dir:
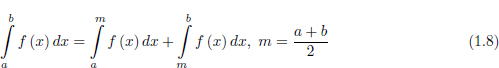
Aquesta relació es pot observar gràficament a la Figura 1.5. Tenint present que la integral representa l’àrea per sota de la corba, cal observar que si la distància entre a i b és prou petita, la seva integral es pot aproximar per l’àrea d’un rectangle de base b − a i al¸cada sin(m):
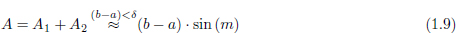
És a dir, que quan a i b sòn prou propers l’error ε comès fent aquesta aproximació es pot considerar negligible.
Ara ja estem en condicions d’escriure l’algorisme que calcula la integral entre a i b de sin(x), el qual es mostra a l’Algorisme 1.6. Com es pot observar, la base de recusivitat es dóna precisament quan aproximem l’integral per l’àrea d’un rectangle. Aquest cas no requereix cap crida recursiva. En canvi, si la distància entre a i b és massa gran, es fan dues crides recursives, una per calcular la integral entre a i m, i l’altre entre m i b. Cal notar que el mateix criteri es torna a aplicar, i per tant si la distància entre a i m és massa gran, l’interval es tornarà a dividir en dues parts iguals, i es tornaran a fer dues crides recursives més, i Així successivament.
Algorisme 1.6: Integral del sin(x) pel Mètode del Trapezi
Com podem saber si la seqüència de crides recursives generada per aquesta algorisme realment acaba? Els paràmetres de les crides recursives sòn parelles de números reals. Per tant hem de poder definir una relació de pre-ordre entre aquestes parelles, i comprovar que tal i com està escrit aquest algorisme els valors dels paràmetres a les crides satisfan aquesta relació. Per començar, definim la relació de pre-ordre de la següent forma:
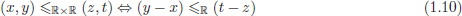
on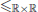 
denota la relació entre parelles de reals, que és el que volem definir, i 
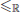denota la relació d’ordenació entre números reals, la qual ja coneixem. El que fa aquesta definició és considerar que una parella de números reals és menor que una altre si la distància entre els dos números de la primera parella és menor que la distància entre els de la segona. Sabent que el nostre algorisme segueix fent crides recursives, precisament, fins que la distància entre a i b és prou petita, es pot veure que aquesta definició sembla prou adequada.
És fàcil comprovar que, efectivament, la relació 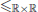és reflexiva i transitiva, ja que sabem que la relació 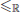sí que ho és.
Ara, però, falta comprovar que els valors dels paràmetres de les crides recursives a l’algorisme satisfan aquesta relació de pre-ordre, és a dir, que ca cada crida recursiva es fa servir un valor més
petit dintre d’aquest pre-ordre:
Així doncs, els paràmetres de les crides satisfan aquesta relació de pre-ordre (anàlogament per (m, b) 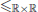(a, b)). La base de recursivitat es satisfá quan a i b estan molt properes, b − a < δ, i aquesta condició representa un mínim dintre del pre-ordre. Per tant podem estar segurs que la seqüència de crides recursives sempre acaba.
Exemple 1.5.3. Escriure una funció recursiva que, donats dos números naturals D i d, retorni el quocient i el reste de dividir D entre d. Considereu que, en el llenguatge pseudocodi utilitzat, és possible que una funció retorni una tupla de valors (en lloc d’un únic valor com és el cas més comú). És a dir, la vostra funció ha de tenir la següent signatura:
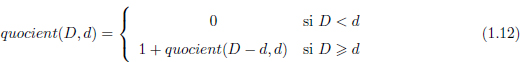
Considereu que només podeu fer servir operacions de suma i resta.
Solució.
Primer de tot cal definir el càlcul del quocient i el reste en funció de sumes i restes. Ja sabem que el quocient, q, de D entre d representa quants cops es pot restar d de D, tal i com es mostra a l’equació 1.12.
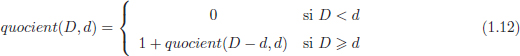
Quan s’arriba a la base de recursivitat, D < d, cal veure que obtenim els valors q := 0 i r := D. A partir d’aquesta informació ja podem escriure la funció recursiva, la qual es mostra a l’Algorisme 1.7.
Per entendre el funcionament d’aquesta funció, vegem la seva execució, pas a pas, per a uns paràmetres concrets, per exemple DIV(15,9). Ja sabem d’entrada que el resultat ha de ser < 2, 3 >, ja
Algorisme 1.7: Quocient i reste de la divisió entera
que el quocient de 15 entre 9 és 2, i el reste 3. A l’equació 1.13 es mostra l’evolució dels paràmetres i les variables locals per a cada una de les tres crides recursives que sòn necessàries en aquest cas concret.
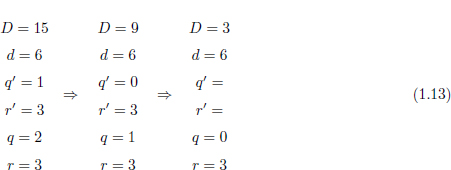
Pel que fa a la relació de pre-ordre entre els paràmetres de les crides recursives que ens assegura que l’algorisme sempre finalitza, aquesta es pot definir com es mostra a l’Equació 1.14.
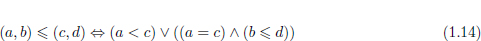
Aquesta relació compara, primer, les primeres components de la parella. Si no sòn iguals, doncs n’hi ha prou només amb aquestes components per saber quina parella és la més gran. Si les primeres components sòn iguals, llavors és necessari comparar les segones.
Tal i com s’ha fet a l’Exemple 1.5.2, es podria fer servir aquesta definició de pre-ordre, juntament amb l’algorisme DIV(), per demostrar que els paràmetres de la seqüència de crides generades per aquest algorisme satisfan la relació de pre-ordre.
Així doncs, a partir dels exemples anteriors es pot veure com tot i que per escriure algorismes recursius ens inspirem en un raonament anàleg al que es fa servir pel Teorema d’Inducció, la correctesa d’un algorisme també es pot garantir tot i que els paràmetres de les crides recursives no siguin un sol número natural. En general, per tal que un algorisme recursiu sigui correcte, ha de ser possible definir una relació de pre-ordre per a qualsevol tipus de dades, de forma que ens assegurem que la seqüència de crides recursives sempre finalitza.
A partir dels exemples anteriors hem pogut distingir dos tipus de recursivitat diferents. La majoria dels exemples ( Factorial (n), Suma(a,b), SumaVector(V,m), etc.) fan servir el que s’anomena Recursivitat Simple. Això vol dir que els algorismes fan únicament una crida a sí mateixos, és a dir, que només es fa una crida recursiva.
En canvi, també és possible escriure un algorisme que faci més d’una crida recursiva. En aquest cas es diu que aquests algorismes tenen Recursivitat Múltiple. Aquest és el cas de l’Exemple 1.5.2 en que es calcula la integral de sin(x) a [a, b] pel Mètode del trapezi, i també l’Exemple 1.4.3 per calcular la successió de Fibonacci. Aquests algorismes realitzen dues crides recursives. En general és possible escriure un algorisme que faci tantes crides recursives com sigui necessari. L’Exercici 1.25, per exemple, proposa un algorisme en el que es fan n crides recursives.
Apart del nombre de crides recursives utilitzades, els algorismes recursius també es poden classificar en funció de si la crida recursiva es fa de forma directe o indirecte. El primer cas és el de tots els exemples que hem vist fins ara, en que una funció (o acció) es crida directament a si mateixa. Per Això s’anomena recursivitat directe. Conceptualment, però, també és possible que una funció F(x) cridi a una funció diferent G(x), la qual crida a F(x). En aquest cas es té recursivitat indirecte, ja que F(x) es crida a si mateixa, tot i que sigui indirectament per mitjà de G(x).
La Figura 1.6 resumeix tots aquests tipus de recursivitat diferents, juntament amb les seves possibles combinacions.
1.7 Transformació d’algorismes recursius en iteratius
Tot algorisme recursiu sempre es pot transformar en un algorisme iteratiu i, recíprocament, tot algorisme iteratiu es pot escriure de forma recursiva. Alguns algorismes sòn més fàcils d’entendre si s’escriuen de forma iterativa, però d’altres resulten més intuïtius si s’escriuen recursivament. Per tant cal ser capa¸c de fer servir qualsevol dels dos tipus d’algorismes, i de saber en quins casos és millor un o l’altre.
L’inconvenient més important de la recursivitat és que introdueix la necessitat de realitzar una sèrie de crides recursives, amb el cost computacional que això suposa. Imaginem, per exemple, el Model de les Còpies descrit a la Secció 1.3.1. La creació de cada còpia requereix d’una certa quantitat de memòria i d’un cert temps de processament. Així doncs, pot ser interessant saber transformar un algorisme recursiu en un algorisme iteratiu equivalent per tal de millorar l’eficiència.
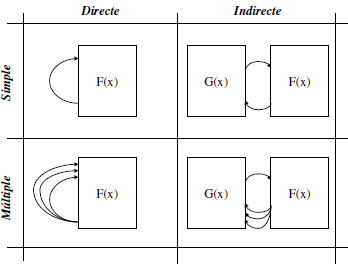
Figura 1.6: Tipus d’algorismes recursius
La transformació d’algorismes recursius en iteratius, en general, pot ser complex. Hi ha alguns casos, però, en que és forc¸a senzill i es pot realitzar de forma mecànica. Per exemple, considerem que disposem d’un algorisme recursiu,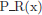 
, que té la forma següent:
on B(x) és la condició que avalua si es dóna o no la base de recursivitat, S és l’acció corresponent a la base de recusivitat, T(x) és la transformació necessária sobre els paràmetres d’entrada que assegura la relació de pre-ordre entre els valors dels paràmetres, i S′ és l’acció realitzada sobre el resultat de la crida recursiva. Cal notar que la majoria dels exemples de recursivitat simple que s’han vist en aquest tema segueixen aquesta estructura. Per exemple, en el cas de l’algorisme del Factorial (n) mostrat a l’Exemple 1.3.1 tenim que B(x) és la condició n = 0 (línia 2 a l’Algorisme 1.1), S és l’acció de retornar 1 (línia 3 a l’Algorisme 1.1), T(x) és el càlcul de n − 1 (línia 5), i S′ consisteix en multiplicar el resultat de la crida recursiva per n (línia 5).
Algorisme 1.8: Funció Factorial(n) - versió iterativa
En els casos d’algorismes recursius amb aquesta estructura la seva transformació en un algorisme iteratiu equivalent es pot fer de forma mecànica sabent que l’algorisme resultant ha de tenir l’estructura següent:
Exemple 1.7.1. Transformar en iteratiu l’algorisme de l’Exemple 1.3.1 per calcular Factorial (n).
Solució.
Aplicat l’esquema anterior s’obté directament l’Algorisme 1.8. Únicament és necessari identificar els components S, B(x), T(x), i S′ de l’algorisme com s’ha escrit abans, i reescriure l’algorisme seguint l’esquema per a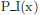 
.
Exemple 1.7.2. Transformar en iteratiu l’algorisme de l’Exemple 1.4.4 per calcular la suma dels elements d’una vector.
Solució.
Es pot veure que l’algorisme iteratiu funcionalment equivalent per aquest cas és el mostrat a l’Algorisme 1.9. Per obtenir aquest algorisme s’han aplicat directament els esquemes donats abans per a P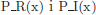 
.
Algorisme 1.9: Suma del elements d’un vector - versió iterativa
Els exemples anteriors de transformació d’un algorisme recursiu en el seu equivalent iteratiu han estat exemples de recursivitat simple. En el cas de la recursivitat múltiple aquesta transformació és bastant més complexa. Per entendre el perquè, considerem el Model de les Còpies de la Secció 1.3.1 pel cas d’un algorisme amb recursivitat múltiple, com per exemple el que calcula el terme n-èssim de la successió de Fibonacci, tal i com s’ha explicat a l’Exemple 1.4.3. Si es volgués calcular Fibonacci (5), s’obtindria l’arbre de Còpies que es mostra a la Figura 1.7. Quan es va estudiar el model de les copies a la Secció 1.3.1 es va veure com la funció Factorial (n) generava una seqüència de Còpies de si mateixa. En el cas de Fibonacci(n), en canvi, obtenim un arbre (binari) en lloc d’una seqüència, perquè l’algorisme d’aquesta funció (veure Exemple 1.4.3, pàgina 18) realitza dues crides recursives, a Fibonacci(n–1) i Fibonacci(n–1) respectivament. A la Figura 1.7 les arestes que indiquen quines Còpies “crea” una copia donada estan etiquetades amb un número que indica l’ordre en que es fan les crides recursives durant la seva execució.
Considerem quèpassaria si es volgués transformar aquest algorisme en iteratiu. D’alguna forma mentre s’està calculant Fibonacci(4) caldrà “recordar” que després encara falta calcular Fibonacci(3) (etiqueta (6)). Anàlogament, mentre s’està calculant Fibonacci(3) (etiqueta (2)) caldrà “recordar” que en acabar s’ha tornar enrera i avaluar Fibonacci(2) (etiqueta (5)).
Així doncs, la transformació d’un algorisme amb recursivitat múltiple al seu equivalent iteratiu, en general, requereix d’algun mecanisme per “recordar” les Còpies de la funció que encara no han estat avaluades. Aquest fet, tot i ser possible, fa que l’algorisme sigui més complex.
Quan es fa servir recursivitat, en canvi, tot aquest procés de “recordar” les crides que encara resten per avaluar està implementat automàticament i per aquesta raó la implementació d’aquests algorismes és més senzilla i intuïtiva si es fa de forma recursiva que no pas de forma iterativa.
Figura 1.7: Model de les Còpies per a Fibonacci(5)
Per últim, de la discussió anterior no s’hauria de concloure que no és possible, per exemple, obtenir una implementació iterativa de la funció Fibonacci(n) que sigui senzilla. Com es pot veure a l’Exercici 2.3 existeix de fet una funció amb aquestes característiques. Això és degut, però, a les característiques específiques de la funció Fibonacci(n). La transformació a un algorisme iteratiu funcionalment equivalent, en aquest cas, no es realitza fent servir cap esquema general tal i com s’ha fet abans amb la funció Factorial (n).
Resumint, per tal d’escriure una algorisme recursiu correcte és necessari:
1. Identificar un o més casos trivials de calcular, anomenats Bases de recurrència, pels quals no es requereix realitzar cap crida recursiva.
2. Escriure un o més casos en que es fa una (o més) crida recursiva. Inspirant-se en el Principi d’Inducció, aquests casos s’escriuen suposant que l’algorisme és correcte pels valors dels paràmetres anteriors.
3. Assegurar-se que la crida (o crides) recursiva es fa de forma que els valors dels paràmetres de la seqüència de crides defineixen una relació de pre-ordre.
4. Tenir present que hi ha algorismes que és millor escriure’ls de forma iterativa, tot i que sigui possible fer-ho de forma recursiva. D’altres, tot i que es puguin escriure de forma iterativa, sòn més intuïtius i fàcils d’entendre si s’escriuen fent servir recursivitat.
Exercici 1.1. Escriure una definició recursiva per a la funció que calcula el producte de dos nombres naturals a i b. Pensa en quin (o quins) és el cas elemental del càlcul, o base de recursivitat, i quin és el cas recursiu.
Exercici 1.2. Escriure una funció recursiva per calcular el producte de dos nombres naturals, suposant que disposem de la funció Suma(a,b).
Exercici 1.3. Escriure una funció recursiva que pren com a paràmetre un número natural i retorna si aquest número és o no un número primer.
Exercici 1.4. Escriure una funció que retorni el nombre de nombres primers entre a i b donats com a paràmetres a la funció (a i b sòn números naturals). Primer de tot cal escriure una funció que retorni si un número qualsevol és o no primer. després, la funció que es demana, vista recursivament, es pot definir com es mostra a l’equació 1.15.
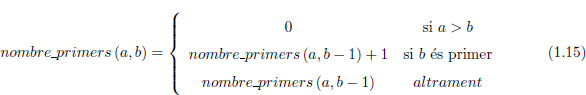
Exercici 1.5. Una cadena de caràcters s’anomena palíndroma (cap i cua) si es llegeix igual de dreta a esquerra que d’esquerra a dreta. Per exemple, la cadena “ABCAD” llegida de dreta a esquerra és “DACBA”. Aquesta cadena no és palíndroma. En canvi “ABCDCBA” sí que ho és.
1. Escriure una funció recursiva que, donada una paraula, retorni si és o no palíndroma.
2. Quina és la relació de pre-ordre entre el(s) paràmetre(s) de les crides que ens assegura que la seqüència de crides recursives sempre acaba?
Exercici 1.6. Escriure una funció que calculi el Màxim Comú Divisor (MCD) de dos nombres naturals fent servir l’anomenat Algorisme d’Euclides. La forma ‘tradicional’ de calcular el MCD requereix que es factoritzin els dos nombres en els seus factors primers, i després s’agafin els factors comuns de menor exponent. Com veurem, però, la factorització en nombres primers és un procés molt ineficient i per tant no és viable quan els nombres sòn molt grans. L’Algorisme d’Euclides no requereix la factorització dels nombres en els seus factors primers, i per tant és molt més eficient. Tot el que cal fer és calcular els restes de les següents divisions fins que un d’ells sigui zero. Siguin a i b els nombres dels quals volem calcular els seu MCD. Calculem els restes de les divisions següents:
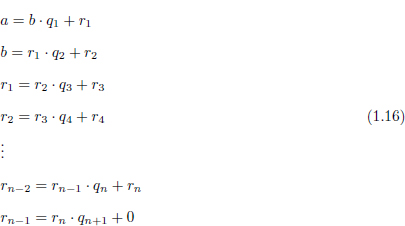
Essent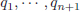 
els quocients i 
els restes de cada divisió. Així doncs els màxim Comú divisor d’a i b seria rn.
Per exemple, si calculéssim el MCD de 200 i 162 fent servir aquest algorisme, obtindríem:
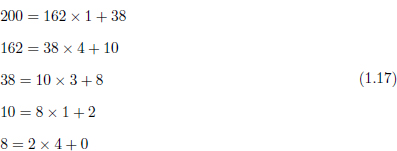
El MCD de 200 i 162 és, doncs, 2.
Exercici 1.7. Blaise Pascal, matemàtic del segle XVII, va demostrar que és possible calcular les potències de 2 fent servir la suma dels termes:
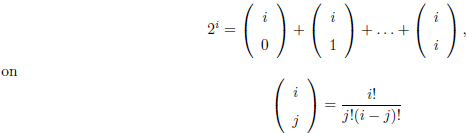
representa el nombre de possibles formes de seleccionar j objectes escollits d’entre un total d’i objectes, i n! és el factorial d’n.
Escriu una funció recursiva, EXPONENT(i, j), que pren i i j com a paràmetres d’entrada i calcula la suma dels termes:
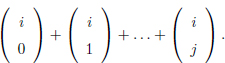
És a dir, EXPONENT(i, i) ha de calcular 2i.
Exercici 1.8. El producte escalar de dos vectors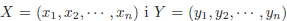 
es pot calcular com 
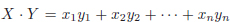. Per exemple, el producte escalar de X = (1, 2, 3) i Y = (4, 5, 6) és X · Y = 32.
1. Escriu una funció recursiva que calculi el producte escalar de dos vectors de nombres reals que es donen com a paràmetres d’entrada a la funció.
2. Quina és la relació de pre-ordre entre els paràmetres de les crides recursives que ens assegura que la cadena de crides recursives sempre acaba?
Exercici 1.9. Una forma de definir la norma d’un vector consisteix en calcular l’arrel quadrada de la suma dels quadrats de les seves components. Per exemple, la norma del vector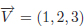 
seria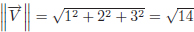 
1. Escriu una funció recursiva que calculi la norma del vector que es dóna com a paràmetre d’entrada a la funció. Pots suposar que disposes d’una funció per calcular l’arrel quadrada d’un nombre real.
2. Quina és la relació de pre-ordre entre els paràmetres de les crides recursives que t’assegura que la cadena de crides recursives sempre finalitza?
Exercici 1.10. Escriu una funció recursiva que determini si els elements d’un vector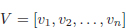 
formen una successió estrictament creixent.
La funció ha de retornar “cert” (1) si els elements satisfan la relació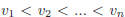 
, i “fals” (0) altrament.
Exercici 1.11. Escriu una funció recursiva que, donats dos vectors de nombres reals de la mateixa mida, calculi el resultat de sumar les components parells i restar les components senars.
Per exemple, considera els vectors V1 = (5, 2, 6, 4, 5) i V2 = (0, 2, 5, 4, 1), el resultat del càlcul de la funció seria:
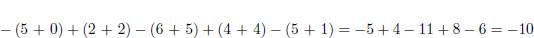
Exercici 1.12. Considera la següent funció:
1. Explica raonadament què retorna aquesta funció.
2. Estàs segur que aquesta funció sempre acaba? Quina és la relació de pre-ordre entre els paràmetres de les crides recursives que t’ho assegura?
Exercici 1.13. Considera la següent funció recursiva:
• Explica raonadament quèretorna la funció amb la crida Misteri(5).
Exercici 1.14. La fórmula tradicional per calcular la mitjana d’un conjunt de valors x1, …, xn és:
L’inconvenient d’aquesta fórmula és que cal sumar tots els valors abans de saber cap a quin valor tendeix la mitjana. Hi ha cops en que és interessant saber el valor de la mitjana tenint present només els k primers valors (per exemple, quan tenim valors molt grans d’n, diguem 500 milions, o potser perquè la resta de valors encara no es coneixen).
Tenint això present, la fórmula tradicional es pot transformar de la següent forma:
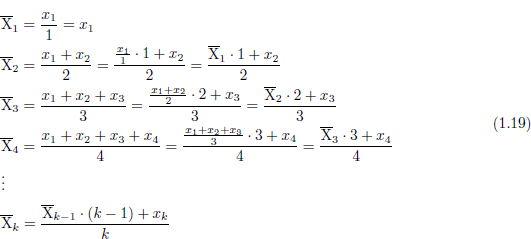
on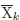 
és la mitjana calculada fent servir només els k primers valors. Podem veure que, efectivament, 
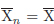, tal i com era de esperar. Així doncs podem obtenir una “aproximació” a la mitjana sense haver de sumar, primer, tots els elements.
Escriu una funció que, donats un vector X = (x1, x2, … , xn) de nombres reals i un valor k natural, retorni la mitjana dels primers k elements del vector fent servir aquest algorisme. Fes-ho o bé iterativament o bé recursivament, segons et sembli més apropiat, i justifica la teva decisió.
Exercici 1.15. Considera la funció següent:
1. Explica de forma raonada què retorna aquesta funció quan es fa la crida misteri (5,0). Identifica clarament quina és la seqüència de totes les crides recursives que es realitzen, i quins sòn els valors dels paràmetres en cada cas.
2. Transforma aquesta funció en una funció iterativa. És a dir, has de escriure una funció que calculi sempre els mateixos resultats que misteri () però sense fer crides recursives.
Exercici 1.16. Per a qualsevol nombre natural n, l’operaciò de ‘invertir i sumar ‘ consisteix en invertir els dígits d’n i sumar-hi el valor d’n. Per exemple, sigui n = 345. Invertint els seus dígits obtenim el número 543. Ara cal sumar n a aquest número, és a dir, n + 543 = 345 + 543 = 888.
Per a la majoria de nombres naturals aquest procés, repetit reiteradament, acaba produint un nombre que és cap i cua. Aquest algorisme s’anomena algorisme 196 , ja que 196 és el número natural més petit pel qual no es coneix que acabi produint un nombre cap i cua.
Escriu una funció recursiva que calculi (mostri per pantalla) la seqüència de nombres que es produeixen aplicant aquest algorisme. Per exemple, aplicat al número 59, es produeix la seqüència 59, 154, 605, i 1111, ja que (59 + 95) = 154, (154 + 451) = 605, i (605 + 506) = 1111. Pots suposar que la crida inicial a la teva funció es farà sempre amb un nombre pel qual, en algun moment, s’obté un nombre cap i cua.
Exercici 1.17. La suma i l’arrel digitals:
La suma digital d’un número natural és la suma dels seus dígits. Per exemple, la suma digital de 492 és 15, ja que 4 + 9 + 2 = 15.
L’arrel digital d’un número n s’obté calculant la suma digital d’n, la suma digital del número obtingut, i així successivament fins a arribar a un número amb un sol dígit (pel qual la suma digital és igual al propi número). Per exemple, l’arrel digital de 492 és 6, ja que la suma digital de 492 és 15, i la suma digital de 15 és 6.
Escriu una funció recursiva ArrelDigital() que prengui un número natural n com a paràmetre i retorni la seva arrel digital.
Exercici 1.18. Imagina que tenim N jugadors de cartes, i que han de jugar tots contra tots, en un joc de cartes que en cada partida enfronta 3 jugadors diferents.
Escriu una acció recursiva que mostra per pantalla totes les possibles partides que s’han de jugar, identificant els 3 jugadors que participen en cada partida. Pots suposar que els jugadors estan numerats d’1 a N.
Exercici 1.19. El desenvolupament de la sèrie de Taylor per a la funció del sinus és la següent:
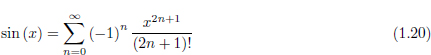
Escriure una funció recursiva per calcular el valor de la funció sin(x) en un punt concret x0 que es dóna com a paràmetre d’entrada. Es pot veure que aquesta sèrie és infinita. Es pot suposar que hi haurá un altre paràmetre d’entrada que indicarà quants termes de la sèrie cal sumar.
Exercici 1.20. Per definició, el número e és el resultat de la sèrie següent:
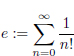
Escriu una funció recursiva que calculi el valor d’aquest número fent servir aquesta sèrie. Pots suposar que hi haurá un paràmetre a la funció que indicarà quants termes de la sèrie cal sumar.
Exercici 1.21. Escriure una funció recursiva per calcular el valor de la integral de la funció cos(x) entre dos números reals a i b que es donen com a paràmetres d’entrada.
• Com estructuraríeu el vostre algorisme si, en lloc de la funció cos(x), haguéssiu de calcular la integral per a qualsevol altre funció f (x)? Per exemple, considereu el mateix problema en el cas de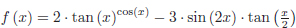 
.
Exercici 1.22. Considera la funció F() següent:
En aquesta funció s’han fet servir les funcions div, que retorna el quocient de la divisió entera dels seus paràmetres, i mod, que retorna el reste.
• Explica quècalcula la funció F().
Exercici 1.23. Considera la funció F() següent:
1. Analitza, pas a pas, quècalcula aquesta funció quan p = 0.
2. Analitza, pas a pas, quècalcula aquesta funció quan p = 1.
3. Analitza, pas a pas, quècalcula aquesta funció quan p = 2.
Exercici 1.24. Considera la funció següent:
1. Explica de forma raonada què retorna aquesta funció quan el paràmetre és n = 11?
2. Explica de formaraonada què retorna aquesta funció quan el paràmetre és n = 16?
Per exemple, les 3! = 6 permutacions dels elements {1, 2, 3} sòn:
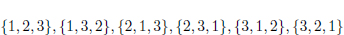
Cal notar que és sempre “més fàcil” mostrar les permutacions d’(N − 1) elements que no pas d’N elements. Així doncs les permutacions d’N elements es poden veure com a N tasques de permutar (N − 1) elements, un cop s’ha fitxat el primer element, de forma que al començar la ‘tasca’ i-èssima el primer element dels que s’han de permutar s’ha intercanviat amb ai.
Exercici 1.26. Suposa que has d’analitzar la correctesa d’una funció que suma els elements d’un vector amb la signatura següent:
on V és el vector que conté els elements que s’han de sumar, posicio representa cada una de les posicions del vector a mesura que es van sumant (comenc¸ant per 1), i midaVector és la dimensió del vector. Quina és la relació de pre-ordre entre els paràmetres d’aquesta funció que ens assegura que sempre acaba?
Exercici 1.27. Transformar a iteratiu l’algorisme proposat a l’Exercici 1.5 per decidir si una paraula és o no palíndroma (cap i cua).
Exercici 1.28. Escriure una funció iterativa que, donat un número n natural, calculi el terme n-èssim de la successió de Fibonacci, definida de forma recurrent per l’equació
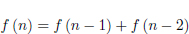
Exercici 1.29. Escriure una funció iterativa que, donats dos números naturals D i d, retorni el quocient i el reste de dividir D entre d. Primer cal escriure la versió recursiva de l’algorisme i després aplicar l’esquema de transformació d’algorismes recursius a iteratius.