1

 

LUCES, CÁMARA, ACCIÓN

 

 

 

Quizás una cosa es simple si puede describirse completamente de varias maneras diferentes sin saber inmediatamente que se está describiendo la misma cosa.

 

RICHARD FEYNMAN

 

 

¿Podría alguien haber sospechado, cuando Feynman era aún un niño, que este llegaría a ser quizás el más grande, y probablemente el más querido, de los físicos de la segunda mitad del siglo XX? No está tan claro, incluso aunque se dieran muchas señales incipientes. Sin duda era listo. Tenía un padre al que le gustaba educar y que lo entretenía con puzles y le infundió el amor por aprender, estimulando su curiosidad innata y alimentando su mente siempre que podía. Y tenía un juego de química y se mostraba fascinado con las radios.

Pero todo eso no era tan raro entre los jóvenes brillantes de la época. En los aspectos más fundamentales, Richard parecía ser un típico chico judío listo de Long Island que se crió después de la Primera Guerra Mundial, y es quizás ese simple hecho más que nada lo que coloreó su futuro lugar en la Historia. Su mente era extraordinaria, sí, pero él permanecía siempre anclado firmemente a la realidad, incluso cuando se dedicaba a explorar las esferas más esotéricas de nuestra existencia. Su desprecio a la pomposidad provenía de una vida temprana en la que no estuvo expuesto a ella, y su falta de respeto a la autoridad provenía no solo de un padre que alimentaba esta independencia sino también de una vida temprana en la que él era marcadamente libre para ser un niño, seguir sus propias pasiones y cometer sus propios errores.

Quizá la primera señal de lo que iba a venir fue la literalmente infatigable capacidad de Feynman para concentrarse en un problema durante horas, hasta el punto de que sus padres empezaban a preocuparse. De adolescente, Feynman hizo un uso práctico de su fascinación por las radios: abrió un pequeño local para repararlas. Pero, a diferencia de los reparadores convencionales, Feynman se deleitaba en resolver los problemas de la radio no meramente chapuceando, sino pensando.

Y combinaba esta notable capacidad para concentrar toda su energía en un problema con un talento innato como comediante. Por ejemplo, la anécdota más famosa de sus reparaciones es que en una ocasión se dedicó a pasearse arriba y abajo pensando mientras la radio rota chillaba delante de su propietario cada vez que se encendía. Finalmente, el joven Feynman sacó dos válvulas y las intercambió, resolviendo así el problema. Sospecho que Feynman dejó que el asunto durase más de lo necesario solo por el efecto que causaba.

Una historia casi análoga se repetiría en una época posterior de su vida. Pero esta última se originó cuando a un escéptico Feynman se le pidió examinar una enigmática fotografía proveniente de una cámara de burbujas, un aparato en el que las partículas elementales dejan trazas visibles. Tras pensar un rato, señaló con su lápiz un lugar preciso en la foto y aseguró que tendría que haber un perno justo allí, donde una partícula había sufrido una colisión imprevista, dando lugar a resultados que de otro modo hubieran sido mal interpretados. Huelga decir que cuando los experimentadores implicados en el pretendido descubrimiento volvieron a examinar su aparato allí estaba el perno.

La teatralidad, aunque contribuyó al conocimiento popular de Feynman, sin embargo no fue importante para su trabajo. Como tampoco lo fue su fascinación por las mujeres, que también apareció más tarde. Sí lo fue su poder de concentración, unido a la energía casi sobrehumana que podía dedicar a cualquier problema. Pero la guinda final y esencial del pastel, que combinada con las dos características anteriores aseguraba definitivamente su grandeza, era simplemente un talento casi incomparable para las matemáticas.

El talento matemático de Feynman empezó a manifestarse cuando estaba en bachillerato. Siendo estudiante aprendió por su cuenta trigonometría, álgebra avanzada, series infinitas, geometría analítica y cálculo diferencial e integral. Y en esa etapa autodidáctica comenzó a materializarse el otro aspecto que hizo a Feynman tan único: remodelaba cualquier conocimiento a su manera, inventando a menudo un nuevo lenguaje o un nuevo formalismo para reflejar su propia forma de entender las cosas. En ciertos casos, la madre de la invención era la necesidad. Al mecanografiar un complejo manual de matemáticas, en 1933, a la edad de quince años, inventó «símbolos mecanográficos» para representar las operaciones matemáticas apropiadas, ya que su máquina de escribir no tenía las teclas para ese fin, y creó una nueva notación para una tabla de integrales que había desarrollado.

Feynman entró en el MIT con la intención de estudiar matemáticas, pero era una idea fuera de lugar. Aunque le encantaban las matemáticas, lo que sobre todo deseaba saber es qué podía «hacer» con ellas. Se lo preguntó al jefe del departamento de Matemáticas y obtuvo dos respuestas: «Cálculos para seguros» y «si tienes que preguntar eso, tu lugar no está en las matemáticas». Ninguna de ellas sintonizaba con Feynman, que decidió que las matemáticas no eran para él, así que se cambió a ingeniería eléctrica. Curiosamente, este cambio fue demasiado extremo. Si las matemáticas no tenían ningún propósito, la ingeniería era demasiado práctica. Sin embargo, como en la sopa del cuento de Ricitos de oro, la física era «justo lo adecuado», y al final de su primer año Feynman había llegado a ser un alumno especializado en física.

Por supuesto, la elección fue un acierto. El talento innato de Feynman le permitió sobresalir en física. Pero poseía otro talento que quizás importaba más, y no sé si era innato o no: la intuición.

La intuición física es un tipo fascinante y efímero de destreza. ¿Cómo saber qué forma de abordar un problema físico será la más fructífera para resolverlo? Sin duda, algunos aspectos de la intuición se adquieren. Esa es la razón de que se les pida a los estudiantes de física que resuelvan tantos problemas. De este modo, empiezan a aprender qué métodos funcionan y cuáles no y aumentan su caja de herramientas técnicas en el camino. Pero lo que es seguro es que no puede enseñarse un aspecto de la intuición física, ese que resuena en cierto lugar y tiempo. Einstein tenía esta intuición, que le fue de gran utilidad durante más de veinte años, desde su histórico trabajo en relatividad especial hasta su logro superior, la relatividad general. Pero su intuición comenzó a fallarle cuando se apartó lentamente de la corriente principal de interés en mecánica cuántica del siglo XX.

La intuición de Feynman era única de manera diferente. Mientras que Einstein desarrolló teorías completamente nuevas sobre la naturaleza, Feynman exploró ideas ya existentes desde una perspectiva completamente nueva y normalmente más fructífera. El único modo en que él podía realmente comprender las ideas físicas era deduciéndolas usando su propio lenguaje. Pero como su lenguaje era normalmente también autoaprendido, los resultados finales diferían radicalmente de lo que producía la sabiduría «convencional». Como veremos, Feynman creó su propia sabiduría.

Pero Feynman adquirió también la intuición por el camino duro, basado en un trabajo incansable. Su enfoque sistemático y la minuciosidad con que examinaba los problemas eran ya evidentes en el bachillerato. Anotaba sus progresos en cuadernos, con tablas de senos y cosenos que él mismo había calculado, y más adelante en su cuaderno exhaustivo de cálculo, titulado Cálculo para el hombre práctico, con extensas tablas de integrales que él mismo había resuelto. Posteriormente, asombraría a la gente proponiendo un modo nuevo de resolver un problema o comprendiendo inmediatamente la esencia de un tema complejo. Casi siempre esto era así porque alguna vez, en las páginas de notas que guardaba al trabajar para comprender la naturaleza, Feynman había reflexionado acerca de ese mismo problema y había explorado no una sino multitud de maneras de resolverlo. Era este deseo de investigar un problema desde todas las perspectivas y de organizar cuidadosamente su pensamiento hasta haber agotado todas las posibilidades —un producto de su profunda inteligencia y de su infatigable capacidad de concentración— lo que lo distinguía.

Quizá «deseo» no sea la palabra correcta. «Necesidad» sería más adecuada. Feynman necesitaba entender cualquier problema que afrontaba partiendo de cero, resolviéndolo a su propia manera y, con frecuencia, de varias maneras distintas. Más adelante, trataría de inculcar esta misma ética a sus estudiantes, uno de los cuales dijo después: «Feynman hacía hincapié en la creatividad —lo que para él significaba desarrollar las cosas desde el principio—. Nos insistía para que cada uno de nosotros crease un universo de ideas propio, de manera que nuestros resultados, incluso si se trataba de ejercicios propuestos en clase, tuvieran un carácter original propio, de la misma manera que su trabajo llevaba el sello único de su personalidad».

No solo era evidente la capacidad de Feynman para concentrarse durante largos periodos cuando era joven, también lo era su capacidad para controlar y organizar sus pensamientos. Recuerdo haber tenido un juego de química cuando era niño y también recuerdo haber mezclado cosas al azar para ver qué pasaba. Pero Feynman, como enfatizó más tarde, «nunca jugaba de manera caótica con las cosas científicas». Más bien, él siempre llevaba a cabo su «juego» científico de manera controlada, siempre atento a lo que estaba sucediendo. De nuevo mucho más tarde, después de su muerte, por sus notas quedó claro que él anotaba cuidadosamente cada una de sus exploraciones. Incluso en una ocasión consideró organizar la vida doméstica con su futura esposa según líneas científicas, antes de que un amigo lo convenciera de que estaba siendo sin remedio poco realista. Al final, su ingenuidad al respecto desapareció, y mucho más tarde le aconsejó a un estudiante: «No puede desarrollarse una personalidad únicamente con la física. El resto de la vida de uno debe entrar en juego». En cualquier caso, a Feynman le encantaba jugar y bromear, pero cuando se trataba de ciencia, lo que empezó pronto y continuó a lo largo de su vida, Feynman podía ser mortalmente serio.

Esperó hasta el final de su primer curso universitario para decidirse a convertirse en estudiante de la especialidad de física, pero las estrellas se habían alineado cuando todavía estaba en el instituto. Retrospectivamente, lo que pudo haber sido el momento clave ocurrió cuando su profesor de bachillerato, Mr. Bader, lo introdujo a uno de los misterios más sutiles y maravillosos del mundo observable, un hecho que se desarrolló a partir de un descubrimiento realizado trescientos años antes de su nacimiento por un brillante y solitario abogado y gran aficionado a las matemáticas, Pierre de Fermat.

Al igual que Feynman, Fermat obtendría reconocimiento público ya en edad madura por algo no relacionado con sus logros más sustanciales. En 1637, Fermat garabateó una breve nota al margen de su copia de Arithmetica, la obra maestra del famoso matemático griego Diofanto, en la que indicaba que había descubierto una prueba sencilla de un hecho notable. La ecuación xⁿ + yⁿ = zⁿ no tiene soluciones enteras si n > 2 (para n = 2 es el conocido teorema de Pitágoras, que relaciona las longitudes de los lados de un triángulo rectángulo). Resulta dudoso que Fermat poseyera realmente esa prueba, que trescientos cincuenta años más tarde requirió casi todos los desarrollos de la matemática del siglo XX y centenares de páginas para completarse. No obstante, si el gran público recuerda de alguna manera a Fermat no es por sus muchas contribuciones fundamentales a la geometría, el cálculo y la teoría de números, sino más bien por esa especulación al margen que será conocida en adelante como «el último teorema de Fermat».

Sin embargo, veinticinco años después de hacer esa dudosa afirmación, Fermat sí presentó una demostración completa de algo distinto: un notable, y casi de otro mundo, principio que establecía un enfoque de los problemas físicos que Feynman usaría posteriormente para cambiar la manera de pensar acerca de la física en el mundo moderno. El tema al cual Fermat dirigió su atención en 1662 tenía que ver con un fenómeno que el científico holandés Willebrord Snell había descrito cuarenta años antes. Snell descubrió una regularidad matemática en la forma en que la luz se refracta, o se dobla, cuando pasa a través de dos medios distintos, tales como el aire y el agua. Esto se llama en la actualidad «la ley de Snell», y se presenta a menudo en las clases de física de bachillerato como otro de los hechos tediosos que deben memorizarse, incluso a pesar de que desempeñara un papel profundo e importante en la historia de la ciencia.

La ley de Snell hace referencia a los ángulos que un rayo de luz forma al atravesar una superficie que separa dos medios. No importa aquí la forma exacta de la ley; lo que es importante es su carácter general y su origen físico. Para entendernos, la ley afirma que cuando la luz pasa de un medio menos denso a otro más denso, la trayectoria del rayo luminoso se dobla al acercarse a la perpendicular de la superficie que los separa (véase la figura).

 

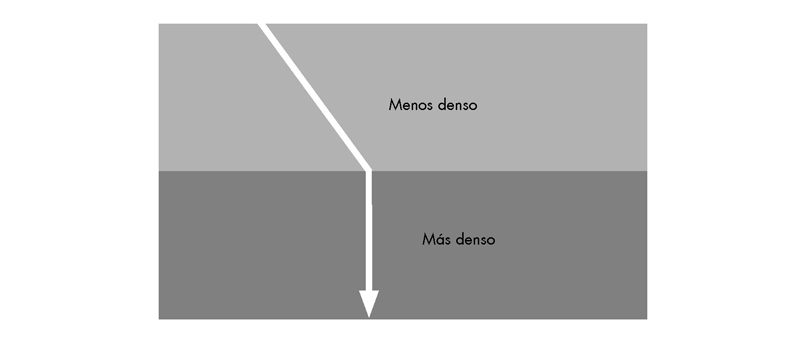
Ley de Snell

 

Ahora bien, ¿por qué se dobla la luz? Bueno, si la luz estuviera constituida de partículas, como creían Newton y otros, podría entenderse esta relación si las partículas ganaran velocidad al pasar de un medio al otro. Serían literalmente arrastradas hacia delante, moviéndose más efectivamente en una dirección perpendicular a la superficie que han cruzado. Sin embargo, esta explicación parecía vidriosa incluso entonces. Después de todo, en un medio más denso cualquiera de esas partículas encontraría presumiblemente mayor resistencia a su movimiento, igual que los coches en una carretera acaban moviéndose más lentamente cuando el tráfico es muy denso.

Existe, sin embargo, otra posibilidad, como demostró el físico holandés Christiaan Huygens en 1690. Si la luz fuera una onda y no estuviera hecha de partículas, entonces de la misma forma que un sonido se dobla hacia dentro cuando va más lento, lo mismo le ocurriría a la luz si también se hiciera más lenta en un medio más denso, de manera que la ley de Snell proporciona una importante evidencia de que la luz se comporta, en este caso, como una onda.

Casi treinta años antes del trabajo de Huygens, Fermat razonó también que la luz debería viajar más lentamente en medios densos que en otros menos densos. Sin embargo, en lugar de razonar en términos de si la luz era onda o partícula, Fermat el matemático mostró que en este caso se podía explicar la trayectoria de la luz en términos de un principio matemático general, que ahora conocemos como «principio de Fermat de tiempo mínimo». Como él demostró, la luz seguiría precisamente la misma trayectoria doblada determinada por Snell si «la luz viaja entre dos puntos dados siguiendo el camino de tiempo mínimo».

Esto puede entenderse heurísticamente de la manera siguiente: si la luz viaja más rápidamente en el medio menos denso, entonces para ir de A a B (véase la figura) en el tiempo más corto, tendría sentido viajar una distancia mayor en ese medio y una distancia menor en el segundo medio, donde viaja más lentamente. Ahora bien, no puede viajar demasiado tiempo en el primer medio, ya que entonces la distancia extra que recorre superaría la ganancia obtenida al viajar a mayor velocidad. No obstante, un camino es precisamente el correcto, y este camino resulta que describe una trayectoria doblada que reproduce exactamente la de la ley de Snell.

 

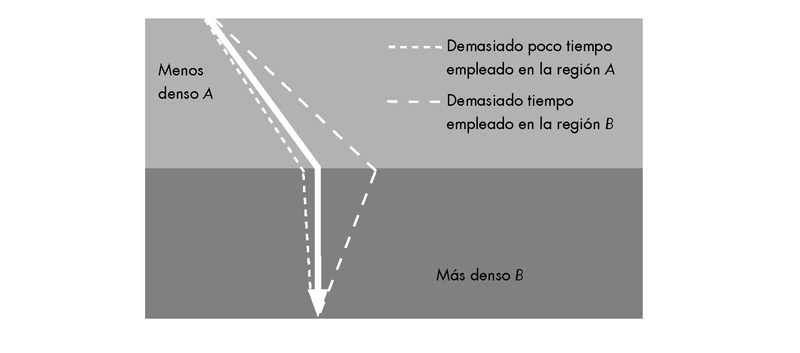
Ley de Snell

 

El principio de Fermat de tiempo mínimo es una manera matemáticamente elegante de determinar el camino que sigue la luz sin recurrir a ninguna descripción mecanicista en términos de ondas o partículas. El único problema es que, cuando se piensa acerca de su base física, este resultado parece sugerir intencionalidad, de manera que, igual que un usuario del transporte público escuchando el informe del tráfico un lunes por la mañana en hora punta, la luz de algún modo considera todos los caminos posibles antes de embarcarse en su viaje y escoge finalmente el que la lleva más rápidamente a su destino.

Pero lo fascinante es que no necesitamos adscribir ninguna intencionalidad a los viajes de la luz. El principio de Fermat es un ejemplo maravilloso de una propiedad de la física aún más notable, una propiedad en el centro del asombroso y a priori inesperado hecho de que la naturaleza es comprensible mediante las matemáticas. Si existe alguna propiedad que fuera un faro guía del enfoque de la física de Richard Feynman, y esencialmente de todos sus descubrimientos, es esta, que él consideraba tan importante que se refirió a ella en dos ocasiones durante su discurso al recibir el Premio Nobel. En primer lugar, escribió:

 

Siempre me parece extraño que las leyes fundamentales de la física, cuando se descubren, puedan aparecer en tantas formas diferentes que no son aparentemente idénticas al principio, y que luego, con una pizca de matemáticas, pueda mostrarse la relación entre ellas... Es algo que he aprendido de la experiencia. Siempre hay otra manera de decir lo mismo que no se parece en nada a la manera en que se había dicho antes... Creo que de algún modo es una representación de la simplicidad de la naturaleza. No sé lo que significa que la naturaleza escoja estas curiosas formas, pero tal vez es una manera de definir la simplicidad. Quizás una cosa es simple si puede describirse por completo de varias formas distintas sin saber inmediatamente que se está describiendo la misma cosa.

 

Y más adelante (y más importante para lo que vendrá después) añadió:

 

Las teorías de lo conocido, descritas mediante ideas físicas distintas, pueden ser equivalentes en todas sus predicciones y son, por consiguiente, imposibles de distinguir científicamente. Sin embargo, no son psicológicamente idénticas cuando se trata de ir de esa base a lo desconocido. Pues diferentes perspectivas sugieren clases diferentes de modificaciones que podrían efectuarse y, por tanto, no son equivalentes en las hipótesis generadas a partir de ellas al intentar entender lo que aún no se entiende.

 

El principio de Fermat del tiempo mínimo representa un claro ejemplo de esa extraña redundancia de la ley física que tanto fascinaba a Feynman, y también de los diferentes «servicios psicológicos» de las distintas prescripciones. Pensar sobre la curvatura de la luz en términos de fuerzas eléctricas y magnéticas en la separación entre los medios revela algo sobre las propiedades de estos. Pensar en términos de la velocidad de la luz en sí misma revela algo sobre el intrínseco carácter ondulatorio de la luz. Y pensar en términos del principio de Fermat puede que no revele nada sobre fuerzas específicas ni sobre la naturaleza ondulatoria de la luz, pero sí revela algo profundo acerca de la naturaleza del movimiento. Felizmente, y lo que es importante, todas esas descripciones dan lugar a predicciones idénticas.

De modo que podemos estar tranquilos. La luz no sabe que está tomando el camino de tiempo más corto; solo actúa así.

 

 

Sin embargo, no fue el principio de tiempo mínimo, sino una idea aún más sutil, lo que cambió la vida de Feynman aquel decisivo día en el instituto de bachillerato. Como Feynman lo describió después: «Cuando estaba en bachillerato, mi profesor de física —que se llamaba Mr. Bader— me llamó un día al acabar la clase y me dijo: “Pareces aburrido; deseo decirte algo interesante”. Entonces me habló de algo que encontré absolutamente fascinante y que, desde entonces, siempre he encontrado fascinante... El principio de mínima acción». «Mínima acción» puede sonar como una expresión más apropiada para describir el comportamiento de un servicio de atención al cliente de la compañía telefónica que para una disciplina como la física, que, después de todo, está centrada en describir acciones. Pero el principio de mínima acción es muy similar al principio de Fermat de tiempo mínimo.

El principio de tiempo mínimo nos dice que la luz siempre sigue el camino de tiempo más corto. Pero ¿qué pasa con los balones de fútbol, las balas de cañón, los planetas y los bumeranes? Ellos no se comportan necesariamente de manera tan simple. ¿Hay algo diferente al tiempo que se hace mínimo cuando estos objetos siguen los caminos prescritos por las fuerzas que actúan sobre ellos?

Considérese cualquier objeto en movimiento; por ejemplo, un cuerpo que cae. Se dice que un objeto tal posee dos clases de energía. Una es la energía cinética, y está relacionada con el movimiento de los objetos (viene de «movimiento» en griego). Cuanto más rápidamente se mueve un cuerpo, mayor es su energía cinética. La otra parte de la energía de un objeto es más sutil, como se refleja en su nombre: energía potencial. Esta clase de energía puede estar oculta, pero es responsable de la capacidad de que un objeto realice trabajo después. Por ejemplo, un objeto pesado que cae desde lo alto de un edificio, aplastando la capota de un coche, producirá más daño, y por tanto más trabajo, que si cayera desde unos centímetros por encima del coche. Claramente, cuanto más alto se halle el objeto, mayor es su potencial para realizar trabajo y, por consiguiente, mayor es su energía potencial.

Ahora bien, lo que afirma el principio de mínima acción es que la diferencia entre la energía cinética de un objeto en cualquier instante y su energía potencial en el mismo instante, calculada en cualquier punto a lo largo de un camino y después sumada a lo largo del camino, será menor para el camino real que toma el objeto que para cualquier otra trayectoria posible. El objeto ajusta su movimiento de manera que la energía cinética y la energía potencial tengan, de media, los valores más cercanos dentro de lo posible.

Si esto parece misterioso y no intuitivo es porque lo es. ¿Cómo demonios se le ocurriría a alguien esa combinación y mucho menos aplicarla al movimiento de objetos cotidianos?

Esto lo hemos de agradecer al matemático italofrancés Joseph Louis Lagrange, más conocido por su trabajo en mecánica celeste. Por ejemplo, determinó los puntos en el sistema solar donde las atracciones gravitatorias de los diferentes planetas se cancelan precisamente entre sí en el sistema de referencia del cuerpo en órbita. Estos son los llamados «puntos de Lagrange». La NASA envía en la actualidad numerosos satélites a estos puntos de manera que pueden permanecer en órbitas estables y estudiar el universo.

Sin embargo, la mayor contribución de Lagrange a la física puede haber tenido que ver con su reformulación de las leyes del movimiento. Las leyes de Newton relacionan el movimiento de los objetos con las fuerzas netas que actúan sobre ellos. Sin embargo, Lagrange logró mostrar que las leyes del movimiento de Newton eran precisamente reproducidas si se usaba la acción, que es la suma sobre una trayectoria de las diferencias entre las energías cinética y potencial, ahora apropiadamente llamada «una lagrangiana», y entonces determinó precisamente qué tipos de movimiento producirían las trayectorias que minimizaban esta cantidad. El proceso de minimización, que requería el uso del cálculo (también inventado por Newton), dio muchas descripciones matemáticas diferentes del movimiento a partir de las leyes de Newton, pero, en el espíritu de Feynman, eran matemáticamente idénticas, aunque fueran «psicológicamente» distintas.

 

 

Fue este extraño principio de mínima acción, llamado frecuentemente «principio de Lagrange», lo que Mr. Bader presentó al quinceañero Feynman. Muchos de esa edad no lo habrían encontrado fascinante o ni siquiera comprensible, pero Feynman sí, o así lo recordaba de viejo.

No obstante, si Feynman había tenido entonces alguna sospecha de que este principio volvería para colorear completamente la historia de su vida, ciertamente no se comportó así cuando empezó a aprender más sobre física al entrar en el MIT. Todo lo contrario. Su mejor amigo en su época de estudiante en el MIT, Ted Welton, con quien trabajó mucho a lo largo de los cursos de grado e incluso de posgrado, describió más tarde cómo «Feynman rehusaba de manera insensata aceptar que Lagrange podía tener algo útil que decir sobre física. Todos los demás estábamos impresionados por la concisión, elegancia y utilidad de la formulación lagrangiana, pero Dick insistía obstinadamente en que la física real reside en identificar todas las fuerzas y resolverlas apropiadamente en componentes».

La naturaleza, como la vida, da muchas vueltas, y, lo que es más importante, es tremendamente insensible a las alegrías y los disgustos de uno. Por mucho que Feynman tratara pronto de focalizarse en entender el movimiento de una manera intrincada con su intuición ingenua, su propia trayectoria hacia la grandeza implicaba un camino muy diferente. No había ninguna mano oculta guiándolo. En cambio, él forzó su intuición a inclinarse a las demandas de los problemas del momento, y no viceversa. El desafío requería incontables horas, días y meses de duro trabajo entrenando su mente para darle vueltas a un problema que las mayores inteligencias de la física del siglo XX no habían sido capaces de resolver hasta entonces.

Cuando realmente lo necesitaba, Feynman se encontraba volviendo una vez más al mismo principio que lo había dirigido hacia la física en primer lugar.