Capítol I. Electrostàtica
1. Introducció
Avui dia sabem que la majoria dels fenòmens físics que es produeixen al nostre voltant són el resultat d’interaccions d’origen electromagnètic. Els cossos mantenen la seva cohesió gràcies a les forces electromagnètiques entre els seus àtoms. La seva duresa o flexibilitat, així com altres propietats, depenen de la intensitat d’aquestes forces. Els xocs entre cossos i les forces de fregament també són el resultat d’aquestes interaccions.
D’altra banda, la comprensió de les interaccions electromagnètiques ha permès desenvolupar molts dels aparells moderns que fem servir avui dia. La nostra vida sense enllumenat elèctric, motors, televisors, ordinadors, etc., seria completament diferent.
Quan parlem d’interaccions electromagnètiques ens estem referint a les forces elèctriques i magnètiques. Fins al segle XIX es pensava que aquestes forces eren dos fenòmens completament diferents. Ara, però, sabem que aquests dos tipus d’interaccions són produïts per una propietat de la matèria que anomenem càrrega elèctrica. Malgrat que els fenòmens elèctrics i magnètics estan íntimament relacionats es poden separar si primer estudiem les càrregues elèctriques en repòs (electrostàtica), com farem en aquest capítol. Les forces magnètiques, que estudiarem en el capítol de Magnetisme, només es manifesten quan les càrregues elèctriques estan en moviment.
La càrrega elèctrica, o senzillament càrrega, pot ser positiva o negativa, de manera que els cossos amb el mateix tipus de càrrega es repel·leixen i els que la tenen de signe oposat s’atrauen. Els cossos que no tenen càrrega s’anomenen cossos elèctricament neutres, o senzillament cossos neutres. L’atracció o repulsió entre càrregues es descriu mitjançant les forces elèctriques. Aquestes forces són difícils d’observar directament perquè la majoria de cossos que ens envolten són neutres.
Aquest capítol l’hem dividit en dues parts. En la primera estudiarem els fonaments de l’electrostàtica i introduirem els conceptes de camp i potencial elèctrics. En la segona veurem com es comporten dos tipus de materials, els conductors i els dielèctrics, en presència d’un camp elèctric. També descriurem el condensador, que és un dels dispositius més simples que es fa servir en el disseny de molts circuits.
2. Fonaments d’electrostàtica
2.1. Càrrega elèctrica i matèria
Pràcticament tota la matèria que ens envolta està formada per tres tipus de partícules, els protons (p), els neutrons (n0) i els electrons (e), que acostumen a estar agrupades formant àtoms. Els protons i els neutrons tenen una massa molt semblant de l’ordre de 1027 kg, mentre que els electrons són unes 2.000 vegades més lleugers (vegeu la taula 1.1).
Taula 1.1

Les dimensions del nucli són de l’ordre de 1015 m 1 fm (1 fermi). En canvi, les dimensions de tot l’àtom són de l’ordre de 1010 m 1 Å (1 àngstrom). Així doncs, els àtoms són pràcticament buits i amb tota la massa en el nucli. (1)
La càrrega d’un neutró és nul·la, la d’un protó és -e i la de l’electró és e, sent e la unitat fonamental de càrrega.
En el Sistema Internacional d’unitats (SI) la unitat de càrrega és el coulomb (C).
El coulomb està relacionat amb e per
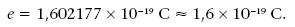
Q = (N p - N e ) e.
Diem que la càrrega és quantitzada ja que tota la càrrega Q present a la naturalesa és un múltiple enter de la càrrega fonamental e. (2)
Normalment, però, la quantització de la càrrega no s’observa macroscòpicament perquè, en els cossos carregats, | N p N e | és quasi sempre un nombre molt gran.
Quan un cos està carregat és perquè ha guanyat o ha perdut electrons. Un àtom amb un excés o un defecte d’electrons rep el nom d’ ió. Si un cos perd electrons, els transfereix a un altre que, per tant, en guanya. En aquest procés la càrrega neta de tots els cossos que intercanvien electrons no es modifica. És a dir, la càrrega es conserva. Aquest fet és una llei fonamental de la naturalesa.
La llei de conservació de la càrrega estableix que la càrrega no es crea, sinó que es transfereix.
Les molècules són agrupacions estables d’àtoms. Els lligams entre els àtoms d’una molècula, anomenats enllaços químics, són d’origen electromagnètic i només depenen dels electrons més externs. Aquests electrons són els més feblement units al nucli i s’anomenen electrons de valència. Els àtoms s’enllacen compartint els electrons de valència, els quals ja no seran d’un únic nucli. En aquest cas es diu que els electrons compartits pertanyen a un orbital molecular en comptes de pertànyer a un orbital atòmic. Les molècules amb un excés o defecte d’electrons també s’anomenen ions.
Les propietats dels materials depenen de com s’enllacen els seus àtoms i molècules. Aquests enllaços també són d’origen electromagnètic. Pel que fa a les propietats elèctriques, els materials poden dividir-se en:
-
Materials conductors, que permeten el desplaçament de càrrega a través seu. Per exemple, els metalls són bons conductors perquè alguns dels electrons no queden lligats a cap àtom o molècula en concret. Són els electrons lliures o de conducció que poden moure’s en el si del material.
-
Materials aïllants, com la fusta o els plàstics, on tots els electrons estan perfectament lligats a algun àtom o molècula proper i no es poden moure lliurement. Els aïllants també s’anomenen dielèctrics.
Parlant amb rigor, no existeixen aïllants perfectes, atès que tots els materials permeten un cert moviment de càrrega i és més correcte parlar de bons i mals conductors.
2.2. Forces elèctriques: llei de Coulomb
L’estudi de les forces elèctriques es fonamenta en la llei de Coulomb, que estableix la força exercida per una càrrega puntual sobre una altra. Sempre que les càrregues siguin molt petites comparades amb la distància que les separa, es pot considerar que són càrregues puntuals.
La llei de Coulomb es pot formular matemàticament de la manera següent: siguin q 1i q 2 dues càrregues puntuals separades una distància r 12, que és el mòdul del vector r 12 que va de la posició de q 1a la de q 2 (com es veu a la figura 1.1), aleshores, la força elèctrica F 12 exercida per q 1 sobre q 2 és
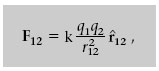
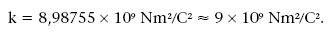
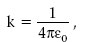
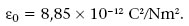
Figura 1.1
Si intercanviessin els subíndexs 1 i 2 en l’equació 1.1 tenim la força F 21 que fa q 2 sobre q 1. En fer aquest canvi, r 21 coincideix amb r 12 , però ȓ 12 = - ȓ 21 i, per tant, F 21 = - F 12 . És a dir, la llei de Coulomb satisfà la tercera llei de Newton, la d’acció i reacció, perquè F 21 té el mateix mòdul i direcció que F 12 , però té sentit oposat.
Segons la llei de Coulomb, si dues càrregues puntuals q 1i q 2 tenen el mateix signe, la força F 12 exercida per q 1 sobre q 2 té el mateix sentit del vector r 12 que va des de q 1 fins a q 2 i, com que F 21 = - F 12 , les dues càrregues es repel·leixen. En canvi, quan q 1i q 2 són de signe diferent F 12 té el sentit oposat al de r 12 i les càrregues s’atreuen.
Exemple 1.1. Aplicació de la llei de Coulomb
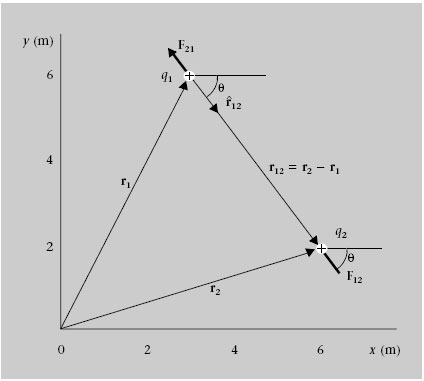
Si a la figura 1.1 considerem que q 1 = 5 nC i q 2 6 = nC, per calcular F 12 i F 21 s’ha de procedir de la forma següent. Com que r 1 (3 m) i (6 m) j i r 2 (6 m) i (2 m) j, tenim que
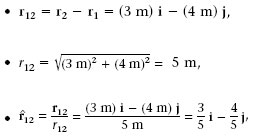
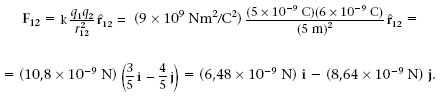
Finalment
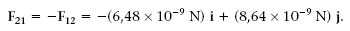
2.2.1. Superposició de les forces elèctriques
En un sistema de càrregues puntuals, la força neta que actua sobre una determinada càrrega és la suma vectorial de cada una de les forces individuals que li fan les altres, i cada una d’aquestes forces individuals ve donada per la llei de Coulomb. Aquest fet s’ha comprovat experimentalment i és conegut com el principi de superposició de les forces elèctriques.
Exemple 1.2. Càlcul de forces elèctriques
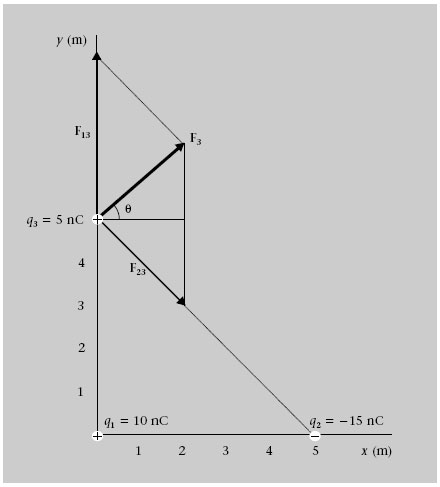
Com s’indica a la figura 1.2, una càrrega positiva q 1 = 10 nC es troba a l’origen de coordenades i una càrrega negativa q 2 = -15 nC està en el punt (5 m,0 m). Quina força fan aquestes dues càrregues sobre una tercera q 3 5 5 nC que està en el punt (0 m, 5 m)?
Tenint en compte que
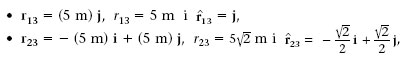
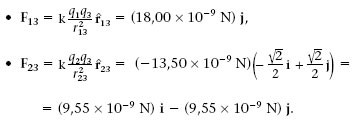
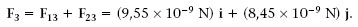
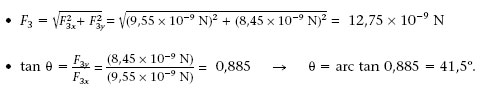
Activitat
1.1. Calculeu la força neta sobre les càrregues q 1i q 2 de l’exemple 1.2.
Resposta
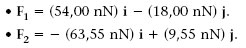
2.3. Camp elèctric
La força elèctrica és una interacció a distància que, com veurem en aquest subapartat, pot formular-se mitjançant el concepte de camp elèctric. Aleshores, la força exercida sobre una càrrega q per un conjunt de càrregues distribuïdes per l’espai s’explica com el resultat de dos processos:
-
D’una banda, una distribució de càrregues crea un camp elèctric E en tot l’espai.
-
De l’altra, el camp elècctric fa una força sobre la càrrega q.
Atès que el camp elèctric és una propietat de tot l’espai, s’ha de descriure mitjançant una funció de la posició. Com veurem tot seguit, aquesta funció assigna un vector a cada punt i, per tant, el camp elèctric és un camp vectorial.
Camps escalars i vectorials
-
Un camp escalar és una funció que a cada punt de l’espai li assigna un escalar (un nombre real). La pressió atmosfèrica és un exemple familiar de camp escalar. Les línies que envolten les depressions i anticiclons del mapa del temps uneixen punts amb la mateixa pressió (isòbares).
-
Un camp vectorial és una funció que a cada punt li assigna un vector. Per a descriure la velocitat del vent (intensitat, direcció i sentit) en un instant determinat s’ha de fer mitjançant un camp vectorial.
El camp elèctric E en un punt es defineix com la força elèctrica F0 per unitat de càrrega que actuaria sobre una càrrega positiva q0 situada en el punt en qüestió. Això és
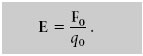
La unitat SI per a E és el newton per coulomb (N/C).
Considerem un sistema de N càrregues puntuals q 1, q 2, ..., q i , ..., q N , situades en els punts r 1 , r 2 , ..., r i , ..., r N , respectivament. La força que actuaria sobre una càrrega d’assaig q 0 situada en el punt r 0 seria la superposició de les forces F i 0 que faria cada q i sobre q 0, això és
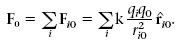
Recordeu que el signe , anomenat sumatori, permet expressar de forma compacta una suma d’elements numerats. Així la suma
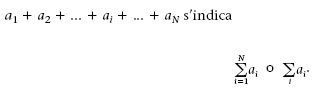
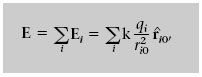
La definició de camp elèctric implica que una càrrega puntual q en presència d’un camp E es veu sotmesa a una força
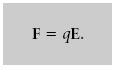
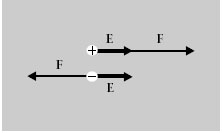
La força que actua sobre una càrrega puntual positiva té el mateix sentit que E i la que actua sobre una càrrega negativa és de sentit oposat (figura 1.3).
Figura 1.3
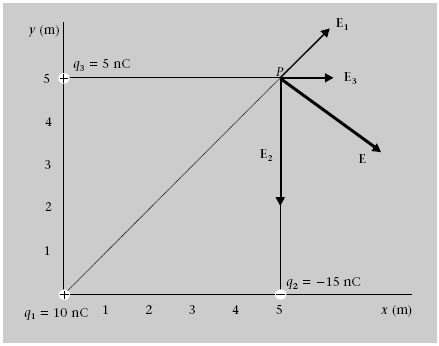
Les càrregues q 1 = 10 nC, q 2 = -15 nC i q 3 5 = nC de l’exemple 1.2 estan en els punts (0 m,0 m), (5 m,0 m) i (0 m,5 m), respectivament (vegeu la figura 1.4). Quin és el camp elèctric creat per les tres càrregues en el punt P = (5 m,5 m)?
Tenint en compte que les distàncies r iP que hi ha des de cada càrrega a P i que els vectors unitat ȓ iP que apunten des de cada càrrega a aquest punt són

Aleshores, el camp elèctric en el punt P és la suma dels tres,
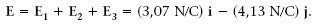
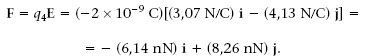
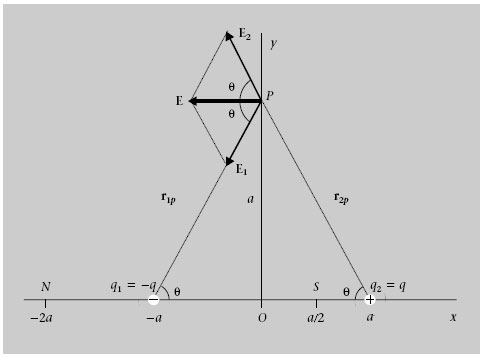
Un dipol elèctric és un sistema format per dues càrregues puntuals de magnitud igual i signe diferent, q + = q i q - = -q (q>0). Quin és el camp E en el punt P de la figura 1.5?
Com que la distància d’ambdues càrregues al punt P = (0,2a) és igual a r + P r - P a √5, els camps elèctrics creats per cada una en aquest punt, E + i E - , tenen el mateix mòdul
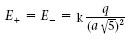
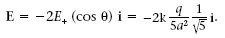
Activitat
1.2. Calculeu el camp elèctric creat pel dipol de l’exemple 1.4 en els punts N (-2a,0), O = (0,0) i S (a/2,0).
Resposta
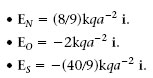
2.4. Línies de camp elèctric
La visualització d’un camp elèctric E es fa mitjançant les línies de camp elèctric.
Una línia de camp elèctric és una línia imaginària que en cada un dels seus punts el vector camp elèctric és tangent a la línea, i que té el seu sentit.
Figura 1.6
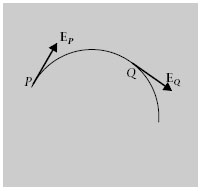
La definició de línia de camp que acabem de donar per al camp E és generalitzable a altres camps vectorials, per exemple les línies de camp gravitatori o les de camp magnètic (que estudiarem en el capítol “Magnetisme”).
Sigui quin sigui el tipus de camp, les línies de camp no es tallen mai. Si una línia de camp es tallés, la seva definició implicaria que en el punt de tall el vector hauria de tenir dues direccions, la qual cosa és absurda.
Els diferents exemples de la figura 1.7 mostren una propietat general del camp elèctric: per a qualsevol distribució de càrregues, les línies del camp elèctric sempre comencen en les càrregues positives (o l’infinit) i acaben en les negatives (o l’infinit).
Figura 1.7
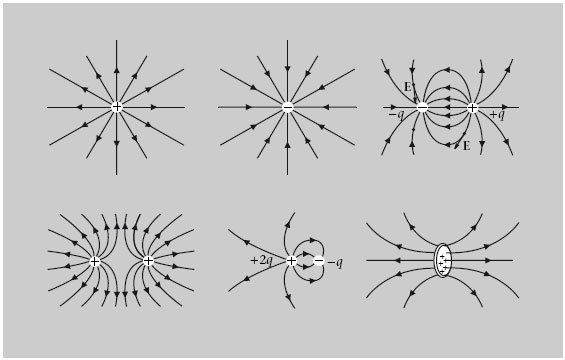
Quan es dibuixen les línies de camp elèctric es fa de manera que el nombre de línies que entren o surten d’una càrrega és proporcional a la càrrega. A més a més, les línies entren o surten de punts distribuïts simètricament al voltant de la càrrega. Seguint aquest conveni, les línies de camp dibuixades satisfan la propietat següent: com més intens és el camp, les línies de camp estan més juntes. Podeu comprovar aquest fet en la figura 1.7 on a mesura que ens apropem a les càrregues, i per tant el camp elèctric és més intens, les línies de camp es van ajuntant.
2.5. Flux del camp elèctric
El nombre de línies de camp elèctric que travessen una determinada superfície està relacionat amb una magnitud matemàtica que s’anomena flux. A continuació definirem el flux del camp elèctric. Aquesta definició és generalitzable a altres camps vectorials.
Producte escalar
Recordeu que el producte escalar entre dos vectors A i B és un nombre real igual a A · B = AB cos θ on A i B són els mòduls dels vectors A i B, i θ és l’angle que formen A i B.

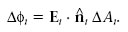
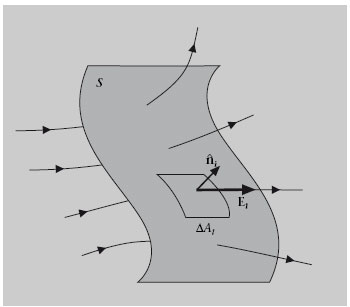
Aleshores, el flux del camp elèctric a través de tota la superfície S es defineix com la suma de tots els Δφ i quan s’ha fet el límit en què l’àrea de cada element tendeix a zero. Una suma definida així és una integral de superfície, i l’expressió matemàtica del flux del camp elèctric és
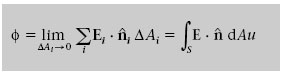
El càlcul general d’integrals de superfície està fora dels objectius d’aquesta assignatura. És important, però, que reconegueu l’expressió del flux en forma d’integral i que entengueu el seu significat. Si és així, en alguns casos el flux elèctric es pot calcular amb certa facilitat. Aquest és el cas del flux d’un camp E uniforme a través d’una superfície plana S d’àrea A.
2.5.1. Flux d’un camp elèctric uniforme a través d’una superfície plana
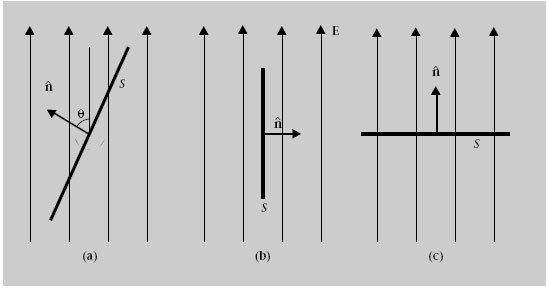
Un camp elèctric uniforme és aquell en què el vector E és el mateix en tots els punts. En aquest cas les línies del camp elèctric són rectes paral·leles que es dibuixen equiespaiades com en la figura 1.9. En una regió de l’espai on un camp elèctric uniforme és el doble d’intens que en una altra regió es dibuixen el doble de línies.
En una superfície plana n és el mateix en tots els punts (figura 1.9) i el seu producte escalar amb un camp E uniforme té un valor constant E · n = E cos θ, on θ és l’angle que forma E amb ṋ (figura 1.9a). Aleshores aquesta constant es pot treure fora de la integral que defineix el flux:
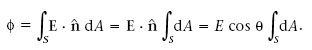
La integral de dA estesa a tota la superfície S és igual a la seva àrea A. Així doncs, tenim que,
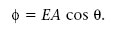
Aquest cas (figura 1.9) mostra una propietat general de qualsevol flux: el flux a través d’una superfície és proporcional al nombre de línies de camp que la travessa.
Fins ara hem considerat que n té el mateix sentit que E. Si haguéssim triat el sentit oposat, hauriem obtingut un flux negatiu (cos(θ + π) = -cos θ). Un flux negatiu indica que les línies de camp travessen la superfície en sentit contrari al que fixem com a positiu quan triem un o altre sentit de n.
Per a evitar l’ambigüitat de signe en el flux a través de superfícies tancades s’ha establert el conveni que el vector normal unitat, n, es tria de manera que sempre està dirigit cap a fora del volum tancat per aquesta.
2.6. Llei de Gauss
Figura 1.10. Superfícies gaussianes
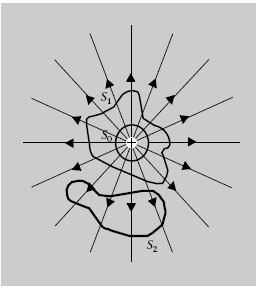
Considerem ara una sola càrrega puntual q i dos tipus de superfícies tancades com les de la figura 1.10: una superfície tancada S 1 que conté q i una superfície tancada S 2 que no la conté. Com es veu a la figura 1.10, el nombre de línies de camp que travessen S 1 és el mateix que el que travessen una superfície esfèrica S 0 de radi R concèntrica amb q. Per tant, el flux del camp elèctric a través de S 1 és el mateix que a través de S 0.
El camp E creat per q en qualsevol punt de S 0 és perpendicular a aquesta superfície, per la qual cosa el vector unitat r que indica la direcció de E en cada punt de S 0 coincideix amb el vector unitat n normal a aquesta superfície i r · n =1. Llavors, en la superfície S 0,
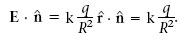
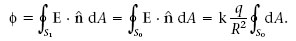
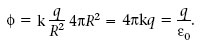
En canvi, com es veu a la figura 1.10, totes les línies de camp que entren a una superfície tancada S 2 que no contingui la càrrega q n’acaben sortint. Per tant, el flux a través de S 2 és nul.
Tenint en compte que el camp E degut a dues càrregues puntuals q 1i q 2 és la suma dels camps E 1 i E 2 creats per cada càrrega per separat, es dedueix que el flux net φ a través d’una superfície tancada S també és la suma dels fluxos φ1 i φ2 produïts per cada càrrega per separat. És a dir,
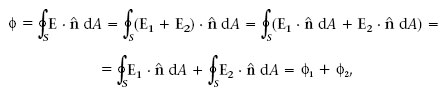
La llei de Gauss estableix que el flux del camp elèctric a través de qualsevol superfície tancada és
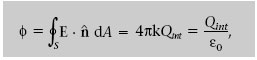
S’entén per Q int la suma del valor de les càrregues positives menys el valor absolut de les negatives (vegeu l’exemple de la figura 1.11).
Figura 1.11. Aplicació de la llei de Gauss
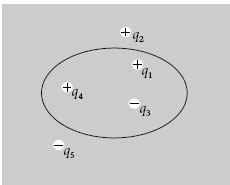
Les superfícies tancades a través de les quals es calcula φ s’anomenen superfícies gaussianes. Si Q int és positiva, φ també ho és, la qual cosa vol dir que el nombre de línies de camp que surten de la superfície gaussiana és més gran que el de les que hi entren. En canvi, si Q int és negativa, φ és negatiu i el nombre de línies de camp que hi entren és més gran que el de les que en surten.
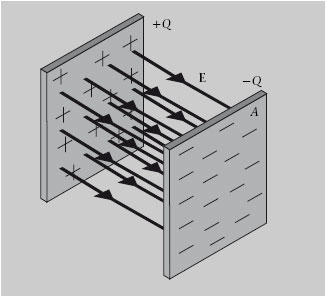
2.7. Camp elèctric prop d’un pla carregat uniformement
Si per una làmina d’àrea A hi ha distribuïda uniformement una càrrega Q, la seva densitat superficial de càrrega és
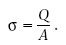
Si considerem un pla infinit carregat uniformement amb una σ > 0, les línies de E s’allunyen del pla (amb sentits oposats a cada costat). Per raons de simetria, E ha de ser perpendicular al pla (figura 1.12) i ha de ser el mateix en tots els punts equidistants al pla.
Figura 1.12. Secció d’un pla infinit carregat amb s > 0
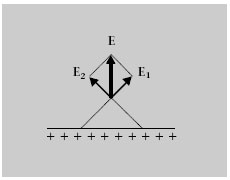
Amb aquesta informació, podem determinar el flux del camp elèctric a través de la superfície d’una caixa cilíndrica com la de la figura 1.13. Les dues bases del cilindre, B 1i B 2, estan a la mateixa distància h del pla i l’àrea de cada una és A b . El flux φ a través d’aquesta superfície gaussiana és igual al flux a través de la superfície lateral del cilindre, S lat , més el flux a través de les bases.
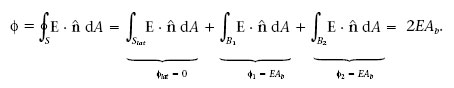
Figura 1.13
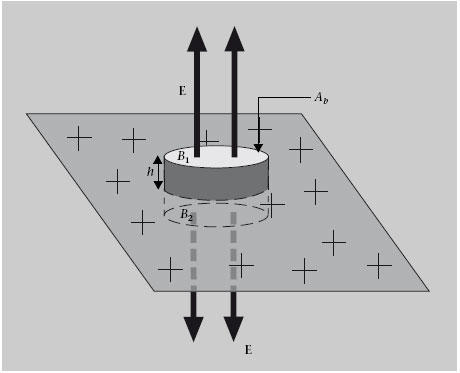
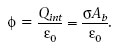
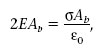
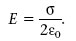
Fixeu-vos que el valor de E és independent de la distància h. És a dir, a cada costat del pla el camp elèctric és uniforme.
Si h és un vector unitat normal a un pla i que assenyala en el sentit que s’allunya del pla, podem considerar que el camp elèctric prop d’un pla carregat uniformement és
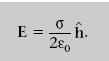
Aquest resultat també és correcte quan el pla està carregat negativament. Si σ < 0, E té sentit contrari a h i assenyala cap al pla.
Exemple 1.5. Camp elèctric prop d’un pla carregat uniformement
Quina força actua sobre una càrrega puntual q = 100 pC que està sobre l’eix z a 20 cm d’un pla molt gran carregat amb σ = 0,3 pC/cm2, que coincideix amb el pla xy (figura 1.14)? Quin és el flux del camp elèctric a través d’una superfície esfèrica S de 10 cm de radi centrada a l’origen de coordenades?
Figura 1.14
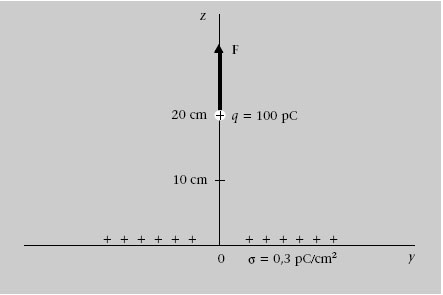
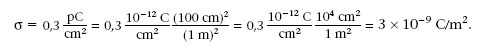
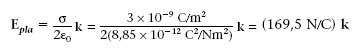
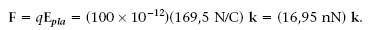

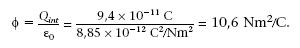
1.3. Considereu el pla i la càrrega puntual de l’exemple anterior. Quina força actuaria sobre una càrrega puntual de -200 pC situada en el punt (0 cm, 5 cm, 20 cm)? Quin seria el flux del camp elèctric a través d’una superfície esfèrica de 10 cm de radi centrada en aquesta nova càrrega?
Resposta
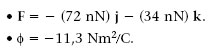
2.7.1. Camp elèctric entre dues làmines paral·leles molt properes amb càrregues oposades
Considerem ara dues làmines paral·leles de la mateixa àrea A i molt properes que estan carregades uniformement, l’una amb una càrrega positiva Q i l’altra amb -Q (figura 1.15). En aquesta situació, el camp E entre les dues làmines lluny dels seus extrems es pot aproximar a la superposició dels camps creats per dos plans infinits carregats amb σ i -σ, respectivament, on σ = Q/A. Entre els dos plans, aquests dos camps són iguals en mòdul (σ/(2ε0)), direcció i sentit. Per tant, el mòdul de E és dues vegades σ/(2ε0). Així, doncs,
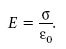
2.8. Treball i energia
En general, quan una força actua sobre un cos que es mou, aquesta realitza un treball. Aquest treball es calcula mitjançant el procediment següent. La trajectòria (o camí) C que ha seguit el cos es divideix en elements prou petits per poder considerar que són segments rectes i que la força en cada un d’aquests desplaçaments és pràcticament constant. Si Δ< i és el vector que va des d’un extrem fins a l’altre del segment i-èsim en el sentit del moviment, el treball fet per la força F i en aquest desplaçament es defineix com
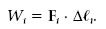
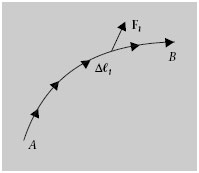
Aleshores, el treball al llarg de tota la trajectòria és la suma de tots els W i en el límit en què els desplaçaments Δ< i són infinitesimals. Una suma així definida és una integral de línia, i l’expressió matemàtica del treball fet per una força sobre un cos que segueix una determinada trajectòria és
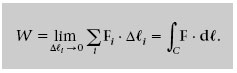
El càlcul general d’integrals de línia està fora dels objectius d’aquesta assignatura. És important, però, que reconegueu l’expressió del treball en forma d’integral i que entengueu el seu significat físic.
Es pot demostrar que el treball fet per la força neta (suma de totes les forces) que actua sobre un cos és igual a la variació de l’energia cinètica (3) del cos, ΔK, això és
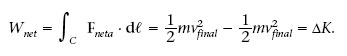
En general, el treball fet per una força depèn de la trajectòria que segueix el cos. Però hi ha un tipus molt important de forces, les forces conservatives, que fan un treball independent de la trajectòria i que només depèn dels punts inicial i final del recorregut. La força gravitatòria n’és un exemple.
Els cossos sotmesos a camps de forces conservatives tenen una propietat anomenada energia potencial, que canvia de valor quan el cos canvia de posició. La variació d’energia potencial produïda per una força conservativa F cons sobre un cos que es mou des d’un punt inicial A fins a un punt final B es defineix com el treball que ha fet la força canviat de signe, això és
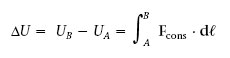
Observació
Com que el treball fet per les forces conservatives només depèn dels punts inicial i final, i no del camí recorregut, en comptes d’acompanyar el signe d’integral amb la lletra C hem indicat els punts A i B en els límits d’integració.
L’energia potencial U d’un cos situat en un punt determinat es defineix com la variació ΔU que es produiria si el cos es desplacés des d’un punt de referència fins al punt en qüestió. És a dir, es tria un punt en el qual s’estableix que U és zero. En principi aquest punt pot ser qualsevol. Així, dues persones que han triat dos punts de referència diferents diran que un mateix cos té valors diferents de U. Aquestes dues persones, però, obtindran els mateixos valors de ΔU. Per tant, només ΔU té un significat físic.
Conservació de l’energia
Recordeu que l’energia potencial gravitatòria prop de la superfície terrestre és mgh (h és l’alçada respecte a un punt on s’ha fixat l’energia potencial igual a zero).
-
Quan alcem un cos, estem fent un treball i li donem energia potencial.
-
Si el deixem anar, el cos cau i la seva energia cinètica va augmentant i la potencial, disminuint.
Si no hi hagués fregament, l’increment de la cinètica seria igual a la disminució de la potencial.
L’energia mecànica d’un cos es defineix com la suma de la cinètica més la potencial.
Tenint en compte la definició de treball (equació 1.12) i l’equació 1.13, la definició de ΔU (equació 1.14) implica que quan sobre un cos només actuen forces conservatives, ΔK ΔU, això és
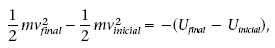
Quan intervenen forces de fregament, que no són conservatives, part de l’energia mecànica es transforma en energia calorífica i, per tant, l’energia mecànica ja no es manté constant. L’energia potencial s’anomena així perquè indica la capacitat de transformar-se en un altre tipus d’energia, cinètica o calorífica per exemple, que es pot aprofitar per realitzar treball.
2.9. Energia potencial electrostàtica d’una càrrega puntual
Es pot demostrar que les forces elèctriques entre càrregues són conservatives. Per tant, una càrrega puntual q en presència d’un camp E creat per altres càrregues té una energia potencial. En aquest cas es parla d’energia potencial electrostàtica.
Com que la força que fa el camp elèctric és F = q E, la variació d’energia potencial electrostàtica d’una càrrega puntual que s’ha desplaçat des d’un punt A fins a un punt B, és
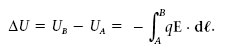
Si un agent extern (F ext), en presència de E, desplaça q des de A fins a B sense modificar la seva energia cinètica, vol dir que (d’acord amb l’equació 1.13) el treball net fet sobre q és nul.
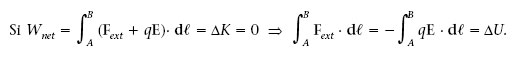
Quan el camp E és degut a càrregues distribuïdes en una regió finita de l’espai, s’acostuma a triar l’infinit com el punt d’energia potencial zero. Seguint aquest conveni, a continuació veurem quina és l’energia potencial electrostàtica U d’una càrrega puntual q 0 deguda al camp E d’una altra càrrega puntual q fixada a l’origen de coordenades. En aquesta situació E = (kq /r 2) r. Aleshores, si q 0 està en el punt r 0 ,
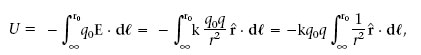
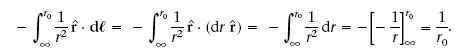
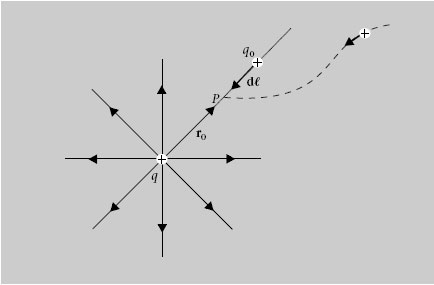
Si substituïm aquest resultat en l’equació anterior veiem que U només depèn de la distància r 0 entre les càrregues. Com que r 0 pot ser qualsevol distància, en el seu lloc escriurem r. Llavors veiem que l’energia potencial electrostàtica d’una càrrega puntual q 0 que està a una distància r d’una altra càrrega puntual q és la següent
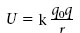
(1.17)
Quan q 0i q 1 són del mateix signe U > 0, i quan són de signe oposat U < 0.
Per trobar l’energia potencial electrostàtica de q 0 deguda al camp E creat per dues càrregues puntuals q 1i q 2 fixades en els punts r 1 i r 2 , respectivament, hem de tenir en compte que E és igual a la suma dels camps E 1 i E 2 deguts a cada una per separat. Si q 0 està en el punt r 0 tenim que
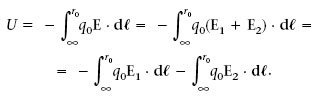
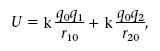
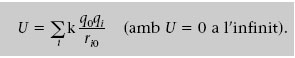
(1.18)
Exemple 1.6. Energia potencial electrostàtica d’una càrrega puntual
Les càrregues q 1 =10 nC i q 2 = -15 nC dels exemples 1.2 i 1.3 estan en els punts (0 m,0 m), (5 m,0 m), respectivament.
a) Quina és l’energia potencial electrostàtica de la càrrega q 3 = 5 nC situada en el punt A = (0 m,5 m)? I si q 3 estigués en el punt B = (2,5 m,0 m)?
b) Quin treball s’ha de fer contra el camp elèctric de q 1i q 2 per portar q 3 de A a B?
a) Per calcular (4) l’energia potencial electrostàtica de q 3 en el punt A, U A , hem de tenir en compte l’equació 1.18 (considerant q 3 en comptes de q 0). Com que les distàncies que hi ha des de q 1i q 2 fins al punt A són r 1 A =5 m i r 2 A = 52m, tenim que
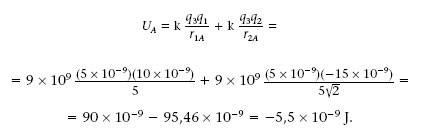
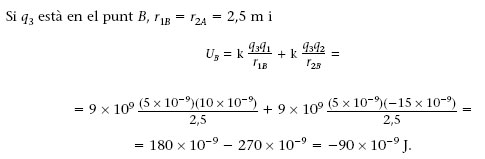
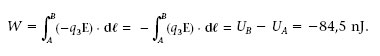
1.4. Considereu les tres càrregues de l’exemple anterior. Si q 3 està en el punt A, quin treball s’ha de fer contra el camp elèctric de les tres càrregues per portar una càrrega q 4 = 2 nC des de l’infinit fins al punt (5 m,5 m)? Quin és el flux del camp elèctric a través d’una superfície esfèrica de 5 m de radi centrada en B?
Resposta
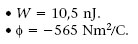
2.10. Potencial elèctric
Com que l’energia potencial electrostàtica d’una càrrega puntual és proporcional al seu valor, és útil introduir el concepte de potencial elèctric.
El potencial elèctric V en un punt es defineix com l’energia potencial electrostàtica U per unitat de càrrega que tindria una càrrega d’assaig positiva q 0 situada en el punt en qüestió. Això és
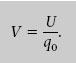
Desplaçant q 0 d’un punt a l’altre es pot trobar V a tots els punts de l’espai. El potencial elèctric és un camp escalar.
La unitat SI per al potencial elèctric és el joule per coulomb (J/C), unitat que s’anomena volt (V).
Electró-volt
En física atòmica i nuclear és adient definir com a unitat d’energia la càrrega fonamental e per un volt:
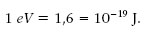
El potencial elèctric degut a un sistema de càrregues puntuals s’obté immediatament dividint l’energia potencial de q 0 deguda a un sistema de càrregues puntuals (equació 1.18) per q 0, això és
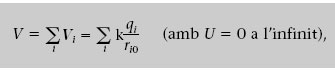
on V i = kq i /r i 0 és el potencial elèctric degut a una sola càrrega puntual.
Fixeu-vos que, de la mateixa manera que el camp E, V és independent de la càrrega d’assaig q 0.
Exemple 1.7. Potencial elèctric degut a càrregues puntuals
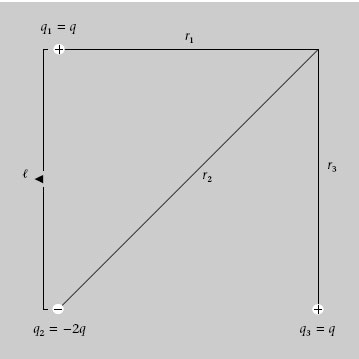
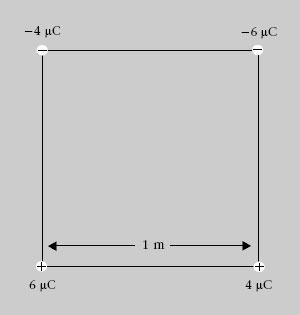
En els vèrtexs d’un quadrat amb costat < = 10 cm, hi ha tres càrregues puntuals (figura 1.18). Les càrregues q 1i q 3 són positives i tenen el mateix valor q = 5 nC. La càrrega q 2 val = 2q. Quin és el potencial elèctric en el vèrtex sense càrrega?
Com que la distància de les dues càrregues positives al vèrtex superior dret és < = 10 cm = 0,1 m, el potencial elèctric creat per cada una en aquest punt és
Figura 1.18
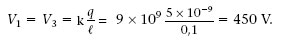
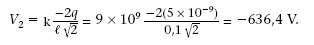
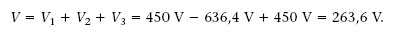
Activitat
1.5. Quin és el potencial elèctric degut al dipol de l’exemple 1.4 i l’activitat 1.2 en els punts P, N, O i S?
Resposta
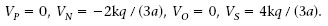
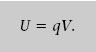
1.6. En el vèrtex sense cap càrrega del quadrat de l’exemple 1.7, hi col·loquem una càrrega puntual positiva igual a q = 5 nC. Quina és la seva energia potencial electrostàtica? A quina força està sotmesa?
Resposta
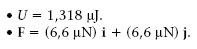
2.11. Diferència de potencial
Com que els valors de l’energia potencial electrostàtica depenen de l’elecció del punt en el qual s’ha fixat U igual a zero, els de V també en depenen. Per tant, només tenen significat físic les diferències de potencial. De les definicions de variació d’energia potencial electrostàtica i de potencial elèctric (equacions 1.16 i 1.19), la diferència de potencial entre dos punts A i B és
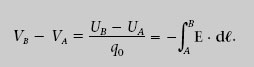
Així, doncs, la diferència de potencial V B – V A és el treball per unitat de càrrega, canviat de signe, que fa el camp elèctric quan una càrrega d’assaig positiva es desplaça des del punt A fins al punt B. També es pot entendre com el treball per unitat de càrrega que s’ha de fer contra el camp elèctric per desplaçar una càrrega d’assaig positiva sense modificar la seva energia cinètica.
Per a calcular la diferència de potencial V B – V A deguda a sistemes de càrregues puntuals, hem de calcular V B i V A mitjançant l’equació 1.20 i restar-los. En altres situacions l’hem de calcular amb la integral de l’equació 1.22.
Activitat
1.7. Sobre l’eix de les x hi ha dues càrregues puntuals q 1 = 2 μC i q 2 =5 -μC. q 2 està 10 cm a la dreta (en el sentit positiu de les x) de q 1.
a) Quin és el camp elèctric 20 cm a l’esquerra de q 1 (punt A)? I 20 cm a la dreta de q 2 (punt B)? b) Quina és la diferència de potencial V B – V A ?
c) En quins punts el camp elèctric és zero?
d) En quins punts de l’eix de les x és zero el potencial elèctric?
Resposta
a) E A 50 × 103 (N/C) i i E B - 925 × 103 (N/C) i.
b) V B – V A = – 105.000 V.
c) A l’eix x, 17,2 cm a l’esquerra de q 1.
d) 6,7 cm a l’esquerra i 2,8 cm a la dreta de q 1.
2.11.1. Diferència de potencial entre dues làmines paral·leles molt properes amb càrregues oposades
A continuació calcularem la diferència de potencial V B – V A entre dues làmines paral·leles i separades una distància d, petita en comparació amb la seva longitud i amplada, que estan carregades amb σ i -σ, respectivament. Recordeu que al subapartat 2.7.1 hem vist que entre les dues làmines el camp es pot considerar uniforme i que les línies de camp van de la làmina positiva a la negativa.
Per calcular V B – V A farem la integral de l’equació 1.22 seguint una línia de camp en sentit contrari, és a dir, des de la làmina negativa a la positiva. Aleshores, com que E i d < són paral·lels i de sentits oposats, E · d < = Ed< i
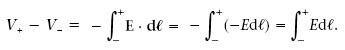
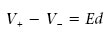
i, tenint en compte que E = σε0 (equació 1.11), obtenim el següent resultat: la diferència de potencial entre dues làmines paral·leles separades una distància d petita i carregades uniformement amb σ i -σ és
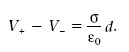
L’equació 1.23 implica que
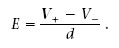
La unitat SI del camp elèctric (NC) també és el volt partit per metre (Vm).
L’equació 1.25 és més útil que l’equació 1.11 perquè V B – V A es pot mesurar amb un voltímetre, mentre que no hi ha aparells per a mesurar directament densitats superficials de càrrega.
La definició de diferència de potencial implica que si una càrrega puntual q es desplaça des d’un punt A fins a un punt B amb potencials V A i V B , respectivament, la seva variació d’energia potencial electrostàtica és
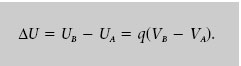
Exemple 1.8. Vàlvula de buit
Un dels dispositius més senzills dels circuits electrònics és el díode (5) . Els primers díodes van ser els de vàlvula de buit, que consisteixen bàsicament en dos elèctrodes a l’interior d’un recipient pràcticament buit. Un dels elèctrodes, l’ànode, està a un potencial més alt que l’altre, el càtode, de manera que hi ha un camp elèctric que va de l’ànode al càtode. Quan el càtode s’escalfa a temperatures prou elevades emet electrons que són accelerats pel camp cap a l’ànode. Considerant que la velocitat inicial dels electrons emesos pel càtode és negligible, quina serà la seva velocitat, v A , quan arribin a l’ànode si el potencial V A de l’ànode és 250 V més alt que el potencial V C del càtode?
La variació d’energia potencial electrostàtica d’un electró que va del càtode a l’ànode és
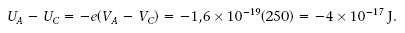
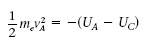
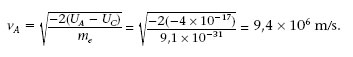
2.12. Superfícies equipotencials
Una superfície equipotencial és aquella en la qual tots els seus punts tenen el mateix potencial.
La definició de potencial elèctric implica que si una càrrega puntual es mou per una superfície equipotencial, el camp elèctric no fa cap treball. Això vol dir que els desplaçaments d entre dos punts molt propers d’una superfície equipotencial són perpendiculars al camp E (E · d < = 0). Per tant, les línies de camp elèctric sempre són perpendiculars a les superfícies equipotencials. Aquesta propietat la podeu comprovar a la figura 1.19.
En el cas d’una càrrega puntual positiva q, les línies de camp s’allunyen de q i el potencial V = kq /r disminueix a mesura que ens allunyem de q. En canvi, si q és negativa les línies s’apropen a q i el potencial disminueix a mesura que ens hi apropem (es fa més negatiu). Per tant, les línies de camp elèctric apunten en el sentit en què el potencial decreix. Aquesta propietat sempre es compleix.
Figura 1.19. Superfícies equipotencials
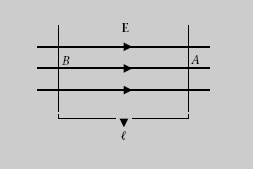
En el cas d’un camp elèctric uniforme, com que les línies de camp són rectes paral·leles, les superfícies equipotencials són plans perpendiculars a les línies de camp (figura 1.20). Per tant, la diferència de potencial entre dos plans equipotencials és igual a la diferència de potencial V B – V A entre dos punts A i B, un de cada pla, units per una línia de camp.
Aleshores, procedint com en el cas de dues làmines paral·leles amb càrregues oposades (subapartat 2.7.1), es demostra que en un camp elèctric uniforme la diferència de potencial entre dos plans equipotencials separats una distància < és
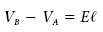
quan les línies de camp van des de B fins a A (si les línies de camp anessin des de A fins a B tindríem
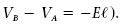
Figura 1.20. Camp E uniforme
2.13. Pantalles de raigs catòdics
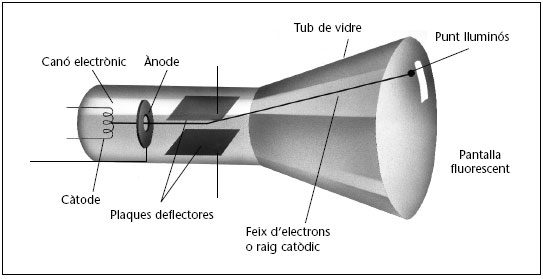
La pantalla d’alguns ordinadors i televisors es fonamenta en el tub de raigs catòdics que hem esquematitzat a la figura 1.21. Aquest dispositiu, en la seva forma més bàsica, consisteix en un tub pràcticament buit (amb gas a molt baixa pressió) que conté un canó electrònic que dispara electrons contra una pantalla fluorescent. Quan els electrons incideixen sobre la pantalla activen substàncies fluorescents i hi produeixen un punt lluminós. Els electrons disparats formen un feix que s’anomena raig catòdic.
El canó electrònic és molt semblant a la vàlvula de buit que hem vist en l’exemple 1.8. El càtode s’escalfa i emet electrons que són atrets per l’ànode que està a un potencial més alt. L’ànode té un petit forat en el centre i els electrons que el travessen surten disparats cap a la pantalla.
En el seu camí cap a la pantalla, els electrons travessen una o més regions amb un camp elèctric o magnètic. Aquests camps fan una força sobre els electrons i els desvien cap a un punt determinat de la pantalla. En els oscil·loscopis (6)
Figura 1.21
En les pantalles de televisor i ordinador, els electrons són desviats per camps magnètics creats per bobines (7) . El feix escombra la pantalla seguint una línia horitzontal, salta cap avall i escombra la línia següent. En un segon la pantalla és escombrada completament unes 30 vegades. En les pantalles de color aquest procés el fan simultàniament tres feixos, cada un dels quals incideix en un punt de la pantalla que produeix un punt lluminós de color vermell, blau o verd.
Avui dia, però, les pantalles fonamentades en el tub de raigs catòdics, a causa del seu volum i del seu consum elèctric, estan deixant pas a les pantalles planes, la qualitat i preu de les quals ha millorat molt els darrers anys. Tots els ordinadors portàtils tenen pantalla plana de cristall líquid controlada per transistors (TFT, thin film transistor), i de mica en mica també es van imposant en els altres ordinadors. D’altra banda, tot i que encara són bastant cars, sembla que els televisors seran amb pantalla plana de plasma. Ambdues tecnologies, la de cristall líquid i la de plasma, són completament diferents entre si i diferents de la de raigs catòdics.
3. Conductors i dielèctrics: condensadors
3.1. Conductors en equilibri electrostàtic
En el subapartat 1.1 d’aquest capítol hem vist que els metalls són bons conductors perquè tenen electrons lliures que es poden desplaçar en el si del material. En aquest apartat estudiarem els conductors metàl·lics en equilibri electrostàtic.
Un conductor en equilibri electrostàtic és aquell en el qual no s’observen càrregues en moviment. Això implica que dintre d’un conductor en equilibri electrostàtic el camp elèctric és igual a zero. Si no fos així les càrregues lliures estarien sotmeses a una força elèctrica que les faria moure. (8)
Com que E és zero, el flux de E a través de qualsevol superfície tancada en l’interior del conductor és nul. Això, segons la llei de Gauss, implica que la càrrega neta a l’interior d’aquestes superfícies és zero. Per tant, no pot haverhi cap excés de càrrega dintre del conductor. En un conductor en equilibri electrostàtic l’excés de càrrega es troba en la seva superfície.
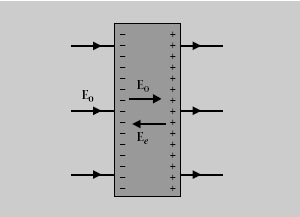
En un metall en equilibri els electrons lliures estan distribuïts de manera que en l’interior la seva càrrega negativa contraresta la positiva dels àtoms ionitzats i només hi ha un excés o defecte d’electrons a la superfície. Quan al metall li apliquem un camp elèctric extern E 0 constant (és a dir, que no canvia en el temps) els electrons lliures es redistribueixen per la superfície i creen un camp addicional E e en l’interior que contraresta el camp extern, E e E 0 , de manera que el camp net a l’interior és nul (vegeu l’exemple de la figura 1.22).
Figura 1.22. Làmina metàl·lica neutra en un camp elèctric extern
A més a més, com que E és nul, la diferència de potencial entre dos punts del conductor també ho és. En fer la integral de línia de l’equació 1.22 seguint un camí interior al conductor, en tots els punts E · d < = 0 i, per tant, aquesta integral també és 0. És a dir, tots els punts d’un conductor en equilibri electrostàtic tenen el mateix potencial elèctric.
Quan es connecten dos conductors carregats, és a dir, els unim amb un cable conductor, es produeix una transferència de càrrega de l’un a l’altre i tots dos queden al mateix potencial. Per tant, dos conductors connectats entre si es comporten com un sol conductor.
La Terra és un conductor que per a molts propòsits es pot considerar infinit i amb una reserva de càrrega il·limitada, fet que implica que el seu potencial sigui constant. Per això, sovint es pren la Terra com a zero del potencial.
3.2. Dielèctrics
Els materials no conductors, com ara el vidre, el paper o els plàstics, s’anomenen dielèctrics. Aquests materials estan formats per molècules neutres que poden ser de dos tipus, polars o no polars.
Per explicar les seves propietats elèctriques primer introduirem el concepte de dipol elèctric: un dipol elèctric és un sistema de dues càrregues puntuals q i q separades una distància d. Els dipols es caracteritzen amb un vector anomenat moment dipolar que es defineix com
p = qd
on d és un vector de mòdul d que assenyala de -q a q.
En un camp E 0 uniforme les càrregues d’un dipol es veuen sotmeses a forces iguals i oposades (figura 1.23) de manera que un dipol tendeix a orientar-se en el sentit de E 0 .
Figura 1.23
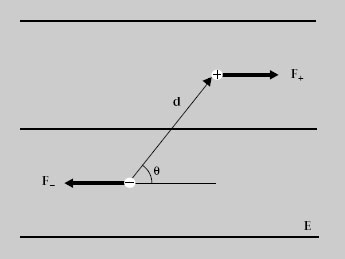
Figura 1.24. Esquema d’un àtom no polar
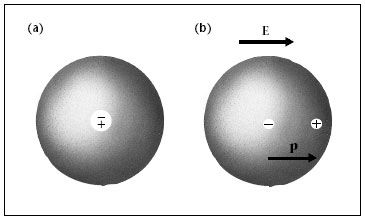
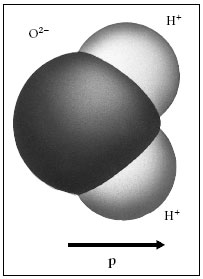
En les molècules polars, com ara la de l’aigua (figura 1.25), el centre de càrrega positiva no coincideix amb el de la negativa i es comporten com un dipol elèctric amb un moment dipolar permanent. Com a conseqüència de l’agitació tèrmica, aquests moments estan orientats a l’atzar de manera que la seva suma és zero. En canvi, en presència d’un camp elèctric extern, els moments tendeixen a orientar-se en el sentit del camp i la seva suma ja no és zero.
Figura 1.25
Quan les molècules d’un dielèctric, polars o no, tenen els moments dipolars predominantment orientats en el sentit d’un camp elèctric extern E 0 , diem que el material està polaritzat. En un material polaritzat els dipols moleculars produeixen un camp elèctric addicional, E b , de sentit oposat a E 0 . Llavors el camp net en l’interior del dielèctric és més feble que el camp E 0 que l’ha polaritzat.
Per entendre millor aquest efecte considerem un bloc d’un material dielèctric en un camp E 0 uniforme com el que es representa en la figura 1.26.
A l’interior del bloc les càrregues positives i negatives dels dipols es compensen. L’efecte net de la polarització és l’aparició d’una distribució superficial de càrrega de signe oposat a les dues cares perpendiculars a E 0 (figura 1.26a). Aquesta distribució de càrregues produeix un camp E b oposat a E 0 (figura 1.26b). Llavors el mòdul del camp net és E = E 0 -E b i, per tant, E < E 0.
Figura 1.26. Polarització
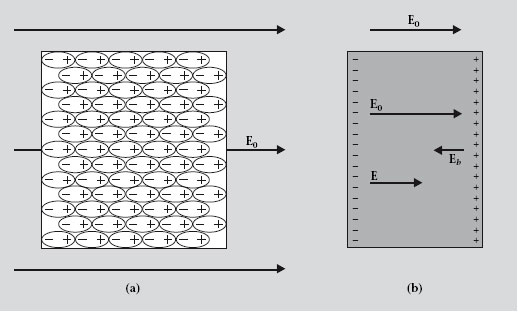
(b) El camp net E dintre del dielèctric és més feble que E 0 .
El camp elèctric E en un medi dielèctric és menys intens que el camp E 0 que hi hauria a l’espai lliure, això és,
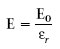
on ε r és una constant adimensional, amb valor igual o superior a 1, característica de cada material que s’anomena constant dielèctrica o permitivitat relativa.
Taula 1.2
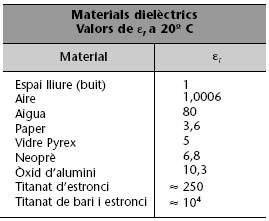
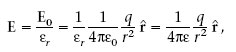
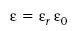
és la permitivitat absoluta del dielèctric.
Fins ara hem estudiat el camp elèctric en l’espai lliure, és a dir, en el buit, sense cap medi dielèctric. Totes les lleis de l’electrostàtica que hem enunciat segueixen sent correctes en un medi dielèctric si en totes les formules substituïm ε0 per ε.
En els materials polars els moments dipolars no estan completament alineats amb el camp elèctric. Com més gran és l’agitació tèrmica, menys alineats estan i, per això, el valor de ε r disminueix quan la temperatura augmenta. En canvi, en els materials no polars ε r es pot considerar independent de la temperatura.
3.3. Condensadors
Un condensador és un dispositiu format per dos conductors molt propers però aïllats l’un de l’altre per un material dielèctric (o el buit).
Independentment de la forma dels dos conductors, cada un s’anomena placa del condensador. La figura 1.27 mostra un condensador de plaques paral·leles format per dues làmines conductores.
D’altra banda, una bateria és un dispositiu que manté una diferència de potencial entre dos terminals metàl·lics. El terminal que està a un potencial més elevat s’anomena born positiu i l’altre és el born negatiu.
Figura 1.27
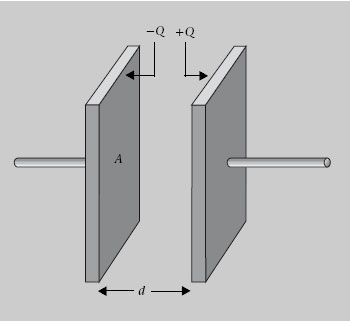
Quan les plaques d’un condensador es connecten als terminals d’una bateria, com s’esquematitza en la figura 1.28, es transfereix càrrega de l’una a l’altra fins que s’assoleix l’equilibri electrostàtic. Aleshores cada placa està al potencial del seu terminal i, per tant, la diferència de potencial entre les plaques és la mateixa que entre els terminals de la bateria.
Figura 1.28
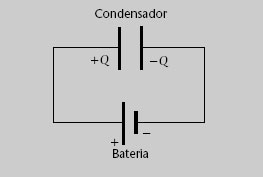
-
El segment més curt del símbol de la bateria representa el born negatiu.
-
Les línies rectes entre el condensador i la bateria representen els fils conductors.
Una vegada assolit l’equilibri, la placa connectada al born positiu té una càrrega positiva Q i l’altra una càrrega -Q. La primera ha perdut electrons que han anat a la segona. Llavors es diu que el condensador està carregat.
Sempre que parlem de la càrrega Q d’un condensador ens referim al valor absolut de la càrrega de cada placa (no a la càrrega neta de les dues, que és zero).
Sovint, una diferència de potencial s’escriu amb la forma abreviada ddp. Si V A és el potencial de la placa carregada positivament, i V B el de l’altra, la ddp V B – V A s’acostuma a indicar amb la lletra V.
Es pot demostrar, i així s’observa experimentalment, que la càrrega Q de tot condensador és proporcional a la ddp V entre les seves plaques.
La raó de proporcionalitat entre la càrrega Q d’un condensador i la diferència de potencial V entre les seves plaques és una propietat de cada condensador que s’anomena capacitat C:
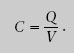
La capacitat d’un condensador ens indica la quantitat de càrrega que pot emmagatzemar per unitat de ddp.
La unitat SI de la capacitat és el coulomb per volt (CV) i rep el nom de farad (F).
El farad és una unitat molt gran i els condensadors que s’utilitzen normalment tenen capacitats compreses entre el picofarad (1 pF = 10-12 F) i el microfarad (1 μF = 10− 6 F).
3.3.1. Condensador de plaques paral·leles
A continuació determinarem la capacitat d’un condensador de plaques paral·leles d’àrea A, separades una distància d, on d és petita en comparació amb la longitud i amplada de les plaques, i que té un dielèctric amb una ε r entre les plaques. Quan aquest condensador té una càrrega Q es comporta com dues làmines paral·leles molt properes carregades amb σ i -σ, on σ Q/A. Llavors, tenint en compte l’equació 1.11 i la 1.29, el camp elèctric entre les plaques és
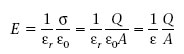
i, d’acord amb l’equació 1.23, deduïm que la diferència de potencial entre les plaques és
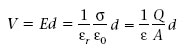
Si substituïm aquest resultat en la definició de capacitat (equació 1.31), veiem que la capacitat d’un condensador de plaques paral·leles és
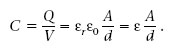
(1.34)
Fixeu-vos que C és independent de Q i V, ja que només depèn de A, d i ε r .
L’equació 1.34 indica una propietat que satisfan tots els condensadors: la seva capacitat, independentment de la forma del condensador, només depèn de la seva geometria i del material dielèctric que hi ha entre les plaques. A més a més, també indica que la capacitat d’un condensador es pot augmentar en:
a) augmentar l’àrea de les seves plaques,
b) disminuir la separació entre les seves plaques,
c) introduir entre les plaques del condensador un material dielèctric amb ε r més gran.
Exemple 1.9. Teclat d’un ordinador
Alguns teclats d’ordinador fan servir interruptors de capacitat. Una placa metàl·lica muntada sobre un èmbol connectat a la tecla actua com a placa superior del condensador (dibuix següent). Quan premem la clau cap avall, la separació entre les plaques varia i, per tant, la seva capacitat també. Aleshores, com que la ddp V es manté constant, la càrrega del condensador es modifica i es dispara el circuit electrònic per introduir la informació a l’ordinador.

La capacitat del condensador abans de prémer és C a εAd a , i després
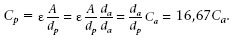
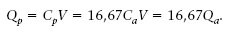
Activitat
1.8. Considereu un condensador de plaques paral·leles, format per dues làmines conductores quadrades de 10 cm de costat i separades 1 mm, que està connectat a una bateria de 12 V. Calculeu-ne la seva capacitat, la seva càrrega i el camp elèctric entre les plaques.
a) Quan l’espai entre les plaques és ple d’aire (ε r ≈1).
b) Quan l’espai entre les plaques és ple de paper (ε r = 3,6).
Resposta
a) 88,5 pF, 1,062 nC i 12 kV/m.
b) 318,7 pF, 3,825 nC i 12 kV/m.
3.3.2. Ruptura del dielèctric
La ddp que es pot aplicar a un condensador i la càrrega que pot emmagatzemar estan limitades pel fet que les molècules del dielèctric es ionitzen en presència de camps elèctrics elevats. Aquest fenomen s’anomena ruptura del dielèctric.
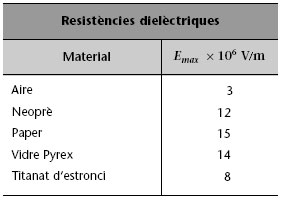
Aleshores els dielèctrics esdevenen conductors, deixen passar càrrega directament d’una placa a l’altra, i el condensador deixa de funcionar com a condensador, és a dir, s’espatlla. La intensitat del camp elèctric a partir de la qual es presenta la ruptura dielèctrica (E max a la taula 1.3) s’anomena resistència dielèctrica del material.
Taula 1.3
3.4. Combinació de condensadors
Per a poder treballar amb ddp més grans i emmagatzemar més càrrega es poden utilitzar combinacions de condensadors.
Sovint, en molts circuits intervenen combinacions de condensadors connectats entre si de formes molt diferents. Aquestes combinacions es poden considerar com un sol condensador amb una capacitat equivalent. La capacitat equivalent d’una combinació de condensadors és la capacitat que hauria de tenir un sol condensador que, quan reemplaça la combinació, produeix els mateixos efectes. Les combinacions més senzilles són les connexions en paral·lel i en sèrie:
1) Condensadors en paral·lel
La figura 1.29a mostra dos condensadors en paral·lel. Les plaques de la dreta dels dos condensadors estan connectades per un fil conductor i, per tant, estan al mateix potencial V A . Les plaques de l’esquerra també estan connectades i estan a un potencial comú V B . Per tant, la ddp V V A V B entre les plaques dels dos condensadors coincideix i les seves càrregues són les que presentem a continuació:
-
Q 1 = C 1 V,
-
Q 2 = C 2 V.
Figura 1.29. Condensadors en paral·lel
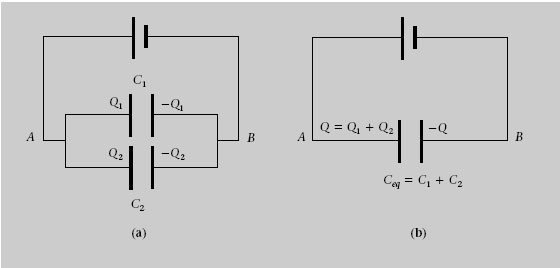
Aquesta combinació de condensadors es comporta com un sol condensador (figura 1.29) amb una ddp V i una càrrega
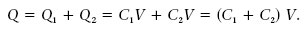
Llavors la capacitat equivalent dels dos condensadors és
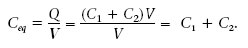
La capacitat equivalent de diversos condensadors en paral·lel és:
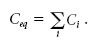
2) Condensadors en sèrie
La figura 1.30a mostra dos condensadors en sèrie. Quan els extrems A i B es connecten a una bateria, aquesta estableix una ddp V = V A - V B > 0, que ha de ser igual a la suma de les diferències de potencial V 1i V 2 de cada condensador, és a dir, V = V 1 + V 2. Per fer-ho, la bateria transfereix electrons de la placa dreta de C 2 a l’esquerra de C 1. Per tant, la placa esquerra de C 1 té una càrrega Q > 0 i la dreta de C 2 té -Q. Com que les càrregues de les plaques d’un condensador han de ser de valor igual absolut però de signe oposat, la placa dreta de C 1 ha de tenir una càrrega -Q i l’esquerra de C 2 ha de tenir Q. És a dir, també es produeix transferència de càrrega entre les plaques connectades pel fil conductor del mig. Aleshores
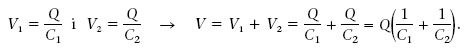
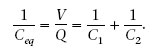
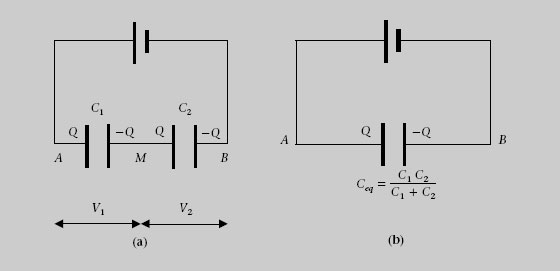
La inversa de la capacitat equivalent de diversos condensadors en sèrie és:
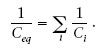
Si associem condensadors en paral·lel aconseguim una capacitat equivalent més gran i, per tant, podem emmagatzemar més càrrega. En canvi, si els associem en sèrie la capacitat equivalent és més petita. L’avantatge de les combinacions en sèrie és que podem aplicar a la combinació una ddp més gran que la que poden aguantar cada condensador per separat, sense que es produeixi la ruptura del dielèctric.
Exemple 1.10. Càlcul de la capacitat equivalent
Quina és la capacitat equivalent entre els punts A i B de la combinació de condensadors de la figura 1.31a, si C 1 = 24 μF, C 2 = 8 μF i C 3 =12 μF? Quina és la càrrega i ddp de cada condensador si entre els terminals A i B apliquem una ddp V = V A +V B 36 V?
C 1i C 2 estan en sèrie i la inversa de la seva capacitat equivalent C 12 és
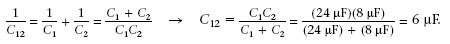
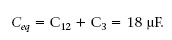
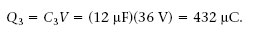
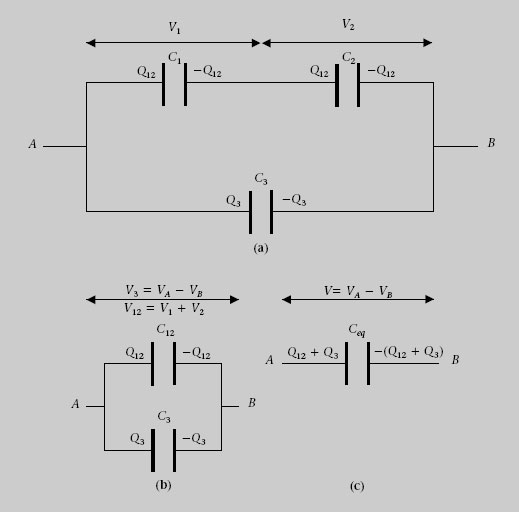
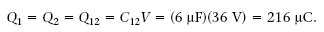
Llavors les diferències de potencial de C 1i C 2 són
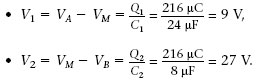
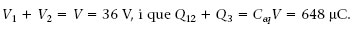
Exemple 1.11. Combinació de condensadors
Disposem de condensadors de 2 μF que poden resistir una ddp màxima de 1.000 V. Com els hem de combinar per tenir un condensador equivalent de 10 μF que resisteixi 4.000 V?
Si connectem 4 condensadors de 2 μF en sèrie a 4.000 V, la ddp de cada un serà de
1.000 V, però la seva capacitat equivalent es reduirà a 0,5 μF. Si connectem en paral·lel 20 d’aquestes combinacions la capacitat equivalent serà de 10 μF.
També es podrien associar 20 condensadors de 2 μF en paral·lel i connectar en sèrie 4 d’aquestes combinacions.
Activitat
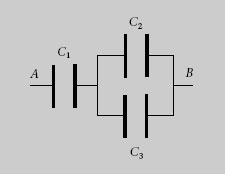
1.9. Quina és la capacitat equivalent entre els punts A i B de la combinació de condensadors de la figura 1.32 si C 1 = 18 μF, C 2 = 4 μF i C 3 =5 μF? Quina és la càrrega i la ddp de cada condensador si entre A i B apliquem 12 V?
Figura 1.32
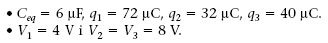
3.5. Energia emmagatzemada en un condensador
Durant el procés de càrrega d’un condensador la bateria transfereix electrons d’una placa a l’altra, de manera que el potencial de la placa que perd electrons (la placa positiva) es va fent més alt que el potencial de la que els guanya (la negativa). Per tant, per portar un electró des de la placa positiva fins a la negativa, la bateria ha de fer un treball per augmentar l’energia potencial de l’electró.
L’energia elèctrica emmagatzemada en un condensador, U, es defineix com l’increment d’energia potencial dels electrons transferits d’una placa a l’altra.
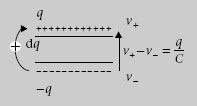
Com que transferir electrons de la placa positiva a la negativa és equivalent a transferir càrrega positiva en sentit contrari, per calcular aquesta energia considerarem el segon procés.
Figura 1.33
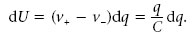
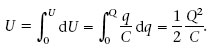
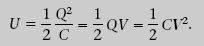
Dos condensadors C 1 = 20 μF i C 2 =15 μF es carreguen amb una ddp V 1 = 24 V i V 2 = 12 V, respectivament. Després es connecten les plaques positives entre si, i les negatives també (figura 1.34). Quina és la variació de la seva energia?
Figura 1.34
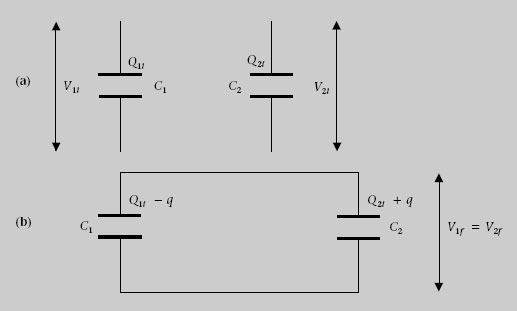
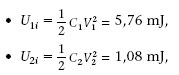
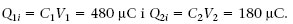
Quan connectem els condensadors entre si la seva ddp ha de ser la mateixa. Això vol dir que part de la càrrega de C 1 ha passat a C 2. Si q és aquesta càrrega, s’ha de satisfer
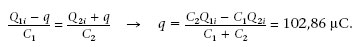
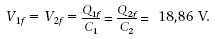
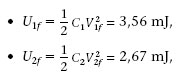
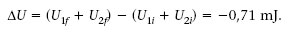
Activitat
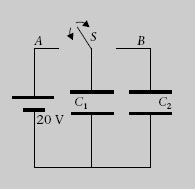
1.10. Dos condensadors de capacitats C 1 = 6 μF i C 2 = 8 μF, inicialment descarregats, es connecten tal com s’indica a la figura 1.35. La bateria proporciona una ddp de 20 V i l’interruptor es pot connectar als punts A o B. Determineu la seva energia després de cada un dels passos següents:
a) Primer connectem l’interruptor al punt A.
b) Després el desconnectem de A i el connectem a B.
c) A continuació el desconnectem de B i el tornem a connectar a A.
d) Finalment el tornem a desconnectar de A i el tornem a connectar a B.
Figura 1.35
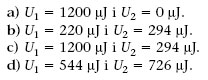
3.5.1. Densitat d’energia d’un camp elèctric
L’energia elèctrica d’un condensador l’hem associat a l’energia potencial de les seves càrregues. Aquesta energia també es pot interpretar com l’energia del camp elèctric entre plaques. En el cas d’un condensador de plaques paral·leles d’àrea A separades una distància d, C = εA/d, i la DDP V i el mòdul del camp elèctric E entre les plaques satisfan V = Ed. Si substituïm C i V en l’equació 1.37, obtenim l’energia del condensador U en funció de E, això és
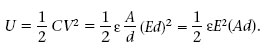
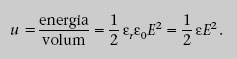
Activitat
1.11. Quina és la densitat d’energia elèctrica a 1 m d’una càrrega puntual de 1 nC submergida en aigua? I en l’espai lliure?
Resposta
-
4,5 pJm3.
-
358 pJm3.
3.6. Condensadors molt petits de gran capacitat
Un dels grans avenços tecnològics actuals és la fabricació de circuits electrònics integrats en xips cada vegada més sofisticats, més petits i més econòmics. Els circuits integrats s’han de complementar amb condensadors que permetin eliminar senyals elèctrics no desitjables i absorbir els excessos de càrrega que podrien espatllar el circuit i alterar el seu funcionament. Així, un dels reptes de la indústria electrònica és aconseguir fabricar condensadors al més petit possibles amb una capacitat prou gran.
En el subapartat 3.3 hem vist que hi ha tres maneres d’augmentar la capacitat d’un condensador. Actualment hi ha dos tipus de condensadors que permeten reunir aquestes tres característiques en el mínim volum possible:
a) Els condensadors ceràmics de capes múltiples (CCCM) estan formats per dues plaques conductores amb les superfícies enfrontades (vegeu figura 1.36). Les plaques estan separades pocs micròmetres (1 μm = 106 m) per un material ceràmic, com el titanat de bari i estronci, que té una constant dielèctrica de l’ordre dels milers.
Figura 1.36. Esquema de la secció d’un CCCM

Les parts grises indiquen les làmines metàl·liques, la zona en blanc correspon al material ceràmic i les dues parts laterals negres representen el conductor que connecta les làmines.
La seva fabricació, explicada molt esquemàticament, consisteix a cobrir per una cara làmines metàl·liques molt fines amb una pel·lícula (capa molt fina) de material ceràmic. Unes quantes desenes d’aquestes làmines s’apilen desplaçades alternativament a dreta i esquerra. Les de la dreta es connecten entre si amb un material conductor, i les de l’esquerra també. Així s’arriben a fabricar condensadors d’uns 4 cm2 d’àrea i un gruix d’uns 40 μm que tenen una capacitat de bastants microfarads (1 μF = 106 F).
b) Els condensadors electrolítics permeten tenir la mateixa capacitat que els CCCM en volums encara més petits. Encara que el seu procés de fabricació és molt més complex, podem pensar que són com un condensador de plaques paral·leles, d’àrea molt gran i molt primes, que s’arruga (com si fos un full de paper) fins a formar un cub molt petit.
Aquests condensadors consten d’una làmina metàl·lica (alumini o tàntal) recoberta d’una pel·lícula d’òxid del mateix metall (que s’obté mitjançant un procés electrolític) amb una pasta conductora per sobre (bari o diòxid de manganès). La capa d’òxid, que pot ser de dècimes de micròmetre, té una constant dielèctrica amb valors compresos entre 5 i 30.
Aquestes tres capes, /làmina metàl·lica/òxid dielèctric/pasta conductora/, constitueixen un condensador molt prim que es pot ‘arrugar’. A causa de les propietats elèctriques dels materials d’aquestes capes, la placa d’un condensador electrolític corresponent a la làmina metàl·lica sempre s’ha de carregar positivament perquè si no el condensador s’espatlla. Per aquesta raó, a diferència dels CCCM, els condensadors electrolítics només es poden fer servir en circuits de corrent continu (en els quals el corrent elèctric sempre circula en el mateix sentit).
Resum
Hi ha dos tipus de càrrega elèctrica, la positiva i la negativa. Les càrregues del mateix signe es repel·leixen i les de signe oposat s’atrauen. Pràcticament tota la matèria que ens envolta està formada per àtoms que tenen un nucli de protons (amb càrrega +e) i neutrons (neutres) que està envoltat d’electrons (amb càrrega -e). Normalment els àtoms tenen tants protons com electrons i per això la majoria dels cossos són neutres. Ara bé, si un cos té un excés o defecte d’electrons té una càrrega neta que és un múltiple enter de e (unitat fonamental de càrrega), és a dir, la càrrega és quantitzada. Si un cos perd electrons (o els guanya) és perquè els ha transferit a un altre cos (o els ha captat), és a dir, la càrrega es conserva.
Dos cossos carregats molt petits comparats amb la distància que els separa es poden considerar càrregues puntuals. En aquesta situació, la força que exerceixen ve donada per la llei de Coulomb. En un sistema de càrregues puntuals, la força neta que actua sobre una càrrega determinada és la suma de cada una de les forces individuals que li fan les altres (principi de superposició de les forces elèctriques).
Un sistema de càrregues crea un camp vectorial anomenat camp elèctric. El camp elèctric en un punt es defineix com la força elèctrica per unitat de càrrega que actuaria sobre una càrrega d’assaig positiva situada en el punt en qüestió. El camp elèctric creat per un sistema de càrregues és la suma dels camps creats per cada una per separat. El camp elèctric es pot representar mitjançant línies de camp. El nombre de línies que travessen una superfície està relacionat amb el flux del camp elèctric. En el cas de superfícies tancades, el flux és proporcional a la càrrega neta a l’interior de la superfície (llei de Gauss).
Les forces elèctriques entre càrregues són conservatives. Per això una càrrega puntual en presència d’un camp elèctric té una energia potencial electrostàtica. El potencial en un punt es defineix com l’energia potencial per unitat de càrrega que té una càrrega d’assaig positiva situada en el punt en qüestió. El potencial degut a un sistema de càrregues és la suma dels potencials deguts a cada una per separat. L’energia potencial i el potencial depenen del punt de referència que es tria com a zero d’aquestes quantitats (en sistemes finits s’acostuma a triar l’infinit) i només tenen significat físic les seves variacions o diferències. La diferència de potencial, V B – V A , es defineix com el treball per unitat de càrrega que s’ha de fer contra el camp elèctric per portar una càrrega d’assaig positiva des de A fins a B, sense modificar la seva energia cinètica. Aquelles superfícies en les quals tots els punts tenen el mateix potencial s’anomenen superfícies equipotencials.
Els materials conductors, com ara els metalls, permeten el moviment de càrrega a través seu. Un conductor en el qual no s’observa moviment de càrregues es troba en equilibri electrostàtic. Aleshores, el camp en el seu interior és nul, tot l’excés de càrrega (si n’hi ha) resideix en la seva superfície i tots els punts del conductor estan al mateix potencial. Els materials no conductors, anomenats aïllants o dielèctrics, tenen molècules que poden ser polars o no polars. Les primeres tenen un moment dipolar permanent i les segones, no. En presència d’un camp elèctric extern, E 0, els dielèctrics es polaritzen i el camp en el seu interior, E, s’afebleix. La raó E 0 E és una propietat de cada material anomenada constant dielèctrica (ε r ).
Dos conductors molt propers separats per un dielèctric formen un condensador. Aquest dispositiu permet emmagatzemar càrrega i energia elèctriques. Quan s’aplica una diferència de potencial (ddp) entre els dos conductors, anomenats plaques, cada una es carrega amb el mateix valor absolut de càrrega però de signes oposats. La raó entre els valors absoluts de la càrrega i la ddp entre plaques és una propietat de cada condensador anomenada capacitat. Com més gran és l’àrea de les plaques enfrontades i més petita és la seva separació, més gran és la capacitat. La capacitat també és més gran com més gran és la constant dielèctrica del material entre les plaques. La capacitat equivalent d’una combinació en paral·lel de condensadors és la suma de les seves capacitats, i la inversa de la capacitat equivalent d’una combinació en sèrie és la suma de les inverses.
Activitat
1. Després d’haver estudiat aquest capítol heu de ser capaços de definir, entendre i relacionar els conceptes següents:
a) Càrrega elèctrica, protó, neutró, electró, nucli atòmic, ió, molècula, càrrega puntual, dipol elèctric, moment dipolar, molècula polar, molècula no polar, raig catòdic, unitat fonamental de càrrega, densitat superficial de càrrega.
b) Llei de Coulomb, constant de Coulomb, permitivitat de l’espai lliure, principi de superposició.
c) Camp escalar, camp vectorial, camp uniforme, camp elèctric, línia de camp elèctric, flux del camp elèctric, llei de Gauss, superfície gaussiana.
d) Conductor, conductor en equilibri electrostàtic, aïllant, dielèctric, moment dipolar induït, moment dipolar permanent, material polaritzat, constant dielètrica, ruptura de dielèctric, resistència dielèctrica, permitivitat relativa, permitivitat absoluta.
e) Treball, força conservativa, energia cinètica, energia potencial, energia mecànica, potencial elèctric, diferència de potencial, superfície equipotencial, densitat d’energia del camp elèctric.
f) Condensador, placa d’un condensador, condensador de plaques paral·leles, energia d’un condensador, condensadors en sèrie, condensadors en paral·lel, capacitat d’un condensador, capacitat equivalent.
Exercicis d’autoavaluació
De selecció
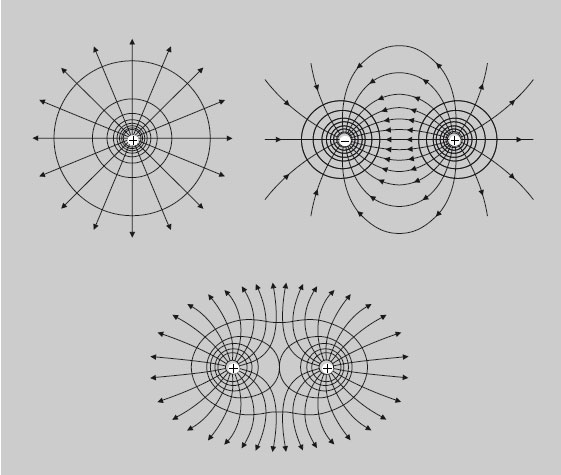
1. En el cas del camp elèctric creat per dues càrregues puntuals idèntiques...
a) hi ha un punt on el camp i el potencial elèctrics són nuls.
b) hi ha un punt on el camp elèctric és nul.
c) hi ha punts on el potencial elèctric és nul.
2. En el cas del camp elèctric creat per un dipol elèctric...
a) hi ha un punt on el camp i el potencial elèctrics són nuls.
b) hi ha un punt on el camp elèctric és nul.
c) hi ha punts on el potencial elèctric és nul.
3. Si el flux del camp elèctric a través d’una superfície tancada és nul...
a) en l’interior de la superfície no hi ha cap càrrega.
b) la càrrega neta a l’interior de la superfície és nul·la.
c) les línies del camp elèctric són tangents a la superfície.
4. Si el flux d’un camp elèctric uniforme a través d’una superfície plana és nul...
a) en l’interior de la superfície no hi ha cap càrrega.
b) la càrrega neta a l’interior de la superfície és nul·la.
c) les línies del camp elèctric són tangents a la superfície.
5. Les línies de camp elèctric...
a) són perpendiculars al camp elèctric i tangents a les superfícies equipotencials.
b) són tangents al camp elèctric i tangents a les superfícies equipotencials.
c) són tangents al camp elèctric i perpendiculars a les superfícies equipotencials.
6. Les línies de camp elèctric...
a) surten de les càrregues positives i apunten en el sentit en què el potencial decreix.
b) surten de les càrregues positives i apunten en el sentit en què el potencial creix.
c) surten de les càrregues negatives i apunten en el sentit en què el potencial decreix.
7. El treball que hem de fer per apropar una càrrega puntual positiva a una càrrega puntual negativa, sense modificar la seva energia cinètica, és...
a) positiu.
b) negatiu.
c) nul si l’apropem seguint una línia de camp.
8. En l’interior d’un conductor en equilibri electrostàtic...
a) el camp elèctric i la càrrega neta són nuls.
b) el camp i el potencial elèctric són nuls.
c) el potencial elèctric i la càrrega neta són nuls.
9. En presència d’un camp elèctric extern, les molècules no polars d’un material dielèctric...
a) tenen un moment dipolar afeblit.
b) no tenen moment dipolar.
c) tenen un moment dipolar induït.
10. Sigui un condensador de plaques paral·leles connectat a una bateria. Si apropem les plaques, la seva energia...
a) augmenta.
b) disminueix.
c) no canvia.
11. Sigui un condensador de plaques paral·leles carregat que no està connectat a cap bateria. Si apropem les plaques, la seva energia...
a) augmenta.
b) disminueix.
c) no canvia.
12. Dos condensadors de plaques paral·leles amb la mateixa àrea i separades la mateixa distància tenen un material dielèctric diferent entre les plaques. Si els connectem en sèrie a una bateria, quin dels dos tindrà més càrrega?
a) El que tingui un material amb la constant dielèctrica més alta.
b) Els dos tindran la mateixa càrrega.
c) El que tingui una ddp entre plaques més alta.
13.Els dos condensadors de la qüestió anterior els connectem en paral·lel a una bateria. Quin dels dos tindrà més càrrega?
a) El que tingui un material amb la constant dielèctrica més alta.
b) Els dos tindran la mateixa càrrega.
c) El que tingui una ddp entre plaques més alta.
Problemes
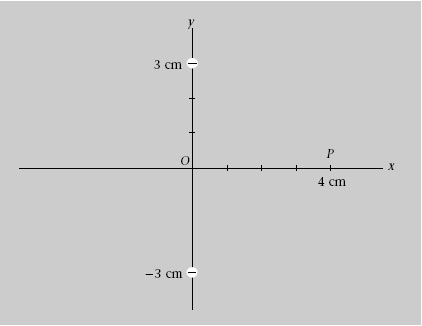
1. Les dues càrregues negatives de la figura 1.37 són iguals a q = 150 pC i estan en els punts (0 cm,3 cm) i (0 cm,-3 cm), respectivament.
a) Quin és el camp elèctric en el punt P = (4 cm,0 cm)?
b) Quina és la diferència de potencial V P = V O que hi ha entre l’origen de coordenades O i el punt P?
c) En quin punt serà nul·la la força que actua sobre una càrrega negativa Q = -0,2 nC?
d) Si Q estigués en el punt P, quina seria la seva energia potencial i a quina força es veuria sotmesa?
e) Considerant que Q està en el punt P, quin és el flux a través d’una superfície esfèrica de 5 cm de radi centrada a l’origen de coordenades?
Figura 1.37
a) Quina és la ddp V B - V A entre un punt A situat a 10 cm del pla i un punt B situat a 5 cm?
b) Quin és el valor absolut del flux del camp elèctric a través d’una superfície plana circular, amb un radi de 5 cm, paral·lela al pla i situada a 15 cm d’aquest?
c) Si a 20 cm del pla hi ha una càrrega puntual negativa Q = -1 nC, quin és el flux del camp elèctric a través d’una superfície esfèrica de 10 cm de radi i amb el centre situat en el pla?
d) En la situació de l’apartat anterior, en quin punt de l’espai serà nul·la la força total que actua sobre una càrrega puntual q = 1 pC?
3. El sistema de càrregues de sota consisteix en un pla, que podem considerar infinit, carregat uniformement amb una densitat superficial de 1 nC/m2, i dues càrregues puntuals -2Q i +Q, amb Q = 0,4 nC, situades a 0,1 m del pla i separades 0,15 m.
Determineu:
a) El camp elèctric en el punt P = (0 cm,0,1 m).
b) El punt de la recta que passa per les dues càrregues puntuals on el camp elèctric total és vertical.
c) El flux del camp elèctric a través d’un cub de 0,5 m de costat centrat en l’origen de coordenades.
d) La ddp V P - V N entre els punts P i N = (0 cm , 0,05 m).
Figura 1.38

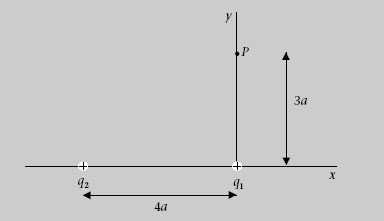
a) El camp i el potencial elèctrics en el punt P = (0,3a).
b)El valor d’una càrrega puntual q 3 i el punt de l’eix de les x en el qual l’hem de situar perquè el camp elèctric en el punt P s’anul·li.
c) El treball que farà el camp elèctric per traslladar q 3 des de P fins a l’infinit.
Figura 1.39
5. El camp elèctric entre les plaques d’un condensador de plaques paral·leles d’1,5 pF és de 40 kV/m. Si la separació entre les plaques és de 5 mm, quina és la seva càrrega? Si un electró s’escapa de la placa negativa amb una velocitat negligible, amb quina velocitat arribarà a la positiva?
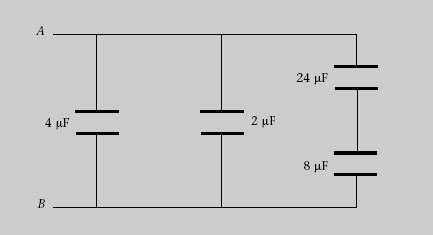
6. Calculeu la capacitat equivalent entre els punts A i B dels dos condensadors de la figura 1.40. Determineu la càrrega i l’energia de cadascun si connectem A i B als terminals d’una bateria de 36 V.
Figura 1.40
7. Connectem el commutador de la figura 1.41 al punt A, i un cop s’ha carregat el condensador de 4 μF, el connectem al punt B. Quines seran la càrrega i la ddp finals de cada condensador?
Figura 1.41
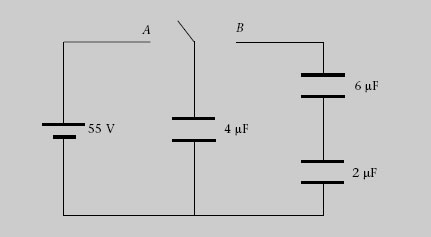
Figura 1.42
Solucionari
Exercicis d’autoavaluació
De selecció
1.b, 2.c, 3.b, 4.c, 5.c, 6.a, 7.b, 8.a, 9.c, 10.a, 11.b, 12.b, 13.a.
Problemes
1.
a) E P = (-864 V/m) i.
b) V P - V O =36 V.
c) (0 cm,0 cm).
d) U P =10,8 nJ i F P (172,8 nN) i.
e) φ = -56,5 Vm.
2. a) V B V A 28,25 V.
b) | φ | = 4,44 Vm.
c) φ = 35,5 Vm.
d) A 32,6 cm del pla, en el punt de la recta normal al pla que passa per Q.
3.
a) E P = (1,92 × 103 V/m) i (56,56 V/m) j.
b) (43,7 cm , 10 cm).
c) φ = 16,95 Vm.
d) V P- - V N 10,83 V.
4.
a) E p k(4q) / (9a 2) (i j), V p = k(28q) / (9a).
b) q 3 = 8√ 2 q en (-3a,0).
c) W= -k(224√ 2)q 2 / (9a).
5. Q = 0,3 nC i V 8,39 × 106 m/s.
6. C eq = 12 μF, Q 4 = 144 μC, Q 2 = 72 μC, Q 8 = Q 24 = 216 μC, U 4 = 2,592 mJ, U 2 = 1,296 mJ,
U 8 = 2,916 mJ i U 24 = 0,972 mJ.
7. Q 4 = 160 μC, Q 2 = Q 6 = 60 μC, V 4 = 40 V, V 2 = 30 V i V 6 = 10 V.
8. E = (23,142 kV/m) i + (115,708 kV/m) j, V = 0 V, u = 0,1356 J/m3.