1

Prehistoria de los cuantos: Kirchhoff, espectros y radiaciones

Aunque el inicio de la física cuántica se sitúa habitualmente en 1900, sus orígenes se remontan mucho más atrás, al siglo XIX. De hecho, los tres primeros capítulos de este libro (estrictamente, los cuatro primeros, ya que 1900 fue el último año del siglo XIX) tienen como escenario aquella centuria. En este primer capítulo me ocuparé básicamente de dos dominios, que, como veremos, resultaron cruciales para el desarrollo de la física cuántica: 1) las líneas espectrales (espectros) que se observaban en las radiaciones emitidas por los diferentes elementos; 2) los esfuerzos teóricos por explicar las propiedades de tales radiaciones y algunos problemas que afectaban a la descripción teórica de ciertos aspectos de la materia. Comencemos por el primero, por el de los espectros, el de la espectroscopia.

ESPECTROS

Fue Isaac Newton (1642-1727) quien descubrió en el siglo XVII que al pasar a través de un prisma de vidrio la luz se descompone en colores diferentes (los colores del arco iris), produciendo lo que se denomina un espectro. Recíprocamente, comprobó que al componer esos colores se recuperaba la luz «normal».

Estimulado por los cursos de óptica de Isaac Barrow (1630-1677) en Cambridge y la teoría de la luz de Descartes (1596-1650), hacia 1664 Newton comenzó a interesarse por los fenómenos ópticos. No fue, sin embargo, hasta 1666 (año que pasó en la finca familiar de Woolsthorpe debido a una epidemia que obligó a cerrar la Universidad de Cambridge en agosto de 1665) cuando intensificó sus esfuerzos, recurriendo a un instrumento simple pero en sus manos extremadamente precioso: un prisma de vidrio. He aquí cómo se refirió al inicio de sus experimentos en el artículo que publicó en el número del 19 de febrero de 1671/72 de las Philosophical Transactions de la Royal Society (Newton 1671/72: 3075-3076): «A comienzos del año 1666 (momento en el que me apliqué a pulir cristales ópticos de formas distintas a la esférica) me proporcioné un prisma triangular de cristal, para ocuparme con él del celebrado Fenómeno de los Colores. Habiendo oscurecido mi habitación, hice un pequeño agujero en una contraventana, para dejar pasar sólo una cantidad conveniente de luz del Sol, y coloqué mi prisma en su entrada, de manera que pudiese ser refractado en la pared opuesta. Al principio, ver los vivos e intensos colores así producidos constituyó una muy entretenida distracción, pero después de un rato intentando considerarlos más cuidadosamente, me sorprendió verlos en forma oblonga, cuando, según las leyes aceptadas de la Refracción, esperaba que hubiese sido circular».

Semejante anomalía le indujo a recurrir a un segundo prisma, con el que llegó a la conclusión de que los colores (observados desde hacía ya siglos) que aparecían al pasar la luz blanca inicial por los prismas no eran «cualidades de luz, derivadas de refracciones o reflexiones de cuerpos naturales (como se cree generalmente), sino propiedades originales o innatas». La luz visible se convertía, en consecuencia, en la combinación de diferentes colores elementales, como muestra con particular claridad el arco iris.

Durante el siglo que siguió a las observaciones de Newton, pocos avances importantes se realizaron en este campo. Uno de ellos tuvo lugar en 1752, cuando Thomas Melvill (f. 1753) se aprovechó de que al calentar los cuerpos sólidos (y los líquidos también), éstos emiten, cuando alcanzan una temperatura suficientemente alta, radiaciones. Melvill hizo pasar por un prisma la luz que emitía una llama producida por sodio y observó un espectro continuo, surcado por una serie de líneas brillantes. Que sepamos, fue la primera observación de un espectro de emisión.

Exactamente cincuenta años después de las observaciones de Melvill, esto es, en 1802, William Hyde Wollaston (1766-1828) advirtió que en el espectro de la luz procedente del Sol aparecían unas pocas líneas oscuras, que Newton no había detectado y que él tomó como los bordes de los colores naturales (Wollaston 1802). Algunos años después (1814-1815), Joseph von Fraunhofer (1787-1826) examinó con mucho más detalle el espectro de la luz del Sol, descubriendo cerca de seiscientas de tales rayas oscuras, que a partir de entonces se conocieron como «líneas de Fraunhofer». Pero no se limitó a descubrir nuevas rayas, sino que también se propuso establecer el lugar del espectro en que se encontraban situadas, determinando la posición de trescientas veinticuatro.

Es interesante señalar que Fraunhofer era un óptico profesional, entre cuyas ocupaciones figuraba la de construir lentes; de hecho, fabricó las mejores lentes acromáticas y prismas que había visto jamás la comunidad óptica. Por este motivo tenía más facilidad que la mayoría de los científicos de su época para utilizar prismas que no «deformasen» demasiado la luz. Su interés por el espectro solar provenía asimismo de su profesión: necesitaba localizar en el espectro un punto de referencia que le permitiera medir con precisión los índices de refracción (grado de desviación de la luz al pasar por un cierto medio) de los distintos materiales con los que construía las lentes de sus instrumentos ópticos.

Gradualmente se fue descubriendo que era posible producir «artificialmente» líneas oscuras en los espectros haciendo pasar la luz a través de diversas sustancias, confirmándose por otra parte el tipo de observación de Melvill: los espectros producidos por algunas llamas estaban atravesados por líneas brillantes.

Naturalmente, se efectuaron varios intentos de explicar y relacionar tales observaciones, pero pasó algún tiempo hasta producirse un avance sustancial. Éste llegó pasado el ecuador del siglo, gracias a las investigaciones de un físico de la Universidad de Heidelberg, Gustav Robert Kirchhoff (1824-1887), que encontró un magnífico apoyo en el químico Robert Wilhelm Bunsen (1811-1899).

GUSTAV KIRCHHOFF Y LA ESPECTROSCOPIA

Formado en la universidad de su ciudad natal, Königsberg, donde se vio influido especialmente por Franz Neumann (1798-1895), Kirchhoff se trasladó a Berlín después de doctorarse en 1847. En la capital prusiana comenzó su carrera docente, al lograr en 1848 el título de Privatdozent (habilitado para dictar cursos en la universidad, sin recibir un salario oficial, únicamente el procedente de las matrículas de los alumnos de sus cursos). En 1850 se incorporó como extraordinarias a la Universidad de Breslau. Allí conoció a Robert Bunsen, pero éste se trasladó a Heidelberg el año siguiente. En 1854, cuando Philipp von Jolly (1809-1884) dejó su cátedra de Física en Heidelberg, Bunsen propuso a Kirchhoff para sucederle, iniciativa que tuvo finalmente éxito. Mantendría este puesto hasta 1875, cuando aceptó una cátedra de Física teórica en la Universidad de Berlín, ciudad en la que falleció el 17 de octubre de 1887. En el capítulo 4 tendremos oportunidad de comprobar que uno de sus alumnos en Berlín fue un estudiante llamado Max Planck.

Tras haberse dedicado al estudio de la elasticidad y la electricidad, hacia 1858 Kirchhoff comenzó a interesarse por el análisis espectral. En esencia, el origen de su interés fue el siguiente: en Heidelberg, Bunsen estaba investigando la posibilidad de analizar sales según los colores que daban al arder, proceso en el que desempeñaba un papel importante un instrumento que Bunsen desarrolló en la década de 1850: el denominado «mechero de Bunsen», con el que el gas inyectado se quemaba con una llama que aunque caliente no era brillante. Y en este punto entra Kirchhoff en la historia, ya que en 1859 señaló a su colega que un método más preciso que el «colorímetro» para llevar a cabo semejante tarea de identificación era a través del espectro al que daban origen tales llamas coloreadas. Unieron sus fuerzas: Bunsen suministrando no sólo su mechero, que para el análisis espectroscópico era aún más útil, sino también sales de gran pureza, mientras que Kirchhoff aportaba el espectroscopio con el que observar las líneas. El poder e importancia del método para la química se mostró muy pronto, al descubrirse con él, como veremos más adelante, dos nuevos elementos químicos, el cesio y el rubidio.

Pero antes de entrar en esta cuestión, es preciso explicar unos detalles muy importantes de la aportación de Kirchhoff.

En el otoño de 1859, mientras llevaba a cabo unos trabajos preliminares para su colaboración con Bunsen, Kirchhoff realizó una sorprendente observación. Se sabía, gracias a trabajos llevados a cabo por León Foucault (1819-1868) en 1849, que las denominadas líneas D (oscuras), observadas en el espectro solar por Fraunhofer en 1814, coincidían con las líneas amarillas brillantes detectadas en las llamas que contenían sodio. Este efecto se podía observar con cierta facilidad haciendo que la luz del Sol llegase a un espectroscopio tras atravesar una llama de sodio; si se debilitaba suficientemente la luz solar, las oscuras líneas de Fraunhofer eran sustituidas por las líneas brillantes provenientes de la llama. El hallazgo de Kirchhoff fue advertir que si la intensidad del espectro solar aumentaba por encima de un cierto límite, las líneas D se hacían todavía más oscuras al interponer una llama de sodio. Intuyó inmediatamente que se trataba de algo fundamental, aunque no sabía cómo explicar el fenómeno.

Un día después se le ocurrió una explicación, que pronto se vio confirmada por nuevos experimentos: una sustancia capaz de emitir una cierta línea espectral posee una gran capacidad de absorber la misma línea; por eso las líneas D, características del sodio, se hacían más oscuras cuando se interponía una llama también de sodio. Otra manifestación de semejante propiedad podía ser que la simple interposición de una llama de sodio de baja temperatura sería suficiente para producir artificialmente las líneas D en el espectro de una fuente de luz intensa que no las mostraba inicialmente, pero este hecho conducía a una conclusión fundamental: las líneas D (oscuras, insisto) que aparecían en el espectro solar tenían que ser debidas a que en la atmósfera del Sol existía sodio, que mediante un fenómeno de absorción originaba las mencionadas rayas espectrales.

Antes de que acabase el año Kirchhoff (1859 a) informó a la comunidad científica de sus ideas, en las que continuó trabajando durante algún tiempo. Un ejemplo en este sentido es la carta que dirigió el 6 de agosto de 1860 al químico Otto Linné Erdmann (1804-1869), y de la que el químico británico Henry Roscoe (1833-1915) publicó un extracto traducido al inglés en el Philosophical Magazine (Kirchhoff 1861 a; 1862, versión en castellano). Escribía en ella:

Desde que remití mi Memoria a la Academia de Ciencias de Berlín, no he dejado de proseguir mis investigaciones en el mismo sentido. Había enunciado yo la ley de que una llama absorbe los mismos rayos que emite; no insistiré sobre las pruebas teóricas que he dado en confirmación de esta ley, ni sobre los experimentos que hemos hecho Mr. Bunsen y yo para demostrar que las rayas brillantes del espectro de una llama pueden servir para caracterizar los metales introducidos en esta llama; mi intención es comunicaros los resultados de mis investigaciones respecto al análisis químico de la atmósfera solar.

El Sol tiene una atmósfera gaseosa, candente, y que envuelve un núcleo cuya temperatura es todavía mucho más elevada. Si pudiésemos observar el espectro de esta atmósfera, notaríamos en él las rayas brillantes características de los metales contenidos en este medio, y por ellas podríamos determinar la naturaleza de estos metales. Pero la luz más intensa emitida por el núcleo solar no permite que el espectro de esta atmósfera se produzca directamente: obra sobre él invirtiéndole, según lo que he expuesto anteriormente; es decir, que sus rayas brillantes parecen oscuras. No vemos el espectro de la atmósfera solar por sí mismo, sino su imagen negativa. Esta circunstancia permite determinar con igual exactitud la naturaleza de los metales contenidos en esta atmósfera, para lo cual basta tener un conocimiento profundo del espectro solar, y de los producidos por cada uno de los diferentes metales.

En este punto Kirchhoff se detenía en explicar el aparato que había hecho posible sus observaciones: un espectroscopio con cuatro prismas (como veremos más adelante, el espectroscopio utilizado en su colaboración con Bunsen fue inicialmente uno más rudimentario: tenía únicamente un prisma).¹ Me detengo en la descripción que hacía de él, entre otros motivos porque con demasiada frecuencia no se hace hincapié en la importancia que los instrumentos tienen en el desarrollo de la ciencia, con lo que la comprensión de ésta resulta gravemente deteriorada. Esto es particularmente cierto en el caso de la espectroscopia, lo que es tanto como decir en apartados básicos de la astrofísica y de la física cuántica. «En los talleres de instrumentos de óptica y de astronomía de Mr. Steinheil», señalaba Kirchhoff, «he tenido la dicha de encontrar un aparato que produce espectros de una intensidad y pureza, a las cuales seguramente no se había llegado todavía. Este aparato se compone de cuatro grandes prismas de flintglass [cristal de roca] y de dos anteojos muy perfectos, y permite ver en el espectro solar millares de rayas, en las cuales es fácil sin embargo orientarse en razón de las diferencias que presentan en su ancho y en su grado de oscuridad, y por los grupos variados que ofrecen». Y continuaba:

Este aparato hace ver el espectro de una luz artificial con la misma intensidad que el espectro solar cuando es suficiente la potencia luminosa de la llama. La del gas común, en la cual se volatilizan las combinaciones metálicas, no basta generalmente, pero la chispa eléctrica da con la mayor limpieza el espectro del metal que constituye los electrodos. Un aparato grande de inducción de Ruhmkorff me produce chispas, que se suceden con bastante rapidez para que pueda observarse este espectro tan cómodamente como el espectro solar.

Una disposición muy sencilla permite comparar con una sola observación los espectros de los dos focos luminosos. Consiste en hacer penetrar por la mitad superior de la hendidura los rayos de uno de los dos focos luminosos, mientras que la mitad inferior deja paso libre a los rayos del otro. En este caso uno de los espectros viene a colocarse inmediatamente debajo del otro, del cual sólo le separa una sencilla línea apenas perceptible. Con facilidad y exactitud se puede estar seguro de si hay coincidencia de ciertas rayas de uno de los espectros con las del segundo.

De esta forma, se había «cerciorado de que todas las rayas brillantes peculiares del hierro corresponden a las rayas oscuras del espectro solar. He podido indicar hasta 72 rayas oscuras en el espectro solar, que corresponden a las rayas brillantes del espectro del hierro: estas rayas están enteramente situadas en el espacio que he reproducido, las cuales son debidas al hierro que existe en la atmósfera solar. Armstrong no ha observado en el espectro de la chispa eléctrica más que tres rayas brillantes del hierro, contenidas en los mismos límites. Mr. Masson apenas ha observado otras más; Mr. Van der Willigen, por su parte, dice que el hierro no hace aparecer con el espectro de la chispa eléctrica más que un corto número de rayas, y que éstas son muy débiles. Debo atribuir a la fuerza de mi aparato el gran número de rayas brillantes, cuya presencia he demostrado con una exactitud completa en el espectro del hierro».

El hierro, como es bien sabido, es un elemento que produce unas tres mil líneas espectrales, lo que da idea de lo compleja que es la tarea de estudiar su estructura espectral. Kirchhoff advirtió este hecho: «El hierro se distingue [...] por el gran número de rayas notables que presenta en el espectro solar». No se limitó, sin embargo, a él: «El magnesio es interesante por el hecho de que presenta en el espectro solar el grupo más aparente de las rayas de Fraunhofer, es decir, el verde, que se compone de tres rayas fuertes. Otras rayas oscuras del espectro solar coinciden claramente, pero son mucho menos notables que las rayas brillantes del cromo y del níquel. Puede, pues, considerarse como demostrada la presencia de estos metales en la atmósfera del Sol. Además, parece que otros muchos metales faltan en ella completamente. Así, los espectros de la plata, del cobre, del zinc, del plomo, del aluminio, del cobalto, del antimonio presentan también rayas extraordinariamente brillantes, pero que no coinciden con ninguna de las rayas oscuras del espectro solar, al menos entre las que son visibles». Momento en que añadía: «Espero dar pronto detalles más minuciosos sobre este punto».

Las consecuencias de los argumentos y observaciones de Kirchhoff eran evidentes. Se hacía posible estudiar por primera vez la composición de los cuerpos celestes sin más que analizar la luz que recibimos de ellos. En otras palabras: nacía una nueva ciencia, la astrofísica, que permitía abordar cuestiones imposibles de resolver para la vieja, varias veces milenaria, astronomía. En sus memorias Roscoe (1906: 69), colaborador de Bunsen durante algún tiempo en Alemania, recordaba la impresión que le suscitó este avance: «Nunca olvidaré la impresión que me produjo mirar a través del magnífico espectroscopio de Kirchhoff, instalado en una de las habitaciones traseras del viejo edificio de la Hauptstrasse, que entonces hacía las funciones de Instituto de Física, y ver la coincidencia de las líneas brillantes en el espectro del hierro con las oscuras líneas de Fraunhofer en el espectro solar. La evidencia de que el hierro, tal y como lo conocemos en esta Tierra, está contenido en la atmósfera solar, aparece instantáneamente como concluyente. Y no han transcurrido aún cuarenta años desde que Comte, argumentando en su Système que los investigadores no deberían malgastar su tiempo intentando lo imposible, utilizase como un ejemplo de lo que quería decir por imposible que el conocimiento de la composición del Sol a una distancia de 91 millones de millas debía permanecer para siempre inalcanzable». «Ya no será necesario tocar un cuerpo para determinar su naturaleza química: bastará verlo», escribía el químico francés Jean-Baptiste-André Dumas (1800-1884; 1861: 484). Y, por supuesto, reconocía, como reconocían todos, que se estaba ante el principio: «Lo que el estado de los instrumentos actuales de óptica permite efectuar en el día de hoy respecto del Sol y las principales estrellas fijas, otros nuevos progresos permitirán que lo intente el hombre respecto de los astros más distantes y luminosos, y reconocer así por medio de qué elementos ha formado Dios los mundos que pueblan el Universo». Treinta años más tarde, las esperanzas fundadas en el nuevo método se habían consolidado, como muestran las palabras que pronunció en su discurso como presidente de la British Association for the Advancement of Science, el astrónomo y espectroscopista William Huggins (1824-1910; 1891: 37), en la reunión anual celebrada en Cardiff: «La astronomía, la más antigua de las ciencias, ha más que renovado su juventud, en ningún momento del pasado ha estado tan encendida con ilimitadas aspiraciones y esperanzas. Nunca fueron sus templos tan numerosos, ni tan grande la masa de sus devotos».

El propio Kirchhoff continuó explorando este campo, como anunciaba en su carta a Erdmann. Sin embargo, no profundizaré en este ámbito de sus actividades, simplemente diré que una de sus publicaciones más acabadas en este campo apareció en dos entregas en 1861 y 1862 (Kirchhoff 1861/62).

KIRCHHOFF Y BUNSEN (1860)

Aunque me he referido a la colaboración de Kirchhoff y Bunsen, no me he detenido todavía en su contenido, centrado como estaba en seguir la línea argumental de las aportaciones espectroscópicas de Kirchhoff. Volvamos, pues, atrás, a esa colaboración, que se concretó en un extenso artículo conjunto, publicado en dos partes (Kirchhoff y Bunsen 1860, 1861).²

Que, al contrario de las memorias de Kirchhoff que he comentado en la sección precedente, basadas bien en interpretaciones teóricas o en observaciones experimentales solares, el trabajo de Bunsen y Kirchhoff estaba dedicado fundamentalmente a aspectos químicos (motivo por el cual la participación de Bunsen se hacía imprescindible) es algo que quedaba claro desde el principio: «Se sabe», escribían (Kirchhoff y Bunsen 1862: 205-207), «que muchas sustancias introducidas en una llama tienen la propiedad de producir en el espectro de ésta rayas brillantes particulares: en la existencia de estas rayas puede fundarse un método de análisis cualitativo que ensancha considerablemente el dominio de las investigaciones químicas y que permite resolver problemas hasta ahora insuperables. Nos limitaremos en esta Memoria a aplicar este método a la investigación de los metales alcalinos y alcalino-térreos, haciendo resaltar su valor con una serie de ejemplos».

A continuación explicaban los instrumentos que habían empleado, sin los cuales, como ya he apuntado, nada habría sido posible. El primero era el mechero de Bunsen, el humilde, familiar, mechero de Bunsen, que —es uno de los puntos que pretendo transmitir en este capítulo— desempeñó de esta forma un papel importante en los orígenes de la física cuántica: «Las rayas del espectro son tanto más visibles, cuanto más elevada es la temperatura de la llama y menor su potencia luminosa. La lámpara de gas, que uno de nosotros ha descrito, produce una llama poco luminosa y de una temperatura muy elevada, y se presta perfectamente al examen de las rayas brillantes que dan ciertos cuerpos». El segundo, el espectroscopio, que era más primitivo que el de cuatro prismas empleado por Kirchhoff, con el que nos encontramos con anterioridad: «El aparato que hemos empleado para la observación del espectro se compone de una caja, ennegrecida por su interior, colocada sobre tres pies, y cuya base es un trapecio. Las dos paredes correspondientes a los lados oblicuos del trapecio forman un ángulo de 58°, y llevan dos anteojos pequeños: el ocular del primero está reemplazado por un disco de latón que tiene una hendidura vertical, la cual se coloca en el foco del objetivo. Delante de esta hendidura se pone la lámpara, de modo que el eje del anteojo pase por el borde de la llama. Un poco más abajo de este punto de encuentro se halla, pendiente de un sustentáculo, un hilo de platino muy fino y encorvado en forma de espiral, en el cual se pone el glóbulo del cloruro que se va a examinar, deshidratado previamente. Entre los objetivos de ambos anteojos hay un prisma de 60°, sostenido por un disco de latón movible sobre un eje vertical, el cual lleva en su parte inferior un espejo, y encima de él una varilla, que sirve para dar vuelta al prisma y al espejo. Delante de este último se halla colocado un anteojo, que sirve para leer las divisiones de una escala horizontal colocada a corta distancia. Dando vueltas al prisma pueden hacerse pasar todas las partes del espectro detrás del retículo vertical del segundo anteojo, y por consiguiente que coincidan todas las rayas del mismo con el retículo. A cada posición del espectro corresponde una división de la escala; y si es poco luminoso, se aclara el hilo del anteojo por medio de una lente que proyecta en él la luz de una lámpara por una abertura lateral practicada en el tubo ocular del segundo anteojo».

En cuanto a elementos químicos, compararon los espectros obtenidos con diversos compuestos (como cloruros puros, yodatos, hidratos, carbonatos y sulfatos) cuando se introducían llamas de, entre otros elementos y compuestos, azufre, hidrógeno, sulfuro de carbono, óxido de carbono y la llama no luminosa del gas del alumbrado. «De nuestras largas y minuciosas investigaciones», manifestaban, «cuyos detalles creemos deber pasar en silencio, resulta que la naturaleza de la combinación en que existe el metal, la diversidad de los fenómenos químicos que se originan en cada llama y la diferencia enorme de temperatura producida por ellas no ejercen ninguna influencia sobre la posición de las rayas del espectro correspondiente a cada metal».

Tras estas explicaciones, llegaba el momento de señalar una de las grandes aplicaciones del método espectral, una de las principales, si no la principal, en lo que a la química se refiere: «También tiene importancia el análisis del espectro bajo otro punto de vista, en cuanto puede conducir al descubrimiento de elementos todavía desconocidos. Si en efecto existen cuerpos diseminados en la naturaleza en cantidades bastante pequeñas para ocultarse a nuestros métodos comunes de análisis, puede esperarse descubrirlos por la simple inspección del espectro. La experiencia nos ha dado ocasión de confirmar esta hipótesis, puesto que fundándonos en los resultados positivos obtenidos por la observación del espectro, creemos poder afirmar con exactitud que además del potasio, del sodio y el litio, existe un cuarto metal alcalino, cuyo espectro es tan característico y tan simple como el del litio. Nuestro aparato no indica para este metal más que dos rayas, una Csβ azul y débil, que corresponde casi a la del estroncio, Srδ, y otra Csα, también azul».

El escenario se encontraba preparado, como vemos, para que intentasen ser los primeros en explotar la posibilidad que acababan de enunciar; esto es, que estaban utilizando un método que «puede conducir al descubrimiento de elementos todavía desconocidos». Lo serían, efectivamente, como explicaban en su segunda memoria (Kirchhoff y Bunsen 1861; 1862, versión castellana). «Tenemos la convicción», explicaban (Kirchhoff y Bunsen 1862: 333-335), «de que este método, que ensancha de un modo tan extraordinario los límites del análisis químico, podrá conducir a descubrir nuevos elementos desapercibidos hasta ahora por los químicos, bien por hallarse diseminados, bien por su analogía con las sustancias conocidas, bien por razón de lo imperfectos que son nuestros métodos de investigación, que no permiten encontrar entre ellos reacciones características. Desde el primer paso que hemos dado en esta senda, hemos visto realizarse lo que habíamos previsto; en efecto, bien pronto hemos reconocido, además del potasio, del sodio y del litio, la existencia de otros dos metales alcalinos, aunque las sales de estos nuevos elementos producen los mismos precipitados que las del potasio, y que sólo se encuentran en pequeñísima cantidad. En efecto, para obtener un peso de materia que suba sólo a algunos gramos, necesario para nuestros experimentos, hemos necesitado operar sobre 44.200 kilogramos de agua madre del agua mineral de Dürkheim, y sobre 150 kilogramos de lepidolita». Y explicaban el procedimiento que habían seguido:

Cuando en la llama del aparato para la observación del espectro se pone una gota de agua madre procedente del agua mineral de Dürkheim, se reconocen únicamente las rayas características del sodio, del potasio, del litio, del calcio y del estroncio. Si entonces, después de haber precipitado por los procedimientos conocidos la cal, la estronciana y la magnesia, se vuelve a tratar con alcohol el residuo, tratado previamente con ácido nítrico para fijar las bases, se obtiene, cuando se le ha privado en lo posible de la litina por medio del carbonato de amoniaco, un agua madre, que en aparato espectral da las rayas del sodio, del potasio, del litio; y además dos rayas azules notables, muy inmediatas la una a la otra, y una de las cuales coincide casi con la raya Srδ; pero no habiendo cuerpo simple conocido que en esta parte del espectro dé dos rayas semejantes, se puede deducir, por consiguiente, la existencia segura de un cuerpo simple hasta ahora desconocido, y que corresponde al grupo de los metales alcalinos.

Proponemos dar al nuevo metal el nombre de cesio (símbolo Cs), de caesius, que entre los antiguos servía para designar el azul de la parte superior del firmamento, cuyo nombre nos parece se justifica por la facilidad con que puede comprobarse con el hermoso color azul de los vapores candescentes de este nuevo cuerpo simple, la presencia de algunas milésimas de miligramo de este elemento mezclado con la sosa, con la litina y con la estronciana.

A continuación describían el camino que los había conducido al descubrimiento del rubidio, Rb, «de rubidus, que entre los antiguos servía para designar el rojo más intenso», por el «magnífico color rojo intenso» de dos de las rayas del nuevo metal. Durante los años siguientes otros elementos serían identificados mediante el análisis espectral: el talio (William Crookes [1832-1919], 1861), el indio (Reich y Ritcher, 1863), el helio, detectado por Norman Lockyer (1836-1920) en 1869 en las protuberancias solares, descubrimiento que fue confirmado (1895) en el laboratorio por William Ramsay (1852-1916) y lord Rayleigh (1842-1919), el galio (Paul E. Lecoq de Boisbaudran [1838-1912], 1875), el escandio (Lars F. Nilson [1840-1899], 1879) y el germanio (Clemens A. Winkler [1838-1904], 1886).

Evidentemente, esto no sucede todos los días, ni todos los investigadores tienen oportunidades del estilo de las que se encontraron en 1859-1861 Kirchhoff y Bunsen: desarrollar un método de una potencia inusitada, que condujo a la creación de una nueva ciencia, fundamental, como es la astrofísica, y a encontrar dos nuevos elementos químicos. Sabemos algo de los sentimientos que la investigación en que estaban inmersos suscitaba en ellos, a través de una carta que Bunsen dirigió a Roscoe el 13 de noviembre de 1859 (Roscoe 1904; 1906: 81-82): «En este momento estoy ocupado con una investigación con Kirchhoff que no nos deja dormir. Kirchhoff ha realizado un descubrimiento totalmente inesperado, en tanto que ha encontrado la causa de las líneas oscuras en el espectro solar y puede producir estas líneas artificialmente intensificadas tanto en el espectro solar como en el espectro continuo de una llama, siendo su posición idéntica a la de las líneas de Fraunhofer. En consecuencia, se abre el camino a la determinación de la composición química del Sol y de las estrellas fijas con la misma certidumbre con que podemos detectar cloruro de estroncio, etc., con nuestros reactivos habituales. Mediante este método también se pueden detectar y separar elementos existentes en el Sol con el mismo grado de precisión que se hace con los que hay en la Tierra; por ejemplo: se puede demostrar la presencia de litio en 20 gramos de agua del mar. En la detección de muchos elementos es preferible este método a todos los procesos conocidos previamente. Una mezcla contiene Li, Ka, Na, Ba, Sr y Ca; todo lo que se necesita es llevar un miligramo de esta mezcla a nuestro aparato para, inmediatamente, con la ayuda de un microscopio, descubrir la presencia de todos estos cuerpos mediante una sola observación. Algunas de estas reacciones tienen un grado de delicadeza maravilloso; así, por ejemplo, se puede detectar la 5/1000 parte de un miligramo de litio con la mayor facilidad. Yo mismo he observado la presencia de este cuerpo en casi todos los especímenes de potasio».

El reconocimiento, los honores no tardaron en llegar; eran obligados. Representativo de ese reconocimiento es lo que Jean-Baptiste-André Dumas (1861: 485) escribió (y no olvidemos que se trataba de un francés, y que con no pequeña frecuencia los galos no han sido excesivamente generosos en sus halagos a alemanes): «Los físicos franceses, que han tratado de estos excelentes estudios, pueden sentir no haber dado a la filosofía natural el impulso que ha recibido de la sabia Alemania: pero la ciencia es de todos los países; sus progresos pertenecen a la humanidad entera; y todo el mundo se felicitará en Francia al saber que S. M. el Emperador, cuyo pensamiento comprende todo lo que puede contribuir al adelanto de las ideas como también a la grandeza y a la felicidad del país, acaba de dar [27 de octubre de 1861], en testimonio del interés constante que manifiesta por las ciencias, la condecoración de oficial a Mr. Bunsen, y la Cruz de la Legión de Honor a Mr. Kirchhoff».

KIRCHHOFF Y LA RADIACIÓN DE UN CUERPO NEGRO

Cualquier texto introductorio de mecánica cuántica, y por supuesto uno que pretenda reconstruir su historia, no deja de señalar el papel que la radiación de un cuerpo negro desempeñó en el descubrimiento realizado por Max Planck en 1900, que puso en marcha la cuantización de la física. Ahora bien, muy pocos de esos mismos textos se detienen en explicar cuándo y por qué surgió la noción de cuerpo negro. Como veremos en la presente sección, su origen está asociado al nombre de Kirchhoff y tiene que ver con los desarrollos que acabo de citar.³

El mismo año en que Kirchhoff (1859 a) publicó sus observaciones e ideas sobre las líneas D observadas en el espectro solar que coincidían con las líneas amarillas brillantes emitidas por llamas que contenían sodio, apareció un segundo trabajo suyo en el que se ocupaba de aspectos teóricos que subyacían en el primero.⁴ En particular, trataba en él de una propiedad específica de los cuerpos que emitían luz y calor («luz invisible», como llamaba a este último): «El cociente entre la capacidad de emisión y la capacidad de absorción, e/a, común a todos los cuerpos», escribía (Kirchhoff 1859 b: 786), «es una función que depende de la longitud de onda [de la radiación emitida o absorbida] y de la temperatura».

Un año después Kirchhoff (1860) publicó un segundo artículo en el que abordaba el mismo problema con mayor detalle, suministrando además una demostración analítica más rigurosa del enunciado anterior. Fue en este trabajo donde, al principio, introdujo la noción de cuerpo negro (estrictamente una ficción, un objeto inalcanzable). «Quiero llamar a semejante cuerpo», fueron sus palabras (Kirchhoff 1860: 277), «cuerpo negro perfecto, o de modo abreviado, negro» («Ich will solche Körper vollkommen schwarze, oder kürzer schwarze neenen»).

No fue, sin embargo, él quien inventó el concepto de cuerpo negro. En, por ejemplo, la Cuestión 6 de la Óptica de Isaac Newton (1704) podemos leer: «¿Acaso la luz no engendra el calor en los cuerpos negros con mayor facilidad que en los de otros colores, debido a que al incidir sobre ellos no se refleja hacia afuera, sino que penetrando en ellos, se refracta y refleja muchas veces en su interior hasta que se absorbe y pierde?». Sí fue Kirchhoff, no obstante, el primero que formuló tal concepto en el sentido técnico preciso que veremos en seguida, y quien lo insertó en un contexto teórico de cuya fecundidad dan testimonio, entre otras ramas de la ciencia, la propia teoría cuántica al igual que la astrofísica. Sin embargo, en lugar de este segundo artículo, a continuación utilizaré otro más breve: el resumen de una conferencia que pronunció en la Sociedad de Historia Natural de Heidelberg, que apareció en el Philosophical Magazine (en el número de abril de 1861; [Kirchhoff 1861 b]) gracias a los servicios de Roscoe, quien, como vemos, se convirtió en uno de los principales mensajeros de los resultados obtenidos por Kirchhoff (también, claro, de Bunsen).

«Hace unos pocos meses», comenzaba su exposición Kirchhoff (1861 b: 241), «comuniqué a la Sociedad ciertas observaciones, que parecían de interés porque dan alguna información sobre la composición de la atmósfera solar y señalan el camino hacia más conocimientos sobre este tema. Estas observaciones conducen a la conclusión de que una llama cuyo espectro consiste de líneas brillantes es parcialmente opaca a rayos de luz del color de estas líneas, mientras que es perfectamente transparente a la luz restante. Esta afirmación explica las líneas oscuras de Fraunhofer en el espectro solar, y justifica la conclusión relativa a la composición de la atmósfera del Sol. El hecho de que una llama sea parcialmente opaca solamente a aquellos rayos que emite fue, como manifesté en su momento, una sorpresa para mí. Desde entonces he llegado, mediante consideraciones teóricas muy simples, a una proposición de la que se deduce inmediatamente la anterior conclusión».

Las «consideraciones teóricas» a las que aludía nos parecen, casi siglo y medio después, más que simples, triviales, pero no lo eran tanto en el contexto en el que Kirchhoff se estaba moviendo (más bien, creando): «Un cuerpo caliente emite rayos de calor. Lo sentimos claramente cerca de una estufa caliente. La intensidad de los rayos de calor que un cuerpo caliente emite depende de la naturaleza y de la temperatura del cuerpo, pero es en general independiente de la naturaleza de los cuerpos sobre los que caen los rayos. Sentimos los rayos de calor solamente en el caso de los cuerpos muy calientes, pero todos los cuerpos los emiten, cualquiera que sea su temperatura, aunque su magnitud disminuye con la de esta. Un cuerpo pierde calor en proporción a lo que radia, y su temperatura debe disminuir salvo que esta pérdida sea compensada. Un cuerpo rodeado por sustancias que se encuentran a su misma temperatura no experimenta un cambio de temperatura. En este caso, la pérdida de calor producida por su propia radiación es compensada exactamente por los rayos que emiten los cuerpos que le rodean, una parte de los cuales absorbe el cuerpo. La cantidad de calor que este cuerpo absorbe en un tiempo dado debe ser igual a la que emite en el mismo intervalo. Esto es válido cualquiera que sea la naturaleza del cuerpo; cuantos más rayos emita un cuerpo, más rayos incidentes debe absorber. La intensidad de los rayos que emite un cuerpo ha sido denominada su capacidad de radiación o emisión; y el número que denota la fracción de los rayos incidentes que se absorben, la capacidad de absorción. Cuanto mayor sea la capacidad de emisión de un cuerpo, mayor debe ser su capacidad de absorción». Y añadía en este punto: «Una consideración más estrecha demuestra que la relación entre las capacidades de emisión y de absorción para una temperatura es la misma para todos los cuerpos. Esta conclusión ha sido verificada en muchos casos especiales, tanto en los últimos diez años como en épocas anteriores».

Ahora bien, Kirchhoff se daba cuenta de que esta conclusión exigía que «todos los rayos de calor considerados sean de una y de la misma clase», que «no fuesen cualitativamente tan diferentes que una parte de ellos fuese absorbida por los cuerpos más que otra parte, ya que en este caso no podríamos hablar de la capacidad de absorción de un cuerpo, simplemente porque sería diferente para rayos diferentes». Y se sabía que, efectivamente, había diferentes tipos de rayos de calor: los rayos «oscuros y luminosos» (es decir, los de diferentes longitudes de onda), y los rayos polarizados de una u otra forma. Pero a la postre fue capaz de superar esta dificultad: «He encontrado», afirmaba (Kirchhoff 1861 b: 243), «que la proposición relativa al cociente entre el poder de emisión y el de absorción sigue siendo cierta, independientemente de lo diferentes que puedan ser los rayos que emiten los cuerpos, siempre que las nociones de capacidad de emisión y de absorción queden confinadas a un tipo de rayo».

Para llegar a este resultado, comenzó «considerando que es posible imaginar cuerpos que, aunque muy delgados, absorben todos los rayos que caen sobre ellos, o cuya capacidad de absorción es igual a 1. Denomino a tales cuerpos perfectamente negros, o simplemente negros». En primer lugar, investigó la radiación de tales cuerpos negros, llegando a la conclusión «de que la capacidad de emisión del cuerpo negro, considerada con respecto a una longitud de onda dada y a un plano de polarización dado, es independiente de su constitución».

Cuando suponía que el cuerpo no era negro, «sino de cualquier otro color», encontraba que la relación entre emisión y absorción permanece constante para todos los cuerpos; es decir que:

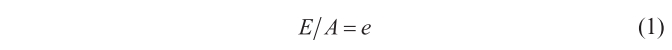
Una ecuación que, obviamente, se puede escribir como

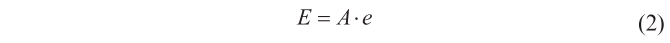
o

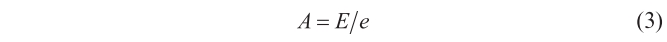
En un cuerpo negro A = 1, y por tanto E = e, así que según la ley de Kirchhoff que acabamos de enunciar, como el cociente E/A permanece constante para todos los cuerpos, dos cuerpos negros diferentes también tendrán la misma capacidad de emisión (E = E’).

Con tal bagaje teórico, Kirchhoff (1861 b: 246) obtenía varias consecuencias importantes. Una, la segunda, le llevaba de vuelta al tema de partida: «El espectro de todos los cuerpos opacos incandescentes es continuo; no contiene líneas brillantes ni oscuras. Por consiguiente, podemos concluir que el espectro de un cuerpo negro incandescente (utilizando el término en el sentido ya definido) debe ser continuo. El espectro de un gas incandescente está formado, al menos casi siempre, de una serie de líneas brillantes separadas entre sí por espacios perfectamente oscuros. Si la capacidad de emisión de tal gas se representa por E, la relación E/e posee un valor apreciable para aquellos rayos que corresponden a las líneas brillantes del espectro del gas, pero tiene un valor despreciable para todos los demás rayos. Sin embargo, según la ecuación [(3)] esta relación es igual a la capacidad de absorción del gas incandescente. En consecuencia, se sigue que el espectro de un gas incandescente será el recíproco de éste [...], cuando está colocado delante de una fuente de luz de suficiente intensidad, que da un espectro continuo; esto es, las líneas del espectro del gas, que antes eran brillantes, se verán como líneas oscuras en un fondo brillante. Una consecuencia notable de mi proposición que mencionaré es que si la fuente de luz más remota es un cuerpo sólido incandescente, la temperatura de este cuerpo debe ser mayor que la del gas incandescente para que tenga lugar tal conversión».

Y así, podía concluir (Kirchhoff 1861 b: 247): «El Sol está formado por un núcleo luminoso, que podría producir por sí mismo un espectro continuo, y por una atmósfera gaseosa incandescente, que podría producir por sí misma un espectro formado por un inmenso número de líneas brillantes características de las numerosas sustancias que contiene. El espectro solar real es el recíproco de éste. Si fuese posible observar el espectro que pertenece a la atmósfera solar con todas las líneas brillantes que posee, nadie se sorprendería de escuchar que, a partir de la existencia en el espectro solar de las líneas brillantes características del sodio, potasio e hierro, se hubiese comprobado la presencia de estos cuerpos en la atmósfera del Sol. Sin embargo, según la proposición que acabo de establecer, tampoco puede existir duda de lo cierto de esa afirmación si viésemos el espectro real de la atmósfera solar».

Había sido, en definitiva, capaz de explicar sus observaciones iniciales, observaciones que surgieron del contexto de su colaboración con Bunsen. Y al hacerlo no sólo había introducido la noción de cuerpo negro, en el sentido técnico moderno, sino que había llegado a resultados que contenían elementos —como la «constancia» entre emisión y absorción, es decir, y utilizando otro lenguaje, que existe, como veremos a continuación, una función universal, Kλ(T)— sin los que la historia de la creación de la física cuántica habría sido otra, en el supuesto, claro está, de que hubiese sido creada.

RECONSTRUCCIÓN TEÓRICA DE LA CONTRIBUCIÓN DE KIRCHHOFF

En la sección anterior he presentado los resultados de Kirchhoff utilizando, básicamente, sus propias palabras. Ahora voy a reconstruir sus razonamientos recurriendo a términos y expresiones más actuales, que nos servirán, además, para establecer una línea de argumentación continua con desarrollos que aparecerán en otros capítulos, al igual que en este mismo.⁵

Consideremos una cavidad esférica de paredes perfectamente absorbentes (es decir, negras), llena de radiación de intensidad K, que se mantiene a una temperatura fija, T. Su interior se llenará de energía radiante de todas las longitudes de onda, X. Si la radiación está en equilibrio, tanto dentro de la cavidad como con las paredes, entonces la magnitud con la que la energía es radiada a través de cualquier superficie o área unidad es independiente de la posición y orientación de esa superficie. En estas circunstancias, el flujo de energía que incide sobre un elemento infinitesimal de superficie, dσ, desde un cono de luz de ángulo sólido dΩ, es K·cosθ·dΩ · dσ, donde θ es el ángulo entre dσ y el eje del cono. Como la radiación contribuye al flujo total con longitudes de onda muy diversas, la intensidad admite una especificación más precisa mediante una función de distribución, K_λ, tal que

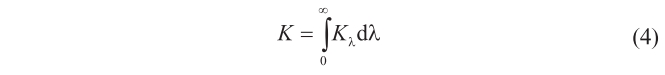
K_λdλ es, evidentemente, la intensidad debida a la radiación de longitud de onda entre λ y λ + dλ.

Determinar la forma de K_λ constituye el problema principal para estudiar la radiación de un cuerpo negro, y en esencia esto es lo que hizo Kirchhoff.

Denotemos ahora como a_λ a la energía de longitud de onda entre λ y λ + dλ que es retenida por dσ, cuando la cavidad se mantiene a la temperatura T. La energía absorbida será proporcional a a_λ·K_λ·dσ. Análogamente, dσ radia (emisión) energía al interior de la cavidad en magnitud que es proporcional a e_λ·dσ.

Imponiendo la condición de que exista equilibrio, es decir, que la absorción total sea igual a la emisión total, se llega a:

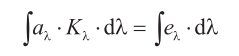
Experimentando (recordemos lo que escribía en 1861: «Esta conclusión ha sido verificada en muchos casos especiales, tanto en los últimos diez años como en épocas anteriores»), Kirchhoff llegó al resultado de que a_λ · K_λ=e_λ para cualquier material. En consecuencia, se tiene que:

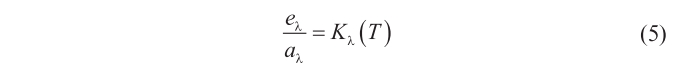
es decir, que existe una función universal, Kλ(T) que depende sólo de λ y de T.

Recurriendo ahora a la condición de «cuerpo negro» (aquel que absorbe toda la radiación; esto es, aquel en el que a_λ = 1) introducida por Kirchhoff en 1860, se sigue inmediatamente que para un cuerpo negro, e_λ=K_λ(T).

Entre los motivos para interesarse por estas expresiones, estaba el que si se conociese la forma de K_λ(T), una vez que se midiese (mediante las oportunas observaciones) la radiación emitida por una estrella, por ejemplo, se podría calcular T, esto es, la temperatura de la superficie de esa estrella.

LA LEY DE RADIACIÓN DE STEFAN

A pesar de lo que acabo de decir, para calcular la temperatura de, por ejemplo, el Sol, no basta con medir experimentalmente el ritmo con que emite radiación y comparar este valor con K_λ(T); hay que conocer también, entre otros factores, qué fracción de la radiación es absorbida por la atmósfera terrestre, que es atravesada por esa radiación antes de llegar al observador terrestre. Curiosamente, fue también en la década de 1860 cuando se publicaron los primeros resultados relevantes en este sentido. Especialmente importante para el desarrollo al que me voy a referir fue un artículo que el irlandés John Tyndall (1820-1893) publicó en el Philosophical Magazine en 1864.⁶ Este artículo (Tyndall 1864) fue traducido al alemán (Tyndall 1865) y leído por Adolph Wüllner, que en un texto que publicó en 1871 —Die Lehre von der Wärme vom Standpunkte der mechanischen Wärmetheorie— señalaba que «la cantidad de calor emitida aumenta considerablemente más rápido que la temperatura, especialmente a temperaturas elevadas», mencionando como apoyo de semejante conclusión algunas de las medidas de Tyndall (cometiendo, por cierto, errores en su transcripción al efectuar ciertas conversiones).⁷

Aun conteniendo errores, el hecho es que lo que Wüllner señalaba en su libro influyó en Josef Stefan (1835-1893), catedrático de Matemáticas Superiores y Física en la Universidad de Viena, donde también dirigía (desde 1869) el Instituto de Física Experimental, que nada menos que Christian Johann Doppler (1808-1853) había fundado en 1850. En un artículo que apareció en 1879, Stefan propuso una ley concreta para la emisión de radiación: «Mencionaré aquí», escribía (Stefan 1879: 421), «el comentario que Wüllner efectua en su libro de texto sobre los experimentos de Tyndall acerca de la radiación de un hilo de platino al que una corriente eléctrica hace brillar, ya que ese comentario fue el que primero me hizo suponer que la radiación calorífica es proporcional a la cuarta potencia de la temperatura absoluta»; esto es: K es igual a una constante multiplicada por T⁴.

El único fundamento para la propuesta de Stefan era experimental, con una base muy pobre, además. Una derivación teórica tendría que esperar algunos años, a 1884. Su autor fue un físico (y pensador) extraordinario, que, como iremos viendo en diversos lugares de este libro, desempeñó un papel central en la génesis de la física cuántica: Ludwig Boltzmann (1844-1906).

La carrera científica de Boltzmann está unida especialmente a la física estadística, de la que fue, como también tendremos ocasión de comprobar (en este mismo capítulo, cuando, en seguida, me refiera a James Clerk Maxwell), uno de sus protagonistas principales. Natural de Viena, allí estudió, teniendo la oportunidad de seguir cursos del mismo Josef Stefan y de Josef Loschmidt (1821-1895). Ocupó numerosos puestos académicos: fue catedrático de Física teórica en las universidades de Graz, Múnich, Viena y Leipzig, de Matemáticas en Viena y de Física Experimental en Graz (tal vez satisfizo con tantos cambios su espíritu viajero, que plasmó en algún escrito memorable: como «El viaje de un profesor alemán a Eldorado»).⁸ Durante su vida se embarcó en profundas y con frecuencia amargas controversias —científicas y filosóficas— con científicos (como Ernst Mach o Wilhelm Ostwald) que negaban la realidad de los átomos, idea en la que se basaban sus trabajos estadísticos. Se suicidó en Duino, cerca de Trieste, el 5 de septiembre de 1906. Sus restos reposan en el cementerio de Viena, adornados por un mausoleo en el que se puede leer su gran fórmula (con la que nos volveremos a encontrar): «S = k · log W».

Veamos a continuación, siguiendo una presentación especialmente clara debida, precisamente, a Max Planck (1906: 61-63), en su libro Vorlesungen über die Theorie der Wärmestrahlung, cómo dedujo Boltzmann (1884) la ley de Stefan.

Si se supone que la radiación está confinada en un cilindro de volumen V, cerrado por un émbolo reflector, se tendrá que si la presión de la radiación realiza un trabajo, aumentando el volumen, V, del cilindro en δV, para que la temperatura se mantenga constante hay que añadir un calor δQ. Ahora bien, de acuerdo con el primer principio de la termodinámica (el de la conservación de la energía),

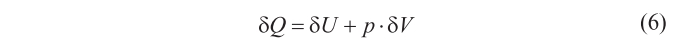
donde U = energía (por otra parte, se tiene que u = U/V, la densidad de energía).

Asimismo, se sabía que una onda plana que incide perpendicularmente sobre una superficie reflectora (o perfectamente conductora) ejerce una presión, p, igual a su densidad de energía; de manera que para radiación isótropa (esto es, aquella igual en todas las direcciones) se tiene p = (1/3) · u. Sustituyendo esta relación en (6), resulta

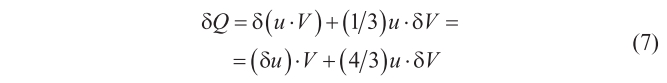
Argumentando ahora que en una situación de equilibrio, el flujo neto de energía a través de una superficie arbitraria, situada en el interior de la cavidad llena de radiación, tiene que ser cero, y que esta condición sólo puede verificarse (en el contexto de la teoría electromagnética de Maxwell) si la energía radiante, u, se relaciona con K según

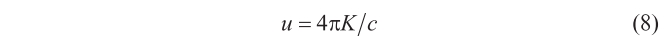
donde c representa la velocidad de la luz, y recordando lo visto con anterioridad acerca de K, se sigue que u = u(T, V), relación que se puede utilizar para deducir

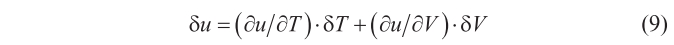
La expansión del volumen, δV, modifica también la entropía de la radiación, S, en una cantidad (como es bien sabido por la termodinámica)

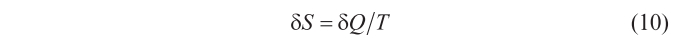
Ahora bien, otro de los requisitos termodinámicos es que δS tiene que ser una diferencial exacta; esto es, que se debe verificar

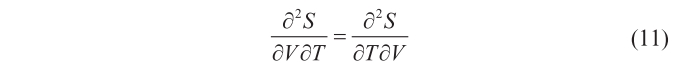
Combinando (9), (10) y (11), y teniendo en cuenta que en los resultados obtenidos por Kirchhoff, K—y por tanto, recordando (8), también u— es función únicamente de T, y no de V (lo que significa que ∂u/∂V = 0, y que ∂u/∂T = du/dT), se llega a que

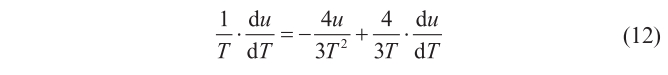
de la que manipulando, se sigue

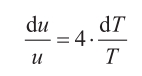
e integrando aparece el logaritmo neperiano (ln)

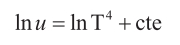
o lo que es lo mismo

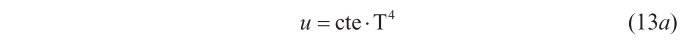
o también,

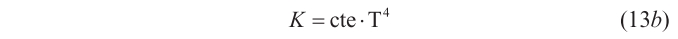
(en el caso de la energía total, lo que se tiene es U = cte · T⁴ · V), esto es, la ley de Stefan, que debido a la participación de Boltzmann en su deducción teórica pasó a denominarse «ley de Stefan-Boltzmann».

JAMES CLERK MAXWELL

Hasta el momento me he ocupado de una secuencia de desarrollos científicos —que tienen en el estudio de la radiación y en disciplinas como la espectroscopia su núcleo vertebrador— que, como veremos, condujeron a «encrucijadas científicas» que desempeñaron un papel decisivo en el nacimiento de la física cuántica. Ahora bien, aunque tales desarrollos constituyen la pieza crucial en esa génesis, es posible —y obligado— identificar también otros elementos. En particular, uno, el principio de equipartición (perteneciente al universo de la física estadística), con el que está asociado uno de los grandes físicos de todos los tiempos: el escocés James Clerk Maxwell (1831-1879). Es tanta la importancia de este científico en la historia de la ciencia que antes de pasar a considerar semejante principio, he considerado conveniente detenerme en algunos detalles de su biografía.

Maxwell nació el 13 de julio de 1831, en Edimburgo, en el seno de una familia acomodada. En su momento heredaría una gran finca (Glenair): alrededor de 1.500 acres de tierra cerca de Dalbeattie, en Galloway, al suroeste de Escocia. Fue allí donde escribió algunos de sus más importantes trabajos científicos.

Aunque había sido educado para abogado, el principal interés de su padre era la tecnología, y de hecho, John Clerk Maxwell fue miembro (fellow) de la Royal Society de Edimburgo. No fue, sin embargo, a su progenitor a quien James debió sus primeras enseñanzas: durante sus ocho primeros años de vida la mayor parte de la educación que recibió procedió de su madre, Frances Cay. Desgraciadamente, en 1839 Frances murió de cáncer, la misma enfermedad de la que fallecería su hijo, cuarenta años más tarde.

John Clerk Maxwell demoró cuanto pudo el enviar a su hijo a la escuela; contrató incluso a un joven para que continuara educándolo, una vez que su esposa falleció. La iniciativa, sin embargo, no tuvo demasiado éxito y James fue enviado, en noviembre de 1842, a la Edinburgh Academy, una escuela que había sido fundada en 1824 por un grupo que incluía al célebre novelista Walter Scott. Allí encontró condiscípulos muy interesantes, que se convertirían en sus amigos para toda la vida. Como Peter Guthrie Tait (1831-1901), que más tarde llegó a ser un distinguido científico: catedrático de Filosofía Natural en la Universidad de Edimburgo. A la amistad que mantuvo con Tait se le sumó más tarde la de otro ilustre científico: nada menos que William Thomson (1824-1907; lord Kelvin a partir de 1892), catedrático en Glasgow y una de las figuras más notables de la historia de la física del siglo XIX. Los tres mantuvieron frecuentes intercambios epistolares; en sus cartas de la década de los años setenta, Thomson y Tait firmaban, respectivamente, como T y T’, y Maxwell como dp/dt, puesto que en uno de los libros de Tait (Sketch of Thermodynamics [Edimburgo, 1868], p. 91) una expresión de la segunda ley de la termodinámica es: dp/dt=JCM (las iniciales de Maxwell).⁹ Otro símbolo que utilizaban era T”, para John Tyndall (Tait, que despreciaba a Tyndall, explicó que T” designaba una «cantidad de segundo orden»).

Maxwell estudió en la Edinburgh Academy cinco años. Durante ese tiempo, antes por tanto de entrar en la universidad, ya dio muestras de su inteligencia y precocidad: a la edad de quince años elaboró su primer artículo científico, que versaba sobre la geometría de curvas cónicas, acerca, en concreto, de una extensión de la teoría estándar de secciones cónicas a curvas con un grado mayor de complicación. No sería, sin embargo, hasta noviembre de 1847 cuando entró en la Universidad de Edimburgo; esperó, por consiguiente, a tener la edad que entonces era normal para entrar en las universidades escocesas. Allí siguió los tres primeros cursos de una carrera que constaba de cuatro. Esto quiere decir que no completó sus estudios y que, por consiguiente, no obtuvo ningún título. Semejante comportamiento no fue ni involuntario, ni era infrecuente. Se trataba de una maniobra habitual para poder estudiar en la más prestigiosa de las universidades británicas de la época, la de Cambridge, que no admitía como alumnos a quienes ya poseyesen un título por otro centro universitario. Tait, por ejemplo, únicamente estudió un año en la Universidad de Edimburgo, entrando en Cambridge, como alumno de Peterhouse (uno de los colleges de la universidad), en 1848, antes, por tanto, que Maxwell.

En octubre de 1850, James se trasladó a Cambridge, y fue admitido en uno de los centros académicos más prestigiosos: Trinity, el antiguo college de Newton. En Cambridge se encontró con un sistema de exámenes muy especial: el Mathematical Tripos, al que me referiré con cierto detalle en el capítulo 3. Pasó el examen en 1854, ocupando el segundo puesto.

Un año después de pasar los exámenes del Tripos, fue nombrado fellow de Trinity. Aquello significaba la seguridad de poder continuar en Cambridge, con muy pocas obligaciones, dedicándose a investigar en lo que desease. Sin embargo, no utilizó durante mucho tiempo tal privilegio, ya que en 1856 pasó a ocupar la cátedra de Filosofía Natural del Marischal College, en Aberdeen. En 1860, no obstante, tuvo que abandonar su cátedra, debido a lo que en la actualidad seguramente denominaríamos un «reajuste de plantilla», consecuencia de la unión del Marischal College con el King’s College, la otra institución universitaria de Aberdeen. De todas maneras, en seguida obtuvo la cátedra del King’s College de Londres. Allí permaneció cinco años, un período que resultó muy provechoso para sus investigaciones. Así, dos de sus artículos clásicos sobre el campo electromagnético se publicaron en aquella época: en 1861-1862 y 1864: «On the physical lines of force» y «A dynamical theory of the electromagnetic field».

En 1865, renunció a su cátedra por voluntad propia, para volver a su finca escocesa de Glenair. En una carta que escribió el 2 de febrero de 1866 (Harman, ed., 1995: 249), a Charles Benjamin Tayler, señalaba que «ahora tengo mi tiempo completamente ocupado con experimentos y especulaciones de tipo físico, algo que no podía emprender mientras tenía deberes públicos». Además de estas razones, también deseaba ocuparse más de su finca, cumpliendo un viejo sueño: ampliar su casa. En Glenair escribió dos libros: uno que podríamos considerar de carácter general, pero que contiene ideas de gran novedad y originalidad (como el «demonio de Maxwell»), Theory of Heat (1871), y el otro, su gran A Treatise on Electricity and Magnetism (1873), una de las obras cumbre de la literatura científica especializada.

El 24 de febrero de 1871, fue designado para ocupar la recién creada cátedra de Física Experimental de la Universidad de Cambridge. Cuando, en el capítulo 3, me detenga en la carrera y contribuciones de Joseph John Thomson, diré algo más acerca de esa cátedra y el laboratorio con que pronto fue dotada.

La salud de Maxwell comenzó a deteriorarse en la primavera de 1877, aunque no recurrió a ningún médico hasta dos años después. Fue entonces cuando se hizo evidente que su gran energía había desaparecido, y cuando los acontecimientos se precipitaron, hasta que el 2 de octubre de 1879, entre grandes dolores, el Dr. Sanders de Edimburgo, que había sido llamado a Glenair, le comunicó que no le quedaba ni siquiera un mes de vida. No obstante, regresó a Cambridge, y murió, de cáncer abdominal, el 5 de noviembre.

MAXWELL, LA FÍSICA ESTADÍSTICA Y EL PRINCIPIO DE EQUIPARTICIÓN

Aunque para muchos Maxwell es recordado especialmente por sus contribuciones a la física del electromagnetismo, figura, asimismo, entre los grandes de la física estadística, disciplina de la que se le puede considerar como uno de los fundadores. De hecho, junto a Ludwig Boltzmann, Josiah Williard Gibbs (1839-1903) y Albert Einstein, forma el grupo de los auténticos grandes de esa disciplina (también se podría incluir a Clausius, que nos aparecerá más adelante, en este y en otro capítulo).

El propósito de la física (o, simplemente, mecánica) estadística es la descripción de propiedades macroscópicas de sistemas formados por un número muy grande de átomos (o moléculas). Se trata de una rama de la física que surgió, durante el siglo XIX, de la teoría cinética de los gases para, fundamentalmente, suministrar una interpretación microscópica, molecular o atómica de las leyes de la termodinámica. Objetivos preferentes de la mecánica estadística incluyen: 1) encontrar expresiones para magnitudes macroscópicas tales como presión, temperatura, energía interna o entropía, en términos de propiedades microscópicas, del tipo de la masa, la velocidad molecular y la energía potencial; 2) deducir ecuaciones de estado (que relacionan entre sí las variables que caracterizan a un sistema) para materiales específicos, y 3) determinar magnitudes termodinámicas que se miden experimentalmente en función de constantes microscópicas fundamentales.

Queda perfectamente claro de lo que acabo de decir que para la física estadística es absolutamente imprescindible la suposición de que la materia está formada por elementos discretos, por átomos. Sin embargo, es importante señalar que no todos aceptaban semejante hipótesis; de hecho, durante la segunda mitad del siglo XIX muchos reaccionaron en contra de los intentos «mecanicistas» y «estadísticos» de construir modelos atómicos —no sólo de la materia sino también del éter electromagnético (o incluso gravitatorio)— y de reducir la termodinámica a magnitudes discretas. Uno de los más activos en esa reacción fue el ya citado físico y filósofo austríaco Ernst Mach (1838-1916). En uno de sus libros, Die Principien der Wärmelehre [Principios de la teoría del calor], podemos leer (Mach 1896; 1986: 335): «Al distinguir entre movimientos ordenados y desordenados e igualar el crecimiento de la entropía con el aumento de los movimientos desordenados, prescindiendo de los ordenados, la concepción mecánica de la segunda ley de la termodinámica me parece un procedimiento muy artificial ... Estoy de acuerdo completamente con F. Wald [Die Energie und ihre Entwerthung, 1889, p. 104] cuando dice: “En mi opinión, las raíces de este teorema [el del crecimiento de la entropía] son más profundas, y si es posible poner en armonía la hipótesis molecular y el teorema de la entropía, es producto de un golpe de suerte para la hipótesis, pero no [una prueba en favor del] teorema de la entropía”». De hecho, en general se ha denominado «energeticismo» (porque en lugar de a los átomos daba un papel central a la energía) al punto de vista de aquellos que se opusieron a las tesis mecánico-estadísticas, un grupo al que pertenecieron, además de Mach, científicos como Wilhelm Ostwald (1853-1932), uno de los fundadores de la química-física, Georg Helm (1851-1923) o Pierre Duhem (1861-1916). Como recordaré más adelante, uno de los momentos decisivos en la dilucidación de la polémica entre mecanicistas y energeticistas tuvo lugar en 1905, con uno de los artículos que Albert Einstein publicó en aquel año (el dedicado al movimiento browniano). Pero todavía estamos lejos de ese momento. Continuemos, pues, con Maxwell, introduciéndonos de su mano en el nacimiento y problemas de la física estadística. Para ello me serviré de un artículo que publicó en 1875, apenas cuatro años antes de su muerte; «On the dynamical evidence of the molecular constitution of bodies» (Sobre la evidencia dinámica de la constitución molecular de los cuerpos) es su título.

Justo al inicio de su escrito, Maxwell (1875; Nye 1984: 213) se refería a la base sobre la que se edificaba la física estadística, defendiendo el punto de vista atómico:

De todas las hipótesis sobre la constitución de los cuerpos, la seguramente más justificable es la que sólo supone que son sistemas materiales y propone deducir de los fenómenos observados tanta información acerca de las condiciones y conexiones del sistema material como estos fenómenos puedan legítimamente proporcionar.

Al estudiar la constitución de los cuerpos nos vemos forzados desde el principio a tratar con partículas que no podemos observar. Ya que cualesquiera que sean nuestras conclusiones últimas sobre las moléculas y átomos, disponemos de evidencia experimental de que los cuerpos se pueden dividir en partes tan pequeñas que no las podemos observar.

Por consiguiente, si somos cuidadosos y recordamos que la palabra partícula significa una parte pequeña de un cuerpo, y que no implica ninguna hipótesis relativa a la divisibilidad última de la materia, podemos considerar a un cuerpo como formado por partículas, y también podemos afirmar que en cuerpos o partes de cuerpos de dimensiones mesurables, el número de partículas es de hecho muy grande.

Y en este punto pasaba a introducir las consideraciones estadísticas:

Lo siguiente que se necesita es un método dinámico para estudiar un sistema material formado por un inmenso número de partículas, formarse una idea de sus configuraciones y movimientos, y de las fuerzas que actúan sobre las partículas, y deducir de la teoría dinámica aquellos fenómenos que, al depender de las configuraciones y movimientos de las invisibles partículas, son capaces de ser observados en partes visibles del sistema.

Los principios dinámicos necesarios para este estudio fueron desarrollados por los padres de la dinámica, desde Galileo y Newton hasta Lagrange y Laplace; pero la adaptación específica de estos principios a los estudios moleculares ha sido en gran medida el trabajo del Prof. Clausius de Bonn, que recientemente nos ha sometido a obligaciones aún más graves, al darnos, además de los resultados de sus elaborados cálculos, una nueva idea dinámica, con cuya ayuda espero que seremos capaces de establecer varias conclusiones importantes sin demasiados cálculos simbólicos.

Maxwell se refería aquí a un artículo de otra de las grandes figuras de la termodinámica y física estadística, Rudolf Clausius (1822-1888), al que volveré con algo más de detalle, en el capítulo 4, el dedicado a Planck, para quien las ideas y aportaciones de Clausius fueron fundamentales. Ahora simplemente diré que el artículo al que aludía Maxwell apareció en 1858 (Clausius 1858). De hecho, el punto real de partida de las investigaciones de Maxwell en la física estadística se produjo cuando leyó la traducción de ese artículo, que se publicó en el número de febrero de 1859 del Philosophical Magazine (Clausius 1859).

Sabemos que Maxwell leyó realmente ese trabajo a través de una carta, muy interesante, que escribió el 30 de mayo de 1859 a George Gabriel Stokes (1819-1903), Lucasian professor en Cambridge.¹⁰ «Querido Stokes», decía, «he visto en el Philosophical Magazine de febrero/59, un artículo de Clausius sobre el “recorrido medio de la trayectoria de una partícula de aire o gas entre colisiones sucesivas”, bajo la hipótesis de que la elasticidad del gas se debe a que la velocidad de sus partículas y sus trayectorias son rectilíneas excepto cuando se acercan mucho entre sí, suceso que puede ser denominado una colisión». Más adelante se refería a sus propias aportaciones: «Como no sabemos nada ni de s [el radio de la esfera de acción de una partícula], ni de N [el número de partículas], pensé que merecía la pena examinar la hipótesis de partículas libres que actúan por impacto y compararlo con fenómenos que parecen depender de este “recorrido medio”. He comenzado, por consiguiente, por el principio y diseñado una teoría de los movimientos y colisiones de partículas libres que actúan solamente por impacto, aplicándola a la fricción interna de gases, y conducción de calor a través de un gas (sin radiación)». Y a continuación resumía los resultados a que había llegado. En apenas cuatro meses desde la publicación de la traducción del artículo de Clausius, Maxwell había elaborado una teoría que no sólo englobaba todas las propiedades de los gases descritas hasta entonces, sino que también incluía los coeficientes de transporte, proporcionando además un poderoso método estadístico para describir el estado de un gas.

Vemos, por consiguiente, que la novedad que había introducido Clausius en su artículo y que atrajo tan poderosamente la atención de Maxwell se encuentra en el hecho de que el físico alemán introducía un concepto completamente nuevo y extremadamente original, el «recorrido medio» de la molécula de un gas, algo que abría el camino a la determinación estadística de movimientos de grandes números de cuerpos que colisionan entre sí. Lo que le interesó no fue el que su colega utilizase una «teoría cinética de gases»; la idea de que la presión en los gases se debiese a impactos aleatorios de moléculas sobre las paredes del recipiente que los contenían había sido sugerida con anterioridad muchas veces (el propio Clausius había escrito dieciocho meses antes un artículo en el que recurría a la teoría cinética).

El resultado de la respuesta de Maxwell al trabajo de Clausius fue un artículo publicado en 1860 en el Philosophical Magazine: «Illustrations of the dynamical theory of gases», uno de los clásicos de la física estadística (Maxwell 1860 a).

Clausius había basado su trabajo en la suposición de que todas las moléculas del gas tenían la misma velocidad, pero era evidente que esto no podía ser cierto. Una de las aportaciones más importantes —seguramente la más importante— de Maxwell en su artículo de 1860 fue la obtención de una fórmula estadística para la distribución de velocidades en un gas a presión uniforme. En concreto, en la «Proposición IV» obtenía la expresión que da el número medio de partículas cuyas velocidades se encuentran entre límites dados (v y v + dv), después de un gran número de colisiones entre un número igualmente elevado de partículas idénticas:

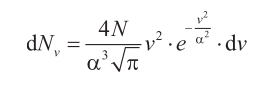
donde α es una magnitud con las dimensiones de una velocidad.

Ésta es una de las expresiones de su famosa «función de distribución», con la que de hecho comenzó una nueva era de la física; una expresión que tenía, además, una forma familiar: «Parece», escribió Maxwell (1860 a; Niven, ed., 1965, vol. I: 382), «de esta proposición que las velocidades están distribuidas entre las partículas de acuerdo con la misma ley con que se distribuyen los errores entre las observaciones en la teoría del método de los mínimos cuadrados. Las velocidades varían entre 0 e ∞, pero el número de las que tienen velocidades grandes es comparativamente pequeño».

La importancia del modo de análisis introducido por Maxwell fue resumida adecuadamente por Gibbs (1889; 1961, vol. II: 265): «Clausius se centró en los valores medios de diversas cantidades que varían enormemente en el tiempo o espacio más pequeño que podemos apreciar. Maxwell se ocupó de la frecuencia relativa de los diversos valores que tienen estas cantidades. En esto fue seguido por Boltzmann. Cuando leemos a Clausius, parece que estamos leyendo mecánica; cuando leemos a Maxwell, y mucho de lo más valioso del trabajo de Boltzmann, parece más bien que estamos leyendo teoría de probabilidades. No hay duda de que la manera más amplía en que Maxwell y Boltzmann plantearon los problemas de la ciencia molecular les permitió obtener en algunos casos una respuesta más satisfactoria y completa, incluso para aquellas cuestiones que a primera vista no parecían necesitar de un tratamiento tan amplio».

Otro resultado al que llegó Maxwell en 1860, y que nos es especialmente necesario resaltar aquí, es que la energía de un sistema debe distribuirse por igual, en promedio, entre todas sus partes: «El estado final», escribía (Maxwell 1860 a; Niven, ed., 1965, vol. 1: 408-409), «de cualquier número de sistemas de partículas en movimiento es uno en el que la vis viva [energía cinética] media de traslación a lo largo de cada uno de los tres ejes es la misma para todos los sistemas, e igual a la vis viva media de rotación sobre cada uno de los tres ejes principales de cada partícula».

Se trata de una manifestación del célebre «teorema de equipartición», que en una forma restringida ya había sido propuesto por John James Waterston (1811-1883) en 1846,¹¹ y que en la terminología moderna viene a señalar que «todo grado de libertad tiene la misma energía». Aplicado a cierto caso referente a los calores específicos, el teorema de equipartición provocaba un importante problema, que llevaba a Maxwell, inmediatamente después de la cita precedente, a declarar: «Este resultado [...] parece decisivo en contra de aceptar sin reservas la hipótesis de que los gases son tales sistemas de partículas duras elásticas».

Recuperemos ahora el artículo de 1875, «On the dynamical evidence of the molecular constitution of bodies», en el que Maxwell explicaba de manera sintética y clara los resultados y problemas a que había llegado en 1860.

En aquel trabajo, inicialmente había estado considerando solamente el movimiento del centro de masas de la molécula; debía, en consecuencia, completar su análisis estudiando el movimiento de los constituyentes de las moléculas con respecto al centro de masas. «Si suponemos», señalaba (Maxwell 1875; Nye 1984: 222), «que los constituyentes de una molécula son átomos, y que cada átomo es lo que se denomina un punto material, entonces cada átomo se puede mover de tres maneras diferentes e independientes, que corresponden a las tres dimensiones espaciales, de forma que el número de variables que se necesitan para determinar la posición y configuración de todos los átomos de la molécula es tres veces el número de átomos». De hecho, reconocía que «para la investigación matemática no es esencial, sin embargo, suponer que la molécula está formada por átomos. Todo lo que hay que suponer es que la posición y configuración de la molécula puede expresarse completamente por un cierto número de variables», un número que denotaba con la letra n (para un cuerpo rígido, por ejemplo, n = 6). «De estas variables», continuaba, «tres deben determinar la posición del centro de masas de la molécula, y las restantes n−3 su configuración relativa a su centro de masas».

Básicamente, esto es todo lo que necesitamos para introducir los comentarios que más adelante Maxwell realizaba sobre sus trabajos de 1860, en los que calculó el calor específico de un gas a volumen y a presión constantes. Los valores que halló para ambos son, respectivamente:

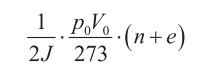
y

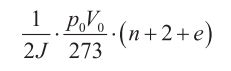
donde p₀ y V₀ son la presión y el volumen por unidad de masa a cero grados centígrados de temperatura, o 273 grados de temperatura absoluta, J el equivalente dinámico del calor y e una «cantidad positiva de valor desconocido, dependiente de la ley de fuerza que una los constituyentes de la molécula».

El problema era, como señalaba Maxwell (1875; Nye 1984: 224), que «si tomamos los valores reales del calor específico, tales como los ha encontrado Regnault, y los comparamos con esta fórmula, encontramos que para el aire y varios otros gases n + e no puede ser mayor que 4,9». Y añadía:

Para el ácido y vapor carbónico es más grande. Obtenemos el mismo resultado si comparamos el cociente de los calores específicos calculados

(2 +n + e) / (n + e)

con el cociente tal y como se ha calculado en experimentos con diversos gases, a saber, 1,408.

Y aquí nos enfrentamos cara a cara con la mayor dificultad que la teoría molecular ha encontrado hasta la fecha; a saber, la interpretación de la ecuación (n + e) =4,9.

Si suponemos que las moléculas son átomos —meros puntos materiales, incapaces de energía rotacional o movimiento interno— entonces n es 3 y e cero, y el cociente de los calores específicos es 1,66, demasiado grande para cualquier gas real.

Pero sabemos gracias al espectroscopio que una molécula puede ejecutar una gran cantidad de diferentes tipos de vibraciones. Deben ser, por consiguiente, sistemas de un muy considerable grado de complejidad, y tener mucho más de seis variables. Ahora bien, cada variable adicional introduce una cantidad suplementaria de capacidad para movimiento interno sin afectar a la presión externa. En consecuencia, toda variable adicional aumenta el calor específico, ya sea considerado a presión constante o a volumen constante. Y lo mismo hace cualquier capacidad que la molécula pueda tener para almacenar energía en forma potencial. Pero el calor específico calculado es ya demasiado grande cuando suponemos que la molécula está constituida solamente por dos átomos. Por consiguiente, todo grado de complejidad adicional que atribuyamos a la molécula únicamente aumentará la dificultad de reconciliar los valores del calor específico observados con los calculados.

[...] Boltzmann ha sugerido que debemos buscar una explicación en la acción mutua entre las moléculas y el medio etéreo que las rodea. Me temo, no obstante, que si recurriésemos a la ayuda de este medio solamente aumentaríamos el calor específico calculado, que ya es demasiado grande.

Las dudas que suscitaron en Maxwell estos resultados debieron de ser muy grandes. Un atisbo de ellas lo encontramos en la frase con la que finalizaba una comunicación que hizo en el congreso de la British Association for the Advancement of Science celebrado en Oxford entre junio y julio de 1860 (Maxwell 1860 b: 16): «Este resultado de la teoría dinámica, diferente de lo que se encuentra en los experimentos, socava toda la hipótesis, no importa lo satisfactorios que puedan ser los otros resultados».

Sin embargo, una de las pocas enseñanzas auténticamente fiables que nos han dejado décadas de esfuerzos por aquellos filósofos de la ciencia del siglo XX que se dedicaron a la metodología de la ciencia, a tratar de descubrir recetas fiables que distingan una teoría científica de otra que no lo es, es que difícilmente existen tales recetas, no al menos recetas simples, entre otros motivos porque ¿cómo refutar una teoría?, ¿a cuál del conglomerado de hipótesis responsabilizar de los problemas o fracasos con que se encuentra un sistema teórico? En el caso al que se refería Maxwell, no era legítimo concluir que «Este resultado de la teoría dinámica [es decir de la física estadística], diferente de lo que se encuentra en los experimentos, socava toda la hipótesis», porque la teoría estadística incluía numerosas suposiciones. Como, por ejemplo, la asociada al principio (también denominado teorema) de equipartición. ¿No podría encontrarse ahí la dificultad?, ¿no podría prescindirse de él manteniendo lo básico del enfoque estadístico? Claro que todo esto es muy fácil de decir... cuando se conoce la solución, una solución que llegaría de la mano de la física cuántica, de otro tipo de planteamiento.

Otro punto que no debe pasar desapercibido es que, como manifestaba Maxwell, las observaciones tomadas del espectroscopio, que revelaban que «una molécula puede ejecutar una gran cantidad de diferentes tipos de vibraciones», constituían una evidencia importante a la hora de mostrar los problemas que surgían a propósito del principio de equipartición. El propio Maxwell (1875; Nye 1984: 226) se daba cuenta de que de ahí podían surgir consecuencias imprevistas: «La teoría de las vibraciones posibles de una molécula no ha sido estudiada todavía, como se debería, con la ayuda de una comparación continua entre la teoría dinámica y la evidencia del espectroscopio. Un estudiante inteligente, armado con el cálculo y el espectroscopio, difícilmente podría dejar de encontrar algún hecho importante sobre la constitución interna de una molécula». Es dudoso, sin embargo, que se imaginase todo lo que ese «estudiante inteligente» —legiones de estudiantes inteligentes, de hecho— podría llegar a encontrar; que se diese cuenta de que sólo una nueva teoría, la teoría cuántica, podría ser a la postre capaz de explicar los «hechos importantes» que irían apareciendo.

Los resultados procedentes de la espectroscopia, como tendremos repetidas ocasiones de comprobar en este libro, constituyeron un elemento básico, imprescindible, en la construcción de la teoría cuántica, y en la medida en que fue ésta la que abrió en gran manera el mundo de la estructura atómica, tenemos que no podía ser más afirmativa la respuesta a una pregunta que se formuló Norman Lockyer (1904: 119-120) en su libro Studies in Spectrum Analysis: «¿Arroja alguna luz el espectroscopio sobre las cuestiones moleculares? ¿Existe alguna esperanza de que cuando se extiendan las investigaciones, el espectroscopio pueda ayudar en el estudio de un tema que se encuentra en la raíz de la investigación química y física?».

LAS «NUBES» DE KELVIN: LA IMPORTANCIA DEL PRINCIPIO DE EQUIPARTICIÓN

Con el tiempo, los problemas derivados del principio de equipartición, lejos de disminuir, aumentarían. Es ésta una cuestión que iremos analizando más adelante. Permítaseme, no obstante, avanzar dos evidencias que muestran la importancia que fue adquiriendo. La primera se encuentra en un artículo célebre de lord Kelvin (1901) titulado «Nineteenth century clouds over the dynamical theory of heat and light» (Nubes del siglo XIX sobre la teoría dinámica del calor y de la luz). En ese trabajo, publicado el mismo año en que comenzaba el siglo XX, Kelvin enumeraba las grandes dificultades («nubes») que en su opinión oscurecían «la belleza y claridad de la teoría dinámica, que afirma que el calor y la luz son modos de movimiento». Dos fueron las nubes seleccionadas por Kelvin, y a fe que su juicio fue certero, ya que cada una de ellas estuvo íntimamente ligada a las dos grandes teorías que marcarían la física del futuro: la relatividad especial y la física cuántica.

La primera nube se basaba en los problemas que surgían para que el éter electromagnético pudiese dar cuenta de fenómenos como la aberración de la luz y experimentos como el de Michelson y Morley, que obligaban a dotar al éter de una estructura difícil de aceptar. «Está claro», señalaba Kelvin (1901: 2-3), «que ni Fresnel ni Young tenían idea de que el éter de su teoría ondulatoria de la luz, con sus vibraciones transversales, es esencialmente un sólido elástico; esto es, materia que resiste el cambio de forma con una fuerza permanente o subpermanente. Si se hubieran dado cuenta de esta idea, habrían advertido la enorme dificultad que representa la laceración que debe de sufrir el éter si se mueve a través de poros o intersticios entre los átomos de la materia».

En cuanto al experimento de Michelson y Morley (que intentaba —a la postre sin éxito— medir el efecto del «viento del éter» cuando la Tierra se movía en sentidos opuestos con respecto a él), no veía ningún problema en su ejecución, pero «una posibilidad de escapar de la conclusión que parece probar puede encontrarse en una brillante sugerencia hecha independientemente por Fitzgerald y Lorentz [...] al efecto de que el movimiento del éter a través de la materia puede alterar ligeramente sus dimensiones lineales», por ejemplo, las del brazo del interferómetro en el que Michelson y Morley hacían las medidas. Nos encontramos aquí con la célebre idea de la contracción de longitudes, que surgía de manera natural dentro del contexto de la visión electromagnética de la materia. Ahora bien, esta vía de escape, que con tanta determinación tomó Hendrik Antoon Lorentz (1853-1928),¹² no era para Kelvin suficiente como para no concluir manifestando: «Me temo que debemos considerar todavía la nube n.° 1 como muy densa». Sería, como es bien sabido, Albert Einstein quien en 1905 la eliminaría del horizonte de la física con su teoría de la relatividad especial.

La segunda nube que seleccionó es la que tiene más importancia para los propósitos del presente libro, ya que estaba dedicada a, precisamente, el principio de equipartición, o, utilizando las palabras de Kelvin, «la doctrina de Maxwell-Boltzmann relativa a la partición de la energía». «Cuando se considera su impacto en la termodinámica», escribía (Kelvin 1901: 11), «y la encontramos en su primera y más obvia aplicación destructiva para la teoría cinética de los gases, de la que Maxwell fue uno de los principales fundadores, no la podemos ver más que como una nube en la teoría dinámica del calor y la luz». De hecho, era esta dificultad, esta nube, la que ocupaba la mayor parte del artículo, puesto que Kelvin no se limitaba a exponerla sino que también se esforzaba por indagar cómo podía ser eliminada, para lo cual pasaba revista detallada a los trabajos que desde el pionero de Waterston, pero sobre todo los de Maxwell y Boltzmann, habían añadido tanta luz como dramatismo al problema. Así, recordaba que Maxwell (1879) «extendió el teorema de la igualdad de las energías cinéticas medias a cualquier sistema de un número finito de puntos materiales [...] actuando entre sí, según una ley de fuerza arbitraria, y moviéndose libremente entre ellos», dando, además, una demostración con coordenadas generalizadas lagrangianas en un sistema arbitrario, con un número de grados de libertad finito o infinitamente grande.

Kelvin mencionaba otro problema que es conveniente resaltar, ya que no tendré más adelante mejor oportunidad para recordarlo. En su artículo, Maxwell (1879: 548) había escrito que la «única suposición que se necesita para la demostración directa [esto es, para obtener los resultados a que me acabo de referir] es que si se deja libre en su actual estado de movimiento al sistema, pasará, más pronto o más tarde, por toda fase que sea consistente con la ecuación de la energía». Kelvin veía que acaso en este punto se encontrase una vía de escape para evitar dar, como se deducía de los resultados de Maxwell, una aplicabilidad tan general al teorema de equipartición. En concreto, Kelvin apuntaba que «nunca he visto la validez de la demostración en la que Maxwell basó su afirmación y siempre me ha parecido improbable que pudiese ser cierta».

No está claro, sin embargo, que este comentario de Kelvin fuese en la dirección correcta, ya que la suposición de Maxwell parece no ser sino una manifestación de otro problema que a finales de siglo afectaba gravemente a la teoría cinética. De un teorema demostrado por Henri Poincaré (1890) se deducía que en un sistema conservativo (es decir, uno en el que se cumplen ciertas condiciones que implican, por ejemplo, que se conserva la energía), en un espacio finito un estado inicial arbitrario pasaría infinitas veces por un estado próximo (infinitamente próximo, de hecho). De ello parecía deducirse que la entropía no podía crecer continuamente, sino que debía experimentar variaciones cíclicas. Esta paradoja de «la recurrencia» fue destacada especialmente por Ernst Zermelo (1871-1953; 1896 a, b), y algunos científicos utilizaron semejante aparente contradicción entre la termodinámica macroscópica y la teoría cinética para argumentar que debía rechazarse esta última. Fue Boltzmann, por supuesto, el que con más fuerza se opuso a semejante conclusión (ver, por ejemplo, su tratado Vorlesungen über Gastheorie, Boltzmann 1896, 1898).

Para la segunda evidencia a la que aludía antes, y con la que finalizaré el presente capítulo, utilizaré las reminiscencias de Oliver Lodge (1851-1940; 1931: 181) sobre lo que Joseph Larmor (1857-1942) manifestó durante el Congreso de la British Association for the Advancement of Science celebrado en Bradford en 1900:

Cuando descubrió en 1860, para su gran sorpresa, que en un sistema de átomos rígidos que colisionan entre sí la energía debe estar siempre dividida por igual entre los movimientos traslacionales y los rotacionales, Maxwell manifestó que para evitar esta desagradable conclusión solamente es necesario suponer que «se nos ha escapado hasta ahora algo esencial para la formulación completa de la teoría física de los choques moleculares».

De otro modo, añadía Lodge, «la energía se disiparía entre los innumerables grados de libertad, y la actividad del universo llegaría a su final». Lodge estaba pensando, especialmente, en el éter, para él muy querido; el problema señalado por Maxwell planteaba, efectivamente, un grave problema: dado que el éter posee infinitos grados de libertad, ¿cómo distribuir la energía entre ellos? Si suponemos que existe una energía finita en el Universo, al ser infinitos, cada grado de libertad debería poseer una energía nula; recíprocamente, si cada grado de libertad posee la misma, no nula, energía, ¿no tendrá que ser la energía total infinita? Pero Lodge, que escribía en 1931, podía ya añadir: «Ahora sabemos lo que se nos había escapado cuando discutíamos la equipartición total; era nada menos que el “cuanto”, para regular el intercambio de energía entre materia y éter».