SOY SOCIABLE Y TRAVIESO: APAREZCO EN TODAS PARTES

2

Ahora que ya me reconociste, quizás recuerdes que me has visto aparecer en muchas otras partes. Por ejemplo, en la fórmula del área del círculo:

O en las fórmulas del área y del volumen de la esfera:

Con el tiempo me verás aparecer en medio de la que, para muchas personas, es la igualdad más hermosa de la matemática, la del gran Leonhard Euler, uno de los héroes de mi historia:

La letra i representa la famosa “unidad imaginaria”, una extraña entidad numérica que los matemáticos tardaron mucho en descubrir, pero que hoy les resulta muy útil para encontrar raíces cuadradas de números negativos. Esta se te hará muy familiar con los años cuando descubras su sencillez, pese a que es llamada número complejo. Además, la letra e denota el importantísimo número de Euler, cuyo valor aproximado es 2,71. Es uno de mis mejores amigos y, aunque suele estar muy ocupado, debería escribir su propia autobiografía.

¿No es hermosa la fórmula de arriba? Aparezco junto a mis amigos i, e, 0 y 1, enlazados por la operación más sencilla, la suma +, y con una igualdad en medio. ¿No te parece curioso que yo pueda multiplicarme con un número imaginario y luego subir juntos como exponentes sobre e para finalmente valer -1?

Con mi amigo e aparecemos juntos en muchas otras situaciones. Una de estas tiene que ver con el factorial de un número (natural), que es el producto de todos los números naturales no mayores que él. Por ejemplo, el factorial de 5
es 1 x 2 x 3 x 4 x 5 = 120 , y se denota 5 ! He visto factoriales apareciendo en muchas partes de la matemática. Sin embargo, un problema que se presenta a menudo es que el factorial se vuelve rápidamente muy grande a medida que el número crece, al punto de que las calculadoras clásicas usualmente colapsan al calcular, por ejemplo, el valor de 100 !,
pues se trata de un número que consta de 158 dígitos. Se requiere entonces de una buena aproximación de n ! que permita aventurar, al menos, qué tan grande es el resultado. Afortunadamente, una excelente fórmula “aproximativa” fue descubierta por James Stirling en el siglo xviii, y ella señala que n ! es bastante parecido a

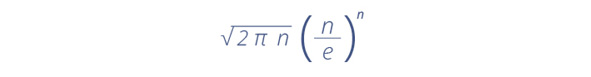
Entonces, para estimar el valor de n ! no necesitas jugar con todos los números inferiores a n sino que te basta con conservarlo y colocarme en medio de la fórmula, junto con mi gran amigo e. Si realizas este procedimiento, por ejemplo, con n = 100, el error en que incurrirás con respecto al valor real de 100 ! es inferior al 1 %. ¡Increíble!

Por cierto, si bien era muy natural que yo apareciera en el perímetro y el área de círculos y esferas, no lo era tanto para la identidad de Euler y la aproximación de Stirling. Pero la verdad es que en muchos procesos hay un círculo escondido y, cada vez que este anda por allí, yo me escurro en medio. Otro ejemplo que tal vez ya hayas estudiado (si no, seguramente pronto lo harás) es el de la distribución “normal” de probabilidades. Esta es la que genera la famosa “campana de Gauss” mediante la función de densidad

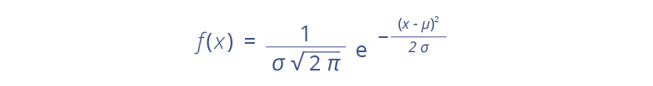
Puede que esta fórmula te parezca un poco difícil pues, además de hacer intervenir (nuevamente) a mi querido e, involucra dos constantes: la esperanza μ y la varianza σ del fenómeno que se está estudiando; además, para implementarla se requieren conocimientos de cálculo integral. Con ella solo quiero mostrarte que puedes verme participando de este proceso con que se calibran los cálculos que gobiernan muchos fenómenos de la naturaleza y de las ciencias humanas.

Ahora bien, si te parece extraño que yo viva también en el mundo de las probabilidades, te puedo contar que hay un experimento muy entretenido de este tipo en el que aparezco de manera mucho más transparente. Este fue ideado en 1733 por Georges Leclerc, más conocido como Buffon, pues era conde de la localidad francesa con ese nombre.

¿En qué consiste? Toma un palito y lánzalo sobre una superficie que tenga rayas paralelas trazadas a una distancia igual al largo del palito. Hazlo muchas veces, digamos 100, y cuenta en cuántas de ellas el palito cayó sobre una de las rayas. Apuesto que esto ocurre un poquito más de 60 veces o un número de veces no muy lejano a este.

¿Es así? ¿Te sorprende que pueda adivinar? Ocurre que, usando argumentos teóricos sofisticados, Buffon calculó la probabilidad de que el evento suceda y concluyó que su valor es igual a . Con 100 lanzamientos, esto corresponde aproximadamente a x 100 = 63,6...¡Es por esto que yo puedo adivinar!

Durante siglos me he dedicado a estudiar la matemática de los seres humanos y he podido constatar que no existe rama de esta ciencia en la que yo no aparezca. Muchas veces me vi sorprendido, pero ya estoy tan acostumbrado que podría apostar que no habrá campo alguno en el futuro en el que no me entrometeré. Y no solo ando por estos rumbos: también lo hago en otras ciencias, como la astronomía. Allí me puedes encontrar, por ejemplo, en medio de la tercera ley de Kepler del movimiento de los planetas:

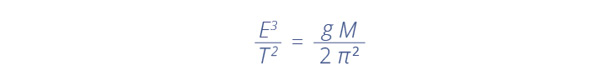
Esta ley sintetiza lo siguiente: cada planeta describe una órbita elíptica en torno al Sol, y el cubo del semieje mayor E de esta elipse (es decir, del mayor segmento que puede trazarse desde el centro de la elipse a uno de los puntos de su contorno) es proporcional al cuadrado del tiempo T que el planeta demora en dar una vuelta (es decir, del periodo); además, la constante de proporcionalidad es, nada más ni nada menos, que el producto de la constante gravitacional universal g por la masa M del Sol, todo esto dividido por dos veces el cuadrado de mi valor.

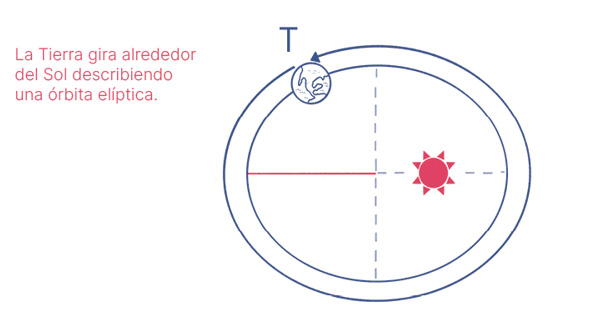
Cada vez que reviso estas fórmulas no deja de sorprenderme la enorme creatividad del ser humano para descubrirlas (¿o quizás inventarlas?, la verdad no lo sé, y creo que nadie tiene claridad sobre esto). Siempre comienzan observando un fenómeno, reflexionan sobre este, leen y estudian mucho al respecto. Luego intentan traducirlo a un lenguaje matemático que, en general, está gobernado por fórmulas. Finalmente, para comprobar que estas son correctas, piensan hasta romperse la cabeza. Intentan una idea, fracasan; tratan otra y se equivocan nuevamente… Pero siguen, saben que incluso un tropiezo es útil, pues los ayuda a vislumbrar el camino cierto, y poco a poco se van acercando. Nunca pierden la ilusión: vuelven a la carga y, a veces, consiguen una justificación apropiada. Y cuando lo logran, son inmensamente felices, ¡casi como si no existiera un placer más grande!

Sin embargo, puede ocurrir que esta justificación (que en matemática suele llamarse “demostración”) sea un poco dura y deba escribirse en un lenguaje difícil, a veces algebraico. De hecho, debo confesar que, pese a que estudié muchísimo para escribir mi autobiografía, no creo recordar de memoria todas las demostraciones de las fórmulas que verás aparecer en estas páginas, y apostaría a que son muy pocos quienes las recuerdan. En ocasiones, al ver alguna de ellas, me veo forzado a repasar varias teorías, ya que una demostración debe basarse en argumentos incuestionables que recurran solo a conocimientos ya adquiridos.

A pesar de este rigor implacable, con el tiempo he aprendido a reconocer que este lenguaje tan preciso de las matemáticas tiene una extraña elegancia. Además, cuando una idea matemática se me vuelve compleja, no logro captar completamente una demostración o, simplemente, si quiero convencerme de que estoy entendiendo bien las cosas, a menudo recurro a mis amigos para compartir opiniones al respecto. Estos encuentros me generan gran entusiasmo: suelo imaginar nuevas formas de entender las cosas y demostrarlas, muchas de ellas más entretenidas que las ya existentes y, por ende, más amenas de enseñar. Una de mis explicaciones favoritas es, precisamente, la de la primera de las fórmulas anteriores, la del área del círculo. Lo sabroso de todo esto es que, desde que descubrimos el sabor de la pizza hace algunos siglos, ¡se las he repetido cientos de veces comiéndonos varias en mi casa!

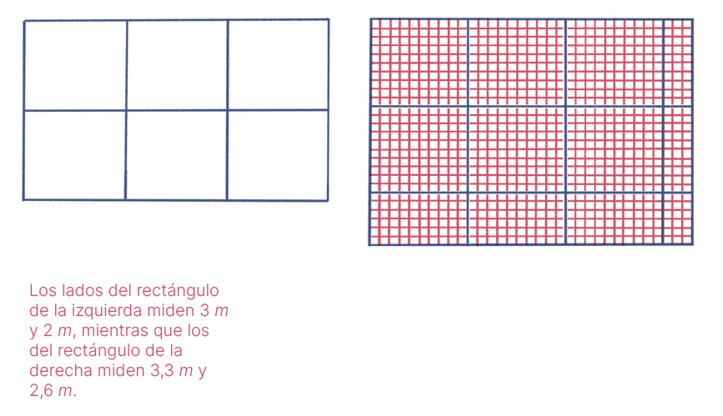
Para comenzar, les explico que el área corresponde a un valor que se le asigna a la amplitud de una región o superficie. ¿Cómo se hace esta asignación de manera natural? Pues bien, si la unidad para medir longitudes es, por ejemplo, el metro, entonces al cuadrado de lado un metro se le asigna naturalmente el valor de un metro cuadrado, que se denota 1 m2. Si ahora se considera un rectángulo de, por ejemplo, lados 3 m y 2 m, este se puede dividir en 3 x 2 = 6 cuadrados de lado 1 m (como en la imagen de abajo a la izquierda). Por lo tanto, lo natural es asignarle un área de 6 m2. Si un rectángulo tiene longitudes más complicadas, como 3,3 m y 2,6 m, entonces se puede dividir en 33 x 26 = 858 cuadrados de lado 0,1 m (tal como se ilustra en la figura de abajo a la derecha). Ahora bien, cada cuadrado de lado 0,1 m tiene área m2, pues 100 de ellos cubren un cuadrado de lado 1 m. Así se concluye que, en metros cuadrados, el área del rectángulo es = 8,58, que equivale al producto 3,3 x 2,6.

Luego, no es difícil convencerlos de que un razonamiento análogo es válido para cualquier rectángulo cuyos lados son números con finitos decimales, lo que permite concluir que su área es el producto de sus lados. Finalmente, con un último esfuerzo, logro probarles que esto es válido para cualquier rectángulo, pues si la medida de alguno de los lados (o ambos) tiene infinitos decimales, entonces el rectángulo puede ser aproximado tanto cuanto se quiera por rectángulos cuyos lados tienen longitudes iguales a números de finitos decimales.

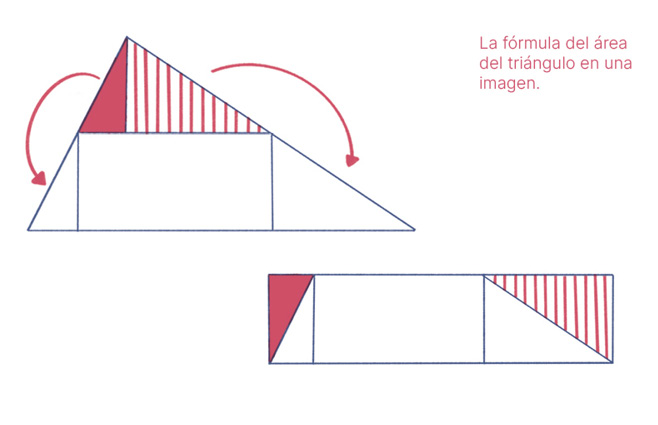
Con el tiempo he entendido que la “única” fórmula para áreas es aquella que señala que su valor para un rectángulo corresponde al producto de la medida de sus lados. Esto, en el sentido de que cualquier otra fórmula se puede deducir de aquella. En algunos casos es sencillo. Por ejemplo, la famosa “regla” que señala que “el área de un triángulo es la mitad del producto de su base por la altura correspondiente” se justifica porque el triángulo es equivalente a un rectángulo cuyos lados son dicha base y la mitad de la altura.

“¡Todo tiene su demostración!”, me han gritado algunos de mis amigos cuando llego a este punto de mi explicación, felices de comprender al fin algo tan fundamental.

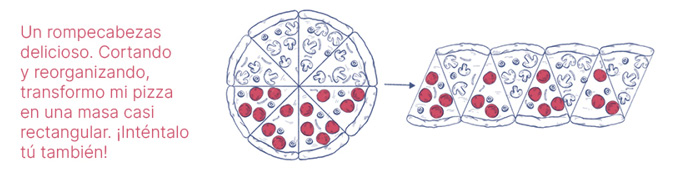
Pasar al caso del círculo me resulta complicado, pues es relativamente claro que este no puede ser transformado en un rectángulo por procedimientos “simples”. Pero uno puede intentar hacerlo de manera aproximada. Para explicar esto, a menudo tomo una pizza y la divido en 8 partes iguales mediante cortes que nacen desde su centro. Se forman entonces dos figuras de 4 trozos cada una que ensamblan una contra la otra para formar algo parecido a un rectángulo. Es la misma pizza, pero dispuesta de una manera distinta. Los lados rectos quedan ligeramente inclinados y corresponden a radios de la pizza. Los otros “lados” son, en realidad, uniones de arcos de circunferencia, y tanto el “lado” de abajo como el de arriba miden la mitad del perímetro de la circunferencia (que no es otra cosa que el borde de la pizza).

Ahora bien, si este proceso lo repitiera con 48 cortes de pizza para repartirla entre más amigos, entonces la figura que resultaría es prácticamente igual a la de un rectángulo cuya base es la mitad del perímetro del círculo y cuya altura es el radio de este. El área de esta figura sería, entonces, muy próxima a la de dicho rectángulo, cuyo valor no es otro que

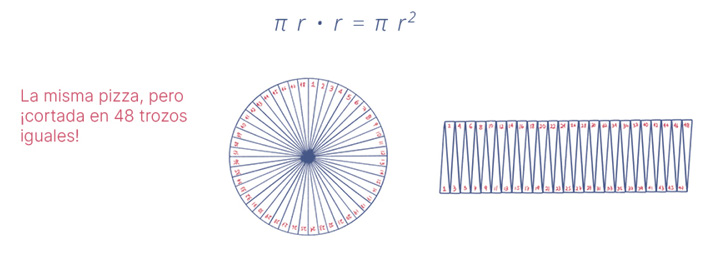
Y si invitara a más y más amigos, habría que dividir la pizza en más y más trozos cada vez más finos. Al ensamblarlos, la diferencia entre la figura resultante y el rectángulo se haría progresivamente menor. Todo el mundo se convencería, entonces, de que el área de la pizza-círculo inicial debe ser igual a la del rectángulo, es decir, a π r2.

¡Es por esto que en la fórmula A = π r2 también me entrometo! Como ves, el razonamiento no es difícil, pero necesita algo de ingenio y de mucha curiosidad. A lo largo de la historia, estos han sido los motores que les han permitido a los seres humanos ir descubriendo centenares de sitios en los que me escondo, y ciertamente seguirán descubriendo otros nuevos en el futuro. Quizás seas tú quien, en algunos años más, descubra uno de estos rincones aún desconocidos.