Vivo y trabajo en New Haven, Connecticut. La ciudad, además de ser conocida por la Universidad de Yale, es famosa por su pizza. Algunos son apasionadamente fieles a la de Sally’s y otros a la de Pepe’s. Viendo sus largas colas se podría pensar que es más difícil entrar en estos restaurantes que en Yale. Eso es porque sus pizzas de almejas están en una liga propia. A riesgo de decantarme por un bando, contemplo una negociación con una pizza de Pepe’s.

Pepe’s les dará a Alice y a Bob una de sus pizzas de almeja de 12 porciones si ambos se ponen de acuerdo en cómo repartirla. Si no lo hacen, Pepe’s seguirá dándoles pizza, pero solo media y, además, con cierto favoritismo: 4 trozos serán para Alice y 2 para Bob.
Hay muchos incentivos para llegar a una resolución. El reto es que hay varios acuerdos que pueden funcionar para ambas partes, unos más favorables para Alice y otros, para Bob. Pero tienen que elegir uno. La mayoría de la gente emplearía una de estas dos perspectivas para que Alice y Bob negociaran un acuerdo:
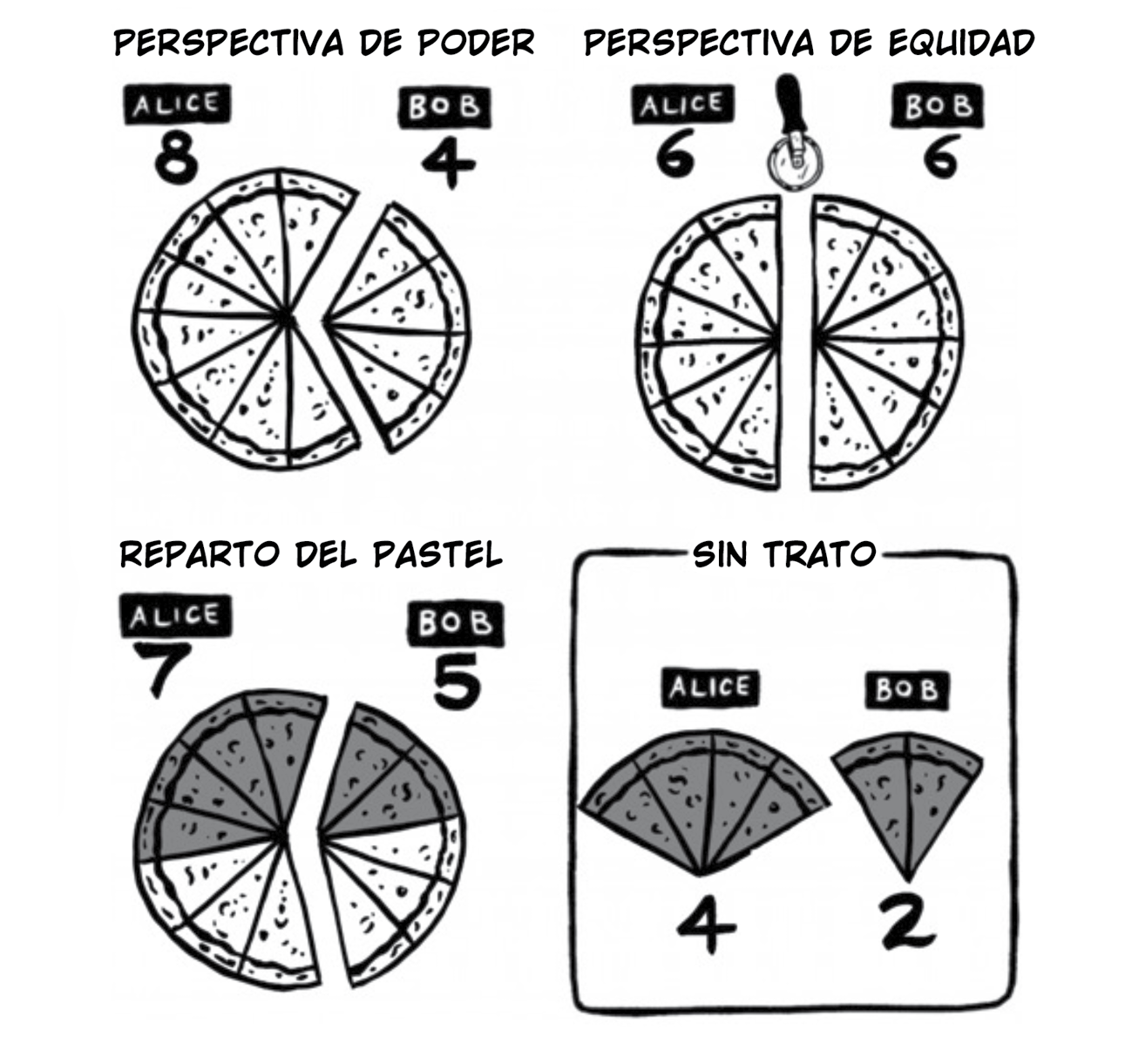
La primera es la perspectiva del poder: Alice comienza con más poder ya que sin acuerdo —su parte es de 4 pedazos, es decir dos veces mejor que la de Bob—, por lo que debería obtener el doble (8 porciones para Alice y 4 para Bob).
La segunda es la perspectiva de la equidad: las dos partes se centran en lo que se lleva cada una. En este caso, dividen la pizza por la mitad (Alice se queda con 6 porciones y Bob con otras 6).
Sin embargo, hay una forma diferente —y más lógica— de repartir la pizza. Es más lógica porque se centra en lo que realmente es la negociación: las 6 porciones extra creadas mediante acuerdo. Si Alice y Bob no llegan a un trato, tendrán un total de 4 + 2 = 6 porciones. Si, por el contrario, se avienen a él, tendrán 12 trozos. El valor de llegar a un acuerdo es pasar de 6 a 12 porciones. Ese aumento de 6 porciones es lo que está en juego o lo que yo llamo el «pastel de la negociación». Para conseguir esas 6 porciones, Alice y Bob se necesitan por igual. Como tienen el mismo poder, las 6 porciones deben repartirse a partes iguales. Además, cada uno recibe su parte de vuelta. Esto lleva a un reparto global de 4 + 3 = 7 porciones para Alice y 2 + 3 = 5 porciones para Bob.
Aunque parezca extraño decir esto, la mayoría de la gente acaba confundida sobre lo que realmente se negocia. Discuten sobre las 12 porciones, en lugar de las 6. Se centran en toda la pizza, no en la parte que corresponde. El pastel de la negociación es como una idea obvia que se esconde a la vista. Una vez que se enmarca la negociación en términos del pastel pertinente, la conclusión lógica es que esa parte que de verdad corresponde debe repartirse equitativamente. Eso es de lo que tengo que convencerte. Luego te daré las herramientas para convencer a los demás.
Como primer paso, quiero explicar lo que está mal en el statu quo. En mi opinión, la perspectiva de poder confunde el poder externo de la negociación con el interno de la negociación. ¿Por qué habría que repartir el importe del total en proporción al no acuerdo? Aunque 8:4 parece un resultado razonable porque imita la proporción de sus respectivas cantidades de no haber un acuerdo, no hay ninguna razón inherente para que el resultado se base en esa proporción.
Una forma de ver la debilidad de este argumento de la proporción es considerar un escenario diferente, uno en el que, si no hay acuerdo, Bob no obtendría ninguna porción, solo algunas migajas. En ese caso, tratar de imitar la proporción del no acuerdo llevaría a proporciones absurdamente altas de porciones (acercándose al infinito), lo que sugiere que de las 12 porciones casi todas serían para Alice.
Se podría argumentar que Bob está en una posición de negociar más débil, ya que solo obtendrá 2 porciones si no hay acuerdo, mientras que Alice obtendrá 4. Este argumento no tiene en cuenta el objetivo de la negociación. Si no llegan a un acuerdo, Alice solo conseguirá sus 4 porciones, y Bob solo 2. Una negociación eficaz consiste en superar el no acuerdo y para eso Alice y Bob son igual de necesarios y, por tanto, igual de poderosos.
El segundo enfoque, un reparto equitativo del total, es una visión exagerada de la equidad. A la hora de repartir los 12 trozos, Alice y Bob no están en igualdad de condiciones. Alice tiene una opción mejor. Si 6:6 es realmente una visión viable de la equidad, debería funcionar cualquier sea la opción de no acuerdo. Pero no es así. Mira qué pasaría si la opción de Alice fuera de 7 trozos en lugar de 4, mientras que la de Bob se quedase en 2 trozos. Si la equidad significa una división 6:6, Alice la rechazaría. Preferiría quedarse con su opción de 7 pedazos antes que aceptar 6. Mientras que en un reparto equitativo este error puede no ser aparente cuando las opciones alternativas son 4 y 2 porciones, sí lo es cuando la alternativa es 7 y 2. Por lo tanto, como regla de equidad, dividir el total en dos es fundamentalmente un error.
Dividir el total es un error común. Digamos que asignamos los trozos que corresponen a Alice y Bob al azar y luego los hacemos negociar. ¿Qué se puede predecir? Un experimento de este tipo fue realizado por Nejat Anbarci y Nick Feltovich1. Si la alternativa de ambas partes es menos de la mitad del total, el 42 % de las veces se lo dividirán a partes iguales. Parece justo y ninguno de los dos bandos sale ganando si no acuerda. Pero en cuanto una de las opciones alternativas superase la mitad, en menos del 8 % de las veces se optaría por un reparto equitativo.
Lo que ocurre es que las dos partes se aferran a una solución que parezca justa. El problema es que no han aprendido a ver el pastel pertinente como 12 – (4 + 2) = 6 porciones y por eso acaban repartiendo el total equivocado. Dividen las 12 porciones, no las 6. Está bien preocuparse por la equidad, pero la equidad debe aplicarse al pastel de negociación pertinente, no al total. Cuando se trata de las 6 porciones del pastel de la negociación, Alice y Bob son perfectamente simétricos, están en la misma posición y son igualmente necesarios. Repartir el pastel de la negociación a partes iguales es lo justo. Bajo la perspectiva del pastel, el pastel de la negociación de 6 se divide en 3 y 3.
Cada parte obtiene su opción alternativa más la mitad del pastel. Alice termina con 4 + 3 = 7 porciones, y Bob obtiene 2 + 3 = 5 porciones.
Repartir el pastel de la negociación no es solo una cuestión de equidad. Alice y Bob tienen el mismo poder. Si Alice no acepta el reparto, dicho pastel se pierde. Lo mismo ocurre con Bob. No se puede decir que ninguna de las partes contribuya más que la otra a crear este pastel de 6. Dentro de la negociación, donde el objetivo es crear un valor creciente más allá del punto de partida de las partes, ambas son totalmente simétricas. Fuera de ella, las dos partes tienen un poder diferencial que se refleja en sus desiguales opciones alternativas, lo cual no influye en la forma de repartir el pastel de la negociación.
Ahora has visto la salsa secreta. En el caso de la pizza puede parecer engañosamente sencillo, al menos en retrospectiva. Cuando aplicamos este enfoque a problemas más complicados del mundo real, el ejemplo de la pizza subyace a todo lo que hagamos.
A partir de ahora, cuando utilice el término «pastel» me referiré siempre al que corresponde a la negociación. Ese es el pastel que importa. Como ya he dicho, lo difícil de la negociación es medir el pastel correctamente. No siempre es tan sencillo como en el ejemplo de la pizza. Puede que tengas que trabajar con la otra parte para descubrir cuál es. Reconocerlo es la clave para conseguir la mitad. Y, una vez resuelto el problema de dividirlo, puedes centrar tu atención en trabajar juntos para hacer que crezca.
Empecemos.