1
Para mi hijo y para mí, él era simplemente «el profesor». Este, por su parte, llamaba a mi hijo con el curioso apelativo de «Raíz Cuadrada», porque tenía la parte superior de la cabeza tan chata y tan recta como el símbolo de esa operación.
—Muchacho, con esta tapadera no se te escapará la inteligencia que tienes debajo —bromeaba, orgulloso, el profesor, mientras le pasaba cariñosamente la mano por el pelo, desgreñándoselo.
Ante esas inocentes muestras de afecto, mi hijo se encogía de hombros mientras recordaba las burlas de sus compañeros de clase cuando se pitorreaban de la curiosa planicie que le remataba el cráneo. Por eso se había acostumbrado a cubrirse la cabeza siempre con una gorra de béisbol.
—Fijaos en esto —dijo un día el profesor mientras pasaba el dedo índice por una esquina de la superficie polvorienta de su escritorio—. Aquí donde lo veis, este pequeño signo representa una operación matemática fundamental. Nos permite ordenar todos los números, incluidos los infinitos y los invisibles. ¿Podéis creerlo?
El profesor acababa de trazar el signo de la raíz cuadrada:
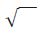
De las incontables cosas que el profesor nos enseñó en los meses que pasé a su servicio, la raíz cuadrada fue lo que a mi hijo y a mí más nos impresionó. Agrandó el modo en que veíamos el mundo, hasta ahora sencillo. Seguramente al profesor no le habría gustado esa expresión, «incontables cosas», ya que para él el mundo entero podría ser expresado mediante las matemáticas. Pero ¿cómo podría describir aquellas cascadas de números primos de cientos de miles de cifras, o magnitudes inabarcables, como el mayor número jamás usado en una demostración matemática, incluido en el Guinness de los récords, o a la inconcebible idea de que hay unos infinitos mayores que otros? Y, sin embargo, pese a la emoción que me causó todo eso, lo más valioso y que con más cariño todavía hoy guardo dentro de mi corazón, son todas aquellas horas en que mi hijo y yo disfrutamos en compañía del profesor.
Recuerdo perfectamente ese día en que, mediante el símbolo de la raíz cuadrada, nos abrió las puertas de aquel maravilloso mundo lleno de secretos. Era una tarde gris y lluviosa de principios de abril, y estábamos los tres en el estudio del profesor, en una penumbra apenas rota por la luz de una bombilla. Guardo en mi memoria la imagen de la mochila de mi hijo, abandonada con descuido sobre la alfombra, y la de los albaricoqueros en flor, inmóviles al otro lado de los cristales de la ventana y con sus hojas expuestas al aguacero.
Cuando el profesor nos animaba a resolver alguna cuestión matemática, no era la solución correcta lo que esperaba de nosotros. Lo que menos le gustaba era que, por cautela, nos quedáramos en silencio cuando no sabíamos qué contestar. Y si para encontrar la respuesta correcta no habíamos argumentado bien, entonces prefería una respuesta inexacta, incluso descabellada. Y es que, fueran correctas o no, le gustaban mucho las respuestas que agrandaban las perspectivas del problema inicial y provocaban nuevas preguntas que iban más allá. Daba la bienvenida a esos errores, reconocía que en cierto modo eran acertados si apuntaban en la dirección adecuada; y para detectar esos errores esclarecedores, el profesor tenía un instinto finísimo, los olfateaba, y nos animaba a seguirles la pista. Así nos llenaba a nosotros de confianza y nos motivaba para dedicar tiempo y esfuerzo a cada desafío que nos planteaba.
—¿Puedo proponeros un reto? —nos preguntó el profesor aquella tarde de lluvia—. ¿Qué os parece si ponemos debajo de la raíz cuadrada un –1?
Mi hijo había estudiado las fracciones en el colegio, y, por otro lado, sabía que había números menores que 0 tras una sesuda lección de casi media hora que el profesor le había dado, con mucha paciencia, de modo que se apresuró a replicar:
—Para eso deberíamos encontrar un número que, multiplicado por sí mismo, nos dé –1, ¿no?
Y puesto que así debía de ser, colocamos el número –1 debajo del signo de la raíz cuadrada: 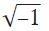 , y, sin tiempo que perder, nos lanzamos a repasar operaciones sencillas, como la raíz cuadrada de 100, que es 10; la de 16, que es 4, o la de 1, que es 1, con la esperanza de que eso nos ayudara a encontrar la raíz cuadrada de –1...
, y, sin tiempo que perder, nos lanzamos a repasar operaciones sencillas, como la raíz cuadrada de 100, que es 10; la de 16, que es 4, o la de 1, que es 1, con la esperanza de que eso nos ayudara a encontrar la raíz cuadrada de –1...
El profesor no nos atosigaba. Le encantaba contemplar nuestras caras cuando reflexionábamos.
—Yo diría —me atreví a intervenir, aunque no las tenía todas conmigo— que no es posible..., que ningún número multiplicado por sí mismo puede dar –1 como resultado.
—Creo que te equivocas. Ese número se encuentra aquí —replicó el profesor, señalándose el pecho—. Se trata de un número muy reservado y que no se muestra a simple vista. Solo podréis contemplarlo con los ojos de la razón, pero, a pesar de su timidez, cumple una función imprescindible en el conjunto de la existencia.
Volvimos a quedarnos en silencio. En mi cabeza revoloteaba la imagen de un número que, a pesar de esa reserva y discreción, ocupaba un lugar propio en la totalidad del universo y lo sustentaba. Me di cuenta de que no se oía más sonido que el de la lluvia, y vi a mi hijo llevarse una mano a la cabeza, como si tratara de asegurarse de que seguía allí, con su forma de raíz cuadrada.
Además de compartir gustoso sus conocimientos, el profesor se mostraba siempre humilde y respetuoso, no solo con nosotros, sino también con todo lo que él desconocía. No desviaba la mirada hacia otro lado, con desdén, cuando algo desafiaba su sabiduría, sino que lo aceptaba con la misma deferencia que tenía hacia aquel 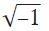 . Eso formaba parte de su carácter atento y tolerante, que mostraba también cuando me pedía algo: lo hacía siempre con mucho respeto, comenzando con un «Perdona que te moleste, pero...», incluso si lo que quería era algo tan trivial como, por ejemplo, que pusiera el temporizador del horno tostador a tres minutos y medio. Recuerdo que, en esos casos, apenas giraba yo el temporizador hasta la franja correspondiente, él se inclinaba hacia el aparato, alargaba el cuello y observaba a través de la portezuela cómo la rebanada de pan adquiría tonos dorados, y así se quedaba, absorto, hasta el final de la cuenta atrás, tan ensimismado como cuando se concentraba en sus complicadas demostraciones hasta encontrar la última proposición, la verdadera y final, como si el tostado del pan que ocurría ante sus ojos fuera un proceso equiparable a la demostración del teorema de Pitágoras.
. Eso formaba parte de su carácter atento y tolerante, que mostraba también cuando me pedía algo: lo hacía siempre con mucho respeto, comenzando con un «Perdona que te moleste, pero...», incluso si lo que quería era algo tan trivial como, por ejemplo, que pusiera el temporizador del horno tostador a tres minutos y medio. Recuerdo que, en esos casos, apenas giraba yo el temporizador hasta la franja correspondiente, él se inclinaba hacia el aparato, alargaba el cuello y observaba a través de la portezuela cómo la rebanada de pan adquiría tonos dorados, y así se quedaba, absorto, hasta el final de la cuenta atrás, tan ensimismado como cuando se concentraba en sus complicadas demostraciones hasta encontrar la última proposición, la verdadera y final, como si el tostado del pan que ocurría ante sus ojos fuera un proceso equiparable a la demostración del teorema de Pitágoras.
Fue en el mes de marzo de 1992 cuando la agencia de empleadas del hogar Aurora me asignó la casa del profesor. La agencia se hallaba en una modesta ciudad del litoral del mar interior de Seto, y yo, pese a mis diez años de experiencia, era la más joven de todas sus empleadas. Podía además presumir de no haber tenido nunca un contratiempo en los numerosos hogares por los que había pasado. Me tomaba mi oficio con gran profesionalidad: nunca expresé la menor queja ante el director por complicado que fuera el hogar que me habían asignado, ni siquiera cuando era uno de los que mis compañeras evitaban.
Y el profesor era uno de esos clientes conflictivos de los que todas huían, o al menos eso se deducía de su ficha. Solo verla ya presagiaba lo peor. Una hilera de nefastos sellos azules en el dorso mostraba el número de empleadas a su servicio que habían sido despedidas: cada sello correspondía a una queja o reclamación por parte del cliente y de su familia lo bastante grave como para provocar la destitución de la empleada y la necesidad de asignar otra nueva. Cuando eso ocurría, el director estampaba diligentemente un sello azul con forma de estrella en el reverso de la ficha —nueve tenía ya la del profesor—, a modo de advertencia para las siguientes incautas que se atrevieran a asumir el relevo. Por lo que a mí respecta, hasta ese momento nunca me había encontrado con un cliente con tantas estrellas.
Cuando visité por primera vez la nueva casa que me habían asignado, la del profesor, me abrió la puerta una anciana de edad avanzada, pulcra, elegante y de porte digno; era esbelta, llevaba un vestido de punto, y el pelo, con mechas de color castaño, recogido en un moño alto. Me invitó a pasar y caminó apoyándose en un bastón negro que sujetaba con su mano izquierda.
—Se trata de mi cuñado —dijo, desvelando así el parentesco que le unía al profesor—. Es a él a quien debe atender, naturalmente, no a mí. Nos daría usted un auténtico disgusto si no consiguiera adaptarse al trabajo. Nos duran poco, ya sabe. Las chicas, digo, y entienda usted que cada vez que viene una nueva, nos vemos obligados a comenzar una vez más desde el punto de partida.
Más adelante supe que el profesor, al que se había referido como «su cuñado», era el hermano pequeño de su difunto marido.
—No voy a pedirle nada particularmente complicado —continuó la anciana—. Su horario será de once de la mañana a siete de la tarde, de lunes a viernes. Primero le preparará la comida a mi cuñado y a continuación se encargará de la limpieza, hará las compras necesarias y preparará la cena. Nada extraordinario, ¿no le parece? —Cada vez que pronunciaba la palabra «cuñado», titubeaba un poco. Por otra parte, con su mano izquierda manoseaba sin descanso la empuñadura del bastón, lo que contrastaba con sus delicados ademanes. Unas veces rehuía mi mirada sin disimular su desconfianza, y otras me observaba fijamente—. Ya lo ve, nada del otro mundo. Me doy plenamente por satisfecha con que le proporcione a mi cuñado las atenciones básicas para que pueda llevar una vida normal. Así lo dejé especificado en el contrato con la agencia y así se lo pido.
—Bien, bien. Y... ¿dónde está ahora? —pregunté.
La anciana alzó el bastón y con él apuntó hacia un jardín interior. Más allá de un seto de fotinia podado con esmero se alzaba una edificación más pequeña, quizá un anejo de la casa en la que nos encontrábamos. Apenas se entreveían, más allá de los árboles del jardín, las tonalidades granates de su tejado de pizarra.
—Debo rogarle encarecidamente que no vaya por capricho de una casa a la otra, que se ciña a la de mi cuñado, pase lo que pase, y le agradecería que, para entrar y salir, utilizara la entrada principal, orientada al norte, que da directamente a la calle. Y no lo olvide: sean cuales sean las dificultades que se le presenten, deberá arreglárselas usted como buenamente pueda, desde casa de mi cuñado, ¿de acuerdo? Espero que lo haya entendido y que así lo haga. Por lo que a mí respecta, no le pido nada más —sentenció, y, como enfatizándolo, golpeó el suelo con el bastón.
Aquello no era nada comparado con las minuciosas normas, a veces disparatadas, que muchos clientes me imponían: que si debía recogerme el pelo en una trenza adornada cada día con un lazo diferente, que si tenía que calentar el agua para el té exactamente a setenta y cinco grados, que si debía unir mis manos para rezar cada tarde en dirección al lucero vespertino...
—Bien, entonces ya solo queda que nos presente y... —Yo había dado por concluido el sermón de la anciana dama.
—No será necesario —atajó, tan firmemente que dudé de si yo había dicho algo inoportuno—. Sería inútil que los presentara a ustedes dos hoy —continuó—. Mañana el profesor no recordaría nada. Por lo tanto, no veo que haya ninguna necesidad.
—Disculpe, no entiendo a qué se refiere...
—Muy sencillo. Anda mal de la memoria, por decirlo claro. De cabeza y todo lo demás está bien, las neuronas le funcionan, pero la memoria... le falla desde un accidente que tuvo hace diecisiete años, de tráfico. Se golpeó la cabeza y todos sus recuerdos se le quedaron paralizados, congelados allí mismo, en el año 1975. Recuerda lo anterior a esa fecha, pero lo posterior, todo lo nuevo que le ocurra, no logra retenerlo en su memoria más que unos minutos y, después, lo olvida. Por ponerle un ejemplo, es capaz de recordar un teorema que descubrió hace treinta años, pero no le pregunte qué cenó la víspera... porque será incapaz de decírselo. Para ser exactos, la memoria le dura ochenta minutos. Solo durante ese breve periodo retiene lo que le ocurre, como un videocasete que, después de registrar imagen y sonido, se borrara al llegar al final de esos minutos fatídicos. —Su tono era resuelto y poco cordial, seguramente por haber repetido esas mismas palabras a cada asistenta nueva.
Yo no lograba hacerme una idea de lo que eso podía significar: ¿una memoria de ochenta minutos? Nunca había oído nada igual. A menudo me había tocado cuidar de enfermos con las más diversas dolencias, pero dudaba de que mi experiencia fuera útil en una situación como la que me describía. Además, no podía quitarme de la cabeza los sellos azules estampados en la ficha del profesor.
Desde allí, la casa del profesor ofrecía un aspecto lastimoso. A través del seto de fotinia alcancé a ver una pequeña puerta de acceso anticuada, y un grueso candado que, cubierto de herrumbre y excrementos de ave, ninguna llave habría abierto en mucho tiempo ni, posiblemente, volvería a abrir.
—¿Estaría usted disponible para comenzar pasado mañana, lunes? —preguntó con frialdad, quizá para evitar más preguntas o fisgoneos por mi parte.
Asentí, y de esa manera me convertí en la nueva empleada del hogar del profesor.
En comparación con la magnífica vivienda de la anciana, en cada metro cuadrado del reducido y frío espacio de la del profesor, de una sola planta, reinaba la austeridad, y en parte también la desidia. A su alrededor, quizá para disimularlo, la frondosa vegetación que la rodeaba crecía con descuido. Mi primer día, frente a la puerta envuelta en la penumbra, me encontré con el primer problema: el timbre ni siquiera funcionaba.
—¿Qué número de zapato calzas? —fue lo primero que salió de la boca del profesor tras abrirme la puerta, y una vez que me presenté. Ni siquiera había hecho una ligera inclinación de cabeza.
—Veinticuatro —repliqué llanamente, siguiendo el precepto de toda asistenta de no responder a una pregunta con otra pregunta.
—¡Qué buen número! ¡Decidido y valiente, factorial de 4, por cierto! —Dicho esto, se cruzó de brazos, cerró los ojos y se quedó en silencio.
Viendo que mi número de calzado era muy importante para mi nuevo cliente, lo aproveché para seguir hablando de eso. ¿Por qué no?, me animé.
—¿Factorial? —dije entonces—. ¿Qué significa eso, si no le importa que se lo pregunte?
—Al multiplicar los números naturales del 1 al 4, obtenemos 24, ¿no es cierto? —explicó el profesor, todavía con los ojos cerrados—. A ver, dime ahora..., ¿cuál es tu número de teléfono?
—El 576-1455.
—¿5.761.455? ¡Asombroso! ¡Verdaderamente asombroso! 5.761.455 es precisamente el total de números primos existentes menores de 100.000.000 −dijo con entusiasmo mientras asentía con la cabeza.
Me pregunté si eso merecía esa exaltación, pero en su tono de voz no había vanidad, solo una emoción intensa, tan honesta como humilde, que enseguida me contagió; tanto, que llegué a pensar que mi número de teléfono podía estar ligado a un destino extraordinario y que a mí, por lo tanto, me esperaba algo similar.
A los pocos días de comenzar mi trabajo allí, caí en la cuenta de que el profesor recurría a los números cuando no sabía de qué hablar. Era su estrategia para relacionarse con los demás. Los números eran como una mano que tendía al otro para saludarlo, y también una gruesa capa bajo la que se escondía y con la que se protegía de los peligros del mundo exterior, una fortaleza que lo mantenía a salvo.
Aquella no fue la única mañana en la que el profesor me recibió hablando de números. Cuando llegaba, en la entrada me esperaban las mismas preguntas todas las mañanas, sin excepción, y eso se repitió hasta mi último día de trabajo en aquella casa. A sus ojos, y en el océano de su memoria, cada día era el primero, el de mi incorporación al trabajo. Los ochenta minutos que le duraban los recuerdos no daban para mucho: todas las mañanas yo me presentaba, y él volvía a sentirse turbado. Aparte del número de teléfono y el del calzado, me preguntaba, según la ocasión, mi código postal, la matrícula de mi bicicleta o el número de trazos que componían los caracteres de mi nombre. A todos ellos les encontraba algún sentido, o establecía con ellos alguna relación, e inmediatamente, sin esfuerzo aparente, los clasificaba en grupos de factoriales, primos o lo que fueran.
El profesor, de sesenta y cuatro años por aquel entonces, había dado clases de teoría de números en la universidad, y no solo aparentaba más años de los que tenía, sino que, además, estaba muy delgado; incluso se le adivinaba cierto grado de raquitismo. Siempre encorvado, nadie habría dicho que medía un metro sesenta de estatura; las arrugas de su cuello flaco y flácido escondían pequeños restos de suciedad, y su cabello blanco y alborotado apenas le cubría las orejas, de grandes pabellones. La voz extenuada y los ademanes parsimoniosos convertían cualquier gesto suyo, cualquier acto, en un proceso laborioso y lento.
Sin embargo, si una lo observaba con atención, entreveía en su rostro unos rasgos tiempo atrás hermosos, rastros de juventud en las líneas de su semblante, en la firmeza de su mentón.
Nunca se quitaba la chaqueta ni la corbata, ni dentro ni fuera de casa, aunque salía en escasas ocasiones. Tenía solo tres trajes (uno de invierno, otro de verano y otro de entretiempo), tres corbatas, seis camisas y un abrigo de lana. En su armario no guardaba ni un jersey, ni unos pantalones de algodón, ni ninguna otra prenda que pudiera complicarme lo más mínimo mi trabajo.
¿Acaso el profesor no sabía que había otras alternativas a la chaqueta? Esa austeridad se debía sin duda a su falta de interés por el aspecto de los demás y, en consecuencia, por el suyo propio. Él no daba a eso ninguna importancia. Lo imaginé abriendo la puerta del armario a primera hora de la mañana y descolgando el único de los tres trajes que no estaba enfundado en una bolsa de la tintorería. En consonancia con el aire y el estilo del profesor, los tres eran de tonos apagados y oscuros, estaban muy gastados y se adaptaban a él como una segunda piel: con o sin funda de la tintorería, supuse que nunca había dudado a la hora de elegir uno u otro.
Pero lo más llamativo de su indumentaria eran los papelitos que cubrían la parte delantera de su chaqueta, de arriba abajo, incluidos bolsillos, cuello, ojales y puños. Los papelitos estaban prendidos a la tela con unas pinzas que, aquí y allá, creaban pliegues que deformaban la chaqueta. Eran en su mayoría simples pedazos de papel rasgados a mano, y algunos, simples jirones que amarilleaban, medio deshechos, con pequeñas notas a lápiz que solo se podían leer si te acercabas. Vi que eran recordatorios de tareas, asuntos que debía tener en cuenta, cosas que necesitaba recordar pasados los ochenta minutos, y que, por tanto, debía conservar a la vista, en un lugar donde no pudiera perderlas. Era una idea bastante razonable, si no fuera porque le daban un aspecto desaliñado y desvalido.
—En fin, adelante. Yo me retiro a mi estudio —me dijo el profesor—. Por favor, mientras trabajo, encárgate de las tareas de la casa como lo consideres oportuno.
Me hizo un gesto para que pasara y los papelitos se movieron, y al rozarse entre sí produjeron un ruido áspero que lo acompañó a cada paso que daba hacia su estudio, tras cuya puerta, al poco, desapareció.
Hablando con las asistentas que habían fracasado en esa casa, me enteré de que la anciana que velaba por el profesor había enviudado del hermano de este, doce años mayor, y que a la muerte prematura de los padres de ambos había heredado la fábrica de telas familiar. El hermano mayor había dado un nuevo impulso al negocio y los vientos que soplaron a su favor le permitieron financiar los estudios de matemáticas de su hermano menor en la prestigiosa Universidad de Cambridge. Tras graduarse y obtener un doctorado, lo contrataron como profesor en un departamento universitario de matemáticas, emancipándose así de la tutela económica familiar, pero poco después el hermano mayor contrajo una hepatitis aguda que acabó con su vida de manera fulminante, dejando a su esposa viuda y sin descendencia. Ella echó el candado al negocio de las telas y, tras demoler las instalaciones, construyó en el solar un edificio de apartamentos, para vivir del alquiler que generaban. Y el tiempo transcurrió sin sobresaltos durante unos años, hasta que el profesor tuvo un accidente de tráfico, por la negligencia de un conductor que cabeceaba al volante, vencido por el sueño; el vehículo invadió el carril contrario hasta colisionar frontalmente con el del profesor. A consecuencia del impacto, este sufrió lesiones cerebrales irreversibles y perdió su puesto en la universidad. A partir de entonces pasaba las horas en la soledad de su hogar, rodeado de montañas de revistas especializadas cuyos problemas matemáticos resolvía y que, en contrapartida, le reportaban premios en metálico, su única fuente de ingresos. Nunca se había casado, tenía ya sesenta y dos años, y seguía dependiendo de la anciana viuda, su cuñada.
—Menudo bicho raro, ese viejo profesor —me comentó una de las compañeras de trabajo que solo había durado en la casa una semana, aunque era de las más veteranas y experimentadas—. Se le ha pegado a la pobre mujer como un parásito y está dilapidando la herencia de su difunto marido. La compadezco.
Sin duda, las frecuentes disertaciones sobre números del profesor habían acabado con la paciencia de mi compañera.
El interior de la vivienda era tan desabrido como el exterior. Solo constaba de dos estancias: el estudio del profesor, que hacía las veces de dormitorio, y un comedor con cocina americana. Más allá de la estrechez del lugar, me llamó la atención aquella austeridad adusta y fría que parecía haberse adueñado de cada metro cuadrado, de cada rincón, con su mobiliario barato e insulso, su papel de pared descolorido y polvoriento, el desagradable crujido de las tablas del suelo resecas; en definitiva, al igual que el timbre de la entrada, todo estaba estropeado, destartalado o con aspecto de encontrarse en las últimas y a punto del desahucio. Descubrí que la ventana del cuarto de baño estaba resquebrajada, que el pomo de la puerta del jardín trasero estaba medio desprendido y que la radio que había sobre el mueble de la vajilla no funcionaba.
Mis primeras dos semanas las pasé sin saber qué hacer; todo era nuevo para mí, me tocaba aprender a desenvolverme, y acababa la jornada agotada, aunque el trabajo no parecía muy cansado ni complicado. Por lo general, cada nuevo hogar requería de un periodo de adaptación que podía prolongarse más o menos, pero nunca me había topado con nada como la casa del profesor, no había manera de encontrar un ritmo o de averiguar en qué consistía mi trabajo. En otros hogares, la dueña o el dueño de la casa me guiaban con un «Encárgate de esto, por favor» o un «No hagas aquello otro de tal manera». Eso, y el trato diario, me permitía ir conociéndolos, algo fundamental para saber a qué debía prestar más atención o cómo evitar complicaciones, y amoldarme a las rutinas y las exigencias de la nueva casa. El profesor, que sin duda no sabía lo que su casa o él mismo necesitaban, no me daba instrucciones. Es más, parecía desear que yo no hiciera nada. Me ignoraba por completo.
Si me atenía a lo que me había indicado la anciana viuda, mi cometido era bien sencillo: en primer lugar, prepararle la comida. Y ciertamente lo intenté, pero ni siquiera en eso empecé con buen pie. Busqué y rebusqué, y en la nevera y el armario de la cocina solo encontré una caja de copos de avena humedecidos y una bolsa de macarrones caducados desde hacía cuatro años.
Me atreví, por tanto, a llamar a la puerta de su estudio. Lo hice una vez. No hubo respuesta. Dos. Tampoco. Aunque sabía que quizá me estaba excediendo, probé a abrir la puerta. Entreví su espalda. Se encontraba, naturalmente, sentado frente a su mesa de trabajo.
—Profesor, disculpe que le interrumpa.
No se movió un milímetro. Me acerqué a él pensando que no me habría oído, que debía de ser un poco sordo o que se habría puesto tapones para aislarse del ruido exterior.
—¿Qué desea que le prepare para almorzar? —pregunté—. ¿Hay alguna cosa que le apetezca en especial? ¿Ingredientes que deba evitar? ¿Algún alimento al que tenga alergia, quizá?
Noté un denso olor a papel, como ocurre en las habitaciones poco ventiladas y atestadas de libros. Y es que los había por todas partes, apilados sobre el suelo y en las estanterías, cubriendo incluso media ventana y, más allá, desperdigados encima de la desgastada colcha de su cama, pegada a la pared. Sobre el escritorio, sin embargo, solo había un cuaderno abierto. No había ordenador. El profesor tampoco tenía en la mano algo con lo que escribir. Se limitaba a mantener la vista fija en un punto del espacio.
—Si no tiene ninguna preferencia, le prepararé algo a mi manera. Pero, por favor, no dude en decirme cuáles son sus platos preferidos.
Me fijé en algunos de los papelitos que llevaba prendidos en la chaqueta. «Error en el método de análisis de...», «Según el decimotercer problema de Hilbert...», «... definida como curva elíptica...», leí, entre símbolos y palabras incomprensibles. En medio de ese maremágnum, solo un papelito me resultó legible, aunque estaba muy sucio, doblado en sus cuatro esquinas, y con la pinza que lo sujetaba oxidada; debía de llevar años allí. Rezaba así: «Mi memoria solo dura ochenta minutos».
—¡No tengo absolutamente nada que decir! —bramó el profesor volviéndose de pronto hacia mí—. ¿No te das cuenta de que estoy trabajando? ¡Me duele más que si me estrangularas! Es como si te hubieras metido de golpe en mi cabeza, pisoteando todo lo que encuentras dentro de ella, mis amados números, mis pensamientos y reflexiones... ¡Es peor que ser espiado en el cuarto de baño!
Me disculpé de inmediato, inclinando varias veces la cabeza, pero el profesor no parecía escuchar. Al poco había vuelto a quedarse inmóvil ante la mesa, con los ojos fijos en un algún punto.
Fue, desde luego, un mal comienzo. Acababa de enfadarse conmigo en mi primer día de trabajo, y yo todavía no había realizado ninguna tarea. Temí acabar convertida fulminantemente en el décimo sello azul de la ficha del profesor, y traté de grabarme a fuego en la mente la norma de no molestarlo bajo ningún concepto cuando estaba pensando.
El problema era que siempre estaba pensando... Alguna vez salía de su estudio y se sentaba a la mesa del comedor o hacía gárgaras en el cuarto de baño, pero incluso entonces seguía pensando. También cuando hacía unos extraños ejercicios para desentumecer los brazos y las piernas. Siempre estaba en las nubes y caminaba casi como un sonámbulo. A la hora de comer, se llevaba la comida a la boca distraídamente y la tragaba apenas sin masticar. Con tal de no distraerlo, no me atrevía ni a preguntarle cómo encender el calentador del agua o dónde guardaba el cubo para fregar. Procuraba no hacer ningún ruido que pudiera molestarlo y hasta aguantaba la respiración cuando estaba cerca de él. Si al menos le diera un pequeño respiro a su cabeza, por breve que fuera...
Un viernes, al final de las dos semanas que llevaba trabajando allí, el profesor se había sentado a la mesa del comedor a eso de las seis de la tarde, y ensimismado, como siempre, se dispuso a cenar estofado con salsa de verduras que le había preparado, para que no tuviese problemas con huesecillos, espinas ni cáscaras —una cena que le proporcionaba todos los nutrientes y proteínas—, cuando me fijé en algo que hasta entonces se me había pasado por alto.
Quizá porque sus padres habían fallecido muy pronto, nadie parecía haberse molestado en corregir sus modales en la mesa: derramaba la comida, se frotaba las orejas con la servilleta sucia y hecha un gurruño, y nunca le oí decir un escueto «que aproveche» antes de llevarse la primera cucharada a la boca... No se quejaba de mis guisos, pero tampoco me hacía ningún cumplido ni se molestaba en darme conversación, aunque me quedaba a su lado mientras cenaba. Pues bien, en lo que me fijé aquel viernes fue en que se había colgado en la manga un nuevo papelito que estaba a punto de acabar dentro de la salsa cada vez que el profesor hundía la cuchara en el plato. La nota decía: «La nueva asistenta», escrito con trazos débiles y caracteres pequeños, seguidos del dibujo de una mujer. A pesar de que el dibujo parecía haberlo hecho un niño de guardería, enseguida comprendí que aquella era yo, con aquel pelo corto, las mejillas redondeadas y el lunar junto a la boca.
Mientras lo oía sorber la salsa, lo imaginé dibujándolo a toda prisa, antes de que se desvaneciera el recuerdo que aún guardaba de mí, llevándose mi imagen. Eso probaba que había dejado a un lado sus valiosas reflexiones matemáticas para dedicarme a mí unos minutos.
—Profesor, ¿quiere que le sirva más? —le ofrecí—. He preparado mucho. Puede repetir todas las veces que quiera.
No respondió. Soltó un eructo. Y sin mirarme, se dirigió hacia su estudio y una vez más desapareció tras la puerta. En su plato no quedaban más que unos trocitos de zanahoria.
El lunes siguiente, en cuanto crucé la puerta de su casa le señalé en su chaqueta el pedacito de papel con mi retrato. Él miró el dibujo y a mí alternativamente, comparándonos, y se quedó en silencio durante unos segundos, tratando de interpretar aquello; después farfulló las habituales preguntas acerca de mi número de calzado y de teléfono.
Sin embargo, vi que algo en él había cambiado respecto a la semana anterior cuando me mostró un legajo de papeles repletos de fórmulas y signos matemáticos garabateados por él y me pidió que lo enviase por correo a la revista Journal of Mathematics.
—¿Me harías ese favor?
Lo dijo con tal amabilidad que no parecía el mismo que se había enfadado cuando lo interrumpí mientras trabajaba en su estudio. Curiosamente, era la primera vez que me pedía algo. Su cabeza se había tomado, por fin, un descanso.
—Sí, claro. Déjelo en mis manos, yo me encargo.
Con esmero, escribí en el sobre, letra a letra, las señas y el departamento al que iba dirigido en un idioma que yo no sabía ni pronunciar, y me fui a buen paso, como impulsada por una ráfaga de entusiasmo, hacia la oficina de correos.
Cuando el profesor no estaba pensando, pasaba bastante tiempo arrellanado en una poltrona situada junto a la ventana del comedor. Ese día aproveché que se había sentado ahí para hacer limpieza en el estudio. Abrí la ventana de par en par, saqué el colchón y la almohada al jardín para que se ventilaran y se secaran bien, y di una buena pasada con el aspirador. La verdad era que, a pesar del desorden, en esa habitación uno no se sentía incómodo, y eso que el aspirador tuvo que vérselas con burujos de pelos bajo la mesa de trabajo y yo con palos de helado cubiertos de moho que encontré entre las montañas de cuadernos y libros que corrían por el suelo, además de unos restos de huesos de lo que debía de haber sido pollo frito en tiempos remotos.
Quizá el bienestar que sentí allí se debía al silencio que reinaba en la habitación, algo que yo no había experimentado hasta entonces. No se trataba simplemente de la ausencia de ruido, sino de un sosiego que, a pesar del desorden, nada, ni restos de pelo ni moho, podía alterar. Era como si el profesor hubiera dejado en el ambiente la impronta de su armonía y su equilibrio matemáticos; era una calma cristalina como la de un lago situado en lo más profundo del bosque.
Ahora bien, a pesar del sosiego que flotaba en ese cuarto, no había nada en él que me llamara la atención, ningún detalle que me diera pistas acerca del pasado del profesor, ninguna fotografía que despertara mi curiosidad, ningún objeto decorativo que me hiciera suspirar de emoción, nada en definitiva que excitara mi imaginación ni me maravillara.
Empecé a pasar el plumero por los estantes y los libros, con títulos como Teoría de grupos continuos, Teoría de números algebraicos o Tratado de teoría de números, y autores como Chevalley, Hamilton, Turing, Hardy o Baker, entre otros muchos. Tantos y tantos libros, y ni uno solo despertaba en mí los menores deseos de leerlo. Además, la mitad de ellos estaban escritos en lenguas extranjeras y yo no entendía los títulos impresos en sus lomos. En su escritorio había ese día un cúmulo de cuadernos de notas, restos consumidos de lápices 4B y pinzas, un panorama desolador, que no tenía nada que ver con lo que yo esperaba de alguien que se dedicaba a una labor intelectual. Había también, esparcidas aquí y allá, virutas de goma de borrar, única prueba del trabajo que el profesor había estado haciendo.
Yo daba por sentado que todo buen matemático poseía material de trabajo a la altura de su nivel académico, en este caso de gama alta, por decirlo de alguna manera: compases que no se encuentran en papelerías corrientes, reglas e instrumentos de medición con complicadas tablas de graduación y calibres. Y pensando en esas cosas fui limpiando los restos de goma de borrar, apilando los cuadernos en un montón y juntando todas las pinzas. Me fijé también en el hoyo que las nalgas del profesor habían dejado en el asiento blando de la silla.
—¿Cuál es la fecha de tu cumpleaños? —me preguntó tras dar el último bocado a la cena. Aquella tarde no parecía dispuesto a desaparecer tras la puerta de su estudio en cuanto se terminó su plato. Me dio la impresión, más bien, de que se mostraba más afable conmigo y trataba de darme conversación mientras yo recogía la mesa.
—El 20 de febrero —contesté.
—No me digas...
El profesor no había tocado la zanahoria que yo había añadido a la ensalada. Allí seguían todos los trozos. Retiré los platos y empecé a pasar un paño por la mesa: su hábito de dejar caer la comida no había desaparecido, pero se lo veía más relajado. Aunque ese día hacía un tiempo primaveral, con la puesta del sol refrescaba y todavía teníamos que encender la estufa de petróleo del comedor.
—¿Siempre envía sus investigaciones a las revistas especializadas? —se me ocurrió preguntarle.
—Más que investigaciones, llamémosles simples ejercicios para revistas de aficionados, una manera entretenida de pasar el rato que, con un poco de suerte, puede reportarle a uno algún que otro beneficio económico. La financiación de los premios corre a cargo de ciertas personas adineradas a las que les apasionan matemáticas. —Repasó con la mirada distintos papelitos hasta dar con uno prendido del bolsillo izquierdo de la chaqueta—. ¡Ah! ¡Ya veo que has enviado hoy mismo mi demostración del teorema del número treinta y siete del Journal of Mathematics! ¡Magnífico! —exclamó.
En efecto, así había sido. Claro está, habían transcurrido más de ochenta minutos desde que la llevé a la oficina de correos aquella misma mañana.
—¡Dios mío! —exclamé yo entonces—. ¡Ahora caigo en la cuenta de que tenía que haberla enviado por correo urgente! Si no llega a tiempo, no le darán el premio, ¿no?
—No te preocupes en absoluto. Por supuesto, es mejor que llegue lo antes posible y se adelante a las demostraciones enviadas por los demás, pero al final lo que cuenta es la demostración en sí, que sea hermosa, impecable y radiante.
—¿Hermosa y qué...? —pregunté—. ¿Qué tiene que ver la belleza con una demostración matemática?
—¿Cómo que qué tiene que ver? —dijo, categórico, el profesor. Se puso en pie. Se acercó a mí, que estaba fregando los platos, y me miró a la cara—. No debe tener fisuras. Su estructura debe sostenerse airosa y elegante, firme, dispuesta perfecta y armónicamente y, por supuesto, sin ninguna contradicción. Aunque no contenga ningún error, podrían ser petulantes, desordenadas, toscas. ¿En qué consiste la hermosura de una estrella? ¿Cuál es el secreto de su belleza? Creo que ninguna explicación racional puede decirlo, ¿verdad? Lo mismo ocurre con una demostración. La intuición es la que, en definitiva, nos dicta el camino.
Dejé de fregar los platos y asentí. Nunca lo había oído hablar tanto y no quería desanimarlo.
—Me has dicho que el día de tu cumpleaños es el 20 de febrero, ¿cierto? —continuó—. Si juntamos el mes y el día forman una cifra fascinante: 220. ¿Por qué? Mira, echa un vistazo. Es el regalo que me dieron en la universidad al ganar el Premio del Rector, con una tesis sobre la teoría de los números trascendentes —dijo quitándose su reloj de pulsera, un magnífico modelo extranjero, que no casaba nada con la austeridad del profesor. Me lo acercó para que pudiera verlo mejor.
—¡Es estupendo! —reconocí.
—Eh..., sí. Eso es lo de menos. Solo quiero que te fijes en el número que está aquí grabado. ¿Llegas a verlo? Es muy pequeño.
Efectivamente, en el dorso había una inscripción que decía «Premio del Rector núm. 284».
—¿Ese número es el número de convocatoria del premio? —pregunté.
—Es probable, no lo sé. Lo que me interesa es el número. Por favor, deja los platos un momento. Prestemos atención a ambos números, el 220 y el 284.
Estaba tan entusiasmado que me tiró del delantal para llevarme hasta la mesa del comedor; me invitó a sentarme, se sacó del bolsillo interior de la chaqueta uno de sus viejos lápices 4B y escribió velozmente los dos números en el reverso de un folleto publicitario, separados uno del otro:
220
284
—Dime, ¿qué te parece? —preguntó.
¿Que qué me parecía? Me parecía que, por bien que hubiera empezado, yo estaba a punto de meterme en un atolladero. Me sequé las manos en el delantal mientras me estrujaba la cabeza para encontrar una respuesta a la altura de lo que él esperaba de mí, cosa que, de todos modos, veía poco probable. Miré y remiré aquellos dos números sin ver en ellos más que lo que eran para mí: números.
—Veamos, eh... —Apurada, solo acertaba a balbucear—. Los dos son de tres cifras y... se parecen un poco, ¿no? Por ejemplo, en el supermercado no vería mucha diferencia entre comprar una bandeja de 220 gramos de carne picada o una de 284. Me decidiría por la que tuviera la fecha de envasado más reciente, sin hacer mucho caso del peso. Vamos, los dos números dan una impresión parecida. Los dos están en la franja de los doscientos, y son pares...
—¡Magnífico! ¡Muy bien visto! —me interrumpió, con un aspaviento que hizo balancearse la correa de cuero del reloj. Esa reacción me desconcertó—. La intuición tiene una importancia vital en matemáticas. Solo ella puede atrapar números con la agilidad con que el martín pescador se lanza hacia el pez al percibir el brillo fugaz de sus escamas bajo el agua —explicó y acercó aún más su silla a la mesa. Desprendía el mismo olor a papel que flotaba en el estudio—. ¿Sabes qué es un número divisor?
—Creo que sí... Pero ha pasado tanto tiempo desde que lo aprendí en el colegio...
—El número 220 podemos dividirlo por 1 y también por sí mismo, ¿verdad?, sin que nos quede ningún resto. Bien, eso nos permite afirmar que tanto 1 como 220 son divisores de 220. Y lo mismo puede decirse de todos los números naturales. Cada número natural es divisible por 1 y por sí mismo. Pero volvamos al 220 y al 284. ¿Por qué otros dos números pueden dividirse?
—Supongo que por 2 y por 10.
—Así es. Lo has comprendido a la perfección. ¿Qué te parece, entonces, si escribimos todos los divisores de ambos números a excepción de sí mismos? Veamos...
220 : 1 2 4 5 10 11 20 22 44 55 110
142 71 4 2 1 : 284
Debido a los trazos redondeados del profesor, cada cifra parecía una figura con la cabeza levemente agachada, mientras la mina del lápiz, maleable, se deshacía y esparcía cuando rasgaba el papel, creando una fina nube de polvo de grafito alrededor de los números.
—¿Cómo se las ha arreglado para encontrar los divisores mentalmente?
—No he ido dividiendo cada número, sino que he echado mano de la intuición, como tú misma has hecho hace unos minutos. Bien, demos un paso más —propuso, y añadió signos de suma entre cada número.
220 : 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 =
= 142 + 71 + 4 + 2 + 1 : 284
—¿Podrías, por favor, hacer estas dos sumas? —me pidió, dándome el lápiz—. Tómate todo el tiempo que necesites; no tenemos prisa.
Tal como me pidió, fui sumando con paciencia las cifras de las dos sumas. Gracias a su entusiasmo y a su amabilidad, en ningún momento tuve la impresión de que estuviera poniéndome a prueba. Al contrario, ya no sentía que me había metido en un atolladero, y que podía lanzarme a desentrañar ese misterio propuesto por el profesor.
Cuando acabé las sumas, las repetí tres veces para asegurarme de que eran correctas. Estaba tan concentrada que no me di cuenta de que se había hecho de noche. De vez en cuando llegaba hasta nuestros oídos el sonido de una gota de agua que se escurría de los platos puestos a secar. El profesor no se movió de mi lado mientras completaba las sumas.
—¡Listo! —exclamé cuando acabé las comprobaciones.
220 : 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
220 = 142 + 71 + 4 + 2 + 1 : 284
—¡Correcto! —exclamó—. ¿Te das cuenta? Es asombroso. El resultado de la suma de los divisores de 220 es 284 y, a su vez, la suma de los divisores de 284 es igual a 220. Es extremadamente raro que entre dos números se establezca una relación como esa. Cuando eso ocurre, a los números que la cumplen se les llama números amigos. Descartes solo llegó a encontrar una pareja de números amigos, y Fermat lo mismo. Creo que puedo afirmar que se trata de un vínculo casi divino. ¿No es eso una evidente muestra de belleza? La fecha de tu cumpleaños y el número grabado en mi reloj de pulsera están unidos por este asombroso nexo.
Nos quedamos largo rato observando las dos sucesiones de números y sus correspondientes sumas garabateadas en un simple folleto publicitario, los trazos del profesor y los míos entrelazados en una sinuosa caligrafía, como una constelación de millones de estrellas titilantes sobre el cielo nocturno.