CAPÍTULO 1
Las matemáticas en la sociedad

1.1. EL MUNDO ES MATEMÁTICO
LA MATEMÁTICA es la reina de las ciencias, y el mundo está organizado de forma misteriosa por el poder del número. Bertrand Russell lo expuso de forma maravillosa en su autobiografía:
Yo he buscado el conocimiento con la misma pasión. He deseado comprender el corazón del hombre. He deseado saber por qué brillan las estrellas y he intentado entender el poder pitagórico por el que los números dominan el flujo.
La matemática está, de una u otra forma, en todo. Ni siquiera el pensamiento más simple puede ser formulado sin que conlleve el concepto fundamental de número (una casa, dos personas…).
Del concepto de número surge otro de indiscutible importancia: la noción de medida. Para medir hay que comparar y, cuando no se compara, se crean medidas estándar.
La aritmética es la rama de la matemática que estudia los números, sus propiedades y transformaciones. Conocidos los números es posible aplicarlos a la evaluación de dimensiones que varían o que son desconocidas, pero que se pueden representar por medio de relaciones y fórmulas. Tenemos así el álgebra.
Estos valores que medimos en la realidad están representados por cuerpos materiales o símbolos, dotados de tres atributos: forma, tamaño y posición. El estudio de estos atributos se llama geometría.
La aritmética, el álgebra y la geometría se apoyan entre ellas, y son la base de todas las ciencias y las artes. La pintura, escultura, arquitectura, la música, la filosofía… no tendrían avance si no fuese por esa herramienta indispensable denominada matemáticas.
De igual forma, el comercio no se desarrollaría, ni habríamos conocido el resto de las ciencias.
Esta intensa presencia de la matemática en nuestra cultura no es algo que vaya a menos, sino todo lo contrario. A juzgar por las tendencias que se manifiestan cada vez con más fuerza, parece claro que el predominio de la madre de las ciencias va a ser un distintivo bien patente de la civilización futura.
Las matemáticas se han convertido en herramienta conceptual para casi todas las ciencias, incluidas las del comportamiento, son un instrumento capaz de facilitar la comprensión de los fenómenos propios de cada disciplina científica y se han instalado en nuestra vida cotidiana: protección a las tarjetas de crédito contra los abusos; envío de datos de las sondas espaciales; diseño de alas de avión; experimentos de laboratorio planteados en la pantalla del ordenador; estadísticas; proyecto genoma; mercados financieros; meteorología; simulación de la realidad y todas las innumerables, crecientes y asombrosas funciones del ordenador y la informática.
Sin embargo, pese a esta importancia, políticos y vacas sagradas de nuestra cultura no suelen tener ningún empacho, sino más bien un extraño y estúpido orgullo, en confesar su ignorancia absoluta en temas relacionados con las matemáticas, contagiando de esta forma al resto de la sociedad.
Muchas veces me he encontrado en la situación de estar con gente con un alto nivel cultural y, sin embargo, ante un sencillo cálculo, lanzar un soy de letras. Impensable sería que yo escribiese burro con «v» y se pasase por alto; sin embargo, el argumentar ante un sencillo cálculo que se es de letras no parece estar mal visto.
En nuestro país, fuertemente escorado hacia las humanidades desde hace siglos, parece que cultura viene a coincidir, más o menos, con música, escultura, cine y otras manifestaciones artísticas.
No digo que sea negativo considerar cultura a estas áreas, que evidentemente lo son, pero sí que se debería tratar a las ciencias, y más en concreto a la madre de todas ellas, como lo que se merecen, buscando su divulgación entre el pueblo.
A lo largo de este capítulo me propongo exponer situaciones en las que sería más que interesante ver con ojos matemáticos situaciones en las que los números intervienen y que muchas veces dejamos de lado, o en las que no percibimos esa incidencia. No es difícil adoptar una postura matemática, solo es perderle el miedo, interpretar de qué forma están los números en nuestra vida y, sobre todo, romper ese bloqueo psicológico que, de entrada, provocan.
1.2. EL TIMO BURSÁTIL
Hay mucho hábil con los números. Por eso es importante tener una buena cultura numérica, de esta forma nos protegemos ante muchos fraudes, como el famoso timo bursátil que a continuación voy a contar y que está basado en hechos reales:
Un determinado estafador se hizo pasar por asesor financiero, enviando 64.000 cartas a potenciales inversores. Las cartas hablan de los importantes contactos que esta persona tiene, contando con información privilegiada, y de los sistemas punteros e informatizados en análisis financiero a los que tiene acceso.
En 32.000 de las cartas predice que las acciones subirán. En las otras 32.000 predice que las acciones bajarán. Evidentemente, habrá acertado en la predicción de 32.000 (en las otras 32.000 habrá fallado y las desestimará).
De las 32.000 acertadas hace una segunda predicción igual a la primera. En 16.000 hablará de una subida, y en las otras 16.000 de una bajada.
Acertará en 16.000, fallará en 16.000.
16.000 predicciones correctas y vuelta a lo mismo. En 8.000 predice subida, y en otras 8.000 bajada. Tras esta tercera predicción habrá acertado en 8.000, y tres veces consecutivas.
Pues bien, siguiendo con el envío de cartas, tendríamos en una cuarta predicción 4.000 correctas. En una quinta, 2.000 correctas. En una sexta, 1.000.
Y ahora imaginemos que después de seis predicciones correctas a un total de 1.000 personas, nuestro asesor nos dice que si queremos una séptima predicción hemos de abonar 500 euros.
Ahora vamos a hacer cuentas:
Aunque solo el 80% de estas mil personas acepten, el asesor-estafador estaría ingresando un total de 400.000 euros (80 personas x 500 euros cada uno).
Después de todo este proceso habría enviado un total de unas 127.000 cartas que, a un total de 50 céntimos cada una, suman 63.500 euros de gastos.
127.000 × 0,50 € = 63.500 €
Como obtuvo unos ingresos de 400.000 euros, y gastos por 63.500 euros:
400.000 – 63.500 = 336.500 €
Por tanto, nuestro hábil estafador bursátil habría obtenido unos beneficios de 336.500 euros (56 millones de pesetas).
1.3. EL TABACO EN NÚMEROS
En mis conferencias casi siempre hago referencia a lo que supone en términos numéricos la adicción al tabaco. De esta forma se da una connotación matemática a algo tan habitual en nuestra sociedad como es el fumar.
Imaginemos a un fumador de un paquete diario, 20 cigarrillos. Un paquete no es tanto para un buen fumador, como bien sabemos. Y, sobre todo, y por eso se magnifica la cantidad, un fumador consume tabaco todos los días.
En términos numéricos, en un mes de 30 días hablaríamos de 600 cigarrillos fumados (20 al día). En un año serían 7.300 cigarrillos (20 × 365). En diez años estamos hablando de 73.000 cigarrillos fumados. Y en veinte años, un fumador de un paquete diario se habrá fumado 146.000 cigarrillos.
Ahora, hagamos el sano ejercicio de imaginar 146.000 cigarrillos uno encima de otro… ¿Sorprende imaginarse tal cantidad de cigarrillos, verdad?
Si cada cigarrillo mide aproximadamente 9 centímetros, si colocamos los 146.000 cigarrillos uno tras otro, recorreríamos un trayecto de 1.314.000 centímetros, que es lo mismo que 13.140 metros, o 13 kilómetros y 140 metros…
Es decir, quien fume un paquete al día, si empieza a fumar a los quince años, cuando tenga treinta y cinco se habrá fumado toda esa cantidad. Cuando tenga cincuenta y cinco se habría fumado el doble (292.000 cigarrillos).
Contenido del cigarrillo: Hay numerosos estudios hechos sobre los efectos del tabaco en la vida y en la salud de las personas. El fumar implica autoexponerse a unas 4.000 sustancias tóxicas, que son las que contiene el humo del cigarrillo. Entre estas podemos citar a las más conocidas (cancerígenas todas ellas): la nicotina, el alquitrán y el monóxido de carbono.
La nicotina: Es una droga adictiva, la sustancia responsable de la aparición de signos y síntomas tras la reducción o supresión, y la que genera la dependencia del tabaco.
Esta sustancia puede ser entre seis y ocho veces más adictiva que el alcohol, pudiendo generar una dependencia más fuerte que la heroína.
La nicotina tarda entre siete y diez segundos en llegar al cerebro tras su inhalación.
El alquitrán: En la calada de un cigarrillo se respiran partículas de alquitrán, las cuales van recubriendo los pulmones.
Pues bien, trasladándolo a términos numéricos, si cada cigarrillo tiene unos 15 miligramos de alquitrán, en veinte años habríamos ingerido, con un paquete de tabaco al día, nada menos que 2,190 kilos de alquitrán. Lo que puede ser una taza de alquitrán al año… Con estos números ahora se comprende mejor el que los pulmones de un fumador tengan una tonalidad «oscura».
Datos económicos
El Banco Mundial ha estimado que el consumo del tabaco supone más de 200 billones de euros de gastos directos e indirectos. Por su parte, los fumadores se gastan unos 100.000 millones de euros en todo el mundo. Ahora, vamos a comprobarlo en economías domésticas, que proporcionalmente genera un impacto en las mismas muy interesante de analizar. Ahí van los datos:
Si cada paquete cuesta 2,50 euros, nos habríamos gastado (fumando un paquete al día) 75 euros en un mes de treinta días; 912,50 euros en un año; 9.125 euros en diez años; 18.250 euros en veinte años.
Ahora, si seguimos calculando, es el equivalente a… todos los años unas vacaciones de quince días a un lugar paradisíaco, en hotel de lujo y con yacusi incorporado, por ejemplo…
Evidentemente, más importante que el gasto económico es el tema de salud y de años de vida (y de calidad de vida) que quita esta adicción. Me he encontrado muchas veces con el anumérico comentario de «tal o cual persona fumó hasta los noventa años»… Y es evidente que hay casos de estos, todos los conocemos. Pero se trata de hablar de matemáticas, de probabilidades, de datos estadísticos fiables; nunca las excepciones han de ser tomadas como datos fiables desde un punto de vista matemático, por ese mismo motivo: son excepciones.
Los datos sobre lo que esta adicción produce son la realidad, verificables, son números a tener en cuenta, ya que cada día mueren 14.000 personas por enfermedades relacionadas con el tabaco o, lo que es lo mismo, una persona cada seis segundos. Es decir, el tabaquismo mata más personas en el mundo que cualquier otra enfermedad.
1.4. LAS MATEMÁTICAS EN EL DEPORTE
Me gustan los deportes en general, soy practicante, y partidario, sin duda alguna, de lo expresado por Platón: Mens sana in corpore sano. Pues bien, ¿nos imaginamos las competiciones deportivas sin números? ¿Acaso en la Fórmula 1 o en las carreras de motos no es fundamental hacer cálculos para determinar si en un determinado momento nos puede venir bien sacar un puñado de puntos y decidir que el riesgo por ganar no merece la pena? ¿O el líder de una carrera ciclista, haciendo cálculos constantemente para regular su ventaja ante eventuales escapadas? Todo ello es puro cálculo y suele salir victorioso, aparte del mejor, el que más cálculos hace y más frío es al valorarlos, midiendo en todo momento el riesgo.
Nos imaginamos una competición de fútbol sin números, no habría clasificaciones. Nos la imaginamos sin goles, también son números… Incluso dentro del terreno de juego se puede calcular el ángulo con el que hay que pegarle a la pelota para que salga de determinada forma.
En pocas facetas se ven tantos ejemplos de imprecisiones, por no decir otra cosa, que en temas deportivos y, sobre todo, en temas futbolísticos.
Escribo esta parte durante el Campeonato Mundial de Fútbol de Alemania 2006, en concreto en vísperas de un partido de octavos de final entre España y Francia. Hace un par de horas tenía la radio puesta y oí a un famoso jugador del Real Madrid y de nuestra Selección hacer el siguiente comentario (aparte de los tópicos evidentes que se dicen en todas las entrevistas futboleras…):
Mañana contra Francia no servirá jugar al 100%, tenemos que jugar al 200%…
De acuerdo, ya sé que es una frase hecha, pero ¿quiere alguien explicarme qué significa jugar al 200%?
Desde luego, yo firmaría, sin lugar a la menor duda, que jugasen al 100%.
Por cierto, antes también escuché que la media de edad de la selección francesa era de 29,5 años, mientras que la española era de 24,5 años (cinco años más joven que la selección gala). También que la altura media de los jugadores franceses era de 182 centímetros, la española se acercaba a los 179 centímetros.
Si entramos en las clasificaciones de los equipos, ahí sí que está lleno de números y de continuos aportes matemáticos, algo muy bonito de analizar y ante lo que sería más que útil que los equipos contratasen a un buen equipo de matemáticos y estadísticos (igual que se hace con médicos fisioterapeutas o psicólogos). A buen seguro que les resultaría de gran utilidad.

1.5. LA MATEMÁTICA Y LA MÚSICA
Leibniz establece una tentadora analogía entre los números y la música:
El placer que nos proporciona la música viene de contar, pero de contar inconscientemente. La música no es más que aritmética inconsciente…
¿Nos imaginamos un mundo sin música? Cuesta trabajo imaginarlo, ¿verdad?
Pues la materia prima para que exista la música son los números. Si te resulta difícil verlo, lee las siguientes páginas.
1.5.1. FUNDAMENTOS MATEMÁTICOS DE LA MÚSICA
La música, desde su aspecto físico-armónico, se fundamenta sobre principios rigurosamente matemáticos. Así de rotundo podemos comenzar nuestro análisis dedicado a la relación entre la música y las matemáticas.
Ya en la antigüedad se constata la llamada «leyenda de la fragua», que relata cómo el maestro Pitágoras escuchó el golpeo de cuatro martillos de herrero sobre un yunque mientras trabajaban el acero. Sorprendido de la perfecta consonancia de los sonidos, hizo pesar los citados martillos, comprobando que el peso de los mismos se hallaba en proporciones numéricas. A partir de esta experiencia, la Escuela Pitagórica continuó sus experimentos en pos de las relaciones aritméticas que regían los sonidos, con campanas, tubos sonoros y cuerdas vibrantes. La importancia de los experimentos pitagóricos radica en la constatación de que la armonía —la belleza— es un concepto que se fundamenta en la proporcionalidad, o lo que es lo mismo, en estructuras mensurables.
En música, el concepto de armonía se basa en leyes sobre las cuales se construyen las tonalidades y los acordes. En lenguaje coloquial, entendemos la armonía cuando resulta «agradable» lo que estamos escuchando.
Un acorde lo constituyen al menos tres sonidos ejecutados simultáneamente que producen ese efecto en nosotros. En el caso de los llamados acordes perfectos mayores, se forman con la 1.a, la 3.a y la 5.a nota de su respectiva escala. Siguiendo con el ejemplo de la tonalidad de do mayor DO-RE-MI-FA-SOL-LA-SI-DO, el acorde está formado por las notas DO-MI-SOL (1.a, 3.a y 5.a). Esta combinación, que se puede trasladar a todas las tonalidades, las cuales tomarán el nombre de su primera nota, resulta en su base matemática en relación numérica en cuanto al número de vibraciones, de ahí que nuestro oído lo perciba como agradable; de lo contrario, si ese número de vibraciones no estuviera en proporción, percibiríamos una especie de «choque» en nuestra percepción auditiva.
Cuando pulsamos una cuerda, por ejemplo de una guitarra, se produce un sonido fundamental, pero curiosamente va acompañado de otros sonidos que lo refuerzan. Estos sonidos, que acompañan siempre al fundamental, son sobre todo el 3.o y el 5.o (aunque hay más, se pueden considerar como nítidos estos dos), que son los que antes mencionaba como base de los acordes.
Imaginemos pulsar una cuerda partiendo de una de las notas DO, por ejemplo la que tiene 128 vibraciones por segundo; si fuéramos dividiendo la cuerda sucesivamente en una, dos, tres, cuatro, cinco, seis partes…, obtendríamos la siguiente relación:
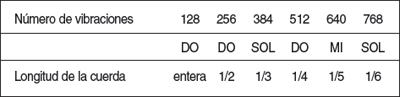
En este cuadro se constata que son las notas del acorde las que aparecen bajo una de esas relaciones proporcionales que están subyacentes en ese «mundo mágico» que es la música.
Uno de los más grandes directores de orquesta que ha habido, Leopold Stokowski (1882-1977), escribió en su libro Música para todos nosotros:
Cuando alguno de nosotros escucha música, toda nuestra conciencia se llena hasta derramarse, con el sentimiento causado por la belleza de los sonidos y la expresión emotiva de la música, pero al mismo tiempo, y aunque no siempre seamos conscientes de ello, hay escondido en el mundo de la música otro mundo. Un mundo inefablemente complejo de ondas, de sonido y de relaciones matemáticas que controlan estas ondas. Puede no ser nunca posible para nosotros oír conscientemente complejidades matemáticas como esas, pero quizá alguna vez podremos encontrar una manera de hacerlas visibles.
Existen en música dos conceptos, uno la afinación, que es la diferencia de nuestras sensaciones causada por sonidos altos o bajos y que es algo subjetivo, y otro la frecuencia, que expresa el número de vibraciones que se producen en un segundo y que es un concepto objetivo.
Resulta que las notas musicales que forman una escala completa están relacionadas por proporciones matemáticas según el número de vibraciones que producen en un determinado intervalo de tiempo.
En música, una escala completa toma el nombre de su primera y su última nota. Así, como ejemplo, si tomamos la llamada escala del tono de DO MAYOR, estaría constituida por los siguientes sonidos, que además llevan asociada una numeración romana:
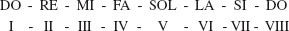
Resulta que entre todas las notas consecutivas existe una distancia sonora que llamamos de un tono, menos entre los intervalos III y IV, es decir, entre MI-FA, y entre el VII y VIII, es decir, de SI a DO, cuyas distancias son de medio tono, también llamado semitono. Pues bien, de esto deducimos que entre todas las notas consecutivas, menos en estos dos últimos casos, al existir un tono de distancia es lo mismo que decir que hay dos medios tonos o semitonos. Si reflexionamos un instante, nos daremos cuenta de que una escala completa tiene una extensión de cinco tonos y dos semitonos o, dicho de otro modo, de doce semitonos. Valga como ejemplo el siguiente esquema:

Entre cada rectángulo consecutivo del anterior esquema hay medio tono, y con los doce semitonos tenemos una escala completa que también se llama en música una extensión de octava.
Es como si, por ejemplo, dividiésemos un metro en doce segmentos iguales o un kilogramo de cualquier sustancia lo repartiésemos en doce partes iguales. Estos dos ejemplos son fáciles de entender para nosotros porque son magnitudes que se «pueden ver». En el caso de las alturas sonoras es más complicado, porque aunque el oído distingue estas variaciones en la altura del sonido, es más difícil, por no decir imposible, que el mismo oído sepa el número de vibraciones de cada sonido. Pero resulta que las doce distancias que hay para completar la escala son similares, medidas en número de vibraciones (Sistema temperado *).
1.5.2. CURIOSIDAD
El compositor Ernst Toch podía retener fácilmente tras su simple audición una serie muy larga de números; pero lo hacía «convirtiendo» la serie de números en una melodía (una melodía compuesta por él mismo, y que «correspondía» a los números).
1.6. LOS NÚMEROS EN LOS JUEGOS DE AZAR
1.6.1. LOS JUEGOS DE CARTAS Y LA RULETA
No recuerdo con exactitud la edad a la que empecé a calcular, pero fue alrededor de los cinco-seis años, y lo que sí recuerdo es que aprendí jugando a las cartas. Y es que este tipo de juegos están repletos de cálculos. La correcta toma de decisiones en cada jugada se basa en las probabilidades y en el buen manejo de los números.
Considero muy importantes los juegos de mesa para desarrollar las habilidades de cálculo e, incluso, para desarrollar otras habilidades como pueden ser la concentración o la memoria.
Yo, ante las jugadas de cartas —tute, mus, brisca, escoba, etc.—, siempre juego calculando. Procuro llevar la cuenta de las cartas que han salido y de los puntos que llevo acumulados y, ante cada jugada, tomo la mejor decisión en función de los puntos que me puede reportar o de si me interesa un grado mayor o menor en el riesgo a tomar.
Jugando de igual a igual, si somos buenos calculadores y controlamos las cartas que van saliendo, tenemos muchísima ventaja y mayor probabilidad de resultar vencedores. Esto es así porque te pueden venir cartas malas y perder, pero jugando con criterio a medio o largo plazo te van a venir cartas de todo tipo.
En los juegos de casino la complicación es mucho mayor, vamos a ver cómo se podría atacar la ruleta.
Si tuviese que escoger un método para tratar de ganar dinero en la ruleta, lo haría basándome en una suposición: «No hay ruleta perfecta, físicamente hablando». Si no hay ruleta perfecta, esto implica que las ruletas son imperfectas. Y si las ruletas son imperfectas, la bola caerá más en unos casilleros que en otros.
¿Cómo determinar en cuáles?
Respuesta sencilla: Estudiando cada ruleta. Esto es, armarse de paciencia, trabajar preferiblemente en equipo para ser lo más discretos posible y tomar nota de la caída de la bola en las ruletas (esto está permitido, sin problema).
Cuantas más tiradas tomemos, pues mejor. A partir de aquí, hacemos un estudio matemático, estadístico. Si la bola cae más en unos casilleros que en otros, podremos concluir que en esa ruleta hay mayor facilidad para caer en esos lugares, con lo que nuestras apuestas se dirigirán a esos sitios concretos.
Eso sí, tenemos que contar con que en la ruleta Europea el Casino tiene un 2,7% de beneficio, con lo cual sería lógico que apostásemos cuando la imperfección superase ese 2,7% (en la ruleta americana el beneficio del casino es del 5,26%, con lo que tendríamos que encontrar ruletas quizá demasiado «imperfectas»).
Otra cuestión a tener en cuenta es que estamos hablando de una tendencia que se dará a largo plazo, con lo cual nuestro éxito, matemáticamente hablando, tendrá lugar también a largo plazo. Esto significa que habría que contar con un capital previo (estamos hablando de tendencias a largo plazo, a corto plazo podríamos perder).
El principio fundamental sobre el que se ha de basar el trabajo en la ruleta es fácil de entender: los 37 casilleros que se reparten alrededor de la circunferencia de una ruleta no son físicamente iguales y, por lo tanto, la bola tiene más facilidad para entrar en unos que en otros, dependiendo de las características físicas de cada casilla.
Otro posible factor que otorgue imperfecciones al juego de la ruleta es que el crupier, cansado de hacer siempre lo mismo, tuviese una tirada un tanto automatizada y lanzara la bola y el plato de la ruleta a una velocidad parecida. Es lógico suponer, entonces, que la bola caería aproximadamente a la misma distancia del sitio en el que salió.
Hay casos de jugadores que trabajaron la ruleta de esta forma y a largo plazo consiguieron ganar mucho dinero. Siempre con disciplina y paciencia y, por supuesto, aplicando siempre un criterio matemático a la hora de jugar.

1.6.2. LOS JUEGOS DE AZAR EN ESPAÑA
Según el INE (Instituto Nacional de Estadística), cada español se gasta al año unos 230 euros de media en juegos de azar. En este apartado vamos a hablar de matemáticas en los juegos de azar, en la que toman el nombre de estadística; vamos a ver en qué juegos hay más probabilidades (o menos) de que nos toque.
Antes, analicemos brevemente en qué consiste esto de la estadística y las probabilidades.
La teoría de probabilidad se utiliza en campos tan diversos como la demografía, la medicina, las comunicaciones, la informática, la economía o las finanzas. A diferencia de otras ramas clásicas de la matemática, su certificación como teoría matemática no se produce hasta los años treinta del siglo XX, gracias al físico y matemático Andrei N. Kolmogorov. Hasta entonces, la teoría de probabilidad se movió entre aquellos que pretendían comprender los juegos de azar, lo que llevó, por ejemplo, a que la clase alta europea durante el siglo XVII se planteara numerosas cuestiones teóricas.
La probabilidad y el azar siempre han estado en la mente del ser humano. Por ejemplo, sumerios y asirios ya utilizaban un hueso (astrágalo) que tallaban para que pudiera caer en cuatro posiciones distintas, por lo que son considerados como los precursores de los dados. En el caso de la civilización egipcia, algunas pinturas encontradas en las tumbas de los faraones muestran tanto astrágalos como tableros para el registro de los resultados. Por su parte, los juegos con dados se practicaron ininterrumpidamente desde los tiempos del Imperio romano hasta el Renacimiento, aunque no se conocen apenas las reglas con las que jugaban. Uno de estos juegos, denominado «hazard», palabra que en inglés y francés significa riesgo o peligro, fue introducido en Europa con la Tercera Cruzada. Las raíces etimológicas del término provienen de la palabra árabe «alazar», que significa «dado». Posteriormente, en el «Purgatorio» de Dante el término aparece ya como «azar».
La estadística tiene su origen mil o dos mil años antes de Cristo, en Egipto, China y Mesopotamia, donde ya se hacían censos para la administración de los imperios. Como ejemplo curioso, los egipcios tuvieron un instrumento llamado «nilómetro», que servía para fijar los impuestos a partir del caudal del Nilo: cuanta más agua se medía, más fértiles eran las orillas del río y, por lo tanto, más impuestos podían pagar los lugareños.
Lotería Nacional
Tendríamos dos tipos de sorteo: el que se celebra semanalmente, en el que se emiten seis series de 100.000 números (00.00099.999), de los cuales 35.450 se llevan algún tipo de premio.
Y el popular sorteo de Navidad, en el que se ponen en juego 170 series de 85.000 billetes, de los cuales 13.334 se llevan premio. Así, por ejemplo, si jugamos un billete de lotería en el premio de Navidad, la probabilidad de que nos toque el premio mayor es de 1 entre 14 millones y medio (170 series × 85.000 billetes), mientras que en un sorteo de los jueves, la probabilidad es de 1 entre 600.000.

La ONCE
En el sorteo de la ONCE los boletos constan de cinco cifras, que representan un total de 100.000 números, y en los sorteos especiales se entrega además un premio especial si coincide también con la serie (150 series). Por ello, acertar el «cuponazo» significa una probabilidad de 1 entre 15 millones (150 series x 100.000 números).
Quiniela de fútbol
En la quiniela tenemos una posibilidad entre casi cinco millones, siempre y cuando hagamos una apuesta sencilla. El cálculo se hace de la siguiente forma: tenemos tres posibles resultados: 1, X, 2, y tenemos un total de 14 partidos. El resultado se obtiene elevando 3 a la 14 (4.782.969). Y como solo tenemos una apuesta, pues esa será nuestra probabilidad de acierto.
En el caso de la quiniela de fútbol, hablamos de probabilidades sin tener en cuenta que algunos resultados son más probables que otros, debido a las diferencias entre los equipos de fútbol en juego.
También podríamos hacer múltiples combinaciones de juego tratando de buscar el mayor beneficio, pero sería complicar demasiado el asunto.
Lotería Primitiva
En el caso de la Lotería Primitiva, haciendo una apuesta sencilla de seis números, la probabilidad de acertar seis es de una entre casi 14 millones. Esto se calcula de la siguiente forma:
Tenemos 49 números, de los que seis resultan ganadores. En el primer número extraído nos resultan favorables seis casos, cualquiera de los nuestros, de entre los posibles cuarenta y nueve; por lo tanto, hay que dividir 6 entre 49. En la segunda extracción, al haber salido ya un número, quedan cinco favorables y cuarenta y ocho posibles, es decir, 5 entre 48, y así, en progresión hasta llegar a la sexta, donde llegaríamos a dividir el último número entre los 44 que nos quedarían posibles. Al hacer estos cálculos, resulta que la probabilidad de ganar el premio mayor con esta apuesta simple es de 1 entre 13.983.816.
1.6.3. LAS PROBABILIDADES DAN MUCHO JUEGO
Te planteo la siguiente pregunta: ¿Cuántas personas, como mínimo, ha de haber en un grupo para que la probabilidad de que dos de ellas compartan cumpleaños supere el 50%?
La respuesta es: solo 23 personas.
Puede parecernos sorprendente, pero la realidad es que entre 23 personas se pueden formar 253 parejas posibles.
Es decir, imaginemos un partido de fútbol. Dentro del rectángulo de juego tenemos 22 jugadores más el árbitro. Pues bien, es más probable que dos de los participantes en el partido cumplan años el mismo día a que no se dé esta circunstancia.
Cuantas más personas superen las 23, mayor es la probabilidad de que dos de ellas cumplan años el mismo día.
Podemos concluir con que, si te gustan las apuestas, puedes, en grupos iguales o mayores a 23 personas, apostar a que dos de ellas comparten cumpleaños. Matemáticamente tendrás mayor probabilidad de acierto que lanzando una moneda al aire y decantándote por cara o cruz.
1.7. LOS MEDIOS DE COMUNICACIÓN
Nuestros medios de comunicación, con contadas excepciones, apenas son capaces de reseñar con mediano sentido de rigor informativo, a no ser copiando de otros medios extranjeros, los hechos más sustanciales que van surgiendo en el mundo de la ciencia en general y de las matemáticas en particular. Todo lo que tenga números parece que se atraganta sin el más mínimo sonrojo.
En los informativos
En cierta ocasión, hace un par de años, estaba de gira impartiendo unas charlas por las maravillosas Islas Canarias. Como en otras muchas ocasiones acudieron los medios informativos, que hicieron sus reportajes y grabaciones. Cuando estaba en el hotel, pude ver en las noticias de la Televisión Canaria acerca de mi presencia en las Islas; la información, de entrada, era la siguiente:
Estos días se encuentra en las Islas el popular Alberto Coto, Récord Guinness y Campeón del Mundo en Velocidad de Cálculo Mental. Entre sus logros está el haber sumado 100 números del 0 al 9 en un increíble crono de 19 minutos y 23 segundos.
Cuando oí la noticia me quedé estupefacto; la presentadora es evidente que leyó lo que alguien le había escrito, pero resulta curioso que alguien pueda tener un Guinness en velocidad de cálculo por haber sumado 100 números sencillos en más de ¡19 minutos! (evidentemente, la realidad son 100 números en 19 segundos y 23 centésimas de segundo…).
Este gazapo apareció en el diario El Mundo en fechas recientes:
Crece un 10,9 %
Un total de 7.853 millones de turistas llegaron a España en agosto, lo que supone un 10,9% más que en el mismo periodo del año pasado.
No deja de ser simpático, ¿verdad? Está claro que es un error, creemos que así es, de imprenta. Lo interesante del tema sería que el lector inmediatamente se dé cuenta de lo que implicaría ese dato, que en muchos casos estoy seguro que pasó desapercibido.
7.853 millones de turistas superarían la población mundial, con lo cual se me antoja un poquito difícil que esta cifra pueda ser correcta. Salvo que durante el pasado mes de agosto nos hayan visitado de otros planetas.
Rebajas en el AVE
En diciembre de 2005 se dio la noticia de la rebaja de las tarifas del AVE entre Madrid y Zaragoza. De esta forma dieron la noticia dos de los más importantes periódicos de nuestro país:
Como término medio, las tarifas de los trenes AVE que circulan por la línea Madrid-Zaragoza-Lérida tendrán una reducción de un 7% en euros por kilómetro y un 16% en todo el conjunto del recorrido.
Caramba, ¿cómo se come esto?
A ver cómo plantea la noticia el periódico número 2, quizá nos saque de la duda…
El secretario de Estado de Infraestructuras, Víctor Morlán, anunció hoy que viajar en el AVE Madrid-Zaragoza-Lleida costará de media a partir de mañana un 16% menos, con lo que se pretende establecer unas tarifas similares a las de la línea que une Madrid-Córdoba-Sevilla.
Morlán, en una conferencia de prensa en la sede de la Delegación del Gobierno en Aragón junto al presidente de Renfe, José Salgueiro, explicó que esta reducción de precios supone que los usuarios del tren entre Madrid-Zaragoza-Lleida pagarán un 7% menos por kilómetro del trayecto.
¿Qué fácil nos lo han puesto, verdad? Por favor, a mí que no me cobren por kilómetro (7% de rebaja), que me cobren por trayecto completo (16% de rebaja).
El precio del cordero
Este titular apareció en el diario Las Provincias:
El precio del cordero se multiplica por 15.
El precio del cordero se multiplica hasta 15 veces desde que el ganadero lo vende y hasta que llega al consumidor, pasando de 4,27 euros/kilo a 19,33 euros/kilo que paga el consumidor final.
Qué barbaridad…, ahora me entero de que 4,27 × 15 = 19,33 euros…
Consumo de helados
Cada español consumió el año pasado ocho litros de helado, dos más que en 2002…
Un crecimiento extraordinario del 33% en un año (de 6 a 8). Pero seguramente falso, si esta otra cifra, que aparece en el texto, es cierta (vaya usted a saber):
Las grandes marcas distribuyeron el año pasado 326 millones de litros, casi un 10% más que en 2002.
326 (millones) entre 40 (millones de españoles) son algo más de ocho litros por cada español. Pero entonces, ¿los dos litros de crecimiento a los que se aludía anteriormente?
Sería recomendable que los niños que han suspendido las matemáticas y están con sus cuadernos de verano no lean los suplementos de los periódicos…
Alergia al polen
Observa el siguiente titular, quizá habría que cambiar lo de alergia al polen por «alergia a los números».
La alergia al polen podría aumentar a la mitad de la población en 20 años.
Alrededor de seis millones de personas sufren alergia al polen en España y se prevé que la cifra aumente…
Y a continuación:
Se calcula, por tanto, que un 22% de la población española sufre alergia a los pólenes…
Algo falla, o que en el periódico no sepan la gente que vive en España, o sencillamente que no saben lo que es un porcentaje.
La sección de economía no se libra
En páginas de prensa económica también aparecen lindezas como la siguiente:
Las mujeres ganan de media un 71,1% menos que los hombres.
No contentos con el titular, la noticia continúa de la siguiente forma:
El salario medio bruto por trabajador se situó en 19.808,06 euros en 2002, correspondiendo 22.174,08 euros a los empleados varones y 15.775,07 euros a las mujeres, lo que sitúa el salario promedio anual femenino un 71,1% por debajo del masculino.
Evidente es que lo que quieren decir y no dicen es que el salario medio de las mujeres es el 71,1% del de los hombres, no «un 71,1% menos». Ahí es nada la diferencia.
Este sí que es curioso
… En las 2.117 bodas del cuarto trimestre del pasado año, contrajeron matrimonio 2.042 varones y 2.092 mujeres.
Sin comentarios…
1.8. LA PSICOLOGÍA DE LOS NÚMEROS
Como bien sabemos, la forma de interpretar o de plantear datos numéricos puede cambiar desde un punto de vista psicológico el efecto que cause en las personas. Todos hemos visto tras unas elecciones cómo parece que el conjunto de los partidos han ganado las mismas. Unos interpretan los datos en función de si han subido o no en número de votos; si así no fuese, lo interpretarían según el porcentaje de votos, o si tampoco fuese así, buscarían resquicios basándose en unas determinadas previsiones que hubiesen resultado más desastrosas en función de determinados hechos acaecidos, etc.
Observa a continuación, con el siguiente ejemplo, cómo influye el factor psicológico según se plantee el problema.
Nos imaginamos que estamos ante un desastre natural y somos los jefes del servicio de salvamento. En peligro hay 900 personas. Se nos abren dos posibles vías de escape:
La primera vía nos dice que, si la tomamos, salvaríamos a 300 personas. Mientras que, si tomamos la segunda vía, hay una probabilidad de un tercio de que las 900 se salven y una probabilidad de dos tercios de que no lo consiga ninguna de las personas afectadas. ¿Qué camino tomarías?
Con encuestas realizadas, la mayoría de la gente eligió la primera vía, pues de este modo es seguro que se salven 300 vidas, mientras que con la segunda opción hay dos tercios de probabilidad de que no se salve ninguna.
Hasta aquí todo correcto, pero ahora vamos a plantear el problema de otra forma.
Imagina que ante la primera vía de escape te dicen que es seguro que conlleve 600 muertos. Mientras que si eliges la segunda vía hay una probabilidad de un tercio de que ninguno muera (y una probabilidad de dos tercios de que caigan todos). ¿Qué ruta elegirías en esta ocasión?
La mayoría de la gente optó por la segunda ruta, justificando su elección en que la primera de ellas nos lleva a 600 muertes seguras, mientras que por la segunda vía hay un tercio de probabilidades de que todos se salven.
Las dos preguntas son idénticas desde un punto de vista matemático. El motivo por el que las respuestas hayan sido completamente distintas depende del modo en que han sido planteadas: en términos de vidas perdidas o de vidas salvadas.
Como este ejemplo que acabamos de citar se dan infinidad de ellos en los medios de comunicación, con otro formato y otro mensaje. Todo depende de qué pretenda la persona que lanza el mensaje, y de lo que le interese respecto a la opinión del gran público. Interesante es saberlo valorar desde un punto de vista matemático.
1.9. EL GENIO NUMÉRICO
Hace unos años leí una historia muy bonita de un matemático árabe, la cual paso a contar de la forma en que la recuerdo:
Vagaban por el desierto un hombre mayor, conocido como el matemático, y su compañero de viaje a lomos de un solo camello, habían sufrido la pérdida del segundo camello y de esta penosa forma consiguieron llegar a un albergue donde poder descansar.
A la mañana siguiente fueron testigos de la discusión acalorada de tres hombres.
El matemático preguntó entonces al mayor de ellos por el motivo de la misma, y este pasó a contarle:
Somos tres hermanos y recibimos como herencia 35 camellos, voluntad expresa de nuestro padre. A mí, por ser el mayor, me corresponden la mitad de los camellos; a mi hermano, el segundo en edad, le corresponde una tercera parte de los 35 camellos, y al pequeño de los tres le corresponde la novena parte de los camellos.
No sabemos cómo hacer la partición, ya que la mitad de los 35 serían 17,5 camellos, y no es posible partir un camello por la mitad. Al mediano le correspondería un tercio, y eso son 11,66 camellos, algo que tampoco es posible. Mientras que al pequeño de los tres le corresponde la novena parte, y 35/9 es casi 3,9 camellos…
Hemos ensayado varias particiones pero ninguno está de acuerdo, ninguna nos resulta satisfactoria.
Yo soy calculador, me comprometo a mediar en la disputa y vosotros diréis si aceptáis la partición que os propongo, intervino el matemático.
Adelante, dijeron los tres hermanos, nada tenemos que perder.
Bien, permitidme, pues, que el camello que nos ha traído a este lugar forme parte del grupo de camellos, de esta forma tendríais 36 camellos y uno más para que podáis repartir.
Los tres hombres miraron asombrados por tal majadería, pero no dijeron nada.
Tenemos 36 camellos y vamos a proceder al justo reparto de los mismos…
Se dirigió entonces al mayor de los tres hombres y le dijo:
Tendrías que recibir la mitad de 35 camellos, que son 17,5. Pues bien, recibirás la mitad de 36, que son 18 camellos, y de esta forma sales ganando.
Se dirigió al segundo de los hermanos y le dijo:
Te corresponde un tercio de 35 camellos, que es menos de 12 camellos. Propongo que recibas un tercio de 36 camellos, que son 12, y también saldrás ganando.
Por último, le dijo al menor de los hermanos:
La voluntad de tu padre es que recibas la novena parte de los 35 camellos, o sea, menos de 4 camellos. Pues bien, recibirás la novena parte de 36 y tendrás así 4 camellos.
Miró entonces a los tres hombres para comprobar que estaban de acuerdo. Los tres asintieron complacidos, ¿cómo no iban a estar de acuerdo si los tres ganaban con el reparto?…
Pues bien, concluyó el matemático, el mayor de los tres recibirá 18 camellos, el mediano 12 y el pequeño 4. Y 18 + 12 + 4 son 34 camellos. De los 36 camellos sobran por lo tanto dos. Uno lo hemos puesto mi amigo y yo, el otro, si me permitís, es de justicia que me corresponda por haber resuelto vuestro problema y haberos dejado satisfechos con el reparto.
Los tres hermanos, satisfechos plenamente, asintieron elogiando y agradeciendo al matemático su brillante intervención.
De esta forma, el matemático y su amigo continuaron ruta por el desierto, cada uno en su camello.
1.10. CÓDIGOS DEL DÍA A DÍA
Nuestra cuenta corriente, la letra del NIF, los códigos de barras o el ISBN de los libros, son cuatro ejemplos que forman parte de nuestro día a día, de nuestro paisaje habitual. Vamos a ver cómo se construyen, pues no están hechos de forma aleatoria, sino que lo están con un procedimiento cuyo objetivo está en poder detectar posibles errores al ser introducidos en un ordenador.
1.10.1. LA LETRA DEL NIF
Como bien sabemos, nuestro NIF (número de identificación fiscal) está formado por nuestro número de DNI (7 u 8 dígitos) y una letra de control.
Esta letra se calcula a través de una fórmula matemática y de una tabla creada con equivalencias. De esta forma, podemos calcular la letra que corresponde a una serie de números y, por otra parte, a partir de una serie de números, puede comprobarse si es correcta la letra que lleva asociada.
Forma de calcular la letra:
Se divide el DNI entre 23 y obtenemos un cociente y un resto. Pues bien, lo que nos interesa sería el resto.
A continuación, la letra se sabe utilizando esta tabla:

Si el resto da 0, la letra será la T; si da 1, la R; si da 17, la V, etc.
1.10.2. EL ISBN DE LOS LIBROS
El ISBN (International Standard Book Number), que aparece en todos los libros, está formado por diferentes bloques que identifican el país, la editorial y libro (en total 9 cifras), y un último dígito (o la letra X) que sirve como dígito de control.
Este dígito de control se calcula de una manera muy sencilla que pasamos a explicar mediante un ejemplo:
Supongamos que las nueve primeras cifras de la izquierda del ISBN de un libro son 84-607-7738. Para calcular el último dígito del ISBN se realizan las siguientes operaciones:
(8 × 1) + (4 × 2) + (6 × 3) + (0 × 4) + (7 × 5) + (7 × 6) + (7 × 7) + + (3 × 8) + (8 × 9) = 8 + 8 + 18 + 0 + 35 + 42 + 49 + 24 + 72 = 256
Es decir, cada una de las cifras del número, leídas de izquierda a derecha, se han ido multiplicando por 1, 2, 3, 4, 5, 6, 7, 8, 9, y luego se han sumado estos resultados.
El último paso es dividir el resultado entre 11 y quedarnos con el resto. 256 entre 11 es 23 de cociente y 3 de resto (si el resto diese 10, pondríamos una X).
Luego, el ISBN de este libro sería 84-607-7738-3.
Actualmente, cualquier programa profesional de ordenador que trabaje con ISBN tiene rutinas que calculan el dígito de control y comprueban si este coincide con el introducido por el usuario. Si no coincide, el ISBN dado es erróneo; si coincide, puede que lo sea o puede que no. Esto es así porque a un número le corresponde un único dígito de control, pero un mismo dígito de control corresponde a muchos números.
1.10.3. CÓDIGO DE LA CUENTA CORRIENTE
Nuestra cuenta corriente tiene un código de 20 cifras. Empezando por la izquierda, los cuatro primeros dígitos identifican a la entidad, los cuatro siguientes a la sucursal, luego vienen dos dígitos de control, y las diez últimas cifras corresponden al número de la cuenta corriente.
El primero de los dígitos de control es el de la entidad/sucursal. El segundo es el dígito de control del número de la cuenta corriente. Un ejemplo enseñará a calcularlos.
Supongamos que el número de una cuenta corriente es el 0123456789; para calcular su dígito de control se realiza la operación:
0 × 10 + 1 × 9 + 2 × 7 + 3 × 3 + 4 × 6 + 5 × 1 + 6 × 2 + 7 × 4 + + 8 × 8 + 9 × 5 = 210
Es decir, cada una de las cifras del número de la cuenta, leídas de izquierda a derecha se han ido multiplicando por 10, 9, 7, 3, 6, 1, 2, 4, 8, 5 y luego se han sumado estos resultados.
Ahora dividimos 210 entre 11 y el resto, que en este caso es 1, es el dígito de control. Si el resto hubiera sido 10, se toma como dígito de control 1.
Sean ahora 0123 el código de una hipotética entidad y 4567 el código de una de sus sucursales. Para calcular el dígito de control de entidad/sucursal se realiza la operación:
0 × 7 + 1 × 3 + 2 × 6 + 3 × 1 + 4 × 2 + 5 × 4 + 6 × 8 + 7 × 5 = 129
Calculamos el resto de 129 entre 11, que es 8, y ya tenemos el dígito de control de entidad/sucursal. Como antes, si el resto es 10, el dígito de control será 1.
Lo mismo que decimos para el ISBN sirve para el Código Cuenta Corriente. Por ejemplo, el programa de ayuda para la declaración del IRPF tiene incorporadas rutinas de cálculo de los dígitos de control, detecta la introducción de un código cuenta corriente erróneo y aparece una ventana de aviso.
1.10.4. LOS CÓDIGOS DE BARRAS

Los códigos de barras están presentes a todas horas en nuestras vidas y, sin embargo, con frecuencia no sabemos exactamente lo que representan. Gracias a los códigos de barras se pueden identificar toda clase de productos y servicios en todo el mundo.
Constan de varios números, siendo el último el dígito de control, fundamental es que sea correcto.
Pues bien, este dígito verificador se obtiene mediante un cálculo efectuado para asegurar la exactitud del código de un producto.
El cálculo que se realiza sería el siguiente:
Primero: Numerar todos los dígitos del código de derecha a izquierda.
Segundo: Sumar todas las posiciones impares del código y multiplicarlas por tres.
Tercero: Sumar todas las posiciones pares del código.
Cuarto: Sumar el resultado final del segundo y tercer paso.
Quinto: El resultado se resta a la decena inmediata superior, de donde resulta el dígito verificador. Este puede ser un número entre 0 y 9.
Ejemplo práctico para un código EAN-13:
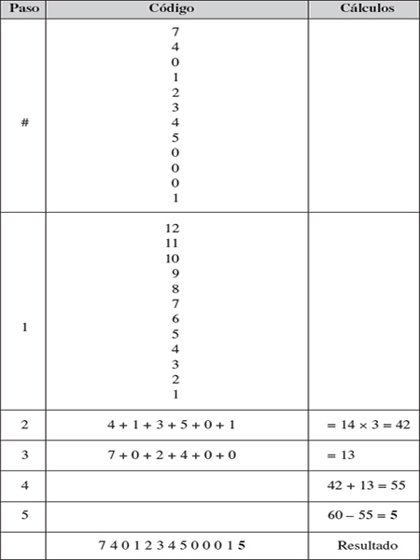
El algoritmo a utilizar para cada uno de los sistemas de codificación es el mismo:
• Para Código UPC: 11 dígitos (el dígito 12 es el dígito de control).
• Para Código EAN-8: 7 dígitos (el dígito 8 es el dígito de control).
1.11. DOS NÚMEROS CON MALA SUERTE: 13 - 666
1.11.1. EL NÚMERO 13
Como bien sabemos, el número 13 está considerado en las sociedades occidentales como el número de la mala suerte.
La superstición en torno a este número no es algo fruto de los tiempos modernos, debemos remontarnos muchos siglos atrás para comprender estos miedos. De hecho, se debe a que en la Última Cena se sentaron los doce apóstoles más Jesucristo, y este murió. Por eso la tradición primitiva cristiana considera que nunca se han de sentar trece personas en una comida o cena, pues existiría el riesgo de que alguna muera antes de terminar el año.
Si continuamos con las tradiciones religiosas, vemos que el capítulo decimotercero del Apocalipsis está dedicado al Anticristo.
De todas formas, no es solo de la religión cristiana, los hindúes ya veían el 13 como un número maldito, el Código de Hammurabi, por ejemplo, lo omite.
Mientras que para nosotros el martes y 13 es el día de la mala suerte, para los anglosajones se mantiene el número 13 pero es el viernes. Sin embargo, para los japoneses el viernes, y si encima es 13, es el día propicio para tener todo tipo de suertes. Como vemos, todo depende de las interpretaciones. Por cierto, cuando alguien tiene miedo al número 13 se dice que padece triscadecafobia.
A modo de curiosidad
Lo cierto es que hay casos que son para pensar que sí que hay algo raro en este número, como lo que le pasó al músico alemán Richard Wagner: nació en un año acabado en 13; la suma de las letras de su nombre y apellido son 13; los números de su año de nacimiento, 1813, suman también 13; compuso 13 óperas y falleció un día 13.
Simplemente son fobias que en mayor o menor medida podemos tener cualquier persona, pero no nos dejemos llevar por ellas. La ciencia no casa con las casualidades. ¿Nos habríamos fijado en este detalle si en lugar de con el 13 el baile de cifras hubiese sido, por ejemplo, con el 24?
No olvidemos nunca que la mayor de las casualidades sería que no las hubiera. Se dan tantos sucesos y hay tantas personas como interpretaciones posibles. Siempre habrá alguien decidido a sacarlas a la luz y a hacernos creer que tienen algún significado.
1.11.2. EL 666
¡Aquí hay sabiduría! El que tiene entendimiento, cuente el
número de la Bestia; pues es número de un hombre. Y su número es 666.
Apocalipsis 13, 18
La Biblia, en el Libro de las Revelaciones o Apocalipsis de San Juan, es quien identifica al 666 como al número de la Bestia, siendo el sello o la marca del Anticristo.
En las doctrinas religiosas será la marca que impondrá el Anticristo en la mano derecha o la frente de cada ser humano, al final de los tiempos de la tierra. Se cree que el hecho de que esa marca sea el 666 implica denotar la trinidad satánica (satanás, el Anticristo y el falso profeta).
Hay más números con cierto significado en las Sagradas Escrituras, por ejemplo:
10 |
= |
Lo completo. |
7 |
= |
Lo perfecto. |
3 |
= |
Da énfasis. |
6 |
= |
Imperfección (pues no alcanza el 7, y el que mencione 3 veces indica énfasis en lo imperfecto… |
Cuadrado Mágico Satánico
Los cuadrados mágicos son una forma antiquísima de acertijo numérico, consistente en formar un cuadrado de números cuyas filas, columnas y diagonales sumen lo mismo. Dice la leyenda que el primer cuadrado mágico nació en el siglo XXIII a. de C., y fue encontrado por el emperador chino de la época en el caparazón de una tortuga que pasaba por el río amarillo. Con este peculiar origen no es de extrañar que siempre hayan tenido un significado cabalístico y mágico, considerando que preservaban de todo tipo de enfermedades.
Durante la Edad Media se utilizaron como amuletos para buenos o malos encantamientos, asociándolos con la religión, la astrología y la alquimia. También se grababan como amuletos en láminas de plata con la creencia de que mantendrían alejada la peste negra.
Pues bien, si se utilizaban en toda clase de supersticiones, observa este cuadrado mágico de orden 6 (6 filas por 6 columnas). Todas sus filas, columnas y diagonales suman 666, es decir, el número del diablo, por eso es conocido como Cuadrado Mágico Satánico.
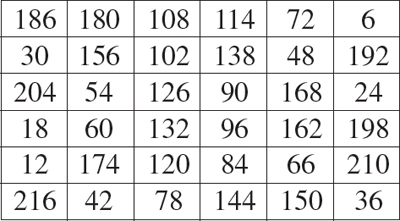
Ricemos el rizo de la fantasía y de la magia, porque el siguiente cuadrado mágico no solo es satánico, sino que además todos los números que lo integran son números primos.
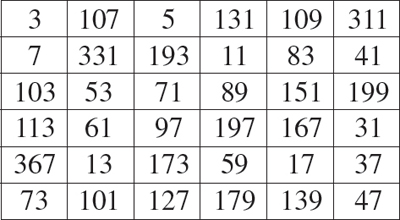
Aunque para las sociedades occidentales el 666 es el número del Anticristo, para los chinos, por el contrario, es de buen augurio, ya que el 6 es sinónimo de suerte.
La cultura oriental, muy supersticiosa en cuestión de números, considera que el 4 es el número de la mala suerte, el 6 es sinónimo de buena fortuna, el 8 de riqueza y el 9 de longevidad y eternidad.
Los chinos sí tendrán una celebración el 8 de agosto de 2008 (8-8-8), ya que fue la fecha elegida para inaugurar los Juegos Olímpicos de Pekín.
* Este es un sistema acordado para corregir pequeñas desviaciones que se producen que se llaman «comas», cuyo análisis excede de los fines de este libro.