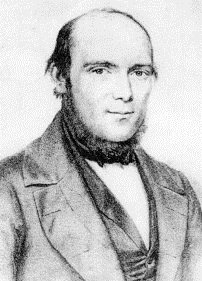Karl Adolf Anderssen (Breslavia, 6 de julio de 1818 - 13 de marzo de 1879).
Que las matemáticas y el ajedrez están muy correlacionados no es ningún secreto. Muchas de las aperturas, defensas, y finales de partidas tienen una gran carga teórica matemática detrás que conviene conocer. Además, no es nada corta la lista de grandes jugadores históricos del ajedrez que también presentaron una más que notable influencia en matemáticas. Son jugadores que lograron compenetrar su indudable capacidad matemática con la aún más interesante habilidad en un juego nada sencillo y completamente indescifrable. Se procede a analizar algunos de los nombres más reconocidos.
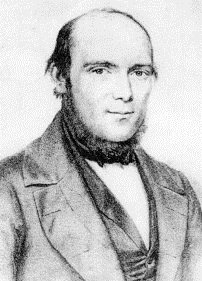Karl Adolf Anderssen (Breslavia, 6 de julio de 1818 - 13 de marzo de 1879).
Nacional de la antigua Alemania. Fue un matemático doctorado en 1847, que compaginó durante toda su vida sus dos grandes pasiones: el ajedrez y las matemáticas.
Fue profesor de matemáticas.
Imagen 1: Adolf Anderssen.
Adolf Anderssen fue considerado el jugador más fuerte de su época, mediados del siglo XIX, en el auge de la Escuela Romántica. Aunque por entonces no había oficialmente un título de campeón del mundo, ya se le consideraba como el mejor jugador del planeta. Sus innumerables aportaciones merecen una especial mención.
Fue un jugador de carácter muy agresivo, y con una gran capacidad combinativa. Su gran habilidad no fue sólo fruto de la suerte o de un talento innato obtenido por nacimiento, sino que fue gracias a un gran entrenamiento y un esfuerzo titánico. Uno de los motivos por los que su evolución fue relativamente tardía fue por el hecho de provenir de una familia humilde, sin demasiados recursos, lo que le impidió asistir a las escuelas de ajedrez y mejorar a un ritmo más elevado. Dicho lo cual, adquieren aún más méritos los logros que obtuvo en vida.
Atrajo la atención del mundo del ajedrez con la publicación en 1842 de un famoso libro de problemas de ajedrez de la época. La publicación de dicha obra le sirvió para lograr años más tarde el puesto de director de una famosa editorial.
En el año 1848 empató un match contra el gran maestro alemán de ajedrez Daniel Harrwitz, cuando todavía Anderssen no era un jugador profesional. Este hecho le sirvió para recibir una invitación para asistir al primer torneo internacional de la historia, que se disputó en Londres en 1851, donde se iban a ver las caras principales maestros del mundo del ajedrez. Anderssen disputó ese torneo y lo ganó dejando atrás a rivales fuertes de la época como Staunton, Kieseritzky o Wyvill. Es por ello por lo que esta victoria le sirvió para ser recordado como campeón del mundo, aunque oficialmente no tuviera tal consideración en aquel momento.
En 1862, también en Londres, Anderssen obtuvo la puntuación más alta en el primer torneo disputado bajo las reglas del ‘round-robin challenge’, aquél en el que cada jugador se enfrenta a todos los demás. Ganó todas las partidas salvo una, en el que se constituye como uno de los mayores méritos de su carrera ajedrecística.
Pero, sin duda, su mayor logro fue ganar el torneo de Baden-Baden (Alemania) en 1870, quedando por delante de otro matemático y gran jugador reconocido, Wilhelm Steinitz, y de otros jugadores muy fuertes como Neumann.
Su último logro fue en 1877, quedando en un meritorio segundo lugar en el torneo de Leipzig (Austria). Dos años más tarde, falleció.
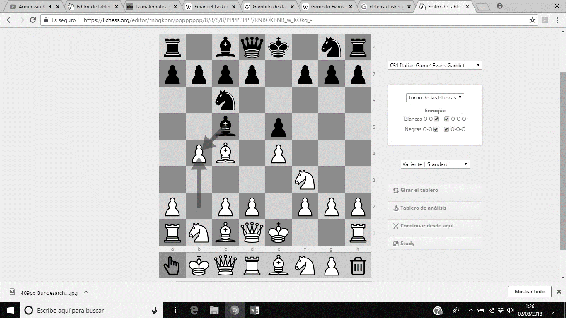
Entre sus aportaciones podemos destacar la apertura de ajedrez que lleva su nombre, la Apertura Anderssen, si bien es cierto que no es demasiado popular en nuestros días. Es utilizada en partidas en los que un rival se cree muy superior al otro, y, de entrada, le interesa realizar movimientos de espera. La apertura comienza con a3…
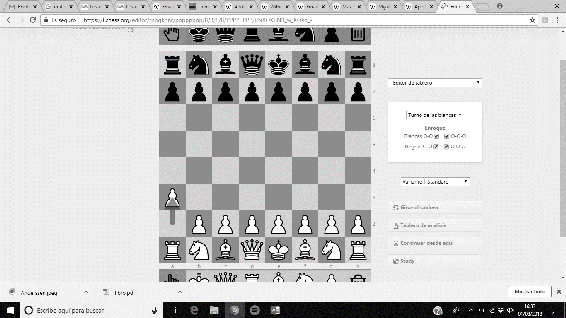
Imagen 2: Apertura Anderssen: a3
Pero hablar de Anderssen no es sólo hablar de su famosa apertura. No podemos dejar pasar sus aportaciones en partidas históricas. Tales fueron el nivel de dichas partidas, que dos de ellas han sido bautizadas y recordadas durante dos siglos. Sus nombres son ‘La Inmortal’ y ‘La siempreviva’, y forman parte de muchos libros de ajedrez.
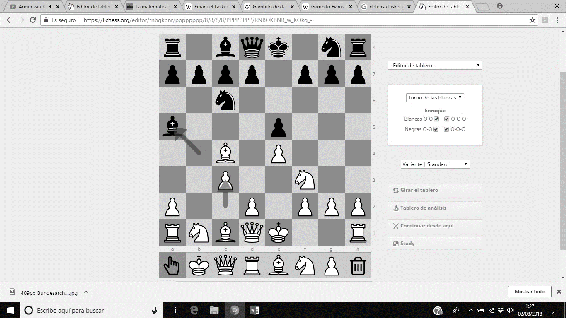
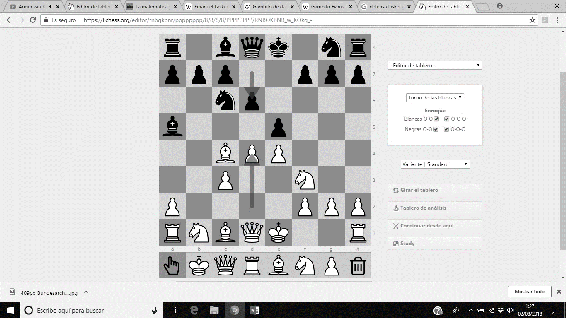
‘La Inmortal’ fue una partida amistosa disputada en Londres, 1851, entre Anderssen (piezas blancas), y Lionel Kieseritzky (piezas negras). Un espectacular sacrificio de la Torre y de la Dama fuerza un Jaque Mate antológico, cuya secuencia es …19. e5 Dxa1+ 20. Re2 Ca6 21. Cxg7+ Rd8 22. Df6+ Cxf6 23. Ae7#.
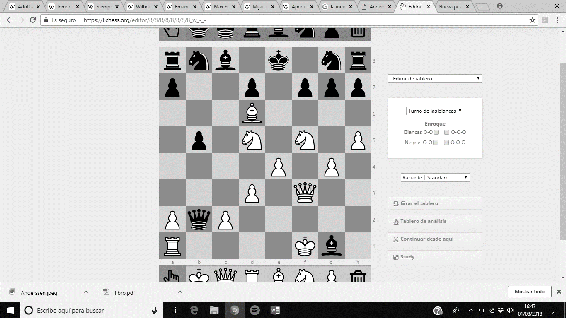
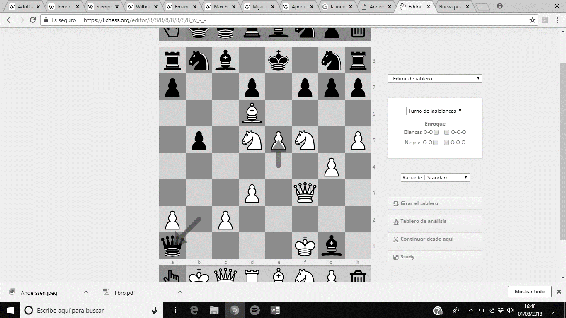
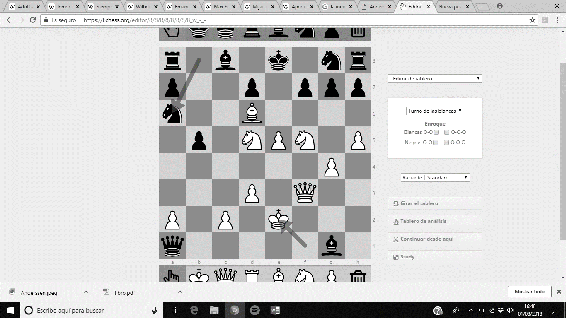
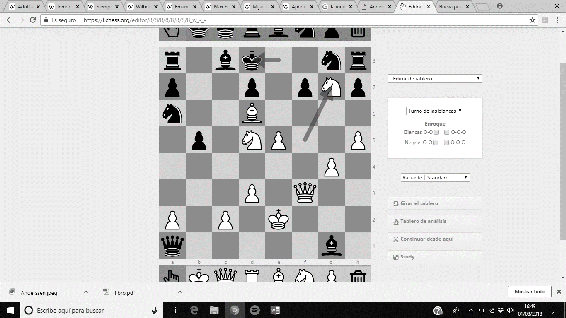
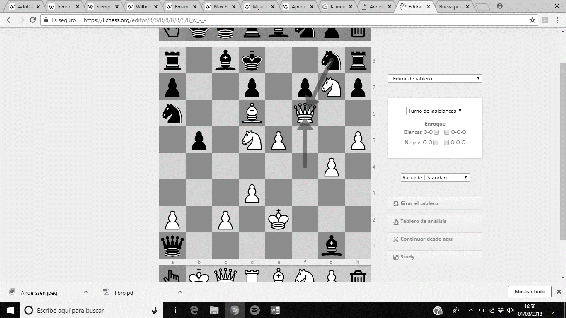
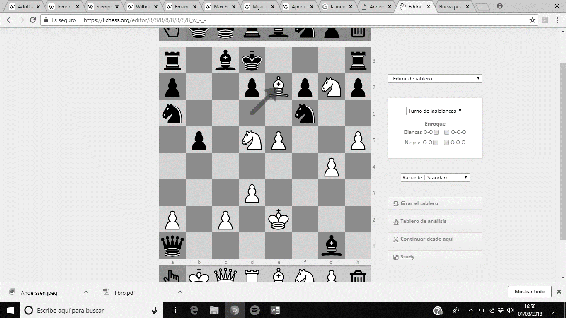
Imágenes 3-8: Secuencia final de la partida ‘La Inmortal’.
No menos espectacular es ‘La siempreviva’, una partida amistosa disputada en Berlín en 1852 entre Anderssen (piezas blancas) y Jean Dufresne (piezas negras). Tras un desarrollo de la partida propio de la Escuela Hipermoderna de Ajedrez, Anderssen logra un precioso Jaque Mate forzado con los Alfiles tras un brillante sacrificio de Dama. La secuencia final de la partida es 21. Dxd7+ Rxd7 22. Af5+ Re8 23. Ad7+ Rf8 24. Axe7#.
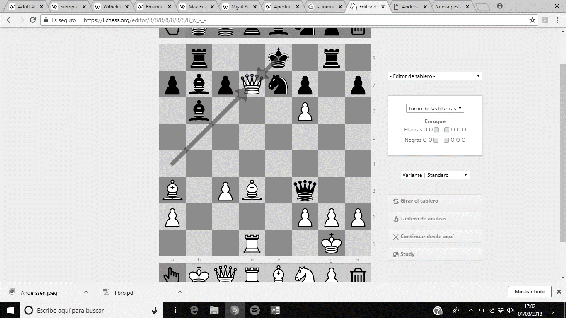
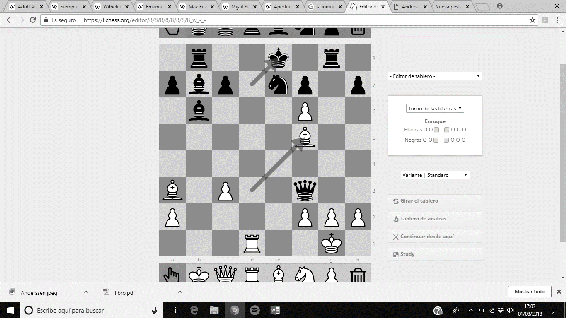
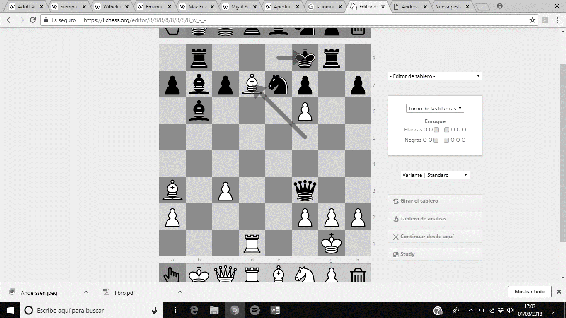
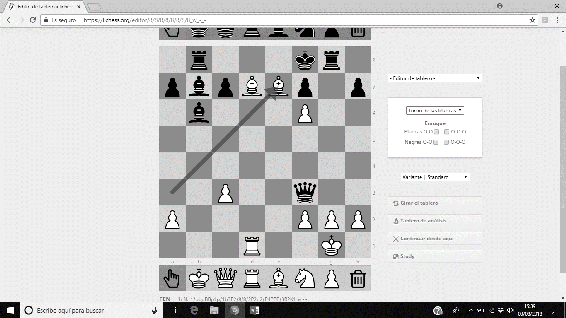
Imágenes 9-12: Secuencia final de la partida ‘La siempreviva’.
Wilhelm Steinitz (Praga, 14 de mayo de 1836 - Nueva York, 12 de agosto de 1900) fue un jugador de ajedrez de origen austríaco (Praga por entonces pertenecía a Austria).
En sus primeros años de vida, destacó por unas excepcionales habilidades en las matemáticas que supo plasmar a la profesión que dedicó durante toda su vida, el ajedrez.
Imagen 13: Wilhelm Steinitz.
Steinitz creció en una modesta familia que se dedicaba a la industria textil y ferretería. Emigró a Viena, la cual era una ciudad con una gran tradición ajedrecística, a continuar con los estudios de Ingeniería en la Universidad. Sin embargo, viendo que sus cualidades como ajedrecista mejoraban muy rápidamente (esto le hacía ganar dinero apostando en partidas que él mismo disputaba en los locales y las cafeterías) hizo que abandonara permanentemente los estudios que estaba cursando para dedicarse a tiempo completo al ajedrez como jugador profesional. Poco tiempo después, Steinitz fue progresando hasta lograr convertirse en uno de los jugadores de ajedrez más fuertes de Viena.
En 1862, disputó el Torneo de Londres, que como se ha mencionado antes, lo ganó Anderssen, quedando Steinitz en segunda posición. Sin embargo, en dicho torneo comenzaron a verse destellos del gran jugador que acabaría siendo.
Derrotó a rivales de nivel como Blackburne o Mongredien. Poco después de esto, se instaló en Londres.
En 1866, se disputó el combate entre Adolf Anderssen y Wilhelm Steinitz, duelo que podría ser considerado como aquél que decidiría quién sería el primer campeón mundial de ajedrez. El duelo finalizó con la victoria para Steinitz, por ocho victorias de este, frente a seis de Anderssen. Sin embargo, todavía no tendría la consideración oficial de título mundial.
Disputó en 1867 el Torneo de París, en el que acabó tercero, y el torneo de Baden-Baden (1870), en el que acabó segundo contra su entonces rival Adolf Anderssen, al que ganó en sus dos enfrentamientos individuales.
Ganó varios torneos con renombre internacional, como el Torneo de Londres (1872) y el Torneo de Viena (1873), tras el cual, Steinitz efectuó un parón competitivo para dedicarse al análisis y estudio teórico de aperturas y posiciones.
Tras el parón voluntario, en 1886 comenzó el primer duelo con la consideración oficial de campeonato mundial de ajedrez, en Nueva York, entre Steinitz y el gran jugador polaco Johannes Zukertort. El duelo finalizó con victoria de Steinitz, lo que le convirtió en el primer campeón oficial del mundo de ajedrez.
En 1889 disputó un intenso duelo con el gran maestro ruso Mijail Chigorin, en La Habana, el cual finalizó con la victoria, de nuevo, para Steinitz.
Entre 1890 y 1891, se disputó otro duelo con el título en juego frente al maestro húngaro Gunsberg, quien tampoco pudo vencer a Steinitz, que retuvo de esta forma el título unos años más.
El ruso Chigorin tuvo la revancha por el título mundial en 1893, en San Petersburgo, tras una tremenda expectación creada en torno a los dos jugadores debido a sus diferencias en temas de aperturas. De nuevo, Steinitz, con 60 años, revalidó el título en un igualado enfrentamiento.
Fue finalmente otro gran matemático, Emanuel Lasker, quien logró derrotar a Steinitz, en 1894, por el título de campeón del mundo de ajedrez. Finalizaba así una gloriosa etapa para la vida de este irrepetible ajedrecista, quien moriría unos años más tarde por problemas mentales, en un asilo de Estados Unidos.
Entre sus aportaciones más destacables al ajedrez teórico, se pueden destacar los grandes estudios que realizó a diversas variantes de defensa que surgen de la Apertura Española y de la Defensa Francesa.
La Defensa Steinitz de la Apertura Española (cuya secuencia es 1.e4 e5 2.Cf3 Cc6 3.Ab5 a6 4.Aa4 d6…) permite un gran contra juego para las piezas negras frente al fuerte ataque de las blancas que provoca la Apertura Española. Diversas variantes fueron estudiadas por Steinitz.
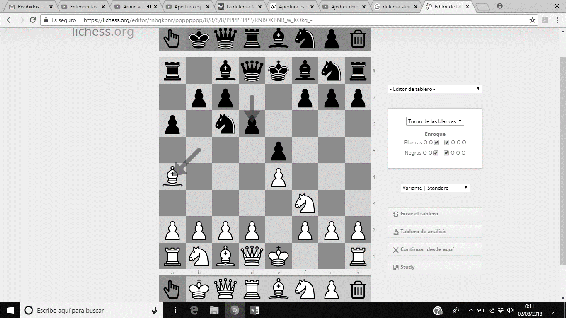
Imágenes 14-17: Secuencia de la Defensa Steinitz de la Apertura Española.
La secuencia principal de movimientos de la Variante Steinitz de la Defensa Francesa es 1. e4 e6 2. d4 d5 3.Cc3 Cf6 4.e5 Cfd7…, y deja a las piezas negras en una posición ‘sana’.
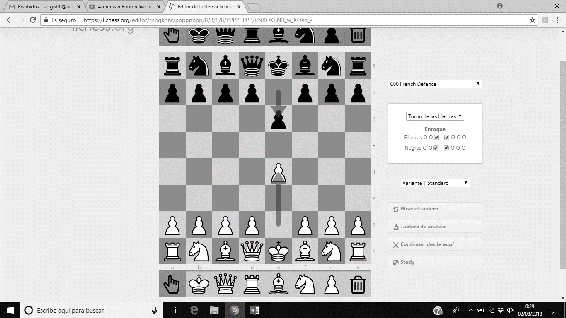
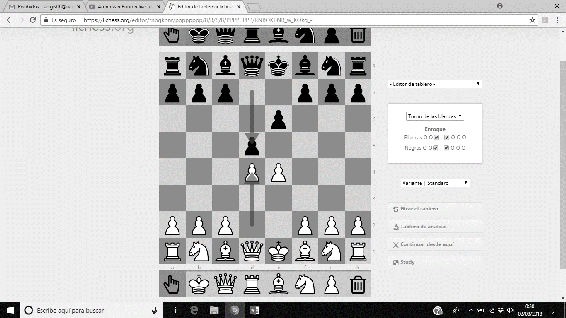
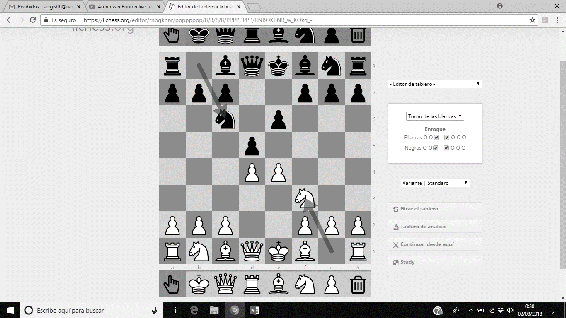
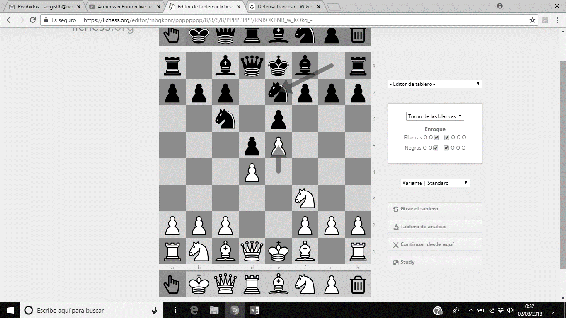
Imágenes 18-21: Secuencia de la Variante Steinitz de la Defensa Francesa.
Wilhelm Steinitz no dedicó su vida (de una forma oficial) a las matemáticas (como sí que hizo Anderssen), pero, sin duda, sus grandes facultades en ellas hicieron de él un fortísimo jugador, y del que se guarda el recuerdo de ser el primer campeón oficial de ajedrez del mundo. Campeones mundiales posteriores, tales como Emanuel Lasker, Harry Pillsbury, Rubinstein, Capablanca o Euwe, entre otros, han tenido siempre como referencia a este genial jugador de ajedrez.
Emanuel Lasker (Berlinchen, Prusia, 24 de diciembre de 1868 - Nueva York, 11 de enero de 1941) fue un gran ajedrecista y un brillante matemático alemán.
Se graduó en matemáticas en la Universidad de Berlín.
Aportó conocimientos al campo del Álgebra Abstracta, y colaboró en la demostración del Teorema de Lasker-Noether, cuyas aplicaciones son notorias a la Teoría de la Relatividad de Einstein, con quien mantuvo una gran amistad.
Imagen 22: Emanuel Lasker.
En su juventud, Lasker demostró unas grandes habilidades tanto en el ajedrez como en matemáticas. Por ello, fue enviado a cursar estudios superiores de matemáticas en la prestigiosísima Universidad de Berlín.
Con poca edad, logró vencer en pequeños torneos secundarios, y obtuvo beneficios monetarios apostando en partidas que él disputaba en cafeterías. Sin embargo, nunca descuidaría los estudios en matemáticas, sino que los compaginó de forma perfecta.
En 1889 obtuvo un triunfo en un torneo regional, con una puntuación del 100%, lo que le valió el título de maestro, y le permitió ser invitado a torneos internacionales. Comenzó en el Torneo de Ámsterdam (1889), donde acabó en segunda posición.
Entre los años 1889 y 1892, derrotó a varios rivales de talla mundial en duelos particulares. Finalmente, tras terminar su carrera matemática, se instaló en Londres para seguir mejorando en su nivel ajedrecístico.
En 1893, retó al campeón, Wilhelm Steinitz, y éste aceptó el reto por el cetro mundial. Entre 1893 y 1894, y tras un inicio de duelo realmente igualado, la balanza se inclinó del lado de Lasker, que obtuvo así el título de campeón del mundo de ajedrez.
Tras la conquista del título mundial, logró retenerlo hasta el 1920, donde claudicó frente al genial jugador cubano José Raúl Capablanca. Sin embargo, nada más lejos de comenzar el declive de su carrera tras la pérdida del título, Lasker mantuvo un nivel altísimo de juego, no logrando, eso sí, recuperar de nuevo la corona, pero sí venciendo en duelos particulares a jugadores realmente fuertes como Max Euwe.
Posee, además, el reconocimiento de haber sido poseedor del título mundial más tiempo que ningún otro jugador de ajedrez.
Emanuel Lasker tuvo una aportación elevada al ajedrez, entre las que se incluyen teorías de aperturas, sistemas de defensa, y diversos análisis para posiciones de finales de partidas con muy pocas piezas, donde era un extraordinario jugador.
Dio nombre a la famosa Defensa Lasker del Gambito de Dama, la cual proporcionaba un contrataque fuerte, y provocaba la promoción de un peón en la séptima fila. Es considerada una de las mejores defensas contra la usual apertura del Gambito de Dama. La secuencia completa, a partir de un Gambito de Dama usual viene dada por 1. d4 d5 2. c4 e5 3. dxe5 d4 4. e3 Ab4 5. Ad2 dxe3…
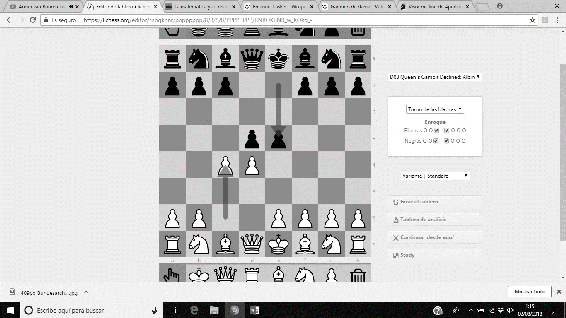
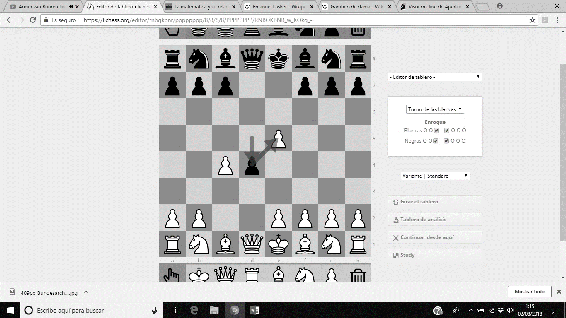
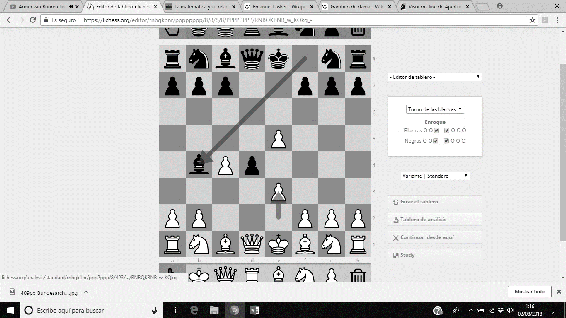
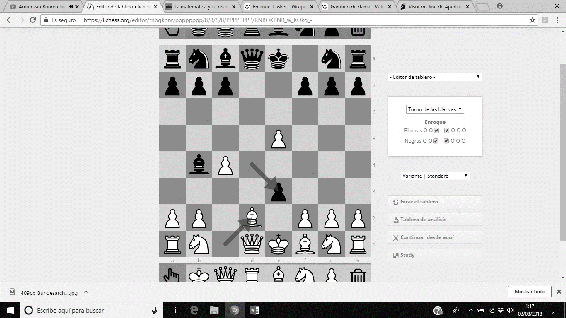
Imágenes 23-26: Secuencia de la Defensa Lasker del Gambito de Dama.
También utilizó una implacable defensa contra el Gambito Evans, una apertura realmente utilizada en la Escuela Romántica de Ajedrez (no tanto en la actualidad). Esta secuencia está considerada la mejor respuesta posible frente a esta apertura. La secuencia de dicha defensa viene dada por 1.e4 e5 2.Cf3 Cc6 3.Ac4 Ac5 4.b4 Axb4 5.c3 Aa5 6.d4 d6.
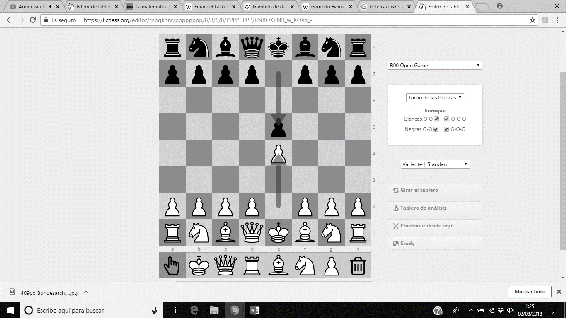
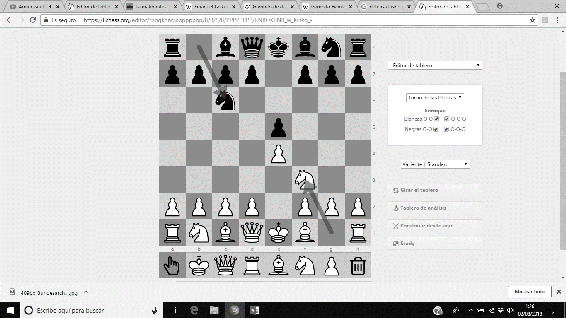
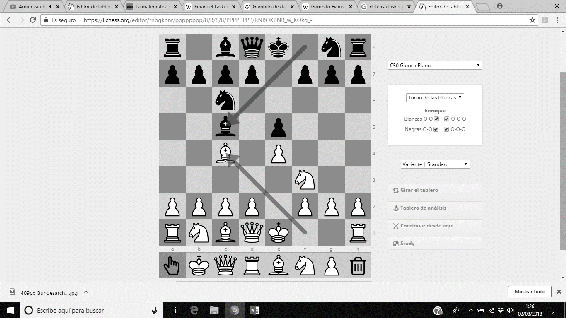
Imágenes 27-32: Secuencia de la Defensa Lasker contra el Gambito Evans.
Emanuel Lasker es uno de los mayores referentes en el ajedrez y matemáticas de toda la historia. Supo utilizar de forma fabulosa sus cualidades en ambas disciplinas.
Machgielis (Max) Euwe (20 de mayo de 1901-26 de noviembre de 1981) fue un matemático y un ajedrecista holandés, nacido cerca de Ámsterdam, donde se licenció en Matemáticas.
Durante su vida, no dejó de lado la matemática aplicada, y fue profesor de matemáticas en Róterdam y en Ámsterdam.
Imagen 33: Max Euwe.
Max Euwe fue un prodigio matemático, y un jugador realmente aventajado de ajedrez. Así lo demuestra el hecho de que, con tan sólo 20 años, lograra obtener el campeonato de los Países Bajos de una forma brillante. Logró retener dicho título durante 14 años, hasta 1935.
A finales de ese mismo año, sus logros en otros torneos de prestigio internacional le sirvieron para obtener el derecho a competir por el título mundial de ajedrez que, hasta entonces, lo ostentaba el gran maestro ruso Alexander Alekhine. Tras 30 partidas disputadas en trece ciudades diferentes, Euwe logró ser campeón mundial por primera vez en su vida.
Tuvo el título en su poder durante dos años, hasta que en 1937 perdió el título en el combate de revancha que disputó contra el propio Alexander Alekhine, quien retendría el título hasta su muerte en 1946.
Siguió compitiendo, años más tarde, en otros torneos de renombre, obteniendo posiciones de mérito, pero sin volver a tener la opción de recuperar el título.
Fue presidente de la FIDE (Federación Internacional de Ajedrez), principal estamento oficial en el mundo del ajedrez, entre 1970 y 1980.
Merece la pena destacar dos aportaciones. Una de ellas en el ajedrez teórico, y otra en la aplicación de sus conocimientos matemáticos al problema de las partidas infinitas utilizando diversos estudios sobre la secuencia Thue-Morse.
Aportó luz sobre una defensa del Gambito de Rey, conocida como la Defensa Euwe, cuya secuencia es 1.e4 e5 2.f4 exf4 3.Cf3 Ae7 4.Ac4 Cf6…
Imágenes 34-37: Secuencia de la Defensa Euwe contra el Gambito de Rey.
Pero donde se puede ver la capacidad de aplicar sus conocimientos matemáticos a la disciplina del ajedrez es en el desarrollo de la conocida como secuencia de Thue-Morse para demostrar que determinadas reglas de la FIDE con respecto al final de partidas deberían cambiar.
La sucesión de Thue-Morse es una sucesión de términos con dígitos binarios (0 o 1) de forma que, comenzando con el 0, se concatenan segmentos de la misma longitud que el que se tiene en el momento, y de manera que los términos de dichos segmentos concatenados nuevos sean el llamado Complemento Booleano de la secuencia original. Por el Complemento Booleano de un dígito binario se entiende el valor contrario a dicho dígito, dado por
Existen multitud de definiciones para dicha sucesión. Entre ellas, merece la pena mencionar aquella que hace uso de una relación de recurrencia (son sucesiones en las que los términos se van obteniendo según los términos anteriores que se disponen hasta el momento), cuya definición viene dada por
La aplicación de dicha sucesión, y de los estudios de Max Euwe se centraron en cambiar una norma de la FIDE, en la que hasta 1929, citaba que una partida acabaría en tablas si se repiten las mismas jugadas tres veces consecutivas. Esto servía para dar por terminadas partidas que parecían no acabar. Sin embargo, Euwe, probó que esto no siempre era así, sino que existían partidas en las que, con tal regla de tablas, podrían no terminar nunca. Este hallazgo sirvió para que la FIDE incorporara al reglamento una nueva normativa de tablas conocida como ‘la regla de los 50 movimientos’, en los que, si no se captura una pieza, o ningún peón avanza, la partida también acaba en tablas, cerrando así la opción de que una partida no acabara nunca.
Mijaíl Moiséyevich Botvínnik (17 de agosto de 1911 - 5 de mayo de 1995) fue un jugador de ajedrez soviético, uno de los mejores de la historia.
Conocido como ‘El Patriarca del Ajedrez Soviético’.
No fue matemático de profesión, era Ingeniero Eléctrico y contribuyó al desarrollo de las primeras computadoras de ajedrez.
Imagen 38: Mijail Botvinnik.
Botvinnik aprendió a jugar al ajedrez a la temprana edad de 12 años, e instantáneamente, apostó por aprender a jugar a nivel de gran maestro.
En 1924, ganó torneos locales y regionales, y hasta se vio obligado a mentir sobre su edad (aumentándola en 3 años) para poder acceder legalmente a la Asamblea de Ajedrez de Petrogrado.
Su primera hazaña llegó con tan sólo 14 años, en 1925, cuando venció al jugador cubano José Raúl Capablanca en una exhibición de partidas simultáneas.
Con 16 años, en 1927, debutó en el Torneo Nacional de la URSS, obteniendo un gran quinto puesto, algo muy brillante para un debutante.
Durante los siguientes años no participó en torneos de una forma frecuente, sino que compaginó sus estudios en Ingeniería, con la mejora y el aprendizaje de la teoría del ajedrez. Esto le sirvió para ganar con 20 años, su primer Torneo Nacional de la URSS, en 1931. Logró este título cinco veces más durante su carrera.
Con 24 años, Botvinnik estaba considerado uno de los tres mejores jugadores de esa época, y sus excepcionales participaciones en Torneos Internacionales, como los de Moscú en 1935, el de Nottingham en 1936, o un sobresaliente tercer puesto en el famoso Torneo de AVRO, uno de los mejores del planeta, disparaban su popularidad dentro del mundo del ajedrez.
Tras la muerte de Alekhine, Botvinnik disputó el Torneo por el campeonato mundial, en 1948, entre las ciudades de La Haya y Moscú, en el cual venció, y obtuvo por primera vez tan ansiado premio.
Logró mantener el título de campeón mundial frente a jugadores de la talla de David Bronstein (en 1951) y Vasili Smyslov (en 1954), en los que fueron dos de los combates más igualados que se recuerdan (ambos duelos acabaron empatados a 12, lo que permitía al campeón retener el título).
En 1957 perdió el título contra Smyslov, pero sólo unos meses después fue capaz de recuperarlo, venciendo en el combate de revancha.
Repitió la historia contra el gran Mijail Tal, cayendo en 1960, pero recuperando el título sólo un año después en el combate de revancha.
En 1963, perdió definitivamente el título de campeón mundial frente a Tigran Petrosian.
A comienzos de la década de 1970, Botvinnik fue progresivamente abandonando el ajedrez de alta competición, para poder combinar su espectacular nivel ajedrecístico con los conocimientos que él tenía en Ingeniería Eléctrica, algo que, junto con el uso de matemática aplicada, sirvieron para desarrollar varios avances importantísimos en materia de programas y módulos de ajedrez.
Fundó, además, una escuela para jóvenes talentos en el mundo del ajedrez. En dicha escuela, fueron alumnos nada más y nada menos que dos de los mejores jugadores de ajedrez de todos los tiempos: Gary Kasparov y Anatoly Karpov.
Entre sus aportaciones podemos destacar, sobre todo, un incesante trabajo en el desarrollo de programas de ajedrez. En los años cincuenta, las ideas más frecuentes sobre la creación de dichos módulos eran las de la ‘fuerza bruta’ o de Tipo ‘A’, es decir, recorrer todas (o la gran mayoría) de las posiciones posibles que surgen tras cada variante y analizarlas todas. Se debía dotar, por tanto, a las computadoras de un procesador muy rápido para poder analizar en un tiempo razonable un número admisible de variantes. El problema radica en que, si se supone que tras cada movimiento existen entre 25 y 30 posibles respuestas, analizando a una profundad de 6, las combinaciones que surgen son de un valor comprendido entre y algo inasumible. Por tanto, comenzaron a surgir las ideas de Tipo ‘B’, donde no se analizarían todas las variantes, sino un número reducido de ellas según las partidas almacenadas en ‘memoria’ o según diversos criterios ajedrecísticos (se verá en el capítulo 4). Así, se ahorraría mucho tiempo computacional, pero con gran frecuencia se pasarían por alto jugadas o variantes más ventajosas que otras, al no estar en aquella época la teoría del ajedrez tan desarrollada como está en la actualidad. Por esto mismo, Botvinnik centró sus últimos años en la creación de diversos algoritmos que combinaran ambas ideas de forma adecuada, pero más orientadas a las de Tipo ‘B’. Sus estudios sobre el tema le llevaron a ser galardonado en el año 1991 con el título de Doctor Honorífico en Matemáticas por la Universidad de Ferrara (Italia).
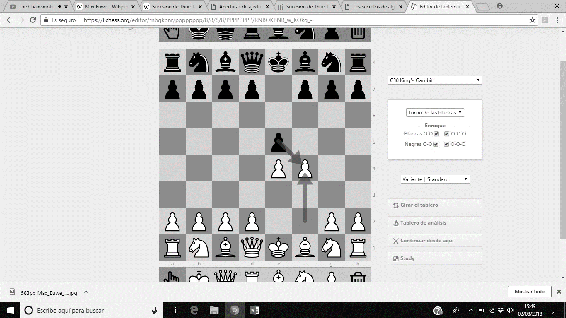
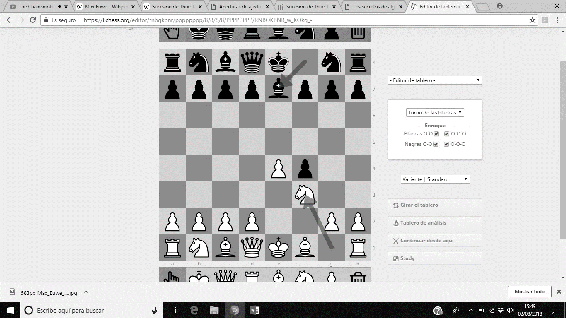
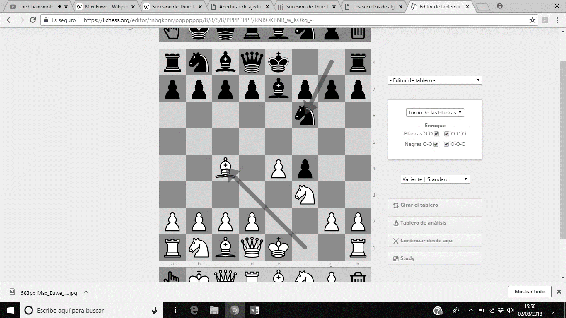
Entre las aportaciones a la teoría ajedrecística, realizó numerosos estudios, y un gran número de análisis a diversas posiciones (era un gran analista). Destaca, sobre todo, el Sistema Botvinnik de la Defensa Semieslava, que permite con una gran eficiencia, dotar a las piezas negras de iniciativa. La secuencia usual es 1. d4 d5 2. c4 c6 3. Cf3 Cf6 4. Cc3 e6 5. Ag5 dxc4 6. e4 b5…
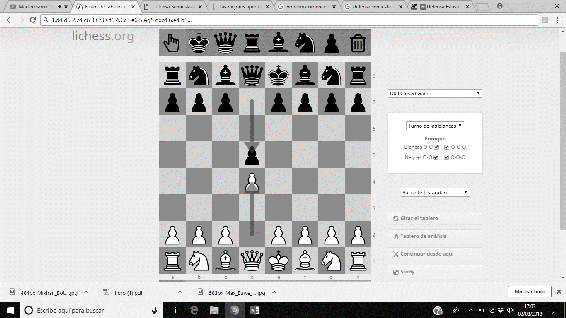
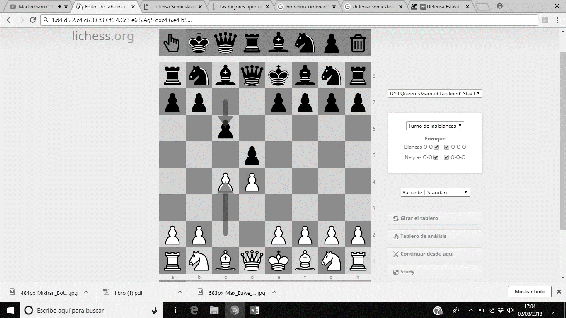
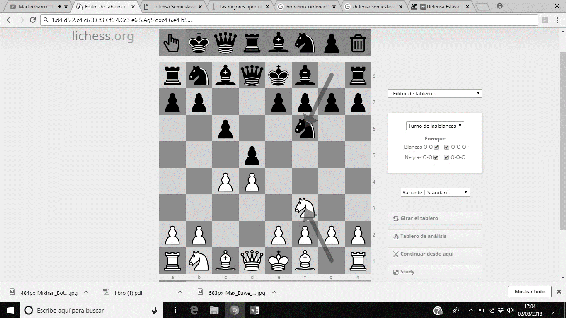
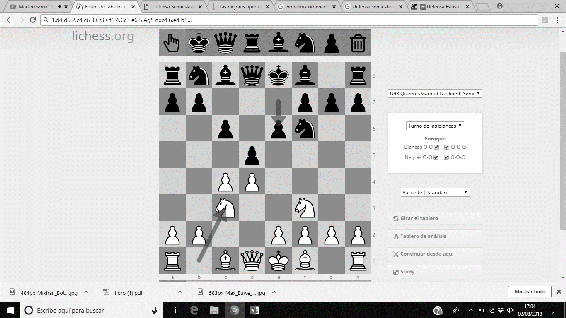
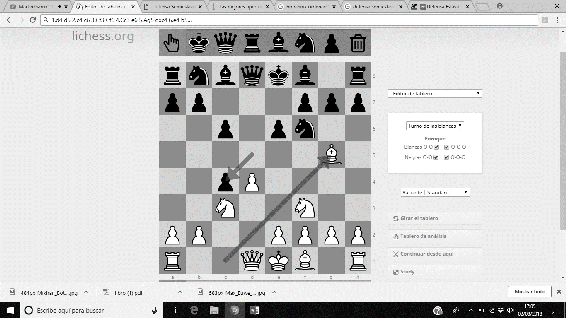
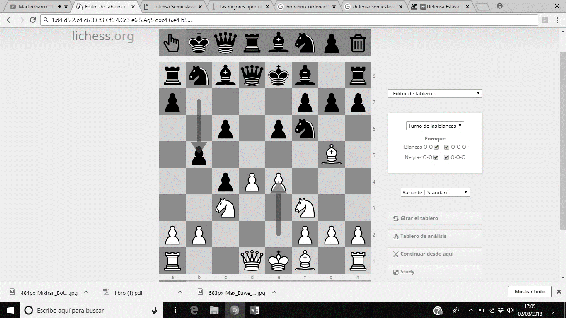
Imágenes 39-44: Secuencia del Sistema Botvinnik a la Defensa Semieslava.
Como se ha podido ver, la lista de grandes ajedrecistas que, a la vez hayan sido matemáticos de una forma profesional, o bien hayan tenido una gran influencia en matemáticas, incluye nombres propios realmente importantes, y cualquier aficionado de este juego podrá reconocer sin muchos problemas cualquiera de estos cinco jugadores mencionados.
No obstante, existen muchos más jugadores, pero no llegaron a la élite del ajedrez como lo hicieron estos. Mención aparte merece el suizo Leonhard Euler, quien no fue un jugador profesional de ajedrez, pero logró resolver diversos problemas matemáticos asociados al ajedrez (por ejemplo, el Problema del Caballo), proporcionando además una certera aproximación de cuál sería el número de soluciones posibles. Euler trató de aplicar sus conocimientos de matemáticas al ajedrez para probar que ambas disciplinas están muy relacionadas.
Recientemente, y sobre todo en últimos años, la lista de jugadores profesionales de ajedrez no incluye en su élite a matemáticos. Esto es motivado, quizá, por la profesionalización del ajedrez, el cual exige a los jugadores la total y completa dedicación del tiempo a la disciplina. Antiguamente, esto no era así, como ya hemos visto, con jugadores que alternaban sus estudios en matemáticas o similares con sus respectivas carreras en el mundo del ajedrez.
En definitiva, se ha podido comprobar que, en el mundo del ajedrez, las matemáticas siempre han sido algo imprescindible, tanto en el desarrollo teórico del ajedrez, el estudio analítico de diversas variantes, y las recientes mejoras en las ciencias de la computación.
Sin mencionar nada concreto, está probado a lo largo de la historia, que jugadores con estudios en ciencias, y, en especial, en matemáticas, tienen una notable facilidad superior a la hora de aprender las reglas, y de obtener jugadas interesantes de este juego. Es por ello, que la mayor parte de los jugadores de élite de los últimos siglos han tenido que ver en mayor o menor medida con los estudios en ciencias, pues sin duda, ayudan en el correcto desarrollo del ajedrez. Incluso hace algunos años, en determinados países como la URSS, el ajedrez era una asignatura más en el colegio como complemento, lo que sin duda potenciaba la capacidad en matemáticas.