 Los inicios del mundo digital
Los inicios del mundo digital Los inicios del mundo digital
Los inicios del mundo digitalSeguramente no habrás oído hablar nunca de Claude Shannon. O quizás sí, a lo mejor te suena el nombre, pero poco más. Y no debería ser así. A este matemático, ingeniero electrónico y criptógrafo le debemos las bases de lo que hoy llamamos «mundo digital», de la digitalización. Sí, todo tiene un padre o una madre, y en este caso el padre es el desconocido Shannon.
Cuando trabajaba en los laboratorios Bell, donde entró muy joven, Shannon inventó un sistema de circuitos eléctricos que recogían los enunciados de Boole y, en concreto, su lógica binaria y los valores lógicos «1» y «0» para denotar los valores discretos «verdadero» y «falso». Así, enunció que, en un circuito eléctrico, cuando dos interruptores en serie estaban conectados con una puerta «OR», bastaba con que uno de ellos estuviera en «1», es decir, encendido, para que la electricidad circulara. En cambio, si estaban conectados con una puerta «AND», ambos tenían que estar en «1», es decir, encendidos, para que esto sucediera. Estos enunciados, que hoy en día parecen triviales, supusieron una revolución cuando se publicó su tesis A Symbolic Analysis of Relay and Switching Circuits. Era el año 1938.
Pero lo que Shannon enunció en su tesis no era más que el paso previo a los postulados de la obra por la que acabaría siendo conocido: A Mathematical Theory of Communication, publicada en 1947. En ella decía que se podían transmitir datos mediante el circuito eléctrico que él mismo había desarrollado, es decir, que todo podía reducirse a unos y ceros. Por primera vez, lo importante no era la información que se transmitía, ni su significado, ni su propósito, sino la cantidad de esta. ¿Y cómo se medía esta cantidad? Shannon propuso que los datos debían medirse en bits, que representan los valores discretos de cero o uno. La denominación no era suya, sino de su colega de los laboratorios Bell, John Tukey, que la había acuñado como una contracción de la frase en inglés «binary digit», ‘dígito binario’.
Esta revolucionaria idea fue adoptada gradualmente por los ingenieros de comunicaciones y estimuló la tecnología que condujo a la era de la información que hoy conocemos. Todas las comunicaciones actuales se miden en bits por segundo, lo que Shannon definió como «capacidad del canal». Su teoría también generó que se emplearan bits para medir el almacenamiento de los ordenadores, las transmisiones de voz y otros datos.
Más allá del trabajo de Shannon, de sus investigaciones y, sobre todo, de cuándo lo pensó, lo que nos debe llamar la atención es cómo sus ideas nos hicieron pasar de un mundo analógico a uno digital. Esto nos permite llevar a cabo un sencillo ejercicio. Vamos a intentar definir el concepto «digital». Sí, podemos caer en la tentación de quedarnos con la primera acepción del diccionario de la Real Academia Española y decir que es aquello «perteneciente o relativo a los dedos». Como broma estaría bien, pero está claro que esa no es la definición que corresponde en este contexto. Por suerte, el diccionario nos ofrece otras acepciones: «referente a los números dígitos» o «que se realiza o transmite por medios digitales», que creo que podríamos tomar como base para profundizar un poco más. A esto podemos añadir la parte que dice «que crea, presenta, transporta o almacena información mediante la combinación de bits». Dígitos, bits, medios digitales… Queda claro que el concepto «digital» es difícil de definir.
Quizás una buena forma de abordar el problema es empezar por el antónimo: «analógico». En nuestro contexto, digital es todo aquello que no es analógico. Pero ¿cuál es la diferencia entre ambas cosas?
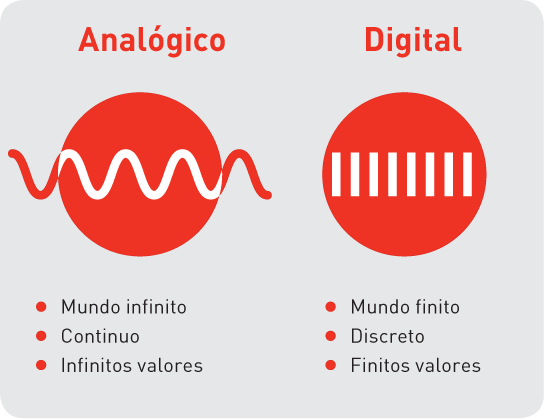
Lo que nos interesa de esta contraposición es la idea de que con lo digital pasamos de un mundo infinito a otro finito. Todo lo analógico es continuo y una cosa continua tiene infinitos valores. En cambio, lo digital es discreto, es «1» o «0», es decir, tiene un número finito de valores. Vamos a poner un ejemplo cotidiano para verlo más claro.
Imaginemos que queremos hacer un pastel y que, para ello, necesitamos 2 tazas de harina, 1 taza de leche y 2 huevos. La parte de la harina es sencilla. Llenamos la taza de harina, volcamos el contenido en el bol donde haremos la mezcla y repetimos el proceso otra vez. Para la leche, algo parecido. Llenamos la taza hasta el límite y volcamos el contenido en el bol. Pero al llegar a los huevos la cosa cambia. Lo que debemos hacer es abrir la huevera, sacar 2 huevos, romperlos y echar la yema y la clara en el bol de la mezcla.
Fíjate en lo que ha pasado. La leche y la harina la hemos medido en tazas con el único requisito de que estuvieran llenas. Esto es una aproximación. En cambio, los huevos los hemos contado. Eran 2. No eran 4, 1 o 9 y ¾. Eran 2. La primera medida era analógica. La segunda, digital. Cuando cuentas algo, obtienes un resultado exacto; en cambio, cuando mides algo, obtienes un resultado aproximado.

Antigua cámara analógica

Móvil actual con cámara digital incorporada
Pongamos otro ejemplo: qué prefieres, ¿enfrentarte a n problemas o a infinitos? ¿A infinitas cosas o a un número finito de ellas? En el terreno de la gestión esto está muy claro: lo que buscamos, queremos, deseamos y soñamos es vivir en un mundo finito. Contable. Palpable. Y el motivo es muy sencillo: lo finito es gestionable, transformable, intercambiable, medible… Por eso, las empresas actuales se han lanzado al proceso de digitalización. Algunas, incluso, han convertido sus bienes en digitales. Un ejemplo claro de esto es la industria musical.
Shannon tenía razón: buscamos un mundo finito y la revolución digital ha llegado a las empresas. La tecnología está ya en todas partes y esto ha generado un auténtico cambio. Es lo que hemos denominado «transformación digital».
Sin embargo, no todo es de color de rosa en este mundo digital. A menudo, lo digital está lleno de voces discordantes, mitos y motivos para el escepticismo. Por ejemplo, hasta enero de 2018, todas las personas que alcanzaban la cima de las montañas más altas del Himalaya debían, a su vuelta, visitar a Elizabeth Hawley. Esta estadounidense no había subido nunca al Everest, pero se había autonombrado «jueza de la montaña». Hawley se enamoró a primera vista de la imponente cordillera en su primera visita a Nepal a finales de la década de 1950; finalmente, decidió instalarse en Katmandú y, desde 1963, se dedicó a documentar los ascensos a la montaña.
Cualquier escalador podía decir que había llegado a las cimas más altas del mundo, por eso tenía que demostrarlo. Hawley tenía que verlo. Mediante fotos, descripciones exactas del recorrido, detalles concretos… Fue ella quien cuestionó en 2009 que la surcoreana Oh Eun-sun hubiese alcanzado la cima del Kanchenjunga, lo que la habría convertido en la primera mujer en conseguir los catorce «ocho miles». Que Howley no validara la última de las catorce cimas de la surcoreana hizo que el honor de ser la primera mujer en alcanzar dicha hazaña recayera en la española Edurne Pasabán.
¿Por qué cuento esto? Porque, a veces, en el mundo digital hacemos de señora Hawley. No nos creemos lo que nos cuentan, dudamos. Nos dicen que se puede hacer esto o lo otro, pero, hasta que no lo vemos, no nos lo creemos. Ahora bien, lo que no podemos hacer en ningún caso es anticiparnos, saber algo antes de que pase. La señora Hawley no podía prever si un escalador alcanzaría o no determinada cima. Y lo mismo sucede con la transformación digital. Podemos llegar a entender qué pasa, pero no anticiparnos. Y esto es lo complicado del mundo digital en el que vivimos, en el que resulta tremendamente importante ser capaz, no solo de entender qué quiere decir «digital», sino de saber afrontar, trabajar y anticipar todo el impacto y la respuesta que este conlleva. Y esto es lo que vamos a tratar de descubrir en este libro.
