1.1. Actualización simple
1.1.1. El descuento comercial
1.1.2. El descuento matemático
1.2. Actualización compuesta
1.2.1. El descuento compuesto
1.3. Rentas constantes, variables y fraccionadas
1.3.1. Descripción
1.3.2. Variables que intervienen
1.1. Actualización simple
Introduciremos el tema de la actualización simple planteando una cuestión, ¿el valor de un euro hoy es mayor o menor que su valor dentro de un tiempo? El tiempo es una cuestión importante en lo que respecta al valor del dinero o capital. Con estas dos variables en juego, capital y tiempo, solo existen dos posibles movimientos en el tiempo, que podemos realizar con el capital, llevarlo hacia delante o traerlo hacia atrás.
A la operación de calcular el valor del capital actual en una fecha futura es decir, adelantar su valor en el tiempo llevándolo a un momento futuro, es lo que conocemos por capitalizar o diferir. A la operación contraria de calcular el valor del capital futuro es decir, en una fecha futura, trayéndolo en el tiempo al presente es lo que conocemos por descontar o actualizar.
Representación gráfica
Vamos a realizar una representación gráfica de los conceptos capitalizar o diferir y descontar o actualizar:
–Capitalizar o diferir, partimos del capital inicial C0 y calculamos Ct que es el valor futuro que tendrá C0. Este cálculo nos permite conocer el valor del capital en el momento presente y situar su valor en un momento fututo.

Esquema de la capitalización
–Descontar o actualizar, partimos del capital en una fecha futura Ct y calculamos C0 que es el valor actual o presente que tendría Ct. Este cálculo nos permite conocer el valor del capital en un momento del futuro y situar su valor en el momento presente.

Esquema del descuento del capital
Importante
La actualización simple o de descuento es una operación financiera que calcula el valor de un capital futuro sustituyéndolo por otro con vencimiento presente. Consiste en la operación contraria o inversa a la capitalización simple, desde el punto de vista matemático.

Tipos de actualización simple
Existen dos tipos de actualización o descuento simple:
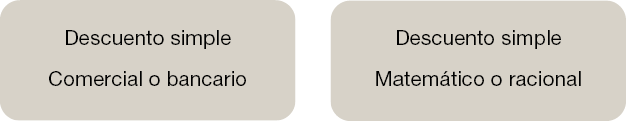
Recuerda
Hemos definido en qué consiste la actualización simple y dentro de ella nos encontramos con el descuento comercial o bancario y el descuento matemático o racional.
En los siguientes puntos definiremos y explicaremos en qué consiste el descuento comercial o bancario y el descuento matemático o racional.

El Capital actual en el momento presente será C0 y siempre será inferior al Capital futuro Cn, es decir descontar el capital y traerlo al momento presente tiene un coste y es la diferencia entre C0 y Cn. Esta diferencia es lo que denominamos descuento D. Su expresión matemática sería:
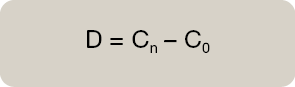
Sabías que
El descuento es la disminución de interés que experimenta el capital futuro al ser adelantado en el tiempo, consecuencia de ese adelanto se produce esa disminución. Matemáticamente sería:


1.1.1. El Descuento Comercial
Partimos de la idea de que actualizar o descontar es la operación financiera contraria a la capitalización, consistente en calcular el valor de un capital futuro en el momento presente. Dentro de este tipo de operaciones financieras se encuentra el descuento comercial o bancario y el descuento matemático o racional.
Definición
El descuento comercial o bancario consiste en anticipar la entrega de un capital, que deberíamos cobrar o tener en un futuro y queremos cobrar o tener en el momento actual.

–Descripción del proceso
1.Empresa que necesita liquidez y tiene pendientes cobros de clientes.
2.La empresa acude a una entidad financiera para realizar el Descuento Comercial.
3.La entidad estudia el caso y ofrece a la empresa las condiciones del descuento comercial.
4.Si la empresa acepta obtiene la liquidez necesaria a cambio de unos costes económicos.
Este tipo de descuento generalmente es utilizado por las empresas y lo realizan las entidades financieras. Encontramos pues dos partes:
|
La empresa |
Necesita liquidez y tiene derechos de cobro sobre sus clientes. Necesita descontar estos derechos de cobro futuros y tener liquidez en el momento actual. |
|
La entidad financiera |
Ofrece el descuento comercial para dar liquidez a la empresa. |
La empresa en su actividad habitual realiza operaciones de venta a sus clientes, ya sea de bienes o servicios, y en ocasiones ofrece un crédito, es decir, un aplazamiento del pago de esa venta. Si la empresa se encuentra en la necesidad de disponer de ese dinero en el momento actual puede dirigirse a una entidad financiera que realice estos servicios financieros y solicitar el descuento comercial de ese crédito. A través de este descuento comercial la entidad financiera adelanta a la empresa el importe de ese crédito pendiente de su cliente que aún no ha vencido. La entidad financiera se encargará cuando llegue el momento del vencimiento del crédito de cobrárselo al cliente de la empresa, no asumiendo ésta ningún riesgo.
La empresa justificará a la entidad financiera debidamente la existencia de este crédito a través de letras de cambio, pagarés, recibos o facturas obteniendo, si se lleva a cabo la operación, la liquidez necesaria en el momento actual. La entidad financiera, realizados los cálculos, adelantará y entregará el importe resultante y a cambio del cobro de una comisión de gestión y los intereses generados.
La entidad financiera es libre de aceptar este tipo de operaciones, habitualmente se realizan estudios de solvencia e incluso se llegan a solicitar, dependiendo del caso y del importe, avales o garantías para aceptar la operación.
Existen dos tipos de descuentos comerciales o bancarios que son de los más utilizados en el mercado español. Son:
|
Línea de descuento |
Operación periódica, permanente y repetitiva entre la empresa y la entidad financiera. La entidad financiera marca un límite de créditos a descontar por parte de la empresa una vez que se ha analizado en factor de riesgo. |
|
Bancario simple o circunstancial |
Operación en la que se negocia el descuento de uno o varios créditos de manera individual y puntual. |
Recuerda
El descuento comercial simple es la operación inversa a la capitalización, en el descuento comercial simple calculamos los intereses que pagaremos por adelantar el capital al momento actual. Descontar conlleva adelantar el capital futuro a un momento presente y eso conlleva un coste.

Vamos a realizar el cálculo del descuento comercial. Primero presentaremos las variables que van a intervenir:
–Dc: Descuento comercial.
–Cn: Valor Final o Nominal.
–C0: Valor actual, inicial o efectivo.
–i o d: interés de la operación.
Ya tenemos las variables o elementos que intervienen en el cálculo del descuento comercial. La operación de descuento comercial genera unos intereses que serán calculados sobre el nominal Cn y un el tipo de interés o descuento que tenga la operación.
Proceso de cálculo

Cálculo del Descuento (Dc) suma de intereses que se van generando en los periodos de vamos adelantando, periodos descontados, que denominaremos (n) sobre el capital que vamos a descontar.
Matemáticamente:
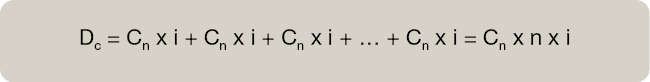
Cálculo del Capital Inicial C0 es la diferencia entre el Capital final (Cn) y el Descuento (Dc) que hemos calculado con la fórmula matemática anterior.
Sería:
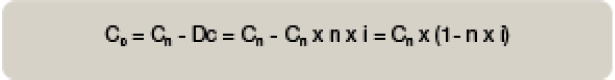
Ejercicio práctico
Una empresa con necesidades de liquidez acude a la entidad financiera para anticipar una deuda de su cliente por importe de 10.000 euros. El vencimiento de esta deuda es dentro de un año y la entidad financiera le ofrece un tanto de interés anual del 10%. Vamos a calcular el Capital inicial C0 y el descuento de la operación Dc.
–Cn = 10.000 euros.
–i = 10%.
–n = 1 año.
Dos opciones para su cálculo:

La principal ventaja para la empresa es obtener liquidez y no esperar a que llegue el vencimiento de los cobros a sus clientes, pero el coste en ocasiones puede llegar a ser alto. Otra ventaja es que la empresa elimina costes en cuanto a la gestión de cobros que es desarrollada por la entidad financiera.
La entidad financiera no asume ningún tipo de riesgo ya que cuando llega el momento del vencimiento del pago gestionará esta operación con el cliente de la empresa y si este no realiza el pago la entidad financiera reclamará a la empresa la totalidad del crédito y una comisión.
Los costes de esta operación son la comisión de gestión y los intereses generados. La comisión de gestión incluye habitualmente la gestión de cobro al cliente y el servicio prestado, dependerá de las condiciones pactadas en el contrato formalizado entre la empresa y la entidad financiera. Los intereses generados se calculan por el tiempo que media entre el momento actual y el momento en que vencía el crédito.
Por lo tanto, este tipo de operación presenta una serie de ventajas y de inconvenientes que tendremos que valorar para elegir entre este tipo de operación u otra que presente otro tipo de ventajas e inconvenientes.
Ventajas
–Flexibilidad
Permite obtener los recursos que necesita la empresa adaptándose a su medida, siempre y cuando la entidad financiera acepte la operación. Podemos negociar con la entidad una línea de descuento abierta. Al tener esta línea abierta solo tenemos que enviar la remesa de documentos que queremos que sean descontados por la entidad.
–Rapidez
Al contar con esa línea de descuento abierta en la entidad financiera la liquidez se obtiene de manera muy rápida. Por lo general aunque no dispongamos de esa línea abierta suele ser una operación rápida.
–Rentabilidad
Para la entidad financiera es una operación en la que los intereses y comisiones se cobran por adelantado. Una vez que la empresa entrega los documentos a descontar y la entidad realiza la operación de descuento entrega a la empresa la cantidad descontada y la entidad ingresa los costes de la operación, aún el vencimiento de los documentos no ha ocurrido.
Inconvenientes
–Riesgos de sobrefinanciación
Una vez que se realiza el descuento no hay forma de retroceder la operación por lo que, debido a su elevado coste, tendremos que realizar una previsión muy exhaustiva de necesidades de liquidez.
–Costes
Dependen de la negociación con la entidad financiera pero los más usuales son costes de la operación, costes de los intereses y comisiones. Uniendo todos estos costes el descuento comercial puede salir caro para las empresas.
–Control
Se debe realizar un control y vigilancia sobre los vencimientos de los créditos que se han descontado. Dependerá del acuerdo con la entidad financiera pero en todo caso si hay algún impago, la entidad nos reclamará la cantidad descontada y además ese impago tendrá unos costes adicionales.
Sabías que
Existe una operación llamada redescuento, en ella son las entidades financieras, una vez realizado el descuento a las empresas, las que van en busca de liquidez a otras entidades bancarias realizando otra operación de descuento, de ahí la expresión redescuento.

1.1.2. El Descuento Matemático
Seguimos dentro de la actualización simple hemos visto el descuento comercial y ahora nos centramos en el descuento matemático o racional.
Definición
El descuento matemático se obtiene aplicando un tipo de interés establecido sobre el Capital efectivo en el momento presente. La tasa de descuento o tipo de interés fijado se calcula sobre el capital en el momento actual, al inicio del periodo.

Una de las desventajas o inconvenientes que presentaba el descuento comercial eran sus elevados costes. El cálculo del descuento comercial es el equivalente a la inversa de la capitalización simple. Partimos de la misma fórmula matemática.
Representemos este descuento gráficamente. La curva que obtenemos en el descuento matemático o racional simple no es una recta, sino que se curva de manera descendiente. Es una curva asintótica al eje de la x y tiende a 0 aunque nunca será un valor negativo, al contrario de lo que puede ocurrir con el descuento comercial.
Comparemos ambos gráficos.
Descuento matemático o racional simple
Cn

Co
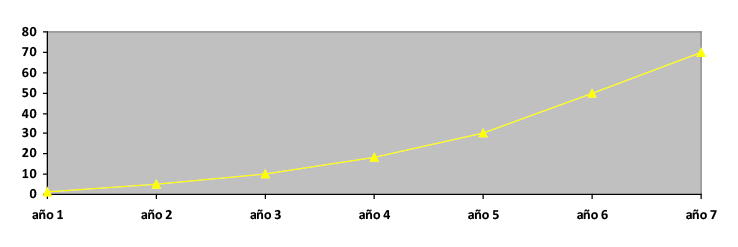
En el eje de ordenadas se representa el efectivo obtenido y en el eje de las abscisas se representa la duración temporal de la operación.
La tasa de interés o de descuento en el descuento comercial se calcula sobre el nominal o capital final Cn mientras que en el descuento matemático o racional se realiza sobre el capital inicial. Podemos ver que el descuento matemático es más interesante a simple vista para la empresa.
Recuerda
El descuento matemático se clasifica dentro de la actualización simple junto con el descuento comercial.

Vamos a desarrollar el cálculo del Descuento matemático o descuento racional. Lo primero tal como hicimos en el descuento comercial es introducir las variables o elementos que van a formar parte del cálculo.
Descuento matemático o racional:
–Dr: Descuento racional o matemático.
–C0: Capital Inicial.
–Cn: Valor o Capital Final. Nominal.
–i o d: Tanto de interés de la operación.
Una vez conocidas las variables que intervienen en el cálculo, que como puedes observar son las mismas que intervienen en el descuento comercial, vamos a proceder a detallarlo. Su cálculo se considera un ahorro de intereses que se calcula sobre el valor inicial C0 aplicando el tipo de interés o de descuento de la operación.
Proceso para el cálculo
–Primero a partir de la fórmula de la capitalización simple despejamos C0 el capital inicial.
–Después por la diferencia entre el Capital Final Cn y el Capital Inicial C0 determinamos el Descuento racional Dr.
Proceso matemático:
Cálculo del capital inicial a partir de la fórmula de capitalización simple despejamos el capital inicial C0.

Una vez que tenemos despejado el Capital Inicial procedemos al cálculo del Descuento por la diferencia entre el Capital Final y el Capital Inicial.

Otra forma de realizar el cálculo sería:
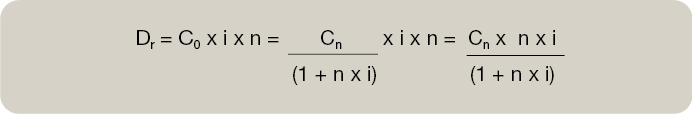
Ejemplo práctico
Calcular el descuento matemático al anticipar 15.000 euros con un interés establecido del 14% durante 12 meses.
Variables que intervienen para el cálculo:
–i = 14%
–n = 1. 12 meses.
–Cn = 15.000 euros.
Desarrollo matemático del cálculo del descuento:

Por su definición y concepto es un tipo de descuento más beneficioso para las empresas que el descuento comercial. Para apoyar este argumento vamos a realizar por un lado una comparación matemática de los descuentos comercial y matemático y además plantearemos la equivalencia que existe entre ellos.
Veamos primero una comparativa entre ambos descuentos: comercial y matemático.
Comparación matemática
–Primera comparación.
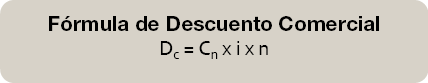
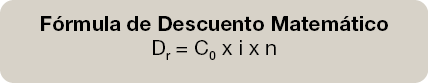
Si observamos ambas fórmula vemos que el descuento comercial realiza los cálculos del interés sobre Cn valor final del capital mientras que, el descuento matemático lo aplica sobre C0 valor inicial del capital que como sabemos, es siempre inferior. La primera comparación nos hace decidirnos por el descuento matemático ya que es más beneficioso para la empresa.
–Segunda comparación
Expresaremos ambas fórmulas en función del capital final o nominal Cn, despejando en ambos casos Dc y Dr en relación al nominal.


Al despejar ambas fórmulas se puede observar que si aplicásemos el mismo tipo de interés o descuento en ambas fórmulas, el resultado al aplicar la fórmula del descuento comercial sería siempre superior que si aplicamos la fórmula del descuento matemático o racional.
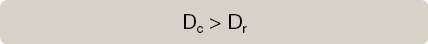
Tras realizar la comparativa matemática y llegar a la conclusión de que el descuento matemático es más beneficioso para la empresa plantearemos a continuación la equivalencia que existe entre ambos descuentos: comercial y matemático.
–Equivalencia entre descuento comercial y descuento matemático
Para llegar a la equivalencia entre ambos descuentos trataremos de encontrar el tipo de interés o descuento, comercial y racional, que aplicado al capital final nos den como resultado el mismo descuento. Tenemos que llegar a este resultado:
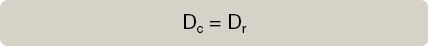
Por tanto, partiendo de las fórmulas del descuento comercial y del descuento matemático Dc y Dr despejaremos los tipos de interés o de descuento. Para diferenciarlos incluiremos en las fórmulas ir expresando el tipo interés o descuento en el descuento matemático y para el tipo de interés o descuento en el descuento comercial incluiremos ic.
Desarrollo:
1.

2.
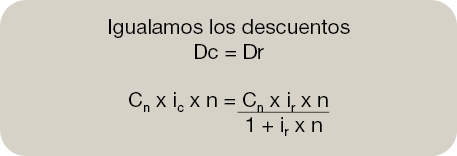
3.

Veamos un ejemplo: Con un tanto de interés o descuento comercial del 10% calcula el tanto de interés o descuento matemático equivalente, con una duración de 12 meses. Una vez obtenidos los tipos de interés o descuento comprueba que son equivalentes para un nominal de 5.000 euros.


Importante
Como hemos comprobado por diferentes métodos podemos concluir que el descuento matemático o racional es más ventajoso para la empresa que el descuento comercial.

1.2. Actualización compuesta
En el apartado anterior definimos y estudiamos el descuento o interés simple operación en la que se generaban intereses o descuento solo en función del capital. En este caso introducimos el concepto de descuento o interés compuesto, en el que los intereses generados se van sumando al capital y junto con este van generando más intereses. El capital por lo tanto va aumentando dependiendo del periodo marcado.
Definición
La actualización compuesta es un cálculo financiero aplicable a productos financieros de activo cuyo fin es calcular el valor de un capital futuro en el momento presente teniendo en cuenta los intereses que se van generando en cada periodo. Aplicaremos para su cálculo matemático la Ley financiera de descuento compuesto.

Como hemos introducido los intereses que genera esta operación se van uniendo al capital, aumentándolo. Lo que significa es que:
–Cuando estos intereses o descuentos son generados se descuentan del capital objeto del cálculo para generar más intereses para el siguiente periodo.
–Los intereses de los periodos son calculados del capital del periodo anterior.
El punto inicial para el cálculo del descuento o actualización compuesta es el capital final o nominal Cn, sabemos su vencimiento y el tipo de interés que se aplica en la operación. Una vez realizados los cálculos se genera el valor del capital futuro en el momento actual C0 que será inferior al capital final Cn. La diferencia entre ambos capitales es el coste de anticipar su vencimiento.
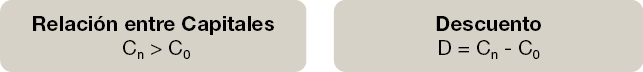
A lo largo de este punto centraremos los contenidos en el descuento compuesto veremos las fórmulas que intervienen en su cálculo, lo compararemos con el descuento simple y profundizaremos en el concepto de tasa de interés. Por último, como ya hemos visto tanto el descuento comercial como el matemático en relación al descuento simple ahora veremos estos dos tipos de descuentos en su cálculo compuesto.
–Descuento compuesto
∙Fórmulas.
∙Comparativa entre descuento simple y descuento compuesto.
∙Tasa de interés compuesta.
∙Descuento compuesto comercial.
∙Descuento compuesto racional.
1.2.1. El Descuento Compuesto
Recuerda
En el descuento o actualización compuesta los intereses generados son incluidos junto con el capital para generar los intereses del siguiente periodo.

Comenzamos este punto con el concepto de Descuento Compuesto como descuento acumulativo, en el que el capital que es descontado se incorpora al capital a descontar en el periodo siguiente y así sucesivamente. Este tipo de descuento suele utilizarse en periodos de tiempo más amplios que el descuento simple generalmente superiores a un año.
Las variables o elementos que van a intervenir son los siguientes:
–D: Descuento.
–C0: Capital Inicial.
–Cn: Valor o Capital Final. Nominal.
–i o d: Tanto de interés de la operación.

El descuento o actualización compuesta es la operación opuesta a la capitalización compuesta. Dentro del descuento compuesto partimos del capital final Cn y matemáticamente calculamos su valor en el momento actual CO.
Recuerda
El descuento o actualización simple es la operación inversa a la operación financiera de capitalización simple.

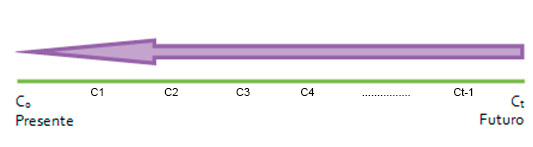
Esquema general del descuento compuesto
Como vemos en el esquema en la parte inferior Ct representa el valor final del capital que en periodos sucesivos se va descontando generando capitales Ct-1 ….C4 C3 C1 cada vez más pequeños hasta llegar al momento actual cuyo capital será C0.
Matemáticamente su cálculo en líneas generales será:

Una vez presentado el concepto de descuento compuesto veamos qué relación y diferencias existen entre el descuento o actualización simple y el descuento o actualización compuesta. Para ello haremos una comparativa.
Situación de partida, disponemos de un capital con el que podemos realizar dos tipos de operaciones de descuento o actualización:
–Descuento o actualización simple.
–Descuento o actualización compuesta.
Recuerda
La actualización simple o de descuento es una operación financiera que calcula el valor de un capital futuro sustituyéndolo por otro con vencimiento presente. Consiste en la operación contraria o inversa a la capitalización simple, desde el punto de vista matemático.
La actualización compuesta es un cálculo financiero aplicable a productos financieros de activo cuyo fin es calcular el valor de un capital futuro en el momento presente teniendo en cuenta los intereses que se van generando en cada periodo.

En primer lugar, realizaremos un esquema con las diferencias entre Descuento o actualización simple y Descuento o actualización compuesta.
|
Descuento o Actualización Simple |
Descuento o Actualización Compuesta |
|
Operaciones generalmente a corto plazo |
Operaciones a mayor plazo que en el simple |
|
El capital sobre el que se realiza el cálculo es constante en cada periodo |
El capital sobre el que se realiza el cálculo aumenta en cada periodo |
Una vez vistos los conceptos y sus diferencias realizaremos un esquema de los conceptos que hemos visto y otros que nos queda por ver en relación al descuento o actualización simple y al descuento o actualización compuesta.
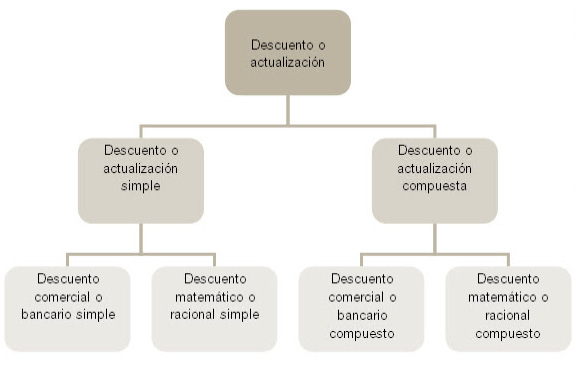
Ya hemos visto el bloque completo de descuento simple con los dos tipos de descuento simple comercial y racional. Hemos realizado una introducción al descuento compuesto y posteriormente veremos los conceptos de descuento comercial compuesto y descuento racional compuesto, sus fórmulas y unos ejercicios prácticos que nos aclaren estos conceptos.
Dentro del descuento compuesto tenemos dos tipos de descuentos:
–Descuento comercial compuesto.
–Descuento racional compuesto.
Nos centramos en el primer descuento compuesto.
Descuento comercial compuesto
Definición
El descuento comercial compuesto es la cantidad que general el capital final en un momento determinado del periodo, es decir, tiempo que dista entre el pago y el vencimiento.

Gráficamente una representación del Descuento comercial compuesto sería:

Esquema gráfico del descuento comercial compuesto
Partimos del capital final o nominal Cn sobre el que calculamos un interés o descuento i por periodo de tiempo n, en tantos por uno. En el periodo n-1 el Capital sería Cn-1, en el periodo n-2 el capital sería Cn-2, en el periodo 2 el capital sería C2, así sucesivamente llevamos al momento 0 y al capital C0.
En el periodo n-1 el capital habrá disminuido a Cn-1. Matemáticamente su desarrollo sería:

Si seguimos con los cálculos llegamos a calcular C0.
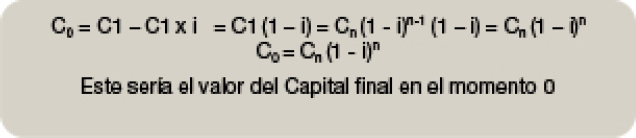
Ya tenemos el valor de Cn y de C0, vamos a expresar matemáticamente el valor del Descuento Comercial Compuesto Dc.

Descuento racional compuesto
Una vez visto el descuento comercial, uno de los tipos de descuento compuesto veamos a continuación el segundo, el descuento racional compuesto.
Definición
El descuento racional compuesto es la cantidad vía intereses que se generan desde que se realiza el pago hasta el momento del vencimiento del capital.

Para anticipar el Capital futuro al momento inicial o o, el periodo de referencia para el cálculo de los intereses será el inicio del periodo en cuestión.
Gráficamente sería:

Esquema gráfico del descuento racional compuesto
Paso a paso el desarrollo de la fórmula matemática sería en primer lugar calcular C0. Para llegar a este concepto primero calculamos Cn en el periodo n, Cn-1 en el periodo n-1 y así sucesivamente hasta llegar al momento 0 y calcular C0.

Sucesivamente llegamos al momento o y al cálculo matemático de C0.

El interés se aplica finalmente sobre el capital Cn, que es el que conocemos inicialmente. Una vez obtenido el capital C0, obtenemos es descuento Dr por la diferencia entre el capital final Cn y el Capital actual C0.

Recuerda
El descuento comercial compuesto es la cantidad que general el capital final en un momento determinado del periodo, es decir, tiempo que dista entre el pago y el vencimiento.
El descuento racional compuesto es la cantidad vía intereses que se generan desde que se realiza el pago hasta el momento del vencimiento del capital.

Hemos realizado el desarrollo gráfico y matemático de los descuentos compuesto comercial y racional. Ahora pasamos a realizar un ejemplo práctico de ambos descuentos.
Ejemplos prácticos de descuentos compuestos
Plantearemos el mismo enunciado y lo resolveremos con los dos procedimientos. Tenemos un capital de 100.000 euros con los que queremos realizar un descuento o actualización compuesta. Este capital tiene un vencimiento de 6 años. Si este capital lo traemos al momento actual momento 0 qué tendremos que pagar si el tipo de interés o de descuento aplicado es del 10%.
Descuento comercial compuesto
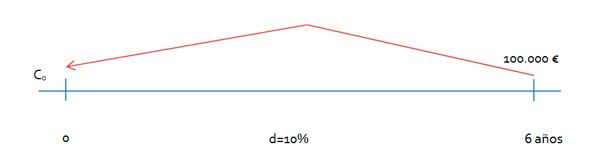
Esquema gráfico ejercicio práctico del descuento comercial compuesto
1.

2.

Descuento racional compuesto
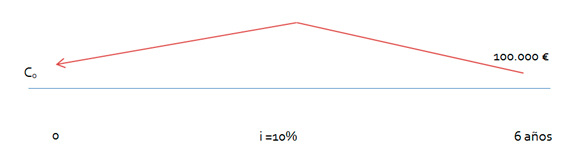
Esquema gráfico ejercicio práctico del descuento racional compuesto
1.

2.

1.3. Rentas constantes, variable y fraccionadas
Hasta este momento todas las operaciones que hemos realizado de descuento, tanto simple como compuesto en sus variedades comercial y racional, se configuraban únicamente con un capital que movíamos en el tiempo adelantándolo de un momento futuro n, al momento actual 0. Pero existen un gran número de operaciones financieras que se componen de un gran número de capitales y si nuestra tarea fuera adelantar cada uno de ellos a un momento concreto o retrasarlos en el tiempo sería poco práctico y poco eficiente.
Por tanto, dado la existencia de este tipo de operaciones con varios capitales surge la necesidad de obtener un sistema matemático que nos permita realizar estas operaciones de una manera más eficiente y con facilidad. Surgen las rentas.
Definición
Las rentas son fórmulas matemáticas que nos permiten de manera rápida y sencilla mover en el tiempo un número determinado de capitales.

–Requisitos
∙Debe existir más de un capital, mínimo dos.
∙Entre las rentas debe existir una constancia temporal, es decir entre los capitales debe existir siempre el mismo espacio temporal.
–Elementos
∙Origen: devengo del primer capital.
∙Final: devengo del último capital.
∙Duración: espacio temporal que transcurre entre el origen y el final.
∙Término: capital.
∙Periodo: espacio de tiempo entre dos capitales. Como requisito siempre debe ser igual.
∙Interés: tasa que se aplica para el movimiento de los capitales.
–Clasificación
|
Criterio |
Clasificación |
|
Dependiendo de la cuantía de los capitales o términos |
Constante: capitales iguales. Variable: al menos un capital es diferente al resto. Dentro de las variables nos encontramos con las que siguen una ley matemática y las que no. Dentro de las que siguen una ley matemática están en progresión geométrica y en progresión aritmética. |
|
Dependiendo del número de capitales o términos |
Temporal: número determinado de capitales todos ellos conocidos. Perpetua: número indeterminado de capitales o muy extenso. |
|
Dependiendo del vencimiento de los capitales o términos |
Pospagable: al final de cada periodo nos encontramos los capitales. Prepagable: al principio de cada periodo es donde encontramos los capitales. |
|
Dependiendo del movimiento y su valoración |
Inmediata: valoración de la renta al inicio o al final. Diferida: valoración de la renta en un momento anterior al momento inicial. Anticipada: valoración de la renta en un momento posterior al momento final. |
|
Dependiendo de la periodicidad |
Entera: los capitales de la renta están expresados en la misma unidad temporal que el tipo de interés. No entera: los capitales de la renta están expresados en unidades temporales distintas a las del tipo de interés. Fraccionada: los capitales que componen la renta están en una unidad temporal inferior a la que está expresado el tipo de interés. |
|
Dependiendo de la ley financiera |
Simple: aplica la ley financiera de interés simple para mover los capitales. Compuesta: aplica la ley financiera de interés compuesta para mover los capitales. |
1.3.1. Descripción
En el apartado anterior introdujimos el concepto general de renta y realizamos una clasificación en función de varios criterios. De entre todas las rentas que hemos clasificado anteriormente vamos a centrarnos en algunas de ellas. Las detallamos en el siguiente gráfico.
Gráfico rentas
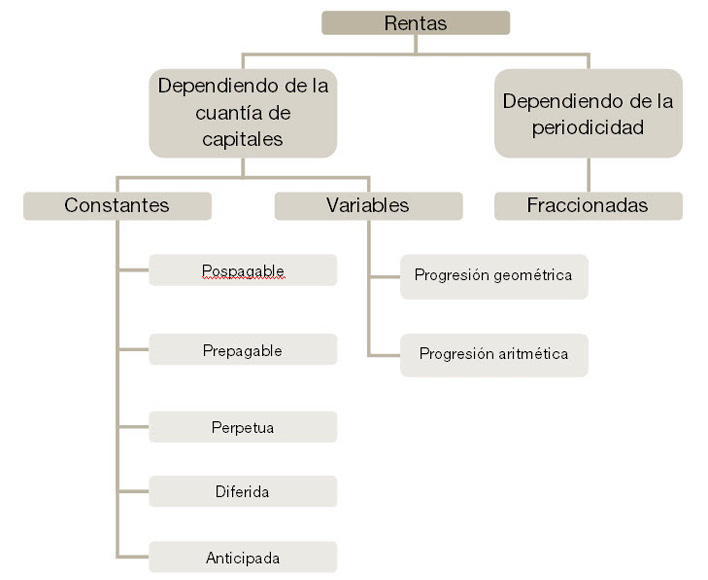
Al realizar la valoración de una renta calculamos la suma de todos sus capitales en un momento dado. Esa suma es el valor financiero o capital. Cuando se lleva al origen se denomina valor actual y cuando se lleva al momento final se denomina valor final.
Esquema general de las rentas:

1.3.2. Variables que intervienen
En este apartado vamos a detallar las variables que intervienen en cada una de las rentas que nos ocupan en este apartado que son:
–Rentas constantes:
∙Rentas constantes pospagables.
∙Rentas constantes prepagables.
∙Rentas constantes perpetuas.
∙Rentas constantes diferidas.
∙Rentas constantes anticipadas.
–Rentas variables:
∙Rentas variables en progresión geométrica.
∙Rentas variables en progresión aritmética.
–Rentas fraccionadas
Rentas constantes
Rentas constantes pospagables
Presentemos las características de este tipo de renta:
–Constante: capitales iguales, mismo valor.
–Temporal: número concreto y definido de capitales.
–Pospagable: los capitales vencen en el momento final de cada periodo.
–Inmediata: cálculo de la renta en el momento final y en el momento presente.
–Entera: capital e interés expresados en la misma unidad temporal.
–Compuesta: sigue la Ley financiera de descuento compuesto.
Variables que intervienen en los cálculos matemáticos:
–V0: Valor inicial de los capitales.
–Vn: Valor final de los capitales.
–c: Capitales.
–i: tasa de interés.
–an]i: muestra el valor inicial de una renta constante de valor distinto a la unidad.
–sn]i: muestra el valor final de una renta constante de valor distinto a la unidad.
–n: periodos de los que se compone la renta.
Cálculo del valor actual de la renta en el momento 0.
Calculamos el valor de los capitales en el momento actual y llevamos todos los capitales al momento 0 realizando con ellos un descuento compuesto al tipo i, desde donde se encuentra cada uno de los capitales hasta el momento inicial.
Matemáticamente:
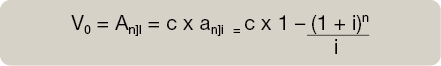
Cálculo del valor final de la renta en el momento n.
Calculamos el valor de los capitales en el momento final y llevamos todos los capitales al momento n realizando una capitalización compuesta al tipo i, desde el momento en el que se encuentra cada uno de los capitales hasta el momento final de la renta.
Matemáticamente:
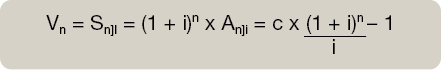
Rentas constantes prepagables
Presentemos las características de este tipo de renta:
–Constante: capitales iguales, mismo valor.
–Temporal: número concreto y definido de capitales.
–Prepagable: los capitales vencen en el momento inicial de cada periodo.
–Inmediata: cálculo de la renta en el momento final y en el momento presente.
–Entera: capital e interés expresados en la misma unidad temporal.
–Compuesta: sigue la Ley financiera de descuento compuesto.
Las variables que intervienen son las que intervenían en la renta anterior para diferenciar las fórmulas incluimos än]i y ¨sn]i
Cálculo del valor actual de la renta en el momento 0.
Calculamos el valor de los capitales en el momento actual y llevamos todos los capitales al momento 0 realizando con ellos un descuento compuesto al tipo i, desde donde se encuentra cada uno de los capitales hasta el momento inicial.
Matemáticamente:
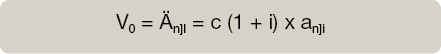
Sabías que
El valor V0 y el valor Vn, es decir el valor inicial y el valor final de las rentas prepagables se calculan a partir de los valores actual y final de las rentas pospagables multiplicados por (1 + i). Matemáticamente realizamos una capitalización del periodo de una renta pospagable.

Rentas constantes perpetuas
Este tipo de rentas se caracteriza por tener un número de periodos de tiempo indefinido en el tiempo, es decir infinito. Por tanto, al no presentar un número finito de periodos desconocemos el valor que tendrá el momento n, es decir el valor de la renta en el momento final Vn es imposible de calcular ya que no lo conocemos. Solo podemos calcular el valor de la renta en el momento actual, es decir el valor de V0.
Cálculo del valor actual de la renta en el momento 0.
Calculamos el valor de los capitales en el momento actual y llevamos todos los capitales al momento 0 realizando con ellos un descuento compuesto al tipo i, desde donde se encuentra cada uno de los capitales hasta el momento inicial. En este caso trabajamos con un número infinito de espacio temporal y capitales por lo que introducimos el término ∞. Matemáticamente se utiliza el término límite y la duración de la renta tiende a ∞.
Matemáticamente expresamos varias opciones en función de matiz de la renta perpetua:

Rentas constantes
Rentas constantes diferidas
Dentro de las rentas constantes las rentas diferidas son aquellas en las que su valor inicial V0, no se valora en el momento actual 0 sino que, se valoran con anterioridad a ese momento. El espacio temporal que media entre el momento 0, el origen y el cálculo de la renta diferida se denomina periodo de diferimiento.
Partimos de una renta:
–Constante.
–Unitaria.
–Temporal.
–Pospagable.
Incluimos dos nuevos conceptos:
–t: va a representar ese valor temporal anterior al momento 0.
–d: muestra lo que anteriormente definíamos como periodo de diferimiento. Tiempo que transcurre entre el momento t y el momento 0.
Cálculo de Vt. Matemáticamente:
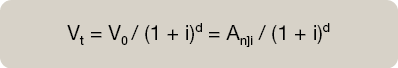
Cálculo de Vn. Matemáticamente:
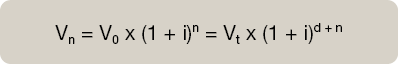
Rentas constantes anticipadas
Esta renta constante anticipada se caracteriza por que el cálculo del valor final de la renta se realiza con posterioridad al momento n. El espacio temporal entre el momento n y el momento del cálculo del valor final de la renta anticipada se denomina periodo de anticipación de la renta.
Variables de este tipo de renta:
–Vn+h: valor final de la renta en el periodo anticipado n+h.
–h: periodo de anticipación, es el periodo que media entre el final de la renta en el periodo n y el más el periodo de anticipación.
Cálculo de Vn+h .Matemáticamente:
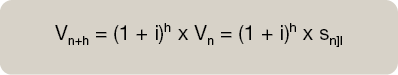
Cálculo de V0 .Matemáticamente:
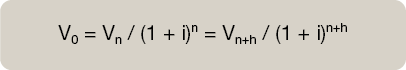
Rentas variables en progresión aritmética
Recuerda
Hasta ahora hemos realizado diferentes cálculos de rentas con una característica común, todas eran constantes. El término constante en una renta nos indica que los capitales están distribuidos en periodos de tiempo iguales y consecutivos.

Pasamos en este punto a tratar con otro tipo de rentas denominadas variables cuyos capitales están distribuidos en el tiempo de forma variable, los periodos entre capitales son diferentes pero siguen una progresión en este caso, una progresión aritmética.
Cada capital es el anterior aumentado o disminuido en la misma cantidad que denominaremos d y siempre se mostrará en unidades monetarias.
Definición
El término d lo podemos definir como la razón de la progresión aritmética.

Partimos de la idea de que en una renta variable en progresión aritmética cada capital es igual al anterior más d, más la razón aritmética. Esta razón aritmética puede tomar dos valores:
–Razón aritmética positiva. d.
–Razón aritmética negativa. –d.
Matemáticamente el cálculo de V0, valor inicial de la renta en función del valor que tome la razón aritmética, sería:
Razón aritmética positiva. d.
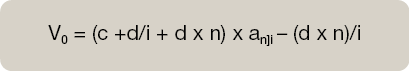
Razón aritmética negativa. –d.
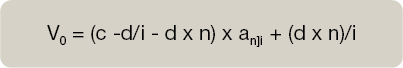
Matemáticamente el cálculo de Vn, valor inicial de la renta en función del valor que tome la razón aritmética, sería:
Razón aritmética positiva. d.
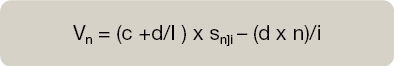
Razón aritmética negativa. –d.
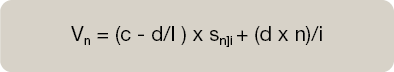
Rentas variables en progresión geométrica
Recuerda
En este apartado tratamos el tipo de rentas denominadas variables cuyos capitales están distribuidos en el tiempo de forma variable.

Los periodos entre capitales en este tipo de rentas son diferentes pero siguen una progresión en este caso, una progresión geométrica. Cada capital es el anterior multiplicado por un número que denominaremos q.
Definición
El término q podemos definirlo como razón de la progresión geométrica de la renta variable.

La razón de la progresión geométrica q, no puede ser negativa. Esta afirmación no quiere decir que la renta variable en progresión aritmética no pueda ser decreciente. Puede ser decreciente pero el valor de q nunca será negativo.
El valor que tome la razón de la progresión geométrica determinará si la renta variable es creciente o decreciente. Valores de referencia para q:
–0<q<1 Renta variable en progresión geométrica decreciente.
–q>1 Renta variable en progresión geométrica creciente.
Calculamos el valor actual V0 y el valor final Vn de una renta variable en progresión geométrica con las siguientes características: temporal, pospagable, inmediata y entera.

Estas rentas muestran una particularidad en cuanto a su valoración financiera. Esta valoración de rentas temporales, variables en progresión geométrica va a depender básicamente de la relación que hay entre la razón de crecimiento q, definida anteriormente y la expresión (1+i). En función de esta relación se plantearán diferentes resultados:
–q<(1+i). Podemos utilizar las fórmulas planteadas anteriormente en este punto.
–q>(1+i). Podemos utilizar las fórmulas planteadas anteriormente en este punto.
–q=(1+i). El resultado que obtendríamos con las expresiones anteriores sería indeterminado. Por tanto en este caso las fórmulas a aplicar serían:
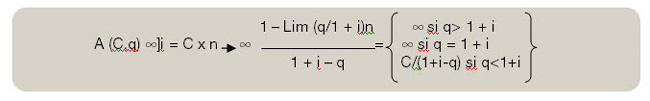
Las rentas fraccionadas son un tipo de rentas en las que se divide cada periodo que dista entre un capital y otro en sub periodos, denominados k. Una renta de n periodos temporales se transformará en una renta fraccionada de n x k términos que en este caso se denominan sub periodos.
Dentro de las rentas fraccionadas vamos a profundizar en:
–Rentas fraccionadas constantes.
–Rentas fraccionadas en progresión geométrica.
–Rentas fraccionadas en progresión aritmética.
Rentas fraccionadas constantes
El interés aplicado en la operación está expresado en una unidad de tiempo superior al que viene expresado el capital de la renta. Para resolver este cálculo vamos a utilizar el método del tanto equivalente.
En este método tratamos de cambiar el tanto de interés por otro que sea equivalente en la misma unidad de tiempo a la que se muestran los capitales que componen la renta. Para la expresión matemática mostramos una renta pospagable:
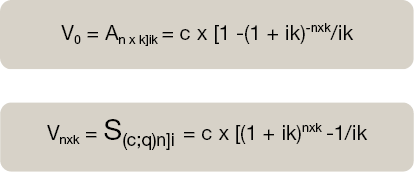
Rentas fraccionadas en progresión geométrica
Aquellas en las que los capitales siguen una progresión cuya variación en la razón se produce en un espacio de tiempo superior al de los capitales. La unidad de tiempo, los capitales y el tipo de interés deben estar expresados en la misma unidad.
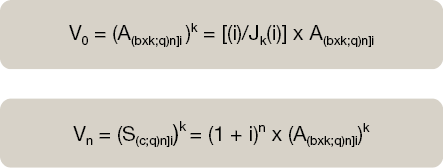
Siendo:
k: la frecuencia de fraccionamiento.
b x k: la suma aritmética de los capitales del primer período de la renta.
q: la razón de la progresión.
n: el número de períodos (en la unidad de tiempo de la razón).
i: el tipo de interés en la unidad de tiempo de la razón.
Rentas fraccionadas en progresión aritmética
Como en la renta fraccionada en progresión geométrica, en la fraccionada en progresión aritmética los capitales varían de forma lineal, esta variación en el tiempo es menor que la que presenta los capitales, con un interés de renta dado.
Para aplicar las siguientes fórmulas los capitales, el interés y la razón deben mostrarse en la misma unidad.
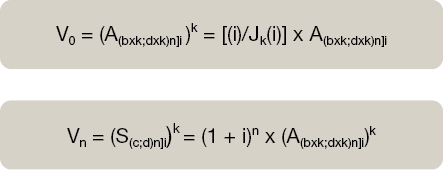
Siendo:
k: la frecuencia de fraccionamiento.
b x k: la suma aritmética de los capitales del primer período de la renta.
d x k: la suma aritmética de los aumentos de un período respecto a otro (razón de la progresión).
n: el número de períodos (en la unidad de tiempo de la razón).
i: el tipo de interés en la unidad de tiempo de la razón.
–La actualización simple o de descuento es una operación financiera que calcula el valor de un capital futuro sustituyéndolo por otro con vencimiento presente. Consiste en la operación contraria o inversa a la capitalización simple, desde el punto de vista matemático.
–El descuento comercial o bancario consiste en anticipar la entrega de un capital, que deberíamos cobrar o tener en un futuro y queremos cobrar o tener en el momento actual.
–El descuento matemático se obtiene aplicando un tipo de interés establecido sobre el capital efectivo en el momento presente. La tasa de descuento o tipo de interés fijado se calcula sobre el capital en el momento actual, al inicio del periodo.
–La actualización compuesta es un cálculo financiero aplicable a productos financieros de activo cuyo fin es calcular el valor de un capital futuro en el momento presente teniendo en cuenta los intereses que se van generando en cada periodo. Aplicaremos para su cálculo matemático la Ley financiera de descuento compuesto.
–El descuento racional compuesto es la cantidad vía intereses que se generan desde que se realiza el pago hasta el momento del vencimiento del capital.
–V0 Calculamos el valor de los capitales en el momento actual y llevamos todos los capitales al momento 0 realizando con ellos un descuento compuesto al tipo i, desde donde se encuentra cada uno de los capitales hasta el momento inicial. Renta Constante pospagable.
–Vn Calculamos el valor de los capitales en el momento final y llevamos todos los capitales al momento n realizando una capitalización compuesta al tipo i, desde el momento en el que se encuentra cada uno de los capitales hasta el momento final de la renta. Renta Constante pospagable.
–V0 Calculamos el valor de los capitales en el momento actual y llevamos todos los capitales al momento 0 realizando con ellos un descuento compuesto al tipo i, desde donde se encuentra cada uno de los capitales hasta el momento inicial. Renta Constante prepagable.
–Vn Calculamos el valor de los capitales en el momento actual y llevamos todos los capitales al momento 0 realizando con ellos un descuento compuesto al tipo i, desde donde se encuentra cada uno de los capitales hasta el momento inicial. En este caso trabajamos con un número infinito de espacio temporal y capitales por lo que introducimos el término ∞. Matemáticamente se utiliza el término límite y la duración de la renta tiende a ∞. Rentas Constantes Perpetuas.
–Dentro de las rentas constantes las rentas diferidas son aquellas en las que su valor inicial V0, no se valora en el momento actual 0 sino que, se valoran con anterioridad a ese momento. El espacio temporal que media entre el momento 0, el origen y el cálculo de la renta diferida se denomina periodo de diferimiento.
–Esta renta constante anticipada se caracteriza por que el cálculo del valor final de la renta se realiza con posterioridad al momento n. El espacio temporal entre el momento n y el momento del cálculo del valor final de la renta anticipada se denomina periodo de anticipación de la renta.
–Las rentas fraccionadas son un tipo de rentas en las que se divide cada periodo que dista entre un capital y otro en sub periodos, denominados k. Una renta de n periodos temporales se transformará en una renta fraccionada de n x k términos que en este caso se denominan sub periodos
1.Capitalizar consiste en...
a.Calcular el valor del capital actual en el momento actual.
b.Calcular el valor del capital actual en un momento futuro.
c.Calcular el valor del capital futuro en el momento actual.
d.Calcular el valor del capital futuro en el momento futuro.
2.¿Qué es el descuento simple de un capital?
a.Calcular el valor del capital futuro en el momento actual.
b.Calcular el valor del capital actual en el momento futuro.
c.Calcular el valor del capital futuro en el momento futuro.
d.Calcular el valor del capital actual en el momento actual.
3.El descuento matemático:
a.Se obtiene aplicando un tipo de interés establecido sobre el capital efectivo en el momento actual.
b.Consiste en calcular el valor del capital actual en el momento futuro.
c.Se obtiene aplicando un tipo de interés establecido sobre el capital efectivo en el momento futuro.
d.Consiste en calcular el valor del capital actual en el momento actual.
4.La actualización compuesta:
a.Calcula el valor de un capital futuro en el momento actual junto con los intereses que va generando.
b.Calcula el valor de un capital futuro en el momento actual.
c.Calcula el valor de un capital actual en el momento actual.
d.Calcula el valor de un capital futuro en el momento futuro junto con los intereses que va generando.
5.Las rentas son:
a.Fórmulas matemáticas que permiten mover en el tiempo un capital al momento actual.
b.Fórmulas matemáticas que permiten mover en el tiempo solamente un capital.
c.Fórmulas matemáticas que permiten mover en el tiempo varios capitales.
d.Fórmulas matemáticas que permiten mover en el tiempo varios capitales solamente al momento actual.
6.Tipos de rentas atendiendo a la cuantía de sus capitales:
a.Constantes y variables.
b.Constantes y fraccionadas.
c.Variables y fraccionadas.
d.Prepagables y fraccionadas.
7.Tipos de rentas variables:
a.Fraccionada y pospagable.
b.Progresión geométrica y progresión aritmética.
c.Perpetua y anticipada.
d.Diferida y en progresión geométrica.
8.Rentas constantes:
a.Distintos capitales y de distinto valor.
b.Distintos capitales y del mismo valor.
c.Iguales capitales y del mismo valor.
d.Iguales capitales y de distinto valor.
9.Renta prepagable:
a.Los capitales de la renta pueden vencer en el momento inicial y en el final del periodo.
b.El capital de la renta vence en el momento final del periodo.
c.Los capitales de la renta vencen en el momento final del periodo.
d.Los capitales de la renta vencen en el momento inicial del periodo.
10.Renta constante anticipada:
a.Cálculo inicial de la renta con posterioridad al momento inicial 0.
b.Cálculo final de la renta con posterioridad al momento inicial 0.
c.Cálculo inicial de la renta con posterioridad al momento n.
d.Cálculo del valor final con posterioridad al momento n.