Capítol I
Què podem arribar a dibuixar
Quan Leonardo Da Vinci, un dels dissenyadors més creatius de la nostra història, feia els seus estudis previs a qualsevol creació elaborava tot tipus de dibuixos i anotacions en els seus quaderns. Si els observem (Isaacson, 2018, figures diverses) en podem distingir de diversos tipus: perspectives d’objectes muntats i desmuntats (vistes explotades), vistes planes i dibuixos geomètrics (que feia servir a manera de «calculadora gràfica»).
Un enginyer ha d’utilitzar el dibuix com una eina per a dissenyar i per a resoldre els seus problemes: des de la concepció d’una idea, amb el que actualment s’anomena pluja d’idees o brainstorming (dibuixos en perspectives parcials o completes, perspectives de vistes explotades d’un conjunt…), passant pels càlculs fets amb dibuix geomètric, fins a arribar als plànols (vistes ortogonals) de peces individuals i de conjunt, on es pot aprofundir en tota la concreció que convingui.
En el capítol següent farem un recorregut pels diferents tipus de dibuix que un enginyer hauria de poder utilitzar.
1. Recorregut pels sistemes de representació d’objectes del dibuix tècnic més habitual en l’enginyeria
Tot i que hi ha moltes branques en l’enginyeria i que cada branca desenvolupa tipologies de dibuix tècnic específic, observem una certa recurrència en l’estructura dels dibuixos.
En aquest capítol intentarem proporcionar els tipus de dibuix més habituals.
En gran mesura, quan volem representar objectes tridimensionals sobre una superfície bidimensional (paper o pantalla plana), les tipologies recurrents es basen en la projecció gràfica.
2. Projecció gràfica
Utilitzem la projecció gràfica com un instrument que ens permet representar un objecte tridimensional sobre una superfície 2D.
Figura 1. Projecció gràfica d’un cub (3D) sobre una superfície plana (2D) a partir dels rajos que s’originen en un punt focal (F)
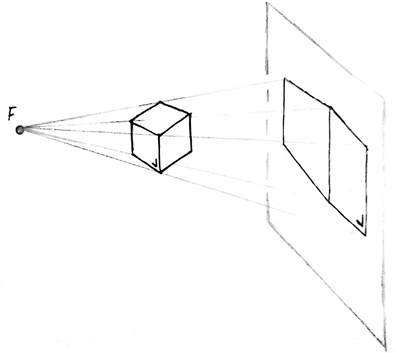
Font: elaboració pròpia
Si tenim un objecte tridimensional flotant a l’espai, ubicat en un focus de projecció, i una superfície plana sobre la qual s’ha de projectar, podem traçar rajos des del focus fins a la superfície plana passant per les arestes i vèrtexs de l’objecte.
Figura 2. Diagrama on es categoritza les diferents tipologies de dibuix tècnic segons els sistemes de representació que acull la projecció gràfica
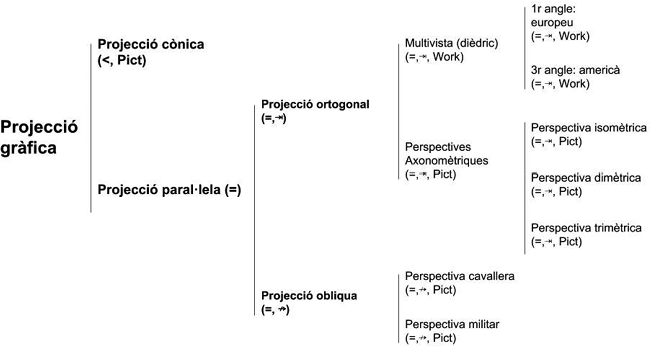
Font: elaboració pròpia
La incidència d’aquests rajos a través de la morfologia de l’objecte ens permet obtenir figures projectades representatives d’aquest objecte.
A partir d’aquesta definició, en l’esquema següent podem fer un recorregut pels diferents tipus de dibuix tècnic segons els elements següents:
- • Paral·lelisme dels rajos projectius
- – Els rajos projectius són originaris d’un o diversos punts focals (<).
- – Els rajos projectius són paral·lels (=), o el que seria equivalent a considerar que provenen d’un punt focal situat a l’infinit.
- • Perpendicularitat dels rajos projectius respecte de la superfície on es projecta
- – Els rajos projectius arriben perpendiculars a la superfície on es projecta (⇥).
- – Els rajos projectius arriben oblics a la superfície on es projecta (↛).
- • Objectiu del dibuix
- – Representació pictòrica: realista i sense rigor com a eina de treball (Pict)
- – Representació simbòlica però amb rigor com a eina de treball (Work)
2.1. Projecció cònica (perspective projection)
La representació gràfica més semblant al que una persona pot percebre visualment és la que es basa en la projecció cònica, en què els rajos projectius provenen d’un o diversos punts focals.
S’anomena projecció cònica perquè els rajos projectius formen un con, l’extrem del qual té origen en l’observador. Lògicament, en aquest cas, els rajos projectius no són paral·lels.
La característica principal és que la mida de l’objecte representat es veu modificada en funció de la distància entre aquest objecte i l’observador.
En la figura 3 observem la comparativa entre dues escenes, una il·luminada pels rajos projectius d’una espelma (esquerra) i l’altra il·luminada per una llum plana, equivalent a la llum del Sol, per exemple (dreta). L’escena es compon, a part de les llums, d’una esfera a cada costat i de dos plans semitransparents (A, proper; B, llunyà) on es veuen projectades les ombres de les esferes corresponents.
Observem com l’ombra generada per l’espelma és més gran si la distància augmenta, perquè tots els rajos s’originen en un sol punt (la flama). En canvi, quan els rajos són paral·lels, l’ombra és idèntica, independentment de la distància del pla on es representa.
Figura 3. Diferència entre projecció cònica (espelma) i paral∙lela (feix de rajos paral∙lels)
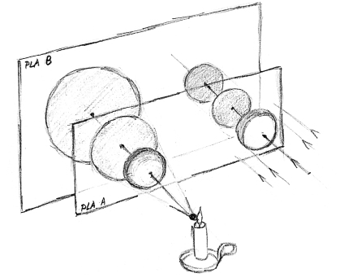
Font: elaboració pròpia
Això determina que, normalment, la majoria de les perspectives còniques es realitzen amb finalitats pictòriques, ja que representen més fidelment la realitat observada des d’un sol punt.
La projecció cònica, també anomenada perspectiva cònica, pot tenir diversos punts de fuga.
Un punt de fuga és un punt abstracte ubicat a l’espai 2D sobre el qual convergeixen els rajos projectius.
Segons les necessitats representatives del dibuix, podrem dibuixar perspectives còniques amb un, dos o més punts de fuga. Es podria afirmar que com més punts de fuga s’afegeixen al sistema de perspectiva cònica el resultat s’assembla més a la percepció de l’ull humà.
- • Un punt de fuga: és molt eficient per a expressar distància, llunyania.
El cas que es representa en la figura 4 il·lustra una fila de rajoles situades al terra que arriben fins a l’horitzó. Teòricament el punt de fuga (F) se situa a l’infinit i representa l’eix de profunditat. La resta d’eixos, amplada i alçària, es representen segons la metodologia de rajos plans.
Figura 4. Exemple de representació amb un sol punt de fuga (F)
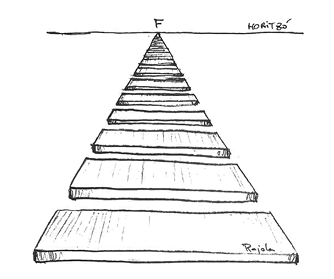
Font: elaboració pròpia
- • Dos punts de fuga: quan s’alineen horitzontalment representen l’horitzó. És utilitzat freqüentment per a representacions pictòriques d’objectes relativament senzills.
Figura 5. Exemple de representació amb dos punts de fuga (F1 i F2)
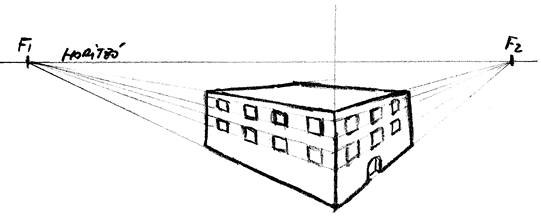
Font: elaboració pròpia
La figura 5 representa una edificació referenciada a l’horitzó, ja que els dos punts de fuga són a sobre d’aquest. Els dos punts de fuga representen l’eix de profunditat i el d’amplada (esquerra-dreta), encara que no són alineats igual que els eixos de profunditat i amplada del punt de vista de l’observador. L’eix vertical no té punt de fuga; per tant, continua treballant amb rajos paral·lels.
- • Tres punts de fuga: també s’utilitza sovint per a representar de manera pictòrica edificacions o entorns que tenen una certa alçària.
Figura 6. Exemple de representació amb tres punts de fuga (F1, F2 i F3)
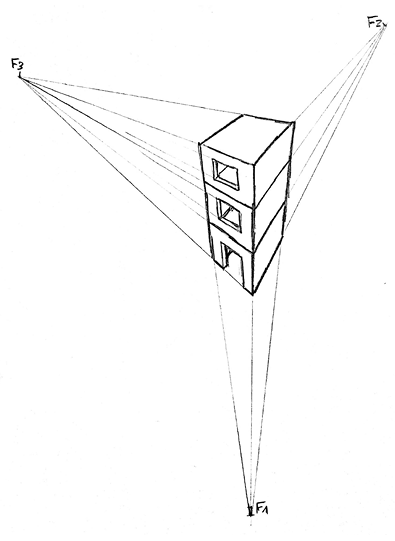
Font: elaboració pròpia
2.2. Projecció paral·lela
La principal característica de la projecció paral·lela és que la mida dels objectes representats no depèn de la distància. Això és així perquè els rajos projectius són paral·lels.
Aquesta particularitat determina unes limitacions importants quan les finalitats són pictòriques. Les limitacions de la projecció paral·lela queden evidenciades en les famoses perspectives impossibles d’escales que sembla que van pujant i al final enllacen amb el principi.
Figura 7. Exemple comparatiu de representació d’un mateix conjunt de peces de quatre maneres diferents: combinant perspectiva isomètrica i perspectiva cònica, amb dos punts de vista diferents
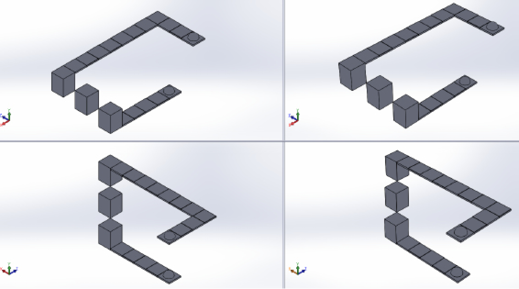
- • Columna esquerra: isomètrica
- • Columna dreta: perspectiva cònica, amb orientació d’eixos idèntica a la isomètrica, però amb rajos NO paral∙lels
- • Fila de dalt: orientació 1
- • Fila de baix: orientació 2
Font: elaboració pròpia
En la figura 7, feta amb ordinador, es pot apreciar un conjunt de peces representat de diverses maneres. Es tracta d’unes rajoles alineades i de blocs de formigó disposats en forma d’escala. A les rajoles de l’extrem hi ha unes semiesferes. Tots els elements leviten a l’espai.
En les dues vistes de l’esquerra s’aprecia que les peces idèntiques es veuen de la mateixa mida quan la perspectiva és isomètrica, independentment de si són properes o llunyanes respecte a l’observador: rajoles, semiesferes, paral·lelepípedes més alts.
En canvi, en les dues vistes de la dreta a l’ordinador hi ha activada la deformació per perspectiva cònica, és a dir, que com més lluny és l’objecte més petit es veu.
També cal observar com hi ha elements que a l’esquerra són estrictament paral·lels, i a la dreta aparentment es trenca aquest paral·lelisme.
A partir de l’esquema de la figura 8, s’observa que la projecció paral·lela inclou, per un costat, la projecció ortogonal i per l’altre, la projecció obliqua. Els objectius de la projecció paral·lela són tan pictòrics com de treball.
Figura 8. Distinció de tipus de projecció paral∙lela: ortogonal i obliqua
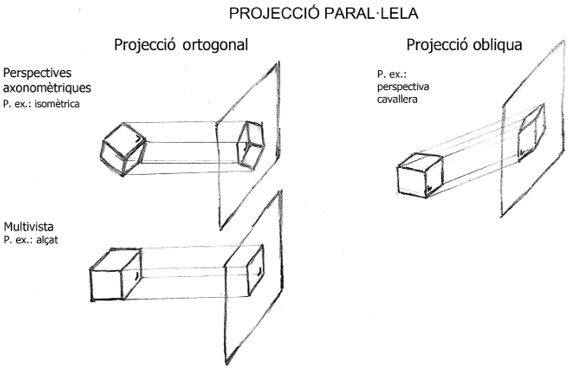
Columna esquerra: projecció ortogonal
- • Dalt: una perspectiva axonomètrica, en aquest cas, isomètrica
- • Baix: sistema multivista, en aquest cas, alçat
Columna dreta: projecció obliqua
- • Dalt: en aquest cas, perspectiva cavallera
Font: elaboració pròpia
En la figura 8 es mostren exemples dels dos tipus de sistemes de projecció paral·lela: ortogonal i obliqua, alhora que s’il·lustra la seva metodologia.
Comprovem que els rajos projectius són paral·lels en totes les representacions.
També constatem que, en la projecció ortogonal, els rajos sempre són perpendiculars a la superfície en què es projecta. En canvi, en la projecció obliqua, els rajos són oblics a la superfície.
En la figura anterior també observem diferències pel que fa a la posició de l’objecte respecte al pla en què es projecta. En el sistema de multivista (alçat, en la figura) la cara que es representa és paral·lela al pla en què es projecta. Aquesta particularitat fa especialment útil el sistema de multivista per a l’enginyeria, ja que, gràcies a això, es pot treballar sempre en veritable magnitud.
2.2.1. Projecció ortogonal (orthographic projection)
Com ja sabem, en la projecció ortogonal els rajos projectants sempre són perpendiculars al pla en què es projecta.
Si repassem altra vegada l’esquema de la figura 8, veiem que la projecció ortogonal inclou el sistema de representació de vistes ortogonals (multiview projection), utilitzat per a treballar en l’enginyeria productiva pel seu rigor, i el sistema de perspectiva axonomètrica (axonometric projection), utilitzat majoritàriament amb finalitats pictòriques.
2.2.1.1. Multivista (dièdric)
La projecció ortogonal és l’essència de la geometria descriptiva, també anomenada sistema dièdric. Gaspard Monge (1799) va idear la geometria descriptiva i a partir de la publicació del seu llibre Géométrie descriptive, es comença a utilitzar la seva proposta de representació. Gràcies a la seva contribució, a partir d’aquell moment qualsevol objecte tridimensional es podia representar completament amb una combinació de vistes 2D. És el que actualment, a la indústria, coneixem com a plànols.
Actualment, la norma espanyola que regula els principis generals de representació és la UNE 1-032-82, regulada per AENOR (equivalent a la ISO 128).
El sistema dièdric es basa en la utilització d’un diedre per a ubicar tots els punts de l’espai.
Un diedre és un sistema format per dos plans perpendiculars que es creuen. Els dos plans són el pla vertical (PV) i el pla horitzontal (PH). La línia que es genera en el creuament dels dos plans s’anomena línia de terra (LT).
També s’utilitza el pla auxiliar anomenat de perfil (PP).
L’espai determinat pel creuament entre els dos plans (PV i PH) en les seves coordenades positives s’anomena primer quadrant, i el determinat en les seves coordenades negatives s’anomena tercer quadrant.
El sistema de projecció ortogonal es deriva de la utilització del sistema dièdric, en la variant simplificada anomenada directe.
En el sistema dièdric directe no s’especifica la línia de terra (LT). També es pot afirmar que el que es projecta en el PV correspon a l’alçat, en el PH, correspon a la planta i en el PP, correspon al pla de perfil (dret o esquerre, segons sigui europeu o americà, respectivament).
Multivista: sistema de projecció de vistes ortogonals (multiview projection)
Quan els professionals de l’enginyeria volem representar un objecte de manera completa i rigorosa el dibuixem amb el sistema de projecció de vistes ortogonals, també anomenat sistema multivista.
En el segle xx comença a ser necessari generar una norma universal que reguli els principis generals de representació basats en el sistema dièdric de Monge. Amb les guerres mundials es veu la necessitat d’intercanviar plànols de maquinàries entre països de diferents cultures.
La conclusió serà contundent: l’expressió gràfica de documentació tècnica ha de ser un llenguatge universal entre els professionals de l’enginyeria.
Actualment hi ha dos sistemes de representació de vistes ortogonals majoritaris al món de l’enginyeria: el sistema europeu i el sistema americà. Tot i que l’essència és la mateixa, l’un representa les vistes de manera oposada respecte de l’altre.
El sistema europeu i, per tant, el que fa servir la norma espanyola, ubica l’objecte que es vol representar en el primer quadrant del sistema dièdric, on les coordenades són totes positives. El sistema americà treballa ubicant l’objecte en el tercer quadrant del diedre, on totes les coordenades són negatives
La norma espanyola que regula els principis generals de representació és la UNE 1-032-82 (equivalent a la ISO 128).
Quan volem representar un objecte segons el sistema europeu el posicionem en el primer quadrant del diedre i projectem les vistes en PV, PH i PP. D’aquí sortiran les tres vistes alçat, planta i perfil dret.
Figura 9. Procés per a representar un objecte en vistes ortogonals utilitzant el primer quadrant del sistema dièdric, en el sistema europeu
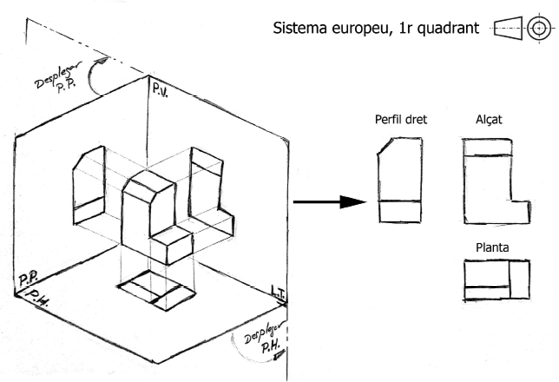
Font: elaboració pròpia
Una manera senzilla de descriure el sistema de representació d’objectes segons el sistema multivista europeu podria ser la següent:
- • Tenim l’objecte que s’ha de representar flotant dins d’una capsa.
- • Tenim una llum (punt d’observació) que impacta sobre l’objecte i que projecta les seves arestes i contorns a la paret oposada de la caixa de cartró (representació de les diferents vistes).
- • La llum és plana, de rajos paral·lels.
- • Un cop fetes les projeccions de l’objecte sobre les parets de la caixa, la despleguem de manera que totes les cares passen a ser coplanars amb el pla vertical (vista frontal, alçat o principal).
- • Per tant, el sistema europeu, o del primer quadrant, dibuixa en la paret oposada la projecció que traspassa l’objecte que volem representar. Així, la vista en planta, que s’observa des de dalt (punt de vista zenital), es dibuixa a la part inferior de l’alçat, és a dir, a sota. De la mateixa manera, el perfil dret es dibuixa a l’esquerra de l’alçat, i així successivament.
- • Una altra manera d’entendre el funcionament d’aquest sistema de representació podria ser aquesta: l’objecte està quiet i l’observador és el que canvia de lloc per captar el punt de vista que vol. El que veu l’observador s’ha de dibuixar a la paret que queda darrere l’objecte.
Figura 10. Procés per a representar un objecte en vistes ortogonals utilitzant el tercer quadrant del sistema dièdric, en el sistema americà
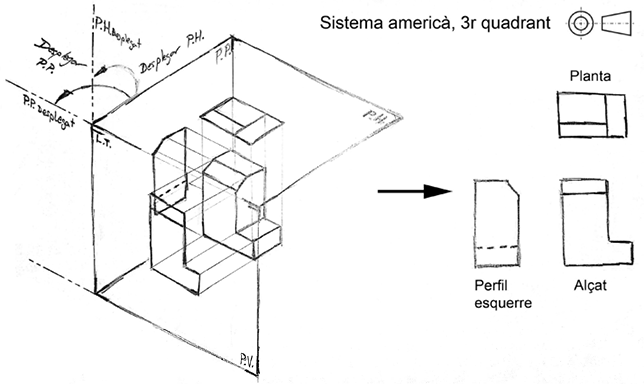
Font: elaboració pròpia
Quan volem representar un objecte segons el sistema americà el posicionem en el tercer quadrant del diedre i projectem les vistes en PV, PH i PP. D’aquí sortiran les tres vistes alçat, planta i perfil esquerre.
Una manera senzilla de descriure el sistema de representació d’objectes segons el sistema multivista americà podria ser la següent:
- • Tenim l’objecte que s’ha de representar flotant dins d’una caixa de cartró.
- • Tenim una llum que no travessa l’objecte i que hi rebota, sempre en sentit oposat a com ha sortit.
- • La llum és plana, de rajos paral·lels.
- • Aquest objecte reflecteix els rajos que surten de l’observador cap a la mateixa paret de la caixa de cartró d’on han sortit, dibuixant les arestes en què han rebotat.
- • Un cop fetes les projeccions de l’objecte sobre les parets de la caixa, la despleguem de manera que totes les cares passen a ser coplanars amb el pla vertical (vista frontal, alçat o principal).
- • Per tant, el sistema americà, o del tercer quadrant, dibuixa a cada lloc el que es veu. És a dir, la vista en planta es dibuixa a dalt de l’alçat i el perfil esquerre a l’esquerra d’aquest.
- • Una altra manera d’entendre el funcionament d’aquest sistema de representació podria ser el següent: l’observador sempre està quiet i es gira l’objecte per a aconseguir l’orientació que correspon a la vista.
2.2.1.2. Projecció axonomètrica
Les perspectives que es deriven de les projeccions axonomètriques són diverses (isomètrica, dimètrica i trimètrica), però en tot cas, són de rajos paral·lels que arriben perpendiculars a la superfície projectada i normalment s’utilitzen per a finalitats pictòriques.
Cal destacar que les perspectives axonomètriques tenen un inconvenient comú: com que s’originen des d’un feix de rajos paral·lels, imposen una distorsió, ja que l’observador humà tendeix a percebre millor quan les representacions s’originen a partir de rajos que provenen d’un sol punt.
El sistema isomètric es caracteritza per una visió en què els tres eixos són igualment representats, és a dir, repartits en angles de 120°. Aquesta particularitat atorga la mateixa escala als tres eixos i, per tant, permet prendre mesures en veritable magnitud en qualsevol de les alineacions als eixos X, Y, Z.
Figura 11. Orientació dels eixos del sistema isomètric a 120° dos a dos
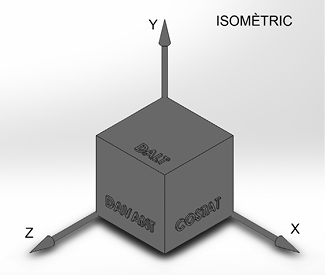
Font: elaboració pròpia
Un inconvenient afegit al sistema isomètric és que sovint hi ha una desafortunada alineació en arestes i contorns de peces amb cares ortogonals i mides coincidents. Com que es basa en la projecció de rajos paral·lels no hi ha disminució de la mida dels objectes a causa de la distància. Aquest efecte dificulta la comprensió de determinades peces, sobretot quan hi ha coincidència en les mides de l’objecte (com passa, per exemple, en un cub).
Els sistemes dimètric i trimètric, en canvi, gestionen els eixos per a orientar la perspectiva en favor d’una de les cares.
Figura 12. Comparativa del repartiment dels angles entre dimètric i trimètric
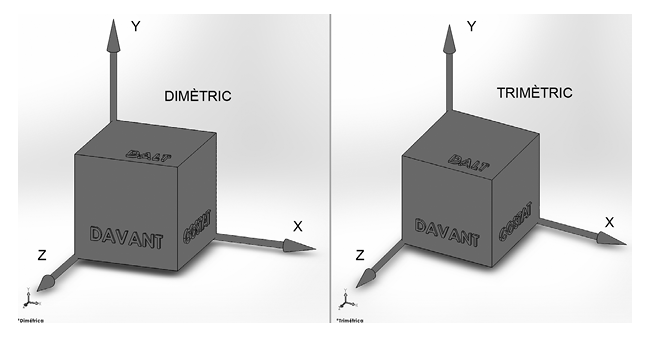
Font: elaboració pròpia
Pel que fa al dimètric, només dos dels tres eixos tenen el mateix angle d’inclinació (116,57°). Això els representa a la mateixa escala. El tercer eix es representa en una inclinació més forçada (126,87°) i se li podria aplicar un factor d’escala diferencial.
Com es veu en la figura 12, això realça un dels tres costats de l’objecte.
Aquest tipus de representació el fa comparable (en angles i en factors d’escala) a la perspectiva cavallera.
Finalment, el sistema trimètric, gestiona cada eix amb un angle diferent, cosa que impedeix obtenir les veritables magnituds encara que les arestes estiguin alineades amb els eixos.
Les inclinacions entre eixos són de 104,04°, 126,87° i 129,09°.
Es podria dir que és un terme mitjà entre la perspectiva isomètrica i la dimètrica.
Figura 13. Comparativa entre les diferents representacions axonomètriques d’un conjunt d’objectes
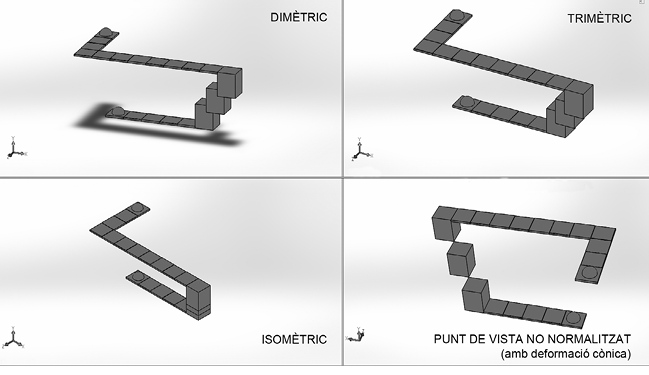
Font: elaboració pròpia
En la figura anterior es pot apreciar com la perspectiva menys afortunada per a la comprensió de l’escena d’objectes 3D implementada en un ordinador és la isomètrica (baix-esquerra). Com que les perspectives dimètrica (dalt-esquerra) i trimètrica (dalt-dreta) tenen un «desempat» en l’alineació dels eixos ortogonals, sovint permeten més claredat en la representació dels objectes.
2.2.2. Projecció obliqua
Tal com observem en la figura 8, en una projecció obliqua els rajos paral·lels de projecció no són perpendiculars al pla en què es representa la vista. La perspectiva cavallera i la militar són els sistemes de projecció obliqua més emprats.
Però, quin sentit té utilitzar un nou sistema de representació de perspectives amb les limitacions de la projecció paral·lela quan el sistema de perspectiva cònic és més versemblant en els seus resultats?
La característica principal de la projecció obliqua és la facilitat amb què es fan les representacions pictòriques, ja que dos dels tres eixos són en veritable magnitud.
És a dir, a partir d’una vista ortogonal (de les multivista) es pot «aixecar» fàcilment la tercera dimensió, que podrà tenir un factor de reducció.
Així, en el sistema de perspectiva cavallera, dues de les tres magnituds (les de l’alçat) es representen en veritable magnitud. La tercera, normalment referida a la profunditat, es desenvolupa per extrusió en 30° (com en la figura 14) o en 45°.
Figura 14. Perspectiva cavallera «aixecada» a partir de l’alçat d’una peça simple
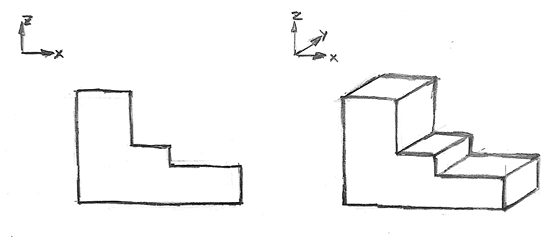
- • Esquerra: alçat (sistema multivista)
- • Dreta: perspectiva cavallera
Font: elaboració pròpia
En la figura 14 observem que, gràcies a tenir els eixos X i Z en veritable magnitud, el desenvolupament de la profunditat de la peça esdevé una tasca senzilla.
Finalment, quan la vista principal de l’objecte és la vista planta es recomana fer servir la perspectiva militar, també anomenada «vista d’ocell».
Figura 15. Perspectiva militar «aixecada» a partir de la planta d’una construcció
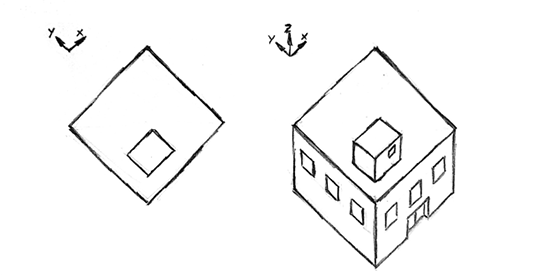
- • Esquerra: planta (sistema multivista)
- • Dreta: perspectiva militar
Font: elaboració pròpia
Una particularitat de la perspectiva militar és la rotació a 45° de la vista de planta, de manera que la planta continua en veritable magnitud, però en diagonal. Així s’aconsegueix il·lustrar la informació «aixecada» dels dos eixos X i Y.