Security Analysis (Edición de 1962)
Capítulo 39. Métodos recientes para la valoración de acciones de crecimiento
Introducción histórica
Hemos definido previamente la acción de crecimiento como aquella que ha aumentado los beneficios por acción durante algún tiempo a un ritmo más rápido que la tasa media y de la que se espera que mantenga esta ventaja durante algún tiempo en el futuro. (Para nuestra comodidad, hemos definido la auténtica acción de crecimiento como aquella de la que se espera que crezca como mínimo a un ritmo anual del 7,2 por ciento –que si se mantiene conseguiría doblar los beneficios al cabo de diez años– aunque otros pueden establecer una tasa mínima más baja). Unos buenos datos en el pasado y un futuro excepcionalmente prometedor siempre han constituido una atracción importante para los inversores así como para los especuladores. En los mercados bursátiles anteriores a los años 20 del pasado siglo, el crecimiento esperado estaba subordinado en importancia, como factor de inversión, a la solidez financiera y a la estabilidad de los dividendos. A finales de la década de los años 20, las posibilidades de crecimiento se convirtieron en la consideración principal de los inversores y especuladores en acciones ordinarias. Se creía que dichas expectativas justificaban los multiplicadores extremadamente altos alcanzados por las emisiones más favorecidas. Sin embargo, los analistas financieros no se esforzaron seriamente en la elaboración de valoraciones matemáticas para las acciones de crecimiento.
La primera base detallada para tales cálculos apareció en 1931 –después del crac– en el libro de S.E. Guild, Stock Growth and Discount Tables. Este enfoque derivó en una completa teoría y técnica en el trabajo de J.B. Williams The Theory of Investment Value, publicado en 1938. El libro describía en detalle la tesis básica de que el valor de una acción ordinaria es la suma de todos sus futuros dividendos, cada uno de ellos descontado a su valor actual. Las estimaciones de las tasas del crecimiento futuro deben utilizarse para establecer el programa de dividendos futuros y, a partir de ellos, calcular el valor total reciente.
En 1938, National Investor’s Corporation fue el primer fondo de inversión que se consagró formalmente a la política de adquirir acciones de crecimiento, a las que identificaba como aquellas que habían aumentado sus beneficios desde la cima de un ciclo económico a la cima del siguiente, y de las que se podía esperar que continuaran a este ritmo. Durante los 15 años siguientes, las compañías que presentaban buenos datos de crecimiento adquirieron una popularidad cada vez mayor, aunque se hicieron escasos esfuerzos para efectuar valoraciones precisas de las mismas.
A finales de 1954 se inició el enfoque actual a la valoración de las acciones de crecimiento en un artículo de Clendenin y Van Cleave, titulado «Growth and Common Stock Values»1. En este artículo se proporcionaban tablas para encontrar los valores presentes de dividendos futuros, sobre diversos supuestos tales como la tasa y la duración del crecimiento, y también el factor de descuento. Desde 1954 se ha producido una verdadera avalancha de artículos en la prensa económica –principalmente en el Financial Analysts Journal– sobre el tema de la valoración matemática de las acciones de crecimiento. Los artículos exponen métodos y fórmulas técnicas, aplicaciones al índice Dow Jones Industrial Average (DJIA), y a numerosas cuestiones individuales, así como algunas evaluaciones críticas de la teoría de las acciones de crecimiento y del comportamiento de mercado de las acciones de crecimiento.
En este capítulo proponemos: 1) examinar de la forma más elemental posible la teoría matemática de la valoración de las acciones de crecimiento tal como se practica actualmente; 2) exponer unos pocos ejemplos de la aplicación de esta teoría, seleccionados de entre la copiosa literatura existente sobre el tema; 3) manifestar nuestras opiniones sobre la fiabilidad de este enfoque, e incluso ofrecer un sustitutivo muy sencillo para sus generalmente complicados cálculos matemáticos.
El método de la «tasa de crecimiento» permanente
Se puede encontrar fácilmente una fórmula aritmética elemental para valorar el crecimiento futuro si damos por sentado que el crecimiento a una tasa fija continuará en el futuro indefinido. Tan solo nos hace falta restar esta tasa fija de la rentabilidad anual exigida por el inversor; la diferencia nos dará la tasa de capitalización para el dividendo actual.
El método puede ejemplificarse a través de una valoración del DJIA realizada en un artículo bastante inicial sobre el tema por un importante teórico en dicho campo.2 Este estudio asumía una tasa de crecimiento permanente del 4 por ciento para el DJIA y un rendimiento global para el inversor (o «tasa de descuento») del 7 por ciento. Sobre esta base, el inversor necesitaría una rentabilidad actual por dividendos del 3 por ciento, y esta cifra determinaría el valor del DJIA. Supondremos que el dividendo aumentará cada año en un 4 por ciento y, por tanto, el precio del mercado también aumentará un 4 por ciento. Entonces, en cualquier año, el inversor obtendrá una rentabilidad por dividendos del 3 por ciento y una revalorización de mercado del 4 por ciento –ambos sobre el valor de partida– o un total de un 7 por ciento anual compuesto. El rendimiento por dividendos exigido puede ser convertido en un multiplicador de beneficios equivalente a base de asumir una tasa de pago estándar. En este artículo, la tasa de pago se situó alrededor de dos tercios; por tanto, el multiplicador de beneficios es de 2/3 de 33 o 22.3
Es importante para el estudioso entender por qué este gratamente simple método de valoración de una acción ordinaria o de un grupo de acciones tiene que ser reemplazado por métodos más complicados, en especial en el campo de las acciones de crecimiento. Funcionaría de forma bastante convincente para presuntas tasas de crecimiento de hasta, digamos, el 5 por ciento. Esta última cifra produce una rentabilidad de dividendos requerida de tan solo el 2 por ciento, o un multiplicador de 33 para los beneficios actuales, si el pago es de dos tercios. Sin embargo, cuando la tasa de crecimiento esperado se va estableciendo progresivamente a un nivel más alto, la valoración resultante de dividendos o beneficios aumenta muy rápidamente. Una tasa de crecimiento del 6,5 por ciento produce un multiplicador de 200 para el dividendo, y una tasa de crecimiento del 7 por ciento o más hace que la emisión valga infinito si paga algún dividendo. En otras palabras, sobre la base de esta teoría y este método, ningún precio sería excesivo para el pago de una acción ordinaria de tales características.4
Hace falta un método diferente
Teniendo en cuenta que una tasa de crecimiento esperado del 7 por ciento es casi el mínimo exigido para calificar a un valor como auténtica «acción de crecimiento» en la estimación de muchos analistas de valores, debería ser evidente que el anterior método de valoración simplificado no puede emplearse en dicha área. Si así se hiciera, todas las acciones de crecimiento de este tipo tendrían un valor infinito. Tanto las matemáticas como la prudencia requieren que el período de alta tasa de crecimiento se limite a un período de tiempo finito –en realidad a uno bastante breve. Después de esto, debe presumirse que el crecimiento se detiene por completo o bien que prosigue a una tasa tan modesta que permita un multiplicador muy bajo de los beneficios más recientes.
El método estándar que se emplea actualmente para las acciones de crecimiento sigue esta prescripción. Suele dar por sentado un crecimiento a una tasa relativamente alta –que varía enormemente entre las diferentes compañías– durante un período de diez años, más o menos. De ahí en adelante, la tasa de crecimiento se prevé tan baja que los beneficios en el décimo año u otro año «objetivo» pueden ser valorados por el sencillo método anteriormente descrito. Esta valoración en el año objetivo se descuenta a continuación al valor actual, como también se hace con los dividendos a recibir durante el período anterior. A continuación, los dos componentes se suman para dar lugar al valor deseado.
La aplicación de este método puede ilustrarse con la formulación de las siguientes hipótesis bastante representativas: 1) una tasa de descuento, o rentabilidad anual requerida del 7,5 por ciento,5 2) una tasa de crecimiento anual de un 7,2 por ciento durante un período de 10 años –es decir, duplicación de beneficios y dividendos en la década–; 3) un multiplicador de 13,5 para los beneficios del décimo año. (Este multiplicador corresponde a una tasa de crecimiento esperado después del décimo año del 2,5 por ciento, requiriendo una rentabilidad por dividendos del 5 por ciento. Está establecido por Molodovsky como un «nivel de ignorancia» con respecto al crecimiento posterior. Nosotros preferiríamos denominarlo «nivel de conservadurismo)». Nuestra última hipótesis sería 4) un pago medio del 60 por ciento. (Este porcentaje puede ser elevado para una compañía con un buen crecimiento).
La valoración por dólar de los beneficios presentes basándonos en dichas hipótesis se calcula de la siguiente forma:
A. Valor presente de la cotización de mercado en el décimo año. Los beneficios del décimo año serán de 2 dólares, su cotización de mercado de 27, y su valor actual un 48 por ciento de 27, es decir, 13 dólares.
B. El valor actual de los dividendos de los diez años siguientes. Comenzarán con 60 centavos, aumentarán hasta 1,20 dólares, la media será de 90 centavos, se acumularán unos 9 dólares, y estarán sujetos a un factor de valor actual de alrededor del 70 por ciento –para un período medio de espera de cinco años. El componente dividendos tiene, por tanto, un valor actual de alrededor de 6,30 dólares.
C. Valor presente total y multiplicador. Los componentes A y B suman 19,30 dólares, o bien un multiplicador de 19,3 de los beneficios actuales.
Valoración del DJIA en 1961 siguiendo este método
En un artículo de 1961, Molodovsky seleccionó el 5 por ciento como la tasa de crecimiento más verosímil del DJIA para el período 1961-1970. Esto daría lugar a un aumento del 63 por ciento en un plazo de diez años, un incremento de los beneficios desde un 1960 «normal» de, digamos, 35 dólares hasta los 57 dólares, y un precio esperado en 1970 de 765, con un valor descontado a 1960 de 365. A esto deben añadirse unos 300 dólares, el 70 por ciento de los dividendos esperados a diez años –o 210 dólares netos. La valoración de 1960 del DJIA calculada de acuerdo con este método es de 575. (Molodovsky la estableció en 590 para 1961).
Similitud con el cálculo del rendimiento de los bonos
El estudioso debería reconocer que el proceso matemático empleado anteriormente es idéntico al utilizado para determinar el precio de un bono correspondiente a un determinado rendimiento y, por tanto, el rendimiento indicado por un determinado precio. El valor, o precio apropiado, de un bono se calcula descontando el pago de cada cupón y también el pago final del principal o capital original a su valor actual, a una tasa de descuento o rendimiento requerido igual al rendimiento designado. En las valoraciones de acciones de crecimiento el precio de mercado presunto en el año objetivo corresponde al reembolso del bono al valor nominal al vencimiento.
Hipótesis matemáticas realizadas por otros
Aunque los cálculos utilizados en el ejemplo del DJIA pueden ser contemplados como bastante representativos del método general, debe señalarse que existe una diversidad bastante amplia en las asunciones específicas, o «parámetros» utilizados por diversos autores. Las tablas originales de Clendemin y Van Cleave llevan los cálculos del período de crecimiento incluso hasta 60 años. Los períodos realmente adoptados por los autores financieros en sus cálculos han incluido 5 años (Bing), 10 años (Molodovsky y Buckley), 12 a 13 años (Bohmfalk), 20 años (Palmer y Burrell), y hasta 30 años (Kennedy). La tasa de descuento también varía mucho –del 5 por ciento (Burrell) al 9 por ciento (Bohmfalk).6
La selección de tasas de crecimiento futuro
La mayoría de los tasadores de acciones de crecimiento utilizarán un período uniforme para proyectar el crecimiento futuro y una tasa de descuento o tasa uniforme de rentabilidad requerida, independientemente de las acciones que estén considerando. (Excepcionalmente, Bohmfalk divide sus acciones de crecimiento en tres clases de calidad, y varía el período de crecimiento entre 12 y 13 años, y la tasa de descuento entre el 8 y el 9 por ciento, según la clase). No obstante, es obvio que la tasa de crecimiento esperado variará de compañía a compañía, es igualmente cierto que la tasa prevista para una determinada compañía variará de un analista a otro.
Parecería que la tasa de crecimiento de cualquier compañía podría establecerse de forma objetiva si estuviera basada enteramente en datos del pasado durante un período de tiempo aceptado. Sin embargo, todos los autores financieros insisten de forma muy apropiada en que la tasa de crecimiento histórica debería considerarse solamente como uno de los factores a tener en cuenta en el análisis de una compañía y no puede aplicarse de modo mecánico para el establecimiento de la tasa de crecimiento para el futuro. Tal vez deberíamos destacar, como observación de precaución, que incluso la tasa de crecimiento histórica parece que se calcula de diferente forma por diferentes analistas.
Multiplicador aplicado a los «beneficios normales»
Los métodos descritos producen un multiplicador por dólar de los beneficios presentes. No se aplica necesariamente a los beneficios reales actuales o recientes, sino a una cifra considerada como «normal» –es decir, a los beneficios actuales tal como aparecerían en una curva de beneficios alisada. Así pues, los multiplicadores del DJIA en 1960 y 1961 eran aplicados generalmente a beneficios «línea de tendencia» que superaban a las cifras reales durante aquellos años que se presumían como «subnormales».
Dividendos frente a beneficios en las fórmulas. Una simplificación
Los métodos «modernos» de valoración de acciones de crecimiento se apartan considerablemente del concepto básico de J.B. Williams respecto a que el valor actual de una acción ordinaria es la suma de los valores presentes de todos los dividendos futuros que se esperan de la misma. Cierto, hoy en día suele realizarse un cálculo de dividendos de diez a veinte años que forma parte del valor final. Sin embargo, a medida que aumenta la tasa de crecimiento esperada de compañía a compañía, el pago previsto también tiende a disminuir, y el componente de los dividendos pierde importancia frente a los beneficios del año objetivo.
Las posibles variaciones en el pago esperado no tendrán un gran impacto en el multiplicador final. Por consiguiente el proceso de cálculo puede simplificarse a base de prever un pago uniforme para todas las compañías del 60 por ciento a lo largo de los diez años siguientes. Si T es la cifra del décimo año conseguida por 1 dólar de los beneficios presentes creciendo a una tasa determinada, el valor de los dividendos de diez años se calcula de la siguiente forma: 2,1 + 2,1T. El valor actual de la cotización de mercado del décimo año es igual al 48 por ciento de 13,5T, o aproximadamente igual a 6,5T. Por tanto, el valor total de 1 dólar de beneficios presentes –o el multiplicador final para las acciones– sería igual a 8,6T + 2,1.
La tabla 39-1 ofrece el valor de T y los consiguientes multiplicadores para diferentes tasas de crecimiento previstas.
Estos multiplicadores son un poco bajos para las pequeñas tasas de crecimiento, puesto que solo suponen un pago del 60 por ciento. Mediante este método el valor actual se calcula enteramente a partir de los beneficios actuales y el crecimiento esperado; el dividendo desaparece como factor que se calcula separadamente. Esta anomalía puede ser aceptada más fácilmente si también se tolera la importancia rápidamente descendente de los pagos de dividendos en el campo de las acciones de crecimiento.
Tabla 39-1
Tasa de crecimiento |
Ganancias del décimo año (T) |
Multiplicador de los beneficios presentes (8,6T + 2,1) |
|---|---|---|
2,5 % |
$1,28 |
13,1x |
4,0 |
1,48 |
14,8x |
5,0 |
1,63 |
16,1x |
6,0 |
1,79 |
17,5x |
7,2 |
2,00 |
19,3x |
8,0 |
2,16 |
20,8x |
10,0 |
2,59 |
24,4x |
12,0 |
3,11 |
28,8x |
14,3 |
4,00 |
36,5x |
17,5 |
5,00 |
45,1x |
20,0 |
6,19 |
55,3x |
Una aparente paradoja en las valoraciones de las acciones de crecimiento
Volvamos a las hipótesis de Molodovsky, utilizadas en nuestro modelo y consideradas como representativas. Su método exige que se presuma que todas las acciones se vendan al cabo de una década a 13,5 veces sus beneficios de dicho año. (Igualmente Bohmfalk prevé que las 100 acciones de crecimiento que valoró en su artículo se vendan entre 11 y 12,5 veces sus beneficios al cabo de 12 a 13 años). Sin embargo, es evidente que los multiplicadores de 1971 variarán de forma importante entre las diferentes compañías, y que aquellas que hayan tenido un buen crecimiento real durante los años 60 se venderán a multiplicadores mucho más altos que aquellas que hayan mostrado ligeros aumentos.
¿Por qué los tasadores no formulan la hipótesis más realista de que sus acciones se venderán en el año objetivo a un multiplicador más o menos proporcional a la tasa de crecimiento prevista? Si una acción dobla sus beneficios en un plazo de 10 años, y se presume que ahora vale 20 veces sus ganancias, ¿Por qué no podría esperarse que se venda en 1971 a no menos de 20 veces sus ganancias? No obstante, si se formula esta hipótesis, el valor actual de la acción tendría que aumentarse a más de 20 veces los beneficios actuales para evitar superar el rendimiento requerido del 7,5 por ciento. Esto sugeriría un multiplicador superior a 20 para los beneficios de 1971, y los ajustes tendrían que repetirse hasta que el valor actual se acerque a infinito.
El hecho matemático es que para cualquier acción que se prevea que ofrezca una rentabilidad por dividendos y un crecimiento que sobrepase la tasa de descuento, el multiplicador previsto en el año objetivo debe ser más bajo que el multiplicador actual derivado. De otro modo, regresaríamos a la valoración infinita que nos hizo descartar la sencilla hipótesis de una tasa de crecimiento perpetua y de una rentabilidad por dividendos que superase el 7 o 7,5 por ciento.
La objeción a la hipótesis de un multiplicador de 13,5 al cabo de 10 años para unos beneficios que se considera que crecen, digamos, a un ritmo del 10 por ciento a lo largo de la década, puede rebatirse si se introducen en el debate la idea de conservadurismo y un factor de seguridad. Una valoración del tipo Molodovsky no debería contemplarse como ese precio presente que, de hecho, produzca una rentabilidad anual del 7,5 por ciento si el crecimiento previsto se materializa, sino como aquel que producirá una rentabilidad superior al 7,5 por ciento bajo tales condiciones. Consideramos perfectamente lógico que el inversor exija este resultado matemático como compensación por el extremado riesgo de que el crecimiento real se produzca por debajo de la cifra estimada.
Dos cálculos adicionales recomendados
Para dar a este punto una expresión concreta para el inversor, aconsejamos a los analistas que su valoración del tipo que hemos estado exponiendo se complemente con uno o dos cálculos adicionales. El primero perseguiría acercar la verdadera tasa de rentabilidad probable al inversor en caso de que se cumpla la tasa de crecimiento estimada. El supuesto más simple para este propósito es que las acciones se vendan en 1971 al mismo multiplicador de sus beneficios tal como es aplicado por el tasador a los beneficios de 1961. Teniendo en cuenta que este superará siempre al multiplicador de 13,5 utilizado en el primer cálculo, producirá una tasa de rentabilidad por encima del 7,5 por ciento básico. La diferencia indicará 1) el beneficio adicional que puede esperarse del cumplimiento de la predicción de crecimiento o 2) la magnitud del factor de seguridad incrustado en la valoración principal. El segundo cálculo de este tipo podría determinar a través de un método similar, hasta qué punto la estimación de la tasa de crecimiento real puede caer y, sin embargo, producir el 7,5 por ciento requerido por el comprador en la primera valoración.
Ilustremos la procedencia de estas cifras adicionales mediante la utilización de un valor con una tasa de crecimiento esperado del 7,2 por ciento. Su multiplicador actual, mostrado en la tabla 39-1, se estableció en 19,3 –basado en un pago del 60 por ciento y en un multiplicador del 13,5 en 1971. Supongamos ahora que el multiplicador real de 1971 sea 19,3 considerado adecuado para 1961, Esto añadirá 11,60 dólares al valor de 1971 de 1 dólar de beneficios presentes. A través de una hábil manipulación de las tablas de interés compuesto podemos establecer que, sobre la nueva base del valor de 1971, la tasa de rentabilidad materializada por el inversor a 19,3 veces los beneficios de 1961 será de alrededor del 10 por ciento en lugar del básico 7,5 por ciento. Igualmente, aunque la tasa de crecimiento real muestre solamente un 5 por ciento de media, pero el multiplicador se mantuviera al 19,3, el inversor todavía obtendría a este precio su rentabilidad objetivo del 7,5 por ciento.
Estos cálculos no están en absoluto libres de contaminación matemática, pero pensamos que no van muy desencaminados en su implicación de que la fórmula de valoración original incluya un factor de seguridad de alrededor de un tercio.
Usos de las valoraciones de las acciones de crecimiento
Es evidente que el uso más directo y positivo de un conjunto de valoraciones de acciones de crecimiento realizadas por cualquiera de los métodos propuesto sería la selección de valores atractivos (infravalorado) y la identificación de los sobrevalorados. Las dos técnicas descritas más arriba –las de Molodovsky y Bohmfalk– se aplicaban de esta forma en los estudios respectivos. La primera descubrió un «valor de inversión» para cada una de las acciones que integraba el DJIA y lo comparó con el precio concurrente. Se descubrió que el nivel de febrero de 1961 de la unidad considerada como un todo (649) estaba un 10 por ciento por encima de su valor de inversión de 590; cinco de los componentes se vendían entre un 75 por ciento y un 95 por ciento de valor; quince entre el 100 y el 120 por cien, y diez entre el 120 y el 153 por ciento. Estas valoraciones, y las indicaciones resultantes respecto a si el mercado estaba barato o caro dependían tanto del enfoque de la fórmula específica utilizada por Molodovsky como de su decisión acerca de las tasas de crecimiento anuales estimadas. La segunda variaba entre un nominal del 1 ½ por ciento de United Aircraft a un máximo del 10 por ciento para Alcoa y Eastman Kodak.
Bohmfalk compara sus valoraciones con el precio actual de un modo diferente. Él calcula la tasa de crecimiento implícita en el precio presente –es decir, la tasa que, a través de sus fórmulas, produciría un valor igual al precio de julio de 1960. Esto se realiza para 93 acciones clasificadas en tres grupos de calidad. (Él utiliza tasas de descuento y períodos de crecimiento moderadamente diferentes para cada grupo). En su mayor parte, sus tasas de crecimiento previstas están bastante cerca de aquellas que están implícitas en el precio de mercado. (Toma el 6,5 por ciento para el DJIA, cifra que descubrió que era tanto su tasa histórica durante los últimos 13 años como la tasa del precio de mercado). No obstante, en dos casos su tasa es prácticamente tres veces la tasa de mercado; en uno de los casos la tasa de mercado está un 40 por ciento por encima de la suya.
Puede ser interesante comparar el crecimiento futuro seleccionado por Molodovsky y Bohmfalk para las nueve acciones que aparecen en ambas listas. Añadimos la tasa «histórica» o de 1946-1959 tal como fue descubierta por Bohmfalk.
La tabla 39-2 indica que las tasas de crecimiento históricas desempeñan un papel importante, aunque de ningún modo determinante, en la previsión de crecimiento futuro, y también que se pueden establecer diferencias de opinión bastante considerables sobre las tasas a adoptar para una determinada compañía por parte de analistas extremadamente competentes.
Tabla 39-2. Comparativa de tasas de crecimiento históricas y previstas de nueve
|
Históricas |
Previsiones de Bohmfalk |
Previsiones de Molodovsky |
|---|---|---|---|
Allied Chemical & Dye |
7,5 % |
10,0 % |
6,0 % |
Alcoa |
12,0 |
13,0 |
10,0 |
Du Pont |
10,0* |
10,0* |
7,0 |
Eastman Kodak |
9,5 |
11,5 |
10,0 |
General Electric |
9,0 |
10,0 |
10,0 |
Goodyear |
12,0 |
9,0 |
5,0 |
International Paper |
4,5 |
8,5 |
3,5 |
Procter & Gamble |
6,0 |
9,0 |
8,0 |
Union Carbide |
9,0 |
9,5 |
5,0 |
*Excluida General Motors
Otras utilizaciones del enfoque de valoración
Una serie de estudios sobre el tema se han consagrado a las diversas interrelaciones existentes entre valor (como multiplicador de beneficios o dividendos presentes), tasa de crecimiento, período de crecimiento y tasa de descuento. Si se empieza con un rentabilidad por dividendos real o prevista (o multiplicador de ganancias) se puede calcular alternativamente 1) qué tasa de crecimiento es necesaria para producir un rendimiento global requerido en el plazo de un número determinado de años, 2) cuántos años de crecimiento a diversas tasas serían necesarios para producir el rendimiento requerido, y 3) qué rentabilidades reales se derivarían de determinadas tasas de crecimiento en determinados períodos8 Sin duda, estas exposiciones son valiosas para el analista porque le hacen consciente de las implicaciones cuantitativas por lo que respecta a las tasas de crecimiento y períodos que deben interpretarse dentro del precio de mercado actual de una acción de crecimiento.
Lecciones de la experiencia pasada
Un estudio de los resultados de inversión reales en grupos de acciones de crecimiento populares hace hincapié en la necesidad de un margen de seguridad sustancial cuando se calculen los valores presentes de tales valores. Sabemos, por supuesto, que cuando unas elevadas tasas de crecimiento se han prolongado durante largos períodos de tiempo, a los inversores les ha ido muy bien con dichos valores, aunque hayan pagado un multiplicador muy alto de los beneficios actuales en aquel momento. El ejemplo más destacado de una experiencia de este tipo nos lo proporciona International Business Machines (IBM). Sus aparentemente altos precios de venta en el pasado siempre han resultado ser bajos a la luz del posterior crecimiento de beneficios y de los posteriores aumentos de su cotización. El multiplicador de 1961 de, digamos, 80 veces, los beneficios actuales también podría demostrar la existencia de una infravaloración si la tasa de crecimiento histórica se mantiene durante un período suficientemente largo en el futuro. En general, los inversores se han sentido tan animados por el brillante rendimiento ofrecido por IBM como para pensar que cualquier compañía que ofrezca unos buenos datos de crecimiento reciente y, supuestamente, con unas excelentes perspectivas de continuidad, se puede adquirir con seguridad a un multiplicador correspondientemente alto.9
Cuando la experiencia de las acciones de crecimiento se contempla como un todo, y no simplemente bajo la luz cegadora de los logros obtenidos por IBM, emerge un cuadro bastante diferente. Se podría haber esperado que el rendimiento general de las acciones de crecimiento a lo largo de las dos últimas décadas hubiera sido decididamente más alto que el del mercado en su conjunto, aunque solo fuera a causa de su creciente popularidad en el mercado y, por tanto, han dispuesto de un factor adicional que ha ayudado a sus cotizaciones de mercado. Los datos disponibles indicarían que los hechos difieren de esta razonable expectativa. Veamos a continuación tres estudios o compilaciones sobre este punto:
1. En un artículo de T.E. Adderley y D.A. Hayes, titulado «The Investment Performance of Selected Growth Stock Portfolios» (Finanacial Analysts Journal, mayo de 1957), los autores rastrean anualmente hasta finales de 1955 los resultados de la inversión en cada una de las cinco carteras de acciones de crecimiento recomendadas en los artículos publicados en una revista económica en 1939, 1940, 1941, 1945 y 1946. Los resultados para cada cartera y cada año, incluidos y excluidos los dividendos, se compararon con los correspondientes resultados del DJIA. En conjunto, el rendimiento es sorprendentemente paralelo. Veamos el resumen a continuación:
Tabla 39-3. Ganancias totales, incluyendo los dividendos recibidos
Período de mantenimiento |
Carteras recomendadas |
DJIA |
|---|---|---|
3 años |
26 % |
22 % |
5 años |
65 |
60 |
10 años |
153 |
165 |
Los aumentos medios totales para los diversos períodos (de 9 a 16 años) hasta el fin de 1955 fueron del 307 por ciento para las carteras y del 315 por ciento para el DJIA.
2. El artículo de Bohmfalk ofrece los datos de 24 acciones de crecimiento seleccionadas para el período 1946-1957. Sus resultados anuales compuestos oscilan entre el 6 por ciento para Air Reduction y el 25 por ciento para IBM. El autor señala que la media de rendimiento de su lista era del 13 por ciento, porcentaje comparable al 13,4 por ciento mostrado en la misma tabla para los 425 valores industriales de Standard & Poor’s.
3. En Investment Companies 1961 de Arthur Wiesenberger se efectúa un análisis independiente de fondos de apreciación por crecimiento. Los resultados para el período 1951-1960 están disponibles para 20 fondos bajo la hipótesis de reinversión de todos los repartos procedentes de los beneficios de los valores y otras fuentes de capital. El rango de aumento total para el período de 10 años oscila desde el 127 por ciento al 392 por ciento, con una media del 289 por ciento. El dato correspondiente para el S & P’s 500 Stock Composite Average es del 322 por ciento.10
Comentario. Los resultados de estos tres estudios señalan los problemas básicos de la selección de valores en la Bolsa basándose principalmente en la tasa de crecimiento futuro esperada. No conocemos el grado de participación de los métodos de valoración matemática en los resultados que hemos comparado con los promedios del mercado. Es posible, aunque de ningún modo seguro, que unas técnicas perfeccionadas del tipo que hemos descrito antes en este capítulo puedan producir un mejor rendimiento comparativo en años futuros. Sin embargo, debemos manifestar una desconfianza muy profunda respecto al empleo de cálculos matemáticos depurados para llegar a valoraciones que en última instancia están basadas en proyecciones inherentemente inexactas de rendimiento de muchos años en el futuro.
Nuestro abordaje a la valoración de las acciones de crecimiento
Los autores de este libro, a nivel individual y colectivo, han trabajado en este problema en los últimos años y han desarrollado varios métodos y fórmulas. A continuación, describiremos brevemente tres de estos planteamientos. Sorprende en cierto modo que los multiplicadores producidos para determinadas tasas de crecimiento muestren tan solo ligeras diferencias entre las respectivas técnicas.
Nuestro primer método procuró aplicar a las acciones de crecimiento el mismo tratamiento básico que hemos recomendado en general para las acciones corrientes, excepto que hemos eliminado el factor dividendos en la valoración. Esto significa que el valor se encontraría a través de la aplicación de un multiplicador adecuado a los beneficios medios de los siete años siguientes. Para cualquier tasa de crecimiento esperado esta media sería aproximadamente igual a la mitad o a los beneficios del cuarto año. (Observe que esto no reduce nuestro período de crecimiento contemplado por debajo de siete años: el multiplicador del dato del séptimo año).
Nuestro rango de multiplicadores se estableció atendiendo a dos consideraciones. La primera fue una limitación de las tasas de crecimiento de siete años a un 20 por ciento anual. Este límite superior contemplaría una expansión de los beneficios de 3,5 veces en siete años –una cifra ciertamente suficiente para cualquier expectativa de inversión. Nuestro segundo paso consistió en establecer un multiplicador máximo similar de 20 veces la media o los beneficios del cuarto año. Este máximo se estableció arbitrariamente al 150 por ciento del multiplicador 13 asignado a empresas sólidas y grandes de perspectivas medias, como el grupo del DJIA en el conjunto, para el cual prevemos un crecimiento futuro del 3,5 por ciento anual. Estas premisas indicarían que los multiplicadores deberían aumentar de forma proporcional de 13 a 20 a medida que la tasa de crecimiento esperado se incremente del 3,5 por ciento al 20 por ciento. La tabla resultante se concretaría de la forma siguiente:
Tabla 39-4
Tasa de crecimiento esperado (durante 7 años) |
Multiplicador de media (beneficios del cuarto año) |
Multiplicador de las beneficios actuales |
|---|---|---|
3,5 % |
13x |
15x |
5,0 |
14x |
17x |
7,2 |
15x |
20x |
10,0 |
16x |
23,5 |
12,0 |
17x |
27x |
14,3 |
18x |
31x |
17,0 |
19x |
35,5 |
20,0 |
20x |
41,5x |
Esta planificación guarda un parecido casual con la técnica de Molodovsky, en el sentido de que todos los multiplicadores de los beneficios proyectados para el séptimo año caerían dentro del estrecho rango de 11,5 a 12,5. Sin embargo, el estudioso debería recordar que los métodos de Molodovsky y la mayor parte de los otros métodos descritos anteriormente conllevan un cálculo de ingresos por dividendos y un factor de descuento, ninguno de los cuales son tenidos en cuenta aquí.
Nuestro segundo enfoque fue desarrollado de forma independiente por Charles Tatham y fue publicado por su firma en 196111. Se ha descrito en su libro en el capítulo sobre «Valoración de las acciones ordinarias de servicio público (capítulo 43).
Por último, nuestro estudio de los diversos procesos matemáticos utilizados por otros expertos nos llevó a formular dos métodos muy simplificados para obtener aproximadamente los mismos resultados que los conseguidos a través de cálculos más complicados. El primero fue nuestro multiplicador «8,6T más 2,1», establecido directamente a partir del concepto de Molodovsky que se ha comentado previament. El segundo es todavía más sencillo y quedaría así:
Valor = beneficios actuales «normales» × (8,5 más 2C), donde C es la tasa de crecimiento anual medio que se espera para los próximos 7 a 10 años
Las cifras concretas de esta fórmula se derivan en gran medida del concepto de que un multiplicador de 8,5 es apropiado para una compañía con un crecimiento esperado nulo, y un multiplicador actual de 13,5 es satisfactorio para otra cuyo crecimiento esperado es del 2,5 por ciento. (Esta última es una hipótesis de Molodovsky). Además, los multiplicadores resultantes de otras tasas previstas parecen tan razonables como aquellos calculados más laboriosamente por otros.
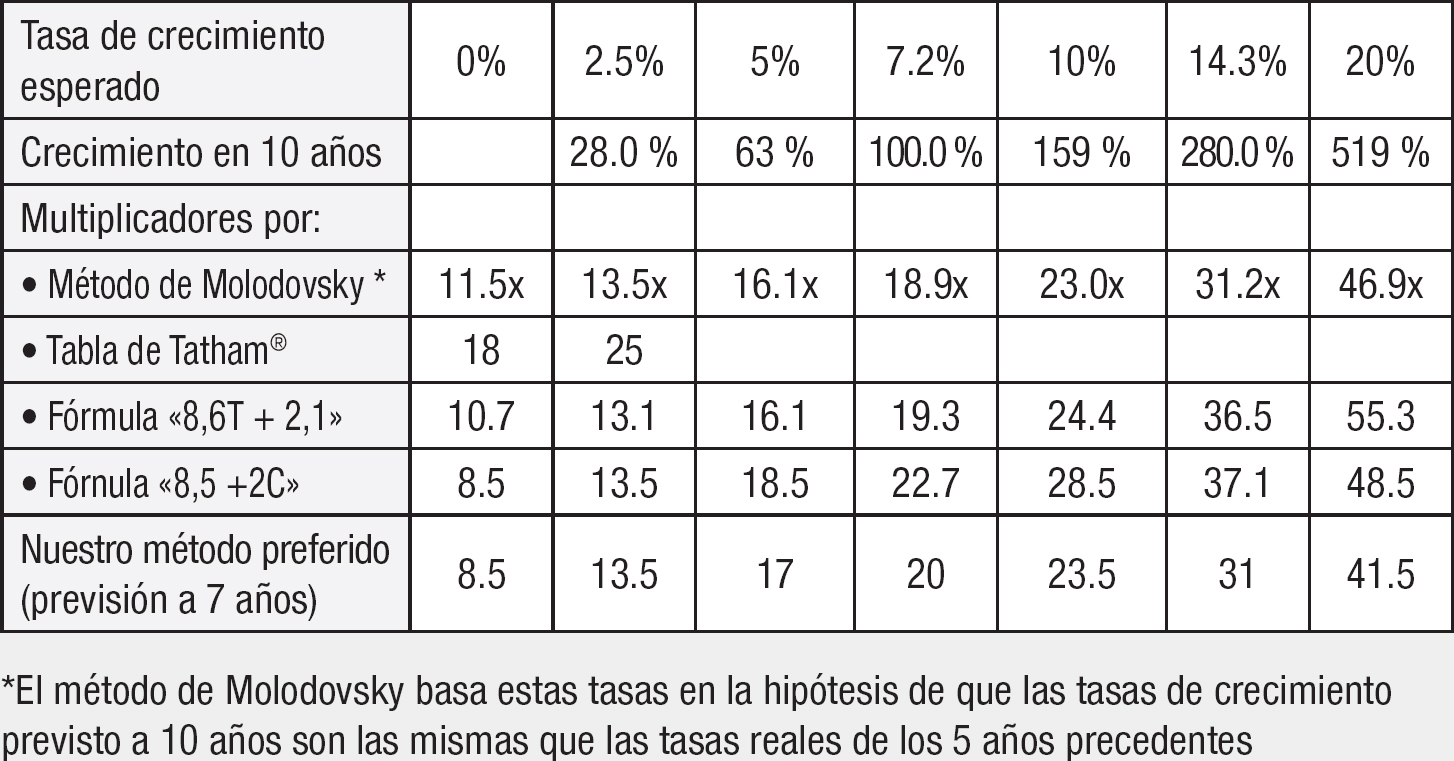
En la tabla 39-5 se refleja una comparación de nuestros cuatro multiplicadores independientes para diversas tasas de crecimiento, junto a los resultados típicos del método de Molodovsky.
Debemos señalar que nuestro método preferido, basado en una previsión de crecimiento a 7 años, produce unos multiplicadores actuales bastante próximos a los derivados de otras fórmulas para tasas de crecimiento de hasta el 10 por ciento. Para tasas más elevadas nuestros multiplicadores recomendados son más conservadores que el resto. Esto es consecuencia en parte del gran impacto del crecimiento del octavo al décimo año de tasas tan optimistas, y en parte de nuestras autoimpuestas limitaciones de 20 veces los beneficios del cuarto año. Como ya hemos manifestado nuestra falta de confianza y seguridad en predicciones de grandes aumentos porcentuales durante muchos años en el futuro, no tenemos nada más que decir para defender nuestro conservadurismo en este intervalo.12
Tabla 39-5
Notas
1. Journal of Finance, diciembre de 1954.
2. Ver N. Molodovsky, «An Approach of the Dow-Jones-Average », Commercial and Financial Chronicle, 30 de octubre de 1958.
3. Molodovsky previó aquí un «nivel de beneficios a largo plazo» de tan solo 25 dólares la unidad en 1959, frente a la cifra real de 34 dólares. Su multiplicador de 22 produjo una valoración de 550 dólares. Más adelante iba a cambiar su método de forma significativa, lo cual comentamos más adelante
4. David Durand ha comentado sobre el paralelismo que existe entre este aspecto de la valoración de acciones de crecimiento y la famosa anomalía matemática conocida como la «Paradoja de Petersburgo». Véase su artículo en el Journal of Finance, setiembre de 1957.
5. Molodosvky adoptó posteriormente esta tasa en lugar de su anterior del 7 por ciento, al descubrir que el 7,5 por ciento era la realización media total de los propietarios de acciones ordinarias entre 1871 y 1959. Estaba integrada por una rentabilidad media por dividendos del 5 por ciento y una tasa de crecimiento anual compuesto de, aproximadamente, el 2,5 en ganancias, dividendos y precio de mercado.
6. Ver R.A. Bing, «Can We Improve Methods of Appraising Growth Stocks?» Commercial & Financial Chronicle, 13 de setiembre de 1956; «The Growth Stock Philosophy», por J. F. Bohmfalk, Jr., Financial Analysts Journal, noviembre de 1960; J.G. Buckley, «A Method of Evaluation Growth Stock», Financial Analysts Journal, marzo de 1960; «A Mathematical Approach to Growth-stock Valuation», por O.K. Burrell, Financial Analysts Journal, mayo de 1960; R.E. Kennedy, Jr., «Growth Stocks: Opportunity or Illusion», Financial Analysts Journal, marzo de 1960; G.H. Palmer, «An Approach to Stock Valuation», Financial Analysts Journal, mayo de 1956; y los diversos artículos de Molodovsky.
7. Observe que la tasa de crecimiento de los últimos 10 años de Dow Chemical fue establecida en 1960 por Kennedy en un 16 por ciento, por Bohmfalk, en un 10 por ciento y por Buckley en un 6,3 por ciento. Ver nota al pie previa.
8. Un artículo escrito por R.Ferguson en el número de mayo-junio de 1961 de Financial Analysts Journal, página 29, contiene una ingeniosa disposición de diversos datos en columnas que pueden utilizarse para realizar fácilmente una serie de cálculos de este tipo.
9. La diferencia entre retrospectiva y prospectiva en la selección de acciones de crecimiento está muy bien ilustrada en este ejemplo de IBM. El estudio de la SEC (Securities and Exchange Commission) (a publicarse en 1962) demuestra que a finales de 1952, los 118 fondos cubiertos tenían solo un 0,5 del 1 por ciento de sus activos en acciones de IBM. Este valor ocupaba el puesto 23 en una lista de los valores más importantes. Estos inversores institucionales actuaban con prudencia debido al multiplicador relativamente alto de las acciones de IBM en 1952. No fueron capaces de prever con la seguridad suficiente su prometedor rendimiento venidero que les empujara a realizar una inversión concentrada en dichas acciones. Aunque participaron hasta cierto punto en su espectacular avance posterior, este beneficio fue relativamente poco importante por el pequeño volumen de los valores en cartera.
10. No se efectúa deducción alguna de estos resultados de rendimiento por las cargas de ventas sobre las participaciones de fondos de inversión o coste de comisión sobre la «cartera» S&P. Véase también el tercer cálculo en la Nota 10, página 741, del Anexo.
11. Price-Earnings Ratio and Earning Growth, Bache & Company, Nueva York, 2 de octubre de 1961.
12. El argumento para no pagar múltiplos extremadamente altos es extraordinariamente persuasivo. En este aspecto, el estudioso debería leer «Price-Earnings Ratios», de S.F. Nicholson en el Financial Analysts Journal, julio-agosto de 1960, páginas 43-45. En un estudio realizado sobre 100 acciones ordinarias, principalmente valores industriales de calidad inversora, entre ellas muchas de las compañías más importantes, en 11 períodos de tiempo seleccionados desde 1939 hasta 1959, el autor descubrió que las acciones que se vendían a los múltiplos más bajos mostraban una apreciación mucho mayor que las acciones que se vendían a los múltiplos más altos, y que los valores individuales que mostraban pérdidas durante dichos períodos o que mostraban una apreciación relativamente leve se encontraban predominantemente en los grupos de múltiplos altos. Un estudio similar de 20 acciones de compañías pertenecientes al sector químico ofreció unos resultados comparables. Por ejemplo, «el 50 por ciento de los valores con los ratios PER más bajos mostraban en promedio una apreciación un 50 por ciento más alta que la de los valores con los ratios PER más elevados». Entre las conclusiones de Nicholson encontramos la siguiente declaración, «al parecer muchos inversores han subestimado la importancia de unas relaciones precio-beneficios razonables».