2
Maestro del sendero
Liu Hui

Liu Hui
Floreció: Cao Wei, China, siglo III d. C.
Zhoubi suanjing (El clásico matemático del gnomon y los senderos circulares del cielo), el texto matemático chino más antiguo que se conoce, data del período de los Reinos Combatientes, entre el 400 y el 200 a. C. Se inicia con un bello pasaje de propaganda educativa:
Tiempo atrás, Rong Fang le preguntó a Chen Zi: «Maestro, recientemente he oído algo sobre su Sendero. ¿Es cierto que su Sendero permite comprender la altura y tamaño del Sol, el área iluminada por su luz, la magnitud de su movimiento diario, las cifras de sus mayores y menores distancias, el alcance de la visión humana, los límites de los cuatro polos, las constelaciones en que se ordenan las estrellas, y la longitud y amplitud de los cielos y la Tierra?».
«Es cierto», dijo Chen Zi.
Rong Fang preguntó: «Aunque no soy inteligente, Maestro, me gustaría que me obsequiara con una explicación. ¿Puede alguien como yo acceder a este Sendero?».
Chen Zi le contestó: «Sí, toda la matemática está a tu alcance. Tu capacidad para la matemática es suficiente para comprender estas cuestiones si reflexionas sobre ellas con tesón».
El libro procede entonces a derivar una cifra para la distancia de la Tierra al Sol con la ayuda de la geometría. Su modelo cosmológico era primitivo: una Tierra plana bajo un cielo circular plano. Pero su matemática era bastante sofisticada. En esencia, usaba la geometría de los triángulos semejantes aplicada a las sombras proyectadas por el Sol.
El Zhoubi demuestra el avanzado estado de la matemática china en una época que corresponde, más o menos, al período helenístico griego, desde la muerte de Alejandro Magno en el 323 a. C. hasta el 146 a. C., cuando la República de Roma anexionó Grecia a su imperio. Este período fue el punto álgido del dominio intelectual griego clásico, la época en que vivieron la mayoría de los grandes geómetras, filósofos, lógicos y astrónomos del mundo clásico. Incluso bajo el dominio romano, Grecia siguió produciendo avances culturales y científicos hasta aproximadamente el 600 d. C., pero los centros de innovación matemática se desplazaron a China, Arabia e India. La frontera del progreso matemático no regresó a Europa hasta el Renacimiento, aunque la Edad Oscura no fue tan oscura como a veces se nos quiere presentar, y en toda Europa se siguieron produciendo pequeños avances.
Los progresos realizados en China son sorprendentes. Hasta hace poco, la mayoría de las historias de la matemática adoptaban una perspectiva eurocéntrica y los ignoraban, hasta que George Gheverghese Joseph escribió sobre la matemática antigua del Lejano Oriente en La cresta del pavo real. Entre los más grandes matemáticos de la antigua China se encuentra Liu Hui. Descendiente del marqués de Zixiang de la dinastía Han, vivió en el estado de Cao Wei durante el período de los Tres Reinos. En 263 editó y publicó un libro con soluciones a los problemas matemáticos presentados en el famoso libro de matemáticas chino Jiuzhang Suanshu [Los nueve capítulos sobre el arte matemático].
Su obra incluye una demostración del Teorema de Pitágoras, de teoremas de geometría de sólidos, una mejora a la aproximación de Arquímedes a π y un método sistemático para resolver ecuaciones lineales con varias incógnitas. También escribió sobre prospección, con especial aplicación a la astronomía. Probablemente visitase Luoyang, una de las cuatro antiguas capitales de China, y midiese la sombra del Sol.

Los registros de la historia antigua de China nos han llegado a través de unos pocos textos posteriores, como las Memorias históricas (hacia el 110 a. C.) de Sima Qian, un escriba de la dinastía Han, y los Anales de bambú, una crónica histórica escrita sobre tiras de bambú, sepultada en la tumba del rey Xiang de Wei en el 296 a. C. y desenterrada en el 281 d. C. Según estas fuentes, la civilización china comenzó en el tercer milenio antes de Cristo con el reino Xia. Los registros escritos comienzan con la dinastía Shang, que rigió del 1600 al 1046 a. C. y nos dejó la prueba más antigua del método de contar de los chinos con huesos de oráculo, huesos marcados para la adivinación. La invasión de los Zhou condujo a un estado más estable con una estructura feudal, que comenzó a desmembrarse tres siglos más tarde, cuando otros grupos comenzaron a cobrar fuerza.
Hacia el 476 a. C. se inició una época de anarquía, un período conocido como los Reinos Combatientes, que se prolongó durante más de dos siglos. El Zhoubi se escribió durante aquellos tiempos turbulentos. Sus principales contenidos matemáticos son lo que hoy conocemos como Teorema de Pitágoras, fracciones y aritmética; también incluye una buena dosis de astronomía. El Teorema de Pitágoras se presenta en una conversación entre el duque de Zhou y el noble Shang Kao. Su discusión sobre los triángulos rectángulos los lleva a enunciar el famoso teorema, del que dan una demostración geométrica. Durante algún tiempo los historiadores creyeron que este descubrimiento había precedido a Pitágoras en medio milenio. En la actualidad, la opinión general es que fue un descubrimiento independiente anterior a Pitágoras, pero no por mucho.
Un importante sucesor del mismo período general es el ya mencionado Jiuzhang, que contiene una gran cantidad de información, como el cálculo de raíces, la resolución de sistemas de ecuaciones, áreas y volúmenes, y, una vez más, sobre los ángulos rectángulos. Una apostilla de Zhang Heng del 130 d. C. da una aproximación a π como 10. El comentario del Zhoubi de Chao Chun Chin, que data del siglo III d. C., añade un método para resolver ecuaciones cuadráticas. El desarrollo más influyente de los que contiene el Jiuzhang se debe al mayor matemático chino de la Antigüedad, Liu Hui, en el año 263 d. C. Presenta el libro con una explicación:
En el pasado, el tirano Qin hizo quemar documentos escritos y destruyó el conocimiento clásico. Más tarde, Zhang Cang, el marqués de Peiping, y Geng Shouchang, vicepresidente del ministro de agricultura, se hicieron célebres por su talento para el cálculo. Como los textos antiguos se habían deteriorado, Zhang Cang y su equipo produjeron una nueva versión eliminando las partes más pobres y rellenando las lagunas. De este modo, revisaron algunas partes, y estas resultaron ser diferentes de las antiguas.
En concreto, Liu Hui proporcionó demostraciones de que los métodos del libro funcionaban, para lo cual utilizó técnicas que hoy en día no consideraríamos rigurosas, de modo parecido a las de Arquímedes en El método. También hizo aportaciones a la prospección, que luego publicó de forma separada con el título de Haidao Suanjing [Manual de matemáticas para islas marinas].

El primer capítulo de Jiuzhang explica cómo calcular las áreas de campos que tengan distintas formas, como rectángulos, triángulos, trapecios y círculos. Sus reglas eran correctas, salvo para el círculo. Aun así, también en este caso la «receta» era correcta: multiplicar el radio por la mitad de la circunferencia. Sin embargo, calculaba la circunferencia como tres veces el diámetro del círculo, lo que equivale a tomar π = 3. Desde un punto de vista práctico, la regla subestima el área en menos del 5%.
A finales del siglo I d. C. el regente Wang Mang solicitó al astrónomo y hacedor de calendarios Liu Hsing que pensara en una medida estándar para el volumen. Liu Hsing fabricó una vasija cilíndrica de bronce muy precisa para que sirviera de patrón, es decir, como una medida de referencia. Se usaron en China miles de copias de esta vasija, cuyo original se encuentra hoy en un museo de Beijing. Sus dimensiones han llevado a algunos a sugerir que Liu Hsing, en términos prácticos, habría utilizado un valor de π en torno a 3,1547. (Cómo se puede obtener una cifra tan precisa a partir de la medición de un contenedor de bronce es algo que se me escapa.) El Sui Shu (la historia oficial de la dinastía Sui) contiene una afirmación que equivale a decir que Liu Hsing habría hallado un nuevo valor para π. Liu Hui señala que, por aquel entonces, el astrólogo de la corte Chang Heng había propuesto calcular π como la raíz cuadrada de 10, que es 3,1622. Está claro que se comenzaba a manejar valores de π claramente mejores.
En su comentario sobre el Jiuzhang, Liu Hui señala que la regla tradicional «π = 3» es errónea: en lugar de la circunferencia del círculo, da el perímetro de un hexágono inscrito, que claramente es menor. Calculó entonces un valor más preciso para la circunferencia (y, de manera implícita, para π). De hecho, fue más allá, pues describió un método de cálculo para estimar π con precisión arbitraria. Su enfoque era parecido al de Arquímedes: aproximarse al círculo mediante polígonos regulares de 6, 12, 24, 48, 96, ... lados. Para aplicar el método exhaustivo, Arquímedes usó una secuencia de polígonos inscritos en el círculo, y una segunda secuencia de polígonos circunscritos, ajustados por fuera. Liu Hui usó únicamente polígonos inscritos, pero al final de su cálculo ofreció un argumento geométrico para acotar el valor verdadero de π por arriba y por abajo. Este método arroja aproximaciones de π de precisión arbitraria sin usar nada más difícil que raíces cuadradas. Estas pueden calcularse sistemáticamente; el método es laborioso pero no más complejo que una larga multiplicación. Un matemático hábil podía obtener diez decimales de π en un día.
Más tarde, hacia el 469 d. C., Zu Chongzhi extendió el cálculo hasta demostrar que
3,1415926 < π < 3,1415927
El resultado quedó registrado, no así su método, que tal vez explicase en su obra perdida Su Shu [Método de interpolación]. Tal vez usase el método de Liu Hui, pero el título del libro sugiere la estimación de un valor más preciso a partir de un par de aproximaciones, una demasiado pequeña y la otra demasiado grande. Métodos como este se encuentran en las matemáticas hasta nuestros días. Hasta no hace mucho se enseñaban en la escuela, para usarlas con las tablas de logaritmos. Zu encontró además dos fracciones simples que dan una aproximación a π: el arquimédico 22/7, con dos decimales de precisión, y 355/113, con seis decimales. La primera todavía se usa en la actualidad, la segunda es bien conocida entre los matemáticos.

Una de las reconstrucciones de la demostración de Liu Hui del Teorema de Pitágoras a partir de las instrucciones que da en su libro es una ingeniosa e inusual disección. El triángulo rectángulo se muestra en color negro. El cuadrado de uno de los lados está dividido en dos por una diagonal (gris claro). El otro cuadrado se escinde en cinco trozos: un pequeño cuadrado (gris oscuro), un par de triángulos dispuestos de forma geométrica y con la misma forma y tamaño que el triángulo rectángulo original (gris medio) y un par de triángulos simétricos que rellenan el espacio sobrante (blanco). Entonces los siete trozos se juntan para formar el cuadrado correspondiente a la hipotenusa.
Hay otras disecciones, más simples, que también sirven para demostrar el teorema.
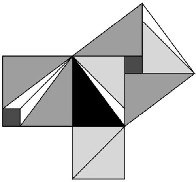
Posible reconstrucción de la demostración de Liu Hui del Teorema de Pitágoras.
Los matemáticos de la antigua China tenían tanto talento como sus contemporáneos griegos, y el curso que siguió la matemática china después del período de Liu Hui incluye muchos descubrimientos que se adelantaron a su aparición en la matemática europea. Por ejemplo, las estimaciones de π halladas por Liu Hui y Zu Chongzhi no fueron superadas en mil años.
Joseph se pregunta si algunas de sus ideas se podrían haber transmitido a la India y Arabia a caballo del comercio, y, por consiguiente, desde allí a Europa. De ser así, los posteriores redescubrimientos europeos podrían no haber sido del todo independientes. En el siglo VI había diplomáticos chinos en la India, y en el siglo VII se realizaron traducciones chinas de libros indios de matemática y astronomía. En cuanto a Arabia, un hadiz (un pronunciamiento de significado religioso) del profeta Mahoma dice así: «Busca el conocimiento, aunque esté tan lejos como China». En el siglo XIV los viajeros árabes nos informan de la existencia de vínculos comerciales formales con China, y el viajero y estudioso marroquí Muhamad ibn Battuta escribió en su rihla (libro de viaje) sobre la ciencia y la tecnología chinas, además de su cultura.
Sabemos de ideas que llegaron a la Europa medieval desde la India y Arabia, como ilustran los dos próximos capítulos, de modo que no es en absoluto imposible que también llegase conocimiento chino. La presencia jesuita en China en los siglos XVII y XVIII sirvió de inspiración a la filosofía de Leibniz, a través de Confucio. Es posible que existiera una red más compleja que transmitiese matemática, ciencia y mucho más entre Grecia, Oriente Medio, India y China. De ser así, quizá la historia convencional de la matemática necesite de una revisión.