1

No perturbéis los círculos

Arquímedes

Arquímedes de Siracusa.

Nacimiento: Siracusa, Sicilia, c. 287 a. C.

Muerte: Siracusa, c. 212 a. C.

El año: 1973. El lugar: la base naval de Skaramangas, cerca de Atenas. Todas las miradas se dirigen, concentradas, a una réplica de madera contrachapada de un navío romano. También se dirigen al navío los rayos del Sol, reflejados por setenta espejos de cobre, cada uno de un metro de ancho y metro y medio de alto.

A los pocos segundos, el navío empieza a arder, envuelto en llamas.

Ioannis Sakkas, un científico moderno, está recreando un posible mito de la ciencia de la antigua Grecia. En el siglo II a. C. el autor romano Luciano escribió que durante el sitio de Siracusa, alrededor de 214-212 a. C., el ingeniero y matemático Arquímedes inventó un ingenio para destruir barcos enemigos con el fuego. Se desconoce si ese ingenio existió y, en su caso, cómo funcionaba. La historia de Luciano podría no ser más que una referencia al uso común de flechas de fuego o trapos ardiendo disparados desde catapultas, pero cuesta imaginar que eso se presentase como un nuevo invento. En el siglo VI, Antemio de Trales sugirió, en Sobre las lentes que queman, que Arquímedes había utilizado una enorme lente. Según la leyenda más extendida, Arquímedes habría usado un espejo gigante, o tal vez una serie de espejos dispuestos en arco para formar una suerte de reflector parabólico.

La parábola es una curva en forma de U, bien conocida por los geómetras griegos. Arquímedes sin duda conocía su propiedad focal: todas las líneas paralelas a su eje, cuando son reflejadas en la parábola, pasan por el mismo punto, llamado «foco». Más incierto es que alguien se percatara de que un espejo parabólico puede enfocar la luz (y el calor) del Sol del mismo modo, dado lo rudimentario del conocimiento de la luz que poseían los griegos. Sin embargo, como muestra el experimento de Sakkas, Arquímedes no habría necesitado espejos dispuestos en parábola. Un montón de soldados, armado cada uno con un escudo reflector que de manera independiente usasen para dirigir los rayos del Sol a la misma parte del barco, habría sido igual de eficaz.

Hasta qué punto es práctico lo que suele conocerse como «rayo de calor de Arquímedes» es algo que se ha discutido acaloradamente. El filósofo René Descartes, un pionero de la óptica, no creía que pudiera funcionar. El experimento de Sakkas sugiere que sí, pero su réplica era de madera fina, y recubierta de una pintura de brea, así que ardía fácilmente. Aun así, en tiempos de Arquímedes era habitual calafatear los barcos con brea para proteger el casco. En 2005 un grupo de estudiantes del MIT repitieron el experimento de Sakkas, y consiguieron prender fuego a una réplica de madera de un barco, pero solo después de enfocar en él los rayos del Sol durante diez minutos mientras se mantenía totalmente quieto. Lo intentaron de nuevo para el programa de televisión Mythbusters [Cazadores de mitos] usando una barca de pescador en San Francisco, y lograron chamuscar la madera y producir unas pocas llamas, pero el fuego no llegó a prender. Mythbusters llegó a la conclusión de que el mito era falso.

Arquímedes fue un polímata: astrónomo, ingeniero, inventor, matemático, físico. Probablemente fuese el mayor científico (por usar el término moderno) de su tiempo. Aparte de importantes descubrimientos matemáticos, concibió inventos que sorprenden por la amplitud de sus ámbitos de aplicación, como el tornillo de Arquímedes para subir agua y el polipasto^* para levantar grandes pesos; descubrió el Principio de Arquímedes sobre la flotación de los cuerpos y la ley (no el artilugio, que apareció mucho antes) de la palanca. También se le atribuye una segunda máquina de guerra, la garra. Supuestamente utilizó este artilugio con aspecto de grúa en la batalla de Siracusa para levantar del agua buques enemigos hasta hundirlos. El documental de televisión Superweapons of the Ancient World [Superarmas del mundo antiguo], producido en 2005, construyó su propia versión de la manus ferrea, y funcionó. En los textos antiguos se encuentran muchas otras intrigantes referencias a teoremas e invenciones atribuidos a Arquímedes, entre ellos una calculadora planetaria mecánica, parecida al célebre mecanismo de Anticitera, de hacia el año 100 a. C., que se descubrió en 1900-1901 en los restos de un naufragio, aunque no logró entenderse hasta hace poco.

Es muy poco lo que sabemos de Arquímedes. Nació en Siracusa, una ciudad histórica siciliana situada hacia el extremo meridional de la costa oriental de la isla. Fue fundada en el 734 o 733 a. C. por colonos griegos, supuestamente dirigidos por el semimítico Arquias tras su exilio voluntario de Corinto. Según Plutarco, Arquias había quedado prendado de Acteón, un joven de gran belleza. Cuando sus intentos por seducirlo fracasaron, intentó secuestrarlo y en la pelea Acteón quedó descuartizado. Las súplicas de su padre Meliso no recibían respuesta, de modo que subió a lo alto de un templo de Poseidón, clamó a los dioses venganza por su hijo, y se tiró a las rocas. A estos dramáticos acontecimientos les siguió una sequía y una hambruna, y el oráculo de la ciudad declaró que solo la venganza apaciguaría a Poseidón. Arquias comprendió el mensaje y se exilió voluntariamente para evitar su sacrificio, se dirigió a Sicilia y fundó Siracusa. Más tarde su pasado lo atrapó cuando Télefo, que de niño también había sido objeto del deseo de Arquias, lo mató.

La tierra era fértil, los nativos, amables, y Siracusa no tardó en convertirse en la ciudad griega más próspera y poderosa de todo el Mediterráneo. En El contador de arena, Arquímedes dice que su padre fue Fidias, un astrónomo. En Vidas paralelas, Plutarco dice que era pariente cercano de Hierón II, tirano de Siracusa. Se cree que el joven Arquímedes estudió en la ciudad egipcia de Alejandría, en la costa del delta del Nilo, donde conoció a Conón de Samos y a Eratóstenes de Cirene. Entre las pruebas de que así era aduce su afirmación de que Conón era amigo suyo, y el hecho de que los prefacios a sus libros El método relativo a los teoremas mecánicos y El problema del ganado están dedicados a Eratóstenes.

Hay también algunas historias sobre su muerte, pero llegaremos a ellas a su debido tiempo.

La reputación matemática de Arquímedes descansa en las obras que han llegado hasta nuestros días, todas ellas como copias posteriores. La cuadratura de la parábola, que adopta la forma de una carta dirigida a su amigo Dositeo, contiene 24 teoremas sobre parábolas, el último de los cuales da el área de un segmento parabólico en función de un triángulo inscrito. La parábola ocupa un lugar destacado en su obra. Es un tipo de sección cónica, una familia de curvas que desempeñaron un importante papel en la geometría griega. Para crear una sección cónica hay que usar un plano para cortar un doble cono, formado por la unión de dos conos idénticos por su ápice. Hay tres tipos principales: la elipse, que es un óvalo cerrado; la parábola, que es una curva abierta en forma de U; y la hipérbola, dos curvas en forma de U que se dan la espalda.

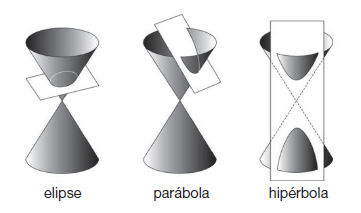
Los tres tipos principales de sección cónica.

La obra Sobre el equilibrio de los planos está formada por dos libros distintos, y establece algunos resultados fundamentales sobre lo que hoy llamamos «estática», la rama de la mecánica que analiza las condiciones bajo las cuales un cuerpo permanece en reposo. El desarrollo posterior de este tema subyace a toda la ingeniería civil, pues permite calcular las fuerzas que actúan sobre los elementos estructurales de puentes y edificios para garantizar que realmente se mantengan en reposo en lugar de ceder y derrumbarse.

El primer libro se centra en la Ley de la Palanca, que Arquímedes enuncia del siguiente modo: «Las magnitudes se encuentran en equilibrio a distancias recíprocamente proporcionales a sus pesos». Una consecuencia de ello es que una palanca larga amplifica una fuerza pequeña. Plutarco nos dice que Arquímedes lo explicó con un toque dramático en una carta al rey Hierón: «Dadme un punto de apoyo y moveré el mundo». Habría necesitado para ello una larguísima palanca rígida, pero el principal inconveniente de las palancas es que, aunque la fuerza aplicada se amplifica, el extremo de la palanca se mueve una distancia mucho más corta que la que recorre la fuerza. Arquímedes habría podido mover la Tierra esa misma (minúscula) distancia simplemente saltando. No obstante, la palanca es muy eficaz, al igual que una variante que Arquímedes también comprendió: la polea. Cuando un escéptico Hierón le pidió una demostración, Arquímedes

en una de las naves reales de carga, de tres palos, recién sacada a tierra firme con gran esfuerzo y abundante mano de obra, introdujo muchos hombres y la carga habitual, y sentado él mismo a distancia, no con esfuerzo, sino sencillamente moviendo con la mano el origen de un polipasto, la acercó suavemente y sin sacudidas y como si corriera sobre el mar.^*

El segundo libro se ocupa principalmente de hallar el centro de gravedad de diversas figuras: triángulo, paralelogramo, trapecio y segmento de una parábola.

Sobre la esfera y el cilindro contiene resultados de los que Arquímedes se sentía tan orgulloso que hizo que los inscribieran en su tumba. Demostró, de forma rigurosa, que el área de una esfera es cuatro veces la de cualquier círculo máximo (como el ecuador de una Tierra esférica); que su volumen es dos tercios del de un cilindro circunscrito a la esfera; y que el área de cualquier segmento de la esfera cortado por un plano es la misma que la del segmento correspondiente de ese cilindro.^** Su demostración se basa en una enrevesada técnica conocida como «método exhaustivo», introducida por Eudoxo para tratar con proporciones que implicasen números irracionales, es decir, que no pueden representarse exactamente en forma de fracción. En términos modernos, demostró que el área de una esfera de radio r es 4πr², y su volumen, 4/3πr³.

Los matemáticos tienen la costumbre de presentar sus resultados finales y pulidos de una forma organizada y bella, escondiendo el proceso, a menudo difícil y embrollado, que les ha llevado hasta ellos. Tenemos la suerte de conocer algo más sobre cómo realizó Arquímedes sus descubrimientos sobre la esfera gracias a El método relativo a los teoremas mecánicos. Esta obra se dio por perdida durante mucho tiempo, hasta que en 1906 el historiador danés Johan Heiberg descubrió una copia incompleta en el llamado «palimpsesto de Arquímedes». Un palimpsesto es un texto que fue lavado o borrado en la Antigüedad para volver a usar el pergamino o el papel. Las obras de Arquímedes fueron compiladas por Isidoro de Mileto hacia el año 530 en Constantinopla (la actual Estambul), capital del imperio bizantino. En 950 fueron copiadas por algún amanuense bizantino en la época en que León de Tesalónica dirigía una escuela de matemáticas que estudiaba las obras de Arquímedes. El manuscrito llegó a Jerusalén, y fue allí, en 1229, donde fue desmontado, lavado (no muy bien), plegado por la mitad y encuadernado de nuevo como una liturgia cristiana de 177 páginas.

En la década de 1840 el estudioso de la Biblia Konstantin von Tischendorf descubrió este texto, que entonces volvía a estar en una biblioteca ortodoxa griega en Constantinopla, y observó que contenía algunos débiles restos de matemáticas griegas. Se llevó una página y la depositó en la Biblioteca de la Universidad de Cambridge. En 1899 Athanasios Papadopoulos-Kerameus tradujo un fragmento mientras catalogaba los manuscritos de la biblioteca. Heiberg se percató de que era obra de Arquímedes, y le siguió el rastro a la página hasta Constantinopla, donde le fue permitido fotografiar el documento completo. Entonces lo transcribió, y publicó el resultado entre 1910 y 1915, y Thomas Heath tradujo el texto al inglés. Tras una compleja serie de acontecimientos, entre ellos una subasta impugnada en un litigio relativo a su propiedad, fue vendido a un americano anónimo por dos millones de dólares. El nuevo propietario lo puso a disposición de los estudiosos, que lo sometieron a diversas técnicas de imagen para sacar a la luz el texto oculto.

El método exhaustivo requiere conocer por adelantado la respuesta, de modo que durante mucho tiempo los estudiosos se preguntaban cómo había logrado conjeturar Arquímedes las reglas para el área y el volumen de una esfera. El método nos da una explicación:

Ciertas cosas las comprendí primero por un método mecánico, aunque hubiera que demostrarlas después por geometría porque su investigación mediante dicho método no proporcionaba una auténtica prueba. Pero naturalmente era más fácil desarrollar la demostración una vez adquirido, por medio del método, algún conocimiento de las cuestiones, que obtenerla sin la ayuda de ningún conocimiento previo.

Arquímedes se imagina que cuelga una esfera, un cilindro y un cono de una balanza, para cortarlos después en rodajas infinitamente pequeñas, distribuidas de tal manera que se preserve el nivel de la balanza. Entonces utiliza el principio de la palanca para relacionar los tres volúmenes (los del cilindro y el cono ya se conocían) y deducir de este modo las magnitudes buscadas. Se ha propuesto que Arquímedes fue un pionero en el uso de los infinitos en las matemáticas. Eso seguramente es ver más de la cuenta en un oscuro documento, pero está claro que El método se anticipa a algunas de las ideas del cálculo.

El resto de las obras de Arquímedes ilustra lo diverso de sus intereses. Sobre las espirales demuestra algunos enunciados fundamentales sobre las longitudes y las áreas relacionadas con la espiral de Arquímedes, la curva descrita por un punto que se mueve a velocidad uniforme a lo largo de una recta en rotación a velocidad uniforme. Sobre conoides y esferoides estudia los volúmenes de segmentos de sólidos formados por la rotación de secciones cónicas alrededor de un eje.

Sobre los cuerpos flotantes es la obra más antigua sobre hidrostática, las posiciones de equilibrio de los objetos en flotación. Incluye el Principio de Arquímedes: un cuerpo sumergido en un líquido está sujeto a una fuerza de flotación igual al peso del fluido desplazado. Este principio es el asunto de una célebre anécdota en la que se solicita a Arquímedes que ingenie un método para determinar si una corona votiva hecha para el rey Hierón II era realmente de oro. Sentado en su baño, le llega de repente la inspiración, y tanto se entusiasma que sale a la calle corriendo y gritando «¡Eureka!» (¡lo encontré!), olvidándose de vestirse primero, aunque la desnudez pública no debía de ser nada particularmente escandaloso en la antigua Grecia. El punto álgido del libro, desde el punto de vista técnico, es una condición para que un paraboloide flotante permanezca estable, un precursor de las ideas básicas de arquitectura naval sobre la estabilidad o tendencia a volcar de los buques.

Sobre la medida de un círculo aplica el método exhaustivo a la demostración de que el área de un círculo es la mitad del radio multiplicado por la circunferencia, lo que hoy escribimos πr². Para demostrarlo, Arquímedes inscribe y circunscribe polígonos regulares de 6, 12, 24, 48 y 96 lados. Con el polígono de 96 lados demuestra un resultado equivalente a una estimación del valor de π, que sitúa entre 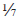3 y 3 .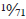

El contador de arena está dedicado a Gelón II, tirano de Siracusa e hijo de Hierón II, lo que aporta una prueba más de que Arquímedes tenía conexiones con la realeza. Explica así su objetivo:

Hay quienes piensan, rey Gelón, que el número de granos de arena es infinito en cantidad ... Pero intentaré mostraros ... que, de las cifras que nombro y que se dan en la obra que envío a Zeuxipo, algunas exceden no solo el número de una masa de arena igual en magnitud a una Tierra llena, sino también al de una masa igual en magnitud al universo.

Aquí Arquímedes promociona su nuevo sistema para nombrar grandes números al tiempo que combate el mal uso habitual del término «infinito» para significar «muy grande». Tiene un claro sentido de la distinción. Su texto combina dos ideas principales. La primera es una extensión de los guarismos griegos ordinarios para que sirvan para números muy superiores a una miríada de miríada (100 millones, 10⁸).^* La segunda es una estimación del tamaño del universo, que fundamenta en la teoría heliocéntrica (centrada en el Sol) de Aristarco. Su resultado final es que, en la notación actual, se necesitarían a lo sumo 10⁶³ granos para llenar el universo.

Existe en la matemática una larga tradición recreativa centrada en los juegos y los puzles. Estos a veces no son más que un entretenimiento, y a veces ocurre que un problema desenfadado arroja luz sobre conceptos más serios. El problema del ganado plantea preguntas que todavía se estudian en la actualidad. En 1773 Gotthold Lessing, un bibliotecario alemán, halló un manuscrito griego, un poema de 44 líneas que invitaba al lector a calcular el número de vacas y toros del rebaño del dios Sol. El título del poema lo presenta como una carta de Arquímedes a Eratóstenes. Comienza así:

Calcula, oh amigo, el número de vacas del Sol que otrora pastaron en los llanos de Sicilia, divididas según su color en cuatro rebaños, unas blancas como la leche, otras negras, otras moteadas y otras rubias. El número de toros es mayor que el número de vacas y las relaciones entre ellas son como sigue.

Da a continuación una lista de siete ecuaciones del tipo de

toros blancos = (½ + ⅓) toros negros + toros amarillos

y prosigue:

Si no puedes, oh amigo, dar el número de toros y vacas de cada tipo, no eres novato en los números, pero no se te podrá considerar de gran destreza. Considera, sin embargo, las siguientes relaciones adicionales entre los toros del Sol:

Toros blancos + toros negros = un número cuadrado,

Toros moteados + toros rubios = un número triangular.

Si has calculado también estos, oh amigo, y hallado la cantidad total de ganado, puedes exaltarte como conquistador, pues has demostrado tener una gran habilidad con los números.

Los números cuadrados son 1, 4, 9, 16, y así sucesivamente, y se obtienen multiplicando cada número entero por sí mismo. Los números triangulares son 1, 3, 6, 10, y así en adelante, formados por la adición de números enteros consecutivos; por ejemplo, 10 = 1 + 2 + 3 + 4. Estas condiciones constituyen lo que hoy llamamos un sistema de ecuaciones diofánticas, por Diofanto de Alejandría, que escribió sobre ellas hacia el 250 d. C. en Arithmetica. La solución debe darse en números enteros, pues es poco probable que el dios Sol tenga media vaca en su rebaño.

El primer conjunto de condiciones conduce a un número infinito de soluciones posibles, la menor de las cuales da 7.460.514 toros negros y números comparables de otros animales. Las condiciones suplementarias seleccionan entre esas soluciones, y conducen a un tipo de ecuación diofántica conocida como ecuación de Pell (capítulo 6). Esta pide enteros x e y tales que nx² + 1 = y², con soluciones como x = 2, y = 3 o x = 12, y = 17. En 1965 Hugh Williams, R. A. German y Charles Zarnke hallaron la solución de menor magnitud coherente con las dos condiciones adicionales, para lo que requirieron la ayuda de dos computadoras IBM. Es aproximadamente 7 · 76 × 10²⁰⁶⁵⁴⁴.

Es imposible que Arquímedes encontrase esta solución a mano, y no hay indicio alguno de que tuviera nada que ver con este problema más allá del título del poema. El problema del ganado todavía atrae la atención de teóricos de los números, y ha inspirado nuevos resultados para la ecuación de Pell.

El registro histórico de la vida de Arquímedes es endeble, pero sabemos algo más acerca de su muerte, suponiendo que los relatos de ella se ajusten a la verdad. Probablemente contengan al menos algo de lo que sucedió.

Durante la segunda guerra púnica, hacia el año 212 a. C., el general romano Marco Claudio Marcelo asedió Siracusa, que capturó al cabo de dos años. Plutarco relata que el anciano Arquímedes estaba examinando un diagrama geométrico en la arena cuando el general envió un soldado para que le dijera que se reuniera con él. Cuando el matemático protestó, alegando que no había concluido su problema, el soldado perdió la paciencia y lo mató con su espada. Las últimas palabras del sabio fueron, presuntamente, «¡No perturbéis los círculos!». Conociendo como conozco a los matemáticos, me parece del todo plausible, pero Plutarco da otra versión en la que Arquímedes intenta rendirse a un soldado, quien cree que los instrumentos que acarrea son valiosos y lo mata para robárselos. En ambas versiones, Marcelo queda molesto con la muerte de su admirado genio matemático.

La tumba de Arquímedes fue decorada con una escultura que representa su teorema favorito, de Sobre la esfera y el cilindro: una esfera inscrita en un cilindro tiene dos terceras partes del volumen de este y la misma área.^* Más de un siglo después de la muerte de Arquímedes, el orador romano Cicerón fue cuestor (auditor del Estado) en Sicilia. Al oír hablar de la tumba, consiguió hallarla en un estado dilapidado cerca de la puerta Agrigentina de Siracusa. Ordenó su restauración, lo que le permitió leer algunas de sus inscripciones, entre ellas el diagrama de la esfera y el cilindro.

En la actualidad, el lugar de la tumba se desconoce, y no parece haber sobrevivido. Pero Arquímedes pervive gracias a sus matemáticas, que en buena parte, dos mil años más tarde, todavía son importantes.