Ya sea que entendamos que se refiere a todos los atenienses o a parte de ellos, por lo que sabemos, se trata de una proposición verdadera, es decir, al sujeto ‘atenienses’ efectivamente le corresponde el predicado ‘griego’ que se está afirmando mediante la cópula verbal ‘son’. Si, a continuación, afirmamos:
(aI) Los atenienses no son griegos,
tendríamos que aceptar esta proposición como falsa, pues ya establecimos que (a) es verdadera y si aceptáramos también (aI) como verdadera, caeríamos en contradicción. Volveremos sobre este punto. De lo expuesto hasta ahora, podemos concluir lo siguiente:
(1) Que la lógica aristotélica entiende la proposición como una unidad de significado que constituye un todo en el que sus partes son el sujeto, el predicado y el verbo.
(2) Que la cópula verbal, al afirmar algún atributo del sujeto, le da el carácter de proposición afirmativa (y no positiva); al negarlo, el carácter de proposición negativa. Así, en esta lógica, la cualidad de la proposición radica en la cópula verbal.
(3) Que solo de las proposiciones puede afirmarse que son verdaderas o falsas.
(4) Que el criterio que se aplica para establecer la verdad o falsedad de una proposición —criterio de verdad— es la correspondencia entre el predicado y el sujeto.
En (2) se establece que hay dos tipos de proposiciones: afirmativas y negativas. Pero hay algo más que debemos analizar para precisar cuáles son los tipos de proposiciones. Retomemos la proposición:
(a) Los atenienses son griegos.
En esta proposición, sin duda, quien la está afirmando se quiere referir a todos los atenienses y no solo a algunos; ello se deduce de la proposición misma y, además, como quiera que interpretemos el sujeto, su valor no cambiará. Sin embargo, es común que nos encontremos con proposiciones poco claras donde la interpretación del sujeto sí puede hacer variar el valor de la proposición.
Por ejemplo, si nos dicen:
(b) Los vegetales son ricos en vitaminas.
¿Cómo debemos interpretarlo?
La tendencia es entenderlo como “Todos los vegetales son ricos en vitaminas”, lo que, evidentemente, es falso. Por esto, sería mucho más exacto decir:
Algunos vegetales son ricos en vitaminas.
Otro ejemplo:
Los alumnos de este curso son muy estudiosos.
Es perfectamente posible que quien afirme esta proposición indefinida se refiera a todos y cada uno de los alumnos. Pero, por nuestra experiencia, es más probable que quiera referirse a la mayoría —y no a todos— de los alumnos. Solo una de las dos interpretaciones del sujeto hará verdadera la proposición y, por lo tanto, a menos que se especifique en qué sentido está tomado el sujeto, no podremos saber con certeza si la proposición es verdadera o falsa.
Por todo esto, se hace necesario cuantificar el sujeto explícitamente. La lógica aristotélica recurre a los términos ‘Todos’ y ‘Ningún’ para indicar que se refiere a toda la clase que denota el sujeto. El término ‘Algunos’ se utiliza para referirse a una parte del sujeto, o sea, a una parte de la clase que denota el sujeto. Cuando el sujeto va precedido del cuantificador ‘Algunos’, se dice que está tomado particularmente.
Asimismo, se dice que el sujeto, cuando va precedido del cuantificador ‘Todos’ o ‘Ningún’, está tomado universalmente.
A esta proposición entendida en la forma sujeto-predicado la llamaremos proposición categórica, porque no es necesario recurrir a nada externo a ella para poder afirmar que es verdadera o falsa, es decir, contiene toda la información requerida para establecer su verdad o falsedad. (Otros tipos de proposiciones que estudiaremos más adelante son las hipotéticas y las disyuntivas).
1.3 Extensión y comprensión
Al referirnos a la necesidad de cuantificar el sujeto, hemos usado la palabra ‘denota’, y con ello estamos optando por una determinada interpretación de la lógica aristotélica. Porque los términos (nombres, sustantivos, etc.) pueden ser analizados desde el punto de vista de la relación que se establece al considerar, por una parte, aquellas características o atributos que nos permiten asociarlos o no a otros términos y, por la otra, en la cantidad de términos a los que podemos aplicar las mismas características o atributos. Y decimos que estos dos aspectos que presentan los términos al ser analizados constituyen una relación entre lo que los lógicos llaman generalmente extensión y comprensión de los términos. Las características: hombre, latinoamericano, nacido en un país llamado Chile, etc., constituyen la comprensión o connotación del término ‘chileno’. El conjunto de personas a las que podemos aplicar estas características con el mismo sentido conforman la extensión o denotación del término ‘chilenos’. Acerca de cómo debe entenderse esta relación entre la comprensión y la extensión de los términos de la proposición se ha escrito mucho. Nos limitaremos a exponer las dos interpretaciones más importantes y a señalar algunos de los problemas que surgen en cada caso.
La primera interpretación —en cierto modo la más consistente con la concepción aristotélica de la proposición— nos dice que la extensión de un término debe entenderse como el conjunto de sujetos de los cuales un término es predicado. Si estamos de acuerdo con Aristóteles en que los individuos solo pueden ser sujeto de la proposición y nunca predicado, significa que, por ejemplo, el nombre ‘Sócrates’ no tiene extensión, puesto que en tanto nombre de individuo no puede predicarse de ningún sujeto.
Sin embargo, si entendemos la extensión o denotación según se plantea en otra interpretación, a saber, como la clase (o dominio) que un término designa, entonces, el nombre ‘Sócrates’ sí tiene extensión y ella consiste en la clase que contiene un solo elemento: el hombre designado por el nombre ‘Sócrates’.
Como se puede apreciar, ambas interpretaciones pueden conducir a resultados diferentes.
En cuanto a la comprensión, para la primera interpretación, debe entenderse como el conjunto de predicados de los que un término puede ser sujeto. Para la segunda interpretación, la comprensión o connotación de un término consiste en el conjunto de atributos, rasgos o propiedades que aplicamos a un término, en razón de lo cual afirmamos que lo que designa pertenece a una clase determinada de “objetos”.
La discusión acerca de estas diferentes interpretaciones de la relación entre extensión y comprensión se ha mantenido durante muchos años. Actualmente, los lógicos tienden a optar por una interpretación de la lógica antigua como una lógica de clases más bien por razones prácticas. Digamos que no se trata de interpretaciones globalmente contradictorias, sino que chocan en determinados puntos que, como ya dijimos, pueden conducir a resultados diferentes. Por otra parte, se ha querido hacer aparecer estas interpretaciones como equivalentes, lo cual es algo más que forzar lo que cada una propone. Lo efectivo es que ambas son importantes y pueden funcionar relativamente bien si se aplican de acuerdo al objetivo que se tenga al trabajar con la lógica aristotélica y teniendo presente que ambas tienen ciertas limitaciones.
Entenderemos por comprensión o connotación todo rasgo o propiedad esencial que nos permita describir un término dado que designe un conjunto de “objetos”. Dada la comprensión de un término, en general, es posible determinar su denotación. Si es dada la extensión o denotación, solo es posible intentar establecer la comprensión si aquella no se da en términos puramente cuantitativos, sino mediante los nombres genéricos de los sujetos que constituyen la extensión. Por ejemplo, ‘hombre’ lo aplicamos a Sócrates, a los atenienses, a los chilenos, etc., porque tanto ‘Sócrates’ como los ‘atenienses’ y los ‘chilenos’ designan objetos que poseen rasgos y propiedades esenciales comunes que están contenidas o resumidas en el término ‘hombre’. Por otra parte, ‘Sócrates’, los ‘atenienses’, los ‘chilenos’ y todos los términos que designen “objetos” análogos, constituyen la extensión o denotación de ‘hombre’.
Otro problema que surge en torno a la relación extensión-comprensión implicada por la mayor parte de las palabras es la idea de algunos lógicos de enunciar una ley que, supuestamente, debe regir esta relación. Usualmente se expresa afirmando que cuando aumenta la extensión de un término, su comprensión disminuye proporcionalmente y viceversa. Supongamos que tenemos una secuencia de términos cuya extensión va aumentando:
‘Sócrates’
‘ateniense’
‘griego’
‘europeo’
‘hombre’
Es evidente que cada uno de estos términos tiene como parte de su extensión la extensión de los anteriores. Según la ley mencionada, la comprensión de estos términos —siguiendo la misma secuencia— debería disminuir “proporcionalmente”. Esta última afirmación no es del todo clara. Porque de acuerdo a la ley, el término ‘ateniense’ debería tener mayor comprensión que el término ‘griego’, pues ‘ateniense’ posee todas las propiedades o atributos de los griegos además de las propias. Aunque en este ejemplo aparece claramente una mayor comprensión, esto no significa que ella sea “proporcional” a su menor extensión en comparación a la del término ‘griegos’.
Si consideramos otros ejemplos veremos que estas variaciones de la comprensión y la extensión de términos comparados no es lo suficientemente clara como para pensar que puedan ser regidas por una ley.
Otros ejemplos:
- El término ‘alacalufe’ ha ido disminuyendo su extensión hasta el extremo de designar un pueblo extinguido, sin embargo, su comprensión no fue variando en la misma proporción en que exterminaron a nuestros indios alacalufes; es más, la comprensión de ‘alacalufe’ sigue siendo la misma.
- Al revés del caso anterior, el término ‘santiaguino’ ha aumentado su extensión (en comparación con la población de 1940, por ejemplo) y no por ello ha disminuido su comprensión (un dialéctico nos diría que lo más probable es que ella también aumente en algún momento o, al menos, que cambie si se produce un “salto cualitativo” resultante del aumento cuantitativo).
En fin, se podrían dar más ejemplos para rechazar el intento de expresar los cambios de la relación extensión-comprensión en términos de una ley, de manera que expresaremos estos cambios sin pretender enunciar una ley sino que sencillamente con la idea de mostrar que dichos cambios efectivamente ocurren en la mayoría de los casos: si anotamos una serie de términos de modo que su comprensión o connotación vaya aumentando, la extensión o denotación de esos mismos términos disminuirá o se mantendrá sin variar y, si es su extensión o denotación lo que aumenta, su comprensión disminuye o se mantiene igual.
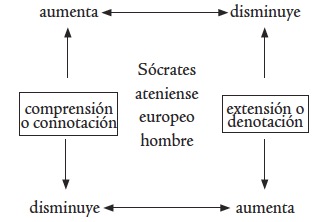
Las palabras ‘aumenta’ y ‘disminuye’ no deben entenderse en un sentido numérico sino más bien como una referencia cuantitativa relativa.
1.4 Tipos de proposición
Habíamos establecido dos tipos de proposiciones, las afirmativas y las negativas. El hecho de ser afirmativas o negativas constituye lo que llamaremos la calidad o cualidad de la proposición.
Ahora que hemos explicado los conceptos de comprensión y extensión podemos aplicarlos y completar los tipos de proposiciones. A esta lógica interesa la extensión de los términos más que su comprensión. Cuando anteponemos algún cuantificador al sujeto de una proposición, estamos indicando explícitamente la extensión en que lo estamos usando; si afirmamos la proposición ‘Todos los S son P’, estamos tomando el sujeto en toda su extensión, o como decíamos antes, universalmente; si la proposición es ‘Algún S es P’, estamos tomando el sujeto en parte de su extensión, o sea, particularmente.
En esto consiste la cantidad de una proposición. Si combinamos la calidad de las proposiciones con su cantidad, obtendremos los cuatro tipos de proposición que establece la lógica aristotélica:
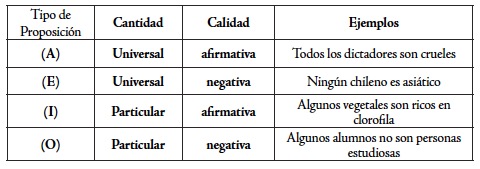
A cada tipo de proposición asignaremos una letra vocal mayúscula —como está anotado entre paréntesis en la tabla— para indicar sintéticamente de qué tipo de proposición se trata.
Solo nos resta, con relación a las proposiciones, explicar lo que en esta lógica ocurre con las proposiciones singulares, como:
Sócrates es ateniense.
Desde el punto de vista aristotélico, los casos de proposiciones singulares son considerados como si se tratara de una universal. A pesar de que hemos mencionado que el cuantificador particular ‘Algunos’ se entiende normalmente como “al menos uno”, lo que nos induce a pensar que cabría clasificar a las proposiciones singulares en la misma categoría que las particulares, Aristóteles no procede así porque un sujeto singular puede constituir por sí solo una clase completa, de la cual él es el único miembro, de modo que lo que se predica de él se predica del mismo modo que si se hiciera de una clase, de un todo. En cambio, cuando interpretamos el cuantificador ‘Algunos’ como “al menos uno”, estamos exigiendo que exista al menos un elemento al cual se aplique un predicado; no sabemos con exactitud cuántos sujetos o elementos constituyen la clase y en este sentido —como afirma Aristóteles— el cuantificador particular es indeterminado. Sabemos con seguridad, eso sí, que cuando aparece ‘Algún’ precediendo a un sujeto, significa que en la clase que le corresponde hay por lo menos uno y que, si hay más, nos referimos no a todos sino a una parte.
En el caso de una proposición singular, nos dice Aristóteles, sabemos con certeza que el todo que denota el sujeto se identifica con él, por lo tanto, debemos proceder como si se tratara de una proposición universal: el atributo se dice de todos y cada uno de los miembros de la clase. Así, podríamos parafrasear la proposición ‘Sócrates es ateniense’ como “(Todo) Sócrates es ateniense”. De modo que, en la interpretación aristotélica, las proposiciones singulares se asimilan a las universales; en una interpretación de la lógica aristotélica como lógica de clases, las proposiciones singulares se consideran como particulares. Por otra parte, algunos autores dan argumentos relevantes para suprimirlas de la lógica, entre ellos, Tarski, Russell, Quine. Pero se trata de una extensa y compleja discusión que corresponde a la filosofía de la lógica y no es posible desarrollarla aquí.
A los cuatro tipos de proposiciones que hemos establecido las llamaremos proposiciones “categóricas”, porque, como ya hemos dicho, es posible establecer su verdad o falsedad a partir de ellas mismas, sin recurrir a otras proposiciones.
1.5 Observaciones
Antes de pasar al tema de la inferencia, mencionaremos una observación crítica respecto a la concepción tradicional de la proposición categórica.
La estructura sujeto-predicado de dicha proposición produce varios problemas. Uno de ellos consiste en la dificultad para presentar en esta forma algunas expresiones de las cuales podemos decir que son verdaderas o falsas —principal requisito de la proposición—, pero cuyo sujeto plantea serios problemas cuando intentamos determinarlo. Expresiones como “hay tormenta”, “hubo una fiesta”, “Estados Unidos perdió la guerra de Vietnam”, etc., son expresiones verdaderas o falsas, sin embargo, resulta complicado determinar sus respectivos sujetos. Obviamente, el requisito esencial de una proposición es la posibilidad de afirmar de ella si es verdadera o falsa; no parece tan esencial la exigencia de que la proposición esté siempre estructurada en la forma sujeto-predicado. Por lo tanto, podremos abandonar esta exigencia cada vez que ello sea necesario o, incluso, cuando resulte más práctico, pero manteniendo claramente el distingo entre la proposición, por una parte, y los términos que la constituyen, por la otra, sin que sea estrictamente necesario especificar siempre esos términos como sujeto y predicado. De todos modos, como en la mayoría de los casos es posible transformar una expresión verdadera o falsa a la forma sujeto-predicado, intentaremos mantener la estructura típica de la proposición categórica (arriesgándonos a veces a presentar proposiciones un tanto forzadas desde el punto de vista del estilo), en tanto desarrollamos la lógica aristotélica.