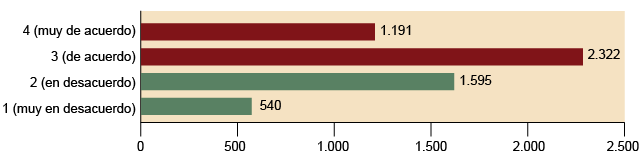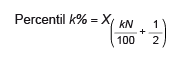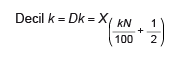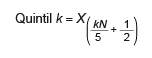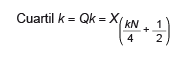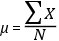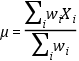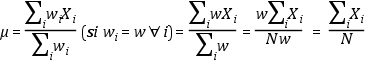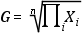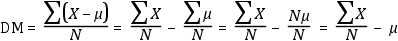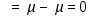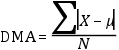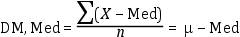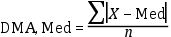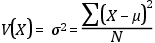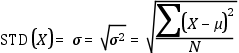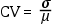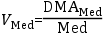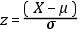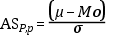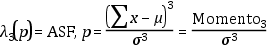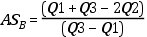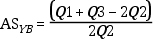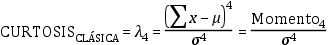Capítulo II
Estadística descriptiva univariante
El análisis univariante proporciona una serie de herramientas para describir, tabular,
representar y sacar gráficos de una variable de las maneras más útiles y eficaces:
¿en qué lugar o posición de una variable se encuentra una observación concreta de
nuestro interés? ¿Cuáles son las observaciones que se encuentran en sus extremos,
en el 5 % más alto, en el 10 % más bajo? ¿Cuáles son las observaciones que se encuentran
«en el centro»? ¿Cuál es la variabilidad o dispersión de nuestra variable? ¿Qué tipo
de forma tiene la variable, por ejemplo, es simétrica, es plana? ¿Cuál es su distribución
de frecuencias completa?
1. Tabulaciones de frecuencias
Las tabulaciones de frecuencias son la herramienta más sencilla e inmediata para obtener
información sobre la distribución de una o más variables.
Tabulaciones de frecuencias
Tablas de distribución de una variable donde se presentan las frecuencias absolutas
de cada categoría de la variable (es decir, el número de veces que se repite cada
categoría), sus frecuencias relativas (es decir, sus porcentajes) o las frecuencias
relativas acumuladas (es decir, el porcentaje acumulado de cada categoría y todas
las precedentes).
A menudo, en una tabulación de frecuencias, se presentan simultáneamente las frecuencias
absolutas, relativas y, quizá, las relativas acumuladas.
A pesar de su simplicidad, las tabulaciones de frecuencias, de una sola variable permiten
conocer, de manera rápida e intuitiva, su distribución, con lo que constituyen una
herramienta indispensable para el análisis de los datos empíricos de los que se dispone.
Las tabulaciones de frecuencias son especialmente útiles para las variables categóricas,
y resultan menos útiles con las variables cuantitativas, ya que obtendríamos un listado
muy largo (por ejemplo, 90 edades diferentes) con frecuencias relativamente bajas
para cada valor.
Ejemplo 1
Tomemos los datos del cuestionario postelectoral español del CIS (Centro de Investigaciones
Sociológicas) correspondiente a las elecciones generales españolas de 2008 (cuestionario
CIS 2757, disponible de manera gratuita, se puede descargar directamente desde la
página web del CIS). Sacaremos una tabla de frecuencias de la variable correspondiente
al género (variable «sexo», en el cuestionario):
Tabla 3. Distribución de frecuencias de la variable «género»
|
Género
|
Frecuencia absoluta (N)
|
Frecuencia relativa (porcentaje)
|
Porcentaje acumulado
|
|
1 (hombre)
|
2.938
|
48,30
|
48,30
|
|
2 (mujer)
|
3.145
|
51,70
|
100,00
|
|
Total
|
6.083
|
100,00
|
|
|
Fuente: CIS, cuestionario 2757. Elaboración propia.
|
La tabla 3 permite observar cómo la muestra del cuestionario postelectoral considerado
contiene, casi, el mismo número de hombres que de mujeres y, por lo tanto, refleja
de forma bastante fiel la distribución de la población estudiada. Efectivamente, de
un total de 6.083 encuestados, 2.938 son hombres y 3.145, mujeres. Estos números representan,
respectivamente, un 48,30 y un 51,70 % de la muestra. En este caso, el porcentaje
acumulado no proporciona información relevante adicional.
Ejemplo 2
Ahora, empleamos la variable correspondiente a la clase social (variable «p69» del
cuestionario).
La tabla 4 (más abajo) permite observar la distribución de la variable ordinal «clase
social». Vemos que, de un total de 6.083 encuestados, la mayoría se sitúa como de
clase media-media (3.682, o un 60,53 % de la muestra) y, en segundo lugar, de clase
media-baja (1.554, o un 25,55 %), mientras que las categorías extremas son muy poco
habituales: solamente 13 de los 6.083 encuestados, o un 0,21 % de la muestra, dicen
ser de clase alta, y 346, o un 5,69 %, manifiestan ser de clase baja. Observad que,
ante una pregunta como esta, hay un porcentaje de casos que o bien no se sabe posicionar,
o bien no contesta. En este caso, el porcentaje acumulado sí proporciona información
relevante adicional. Por ejemplo, nos permite saber que un 5,10 % de la muestra se
posiciona como de clase media-alta o más alta, o que un 96,86 % proporciona algún
tipo de respuesta posicionándose en una de las clases ofrecidas por los encuestadores.
Tabla 4. Distribución de frecuencias de la variable «clase social»
|
Clase social
|
Frecuencia absoluta (N)
|
Frecuencia relativa (porcentaje)
|
Porcentaje acumulado
|
|
1 (alta)
|
13
|
0,21
|
0,21
|
|
2 (media-alta)
|
297
|
4,88
|
5,10
|
|
3 (media-media)
|
3.682
|
60,53
|
65,63
|
|
4 (media-baja)
|
1.554
|
25,55
|
91,17
|
|
5 (baja)
|
346
|
5,69
|
96,86
|
|
8 (no sabe)
|
111
|
1,82
|
98,68
|
|
9 (no contesta)
|
80
|
1,32
|
100,00
|
|
Total
|
6.083
|
100,00
|
|
|
Fuente: CIS, cuestionario 2757. Elaboración propia.
|
Ejemplo 3
Ahora, empleamos la variable correspondiente al estado civil («p59»).
Tabla 5. Distribución de frecuencias de la variable «estado civil»
|
Estado civil
|
Frecuencia absoluta (N)
|
Frecuencia relativa (porcentaje)
|
Porcentaje acumulado
|
|
1 (casado/a)
|
3.585
|
58,93
|
58,93
|
|
2 (soltero/a)
|
1.764
|
29,00
|
87,93
|
|
3 (viudo/a)
|
483
|
7,94
|
95,87
|
|
4 (separado/a)
|
127
|
2,09
|
97,96
|
|
5 (divorciado/a)
|
106
|
1,74
|
99,70
|
|
9 (no contesta)
|
18
|
0,30
|
100,00
|
|
Total
|
6.083
|
100,00
|
|
|
Fuente: CIS, cuestionario 2757. Elaboración propia.
|
La tabla 5 permite observar la distribución de la variable «estado civil», una variable
nominal. Observemos que, de un total de 6.083 encuestados, la mayoría están casados
(3.585, o un 58,93 % de la muestra), seguidos por los solteros (1.764, o un 29,00
%), mientras que las categorías extremas son bastante menos habituales. Fijaos en
que esta parece ser una pregunta menos sensible que la de la clase social, y solamente
dieciocho individuos, un 0,30 %, opta por no contestar. Dado que la ordenación de
las categorías es arbitraria, el porcentaje acumulado no tiene sentido.
Las tabulaciones de frecuencias también son muy útiles para comprobar que las recodificaciones
de las variables llevadas a cabo han sido realizadas correctamente. Esto se puede
hacer tanto mediante una tabla de contingencia (como se verá en el capítulo siguiente)
como mediante la comparación de la tabla de distribución de frecuencias de la variable
recodificada y de la variable original.
Tabla 6. Distribución de frecuencias de la variable «clase social» (recodificada)
|
Clase social
|
Frecuencia absoluta (N)
|
Frecuencia relativa (porcentaje)
|
Porcentaje acumulado
|
|
1 (alta)
|
13
|
0,22
|
0,22
|
|
2 (media)
|
5.533
|
93,91
|
94,13
|
|
3 (baja)
|
346
|
5,87
|
100,00
|
|
Total (válidos)
|
5.892
|
100,00
|
|
|
Fuente: CIS, cuestionario 2757. Elaboración propia.
|
Una comparación rápida de la tabla 6 con la tabla 4 permite comprobar que la recodificación
ha sido llevada a cabo correctamente. Por ejemplo, la diferencia en el número de casos
(6.083 – 5.892 = 191) corresponde a la suma de aquellos que no saben o no quieren
contestar a la pregunta (111 + 80 = 191). Por otro lado, si sumamos el número de casos
de clase media-alta, media-media y media-baja en la tabla 4 (297 + 3.682 + 1.554 =
5.533), el resultado es el mismo que el número de casos de clase media en la tabla
6.
Observad que todas las tablas están encabezadas por un título y que llevan un pie
de tabla donde se indica la fuente de procedencia de los datos. Esta información es
fundamental, y se debe incluir siempre en la presentación de tablas en un trabajo
(de investigación), tanto si se trata de tablas de frecuencias como de cualquier otro
tipo. Dado que la codificación de las variables estaba incluida en las tablas, no
era necesario añadir información adicional, pero si no fuera así, sería necesario
incluir también la codificación al pie de la tabla:
Tabla 7. Distribución de frecuencias de la variable «clase social» (recodificada 2)
|
Clase social
|
Frecuencia absoluta (N)
|
Frecuencia relativa (porcentaje)
|
Porcentaje acumulado
|
|
1
|
13
|
0,22
|
0,22
|
|
2
|
5.533
|
93,91
|
94,13
|
|
3
|
346
|
5,87
|
100,00
|
|
Total (válidos)
|
5.892
|
100,00
|
|
|
1: clase alta; 2: clase media; 3: clase baja.
Fuente: CIS, cuestionario 2757. Elaboración propia.
|
2. Gráficos univariantes
Resulta extremadamente útil acompañar los análisis empíricos con gráficos. Si se usan
bien, los gráficos permiten resumir y presentar la información de manera extremadamente
sintética, intuitiva y fácil de recordar para el lector. Como hay muchos gráficos
al alcance de los investigadores, discutiremos solo algunos de los más populares.
Gráficos de pastel
Gráficos con forma circular o de pastel que representan cada valor de la variable
con un área o «porción del pastel» proporcional a su frecuencia.
Ejemplo
Se presenta un gráfico de pastel de la variable «remordimiento» (variable «p505» del
cuestionario), que recoge en qué medida los encuestados están de acuerdo con la afirmación
según la cual se sentirían fatal si no hubieran votado y su partido preferido hubiera
perdido por un solo voto, debidamente recodificada para prescindir de los individuos
que no saben o no quieren contestar y para que la escala sea creciente con el grado
de acuerdo con la afirmación (originalmente, la escala estaba invertida).
Figura 1. Gráfico de pastel de la variable «remordimiento» (recodificada)
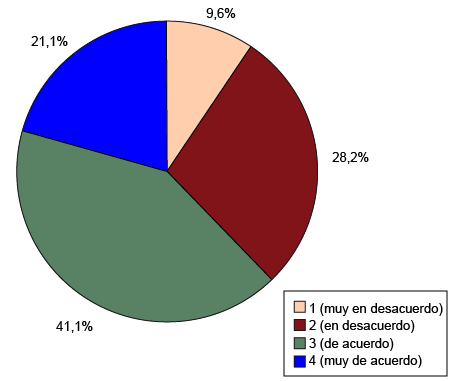
Fuente: CIS, cuestionario 2757. Elaboración propia.
Gráficos o diagramas de barras
Gráficos que representan la frecuencia de cada valor de una variable proporcionalmente
a la longitud horizontal de cada una de ellas en el gráfico.
Ejemplo
Se presenta un gráfico de barras (o, según algunos autores, un diagrama de Pareto;
unas líneas más abajo se discute este punto) de la misma variable, «remordimiento»,
una variable cualitativa con cuatro categorías:
Figura 2. Gráfico de barras de la variable «remordimiento» (recodificada)
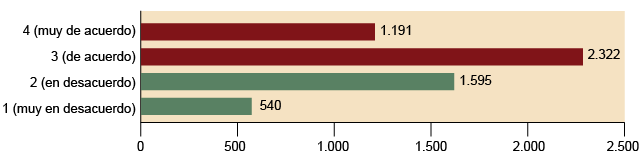
Fuente: CIS, cuestionario 2757. Elaboración propia.
Observad que, en este gráfico, se ha decidido resaltar la diferencia entre las categorías
que manifiestan acuerdo y las categorías que manifiestan desacuerdo mediante su representación
en tonos diferentes. ¿Estáis de acuerdo en que permite diferenciar más fácilmente
entre ambos grupos?
Observad también que en lugar de las frecuencias relativas (porcentajes) se ha optado
por representar las frecuencias absolutas (casos). Sería perfectamente posible representar
porcentajes con un gráfico de este tipo: para pasar de un gráfico con casos a uno
de porcentajes (o viceversa), solo es necesario cambiar la escala (Wonnacott; Wonnacott,
1979, pág. 32).
Algunos autores (Peña, 2001, págs. 51-52) reservan el término de diagrama de barras
(el cual, en nuestra notación, se subdivide en los gráficos de barras y en los gráficos
de columnas, como veremos dentro de poco) para las variables cuantitativas discretas,
y prefieren emplear el término de diagramas de Pareto para los gráficos correspondientes
para variables cualitativas.
Gráficos o diagramas de Pareto
Gráficos que representan la frecuencia de las categorías de variables cualitativas
mediante un rectángulo cuya longitud o altura es proporcional a tales frecuencias
(Peña, 2001, págs. 50-51).
Por lo tanto, si se siguiera este criterio, la figura 2 sería un ejemplo de un diagrama
de Pareto, y no de de barras. Sin embargo, otros autores (Spiegel, 1991, págs. 19-23)
no establecen esta diferencia.
Por otro lado, muchos autores utilizan el término gráfico de barras para hacer referencia tanto a los gráficos en los que las barras se representan de
forma horizontal como a los que las representan de forma vertical (Spiegel, 1991,
págs. 19-23). Aquí, reservaremos el término para los primeros, y denotaremos a los
segundos con el nombre de gráficos de columnas, los cuales se estudian a continuación.
Gráficos de columnas
Gráficos que representan la frecuencia de las categorías de las variables proporcionalmente
mediante la altura de cada una de ellas en el gráfico.
Ejemplo 1
Gráfico de columnas de la variable «remordimiento»:
Figura 3. Gráfico de columnas de la variable «remordimiento» (recodificada), porcentajes

Fuente: CIS, cuestionario 2757. Elaboración propia.
Observad que, en este gráfico, se ha decidido resaltar la categoría más frecuente
mediante su representación en otro color:
Ejemplo 2
A continuación, se presenta un gráfico de la variable «tasa de paro», tomada de EUROSTAT
para los países europeos (y con fines comparativos), para Estados Unidos y Japón;
en concreto, de la tasa de paro no ajustada estacionalmente para 2008 (conviene advertir
que el gráfico que se presentará ahora es mejorable, tal como quedará patente en la
discusión que lo sigue):
Figura 4. Tasa de paro de los países de la UE, 2008 (gráfico no aconsejado)
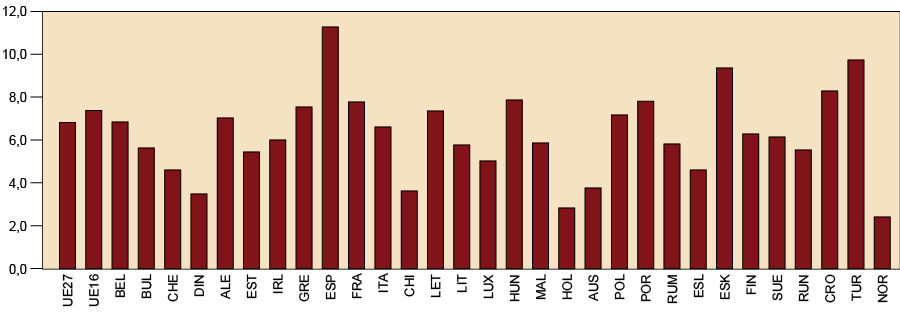
Fuente: EUROSTAT. Elaboración propia.
Como se puede ver, tal como ha sido presentado, el gráfico no es muy cómodo de leer,
y no incluye ni detalles sobre cómo se ha calculado la tasa ni las claves de las etiquetas
de los países. Ahora, considerad un gráfico sobre los mismos datos, pero hecho con
más cuidado:
Figura 5. Tasa de paro de los países de la UE, 2008 (gráfico más aconsejable)
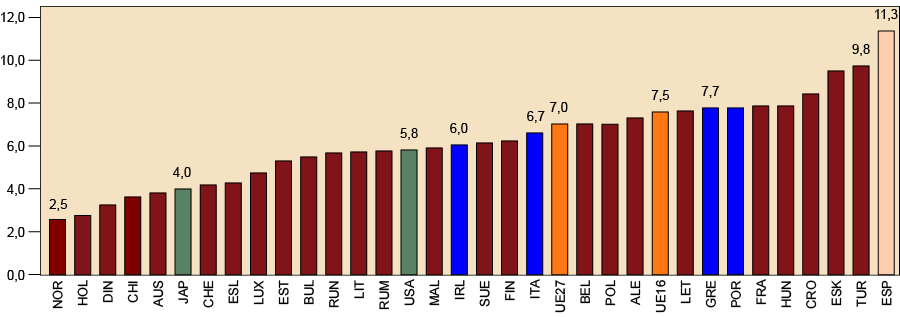
Fuente: EUROSTAT. Datos de la tasa de paro no ajustada estacionalmente. Elaboración
propia. Clave: NOR: Noruega; HOL: Holanda; DIN: Dinamarca; CHI: Chipre; AUS: Austria;
JAP: Japón; CHE: República Checa; ESL: Eslovenia; LUX: Luxemburgo; EST: Estonia; BUL:
Bulgaria; RUN: Reino Unido; LIT: Lituania; RUM: Rumanía; USA: Estados Unidos; MAL:
Malta; IRL: Irlanda; SUE: Suecia; FIN: Finlandia; ITA: Italia; UE27: Unión Europea
(27 países); BEL: Bélgica; POL: Polonia; ALE: Alemania; UE16: Unión Europea (16 países);
LET: Letonia; GRE: Grecia; POR: Portugal; FRA: Francia; HUN: Hungría; CRO: Croacia;
ESK: Eslovaquia; TUR: Turquía; ESP: España.
En este nuevo gráfico, además de incluir toda la información relevante al pie de la
tabla, los países se han ordenado según su tasa de paro, lo que hace mucho más fácil
detectar la posición relativa de cada uno en esta dimensión. Además, se han rellenado
con tonos diferentes las barras de nuestro país y del resto de «PIGS» (Portugal, Italia,
Irlanda y Grecia). Finalmente, se han añadido etiquetas con los valores de la tasa
de paro para algunos de los países. Como se puede observar, este gráfico es mucho
más atractivo que el precedente.
Histogramas
Gráficos empleados para representar la distribución de frecuencias de datos cuantitativos
(en principio, continuos, a pesar de que esto no sería estrictamente necesario) agrupados.
Cada rectángulo representa uno de los intervalos de agrupación o de clase, de manera
parecida a lo que hacían los gráficos de columna. Las bases de los rectángulos son
proporcionales al ancho de cada intervalo, y su altura es tal que las áreas son proporcionales
a la frecuencia de cada clase. Observad que cuando los anchos de todos los intervalos
son los mismos, entonces la altura es proporcional a la frecuencia, con lo que su
construcción resulta idéntica a la de los gráficos de columna.
A continuación, se muestran dos histogramas para dos variables del estudio 2757 del
CIS. En el panel izquierdo, se muestra un histograma para la variable «edad», que
se mueve en un rango de 18 a 97. Se ha pedido un histograma con cuatro intervalos
iguales (que irían de 18 a 37, de 38 a 57, de 58 a 77, y de 78 a 97). En el panel
derecho, se muestra un histograma para la identificación ideológica (variable «p41»).
Se han tratado como perdidos los casos de los encuestados que no saben o no contestan,
y se han construido intervalos de 1 a 3 para la izquierda, 4 a 5 para el centro, y
6 a 10 para la derecha; se han elegido estos intervalos únicamente para facilitar
la visualización gráfica del histograma y mostrar cómo se vería un histograma con
anchos variables, que son las cuestiones que nos interesan aquí.
Figura 6. Histogramas con amplitud fija y variable («edad» e «ideología»)
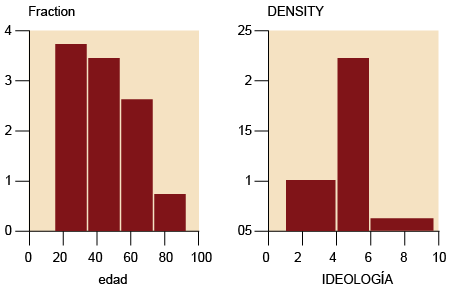
Fuente: CIS, cuestionario 2757. Elaboración propia.
El primer histograma tiene todos los intervalos del mismo ancho, y esto hace que su
interpretación sea muy parecida a la de los gráficos de columna. De hecho, la proporción
de casos de los cuatro intervalos (de 18 a 37, de 38 a 57, de 58 a 77, y de 78 a 97)
es, respectivamente, de un 36,3, 33,3, 24,6 y 5,8 %: las cifras correspondientes a
las alturas del histograma de la izquierda son precisamente estas (pero divididas
por 100). Sin embargo, el segundo histograma tiene anchos diferentes, y lo que es
proporcional a la probabilidad de cada intervalo no es ya la altura, sino el área
de los rectángulos asociados a cada intervalo. La tabla siguiente nos ayudará a comprender
la interpretación del panel de la derecha:
Tabla 8. Detalles para la comprensión del panel derecho de la figura 6
|
IDEOLOGÍA
|
Casos
|
Área
|
Inicio
|
Final
|
Ancho
|
Alto
(= Área/Ancho)
|
|
1_3_izquierda
|
1.520
|
29,2
|
1
|
4
|
3
|
9,7
|
|
4_5_centro
|
2.370
|
45,5
|
4
|
6
|
2
|
22,8
|
|
6_10_derecha
|
1.318
|
25,3
|
6
|
10
|
4
|
6,3
|
|
Total
|
5.208
|
100,0
|
|
|
|
|
|
Fuente: CIS, cuestionario 2757. Elaboración propia.
|
En efecto, el primer intervalo corresponde a un 29,2 % de los casos; el segundo, a
un 45,5 %, y el tercero, a un 25,3 %. Ahora bien, el primer intervalo tiene un ancho
de 3 puntos (digamos, para simplificar, que va de 1 a 4), el segundo, de 2 puntos
(digamos que de 4 a 6) y el tercero, de 4 puntos (de 6 a 10). Entonces, para que las
áreas sean proporcionales, podemos calcular las alturas dividiendo los porcentajes
de casos por los anchos de los intervalos: 29,2/3 = 9,7; 45,4/2 = 22,8; y 25,3/4 =
6,3. Observad que las alturas de los intervalos son exactamente estos números divididos
por 100.
Gráficos de líneas (o de tendencia)
Gráficos que representan la frecuencia (absoluta o relativa) de las categorías de
las variables proporcionalmente mediante la altura de cada una de ellas en el gráfico,
y que conectan los valores con una línea. Son especialmente útiles para representar
la evolución temporal de las variables.
Ejemplo
Gráfico de líneas de la variable «tasa de paro»
Figura 7. Evolución de la tasa de paro en España, 1998-2008
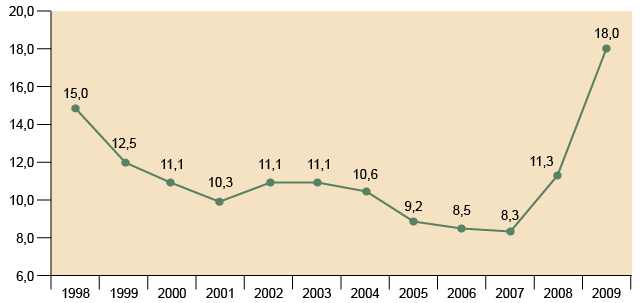
Fuente: EUROSTAT. Datos anuales de la tasa de paro no ajustada estacionalmente.
Como se puede ver, los gráficos de líneas resultan muy adecuados para representar
la evolución temporal de una variable –y, de hecho, también de más variables. Estos
gráficos se pueden enriquecer señalando la ocurrencia de circunstancias que pueden
dar cuenta de los cambios de tendencia, como, por ejemplo, las crisis económicas o
los cambios de gobierno.
A pesar de que cada vez hay más tipos de gráficos univariantes potencialmente útiles,
estos son, probablemente, los más utilizados y, si los empleáis bien, podréis representar
de manera gráfica la mayoría de los rasgos que queráis de una variable dada.
3. Estadísticos descriptivos univariantes
3.1. Medidas de localización
Las medidas de localización permiten establecer qué elemento de una variable ocupa
una determinada posición dentro de ésta, por ejemplo, qué observación está, precisamente,
en el 10 % más bajo o en el 5 % más alto. También permiten saber qué valor toma la
variable en una posición dada: por ejemplo, cuál es la nota de un estudiante que sólo
tiene a un 2% de estudiantes por encima. Obviamente, para que estas medidas tengan
sentido, es necesario que los elementos de la variable estén ordenados en términos
de valor, sea de manera ascendente o descendente.
3.1.1. Percentil
El percentil k % es el elemento situado en la posición correspondiente al k % de los
datos cuando estos están ordenados. Así, el percentil 85 % tiene un 85 % de casos
por debajo (con valores inferiores) y un 15 %, con valores mayores. Sin tener en cuenta
el mínimo y el máximo (a los que se podría aludir como percentil 0 % y 100 %, respectivamente),
hay 99 percentiles, que permiten dividir la variable en cien divisiones iguales. Cada
división contiene una centésima parte de las observaciones.
Los pediatras usan mucho los percentiles para decirle a los padres si su bebé pesa
poco o mucho: «cuidado, debe insistir en que coma, está en el percentil 8». Las universidades
prestigiosas (como la tuya) aplican los percentiles en sus procesos de selección,
por ejemplo, si aceptan sólo a los estudiantes que se hayan situado en el percentil
97 % o superior en alguna prueba. La nota de corte para entrar en la universidad (digamos
que 480 puntos sobre 500) sería el valor del percentil 97 %.
Si hay 300 personas y están ordenadas en orden creciente según la altura, el percentil
1 % sería la tercera persona, y el percentil 50 %, la persona número 150. De manera
más general, si hay N personas, el percentil k estará en la posición N * k / 100.
Hilando más fino
Si se quiere ser más riguroso, habrá que realizar un ajuste. ¿Por qué? Veámoslo con
el ejemplo siguiente. La definición del percentil 50 %, por analogía a la del percentil
1 %, es la del elemento situado en la posición correspondiente a un 50 % de los datos
cuando estos están ordenados. Tomemos el percentil 50 % de una variable con cuatro
observaciones (1, 3, 5 y 6). Con estos cuatro elementos, si se tomara simplemente
el segundo, el valor del percentil 50 % sería 3, correspondiente al segundo elemento.
Ahora bien, resulta evidente que este valor no recoge bien el valor del 50 % de la
variable, sino que, entre los cuatro elementos, lo más adecuado sería hacer una media
entre el segundo y el tercer elemento, dado que lo que está en medio sería el «elemento
segundo y medio», el cual, lógicamente, no existe.
Este procedimiento se puede generalizar a cualquier otro percentil. El percentil 17
% de una variable de N = 2000 casos (ordenados de menor a mayor) se encuentra en la
posición (2000 x 17 / 100) + (1/2) = 340,5. Por lo tanto, se ha de realizar una media
entre el valor de los individuos que caen en las posiciones 340 y 341.
De acuerdo con las consideraciones arriba mencionadas, para el percentil k %, la fórmula
es:
3.1.2. Decil
El decil k es el elemento situado en la posición correspondiente a un k × 10 % de
los datos (cuando estos están ordenados). El decil 1 (D1) está en la posición 10 %
de los datos, el decil 2 (D2) está en la posición 20 % (= 2 x 10) de los datos, y
así, sucesivamente.
Habrás notado que el primer decil coincide con el décimo percentil (D1 = P10), el
segundo decil, con el vigésimo percentil (D2 = P20), etcétera:
-
-
-
-
(tres equivalencias omitidas)
-
-
-
Habrás notado también que he usado un signo de igualdad un poco raro, con tres líneas
en lugar de con dos. No se trata de un error tipográfico, el triple igual se emplea
para indicar que una relación es de identidad. Decimos que existe una relación de identidad entre dos términos cuando se da una
relacion de igualdad entre ellos por pura definición de los mismos. Es decir, tal
y como están definidos los términos, sería lógicamente imposible que no fueran iguales.
Hay nueve deciles (más allá del mínimo de la variable o «decil 0» y del máximo o «decil
10»), que dividen la variable o el conjunto de datos en diez partes iguales, con sendas
décimas partes de las observaciones.
El primer y último decil se emplean a menudo en estudios sobre desigualdades. Generalmente,
se calcula o bien (a) la renta del individuo situado en el decil 9 dividida por la
del individuo situado en el primer decil; o bien (b) la renta media de todos los individuos
pertenecientes al último decil (en este contexto, se entiende que son todos los individuos
entre el percentil 90 % y el percentil 100 %) dividida entre la renta media de todos
los individuos pertenecientes al primer decil (todos los que están entre el percentil
0 % y el percentil 10 %).
Figura 8. Los deciles y su utilización para medir la desigualdad
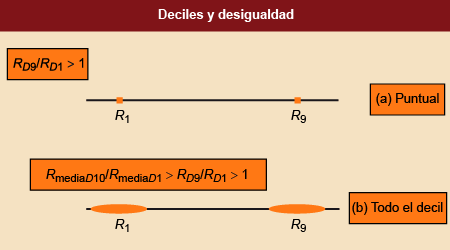
Fuente: Elaboración propia.
En cualquiera de los dos casos, cuanto mayor sea el cociente, mayor será la desigualdad.
Este cociente cumple, además, dos propiedades:
-
Propiedad 1: el cociente es siempre mayor si se emplea el método (b), del intervalo,
que el método (a), puntual. Observad que la renta media del último decil (RmediaD10) hace una media entre D9 (la renta de la persona situada precisamente en el decil 9) y la renta de personas
que tienen todas una renta mayor (observad que D9 es el extremo inferior de RmediaD10). Por lo tanto, RmediaD10 > RD9. Ved, también, que D1 es el extremo superior de RmediaD1. Por lo tanto, RmediaD1 < RD1. Lógicamente, la ratio del método (b), RmediaD10 / RmediaD1, es mayor que la ratio del método puntual, RD9 / RD1, dado que, en el primero, el numerador es más grande y el denominador, más pequeño.
-
Propiedad 2: ambos cocientes son mayores que 1. Basta con demostrar que RD9 / RD1 > 1, dado que la otra ratio siempre es mayor. Por definición, la renta de la persona
del decil 9 es superior a la del decil 1.
3.1.3. Quintil
El quintil k es el elemento situado en la posición correspondiente a un k × 20 % de
los datos cuando estos están ordenados. El primer quintil es el elemento en la posición
20 % (= 1 x 20) de los datos, el segundo quintil es el elemento en la posición 40
% (= 2 x 20) de los datos, y así, sucesivamente.
Habrás notado que puedes establecer una serie de equivalencias: el primer quintil
coincide con el segundo decil y con el vigésimo percentil, el segundo quintil coincide
con el cuarto decil (y con el cuadragésimo percentil), etcétera:
Nuevamente, he usado el signo ‘≡’ para denotar que las relaciones indicadas son de
identidad, y no solo de mera igualdad. Sin contar el elemento en el mínimo y en el
máximo, hay cuatro quintiles que dividen los datos en cinco partes iguales.
El primer y el último quintil son los más utilizados, y se emplean, sobre todo, en
estudios sobre desigualdades. Al igual que con los deciles, se pueden calcular cocientes
tanto por el método puntual como por el de los intervalos. En cualquiera de los dos
casos, cuanto mayor sea el cociente, mayor será la desigualdad.
Figura 9. Los quintiles y su utilización para medir la desigualdad
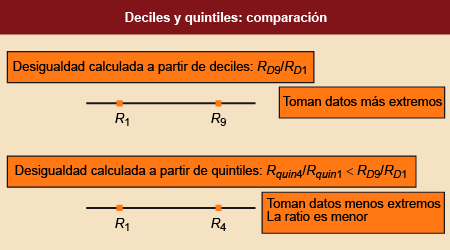
Fuente: Elaboración propia.
3.1.4. Cuartil
El cuartil k es el elemento situado en la posición correspondiente a un k × 25 % de
los datos (cuando estos están ordenados). El primer cuartil es el elemento en la posición
25 % (= 1 x 25) de los datos, el segundo cuartil es el elemento en la posición 50
% (= 2 x 25), y el tercer cuartil es el elemento en la posición 75%. Sin contar el
mínimo y el máximo, hay estos tres cuartiles, que dividen a los datos en cuatro partes
iguales. A veces, se usa el término cuartil para referirse a cada una de estas partes.
Veamos sus equivalencias con las medidas de posición estudiadas en los párrafos precedentes
(el signo ‘≡’ denota que las relaciones son de identidad):
-
-
Cuartil 2 ≡ Q2 ≡ P50 ≡ D5;
-
Los cuartiles se utilizan, entre otras cosas, para construir medidas de dispersión
de las variables, como el rango intercuartílico.
3.1.5. Mediana
Véase en la sección siguiente.
3.2. Medidas de tendencia central
3.2.1. Mediana
Elemento situado en el medio o en el centro de un grupo de elementos ordenados; es
decir, en el 50 % de los datos.
Obviamente, solo hay una mediana, y divide los datos en dos partes iguales. Por definición,
la mediana coincide con el segundo cuartil y el quinto decil:
-
Mediana (Med) ≡ Q2 ≡ D5 ≡ P50;
Por su definición, es evidente que la mediana puede ser considerada no solamente una medida de localización sino también de tendencia
central.
La mediana siempre es una medida adecuada de los datos «típicos», incluso cuando hay
unos pocos datos con valores muy extremos. Este puede ser el caso de variables como
los ingresos o la riqueza, debido a la existencia de unos cuantos multimillonarios
(actores de cine, estrellas del rock, futbolistas profesionales, nobles terratenientes
y directivos de multinacionales) con niveles espectaculares de renta o de riqueza.
Con este tipo de variables (técnicamente, decimos que tienen distribuciones asimétricas; más adelante, se explicará qué significa eso), muchas veces, se prefiere acudir
a la mediana en lugar de a la media (posiblemente, el estadístico más conocido de
todos, el cual veremos a continuación), porque el pequeño contingente de multimillonarios
afecta mucho a la media, pero no a la mediana, que seguirá recogiendo bien «la renta
de una persona típica».
Por esta misma razón, algunas de las medidas más utilizadas para estudiar la pobreza
la definen en relación con la renta mediana (por ejemplo, establecen el umbral de
pobreza en un 50 % de la renta mediana) en lugar de hacerlo en relación con la renta
media.
Otro campo de aplicación muy conocido de la mediana es el de los estudios electorales.
Según la teoría del votante mediano (inspirada en el conocido modelo de Hotelling
del vendedor de helados, y desarrollada principalmente por Anthony Downs, en su libro
de 1957, An Economic Theory of Democracy), los partidos políticos se situarán tan cerca como sea posible de las preferencias
del votante mediano. Lo que importa, según esta línea de pensamiento, es tener a la
mitad más uno de los votantes a favor, y no la intensidad de la preferencia de los
votantes hacia el partido (por cierto: la intensidad estaría relacionada con la preferencia
media).
3.2.2. Media aritmética
Suma de los valores (de un grupo o variable) dividida por el número de valores (del
grupo o variable).
En términos estrictos, la fórmula mostrada se refiere a datos de poblaciones y, cuando
se trabaja con datos de muestras, hay que modificar la notación: por un lado, la letra
griega µ se usa para aludir a la media poblacional, y para la media muestral, se usa una x con una barra encima; y, por otra parte, el número de observaciones en la población
se indica con mayúscula (N) y, en la muestra, con minúscula (n).
La media es una buena medida de tendencia central de los datos «típicos» cuando la
distribución es simétrica. A veces, la media será preferible a la mediana también
cuando la distribución es asimétrica. Precisamente por el hecho de que la mediana
siempre resulta una medida adecuada de los datos «típicos», no es sensible a la influencia
de los datos atípicos, de las observaciones con un papel potencialmente más importante.
Ejemplo 1
La existencia de personas de rentas muy elevadas puede resultar importante en términos
de las posibilidades para el desarrollo de la industria local.
Ejemplo 2
De manera parecida, la existencia de un grupo (reducido) de estudiantes con una nota
de cero (que podría dar pie a un caso de distribución asimétrica negativa) podría
indicar que el profesor no es capaz de motivar a los alumnos menos interesados o con
menos preparación previa.
Media (aritmética) ponderada
Intuitivamente, es una media aritmética con la particularidad de que se asignan pesos
o ponderaciones (wi). Dicho de manera más técnica, es la suma ponderada de los valores (de un grupo o
variable) dividida por la suma de las ponderaciones.
Media aritmética simple
La media aritmética simple es un caso especial de la media aritmética ponderada en
el que todos los elementos reciben el mismo peso o ponderación.
En efecto: si todos los pesos valen lo mismo, es decir, si wi = w = constante, entonces, como, en un sumatorio, una constante se puede sacar y poner
delante, multiplicando al sumatorio, el numerador sera w premultiplicado por el sumatorio
de Xi. Por lo mismo, el denominador será w por el sumatorio de 1 o, simplemente, w por
N. Simplificando por w, que está tanto en el numerador como en el denominador, se
sigue que la media ponderada es equivalente, en este caso, a la media aritmética simple:
Intuitivamente, diríamos que todos los valores reciben la ponderación de la inversa
de la medida del grupo: 1/N o 1/n, según se trate de una población o de una muestra.
Ejemplo
Consideremos el precio del pan en los países de la Unión Europea. Imaginemos que tenemos
una tabla con el valor del pan en estos países. ¿Cuál es el «valor central» en torno
al cual oscila el precio del pan en Europa? Una opción es sumar el precio del pan
en cada país y dividir por el número de países integrantes de la Unión –es decir,
hacer la media aritmética simple. No obstante, este procedimiento supone darle, implícitamente,
la misma importancia a Luxemburgo que a Francia. Para muchas finalidades, esta no
será la mejor estrategia. Quizá queramos ponderar por el número de habitantes, por
el número de toneladas consumidas o producidas, o por otros criterios. Así, si viajamos
por Europa y pasamos cinco días en Francia, ocho en Italia, dos en Luxemburgo, y no
visitamos ningún otro país, para nuestros propósitos, le tendríamos que dar un peso
de 5/15 a Francia, 8/15 a Italia, 2/15 a Luxemburgo, y 0/15 al resto de los países,
ya que, dado nuestro plan de viaje, lo que nos interesa es cuán a menudo nos enfrentaremos
al precio del pan en cada uno de los países. Observad que la determinación de cuáles
son las ponderaciones más adecuadas depende de la finalidad para la que estamos calculando
el «valor central del pan» en la Unión Europea.
3.2.3. Moda
Valor con mayor frecuencia de ocurrencia.
Dependiendo del hecho de si la moda es única o no, las distribuciones pueden ser unimodales
o multimodales.
Distribución unimodal
Distribución en la que la única moda local es la moda global; en la que no existe
ningún valor que sea mayor que todos los valores de su entorno si no es también mayor
que todo el resto de los valores.
En términos prácticos, una distribución unimodal es una distribución con un único
máximo o «pico» de frecuencias.
Ejemplo
A continuación, se presenta un histograma de la variable «RENTA» del cuestionario
postelectoral español de 2008, ya visto antes. Esta variable mide, en una escala de
0 al 10, en cuál de los intervalos de renta se sitúan los encuestados, y ha sido recodificada
a partir de la variable «p68» para excluir la categoría de no respuesta «no contesta»
(un 31,7 % de la muestra):
Figura 10. Ejemplo de una distribución multimodal. Distribución de «RENTA»
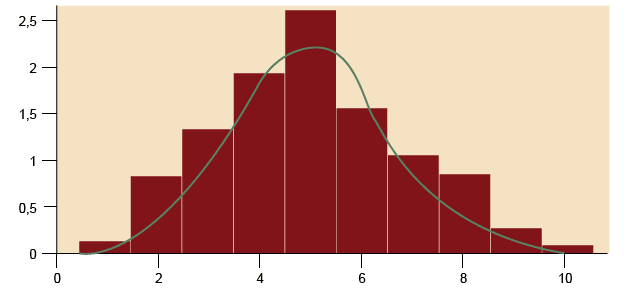
Fuente: CIS, cuestionario 2757. Elaboración propia.
Como se puede ver, la variable «RENTA» tiene un solo pico de frecuencias, es decir,
tiene una única moda, correspondiente a la categoría «5» de renta (de 1201 a 1800
€).
Distribución multimodal
Distribución en la que hay varias modas (o máximos) locales diferentes.
En términos prácticos, una distribución multimodal es una distribución con más de
un máximo o «pico» de frecuencias.
Ejemplo
Se presenta un histograma de la variable «ETA_DIÁLOGO», tomada también del cuestionario
postelectoral español de 2008. Esta variable mide, en una escala de 0 al 10, en qué
medida los encuestados creen que, para acabar con ETA, es necesario derrotarla policialmente
(0) o también hace falta diálogo (10), y ha sido recodificada a partir de la variable
«p10» para excluir las categorías de no respuesta («no sabe» y «no contesta»: un 6,0
% y un 1,1 % de la muestra, respectivamente):
Figura 11. Ejemplo de una distribución multimodal. Distribución de «ETA_DIÁLOGO»

Fuente: CIS, cuestionario 2757. Elaboración propia.
Como se puede ver, las opiniones se polarizan, y hay un grupo sustancial de individuos
que opta por la solución puramente policial (0), y otro grupo claramente en favor
del diálogo (10). Aparte de estos dos grupos, también hay un grupo de gente que ve
la necesidad de ambas estrategias. Esta configuración de opiniones da lugar a una
distribución con tres modas de la variable, dos en los extremos, y una en el centro
(0, 5 y 10).
En general, cuando la distribución de preferencias es bimodal («de dos jorobas»),
es poco probable que las decisiones basadas en la mediana o en la media sean acertadas:
en una sociedad con grandes desigualdades de ingresos, puede ser mejor elegir un producto
de coste bajo dirigido a una demanda de mercado centrada en el precio, o bien un producto
de gama alta aunque sea costoso, pero no uno de gama media, que podría resultar demasiado
caro para quienes se fijan primordialmente en el precio y demasiado vulgar para quienes
se fijan en la calidad.
Aplicación: distribuciones unimodales, multimodales y el «bien colectivo»
El carácter unimodal o multimodal de las distribuciones reviste una enorme importancia
en relación con las preferencias colectivas y la posibilidad de encontrar métodos
de agregación de las preferencias individuales. El teorema general de la posibilidad,
más conocido como teorema general de la imposibilidad, formulado por Kenneth Arrow,
demuestra que, bajo ciertas condiciones mínimas (cualquier preferencia individual
es posible; ninguna preferencia individual es excluida como posible preferencia colectiva;
ausencia de un dictador; ausencia de normas externas que dictaminen cuál es el resultado),
ningún método de agregación de las preferencias individuales podrá garantizar la ausencia
de ciclos. El teorema de Black demuestra que, en espacios de decisión unidimensionales,
cuando las preferencias de los actores entre diferentes alternativas son unimodales,
sí hay métodos para agregar las preferencias individuales que no generan ciclos en
las preferencias colectivas. El carácter unimodal o no de las distribuciones de preferencias
individuales tiene, por lo tanto, una enorme importancia en cuanto a la posibilidad
de agregar preferencias individuales para determinar un eventual o hipotético «bien
común».
Desde un punto de vista matemático, una distribución unimodal se corresponde con una
ecuación cuadrática (del tipo y = ax2 + bx + c), dado que ésta tiene, a lo sumo, un único máximo. Una distribución multimodal
se corresponde con una ecuación de cuarto grado o superior (del tipo y = ax4 + bx3 + cx2 + dx + e), dado que, para tener varios máximos locales, una ecuación debe ser de
cuarto grado o mayor.
3.2.4. Media geométrica (G)
Producto de los valores (de un grupo o variable) elevado a la inversa del número de
valores (del grupo o variable).
Es decir, la raíz n-ésima del producto de los valores de un grupo o variable (en el que hay n elementos):
La media geométrica se suele utilizar cuando se supone que una variable presenta procesos
de crecimiento a una tasa constante. Habitualmente, se extraen medias geométricas
para porcentajes, tasas e índices.
3.3. Medidas de dispersión
Las medidas de dispersión resumen la variabilidad y permiten estudiar la representatividad
de las medidas de tendencia central. ¿Hasta qué punto representan las medidas de tendencia
central los valores de una variable? ¿Hasta qué punto sintetizan adecuadamente la
información de esta variable?
Claramente, si la medida de tendencia central es, por poner un ejemplo, la media (aritmética
simple), la respuesta dependerá de si los valores están considerablemente agrupados
en torno a esta media o considerablemente alejados de ella.
Veamos el ejemplo siguiente, en el que tres empresas de siete vendedores cada una
proporcionan los datos de ventas siguientes:
Tabla 9. Utilidad de las medidas de dispersión
|
Vendedores
|
A – Ventas (miles €)
|
B – Ventas (miles €)
|
C – Ventas (miles €)
|
|
1
|
15
|
0
|
0
|
|
2
|
15
|
1
|
1
|
|
3
|
15
|
15
|
2
|
|
4
|
15
|
15
|
15
|
|
5
|
15
|
15
|
28
|
|
6
|
15
|
29
|
29
|
|
7
|
15
|
30
|
30
|
|
MEDIA
|
15
|
15
|
15
|
|
MEDIANA
|
15
|
15
|
15
|
|
MODA
|
15
|
15
|
No hay
|
Como se puede comprobar, las medidas de tendencia central son casi iguales (la única
diferencia, en este sentido, sería la ausencia de moda en el último caso). Esto significa
que, si los gerentes de las tres empresas recibieran solamente información de la media
de ventas, llegarían a conclusiones muy parecidas. No obstante, la tabla revela que
las diferencias entre las empresas son considerables.
La clave es la variabilidad, la dispersión de los datos: mientras que en la empresa
A las medidas de tendencia central representan de forma extremadamente fidedigna la
situación (los datos se aglomeran en torno a la tendencia central), en las empresas
B y C las medidas de tendencia central no aportan toda la información necesaria, dado
que los datos están considerablemente alejados de las medidas de tendencia central.
Figura 12. Diferencias de ventas a pesar de una misma tendencia central
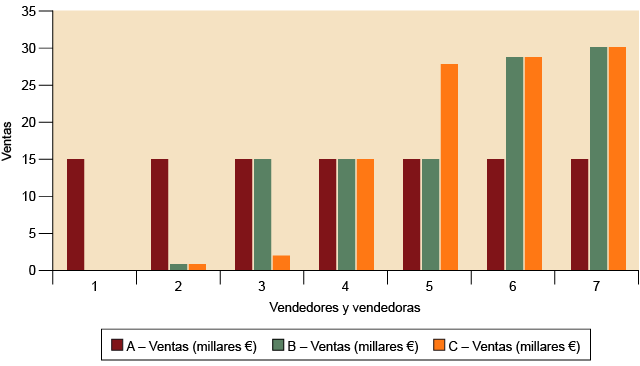
3.3.1. Rango o recorrido (R)
Diferencia entre el valor máximo y el valor mínimo de una distribución.
R(X) = máx{X} - mín{X}
El rango es sensible únicamente a valores extremos, y no tiene en absoluto en cuenta
el resto de los valores.
Ejemplo
Considerad X = {1,2,3,4,5,6,7,8,9} e Y = {3,3,3,3,3,3,9,11,11}. Como podéis ver, para
ambas, la media es 5 y el recorrido, 8. Este ejemplo demuestra que distribuciones
con una misma media (μ = 5) y un mismo rango (R = 8) pueden ser considerablemente
diferentes.
3.3.2. Rango o recorrido intercuartílico (RI)
Diferencia entre el valor del tercer y del primer cuartil, esto es, entre el percentil
75 y el percentil 25.
RI(X) = Q3 - Q1 = P75 - P25
Este rango se puede utilizar para matizar la sensibilidad a valores extremos del rango,
o para estudiar cuestiones más específicas –como, por ejemplo, cuál es el rango en
el que se encuentran las «observaciones centrales». A veces, se utilizan otros rangos
modificados, como el rango entre el percentil 95 y el percentil 5, o entre el percentil
90 y el percentil 10.
3.3.3. Desviación media, varianza y desviación estándar
Desviación Media
Media del valor de la diferencia entre cada valor y la media.
Naturalmente, esta media es, simplemente, 0, puesto que, por definición, las diferencias
positivas entre cada valor y la media se compensan con las diferencias negativas:
Por lo tanto, la desviación media, como tal, es un parámetro igual a cero, no sirve
para medir la variabilidad de una distribución y, naturalmente, no se utiliza. No
obstante, se puede modificar levemente la definición para evitar que los valores positivos
y los negativos se compensen. Eso es lo que hacen los cuatro estadísticos que vienen
a continuación:
Desviación media absoluta
Media del valor absoluto de la diferencia entre cada valor y la media.
Al tomar valores absolutos, los valores positivos y los negativos ya no se compensan,
con lo que esta medida deja de ser un parámetro.
Desviación media respecto a la mediana
Media de la diferencia entre cada valor y la mediana.
El cálculo es análogo al presentado para la media aritmética, pero se sustituye esta
por la mediana:
Esta medida es un parámetro, dado que tanto la media (μ) como la mediana (Med) son
parámetros, y la diferencia de parámetros es un parámetro. ¿Qué información proporciona,
entonces, esta medida (paramétrica) de dispersión? La información que nos proporciona
esta medida es hasta qué punto dos de las medidas de tendencia central, la media y
la mediana, se diferencian una de la otra. Cuando la media y la mediana coinciden,
la desviación media respecto a la mediana valdrá cero.
Desviación media absoluta respecto a la mediana
Media del valor absoluto de la diferencia entre cada valor y la mediana.
Es decir, aplica simultáneamente las ideas de los dos últimas propuestas: tomar valores
absolutos de las diferencias y calcular éstas en relación con la mediana. Del mismo
modo que en el caso de la desviación media absoluta, al tomar valores absolutos, los
valores positivos y los negativos ya no se compensan, con lo que esta medida deja
de ser un parámetro igual a cero por definición.
Varianza
Media del cuadrado de la diferencia entre cada valor y la media.
Para muestras, cambiaría la notación: se usaría ‘s’ en lugar de ‘σ’, la x con la barra
en lugar de ‘μ’ y una ‘n’ minúscula en lugar de la ‘N’ mayúscula en el denominador.
De hecho, por razones que no merece la pena desarrollar aquí, se pone ‘n-1’ en lugar
de ‘N’. La varianza es muy similar en su construcción a la DMA (desviación media absoluta),
pero, para evitar que los positivos y negativos se compensen, en lugar de tomar valores
absolutos, toma cuadrados (como se eleva al cuadrado, siempre será positiva).
-
Desventaja: una desventaja de la varianza es que sus unidades son difíciles de interpretar,
dado que, al tomar cuadrados, no se está en la misma escala que la distribución a
partir de la cual se construye. Por ejemplo, si la variable original está definida
en euros, la varianza estará expresada en euros al cuadrado. Pero ¿qué es un euro
al cuadrado? ¿Cómo debemos interpretar una varianza de tantos o cuantos euros al cuadrado?
-
Varianza como segundo momento: si se retoma la fórmula inicial, se apreciará que la
varianza es, a su vez, una media aritmética, ya que suma algo (en este caso, desviaciones
al cuadrado) para un grupo o variable, y divide esta suma entre el número de valores.
Desviación estándar
Raíz cuadrada de la varianza.
Es decir, raíz cuadrada de la suma del cuadrado de la diferencia entre cada valor y la media, dividida entre la raíz cuadrada de
la medida poblacional:
Desde un punto de vista interpretativo, por el hecho de tomar la raíz cuadrada de
la varianza, las unidades de la desviación estándar vuelven a ser coherentes con las
unidades de la distribución de la que proceden, es decir, vuelven a estar en la misma
escala.
3.3.4. Medidas de dispersión adimensionales
Además de las medidas presentadas hasta ahora, todas dimensionales, en el sentido
de que dependen de las unidades de medida empleadas, hay también medidas diseñadas
para no depender de las unidades de medida ni, por lo tanto, de cuestiones de escala.
En la literatura, es común hablar de medidas de dispersión relativas o adimensionales
para referirse a estas medidas que no dependen de la unidad de medida ni de la escala
de las variables, en oposición a las medidas de dispersión absolutas o dimensionales,
que sí dependen de la unidad de medida.
Coeficiente de variación de Pearson (CV)
Cociente entre la desviación estándar y la media aritmética.
Se trata, por lo tanto, de un «índice de dispersión respecto a la media». Su fórmula
es:
Como recordaréis de la discusión reciente sobre las unidades de medida de la varianza
y de la desviación estándar, esta última tiene las mismas unidades de medida que la
variable original y, por lo tanto, que la media. Al tener la misma unidad de medida
en el numerador y en el denominador, el CV no tiene unidades, es adimensional. El
coeficiente de variación también se puede expresar en tantos por cientos para facilitar
su interpretación.
-
Interpretación del CV: en cuanto a su interpretación, cuanto mayor sea el CV, mayor
es la desviación estándar en relación con la media y, por lo tanto, menos representativa
es la media de la distribución.
-
Propiedades y restricciones del CV: los valores del CV no están acotados, con lo que
pueden variar entre menos infinito y más infinito. Conviene remarcar que no resulta
adecuado utilizar el CV cuando la media es cero, dado que, en este caso, el CV no
estaría definido, ya que el resultado de dividir cualquier número por cero no está
definido. Tampoco sería adecuado utilizar el CV cuando la media es negativa, puesto
que, en este caso, no sería posible interpretar el valor del CV.
Índice de dispersión respecto a la mediana
Cociente entre la desviación media absoluta respecto a la mediana, en el numerador,
y la mediana, en el denominador.
El objetivo de este índice es similar al del CV, pero para la mediana. En lugar de
usar la desviación estándar en el numerador, se utiliza la desviación media absoluta
con respecto a la mediana y, en lugar de usar la media en el denominador, se emplea
la mediana.
3.4. Discusión: variables tipificadas o estandarizadas
Variable a la que se le sustrae la media aritmética y, después, el resultado de esta
diferencia se divide por la desviación estándar. Por construcción, la media de una
variable estandarizada es cero y su desviación estándar es igual a la unidad.
El proceso descrito se denomina «tipificación» o «estandarización» y su objetivo es
permitir la comparación entre variables que, sin estandarizar, no serían comparables,
porque hacían alusión a conceptos diferentes o estaban medidas en escalas diferentes.
Las variables resultantes no tienen unidades, son adimensionales. ¿Podéis decir por
qué? Efectivamente, ya sabemos –lo hemos comentado un par de veces– que la media tiene
las mismas unidades que la variable considerada, y que la desviación estándar también.
Observad que, dado que su media es nula, no se puede utilizar el CV para estas variables.
3.5. Medidas de forma
Además de las medidas de localización, de tendencia central y de dispersión, hay otros
dos tipos de medidas, ambas relacionadas con la forma de la distribución, que son
útiles para caracterizar y describir de manera sucinta los rasgos fundamentales de
una distribución: las medidas de simetría y las de apuntamiento o curtosis.
3.5.1. Medidas de simetría
Una de las cuestiones más importantes relacionadas con la forma de una distribución
es si esta es simétrica, asimétrica positiva o asimétrica negativa.
A continuación, explicaremos qué significan estos términos y presentaremos algunas
de las medidas más utilizadas para evaluar el grado de asimetría de una distribución.
Entre las aplicaciones que tiene la información sobre el grado de asimetría de una
distribución destaca el hecho de que la distribución normal, la cual se asume en un
gran número de contrastes estadísticos, es asimétrica. Las medidas de asimetría permiten,
entre otras cosas, comprobar si la asunción sobre la normalidad de la distribución
es razonable o no.
Distribución simétrica
Distribución en la que «el lado derecho» (con respecto a la mediana, para variables
continuas, y con respecto a la media, para variables discretas) de la gráfica es «igual»
al «lado izquierdo». Dicho de otro modo, cada lado es la imagen especular del otro.
Esta definición implica que una distribución simétrica es una distribución en la que
la media y la mediana coinciden –y, si la distribución es unimodal, también coinciden
con la moda.
A continuación, se vuelve a presentar un histograma de la variable «RENTA», creada
a partir de la variable «p68» del cuestionario CIS 2757, dado que, además de servir
para ejemplificar una distribución unimodal, también representa un buen ejemplo de
una distribución simétrica:
Figura 13. Ejemplo de una distribución simétrica. Distribución de «RENTA»
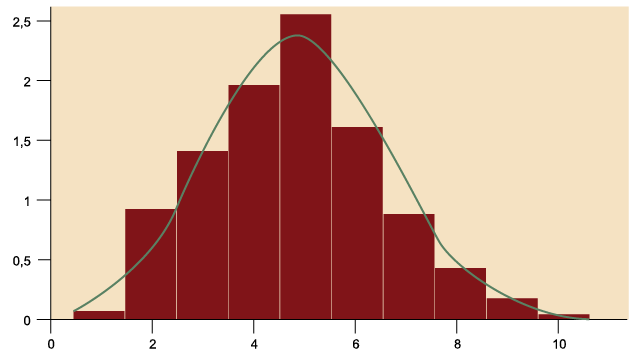
Fuente: CIS, cuestionario 2757. Elaboración propia.
Como se puede ver, la variable «RENTA» es muy simétrica, a pesar de que las categorías
a la izquierda de la mediana tienen algo más de datos que las categorías a la derecha
(es decir, si somos muy estrictos, deberemos reconocer que tiene una pequeña cola
a la derecha). Conviene tener en cuenta que, en la práctica, será muy raro encontrar
una distribución perfectamente simétrica. Por ello, se considerará que es simétrica
si es aproximadamente simétrica. El elevado grado de simetría de la variable «RENTA»
se debe a que esta ha sido codificada en intervalos. Cuando se piden estimaciones
precisas de la renta, esta resulta mucho más asimétrica.
Distribución asimétrica positiva (a la derecha)
Distribución en la que la cola de la derecha es más larga y la masa de la distribución
se concentra hacia la izquierda. Es decir, gráficamente, tienen una «cola» a la derecha.
Ejemplo
Se presenta el histograma de la variable «edad», tomada también del cuestionario postelectoral
español de 2008.
Figura 14. Ejemplo de una distribución asimétrica positiva o a la derecha (variable
«edad»)
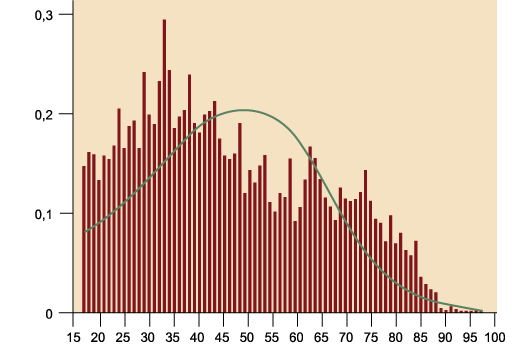
Fuente: CIS, cuestionario 2757. Elaboración propia.
Como se puede apreciar, las observaciones de las personas con edades avanzadas, a
pesar de no ser excesivamente numerosas, conforman una «cola a la derecha» que «arrastra»
la media hacia la derecha, dado que «pesan» más que las observaciones de los más jóvenes.
Esto hace que la media (47) sea algo mayor que la mediana (45).
Distribución asimétrica negativa (a la izquierda)
Distribución en la que la cola de la izquierda es más larga y la masa de la distribución
se concentra hacia la derecha. Es decir, gráficamente, tienen una «cola» a la izquierda.
Normalmente, la media es menor que la mediana y esta es, a su vez, menor que la moda.
Coeficiente de asimetría de Pearson
Diferencia entre la media y la moda dividida entre la desviación estándar.
Observad que el coeficiente de asimetría de Pearson no tiene unidades, es adimensional,
puesto que la desviación estándar está expresada en las mismas unidades que la media
y la moda.
Interpretación:
Este coeficiente se basa en el hecho de que, en las distribuciones simétricas unimodales
y campaniformes, la media es igual a la moda. Si la media y la moda son iguales, el
coeficiente será cero, lo que sugiere que se trata de una distribución simétrica.
Si la media es superior a la moda, estará a su derecha, y el coeficiente será positivo,
lo que indica que la distribución será una distribución asimétrica positiva, con una
cola hacia la derecha de la distribución; si la media es inferior a la moda, estará
a la izquierda de la moda, y el coeficiente será negativo, lo que indica que la distribución
será asimétrica negativa, con una cola hacia la izquierda de la distribución.
Aplicabilidad y restricciones:
Conviene tener siempre presente que este coeficiente no se puede aplicar a cualquier
tipo de distribución; solamente se puede utilizar para distribuciones unimodales,
campaniformes y moderadamente asimétricas. El requisito de una única moda no necesita
casi explicación, dado que lo que se mide es precisamente la diferencia entre la media
y la moda. El requisito de forma campaniforme, sumado al de una única moda, garantiza
que la moda esté en el interior de la distribución, y no en uno de sus extremos, y,
por lo tanto, que la moda sea un buen indicador como medida de tendencia central de
la distribución, a partir de la cual tenga sentido comprobar si ambos lados, el lado
que cae a la izquierda de la moda y el lado que cae a su derecha, son, aproximadamente,
una imagen especular uno del otro o no.
Coeficiente de asimetría de Fisher (λ3)
Cociente entre el momento de tercer orden y la desviación estándar elevada a la tercera
–es decir, el «tercer momento estandarizado».
En estas fórmulas, y en la definición del coeficiente de Fisher, hemos introducido
el término momento. Veamos su significado:
Momento de orden n
De manera general, el momento de orden n es el sumatorio de las desviaciones con respecto a la media, elevadas a la n-ésima potencia.
Momento estandarizado de orden n
El momento estandarizado de orden n (o momento de orden n estandarizado) es el resultado
de dividir el momento de orden n por la n-ésima potencia de la desviación estándar.
Observad que el primer momento es igual a la desviación media (DM) por el número de
observaciones. Como DM es cero, el primer momento es cero. Observad también que todos
los momentos estandarizados son adimensionales. Volviendo al coeficiente de asimetría
de Fisher, es inmediato comprobar que éste no tiene unidades, dado la desviación estándar
está expresada en las mismas unidades que las diferencias respecto a la media.
La lógica que motiva la construcción de este coeficiente es la siguiente: si la distribución
es simétrica, existirá el mismo número de valores a la izquierda que a la derecha
de x; si es asimétrica negativa, existirán más valores a la izquierda que a la derecha
de x; y si es asimétrica positiva, habrá menos valores a la izquierda que a la derecha
de x. Las desviaciones elevadas a una potencia impar permitirán mantener los signos
de las desviaciones: si la distribución es asimétrica negativa, el signo del sumatorio
elevado al cubo, a la quinta o a la séptima será negativo, y si es asimétrica positiva,
este sumatorio tendrá un signo positivo. Naturalmente, si se elevan a una potencia
par, todos resultarán positivos. Por otro lado, la potencia más simple que se puede
utilizar es tres, puesto que, por definición, el momento de primer orden es cero.
Por ello, este coeficiente de simetría utiliza el tercer momento. En consecuencia,
la interpretación del coeficiente es la siguiente:
-
λ3 < 0: la distribución será asimétrica negativa, con una cola hacia la izquierda de
la distribución;
-
λ3 = 0: la distribución será simétrica, sin colas;
-
λ3 > 0: la distribución será asimétrica positiva, con una cola hacia la derecha de la
distribución;
Coeficiente de asimetría de Bowley (ASB)
Diferencia entre la suma de Q1 y Q3 menos dos veces la mediana, dividida por la diferencia
entre Q3 y Q1.
Para entender la lógica de esta medida, convendrá definir las siguientes distancias:
d32 = (Q3 – Q2), la distancia entre el tercer cuartil y la mediana; y d21 = (Q2 – Q1), la distancia entre la mediana y el primer cuartil.
-
En una distribución asimétrica negativa, o a la izquierda, Q3 estará a menos distancia
de Q2 que Q1, es decir, d32 < d21. Por lo tanto, (Q3 – Q2) – (Q2 – Q1) = d32 – d21 < 0, y ASYB < 0.
-
En una distribución simétrica, Q1 y Q3 estarán a la misma distancia de Q2. Por lo
tanto, (Q3 - Q2) – (Q2 – Q1) = d32 – d21 = 0, y ASYB = 0.
-
En una distribución asimétrica positiva, o a la derecha, Q3 estará a más distancia
de Q2 que Q1, es decir, d32 > d21.
Propiedades:
Claramente, en este caso, el coeficiente estará entre –1 y 1, y no depende de los
cambios de origen o de escala. En efecto, observad que el denominador se puede expresar
como (Q3 – Q1) = (Q3 – Q2) + (Q2 – Q1) = d32 + d21. Por lo tanto, ASYB = (d32 – d21) / (d32 + d21), el cual está, evidentemente, comprendido en el rango [–1, 1]. En cuanto a la escala,
está claro que, como las unidades en el numerador y en el denominador son las mismas,
este coeficiente es adimensional y no depende de los cambios de escala.
Coeficiente de asimetría de Yule Bowley (ASYB)
Diferencia entre la suma de Q1 y Q3 menos dos veces la mediana, dividida por el doble
de la mediana.
La lógica de este coeficiente es muy parecida a la del coeficiente de Bowley, lo único
que varía es que, en lugar de dividir por la diferencia entre Q3 y Q1, lo hace entre
el doble de Q2. Obviamente, también en este caso, el coeficiente estará entre –1 y
1, y tampoco depende de los cambios de origen o de escala.
3.5.2. Medidas de curtosis
Intuitivamente, la curtosis mide «la variabilidad de la variabilidad», la «dispersión
de la dispersión», la «varianza de la varianza». Gráficamente, es habitual escuchar
la interpretación de que la curtosis mide el grado de apuntamiento de la distribución
de una variable.
La curtosis es mínima cuando todas las observaciones están igual de alejadas de la
media (por ejemplo, todas son ceros o unos y la media es 0,5), porque todas contribuyen
igual a la variabilidad. La curtosis es máxima cuando toda la variabilidad está provocada
por dos valores extremos. De manera más general, la curtosis es baja cuando una parte
importante de la varianza está provocada por desviaciones frecuentes y de poca magnitud,
y es alta cuando una parte importante de la varianza es consecuencia de desviaciones
extremas pero poco frecuentes.
En los trabajos clásicos, la curtosis se definía como el cuarto momento estandarizado, es decir, como el cociente entre el momento de cuarto orden y la desviación estándar
elevada a la cuarta.
El apuntamiento o curtosis debe evaluarse de manera comparativa, con respecto a alguna
distribución de referencia. Para ello, se utiliza la distribución normal. La distribución
normal tiene una curtosis de 3 (en la definición clásica). Esto ha llevado a definir
el exceso de curtosis como el coeficiente de curtosis menos tres. Obviamente, la distribución normal tiene
un exceso de curtosis de cero.
Distribución mesocúrtica
Distribución con un exceso de curtosis igual a cero.
Dado que esta es característica de la distribución normal, es habitual encontrar definiciones
alternativas de las distribuciones mesocúrticas como aquellas que tienen una curtosis
igual a la normal (estadístico λ4 = 3):
Distribución leptocúrtica
Distribución con un exceso de curtosis positivo o una curtosis mayor que la de la distribución normal (λ4 > 3).
Las distribuciones leptocúrticas tienen un pico más alto, pero más estrecho que el
de las distribuciones mesocúrticas, y unas colas más gruesas, «más largas».
Distribución platicúrtica
Distribución con un exceso de curtosis positivo o una curtosis menor que la de la distribución normal (λ4 < 3).
Las distribuciones platicúrticas tienen un pico más bajo, pero más ancho o grueso
que el de las distribuciones mesocúrticas, y unas colas más finas, «más cortas».
Bibliografía
Barbancho, A. G. (1973). Estadística elemental moderna. Barcelona: Ariel.
Downs, A. (1957). An Economic Theory of Democracy. Nueva York: Harper & Row.
Ferejohn, J. A.; Fiorina, M. P. (1974). «The Paradox of Not Voting: A Decision Theoretic Analysis». The American Political Science Review (vol. 68, núm. 2, págs. 525-536).
Hamilton, L. C. (1992). Regression with Graphics: A Second Course in Applied Statistics. Pacific Grove (CA): Brooks/Cole.
Peña, D. (2001). Fundamentos de Estadística. Madrid: Alianza Editorial.
Spiegel, M. R. (1991). Estadística (2.ª ed.). Madrid: McGraw-Hill.
Wonnacott, T. H.; Wonnacott, R. J. (1979). Introducción a la Estadística. México: Limusa.