Erwin Rudolf Josef Alexander Schrödinger vino al mundo bajo los mejores auspicios, un 12 de agosto de 1887, en la ciudad de Viena. Si las biografías del Renacimiento se abrían precisando las posiciones de los astros en el momento del parto, en el caso de Schrödinger no hace falta remontarse hasta el firmamento para buscar presagios. Se puede decir que la ciencia hizo guardia junto a su cuna. Su abuelo materno, Alexander Bauer, fue catedrático de química y solo moderó su pasión investigadora después de perder un ojo en un accidente de laboratorio, al reventarle un matraz. La ciencia actuó también de celestina entre los padres: Rudolf Schrödinger fue alumno de Alexander en la Technische Hochschule de Viena (la actual Universidad de Tecnología) y así vino a tratar a una de sus hijas, Georgine Bauer, que se convertiría en su mujer en 1886. Poco podían imaginar el padre y el abuelo que el pequeño Erwin crecería para explicar, con una sola ecuación, toda la química que ellos habían aprendido.
Rudolf heredó una modesta empresa familiar dedicada al comercio de linóleo, que le procuró una vida desahogada hasta que el desastre austriaco de la Primera Guerra Mundial lo arrastró a la quiebra. Para él supuso un regalo envenenado, del que renegaba cada mañana al levantarse, por las horas que le robaba a sus verdaderos intereses: la pintura italiana, la cerámica oriental y el estudio de la filogenia. Schrödinger atribuyó a sus padres el origen de sus dos principales fascinaciones, la pasión por el conocimiento y el universo femenino:
Para un hijo en pleno desarrollo, [mi padre] fue un amigo, un maestro y un infatigable interlocutor, la corte de apelación para cualquier asunto que de verdad pudiera interesarle […]. Al margen de su entrega sacrificada, le debo agradecer [a mi madre], según creo, mi estima hacia las mujeres.
La familia de la abuela materna, de apellido Russell, era de origen anglosajón. Una de las tías de Schrödinger, Minnie, quiso preservar los genes insulares en suelo austriaco y, esgrimiendo un libro con historias de la Biblia, le enseñó al niño la lengua de Shakespeare antes de que aprendiera a escribir en alemán. Su madre también podía decretar en cualquier momento que durante el resto del día se hablara en inglés. Esta disciplina improvisada resultó providencial décadas después, cuando la ola nacionalsocialista barrió Alemania y Austria.
El abuelo Alexander aprovechó su carrera académica como trampolín para introducirse en la alta sociedad vienesa, donde se hizo merecedor de dos títulos, uno de ellos oficial, de Hofrat, o consejero de Estado, y otro, más informal pero no menos distinguido, de salönlowe («león de los salones»), que señalaba a quienes sobresalían por su gracia y maneras en los círculos elegantes. Su buena fortuna le permitió comprar un edificio de cinco plantas en uno de los mejores barrios de la ciudad. El último piso lo alquiló a su yerno y allí vivió Schrödinger mientras permaneció en Viena, hasta 1921. En este espacio privilegiado, con dos habitaciones para él solo, que daban a un patio interior, Erwin, hijo único, se crió en un entorno emocional entregado, servido por su madre, sus tías Minnie y Rhoda, y una corte de criadas y niñeras.
La enseñanza de Schrödinger se confió a tutores privados hasta los once años. Cuando llegó la hora de someterse a la educación pautada por el Estado, no halló ningún problema para integrarse, aunque era un año mayor que el resto de los alumnos. En el otoño de 1898 ingresó en el Akademisches Gymnasium, donde recibió una sólida formación humanística, que en su madurez le permitiría traducir a Homero del griego al inglés y a los trovadores provenzales, al alemán. Ya entonces su endiablada facilidad para la física y las matemáticas llamó la atención de uno de sus compañeros de clase:
[…] poseía un don para la asimilación que le permitía, sin necesidad de estudiar en casa, comprender y aplicar la materia de forma inmediata y directa durante las horas de clase. Después de que nuestro profesor Neumann […] completara su exposición, podía llamar de inmediato a Schrödinger a la pizarra y plantearle problemas que él resolvía con una facilidad festiva. A los estudiantes normales, las asignaturas de física y matemáticas nos resultaban aterradoras, pero él las consideraba sus áreas de conocimiento preferidas.
Desde muy joven Schrödinger alimentó inquietudes muy diversas, entre ellas la afición por el teatro, en particular por las obras del dramaturgo austriaco Franz Grillparzer. Le gustaba coleccionar los programas de las funciones a las que asistía y cubrir los márgenes de notas con sus impresiones. Su padre lo introdujo, no del todo convencido, en la teoría de la evolución, una materia que se estigmatizaba en las escuelas. Después de devorar las casi mil páginas de El origen de las especies, Schrödinger se declaró «un darwinista entusiasta, naturalmente».
Al calor de la pubertad despegó su carrera de donjuán. Aunque nunca pudo presumir del repertorio que desgranaba Leporello al admirar las conquistas de su amo Don Giovanni en la ópera de Mozart, durante toda su vida Schrödinger llevó por escrito la cuenta de las mujeres que seducía. La lista llegó a ser casi tan extensa como la de los artículos científicos que publicó. El primer amor del que nos queda constancia era la hermana de su mejor amigo del instituto y se llamaba Lotte.
En el otoño de 1906 Schrödinger comenzó sus estudios de física en la Universidad de Viena, donde de nuevo atrajo la atención la facilidad de su inteligencia. Los demás alumnos descubrieron en él «un espíritu de fuego en acción, que siempre sabía abrirse camino hasta algo original en cualquier investigación». Su mejor amigo durante los años de universidad fue Franz Frimmel, un estudiante de botánica, con quien debió de recorrer entera la ciudad de Viena, mientras discutían hasta el agotamiento sobre el sentido de la vida, que siempre se les terminaba escapando al doblar la última esquina. La capital del Imperio austro-húngaro, por la que paseaban, era un caldero donde se cocinaban toda clase de revoluciones. Los aficionados a la pintura podían escandalizarse ante los desnudos de Klimt y Schiele; los melómanos, criticar las sinfonías de Mahler o silbar a Schoenberg; cualquier ciudadano de a pie, exigir la demolición de las casas cubistas de Adolf Loos; y todos ellos podían exorcizar sus demonios interiores en el diván de Sigmund Freud. Las clases acomodadas se arrimaban a la lumbre de un esplendor cultural sin precedentes, que también iluminó a la ciencia.
BOLTZMANN: EL ÁTOMO O LA VIDA
Ludwig Boltzmann (1844-1906) compartía con Schrödinger la afición desde niño por las ciencias naturales y una admiración sin límites hacia la obra de Charles Darwin. Así la expresó, por ejemplo, en una conferencia que pronunció en la Academia de Ciencias de Berlín, en 1886:
Si me preguntasen cuál es mi convicción íntima, si el siglo XIX será recordado algún día como el siglo del acero, o el siglo de la máquina de vapor, o el siglo de la electricidad, respondería sin la menor vacilación que se llamará el siglo de la concepción mecanicista de la naturaleza, el siglo de Darwin.
Schrödinger estiró un poco la denominación para hacer sitio al físico de Viena y hacer del XIX también el siglo de Boltzmann. Fue uno de los fundadores de la mecánica estadística, una disciplina que supo reescribir la termodinámica en torno a la hipótesis de que la materia se compone de átomos. Del caos aparente en el que bulle un pandemónium de moléculas, emerge el orden del mundo que conocemos, ligado por leyes macroscópicas de apariencia continua y determinista. En particular, Boltzmann dotó a la entropía de su interpretación estadística y fundamentó la segunda ley de la termodinámica sobre principios mecánicos. La ecuación que vincula la entropía con el número de posibles configuraciones microscópicas compatibles con un estado macroscópico fue grabada en el monumento funerario que decora su sepultura en un cementerio de Viena.
La pasión por la ciencia
El nombre de Boltzmann adorna leyes y constantes fundamentales, y muchos de los conceptos que forjó fueron herramientas que inspiraron, o sirvieron directamente para armar, la mecánica cuántica. De ahí que los fundadores de la primitiva teoría, como Einstein o el propio Schrödinger, convirtiesen su obra en objeto de culto. A Boltzmann le gustaba relatar que su carácter ciclotímico se fraguó en el mismo instante de su nacimiento, una noche de carnaval. Así, el contraste entre la fiesta de disfraces que se desarrollaba en la taberna situada debajo de su casa y el sufrimiento de su madre durante el parto dejaría una impronta en su temperamento. Su vida tuvo algo de torbellino, en su constante mudanza de un puesto académico al siguiente, de Viena a Graz, pasando por Heidelberg y Berlín, Viena de nuevo, y de vuelta a Graz, después a Múnich, para regresar a Viena, partir hacia Leipzig y retornar a Viena, de la que nunca terminaba de marcharse, y en los vaivenes violentos de su ánimo, que lo mismo lo encumbraban que lo hundían en una sima sin esperanza. Montado en este carrusel de emociones atravesó también sus polémicas científicas. Ciertamente sus puntos de vista encontraron resistencias entre grandes personalidades, como el premio Nobel de Química Wilhelm Ostwald y Ernst Mach, pero tampoco le faltaron los apoyos. Sus adversarios negaban la realidad de los átomos, el cimiento de sus teorías, al considerarlos una licencia excesiva de la especulación, que no se podía verificar mediante un experimento directo. Boltzmann se sintió acorralado, más por un espejismo de su espíritu atormentado que por los motivos que pudiera dictarle la razón. La mala salud también lo hostigaba, con jaquecas frecuentes y una pérdida de visión que le impedía leer. Ya había coqueteado con el suicidio en Leipzig. El 5 de septiembre de 1906, consumó finalmente el idilio en las horas de luz más intensa del verano. Se ahorcó mientras su mujer y su hija se bañaban al pie de las montañas, en la bahía de Trieste.

Dentro de la física, el foco de la polémica se centraba en Ludwig Boltzmann. Después de completar su último año en el instituto, Schrödinger había pasado el verano contando las semanas y los días, anhelando que llegase la inauguración del nuevo curso para atender a sus clases. Las lecciones sobre filosofía de Boltzmann se abarrotaban de un público que desbordaba la sala y se derramaba hasta el arranque de las escaleras. Sin embargo, el encuentro nunca llegaría a materializarse. Hundido en el pozo de un humor sombrío, Boltzmann se quitó la vida nada más comenzar el mes de septiembre.
Aunque no llegaron a conocerse, Schrödinger se inició en la física bajo la tutela espiritual del padre de la termodinámica moderna. Los profesores que ejercieron una mayor influencia en sus años de formación, Fritz Hasenöhrl y Franz Exner, habían sido discípulos de Boltzmann, a los que un golpe del destino encomendaba ahora la tarea de administrar su legado. Una herencia que se podía resumir en un lema de batalla: «los fundamentos atómicos de la materia impregnan toda la física con su naturaleza estadística». En particular, las clases del sucesor en la cátedra de Boltzmann, Fritz Hasenöhrl, fortalecieron la inclinación de Schrödinger hacia la física teórica.
LA VICTORIA DEL DESORDEN
Las leyes de la termodinámica se establecieron de modo empírico a lo largo del siglo XIX, mediante un proceso lento y laborioso. Un repaso a su historia nos enfrenta a un rosario de engranajes, calderas y pistones. Los títulos de los primeros clásicos de la disciplina, como las Reflexiones sobre la potencia motriz del fuego (1824), de Sadi Carnot, o Acerca de la fuerza motriz del calor (1850), de Rudolf Clausius, transpiran el esfuerzo por sacarle el máximo rendimiento industrial al calor. No en vano muchos de sus cultivadores fueron ingenieros, que con frecuencia abandonaban la mesa de sus reflexiones para solicitar una patente sobre lo que acababan de descubrir. Su gran legado fueron las tres leyes de la termodinámica, que extienden su jurisdicción a sistemas infinitamente más sofisticados que las máquinas de vapor que en primera instancia las inspiraron. Su labor demostró que es posible analizar sistemas de una gran complejidad y formular leyes sobre ellos ignorando por completo los detalles de su estructura interna. Para estudiar el comportamiento del viento o los flujos de calor no es preciso contar con una radiografía que exponga sus componentes.
La primitiva termodinámica se ocupaba de la materia y de sus propiedades, pero no se molestaba en formular preguntas incómodas acerca de su constitución. A medida que se desarrollaba, fue reuniendo su particular juego de herramientas, con magnitudes que en ocasiones poseían un significado claro, como el volumen; en otras, resultaban más imprecisas pero intuitivas, caso de la temperatura y la presión; también las había que rayaban con la metafísica, como el calor y la energía, hasta caer en lo manifiestamente esotérico, con la entropía. Sadi Carnot estableció su ciclo para optimizar el trabajo de las máquinas térmicas sin necesidad de hablar de moléculas o incluso guiado por la idea de que el calor era un fluido.
Ludwig Boltzmann, James Clerk Maxwell y Josiah Gibbs iluminaron esta termodinámica arcaica al someterla a una interpretación estadística. Partieron de la hipótesis atómica, considerando que la materia está formada por una enorme cantidad de partículas, que pueden ser átomos o moléculas, gobernadas por la mecánica de Newton, y la aplicaron con un éxito sin precedentes a los gases ideales, es decir, a gases cuyas moléculas no sienten prácticamente ninguna atracción eléctrica mutua. Las leyes de la probabilidad son pésimas adivinas cuando se aplican a números pequeños, pero se vuelven casi infalibles con los números grandes. La materia ofrecía una cantidad abrumadora de elementos con los que jugar, del orden de 2·1019 moléculas en un 1 cm3 de aire. Con su obra, Boltzmann, Maxwell y Gibbs tendieron un puente entre la física de nuestro entorno cotidiano y la escala molecular. Las viejas variables termodinámicas se despojaron así de sus velos y opacidades. La presión era el efecto de la colisión de billones de moléculas contra las paredes de un recipiente, la temperatura medía su agitación térmica media… Relaciones bien conocidas, como la correspondencia inversa entre el volumen y la presión de un gas, establecida en el laboratorio por Robert Boyle, adquirían un sentido inmediato: al disminuir el espacio disponible para las moléculas, estas regresaban antes a las paredes y chocaban con mayor frecuencia contra ellas. Su propio éxito operó en los dos sentidos y supuso una ratificación de la hipótesis molecular. Al asociarse con la física, la estadística actuó como una sonda, que permitía atisbar lo que sucedía en los niveles más profundos, inaccesibles entonces a la experimentación. Esta rama de las matemáticas permitía poner a prueba modelos atómicos de la materia, extrapolando su comportamiento a gran escala y confrontando sus predicciones con magnitudes observables. Un buen ejemplo lo encontramos en el análisis de Einstein de las trayectorias caóticas que desarrollan partículas muy pequeñas suspendidas en líquidos (movimiento browniano) y que responden al hostigamiento de millones de moléculas de agua, que chocan sin cesar contra ellas.
La gran innovación que aportó la termodinámica clásica fue el concepto de entropía. A su vez, fue uno de los que iluminó con más acierto su interpretación estadística. La entropía se define a menudo como una medida del grado de desorden de un sistema. Los trillones de moléculas que integran un gas o una sustancia pueden variar sus posiciones y velocidades individuales sin que, desde nuestro punto de vista, se altere el estado general de los sistemas que componen. Vale decir que infinidad de situaciones distintas, vistas desde la perspectiva de un átomo (ámbito microscópico), se vuelven indistinguibles a nuestra escala (ámbito macroscópico). En la terminología termodinámica se habla de distintas configuraciones que corresponden a un mismo estado. Las moléculas del aire en una habitación cambian sin descanso sus posiciones sin que sus ocupantes perciban ninguna mudanza en la temperatura, la presión o el volumen que ocupan. La entropía mide precisamente el número de cambios microscópicos que se pueden introducir en un sistema sin que nos demos cuenta. Una noción que se puede relacionar de modo natural con el orden: cuanto más ordenado está un sistema, más fácil es detectar cualquier cambio en él, y viceversa. Los padres estiman pocas disposiciones de los juguetes de sus hijos como ordenadas. Por contra, una infinidad de ellas les parecen desordenadas. El cuarto infantil puede mostrarse desordenado de muchas maneras y de muy pocas en orden. Además, una vez ordenado, cualquier accidente siembra de nuevo el desbarajuste.
LA SEGUNDA PARADOJA DE SCHRÖDINGER

Escultura dedicada a la entropía en la Universidad de Monterrey, México.
Eclipsada por la celebridad cuántica del gato (véase el capítulo 4), existe una segunda paradoja de profundas implicaciones filosóficas, surgida de la inquieta imaginación de Schrödinger. Este la presentó en público en 1943, durante una serie de conferencias en el Trinity College de Dublín, donde, ante una audiencia muy diversa, en la que se confundían diplomáticos, religiosos, estudiantes y damas de la alta sociedad, trató de responder a la pregunta: ¿Qué es la vida? Si nos proporcionan 60 kg de átomos de calcio, fósforo, carbono, hidrógeno, nitrógeno y oxígeno, con trazas de otros elementos, como el azufre y el sodio, el azar dicta muchísimas combinaciones donde no adivinaríamos ninguna clase de orden. Todas ellas ganarían una puntuación entrópica muy elevada. Al barajar los átomos, seríamos incapaces de registrar ninguna modificación. Tras un intervalo de tiempo que nos costaría distinguir de la eternidad, los átomos podrían disponerse en largas cadenas de moléculas, que se enroscarían quizá en proteínas, para organizarse en células, fabricar tejidos, componer órganos, hasta construir un ser vivo. En él, como en el cuarto ordenado de un niño, los pequeños cambios saltarían de inmediato a la vista. Los organismos puntúan muy bajo en entropía. Schrödinger enunció así su paradoja:
¿Cómo consigue un organismo concentrar una corriente de orden en sí mismo y escapar de ese modo a la desorganización del caos atómico prescrito por la segunda ley de la termodinámica?
Para responder, abrió un poco el foco en torno a los seres vivos. El precio por el orden que representa cada organismo se paga con un aumento en la entropía neta de su entorno. Los seres vivos bombean organización, pero la compensan con el desorden que desatan a su paso, acumulando residuos, generando gases y excrementos, degradando las formas de energía que consumen. La vida, por tanto, prospera a costa de un balance positivo de entropía.
Existe una relación entre el orden de una configuración y su probabilidad. Si el destino de los juguetes se deja por completo en manos del azar, resulta casi imposible que acaben repartidos en una disposición que los padres puedan considerar ordenada. Ellos saben por experiencia del segundo principio de la termodinámica: el cuarto de los niños tiende siempre a aumentar su desorden.
Los sistemas en la naturaleza evolucionan de modo espontáneo de forma que sus elementos tienden a distribuirse según sus configuraciones más probables, o de máxima entropía, que también coinciden con aquellas que presentan un grado mayor de desorden. Dejándose arrastrar por una corriente de pura aleatoriedad, la materia tiende a acomodar sus átomos en combinaciones cada vez más desorganizadas.
Según Boltzmann, había que interpretar la segunda ley en un sentido estadístico. Nada impedía a un sistema evolucionar hacia configuraciones menos probables y más organizadas, pero solo como una etapa más de su evolución azarosa. Aunque improbable, las moléculas de aire dentro de una habitación podrían concentrarse en una de sus esquinas, a causa de una combinación muy particular de todos sus movimientos individuales y aleatorios. La probabilidad existe, pero es tan baja que habría que esperar la edad del universo para asistir a su advenimiento.
Los gases ideales, que la mecánica estadística había logrado someter, formaban un pequeño protectorado de la materia. Los físicos no tardaron en diseñar nuevos planes de conquista para extender los dominios de su nueva termodinámica y a continuación fijaron su atención en la interacción entre la materia y la luz. Antes de examinar esta cuestión, sin embargo, conviene hacer un rápido repaso de qué entendían por «luz» los científicos de la época.
LO VISIBLE Y LO INVISIBLE
La mecánica cuántica es una teoría que trata de las relaciones entre la luz y la materia. En la época en que se desarrolló, los científicos acababan de adquirir una perspectiva nueva y muy moderna sobre la luz. Al unificar los fenómenos eléctricos y magnéticos, Maxwell había encontrado en sus ecuaciones que cualquier perturbación en una distribución de cargas o de imanes, o en una corriente, se propaga a través del espacio en forma de onda, cuya velocidad coincidía de modo asombroso con la de la luz en el vacío. De hecho, concluyó Maxwell, la radiación electromagnética y la luz eran lo mismo. Siguiendo su criterio, a partir de este momento utilizaremos ambas expresiones como equivalentes. Por esta vía inesperada, se estableció un primer nexo entre la materia, donde residían las cargas, y la radiación.
Aunque asociamos la luz con la visión, para un físico los ojos son prácticamente ciegos a la radiación electromagnética. Dentro de esa pequeña ventanilla que nos abren los sentidos, modificar λ equivale a cambiar el color. Cuando una onda se estira más allá de los 700 nm desaparece de nuestra vista, para esfumarse en la región infrarroja. Cuando se encoge por debajo de los 400 nm vuelve a desvanecerse, ya que la retina no se aventura en la región ultravioleta (figura 1, página siguiente).
El pionero que se adentró por primera vez en este territorio incierto fue el astrónomo alemán William Herschel, en 1800, mediante un sencillo experimento que cualquiera puede reproducir en casa. Siguiendo los pasos de Newton, descompuso un rayo de luz en sus componentes mediante un prisma. A continuación fue situando un termómetro en cada una de las franjas de color que se desplegaban. Al llegar al rojo, no se detuvo, y observó que la temperatura variaba también en la zona de oscuridad inmediata (en el infrarrojo). Esta experiencia pone de manifiesto que la radiación que no vemos también posee energía. Se puede decir lo mismo de las ondas de radio que agitan los electrones de una antena o de los rayos gamma que escapan de los núcleos atómicos.
La radiación no dialoga del mismo modo con todos los cuerpos. Basta con introducir en un microondas un vaso de agua o una pieza de aluminio para comprobarlo. El agua absorbe con intensidad las microondas, mientras que el aluminio las refleja. La atmósfera se muestra opaca ante la luz ultravioleta, pero transparente a las ondas de radio.
FIG. 1

¿Qué leyes ordenan la interacción de la luz con la materia? ¿Cómo emiten radiación los cuerpos? ¿Cómo la absorben? Si bien los científicos presumían de una imagen muy nítida de la luz después de que Maxwell la retratara como una onda en sus ecuaciones, la materia mostraba una imagen más borrosa. La termodinámica y la electrodinámica se alzaban como las dos joyas de la corona de la física decimonónica. Con ellas, los investigadores sentían una confianza razonable antes de lanzarse al abordaje de las asociaciones más esquivas y nebulosas de los átomos y las moléculas. La pista de que les haría falta una ciencia nueva la ofrecería, una vez más, la estadística, ejerciendo su papel de sonda de las profundidades.
ESPECTROS DE EMISIÓN
Los cuerpos calientes generan radiación electromagnética, aunque no siempre podamos verla. Un radiador de agua, por ejemplo, emite ondas de frecuencias que corresponden a la luz visible, pero con tan poca intensidad que nuestros ojos no alcanzan a percibirlas ni siquiera en la oscuridad. En general, un sólido produce luz dentro de un abanico muy amplio de longitudes de onda a cualquier temperatura, pero el grueso de la energía se concentra en torno a un valor determinado. A medida que aumenta la temperatura del cuerpo, esa λ de referencia decrece. Para expresarlo con más claridad, pensemos en la distribución de pesos en una población muy amplia. Los datos se repartirán a lo largo de un rango extenso de valores, pero la mayoría se agrupará alrededor de la media. Si cambiamos de población, también lo hará la media. En una región bien alimentada, el peso promedio será superior que en otra con escasos recursos, aunque encontremos personas extremadamente delgadas o muy obesas en ambas poblaciones. Podemos establecer una analogía entre el grado de alimentación general de una población y la temperatura de los cuerpos. El grueso de la energía se concentra en torno a una longitud de onda (como la media en los pesos) que se va desplazando a medida que varía la temperatura (la calidad y la cantidad de la alimentación en la población).
Nuestros ojos pueden asistir a este desplazamiento de frecuencias solo cuando sobreviene dentro de la franja entre los 400 y los 700 nm. En una fragua, el acero adquiere un color rojo pálido cerca de los 500 ºC, que gana en intensidad a medida que se aproxima a los 600. A medio camino entre los 700 y los 800 ºC, se tiñe de un tono cereza, que se vuelve salmón cuando rebasa los 840. El naranja se impone pasados los 900 ºC y el color limón, bordeando los 1 000. Al superar la barrera de los 1 200 ºC, el metal se despoja de sus matices amarillos, llega a ser blanco y se prepara para la temperatura de fusión.
De modo parecido a como se muestra gráficamente la distribución de pesos en una población, se puede dibujar cómo se reparte la densidad de energía para cada longitud de onda en un cuerpo a una temperatura dada. Esta clase de representaciones recibe el nombre de «espectro energético».
LAS VARIEDADES DE LA LUZ
Al representar la luz como una onda, se recurre a dos rasgos para caracterizarla: la amplitud (o altura de la onda) y su longitud o frecuencia (su grado de estiramiento o compresión). Para verlo con más claridad, imaginemos un corcho que flota sobre la superficie de un mar cuyas olas viajan siempre con la misma velocidad. El corcho no se desplaza en sentido horizontal: se limita a subir y bajar siguiendo el ritmo que le impone el paso de la onda. Su punto más alto corresponde a las crestas del agua y el más bajo, a sus valles. La extensión de este recorrido vertical determina la amplitud.
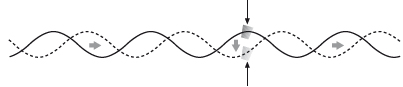
El grado de agitación del corcho se puede considerar como una medida intuitiva de la energía que transportan las ondas. Depende de la frecuencia (ν) o de la longitud de onda (λ). Ambas magnitudes reflejan la misma información y una es la inversa de la otra: una longitud de onda larga corresponde a una frecuencia corta, y viceversa. En el caso de la luz, que se desplaza en el vacío con velocidad constante c: c = λ · ν. Para que c se mantenga constante, el incremento de cualquiera de las dos variables impone la disminución de la otra. En la figura siguiente se muestra λ como la distancia entre dos cumbres seguidas de la ola. Valdría también la distancia entre otros dos puntos consecutivos cualesquiera situados a la misma altura y con la misma pendiente.

Si ahora dirigimos dos ondas de la misma velocidad contra el corcho, una con λ corta (A), y otra, con λ larga (B), se aprecia cómo la primera lo hará subir y bajar muchas veces en poco tiempo, mientras que la segunda le dará un tratamiento más suave:
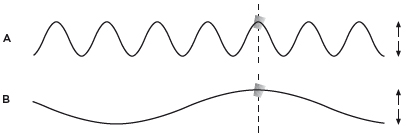
La altura del corcho se relaciona con la altura de la onda en el punto donde se encuentra con él. Igual que la onda reitera su sucesión de crestas y depresiones, el corcho reproduce su recorrido arriba y abajo, una y otra vez. Por eso una λ corta, frenética, se asocia con una ν alta (el corcho pasa por las mismas posiciones con mucha frecuencia) y una λ larga, plácida, con una ν baja (el corcho repite las posiciones más despacio, con una frecuencia menor). Por supuesto, las ondas de λ corta consumen mucha más energía que las largas, puesto que comunican una agitación mayor.
A la hora de estudiar la relación entre la materia y la luz, convenía identificar una situación experimental libre, en lo posible, de interferencias con otros fenómenos que estorbaran o complicaran el análisis. Los físicos buscaron un territorio que permitiera a los átomos y a las ondas electromagnéticas manifestar de la manera más desenvuelta y clara sus vínculos. Encontraron la respuesta en los hornos. Descubrieron que cuando un horno se calienta a una temperatura y se mantiene aislado de su entorno, al llegar al equilibrio, en su interior se desarrolla un espectro de radiación universal, que solo depende de la temperatura. Es decir, da igual el material de las paredes del horno o cuál sea su forma, o su tamaño, todos los hornos a la misma temperatura desarrollan un espectro idéntico. Esta universalidad apuntaba a que en el interior del horno el diálogo materia-radiación se establecía de un modo profundo y directo.
En los laboratorios, al abrir el horno se medía el espectro que se muestra en la figura 2. Se aprecia cómo la energía se concentra sobre todo en torno al punto más alto de cada curva y cómo la λ que corresponde a ese valor extremo se desplaza hacia las longitudes de onda más cortas (más energéticas) a medida que se incrementa la temperatura (T). Este desplazamiento fue enunciado en 1893 por el físico alemán Wilhelm Wien y se resalta en la gráfica con una línea discontinua: la λ máxima es inversamente proporcional a T. Según se eleva la temperatura, la λ máxima se acorta. Se trata de una tendencia esperable: las longitudes de onda cortas se asocian a grandes energías, igual que una temperatura alta.
FIG. 2
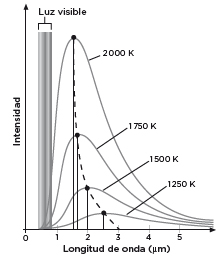
FIG. 3
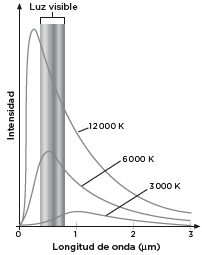
Para las temperaturas consideradas, la mayor parte de la luz cae fuera del espectro visible, una situación que cambia a medida que T sigue creciendo y λ, menguando (figura 3). En estas curvas se puede leer otro gran resultado relacionado con la emisión luminosa de los sólidos. La densidad de energía total emitida por el horno, que es el área encerrada debajo de cada curva, aumenta con la cuarta potencia de la temperatura si esta se expresa en grados Kelvin. Es la llamada ley de Stefan-Boltzmann, que descubrió primero en el laboratorio el físico austriaco Josef Stefan y que cinco años después dedujo su discípulo Ludwig Boltzmann, valiéndose de argumentos termodinámicos.
FIG. 4
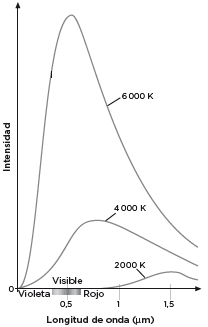
En la figura 4, el área bajo la curva que corresponde a 6000 K es 81 veces mayor que la superficie que limita el espectro de radiación a 2000 K:

El espectro de radiación del horno acotó los límites del terreno de juego donde se resolvería el desafío. La física clásica, que tan bien había modelizado los gases o la propia luz, ¿podía ofrecer una justificación teórica para estas curvas? Ese es el empeño al que se consagró un científico prusiano poco amigo de las sorpresas y que, tras cuarenta años de vida ordenada, no parecía llamado a grandes aventuras.
UNA REVOLUCIÓN INVOLUNTARIA
Aunque se pueden señalar indicios en la obra de científicos anteriores, se suele considerar que el certificado de nacimiento de la mecánica cuántica lo extendió Max Planck el 14 de diciembre de 1900, cuando presentó ante la Sociedad Alemana de Física los resultados de su investigación Sobre la teoría de la ley de distribución de energía en el espectro normal. Lo hizo con un sentido dramático de la oportunidad, el último mes del último año del siglo XIX. Así clausuraba cien años de ciencia particularmente feliz con el hallazgo que derrumbaría los pilares en los que se fundamentaba.
Hasta entonces, Planck había consagrado su carrera científica al estudio y aplicación de la segunda ley de la termodinámica. El principal motor de su curiosidad era la búsqueda de leyes absolutas, de principios que permanecieran «para siempre y para todas las culturas», de ahí que la radiación universal del horno llamara su atención. Con frecuencia se le ha tildado de «revolucionario poco entusiasta», un apelativo que no hace del todo justicia a su tenacidad. Seguramente se trata del científico que partió de presupuestos más conservadores entre quienes participaron en la creación de la teoría cuántica. Durante años negó la existencia de los átomos, defendiendo la continuidad de la materia, una postura que se puede entender dada su especialización en la termodinámica clásica, que no necesita hurgar en las entrañas de los sistemas que investiga. Con tales antecedentes resulta irónico que recayera en él la responsabilidad de asestar el golpe de gracia a la continuidad clásica. Tampoco aceptaba la interpretación estadística de la segunda ley, convencido de que el incremento de la entropía era un absoluto. No temía la posibilidad de que todas las moléculas de su habitación se concentraran en un rincón y lo asfixiaran, pero le repugnaba el trasfondo anárquico de la idea. La mezcla de su determinación por comprender y de sus prejuicios lo colocó en una situación comprometida. En algunos puntos de sus artículos muestra la circunspección de un profesional del póquer que se está jugando una fortuna y resulta difícil adivinar la motivación de muchas de sus jugadas.
Antes de justificarla teóricamente, Planck había hallado en octubre de 1900 la curva matemática del espectro de radiación que hemos considerado en las gráficas del apartado anterior. Es decir, había descubierto una función que dependía de la frecuencia y de la temperatura, tal que, al dar valores numéricos a ν y T, dibujaba las mismas curvas que se obtenían en el laboratorio. Había atrapado, por así decir, la huella matemática de la ley de radiación que estaba buscando. Este resultado por sí solo suponía un mérito más que notable, pero la ambición de Planck no era escribir la fórmula, sino derivarla de un modelo físico del mundo del que se desprendiera lógicamente. Él reconocía sin ambages su determinación: «Desde el mismo instante en que formulé [la ley], me dediqué a la tarea de dotarla de sentido físico». Lo que no podía sospechar era la naturaleza desconcertante de ese sentido que buscaba.
De entrada, le faltaban piezas importantes para poder afinar la imagen de lo que sucedía en el interior del horno. En el momento en el que Planck se enfrentó a la tarea no se conocían, por ejemplo, los neutrones ni los protones. Los electrones acababan de llegar a la física tres años atrás, en 1897.
Sin embargo, contaba con el auxilio de las dos grandes creaciones de la física del siglo XIX, la termodinámica y la electrodinámica de Maxwell. El matemático escocés sostenía que al agitar una carga eléctrica se generan ondas electromagnéticas. Así funcionan las antenas emisoras, que no tardarían en revolucionar el mundo de las telecomunicaciones y que cada día nos envuelven en las microondas que producen los teléfonos móviles. De manera simétrica, una onda electromagnética también pone en movimiento los electrones que encuentra a su paso, por ejemplo, en la antena receptora de una radio. Por tanto, las paredes del horno hablarían con la radiación del interior a través del vaivén de sus electrones. Estos quedarían anclados en sus átomos y oscilarían en torno a posiciones fijas. Planck en su artículo no se refiere en ningún momento a los electrones o a la materia, habla solo de «osciladores».
Con el horno vacío y apagado no tendríamos luz. En el momento en el que se comunica temperatura al sistema, comienza el ajetreo de los electrones y la producción de radiación electromagnética. Las ondas generadas se propagan, cruzan la cavidad y terminan arribando a otras paredes e incidiendo sobre nuevos electrones. Estos, con su actividad, se comportan como antenas que reciben y emiten. El intercambio entre la luz y la materia se ha puesto en marcha. Pasado un tiempo, se alcanza una situación estable, con el horno lleno de radiación, repartida entre las diversas frecuencias, en función de la curva espectral conocida.
Planck aprovechó la circunstancia de que llegado el equilibrio se cumpliría la segunda ley de la termodinámica. El horno podía atravesar toda clase de vicisitudes, pero el paso del tiempo acabaría premiando el desorden. Tenía que delimitar todas las configuraciones microscópicas asociadas a cada estado macroscópico de su sistema, asignar una probabilidad a cada uno y decantarse por el más probable (el de máxima entropía). En este punto su determinación de avanzar ya había ganado la partida a sus prejuicios, porque se vio obligado a acatar la interpretación estadística de Boltzmann y considerar que la probabilidad de cada estado era proporcional al número de configuraciones microscópicas compatible con él. Para resolver la tarea de adjudicar probabilidades, recurrió también a un truco del físico vienés.
A la hora de hacer cuentas con la entropía se pueden manejar dos clases de variables: discretas o continuas. Si tratamos de repartir un grupo de veinte espectadores en el patio de butacas de un cine, las posiciones que pueden ocupar son finitas, están numeradas. Un espectador no puede pasar de una butaca a otra sin transición. Visto sobre un plano del local, cada cambio de sitio se traduce en un salto abrupto. En este caso, la posición es una variable discreta. Sin embargo, si hemos de repartir un grupo de veinte moléculas en el espacio de una caja, ahora las posibilidades se vuelven infinitas. Para cambiar de localización, la molécula no precisa ningún salto brusco: con desplazarse una distancia tan pequeña como quiera ya se verá en una posición nueva.
Desde un punto de vista matemático resulta mucho más cómodo operar en el caso discreto que en el continuo. El truco de Boltzmann consiste en parcelar el espacio continuo y tratarlo como si fuera discreto. Para verlo, partamos de una superficie cuadrada (figura 5). Dentro de sus límites, una partícula puntual puede ocupar infinitas posiciones. ¿Cómo contabilizar todos estos estados y determinar su probabilidad? Dividamos la superficie en una cuadrícula y asignemos a cualquier punto en el interior de uno de los cuadros pequeños que se forman la misma posición (figura 6). Ahora resulta sencillo numerar los estados, como en las butacas de un cine, y contarlos. La probabilidad de que una partícula se encuentre en uno de los cuadros pequeños será el cociente entre su área y la de la superficie total. Esta aproximación será mejor cuanto más menuda sea la fragmentación (figura 7).
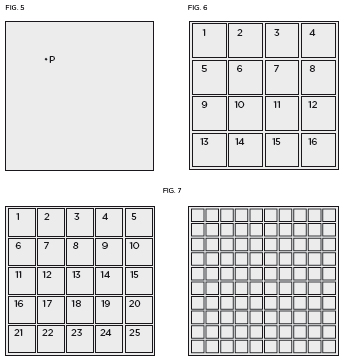
En el límite en el que el tamaño de los cuadros sea cero (→0), recuperamos el escenario continuo de infinitos puntos. Por tanto, al trabajar con variables continuas la estrategia consiste en trocear el rango de posibilidades, lo que permite armar la estructura matemática para contabilizar los estados y definir las probabilidades. Hecho esto se retira el andamio, es decir, se hace tender a cero el tamaño de cada trozo, y del cálculo discreto se deriva el cálculo continuo.
Al enfrentarse al problema del horno, Planck tenía que repartir la energía disponible entre los osciladores de las paredes y la radiación del interior. Para llevar a cabo las cuentas, decidió «trocear» la energía en paquetes discretos: ε=h·ν, siendo h una constante y ν la frecuencia de la radiación. Cuando definiera la probabilidad de cada estado e hiciera tender h a cero, recuperaría el caso continuo y alcanzaría el resultado que andaba buscando. Lo más desconcertante, sin embargo, fue que antes de dar ese último paso, con la energía todavía despedazada, se encontró con la fórmula correcta de la radiación. ¿Qué pasaba si insistía en tomar el límite? Entonces obtenía una divergencia que disparaba la energía hacia un valor infinito. En la práctica esto implicaba que, al abrir el horno, de su interior escaparía una ráfaga letal de rayos ultravioleta. Esa era la predicción de la física clásica.
Por tanto, h no podía encogerse a capricho. Además aparecía en la ecuación de la radiación y al comparar la curva teórica con la experimental, la constante adquiría un valor preciso que no menguaba: 6,62·10−34 J s. Es decir, un oscilador forzado a completar un vaivén en 1 s ganaría una energía de 6,62 ·10−34 J. Es una cantidad francamente minúscula, sobre todo si se tiene en cuenta que en el caso de 1 J ya se está hablando de una energía modesta (es, por ejemplo, la energía necesaria para lanzar una pelota de frontón hacia arriba y que recorra 1 m).
Einstein llamó poco después a cada uno de los paquetes de energía «cuanto» y al proceso de división, «cuantización». La mecánica cuántica acuñaba así las primeras palabras de su hermético vocabulario, que además servían para denominarla. Como homenaje a su creador, h recibió el nombre de «constante de Planck». Funciona como un calibrador, que señala a partir de qué escala hay que tomar en consideración las intermitencias de la energía. El troceado que impone es finísimo, de ahí que para la perspicacia limitada de nuestros sentidos resulte indistinguible de la continuidad. Esta circunstancia explicaba que la naturaleza discreta de la energía hubiera pasado desapercibida hasta entonces, pero eso no reducía la perplejidad de Planck. Cuando uno se levanta y comienza a correr, imagina que su energía cinética parte de cero y aumenta atravesando un continuo de valores, no que progresa a saltos, por muy imperceptibles e insignificantes que sean. La idea no podía resultar más ajena al espíritu clásico.
Muchos años después, en 1931, Planck recordaba así su situación:
Se puede describir lo que hice como un acto de desesperación, ya que por naturaleza soy pacífico y rechazo cualquier aventura dudosa. Pero por entonces llevaba luchando sin éxito seis años (desde 1894) con el problema del equilibrio entre radiación y materia […]. Tenía que encontrar, al precio que fuera, una justificación teórica.
Planck se hallaba tan incómodo con la cuantización de la energía que intentó relativizarla y confinarla a un caso particular. Prefirió pensar que se trataba de un rasgo accidental, asociado al mecanismo singular de intercambio entre osciladores. Se puede establecer un paralelismo con un cubo con el que se extrae agua de un pozo. Las cantidades que se retiran del fondo son múltiplos del volumen del cubo, pero el líquido que transporta (la energía) es continuo y fuera del recipiente se puede presentar en cualquier proporción.
Un joven licenciado que se ganaba mal la vida dando clases particulares y que andaba ya comprometido con otras ideas para poner la física patas arriba, leyó con mucha atención los artículos de Planck. Albert Einstein gozaba de un don especial para la generalización y su agudísimo sentido físico encontró en el horno razones inmejorables para ejercitarlo a fondo.
En 1905, desde la más absoluta marginalidad académica, publicó una serie de artículos que lo ubicaron de golpe, no ya en el mapa de la ciencia, sino en un puesto de honor de su historia. En una carta a su amigo Conrad Habicht solo destacaba uno de ellos con la distinción de «muy revolucionario». ¿Se refería quizá a su esbozo de la relatividad especial? ¿Al apéndice donde establecía su ecuación E = mc2? En absoluto, estaba hablando de Sobre un punto de vista heurístico concerniente a la producción y transformación de la luz, el artículo donde abordaba la hipótesis cuántica de Planck. Einstein abría sus reflexiones apuntando a un malestar de índole conceptual:
Según la teoría de Maxwell, se considera que la energía es una función espacial continua para todos los fenómenos puramente electromagnéticos y, por tanto, también para la luz, mientras que, según la opinión actual de los físicos, la energía de un cuerpo ponderable debería representarse como una suma sobre los átomos y los electrones. La energía de un cuerpo ponderable no puede descomponerse en un número arbitrario de partes, arbitrariamente pequeñas, pero de acuerdo con la teoría de Maxwell (o, de un modo más general, de acuerdo con la teoría ondulatoria) la energía de un rayo de luz emitido desde una fuente puntual se extiende de forma continua sobre un volumen cada vez mayor.
Existía un desacuerdo profundo entre la continuidad de la luz y la discontinuidad de la materia. Einstein halló en el trabajo de Planck una manera de armonizarlos, a base de romper la energía: «Él mostró de modo convincente que, además de la estructura atomística de la materia, existe una forma de estructura atomística de la energía». El propio Planck no estaba de acuerdo, por supuesto, con esta interpretación de su trabajo:
[…] yo soy de la opinión de que […] se puede salir adelante con éxito buscando el significado del cuanto de energía h·ν solo en las acciones mutuas con las que los osciladores se influyen entre sí.
Einstein, sin embargo, defendía que la segmentación era consustancial a la radiación y que de hecho se mantenía cuando viajaba por el espacio lejos de la materia. Solo vista desde muy lejos, una densidad alta de cuantos luminosos adoptaba el contorno familiar de una onda clásica, maxwelliana.
La magnitud de la constante de Planck resulta tan diminuta que a nuestra escala no se revela la naturaleza discreta de la energía, igual que las pinceladas impresionistas no se aprecian a diez metros del cuadro. Las oleadas de color, que parecen extenderse en transiciones suaves, se descomponen en manchas a medida que nos aproximamos. Lo mismo sucede con el impresionismo cuántico de la luz. No obstante, en su diálogo con la materia no se puede soslayar su condición fragmentaria. Una realidad profunda que la sonda de la estadística acababa de poner en evidencia.
En su primer artículo cuántico, Einstein sacó el fraccionamiento de la energía del horno de Planck y, para demostrar que trascendía el capricho de los osciladores, lo aplicó para esclarecer tres fenómenos conocidos. El que le granjearía una mayor notoriedad sería el llamado «efecto fotoeléctrico». Años después, proporcionaría la excusa a la Real Academia de Ciencias de Suecia para concederle el premio Nobel, en vista de que se resistían a tomar en consideración las dos teorías de la relatividad, especulaciones teóricas demasiado aventuradas que el tiempo podía echar por tierra.
Con el curso de los años, Einstein extremó más todavía la cuantización. Puesto que, de acuerdo con su famosa ecuación relativista (E=mc2), la energía implica la presencia de masa, también cabía leer los cuantos en clave de partículas. Fueron bautizadas con el nombre de fotones, proyectiles luminosos que podían chocar contra los electrones, por ejemplo, y desviarlos de su trayectoria. Arthur Compton confirmó su hipótesis en un laboratorio de Missouri, en 1923, tras ametrallar átomos con rayos X (luz de longitud de onda muy corta).
Planck, asustado ante las consecuencias de su éxito, rogaba moderación a los físicos: «La introducción del cuanto debe hacerse con el ánimo más conservador posible, es decir, solo deberían introducirse alteraciones que demuestren por sí mismas ser absolutamente necesarias». Desde luego, no era el espíritu de los tiempos.
EN LA GUERRA
Muchas de las obras primerizas de Schrödinger, dominadas por los intereses de sus maestros, pertenecen a una física híbrida, incompleta, que mantenía un pie en un mundo clásico que ya se desvanecía, mientras el otro se aventuraba en un paisaje neblinoso que todavía no se atisbaba con claridad. Son los frutos de una ciencia de transición, que erradicaría el triunfo de la teoría cuántica.
EL EFECTO FOTOELÉCTRICO
Al dirigir un haz luminoso contra una lámina metálica se liberan electrones (figura 1). En 1902, el físico húngaro Philipp Lenard había hallado que la velocidad de las partículas que escapan del metal aumentaba con la frecuencia de la luz incidente, pero no con su intensidad (figuras 2 y 3). Einstein explicó el misterio al suponer que la luz se componía de cuantos. La carga energética que transporta cada uno de ellos depende de la frecuencia, así que al incrementarla se emiten paquetes más energéticos que ceden más energía a los electrones, haciendo a su vez que se desplacen más rápido. Un aumento de la intensidad del haz se traduce, sin embargo, en un mayor número de paquetes, que alcanzan con la misma energía a más electrones. Por tanto, en ese caso escapan más partículas pero con la misma velocidad.
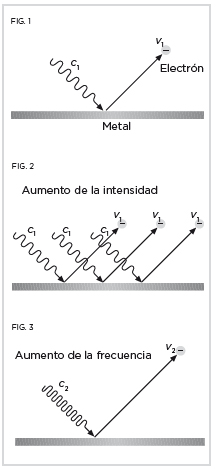
Cada cuanto c1, con frecuencia ν1, arranca un electrón con velocidad v1. Los cuantos c2, con frecuencia ν2, arrancan electrones con velocidad v2.
En mayo de 1910 Schrödinger conquistó el grado de doctor, gracias a un trabajo Sobre la conducción de la electricidad en la superficie de aislantes en presencia de aire húmedo. Desde el título cuesta adivinar ese «espíritu de fuego en acción, que siempre sabía abrirse camino hasta algo original en cualquier investigación», que habían admirado sus compañeros de clase. El artículo recogía una colección de medidas disciplinadas, que registraban los efectos del agua atmosférica sobre la capacidad de ciertos aislantes, como el vidrio, la ebonita o el ámbar, para conducir la electricidad. Su principal interés residía en su relación con el aislamiento del instrumental científico expuesto a los rigores meteorológicos.
Nada más completar sus estudios, quedó libre una plaza de ayudante en el departamento de Física Teórica. Atendiendo a los méritos académicos, el puesto le hubiera correspondido a Schrödinger, que contaba con el mejor expediente. Sin embargo, se interpusieron en su camino el servicio militar y el accidente que sufrió su compañero de universidad Hans Thirring, mientras esquiaba en los alrededores de Mariazel, un pueblo pintoresco situado en los Alpes estirios. A consecuencia de una mala caída, Thirring se rompió un pie, se liberó de sus obligaciones castrenses y, en una última carambola, se hizo con la plaza de ayudante.
Cuando un año después Schrödinger se reincorporó a la vida civil, tuvo que conformarse con un puesto de ayudante en el Instituto de Física Experimental que dirigía Exner, que cuadraba mucho menos con su temperamento científico. Contamos con su testimonio de cómo se desenvolvió en el laboratorio:
Aprendí dos cosas durante aquellos años: primero, que yo mismo no estaba dotado para el trabajo experimental. Segundo, que la tierra donde vivía, y la gente con la que vivía, no estaban mejor dotados que yo para lograr un progreso experimental de primer orden.
Lo cierto es que aprendió algunas cosas más. Jugando con la colección de instrumentos ópticos del departamento, descubrió una anomalía en su percepción de los colores, que reducía su sensibilidad al verde y realzaba la gama de matices rojos. Su bagaje experimental también le permitió presumir de pertenecer «a ese grupo de teóricos que saben por observación directa lo que quiere decir realizar una medición».
Pasada la Navidad de 1913 coronó el siguiente rellano de su escalada académica: la obtención de la llamada venia legendi. El título le autorizaba a dar clases como Privatdozent, a cambio de unos modestos honorarios que corrían a cargo de los estudiantes que lograra atraer a sus cursos.
En sus primeros artículos científicos Schrödinger exhibió un notable virtuosismo matemático que, no obstante, se apoyaba en una intuición física todavía sin afilar. El aislamiento de Viena, apartada de las corrientes de la vanguardia tras la muerte de Boltzmann, frenó su maduración, sin enfrentarlo a retos que de verdad pusieran a prueba sus capacidades.
Además, otra clase de desafíos distraía su atención, hasta el punto de comprometer su incipiente carrera. La amenaza tenía nombre propio: Felicie. El atractivo o la inteligencia de los pretendientes no pesaba lo más mínimo en la balanza del matrimonio burgués y la madre de Felicie, la baronesa Krauss, tenía claro que Erwin no estaba a la altura de sus aspiraciones. Este, desde luego, no podía sostener el tren de vida de la joven con sus ingresos casi inexistentes como Privatdozent. Desesperado, le pidió a su padre que lo introdujera en el negocio del linóleo. Rudolf se opuso con la misma determinación que la baronesa al matrimonio, así que el compromiso que habían establecido en secreto los enamorados naufragó sin remedio. Quizá la frustración de este amor, por el que se había mostrado dispuesto a sacrificarlo todo, templó el entusiasmo de Schrödinger ante el matrimonio convencional, justificando el circo de tres pistas en el que se convertiría más adelante su vida sentimental.
Aunque ya de capa caída, la física atmosférica y la radiactividad eran dos especialidades tan vienesas como la tarta Sacher. En el verano de 1913 la universidad enroló a Schrödinger en la recogida de datos de una de las estaciones, instalada en Seeham, cerca de Salzburgo. El registro de trazas de radón en el aire podía matar de aburrimiento, pero la localidad era un pueblecito popular durante las vacaciones estivales, a orillas del lago Mattsee, y Schrödinger supo hallar el modo de mitigar su tedio. Sobre todo después de que el director del proyecto le presentara a la canguro de sus hijos: Annemarie Bertel. Cuando la adolescente, hija de un fotógrafo de la corte, encontró al joven profesor «muy bien parecido», el radón quedó relegado definitivamente a un segundo plano. Parece que Schrödinger se sintió algo frenado por la diferencia de edad, así que prefirió aguardar unos cuantos años antes de casarse con ella.

Erwin Schrödinger con sus padres y su tía Minnie (derecha) en Innsbruck en 1892.

El físico austriaco cuando tenía siete años.

En 1898, Schrödinger ingresó en el Akademisches Gymnasium de Viena, donde estudió durante ocho años. La imagen es de hacia 1905.

El soldado austriaco Erwin Schrödinger en 1915. Un año después, mientras estaba destinado en el frente de Prosecco, dedicó parte de su tiempo libre a estudiar la relatividad general de Einstein.
La escritora Edith Wharton recordaba cómo una hermosa tarde de junio de 1914 se había acercado a los corrillos que se arremolinaban en torno a los cafés de Auteuil: «¿No lo has oído? El archiduque Fernando asesinado… en Sarajevo… ¿Dónde está Sarajevo? Su esposa iba con él. ¿Cómo se llamaba? Han muerto los dos». Wharton reconocía que para la mayoría el archiduque era un perfecto desconocido y que la conversación pronto había derivado de vuelta hacia el último libro publicado, el último cuadro adquirido por el Louvre, la última exposición… La noticia de que un joven nacionalista serbio había abatido a disparos al archiduque de Austria tampoco suscitó una gran conmoción en Viena. Hasta parece que el viejo emperador, contrariado con el heredero que le había asignado la línea sucesoria, quedaba más contento con el siguiente. En el resto de Europa nadie supo leer los signos de la tormenta que se avecinaba, la grieta invisible que se abría en la cúpula de cristal de sus salones de baile y que se extendía como una destructora tela de araña.
El último día de julio de 1914, Rudolf Schrödinger se presentó por sorpresa en el despacho donde trabajaba su hijo, en el Instituto de Física, para entregarle la orden de alistamiento que acababa de llegar a casa. Juntos salieron a comprar un par de pistolas, que Erwin no llegó a disparar contra nadie. El tratamiento fue recíproco y tampoco sirvió de blanco para la puntería de ningún soldado enemigo.
Durante los años siguientes conoció diferentes destinos como oficial de artillería, a cargo de diversas baterías en el frente italiano. Primero recaló en Predilsattel, donde el acontecimiento más reseñable fue que por primera y última vez en su vida contempló unos fuegos de Santelmo. A partir del verano de 1915 las órdenes del estado mayor lo arrimaron a otras pirotecnias más comprometidas. A finales de año se distinguió por su valor en la tercera gran batalla del Isonzo, donde cayeron 80000 soldados austrohúngaros y 125 000 italianos. Su principal responsabilidad era una aplicación rigurosa de la física newtoniana: calcular la trayectoria de los proyectiles y orientar los cañones, cosa que hizo con entereza a pesar del intenso fuego enemigo.
En la medida de sus posibilidades trató de sacarle provecho a su condición de físico teórico, que a fin de cuentas no precisaba de más laboratorio que el que cargaba ya sobre los hombros. Fue durante la guerra cuando entró en contacto con la relatividad general: «Mi primer encuentro con la teoría de Einstein de 1916 fue en Prosecco. Contaba con un montón de tiempo a mi disposición, pero tuve grandes dificultades para comprenderla». Hay que leer entre las líneas de su modestia, ya que dominó el complejo formalismo de la teoría hasta el punto de publicar dos artículos que llamaron la atención del propio Einstein, un logro al alcance de pocos físicos de la época. Uno de sus artículos apuntaba a uno de los aspectos más delicados de la teoría, la ambigüedad a la hora de definir la energía gravitatoria.
En los momentos en los que no tenía acceso a la literatura científica las condiciones de la guerra se le presentaban en toda su crudeza. También lo asaltaban extrañas epifanías, en sueños que protagonizaba Lotte, su primera novia del instituto: «Es como si todavía estuviera bajo el encantamiento de aquella tarde cuando por primera vez tendí su mano sobre la mía».
Su profesor Fritz Hasenöhrl murió bajo la explosión de una granada, el 7 de octubre de 1915, durante un asalto al monte Plaut, en Trento. En la primavera de 1916, Schrödinger fue promovido al grado de Oberleutnant y un año después se produjo el traslado a Viena. Su nuevo destino revestía escasos peligros. Consistía en enseñar un primer curso de meteorología en una escuela de oficiales situada al sur de Viena, en la ciudad de Wiener Neustadt. Allí entretuvo el tiempo hasta el armisticio de 1918.
Para vadear la desolación anímica y la malnutrición de la posguerra, se volcó en la filosofía, como ya había hecho durante las horas más bajas en el frente. Leyó las obras completas de Schopenhauer, que le abrieron la puerta al pesimismo, la misantropía bien documentada y la filosofía oriental. Llenó páginas y páginas en sus cuadernos con los pensamientos que le inspiraba la lectura de los Upanishads, en un trance casi alucinatorio. Esta fiebre por los textos sagrados de los hindúes lo consumió con la misma avidez que años antes el amor de Felicie. Cuando le ofrecieron un puesto de profesor de física teórica en Chernivtsi, aceptó con el secreto propósito de limitar la ciencia a las aulas y consagrar todas sus horas libres a profundizar en el Vedanta. La desintegración del Imperio austro-húngaro frustró su inmersión orientalista:
Mi ángel de la guarda intervino: pronto Chernivtsi dejó de pertenecer a Austria. Todo quedó en agua de borrajas. Me tuve que mantener fiel a la física teórica y, para mi sorpresa, alguna que otra vez, algo salió de ella.