La etapa de la infancia y adolescencia de Heisenberg coincide con el período inicial de la teoría cuántica. Poco después de su ingreso en la Universidad de Múnich empezó su contribución al desarrollo de la reciente física atómica. La Primera Guerra Mundial y la posguerra ayudaron a conformar el entramado social en el que se movían los científicos que crearon y desarrollaron la nueva teoría.
La familia Heisenberg dispone de un árbol genealógico muy completo, que cubre unas seis generaciones. Lo empezó Werner Heisenberg en la década de 1930, cuando tuvo que acreditar su pureza aria ante las autoridades nazis. En la familia paterna abundaban los artesanos, como toneleros o cerrajeros, mientras que la materna estaba formada por campesinos y granjeros. En el último tercio del siglo XIX, el desarrollo económico e industrial del Imperio alemán abrió una puerta a la promoción social de las clases medias, cuyos miembros podían acceder a la educación superior y convertirse en médicos, abogados, jueces o funcionarios del Imperio. El abuelo materno, Nikolaus Wecklein, estudió lenguas clásicas, y fue director del Max Gymnasium, un selecto centro de educación secundaria de Múnich. Por su parte, el padre, August Heisenberg, fue profesor de griego y latín. En aquella época, la elección de las lenguas clásicas como vía de promoción social era más eficaz que en la actualidad.
Al finalizar la enseñanza primaria se orientaba a los niños a una formación técnica o bien a una formación preparatoria a la universidad. Esta última, dirigida sobre todo a las clases alta y media, tenía lugar en el Gymnasium. Con este nombre se referían los antiguos griegos a la institución pública donde adolescentes y jóvenes practicaban ejercicios físicos diversos, a la vez que se instruían en filosofía, literatura, oratoria, arte o música. Desde el siglo XVI se usó el mismo nombre en distintos países europeos para designar un lugar de enseñanza pública y, con el tiempo, se reservó a un centro de enseñanza secundaria.
August Heisenberg obtuvo su doctorado y empezó a dar clases en el Max Gymnasium. Al mismo tiempo, siguió con sus trabajos e investigaciones sobre el griego clásico para preparar su «habilitación», una especie de segundo doctorado imprescindible para poder dar clases en la universidad. En 1899 se casó con Annie Wecklein, una de las dos hijas de su director. Tras el nacimiento del primer hijo, Erwin, el matrimonio se trasladó a Würzburg, ciudad situada a unos 200 km al norte de Múnich, puesto que August había sido nombrado profesor de su Gymnasium. En Würzburg nació Werner Karl, el 5 de diciembre de 1901, año y medio después de su único hermano y uno más tarde del año que se considera que nació la teoría cuántica.
La muerte repentina del catedrático de griego de la Universidad de Múnich supuso un cambio en la vida de los Heisenberg. Normalmente, al producirse una vacante o crearse una nueva plaza, la universidad consultaba a diversos expertos, dentro y fuera del país, con el fin de proponer al ministerio una terna ordenada de candidatos. Pero en este caso se propuso un único nombre, debido a las muy buenas referencias que acompañaban al candidato y a la urgencia para cubrir la plaza. De esta manera, a principios de 1910, August Heisenberg empezó sus funciones como titular de la única cátedra de filología bizantina existente en Alemania.
En una entrevista realizada en los años 1960, Werner Heisenberg evocaba dos aspectos importantes de la influencia paterna en su vida. Decía que como su padre era un buen maestro, utilizaba juegos para educar a sus dos hijos, tratando de fomentar la competencia entre ellos. Entre esos juegos incluyó los problemas de matemáticas que tenía que resolver el hermano mayor. Ese hecho fue para Werner un modo de estimulación precoz, pues descubrió que podía resolver rápidamente esos problemas, y a partir de ese momento desarrolló un interés especial por las matemáticas. Por otro lado, el padre también estimuló la afición de sus hijos por la música. Heisenberg empezó a estudiar violonchelo, pero pronto se pasó al piano. A menudo acompañaba a su padre, que cantaba lieder y arias para tenor. Heisenberg siguió cursos de piano y tocó dicho instrumento durante toda su vida, alcanzando un nivel muy alto para un aficionado. La música, en particular la de cámara, ocupó siempre un lugar destacado en su vida intelectual y emocional.
LA ENSEÑANZA SECUNDARIA
En Alemania, desde la reforma educativa de Humboldt en el siglo XIX, el objetivo principal de un Gymnasium era proporcionar una formación humanística, basada en el conocimiento de los clásicos griegos y latinos, como mejor modo de impartir una educación moral e intelectual a quienes más tarde formarían la élite de la sociedad. El Gymnasium era la vía obligatoria para acceder a la universidad, y prácticamente la única forma de promoción social para la clase media.
Aunque a principios del siglo XX las necesidades de la sociedad abrieron otros centros de formación, el Gymnasium siguió conservando su carácter elitista. Los profesores de latín y griego gozaban de un gran prestigio e importancia en la sociedad. Además, se les exigía el grado de doctor para poder titularse en uno de estos centros, algo que no se requería a los profesores de otras materias.
En septiembre de 1911, Heisenberg empezó la enseñanza secundaria en el Max Gymnasium, dirigido por su abuelo hasta el retiro de este en 1913. Los alumnos estudiaban durante nueve cursos, normalmente desde los once hasta los diecinueve años. Del total de horas de clase se dedicaba casi el 40% a las lenguas y literatura clásicas, y un 24% al alemán y a las matemáticas. Las restantes horas de clase cubrían, con irregular distribución, materias como historia, religión, francés o dibujo. Las clases de física se reducían a dos horas semanales durante los tres últimos cursos.
Los informes escolares de los profesores de Heisenberg destacaban sus excelentes cualidades y amplios conocimientos. No en vano fue uno de los mejores alumnos de su clase y siempre obtuvo las máximas calificaciones en matemáticas. Tal vez gracias a los juegos competitivos que su padre establecía entre los dos hermanos, al llegar al Gymnasium tenía conocimientos más avanzados de lo que se requería en su nivel. Además, tuvo un profesor de matemáticas que le estimulaba proponiéndole problemas especiales, al margen de los que trataban en las clases. Su padre, consciente del interés de su hijo por las matemáticas, le consiguió algunos libros… pero escritos en latín, para matar dos pájaros de un tiro. De hecho, debía de tener una idea elevada sobre las posibilidades de su hijo, y al mismo tiempo escasos conocimientos de matemáticas porque, entre otros libros, le facilitó una copia de la tesis doctoral sobre teoría de números, del famoso matemático Kronecker, publicada en 1845. Aunque no entendió muchas cosas, Heisenberg descubrió así las propiedades de números enteros como números primos, criterios de divisibilidad, el teorema de Fermat, etc. Sin saberlo, el padre había acertado, pues, en 1916, los temas de máximo interés para Heisenberg eran la música y la teoría de números.
LA MAGIA DE LOS NÚMEROS ENTEROS
Un antecedente de la física cuántica tiene que ver precisamente con números enteros, en relación con los espectros atómicos. Pero antes conviene que hablemos de los conceptos de continuo y discreto, a los que haremos referencia en breve. Pensemos en todos los números decimales que empiezan por cero, como 0,73649100093. Existe un número infinito de ellos, pues siempre podemos añadir cifras y cifras sin límite detrás de la coma decimal. Estos números forman un conjunto continuo, porque dados dos cualesquiera de ellos siempre se puede encontrar otro que esté comprendido entre ambos. Sin embargo, de este conjunto infinito de números se pueden extraer series particulares, como por ejemplo 1/2, 1/3, 1/4, 1/5…, o 1/22, 1/32, 1/42, 1/52… Estas series contienen también un número infinito de términos, pero no forman un conjunto continuo, porque no siempre se cumple la propiedad anterior: por ejemplo, entre 1/3 y 1/4 no hay ningún otro número de la serie. Se dice que estos números forman un conjunto discreto, y ese carácter discreto se refleja en la presencia de números enteros. Aclarado esto, volvamos ahora a los espectros atómicos.
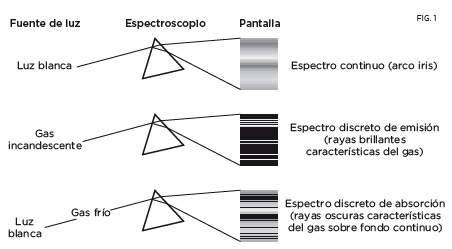
Cuando la luz del Sol atraviesa un prisma se forma un arco iris, un degradado continuo de colores. Cada color de este espectro continuo se caracteriza por una frecuencia o, equivalentemente, por una longitud de onda. Ambas magnitudes están relacionadas: el producto de la frecuencia por la longitud de onda es igual a la velocidad de propagación de la onda. Consideremos ahora un gas calentado hasta alcanzar la incandescencia, como sucede en un tubo fluorescente o en las lámparas que iluminan las carreteras. Si esa luz emitida por el gas se hace pasar por un prisma no se observa un degradado de colores, sino solamente unas líneas brillantes en ciertos valores de la frecuencia; por eso se habla en este caso de espectro discreto. Además, si se analiza mediante un prisma la luz blanca que ha pasado antes a través de un gas, se observa que sobre el espectro continuo aparecen superpuestas unas rayas oscuras, precisamente a las frecuencias de las rayas brillantes emitidas por ese mismo gas incandescente.
En 1860, los alemanes Kirchhoff y Bunsen mostraron que los espectros discretos permiten identificar los elementos, al igual que hoy en día los productos envasados se identifican mediante un código de barras. Para ello, convenía hacer un catálogo detallado de las frecuencias correspondientes a cada elemento, es decir, una lista con los valores medidos. Además, para entender el origen de las rayas espectrales había que encontrar relaciones entre las frecuencias observadas, no solamente del espectro visible —el que podemos ver con nuestros ojos—, sino también de los espectros infrarrojo y ultravioleta, que se observan mediante detectores adecuados. La cosa no era sencilla, pues el número de rayas de ese código puede ser enorme, por ejemplo, varios miles en el caso del hierro.
LOS ESPECTROS
Los gases incandescentes emiten radiación, que puede analizarse mediante un espectrómetro. El elemento esencial de este aparato es un prisma, y los demás componentes, como escalas, lentes y otros dispositivos ópticos, sirven para poder medir con precisión las longitudes de onda o frecuencias luminosas, tanto en el espectro visible como en el ultravioleta o el infrarrojo. Según se refleja en la figura 1, cuando se hace pasar luz blanca por el prisma se observa un espectro continuo, un degradado de colores. En cambio, cuando se hace pasar la luz emitida por un gas incandescente solo se ven unas líneas brillantes en ciertos valores de la frecuencia, y por eso se habla en ese caso de espectro discreto. Además, si se analiza mediante un prisma la luz blanca que ha pasado antes a través de un gas, se observa que en el espectro continuo aparecen unas rayas oscuras, precisamente a las frecuencias que corresponden a las rayas brillantes emitidas por ese mismo gas incandescente. En la figura 2 se muestra una porción del espectro del hidrógeno y del mercurio, con longitudes de ondas comprendidas entre 660 y 190 nm (nanómetros, es decir, una mil millonésima de metro). El espectro visible corresponde a 700-400 nm. La frecuencia de cada línea se obtiene dividiendo la velocidad de la luz (300000 km/s) por la correspondiente longitud de onda. Esta frecuencia es proporcional a la diferencia de dos energías. Lo que se pretendía conseguir en los inicios de la física atómica era deducir los valores de estas energías, que dependen de ciertos números cuánticos, a partir de sus diferencias. Pronto se descubrió que no aparecían todas las posibles diferencias, lo que se reflejó en unas reglas de selección, que había que escribir en función de números cuánticos.
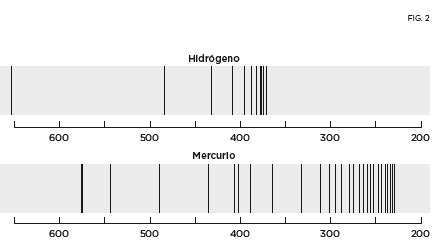
El espectro atómico más sencillo es el del átomo de hidrógeno. En la zona visible del espectro aparecen solo cuatro rayas, cuyas longitudes de onda fueron medidas con gran precisión en 1884 por el sueco Anders Ångström. Al año siguiente intervino en este punto el suizo Johann Balmer, un profesor de matemáticas que daba clases en escuelas técnicas y colegios femeninos de Basilea, su ciudad natal. Más de veinte años después de doctorarse, Balmer obtuvo la habilitación y pudo dar algunas clases en la universidad. El científico suizo decía a sus amigos y colegas que si le daban una serie de números, podía encontrar una fórmula matemática que los relacionara. Un colega suyo le retó a que lo hiciera con las recientes medidas del espectro de hidrógeno, y Balmer lo consiguió. Fue un hallazgo muy afortunado, que adquirió un interés mayor cuando otros científicos lo generalizaron y pudieron caracterizar el espectro completo del hidrógeno, empezando así a poner orden en los «códigos de barras» espectrales. Las frecuencias de las líneas espectrales son proporcionales a las inversas de dos números enteros al cuadrado. La expresión matemática, conocida como relación de Rydberg-Ritz, es:
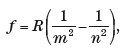
donde m y n son dos números enteros (m<n), y R es la constante de Rydberg.
Sin embargo, no había justificación alguna para la fórmula de Balmer, que era pura numerología. Dicho esto, vamos a comprobar ahora que en el nacimiento de la teoría cuántica también aparecieron números enteros.
LAS DISCONTINUIDADES CUÁNTICAS
El nacimiento de la teoría cuántica tuvo que ver con un problema más bien técnico. En la segunda mitad del siglo XIX, científicos e ingenieros se interesaban en el estudio del cuerpo negro, un objeto ideal llamado así porque es capaz de absorber toda la radiación que le llega. Llevado a la práctica, un cuerpo negro es una cavidad, mantenida a temperatura constante, cuya radiación interior se observa a través de un pequeño orificio. El interés de este objeto ideal se puso de manifiesto cuando Kirchhoff demostró que la intensidad de la radiación (de manera más precisa, la energía de la radiación por unidad de volumen y por unidad de frecuencia en el interior de la cavidad) es independiente de la naturaleza de las paredes, y solo depende de la frecuencia de la radiación y de la temperatura de la cavidad. Así, el estudio del cuerpo negro adquirió una gran importancia práctica para la obtención de patrones de fuentes luminosas.
LA NUMEROLOGÍA DE BALMER

¿Cómo pudo razonar Balmer para llegar a su fórmula mágica? El punto de partida son los valores, en nm (nanómetros), de las cuatro longitudes de onda:
656,21: 486,07: 434,01: 410,12.
Para empezar, los dividiremos por el más pequeño. Sin necesidad de escribir todos los decimales de las divisiones, los nuevos números son:
1,6:1,185:1,058:1.
Los dos puntos indican que se representan cocientes de números. Ahora hay que encontrar la manera de escribirlos como números racionales, es decir, cocientes de dos números enteros. Después de unos tanteos, podemos ver que si multiplicamos los cuatro números por 9/8 obtenemos:
9/5:4/3:25/21:9/8.
Sería conveniente que los denominadores aparecieran en orden creciente, y podemos conseguirlo si multiplicamos el segundo y cuarto números por 4/4, que, evidentemente, es 1. La nueva serie de números es:
9/5; 16/12; 25/21; 36/32.
Sin duda, este es el resultado al que llegó Balmer. ¿Se aprecia alguna regularidad en estos números? A Balmer no se le escapó que los numeradores son cuadrados de números enteros sucesivos (3, 4, 5, 6) y los denominadores se obtienen restando a los numeradores el número 4, convenientemente escrito como el cuadrado de 2. Y llegamos al final: si a cada línea espectral se le asocia un número entero n, las longitudes de onda son proporcionales al cociente n2/(n2–22), donde n toma los valores 3, 4, etc. El lector puede verificar que la constante de proporcionalidad vale 364,56 nm. Como es natural, esta expresión no contiene ninguna información física, es simplemente un juego con números. Pero como el propio Balmer conjeturó, se pudo extender a otras líneas espectrales al reemplazar 22 por los cuadrados de los siguientes enteros. Si se quiere considerar las frecuencias, dado que son inversamente proporcionales a las longitudes de onda, se obtiene que, salvo por una constante global, vienen dadas por la serie 1/22–1/n2.
En su momento, la intensidad de la radiación se midió sin demasiados problemas. Al representarla en función de la frecuencia se obtiene una curva que tiene su inicio en cero, pasa por un máximo y vuelve a cero cuando la frecuencia aumenta. La curva parece una campana no simétrica, cuyas altura y anchura dependen de la temperatura. Pero esta bonita curva no se podía deducir ni justificar a partir de las teorías conocidas. A finales de 1900, el alemán Max Planck consiguió de manera empírica una fórmula matemática que reproducía los datos observados para cualquier frecuencia y cualquier temperatura. Cuando quiso justificarla a partir de consideraciones teóricas generales tuvo que hacer una hipótesis muy especial (un «acto de desesperación», en sus propias palabras), y tuvo que suponer que la radiación de frecuencia f no puede intercambiar con la materia cualquier valor de la energía, sino que solo puede hacerlo en múltiplos enteros de una cantidad mínima proporcional a la frecuencia de la radiación. Los intercambios de energía son cantidades discretas nhf donde la constante de proporcionalidad h se denominó cuanto de acción —así se llama en física al producto de una energía por un tiempo—, pero pronto recibió su nombre actual de constante de Planck. En unidades del sistema internacional, o unidades a escala humana (kilogramos, metros, segundos…), el valor de esta constante o cuanto de acción es pequeñísimo: h ≈ 6,6 · 10–34. Al ser su valor tan pequeño, está claro que la hipótesis de Planck no tiene efectos prácticos en la vida cotidiana, pero esto es algo que se matizará más adelante. En ocasiones se habla de la «hipótesis revolucionaria» de Planck, pero lo cierto es que en su día nadie advirtió tal revolución. Los científicos interesados en el cuerpo negro solo consideraban su fórmula maravillosa, cuya validez se confirmaba cada vez con mayor precisión, y no daban ninguna importancia al razonamiento que había seguido Planck para deducirla.
LA DUALIDAD ONDA-CORPÚSCULO
En este marco, Einstein fue una excepción y no solo tomó en serio la hipótesis de Planck sino que la llevó más lejos, atribuyéndole conscientemente un carácter revolucionario. En uno de sus famosos artículos de 1905 —su annus mirabilis—, el que lleva por título «Sobre un punto de vista heurístico concerniente a la producción y transformación de la luz», sugirió que la luz está formada por cuantos de energía, por partículas que, desde 1924, llamamos fotones. Es decir, si la radiación solo intercambia energía en cantidades discretas, es porque ella misma está constituida por entidades discretas. Con esta nueva hipótesis, Einstein pudo explicar dos resultados experimentales intrigantes. Uno de ellos es el efecto fotoeléctrico, que consiste en la emisión de electrones por un metal al ser iluminado con luz ultravioleta; se trata del fenómeno que subyace a las actuales células fotoeléctricas. Einstein explicó las medidas obtenidas en 1902 por Philipp Lenard, y predijo resultados que fueron confirmados en 1916 por Robert Millikan. El otro resultado intrigante se refiere al calor específico de los sólidos, una medida de cómo varía la temperatura de los sólidos al ser calentados. Desde principios del siglo XIX se sabe que el calor específico de los sólidos es constante a temperaturas suficientemente altas, algo que se explica con facilidad en el marco de la física clásica. Sin embargo, a temperaturas bajas aparecían cada vez más excepciones a la explicación clásica. En un estudio que fue posteriormente refinado por el holandés Debye, Einstein demostró que los cuantos de energía reproducían las observaciones a cualquier temperatura. De esta manera, una hipótesis hecha por Planck especialmente para resolver un problema —la emisión de radiación por el cuerpo negro— fue extendida por Einstein a otros problemas muy distintos, y logró reproducir las observaciones experimentales de modo muy satisfactorio.
EL CUERPO NEGRO
La curva de emisión de un cuerpo negro se parece a una campana asimétrica, cuya forma exacta depende de la temperatura. Cabe precisar que no siempre las palabras utilizadas en física se corresponden con su uso cotidiano: las estrellas se comportan como un cuerpo negro, y la medida de su curva de emisión permite conocer la temperatura de su superficie. Así se sabe que el Sol tiene una temperatura en su superficie de unos 6000 °C, en números redondos. Del estudio de la radiación de fondo existente en el universo se deduce que este está a una temperatura de unos 3 K.
Densidad de potencia emitida (unidades arbitrarias)
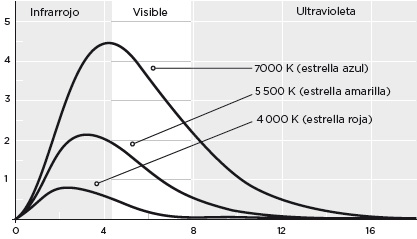
Frecuencia (1014 Hz)
Pero esta hipótesis de los fotones planteaba otro problema. A lo largo del siglo XIX se habían ido acumulando evidencias de que la luz es una onda electromagnética. Por tanto, si la luz está formada por partículas, ¿qué ocurre con la teoría ondulatoria? Einstein era consciente de la dificultad, y por eso el título de su artículo se refería a «un punto de vista heurístico», que es una manera erudita de decir que no se demuestra rigurosamente, sino mediante una comparación con las observaciones. La hipótesis de los fotones fue confirmada en 1922 por el estadounidense Compton. En su experimento envió un haz de rayos X sobre electrones, y demostró que las observaciones se explicaban perfectamente admitiendo que los rayos X estaban constituidos por partículas. Entonces, ¿la luz es una onda o es un conjunto de partículas? En opinión de Einstein, ambas teorías de la luz debían mantenerse, a pesar de que no haya entre ellas ninguna conexión lógica. Él pen-
MAX PLANCK

Max Karl Ernest Ludwig Planck (18581947) fue uno de los eminentes alumnos del Max Gymnasium de Múnich, el mismo centro en el que estuvo Werner Heisenberg años más tarde. Estudió en Berlín, con Hermann von Helmholtz y Gustav Kirchhoff, entre otros, y en 1879 se doctoró en Múnich con una tesis sobre la segunda ley de la termodinámica. Catedrático de física teórica de la Universidad de Berlín desde 1887, Planck es conocido sobre todo por su estudio, en 1900, del cuerpo negro, que representa el nacimiento de la moderna mecánica cuántica y por el que recibió el premio Nobel de Física de 1918. Este ilustre científico alemán gozó de un inmenso prestigio entre el resto de los científicos de su país, tanto por sus cualidades científicas como morales. La más prestigiosa institución alemana actual de investigación lleva su nombre: la Sociedad Max Planck, que engloba institutos en los que se desarrolla investigación de excelencia en ciencias naturales, sociales y humanas. saba que se acabaría llegando a una especie de fusión de las teorías ondulatoria y corpuscular. De hecho, algo de eso pasó, pero no en la forma que hubiera preferido Einstein.
En 1923, el francés Louis de Broglie llevó la idea de Einstein a otro terreno. Pensó que si la luz se describe como una onda formada por partículas, se podría decir algo semejante, pero al revés, del electrón: será una partícula asociada a una onda. De Broglie mostró que el producto del momento p del electrón —el resultado de multiplicar la masa del electrón por su velocidad— por la longitud de onda λ (se pronuncia «lambda») asociada es igual a la constante de Planck, y se escribe así: p·λ=h. Esta relación fue verificada en 1927 por dos grupos independientes, en Estados Unidos y en el Reino Unido. Con diferentes diseños, estos grupos observaron que los electrones producen interferencias, que es la signatura por excelencia de un fenómeno ondulatorio, y confirmaron cuantitativamente la relación deducida por De Broglie.
PARTÍCULAS Y ONDAS EN LA FÍSICA CLÁSICA
La dualidad onda-partícula es una cuestión clave en la física cuántica. Por ello conviene recordar algunas propiedades de estos objetos según la física clásica. Imaginemos que lanzamos un guijarro sobre la superficie de un estanque. El guijarro está en nuestra mano, en el aire, en la superficie del agua, etc., pero solo ocupa una porción definida en el espacio, la de su propio volumen. Al ser lanzado, el guijarro sigue una trayectoria concreta y no se encuentra a la vez en dos o más sitios. En este movimiento se propaga una masa, la del guijarro. Cuando impacta en la superficie del agua, se origina una perturbación que se propaga por todo el estanque. Se forman círculos concéntricos, centrados en el punto de impacto, en los que el agua oscila verticalmente. Esta perturbación es un ejemplo de onda.

Desplazamientos sin masa
Da la impresión de que el agua se desplaza, pero si colocamos un corcho veremos que este solo sigue las oscilaciones verticales del agua. No se desplaza una masa, sino la perturbación; son las oscilaciones entre puntos próximos las que nos producen la sensación de movimiento. Al cabo de cierto tiempo la serie de círculos concéntricos cubre todo el estanque: la onda está definida en todo el espacio. Si dejamos caer dos guijarros en la superficie del agua, veremos formarse las ondas producidas por cada uno de ellos y, pasado un tiempo, el estanque estará afectado por una perturbación que resulta de la superposición de los dos movimientos ondulatorios iniciales. Pero el resultado es algo más que dos series superpuestas de círculos concéntricos. Hay puntos donde las alturas de cada uno de los movimientos están por encima o por debajo del nivel del agua, y se amplifica el resultado. Hay otros en los que, por separado, una altura está por encima y la otra por debajo, y se restan los efectos. A este fenómeno se le llama interferencia, y es una signatura característica de las ondas.
Por tanto, el comportamiento extraño de la luz, que se puede manifestar como onda o como partícula, también lo exhiben los electrones y, en general, todo tipo de partículas subatómicas. Más adelante volveremos a ella; ahora vamos a ver la última pieza del rompecabezas inicial de la teoría cuántica, que tiene que ver con la física atómica.
LOS ÁTOMOS
Los antiguos griegos elaboraron en el siglo V a.C. diferentes doctrinas sobre la constitución de la materia. El atomismo era una de ellas. La materia está constituida por corpúsculos dotados de cualidades ideales: invisibles, indivisibles —eso es lo que significa átomo—, llenos, eternos y de formas diversas. Pero la doctrina que subsistió en el mundo occidental durante más de veinte siglos afirmaba que las sustancias son una sutil mezcla de cuatro elementos: aire, fuego, tierra y agua.
En el siglo XIX, los experimentos químicos descartaron esta doctrina y sugirieron una nueva idea de átomo. Por un lado, el francés Lavoisier llamó «elementos» a aquellas sustancias que no podían descomponerse en otras más simples, lo que excluía el agua, el aire, la tierra y el fuego. Por otro, el inglés Dalton mostró que las regularidades observadas en las reacciones químicas se explicaban con facilidad aceptando la existencia de cantidades discretas extremadamente pequeñas, a las que llamó átomos. Sin embargo, aunque las evidencias experimentales eran cada vez más numerosas en favor de estos nuevos átomos, su realidad no se aceptó de forma unánime. Filósofos como Renan, Comte y Hegel, o científicos como Berthelot, Mach y Ostwald, eran contrarios a aceptar la existencia de algo que, en principio, era inobservable. Pero dejemos aquí la apasionante historia de la idea moderna de átomo para situarnos en 1911, cuando se descubrió lo inapropiado de su nombre.
Los experimentos realizados en Manchester por el grupo de científicos del neozelandés Ernest Rutherford (1871-1937) pusieron de manifiesto que los átomos tienen estructura. En su centro existe un núcleo de carga positiva, que contiene prácticamente toda la masa del átomo, y a su alrededor hay electrones, con carga negativa, en número suficiente para asegurar que el átomo tenga carga eléctrica nula. La imagen que resulta es una especie de sistema planetario, donde la interacción gravitatoria es reemplazada por la interacción electromagnética. Pero este modelo planetario es inestable según las propias leyes del electromagnetismo, pues toda carga eléctrica acelerada emite radiación. Ese es precisamente el fundamento de cualquier antena: la información transmitida por una emisora de radio o de televisión se transforma en variaciones de corriente, es decir, en aceleraciones de las cargas de la antena. Estas cargas emiten ondas electromagnéticas que son captadas por otra antena y traducidas en forma de sonido e imagen en el receptor. Pues bien, un electrón que gira alrededor del núcleo es una carga eléctrica sometida a aceleración, y por tanto emite radiación. Como nada repone la energía emitida, según esta imagen los electrones perderían su energía y colapsarían con el núcleo en un intervalo muy corto de tiempo.
Por otro lado, parece evidente que los espectros atómicos proporcionan información acerca de la estructura interna de los átomos. En 1913, Bohr propuso una salida al problema haciendo intervenir la cuantificación. En sus propias palabras: «Cualquiera que sea la modificación a las leyes del movimiento de los electrones, parece necesario introducir una cantidad ajena a la electrodinámica clásica; esta cantidad es la constante de Planck». En el capítulo siguiente veremos con más detalle los primeros modelos atómicos; ahora es el momento de volver con nuestro protagonista.
LA PRIMERA GUERRA MUNDIAL
La guerra se inició el 1 de agosto de 1914 con el enfrentamiento entre los países de la Triple Entente (Francia, Reino Unido y Rusia) y los Imperios alemán y austrohúngaro, implicando después a más países. El conflicto acabó el 18 de noviembre de 1918, y en términos de la vida escolar de Heisenberg abarcó desde el cuarto hasta el octavo curso de secundaria. El comienzo de la guerra fue acogido con entusiasmo por los países implicados, en una ola de nacionalismo y unidad que dejó de lado los conflictos sociales existentes. Ningún país se veía como agresor, sino como víctima, pero lo cierto es que todos llevaban varios años preparándose para la contienda.
La estrategia militar alemana pasó por invadir Bélgica, que era país neutral. Los terribles daños originados, materiales y humanos, así como el incendio de la biblioteca de la Universidad de Lovaina, provocaron que los miembros de la Triple Entente desataran una campaña mediática en contra de Alemania, acusada de ser un país de bárbaros, agresores y destructores de la cultura. Así las cosas, un grupo de noventa y tres profesores universitarios alemanes reaccionó con un «Manifiesto al mundo civilizado». Dando por buena la versión del ejército alemán, denunciaban la campaña de «mentiras y calumnias con las que nuestros enemigos intentan empañar el honor de Alemania», y suscribían frases como «si no fuera por el militarismo alemán, la civilización alemana habría sido extirpada hace tiempo». Este manifiesto tuvo una réplica pacifista, escrita por Georg Nicolai, profesor de fisiología de la Universidad de Berlín. Pero solo recogió tres firmas más: la del físico Albert Einstein, la del astrónomo Wilhelm Förster y la del filósofo Otto Buek. En su «Manifiesto a los europeos» afirmaban, entre otras cosas, que la guerra «difícilmente tendrá un vencedor, probablemente solo perdedores», hacían un llamamiento a la unidad europea y, en una especie de premonición, pedían «evitar que las condiciones para la paz sean fuente de futuras guerras». Pero el Manifiesto de los 93 reflejaba sentimientos mayoritarios en la sociedad alemana y tuvo una gran influencia en el mundo académico.
El padre de Heisenberg, como muchos otros profesores, fue movilizado. El Max Gymnasium mantuvo durante la duración de la contienda un programa de adoctrinamiento patriótico que, en la línea del Manifiesto de los 93, identificaba la cultura alemana con el militarismo. En 1910, un grupo de militares de Múnich había creado una asociación, la Wehrkraftverein, dirigida a los alumnos de los últimos años de secundaria para ofrecerles una preparación militar fuera del horario escolar. Se trataba de una versión paramilitar del movimiento de exploradores (Boy Scouts), que había llegado a Alemania el año anterior. Tras el estallido de la guerra, la Wehrkraftverein tomó un protagonismo particular. Una vez rebasada la edad de quince años, la mayoría de los alumnos de secundaria recibían en ella una formación dirigida a su futuro alistamiento, posible a partir de los diecisiete años. Heisenberg se integró en la sección de su Gymnasium en 1916, y durante sus vacaciones participaba en tareas agrícolas para suplir la falta de mano de obra. Finalmente, no llegó a alistarse porque el armisticio se firmó un mes antes de que cumpliera la edad mínima. Su hermano Erwin, en cambio, pasó más de un año en el frente.
El entusiasmo popular de los primeros años se fue mitigando debido a la larga duración de la guerra, a las pérdidas humanas y a la escasez de alimentos y combustible. Las tensiones sociales, diluidas en la ola patriótica inicial, volvieron a aflorar. En enero de 1918 surgieron por todo el país huelgas y manifestaciones en demanda de alimentos y de paz que fueron reprimidas por el ejército. El 8 de noviembre de 1918 se proclamó la República Socialista de Baviera; al día siguiente, Guillermo II abdicó como rey de Prusia y emperador de Alemania, y en Berlín se proclamó la República Alemana. Cuando se firmó el armisticio, sectores conservadores y derechistas se negaban a reconocer la derrota, argumentando que Alemania no había sido invadida y que una parte importante del ejército permanecía intacta. Por lo tanto, decían, el armisticio había sido una «puñalada por la espalda» de civiles traidores, principalmente bolcheviques y judíos. Durante varios años se mantuvo una situación política caótica, con asesinatos, luchas callejeras, intentos de golpes de Estado y levantamientos revolucionarios y contrarrevolucionarios en casi todo el país. Todos estos acontecimientos modelaron las ideas sociales y políticas de Heisenberg sobre la nación y sobre los deberes de los individuos frente a la patria, y son una clave importante para entender su comportamiento en los años posteriores.
EL FINAL DE LA ADOLESCENCIA
En Múnich se proclamó formalmente la República Soviética de Baviera en abril de 1919. El Gobierno de Berlín mandó unidades del ejército, junto con grupos paramilitares, para sofocar la insurrección. Estos grupos estaban formados por veteranos de guerra y aventureros, de ideas monárquicas o derechistas, que se oponían por igual a la república y a la revolución. Las autoridades universitarias instaron a los estudiantes a que se alistaran en ellos para defender Baviera del bolchevismo. Se impuso un bloqueo económico de Múnich y se empezó a preparar una revuelta desde el interior, en contacto con el ejército sitiador. A través de la Wehrkraftverein fueron reclutados estudiantes de secundaria, y Heisenberg fue adscrito, de abril a junio, a un regimiento gubernamental. Sus tareas eran hacer de guía y de escribiente, transportar armas y llevar a cabo guardias en edificios y lugares estratégicos o custodiar a los prisioneros, cuyo destino no era ningún secreto: cuando a principios de mayo las tropas del Gobierno controlaron Múnich, hubo más de mil fusilamientos en juicios sumarísimos en poco menos de una semana.
Al acabar la guerra, diversos grupos juveniles propusieron una renovación de la Wehrkraftverein, alejada del carácter militar y de la tutela de los adultos en que habían estado hasta entonces, para formar los Nuevos Exploradores (en alemán, Neupfadfinder). Un grupo de alumnos del Max Gymnasium, de en torno a los catorce años, decidió organizarse según el nuevo espíritu y pidió a Heisenberg que aceptara ser su jefe. No deja de llamar la atención que esto sucediera a mediados de abril de 1919, en el cénit de la República Soviética de Baviera. A principios de agosto, más de doscientos jefes de grupos de Alemania y Austria se reunieron en un castillo medieval próximo a Ratisbona para debatir sobre la reforma del movimiento juvenil. Los reunidos estaban muy afectados por el desenlace de la guerra. De alguna manera, se sentían traicionados por sus mayores, responsables del conflicto y de la derrota, y de una sociedad dominada por la avaricia y la hipocresía, en la que el individuo desaparecía en el anonimato urbano. Propugnaban una vuelta a la naturaleza, cuyos valores fundamentales permitirían restablecer la verdad y la virtud en los individuos y en la sociedad. En muchos aspectos, defendían los valores del romanticismo alemán, con frecuentes ataques a la ciencia y al racionalismo, y adoptaban una actitud apolítica en general. Esta fue la posición de Heisenberg, aunque para él la ciencia, la música, la poesía y la filosofía se situaban en otro plano de la realidad cotidiana, y contenían una verdad eterna.
El grupo de Heisenberg compartía las ideas de los Nuevos Exploradores, pero siempre mantuvo su independencia. Hacían excursiones semanales de un día y salidas más largas durante las vacaciones. Además, organizaban reuniones, generalmente en casa de Heisenberg, dedicadas a la música, la poesía, discusiones filosóficas o partidas de ajedrez. Sobre este último punto, hay que decir que Heisenberg fue un buen ajedrecista, capaz de jugar mentalmente con sus amigos mientras caminaban por la montaña, y de reconstruir la partida a su regreso. Heisenberg estuvo al frente de su grupo hasta que se marchó de Múnich tras obtener su tesis doctoral, pero mantuvo el contacto e hizo muchas salidas con su grupo hasta que los nazis prohibieron este tipo de organizaciones. La participación de Heisenberg en los movimientos juveniles desarrolló en él un profundo sentimiento patriótico que ayuda a entender su comportamiento durante y después de la Segunda Guerra Mundial. Además, las relaciones con su grupo de exploradores influyeron en su carácter y en su actitud vital. Durante muchos años Heisenberg parecía un eterno adolescente, y tenía a menudo una actitud de boy scout, como a veces le decía Wolfgang Pauli en tono irónico.
En los últimos años de la guerra se suspendieron las clases durante el invierno por falta de carbón para la calefacción. Los alumnos debían trabajar en casa y solo acudían al Gymnasium para recoger y entregar los deberes. Como es de imaginar, Heisenberg estudió por su cuenta mucho más allá del nivel escolar en que estaba. Por ejemplo, aprendió cálculo infinitesimal e integral. Este tipo de cálculo se basa en unas reglas bastante sencillas, pero exige mucha práctica y resolver una gran variedad de casos para desarrollar la intuición que permite ver en seguida cómo abordar nuevos problemas.

Heisenberg sentado a bordo de un automóvil con varios miembros de su familia. En la parte delantera, además de Werner (en el centro) se encuentran su padre y su hermano Erwin.

Heisenberg, de pie a la izquierda, con su hermano Erwin y sus padres hacia el final de la Primera Guerra Mundial.
Heisenberg se interesó por los átomos, fundamentalmente por razones filosóficas, y a ello hace referencia en el primer capítulo de sus memorias: nos referimos así a su libro Diálogos sobre la física atómica. El científico alemán recuerda que su libro de física contenía unos dibujos de átomos, con ganchos y anillas para explicar una reacción química, algo que le parecía absurdo. Él pensaba que la unión de átomos para formar una molécula no ha de depender de una representación tan arbitraria como ganchos y anillas. Sin embargo, su biógrafo Cassidy afirma que el libro en cuestión no tiene ni ganchos ni anillas. Solo en una ocasión se representa la molécula de agua tal como se ve aún en nuestros días, como tres bolitas unidas por dos barras, para simbolizar los enlaces. Parece que Heisenberg aplicaba sus ideas presentes con efecto retroactivo, algo frecuente en las memorias autobiográficas. También menciona el Timeo de Platón, que leía en su versión griega, como parte de su actividad escolar. En ese diálogo, Platón asocia cada elemento, tierra, fuego, agua y aire, a uno de los cuatro poliedros regulares que se conocían entonces: cubo, tetraedro, icosaedro y octaedro, respectivamente. Heisenberg pensaba que todo eso eran solo especulaciones fantásticas, sin fundamento alguno, y no entendía que un pensador tan sutil como Platón creyera realmente ese tipo de cosas. Su conclusión fue que para conocer las propiedades de la materia había que conocer sus constituyentes elementales, y a eso se dedicaba ya la física atómica.
Heisenberg se interesó también por la teoría de la relatividad, y leyó un folleto escrito por Einstein especialmente para alumnos de secundaria. Más tarde estudió el libro de Hermann Weyl Espacio, tiempo, materia, publicado en 1918. Se trata de un libro de nivel muy avanzado, que presenta con detalle la relatividad general, con todos los útiles matemáticos necesarios. Pero el interés de Heisenberg por estos temas no tenía que ver con la física, sino más bien con la filosofía; estaba entonces fascinado por la idea de que había que revisar los conceptos de espacio y de tiempo:
Me atraía Kant y me gustaba Platón, en parte como poeta y en parte como filósofo. Pero quedé muy impresionado por la manera como Einstein planteó su teoría de la relatividad, por su idea de cambiar el concepto de tiempo, que me había preocupado mucho y que tanto me interesaba.
A finales de junio de 1920, Heisenberg hizo el examen final para obtener el certificado (Abiturzeugnis) que permitía el acceso a la universidad e ingresó en la Universidad de Múnich con la idea de estudiar matemáticas.